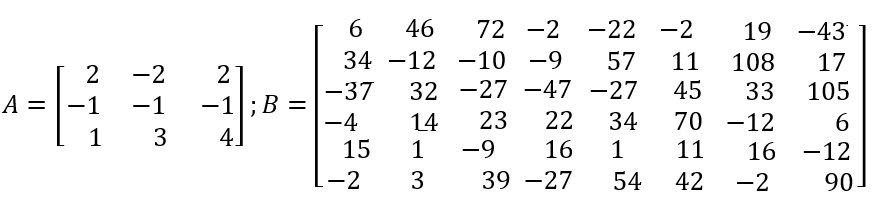Fondo Editorial Pascual Bravo
Título de la obra: Principios de Álgebra lineal
PRINCIPIOS DE ÁLGEBRA LINEAL
Autores:
John Jairo García Mora
Sonia Jaquelliny Moreno Jiménez
Margarita Emilia Patiño Jaramillo
Diseño del contenido: John Jairo García Mora
Revisión del texto: Juan Guillermo Rivera Berrío
Actualización: Joel Espinosa Longi
Código JavaScript para el libro: Joel Espinosa Longi, IMATE, UNAM.
Recursos interactivos: DescartesJS
Fuentes: Lato y UbuntuMono
Fórmulas matemáticas: $\KaTeX$
Fondo Editorial Pascual Bravo
Calle 73 73A-226
PBX: (574) 4480520
Apartado 6564
Medellín, Colombia
www.pascualbravo.edu.co
ISBN: 978-958-56858-8-8
LICENCIA

El álgebra de matrices es una herramienta básica para casi todas las ramas de la matemática, así como para disciplinas afines tales como la física, la ingeniería y la computación, y temas como el encriptamiento de mensajes, el control analógico y digital, solucionar ecuaciones lineales, entre otras.
Las notas no presuponen ningún conocimiento previo de álgebra lineal, pero si requiere de conocimiento de propiedades de los números reales y estructuras que provienen de la aritmética elemental.
Uno de los problemas que soluciona el algebra lineal, es la solución de sistemas de ecuaciones. Pese a que existen métodos iterativos, como el de Gauss, su cálculo manual se vuelve muy laborioso y más expuesto a cometer errores. Una alternativa, es usar la matriz inversa para calcular el vector de incógnitas de las ecuaciones.
Desde este punto de vista, en este texto calcularemos matrices inversas y resolveremos sistemas lineales de ecuaciones ya sea por la denominada matriz inversa o el método de eliminación de Gauss.
Algunas de las escenas interactivas fueron adaptaciones de las escenas que aparecen en el proyecto Un100http://prometeo.matem.unam.mx/recursos/Licenciatura/Un100/, dirigido por José Luis Abreu León de la UNAM.
Los vídeos son autoría propia de los autores realizados con licencia propia del software Camtasia versión 2019 de la empresa TechSmith.
Las imágenes empleadas fueron obtenidas por suscripción a Pngtreehttps://es.pngtree.com/free-graphic-design, entre ellas podemos citar la imagen que nos indica la finalización de cada capítulo tal como se puede observar en la siguiente página.
En cada capítulo aparecen las ecuaciones numeradas con un carácter en mayúsculas y un digito.
Por último, aparecen las referencias bibliográficas en las cuales se apoyo el presente libro de nociones de Álgebra Lineal.

 Una ecuación es una afirmación de que dos expresiones son iguales, cuando se igualan entre sí dos expresiones, y al menos una de ellas contiene una variable, entonces la proposición matemática es una ecuación en una variable, si tiene dos variables diferentes se denomina ecuación en dos variables y así sucesivamente.
Una ecuación es una afirmación de que dos expresiones son iguales, cuando se igualan entre sí dos expresiones, y al menos una de ellas contiene una variable, entonces la proposición matemática es una ecuación en una variable, si tiene dos variables diferentes se denomina ecuación en dos variables y así sucesivamente.
Una solución o raíz de una ecuación es cualquier número que, al reemplazar la(s) variable(s), la convierte en una proposición verdadera. Se dice que un número satisface una ecuación si es una solución de la ecuación. Resolver una ecuación significa hallar todas sus soluciones.
Solucionar una ecuación es hallar sus RAÍCES o CEROS.
Un sistema de ecuaciones algebraicas es un conjunto de dos o más ecuaciones con varias incógnitas que conforman un problema matemático que consiste en encontrar los valores de las incógnitas que satisfacen dichas operaciones. En un sistema de ecuaciones algebraicas las incógnitas son valores numéricos menores a la constante (o más generalmente elementos de un CUERPO sobre el que se plantean las ecuaciones.
Mientras que en una ecuación diferencial las incógnitas son funciones o distribuciones de un cierto conjunto definido de antemano. Una solución de dicho sistema es por tanto, un valor o una función que substituida en las ecuaciones del sistema hace que éstas se cumplan automáticamente sin que se llegue a una contradicción.
En álgebra abstracta, un CUERPO es una estructura algebraica en la cual las operaciones llamadas adición y multiplicación se pueden realizar y cumplen las propiedades: asociativa, conmutativa y distributiva de la multiplicación respecto de la adición, además de la existencia de inverso aditivo, de inverso multiplicativo y de un elemento neutro para la adición y otro para la multiplicación, los cuales permiten efectuar las operaciones de sustracción y división.
El concepto de ecuación lineal se encuentra asociado a las rectas en el plano que tienen como expresión algebraica:
$$\tag{E1}y=mx\pm{b}$$En donde se tiene:
Veamos algunos ejemplos de este tipo de ecuaciones lineales:
En este texto trabajaremos con este tipo de ecuaciones lineales: con dos variables, ecuaciones lineales con una sola variable implica que la otra variable vale CERO, como en los ejemplos 3 y 4.
En general, un sistema con $m$ ecuaciones lineales y $n$ incógnitas puede ser escrito en forma normal como:
$$\tag{E2}\begin{matrix}{a_{11}x_1}&{+}&{a_{12}x_2}&{+}&{...}&{+}&{a_{1n}x_n}&{=}&{b_1}\\ {a_{21}x_1}&{+}&{a_{22}x_2}&{+}&{...}&{+}&{a_{2n}x_n}&{=}&{b_2}\\ {...}&{+}&{...}&{+}&{...}&{+}&{...}&{=}&{...}\\ {a_{m1}x_1}&{+}&{a_{m2}x_2}&{+}&{...}&{+}&{a_{3n}x_n}&{=}&{b_m}\end{matrix}$$Un sistema lineal de dos ecuaciones con dos incógnitas tiene la forma que podemos apreciar en la ecuación (3) de la siguiente página:
En la solución de este sistema se deben tener en cuenta algunas propiedades del álgebra:
Al momento de hallar las RAÍCES de un sistema lineal $2×2$ nos podemos encontrar que:
En la escena interactiva de la siguiente página podemos visualizar estos resultados.Los anteriores resultados también ocurrir en el espacio tridimensional con las ecuaciones de tres planos de ese espacio.
Haz clic en el botón que aparece en la esquina superior derecha para ampliar e interactuar con el recurso.
Para ello seguimos los siguientes pasos empleando las propiedades de las igualdades:

Dadas las ecuaciones $a$ y $b$ siguientes hallar los valores de $x$ e $y$ para que se conviertan en una identidad:
$$\begin{matrix} {(a)}&{5x}&{+}&{3y}&{=}\frac{11}{3} \\ {(b)}&{-x} & {-}&{7y}&{=}{-5} \end{matrix}$$Paso 1: despejar la misma variable en ambas ecuaciones:
De $(a)$ despejamos $x$:
$$5x+3y-3y=\frac{11}{3}-3y\Longrightarrow5x=\frac{11}{3}-3y$$ $$\frac{5x}{5}=\frac{\frac{11}{3}-3y}{5}\Longrightarrow x=\frac{\frac{11}{3}-3y}{5}\Longrightarrow x=\frac{11-9y}{15}$$De $(b)$ despejamos $x$:
$$-x+x-7y=x-5\Longrightarrow-7y=x-5$$Paso 2: igualamos esos resultados obtenidos:
$$\frac{11-9y}{15}=5-7y\Longrightarrow\frac{11-9y}{15}(15)=(5-7y)(15)$$ $$11-9y=75-105y\Longrightarrow 11-9y+105y=75-105y+105y$$ $$11+96y=75\Longrightarrow 11-11+96y=75-11\Longrightarrow96y=64$$Paso 3: despejar para esa variable.
$$\frac{96y}{96}=\frac{64}{96}\Longrightarrow y=\frac{64}{96}\Longrightarrow y=\frac{2}{3}$$Paso 4: sustituimos el valor de esa variable en cualquiera de las ecuaciones del paso 1 y solucionamos para esa variable (paso 5).
$$x=5-7*\frac{2}{3}\Longrightarrow x=5-\frac{14}{3}\Longrightarrow x=\frac{1}{3}$$Paso 6: sustituimos el valor de las variables en cualquiera de las ecuaciones dadas inicialmente.
$$5*\frac{1}{3}+3*\frac{2}{3}=?\Longrightarrow \frac{5}{3}+\frac{6}{3}=?\Longrightarrow \frac{11}{3}=\frac{11}{3}$$Para ello seguimos los siguientes pasos empleando las propiedades de las igualdades:

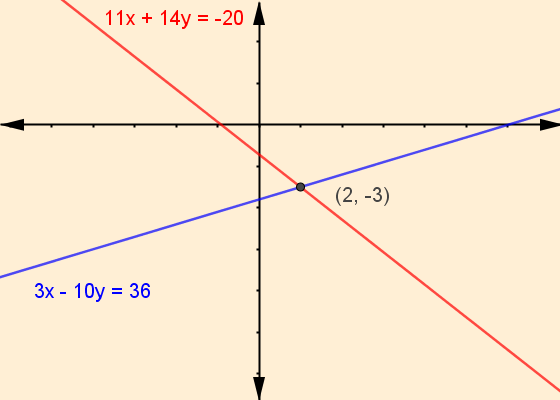
Sean las ecuaciones:
$$\begin{matrix} {(a)}&{11x}&{+}&{14y}&{=}-20 \\ \\ {(b)}&{3x} & {-}&{10y}&{=}\quad{36} \end{matrix}$$Paso 1: despejamos una de las variables en cualquiera de las ecuaciones, de (b) despejaremos la variable $x$.
$$3x-10y+10y=36+10y\Longrightarrow 3x=36+10y$$ $$3x*\frac{1}{3}=(36+10y)*\frac{1}{3}\Longrightarrow x=\frac{36+10y}{3}\Longrightarrow x=12+\frac{10y}{3}$$Paso 2: el valor obtenido lo reemplazamos en la ecuación 1 (La OTRA ecuación):
$$11\left(12+\frac{10y}{3}\right)+14y=-20$$ $$132+\frac{110}{3}y+14y=-20\Longrightarrow 132-132+\frac{152}{3}y=-20-132$$ $$\frac{152}{3}y=-152$$Paso 3. Despejamos la variable de la ecuación obtenida.
$$\frac{152}{3}y=-152\Longrightarrow\frac{152}{3}y*\frac{3}{152}=-152*\frac{3}{152} \Longrightarrow y=-3$$Paso 4. El valor de la variable y se reemplaza en la ecuación obtenida en el paso 1 y resolvemos (Paso 5).
$$x=12+\frac{10}{3}*{(-3)}\Longrightarrow=12-10=2$$Paso 6. Comprobamos en la ecuación (a) los resultados obtenidos:
$$11(2)+14(-3)=?\Longrightarrow 22-42=?\Longrightarrow -20=-20$$Podemos entonces afirmar que el par ordenado $(2, -3)$ es el punto común a las dos rectas citadas como se observa en la figura construida con GeoGebra:
En la siguiente escena aparecen dos ecuaciones, haz clic en el botón paso a paso para ver el proceso. También encontraras dos botones de color rojo para que selecciones la variable a despejar y un botón con el rótulo "Cambiar": con él cambiarás la ecuación en la cual se ha de despejar la variable.
Se trata de reducir el sistema a una sola ecuación:

Dadas las ecuaciones $a$ y $b$ siguientes hallar los valores de $p$ y de $q$ para que se conviertan en una identidad:
$$\begin{matrix} {(a)}&{4x}&{+}&{3y}&{=}\quad{10} \\ \\ {(b)}&{5x} & {-}&{6y}&{=}{-7} \end{matrix}$$Paso 1: sumamos las ecuaciones para saber si alguna de las variables se cancela:
$$\begin{matrix}&{4x}&{+}&{3y}&{=}&{10}\\ &{5x}&{-}&{6y}&{=}&{-7}\\ \hline \end{matrix}$$ $$\begin{matrix}{9x}&{-}&{3y}&{=}&{3}\end{matrix}$$Paso 2. Como la suma continúa con las dos variables procedemos a multiplicar ambas ecuaciones por números enteros de tal manera que al sumar se consiga lo propuesto.
Lo ideal es aprovechar la variable de ambas ecuaciones que posean signo diferente, para nuestro caso observamos que la variable $y$ nos facilita el propósito. Procedemos a multiplicar por números enteros
$$(a)*(2)\quad{8x}\quad{+}\quad{6y}\quad{=}\quad{20}$$ $$(b)*(1)\quad{5x}\quad{-}\quad{6y}\quad{=}\quad{-7}$$ $$\begin{matrix}&{8x}&{+}&{6y}&{=}&{20}\\ &{5x}&{-}&{6y}&{=}&{-7}\\ \hline \end{matrix}$$ $$\begin{matrix}{13x}&{+}&{0y}&{=}&{13}\end{matrix}$$Ahora solucionamos para la única variable en la ecuación:
$$13x=13\Longrightarrow 13x\left(\frac{1}{13}\right)=13\left(\frac{1}{13}\right)\Longrightarrow x=1$$El próximo paso es reemplazar la variable $x$ por su valor en cualquiera de las ecuaciones originales para determinar el valor de la otra variable:
$$5\left(1\right)-6y=-7\Longrightarrow 5-6y=-7\Longrightarrow -6y=-7-5$$ $$-6y=-12\Longrightarrow -6y=-12 \Longrightarrow -6y\left(\frac{1}{6}\right)=-12\left(\frac{1}{12}\right)$$ $$y=2$$Ahora comprobemos:
$$4(1)+3(2)=?\Longrightarrow 4+6=10 \Longrightarrow 10=10$$Este método a veces requiere que se complemente con herramientas algebraicas: en el vídeo observaremos la solución de un sistema $2×2$ que contiene las variables en el denominador de una expresión racional.

Práctica con los ejercicios de la siguiente página.
Utiliza el método propuesto en cada numeral.
Un sistema en el espacio tridimensional $ℝ^3$, es una ecuación de la forma:
$$\tag{E4} Ax + By + Cz + D = 0$$En esa expresión los coeficientes $A$, $B$, $C$ y $D \in ℝ$ y al menos uno de ellos es $≠$ de CERO y representa un plano. En un sistema de dos ecuaciones en tres variables se pueden presentar las siguientes situaciones:
Un sistema de tres ecuaciones o $3×3$ representa las siguientes posibilidades:
En la escena interactiva de la siguiente página se puede observar el comportamiento básico de esos planos.
Una generalización del método de reducción, utilizado para resolver sistemas de dos ecuaciones con dos incógnitas, es el método de Gauss. El método consiste en triangular el sistema, y para conseguirlo, utilizamos los criterios de equivalencia que detallaremos a continuación, de manera que consigamos hacer 0 los valores que están debajo de los elementos de la diagonal principal.
SISTEMA EQUIVALENTE. Se dice que dos sistemas de ecuaciones son equivalentes cuando tienen las mismas soluciones.
Expresado de otra manera, son aquellos sistemas donde toda solución del primero es solución del segundo y viceversa. Si dos ecuaciones lineales son equivalentes entonces tienen el mismo número de incógnitas aunque no necesariamente igual número de ecuaciones. Es evidente que si se cambia el orden de las ecuaciones, el sistema resultante no sólo es equivalente al inicial, sino que es el mismo.
Lo anterior ya lo habíamos practicado en el método de reducción, allí nos dimos cuenta que si en un sistema lineal de ecuaciones sustituimos una ecuación cualquiera por la ecuación que resulta al multiplicarla por un número cualquiera no nulo y sumarla, miembro a miembro, a otras ecuaciones del sistema (después de multiplicar estas últimas por un número cualquiera) el nuevo sistema lineal que obtenemos es equivalente al primero (tiene las mismas soluciones que el primero).
CRITERIOS DE EQUIVALENCIA, cuando determinamos sistemas de ecuaciones equivalentes debemos tener en cuenta:
Si se multiplican los dos miembros de una ecuación de un sistema por un número distinto de cero, resulta otro sistema equivalente al dado.
Si a una ecuación de un sistema se le suma o resta otra ecuación del mismo, resulta otro sistema equivalente.
Es de anotar que si al aplicar el método de Gauss que veremos a continuación llegamos a una ecuación del tipo $0x + 0y + 0z = 0$, se suprime. Si quedan menos ecuaciones que incógnitas, el sistema tiene infinitas soluciones y se conoce como sistema indeterminado. Veamos el esquema triangular que debemos obtener por el método de Gauss:
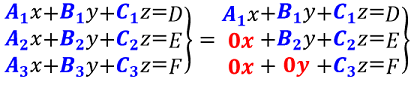

Solucionemos el sistema aplicando el método de Gauss.
$$\begin{cases} 1)\qquad 2x - 3y + 5z & = & -6 \\ 2)\qquad 4x + 2y + 12z & = & 16\\ 3)\qquad 3x - 7y - 4z & = & 4\\ \end{cases}$$Ahora hallaremos ecuaciones equivalentes entre la 1ª la 3ª de tal manera que al sumarlas el valor de $3x$ se convierta en $0x$.
Ello implica que debemos determinar el mcm entre los coeficientes de la variable $x$ de ambas ecuaciones:
Reescribimos nuestro sistema:
$$\begin{cases} 1)\qquad 2x - 3y + 5z & = & -6 \\ 2)\qquad 4x + 2y + 12z & = & 16\\ 3)\qquad {\color{red}0x} - 5y - 23z & = & 26\\ \end{cases}$$Nuestro siguiente paso es hallar ecuaciones equivalentes entre la 1ª la 2ª de tal manera que al sumarlas el valor de $4x$ se convierta en $0x$. Sumaremos la ecuación 1 multiplicada por ($-2$) y la ecuación 2 multiplicada por $1$.
$$\begin{cases} 1)*(-2)\\ 2)*(1)\\ \\ \end{cases}\begin{cases} 1)\qquad -4x + 6y - 10z & = & 12 \\ 3)\qquad \quad 4x + 2y + 12z & = & 16\\ R)\qquad \quad {\color{red}0x} + 8y + 2z & = & 28\\ \end{cases}$$Reescribimos nuestro sistema:
$$\begin{cases} 1)\qquad 2x - 3y + 5z & = & -6 \\ 2)\qquad {\color{red}0x} + 8y + 2z & = & 28\\ 3)\qquad {\color{red}0x} - 5y - 23z & = & 26\\ \end{cases}$$Nuestro siguiente paso es hallar ecuaciones equivalentes entre la 2ª la 3ª de tal manera que al sumarlas el valor de $-5y$ se convierta en $0y$. Sumaremos la ecuación 2 multiplicada por $5$ y la ecuación 3 multiplicada por $8$.
Reescribimos nuestro sistema:
$$\begin{cases} 1)\qquad 2x - 3y + 5z & = & -6 \\ 2)\qquad {\color{red}0x} + 8y + 2z & = & 28\\ 3)\qquad {\color{red}0x} + {\color{red}0y} - 174z & = & 348\\ \end{cases}$$Tomemos la tercera ecuación y solucionemos:
$$ -174z\left(\frac{1}{-174}\right)=348\left(\frac{1}{-174}\right)\Longrightarrow {\Large{z}={\color{red}-2}}$$Ahora reemplazamos $z=-2$ en la ecuación 2:
$$8y + 2(-2)=28 \Longrightarrow 8y-4=28 \Longrightarrow 8y-4+{\color{red}4}=28+{\color{red}4}$$ $$8y=32 \Longrightarrow 8y\left(\frac{1}{8}\right)=32 \left(\frac{1}{8}\right)\Longrightarrow {\Large{y}={\color{red}4}}$$Por último, reemplacemos $y=4$ y $z=-2$ en la ecuación 1:
$$2x-3(4)+5(-2)=-6 \Longrightarrow 2x-12-10=-6$$ $$ \Longrightarrow 2x-22=-6 \Longrightarrow 2x-22+{\color{red}22}=-6+{\color{red}22} \Longrightarrow 2x=16$$ $$2x=16 \Longrightarrow 2x\left(\frac{1}{2}\right)=16 \left(\frac{1}{2}\right)\Longrightarrow {\Large{x}={\color{red}8}}$$

En los numerales 1 a 10 utilice el método de Gauss para solucionar el sistema dado:
$$ 1) \begin{cases} x + y + 2z = 19 \\ 2x + 4y - 3z = 1\\ 3x + 6y = 5z\\ \end{cases}\qquad \qquad 2) \begin{cases} 2x + y = z \\ x + 3y + 2z = 5\\ x + 4y + 9 = y\\ \end{cases}$$

El Álgebra Lineal estudia los conjuntos denominados espacios vectoriales o espacios euclidianos. Un espacio euclidiano es el conjunto de $n$-adas ordenadas, también conocido por espacio $n$-dimensional y se denota por $ℝ^n$ este es una sucesión de n números reales ejemplo $(a_1,a_2,...,a_n)$ donde los vectores $ℝ^n$ se clasifican así:
Un vector es una forma de representar determinados objetos en el plano y en el espacio, es un conjunto ordenado de números escritos en forma de renglones o en forma de columnas.
Un Vector renglón de $n$ componentes es un conjunto ordenado de $n$ números escritos así:
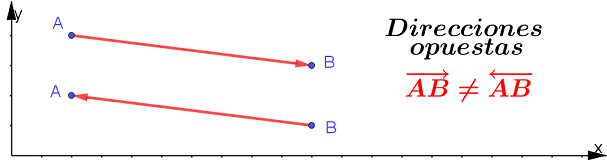
$$\large {\tag{V1}(x_1, x_2, ... , x_n)}$$Sean $A$ y $B$ dos puntos cualesquiera en el plano, el segmento de recta dirigido de $A$ hasta $B$ y el conjunto de todos los segmentos equivales a él se denominan vectores. Desde el punto de vista algebraico, un vector en el plano es el par ordenado de números reales $(a, b)$. Los números $a$ y $b$ se denominan componentes del vector:
$$\large {\tag{V2}\overline{AB}=\overrightarrow{v}=(a, b)}$$En la gráfica, podemos observar que no obstante los segmentos de recta posean igual punto de inicio e igual punto final, la dirección del vector es diferente.
Dado que un vector es la representación del conjunto de segmentos de rectas equivalentes, se define como módulo, magnitud o medida del vector a la longitud de cualquiera de esos segmentos con igual dirección y sentido.

Ese módulo es la resultante de aplicar el denominado Teorema de Pitágoras, puesto que las componentes del vector son las proyecciones del mismo en los ejes coordenados. Esas componentes se obtienen de la siguiente manera:
El módulo de un vector $v$ es un escalar y se representa por: $$\large{\tag{V3}|v|}$$
La dirección de esos vectores equivalentes es la dirección del vector equipolente (vector que tiene su punto de inicio en el origen de coordenadas del plano cartesiano), esta dado por el ángulo cuya tangente es la razón entre la componente en y dividida por la componente en $x$. Es el ángulo que forma con el eje $x$ positivo.
$$\tag{V4}{\large{\overrightarrow{v}=[ x_2-x_1,y_2-y_1 ]=[ \, ]}}$$ $$\tag{V5}{\large|\overrightarrow{v}|=\sqrt{{\overrightarrow{v_x}}^2+{\overrightarrow{v_y}}^2}}$$ $$\tag{V6}{\theta=Tan^{-1}\left(\frac{\overrightarrow{v_y}}{\overrightarrow{v_x}}\right)}$$
Un vector $u$ tiene su punto final en el cuarto cuadrante del plano cartesiano y sus coordenadas están representadas por el par ordenado $(-4,-6)$ y su punto de origen está ubicado en las coordenadas $(8,-1).$
Determinar el valor de las componentes rectangulares, su magnitud y su dirección.
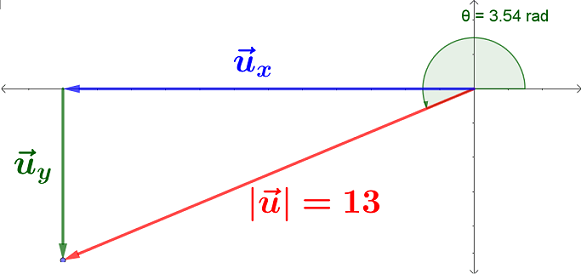
Podemos observar que es necesario recurrir a otras relaciones trigonométricas del triángulo rectángulo: el seno y el coseno, veamos:
$$\theta = Sen^{-1}\left(\frac{\overrightarrow{v_y}}{13}\right) ∴ \overrightarrow{v_y}= 13*Sen \theta \cong -4.97 U$$ $$\theta = Cos^{-1}\left(\frac{\overrightarrow{v_x}}{13}\right) ∴ \overrightarrow{v_x}=13*Cos \theta \cong -12.01 U$$
Para un vector $\overrightarrow{w}$ dado determinar:
Coordenada en $x$:
$$|\overrightarrow{w}|=\sqrt {(x-1)^2+(3-(-3))^2}=\sqrt{157}$$ $$(x-1)^2+(6)^2=157 \Longrightarrow x^2-2x+1+36=157$$ $$x^2-2x+37-{\color{red}{157}}=157-{\color{red}{157}} \Longrightarrow x^2-2x-120=0$$Por fórmula general:
$$x=\frac{-(-2)\pm \sqrt{(-2)^2-4(1)(-120)}}{2(1)}\Longrightarrow x=12 \quad o \quad x=-10$$La dirección del vector $\overrightarrow{w}$
$$\theta= Tan^{-1}\left(\frac{6}{11}\right)= 28.61°$$Luego de recordar la información haz clic en el botón Cerrar y podrás visualizar un nuevo vector desplazando los puntos azules.

Simplemente es un vector cuyas componentes son proporcionales al escalar dado y se presentan las siguientes opciones:

Una fuerza equivalente a $200$ Newton se aplica a un objeto formando un ángulo de $30°$ con la horizontal, determinar el incremento o disminución de sus componentes si la esa fuerza se duplica. ¿Será que la magnitud de esas componentes también se duplica?
El producto escalar de dos vectores es un número real que resulta al multiplicar el producto de sus módulos por el coseno del ángulo que forman, es también conocido como producto interno o producto punto.
Geométricamente, es el producto de dos magnitudes euclidianas de dos vectores $u = (a_1, b_1)$ y $v = (a_2, b_2)$ por el coseno del ángulo $θ$ formado por esos dos vectores:
$$\tag {V8} \large{uv = |u||v|Cos θ}$$Analíticamente el producto punto se expresa como:
$$\tag {V2}\large {uv = a_1a_2 + b_1b_2}$$$θ$ es el ángulo no negativo más pequeño de esos dos vectores equipolentes o sea que tienen el origen de coordenadas como su punto inicial y estará comprendido en el intervalo $[0, π]$.
Según esta definición, podemos calcular el ángulo
$$\tag{V9} θ=Cos^{-1}\left(\frac{uv}{|u||v|}\right)$$
En la gráfica vemos el vector $u = (4,-6)$ y el vector $v = (3,6)$, determinar el ángulo $θ$ formado por ellos:

Dado que dos vectores $u$ y $v$ son paralelos si el ángulo entre ellos es $0$ o $\pi$, además de ello tienen la misma dirección o direcciones opuestas.

Vamos a determinar las coordenadas $(-5, b1)$ del vector $u$ de $|u|= \sqrt{29}$ para que sea paralelo al vector $v = (10,4)$.
Observamos que la respuesta correcta es $\large {b_1=-2}$
Dos vectores $u$ y $v$ diferentes de CERO, son ortogonales si el ángulo entre ellos es $π/2$, ello equivale a decir que el coseno del ángulo vale CERO o que el producto punto vale CERO.
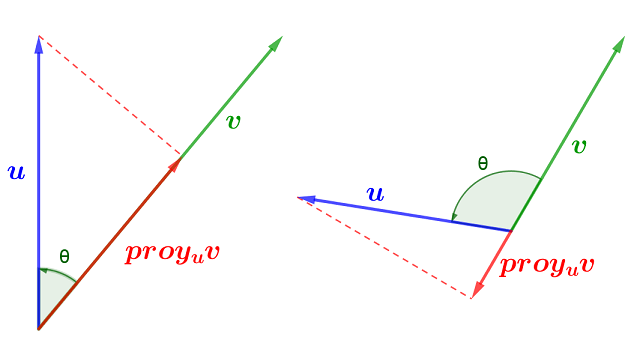
Sean $u$ y $v$ dos vectores diferentes de CERO, entonces la proyección de $u$ sobre $v$ es un vector denominado como:
$$\tag{V10}\large {proy_vu=\frac{u \cdot v}{|v|^2}\cdot v}$$Mueve los puntos $A$ y $B$ para que puedas visualizar la proyección de $u$ sobre $v$.

Vamos a determinar las coordenadas del vector que proyecta el vector $u = (-6,5)$ sobre el vector $v = (2,-2)$
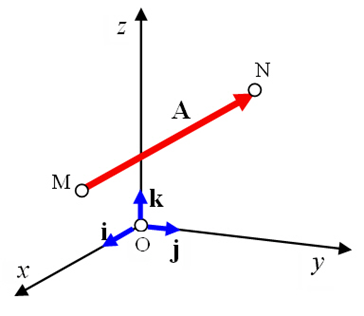
Un vector en el espacio tridimensional analizado desde el punto de vista algebraico es una terna o triada de números reales $(x, y, z)$ donde los números $x$, $y$ y $z$ se denominan componentes del vector.
Dados los puntos $P = (x_1, y_1, z_1)$ y $Q = (x_2, y_2, z_2)$, podemos definir las coordenadas del vector $u$ que va desde $P$ hasta $Q$ como:
Al igual que los vectores en $ℝ^2$ el módulo será la distancia entre en punto inicial y el punto final del vector:
$$|u|=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2+(z_2-z_1)^2}$$Ahora realizaremos algunos cálculos con respecto a los vectores en el espacio tridimensional.

Calcular el módulo del vector $u$ que tiene su origen en $P = (-3, 2, 4)$ y va hasta el punto $Q = (4, 0, -4)$:
$$\sqrt{(4-(3))^2+(0-2)^2+((-4)-4)^2}$$ $$\sqrt{(7)^2+(-2)^2+(-8)^2}=\sqrt{161}$$Hemos calculado la norma del vector $u=[7, -2,-8]$
La disposición más común para representar un vector en el espacio sigue la denominada regla de la mano derecha, donde los dedos extendidos señalan la dirección positiva de los ejes coordenados.

Los ejes coordenados así dispuestos determinan tres planos coordenados y se denominan plano $xy$ (nuestro plano habitual en dos dimensiones), el plano $xz$ y el plano $yz$.
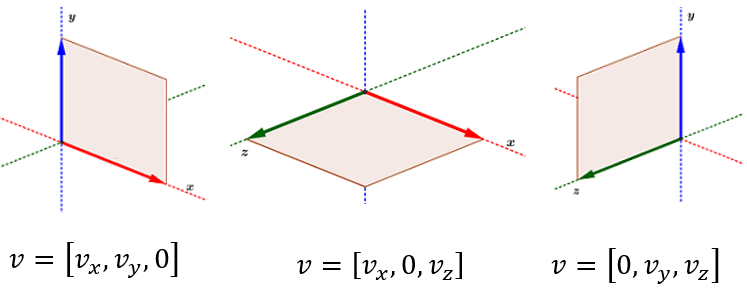

Los vectores en el espacio tridimensional forman un ángulo con cada uno de los ejes coordenados.
En una base ortonormal (Una base es ortogonal si los vectores de la base son perpendiculares entre sí), se llaman cosenos directores del vector $u = [u_x, u_y, u_z]$, a los cosenos de los ángulos que forma el vector u con los vectores de la base.
Dado el vector $u = [u_x, u_y, u_z]$, cada una de esas componentes forma un ángulo $\theta$ que se determina por:
$$\tag{V11} \theta_x=Cos^{-1}\left(\frac{u_x}{|u|}\right);\theta_y=Cos^{-1}\left(\frac{u_y}{|u|}\right)$$$$\theta_z=Cos^{-1}\left(\frac{u_z}{|u|}\right)$$Con esos cosenos directores se cumple que:
$$\tag{V12} Cos^2(\theta_x)+Cos^2(\theta_y)+Cos^2(\theta_z)=1$$
Determinar los ángulos que el vector $u = [-1, 4, 3]$ forma con los ejes coordenados.
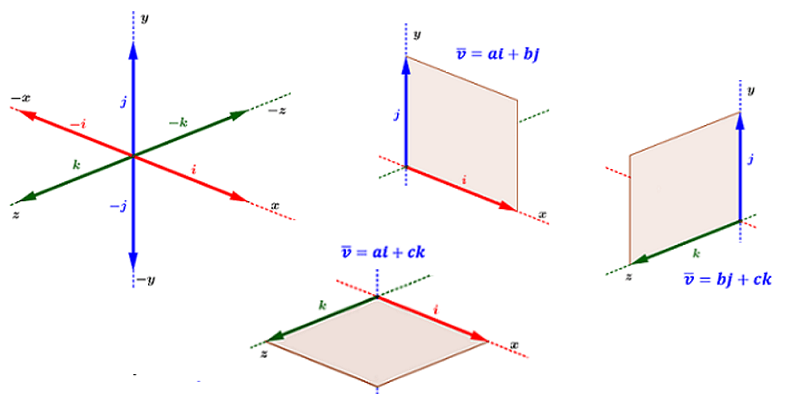
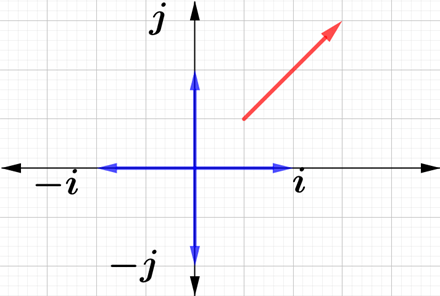
En $ℝ^2$ existen dos vectores que nos permiten especificar cualquier vector en función de ellos, son vectores de magnitud $1$, el primero de ellos es el vector $(1,0)$ que se denota por $i$. El otro vector es el vector $(0,1)$ denotado por $j$. Así, el vector $v = (3,7)$ puede expresarse como $v = 3i + 7j$.
De igual manera en el espacio tridimensional existen tres vectores unitarios que nos permiten representar cualquier vector:
En la gráfica se puede ver más detenidamente las descripción y posición de los vectores unitarios.
Sea $u$ un vector unitario y $v$ otro vector diferente de CERO, entonces podemos determinar un vector unitario que tiene la misma dirección de $v$ mediante:
$$\tag{V13} u=\frac{v}{|v|}$$
Determinar los vectores unitarios que tengan la misma dirección de:
a) $m$ = $(-5,\; 6,\; 4)$,$\quad$ b) $n$ = $(0,\; -3,\; 7)$ y,$\quad$ c) $p$ = $\large {(\frac{1}{8},-\frac{3}{8},\frac{5}{8})}$.
a)$\qquad |m|=\sqrt{(-5)^2+(6)^2+(4)^2}=\sqrt{77}$
$$\large {u=\frac{[-5,6,4]}{\sqrt{77}}}=\left[-\frac{5}{\sqrt{77}},\frac{6}{\sqrt{77}},\frac{4}{\sqrt{77}}\right]$$b)$\qquad |n|=\sqrt{(0)^2+(-3)^2+(7)^2}=\sqrt{58}$
$$\large {u=\frac{[0,-3,7]}{\sqrt{58}}}=\left[0,-\frac{3}{\sqrt{58}},\frac{7}{\sqrt{58}}\right]$$c)$\qquad |p|=\sqrt{(\frac{1}{8})^2+(-\frac{3}{8})^2+(\frac{5}{8})^2}=\sqrt{\frac{35}{64}}=\frac{\sqrt{35}}{8}$
$$\large {u=\frac{8}{\sqrt{35}}} \cdot \left[\frac{1}{8},-\frac{3}{8},\frac{5}{8}\right]=\left[\frac{1}{\sqrt{35}},-\frac{3}{\sqrt{35}},\frac{5}{\sqrt{35}}\right]$$Sean los vectores $u = a_1i + b_1j + c_1z$ y $v = a_2i + b_2j + c_2z$, el vector suma al que llamaremos $r = u + v$ es igual a la suma de las componentes respectivas de los vectores $u$ y $v$, se expresa como: $d = (a_1 + a_2)i + (b_1+b_2)j + (c_1+c_2)z$. Otra forma de expresar esa suma es $ = (a_1 + a_2, b_1 + b_2 , c_1 + c_2)$.
Sean los vectores $u = a_1i + b_1j + c_1z$ y $v = a_2i + b_2j + c_2z$, el vector diferencia al que llamaremos $d = u - v$ (será la suma de $u$ con el opuesto de $v$) será igual a la diferencia de las componentes
respectivas de los vectores $u$ y $v$, y se expresa como: $d = (a_1 - a_2)i + (b_1 - b_2)j + (c_1 - c_2)z$. Otra forma de expresar esa diferencia es $d = (a_1 - a_2, b_1 - b_2 , c_1 - c_2)$.
Dado que el método gráfico no posee la precisión ideal para realizar estas operaciones, ni con el denominado cabeza con cola y el método del paralelogramo, lo ideal es realizar la suma algebraica de los componentes rectangulares de todos los vectores involucrados en la operación.

Dados el vector $u = 3i -4j + 2k$ y el vector $v = -i + j -2k$, determinar el módulo del vector resultante de la siguiente operación: $3u + 2v$.
En la escena se encuentran tres vectores que puedes mover a placer con el desplazamiento de sus puntos de inicio y de aplicación. A la derecha de los vectores podrás observar unas diferentes operaciones de suma y resta que podemos realizar con ellos.
También conocido como producto interno es una operación que se define solo en $ℝ^3$ puesto que a diferencia del producto punto cuyo resultado es un escalar, el resultado aquí es otro vector. Para el vector $u = a_1i + b_1j + c_1k$ y el vector $u = a_2i + b_2j + c_2k$, el producto vectorial está definido como:
$u$ x $v$ = $(b_1c_2 - c_1b_2)i + (c_1a_2 - a_1c_2)j + (a_1b_2 - b_1a_2)k \quad {(V11)}$
El resultado es un vector perpendicular a los vectores que se multiplican, y por lo tanto normal al plano que los contiene. Debido a su capacidad de obtener un vector perpendicular a otros dos vectores, cuyo sentido varía de acuerdo al ángulo formado entre estos dos vectores, esta operación es aplicada con frecuencia para resolver problemas matemáticos, físicos o de ingeniería como el torque de una fuerza, la velocidad angular y la dirección del campo magnético entre algunas de ellas.
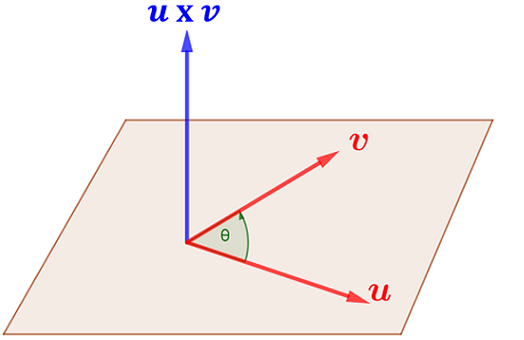
La dirección de esa resultante está dada por la regla de la mano derecha, si denominamos el producto vectorial como el vector $w$, entonces $u$, $v$ y $w$ forman (en ese orden) la tríada de la mano derecha. Si hacemos rotar el vector $u$ en sentido contrario a las manecillas del reloj hasta que sea colineal con el vector $v$. la resultante es el vector $w$, en caso contrario de hacer rotar el vector $v$ en el mismo sentido de las manecillas del reloj hasta que sea colineal con $u$, la resultante sería $-w.$
$$\tag{V14} u \times v=-(u\times v)$$Si $\theta$ es el ángulo entre los vectores $u$ y $v$ (siempre menor o igual a $180°$), entonces la magnitud de su producto cruz esta dado por:
$$\tag{V15} |u \times v| = |u| |v| Sen(\theta)$$Los productos vectoriales de los vectores unitarios $i$, $j$, $k$ están dados por:
$$i \times i = 0 \qquad i \times j = k \qquad i \times k = - j$$ $$j \times j = 0 \qquad j \times i = - k \qquad j \times k = i$$ $$k \times k = 0 \qquad k \times i = j \qquad k \times j = - i$$Considerando que los vectores $u$ y $v$ tienen el mismo origen, existe la interpretación desde la geometría elemental que son los lados adyacentes de un paralelogramo.

Determinar el ángulo que forman y el área del paralelogramo cuyos lados adyacentes son los vectores $u = [7,2,0]$ y $v = [6,7,0]$. Dado que los vectores se encuentran en el plano $xy$, el producto vectorial será en la dirección $k$. Recordemos que:
$$\theta =Cos^{-1}\left(\frac{u \cdot v}{|u||v|}\right)$$Consideremos ahora el producto cruz de $u$ y $v$ y el vector resultante $w$, si esos vectores no se encuentran en el mismo plano, se convierten en los lados de un paralelepípedo en el espacio (volumen).
El cálculo de ese volumen se conoce como el triple producto escalar de $u$ y $v$. Existe la condición de que No sean nulos, No paralelos de dos en dos dos y NO coplanares. Ese volumen es el resultado del producto punto de uno de los vectores por el producto escalar de los otros dos.
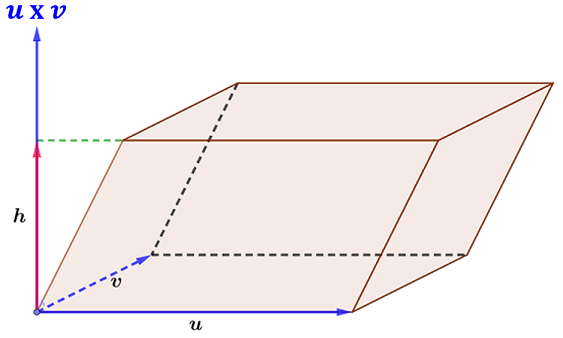

Dados los vectores $u = i, -5j, -3k$; $v = -i, -j, 2k$ y $w = i$, determinar si el volumen existe y su valor.
$| w \cdot (u \times v ) | = | (1)(-13) + ( 0)(1) + ( 0)(-6) | = | -13 | = 13 U^3$
Lo anterior es diferente al triple producto cruz de 3 vectores $u$, $v$ y $w$ en $ℝ^3$ que está dado por:
$$\tag{V17} u \times ( v \times w) = (u \cdot w)v - (u \cdot v)w$$Otros conceptos a considerar en los espacios vectoriales son 1) Dependencia lineal y, 2) Independencia lineal. Ello lo podemos expresar como: dos vectores en un espacio vectorial son linealmente dependientes y solo si uno de ellos es múltiplo escalar del otro.
Sean $v_1, v_2, ..., v_n$ vectores en un espacio vectorial, se dice que esos vectores son linealmente dependientes si existen $n$ escalares $c_1, c_2, ... , c_n$ no todos iguales a CERO y que cumplan:
$$\tag{V18} c_1v_1 + c_2v_2 + \dotso + c_nv_n = 0$$


Un concepto clave en álgebra lineal es el de matriz, definida como un arreglo bidimensional de números. Dado que puede definirse tanto la suma como el producto de matrices, en mayor generalidad se dice que son elementos de un anillo. Una matriz se representa por medio de una letra mayúscula ($A,B,...$) y sus elementos con la misma letra en minúscula ($a,b,...$), con un doble subíndice donde el primero indica la fila y el segundo la columna a la que pertenece.
Los elementos individuales de una matriz $m × n$, a menudo denotados por $ai$, $aj$, donde el máximo valor de sus elementos $(i,j)$ en $i$ es $m$, y el máximo valor de $j$ es $n$. Siempre que la matriz tenga el mismo número de filas y de columnas que otra matriz, estas se pueden sumar o restar elemento por elemento.
Las matrices se utilizan para múltiples aplicaciones y sirven, en particular, para representar los coeficientes de los sistemas de ecuaciones lineales que vimos en el capítulo anterior o para representar transformaciones lineales dada una base. En este último caso, las matrices desempeñan el mismo papel que los datos de un vector para las aplicaciones lineales.
Las matrices y los determinantes son herramientas del álgebra que facilitan el ordenamiento de datos, así como su manejo. Los conceptos de matriz y todos los relacionados fueron desarrollados básicamente en el siglo XIX por matemáticos como los ingleses J.J. Sylvester y
Arthur Cayley y el Irlandés William Hamilton. Las matrices se encuentran en aquellos ámbitos en los que se trabaja con datos regularmente ordenados y aparecen en situaciones propias de las Ciencias Sociales , Económicas y Biológicas.
Se denomina Matriz a una forma rectangular compuesta de filas ($m$) y columnas ($n$), donde cada elemento lleva asociado un doble índice, el primero ($i = 1, 2, ..., m$) para indicar la fila y el segundo ($j = 1, 2, ..., n$) para indicar la columna. El orden de la matriz ($m \times n$) expresa las filas y columnas que componen la matriz. Se designa como $m \times n$ o como un conjunto de sus elementos ($aij$). Si $I=\{1, 2, ..., m\}$ y $J=\{1, 2, ..., n\}$, una Matriz de $m$ filas y $n$ columnas y coeficientes reales se representa como $M(m\times n; R)$.
Un cuerpo $R$ es un conjunto no vacío, junto con dos operaciones binarias internas que normalmente denominamos: 1°) Operación suma representada por $+$ y, 2°) Operación producto representada por $·$, operaciones que verifican las siguientes propiedades:

Vamos a construir una matriz $A$ de orden $3 \times 3$ que cumpla las siguientes condiciones:
Paso 1. Construimos una matriz genérica de $3 \times 3$
\[ A=\left[ \begin{array}{rrr} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \\ \end{array} \right] \]Paso 2. Aplicamos la primera condición: $a_{ij} = 5$. Con la condición de que $i = j$. Dicho de otra forma cambiaremos los elementos $a_{11}$, $a_{22}$ y $a_{33}$ por $5$.
\[ A=\left[ \begin{array}{ccc} 5 && a_{12} && a_{13} \\ a_{21} && 5 && a_{23} \\ a_{31} && a_{32} && 5 \\ \end{array} \right] \]Paso 3. Aplicamos la segunda condición de que $i ≠ j$. Dicho de otra forma cambiaremos los elementos $a_{12}$, $a_{13}$, $a_{21}$, $a_{23}$, $a_{31}$, $a_{32}$ por $0$.
\[ A=\left[ \begin{array}{ccc} 5 & 0 & 0 \\ 0 & 5 & 0 \\ 0 & 0 & 5 \\ \end{array} \right] \]Acabamos de construir una matriz escalar donde todos los elementos de la diagonal principal son iguales a $5$.

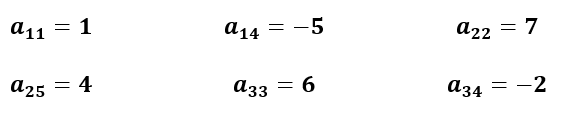
La suma de dos matrices es otra matriz que resulta de sumar los elementos que corresponden a la misma fila y a la misma columna. Ambas matrices deben ser del mismo orden.
$$A = (a_{ij}), B = (b_{ij}) ∈ Mm, n ;$$ $$A + B = C = (c_{ij}) ∈ Mm, n$$ tal que $$\tag{M2}c_{ij}=a_{ij}+b_{ij}$$
Sumar las matrices $A$ y $B$ que se presentan en la siguiente página.
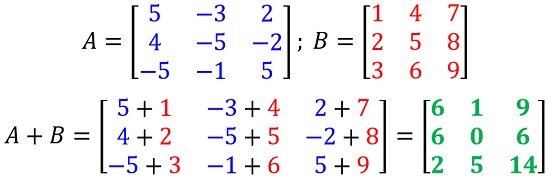

El producto de una matriz por un escalar es otra matriz que resulta de multiplicar el escalar por cada uno de los elementos de la matriz.
Dadas $A = (a_{ij}) ∈ Mm, n y φ ∈ K → φA=(φa_{ij})$
Sea $\large {φ = ¾}$, determinar la matriz resultante de $\large{φA}$.
Únicamente podemos multiplicar dos matrices $A$ y $B$ si el número de columnas de $A$ es igual al número de filas de $B$, podemos expresar que $A$ y $B$ son compatibles bajo la multiplicación. De lo contrario se denominan incompatibles.
Sea $A=a_{ij}$ un matriz $m \times n$, y $B=b_{ij}$ una matriz $n \times p$, entonces el producto de $A$ y $B$ es una matriz $m \times p$, $C=c_{ij}$, caracterizada por:
$\large c_{ij}$ = (renglón $i$ de $A$)$*$(columna $j$ de $B$)
La siguiente escena es una adaptación del proyecto Un100.

Aunque esta aplicación puede realizarse sin emplear matrices, veremos su utilidad en la situación propuesta. Para una temporada escolar que se avecina, un vendedor al menudeo solicita cotización (en miles de unidades) a tres distribuidores mayoristas de los artículos que más le solicitan sus clientes y realiza la siguiente tabla expresada en dólares:

Vamos a determinar con cual de los mayoristas es más económico para el vendedor si compra 12 millares de cuadernos, 7 millares de colores, 5 millares de carpetas, 25 millares de lápices y 6 millares de borradores.
Sea $A$ la matriz de las cotizaciones y $B$ la matriz de la posible compra por el vendedor minorista:
\[ AB=\left[ \begin{array}{ccccc} 305 & 42 & 30 & 12 & 70 \\ 315 & 40 & 28 & 10 & 75 \\ 307 & 38 & 30 & 13 & 85 \\ \end{array} \right] \left[ \begin{array}{c} 12 \\ 5 \\ 25 \\ 6 \\ 7 \\ \end{array} \right] \]El costo de la compra con el mayorista $A$:
$$(305)(12)+(42)(5)+(30)(25)+(12)(6)+(70)(7)=5182$$El costo de la compra con el mayorista $B$:
$$(315)(12)+(40)(5)+(28)(25)+(10)(6)+(75)(7)=52265$$El costo de la compra con el mayorista $C$:
$$(307)(12)+(38)(5)+(30)(25)+(13)(6)+(85)(7)=5297$$De acuerdo a lo anterior, para esa compra al vendedor minorista le es más económico comprarle al mayorista $A$, un estudio completo implica los niveles de ganancia, el impuesto al valor agregado, entre muchas variables que no son competencia de este texto.
La siguiente escena es otra adaptación del proyecto Un100 descrito al inicio de este texto:
Si $A = a_{ij}$ con $m \times n$, entonces $A^t = a_{ji}$ con $n \times m$. Es decir, la transpuesta de una matriz se obtiene intercambiando las filas y las columnas de esta.
El propósito con las transformaciones elementales es convertir una matriz concreta en otra matriz mas fácil de estudiar.
En concreto, siempre será posible conseguir una matriz escalonada: "Sea $A$ una matriz y $F$ una fila de $A$. Diremos que $F$ es nula si todos los números de $F$ coinciden con el cero.
Si $F$ es no nula, llamamos PIVOTE de $F$ al primer número distinto de cero de $F$ contando de izquierda a derecha en ese renglón. Una MATRIZ ESCALONADA es aquella que verifica las siguientes propiedades:
Una matriz escalonada se dice reducida si la columna arriba de cada pivote también es de ceros.
Veamos las siguientes matrices: $A$ no es escalonada, $B$ es escalonada por (2) y $C$ es escalonada por (3).
\[ A=\left[ \begin{array}{rrr} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 1 & 3 \\ \end{array} \right] \; B=\left[ \begin{array}{rrr} 1 & 0 & 2 \\ 0 & 1 & 6 \\ 0 & 0 & 0 \\ \end{array} \right] \; C=\left[ \begin{array}{rrr} 1 & 3 & 2 \\ 0 & 1 & 5 \\ \end{array} \right] \]En una matriz escalonada $E$ se define su RANGO como $rg(E)$ como el número de filas de esa matriz.
Podemos transformar una matriz no escalonada en una matriz escalonada mediante las siguientes transformaciones por filas:

Partiendo de cualquier matriz $A$ se puede llegar, mediante una cantidad finita de transformaciones elementales, a una matriz escalonada $E$. En el siguiente video se aplican algunas transformaciones:

Rango de una matriz
Para cada matriz cuadrada $A$, podemos asociar un número llamado determinante de $A$. Al hallar el determinante de una matriz se sustituyen los corchetes por barras verticales Se dice que un determinante de una matriz de $n \times n$ es un determinante de orden $n$ o un determinante de $n$-ésimo orden. Se expresa como $det A$ ó $|A|$.
Para una matriz cuadrada $2 \times 2$ el determinante se calcula:
Geométricamente el determinante se interpreta como el área orientada del paralelogramo que determinan los vectores fila linealmente independientes:
$$\large {\vec{a}=[a_{11},a_{12}]\qquad \vec{b}=[b_{11},b_{12}]} $$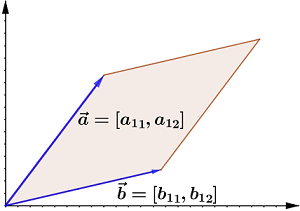

Si $|A| = - 12$, determinar el valor de $a_{21}$ sabiendo que $a_{11}$ tiene un valor igual a $-5$, $a_{12}$ es igual $8$ y $a_{22}$ es igual a $12$
$$\large {-12= (-5)(12)-(8)(a_{12})}$$ $$\large {-12= -60-8(a_{12}) ∴ -12+60=-60+60-8(a_{12})}$$Como ya conocemos la manera de hallar el determinante de una matriz cuadrada $2 \times 2$ entenderemos con mayor propiedad el procedimiento que se describe a continuación y que explicaremos en el vídeo:
Sea $A$ una matriz cuadrada de orden $3$, se llama determinante de $A$ al número que se obtiene calculando la suma de los productos de los elementos de la diagonal principal menos los productos la diagonal secundaria.
Otra forma práctica de recordar la definición es la siguiente: Se escriben a la derecha (o debajo) de la matriz las dos primeras líneas. La diagonal principal y sus dos paralelas llevan el signo $+$ (positivo), la diagonal secundaria y sus dos paralelas llevan el signo $-$ (negativo).
Comprobemos calculado el determinante de la matriz $A$:
\[ A=\left[ \begin{array}{ccc} 2 & 4 & 5 \\ 2 & 4 & 5 \\ 0 & -2 & 0 \\ \end{array} \right] \]
Calcular el determinante de la matriz $A$.
Definición 1. Si $A = (a_{ij})$ es una matriz cuadrada de orden $n$, se llama menor complementario del elemento $a_{ij}$, y se representa por $M_{i j}$, al determinante de la submatriz que se obtiene al suprimir de $A$ la fila $i$ y la columna $j$.
Nota. El adjunto de un elemento es igual a su menor complementario si la suma de subíndices es par, y a su opuesto si es impar. Ejemplo: El adjunto del elemento $a_{21}=-1$, de la matriz que vemos a continuación es $A_{2 1} = -25$.
\[ A=\left[ \begin{array}{rrr} 1 & 3 & 4 \\ -1 & 0 & 1 \\ 4 & 1 & -7 \\ \end{array} \right] ∴ M_{21}=\left[ \begin{array}{rrr} 3 & 4 \\ 1 & -7 \\ \end{array} \right]=-25 \]Definición 2. Se llama adjunto del elemento $a_{i j}$ a:
$$\large {A_{i j} = (-1)i + j M_{i j}}$$Proposición 1. Un determinante es igual a la suma de los productos de los elementos de una línea cualquiera por sus respectivos adjuntos.

Calcular el determinante de la matriz $A$. Seleccionamos la fila o columna que incluya la mayor cantidad de elementos nulos:
\[ A=\left[ \begin{array}{cccc} 3 & 3 & 1 & 1 \\ -2 & 1 & -1 & 1 \\ 1 & 0 & -1 & 2 \\ 0 & 2 & 0 & 1 \\ \end{array} \right] \]Dada la matriz $A$ podemos visualizar que la fila $4$ posee la mayor cantidad de elementos nulos, por lo tanto el cálculo de $|A|$ debe considerar el signo de sus adjuntos:
\[ Adj=\left[ \begin{array}{cccc} + & - & + & - \\ - & + & - & + \\ + & - & + & - \\ - & + & - & + \\ \end{array} \right] \]Calculemos el adjunto de $a_{41}$ que debe ir precedido de signo negativo:
\[ Adj(a_{41})=({\color{red}{\textbf{-}}})(0)\left[ \begin{array}{rrr} 3 & 1 & 1 \\ 1 & -1 & 1 \\ 0 & -1 & 2 \\ \end{array} \right]=({\color{red}{\textbf{-}}})(0)(-6)=0 \]Calculemos el adjunto de $a_{42}$ que debe ir precedido de signo positivo:
\[ Adj(a_{42})=({\color{red}{\textbf{+}}})(0)\left[ \begin{array}{rrr} 3 & 1 & 1 \\ -2 & -1 & 1 \\ 1 & -1 & 2 \\ \end{array} \right]=({\color{red}{\textbf{+}}})(2)(5)=10 \]Calculemos el adjunto de $a_{43}$ que debe ir precedido de signo negativo:
\[ Adj(a_{43})=({\color{red}{\textbf{-}}})(0)\left[ \begin{array}{rrr} 3 & 1 & 1 \\ -2 & 1 & 1 \\ 1 & 0 & 2 \\ \end{array} \right]=({\color{red}{\textbf{-}}})(0)(20)=0 \]Calculemos el adjunto de $a_{44}$ que debe ir precedido de signo positivo:
\[ Adj(a_{44})=({\color{red}{\textbf{+}}})(0)\left[ \begin{array}{rrr} 3 & 3 & 1 \\ -2 & 1 & -1 \\ 1 & 0 & -1 \\ \end{array} \right]=({\color{red}{\textbf{+}}})()(-13)=-13 \]El determinante de esa matriz es la suma de los valores calculados, he aquí la conveniencia de utilizar la fila o columna que mayor cantidad de valores nulos posea.
$$|A|=Adj(a_{41})+Adj(a_{42})+Adj(a_{43})+Adj(a_{44})$$ $$\large {|A|=0+10+0-13=-3}$$Una matriz cuadrada $A$, se dice invertible o que tiene matriz inversa, si existe una matriz cuadrada del mismo orden, que se denota por $A^{-1}$, tal que:
$$\tag{M4} \large {A^{-1}* A = a * A^{-1} = I_{n}}$$No toda matriz cuadrada es invertible. Cuando $A$ tiene inversa se dice que $A$ es regular; en caso contrario diremos que $A$ es singular.
$(A*B)^{-1} = B^{-1} * A^{-1} ∀ A,B ∈ M_{m \times n}$; $A$, $B$ Regulares.
La inversa de una matriz $2 \times 2$ por su definición y su equivalente práctica:
\[ \tag {M5} A^{-1}=\frac{1}{|A|}(adj A)^t=\frac{1}{|A|}\left[ \begin{array}{rrr} a_{11} & -a_{12} \\ -a_{21} & a_{22} \\ \end{array} \right] \]Sí
\[ A=\left[ \begin{array}{cc} a & b \\ c & d \\ \end{array} \right]\Longrightarrow A^{-1}=\frac{1}{ad-bc}\left[ \begin{array}{rr} d & -b \\ -c & a \\ \end{array} \right] \]
Dada la matriz $A$, calcular la matriz inversa a partir de la definición:
Si multiplicamos ambas matrices para obtener la matriz identidad $2 \times 2$ tenemos dos sistemas de ecuaciones lineales que permiten esclarecer el porqué de la parte $b$ de la ecuación $(M7)$:
$$ \left. \begin{array}{rcr} 2a+3b & = & 1 \\ -3a+2b & = & 0 \end{array} \right\}\qquad \left. \begin{array}{rcr} 2c+3d & = & 0 \\ -3c+2d & = & 1 \end{array} \right\} $$Solucionando ambos sistemas se obtiene que:
$$a=\frac{2}{13}\qquad b=\frac{3}{13} \qquad c=-\frac{3}{13} \qquad d=-\frac{2}{13}$$ \[ \left[ \begin{array}{rrr} 2 & 3 \\ -3 & 2\\ \end{array} \right]{\large \left[ \begin{array}{rrr} \frac{2}{13} & -\frac{3}{13} \\ \\ -\frac{3}{13} & \frac{2}{13} \\ \end{array} \right]}=\left[ \begin{array}{rrr} 1 & 0 \\ 0 & 1 \\ \end{array} \right] \]En nuestro siguiente ejercicio vamos a comprobar que dada la matriz $A$ y multiplicada por $A^{-1}$ se obtiene la matriz identidad.

Dadas las matrices $A$ y $A^{-1}$ comprobar si su producto es la matriz identidad:
\[ A=\left[ \begin{array}{rrr} 2 & -3 & 4 \\ 1 & 1 & -1 \\ 2 & 0 & 1 \\ \end{array} \right]\qquad A^{-1}=\left[ \begin{array}{rrr} \frac{1}{3} & 1 & -\frac{1}{3} \\ \\ 1 & 1 & -1 \\ \\ -\frac{2}{3} & -2 & \frac{5}{3}\\ \end{array} \right] \] $\qquad{\color{red}{a_{11}}}=(2)\left(\frac{1}{3}\right)+(-3)(-1)+(4)\left(-\frac{2}{3}\right)=1$Hemos comprobado que:
\[ \left[ \begin{array}{rrr} 2 & -3 & 4 \\ 1 & 1 & -1 \\ 2 & 0 & 1 \\ \end{array} \right]\left[ \begin{array}{rrr} \frac{1}{3} & 1 & -\frac{1}{3} \\ \\ 1 & 1 & -1 \\ \\ -\frac{2}{3} & -2 & \frac{5}{3}\\ \end{array} \right]=\left[ \begin{array}{rrr} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{array} \right] \]El cálculo de la matriz inversa por el método de Gauss supone transformar una matriz en otra equivalente por filas para lograr:
Una matriz aumentada, o matriz ampliada, se obtiene al combinar dos matrices.
Para hallar la matriz inversa combinaremos la matriz cuadrada dada con la respectiva matriz identidad, se representa como: $(A|I)$ tal y como se muestra a continuación:
$$\tag{M6} A\textbf{|}I\rightarrow I\textbf{|}A^{-1}$$Ejemplo de matriz $2 \times 2$ ampliada con la matriz identidad $2 \times 2$.
\[ A\textbf{|}I=\left[ \begin{array}{rrr} 3 & 2 & \textbf{|} & \color{red}{1} & \color{red}{0}\\ 4 & 1 & \textbf{|} & \color{red}{0} & \color{red}{1}\\ \end{array} \right] \]A continuación en el vídeo ilustraremos el procedimiento para hallar la matriz inversa de un sistema $2 \times 2$:

Ahora veamos mediante este ejercicio las transformaciones necesarias para hallar la matriz inversa de una matriz $3 \times 3$
\[ A=\left[ \begin{array}{rrr} 0 & 2 & -1 \\ 2 & 0 & -2 \\ -1 & 1 & 0 \\ \end{array} \right] \] \[ A\textbf{|}I=\left[ \begin{array}{ccccc} 0 & 2 & -1 & \textbf{|} & \color{red}{1} & \color{red}{0} & \color{red}{0}\\ 2 & 0 & -2 & \textbf{|} & \color{red}{0} & \color{red}{1} & \color{red}{0}\\ -1 & 1 & 0 & \textbf{|} & \color{red}{0} & \color{red}{0} & \color{red}{1}\\ \end{array} \right] \]Observamos que todos los elementos de la diagonal principal son CERO y por ello debemos cambiar $F_1$ como punto de partida:
$$F_1=F_1+F_2 \longrightarrow A\textbf{|}I=\left[ \begin{array}{ccccc} \color{red}{2} & \color{red}{2} & \color{red}{-3} & \textbf{|} & \color{red}{1} & \color{red}{1} & \color{red}{0}\\ 2 & 0 & -2 & \textbf{|} & 0 & 1 & 0\\ -1 & 1 & 0 & \textbf{|} & 0 & 0 & 1\\ \end{array} \right]$$ $$F_2=F_2-F_1 \longrightarrow A\textbf{|}I=\left[ \begin{array}{ccccc} 2 & 2 & -3 & \textbf{|} & 1 & 1 & 0\\ \color{red}{0} & \color{red}{-2} & \color{red}{1} & \textbf{|} & \color{red}{-1} & \color{red}{0} & \color{red}{0}\\ -1 & 1 & 0 & \textbf{|} & 0 & 0 & 1\\ \end{array} \right]$$ $$F_3=2F_3+F_1 \longrightarrow A\textbf{|}I=\left[ \begin{array}{ccccc} 2 & 2 & -3 & \textbf{|} & 1 & 1 & 0\\ 0 & -2 & 1 & \textbf{|} & -1 & 0 & 0\\ \color{red}{0} & \color{red}{4} & \color{red}{-3} & \textbf{|} & \color{red}{1} & \color{red}{1} & \color{red}{2}\\ \end{array} \right]$$ $$F_3=F_3+2F_2 \longrightarrow A\textbf{|}I=\left[ \begin{array}{ccccc} 2 & 2 & -3 & \textbf{|} & 1 & 1 & 0\\ 0 & -2 & 1 & \textbf{|} & -1 & 0 & 0\\ \color{red}{0} & \color{red}{0} & \color{red}{-1} & \textbf{|} & \color{red}{-1} & \color{red}{1} & \color{red}{2}\\ \end{array} \right]$$Lo realizado en a través del ejercicio desarrollado implica que la matriz $A$ se convierte en la matriz identidad y la matriz $B$ (Identidad) se convierte en la matriz inversa de la matriz $A$.
La matriz adjunta, de adjuntos o de cofactores de la matriz $A$, que denotamos por $Adj(A)$ o $A*$, es la matriz cuyo elemento $(i , j)$ (fila $i$ y columna $j$) es el adjunto $ad i$, $j = ( - 1 ) i + j · det( A i , j )$ donde la matriz $A i , j$ es la matriz que resulta al quitar a la matriz $A$ la fila $i$ y la columna $j$.
Ello implica que para la matriz de adjuntos de un sistema $2 \times 2$ debemos tener en cuenta los siguientes signos de sus componentes:
$$\bf {Adj(A)=A^{*}=\left[ \begin{array}{cc} + & -\\ - & +\\ \end{array} \right]} $$Se cumple que la matriz inversa de $A$, $A^{-1}$ se puede escribir en función de su adjunta como
$$\tag{M7} \bf {A^{-1}=\frac{(Adj(A))^t}{|A|}=\frac{(A^t)^*}{|A|}}$$Donde la notación de la potencia $t$ expresa la traspuesta de $A$.

Dada la matriz $A$ determinar su inversa por cofactores:
$\qquad Adj_{11}=(-1)^2det(3)=3$
$\qquad Adj_{12}=(-1)^3det(1)=-1$
$\qquad Adj_{21}=(-1)^3det(-1)=1$
$\qquad Adj_{22}=(-1)^4det(5)=5$
$$\bf {Adj(A)=A^*=\left[ \begin{array}{cr} 3 & -1\\ 1 & 5\\ \end{array} \right]}$$Al igual que la adjunta de un sistema $2 \times 2$, la adjunta de un sistema $3 \times 3$ implica que debemos tener en cuenta los signos de sus componentes como se presenta a continuación:
$$\bf {Adj(A)=\left[ \begin{array}{ccc} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23}\\ a_{31} & a_{32} & a_{33} \end{array} \right]=\left[ \begin{array}{ccc} + & - & +\\ - & + & -\\ + & - & + \end{array} \right]} $$La matriz de cofactores tendría la siguiente estructura donde se resalta el signo correspondiente a cada elemento:
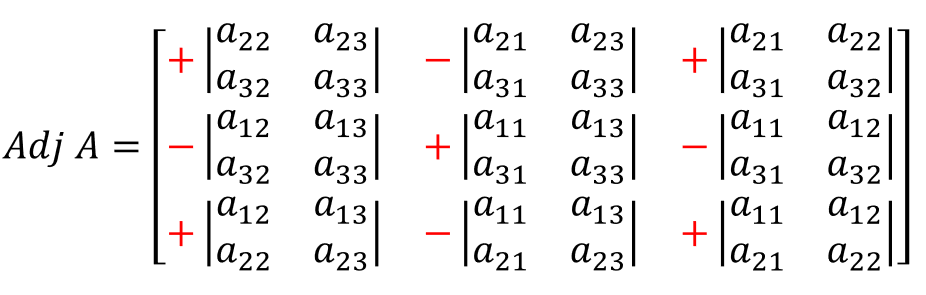

Dada la matriz $A$ determinar su inversa por cofactores:
$$\bf {A=\left[ \begin{array}{ccc} 2 & 2 & 2\\ 1 & -1 & 0\\ 0 & 3 & 4 \end{array} \right]} $$$\qquad a_{11}=(-1)^{1+1}[(-1)(4)-(0)(3)]=-4$
$\qquad a_{12}=(-1)^{1+2}[(1)(4)-(0)(0)]=-4$
$\qquad a_{13}=(-1)^{1+3}[(1)(3)-(1)(0)]=3$
$\qquad a_{21}=(-1)^{2+1}[(2)(4)-(3)(2)]=-2$
$\qquad a_{22}=(-1)^{2+2}[(2)(4)-(0)(2)]=8$
$\qquad a_{23}=(-1)^{2+3}[(2)(3)-(2)(0)]=-6$
$\qquad a_{31}=(-1)^{3+1}[(2)(0)-(-1)(2)]=2$
$\qquad a_{32}=(-1)^{3+2}[(2)(0)-(1)(2)]=2$
$\qquad a_{33}=(-1)^{3+3}[(2)(-1)-(2)(1)]=-4$
Al principio del libro se realizó un recuento de cómo resolver muchos problemas matemáticos a través del planteamiento de un sistema de ecuaciones lineales. Existen diversos métodos para resolverlos (recodemos los conocidos método de igualación, substitución e igualación).
Pero, si dichos sistemas están formados por gran cantidad de ecuaciones e incógnitas, el aplicar los métodos anteriores resulta ser una tarea sumamente dificultosa y que, muy probablemente, conducirá a resultados erróneos. Para solventar este problema, los sistemas de ecuaciones lineales se pueden plantear matricialmente y resolverlos haciendo uso de la matriz inversa.
En el próximo capitulo solucionaremos algunas aplicaciones de la vida real empleando la matriz inversa.

Las matrices constituyen una herramienta que nos permite saber rápidamente si un sistema de ecuaciones lineales (SEL) tiene soluciones y el tipo de soluciones: un sistema puede no tener solución, tener una única solución o tener infinitas soluciones.
Para estas aplicaciones se requiere comprender los conceptos relacionados con las matrices: matrices regular, inversa y adjunta y el rango de una matriz.
Una vez clasificado el SEL se procede a calcular, en caso de haberlas, sus soluciones. Para ello disponemos de varios métodos: El método de Gauss, la Regla de Cramer y el de la matriz inversa si el SEL es compatible determinado, y la eliminación de Gauss o de Gauss-Jordan si es un sistema indeterminado. Para esa solución trabajamos el SEL como un sistema matricial (matriz de coeficientes y matriz o vector de términos independientes).
A partir de su matriz ampliada del SEL (matriz de coeficientes con el vector de términos independientes), el teorema de Rouché-Frobenius, nos permite clasificar un SEL según el tipo de solución.
En esta sección emplearemos las matrices para solucionar sistemas de ecuaciones de $n$ ecuaciones lineales y $n$ variables.
Para solucionar ecuaciones lineales vamos a recurrir a:
Un sistema lineal lo podemos escribir como una ecuación de matrices:
$$A \cdot X = B$$Donde $A$ es la matriz de coeficientes del sistema, $X$ es la matriz de las variables (para este ecuación la variable es $x$) y $B$ es la matriz de los términos independientes.
$$A=\begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n}\\ a_{21} & a_{22} & \cdots & a_{2n}\\ \vdots & \vdots & \vdots & \vdots\\ a_{m1} & a_{m2} & \cdots & a_{mn}\\ \end{bmatrix};X=\begin{bmatrix} x_1\\ x_2\\ \vdots\\ x_n\\ \end{bmatrix};B=\begin{bmatrix} b_1\\ b_2\\ \vdots\\ b_n\\ \end{bmatrix}$$Sistema lineal $2 \times 2$, ilustraremos el proceso de solución con un ejemplo paso a paso y una aplicación:
Resolver el sistema:
$$\begin{array}{rrrr} E_1&&&3x&-&12y&=-&27 \\ E_2&&-&5x&+&3y&=&11 \end{array}$$Paso 1. Escribir la ecuación de matrices:
$$ \begin{bmatrix} 3 & -12\\ -5 & 3\\ \end{bmatrix} \begin{bmatrix} x\\ y\\ \end{bmatrix}= \begin{bmatrix} -27\\ 11\\ \end{bmatrix} $$Paso 2. Verificar si el determinante de la matriz de coeficientes es diferente de CERO.
$$det(A)=|A|=(3)(3)-(-5)(-12)=-51$$Paso 3. Determinar la matriz inversa de la matriz de coeficientes, se emplea uno de los métodos descritos en el capitulo anterior y comprobamos que se obtiene la matriz identidad:
$$ \begin{bmatrix} 3 & -12\\ -5 & 3\\ \end{bmatrix} \begin{bmatrix} 3 & 5\\ 12 & 3\\ \end{bmatrix}=-\frac{1}{51} \begin{bmatrix} -51 & 0\\ 0 & -51\\ \end{bmatrix}= \begin{bmatrix} 1 & 0\\ 0 & 1\\ \end{bmatrix} $$Ello implica que:
$$ \begin{bmatrix} x\\ y\\ \end{bmatrix}= -\frac{1}{51}\begin{bmatrix} -\frac{3}{51} & -\frac{12}{51}\\ &\\ -\frac{5}{51} & -\frac{3}{51}\\ \end{bmatrix}\begin{bmatrix} -27\\ 11\\ \end{bmatrix}=\begin{bmatrix} -1\\ 2\\ \end{bmatrix} $$Ahora comprobemos en $E_1$y en $E_2$:
$$3(-1)-12(2)=?\Longrightarrow -3-24=-27$$ $$-5(-1)+3(2)=?\Longrightarrow 5+6=11$$Aplicación
En un remate de aduanas ofrecen un lote compuesto de: $400$ celulares tipo $A_1$ y 1500 celulares del tipo $Z_3$ por $110500$ dólares. Otro lote ofrecido consta de $1500$ celulares del tipo $A_1$ y $600$ celulares del tipo $Z_3$ por $138000$ dólares. ¿Cuál es el precio de cada tipo de celular?
Establecemos el sistema de ecuaciones y emplearemos como variables la misma denominación de los tipos de celular:
$$\begin{array}{rrrr} E_1&&&400A_1&+&1500Z_3&=110500 \\ E_2&&&1500A_1&+&600Z_3&=138000 \end{array}$$Paso 1. Establecemos la ecuación de matrices:
$$\begin{bmatrix} 400 & 1500\\ 1500 & 600\\ \end{bmatrix} \begin{bmatrix} A_1\\ Z_3\\ \end{bmatrix}=\begin{bmatrix} 110500\\ 138000\\ \end{bmatrix}$$Paso 2. Verificar si el determinante de la matriz de coeficientes es diferente de CERO.
$$|A|=(400)(600)-(1500)(1500)\Longrightarrow |A|=240000-2250000$$ $$\Longrightarrow |A|=-2010000$$Paso 3. Determinar la matriz inversa de la matriz de coeficientes, se emplea uno de los métodos descritos en el capitulo anterior y comprobamos que se obtiene la matriz identidad:
$$ \begin{bmatrix} 400 &1500\\ 1500 &600\\ \end{bmatrix} \begin{bmatrix} 600 & -1500\\ -1500 & 400\\ \end{bmatrix}\Longrightarrow$$ $$=-\frac{1}{2010000} \begin{bmatrix} -2010000 & 0\\ 0 & -2010000\\ \end{bmatrix}=\begin{bmatrix} 1 & 0\\ 0 & 1\\ \end{bmatrix} $$Este arreglo matricial nos lleva a:
$$ \begin{bmatrix} A_1\\ Z_3\\ \end{bmatrix}= -\frac{1}{2010000}\begin{bmatrix} 600 & -1500\\ &\\ -1500 & 400\\ \end{bmatrix}\begin{bmatrix} 110500\\ 138000\\ \end{bmatrix} $$ $$ \begin{bmatrix} A_1\\ Z_3\\ \end{bmatrix}=-\frac{1}{201000} \begin{bmatrix} -140700000\\ -110550000\\ \end{bmatrix}=\begin{bmatrix} 70\\ 55\\ \end{bmatrix} $$Le dejamos al lector la comprobación de las ecuaciones mediante la sustitución de $A_1$ con el valor de $70$ dólares y de $Z_3$ con un costo de $55$ dólares.
Sistema lineal $3 \times 3$, al igual que en el apartado $A$, ilustraremos el proceso de solución con un ejemplo paso a paso y una aplicación:

En el siguiente ejercicio hallaremos la solución de un sistema $3 \times 3$
Hallar los valores de $x_1$, $x_2$ y de $x_3$ que satisfacen el siguiente sistema:
$$\begin{alignedat}{3} 4&x_1+&5&x_2-8&x_3 = -9 \\ 7&x_1-&12&x_2+5&x_3 = -2\\ -3&x_1+&9&x_2+10&x_3=61 \end{alignedat} $$Paso 1. Establecemos la ecuación de matrices:
$$ \begin{bmatrix} 4 & 5 & -8\\ 7 & -12 & 5\\ -3 & 9 & 10\\ \end{bmatrix} \begin{bmatrix} x_1\\ x_2\\ x_3\\ \end{bmatrix}=\begin{bmatrix} -9\\ -2\\ 61\\ \end{bmatrix} $$Paso 2. Verificar si el determinante de la matriz de coeficientes es diferente de CERO mediante los elementos de la primera línea:
$$|A|=4[(-12)-(10)-(9)(5)]$$ $$-5[(7)(10)-(-3)(5)]$$ $$-8[(7)(9)-(-3)(-12)]=-1301$$Paso 3. Hallar $A^{-1}$ ya que $|A| ≠ 0$, iniciamos con la matriz de adjuntos:
Paso 4. Ahora su traspuesta:
$$(Adj(A))^{T}=(A^{*})^{T}=\begin{bmatrix} -165 & -122 & -71\\ -85 & 16 & -76\\ 27 & -51 & -83\\ \end{bmatrix}$$Paso 5. Determinemos $A^{-1}$ mediante:
$$A^{-1}=\frac{1}{|A|}(Adj(A))^{T}$$Paso 6. Solucionemos la ecuación matricial:
$$\begin{bmatrix} x_1\\ x_2\\ x_3\\ \end{bmatrix}=\begin{bmatrix} \frac{165}{1301} & \frac{122}{1301} & \frac{71}{1301}\\ \frac{85}{1301} & \frac{16}{1301} & \frac{76}{1301}\\ -\frac{27}{1301} & \frac{51}{1301} & \frac{83}{1301}\\ \end{bmatrix}\begin{bmatrix} -9\\ -2\\ 61\\ \end{bmatrix}$$ $$\begin{bmatrix} x_1\\ x_2\\ x_3\\ \end{bmatrix}=\begin{bmatrix} \frac{165}{1301}(-9) + \frac{122}{1301}(-2) + \frac{71}{1301}(61)\\ \frac{85}{1301}(-9) + \frac{16}{1301}(-2) + \frac{76}{1301}(61)\\ -\frac{27}{1301}(-9) + \frac{51}{1301}(-2) + \frac{83}{1301}(61)\\ \end{bmatrix}=\begin{bmatrix} 2\\ 3\\ 4\\ \end{bmatrix}$$El sistema tiene como solución: $x_1 = 2$ ; $x_2 = 3$ ; $x_3 = 4$, es consistente determinado.
Aplicación
Una ecuación cuadrática tiene como gráfica una parábola representada por el polinomio:
$$p(x)=a_0\pm a_1x\pm a_2x^{2}$$Vamos a determinar los coeficientes del polinomio que representa la parábola que pasa por los puntos dados en la figura:
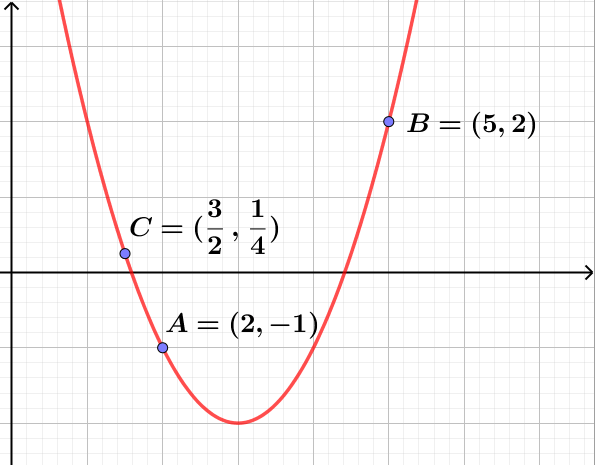
Cada par ordenado debe satisfacer la ecuación del polinomio dado, por lo tanto se forma el sistema:
$$\begin{alignedat}{3} &a_0+&2&a_1+4&a_2 = 1 \\ &a_0+&5&a_1+25&a_2 = 2\\ 4&a_0+&6&a_1+9&a_2=1 \end{alignedat}$$Vídeo solución del problema planteado:

Independiente de su valor posicional en el sistema decimal, la suma de las cifras un número menor de $1000$ y mayor de $100$ es igual a $17$. Si al número original se le restan $297$ unidades el número se invierte posicionalmente. Además, en el número original la suma de las cifras las unidades y la de las centenas excede en $5$ unidades a la cifra de las decenas. ¿Cuál es ese número?
Establecemos las variables
$$A = A*10^{2} \qquad\qquad B = B*10^{1} \qquad \qquad C = C* 10^{0}$$Acorde con ello, la traducción del lenguaje Vernáculo genera las siguientes ecuaciones:
Ecuación 1:
$$a+b+c=17$$Ecuación 2:
$$100A+10B+C-297=100C+10B+A$$Ecuación 3:
$$A+C=B+5$$El sistema generado luego de simplificar es entonces:
$$A+B+C=17$$ $$A-C=3$$ $$A-B+C=5$$Ahora la matriz ampliada $\color{red}A|B$:
\[ \left[ \begin{array}{lrrcr} 1 & 1 & 1 & \color{blue}\vert & \color{red}17\\ 1 & 0 & -1 & \color{blue}\vert & \color{red}3\\ 1 & -1 & 1 & \color{blue}\vert & \color{red}5\\ \end{array} \right] \]Solución por el método de Gauss escalonando la matriz ampliada:
$$F_2=F_2-F_3 \Longrightarrow$$ \[ \left[ \begin{array}{lrrcr} 1 & 1 & 1 & \color{blue}\vert & \color{red}17\\ 0 & 1 & -2 & \color{blue}\vert & \color{red}-2\\ 1 & -1 & 1 & \color{blue}\vert & \color{red}5\\ \end{array} \right] \]El nuevo sistema reducido:
$$\left. \begin{array}{rcr} A+B+C & = & 17 \\ B-2C & = & -2 \\ -4C & = & -16 \end{array} \right\}$$De este sistema reducido solucionamos de atrás hacia adelante:
$$-4C=-16 \Longrightarrow -4C \left(\frac{1}{-4}\right)=-16\left(\frac{1}{-4}\right)\Longrightarrow C=\color{red}4$$Conocido el valor de $C$ tenemos:
$$B-2C=-2 \Longrightarrow B-2(4)=-2 \Longrightarrow B-8=-2$$ $$B - 8 + 8 = -2 + 8 \Longrightarrow B = \color{red}6$$Conocido los valores de $B$ y de $C$ tenemos:
$$A + 6 + 4 = 17 \Longrightarrow A + 10 = 17 \Longrightarrow A + 10 - 10 = 17 - 10$$ $$A = \color{red}7$$El número buscado es:
$$A(10^2)+b¿B(10^1)+C(10^0)\Longrightarrow$$ $$7(100)+6(10)+4(1)=700+60+4=764$$Otro de los campos dónde existen los sistemas de ecuaciones es la solución de circuitos eléctricos, en el siguiente vídeo veremos una solución por el método de mallas.
En el capítulo 2 se aplicaron ciertas propiedades a los conjuntos de
vectores en el plano ($ℝ^2$) y los vectores en el espacio ($ℝ^3$) de tal manera que, si sumamos dos o más vectores en el plano su resultante es otro vector en el mismo espacio, de igual manera sucede lo mismo con vectores en el espacio, expresado de otra forma se aplican las propiedades conmutativa y asociativa para la suma y la propiedad distributiva para la multiplicación por un escalar.
Definición: un espacio vectorial real V es un conjunto de objetos en $ℝ^2$ y $ℝ^3$ con dos operaciones que obedecen las reglas de suma de vectores y multiplicación por un escalar.
Es de resaltar que esos objetos se denominan vectores pero no siempre serán objetos que tienen dirección, magnitud y sentido como las fuerzas, velocidades y aceleraciones tal como veremos en algunos ejercicios resueltos.
Ejemplos de espacios vectoriales:
Para que un conjunto dado sea un espacio vectorial $V$ es necesario que se cumplan los siguientes axiomas:
Dado un conjunto $V$, con solo demostrar que no cumple uno solo de los anteriores axiomas es razón suficiente para declarar que no es un espacio vectorial.
Espacio vectorial trivial. Se denomina así al conjunto $V = { 0 }$, puesto que cumple todos los axiomas descritos ya que el CERO es su único elemento.

Verificar y la recta que pasa por los puntos $A(1,0$) y $B(4,0)$ constituye un espacio vectorial.
De la Geometría Analítica tenemos que su ecuación es:
$$\frac{y-1}{x-0}=\frac{0-1}{4-0}\Longrightarrow y=-\frac{x}{4}+1$$Ahora construyamos una tabla de valores que nos permitirá realizar la comprobación de los axiomas de los espacios vectoriales:

Dado que $V = {(x,y)|y = -0.25x + 1}$, ahora vamos a comprobar que:
$$(x_1,y_1)+(x_2,y_2)=(x_1+x_2,y_1+y_2)$$ $$(1,0)+(4,0)=(1+4,0+0)=(5,0)$$Podemos observar que el par ordenado $(5,0)$ no se encuentra en los pares ordenados de la tabla, es decir no cumple la propiedad de cerradura para la suma. Por lo tanto:
$$V = {(x,y)| y = -0.25x + 1}$$NO es un espacio vectorial

Verificar si las matrices invertibles $A$ y $B$ forman o no forman un espacio vectorial.
\[ A=\left[ \begin{array}{rrr} 1 & 2 & 3 \\ 0 & 1 & -1 \\ 1 & 0 & -2 \\ \end{array} \right] \] \[\color{#0000FF} B=\left[ \begin{array}{rrr} 2 & 1 & 0 \\ 1 & 0 & 1 \\ 1 & 2 & 3 \\ \end{array} \right] \]Recordemos que una matriz es invertible si su determinante es diferente de CERO.
$$|A|=\begin{vmatrix} 1 & 2 & 3 \\ 0 & 1 & -1\\ 1 & 0 & -2\\ 1 & 2 & 3 \\ 0 & 1 & -1 \end{vmatrix}\Longrightarrow|A|=[-4]-[3]=-7$$ $$\color{#0000FF}|B|=\begin{vmatrix} 2 & 1 & 0 \\ 1 & 0 & 1\\ 1 & 2 & 3\\ 2 & 1 & 0 \\ 1 & 0 & 1 \end{vmatrix}\Longrightarrow|B|=[1]-[7]=-6$$Es diferente de:
$$B \times A= \begin{vmatrix} 2 & 5 & 5 \\ 2 & 2 & 1\\ 4 & 4 & -5 \end{vmatrix}$$Podemos afirmar que si $V = M_{mn}$ denota el conjunto de matrices de orden $m \times n$ con componentes reales, entonces con la suma de matrices y multiplicación por un escalar usuales se puede verificar que $M_{mn}$ es un espacio vectorial cuyo neutro aditivo es la matriz de ceros de dimensiones $m \times n$ es un espacio vectorial pero no la multiplicación de matrices puesto que no es conmutativa.
Podemos concluir que las matrices dadas no forman un espacio vectorial.
Se dice que $W$ es un subespacio vectorial de $V$ si $W$ es un subconjunto no vacío de $V$, y $W$ es un espacio vectorial, junto con las operaciones de suma $\oplus$ entre vectores y multiplicación por un escalar $\otimes$ definidas para $V$.
Un subconjunto no vacío $W$ de un espacio vectorial $V$ es un subespacio de $V$ si se cumplen las dos reglas de cerradura.
Reglas que permitan determinar si un subconjunto NO vacío es un sub-espacio vectorial, esas dos reglas las podemos discriminar como:

Determinar si $W = \{(x_1, x_2, x_3) \in ℝ^3 \; | \; 5x_1 − 3x_3 = 0 \}$ es un sub-espacio vectorial de $ℝ^3$.
Este vector lo sustituimos en la ecuación implícita dada:
$$5(x_1 + x_2) − 3(z_1 + z_2) = 0$$Aplicamos la propiedad distributiva:
$$5 x_1 + 5 x_2 − 3 z_1 − 3 z_2 = 0$$Como $W_1$, $W_2 ∈ W$, $∴ 5 x_1− 3 z_1 = 0$ (1); $5 x_2 − 3 z_2> = 0$ (2) y reescribiendo la ecuación de la línea anterior tenemos:
$$\color{red}{5 x_1 − 3 z_2} + \color{blue}{5 x_2 − 3 z_2} = 0 ; 0 + 0 = 0$$Reemplazando en la ecuación implícita:
$$5 \alpha x_1 − 3 \alpha x_3 = 0$$Obteniendo un factor común:
$$\alpha (5x_1 − 3 x_3) =0;0=0$$Dado que hemos demostrado que se cumplen las tres condiciones, podemos afirmar que $W$ es un sub-espacio vectorial de $V$.
Si $S$ y $W$ son sub-espacios de $V$ que cumplen las operaciones de $⊕$ y $⊗$ se realizan las siguientes operaciones entre ellos:
En general la unión de sub-espacios NO es un sub-espacio de $V$.
La intersección de sub-espacios es un sub-espacio de $V$.
Si $S ∩ W = {0}$
$$S ∩ W = {u ∈ V | u ∈ S ∧ u ∈ W}$$A esa intersección se le denomina suma directa y se expresa como $S ⊕ W$. A este se le denomina sub-espacio trivial formado por el vector nulo.
Ahora podemos hablar de la combinación lineal en esos subespacios vectoriales.
Una combinación lineal de vectores $v_1$, $v_2$, $v_3$, $...$, $v_n$ es en un espacio vectorial $V$, es la suma que tiene la forma:
$$\alpha_1v_1 + \alpha_2>v_2 + \alpha_3v_3 + ... + \alpha_nv_n$$Donde $α_1, α_2, α_3, ..., α_n$ son escalares.
En un espacio vectorial $V$, los vectores $v_1, v_2, v_3, ..., v_n$ generan a $V$ si todo vector en $V$ se puede expresar como una combinación lineal de $v_1, v_2, v_3, ..., v_n$
Expresado de otra manera, dados dos vectores: $v_1$ y $v_2$, y dos números: $a$ y $b$, el vector resultante de $av_1 + bv_2$ se dice que es una combinación lineal de $v_1$ y $v_2$.
Una combinación lineal de dos o más vectores es el vector que se obtiene al sumar esos vectores multiplicados por sendos escalares. Cualquier vector se puede poner como combinación lineal de otros dos que tengan diferente dirección. Esta combinación lineal es única.

Dados $v_1 = [-3,2]$ y $v_2 = [3,4]$, hallar la combinación lineal $m = 3v_1 + 2v_2$
$$m = 3[-3,2] + 2[3,4] = [-9,6] + [6,8]\Longrightarrow $$ $$m = [-9+6, 6+8]\Longrightarrow m = [-3,14]$$En la gráfica de la página siguiente se aprecia la combinación lineal de los vectores $v_1$ y $v_2$.


¿Existirán escalares $C_1$ y $C_2$ de tal manera que el vector
$$v = [2, 6]$$sea la combinación lineal de los vectores
$$v_1 = [4, 1] \quad y \quad v_2 = [-1, 2]$$ $$\begin{bmatrix} -2 \\ 6 \end{bmatrix}=C_1\begin{bmatrix} 4\\ 1 \end{bmatrix}+C_2\begin{bmatrix} -1 \\ 2 \end{bmatrix}$$Establecemos el sistema de ecuaciones:
$$\begin{cases} 4C_1 - C_2 = -2 \\ C_1 + 2C_2 = 6 \end{cases}$$La matriz ampliada y la reducción por Gauss es:
\[ \left [ \begin{array}{rrcr} 4 & -1 & \color{blue}{\vert} &-2\\ 1 & 2 & \color{blue}{\vert} &6\\ \end{array} \right] \]Reduciendo $F_2 = 4F_2 - F_1$ se obtiene:
\[ \left [ \begin{array}{rrcr} 4 & -1 & \color{blue}{\vert} &-2\\ 0 & 9 & \color{blue}{\vert} &26\\ \end{array} \right] \]Escribiendo el nuevo sistema equivalente:
$$\begin{cases} 1)&4C_1 - C_2 = -2 \\ 2)&9C_2 = 26 \end{cases}$$Despejando en $C_2$ en la ecuación (2) y reemplazando el valor obtenido en la ecuación (1) se obtiene que $C_1 = 2/9$ y que $C_2 = 26/9$.
Podemos expresar que los vectores serían combinación lineal cuando $v_1$ es multiplicado por $C_1$ y $v_2$ es multiplicado por $C_2$.

Vamos a determinar si los vectores $v_1 = [1,2,-1]$, el vector $v_2 = [0,-1,2]$ y el vector $v_3 = [1,1,-1]$ pueden ser la combinación lineal del vector descrito como $v = [-3,-7,9]$.
$$ {\color{red}a}\begin{bmatrix} \quad1 \\ \quad2 \\ -1 \end{bmatrix}+{\color{red}b}\begin{bmatrix} \quad0 \\ -1 \\ \quad2 \end{bmatrix}+{\color{red}c}\begin{bmatrix} \quad1 \\ \quad1 \\ -1 \end{bmatrix}=\begin{bmatrix} -3 \\ -7\\ \quad9 \end{bmatrix}$$En el vídeo veremos la solución a la inquietud planteada, trataremos de hallar los valores de $a$, $b$ y $c$ que permitan verificar esa combinación lineal.
Plantearemos el sistema de ecuaciones que describe la situación, además, la matriz ampliada generada:
Dos vectores en un espacio vectorial son linealmente dependientes si y sólo si uno de ellos es un múltiplo escalar del otro.
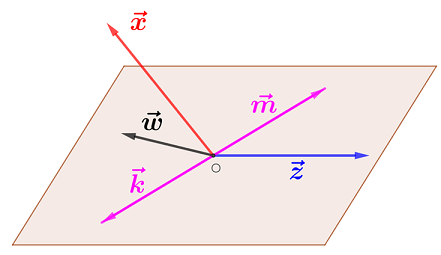
Vectores linealmente dependientes. Varios vectores libres del plano se dice que son linealmente dependientes si hay una combinación lineal de ellos que es igual al vector cero, sin que sean cero todos los coeficientes de la combinación lineal. También se cumple el reciproco: si un vector es combinación lineal de otros, entonces todos los vectores son linealmente dependientes.
Si un determinado conjunto de vectores son linealmente dependientes se dice que son vectores $LD$.
Si un determinado conjunto de vectores son linealmente independientes se dice que son vectores $LI$.
$$Sean \quad v_1, v_2, v_3 ... v_k \in ℝ$$ $$ a_1v_1+a_2v_2+ ... + a_kv_k = 0$$ $$\tag{A2} {\color{red}a_1} \begin{bmatrix} v_1 \\ v_2 \\ \end{bmatrix}+{\color{red}a_1} \begin{bmatrix} u_1 \\ u_2 \\ \end{bmatrix}+...+{\color{red}a_k} \begin{bmatrix} w_1 \\ w_2 \\ \end{bmatrix}= \begin{bmatrix} 0\\ 0\\ \end{bmatrix}$$ $${\color{red}a_1} \begin{bmatrix} v_1 \\ v_2 \\ v_3 \end{bmatrix}+{\color{red}a_2} \begin{bmatrix} u_1 \\ u_2 \\ u_3 \end{bmatrix}+...+{\color{red}a_k} \begin{bmatrix} w_1 \\ w_2 \\ w_3 \end{bmatrix}= \begin{bmatrix} 0\\ 0\\ 0 \end{bmatrix}$$Si el sistema de ecuaciones así formado indicará que los vectores son $LD$ si y solo sí presenta soluciones no triviales.
Si el sistema de ecuaciones establecido NO tiene solución diremos que los vectores son $LI$.
Un conjunto de $n$ vectores en $ℝ^m$ es linealmente independiente si $n > m$.

Vamos a determinar si $v_1 = [2,2]$ y $v_2 = [-3,4]$ son $LI$ o son $LD$.
$${\color{red}a_1} \begin{bmatrix} 2 \\ 2 \\ \end{bmatrix}+{\color{red}a_2} \begin{bmatrix} -3\\ \quad 4\\ \end{bmatrix}= \begin{bmatrix} 0\\ 0\\ \end{bmatrix}$$Ahora emplearemos el método de reducción de Gauss para la matriz ampliada:
\[ \left [ \begin{array}{rrrcr} 2 & -3 &\color{red}{\vert} &0\\ 2 & 4 &\color{red}{\vert} &0\\ \end{array} \right] F_2=F_2-F_1\left [ \begin{array}{rrrcr} 2 & -3 &\color{red}{\vert} &0\\ 0 & 7 &\color{red}{\vert} &0\\ \end{array} \right] \]Esta reducción nos expresa en $F_2$ que $7c_2 = 0$ y por lo tanto $c_2 = 0$. Reemplazando en $F_1$ nos dice que $c_2 = 0$. El resultado así obtenido es la solución trivial que determina que los vectores dados son $LI$.

Determinar la dependencia o independencia lineal de los siguientes vectores:
$$\begin{bmatrix} -2 \\ \quad 4\\ -12 \end{bmatrix}; \begin{bmatrix} 1 \\ 0\\ 2 \end{bmatrix}; \begin{bmatrix} 4\\ 1\\ 6 \end{bmatrix}$$Ahora vamos a formalizar la ecuación teórica con los escalares $a$, $b$ y $c$. A continuación nuestra sistema de ecuaciones que resolveremos por la regla de Cramer:
$${\color{red}a}\begin{bmatrix} -2 \\ \quad 4\\ -12 \end{bmatrix}+{\color{red}b} \begin{bmatrix} 1 \\ 0\\ 2 \end{bmatrix}+{\color{red}c} \begin{bmatrix} 4\\ 1\\ 6 \end{bmatrix}= \begin{bmatrix} 0 \\ 0 \\ 0 \end{bmatrix}$$ $$ \left. \begin{array}{rcr} -2a+b+4c & = & 0 \\ 4a+c & = & 0 \\ -12a+2b+6c & = & 0 \end{array} \right\} $$Aplicando Sarrus calculemos el determinante del sistema, necesario para aplicar Cramer:
Podemos concluir que si el determinante de la matriz de coeficientes es igual a $0$, el sistema no tiene solución. Por lo tanto los vectores dados son $LI$.

Determinar si los polinomios $P_1(x) = x^2 − 5x + 6$, $P_2(x) = x^2 − x$ y $P_3(x) = x − 2$ son $LI$ o son $LD$.
$$\color{red}{a} (x^2 − 5x + 6)+\color{red}{b} (^2 − x)+\color{red}{c} (x − 2)=0$$Aplicando la propiedad distributiva, agrupando términos semejantes y factorizando se tiene:
$$ax^2-5ax+6a+bx^2-bx+cx-2c=0$$ $$(ax^2+bx^2)+(-5ax-bx+cx)+(6a-2c)=0$$ $$x^2(a+b)+x(-5a-b+c)+x^0(6a-2c)=0x^2+0x^1+0x^0$$Nuestro sistema de ecuaciones:
$$\left. \begin{array}{rrcr} a+b& = & 0 \\ -5a-b+c & = & 0 \\ 6a -2c & = & 0 \end{array} \right\}$$Hallemos el determinante de la matriz de coeficientes por Sarrus, necesario para solucionar el sistema por la regla de Cramer:
$$\begin{vmatrix} \quad1&\quad1&\quad0\\ - 5&-1&\quad1\\ \quad6&\quad0&- 2 \end{vmatrix}\begin{matrix} \quad1 & \quad1 \\ - 5 & -1\\ \quad 6 & \quad 0 \end{matrix}$$ $${(1)(-1)(2)+(1)(1)(6)+(0)(-5)(0)}-$$ $${(6)(-1)(0)+(0)(1)(1)+(-2)(-5)(1)}=-2$$ $$a=\frac{\begin{vmatrix} 0&\quad1&\quad0\\ 0&-1&\quad1\\ 0&\quad0&- 2 \end{vmatrix}\begin{matrix} 0 & \quad1 \\ 0 & -1\\ 0 & \quad 0 \end{matrix}}{-2}=\frac{0}{-2}=0$$ $$b=\frac{\begin{vmatrix} \quad1&0&\quad0\\ -5&0&\quad1\\ \quad6&0&- 2 \end{vmatrix}\begin{matrix} \quad 1 & 0 \\ -5 & 0\\ \quad6 & 0 \end{matrix}}{-2}=\frac{0}{-2}=0$$ $$c=\frac{\begin{vmatrix} \quad1&\quad1&0\\ -5&-1&0\\ \quad6&\quad0&0 \end{vmatrix}\begin{matrix} \quad 1 & \quad1 \\ -5 & -1\\ \quad6 & \quad0 \end{matrix}}{-2}=\frac{0}{-2}=0$$Siendo la solución del sistema trivial podemos decir que los polinomios son $LI$.

Determinar la $LI$ o $LD$ de las matrices $A_1$; $A_2$ y $A_3$.
Establecemos la ecuación matricial y reemplazamos:
\[ {\color{red}{a}}\left[ \begin{array}{rrr} 1 & 2 & 1 \\ 0 & 1 & 1 \\ \end{array} \right]+{\color{red}{b}}\left[ \begin{array}{rrr} 0 & 1 & 1 \\ 1 & 1 & 1 \\ \end{array} \right]+{\color{red}{c}}\left[ \begin{array}{rrr} 2 & 1 & 2 \\ 1 & 0 & 2 \\ \end{array} \right]=\left[ \begin{array}{rrr} 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} \right] \] \[ \left[ \begin{array}{rrr} a & 2a & a \\ 0 & a & a \\ \end{array} \right]+\left[ \begin{array}{rrr} 0 & b & b \\ b & b & b \\ \end{array} \right]+\left[ \begin{array}{rrr} 2c & c & 2c \\ c & 0 & 2c \\ \end{array} \right]=\left[ \begin{array}{rrr} 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} \right] \]Sumando $A_1$; $A_2$ y $A_3$ y reescribiendo le ecuación matricial:
\[ \left[ \begin{array}{rrr} a+2c & 2a+b+c & a+b+2c \\ b+c & a+b & a+b+2c \\ \end{array} \right]=\left[ \begin{array}{rrr} 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} \right] \]Hemos obtenido un sistema homogéneo de seis (6) ecuaciones con las variables $a$, $b$ y $c$.
$${\color{red}{E_1}} \quad a+2c=0 \qquad {\color{red}{E_2}} \quad 2a+b+c=0$$ $${\color{red}{E_3}} \quad a+b+2c=0 \qquad {\color{red}{E_4}}\quad b+c=0$$ $${\color{red}{E_5}} \quad a+b=0 \qquad {\color{red}{E_6}}\quad a+b+2c=0$$Si de (4) despejamos $b$ y reemplazamos en (2) obtenemos que $2a = 0$, entonces $a = 0$. Si de (1) despejamos $a$ y reemplazamos en (3) que es igual a (6) obtenemos que $b = 0$, y si reemplazamos $b = 0$ en (4) obtenemos que $c = 0$. El sistema tiene una solución trivial lo que indica que $A_1$; $A_2$ y $A_3$ son $LI$.
Conjunto generador. Los vectores $v_1$, $v_2$, $...$, $v_n$ de un espacio vectorial $V$ generan a $V$ si todo vector en $V$ se puede escribir como una combinación lineal de los mismos. Para todo vector perteneciente al espacio vectorial $V$ existen escalares $α_1$, $α_2$, $...$, α_n$ tales que:
$$\tag{A2}v = α_1v_1 + α_2v_2 + ... + α_nv_n$$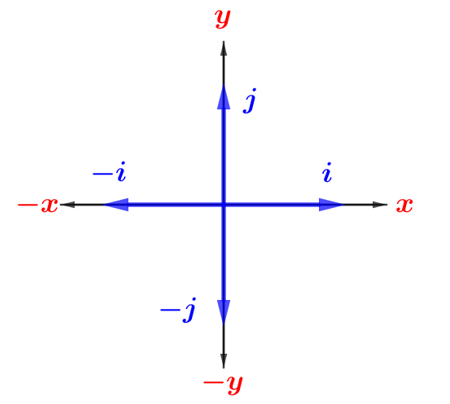

Sean $v_1$, $v_2$, $...$, $v_k$, $k$ vectores de un espacio vectorial $V$. El espacio generado por $\{v_1, v_2, ... , v_k\}$ es el conjunto de combinaciones lineales $v_1$, $v_2$, $...$, $v_k$. Teniendo presente que $α_1$, $α_2$, ... , $α_k$ son escalares arbitrarios tenemos:
Para solucionar problemas acerca del conjunto generador de un espacio vectorial se requiere conocer su rango.
El rango de una matriz coincide con el número de vectores independientes que conforman la matriz.
El $rg$ de la matriz es igual al número de filas distintas de cero en la matriz después de reducirla a la forma escalonada de la fila usando transformaciones elementales sobre las filas de la matriz.
Veamos en este ejemplo de rango de una matriz $M_{2x3}$:
\[ A=\left[ \begin{array}{rrr} -1 & 2 & 0 \\ -1 & 3 & 2 \\ \end{array} \right] F_2=F_2-F_1 \left[ \begin{array}{rrr} -1 & 2 & 0 \\ \quad 0 & 1 & 2 \\ \end{array} \right] ∴ {\color{red}{rg=2}} \]Debido a que $A$ es una matriz $2 \times 3$ y luego de la única transformación elemental realizada ninguna fila está formada por CEROS, el rango es igual al número de filas inicial.

Determinemos el rango de la matriz $A$
\[ A=\left[ \begin{array}{rrrrr} 3 & -3 & -3 & -1 & 2\\ 4 & 0 & 0 & -1 & 0\\ -3 & 3 & 3 & 1 & 2 \\ \end{array} \right] \]Realizar las transformaciones elementales donde la primera a realizar es para lograr que $a_{21}$ sea igual a CERO:
$$F_2=F_2-\frac{4}{3}F_1$$Al ser la última fila compuesta de CEROS, el rango es el número de filas diferentes a ese valor o sea que el rango es igual a $2$.
Ya definido que es el rango de una matriz retomemos el la idea de conjunto generador de un espacio vectorial.
Normalmente el conjunto generador se denota por la expresión $S = [v_1, v_2, ... , v_n]$ o también como $gen[v_1, v_2, ... , v_n]$.
Si $gen(S) = V$, entonces se dice que $V$ es generado por $[v_1, v_2, ..., v_n]$ o que $S$ genera a $V$.
Si $S = [v_1, v_2, ... , v_n]$ es un conjunto de vectores en un espacio vectorial $V$, entonces $gen(S)$ es el menor sub-espacio de $V$ que contiene a $S$; ello implica que cualquier otro sub-espacio de $V$ que contenga a $S$ debe contener a $gen(S)$.
Determinar un conjunto generador requiere que:
$$ {\color{red}{(1)}}\qquad [v_1, v_2,...,v_k]\subset R^n$$ $$ {\color{red}{(2)}}\qquad rg=[v_1, v_2,...,v_k]=n$$Si solamente tenemos un vector $v$, entonces el conjunto generado por $v$ es el conjunto de todos los vectores paralelos a $v$ o sea que tienen la forma $αv$:
$$ \tag{A6} gen(v) = {α v | α ∈ ℝ}$$De manera general podemos expresar que si $v$ es un es un vector diferente de CERO en $ℝ^n$, el conjunto generado es una recta que pasa por el origen.
Cuando se tienen dos vectores $v_1$ y $v_2$, entonces el conjunto generado por esos dos vectores tiene la forma:
$$\tag{A7} gen(v_1, v_2) = {α v1 + β v2| α, β ∈ ℝ}$$En general si se tienen dos vectores $v_1$ y $v_2$ diferentes de CERO, el conjunto generado es un plano que pasa por el origen.

Encontremos por medio de restricciones en las entradas de los vectores el conjunto generado por $v_1$ y $v_2$. Buscaremos las condiciones de un vector $v = [a,b,c]$ tal que haya solución al sistema.
$$ gen\begin{Bmatrix} v_1=\begin{bmatrix} 1 \\ 2 \\ 1 \\ \end{bmatrix}; & v_2=\begin{bmatrix} 2 \\ 0 \\ 3 \end{bmatrix} \\ \end{Bmatrix}$$ $$ \begin{bmatrix} a \\ b \\ c\\ \end{bmatrix}=c_1\begin{bmatrix} 1 \\ 2 \\ 1\\ \end{bmatrix}+c_2\begin{bmatrix} 2 \\ 0 \\ 3\\ \end{bmatrix}\Longrightarrow \begin{cases} 1)&C_1 + 2C_2 = a\\ 2)& 2C_1= b\\ 3)&C_1+3C_2=c \end{cases} $$Veamos la matriz de coeficientes y la respectiva matriz ampliada $B$:
\[ A=\left[ \begin{array}{rrr} 1 & 2 \\ 2 & 0 \\ 1 & 3 \\ \end{array} \right] \] \[A|B= \left [\begin{array}{rrrcr} 1 & 2 &\color{red}{\vert} &a\\ 2 & 0 &\color{red}{\vert} &b\\ 1 & 3 &\color{red}{\vert} &c\\ \end{array} \right] \]Ahora realizamos las transformaciones elementales de la matriz ampliada y establecemos su rango, si es diferente al rango de la matriz de coeficientes que es igual a $3$ el sistema no tendrá solución:
\[A|B= \left [\begin{array}{rrrcr} 1 & 2 &\color{red}{\vert} &a\\ 2 & 0 &\color{red}{\vert} &b\\ 1 & 3 &\color{red}{\vert} &c\\ \end{array} \right] \rightarrow F_2 = F_2-2F_1 \] \[A|B= \left [\begin{array}{rrrcr} 1 & 2 &\color{red}{\vert} & a\\ 0 & -4 &\color{red}{\vert} & -2a+b\\ 1 & 3 &\color{red}{\vert} &c\\ \end{array} \right] \rightarrow F_3 = F_3-F_1 \] \[A|B= \left [\begin{array}{rrrcr} 1 & 2 &\color{red}{\vert} &a\\ 0 & -4 &\color{red}{\vert} &-2a+b\\ 0 & 0 &\color{red}{\vert} &-6a+b+4c\\ \end{array} \right] \]Observamos que NO existe ninguna fila formado por ceros únicamente en la matriz ampliada, por lo tanto su rango es $3$, y el rango de la matriz escalonada es $2$:
$rg(A)>rg(A|B) \lor rg(A)<{rg(A|B)}$, es un sistema incompatible.
En la tercera fila encontramos una contradicción y la forma de evitarla es igualando a CERO, es una restricción. Es equivalente a decir que $0 = − 6a + b + 4c$ es la ecuación de un plano que pasa por el origen.
En la gráfica vemos ese plano que satisface el conjunto generado con restricciones:

Vamos a determinar si los vectores $v_1 = [1,1,0]$; $v_2 = [1,0,1]$ y $v_3 = [0,1,1]$ constituyen un sistema generador en $ℝ^3$.
El primer paso es establecer un vector $ℝ^3$ genérico $= [a,b,c]$.
Luego establecemos nuestra ecuación matricial, el sistema de ecuaciones generado y la respectiva matriz ampliada:
Nuestro próximo paso es obtener una matriz superior mediante la reducción de Gauss: \[ F_2=F_2-F_1 \to \left [ \begin{array}{rrrcr} 1 & 0 & 1 &\color{red}{\vert} &a\\ 0 & 1 & -1 &\color{red}{\vert} &-a+b\\ 0 & 1 & 1 &\color{red}{\vert} &c\\ \end{array} \right] \] \[ F_3=F_3-F_2 \to \left [ \begin{array}{rrrcr} 1 & 0 & 1 &\color{red}{\vert} &a\\ 0 & 1 & -1 &\color{red}{\vert} &-a+b\\ 0 & 0 & 2 &\color{red}{\vert} &a-b+c\\ \end{array} \right] \]
Lo anterior indica que el rango de la matriz ampliada es $3$, el mismo rango de la matriz de coeficientes. Nuestro nuevo sistema de ecuaciones es:
$$\begin{cases} 1)&C_1 + C_3 = a\\ 2)&C_2 - C_3 = -a+b\\ 3)&2C_3 =a-b+c \end {cases} \Longrightarrow $$Obtenemos las restricciones de las variables, las que estarán expresadas en términos de las componentes $a$, $b$ y $c$:
De la ecuación 3:
$$C_3=\frac{a-b+c}{2}$$El valor de $C_3$ en la ecuación 2:
$$C_2-\frac{a-b+c}{2}=-a+b$$ $$C_2=-a+b+\frac{a-b+c}{2}=\frac{-2a+2b+a-b+c}{2}$$ $$C_2=\frac{-a+b+c}{2}$$El valor de $C_3$ en la ecuación 1:
$$C_1+\frac{a-b+c}{2}=a$$ $$C_1=a-\frac{a-b+c}{2}=\frac{2a-a+b-c}{2}$$ $$C_1=\frac{a+b-c}{2}$$Entonces cualquier vector $[a,b,c]$ es un espacio generado por la combinación lineal expresada como:
$$\begin{bmatrix} a \\ b \\ c\\ \end{bmatrix}=\frac{a+b-c}{2}\begin{bmatrix} 1 \\ 1 \\ 0\\ \end{bmatrix}+\frac{-a+b+c}{2}\begin{bmatrix} 1 \\ 0 \\ 1\\ \end{bmatrix}+\frac{a-b+c}{2}\begin{bmatrix} 0 \\ 1 \\ 1\\ \end{bmatrix}$$
Determinar las componentes del vector $v_1 = [3,-2,-3]$ en la base $B$ generada por los vectores $v_2 = [0, 1, 1]$; $v_3 = [-1,-1, 1]$ y $v_4 = [0, -1, 1]$, es decir si son una combinación lineal que genera un espacio vectorial.
Paso 1. Verificar si es un conjunto generador de un vector genérico $[a,b,c]$, ¿existen valores para las constantes $x$, $y$ y $z$?
$$a\begin {bmatrix} 0 \\ 1 \\ 1\\ \end{bmatrix}+b\begin{bmatrix} -1 \\ -1 \\ 1\\ \end{bmatrix}+c\begin{bmatrix} 0 \\ -1 \\ 1\\ \end{bmatrix}=\begin{bmatrix} x \\ y \\ z\\ \end{bmatrix} $$ $$\begin {bmatrix} 0 \\ a \\ a\\ \end{bmatrix}+\begin{bmatrix} -b \\ -b \\ b\\ \end{bmatrix}+\begin{bmatrix} 0 \\ -c \\ c\\ \end{bmatrix}=\begin{bmatrix} x \\ y \\ z\\ \end{bmatrix}$$El sistema de ecuaciones generado y la matriz ampliada de ese sistema:
$$\begin{cases} & - b = x\\ & a - b - c = y\\ & a + b + c =z \end {cases} $$ \[ \left [ \begin{array}{rrrcr} 0 & -1 & 0 &\color{red}{\vert} &x\\ 1 & -1 & -1 &\color{red}{\vert} &y\\ 1 & 1 & 1 &\color{red}{\vert} &z\\ \end{array} \right] \]Aplicamos Gauss para determinar el valor de $x$, $y$ y $z$:
\[ \left [ \begin{array}{rrrcr} 0 & -1 & 0 &\color{red}{\vert} &x\\ 1 & -1 & -1 &\color{red}{\vert} &y\\ 1 & 1 & 1 &\color{red}{\vert} &z\\ \end{array} \right]\updownarrow \frac{F_3}{F_1} \]Ahora reemplazando $c$ en $b$ y luego $c$ y $b$ en $a$ tenemos:
$$\begin{cases} & \Large a = z - b - c\\ \\ & \Large b = \frac {y-z}{-2}- \color{blue}{\frac{2x-y+z}{2}}= \color{blue}{-x+y-z}\\ \\ & \Large c = \frac{2x-y+z}{2} \end {cases}$$ $$\begin{cases} & \Large a =\ z -(-x+y-z) - \frac{2x-y+z}{2}= \color{blue}{\frac{-y+3z}{2}}\\ \\ & \Large b = \frac {y-z}{-2}- {\frac{2x-y+z}{2}}= \large \color{blue}{-x+y-z}\\ \\ & \Large c = \color{blue}{\frac{2x-y+z}{2}} \end {cases}$$Podemos expresar entonces que:
$$\begin{bmatrix} x \\ y \\ y\\ \end{bmatrix}= \color{red}{\frac{-y+3z}{2}} \color{black} \begin{bmatrix} 0 \\ 1 \\ 1\\ \end{bmatrix}+\color{red}{(-x+y-z)} \color{black} \begin{bmatrix} -1 \\ -1 \\ \quad 1\\ \end{bmatrix}+\color{red}{\frac{2x-y+z}{2}} \color{black} \begin{bmatrix} \quad 0 \\ -1 \\ \quad 1\\ \end{bmatrix}$$Paso 2. Hallar las coordenadas del vector $v_1 = [3,-2,-3]$ en la base generada por los vectores dados.
$$\begin{bmatrix} \quad 3 \\ -2 \\ -3\\ \end{bmatrix}= \color{red}{\alpha} \color{black} \begin{bmatrix} 0 \\ 1 \\ 1\\ \end{bmatrix}+\color{red}{\beta} \color{black} \begin{bmatrix} -1 \\ -1 \\ \quad 1\\ \end{bmatrix}+\color{red}{\gamma} \color{black} \begin{bmatrix} \quad 0 \\ -1 \\ \quad 1\\ \end{bmatrix}$$ $$\begin{cases} & \large -\beta = 3 \\ & \large \alpha - \beta - \gamma = -2\\ & \large \alpha + \beta + \gamma = -3\\ \end {cases} \Longrightarrow \begin{cases} & \large \beta = -3 \\ & \large \alpha = - \frac{5}{2}\\ & \large \gamma = \frac{5}{2}\\ \end {cases} $$ $$\begin{bmatrix} \quad 3\\ -2 \\ -3\\ \end{bmatrix}= \begin{bmatrix} \color{red}{-3}\\ \\ \color{red}{\Large -\frac{5}{2}}\\ \\ \color{red}{\Large \quad \frac{5}{2}}\\ \end{bmatrix} $$Son las coordenadas del vector especificado.
Introducción. Según lo expresa el diccionario de la Real Academia Española (RAE) criptografía es una combinación de dos vocablos griegos: crypto, que significa “oculto” o “secreto”, y grapho, que significa “escritura”.
Así, la criptografía es el arte de escribir en códigos o de manera enigmática. Un sistema criptográfico de comunicación implica que exista una codificación y una decodificación que tanto el remitente como el destinatario del mensaje conozcan:
Una regla de correspondencia específica entre un conjunto de símbolos (como las letras del alfabeto y los signos de puntuación que componen los mensajes) y un conjunto de números enteros.
Una matriz $A$ no singular especificada, recordando que una matriz es singular si y sólo si su determinante es nulo.
La criptografía es la ciencia que se encarga de diseñar métodos para mantener confidencial a la información que es enviada por un medio inseguro. Casi todos los medios de comunicación son inseguros, es decir, un espía siempre puede intervenir una comunicación, y en tal caso conocer su contenido, alterar el contenido, borrar el contenido, etc.

Lester Hill en el año 1929 propuso un método que consiste en cifrar en bloque mediante el empleo de matrices y otras operaciones algebraicas, el cual surgió como respuesta a la gran vulnerabilidad que presentan los cifrados monográficos, como el cifrado afín, estos eran desencriptados con facilidad empleando técnica estadística.
Lo anterior es sólo una posibilidad, también podrían asignarse las letras en orden decreciente o comenzando por el número 3, etc.
A las letras del alfabeto se le asignan los números del 1 al 27. Al espacio en blanco se le asigna el número 0, para poder separar palabras como se ve en la siguiente tabla, la cual emplearemos para nuestro ejemplo:
Tabla 1. Asignación para encriptar nuestro ejemplo.
.png)
Cuando se habla de cifrado usando la matemática, las matrices inversas se pueden usar para proporcionar un procedimiento simple y efectivo para codificar y decodificar mensajes. Para codificar un mensaje los elementos que se requieren son: un emisor, un receptor, un mensaje y un código.
La referencia a un código, expresa un método de codificación, se refiere a un algoritmo biunívoco (una función biyectiva) que asigna a cada carácter del mensaje otro carácter. Este método hace que el mensaje enviado por el emisor se transforme en una cadena de símbolos ilegibles para el resto de los receptores que no sean legales.
Dependiendo de la calidad del método de codificación, el mensaje será más o menos difícil de descifrar si es capturado por receptores no autorizados.
Cualquier matriz cuyos elementos sean enteros positivos y sea invertible se puede usar como matriz de codificación. Si la matriz de código es de $n \times n$ se construye con el mensaje una matriz de $n$ filas y tantas columnas como sean necesarias, escribiendo los números por columna y rellenando al final con espacios en blanco si fuera necesario. Luego se multiplica a izquierda por la matriz de código y el resultado es el mensaje codificado.
Para recuperar el mensaje se multiplica la matriz anterior a izquierda por la inversa de la matriz de código. Después, el mensaje es convertido a números dividido en vectores fila sin codificar, cada uno con "$n$" elementos, teniendo en cuenta que para codificar el mensaje se elige una matriz invertible $A$, de orden $n \times n$ y las matrices renglón no codificada se multiplican por $A$, para así obtener las matrices renglón codificadas.
Ilustraremos el proceso con el mensaje:
“En el año 2007 el Instituto Tecnológico Pascual Bravo se transformó en Institución Universitaria, y fue uno de los primeros colegios públicos, así mismo, primer colegio técnico del país, con más de 80 años de existencia”
El mensaje se ha dividido en matrices de $1 \times 3$, ellas son:
\[\left[ \begin{array}{rrr} 5 & 14 & 5 \\ \end{array}\right];\left[ \begin{array}{rrr} 12 & 1 & 15 \\\end{array}\right];\left[ \begin{array}{rrr} 16 & 30 & 28 \\\end{array}\right];\left[ \begin{array}{rrr} 28 & 5 & 12 \\\end{array}\right] \] \[\left[ \begin{array}{rrr} 9 & 14 & 20 \\ \end{array}\right];\left[ \begin{array}{rrr} 21 & 9 & 21 \\\end{array}\right];\left[ \begin{array}{rrr} 22 & 21 & 16 \\\end{array}\right];\left[ \begin{array}{rrr} 21 & 5 & 3 \\\end{array}\right] \] \[\left[ \begin{array}{rrr} 14 & 16 & 12 \\ \end{array}\right];\left[ \begin{array}{rrr} 16 & 7 & 9 \\\end{array}\right];\left[ \begin{array}{rrr} 3 & 16 & 17 \\\end{array}\right];\left[ \begin{array}{rrr} 1 & 20 & 3 \\\end{array}\right] \]La matriz de codificación es la matriz inversa de la matriz $A$ que detallamos como:
\[A=\left[ \begin{array}{rrr} 1 & 3 & 3 \\ 1 & 4 & 3 \\ 4 & 3 & 4 \\ \end{array} \right] \]El mensaje que se pretende leer, ya está dividido en matrices de $1 \times 3$ y la matriz de codificación es la de la derecha, la matriz $A$, así entonces, si $X = [x_1, x_2, ..., x_n]$ es una matriz no codificada, al ser multiplicada por la matriz $A$ invertible, entonces $Y = XA$, donde $Y$ es la matriz codificada correspondiente, y la matriz para descifrar el mensaje, quien
lo recibe, es la inversa de $A$, veamos las cuatro primeras:
\[\left[ \begin{array}{rrr} 5 & 14 & 5 \\ \end{array} \right] \times \left[ \begin{array}{rrr} 1 & 3 & 3 \\ 1 & 4 & 3 \\ 4 & 3 & 4 \\ \end{array} \right]= \left[ \begin{array}{rrr} 24 & 86 & 77 \\ \end{array} \right] \] \[\left[ \begin{array}{rrr} 12 & 1 & 15 \\ \end{array} \right] \times \left[ \begin{array}{rrr} 1 & 3 & 3 \\ 1 & 4 & 3 \\ 4 & 3 & 4 \\ \end{array} \right]= \left[ \begin{array}{rrr} 18 & 55 & 59 \\ \end{array} \right] \] \[\left[ \begin{array}{rrr} 16 & 30 & 28 \\ \end{array} \right] \times \left[ \begin{array}{rrr} 1 & 3 & 3 \\ 1 & 4 & 3 \\ 4 & 3 & 4 \\ \end{array} \right]= \left[ \begin{array}{rrr} 74 & 252 & 250 \\ \end{array} \right] \] \[\left[ \begin{array}{rrr} 28 & 5 & 12 \\ \end{array} \right] \times \left[ \begin{array}{rrr} 1 & 3 & 3 \\ 1 & 4 & 3 \\ 4 & 3 & 4 \\ \end{array} \right]= \left[ \begin{array}{rrr} 45 & 140 & 147 \\ \end{array} \right] \]El lector puede verificar las demás multiplicaciones con la matriz $A$. Por lo tanto, la serie de matrices renglón cifradas es:
\[\left[ \begin{array}{rrr} 24 & 86 & 77 \\ \end{array}\right];\left[ \begin{array}{rrr} 18 & 55& 59 \\\end{array}\right];\left[ \begin{array}{rrr} 74 & 252 & 250 \\\end{array}\right] \] \[\left[ \begin{array}{rrr} 45 & 140 & 147 \\ \end{array}\right];\left[ \begin{array}{rrr} 43 & 143 & 149 \\\end{array}\right];\left[ \begin{array}{rrr} 51 & 162 & 174 \\\end{array}\right] \] \[\left[ \begin{array}{rrr} 59 & 198 & 193 \\ \end{array}\right];\left[ \begin{array}{rrr} 29 & 92 & 90 \\\end{array}\right];\left[ \begin{array}{rrr} 42 & 142 & 138 \\\end{array}\right] \] \[\left[ \begin{array}{rrr} 32 & 103 & 105 \\ \end{array}\right];\left[ \begin{array}{rrr} 36 & 124 & 125 \\\end{array}\right];\left[ \begin{array}{rrr} 24 & 92 & 75\\\end{array}\right] \] \[\left[ \begin{array}{rrr} 35 & 106 & 117 \\ \end{array}\right];\left[ \begin{array}{rrr} 22 & 85 & 67 \\\end{array}\right];\left[ \begin{array}{rrr} 59 & 193 & 197\\\end{array}\right] \]Para quienes desconozcan la matriz $A$ es difícil descifrar el mensaje, sin embargo, para un receptor autorizado que conozca la matriz $A$ descifrarlo es sencillo, simplemente se debe multiplicar por $A^{-1}$ las matrices renglón cifradas para recuperar las matrices no cifradas, por lo tanto, $Y$ (matriz codificada) al ser multiplicada por $A^{-1}$ para obtener:
$$\tag{A8} YA^{-1} = (XA)A^{-1} = X $$Así entonces, hay que obtener la matriz inversa, la que ya calculada mediante el método de Gauss Jordan es:
\[ A^{-1}=\left[ \begin{array}{rrr} 7 & -3 & -3 \\ -1 & 1 & 0 \\ -1 & 0 & 1 \\ \end{array} \right] \]Realizado este proceso, se ha obtenido la serie de matrices ya descifradas, con las que se puede leer el mensaje enviado, veamos las primeras cinco (dejamos la verificación del resto al lector):
\[\left[ \begin{array}{rrr} 24 & 86 & 77 \\ \end{array} \right] \times \left[ \begin{array}{rrr} 7 & -3 & -3 \\ -1 & 1 & 0 \\ -1 & 0 & 1 \\ \end{array} \right]= \left[ \begin{array}{rrr} 5 & 14 & 5 \\ \end{array} \right] \] \[\left[ \begin{array}{rrr} 18 & 55 & 59 \\ \end{array} \right] \times \left[ \begin{array}{rrr} 7 & -3 & -3 \\ -1 & 1 & 0 \\ -1 & 0 & 1 \\ \end{array} \right]= \left[ \begin{array}{rrr} 12 & 1 & 15 \\ \end{array} \right] \] \[\left[ \begin{array}{rrr} 74 & 252 & 250 \\ \end{array} \right] \times \left[ \begin{array}{rrr} 7 & -3 & -3 \\ -1 & 1 & 0 \\ -1 & 0 & 1 \\ \end{array} \right]= \left[ \begin{array}{rrr} 16 & 30 & 28 \\ \end{array} \right] \] \[\left[ \begin{array}{rrr} 45 & 140 & 147 \\ \end{array} \right] \times \left[ \begin{array}{rrr} 7 & -3 & -3 \\ -1 & 1 & 0 \\ -1 & 0 & 1 \\ \end{array} \right]= \left[ \begin{array}{rrr} 28 & 5 & 12 \\ \end{array} \right] \] \[\left[ \begin{array}{rrr} 43 & 143 & 149 \\ \end{array} \right] \times \left[ \begin{array}{rrr} 7 & -3 & -3 \\ -1 & 1 & 0 \\ -1 & 0 & 1 \\ \end{array} \right]= \left[ \begin{array}{rrr} 9 & 14 & 20\\ \end{array} \right] \]Las matrices que se han descifrado corresponden a las que se definieron inicialmente al obtener las matrices renglón $1 \times 3$, y así se
logra descifrar el mensaje, al remplazar cada uno de los elementos de la matriz por la letra correspondiente.
El remitente del mensaje lo codificará por medio de una matriz $A$ no singular y el destinatario del mensaje codificado lo decodificará por medio de la matriz $A^{-1}$ (única). La matriz $A$ se llama matriz de codificación y $A^{-1}$ se llama matriz de decodificación. El mensaje numérico se escribirá ahora como una matriz $M$.
La matriz de codificación $A$ y la matriz de decodificación $A^{-1}$ se elaboran de tal manera que:

Codificar el mensaje "EL JUEGO DE TRONOS"
$5 \quad 12 \quad 0 \quad 10 \quad 22 \quad 5 \quad 7 \quad 16 \quad 0 \quad 4 \quad 5 \quad 0 \quad 21 \quad 19 \quad 16 \quad 14 \quad 16 \quad 20$
Por lo tanto podemos emplear cualquiera de las matrices $3 \times 6$, $6 \times 3$, $9 \times 2$ o una matriz $2 \times 9$.
Emplearemos dos matrices $M_1$ y $M_2$ de $3 \times 3$, ello nos permitirá codificar el mensaje empleando una matriz $3 \times 3$.
\[ M_1= \left[ \begin{array}{rrr} 5 & 12 & 0 \\ 10 & 22 & 5 \\ 7 & 16 & 0 \\ \end{array} \right]; \] \[ M_2= \left[ \begin{array}{rrr} 4 & 5 & 0 \\ 2 & 19 & 16 \\ 14 & 16 & 20 \\ \end{array} \right] \]Por la regla de Sarrus tenemos:
$$|A|=[(1)(-1)(2)+(2)(-2)(-1)+(3)(0)(1)]$$$$-[(-1)(-1)(3)+(1)(-2)(1)+(2)(0)(2)]=1$$El mensaje codificado contiene las mismas 18 entradas pero algunas de ellas son números enteros negativos lo que dificulta el proceso de decodificación si no se conoce la matriz inversa.
Con la matriz $M_1$
$$M_1AA^{-1}= \left[ \begin{array}{rrr} 5 & -2 & -9 \\ 5 & 3 & -4 \\ 7 & -2 & -11 \\ \end{array} \right] \left[ \begin{array}{rrr} 0 & -1 & -1 \\ 2 & 5 & 2 \\ -1 & -3 & -1 \\ \end{array} \right] $$ $$M_1AA^{-1}=\left[ \begin{array}{rrr} 5 & 12 & 0 \\ 10 & 22 & 5 \\ 7 & 16 & 0 \\ \end{array} \right] $$Con la matriz $M_2$
$$M_2AA^{-1}= \left[ \begin{array}{rrr} 4 & 3 & 2 \\ -14 & 1 & 0 \\ -6 & 32 & 50 \\ \end{array} \right] \left[ \begin{array}{rrr} 0 & -1 & -1 \\ 2 & 5 & 2 \\ -1 & -3 & -1 \\ \end{array} \right] $$ $$M_1AA^{-1}=\left[ \begin{array}{rrr} 4 & 5 & 0 \\ 2 & 19 & 16 \\ 14 & 16 & 20 \\ \end{array} \right] $$Observamos que mediante la matriz de decodificación se obtiene el mensaje enviado:
$5 \quad 12 \quad 0 \quad 10 \quad 22 \quad 5 \quad 7 \quad 16 \quad 0 \quad 4 \quad 5 \quad 0 \quad 21 \quad 19 \quad 16 \quad 14 \quad 16 \quad 20$
E L _ J U E G O _ D E _ T R O N O S
En los dos ejemplos desarrollados se nota que no existe una regla que nos indique como se ha de dividir el mensaje de acuerdo a su correspondencia natural.
En el primero se dividieron en matrices de $3 \times 1$, en el segundo en matrices de $3 \times 3$, solo se hace necesario que cumpla las propiedades de la multiplicación de matrices.

Empleando el mismo procedimiento realizado, decodifique el mensaje dada la matriz $A$ de codificación y $B$ la matriz codificada. Son sentencias atribuidas al llamado "Hombre Universal": Leonardo Da Vinci.
Para efectos de la realización de los siguientes ejercicios propuestos se ha utilizado la tabla N° 1.
Haz clic en la imagen para obtener una vista ampliada del ejercicio propuesto.
Ejercicio 1.

Ejercicio 2.
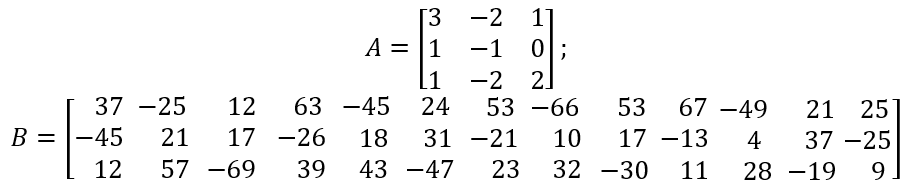
Ejercicio 3.
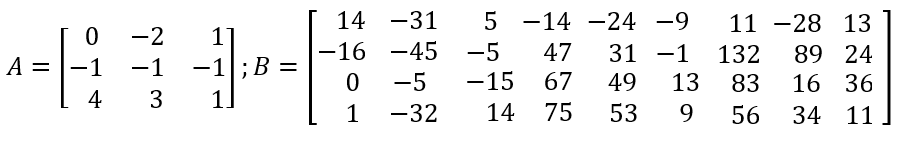
Ejercicio 4.