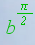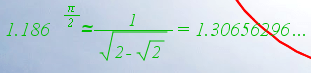LA ESPIRAL LOGARÍTMICA CORDOBESA

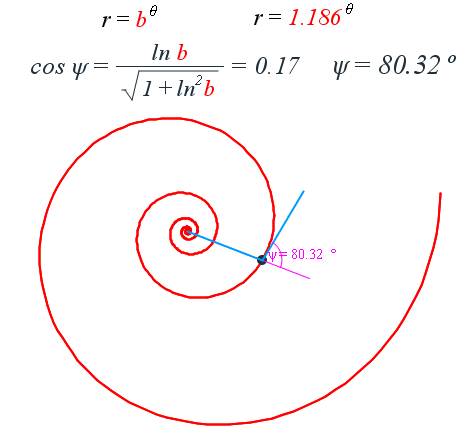
La espiral logarítmica es equiangular, es decir, el radio vector y la recta tangente en cualquier punto de la espiral forma siempre un ángulo constante. Puede consultarse nuestro recurso interactivo "La espiral logarítmica, geométrica o equiangular".

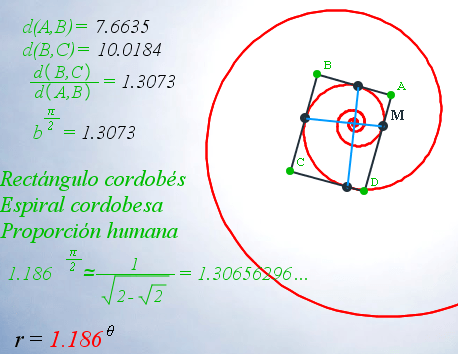
Ángulo formaddo por el radio vector y la recta tangente en un punto Rectángulo circunscrito a la espiral a partir de radios vectores que se diferencian pi/2 radianes

Gracias a ser equiangular, si se consideran cuatro puntos cualesquiera de la espiral en los que su ángulo polar difiera en pi/2 radianes, se puede construir un rectángulo que circunscribe a la espiral y cuyo módulo o razón entre sus lados es:

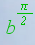
Cuando en particular b es aproximadamente igual a 1.186, el módulo anterior se corresponde con el número denominado cordobés y con la denominada proporción cordobesa o humana. De ahi que a ese rectángulo se le denomine rectángulo cordobés.

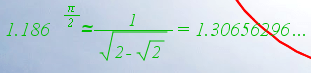
Y por ello, a la espiral logarítmica correspondiente a ese valor de b, a ese rectángulo circunscrito, la denominamos espiral logarítmica cordobesa.

EL CRECIMIENTO GNOMÓNICO DISCRETO

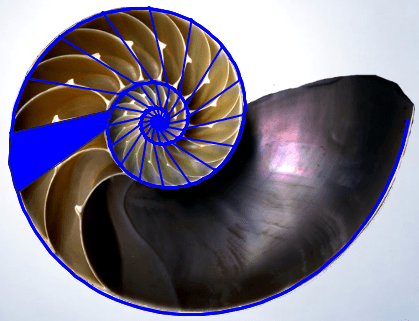
En la siguiente imagen puede observarse el gnomon aristotélico --figura que al añadirla a otra conduce a una semejante-- correspondiente a un crecimiento gnomónico discreto de paso 2pi/16 --dieciséis son las cámaras de flotación en cada una de las vueltas--. Éste se construye en base a dos radios vectores que se diferencian en un ángulo de 2pi/16 y las tangentes  respectivas en cada uno de esos puntos.

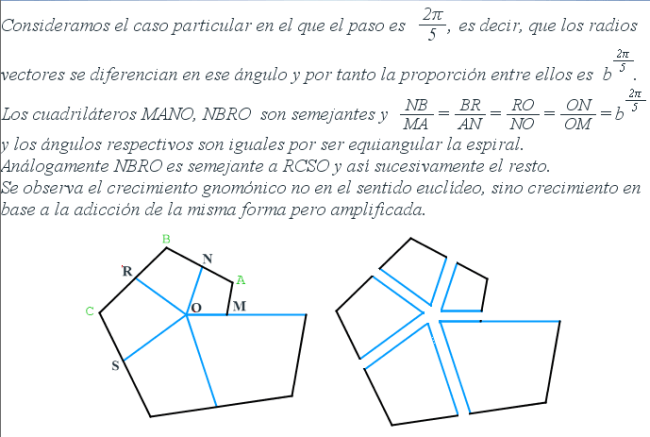
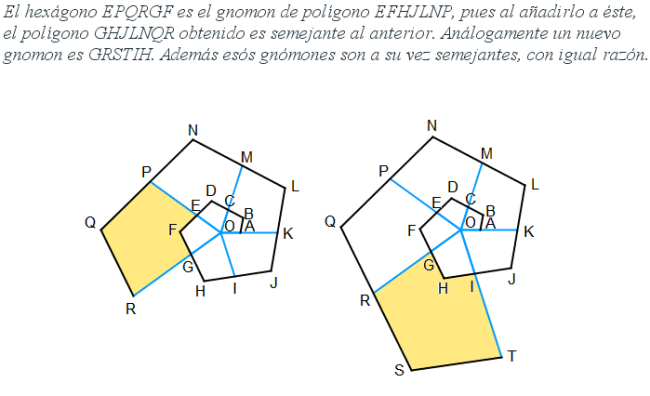
En las dos imágenes siguientes podemos observar el crecimiento gnomónico discreto para el caso particular de paso 2pi/5 y la demostración de que efectivamente es un gnomon. Se ha considerado este paso concreto como ejemplo, porque permite observar mejor las figuras, pero análoga situación acontece al considerar cualquier otro.

Cuando se considera más de una vuelta esos cuadriláteros se superponen y consecuentemente el gnomon realmente es hexagonal.