Matemáticas de secundaria:
Grados 8 - 9
INTERACTIVO

Carlos Alberto Rojas Hincapié
Red Educativa Digital Descartes, Colombia
1ª edición – 2022
Córdoba (España)
2022
Título de la obra
Matemáticas de secundaria:
Grados 8 - 9
Autor
Carlos Alberto Rojas Hincapié
Primera edición: 2022
Código JavaScript para el libro: Joel Espinosa Longi, IMATE, UNAM.
Recursos interactivos: DescartesJS
Fuentes: Lato y UbuntuMono
Fórmulas matemáticas: $\KaTeX$

Diseño de personajes:
Orlando Antonio Martinez Hoyos
Red Educativa Digital Descartes
Córdoba (España)
descartes@proyectodescartes.org
https://proyectodescartes.org
Proyecto iCartesiLibri
https://proyectodescartes.org/iCartesiLibri/index.htm
https://prometeo.matem.unam.mx/recursos/VariosNiveles/iCartesiLibri/
ISBN: 978-84-18834-49-3
Esta obra está bajo una licencia Creative Commons 4.0 internacional: Reconocimiento-No Comercial-Compartir Igual.
Tabla de contenido
Este libro digital interactivo se ha diseñado con fundamento en la filosofía del Proyecto DescartesJS: "Trabajando altruistamente por la comunidad educativa de la aldea global", que sólo busca desarrollar contenidos educativos para el provecho de la comunidad académica, esperando únicamente como retribución el uso y difusión de estos contenidos. El contenido del libro, al igual que los objetos interactivos se han diseñado de tal forma que se puedan leer en ordenadores y dispositivos móviles sin necesidad de instalar ningún programa o plugin. El libro se puede descargar para su uso en local sin dependencia con la red, a excepción de algunos vídeos incluidos en el texto. Todos los objetos interactivos se han diseñado con el Editor DescartesJS.
Véase https://proyectodescartes.org/iCartesiLibri/descripcion.htm.
El contenido de este libro se basa en un curso de capacitación del editor DescartesJS para docentes que, por la dificultad de concertar un horario presencial, permite una opción autodidacta acompañada de material interactivo para una mayor comprensión de los temas tratados.
Retomando la introducción a la documentación de DescartesJS de Radillo, Abreu y Espinosa, podríamos coincidir en que este libro está destinado tanto a personas que no han usado DescartesJS como a personas que tienen cierta experiencia y desean mejorarla. En cada apartado del libro se proponen ejercicios y se incluyen ejemplos para que el lector pueda comprender paso a paso la funcionalidad de DescartesJS y su enorme potencial para crear objetos interactivos de aprendizaje.
El Estado colombiano, decidido a elevar la calidad de la educación, introdujo el enfoque basado en el desarrollo de competencias en los estudiantes, lo cual supone el tránsito desde el aprendizaje que centra la atención en el dominio de contenidos, a una educación basada en competencias que no se agota en el sistema educativo, sino que se desarrolla de manera permanente en interacción con el mundo.
De esta manera, consolidar una política de calidad enmarcada en el desarrollo de competencias implica, entonces, una transformación de fondo de las prácticas pedagógicas, del funcionamiento de la institución educativa y del papel de los actores educativos, teniendo como protagonista al estudiante. Buscando desarrollar este modelo se han realizado esfuerzos por elevar la calidad de la educación en el país; en este sentido, el Ministerio de Educación Nacional (MEN) ha puesto a disposición de docentes, directivos docentes, padres de familia y público en general herramientas pedagógicas como:
Herramientas que constituyen el punto de partida y sustento de todas las estrategias de mejoramiento, además son un importante insumo para el diseño curricular y el cambio en las prácticas pedagógicas
Elementos que contribuyen a mejorar los procesos de evaluación por competencias y las prácticas en el aula de clase por parte de los docentes para alcanzar cada vez mejores resultados y hacer que la educación en Colombia mejore su calidad. Ampliar imagen
5 categorías conceptuales que conforman esta asignatura según los Lineamientos y los Estándares Básicos de Competencia diseñados por el Ministerio de Educación Nacional, los cuales son:
1. Pensamiento numérico y sistemas numéricos.
Se asocia con "la organización de actividades centradas en la comprensión del uso y de los significados de los números y de la numeración; el desarrollo de diferentes técnicas de cálculo y estimación".
2. Pensamiento espacial y sistemas geométricos.
Contempla las actuaciones del sujeto en todas sus dimensiones y relaciones espaciales para interactuar de diversas maneras con los objetos situados en el espacio, hacer acercamientos conceptuales que favorezcan la creación y manipulación de nuevas representaciones mentales.
3. Pensamiento métrico y sistemas de medidas.
Hace referencia a la comprensión general que tiene una persona sobre las magnitudes y las cantidades, su medición y el uso flexible de los sistemas métricos o de medidas en diferentes situaciones.
4. El pensamiento variacional y sistemas algebraicos y analíticos.
Comprensión y uso de los conceptos y procedimientos de las funciones y sus sistemas analíticos, para el aprendizaje con sentido del cálculo numérico y algebraico.
5. Pensamiento aleatorio y sistemas de datos.
El pensamiento aleatorio se apoya directamente en conceptos y procesos de la teoría de probabilidades y de la estadística inferencial, e indirectamente, en la estadística descriptiva y en la combinatoria.
Competencias específicas del área de matemáticas.
Son las encargadas de desarrollar la capacidad de formular, resolver y modelar fenómenos de la realidad; comunicar, razonar, comparar y ejercitar procedimientos para fortalecer la adquisición de conocimientos, habilidades, actitudes y comprensiones del pensamiento matemático, relacionándolos entre si para facilitar el desempeño flexible, eficaz y con sentido. Las competencias específicas en el área de matemáticas que evalúa la prueba Saber desde los grados 1° a 9° se reagrupan en las siguientes:
La capacidad del estudiante para expresar ideas, interpretar, usar diferentes tipos de representación, describir relaciones matemáticas, describir situaciones o problemas usando el lenguaje escrito, concreto, pictórico, gráfico y algebraico, manipular expresiones que contengan símbolos y fórmulas, utilizar variables y describir cadenas de argumentos orales y escritas, traducir, interpretar y distinguir entre diferentes tipos de representaciones, interpretar lenguaje formal y simbólico así como traducir de lenguaje natural al simbólico formal y viceversa, que se resume en decodificar de manera entendible aquello expresado matemáticamente en palabras sencillas y manejables.
Es la capacidad para formular problemas a partir de situaciones dentro y fuera de las matemáticas, desarrollar, aplicar diferentes estrategias y justificar la elección de métodos e instrumentos para la solución de problemas, justificar la pertinencia de un cálculo exacto o aproximado
en la solución de un problema y lo razonable o no de una respuesta obtenida, verificar e interpretar resultados a la luz del problema original y generalizar soluciones y estrategias para dar solución a nuevas situaciones problema.
Está relacionada con la capacidad para dar cuenta del cómo y del porqué de los caminos que se siguen para llegar a conclusiones, justificar estrategias y procedimientos puestos en acción en el tratamiento de situaciones problema, formular hipótesis, proponer opiniones e ideas, explorar ejemplos y contraejemplos, probar y estructurar argumentos, generalizar propiedades y relaciones, identificar patrones y expresarlos matemáticamente y plantear preguntas, reconocer distintos tipos de razonamiento y distinguir y evaluar cadenas de argumentos.
Tomado Saber 3° Guía de orientación(2017).
¿Qué son los Derechos Básicos de Aprendizajes (DBA)?
Los DBA, en su conjunto, explicitan los aprendizajes estructurantes para un grado y un área particular. Se entienden los aprendizajes como la conjunción de unos conocimientos, habilidades y actitudes que otorgan un contexto cultural e histórico a quien aprende.
Los DBA se organizan guardando coherencia con los Lineamientos Curriculares y los Estándares Básicos de Competencias (EBC). Su importancia radica en que plantean elementos para construir rutas de enseñanza que promueven la consecución de aprendizajes año a año para que, como resultado de un proceso, los estudiantes alcancen los EBC propuestos por cada grupo de grados.
DERECHOS BÁSICOS DE APRENDIZAJE (DBA)
DBA.1. Reconoce la existencia de los números irracionales como números no racionales y los describe de acuerdo con sus características y propiedades.
DBA.2. Construye representaciones, argumentos y ejemplos de propiedades de los números racionales y no racionales.
DBA.3. Reconoce los diferentes usos y significados de las operaciones (convencionales y no convencionales) y del signo igual (relación de equivalencia e igualdad condicionada) y los utiliza para argumentar equivalencias entre expresiones algebraicas y resolver sistemas de ecuaciones..

DESEMPEÑOS / ESTÁNDAR
Pensamiento numérico.
1.1 M.IV Utilizo números reales en sus diferentes representaciones y en diversos contextos. DBA 1, 2.
1.2 M.IV Resuelvo problemas y simplifico cálculos usando propiedades y relaciones de los números reales y de las relaciones y operaciones entre ellos. DBA 3.
1.3 M.IV Utilizo la notación científica para representar medidas de cantidades de diferentes magnitudes. DBA 2.
El desarrollo de estos Estándares Básicos de Competencia permitirá fortalecer los procesos de formulación, modelación y resolución de problemas.
Capitulo I. Conceptos preliminares $\qquad$
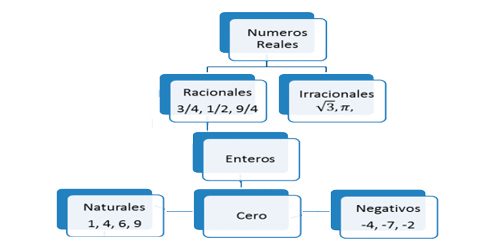
El sistema de los números Reales ($\mathbb{R}$) lo conforman los conjuntos:
N = { 1, 2, 3, 4, 5, 6, 7,.......}
Se denomina el conjunto de los números Naturales o enteros positivos, están definidas las operaciones básicas: adición y multiplicación. El conjunto de los números Naturales surgió de la necesidad de contar, lo cual se manifiesta en el ser humano desde sus inicios, este conjunto se caracteriza porque tiene un número ilimitado de elementos.
Z = { .... –3, -2, -1, 0, 1, 2, 3,...}
El Conjunto de los números Enteros surge de la necesidad de dar solución general a la sustracción (resta), pues cuando el sustraendo es mayor que el minuendo, esta sustracción no tiene solución en los números Naturales (por ejemplo: 5 – 20 = ¿?). Debido a esto, la recta numérica se extiende hacia la izquierda, de modo que a cada punto que representa un número Natural le corresponda un punto simétrico, situado a la izquierda del cero; Punto simétrico es aquel que está ubicado a igual distancia del cero (uno a la derecha y el otro a la izquierda de él), se dividen en:
Un número Racional es un número que puede expresarse de la forma:
$$\frac{a}{b}=\frac{Numerador}{Denominador}, \quad con \quad b \equiv\not 0 $$
Este conjunto se creó debido a las limitaciones de cálculo que se presentaban los números Naturales y números Enteros, para solucionar esta dificultad, se creó este conjunto, podemos identificar dos tipos de fracciones:
Una fracción propia es una fracción donde el valor del numerador es más pequeño que el valor del denominador.
 xploremos.
xploremos.
Ejemplos de fracciones propias representadas en la recta numérica, oprime el botón otro ejemplo para ver más fracciones.
Capitulo I. Conceptos preliminares $\qquad$
Se representa gráficamente, dividiendo cada intervalo de una recta numérica en espacios iguales, que representen números enteros.
Q = {....- ¾, - ½, - ¼ , 0, ¼ , ½, ¾,.....}

Una fracción impropia es una fracción donde el valor del numerador es más grande que el valor del denominador, veamos algunos ejemplos de fracciones impropias en la recta numérica.
 xploremos.
xploremos.
Ejemplos de fracciones impropias representadas en la recta numérica, oprime el botón otro ejemplo
para ver más fracciones.

Ingresa el numerador y denominador, oprime la tecla "enter <┘", el botón solución y observa la gráfica de la fracción.
Una fracción impropia, se puede representar como un  ¡Número Mixto!, estos, se componen por un número entero y una fracción propia, por ejemplo:
¡Número Mixto!, estos, se componen por un número entero y una fracción propia, por ejemplo:
$$\displaystyle\textrm{\Huge 3}\dfrac{1}{5}=\frac{(3)(5)+1}{5}=\frac{16}{5}$$
¿Sabes como se convierte un fracción impropia a un número mixto?
Capitulo I. Conceptos preliminares $\qquad$
Cada una de estas subdivisiones representa una fracción con denominador igual al número de partes de la subdivisión. Cada fracción es un número racional y cada número racional consta de infinitas fracciones equivalentes.
Conjunto de Números Decimales Infinitos no Periódicos. Este conjunto surgió de la necesidad de reunir a ciertos números que no pertenecen a los conjuntos anteriores; entre ellos se pueden citar a las raíces inexactas, el número Pi, etc. A él pertenecen todos los números decimales infinitos puros, es decir aquellos números que no pueden transformarse en una fracción.
No deben confundirse con los números racionales, porque éstos son números decimales finitos, infinitos periódicos e infinitos semiperiódicos que sí pueden transformarse en una fracción.
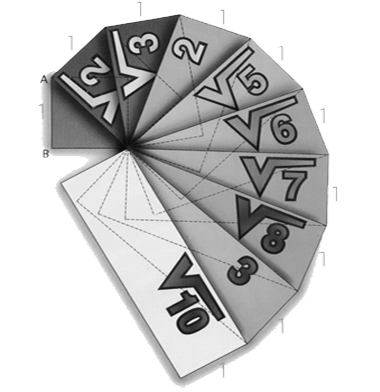
Un número Irracional no se puede expresar como una fracción o el cociente de dos números, algunos ejemplos:
$$ \pi\approx 3,14159265358979323846…$$ $$ e\approx 2,718281828459045235360…$$
Las raíces inexactas representan números Irracionales.
$$\sqrt{2}\approx 1,41421356237309504880...$$
El conjunto de los números Reales ($\mathbb{R}$) está conformado por la unión de los números Racionales ($\mathbb{Q}$) y los números Irracionales ($\mathbb{Q^*}$).
$$\color{blue} \mathbb{R} = \mathbb{Q} \cup \mathbb{Q^*}$$
Los números Racionales ($\mathbb{Q}$) incluye a los números Naturales ($\mathbb{N}$) y los números Enteros ($\mathbb{Z}$) y el cero (0).
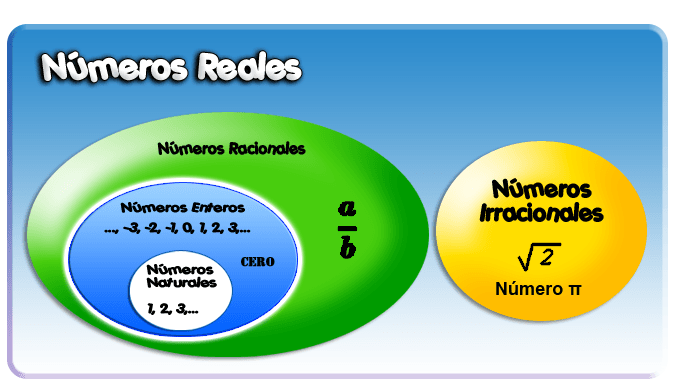
La figura representa la gráfica del conjunto de los números Reales, teniendo en cuenta esto, se puede representar gráficamente el conjunto de los números Reales en una recta numérica, en la que cada punto representa un número.
Capitulo I. Conceptos preliminares $\qquad$
Representaciones numéricas de los conjuntos.
$\mathbb{N} = \left\lbrace 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12,...\right\rbrace$
$\mathbb{Z} = \left\lbrace ... -6, -5, -4, -3, -2, -1\right\rbrace \cup \left\lbrace 0 \right\rbrace \cup \left\lbrace 1, 2, 3, 4, 5, 6,...\right\rbrace$
$\displaystyle \mathbb{Q} = \left\lbrace ...-3, -\frac{5}{2}, -2, -\frac{3}{2}, -1,-\frac{3}{4}, -\frac{1}{2}, 0, \frac{1}{2}, \frac{3}{4}, 1, -\frac{3}{2}, 2, \frac{5}{2},...\right\rbrace$
Los números Racionales es un número que se expresa de la forma:
$$\frac{a}{b} , \quad con \quad b \equiv\not 0$$
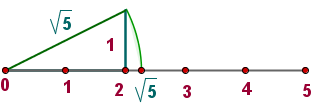
En otras palabras, se representa como el cociente de dos números, donde a y b son números enteros. (Recordemos que la división por cero no existe), un número Irracional ($\mathbb{Q^*}$) no se puede expresar como una fracción o el cociente de dos números.
Su característica principal es que al expresarlos en forma decimal, su parte decimal no termina ni se repiten, es un decimal infinito (es decir, con infinitas cifras), son decimales no periódicos.
$$\sqrt{5}\approx 2,236067976...$$
Expresando informalmente, como en muchos ámbitos de la educación, los números decimales son aquellos que poseen una parte decimal, en contraposición a los números enteros, que carecen de esta, es decir, un número decimal $\textit{\textbf{x}}$ se puede representar como:
$$ x = a,dddddd....$$ donde $\textit{\textbf{a}}$ es un número entero o cero y $\textit{\textbf{d}}$ dígitos decimales, por ejemplo:
$$\space\space \frac{1}{6} \approx 1,6666666666666...$$
Dada la definición anterior, observa el siguiente esquema:
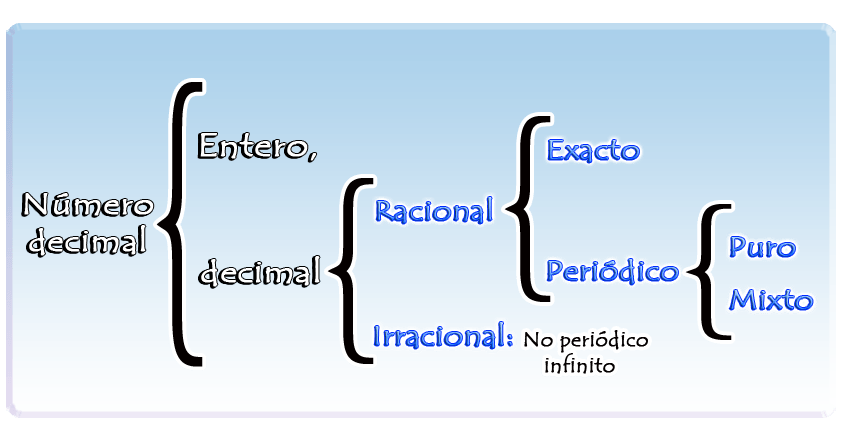
Un número decimal que tiene en su parte decimal dígitos que se repiten infinitamente, se conocen como un decimal periódico.
Capitulo I. Conceptos preliminares $\qquad$
La parte que se repite se llama periodo, y se puede representar mediante una barra en la parte que se repite, por ejemplo:
$$ \frac{1}{6} \approx 1,6666666666666... = 1,\bar{6}$$
Teniendo en cuenta el esquema de la figura 1.3 , una fracción se puede representar como un número decimal que puede ser:
 Video. Observa y complementa la información dada.
Video. Observa y complementa la información dada.
Si se tiene un número decimal exacto, periódico puro o periódico mixto, se puede encontrar la fracción que lo representa, esta fracción se conoce como fracción generatriz.
Capitulo I. Conceptos preliminares $\qquad$

 Video. Observa y complementa la información dada.
Video. Observa y complementa la información dada.
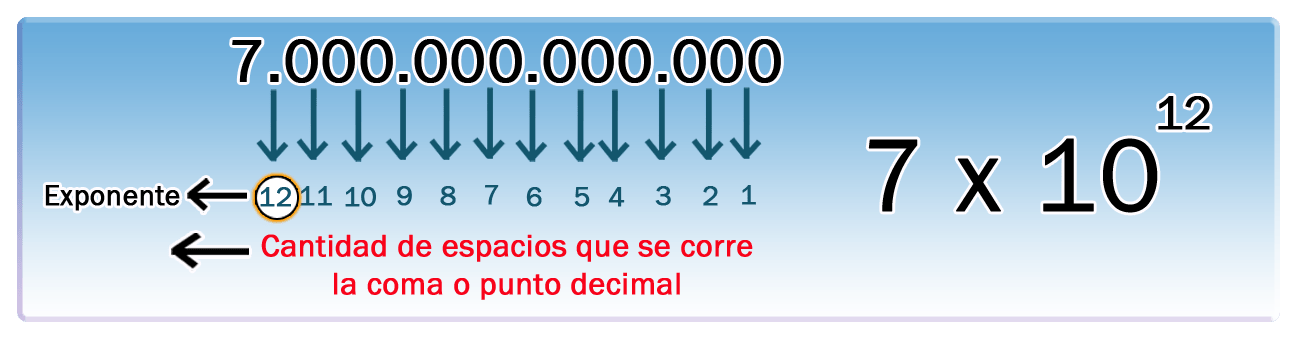
La representación de un número en notación científica es una forma de escribir números demasiado grandes o demasiado pequeños utilizando potencias de 10.

Entre las partes que componen un número representado en notación científica (figura 1.4) tenemos:

Potencia de $10 (+)$. Siempre que movemos la coma decimal hacia la izquierda. ( ← )
Potencia de $10 (-)$. Siempre que movemos la coma decimal hacia la derecha. ( → ).
Capitulo I. Conceptos preliminares $\qquad$
En el sistema decimal, cualquier número $\mathbb{R}$ puede expresarse en notación científica, veamos la representación del siguiente número:
 xploremos.
xploremos.
Notación científica.
 Escribe un número en notación científica y oprime el botón expresar para ver en forma decimal.
Escribe un número en notación científica y oprime el botón expresar para ver en forma decimal.
Para sumar o restar números en notación científica, éstos deben tener el mismo exponente en la potencia de 10.
Una vez todos los números tienen el mismo exponente, tan sólo hay que sumar y restar los números que multiplican a la potencia de base 10, sacando factor común a la potencia de 10.

= 5,5 x 1018 + 3 x 1018
= 1018 . ( 5,5 + 3 ) $\quad {\displaystyle \longrightarrow } \quad$ Factor común.
= 8,8 x 1018 $\quad {\displaystyle \longrightarrow } \quad$ Suma números decimales.
Para multiplicar o dividir números en notación científica, hay que tener en cuenta las propiedades de las potencias.
= ( 3,2 x 3 ) x 1025 - 18 $\quad {\displaystyle \longrightarrow } \quad$ Propiedades de potencias.
= 9,6 x 107 $\quad {\displaystyle \longrightarrow } \quad$ Multiplicación números decimales.
Se pueden presentar expresiones combinadas entre operaciones.
Capitulo I. Conceptos preliminares $\qquad$
 jercicio 1. Clasificación de los números.
jercicio 1. Clasificación de los números.
Arrastrar los números a cada recuadro según su conjunto numérico, ubicarlo en el conjunto más pequeño al que pertenezcan.
Indicación. Arrastrar el número al recuadro que corresponda, según el primer conjunto al que pertenece.

¡Recuerda! , todos los conjuntos numéricos pueden ser representados en la recta numérica.
 Proyecto Descartes.org.
Proyecto Descartes.org.
 jercicio 2. Identifica el conjunto numérico.
jercicio 2. Identifica el conjunto numérico.
$\mathbb{N}$ (Naturales), $\mathbb{Z}$ (Enteros), $\mathbb{Q}$ (Racional), $\mathbb{Q*}$ (Irracional) o $\mathbb{R}$ (Reales).
Oprime el botón correspondiente al conjunto numérico al cual pertenece el número dado y verifica tu respuesta.
Capitulo I. Conceptos preliminares $\qquad$
 jercicio 3.
jercicio 3.
Práctica resolviendo los siguientes ejercicios con números reales en operaciones básicas, realiza paso a paso su debido procedimiento.

 Actividad complementaria.
Actividad complementaria.
$\space$ Descargar para imprimir
 Evaluamos lo aprendido.
Evaluamos lo aprendido.
Prepárate para la evaluación y mide tus conocimientos de lo aprendido en este capítulo, responde las preguntas a continuación:
 Evaluación - 5x2 preguntas con límite de tiempo - (20 minutos)
Evaluación - 5x2 preguntas con límite de tiempo - (20 minutos)
Clic en el link, responde y envía los resultados por e-mail.

 $\quad$ Envía tu evaluación
$\quad$ Envía tu evaluación
$\space$ Evaluación: Capítulo I
Tomada de la Red Educativa Digital Descartes.
"Las matemáticas son la puerta y la llave a la ciencia".
Roger Bacon
DERECHOS BÁSICOS DE APRENDIZAJE (DBA)
DBA.2. Construye representaciones, argumentos y ejemplos de propiedades de los números racionales y no racionales.
DBA.3. Reconoce los diferentes usos y significados de las operaciones (convencionales y no convencionales) y del signo igual (relación de equivalencia e igualdad condicionada) y los utiliza para argumentar equivalencias entre expresiones algebraicas y resolver sistemas de ecuaciones..

DESEMPEÑOS / ESTÁNDAR
Pensamiento numérico.
1.2 M.IV Resuelvo problemas y simplifico cálculos usando propiedades y relaciones de los números reales y de las relaciones y operaciones entre ellos. DBA 3.
1.4 M.IV Identifico y utilizo la potenciación, la radicación y la logaritmación para representar situaciones matemáticas y no matemáticas y para resolver problemas. DBA 3.
El desarrollo de estos Estándares Básicos de Competencia permitirá fortalecer los procesos de formulación, modelación y resolución de problemas.
Capitulo II. Potenciación, Radicación y Logaritmación $\qquad$
En la nomenclatura de la potenciación se diferencian tres partes, la base, el exponente y la potencia.

Una potencia es el resultado de multiplicar un número por sí mismo varias veces. El número que multiplicamos se llama base, el número de veces que multiplicamos la base se llama exponente.


Capitulo II. Potenciación, Radicación y Logaritmación $\qquad$
Las propiedades de la potenciación son válidas para todos los conjuntos numéricos.

$a^0=1$
 xploremos
xploremos
Verifica lo aprendido en esta sección, oprime las fechas y sigue paso a paso como aplicar la propiedad de potencia de una potencia.

( ae1 )e2 = a (e1 . e2)
Capitulo II. Potenciación, Radicación y Logaritmación $\qquad$

Indicaciones.
 Para iniciar, haz click en el botón
ejercicio
, soluciona el ejercicio propuesto,
ingresa los resultados en el campo indicado, el exponente, la base y pulsa la tecla "enter <┘", verifica tu respuesta oprime el botón
solución
.
Para iniciar, haz click en el botón
ejercicio
, soluciona el ejercicio propuesto,
ingresa los resultados en el campo indicado, el exponente, la base y pulsa la tecla "enter <┘", verifica tu respuesta oprime el botón
solución
.
 Las expresiones radicales son expresiones que incluyen un radical, el cual es el símbolo de calcular una raíz.
Las expresiones radicales son expresiones que incluyen un radical, el cual es el símbolo de calcular una raíz.
En la nomenclatura de la radicación se tienen las siguientes partes:

Capitulo II. Potenciación, Radicación y Logaritmación $\qquad$

$$(\sqrt[3]{x^2})^4 = (x^\frac{2}{3})^4 = x^\frac{8}{3} = \sqrt[3]{x^8}$$ $$(\sqrt[3]{x^2})^4 = \sqrt[3]{x^8}$$
Para operar sumas o restas de expresiones radicales, deben tener el mismo índice y el mismo radicando, o sea radicandos semejantes.
Simplificar expresiones radicales.
Para simplificar expresiones radicales con diferente índice, buscamos términos exponenciales dentro del radical, aplicamos la descomposición en factores primos y las reglas de los exponentes.
Se debe llevar a un índice común (m.c.m.) y se expresa en una sola raíz, simplificando la expresión si es posible, como por ejemplo:
$$\frac{\sqrt[3]{4}}{\sqrt{2}}=\frac{\sqrt[3x2]{4^2}}{\sqrt[2x3]{2^3}}=\frac{\sqrt[6]{4^2}}{\sqrt[6]{2^3}}=\sqrt[6]{\frac{4^2}{2^3}}=$$ $${\left(\frac{2^4}{2^3}\right)}^{\frac16}={\left( 2 \right)}^{\frac16}=\sqrt[6]{2}$$
$$\frac{\sqrt[n]{x}}{\sqrt[n]{y}}=\sqrt[n]{\frac{x}{y}}$$
Capitulo II. Potenciación, Radicación y Logaritmación $\qquad$


Indicaciones
Practica lo aprendido en esta sección, resuelve los 10 ejercicios propuestos.

Capitulo II. Potenciación, Radicación y Logaritmación $\qquad$
La racionalización consiste en eliminar los radicales del denominador.
Una expresión es considerada simplificada solo si no tiene signos de radical en el denominador. Si tenemos un radical en el denominador, tenemos que racionalizar dicho denominador.
Para racionalizar un denominador, se puede presentar:
En este caso, se logra multiplicando tanto el numerador como el denominador por el mismo radical que tiene el denominador.
$$\frac{2}{\sqrt{5}}=\frac{2}{\sqrt{5}}.\frac{\color{blue}\sqrt{5}}{\color{blue}\sqrt{5}}=\frac{2 \sqrt{5}}{(\sqrt{5})^2}= \frac{2 \sqrt{5}}{5}$$
Para este caso, multiplicamos tanto el numerador como el denominador por el mismo radical que tiene el denominador elevado a la diferencia entre el índice de la raíz y su exponente.
 $$\frac{3}{6\sqrt[5]{3}}=\frac{3}{6\sqrt[5]{3}}.\frac{\color{blue}\sqrt[5]{3^{5-1}}}{\color{blue}\sqrt[5]{3^{5-1}}}=\frac{3}{6\sqrt[5]{3}}.\frac{\color{blue}\sqrt[5]{3^{4}}}{\color{blue}\sqrt[5]{3^{4}}}=$$ $$=\frac{3\sqrt[5]{3^{4}}}{6\sqrt[5]{3}\sqrt[5]{3^{4}}}=\frac{3\sqrt[5]{3^{4}}}{6\sqrt[5]{3^{5}}}=\frac{\cancel{3}\sqrt[5]{3^{4}}}{6.\cancel{3}}=\frac{\sqrt[5]{3^{4}}}{6}$$
$$\frac{3}{6\sqrt[5]{3}}=\frac{3}{6\sqrt[5]{3}}.\frac{\color{blue}\sqrt[5]{3^{5-1}}}{\color{blue}\sqrt[5]{3^{5-1}}}=\frac{3}{6\sqrt[5]{3}}.\frac{\color{blue}\sqrt[5]{3^{4}}}{\color{blue}\sqrt[5]{3^{4}}}=$$ $$=\frac{3\sqrt[5]{3^{4}}}{6\sqrt[5]{3}\sqrt[5]{3^{4}}}=\frac{3\sqrt[5]{3^{4}}}{6\sqrt[5]{3^{5}}}=\frac{\cancel{3}\sqrt[5]{3^{4}}}{6.\cancel{3}}=\frac{\sqrt[5]{3^{4}}}{6}$$
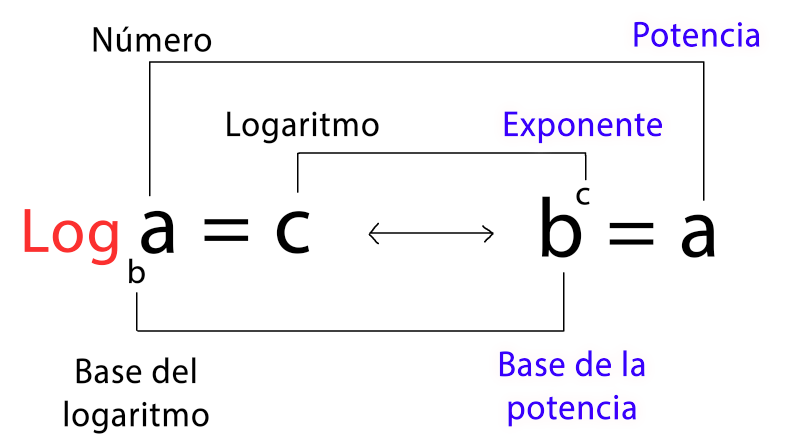
El logaritmo es el exponente de una potencia con cierta base, el logaritmo de un número debe ser positivo, es decir, el número y la base de un logaritmo corresponde a números $\mathbb{R}$ (números positivos).
El logaritmo de $a$ en base $b$ es otra forma de expresar la potenciación con $b>0$ y $a$ un número $\mathbb{R}$ positivo, se denota como:

Capitulo II. Potenciación, Radicación y Logaritmación $\qquad$
Propiedades de los logaritmos.
Si $m$ y $n$ son números positivos y $a$ es un número $\mathbb{R}$, entonces:

$$\log_5 (25)=\log_5(5^2)=2\cdot\log_5(5)=2\cdot(1)=2$$
$$\log_4{(2)} + log_4{(32)}$$
Solución.
$$\log_4{(2)} + \log_4{(32)} = \log_4{(2.32)} = \log_4 {(64)} $$
$$\log_4{(4^3)} = 3\cdot \log_4{(4)} = 3\cdot(1) = 3$$
 jercicio 1.
jercicio 1.
Resuelve y simplifica aplicando las propiedades de potenciación.

 Actividad complementaria.
Actividad complementaria.
$\space$ Descargar para imprimir
Capitulo II. Potenciación, Radicación y Logaritmación $\qquad$
 jercicio 2.
jercicio 2.
Resuelve los ejercicios propuesto a continuación.
 Indicaciones
Indicaciones
Resuelve y simplifica aplicando las propiedades de potenciación.

 Evaluamos lo aprendido.
Evaluamos lo aprendido.
Prepárate para la evaluación y mide tus conocimientos de lo aprendido en este capítulo, responde las preguntas a continuación:
 Evaluación - 12 preguntas con límite de tiempo - (12 minutos)
Evaluación - 12 preguntas con límite de tiempo - (12 minutos)
Clic en el link, responde y envía los resultados por e-mail.

 $\quad$ Envía tu evaluación
$\quad$ Envía tu evaluación
$\space$ Evaluación: Capítulo II
Plantillas con Descartes-JS
"La vida es buena por sólo dos cosas, descubrir
y enseñar las matemáticas".
Simeon Poisson
DERECHOS BÁSICOS DE APRENDIZAJE (DBA)
DBA.1. Reconoce la existencia de los números irracionales como números no racionales y los describe de acuerdo con sus características y propiedades.
DBA.2. Construye representaciones, argumentos y ejemplos de propiedades de los números racionales y no racionales.
DBA.3. Reconoce los diferentes usos y significados de las operaciones (convencionales y no convencionales) y del signo igual (relación de equivalencia e igualdad condicionada) y los utiliza para argumentar equivalencias entre expresiones algebraicas y resolver sistemas de ecuaciones..
DBA.8. Identifica y analiza relaciones entre propiedades de las gráficas y propiedades de expresiones algebraicas y relaciona la variación y covariación con los comportamientos gráficos, numéricos y características de las expresiones algebraicas en situaciones de modelación.
DBA.9. Propone, compara y usa procedimientos inductivos y lenguaje algebraico para formular y poner a prueba conjeturas en diversas situaciones o contextos.

DESEMPEÑOS / ESTÁNDAR
Pensamiento numérico
1.1 M.IV Utilizo números reales en sus diferentes representaciones y en diversos contextos. DBA 1, 2.
Pensamiento variacional y sistemas algebraicos y analíticos
5.2 M.IV Construyo expresiones algebraicas equivalentes a una expresión algebraica dada. DBA 3, 9.
5.3 M.IV Uso procesos inductivos y lenguaje algebraico para formular y poner a prueba conjeturas. DBA 8.
Capitulo III. Expresiones algebraicas $\qquad$
Definiciones preliminares
1. Expresión algebraica:
Combinación de números, letras, signos de agrupación, con operaciones indicadas, por ejemplo:
2. Términos en una expresión algebraica:
Se llama término en una expresión algebraica, a cada parte de ella que viene a ser separada por el signo mas $( + )$ ó el signo menos $( - )$. Los términos están formados por números y letras o expresiones combinadas multiplicadas entre sí (llamados factores).

3. Términos semejantes:
Aquéllas expresiones que poseen una misma parte, bien sea literal (letras) o radical (raíces), por ejemplo:

 xploremos.
xploremos.
Ingresa los valores de $x, y, z$ y evalúa la expresión propuesta.
Capitulo III. Expresiones algebraicas $\qquad$
 xploremos
xploremos
Observa las siguientes expresiones algebraicas, pulsa los controles para desplazarse por las diferentes frases y observa la escritura matemáticas de la expresión algebraica.
Escena de Consolación Ruiz Gil con licencia CC by-nc-sa
Cuándo un término en apariencia no presenta coeficiente numérico, como en la expresión algebraica "$b \space – \space 4c$" en donde $b$ es el término que en apariencia no presenta coeficiente numérico, se asume la unidad como su coeficiente numérico, donde, el término $b = 1b$.
 xploremos.
xploremos.
Identifica los términos de una expresiones algebraicas.

Indicaciones. Sigue las instrucciones que se muestran en cada pantalla, oprime las flechas para avanzar o retroceder a otra escena.

 Proyecto Descartes.org.
Proyecto Descartes.org.
Modalidad en el sistema Educativo de México.
Capitulo III. Expresiones algebraicas $\qquad$
Para simplificar monomios que se suman o restan, estos deben contener términos semejantes, los coeficientes de cada monomio que tienen la misma parte literal se suman o restan, y se deja igual la parte literal, por ejemplo, simplifiquemos la expresión algebraica
$$\quad 20x^2y + 12x^2y - 3x^2y$$
Término semejante (llamaremos factor común) $\quad {\displaystyle \longrightarrow } \quad x^2y$.
Operación con los coeficientes $\quad {\displaystyle \longrightarrow } \quad 20+12-3=29 $.
$$20x^2y + 12x^2y - 3x^2y = 29x^2y$$ 


 Actividad complementaria.
Actividad complementaria.
$\space$ Descargar para imprimir
Capitulo III. Expresiones algebraicas $\qquad$
¿Que es un polinomios?
Son expresión algebraica con características especiales, así por ejemplo un polinomio en la variable $x$, es una expresión de la forma:
P(x) = an xn + an-1xn-1 + an-2xn-2 + … + a1x + a0
El grado de un polinomio $P(x)$ es el mayor exponente al que se encuentra elevada la variable $x$.
Elementos de un polinomio:

Veamos el proceso para sumar dos polinomios, sean $P_1(x)$, $P_2(x)$:
$$P_1(x) = x^3 + 2x^2 – 5x + 7$$ $$P_2(x) = 4x^3 – 5x^2 + 3$$
$P_1 + P_2 = ( x^3 + 2x^2 – 5x + 7 ) + ( 4x^3 – 5x^2 + 3 )$
$P_1 + P_2 = x^3 + 2x^2 – 5x + 7 + 4x^3 – 5x^2 + 3$
Si a un signo de agrupación (paréntesis, llaves, corchetes) lo antecede un signo mas (+), al eliminar el signo de agrupación, todos los términos que haya dentro de él quedarán con los mismos signos, pero si al signo de agrupación lo antecede un signo menos (-), o sea en la resta, al eliminar el signo de agrupación todos los términos dentro de éste cambian de signo.
Capitulo III. Expresiones algebraicas $\qquad$
$P_1 + P_2 =( x^3 + 4x^3 ) + ( 2x^2 – 5x^2 ) – 5x + ( 7 + 3 )$
Por lo tanto, el resultado de la suma de $P_1 + P_2$ es:
$P_1 + P_2 = 5x^3 - 3x^2 – 5x + 10$
 xploremos.
xploremos.
Dados los polinomios $P_1(x)$, $P_2(x)$ de grado 3, observa la suma entre ellos, oprime el botón otro ejemplo
para ver diferentes polinomios.

 xploremos.
xploremos.
Polinomios - suma y resta de expresiones algebraicas.
Verifica los conocimientos de lo visto en esta sección, explora la siguiente escena interactiva.
Indicaciones.
Sigue las instrucciones que se muestran en cada pantalla, oprime las flechas para avanzar o retroceder a otra escena.

 Proyecto Descartes.org.
Proyecto Descartes.org.
Modalidad en el sistema Educativo de México.
Capitulo III. Expresiones algebraicas $\qquad$
|
|
|
|---|---|
|
$( - ) \cdot ( - ) = ( + )$ |
$( - ) \cdot ( + ) = ( - )$ |
$$ b^m b^n = b^{m+n}$$
Para multiplicar polinomios entre sí, se aplica la propiedad distributiva, multiplicando cada término del primer polinomio por todo el segundo polinomio, ejemplo:
$(3x + 4) \cdot (5x – 7) = 3x \cdot(5x – 7) + 4 \cdot (5x – 7)$
Se aplica propiedad distributiva.
$= [ (3x) \cdot (5x) – 7 \cdot (3x) ] + [ 4 \cdot (5x) – (4) \cdot (7) ] $

$$ b^m b^n = b^{m+n}$$
Suma de términos semejantes.
$= 15x^2 – 21x + 20x – 28 $
por tanto, el producto de los polinomios es:
$(3x + 4) \cdot(5x – 7) = 15x^2 – x – 28$
Se debe tener en cuenta la ley de signos entre los términos a multiplicar, donde los positivos son aquéllos términos que los antecede un signo mas ( + ) ó aquéllos términos que en apariencia no poseen signo que los anteceda; y los negativos son aquéllos términos que los antecede un signo menos ( - ).
Capitulo III. Expresiones algebraicas $\qquad$
 xploremos.
xploremos.
Binomios - multiplicación y división de expresiones algebraicas.
Verifica los conocimientos de lo visto en esta sección, explora la siguiente escena interactiva.
Indicaciones.
Sigue las instrucciones que se muestran en cada pantalla, oprime las flechas para avanzar o retroceder a otra escena.

 Proyecto Descartes.org.
Proyecto Descartes.org.
Modalidad en el sistema Educativo de México.
Productos que tienen su base en la potenciación de polinomios.
1. Cuadrado de la suma de dos términos
Corresponde al cuadrado del primer término, mas el doble producto del primer término por el segundo término, mas el cuadrado del segundo término, veamos como se genera:
$(a + b)^2 = (a + b) . (a + b) \quad {\displaystyle \longrightarrow } \quad$ Definición de potencia
(a + b)2 = a2 + 2ab + b2
$(2m + 3)^2 = (2m)^2 + 2 . (2m) . (3) + (3)^2 = 4m^2 + 12m + 9$
2. Cuadrado de la diferencia de dos términos
Corresponde al cuadrado del primer término, menos el doble producto del primer término por el segundo término, mas el cuadrado del segundo término, veamos como se genera:
$(a - b)^2 = (a - b) . (a - b) \quad {\displaystyle \longrightarrow } \quad$ Definición de potencia
(a - b)2 = a2 - 2ab + b2
$(y - 5x)^2 = (y)^2 - 2 . (y) . (5x) + (5x)^2 = y^2 - 10xy + 25x^2$
Capitulo III. Expresiones algebraicas $\qquad$
Si se tienen tres o más términos elevados al cuadrado, se agrupan de tal forma que formen un binomio y se aplica la misma definición:
(a + b + c)2 = [( a + b ) + c]2
(a + b + c)2 = a2 + b2 +c 2+ 2ab + 2ac + 2b
 xploremos.
xploremos.
Aplicación de productos notables. 
Escribe los valores de los coeficientes, los exponentes, pulsa "enter <┘" y observa el resultado cuando tiene diferentes exponentes dentro de los términos del binomio.
Observa la descomposición al modificar los valores de los coeficientes $a$ y $b$, los exponentes $n$ y $m$ para obtener el binomio $(ax^n + by^m )^2$.
 xploremos.
xploremos.
Productos notables y factorización.
Verifica los conocimientos de lo visto en esta sección, explora la siguiente escena interactiva.
Indicaciones.
Sigue las instrucciones que se muestran en cada pantalla, oprime las flechas para avanzar o retroceder a otra escena.

 Proyecto Descartes.org.
Proyecto Descartes.org.
Modalidad en el sistema Educativo de México.
Capitulo III. Expresiones algebraicas $\qquad$
3. Potencias de binomios
Los binomios se desarrollan de la siguiente forma:
(a + b)0 = 1
(a + b)1 = a + b
(a + b)2 = a2 + 2ab + b2
(a + b)3 = a3 + 3a2b + 3ab2 + b3
(a + b)4 = a4 + 4a3b + 6a2b2 + 4ab3 + b4
Detallando el desarrollo de los binomios se tiene que:
Triángulo de Pascal.

Los términos simétricos tienen los mismos coeficientes, la simetría de los términos permite disponer los coeficientes de cada binomio en forma de un triángulo como se muestra a continuación:

Con el triángulo de Pascal, se deduce:
$(m)^5 – 5(m)^4(2n) + 10(m)^3(2n)^2 – 10(m)^2(2n)^3+ 5(m)(2n)^4 – (2n)^5$
$(m – 2n)^5 = m^5 – 10m^4n + 40m^3n^2 – 80m^2n^3 + 80mn^4 – 32n^5$
Capitulo III. Expresiones algebraicas $\qquad$
1. División de monomios
Para dividir dos monomios:
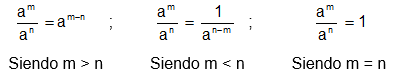
Sólo se pueden dividir monomios con la misma parte literal y con el grado del dividendo mayor o igual que el grado de la variable (letra) correspondiente del divisor.

En la división de los coeficientes de cada monomios también se aplica la ley o regla de los signos, ya que la división algebraica de monomios consiste en una operación aritmética.

Simplifique la siguiente expresión algebraica que contienen división entre monomios.
Indicaciones. 
Capitulo III. Expresiones algebraicas $\qquad$
2. División de un polinomio por un monomio
Para dividir un polinomio por un monomio, se divide cada término del polinomio por el monomio, teniendo en cuenta la ley de signos y las propiedades de la potencia de bases iguales.
3. División de un polinomio por otro polinomio
Tengamos en cuenta los siguientes pasos:
Para hacer la división, se dividen los monomios de mayor grado, luego, se multiplican cambiando de signo, y se suman, este proceso se repite hasta obtener un resto de grado menor que el del divisor.
El grado del cociente es la resta del grado del dividendo y del divisor; cuando el resto es cero, el divisor divide exactamente al dividendo. Observemos por medio de la escena la división de polinomios:
Escena de Consolación Ruiz Gil con licencia CC by-nc-sa
Capitulo III. Expresiones algebraicas $\qquad$
 División de polinomios con los coeficientes.
División de polinomios con los coeficientes.
Se escriben los coeficientes del dividendo y del divisor, se dividen los primeros coeficientes, se multiplica el resultado por el divisor del último coeficiente y se resta al dividendo.
 xploremos.
xploremos.
Observa los tres niveles de la escena:
Escena de Consolación Ruiz Gil con licencia CC by-nc-sa
 jercicio 1.
jercicio 1.
Simplifique la siguiente expresión algebraica que contienen operaciones de sumas, restas, productos, cocientes o potencias. 
Indicaciones.
Capitulo III. Expresiones algebraicas $\qquad$
 jercicio 2.
jercicio 2.
Mide tus conocimientos en la siguiente actividad interactiva.
Ten cuidado al soltar el objeto, es posible que quede debajo de otro, si esto ocurre, aparecerá un cuadrado de color verde. 
 Proyecto Descartes.org.
Proyecto Descartes.org.
 Evaluamos lo aprendido.
Evaluamos lo aprendido.
Prepárate para la evaluación y mide tus conocimientos de lo aprendido en este capítulo, responde las preguntas a continuación:
 Evaluación - 10 preguntas con límite de tiempo - (10 minutos)
Evaluación - 10 preguntas con límite de tiempo - (10 minutos)
Clic en el link, responde y envía los resultados por e-mail.

 $\quad$ Envía tu evaluación
$\quad$ Envía tu evaluación
$\space$ Evaluación: Capítulo III
Tomada de la Red Educativa Digital Descartes.
"Las matemáticas consisten en demostrar
las cosas más obvias de la forma menos obvia".
George Polye
DERECHOS BÁSICOS DE APRENDIZAJE (DBA)
DBA.3. Reconoce los diferentes usos y significados de las operaciones (convencionales y no convencionales) y del signo igual (relación de equivalencia e igualdad condicionada) y los utiliza para argumentar equivalencias entre expresiones algebraicas y resolver sistemas de ecuaciones..
DBA.5. Utiliza teoremas, propiedades y relaciones geométricas (teorema de Tales y el teorema de Pitágoras) para proponer y justificar estrategias de medición y cálculo de longitudes.
DBA.9. Propone, compara y usa procedimientos inductivos y lenguaje algebraico para formular y poner a prueba conjeturas en diversas situaciones o contextos.

DESEMPEÑOS / ESTÁNDAR
Pensamiento espacial
2.4 M.IV Uso representaciones geométricas para resolver y formular problemas en las matemáticas y en otras disciplinas. DBA 5.
Pensamiento variacional y sistemas algebraicos y analíticos
5.2 M.IV Construyo expresiones algebraicas equivalentes a una expresión algebraica dada. DBA 3, 9.
El desarrollo de estos Estándares Básicos de Competencia permitirá fortalecer los procesos de formulación, modelación y resolución de problemas.
Capitulo IV. Factorización $\qquad$
 Factorizar un polinomio es expresarlo como el producto de otros polinomios que tengan menor grado que éste. Casos de factorización:
Factorizar un polinomio es expresarlo como el producto de otros polinomios que tengan menor grado que éste. Casos de factorización:
Hace referencia al término común de un polinomio, pueden ser factores numéricos o factores literales. Para encontrar el factor común, se realiza lo siguiente:
Encontrar el factor común para el polinomio: $3m^3 – 6m^2n$
Factor común numérico: $\quad {\displaystyle \longrightarrow } \quad MCD (3,6) = 3$
Factor común literal: $\quad {\displaystyle \longrightarrow } \quad m^2$
por tanto, el factor común del polinomio es : $\quad 3m^3 – 6m^2n = 3m^2$
 xploremos.
xploremos.
Veamos por medio de un paso a paso como hallar el factor común de un polinomio, pulsa en botón para cada paso y sigue las instrucciones.
Capitulo IV. Factorización $\qquad$
Una vez encontrado el factor común a los términos del polinomio, se procede a encontrar los términos que quedan al sacar el factor común, dividiendo cada término del polinomio por este factor, quedando en ésta forma factorizado completamente el polinomio.
Se caracteriza por ser una diferencia (resta) entre dos términos que poseen raíz cuadrada exacta.
 Expresar la raíz cuadrada de cada termino.
Expresar la raíz cuadrada de cada termino.
$$9a^2 – b^2$$
Raíz cuadrada del primer término $\quad {\displaystyle \longrightarrow } \quad 3a$
Raíz cuadrada del segundo término $\quad {\displaystyle \longrightarrow } \quad b$
Una diferencia de cuadrados se factoriza como la suma de las raíces cuadradas, multiplicada por la diferencia de las mismas, simbólicamente se tiene:
a2 – b2 = ( a + b )( a – b )
Factorizar: $\quad 25p^2-4q^2$
$\sqrt{25p^2}\qquad \sqrt{4p^2}\quad$
$\quad 5p \qquad \qquad 2q \quad {\displaystyle \longrightarrow } \quad $ Raíz cuadrada de cada termino
Por tanto, $\quad 25p^2-4q^2=(5p-2q)(5p+2q)$

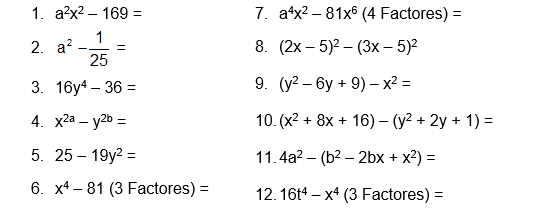
Capitulo IV. Factorización $\qquad$
 xploremos.
xploremos.
Productos notables y factorización.
Verifica los conocimientos de lo visto en esta sección, explora la siguiente escena interactiva.
Indicaciones.
Sigue los pasos para la demostración gráfica.

 Proyecto Descartes.org.
Proyecto Descartes.org.
Modalidad en el sistema Educativo de México.
El trinomio de la forma $x^2 + bx + c$, siempre que $x^2 + bx + c=0$ tenga solución, equivale al producto de dos binomios o factores, estos trinomios se factorizan de la siguiente forma:
x2 + bx + c = ( x + p )( x + q )
Donde el primer término de cada binomio, es la raíz cuadrada del primer término del trinomio "$x$" y los segundos términos de cada binomio son los números $p$ y $q$, donde
La suma $\quad {\displaystyle \longrightarrow } \quad p + q = b$
El producto $\quad {\displaystyle \longrightarrow } \quad p\cdot q = c$

$x^2 + 8x + 15 = ( x + 3 )( x + 5 ) \quad $ entonces, $$\sqrt{x^2}=x, \qquad 8=3+5, \qquad 15=(3).(5)$$
Capitulo IV. Factorización $\qquad$

Ingresa los coeficientes $p, q$, pulsa la tecla "enter <┘", cambia los signos de cada factor con el botón + o - y oprime el botón verificar
Se puede presentar el trinomio con la forma: $\quad$x2n + bxn + c
Se factoriza de igual manera, donde,
$\begin{cases} b = (-3 + 2) = -1 \\ c = (-3)(2) = -6 \end{cases}$ $\quad {\displaystyle \longrightarrow } \quad x^4 – x^2 – 6 = ( x^2 - 3 )( x^2 + 2 )$
Estos trinomios se factorizan de la siguiente forma:
Se caracterizan por ser muy parecidas a la forma $x^{2n} + bx^n + c$, con la diferencia de que la variable $x^{2n}$ ya tiene un coeficiente "$a$" diferente de cero y uno.

$2x^2 + 7x – 15$, $\quad 3x^2 + 17x + 10,$ $\quad 5x^2 – 17x + 6$
Simbólicamente se tiene que:
$ax^{2n} + bx^n + c \quad \to \quad$ trinomio dado,
$\displaystyle \frac{a(x^{2n} + bx^n + c)}{a} \quad \to \quad$ multiplicamos y dividimos por $a$,
$\displaystyle \frac{ax^{2n} + (a)bx^n + a.c}{a} \quad \to \quad$ aplicamos propiedad distributiva,
El primer termino de cada binomio será: $\quad ( ax^n + p )( ax^n + q )$
por tanto, $\quad (ax^n)^2 + b(ax^n) + ac = ( ax^n + p )( ax^n + q )$,
donde $\quad \sqrt{(ax^n)^2}=ax^n, \qquad b=p+q, \qquad a\cdot c=p \cdot q$
Capitulo IV. Factorización $\qquad$
Multiplicamos y dividimos por $3 \quad {\displaystyle \longrightarrow } \quad \frac33 \cdot (x^{2} + 17x + 10)$
Aplicamos propiedad distributiva $\quad {\displaystyle \longrightarrow } \quad \displaystyle \frac{3x^{2} + 17(3x) + 30}{3}$
$\begin{cases} 17=15+2 \\ 30=(15)(2) \end{cases} \quad {\displaystyle \longrightarrow } \quad \displaystyle \frac{(3x+15)(3x+2)}{3} = \frac{3(x+5)(3x+2)}{3}$
$\qquad \qquad \qquad \space \space \quad {\displaystyle \longrightarrow } \quad 3x^2 + 17x + 10=(x+5)(3x+2)$

Ingresa los coeficientes $c_1, c_2, p, q$, pulsa la tecla "enter <┘", cambia los signos de cada factor con el botón + o - y oprime el botón verificar
 xploremos.
xploremos.
Productos notables y factorización.
Verifica los conocimientos de lo visto en esta sección, explora la siguiente escena interactiva.
Indicaciones.
Utilizar la piezas dadas para formar un rectángulo del área dada.

 Proyecto Descartes.org.
Proyecto Descartes.org.
Modalidad en el sistema Educativo de México.
Capitulo IV. Factorización $\qquad$
Se trata de suma entre dos términos cuya característica es que pueden expresarse como cantidades que se pueden elevar al cubo, por lo tanto cada término posee raíz cúbica exacta.
a3 + b3 = (a + b)(a2 - ab + b2)
Para factorizar una suma de cubos, se tiene en cuenta lo siguiente:
Se tiene que: $\quad x^3 + 27 = x^3 + 3^3$
Raíz cúbica del primer término $\quad {\displaystyle \longrightarrow } \quad x$
Raíz cúbica del segundo término $\quad {\displaystyle \longrightarrow } \quad 3$
$\begin{cases}\sqrt[3]{y^3}=y \\ \sqrt[3]{64x^3}=4x \end{cases},\quad$ donde $\quad (y + 4x)(y^2 - 4xy + 16y^2)$
Se trata de resta entre dos términos cuya característica es que pueden expresarse como cantidades que se pueden elevar al cubo, por lo tanto cada término posee raíz cúbica exacta.
a3 - b3 = (a - b)(a2 + ab + b2)
Para factorizar una diferencia de cubos, se tiene en cuenta lo siguiente:
Raíz cúbica del primer término $\quad {\displaystyle \longrightarrow } \quad p$
Raíz cúbica del segundo término $\quad {\displaystyle \longrightarrow } \quad 2k$
$\begin{cases}\sqrt[3]{y^3}=y \\ \sqrt[3]{64x^3}=4x \end{cases},\quad$ donde $\quad (y - 4x)(y^2 + 4xy + 16y^2)$
Capitulo IV. Factorización $\qquad$
Ahora, veamos algunos ejemplos de la factorización de suma y diferencia de cubos.
Algunos polinomios no se pueden factorizar directamente, mediante la aplicación de los casos vistos hasta ahora, sino que es necesario agrupar adecuadamente los términos antes de factorizar
 jercicio 1.
jercicio 1.
Factorizar los polinomios si se posible.

 Actividad complementaria.
Actividad complementaria.
$\space$ Descargar para imprimir
Capitulo IV. Factorización $\qquad$
 jercicio 2.
jercicio 2.
Mide tus conocimientos de lo aprendido en esta sección y resuelve la actividad interactiva siguiente.
Indicaciones
Factorizar diferencia de cuadrados.
Arrastrar las imágenes al recuadro en el orden que se realiza la factorización, ten presente que no queden imágenes montadas.

 Proyecto Descartes.org.
Proyecto Descartes.org.
 Evaluamos lo aprendido
Evaluamos lo aprendido
Prepárate para la evaluación y mide tus conocimientos de lo aprendido en este capítulo, responde las preguntas a continuación:
 Evaluación - 10 preguntas con límite de tiempo -
Evaluación - 10 preguntas con límite de tiempo -
Clic en el link, responde y envía los resultados por e-mail.

 $\quad$ Envía tu evaluación
$\quad$ Envía tu evaluación
$\space$ Evaluación: Capítulo IV
Tomada de la Red Educativa Digital Descartes.
"Ninguna investigación humana puede ser llamada verdadera
ciencia si no puede ser demostrada matemáticamente".
Leonardo da Vinci
DERECHOS BÁSICOS DE APRENDIZAJE (DBA)
DBA.3. Reconoce los diferentes usos y significados de las operaciones (convencionales y no convencionales) y del signo igual (relación de equivalencia e igualdad condicionada) y los utiliza para argumentar equivalencias entre expresiones algebraicas y resolver sistemas de ecuaciones..
DBA.8. Identifica y analiza relaciones entre propiedades de las gráficas y propiedades de expresiones algebraicas y relaciona la variación y covariación con los comportamientos gráficos, numéricos y características de las expresiones algebraicas en situaciones de modelación.
DBA.9. Propone, compara y usa procedimientos inductivos y lenguaje algebraico para formular y poner a prueba conjeturas en diversas situaciones o contextos.

DESEMPEÑOS / ESTÁNDAR
Pensamiento variacional y sistemas algebraicos y analíticos
5.2 M.IV Construyo expresiones algebraicas equivalentes a una expresión algebraica dada. DBA 3, 9.
5.3 M.IV Uso procesos inductivos y lenguaje algebraico para formular y poner a prueba conjeturas. DBA 8.
El desarrollo de estos Estándares Básicos de Competencia permitirá fortalecer los procesos de formulación, modelación y resolución de problemas.
Capitulo V. Operaciones Algebraicas $\qquad$

Una fracción aritmética está simplificada cuando el único factor común al numerador y al denominador es el número "$1$".
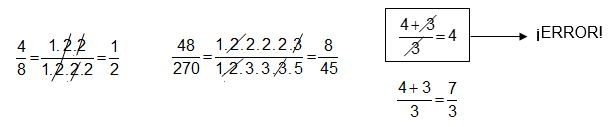
Para simplificar, cancelamos los factores comunes al numerador y al denominador.
Cuándo el denominador de una fracción es cero "$0$" se dice que la fracción no existe o no está definida.
Al igual que las fracciones aritméticas, decimos que una fracción algebraica está simplificada, cuando el único factor común al numerador y al denominador es el número "$1$", es decir, cuando el numerador y el denominador sean primos entre sí.
Para simplificar fracciones algebraicas procedemos de la forma:
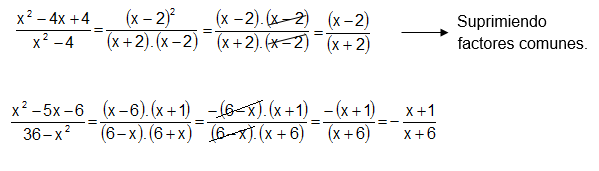
 En ocasiones, se requiere cambiar el orden de los términos de uno o varios factores, como en el ejemplo 2, el orden del factor $(x – 6)$, por eso se le antecedió con un signo menos antes del paréntesis y se cambió el orden de los términos dentro del paréntesis, quedando $-(6 - x)$.
En ocasiones, se requiere cambiar el orden de los términos de uno o varios factores, como en el ejemplo 2, el orden del factor $(x – 6)$, por eso se le antecedió con un signo menos antes del paréntesis y se cambió el orden de los términos dentro del paréntesis, quedando $-(6 - x)$.Capitulo V. Operaciones Algebraicas $\qquad$

Escena de Consolación Ruiz Gil con licencia CC by-nc-sa
Para sumar o restar fracciones racionales hacemos lo siguiente:

Simplificar $\quad\displaystyle x+3+\frac{6}{x-5}$
Expresamos el término $(x+3)$ como un fracción, se coloca de denominador un "$1$", y se opera con la otra fracción:
$\quad\displaystyle \frac{x+3}{1}+\frac{6}{x-5}= \frac{(x+3)(x-5) + 6}{x-5}=$
Aplicamos propiedad distributiva y se agrupan los términos semejantes, se verifica si es posible simplificar la expresión final obtenida.
$\quad\displaystyle \frac{x^2+3x-5x-15+6}{x-5}=\frac{x^2-2x-9}{x-5}$
Capitulo V. Operaciones Algebraicas $\qquad$

Para multiplicar fracciones racionales hacemos lo siguiente:



Resuelva el ejercicio propuesto, oprima el botón solución , verifique el procedimiento, para un nuevo ejercicio, oprima el botón ejercicio y repita los pasos.
Capitulo V. Operaciones Algebraicas $\qquad$
Para dividir fracciones racionales hacemos lo siguiente:
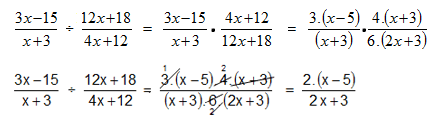
 ¡Recuerda!
, en la división de fracciones, se multiplica en cruz o multiplicamos por el inverso multiplicativo de la 2° fracción:
¡Recuerda!
, en la división de fracciones, se multiplica en cruz o multiplicamos por el inverso multiplicativo de la 2° fracción:

Resuelva el ejercicio propuesto, oprima el botón solución para verificar el procedimiento, para un nuevo ejercicio, oprima el botón ejercicio y repita los pasos.

Capitulo V. Operaciones Algebraicas $\qquad$
 jercicio 1.
jercicio 1.
Simplifica las expresiones racionales dadas que contienen sumas, restas, productos o divisiones.

Indicaciones.
 jercicio 2.
jercicio 2. 
Simplifica las expresiones racionales dadas que contienen diferentes operaciones básicas como: sumas, restas, productos o divisiones.
1. Simplifica las expresiones racionales con contienen sumas y restas.
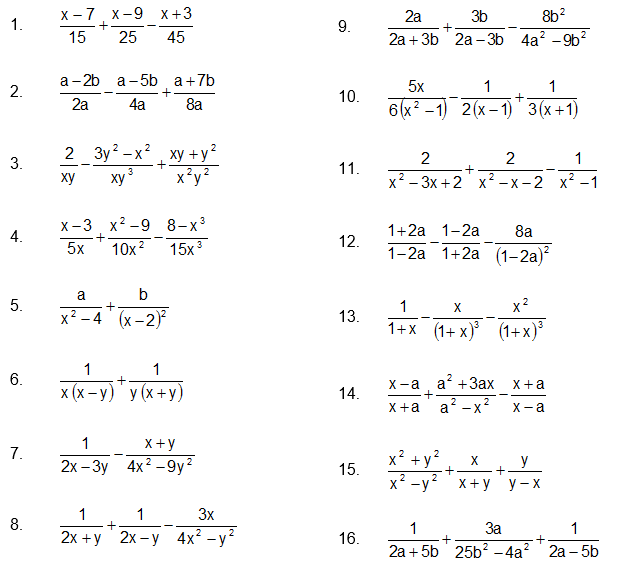
Capitulo V. Operaciones Algebraicas $\qquad$
2. Simplificar productos con expresiones racionales:
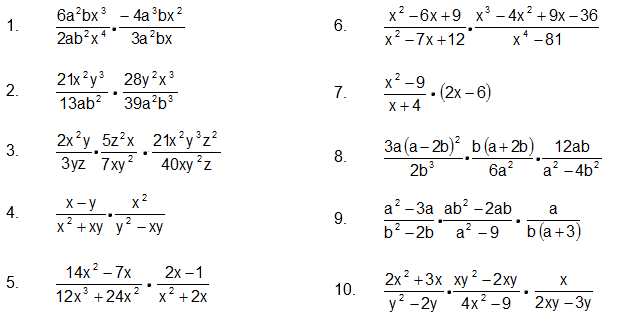
3. Simplificar divisiones con expresiones racionales.
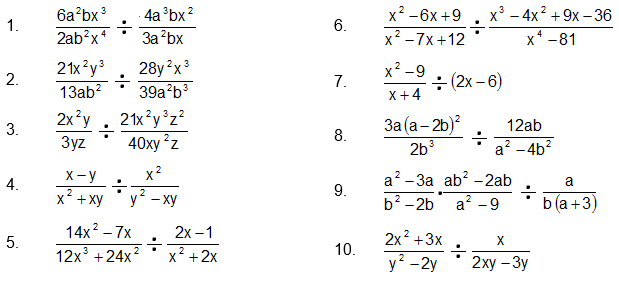

 Actividad complementaria.
Actividad complementaria.
$\space$ Descargar para imprimir
 Evaluamos lo aprendido.
Evaluamos lo aprendido.
Prepárate para la evaluación y mide tus conocimientos de lo aprendido en este capítulo, responde las preguntas a continuación:
 Evaluación - 5x2 preguntas con límite de tiempo - (25 minutos)
Evaluación - 5x2 preguntas con límite de tiempo - (25 minutos)
Clic en el link, responde y envía los resultados por e-mail.

 $\quad$ Envía tu evaluación
$\quad$ Envía tu evaluación
$\space$ Evaluación: Capítulo V
Tomada de la Red Educativa Digital Descartes.
"La matemática es la reina de la ciencia,
y la aritmética la reina de la matemática".
Carl Friedrich Gauss
DERECHOS BÁSICOS DE APRENDIZAJE (DBA)
DBA.1. Reconoce la existencia de los números irracionales como números no racionales y los describe de acuerdo con sus características y propiedades.
DBA.2. Construye representaciones, argumentos y ejemplos de propiedades de los números racionales y no racionales.
DBA.8. Identifica y analiza relaciones entre propiedades de las gráficas y propiedades de expresiones algebraicas y relaciona la variación y covariación con los comportamientos gráficos, numéricos y características de las expresiones algebraicas en situaciones de modelación.
DBA.9. Propone, compara y usa procedimientos inductivos y lenguaje algebraico para formular y poner a prueba conjeturas en diversas situaciones o contextos.

DESEMPEÑOS / ESTÁNDAR
Pensamiento numérico
1.2 M.IV Resuelvo problemas y simplifico cálculos usando propiedades y relaciones de los números reales y de las relaciones y operaciones entre ellos. DBA 1, 2.
Pensamiento variacional y sistemas algebraicos y analíticos
5.1 M.IV Identifico relaciones entre propiedades de las gráficas y propiedades de las ecuaciones algebraicas. DBA8, 9
5.5 M.IV Identifico diferentes métodos para solucionar sistemas de ecuaciones lineales. DBA2, 8.
El desarrollo de estos Estándares Básicos de Competencia permitirá fortalecer los procesos de formulación, modelación y resolución de problemas.
Capitulo VI. Ecuaciones $\qquad$
Una ecuación consta de dos expresiones algebraicas relacionadas mediante una igualdad que contiene uno o más números desconocidos llamados incógnitas, por ejemplo:
$$ 6x - \frac{2}{3}x +2 = 5x - \frac{1}{3} \qquad (1)$$ 
La expresión a la izquierda del igual se conoce como primer miembro de la ecuación y la del lado derecho como segundo miembro de la ecuación.
Habitualmente a la incógnita la representamos con la letra $x$, que denominamos variable, en este caso, es una ecuaciones con una sola incógnita (letra en la ecuación).
Se puede presentar que en algunas ecuaciones se obtienen varias soluciones y se conocen como conjunto solución o raíces de la ecuación.
Solucionar una ecuación es encontrar el valor de la incógnita que hacen verdadera la igualdad, transformando la ecuación a un equivalente de la forma $\color{blue}x = a$ utilizando diferentes propiedades, donde $\color{blue}a$ es solución o raíz de la ecuación original.
Para encontrar las soluciones de una ecuación, intentamos aislar la incógnita en uno de los miembros usando propiedades de los números reales y sus operaciones de forma que conserven la igualdad, observa el proceso de solución de la ecuación (1).
$$ 6x - \frac{2}{3}x + 2 = 5x - \frac{1}{3}$$ $$ 18x - 2x + 6 = 15x - 1 $$ $$ 18x - 2x - 15x = -6 - 1 $$ $$ x = -7 $$ ¿Identificas cada paso? (Ver explicación).
Las ecuaciones son nombradas según el grado, el cual corresponde al grado del polinomio, por ejemplo:
$ \qquad 18x - 2 = -6 \quad {\displaystyle \longrightarrow } \quad $ Ecuación de primer grado o lineal.
Capitulo VI. Ecuaciones $\qquad$
 ¡Recuerda!
, llamamos solución de la ecuación a los valores de $\color{blue}x$ que al sustituirlos en la ecuación resultan en una igualdad numérica. Decimos, entonces, que tal valor satisface la ecuación.
¡Recuerda!
, llamamos solución de la ecuación a los valores de $\color{blue}x$ que al sustituirlos en la ecuación resultan en una igualdad numérica. Decimos, entonces, que tal valor satisface la ecuación.Observa la siguiente ecuación de primer grado con una incógnita:
$$ 4 - 6x = -2x -4(x-1)$$ $$ 4 - 6x = -2x -4x + 4$$ $$-6x + 6x = 4 - 4 $$ $$\qquad 0 = 0 $$
Cualquier valor que tome la incógnita, es solución de la ecuación:
Si $\quad x = 1 \quad {\displaystyle \longrightarrow } \quad 4 - 6(1) = -2(1) -4((1)-1)$
$\qquad\qquad\qquad\qquad\qquad\space -2 = -2 $
Si $\quad x = -3 \quad {\displaystyle \longrightarrow } \quad 4 - 6(-3) = -2(-3) -4((-3)-1)$
$\qquad\qquad\qquad\qquad\qquad\qquad 22 = 22 $
Por tanto, el conjunto solución son todos los números Reales ($\mathbb{R}$) 
De lo anterior, podemos deducir que una ecuación de primer grado con una incógnita, su solución puede ser: 

Capitulo VI. Ecuaciones $\qquad$
¿Estrategia para enfrentar una situación problema?
Si las variables que aparecen en un problema están relacionadas mediante una formula determinada, el problema se reduce a despejar y sustituir valores.
Algunas veces, las relaciones entre las variables del problema no vienen dadas en ninguna formula y es necesario determinar una ecuación que exprese la relación.
Para hacerlo es necesario estar bien familiarizado con el lenguaje cotidiano y expresarlo en forma adecuada por medio de expresiones algebraicas en lenguaje matemático.
Para la resolución de una situación problema, se tienen el siguiente método de análisis:
 Método de resolución de problemas de Polya.
Método de resolución de problemas de Polya.
Método que fue generalizado por el matemático George Polya para analizar situaciones problema en cuatro pasos.

Al intentar resolver un problema es útil aplicar los siguientes pasos:
Generalmente es necesario leer varias veces el problema hasta estar seguro de entender el significado y poder realizar la situación.
En esta etapa no es necesario escribir ni formular ecuaciones, pero es conveniente en algunos casos hacer un diagrama que ilustre la situación planteada y ayude a entender el problema.
En este punto, se deben expresar las condiciones y datos del problema en el lenguaje algebraico, con lo que obtenemos una o varias ecuaciones.
Resolvemos las ecuaciones empleando los métodos ya conocidos para resolverlas.

Es conveniente verificar que la solución obtenida satisface las condiciones del problema dado.

 Lista de chequeo.
Lista de chequeo.
Método de resolución de problemas
Capitulo VI. Ecuaciones $\qquad$
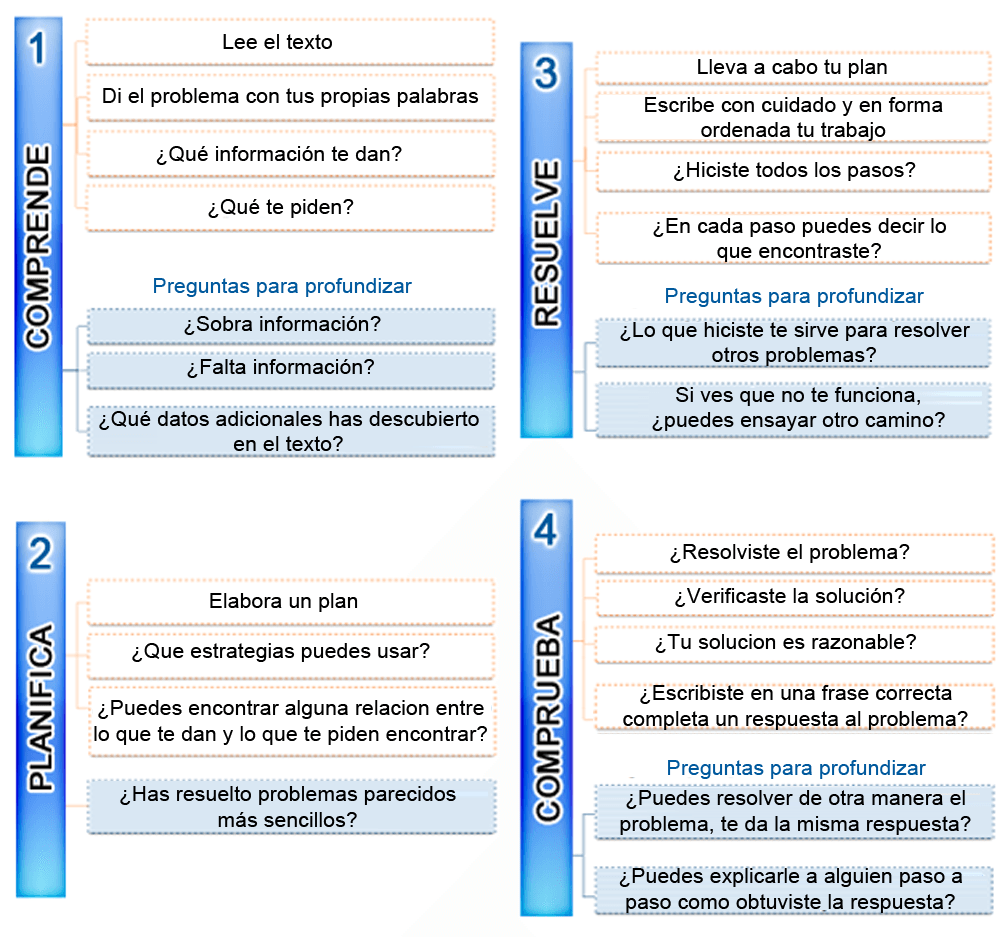

 Preguntas orientadoras.
Preguntas orientadoras.
Método de resolución de problemas
Es conveniente estar familiarizado con la forma de expresar algebraicamente gran cantidad de expresiones que con frecuencia se presentan en la cotidianidad.
Por ejemplo, símbolos como $=, <,>, +$ en otros, hacen parte de nuestro lenguaje, analicemos los siguientes frases expresadas en forma algebraica, donde "$x$" representa un número indeterminado.
| El triple de un número | $\color{blue}3x$ |
| Un número aumentado en 3 | $\color{blue}x + 3$ |
| La tercera parte de un número | $\color{blue}\frac{x}{3}$ |
| Tres enteros consecutivos | $\color{blue}x$, $\color{blue}\;\;(x + 1)$, $\color{blue}\;\;(x + 2)$ |
| Un número par o un número impar | $\color{blue}2x$, $\color{blue}\;\;(2x +1)$ |
| Dos números que su suma es 40 | $\color{blue}x$, $\color{blue}\;\;(40 - x)$ |

Capitulo VI. Ecuaciones $\qquad$
 xploremos.
xploremos.
Expresiones escritas en lenguaje matemático, por ejemplo:
Indicaciones.
Arrastra la expresión al lugar adecuado para formar la ecuación.

 Proyecto Descartes.org.
Proyecto Descartes.org.
Modalidad en el sistema Educativo de México.

 Indicaciones
Indicaciones
Solucionar el problema y verificar las respuestas.
Se plantea el problema en lenguaje algebraico y se expresa el significado que le damos a la incógnita, se escribe la ecuación o las ecuaciones que se generan.
Oprime el botón otro problema para ver otros problemas o el botón datos diferentes para cambiar los datos del problema.
Responde a la siguiente pregunta:
Capitulo VI. Ecuaciones $\qquad$

 Indicaciones
Indicaciones
Soluciona completamente el problema, intenta resolverlos antes de ver su solución, no memorizarlos, serán de gran ayuda para resolver los problemas propuestos al final del capítulo.
Oprime el botón solución y analiza la solución del problema, oprime el botón ejercicio para plantear un nuevo problema.

La ecuación cuadrática o también conocida como ecuación de segundo grado, donde $a, b$ y $c$ son números $\mathbb{R}$ con $a \equiv\not 0$, se expresa de la forma:
$$\color{blue}f(x) = a x^2 + bx + c$$La ecuación cuadrática puede presentar las siguientes soluciones:
Para resolver o encontrar las posibles soluciones de una ecuación cuadrática, igualamos a cero la ecuación, es decir, $a x^2 + bx + c = 0$ y se aplica una de las tres alternativas siguientes:
Para verificar si la ecuación tiene solución, se puede utilizar la expresión que se encuentra dentro la raíz cuadrada de la ecuación (1) llamada discriminante,
$$d = b^2 - 4ac\qquad(2)$$
Capitulo VI. Ecuaciones $\qquad$
Se puede presentar uno de lo siguientes casos si se analiza el valor del discriminante, expresión (2), teniendo presente lo siguiente:
Verifica ingresando los coeficientes $a, b$ y $c$ de la ecuación dada:

 Existen varios métodos para resolver las ecuaciones de segundo grado, mencionados anteriormente.
Existen varios métodos para resolver las ecuaciones de segundo grado, mencionados anteriormente.
El método apropiado para resolver una ecuación cuadrática depende del tipo de ecuación que se va a resolver.
Veamos algunos casos que se presentan:
1° caso. Ecuación de la forma $\quad \color{blue}a x^2 + c = 0$
Para este caso despejamos la variable, en nuestro caso, $x$, entonces la solución o raíces serán:
$$ x_1 = \sqrt[]{\frac{c}{a}},\quad x_2 = -\space\sqrt[]{\frac{c}{a}},\qquad con\quad\frac{c}{a}> 0$$Capitulo VI. Ecuaciones $\qquad$
2° caso. Ecuación de la forma $\quad \color{blue}a x^2 + bx = 0$
En este caso tenemos la variable $x$ en los dos términos, por lo tanto, podemos sacar un factor común $x$, es decir,
$$x (a x + b) = 0,\qquad donde\quad x = 0,\space \quad ax + b = 0$$ entonces la solución o raíces serán: $$x_1 = 0,\quad x_2 = \frac{b}{a}$$Por tanto, las soluciones de la ecuación dada, corresponden a dos raíces reales diferentes. 
3° caso. Ecuación de la forma $\quad \color{blue}a x^2 + bx + c = 0$
Para este tipo de ecuaciones se pueden presentar varias situaciones, una de ellas es, si el trinomio es factorizable
Para utilizar este método la ecuación cuadrática debe estar igualada a cero y factorizamos el trinomio de la forma $x^2 + bx + c = 0$ o $a x^2 + bx + c = 0$.
Sacando la raíz cuadrada de ambos lados, entonces, las soluciones son dos raíces reales iguales: $$x + 1= 0$$ $$ x_1 = x_2 = -1$$
En este caso, la ecuación $(x + 1)^2= 0$ corresponde a un trinomio cuadrado perfecto, por tanto se dice que la raíz tiene multiplicidad 2, lo que equivale a tener dos soluciones o raíces iguales.

Capitulo VI. Ecuaciones $\qquad$
Vamos a reescribir esta ecuación completando cuadrados, sumando a ambos lados de la igualdad la cantidad $(\frac{4}{2})^2$
$$x^2 - 4x + (\frac{4}{2})^2 = -1 + (\frac{4}{2})^2$$ $$x^2 - 4x + 4 = -1 + 4$$ $$(x - 2)^2 = 3$$Sacando la raíz cuadrada de ambos lados, obtenemos:
$$x - 2= \sqrt[]{3}$$por tanto, las soluciones son dos raíces reales diferentes:
$$ x_1 = 2 - \sqrt[]{3},\quad x_2 = 2 + \sqrt[]{3}$$
 ¡Recuerda!
, para completar el cuadrado en una expresión de la forma $x^2 + bx$, se suma la expresión $(\frac{b}{2})^2$ a ambos lados de la igualdad, y la expresión se vuelve:
$$x^2 + bx + (\frac{b}{2})^2 = (x + \frac{b}{2})^2$$
¡Recuerda!
, para completar el cuadrado en una expresión de la forma $x^2 + bx$, se suma la expresión $(\frac{b}{2})^2$ a ambos lados de la igualdad, y la expresión se vuelve:
$$x^2 + bx + (\frac{b}{2})^2 = (x + \frac{b}{2})^2$$Cualquiera que sea la ecuación cuadrática, la fórmula general es de gran utilidad para encontrar las raíces de la ecuación de 2° grado.
donde $\space a = 3,\space b = 4,\space c = -15,\space $ si analizamos el discriminante:
$$d = (4)^2-4(3)(-15)$$ $$d = 196$$Como $ d > 0$, se tendrán dos soluciones reales diferentes, remplazando entonces, en la ecuación cuadrática, se tiene:
$$x = {-4 \pm \sqrt{196} \over 2(3)}$$ $$x_1 = {-4 + 14 \over 6},\quad x_2 = {-4 - 14 \over 6}$$ $$\qquad\qquad\qquad x_1 = \frac{5}{3},\quad x_2 = -3 $$
$$\qquad\qquad\qquad x_1 = \frac{5}{3},\quad x_2 = -3 $$
Por tanto, se tienen dos raíces reales diferente.
Responde de acuerdo a lo visto en la sección:
Capitulo VI. Ecuaciones $\qquad$
 Ecuaciones de 2° grado.
Ecuaciones de 2° grado.
 Indicaciones
Indicaciones
Encuentra las raíces de la ecuación cuadrática.
La gráfica de la ecuación cuadrática corresponde a una parábola, donde, las soluciones o raíces son las intersecciones con el eje $x$.
Veamos en la siguiente imagen, las posibles gráficas que se presentan de la ecuación cuadrática según el valor del discriminante $(d)$:
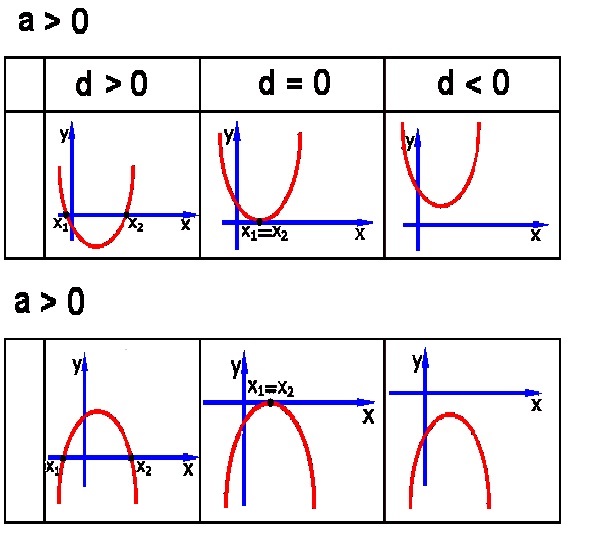
En la figura se ve la solución gráfica que puede presentar una ecuación cuadrática $f(x) = ax^2 + bx + c$, donde el signo del coeficiente $a$, me indica si la parábola abre hacia arriba o hacia abajo. 
Se puede observar que hay soluciones reales diferentes, iguales o no tener soluciones.
Las soluciones o raíces corresponden a las intersecciones o cortes en el eje $x$.
Capitulo VI. Ecuaciones $\qquad$
 xploremos.
xploremos.
Observa la gráfica de la ecuación cuadrática.
Verifica los conocimientos de lo visto en esta sección, explora la siguiente escena interactiva.
Indicaciones.
Encuentra y comprueba las soluciones de la ecuación cuadrática dada según su gráfica.

 Proyecto Descartes.org.
Proyecto Descartes.org.
Modalidad en el sistema Educativo de México.
Observemos la solución gráfica de la ecuación $\quad\color{blue}ax^2 + bx + c = 0$.
Este tipo de ecuación, es llamada ecuación bicuadrada: $$ax^4 + bx^2 + c = 0$$ Se resuelve como una ecuación cuadrática haciendo un cambio de variable, cambiando $x^2$ por $y$, por ejemplo:
$$x^4 - 12x^2 + 9 = 0$$ $$(x^2)^2 - 12(x^2) + 9 = 0$$ $$y^2 - 12y + 9 = 0$$Capitulo VI. Ecuaciones $\qquad$
Otra forma de la ecuación cuadrática se puede presentar como: $$a (f(x))^2 + b(f(x)) + c = 0$$ donde $f(x)$ es una función de x, se dice que es una ecuación cuadrática, por ejemplo:
Como hallar la ecuación cuadrática dadas sus raíces:
La suma de las raíces, es igual al negativo del cociente entre los coeficientes de $x^2$ y $x$.
$\qquad\qquad\qquad x_1 + x_2 = -\frac{b}{a} =-b$
 El producto de las raíces, es igual al cociente del término constante y el coeficiente de $x^2$.
El producto de las raíces, es igual al cociente del término constante y el coeficiente de $x^2$.
$\qquad\qquad\qquad (x_1)(x_2 )= \frac{c}{a}= c$
La ecuación cuadrática se expresa como:
$\quad\color{blue}x^2 -(x_1+x_2)x + (x_1)(x_2) = 0$
Suma de las soluciones $\quad {\displaystyle \longrightarrow } \quad S = x_1 + x_2 = 3 - 2 = 1 $
Producto de las soluciones $\quad {\displaystyle \longrightarrow } \quad P = x_1\cdot x_2 = (3)(- 2) = 6 $
por lo tanto, la ecuación es: $\quad x^2 - x - 6 = 0$

 Indicaciones
Indicaciones
Soluciona ecuaciones de segundo grado con una incógnita.
Capitulo VI. Ecuaciones $\qquad$
Con alguna frecuencia se nos presentan algunos problemas que llevados al lenguaje matemático se plantean las situaciones a través de una ecuación cuadrática o de segundo grado.
$\qquad \quad x: \quad$ Representa uno de los números.
$\quad 25 - x :\quad$ Representa el otro número.
Según los datos dados en el problema, se tiene que:
Solucionando la ecuación por factorización, se tiene que:
Si $\quad x = 12\quad {\displaystyle \longrightarrow } \quad 25 - x = 25 - 12 = 13$
Si $\quad x = 13 \quad {\displaystyle \longrightarrow } \quad 25 - x = 25 - 13 = 12$
Por tanto, las dos soluciones satisfacen la situación problema.
 Cuándo se resuelve la ecuación, es posible que alguna de sus raíces no satisfagan las condiciones del problema y en consecuencia debe rechazarse,
es conveniente, examinar las raíces y determinar aquellas que resuelvan satisfactoriamente las situaciones planteadas.
Cuándo se resuelve la ecuación, es posible que alguna de sus raíces no satisfagan las condiciones del problema y en consecuencia debe rechazarse,
es conveniente, examinar las raíces y determinar aquellas que resuelvan satisfactoriamente las situaciones planteadas. xploremos.
xploremos.
Situaciones que involucran ecuaciones de 2° grado.
Analiza las dos situaciones problema que se plantean a continuación:

 Proyecto Descartes.org.
Proyecto Descartes.org.
Modalidad en el sistema Educativo de México.
Capitulo VI. Ecuaciones $\qquad$
 Aplicación de física.
Aplicación de física.Situación problema. Se va a construir un corral con área de forma rectangular, expresada mediante una función cuadrática.
 Indicaciones
Indicaciones
Soluciona la siguiente situación problema.

Escena de Carlos Mario Restrepo Restrepo. CC by-nc-sa
 Aplicación de física.
Aplicación de física. Situación problema, piensa y analiza.
Situación problema, piensa y analiza.
¿Cómo se debe lanzar una pelota, para que alcance la máxima distancia horizontal?, ¿Cómo se llama esta trayectoria?. ¿Desde las matemáticas, cómo se puede interpretar este movimiento?
Oprime la botón  para avanzar o retroceder en las situaciones.
para avanzar o retroceder en las situaciones.
Capitulo VI. Ecuaciones $\qquad$
Para $n>2$, se tiene la siguiente ecuación:
an xn + an-1xn-1 + an-2xn-2 + … + a1x + a0 = 0
Este tipo de ecuación se puede descomponer en factores de primer y segundo grado, entonces basta igualar a cero cada uno de los factores y resolver las ecuaciones de primer grado y de segundo grado resultantes.
 xploremos.
xploremos.
Analiza y explora las siguientes escenas interactivas, observa las gráficas de las ecuaciones que se plantean según la situación.

 Proyecto Descartes.org.
Proyecto Descartes.org.
Modalidad en el sistema Educativo de México.
También, se puede utilizar la regla de Ruffini, para reducir polinomios de tercer grado o mayor. A continuación veremos algunos teoremas, que nos servirán para factorizar polinomios y la relación con las raíces del polinomio.
Capitulo VI. Ecuaciones $\qquad$
Teorema del Residuo

Este teorema permite conocer el residuo sin efectuar la división de un polinomio $P(x)$ entre un binomio de la forma $(x-a)$:
"Si el polinomio $P(x)$ se divide entre $(x-a)$, el residuo es igual a $P(a)$."
"Si el polinomio $P(x)$ se anula para $x = a$, entonces el polinomio $P(x)$ es divisible por $(x - a)$."
Esto es, si $P(a)= 0$ entonces $(x - a)$ es un factor de $P(x)$.
Usando el teorema del residuo y el teorema del factor, factorice completamente el polinomio.
$$P(x) = x^4 + x^3 - 7x^2 - x + 6$$Para empezar, debemos buscar los posibles factores de la forma $(x-a)$ del polinomio dado. Esto equivale a buscar los números $a$ tales que $P(a)=0$.
Los posibles valores para hacer que el polinomio se anule son precisamente los divisores del término independiente, que en este caso es 6.
Divisores de 6 = $ \pm1; \pm2; \pm 3; \pm 6 $.
Evaluamos con cada divisor el polinomio $P(x)$:

Entonces, los divisores $a$ tales que $P(a)=0$, son los factores del polinomio, por tanto:
$$P(x) = x^4 + x^3 - 7x^2 - x + 6$$ $$P(x) = (x+1)(x-1)(x - 2)(x + 3)$$Capitulo VI. Ecuaciones $\qquad$
La regla de Ruffini es un método que permite:

Apliquemos los siguiente pasos al polinomio organizado de manera ordenada (las variables de mayor a menor grado).
Los divisores de 28 son: $\pm 1, \pm 2, \pm 4, \pm 7, \pm 14, \pm 28$
¿Cuales de estos divisores son válidos aplicando el método?
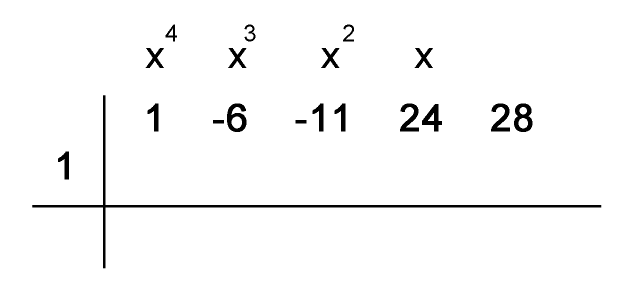
Ahora multiplicamos el primer divisor (el 1ª la izquierda de la raya vertical) por el primer coeficiente del polinomio (el 1 que lo tienes debajo de la raya horizontal) y el resultado del producto lo colocas debajo del segundo coeficiente (el -6).
Se Suma -6 + 1 = -5, este resultado lo colocamos debajo de la línea horizontal y a la altura del segundo coeficiente, realizamos los mismos pasos hasta llegar al termino independiente.
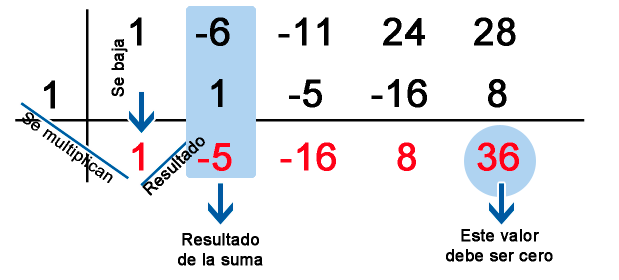
El divisor (1), no es solución porque la última suma es 36 y para que sea raíz o solución debe ser igual CERO.
Capitulo VI. Ecuaciones $\qquad$
Se realiza el mismo proceso con cada divisor, hasta encontrar como resultado en su ultima operación el CERO.
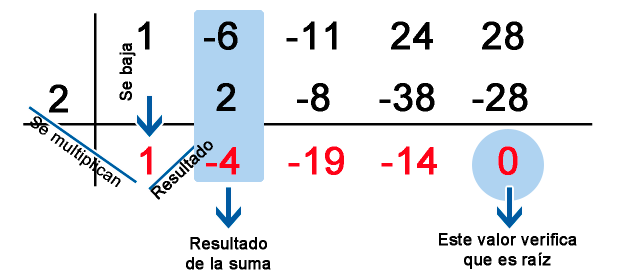
Esta vez comprobamos que obtengo al final un cero, lo que significa que el divisor es una raíz, osea. $(x - 2)$

Lo que significa que el divisor (-2) es una raíz, osea. $(x + 2)$
Por lo tanto, tenemos: $(x - 2)(x + 2)(x^2 -6x - 7)$
Además, con los últimos coeficientes obtenemos un trinomio, el cual podemos factorizan directamente:
$$x^2 -6x - 7 = (x - 7)( x + 1)$$Por lo tanto, la factorización del polinomio es:
$$x^4 - 6x^3 - 11x^2 + 24x + 28 = ( x + 1)(x - 2)(x + 2)(x - 7)$$Se puede comprobar que al sustituir a $x$ por $-2, -1, 2$ y $7$ obtenemos como resultado el cero en la ecuación.
Observemos la solución gráfica en la siguiente figura:
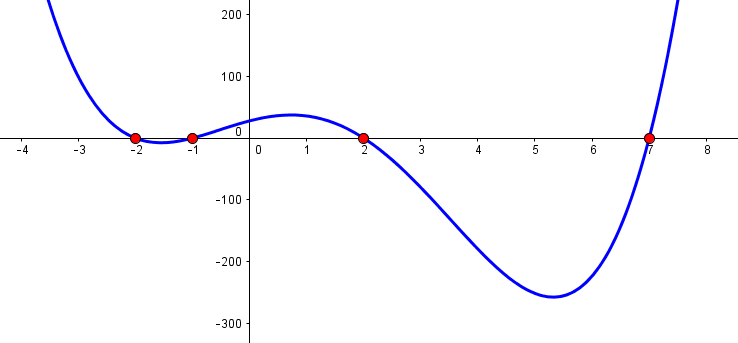

Capitulo VI. Ecuaciones $\qquad$

 Indicaciones
Indicaciones
Aplicamos la Regla de Ruffini o uno de los métodos de solución.
La expresión exponencial es la inversa de la función logarítmica , y se representa en función de $x$ de la forma:
¿Cómo se resuelve una ecuación logarítmica o exponencial?
Para hallar el valor de $x$ en una ecuación logarítmica o exponencial, es conveniente seguir los siguientes pasos:
Cuándo se resuelven ecuaciones de tipo algebraicas, normalmente se basan en la idea de que se puede cambiar en ambos lados de la ecuación de la misma manera y obtener una ecuación válida.
Esto también aplica para los logaritmos y exponenciales, no importa cual sea la base $b$, si:
$x = y \quad {\displaystyle \longrightarrow } \quad \log_b(x) = \log_b(y)$.
$x = y \quad {\displaystyle \longrightarrow } \quad b^x = b^y$.
Capitulo VI. Ecuaciones $\qquad$
Tomamos logaritmos en base $2$ a ambos lados de la ecuación:
$$\ce{log_2 {(2^{x+3})} = log_2 {(126)}}$$ $${(\ce{x}+3) \cancel{\ce {log_2 {(2)}}} = \ce{log_2 {(126)}}}$$ $$\ce{x}+3 = \ce{log_2 {(126})}$$ $$\ce{x = log_2 {(126)}} - 3$$ Si deseamos encontrar el valor exacto de la incógnita, se hace un cambio de base y se evalúa en calculadora.
Si deseamos encontrar el valor exacto de la incógnita, se hace un cambio de base y se evalúa en calculadora.
Para verificar el resultado, se sustituye el valor hallado en la ecuación inicial.
$$2^{(3,9773)+3} = 126$$
Despejamos los logaritmos a un solo lado de la ecuación aplicando las leyes para simplificar:
$$ \log{(x+3)}- \log{(x+2)}=5$$ $$ \log{\bigg(\frac{x+3}{x+2}\bigg)}=5$$Para eliminar el logaritmo, aplicamos la base en forma exponencial a ambos lados de la ecuación, simplificando asi el logaritmo.
$$ 10^{\log{\big(\frac{x+3}{x+2}\big)}}=10^5$$ $$ \frac{x+3}{x+2}=10^5$$ $$ x+3=10^5 (x+2)$$ $$ x+3=10^5x+(2)10^5$$ $$ x-10^5x=(2)10^5-3$$ $$ x(1-10^5)=200000-3$$
$$ x=\frac{199997}{1-10^5}$$
$$x \approx -1,99999$$
$$ x(1-10^5)=200000-3$$
$$ x=\frac{199997}{1-10^5}$$
$$x \approx -1,99999$$
Capitulo VI. Ecuaciones $\qquad$
 xploremos.
xploremos.
Observa la gráfica de una función logarítmica y exponencial:
Piensa y analiza
Analicemos, las gráficas de las expresiones logarítmicas $y=\log_b(x)$ y exponencial $y = b^x$ (estas expresiones llamadas funciones).

 jercicio 1.
jercicio 1.
Pongamos en práctica lo visto en esta sección
 Indicaciones
Indicaciones
Soluciona ecuaciones de primer grado con una incógnita.
Capitulo VI. Ecuaciones $\qquad$
 jercicio 2. Situaciones problema de 1° grado
jercicio 2. Situaciones problema de 1° grado
Analiza, plantea y resuelve las siguientes situaciones problema.

 Actividad complementaria.
Actividad complementaria.
Situaciones problemas para imprimir
 jercicio 2. Situaciones problema de 2° grado.
jercicio 2. Situaciones problema de 2° grado.
 Pongamos en práctica lo visto en esta sección, analiza, plantea y resuelve las siguientes situaciones problema.
Pongamos en práctica lo visto en esta sección, analiza, plantea y resuelve las siguientes situaciones problema.


 Actividad complementaria.
Actividad complementaria.
Situaciones problemas para imprimir
Capitulo VI. Ecuaciones $\qquad$
 jercicio 3.
jercicio 3.
Resuelve las siguientes ecuaciones con logaritmos.
Indicaciones

 Evaluamos lo aprendido.
Evaluamos lo aprendido.
Prepárate para la evaluación y mide tus conocimientos de lo aprendido en este capítulo, responde las preguntas a continuación:
 Evaluación - 5x2 preguntas con límite de tiempo - (20 minutos)
Evaluación - 5x2 preguntas con límite de tiempo - (20 minutos)
Clic en el link, responde y envía los resultados por e-mail.

 $\quad$ Envía tu evaluación
$\quad$ Envía tu evaluación
$\space$ Evaluación: Capítulo VI
Tomada de la Red Educativa Digital Descartes.
"Ningún empleo puede ser controlado sin aritmética,
ninguna invención mecánica sin geometría".
Benjamin Franklin
DERECHOS BÁSICOS DE APRENDIZAJE (DBA)
DBA.1. Reconoce la existencia de los números irracionales como números no racionales y los describe de acuerdo con sus características y propiedades.
DBA.2. Construye representaciones, argumentos y ejemplos de propiedades de los números racionales y no racionales.
DBA.8. Identifica y analiza relaciones entre propiedades de las gráficas y propiedades de expresiones algebraicas y relaciona la variación y covariación con los comportamientos gráficos, numéricos y características de las expresiones algebraicas en situaciones de modelación.
DBA.9. Propone, compara y usa procedimientos inductivos y lenguaje algebraico para formular y poner a prueba conjeturas en diversas situaciones o contextos.

DESEMPEÑOS / ESTÁNDAR
Pensamiento numérico
1.2 M.IV Resuelvo problemas y simplifico cálculos usando propiedades y relaciones de los números reales y de las relaciones y operaciones entre ellos. DBA 1, 2.
Pensamiento variacional y sistemas algebraicos y analíticos
5.1 M.IV Identifico relaciones entre propiedades de las gráficas y propiedades de las ecuaciones algebraicas. DBA8, 9
5.5 M.IV Identifico diferentes métodos para solucionar sistemas de ecuaciones lineales. DBA2, 8.
El desarrollo de estos Estándares Básicos de Competencia permitirá fortalecer los procesos de formulación, modelación y resolución de problemas.
Capitulo VII. Sistemas de Ecuaciones $\qquad$
Un sistema de ecuaciones esta formado por dos o más ecuaciones con varias incógnitas en la que deseamos encontrar una solución común, se tomará la ecuación donde $a, b, c$ son los coeficientes y las incógnitas $x$, $y$ expresada de la forma:
$$\color{blue} ax + by = c$$Los sistemas de solución de ecuaciones, también conocidos como:
Para resolver un sistema (compatible determinado) necesitamos tener al menos tantas ecuaciones como incógnitas.
Resolver un sistema de ecuaciones, es encontrar el valor de cada incógnita para que se satisfagan todas las ecuaciones del sistema, estas aparecen en varias de las ecuaciones, pero no necesariamente en todas, lo que hacen estas ecuaciones es relacionar las incógnitas entre sí.

Como resolver un sistema de dos ecuaciones lineales con dos incógnitas por diferentes métodos de solución
Cuándo se soluciona un sistema de ecuaciones utilizando el método gráfico, para este caso, un sistema 2 x 2 se tiene que:

Capitulo VII. Sistemas de Ecuaciones $\qquad$
El método gráfico puede presentar las siguientes soluciones: Unica solución, no tener solución o infinitas soluciones.
 Secantes:
Secantes:  Paralelas:
Paralelas: Coincidentes:
Coincidentes: xploremos.
xploremos.
Veamos la solución gráfica de un sistema lineal de ecuaciones 2 x 2, para ver diferentes ejemplos, oprime el botón otro ejemplo .

Como es de esperar, en el método gráfico se representan las gráficas asociadas a las ecuaciones del sistema para deducir su solución ahora veamos, como resolver sistemas de ecuaciones lineales de forma analítica.
Capitulo VII. Sistemas de Ecuaciones $\qquad$
El método consiste en multiplicar una ó las dos ecuaciones por un número de modo que obtengamos un sistema en que los coeficientes de $x$ o de $y$ sean iguales con signo contrario, para eliminar dicha incógnita al sumar las dos ecuaciones.
El método consiste en despejar una de las incógnitas de una de las ecuaciones y reemplazar este valor en la otra ecuación, de esta forma se llega a una ecuación de primer grado con una incógnita.

Capitulo VII. Sistemas de Ecuaciones $\qquad$
El método consiste en una pequeña variación del método de sustitución, para resolver el sistema de ecuaciones hay que despejar una incógnita, la misma, en las dos ecuaciones e igualar el resultado de ambos despejes, con lo que se obtiene una ecuación de primer grado con una incógnita.
 xploremos.
xploremos.
Solución de un sistema de ecuaciones lineales analítica y gráficamente paso a paso.
 Indicaciones.
Indicaciones.
Resuelve primero y luego verifica la respuesta, oprime las flechas para obtener los coeficientes $a, b, c, d, e, f$ de cada variable del sistema de ecuaciones.

 Proyecto Descartes.org.
Proyecto Descartes.org.
Modalidad en el sistema Educativo de México.
Capitulo VII. Sistemas de Ecuaciones $\qquad$

Oprime el botón ejercicio para generar un sistema de ecuaciones lineales, utiliza uno de los métodos para solucionar el sistema.
 Verifica la solución por medio del método gráfico, ingresa los coeficientes $a, b, e, d$ y las constantes $c$ y $f$ respectivamente.
Verifica la solución por medio del método gráfico, ingresa los coeficientes $a, b, e, d$ y las constantes $c$ y $f$ respectivamente.
Oprime el botón solución para verificar la solución gráfica.
Para resolver un sistema de ecuaciones lineales existe también un método, llamado método de determinantes.
Consideremos el siguiente sistema de ecuaciones 2 x 2:
$$\color{blue} a_1x + b_1y = c_1 \qquad (1)$$ $$\color{blue} a_2x + b_2y = c_2 \qquad (2)$$El número real $\color{blue} \triangle = a_1 . b_2 - a_2 . b_1$, se llama determinante ($\triangle$) de orden 2 y se esquematiza de la forma:
$$\color{blue} \triangle = \begin{vmatrix} a_1 & b_1 \\ a_2 & b_2 \end{vmatrix} = a_1 . b_2 - a_2 . b_1$$Donde la primera columna corresponde a los coeficientes de la incógnita $x$ y la segunda columna a los coeficientes de la incógnita $y$.
Para hallar $x$ y $y$, se pueden expresar como cocientes de determinantes de la siguiente forma:
$$ x = {c_1.b_2 - c_2.b_1 \over a_1 . b_2 - a_2 . b_1} = {\begin{vmatrix} {\color{red}c_1} & b_1 \\ {\color{red}c_2} & b_2 \end{vmatrix} \over \begin{vmatrix} a_1 & b_1 \\ a_2 & b_2 \end{vmatrix}}$$ $$ y = {a_1.c_2 - a_2.c_1 \over a_1 . b_2 - a_2 . b_1} = {\begin{vmatrix} a_1 & {\color{red}c_1} \\ a_2 & {\color{red}c_2} \end{vmatrix} \over \begin{vmatrix} a_1 & b_1 \\ a_2 & b_2 \end{vmatrix}}$$Capitulo VII. Sistemas de Ecuaciones $\qquad$
Según las expresiones anteriores, se tiene lo siguiente:

 Para resolver un sistema de ecuaciones 3 x 3, se puede utilizar cualquiera de los métodos ya vistos en esta sección.
Para resolver un sistema de ecuaciones 3 x 3, se puede utilizar cualquiera de los métodos ya vistos en esta sección.Para resolver un sistema de 3 x 3, necesitamos tener al menos tantas ecuaciones como incógnitas, el sistema está formado por (3) ecuaciones, (3) incógnitas, así:
$$ a_1x + b_1y +c_1z = d_1 \qquad (1)$$ $$ a_2x + b_2y +c_2z = d_2 \qquad (2)$$ $$ a_3x + b_3y +c_3z = d_3 \qquad (3)$$El determinante ($\triangle$) de orden 3 se esquematiza de la forma: $$\color{blue} \triangle = \begin{vmatrix} a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \\ a_3 & b_3 & c_3 \end{vmatrix} = a_1 . \begin{vmatrix} b_2 & c_2 \\ b_3 & c_3 \end{vmatrix} - b_1 . \begin{vmatrix} a_2 & c_2 \\ a_3 & c_3 \end{vmatrix} + c_1.\begin{vmatrix} a_2 & b_2 \\ a_3 & b_3 \end{vmatrix} $$
La solución del sistema se determina por:
$$x = {\begin{vmatrix} d_1 & b_1 & c_1 \\ d_2 & b_2 & c_2 \\ d_3 & b_3 & c_3 \end{vmatrix} \over \triangle} \qquad y = {\begin{vmatrix} a_1 & d_1 & c_1 \\ a_2 & d_2 & c_2 \\ a_3 & d_3 & c_3 \end{vmatrix} \over\triangle} \qquad z = {\begin{vmatrix} a_1 & b_1 & d_1 \\ a_2 & b_2 & d_2 \\ a_3 & b_3 & d_3 \end{vmatrix} \over \triangle}$$Capitulo VII. Sistemas de Ecuaciones $\qquad$
Se observa que cada incógnita es una fracción cuyo denominador es el determinante $\triangle$ y el numerador es el determinante que se obtiene cambiando la columna de los coeficientes de la incógnita por los términos independientes, veamos diferentes ejemplos de un sistema 3x3 utilizando Regla de Cramer:

 1. Oprime el botón sistema
y generar un sistema de ecuaciones lineales 2x2, soluciona y verifica tus respuestas.
1. Oprime el botón sistema
y generar un sistema de ecuaciones lineales 2x2, soluciona y verifica tus respuestas.
Ingresa los coeficientes, oprime el botón solución y observa.
Capitulo VII. Sistemas de Ecuaciones $\qquad$
2. Oprime el botón sistema y generar un sistema ecuaciones de 3x3.
Es conveniente estar familiarizado con la forma de expresar algebraicamente gran cantidad de expresiones que con frecuencia se presentan en la cotidianidad.
Con alguna frecuencia se nos presentan algunos problemas que llevados al lenguaje matemático se plantean las situaciones a través de un sistema de ecuaciones.
Dos números suman 25 y el doble de uno de ellos es 14. ¿Cuales son los números?
$\qquad x: \quad$ Es un número
$\qquad y: \quad$ El otro número
Entonces el sistemas de ecuaciones es:
$$x + y = 25 \qquad (1) \qquad \qquad \quad$$ $$2x + 0y = 14 \qquad (2)$$
$$2x + 0y = 14 \qquad (2)$$
Verifica que la solución es: $\quad x = 7$, $\quad y = 18$
Capitulo VII. Sistemas de Ecuaciones $\qquad$

 Situaciones problema, que generan sistemas de ecuaciones lineales de 2x2, intenta resolverlos antes de ver su solución.
Situaciones problema, que generan sistemas de ecuaciones lineales de 2x2, intenta resolverlos antes de ver su solución.
Para ver el planteamiento y su respuesta, oprime el botón solución , para un nuevo problema, oprime el botón ejercicio .
 jercicio 1. Situaciones problema.
jercicio 1. Situaciones problema.

 Actividad complementaria.
Actividad complementaria.
Situaciones problemas para imprimir
Capitulo VII. Sistemas de Ecuaciones $\qquad$
 jercicio 2. Sistemas de ecuaciones lineales
jercicio 2. Sistemas de ecuaciones lineales
Pongamos en práctica lo visto en esta sección.
 Oprime el botón para generar un ejercicio aleatorio, utiliza uno de los métodos de solución de sistemas de ecuaciones.
Oprime el botón para generar un ejercicio aleatorio, utiliza uno de los métodos de solución de sistemas de ecuaciones.
 Evaluamos lo aprendido.
Evaluamos lo aprendido.
Prepárate para la evaluación y mide tus conocimientos de lo aprendido en este capítulo, responde las preguntas a continuación:
 Evaluación - 10 preguntas con límite de tiempo - (10 minutos)
Evaluación - 10 preguntas con límite de tiempo - (10 minutos)
Clic en el link, responde y envía los resultados por e-mail.

 $\quad$ Envía tu evaluación
$\quad$ Envía tu evaluación
$\space$ Evaluación: Capítulo VII
Plantillas con Descartes-JS
"La única forma de aprender matemáticas es hacer matemáticas".
Paul Halmos
DERECHOS BÁSICOS DE APRENDIZAJE (DBA)
DBA.1. Reconoce la existencia de los números irracionales como números no racionales y los describe de acuerdo con sus características y propiedades.
DBA.2. Construye representaciones, argumentos y ejemplos de propiedades de los números racionales y no racionales.
DBA.8. Identifica y analiza relaciones entre propiedades de las gráficas y propiedades de expresiones algebraicas y relaciona la variación y covariación con los comportamientos gráficos, numéricos y características de las expresiones algebraicas en situaciones de modelación.
DBA.9. Propone, compara y usa procedimientos inductivos y lenguaje algebraico para formular y poner a prueba conjeturas en diversas situaciones o contextos.

DESEMPEÑOS / ESTÁNDAR
Pensamiento numérico
1.2 M.IV Resuelvo problemas y simplifico cálculos usando propiedades y relaciones de los números reales y de las relaciones y operaciones entre ellos. DBA 1, 2.
Pensamiento variacional y sistemas algebraicos y analíticos
5.1 M.IV Identifico relaciones entre propiedades de las gráficas y propiedades de las ecuaciones algebraicas. DBA8, 9
5.5 M.IV Identifico diferentes métodos para solucionar sistemas de ecuaciones lineales. DBA2, 8.
El desarrollo de estos Estándares Básicos de Competencia permitirá fortalecer los procesos de formulación, modelación y resolución de problemas.
Capitulo VIII. Inecuaciones $\qquad$
Una inecuación es una desigualdad entre dos expresiones algebraicas, donde su solución posee infinitas soluciones, como es el caso: $$ 4 < x + 2 < 7$$ $$ 2 < x < 5$$
Todos los valores de $x$ entre $2$ y $5$ verifican la desigualdad, por tanto el conjunto solución de la desigualdad puede verse intuitivamente como el tramo de la recta real entre $2$ y $5$ .
¿Qué es una desigualdad?
Una desigualdad es un enunciado matemático que compara dos expresiones (numéricas o algebraicas) usando algún signo de desigualdad $>,<,≥ o ≤$.
En una desigualdad, una expresión de la desigualdad puede ser más grande o más chica que la otra expresión, se utilizan símbolos especiales en estos enunciados.
Dados los números reales $a, b$ que cumplen $a < b$ o $a> b$, donde el símbolo "$<$ o $>$" indican que no incluye el limite dado y el símbolo "$\le$ o $≥$" indican que incluye los limites, se definen así:
 xploremos.
xploremos.
Intervalos Acotados.
Es el conjunto de los números comprendidos entre los límites $a$ y $b$:
|
|
$x \in \mathbb{R}$ |
|
| Abierto $\quad (a, b)$ |
|

|
| Cerrado $\quad [a, b]$ |
|

|
| Abierto izquierda $(a, b]$ |
|

|
| Abierto derecha $[a, b)$ |
|

|
Capitulo VIII. Inecuaciones $\qquad$
 xploremos.
xploremos.
Intervalos no Acotados.
Este tipo de intervalos aparece cuando se conoce solo uno de los extremos y el otro es el infinito, al no poderse incluir el infinito en el intervalo, estos se consideran siempre abiertos en el infinito:
|
|
$x \in \mathbb{R}$ |
|
| Abierto izquierda $(a, +\infty)$ |
|

|
| Cerrado izquierda $[a, +\infty)$ |
|

|
| Abierto derecha $(-\infty, b)$ |
|

|
| Cerrado derecha $(-\infty, b]$ |
|

|
| Todos los $\mathbb{R} (-\infty, +\infty)$ |
|

|

Capitulo VIII. Inecuaciones $\qquad$
Sean $a, b, c$ números $\mathbb{R}$, se cumple que:

$\quad a ≤ b ⇔ a ± c ≤ b ± c$
$\quad c > 0 \quad {\displaystyle \longrightarrow } \quad a ≤ b ⇔ ca ≤ cb$.
$\quad c > 0 \quad {\displaystyle \longrightarrow } \displaystyle \quad a ≤ b ⇔ {a \over c} ≤ {b \over c}$.
$\quad c < 0 \quad {\displaystyle \longrightarrow }\quad a ≤ b ⇔ ca ≥ cb$.
$\quad c < 0 \quad {\displaystyle \longrightarrow }\quad \displaystyle a ≤ b ⇔ {a \over c} ≥ {b \over c}$.
El sentido de una desigualdad se conserva al multiplicar o dividir sus dos miembros por un mismo número positivo, se invierte si dicho número es negativo.
Resolver una desigualdad o inecuación es encontrar todos los valores que tiene $x$ para que la desigualdad se cumpla.
Si $a,b \in \mathbb{R}$ con $a =\not 0$, cualquiera de las siguientes expresiones se llama inecuación lineal de una variable, inecuaciones del tipo:
$$ax + b < 0 ,\quad x> b, \quad ax < b, \quad ax ≥ b, \quad ax ≤ b$$ xploremos.
xploremos.
Pasos para resolver una inecuación lineal.
Primero se aísla la incógnita en un lado de la desigualdad, dejando en el otro solo números, para ello debe tenerse en cuenta las propiedades de las desigualdades, luego se procede de igual forma que al resolver una ecuación lineal con una incógnita.
Oprime el botón Siguiente paso y observa los ejemplos:
Capitulo VIII. Inecuaciones $\qquad$
 xploremos.
xploremos.
Ejemplos de inecuaciones lineales.
Indicaciones

 Veamos los siguientes ejemplos de la solución de una inecuación, encontrando los valores de $x$ que cumplen la desigualdad y la representación de su solución gráfica:
Veamos los siguientes ejemplos de la solución de una inecuación, encontrando los valores de $x$ que cumplen la desigualdad y la representación de su solución gráfica:
Resolver la inecuación no acotada $\quad 3x - 10 > 5$ $$ 3x > 5 - 10 \quad \quad $$ $$ x > {-5 \over 3} \quad \quad \quad$$
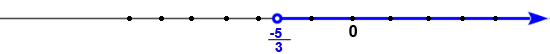
Resolver la inecuación acotada $\quad \displaystyle 2 < 3x - 7 \le {2x-7 \over 4}$ $$ 2 < 3x-7 \land\quad 3x-7\le {2x-7 \over 4}$$ $$ 9 < 3x \quad\land\quad 12x-28\le 2x-7$$ $$ 3 < x \quad\land\quad x\le {21 \over 10}$$

Capitulo VIII. Inecuaciones $\qquad$
 xploremos.
xploremos.
Ejemplos de soluciones de inecuaciones lineales.
Observa la representación de un intervalo acotado, la desigualdad y su representación gráfica, oprime el botón otro ejemplo para ver diferentes ejemplos.
Los puntos de color rojo, representan los extremos del intervalo:
$\color{red} \circ \quad {\displaystyle \longrightarrow } \quad$ No se incluye el extremo, intervalo abierto $(\space)$.
$\color{red} \bullet \quad {\displaystyle \longrightarrow } \quad$ Si se incluye el extremo, intervalo cerrado $[\space]$.


Resuelve el ejercicio planteado, verifica con el botón solución , para generar un nuevo ejercicio, oprime el botón ejercicio , veamos primero el siguiente ejemplo:
$$ - 10 < 2x - 2 \le -2$$ $$ 2 - 10 < 2x \le -2 + 2$$ $$ -8 < 2x \le 0$$ $$ {-8 \over 2} < x \le {0 \over 2}$$ $$ -4 < x \le 0$$
Capitulo VIII. Inecuaciones $\qquad$

 Se plantean 4 inecuaciones lineales a continuación:
Se plantean 4 inecuaciones lineales a continuación:

Primero que debemos hacer, recordemos las propiedades de las ecuaciones de 2° grado, teniendo en cuenta sus diferentes soluciones analizando el discriminante $d = b^2 -4ac$ que indica que tipo de solución tiene la ecuación (

Con la información anterior obtenida, el proceso de solución de la inecuación consiste en:
Capitulo VIII. Inecuaciones $\qquad$
Ubicamos los valores encontrados y identificamos los intervalos generados, sustituimos un valor de cada intervalo en el factor para obtener el signo que se determina.
Observemos el signo del factor $x - 7$:
Si $x < 7,$ sustituimos $x$ por $1 \quad {\displaystyle \longrightarrow } \quad 1-7=-6 \quad {\displaystyle \longrightarrow } \quad (-)$.
Si $x > 7,$ sustituimos $x$ por $9 \quad {\displaystyle \longrightarrow } \quad9-7 = 2 \quad {\displaystyle \longrightarrow } \quad (+)$.

Observemos el signo del factor $x + 6$:
Si $x < -6,$ sustituimos $x$ por $-8 \space {\displaystyle \longrightarrow } \space -8+6=-2 \space {\displaystyle \longrightarrow } \quad (-)$.
Si $x > -6,$ sustituimos $x$ por $2 \quad {\displaystyle \longrightarrow } \quad 2+6 = 8\quad {\displaystyle \longrightarrow } \quad (+)$.
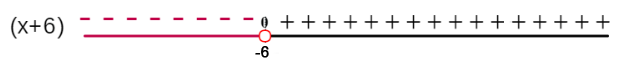
¿Que sucede en el caso que la ecuación no tenga solución real?
Por tanto la solución de la inecuación $x^2 - x -42 < 0$, son los valores donde los intervalos son negativos:
por tanto, la solución es: $\quad -6 < x < 7=(-6, 7)$
Si la inecuación fuera $x^2 - x -42 \le 0$, significa que ahora se admiten valores que al evalúar el polinomio el resultado sea cero: $$(-6)^2 - (-6) -42 \le 0$$ $$(7)^2 - (7) -42 \le 0$$ Por tal motivo, se incluye $-6$ y $7$ en la solución: $\quad [-6, 7]$.
Podemos expresar la solución de la inecuación mediante una representación gráfica o un intervalo.
Si la desigualdad tiene este signo $≥ o ≤$, los valores en la recta son un circulo relleno y se ubica en corchetes en la solución.
Capitulo VIII. Inecuaciones $\qquad$
 xploremos.
xploremos.
Ejemplos de la solución de una inecuación cuadrática.
Comprueba la solución, toma un valor de cada intervalo, remplaza en el polinomio inicial y verifica el signo del resultado obtenido.
Seleccione el signo de la desigualdad para cambiar la inecuación, oprime el botón ejemplo para ver diferentes ejemplos.
Responde a la siguiente pregunta:
Cuándo tenemos inecuaciones con expresiones racionales se realizan los siguientes pasos:
 xploremos.
xploremos.
Observa ejemplos de inecuaciones con expresiones racionales:
Capitulo VIII. Inecuaciones $\qquad$
 jercicio.
jercicio.
Resuelve las siguientes inecuaciones cuadráticas y racionales.
 Indicaciones
Indicaciones
Analiza la inecuación propuesta.

 Evaluamos lo aprendido.
Evaluamos lo aprendido.
Prepárate para la evaluación y mide tus conocimientos de lo aprendido en este capítulo, responde las preguntas a continuación:
 Evaluación - 10 preguntas con límite de tiempo - (10 minutos)
Evaluación - 10 preguntas con límite de tiempo - (10 minutos)
Clic en el link, responde y envía los resultados por e-mail.

 $\quad$ Envía tu evaluación
$\quad$ Envía tu evaluación
$\space$ Evaluación: Capítulo VIII
Tomada de la Red Educativa Digital Descartes.
"Las matemáticas son la ciencia de lo que está claro por sí mismo".
Carl Gustav Jacob Jacobi
DERECHOS BÁSICOS DE APRENDIZAJE (DBA)
DBA.2. Construye representaciones, argumentos y ejemplos de propiedades de los números racionales y no racionales.
DBA.5. Utiliza teoremas, propiedades y relaciones geométricas (teorema de Tales y el teorema de Pitágoras) para proponer y justificar estrategias de medición y cálculo de longitudes.
DBA.8. Identifica y analiza relaciones entre propiedades de las gráficas y propiedades de expresiones algebraicas y relaciona la variación y covariación con los comportamientos gráficos, numéricos y características de las expresiones algebraicas en situaciones de modelación.
DBA.9. Propone, compara y usa procedimientos inductivos y lenguaje algebraico para formular y poner a prueba conjeturas en diversas situaciones o contextos.

DESEMPEÑOS / ESTÁNDAR
Pensamiento numérico
1.2 M.IV Resuelvo problemas y simplifico cálculos usando propiedades y relaciones de los números reales y de las relaciones y operaciones entre ellos. DBA 2.
Pensamiento espacial
2.4 M.IV Uso representaciones geométricas para resolver y formular problemas en las matemáticas y en otras disciplinas. DBA 5.
Pensamiento variacional y sistemas algebraicos y analíticos
5.1 M.IV Identifico relaciones entre propiedades de las gráficas y propiedades de las ecuaciones algebraicas. DBA8, 9
5.5 M.IV Identifico diferentes métodos para solucionar sistemas de ecuaciones lineales. DBA2, 8.
Capitulo IX. Números Complejos $\qquad$
Si se llega a la siguiente situación al resolver una ecuación, donde:
$$x^2 = -1$$ $$x = \sqrt{-1}$$ Este tipo de ecuación o similar, no tiene solución en el conjunto de los números reales ($\mathbb{R}$).
Este tipo de ecuación o similar, no tiene solución en el conjunto de los números reales ($\mathbb{R}$).
En esta sección se analizará el estudio de números no reales que provienen de una raíz par de un número negativo, para esto, veamos la siguiente definición:
Un número Imaginario ($\mathbb{I}$) puede describirse como el producto de un número real por la unidad imaginaria $i$, es decir, la expresión $bi$, donde $i = \sqrt{-1}$ llamada unidad imaginaria. Este número Imaginario $i$ se le conoce también como constante imaginaria, ejemplos:
$$\quad \sqrt{-4} =\sqrt{4}.\sqrt{-1} = 2i$$ $$-\sqrt{-25}=-5i, \qquad \sqrt{-{4 \over 9}}={2 \over 3}i, \qquad \sqrt{-5}=\sqrt{5}i$$Este tipo de números se conocen como números imaginarios puros y se representan también como una pareja ordenada de la forma $(0, b)$, donde la primera componente es nula.
$$ 3i = (0, 3)$$Análisis de las potencias de $i$
$i = \sqrt{-1}$
$i^2 = (\sqrt{-1})^2 = -1$
$i^3 = (\sqrt{-1})^3 = (\sqrt{-1})^2.(\sqrt{-1}) = -\sqrt{-1} = -i$
$i^4 = (\sqrt{-1})^4 = (\sqrt{-1})^2.(\sqrt{-1})^2 = 1$
$i^5 = (\sqrt{-1})^5 = (\sqrt{-1})^2.(\sqrt{-1})^3 = (-1)(-\sqrt{-1}) = \sqrt{-1} = i$
$i^6 = (\sqrt{-1})^6 = (\sqrt{-1})^2.(\sqrt{-1})^4 = (-1)(1) = -1$
$i^7 = (\sqrt{-1})^7 = (\sqrt{-1})^2.(\sqrt{-1})^5 = (-1)(\sqrt{-1}) = -\sqrt{-1} = -i$
$i^8 = (\sqrt{-1})^8 = (\sqrt{-1})^2.(\sqrt{-1})^6 = (-1)(-1) = 1$
$i = i^5 = i^9 = i^{13}...... = i \quad \quad{\displaystyle \longrightarrow } \quad$ Múltiplos de 4 más 1
$i^2 = i^6 = i^{10} = i^{14}... = -1 \quad {\displaystyle \longrightarrow } \quad$ Múltiplos de 4 más 2
$i^3 = i^7 = i^{11} = i^{15}... = -i \quad {\displaystyle \longrightarrow } \quad$ Múltiplos de 4 más 3
$i^4 = i^8 = i^{12} = i^{16}... = 1 \quad \quad{\displaystyle \longrightarrow } \quad$ Múltiplos de 4
Si $n$ es par $(-1)^n = 1$
Si $n$ es impar $(-1)^n = -1$

$i^{47}= (i^2)^{23}.i = (-1)^{23}.i = (-1).i = -i = -\sqrt{-1}$
$i^{80}= (i^2)^{40} = (-1)^{40} = (1)$
Capitulo IX. Números Complejos $\qquad$
Los números complejos ($\mathbb{C}$), están formados por una parte real "$a$" y una parte imaginaria "$bi$", donde $a, b$ son números $\mathbb{R}$ que representan una pareja ordenada $(a, b)$ y se expresan en forma binómica:
$$z =(a, b)= a + bi $$
En el caso en que $b=0$, se tendrá un número de la forma $a+0i$, el cual corresponde a un número $\mathbb{R}$, por lo que se puede concluir que todos los números $\mathbb{R}$ son también números Complejos, donde la parte imaginaria sería cero, observa la escritura de algunos números complejos:
|
|
|
|
|---|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Generalmente un número complejo se representa por medio de un vector, veamos en el plano la representación de un número Complejo $(a, b)$ y su forma binómica $z = a + bi$:
 xploremos.
xploremos.
Mueve el control o ingresa los valores para cada componente, observa el vector que se genera del complejo $z=(a, b)=a + bi$.
Capitulo IX. Números Complejos $\qquad$
Para sumar o restar números complejos se suman o se restán las partes reales y las partes imaginarias, si se tienen dos números complejos en forma binómica, entonces la suma o resta será:
$$z_1 = a+bi, \quad z_2 = c+di$$ $$z_1 \pm z_2 = (a \pm c)+ (b \pm d)i$$
 Ingresa los valores para cada componente del número complejo, observa la suma de los números.
Ingresa los valores para cada componente del número complejo, observa la suma de los números.
Si los números complejos están en forma de pareja ordenada, su suma o diferencia se expresa similar a la forma binómica.
Si los números están como pareja ordenada, la primera componente es la suma o resta de las partes reales $(a_1 \pm a_2)$ y la segunda componente es la suma o resta de las partes imaginarias $(b_1 \pm b_2)i$. $$z_1 \pm z_2 =(a, b) \pm (c, d) = (a \pm c, b \pm d)$$ $$ (3, 5) + (2, -3) = (3+2, 5+(-3)) = (5, 2) = 5 + 2i$$
Responde a la siguiente pregunta:
Representación de operaciones en el plano 
Para sumar dos vectores gráficamente de manera sencilla, es utilizado el método del paralelogramo.
Consiste en colocar los dos vectores iniciales con su magnitud, dirección y sentido en el origen, de manera que los dos vectores inicien en el mismo punto.
Los dos vectores forman dos lados adyacentes del paralelogramo, los otros lados se construyen trazando líneas paralelas a los vectores opuestos de igual longitud.
El vector suma resultante se representa mediante un vector dado por la diagonal del paralelogramo, partiendo del origen en el que se unen los vectores hasta la intersección de las paralelas trazadas.
Capitulo IX. Números Complejos $\qquad$
 xploremos.
xploremos.
Método del paralelogramo para sumar números complejos.
 Ingresa los valores para cada componente del número complejo, observa su gráfica.
Ingresa los valores para cada componente del número complejo, observa su gráfica.

Para realizar la multiplicación de números complejos, se opera como una multiplicación entre binomios, se aplica la propiedad distributiva. Si se tienen dos números complejos, entonces la multiplicación será:
$$z_1 = a+bi$$ $$z_2 = c+di$$ $$z_1 \cdot z_2 = (a + bi)(c + di) = ac + (ad)i + (bc)i + (bd)i^2$$ $$z_1 \cdot z_2 = (ac - bd)+ (ad + bc)i$$Componente real: $\displaystyle\quad a = {a \over a^2+b^2} = {-3 \over (-3)^2 + 5^2} = {-3 \over 34}$
Componente imaginario: $\displaystyle\quad bi = {-b \over a^2+b^2} = {-5 \over (-3)^2 + 5^2} = {-5 \over 34}$
Por lo tanto, el inverso multiplicativo es: $\displaystyle\quad z^{-1} = -{3 \over 34} - {5 \over 34}i$
Capitulo IX. Números Complejos $\qquad$

 Ingresa los valores para cada componente del número complejo, observa las respuestas.
Ingresa los valores para cada componente del número complejo, observa las respuestas.
El sistema de los números complejos tiene la propiedad de la existencia del inverso multiplicativo o recíproco para todo número distinto de cero. La propiedad del inverso multiplicativo se refiere a que para cada número $z$, distinto de cero, existe un número, llamado el inverso, denotado por $z^{−1}$, que cumple:
$$z\cdot z^{-1} = 1$$El complejo conjugado, o simplemente la conjugada, de un número complejo $z = a + bi $, es otro complejo, y esta dado porla expresión:
$$\bar{z} = a - bi = (a, -b)$$La conjugada es: $\quad \bar{z} = -3 - 5i = (-3, -5)$
 xploremos.
xploremos.
Observa un número complejo y su conjugada:
 Ingresa los valores para cada componente del número complejo, observa la conjugada.
Ingresa los valores para cada componente del número complejo, observa la conjugada.
Capitulo IX. Números Complejos $\qquad$
 $$(c + di).(c - di)=c^2-(di)^2$$
donde $\quad i^2=(-1), \quad$ entonces, se tiene que:
$$c^2-d^2(i)^2=c^2-d^2(-1)=(c^2+d^2) \in \mathbb{R}$$
$$(c + di).(c - di)=c^2-(di)^2$$
donde $\quad i^2=(-1), \quad$ entonces, se tiene que:
$$c^2-d^2(i)^2=c^2-d^2(-1)=(c^2+d^2) \in \mathbb{R}$$
Conjugada de $\quad z=5 + 2i\quad {\displaystyle \longrightarrow } \quad \bar{z}=5 + 2i$
$z\cdot\bar{z}=(5 + 2i)(5 - 2i)=5^2+2^2=14$
Para dividir por un número complejo, se multiplica el dividendo y el divisor por el conjugado del divisor, veamos el siguiente proceso en la división de dos números: $$z_1 = a+bi$$ $$z_2 = c+di$$
Conjugada del divisor $\quad {\displaystyle \longrightarrow } \quad \bar{z_2} = c-di$
$${z_1 \over z_2} = {(a + bi) \over (c + di)}.{(c - di) \over (c - di)}$$Para este ejemplo, se tiene que la parte real es cero, por tanto, el número complejo se representa como: $$z =(0, -{14 \over 5})=0 -{14 \over 5}i$$
Responde a la siguiente pregunta:

¡Recuerda! , que al multiplicar un número complejo por su conjugada, se obtiene un número real, la parte imaginaria es cero.
$$z.\bar{z}=(c + di).(c - di)=c^2+d^2$$Capitulo IX. Números Complejos $\qquad$
 jercicio.
jercicio.
Operaciones entre números complejos-
 Resuelve los 6 ejercicios propuestos con número complejos y verifica tus respuestas, oprime el botón solución
.
Resuelve los 6 ejercicios propuestos con número complejos y verifica tus respuestas, oprime el botón solución
.
 Evaluamos lo aprendido.
Evaluamos lo aprendido.
Prepárate para la evaluación y mide tus conocimientos de lo aprendido en este capítulo, responde las preguntas a continuación:
 Evaluación - 12 preguntas con límite de tiempo - (12 minutos)
Evaluación - 12 preguntas con límite de tiempo - (12 minutos)
Clic en el link, responde y envía los resultados por e-mail.

 $\quad$ Envía tu evaluación
$\quad$ Envía tu evaluación
$\space$ Evaluación: Capítulo IX
Plantillas con Descartes-JS
"La naturaleza está escrita en lenguaje matemático".
Galileo Galilei