Matemáticas Operativas
INTERACTIVO
Marco Tulio Mesa Cardona
Institución Universitaria Pascual Bravo

Fondo Editorial Pascual Bravo
Medellín
2020
Título de la obra:
Matemáticas Operativas
Autor:
Marco Tulio Mesa Cardona
Diseño del libro: Juan Guillermo Rivera Berrío
Código JavaScript para el libro: Joel Espinosa Longi, IMATE, UNAM.
Recursos interactivos: DescartesJS
Fuentes: Lato y UbuntuMono
Fórmulas matemáticas: $\KaTeX$
Colaborador: Juan Guillermo Arango Arango
Fondo Editorial Pascual Bravo
Calle 73 73A-226
PBX: (574) 4480520
Apartado 6564
Medellín, Colombia
www.pascualbravo.edu.co
ISBN: 978-958-52584-7-1
LICENCIA
Este libro de texto "Matemáticas Operativas" se ha trabajado para hacer del estudio de las matemáticas una actividad interesante, agradable e interactiva, manteniendo el rigor matemático inherente a la asignatura. Con este objetivo en mente, el contenido se ha desarrollado y organizado para proporcionar una progresión lógica de conceptos fundamentales a conceptos más avanzados, basándose en lo que los estudiantes ya han aprendido y enfatizando en las conexiones entre temas y entre teoría y aplicaciones. El objetivo es permitir que los estudiantes no solo reconozcan los conceptos, sino que trabajen con ellos de manera que sean útiles en cursos posteriores y carreras futuras.
La obra incluye 110 escenas interactivas, diseñadas en DescartesJS y GeoGebra, lo que facilita un mayor acercamiento a los conceptos trabajados. Se incluyen, también, 15 vídeos subidos a YouTube de diversos autores, que apoyan el desarrollo de los contenidos de la obra.
La obra se ha dividido en cinco capítulos, que responden al currículo de la asignatura "Matemáticas Operativas" de la Institución Universitaria Pascual Bravo; no obstante, el texto también es útil en niveles de secundaria o para otras instituciones de educación superior, que incorporan, en sus planes de estudio, cursos de matemáticas en un nivel básico o, si se prefiere, de nivelación postsecundaria.
Para evitar, al máximo, la dependencia con la conectividad en la red, las expresiones matemáticas se han construido recurriendo al API de $\KaTeX$.

El conjunto se formalizó para dar respuesta a la necesidad de contar en una base generalizada, la base $10$. Con los dígitos se forma cualquier número natural. El conjunto de los números naturales, se denota por $ℕ$, y se representa así:
$$\color{brown}ℕ=\{ 1,2,3,4,5,6,7,...\}$$El conjunto surge de la necesidad de dar solución general a la sustracción, cuando el sustraendo es mayor que el minuendo, esta sustracción no tiene solución en los números Naturales. Por ejemplo: $5-20$? Se denota por (ℤ) y se representa así:
$$\color{brown}ℤ=\{ ...,-3,-2,-1,0,1,2,3,...\}$$Son un subconjunto de los números reales, conformado por el conjunto de los enteros (ℤ) y los naturales (ℕ). Es el resultado del cociente entre dos enteros $\frac{p}{q}$, siempre y cuando el denominador ($q$) sea diferente de cero.
$$\color{brown}ℚ=\bigg\lbrace\dfrac{p}{q}\bigg|p\hspace{0.1cm}y\;q\;\text{\;son\;números\;enteros},\;q=\not 0\bigg\rbrace$$Los números racionales se ubican en una de las siguientes características: Ser entero, tener una expresión decimal finita, o tener una expresión decimal infinita periódica.
 Ejemplos con fracciones
Ejemplos con fracciones$\cfrac{10}{2} = 5, \quad \cfrac{30}{8} = 3,75$ y $\cfrac23 = 0,66666666$
En la siguiente escena interactiva, diseñada por Carlos Rojas HincapiéCarlos Rojas Hincapié es un autor de la red Descartes, que publicó el libro "Matemáticas Básicas", del cual seleccionaremos algunas escenas interactivas en el resto de esta obra., lo cual permitirá que se presente una representación gráfica, dividiendo cada intervalo de una recta numérica en espacios iguales que representan números enteros. También, puedes hacer uso del zoom para visualizar mejor la partición en la recta numérica o, si lo deseas, hacer clic en el botón ampliar para ver la escena en un tamaño más grande.
Prueba con las siguientes fracciones: $\cfrac{3}{4}$, $\cfrac{7}{5}$, $\ldots$
Es el conjunto de números cuya expresión decimal no es finita ni periódica, estos números no pueden transformarse en una fracción. Se denota con la letra (ℚ'). Como ejemplos de ellos tenemos todas las raíces no exactas como $\sqrt{3}$, $\sqrt{5}$, etc., igualmente el número $\pi$, la constante "e" de la base de los logaritmos naturales, entre otros.
Representación gráfica del conjunto de los números reales: En la Figura 1, se puede visualizar la representación gráfica de los números reales.

Figura 1. Conjuntos numéricos (adaptado del libro Precálculo de Stewart).
Es el conjunto de números formado por la unión de los números Racionales (ℚ) y los Irracionales (ℚ'). Se denota por la letra $ℝ$ y se representa así:
$ℝ = \{ ℚ \cup ℚ' \}$
Veamos algunas de ellas: Sean $a$, $b$ y $c$ números reales cualesquiera. Puedes ampliar la imagen al hacer clic sobre ella.

Tabla 1. Propiedades de las operaciones en ℝ.
Es el conjunto formado por la unión de los números reales y los números imaginarios. Un número complejo puede representarse de la forma $a + bi$, que es la suma de un número real y un número imaginario. Se denota por ℂ y se representa así:
$ℂ = \{ ℝ \cup i \}$
Los números imaginarios son números complejos, cuya parte real es igual a cero, por ejemplo: los números $5i$, $i$ o $–i$ son números imaginarios, donde la letra $i$ denota la raíz cuadrada de $-1$. Esto es:
Antes de empezar a clasificar los números propuestos en la escena interactiva, de nombre “Clasifica los siguientes números” y así dar inicio a las operaciones básicas que te abrirán el camino para resolver ejercicios en contexto aplicando conjuntos numéricos y propiedades de las expresiones aritméticas, en el siguiente video, realizado por César Moisés Grillo Soliz, recordarás lo que se ha visto hasta el momento.
En la siguiente escena interactiva, diseñada por Carlos Rojas Hincapié, podrás identificar el número dado, al oprimir los botones correspondientes según el conjunto numérico al cual pertenece.
Basta con oprimir el botón correspondiente ℕ (Naturales), ℤ (Enteros), ℚ (Racional), ℚ' (Irracional) o ℝ (Real) y verifica la respuesta. Intenta obtener la mayor cantidad de aciertos, recuerda que un racional puede ser un entero.
Podrás observar, como un número a parte de pertenecer al conjunto de los reales, puede ser ℕ (Natural) y/o, ℤ (Entero) y/o, ℚ(Racional) y/o, ℚ' (Irracional), según el caso.
como ejemplos, de lo que puedes encontrar en la escena interactiva, podemos mencionar: $-79$, que es un entero, racional y real al mismo tiempo, o ${\sqrt{80}}$, que es irracional y real, o $-\cfrac{18}{15}$ que es racional y real.
Cuando se realizan operaciones entre los conjuntos numéricos, se debe tener en cuenta la aplicación de las propiedades mencionadas anteriormente.
En caso de presentarse signos de agrupación, como llaves, corchetes o paréntesis, se recomienda tener en cuenta las siguientes indicaciones:
$\bullet\hspace{0.3cm}$Los signos de agrupación indican el orden en que se deben realizar las operaciones.
$\bullet\hspace{0.3cm}$Los paréntesis deben estar dentro de los corchetes y los corchetes dentro de llaves.
$\bullet\hspace{0.3cm}$Cuando se eliminan signos de agrupación, es recomendable iniciar con los más internos.
$\bullet\hspace{0.3cm}$Un signo negativo, antes de un signo de agrupación, cambia todos los signos internos.
$\bullet\hspace{0.3cm}$No olvides la ley de los signos que se muestran en la gráfica.
$\bullet\hspace{0.3cm}$Se quitan primero los parénesis, luego los corchetes y finalmente las llaves.
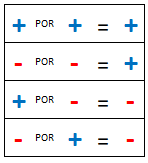
$\bullet\hspace{0.3cm}$Se tienen en cuenta los signos de las diferentes operaciones aritméticas, sin olvidar que signos iguales dan positivo y signos contrarios dan negativo.
$\bullet\hspace{0.3cm}$En operaciones aritméticas mixtas, primero se realizan las multiplicaciones y divisiones y luego las sumas y restas.

Figura 2. La jerarquía de las operaciones.
Fuente: https://www.twinkl.com
 Ejemplos de operaciones con los reales.
Ejemplos de operaciones con los reales.En los siguientes ejemplos, podrás observar el orden en que se deben hacer las operaciones, para eliminar los signos de agrupación.
1. 13 + {2 + [6 + 3 + (8 + 7) ] }
13 + { 2 + [ 6 + 3 + ( 8 + 7 ) ] } = 13 + { 2 + [ 9 +15 ] }
13 + { 2 + [ 9 + 15 ] }
13 + { 2 + 24 }
Se eliminaron los paréntesis y se agrupan, $8+7$, al mismo tempo se agrupan $6+3$ y $9+15$.
Se suma la cantidad entre llaves, { 2 + 24 }
13+26
39
Se eliminaron las llaves y se agrupan $2+24$.
Se agrupan $13+26$.
2. 13 - { 2 + [ 6 +3 - ( 8 + 7 ) ] }
13 - { 2 + [ 6 + 3 - ( 8 + 7 ) ] } = 13 - { 2 + [ 9- ( 15 ) ] }
13 - { 2 + [ 9 - 15 ] }
13 - { 2 + [ - 6 ] }
13 - { 2 - 6 }
13 - { -4 }
13 + 4
17
Se eliminaron los paréntesis, haciendo operación de signos y agrupando.
Se eliminaron los corchetes, haciendo operación de signos y agrupando.
Se eliminan las llaves y se hacen las operaciones de signos y agrupando.
3. 20 - { 7 + 2 [ 3 - 2 ( 7 + 9 ) + 5 ( 6 - 2 ) ] }
20 - { 7 + 2 [ 3 - 2 ( 7 + 9 ) +5 ( 6 - 2 ) ] } = 20 - {7 + 2 [3 - 2 (16) + 5 (4 ) ] }
20 - { 7 + 2 [ 3 - 32 + 20 ] }
20 - { 7 + 2 [ - 9 ] }
20 - { 7 - 18 }
20 - { -11 }
20 + 11
31
En la siguiente escena interactiva, diseñada por Leopoldo Aranda Murcia.Leopoldo Aranda Murcia, es un autor de la red GeoGebra, que publicó la escena interactiva "Suma de enteros en el Mar versión 2"., podrás realizar sumas y restas de números enteros.
No debes olvidar que signos iguales se suman y se coloca el mismo signo, signos contrarios se restan y se coloca el signo del mayor.
En la siguiente escena interactiva, diseñada por Ceferino A.Ceferino A., es un autor de la red GeoGebra, que publicó la escena interactiva "Operanteros"., puedes seguir realizando operaciones con números enteros.
TEOREMA FUNDAMENTAL DE LA ARITMÉTICA.
Todo entero positivo se puede representar de forma única como producto de factores primos excepto por el orden.
 Ejemplo del Teorema fundamental de la aritmética
Ejemplo del Teorema fundamental de la aritméticaNÚMEROS PRIMOS.
Eratóstenes de Cirene (276-194 a de C) Matemático griego, ideó una forma de determinar los primeros números primos al construir la denominada Criba de Eratóstenes.
En la siguiente tabla encontrarás los primeros 100 números primos, que te serán de utilidad cuando estés descomponiendo números para determinar el m.c.m y el M.C.D, amplia haciendo clic sobre ella.
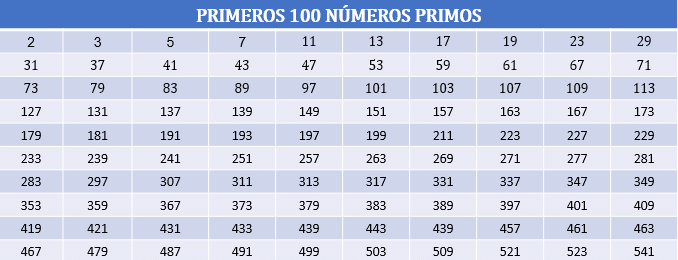
Tabla 2. Primeros 100 números primos.
MÍNIMO COMÚN MÚLTIPLO
Hallar al m.c.m entre $4, 8$ y $12$
$m_{\left( 4\right) }=\left\{ 4,8,12,16,20,\red{24},\ldots\right\}$
$m_{\left( 8\right) }=\left\{ 8,16,\red{24},\ldots\right\}$
$m_{\left( 12\right) }=\left\{ 12,\red{24},\ldots\right\}$
Así, el $m_{\left(4,8,12\right) }=\left\{\red{24}\right\}$
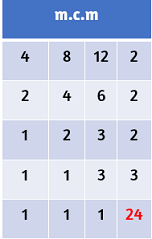
Por el método abreviado, se descomponen en todos los números en sus factores primos a la vez, teniendo en cuenta que si en alguno no coincide con el factor que se está sacando, se baja el número, hasta llegar a la unidad y luego se multiplican los factores verticalmente.
Otro método es descomponer los números en factores primos y tomar los factores comunes y no comunes con su mayor exponente.
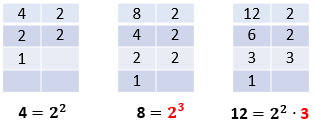
$m.c.m_{\left(4,8,12\right) }=\left\{\red{2^3\times3}\right\}$
$m.c.m_{\left(4,8,12\right) }=\left\{\red{24}\right\}$
MÁXIMO COMÚN DIVISOR
$M.C.D_{\left(48,60\right) }=\left\{\red{2^2\times3}\right\}$
$M.C.D_{\left(48,60\right) }=\left\{\red{12}\right\}$
Por el método abreviado, se descomponen todos los números en sus factores primos a la vez, teniendo en cuenta que si en alguno no coincide con el factor que se está sacando, se baja el número, hasta llegar a la unidad y luego se multiplican los factores comunes a todos.
$M.C.D_{\left(48,60\right) }=\left\{\green{12}\right\}$

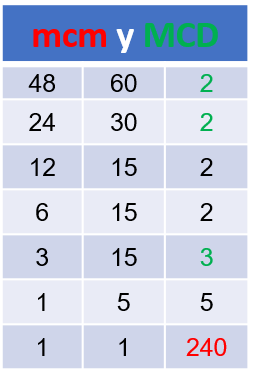
Hallar el M.C.D y el m.c.m entre:
Puedes utilizar la siguiente escena interactiva, adaptada de Eduardo Barbero Corral, sólo necesitas ingresar cada número en la casilla inferior derecha y pulsar "Enter" y con los resultados obtenidos determinar el M.C.D y el m.c.m.
 Ejemplo para hallar el M.C.D y el m.c.m
Ejemplo para hallar el M.C.D y el m.c.mPara hallar el M.C.D, son los factores primos comunes, con su menor exponente.
Para hallar el m.c.m, son los factores primos comunes y no comunes, con su mayor exponente.
$\;\;\;\;M.C.D_{\left(148,156\right) }=\red{4}$
$\;\;\;\;m.c.m_{\left(148,156\right) }=\left\{{4\times3\times13\times37}\right\}$
$\;\;\;\;m.c.m_{\left(148,156\right) }=\red{5772}$
Observa la forma abreviada y compara con los resultados anteriores.
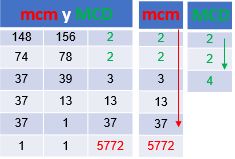
En la siguiente escena interactiva, encontrarás seis ejercicios de aplicación de mínimo común múltiplo (mcm) y de máximo común divisor (MCD), en la cual podrás identificar en que tipo de problemas puedes utilizar cada uno de ellos.
Debes identificar cual de los dos debes utilizar mcm=1 o MCD=2, e ingresarlo en la casilla "Elegir". Cuando la escena te indique que es "¡CORRECTO!" habilita las "Respuestas" y te da la posibilidad de ingresar los datos que te plantea el problema en estricto orden en las casillas correspondientes, no olvides ingresar uno de los datos en las casillas restantes en caso de ser necesario, es decir, cuando el
problema plantea dos o tres datos para analizar ingresa uno de los dos o tres en la casilla restante.
CRITERIOS DE DIVISIBILIDAD
En tu cuaderno, para la siguiente tabla; escriba sí o no para indicar si el número de la primera columna es divisible por cada uno de los números de la fila superior.
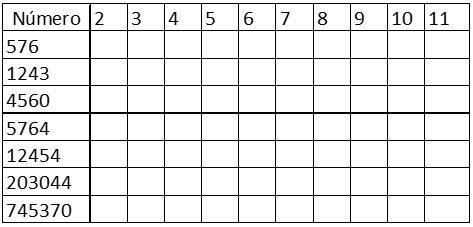
Un número es divisible por otro, cuando cumple las condiciones que presentan a continuación:

Tabla 3. Criterios de divisibilidad.
$\dfrac{a}{b},\;\;con \;\; b=\not0$
Fracciones equivalentes
Dos fracciones son equivalentes cuando el producto de extremos es igual al producto de medios.
Si se multiplica o divide el numerador y el denominador de una fracción por un número entero, distinto de cero, se obtiene otra fracción equivalente a la dada. Al primer caso le llamamos amplificar, al segundo simplificar.
 Ejemplos de fracciones equivalentes
Ejemplos de fracciones equivalentesAmplificar los siguientes racionales
Simplificarlos siguientes racionales
Solución
Amplificar
$\hspace{0.1cm}$
Simplificar
$\hspace{0.1cm}$
Con base en los ejemplos realizados anteriormente y con los que se plantean a continuación, puedes simplificar las expresiones racionales propuestas.
 Ejemplos de simplificación de expresiones racionales
Ejemplos de simplificación de expresiones racionalesPara simplificar expresiones racionales, puedes utilizar los criterios de divisibilidad e ir simplificando paso a paso, o buscar el M.C.D entre el numerador y el denominador y luego, los divides por el valor encontrado.
Utiliza la escena interactiva de la página 38, para que puedas encontrar con facilidad el M.C.D.
Se descompone el numerador y el denominador en sus factores primos:
$45=3^2\times 5$ $\;\wedge\;$ $120=2^3\times 3\times 5$Por la definición del M.C.D, se obtiene:
$\;\;\;\;M.C.D_{\left(45,120\right) }=3\times 5$
$\;\;\;\;M.C.D_{\left(45,120\right) }=$$15$
Ahora se divide numerador y denominador, por el el M.C.D.
$\;\;\dfrac{45\div15}{120\div15}=$$\dfrac{3}{8}$
Factores primos:
$370=2\times 5\times 37$ $\;\wedge\;$ $444=2^2\times 3\times 37$$\;\;\;\;M.C.D_{\left(370,444\right) }=2\times 37$
$\;\;\;\;M.C.D_{\left(370,444\right) }=$$74$
Ahora se divide.
$\;\;\dfrac{370\div74}{44\div74}=$$\dfrac{5}{6}$
Es el momento de poner en práctica los conocimientos adquiridos, realiza los siguientes ejercicios. Recuerda que puedes cambiar el tamaño de la imagen al hacer clic en Tabla 4, o sobre sobre la misma imagen.
Propiedades de las fracciones
En Tabla 4, podrás observar algunas propiedades de las fracciones.

Tabla 4. Propiedades de las fracciones.
Tipos de fracciones
Fracciones Propias:$\hspace{0.1cm}$Cuando el numerador es menor que el denominador. Su valor es mayor que 0 y menor que 1.
Estos son algunos ejemplos de fracciones propias: $\dfrac{2}{5}, \;\dfrac{3}{7} \;y\;\dfrac{9}{11}$
Fracciones Impropias: cuando el numerador es mayor o igual que el denominador. Su valor es mayor o igual a uno.
Ejemplos: $\hspace{0.2cm}\dfrac{5}{2}, \;\dfrac{7}{3}, \;\dfrac{11}{9}\;y\;\dfrac{5}{5}$
En la siguiente escena interactiva, adaptada de Fernanda Mejía Palomino y otroFernanda Mejía Palomino y otro, son autores de la red GeoGebra, que publicaron la escena interactiva "Fracción propia e impropia"., podrás entender la diferencia entre fracciones propias e impropias, en el momento que hagas uso de los deslizadores.
Fracciones Mixtas: Este tipo de fracciones está compuesta de una parte entera y otra fraccionaria. Se obtienen de una fracción impropia, donde la parte entera corresponde al cociente y la fraccionaria del residuo (numerador), dividido por el divisor (denominador), como se muestra en la imagen de la página siguiente.
Ejemplos:
$3\dfrac{2}{5}, \;1\dfrac{3}{7}, \;5\dfrac{9}{11}$Para facilitar su comprensión, analizaremos la fracción impropia $\dfrac{17}{5}$
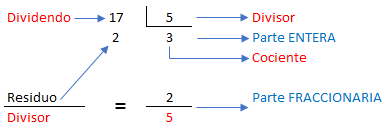
$3\dfrac{2}{5}$
Para pasar un número mixto a una fracción impropia se procede de la siguiente manera:
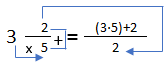
a. Se multiplica la parte entera por el denominador de la parte fraccionaria.
b. Se le suma el numerador de la parte fraccionaria.
c. Luego se divide por el denominador de la parte fraccionaria.
$$\dfrac{17}{5}$$Suma y resta de fracciones: En la suma y resta de fraccionarios se pueden presentar dos tipos de operaciones, cuando tienen el mismo denominador (homogéneas) y cuando su denominador es diferente (heterogéneas).
$\bullet\hspace{0.3cm}$Suma y resta de fracciones homogéneas: En este caso se suman o restan los numeradores y se pone el mismo denominador.
En la siguiente escena interactiva, podrás realizar los ejercicios propuestos al pulsar "Otro ejercicio", para que te familiarices con el procedimiento.
$\bullet\hspace{0.3cm}$Suma y resta de fracciones heterogéneas: Se puede hacer lo siguiente.
Para la suma o resta de dos fraccionarios, con denominadores pequeños (menores que 10), se recomienda aplicar la siguiente propiedad:
 Ejemplos de suma y resta de fracciones
Ejemplos de suma y resta de fracciones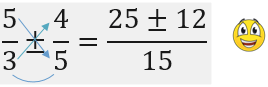
Para la suma o resta de dos fraccionarios, con denominadores grandes (mayores que 10), se recomienda encontrar el (m.c.m) entre los denominadores y hacer lo siguiente:
a. Determinar el m.c.m de los denominadores.
b. Dividir el m.c.m encontrado, por el denominador de la primer fracción.
c. Multiplicar resultado anterior, por el numerador de la primer fracción.
d. Se repite el mismo procedimiento para cada uno de las demás fracción.
e. Finalmente se realizan las operaciones y se simplifica, si es posible.
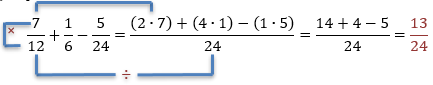
$\bullet\hspace{0.3cm}$ Suma y resta de fracciones mixtas: Para sumar o restar fracciones mixtas, lo más conveniente es convertirlas en fracciones impropias y realizar las sumas o restas como se indicó anteriormente.
También se pueden convertir las fracciones en fracciones equivalentes y de esta forma llevar las operaciones con fracciones heterogéneas. a homogéneas
En el siguiente ejemplo se realiza el procedimiento.
 Ejemplo de suma y resta de fracciones
Ejemplo de suma y resta de fracciones $\dfrac{7}{12}+\dfrac{1}{6}-\dfrac{5}{24}$
Debes realizar los siguientes pasos:
a. Determinar el m.c.m de los denominadores (en el ejemplo es 24).
b. Convertir las fracciones heterogéneas en homogéneas, utilizando el concepto de fracciones equivalentes, esto es, multiplicando numerador y denominador por el factor que haga falta para que el denominador de cada fracción sea igual al m.c.m.
Veamos:
Se realizan las operaciones para obtener fracciones HOMOGÉNEAS.
$\hspace{2.1cm}= \dfrac{14}{24}+\dfrac{4}{24}-\dfrac{5}{24}$
Recuerda que para realizar operaciones con fracciones homogéneas, se toma el mismo denominador y se hacen las operaciones de los numeradores.
$\hspace{2.1cm}= \dfrac{27}{45}-\dfrac{15}{45}+\dfrac{10}{45} \hspace{2.1cm}$
En la siguiente escena interactiva, diseñada por José Luis Abreu León y otrosJosé Luis Abreu León y otros, son autores de la red Descartes, que publicaron la escena interactiva "Fracciones 2"., puedes interactuar, determinando el m.c.m de los denominadores y practicar lo aprendido en las páginas anteriores, y sólo podrás avanzar si aciertas con la información solicitada.
En el siguiente escena interactiva, diseñada por Diego Luis Feria GómezDiego Luis Feria Gómez, es un autor de la red Descartes, que publicó la escena interactiva "Suma de fracciones"., puedes interactuar y ampliar los conocimientos adquiridos.
$\bullet\hspace{0.3cm}$Producto de fracciones: Para multiplicar fraccionarios, se multiplican numeradores y denominadores entre sí. Se aplica la siguiente propiedad:
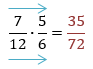
$\bullet\hspace{0.3cm}$División de fracciones: Se multiplica el numerador del primer fraccionario, por el denominador del segundo fraccionario (será el numerador) y el denominador del primero por el numerador del segundo (será el denominador). En conclusión, se multiplican en cruz. Se aplica la siguiente propiedad:
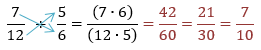
Antes de explicar algunos ejemplos de aplicación sobre operaciones con fracciones, es importante que trates de comprender como se convierte un lenguaje verbal en un lenguaje matemático.
Ejemplo
Expresión Matemática
Ejemplo
Expresión Matemática
 Ejercicios de aplicación
Ejercicios de aplicacióna. La población de un pequeño pueblo disminuyó de 1750 a 1700 habitantes. ¿Cuál es el porcentaje de decrecimiento?
R. $\dfrac{1750-1700}{1750}\times100\%=0.0285714\times100\% =2.86\%$
b. El salario por hora de trabajo de un estudiante se elevó de $5.25$ dólares a $5.75$. ¿Cuál es el porcentaje de incremento?
R. $\dfrac{5.25-5.75}{5.25}\times100\%=0.952381\times100\%=9.52\%$
c. ¿Cuál es el descuento y el precio de oferta de un balón de volibol si el precio normal es de $\$28,60$ y hay $25\%$ de descuento?
R. Descuento $= \$28.6\times0.25\%=\$7.15$
Precio Oferta $= \$28.6\times0.75\%=\$21.45$
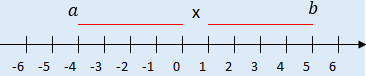
De la gráfica de la recta numérica se puede concluir que $a < x < b$.
$a < x < b$
Si, $a < b, \;a=b \;\vee\; a> b$, se llama ley de tricotomía.
Si, $a < b \wedge b < c,\Rightarrow \hspace{0.1cm}a < c$
Se conoce como Propiedad transitiva.
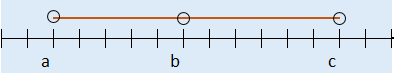
 Ejemplos de de la recta numérica
Ejemplos de de la recta numéricaSi, $x <12 \wedge 12 <y$, concluimos de la propiedad anterior que $x <y$. Veamos el ejemplo gráficamente.
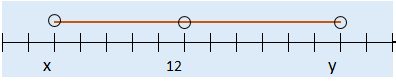
Los intervalos pueden ser abiertos o cerrados, los abiertos se representan con paréntesis y los cerrados con corchetes.
En la siguiente escena interactiva puedes darte cuenta del significado de lo que es un intervalo abierto y un intervalo cerrado. Observa cuando la escena te muestra en las opciones de intervalos, como incluye el valor cuando se trata de un intervalo cerrado y como se acerca con muchas cifras decimales, pero no lo toma cuando se trata de un intervalo abierto. También podrás ver como puedes desplazar el punto rojo, sólo hasta donde el intervalo te lo permite.
Realiza diferentes modificaciones en "Seleccione intervalo" y en el valor del "Extremo inferior" y observa los cambios en la escena interactiva.
En la siguiente escena interactiva, adaptada de Alfredo Cortés SánchezAlfredo Cortés Sánchez, es un autor de la red GeoGebra, que publicó la escena interactiva "Intervalos"., podrás interactuar realizando cambios en los rangos para que profundices en tus conocimientos.
En la siguiente escena interactiva diseñada por Juan Guillermo Rivera, al realizar los ejercicios propuestos, pondrás a prueba los conocimientos adquiridos.
Unión e Intersección de intervalos.
Unión de intervalos: En la unión de intervalos, se encuentran todos los elementos que pertenecen a los conjuntos numéricos en referencia.
 Ejemplo de unión de intervalos
Ejemplo de unión de intervalosSea $A$=$[-1,2)$, $B$ = $\left[ 1,4\right] \wedge C=\left( -3,\infty \right)$
Gráficamente lo podemos representar de la siguiente forma:

En los siguientes ejercicios, podrás ver la respuesta al frente de cada uno para su análisis
Intersección de intervalos: En la intersección de intervalos, se encuentran SÓLO los elementos comunes que pertenecen a los conjuntos numéricos en referencia.
Para una mejor comprensión, se continuará con el mismo ejemplo.
 Ejemplo de intersección de intervalos
Ejemplo de intersección de intervalosSea $A$=$[-1,2)$, $B$ = $\left[ 1,4\right] \wedge C=\left( -3,\infty \right)$
Gráficamente lo podemos representar de la siguiente forma:

Hallar:
Observa que no se incluye el número 2 en la intersección, ya que NO ES COMÚN para el conjunto A.
En la siguiente escena interactiva, adaptada de EducaticMeta EducaticMeta son autores de la red GeoGebra, que publicaron la escena interactiva "ov2 operaciones con intervalos"., podrás interactuar realizando cambios en los rangos para que profundices en tus conocimientos.
En la escena que se presenta, puedes modificar los rangos, utilizando los deslizadores y de forma similar a la escena anterior, puedes cambiar los intervalos, interactuando entre abiertos y cerrados.
En el siguiente video realizado por Matemáticas Profe AlexMatemáticas Profe Alex son autores de la red YouTube, que publicaron el video "Unión e Intersección de intervalos"., vas a repasar los conceptos de intervalos abiertos y cerrados explicados anteriormente y podrás ver cómo influyen en la solución de la unión de intervalos.
De igual forma podrás ver la representación gráfica y en forma de intervalos de la respuesta final.
En el siguiente video realizado por Matemáticas Profe AlexMatemáticas Profe Alex son autores de la red YouTube, que publicaron el video "Unión e Intersección de intervalos"., vas a repasar los conceptos de intervalos abiertos y cerrados explicados anteriormente y podrás ver cómo influyen en la solución de la intersección de intervalos.
De igual forma podrás ver la representación gráfica y en forma de intervalos de la respuesta final.
El valor absoluto de un número $a$, denotado por $\left| a\right|$, es la distancia desde $a$ hasta $0$ sobre la recta numérica. La distancia es siempre positiva o cero, de modo que tenemos para cada número a $\left| a\right| \geq 0$. Tenga en cuenta que $\text–a$ es cuando $a$ es negativa.
Hallar:
En la tabla siguiente, encontrará las principales propiedades del valor absoluto. Así como un ejemplo de cada una de ellas y su descripción.

Tabla 5. Propiedades del valor absoluto.
Distancia entre dos puntos.
Si $a$ y $b$ son números reales, entonces la distancia entre ellos en la recta numérica es:
 Ejemplos de distancia entre dos puntos
Ejemplos de distancia entre dos puntos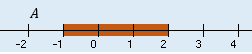
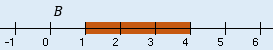
Es un mecanismo matemático que sirve para la solución de problemas que tienen una relación de proporcionalidad, se deben conocer tres datos y con su utilización, se encuentra el cuarto. Siempre que existe un cambio en uno de los datos, los otros cambiarán en forma proporcional.
 Ejemplos de regla de tres simple
Ejemplos de regla de tres simple$\hspace{1cm}$Supuesto$\ldots\ldots\;4\hspace{0.1cm} libros\ldots\ldots\$ 8$
$\hspace{1cm}$Pregunta$\ldots\ldots15\hspace{0.1cm} libros\ldots\ldots\$ x$ $\hspace{3.8cm}\text + \hspace{0.5cm}\\[3pt] \hspace{3.1cm}\overline{}{\hspace{0.5cm}}$Comparamos:
A más libros más pesos; luego, estas magnitudes son directamente proporcionales: ponemos $(+)$ debajo de los libros y $(\text–)$ encima; ponemos $(+)$ también a $\$ 8$. Ahora, el valor de $x$ será igual al producto de $8$ por $15$, que son los que tienen el signo $(+)$, partido por $4$ que tiene $(-)$, y tendremos:
Se define con la variable $x$ = la cantidad de huevos que se necesitan para la elaboración de las 7 tortas.
Solución: $\hspace{3.1cm}{\hspace{0.5cm}}\\[-1pt] \hspace{3.8cm}\text - \hspace{2.2cm}\text + $$\hspace{1cm}$Supuesto$\ldots\ldots\;1\hspace{0.1cm} Torta\ldots\ldots\ 5 \;Huevos$
$\hspace{1cm}$Pregunta$\ldots\ldots7\hspace{0.1cm} Tortas\ldots\ldots\ x\; Huevos$ $\hspace{3.8cm}\text + \hspace{0.5cm}\\[3pt] \hspace{3.1cm}\overline{}{\hspace{0.5cm}}$Al realizar el mismo procedimiento del ejemplo anterior, nos queda:
Como existe una proporcionalidad o equivalencia, lo podemos resolver teniendo en cuenta la definición vista en la pagina 39 para fracciones equivalentes.
Lo que sería:
Luego,
$\dfrac{1}{7}=\dfrac{5}{x}$, se lee uno $(1)$ es a siete $(7)$, como cinco $(5)$ es a $x$.
Aplicamos la definición de fracciones equivalentes y se resuelve de igual forma:
$( 1 ) x = 7 \cdot 5 $, luego:
$\hspace{1cm}$Supuesto$\ldots\ldots 4\hspace{0.1cm} Hombres\ldots\ldots\ 12\;d\text{í}as$
$\hspace{1cm}$Pregunta$\ldots\ldots 7\hspace{0.1cm} Hombres\ldots\ldots\ x\;d\text{í}as$ $\hspace{3.8cm}\text - \hspace{0.5cm}\\[3pt] \hspace{3.1cm}\overline{}{\hspace{0.5cm}}$Comparamos:
A más hombres, menos días; luego, son inversamente proporcionales.
Ponemos $(-)$ debajo de hombres y $(+)$ arriba; ponemos $(+)$ también a $12$ días. Ahora, el valor de $x$ será igual al producto de $12$ por $4$, que son los que tienen signo $(+)$ dividido por $7$ que tiene $(-)$, y tendremos:
 Ejemplo de regla de tres compuesta
Ejemplo de regla de tres compuesta$\hspace{0.1cm}$Tres $(3)$ hombres trabajando $8$ horas diarias han hecho $80$ metros de una obra en $10$ días. ¿Cuántos días necesitarán $5$ hombres trabajando $6$ horas diarias para hacer $60$ metros de la misma obra?
Solución:$\hspace{-1cm}$Supuesto$\ldots 3\hspace{0.1cm} Hombres\ldots8\hspace{0.1cm} Horas(d\text{í}a)\ldots80\hspace{0.1cm} m.\ldots10\hspace{0.1cm}d\text{í}as$
$\hspace{-1cm}$Supuesto$\ldots 5\hspace{0.1cm} Hombres\ldots6\hspace{0.1cm} Horas(d\text{í}a)\ldots60\hspace{0.1cm} m.\ldots \; x \hspace{0.1cm} d\text{í}as$ $\hspace{2.3cm}\text - \hspace{2.2cm}\text{-}\hspace{2cm}\text{+}\hspace{1.3cm}\\[3pt] \hspace{3.1cm}\overline{}{\hspace{0.5cm}}$Comparamos:
A más hombres, menos días; ponemos $(\text–)$ debajo de hombres y $(+)$ encima; a más horas diarias de trabajo, menos días en hacer la obra; ponemos $(\text–)$ debajo de horas diarias y $(\text+)$ encima; a más metros, más días, ponemos $(\text+)$ debajo de metros y $(\text–)$ encima; ponemos $(\text+)$ también a $10$ días.
En la siguiente escena interactiva, adaptada de Leslye RS, Fabián ColomboLeslye RS, Fabián Colombo, Fabián Colombo son autores de la red GeoGebra, que publicaron la escena interactiva "Fracciones, decimales y porcentajes"., podrás observar que el denominador determina en cuantas partes se divide una unidad y el numerador determina la fracción (parte del denominador) o porcentaje que se toma. En la escena interactiva el “lado”, elevado al cuadrado determina el denominador y el deslizador es el numerador.
Observa lo que sucede al ingresar los lados $10, 8, 6$ y mueve el deslizador (numerador) a $50, \;32 \;y\; 18$ respectivamente; en cada uno de ellos.
En cada cambio que realices, sobre la escena interactiva puedes hacer clic izquierdo en tu mouse y dejarlo presionado, desplazando hacia la izquierda o derecha para una mejor visualización de la escena.
Puedes realizar diferentes cambios en el "lado" de la escena interactiva y mover el deslizador para que observes como cambia el fraccionario, el decimal y el porcentaje, en cada uno de los ejercicios que te propongas realizar.
 Ejemplo de fracciones y porcentajes
Ejemplo de fracciones y porcentajes
1.$800.000 - \dfrac{1.800.000\times15}{100 }= 1.800.000 - 270.000 = 1.530.000$. Que sería equivalente a pagar: $1.800.000\times0.85 = 1.530.000$
$1.800.000 - \dfrac{1.800.000\times15}{100 }= 1.800.000 - 270.000 = 1.530.000$. Que sería equivalente a pagar: $1.800.000\times0.85 = 1.530.000$
$1.980.000 + \dfrac{1.980.000\times25}{100}= 1.980.000 + 495.000 = 2.475.000$. Que sería equivalente a pagar: $1.980.000\times 1.25 = 2.475.000$
$\dfrac{290.000 - 250.000}{250.000} = 0.16\times100% = 16\%$
También puedes dividir las ventas de febrero por las ventas de enero y obtienes el incremento $\dfrac{290.000}{250.000}= 1.16$, esto quiere decir que las ventas se incrementaron un $16\%$
En la siguiente escena interactiva, diseñada por @prende.mx@prende.mx son autores de la red Descartes, que publicaron la escena interactiva "Porcentajes y fracciones"., podrás interactuar para observar las distintas maneras de representar porcentajes, explorar la relación existente entre porcentajes y fracciones, aprender a representar porcentajes y fracciones y finalmente podrás a prueba los conocimientos adquiridos al responder sin limite de tiempo 10 preguntas. !Buena Suerte!.
En las siguientes escenas interactivas, diseñadas por Javier Cayetano RodriguezJavier Cayetano Rodriguez es un autor de la red GeoGebra, que publicó la escena interactiva "Aumentos y Disminuciones porcentuales". , podrás resolver los ejercicios planteados con aproximación de dos cifras decimales y pondrás a prueba tus conocimientos.
En las siguientes escenas interactivas, adaptadas de Juan Guillermo Rivera, podrás resolver los ejercicios planteados sobre operaciones con fraccionarios y pondrás a prueba tus conocimientos.
En cada escena interactiva dispones de 45 minutos para realizar los ejercicios e ir eligiendo la respuesta correcta en el cuestionario. Al finalizar tendrás la posibilidad de ingresar tu nombre y enviar las respuestas a tu docente ingresando su correo en el espacio destinado para ello.
Al solucionar los ejercicios propuestos en las escenas interactivas, estarás en capacidad de resolver los ejercicios propuestos para el capitulo 1.
Opción 1. Operaciones con fraccionarios.
Opción 2. Operaciones con fraccionarios.
Opción 3. Operaciones con fraccionarios.
En la potenciación se distinguen tres partes importantes, una base, un exponente y una potencia. El exponente son las veces que se debe multiplicar la base por sí misma y el resultado de este producto, es la potencia.


 Ejemplos de potenciación
Ejemplos de potenciaciónEn la siguiente escena interactiva, adaptada de Orlando, El SuenieroOrlando, El Sueniero, es un autor de la red GeoGebra, que publicó la escena interactiva "Problemas de porcentajes"., podrás resolver los ejercicios planteados y de esta manera ampliar tus conocimientos en potencias de números enteros.
En la siguiente escena interactiva, diseñada por José Luis Abreu León y otrosJosé Luis Abreu León y otros, son autores de la red Descartes, que publicaron la escena interactiva "Potencias y radicales.", podrás analizar las propiedades de las potencias y los radicales con ejercicios propuestos.
Con lo que aprendas en la escena interactiva, estarás en capacidad de resolver correctamente los ejercicios que se presenten sobre potenciación.
En la Tabla 6, se resumen las propiedades de las potencias y las podrás utilizar para realizar las actividades propuestas en la siguiente escena interactiva.
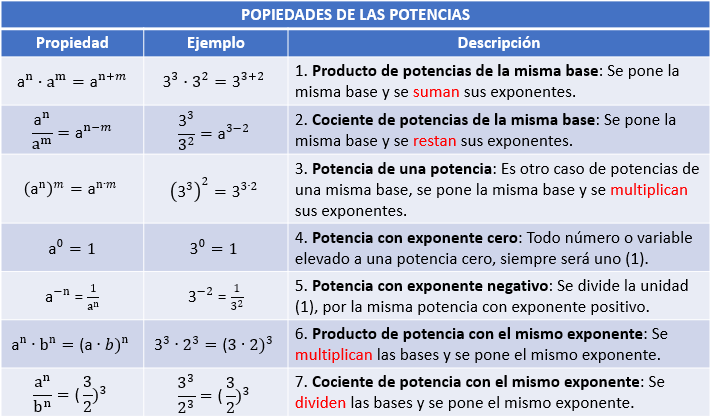
Tabla 6. Propiedades de las potencias.
En la siguiente escena interactiva, diseñada por Erika Paulina Tovilla QuesadaLa escena interactiva fue desarrollada en el ILCE por el Grupo Descartes de México., puedes interactuar y practicar con las propiedades de las potencias.
 Ejemplos de operaciones con potencias potencias
Ejemplos de operaciones con potencias potenciasPara realizar operaciones con potencias, se debe tener en cuenta la aplicación de las propiedades que se vieron con anterioridad, no olvidar que sólo se pueden sumar o restar aquellas potencias idénticas, es decir, que tengan la misma base y el mismo exponente.
Posteriormente se deben realizar las simplificaciones respectivas. A continuación se realizarán algunos ejemplos.
$\bullet\hspace{0.3cm}$Suma:
$$\color{black}\begin{aligned} 5(2^2)+12 &= 5(2^2)+3(2^2)\\[15pt] &= 8(2^2)\\[15pt] &=8(4)=\color{brown}32 \end{aligned}$$$\bullet\hspace{0.3cm}$Resta:
$$\color{black}\begin{aligned} 5(2^2)-12 &= 5(2^2)+3(2^2)\\[15pt] &= 2(2^2)\\[15pt] &=2(4)=\color{brown}8 \end{aligned}$$$\bullet\hspace{0.3cm}$Producto:
$$\color{black}\begin{aligned} 5(2^2)\times12 &= 5(2^2)\times3(2^2)\\[15pt] &= 15(2^4)\\[15pt] &=15(16)=\color{brown}240 \end{aligned}$$Por ser potencias idénticas, se pueden sumar
Se puede observar que el resultado es $\color{brown}32$.
Por ser potencias idénticas, se pueden restar
Se puede observar que el resultado es $\color{brown}8$.
Se descompone el 12 en sus factores primos y por ser potencias idénticas, se pueden multiplicar los coeficientes de las potencias y aplicar las propiedades.
Se puede observar que el resultado es $\color{brown}240$.
$\bullet\hspace{0.3cm}$Cociente:
$$\color{black}\begin{aligned} \dfrac{5(2^2)}{12} &= \dfrac{5({\color{Red}\bcancel {{\color{black}2^2}}})}{3({\color{Red}\bcancel {{\color{black}2^2}}})}\\[15pt] &=\color{brown} \dfrac{5}{3} \end{aligned}$$Se descompone el 12 en sus factores primos y por ser potencias idénticas, se pueden dividir los coeficientes y simplificar las potencias aplicando las propiedades.
Se puede observar que el resultado es $\color{brown}\dfrac{5}{3}$.
Para simplificar expresiones aritméticas racionales con potencias, se aplican las propiedades tanto al numerador y al denominador y luego se simplifica (si es posible).
 Ejemplos de simplificación de expresiones con potencias
Ejemplos de simplificación de expresiones con potenciasEjemplo 1: Se aplican las propiedades de las potencias al numerador y al denominador.
$$\color{black}\begin{aligned} \dfrac{2(3^3)^\frac{1}{3}\cdot5(3^2)^2\cdot3(3^2)^\frac{5}{2}}{3(3^2)^2\cdot4(3^\frac{1}{2})^2\cdot5(3^4)^\frac{1}{2}}&=\dfrac{2(3)\cdot5(3^4)\cdot3(3^5)}{3(3^4)\cdot4(3)\cdot5(3^2)}\\[15pt] &=\dfrac{\quad {\color{Red}\bcancel {{\color{black}30}}}(3^{{\color{Red}\bcancel {{\color{black}10}}}})}{\quad {\color{Red}\bcancel {{\color{black}60}}}({\color{Red}\bcancel {{\color{black}3^7}}})} \end{aligned}$$Se multiplican los coeficientes, luego por ser potencias de la misma base, se suman sus exponentes y finalmente se simplifica.
$$\color{black}\begin{aligned} \dfrac{2(3^3)^\frac{1}{3}\cdot5(3^2)^2\cdot3(3^2)^\frac{5}{2}}{3(3^2)^2\cdot4(3^\frac{1}{2})^2\cdot5(x^4)^\frac{1}{2}}&=\dfrac{\quad {\color{Red}\bcancel {{\color{black}30}}}(3^{{\color{Red}\bcancel {{\color{black}10}}}})}{\quad {\color{Red}\bcancel {{\color{black}60}}}({\color{Red}\bcancel {{\color{black}3^7}}})}\\[15pt] &=\dfrac{3^3}{2}\\[15pt] &=\color{brown}\dfrac{27}{2} \end{aligned}$$Ejemplo 2: Para simplificar expresiones con variables, se procede de igual forma. En el ejemplo se puede ver el procedimiento.
$$\color{black}\begin{aligned} \dfrac{2(x^3)^\frac{1}{3}\cdot5(x^2)^2\cdot3(x^2)^\frac{5}{2}}{3(x^2)^2\cdot4(3^\frac{1}{2})^2\cdot5(x^4)^\frac{1}{2}}&=\dfrac{2(x)\cdot5(x^4)\cdot3(x^5)}{3(x^4)\cdot4(3)\cdot5(x^2)}\\[15pt] &=\dfrac{\quad {\color{Red}\bcancel {{\color{black}30}}}(x^{{\color{Red}\bcancel {{\color{black}10}}}})}{\quad {\color{Red}\bcancel {{\color{black}60}}}({\color{Red}\bcancel {{\color{black}x^7}}})} \end{aligned}$$Se cambió el $3$ por la "$x$" para mostrar que se procede de las misma forma.
Con lo que estudiaste en los ejemplos anteriores, estas en capacidad de resolver los siguientes ejercicios.

El primer intento por representar números demasiados grandes fue emprendido por el matemático y filósofo griego Arquímedes, descrito en su obra El contador de Arena en el siglo III a. C. Ideó un sistema de representación numérica para estimar cuántos granos de arena existían en el universo. El número estimado por él era de 1063 granos.
A través de la notación científica fue concebido el modelo de representación de los números reales mediante coma flotante. Esa idea fue propuesta por Leonardo Torres Quevedo (1914), Konrad Zuse (1936) y George Robert Stibitz (1939). (Wikilibros, 2019)
En la siguiente escena interactiva, adaptada de Juan Guillermo Rivera BerríoJuan Guillermo Rivera Berrío, es un autor de la red Descartes, que publicó la escena interactiva "Emparejamiento tipo 2 (imagen-imagen)." para el presente libro, podrás interactuar y mediante emparejamiento, recordarás y poner a prueba los conocimientos adquiridos.
En la siguiente escena interactiva, podrás comprobar lo que has aprendido sobre potencias, poniendo a prueba tus conocimientos con 8 preguntas que debes responder en 5 minutos.
La expresión $\LARGE\color{brown}\sqrt [b] {c^a}$, que representa la raíz $ n-\text ésima$ principal de $c$ se llama radical, el entero $b$ es el índice del radical y el número real $c$ se llama radicando, con un exponente $a$. Si el índice b es 2, normalmente se omite del radical.

Para convertir expresiones radicales en potencias, debes tener cuenta la siguiente imagen para su conversión.

Expresión en Radicales
$\LARGE\color{brown}\sqrt [b] {c^a}$
Expresión en Exponentes
$\LARGE\color{brown}c^{\frac {a}{b}}$
En la siguiente escena interactiva, diseñada por Miguel Angel Cabezón OchoaMiguel Angel Cabezón Ochoa, es un autor de la red Descartes, que publicó la escena interactiva "Propiedades de los radicales.", podrás analizar las propiedades de los radicales para convertir radicales en potencias en cada uno de los ejercicios propuestos. Analiza las indicaciones de la página anterior.
 Ejemplos con radicales
Ejemplos con radicales$\sqrt {125}=\sqrt {5^2\cdot5}=\color{brown}5\sqrt {5}$
$\sqrt [5] {-32}=\sqrt [5] {-2^5}=\color{brown}-2$
$\sqrt [3] {125}=\sqrt [3] {5^3}=\color{brown}5$
$\sqrt [4] {\dfrac{1}{81}}=\dfrac{\sqrt [4]{1}}{\sqrt[4]{3^4}}=\color{brown}\dfrac{1}{3}$
En la Tabla 7, se resumen las propiedades de la radicación y las podrás utilizar para realizar las actividades propuestas en la siguiente escena interactiva.

Tabla 7. Propiedades de la radicación
En la siguiente escena interactiva, diseñada por Hernán Darío Ortiz AlzateHernán Darío Ortiz Alzate, es un autor de la red Descartes, que publicó la escena interactiva "Radicación"., puedes interactuar y comprender la relación entre la radicación y la potenciación.
En las siguientes escenas interactivas, diseñadas por Carlos Rojas Hincapié, puedes realizar sumas o restas de expresiones radicales, teniendo en cuenta que debes convertirlas en expresiones semejantes (mismo índice y mismo radicando). Intenta encontrar la solución con la ayuda de la escena "Descomposición factorial del número" diseñada por Eduardo Barbero Corral.
Antes de pasar a la siguiente página, te recomiendo que analices los siguientes ejemplos.
 Ejemplos de suma y resta de expresiones radicales
Ejemplos de suma y resta de expresiones radicalesEjemplo 1: Para la primera escena interactiva, si el ejemplo fuera.
$\sqrt {810}+4\sqrt {10}$
Con la ayuda de la escena interactiva "Descomposición factorial del número", busca los factores primos de 810.
Observa que $810=2\cdot3^4\cdot5$, por lo que sale el $3^2=9$, quedando $\sqrt {2\cdot5}=\sqrt{10}$ dentro del radical. Ahora puedes sumar radicales semejantes.
Luego de realizar los cálculos, puedes presionar "SOLUCIÓN" en la escena interactiva y confirmar el resultado.
Realiza el procedimiento anterior y continua con otros ejercicios propuestos en la escena interactiva.
Ejemplo 2: Para la segunda escena interactiva, si el ejercicio fuera.
Con la ayuda de la escena interactiva "Descomposición factorial del número", busca los factores primos de 512 y 128.
Observa que $512=2^9$, por lo que sale el $2^4=16$, quedando $\sqrt {2}$ dentro del radical y para el $128=2^7$ sale el $2^3$, quedando el $2$ dentro del radical. Ahora puedes restar radicales semejantes.
Luego de realizar los cálculos anteriores, puedes presionar "SOLUCIÓN" en la escena interactiva y confirmar el resultado.
Realiza el procedimiento anterior y continua con otros ejercicios propuestos en la escena interactiva diseñada por Carlos Rojas Hincapié.
Luego de analizar los dos ejemplos anteriores, estas preparado para resolver los ejemplos y ejercicios que se proponen en las siguientes escenas interactivas. Recuerda hacer uso de la escena "Descomposición factorial del número" para que puedas obtener las respuestas acertadas.
En caso de presentarse algún error, la escena interactiva mostrará el procedimiento.
 Ejemplos de producto y división de expresiones radicales
Ejemplos de producto y división de expresiones radicalesPara multiplicar dividir expresiones radicales que tienen diferente índice, es conveniente convertir las expresiones en forma de potencias, amplificar los exponentes para que queden con el mismo denominador
Ejemplo 1: $\hspace{0.1 cm}\sqrt{2}\cdot\sqrt[3]{3}$
$$\color{black}\begin{aligned} \sqrt{2}\cdot\sqrt[3]{3}&=2^\frac{1}{2}\cdot3^\frac{1}{3}\\ &= 2^\frac{3}{6}\cdot3^\frac{2}{6} \\ &= \left(2^3\cdot3^2\right)^\frac{1}{6}\\ &= \left(8\cdot9\right)^\frac{1}{6} \end{aligned}$$Ejemplo 2: $\hspace{0.1 cm}\cfrac{\sqrt{2}}{\sqrt[3]{3}}$
$$\color{black}\begin{aligned} \cfrac{\sqrt{2}}{\sqrt[3]{3}}&=\cfrac{2^\frac{1}{2}}{3^\frac{1}{3}}\\ &= 2^\frac{3}{6}\cdot3^\frac{2}{6} \\ &= \left(2^3\cdot3^2\right)^\frac{1}{6}\\ &= \left(8\cdot9\right)^\frac{1}{6} \end{aligned}$$Para simplificar expresiones radicales, debe tener en cuenta lo siguiente:
 Ejemplos de simplificación de expresiones radicales
Ejemplos de simplificación de expresiones radicalesEjemplo 1:$\;\;\sqrt [10] {6561}$
Se descompone el $10$ y el $8$ en sus factores primos, $10 = 2 \cdot5$5 y $8 = 2^3$. El $M.C.D_{(10,8)}=2$. Se divide el índice y el exponente del radicando por 2.
Se simplifican las fracciones del índice del radical y el exponente del radicando.
Ejemplo 2: $\;\;\dfrac{\sqrt3(\sqrt{3125}+\sqrt{245})}{\sqrt{19683}+\sqrt{27}-\sqrt{2187}}$
Se descompone los radicandos en sus factores primos, se sacan las raíces y se realizan las operaciones dentro del paréntesis.
$$\color{black}\begin{aligned} \dfrac{\sqrt3(2\sqrt{3125}+\sqrt{245})}{\sqrt{19683}+\sqrt{27}-\sqrt{2187}}&=\dfrac{\sqrt3(2\sqrt{5^5}+\sqrt{7^2\cdot5})}{\sqrt{3^9}+\sqrt{3^3}-\sqrt{3^7}}\\[13pt] &=\dfrac{\sqrt3(2\cdot5^2\sqrt{5}+7\sqrt{5})}{3^4\sqrt{3}+3\sqrt{3}-3^3\sqrt{3}} \end{aligned}$$Ahora ya se tienen radicales semejantes, se realizan las operaciones y se simplifica.
$$\color{black}\begin{aligned} \dfrac{\sqrt3(2\sqrt{3125}+\sqrt{245})}{\sqrt{19683}+\sqrt{27}-\sqrt{2187}}&=\dfrac{\sqrt3(50\sqrt{5}+7\sqrt{5})}{81\sqrt{3}+3\sqrt{3}-27\sqrt{3}}\\[15pt] &=\dfrac{{\color{Red}\bcancel {{\color{black}\sqrt3}}}({\color{Red}\bcancel {{\color{black}57}}}\sqrt{5})}{{\color{Red}\bcancel {{\color{black}57}}}{\color{Red}\bcancel {{\color{black}\sqrt{3}}}}} \end{aligned}$$Ejemplo 3: $\;\;\dfrac{\sqrt3(\sqrt{3125}-\sqrt{245})}{\sqrt{19683}-\sqrt{27}+\sqrt{2187}}$
Se descompone los radicandos en sus factores primos, se sacan las raíces y se realizan las operaciones dentro del paréntesis.
$$\color{black}\begin{aligned} &=\dfrac{\sqrt3(5^2\sqrt{5}-7\sqrt{5})}{3^4\sqrt{3}-3\sqrt{3}+3^3\sqrt{3}}\\[13pt] &=\dfrac{\sqrt3(25\sqrt{5}-7\sqrt{5})}{81\sqrt{3}-3\sqrt{3}+27\sqrt{3}}\\[13pt] &=\dfrac{{\color{Red}\bcancel {{\color{black}\sqrt3}}}({\color{Red}\bcancel {{\color{black}18}}}\sqrt{5})}{{\color{Red}\bcancel {{\color{black}105}}}{\color{Red}\bcancel {{\color{black}\sqrt{3}}}}} \end{aligned}$$En la siguiente escena interactiva, diseñada por Miguel Angel Cabezón Ochoa, podrás analizar las propiedades de los radicales para simplificar los ejercicios propuestos.
NOTA: En algunos ejercicios en más conveniente expresar los radicales en forma de exponentes, aplicar las propiedades y simplificar.
En la siguiente escena interactiva, diseñada por Miguel Angel Cabezón OchoaMiguel Angel Cabezón Ochoa, es un autor de la red Descartes, que publicó la escena interactiva "Propiedades de los radicales.", podrás analizar las propiedades de los radicales para simplificar el índice con el exponente del radicando en los ejercicios propuestos.
Cuando se trata de racionalizar, por lo general se trata de eliminar los radicales que se presenten en los denominadores. Para hacerlo se debe multiplicar el radical por una fracción que lo elimine o hacer uso de la conjugada. Resuelve los ejercicios en tu cuaderno.
En la siguiente escena interactiva, diseñada por Miguel Angel Cabezón Ochoa, podrás analizar las propiedades de los radicales para racionalizar los ejercicios propuestos.
En la siguiente escena interactiva, diseñada por Miguel Angel Cabezón Ochoar, podrás analizar las propiedades de los radicales para racionalizar los ejercicios propuestos.
Cuando se presenten binomios, en el numerador o en el denominador y se busque racionalizar, se debe multiplicar por la conjugada.
No olvides que para obtener la conjugada, se le cambia el signo al segundo término del binomio que se desee racionalizar.
Con lo que estudiaste en los ejemplos anteriores, estas en capacidad de resolver los siguientes ejercicios.
En la siguiente escena interactiva, diseñada por Miguel Angel Cabezón OchoaMiguel Angel Cabezón Ochoa, es un autor de la red Descartes, que publicó la escena interactiva "Propiedades de los radicales.", podrás analizar las propiedades de los radicales para simplificar.
Amplia la escena interactiva y trata de resolver los 10 ejercicios propuesto, sin olvidar los índices radicales de cada uno de los ejercicios propuestos.
Una variable es una letra que representa a cualquier número de un conjunto dado de números. Si empezamos con variables $x,y,z$ y algunos números reales, y los combinamos usando la resta, multiplicación, división, potencias y raíces obtenemos una expresión algebraica.
Un monomio es una expresión de la forma $ax^k$, donde $a$, es el coeficiente y por lo general un número real, la $x$ representa la variable y la $k$ el exponente de la expresión algebraica. Dicho valor representa el grado del polinomio y la cantidad de términos su nombre.
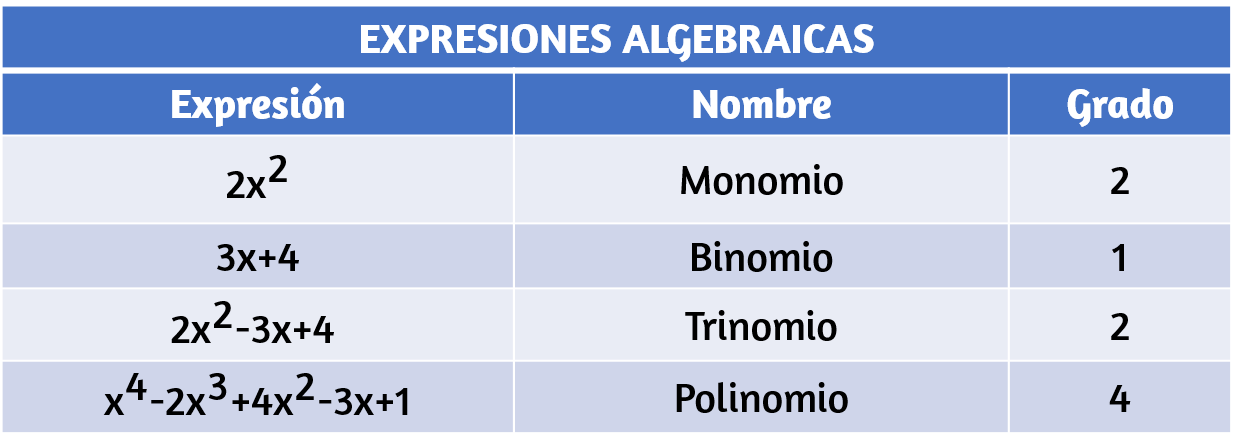
Las operaciones de suma y producto definidas en las expresiones algebraicas (números y letras – variables), cumplen las mismas propiedades de los números reales. Veamos algunas de ellas: Sean $a$, $b$ y $c$ números reales cualesquiera.
En la Tabla 8, se resumen las propiedades de las expresiones algebraicas y las podrás utilizar para realizar las actividades propuestas en la siguientes escenas interactiva.
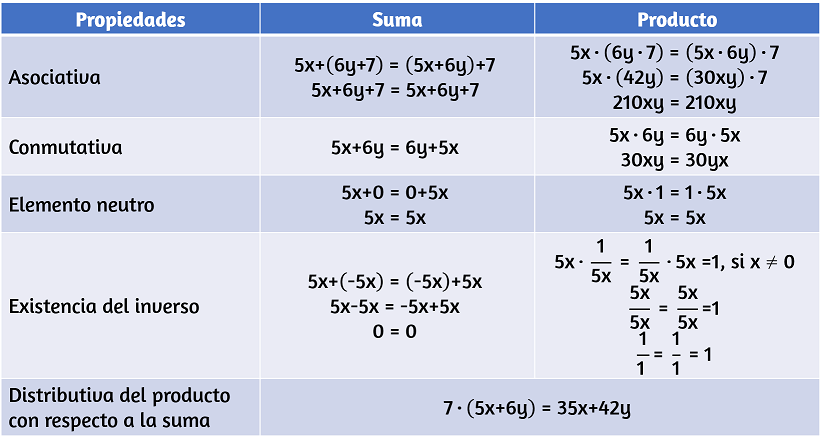
Tabla 8. Propiedades de las expresiones algebraicas.
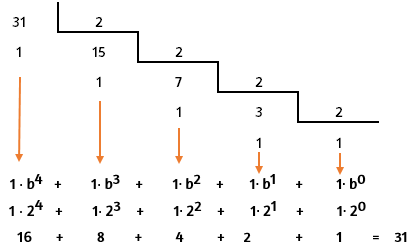
El sistema de numeración binario o digital (base=2), utiliza el 0 y el 1 para la representación de un determinado número por medio de un polinomio, el cual representa un lenguaje máquina, que después puede ser utilizado a mayor escala por los desarrolladores en un lenguaje de programación.
En la informática es apropiado para definir si por un circuito pasa o no una descarga eléctrica, siendo el cero (0) la respuesta negativa y el uno (1) la respuesta afirmativa.
A continuación se ilustra la forma de convertir un número natural en su representación binaria:
En las siguientes escenas interactivas, diseñadas por Miguel Angel Cabezón OchoaMiguel Angel Cabezón Ochoa, es un autor de la red Descartes, que publicó la escena interactiva "Propiedades de los radicales.", podrás jugar al adivino y darte cuenta la importancia de los polinomios y sus propiedades en la vida cotidiana.
Para el primer juego de adivino, elige inicialmente la figura  , que corresponde a la figura número 31 del juego, iniciando su conteo en cero para la primer imagen. Al terminar el juego, te darás cuenta que corresponde a la figura seleccionada.
, que corresponde a la figura número 31 del juego, iniciando su conteo en cero para la primer imagen. Al terminar el juego, te darás cuenta que corresponde a la figura seleccionada.
En la escena interactiva anterior, elige la misma figura  , que habías elegido y compara el resultado obtenido.
, que habías elegido y compara el resultado obtenido.
Con las expresiones algebraicas se pueden representar infinidad de cálculos matemáticos, a continuación encontrarás algunas escenas diseñadas por Juan Guillermo Rivera y otros que dan cuenta de ello.
Los polinomios, no son sólo herramientas para la solución de ecuaciones, son una necesidad para la aplicación de fórmulas en el cálculo de áreas y volúmenes.
En las siguientes escenas interactivas, tendrás la oportunidad de buscar la solución a diferentes situaciones y en caso de no acertar, puedes encontrar ayuda en los botones diseñados para tal fin.
Cuando se realicen las operaciones entre expresiones algebraicas, se deben tener cuenta las propiedades que se vieron en la página 96 o puedes hacer click en la Tabla 8 para recordarlas.
 Ejemplos de suma, resta y producto de expresiones algebraicas
Ejemplos de suma, resta y producto de expresiones algebraicasA continuación se realizarán algunos ejemplos para la suma, resta y producto de expresiones algebraicas. La división se explicará más adelante.
Sean los polinomios: $P(x) = ( x^3 - 6x^2 + 2x + 4 )\wedge Q(x) = ( 6x^2 + 2x + 4 )$
Suma:$P(x) + Q(x)$
$x^3 - {\color{Red}\bcancel {{\color{black}6x^2}}} + 2x + 4$
$\underline{\hspace{0.8cm}{\color{Red}\bcancel {{\color{black}6x^2}}} + 2x + 4}$
${\hspace{1.8cm}\color{brown}4x + 8}$
Se recomienda ubicar un polinomio debajo del otro para que se facilite la suma de los términos semejantes.
Resta: P(x) - Q(x)
$x^3 - 6x^2 + {\color{Red}\bcancel {{\color{black}2x}}} + {\color{Red}\bcancel {{\color{black}4}}}$
$\underline{\hspace{0.5cm}-6x^2 - {\color{Red}\bcancel {{\color{black}2x}}} - {\color{Red}\bcancel {{\color{black}4}}}}$
${\color{brown}x^3 - 12x^2}$
Se recomienda ubicar un polinomio debajo del otro para que se facilite la suma de los términos semejantes. No debes olvidar cambiar todos los signos a Q(x), el segundo polinomio.
Producto:$\;\;P(x)\cdot Q(x)$
$\hspace{0.1cm}6x^5+2x^4+\;\;4x^3$
$\hspace{0.6cm}-36x^4-{\color{Red}\bcancel {{\color{black}12x^3}}}-{\color{Red}\bcancel {{\color{black}24x^2}}}$
$\hspace{2cm}{\color{Red}\bcancel {{\color{black}12x^3}}}+\;\;4x^2+8x$
$\underline{\hspace{3.1cm}{\color{Red}\bcancel {{\color{black}24x^2}}} +8x+16}$
$\color{brown}6x^5-32x^4+4x^3+\;\;4x^2+16x+16$
Se aplica la propiedad distributiva y se ubican los términos semejante, uno debajo del otro. No debes olvidar hacer la operación de los signos.
 Ejemplos de suma y resta de polinomios
Ejemplos de suma y resta de polinomiosUtiliza la siguiente escena interactiva, diseñada por Carlos Rojas Hincapié, para resolver los siguientes ejemplos.
No te inquietes al resolver los dos primeros ejemplos, por estar en términos de $x \wedge y$. Recuerda que sólo tienes que sumar o restar los coeficientes de los términos semejantes y para hacerlo con la escena interactiva, asume que x ocupa el espacio de $x^2 \wedge y$, ocupa el espacio de $x$. Recuerda que si vas a restar, debes cambiar los signos del segundo polinomio.
En la siguiente escena interactiva, diseñada por TelesecundariaTelesecundaria, son autores de la red Descartes, que publicó la escena interactiva "Suma y resta de expresiones algebraicas.", podrás jugar al adivino y darte cuenta la importancia de los polinomios y sus propiedades.
Ciertos productos de binomios se presentan con tanta frecuencia que debes aprender a reconocerlos. Empezamos con el producto de dos binomios:
$\left(x + a\right)\left(x + b\right)= x^2 + \left(a + b\right)x + ab$
$\left(ax^n + b\right)\left(cx^n + d\right)= acx^{2n} + \left(ad + bc\right)x^n + bd$
 Ejemplos del Producto de dos binomios
Ejemplos del Producto de dos binomiosSe aplica la definición de Producto de dos binomios y se realizan las operaciones.
$\color{black}\begin{aligned} \left(x + 3\right)\left(x + 2\right)&=x^2 + \left(3 + 2\right)x + \left(3 \cdot2\right) \end{aligned}$Se tiene en cuenta la ley de los signos y se realizan las operaciones.
$$\left(x - 3\right)\left(x + 2\right)=x^2 + \left(-3 + 2\right)x + \left(-3 \cdot2\right)$$$\left(a\pm b\right)^2= a^2\pm 2ab + b^2$
Se lee así:
En las siguientes escenas interactivas, diseñadas por Miguel Angel Cabezón OchoaMiguel Angel Cabezón Ochoa, es un autor de la red Descartes, que publicó la escena interactiva "Propiedades de los radicales.", podrás analizar la definición del cuadrado de la suma y diferencia de polinomios.
Pulsa los botones  para analizar las escenas en forma individual, rebobinar, pausar, adelantar o retroceder.
para analizar las escenas en forma individual, rebobinar, pausar, adelantar o retroceder.
Al utilizar los dos últimos botones, para iniciar la escena interactiva y pausarla, podrás observar que se aplica la propiedad distributiva y posteriormente se suman los términos semejantes
 Ejemplos de Binomio al cuadrado
Ejemplos de Binomio al cuadradoSe aplica la definición del cuadrado de un binomio y las propiedades de las potencias..
En la siguiente escena interactiva, adaptada de José RosasJosé Rosas, es un autor de la red GeoGebra, que publicó la escena interactiva "Diferencia de cuadrados.", podrás analizar la definición del producto de la suma por la diferencia.
De la escena interactiva anterior, se puede concluir que:
$\left(a+b\right)\left(a-b\right)= a^2 -b^2$
Por lo anterior, podemos decir que:
 Ejemplos del Producto de la suma por la diferencia
Ejemplos del Producto de la suma por la diferenciaSe aplica la definición del Producto de la suma por la diferencia.
$\left(a\pm b\right)^3= a^3 \pm 3a^2b+3ab^2\pm b^3$
 Ejemplos de Binomio al cubo
Ejemplos de Binomio al cuboSe aplica la definición del cubo de un binomio, se utilizan las propiedades de las potencias y se realizan las operaciones.
En la siguiente escena interactiva, diseñada por Miguel Angel Cabezón Ochoa, podrás analizar la definición del cubo de la suma de polinomios. Recuerda que para la diferencia, es el mismo procedimiento y sólo se alternan los signos (+ - + -) para el segundo factor.
$\left(ax + by + c\right)^2 = (ax)^2 +2(ab)xy+2(ac)x+(by)^2+2(bc)y+c^2$
Por lo anterior, podemos decir que:
 Ejemplos de Trinomio al cuadrado
Ejemplos de Trinomio al cuadradoSe aplica la definición del Trinomio Cuadrado y se realizan las operaciones indicadas.
En la siguiente escena interactiva sólo tienes que seleccionar el producto notable con el que desees practicar, puedes cambiar a otra expresión pulsando "Otro ejercicio", utiliza tu cuaderno para resolver los ejercicios planteados e ingresa los resultados. Para ingresar los exponentes, presiona Alt ( sostenido ) y 94, libera el Alt y luego digita el valor del exponente.
En la siguiente escena interactiva, diseñada por AdriánAdrián, es un autor de la red GeoGebra, que publicó la escena interactiva "Productos Notables"., podrás analizar la definición del producto de la suma por la diferencia.
Antes de intentar realizar una división de polinomios, es conveniente recordar los términos de la división.

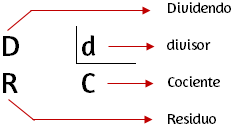
Propiedades de la división de polinomios
Prueba de la división
Al producto del cociente ($C$) por el divisor ($d$), se le suma el residuo ($R$) y tiene que ser igual al dividendo ($D$).
 Ejemplos de la división y su prueba
Ejemplos de la división y su prueba
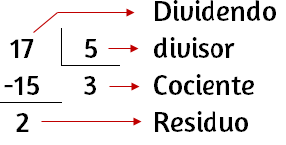
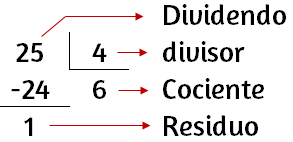
Prueba:
$C \times d + R = D$
$3 \cdot 5 + 2 = 17$
$15 + 2 = 17$
$C \times d + R = D$
$6 \cdot 4 + 1 = 17$
$24 + 1 = 17$
Observa que en el ejemplo 1, en la división se busca un número en el cociente "$C$" que al multiplicarlo por el divisor "$d$", sea igual o se acerque al dividendo. El número que más se acerca es el tres, ya que $5\cdot3=15$ y es el que más se acerca al $17$. Tienes que tener en cuenta que el producto $15$, pasa con signo contrario.
Lo anterior va ser de mucha utilidad, cuando estés haciendo divisiones de polinomios. En el siguiente ejemplo lo podrás evidenciar.
Siempre que vayas a realizar una división de polinomios, debes tener en cuenta ordenar los exponentes de las variables, tanto el dividendo (numerador) como el denominador (divisor) de mayor a menor grado y en caso de que falte uno, deja un espacio que puedes llenar con un cero.
En el ejemplo que se plantea, observa que el polinomio está ordenado $4$, $3$, $2$, $1$ para el dividendo y $2$, $1$ para el divisor.
Existen dos formas de hacer la división, una es la división larga y la otra la división sintética.
Esta forma de división permite que el divisor sea de un grado superior a uno, mientras que la división sintética, sólo permite que el divisor sea de grado uno ($1$). Para el ejemplo que se presenta no se puede hacer la división sintética.
En el ejemplo, $P(x)=-9x^4+9x^3-14x^2+18x$ y $Q(x)=3x^2-2x$. Al finalizar el proceso de la división larga se hará la prueba, para lo cual hallaremos $F\left( x\right) =P\left( x\right) \cdot Q\left( x\right) +R\left( x\right)$, con un residuo $R(x)=0$ o el grado de $R(x)$, menor que el grado de $P(x)$.
${\color{Red}\bcancel {{\color{black}-9x^4}}}+9x^3-14x^2+18x$ $\hspace{1cm}|$ $\hspace{-0.1cm}\underline{3x^2-2x\color{white}.......}\\[3pt] \hspace{0.2cm}\underline{{\color{Red}\bcancel {{\color{black}9x^4}}}-6x^3\color{white}.........................}\hspace{0.8cm}\color{brown}\underbrace{-3x^2+x-4}\\[3pt] \hspace{1.1cm}\color{black}+{\color{Red}\bcancel {{\color{black}3x^3}}}-14x^2+18x\hspace{1.2cm}\color{brown}Cociente\\[3pt] \hspace{1.1cm}\color{black}\underline{-{\color{Red}\bcancel {{\color{black}3x^3}}}+2x^2\color{white}.............}\\[3pt] \hspace{1.7cm}\color{black}-{\color{Red}\bcancel {{\color{black}12x^2}}}+18x\\[3pt] \hspace{1.7cm}\underline{+{\color{Red}\bcancel {{\color{black}12x^2}}}-\;\;8x\color{white}....}\\[3pt] \hspace{2.8cm}\color{blue}\underbrace{+10x}\\[3pt] \hspace{2.6cm}Residuo$Prueba de la división
$F\left( x\right) =P\left( x\right) \cdot Q\left( x\right) +\color{blue}R\left( x\right)$
$F(x)=(-3x^2+x-4)\cdot(3x^2-2x)+\color{blue}10x$$\hspace{0.1cm}-9x^4+6x^3$
$\hspace{1cm}+3x^3-2x^2$
$\underline{\hspace{1.8cm}-12x^2+8x}$
$-9x^4+9x^3-14x^2+8x+\color{blue}10x$
$F(x)=\color{brown}-9x^4+9x^3-14x^2+18x$En la siguiente escena interactiva, adaptada de David MartínezDavid Martínez, es un autor de la red GeoGebra, que publicó la escena interactiva "División de polinomios. Practica"., podrás realizar ejercicios de división de polinomios y poner en práctica los conocimientos adquiridos con la explicación y los ejemplos anteriores.
Para realizar la división sintética, debes tener en cuenta que el grado del divisor debe ser uno (1); de lo contrario se debe hacer la división larga.
Al realizar una división sintética de polinomios, debes hacer lo siguiente:
$\bullet\hspace{0.3cm}$ Verificar que el grado del divisor sea uno (1).
$\bullet\hspace{0.3cm}$ Ordenar el polinomio del dividendo de mayor a menor grado.
$\bullet\hspace{0.3cm}$ En caso de que falte algún grado en el dividendo, se debe reemplazar por un cero.
$\bullet\hspace{0.3cm}$ Se despeja la variable del divisor.
$\bullet\hspace{0.3cm}$ El valor despejado (con su signo), se coloca en la parte inferior izquierda de la tabla para la división sintética.
$\bullet\hspace{0.3cm}$ Se baja el coeficiente del primer término del polinomio a la parte inferior de la tabla.
$\bullet\hspace{0.3cm}$Se multiplica el valor anterior por el valor despejado y que se ubico en la parte inferior izquierda.
$\bullet\hspace{0.3cm}$El resultado anterior se coloca debajo del coeficiente del segundo término de polinomio.
$\bullet\hspace{0.3cm}$Se suman o se restan los valores y se repite el paso anterior.
Una vez terminado el procedimiento, se le baja un grado al polinomio inicial y se utilizan los valores obtenidos anteriormente.

Paolo Ruffini, nacido en 1765 en Valentano, Estados Papales (ahora Italia), fue un matemático, médico y filósofo. Profesor de matemáticas en la Universidad de Módena desde 1788, fue despedido por negarse al juramento de lealtad a Napoleón Bonaparte. Más tarde, en 1799, fue readmitido. En 1806 recibió la cátedra de Matemática Aplicada en la escuela militar de Módena, en 1814 fue nombrado director de la Universidad de Módena y en 1816, presidente de la Sociedad
Italiana Dei Quaranta. Su aportación más conocida en las matemáticas es la Regla de Ruffini (~1809), que permite obtener los coeficientes del cociente de un polinomio por el binomio $x - n$, siendo $n$ una de las raíces (enteras) del polinomio. Además, este método facilita, como veremos a continuación, la obtención de las raíces del polinomio. (matesfacil.com, 2019)
Continuando con los ejemplos de la división, se plantea el siguiente:
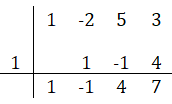
El cociente $P(x)$, sería $x^2-x+4$ y con residuo $R(x)=7$
Observa que en la división sintética para obtener el cociente $P(x)$ se le bajó un grado al polinomio, por haber divido por $x-2$, esto es $\dfrac{x^3}{x}=x^2$
Prueba de la división
$F\left( x\right) =P\left( x\right) \cdot Q\left( x\right) +\color{blue}R\left( x\right)$
$F(x)=(x^2-x+4)\cdot(x-1)+\color{blue}7$$\hspace{0.1cm}x^3-x^2$
$\hspace{0.8cm}-x^2+x$
$\underline{\hspace{1.6cm}+4x-4}$
$x^3-2x^2+5x-4+\color{blue}7$
$F(x)=\color{brown}x^3-2x^2+5x+3$Antes de practicar en la escena interactiva, intenta realizar los siguientes ejercicios, los cuales tienen la respuesta para que puedas confrontar tu solución.
Respuesta:$\hspace{0.2cm}(3x^3-3x^2+x)$, con residuo $R(x)=-3$
Respuesta:$\hspace{0.2cm}(x^4+x^3-x^2-x-2)$, con residuo $R(x)=-1$
Respuesta:$\hspace{0.2cm}(2x^2-5x+13)$, con residuo $R(x)=-27$
En la siguiente escena interactiva, adaptada de MatematicaulaMatematicaula, son autores de la red GeoGebra, que publicaron la escena interactiva "Método de Ruffini"., podrás realizar ejercicios de división sintética de polinomios y poner en práctica los conocimientos adquiridos con la explicación y los ejemplos anteriores.
En las siguientes escenas interactivas, adaptadas de Juan Guillermo Rivera, podrás resolver los ejercicios planteados sobre operaciones algebraicas y productos notables, para pongas a prueba tus conocimientos.
En cada escena interactiva dispones de 60 minutos para realizar los ejercicios e ir eligiendo la respuesta correcta en el cuestionario. Al finalizar tendrás la posibilidad de ingresar tu nombre y enviar las respuestas a tu docente ingresando su correo en el espacio destinado para ello.
Al solucionar los ejercicios propuestos en las escenas interactivas, estarás en capacidad de resolver los ejercicios propuestos para la sección 3.3
Opción 1. Operaciones algebraicas y productos notables.
Opción 2. Operaciones algebraicas y productos notables.
Opción 3. Operaciones algebraicas y productos notables.
Factorizar es expresar un polinomio, como el producto de otros polinomios de menor grado.
Como su nombre lo indica, es buscar los elementos comunes, tanto de los coeficientes numéricos como de las variables (literales) con su menor exponente.
 Ejemplos de factor común
Ejemplos de factor común$\hspace{0.2cm}3x^2 + 6x = 3x \left(\hspace{0.7cm}\right)$
$\hspace{0.2cm}3x^2 + 6x = 3x ( x + \hspace{0.3cm})$
$\hspace{0.2cm}3x^2 + 6x = 3x ( x + 2)$
Encontrar el factor común entre los coeficientes $(MCD=3)$ y entre las variables (literales), $x$. Ahora ya se tiene el primer factor. Para encontrar el segundo, se aplica la propiedad distributiva.
Qué le falta a $3x$, para que al multiplicarlo se obtenga como resultado $3x^2$?. Claro!, como ya tienes $3x$, sólo falta una $x$.
Qué le falta a $3x$, para que al multiplicarlo se obtenga como
resultado $6x$?. Claro!, como ya tienes $3x$, sólo falta un $2$.
Otro caso del factor común, es el de agrupación de términos y se deben agrupar aquellos que tengan algo el común.
Observa que el factor común para el primer y segundo término es la $a$ y para el tercero y cuarto, es la $x$.
$a^2 + ab + ax + bx = a (\hspace{0.3cm}+ \hspace{0.3cm}) + x (\hspace{0.3cm}+ \hspace{0.3cm})$
Ahora ya se tiene los factores $a$ y $x$, procedemos a completar los paréntesis aplicando la propiedad distributiva.
$a^2 + ab + ax + bx$ = $a$$(a + b)$ + $x$$(a + b)$
Como puedes observar, ha quedado $(a + b)$, como un nuevo factor común.
En las siguientes escenas interactivas, diseñada por Carlos Rojas HincapiéCarlos Rojas Hincapié es un autor de la red Descartes, que publicó el libro Matemáticas Básicas, del cual seleccionaremos algunas escenas interactivas en el resto de esta obra., puedes interactuar,pulsando "Otro ejemplo" e ir observando los resultados obtenidos. En la segunda escena, puedes seguir el paso a paso, ubicando los factores comunes para los coeficientes y las variables (literales), pulsar "enter" e ir observando los resultados.
Para interactuar en la siguiente escena interactiva, debes seguir el paso a paso e ir dando "enter" para continuar.
Pulsa en la figura  , determina el MCD (factor numérico) y finaliza con enter.
, determina el MCD (factor numérico) y finaliza con enter.
Pulsa en la figura  , selecciona cada variable para determinar el factor común entre ellas y finaliza con enter.
, selecciona cada variable para determinar el factor común entre ellas y finaliza con enter.
NOTA:
Debes recordar lo siguiente:
$a^2-b^2=\left(a+b\right)\cdot\left(a-b\right)$
 Ejemplos de diferencia de cuadrados
Ejemplos de diferencia de cuadradosSe saca raíz cuadrada a cada uno de los términos y se multiplica, la suma por la diferencia de las raíces cuadradas.
$\hspace{0.2cm}2m\hspace{0.5cm}3n$
En la siguiente escena interactiva, adaptada de José RosasJosé Rosas, es un autor de la red GeoGebra, que publicó la escena interactiva "Diferencia de cuadrados"., podrás analizar la definición de la diferencia de cuadrados.
$x^2 + bx + c = \left(x + p\right)\left(x + q\right)$
El primer término de cada factor, es la raíz cuadrada del primer término del trinomio, $bx$ es la suma de $px + qx$ y el producto de $p \cdot q$, corresponde al término independiente $c$.
 Ejemplos de Trinomio de la forma $\\[0.1cm]\hspace{1.5cm}x^2 + bx + c$
Ejemplos de Trinomio de la forma $\\[0.1cm]\hspace{1.5cm}x^2 + bx + c$| $\large12$ | $\large2$ |
|---|---|
| $\large6$ | $\large2$ |
| $\large3$ | $\large3$ |
| $\large1$ | $\large12=2^2\times3$ |
Se descompone el $12$ en sus factores primos.
Por la descomposición del $12$ en sus factores primos, se puede observar que $4 \times 3$, cumple con lo que se necesita. Observen que su producto equivale al último término y su suma, corresponde al término de la mitad; luego:
| $\large24$ | $\large2$ |
|---|---|
| $\large12$ | $\large2$ |
| $\large6$ | $\large2$ |
| $\large3$ | $\large3$ |
| $\large1$ | $\large24=2^3\times3$ |
Se descompone el $24$ en sus factores primos.
Por la descomposición del $24$ en sus factores primos, se puede observar que $8 \times 3$, cumple con lo que se necesita. Observen que su producto equivale al último término y su diferencia, corresponde al término de la mitad; luego:
| $\large54$ | $\large2$ |
|---|---|
| $\large27$ | $\large3$ |
| $\large9$ | $\large3$ |
| $\large3$ | $\large3$ |
| $\large1$ | $\large54=2\times3^3$ |
Se descompone el $54$ en sus factores primos.
Por la descomposición del $54$ en sus factores primos, se puede observar que $9 \times 6$, cumple con lo que se necesita. Observen que su producto equivale al último término y su diferencia, corresponde al término de la mitad; luego:
En la siguiente escena interactiva, diseñada por Rojas Hincapié, puedes interactuar, ingresando en el espacio destinado para coeficientes 1 y 2, los factores primos del término independiente que cumplen con las indicaciones dadas. Luego de ingresar los coeficientes, pulsa  para cambiar los signos de los factores (por defecto se toma el signo +), y luego pulsa "verificar". Si deseas seguir practicando, pulsa "ejercicio". ¡Buena suerte!
para cambiar los signos de los factores (por defecto se toma el signo +), y luego pulsa "verificar". Si deseas seguir practicando, pulsa "ejercicio". ¡Buena suerte!
Como el caso anterior, se resuelve por ensayo y error; adicional se debe descomponer el coeficiente "$a$" en sus factores primos.
 Ejemplos de Trinomio de la forma $\\[0.1cm]\hspace{1.5cm}ax^2 + bx + c$
Ejemplos de Trinomio de la forma $\\[0.1cm]\hspace{1.5cm}ax^2 + bx + c$Se abren dos paréntesis (factores), se descompone la "$a$" ($6$) y la "$c$" ($5$) en sus factores primos y se tantea la solución.
$6x^2 + 7x - 5 = (\hspace{0.35cm} + \hspace{0.35cm})(\hspace{0.35cm} - \hspace{0.35cm})$
| $\large6$ | $\large2$ |
|---|---|
| $\large3$ | $\large3$ |
| $\large1$ | $\large6=\color{blue}2\times3$ |
| $\large5$ | $\large5$ |
|---|---|
| $\large1$ | $\large5=\color{brown}5\times1$ |
Se colocan los factores primos de "$a$" (por lo general los más cercanos), en cada uno de los paréntesis (en este caso $3\times2$), acompañados de la raíz cuadrada de la variable y luego los factores de "$c$".
Se verifica que este correcto, observa que al aplicar la propiedad distributiva se obtiene el trinomio inicial.
Se abren dos paréntesis (factores), se descompone la "$a$" ($24$) y la "$c$" ($5$) en sus factores primos y se tantea la solución.
$24x^2 + 37x - 5 = (\hspace{0.35cm} + \hspace{0.35cm})(\hspace{0.35cm} - \hspace{0.35cm})$
| $\large24$ | $\large2$ |
|---|---|
| $\large12$ | $\large2$ |
| $\large6$ | $\large2$ |
| $\large3$ | $\large3$ |
| $\large1$ | $\large24=\color{blue}8\times3$ |
| $\large5$ | $\large5$ |
|---|---|
| $\large1$ | $\large5=\color{brown}5\times1$ |
Se colocan los factores primos de "$a$" (por lo general los más cercanos), en cada uno de los paréntesis (en este caso $8\times3$), acompañados de la raíz cuadrada de la variable y luego los factores de "$c$".
$\color{blue}8x\cdot\hspace{0.5cm}\color{brown}5=\color{black}40x\\[3pt] \underline{\color{blue}3x}\cdot\underline{\hspace{0.2cm}\color{brown}-1}=\underline{-3x}\\[3pt] 24x\;\hspace{0.0cm}-5\hspace{0.6cm}37x$Como puedes observar, $8\times5 = 40$, $3\times1 = 3$ y la diferencia entre $40$ y $3$ es $37$, por lo que se debe poner negativo el $1$.
La respuesta será colocar los factores, haciendo una "$x$". Por tanto se obtiene:
$24x^2 + 37x - 5 = \color{brown}(\color{blue}8x - \color{brown}1)(\color{blue}3x + \color{brown}5)$
Para verificar si la solución es correcta, se realiza tal como se indicó en el ejemplo anterior.
| $\large8$ | $\large2$ |
|---|---|
| $\large4$ | $\large2$ |
| $\large2$ | $\large2$ |
| $\large1$ | $\large24=\color{blue}8\times3$ |
| $\large36$ | $\large2$ |
|---|---|
| $\large18$ | $\large2$ |
| $\large9$ | $\large3$ |
| $\large3$ | $\large3$ |
| $\large1$ | $\large36=\color{brown}2^2\times3^2$ |
Como puedes observar, $4\times12 = 48$, $2\times3 = 6$ y la suma de $48$ y $6$ es $54$, por lo que se deben poner negativos el $12$ y el $3$.
La respuesta será colocar los factores, haciendo una "$x$". Por tanto se obtiene:
A continuación encontrarás algunos ejemplos con respuesta, para que intentes resolverlos de acuerdo con las explicaciones de los ejemplos anteriores.
En la siguiente escena interactiva, diseñada por Carlos Rojas Hincapié, puedes interactuar, ingresando en los espacios a lado y lado de de los coeficientes 1 y 2  (los números corresponden al ejemplo anterior), los factores primos de "$a$" y los factores primos de "$c$" respectivamente, que cumplen con con el trinomio. Luego pulsa
(los números corresponden al ejemplo anterior), los factores primos de "$a$" y los factores primos de "$c$" respectivamente, que cumplen con con el trinomio. Luego pulsa  para cambiar los signos de los factores (por defecto se toma el signo +), y luego pulsa "verificar". Si deseas seguir practicando, pulsa "ejercicio".
para cambiar los signos de los factores (por defecto se toma el signo +), y luego pulsa "verificar". Si deseas seguir practicando, pulsa "ejercicio".
$a^2\pm 2ab + b^2 = (a \pm b)^2$
Este caso corresponde a la solución del producto notable "cuadrado de un binomio" y para identificarlo, se debe tener en cuenta lo siguiente:
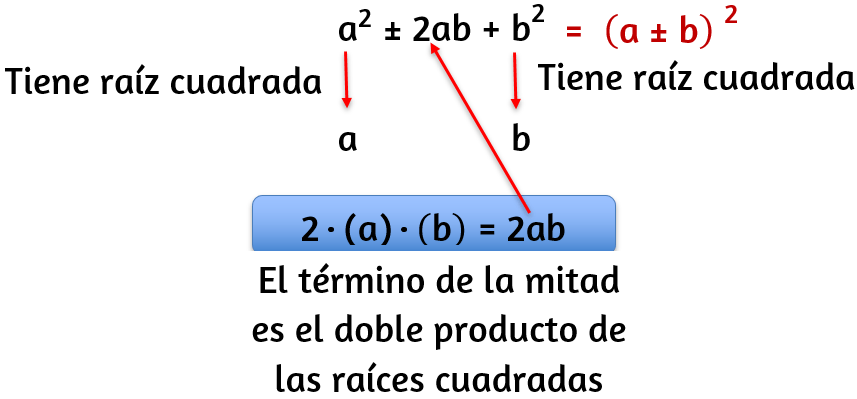
 Ejemplos Trinomio cuadrado perfecto
Ejemplos Trinomio cuadrado perfectoSolución:
1.
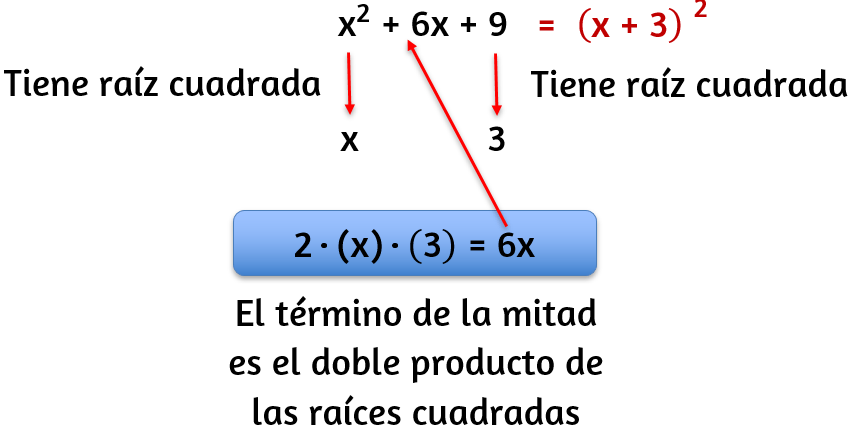
2.
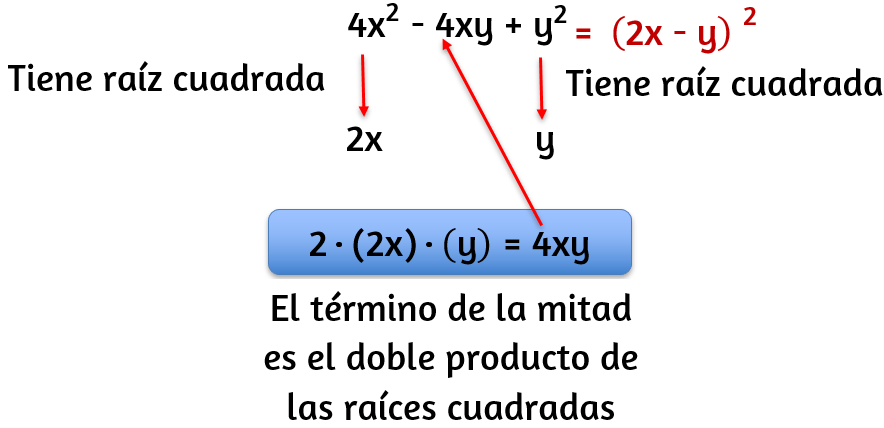
3.$\hspace{0.2cm}9x^4-42x^2+49=\color{brown}(3x^2-7)^2$
En la siguiente escena interactiva, adaptada de Jesús AlvarezJesús Alvarez, es un autor de la red GeoGebra, que publicó la escena interactiva "Factorización de un Trinomio cuadrado perfecto., practica modificando el binomio al cuadrado.
En la solución debes incluir en el coeficiente de x, el número uno (1), en caso de necesitarse.
Existen trinomios, donde el primer y tercer término tienen raíz cuadrada exacta, pero el término de la mitad, no es igual al doble producto de sus raíces cuadradas.
Para convertir un trinomio de esta forma, en un trinomio cuadrado perfecto, se debe sumar y restar la cantidad que haga falta para
obtener el doble producto de las raíces cuadradas del primer y último término.
 Ejemplos de Trinomio cuadrado perfecto por adición y sustracción
Ejemplos de Trinomio cuadrado perfecto por adición y sustracciónComo puedes observar, $\color{brown}\sqrt{a^4}=a^2$ y $\sqrt{1}=1$, pero su doble producto es $2(a^2)(1) = 2a^2$
$a^4 + a^2 +1 = a^4 + a^2 + 1 + a^2 - a^2$
Sumamos las $a^2$ positivas y nos queda:
$a^4 + a^2 +1 = a^4 + 2a^2 + 1 - a^2$
Ahora ya tenemos un trinomio cuadrado perfecto en los tres primeros términos y se soluciona como se explicó anteriormente y será de mucha ayuda los ejercicios que se repasaron en la escena interactiva.
$a^4 + a^2 +1 = (a^2 + 1)^2 - a^2$Se soluciona la diferencia de cuadrados, que es igual a la suma por la diferencia de las raíces cuadradas de los dos términos. Eliminamos signos de agrupación y finalmente queda:
$a^4 + a^2 +1 = [(a^2 + 1) + a ] [(a^2 + 1) - a]$
Siguiendo el procedimiento realizado en el ejemplo 1, podemos observar que se tienen raíces cuadradas exactas, para el primer y tercer término, pero para el segundo término, faltan $25x^4y^4$, por lo que se le debe sumar y restar esta cantidad.
$4x^8 - 53x^4y^4 + 49y^8 = 4x^8 - 53x^4y^4 + 49y^8 + 25x^4y^4 - 25x^4y^4$
Ahora podemos sumar los términos que se requieren para tener un trinomio cuadrado perfecto
$4x^8 - 53x^4y^4 + 49y^8 = 4x^8 - 28x^4y^4 + 49y^8 - 25x^4y^4$
Solucionando el trinomio cuadrado perfecto, quedaría:
$4x^8 - 53x^4y^4 + 49y^8 = (2x^4 - 7y^4)^2 - 25x^4y^4$
Es el momento de solucionar la diferencia de cuadrados.
$4x^8 - 53x^4y^4 + 49y^8 = [(2x^4 - 7y^4) + 5x^2y^2][(2x^4 - 7y^4) - 5x^2y^2]$
En la siguiente escena interactiva, podrás realizar ejercicios con Trinomio cuadrado perfecto por adición o sustracción y pondrás en práctica los conocimientos adquiridos sobre la solución de trinomio cuadrado perfecto y diferencia de cuadrados.
$a^3 - b^3 = (a - b)(a^2 + ab + b^2)$
Podemos concluir que para solucionar una diferencia de cubos, se procede de la siguiente forma:
$a^3 + b^3 = (a + b)(a^2 - ab + b^2)$
De forma similar,
 Ejemplo de suma y diferencia de cubos
Ejemplo de suma y diferencia de cubosSe aplica la definición de la diferencia de cubos.
Se aplica la definición de la suma de cubos.
Ahora, en la siguiente escena interactiva, adaptada de Carlos Rojas Hincapié, podrás ver y analizar algunos ejemplos de suma y diferencia de cubos.
En la siguiente escena interactiva, diseñada por Miguel Angel Cabezón Ochoa, podrás realizar una prueba de conocimiento, sin limite de tiempo que te permitirá poner en practica los conocimientos adquiridos sobre operaciones con polinomios. Si requieres hacer uso de la calculadora, podrás utilizar la de Descartes, haciendo clic sobre la imagen. 
En la siguiente escena interactiva, diseñada por José Luis Abreu León y Valentina Muñoz Porras.José Luis Abreu León y Valentina Muñoz Porras, son autores de la red Descartes, que publicaron la escena interactiva "Productos notables y factorización., podrás recordar lo que se ha visto sobre productos notables y factorización y mediante el desplazamiento de las figuras, para completar adecuadamente los rectángulos, te darás cuenta que lo que realmente harás es factorizar.
Para realizar operaciones entre fracciones algebraicas, se deben tener en cuenta lo aprendido en las operaciones con fracciones numéricas. En caso de presentarse una suma o resta, se debe encontrar el m.c.m.
Es conveniente, antes de realizar las operaciones, factorizar y simplificar, si es posible
$\bullet\hspace{0.3cm}$Suma de fracciones algebraicas homogéneas
Se presenta cuando encontramos expresiones, tales que:
Como puedes observar, se tiene el mismo denominador.
 Ejemplos de suma y resta de fracciones algebraicas homogéneas
Ejemplos de suma y resta de fracciones algebraicas homogéneas$\hspace{3.9cm}=\dfrac{x^3-1}{x^2+x+1}$
Se puede factorizar, resolviendo la diferencia de cubos .
$\hspace{1.8cm}a^3-b^3=(a-b)(a^2+ab+b^2)$$\dfrac{(x^3-1)}{(x^2+x+1)}=\dfrac{(x-1){\color{Red}\bcancel {{\color{black}(x^2+x+1)}}}}{{\color{Red}\bcancel {{\color{black}(x^2+x+1)}}}}$
$\hspace{3.5cm}=\dfrac{x^2+5x+6}{x+3}$
Se puede factorizar, resolviendo el trinomio de la forma $x^2+bx+c$
$\dfrac{x^2+5x+6}{x+3}=\dfrac{{\color{Red}\bcancel {{\color{black}(x+3)}}}(x+2)}{{\color{Red}\bcancel {{\color{black}(x+3)}}}}$
$\hspace{4cm}=\dfrac{x^3+1}{x^2-x+1}$
$\dfrac{(x^3+1)}{(x^2-x+1)}=\dfrac{(x+1){\color{Red}\bcancel {{\color{black}(x^2-x+1)}}}}{{\color{Red}\bcancel {{\color{black}(x^2-x+1)}}}}$
$\hspace{3.5cm}=\dfrac{x^2+4x+4}{x+2}$
Se puede factorizar, resolviendo el trinomio cuadrado perfecto.
$\dfrac{x^2+4x+4}{x+2}=\dfrac{(x+2)^{\color{Red}\bcancel {{\color{black}2}}}}{{\color{Red}\bcancel {{\color{black}(x+2)}}}}$
$\color{brown}\hspace{1.9cm}=x+2$$\bullet\hspace{0.3cm}$Suma de fracciones algebraicas heterogéneas
Se presenta cuando encontramos expresiones, tales que:
 Ejemplos de suma y resta de fracciones algebraicas homogéneas
Ejemplos de suma y resta de fracciones algebraicas homogéneasComo puedes observar, se tiene distinto denominador. Para la solución, se procede a factorizar los denominadores, con el fin de obtener el mínimo común múltiplo (m.c.m).
$\;\;\dfrac{1}{m+1}+\dfrac{2m}{m^2-1}-\dfrac{1}{m+1}$
$=\dfrac{1}{m+1}+\dfrac{2m}{(m+1)(m-1)}-\dfrac{1}{m+1}$
$=\dfrac{(m-1)+2m-(m+1)}{(m+1)(m-1)}$
$=\dfrac{{\color{Red}\bcancel {{\color{black}m}}}-1+2m-{\color{Red}\bcancel {{\color{black}m}}}-1}{(m+1)(m-1)}$
Se suman o restan los términos semejante, según el caso.
$=\dfrac{2m-2}{(m+1)(m-1)}$
Se saca factor común en el numerador y se simplifica.
$=\dfrac{2{\color{Red}\bcancel {{\color{black}(m-1)}}}}{(m+1){\color{Red}\bcancel {{\color{black}(m-1)}}}}$
$=\;\;\dfrac{1}{x+2}-\dfrac{x-2}{(x+2)^2}-\dfrac{x-1}{(x+2)^3}$
Luego de factorizar podemos observar que el m.c.m es $(x+2)^3$, se procede a realizar las operaciones.
$=\;\;\dfrac{(x+2)^2-(x-2)(x+2)-(x-1)}{(x+2)^3}$
$=\;\;\dfrac{x^2+4x+4-(x^2-4)-x+1}{(x+2)^3}$
$=\;\;\dfrac{{\color{Red}\bcancel {{\color{black}x^2}}}+4x+4-{\color{Red}\bcancel {{\color{black}x^2}}}+4-x+1}{(x+2)^3}$
$=\;\;\dfrac{3x+9}{(x+2)^3}$
Se saca factor común en el numerador y se simplifica.
$\bullet\hspace{0.3cm}$Producto de expresiones algebraicas racionales
Se factorizan, tanto el numerador como el denominador y se simplifica. Cuando se trata de producto, al simplificar , ten en cuenta que siempre se toman los términos semejantes de los numeradores con los de los denominadores
 Ejemplos de producto de expresiones algebraicas racionales
Ejemplos de producto de expresiones algebraicas racionalesComo puedes observar, el trinomio cuadrado perfecto del segundo término, se expreso como $(5x+1)(5x+1)$ para facilitar la comprensión de la simplificación
$=\dfrac{{\color{Red}\bcancel {{\color{black}x}}}}{{\color{Red}\bcancel {{\color{black}(5x+1)}}}(x+4)}\cdot\dfrac{{\color{Red}\bcancel {{\color{black}(5x+1)}}}(5x+1)}{{\color{Red}\bcancel {{\color{black}x}}}(3x+1)}$$\;\;\dfrac{x^2+8x+16}{x^2-5x}\cdot\dfrac{x-5}{x^2-16}=\dfrac{(x+4)^{\color{Red}\bcancel {{\color{black}2}}}}{x{\color{Red}\bcancel {{\color{black}(x-5)}}}}\cdot\dfrac{{\color{Red}\bcancel {{\color{black}x-5}}}}{{\color{Red}\bcancel {{\color{black}(x+4)}}}(x-4)}$
$\bullet\hspace{0.3cm}$División de expresiones algebraicas racionales
De igual forma que el producto, se factorizan, tanto los numeradores como los denominadores y se simplifica. Cuando se trata de división, al simplificar , ten en cuenta que siempre se toman los términos
semejantes entre los numeradores y los denominadores.
 Ejemplos de división de expresiones algebraicas racionales
Ejemplos de división de expresiones algebraicas racionalesEn las siguientes escenas interactiva, diseñadas por José Luis Abreu Leon y otros, podrás:
Simplificar expresiones algebraicas, usando los productos notables para factorizar los numeradores y denominadores de los polinomios. Puedes pulsar "Solución", para ver el resultado paso a paso y si lo deseas, puedes pulsar "Ejercicio", para analizar la simplificación de otros polinomios y de esta forma ampliar los conocimientos adquiridos en las páginas anteriores.
Es recomendable que uses papel y lápiz para tratar de llegar a la solución y luego observar y analizar el ejercicio resuelto, paso a paso que se presenta en la escena interactiva.
Escena 1. Simplificar expresiones algebraicas
Realizar las operaciones con fracciones algebraicas, analizando el paso a paso de los ejercicios resueltos de las operaciones de suma y resta, producto, cociente y una serie de mezclas que te ayudarán a fortalecer los conocimientos adquiridos.
Se recomienda que uses papel y lápiz y trates de resolver los ejercicios, antes de consultar la solución.
Escena 2. Operaciones con fracciones algebraicas
Generalmente la racionalización consiste en utilizar operaciones matemáticas que permitan eliminar los radicales, ya sea en el numerador o en el denominador según el caso. Para ello es muy común el uso de la conjugada, que no es más que la expresión que tiene los mismos términos literales, pero se diferencian por el signo de la mitad.
Antes de aprender a racionalizar expresiones algebraicas, observa la escena interactiva, diseñada por http://matematicaula.com.es/http://matematicaula.com.es/, son autores de la red GeoGebra, que publicaron la escena interactiva "Racionalización"., en la escena interactiva podrás aprender a racionalizar expresiones aritméticas.
$\bullet\hspace{0.3cm}$Racionalización del numerador
Para racionalizar el numerador, se debe multiplicar el numerador y el denominador por una expresión que al realizar las operaciones, se elimine la raíz o las raíces del numerador (la conjugada).
Recuerda que para hallar la conjugada de un binomio, debes cambiar el signo al segundo término del binomio, luego hacer una fracción con dicho binomio y multiplicarla por el racional que se desea racionalizar.
 Ejemplos de racionalización de numeradores
Ejemplos de racionalización de numeradoresObserva que el numerador se ha convertido en el producto de la suma por la diferencia, que nos da como resultado una diferencia de cuadrados, por lo que basta (elevar en la diferencia) cada término al cuadrado.
$\hspace{3cm}=\dfrac{\left( \sqrt {x+h}\right) ^{2}-\left( \sqrt {x}\right)^{2}}{h\cdot(\sqrt{x+h}+\sqrt{x})}$
$\hspace{3cm}=\dfrac{{\color{Red}\bcancel {{\color{black}x}}}+{\color{Red}\bcancel {{\color{black}h}}}-{\color{Red}\bcancel {{\color{black}x}}}}{{\color{Red}\bcancel {{\color{black}h}}}\cdot(\sqrt{x+h}+\sqrt{x})}$
Al igual que en el ejemplo anterior, el numerador se ha convertido en el producto de la suma por la diferencia, pero en el denominador se debe aplicar la propiedad distributiva y sumar términos semejantes.
$\hspace{1.3cm}=\dfrac{\left( 2\sqrt {a}\right) ^{2}-\left( 3\sqrt {b}\right) ^{2}}{(2a-3b+\sqrt{ab})\cdot(2\sqrt{a}-3\sqrt{b})}$
$\hspace{2cm}=\dfrac{ 4a-9b}{4a\sqrt{a}-6a\sqrt{b}-6b\sqrt {a}+9b\sqrt{b}+2a\sqrt{b}-3b\sqrt{a}}$
$\hspace{4cm}\uparrow\underline{\color{brown}\;\;\;\;\;\;\;\;\;-4a\sqrt{b}\;\;\;\;\;\;\;\;\;\;\;\;}\hspace{0.0cm}\uparrow\\$ $\hspace{5.3cm}\uparrow\underline{\color{brown}\;\;\;\;\;\;\;\;\;-9b\sqrt{a}\;\;\;\;\;\;\;\;\;\;\;\;}\hspace{0.0cm}\uparrow\\$$\hspace{2cm}=\dfrac{ 4a-9b}{4a\sqrt{a}-4a\sqrt{b}-9b\sqrt {a}+9b\sqrt{b}}$
Ahora se saca factor común por agrupación de términos en el denominador.
$\hspace{2cm}=\dfrac{ 4a-9b}{4a(\sqrt{a}-\sqrt{b})-9b(\sqrt {a}-\sqrt{b})}$
Nuevamente se tiene un factor común en el denominador.
$\hspace{2cm}=\dfrac{ {\color{Red}\bcancel {{\color{black}4a-9b}}}}{{\color{Red}\bcancel {{\color{black}(4a-9b)}}}(\sqrt{a}-\sqrt{b})}$
Luego de simplificar, se obtiene:
$\bullet\hspace{0.3cm}$Racionalización del denominador
Es el más utilizado en las operaciones matemáticas, para racionalizar el denominador, se debe multiplicar el numerador y el denominador por una expresión que al realizar las operaciones, se elimine la raíz o las raíces del denominador (la conjugada).
 Ejemplos de racionalización de denominadores
Ejemplos de racionalización de denominadoresObserva la diferencia de cuadrados en el denominador, se resuelve y se aplica la propiedad distributiva en el numerador.
$\hspace{0cm}=\dfrac{({3x-4y}-\sqrt{xy})\cdot(3\sqrt{x}+4\sqrt{y})}{\left( 3\sqrt {x}\right) ^{2}-\left(4\sqrt {y}\right) ^{2}}$
$\hspace{2.3cm}\underline{\color{brown}\hspace{1.6cm}9x\sqrt{y}\hspace{1.8cm}}{\hspace{0.5cm}}\\$ $\hspace{2.2cm}\downarrow\hspace{1.0cm}\hspace{3.1cm}\downarrow\\$$=\dfrac{{9x\sqrt{x}+12x\sqrt{y}-12y\sqrt{x}-16y\sqrt{y}-3x\sqrt{y}-4y\sqrt{x}}}{9x-16y}$ $\hspace{3.4cm}\uparrow\underline{\color{brown}\hspace{1.3cm}-16y\sqrt{x}\hspace{1.3cm}}\hspace{0.0cm}\uparrow\\$
Se agrupan términos semejantes del numerador.
$\hspace{1cm}=\dfrac{{9x\sqrt{x}+9x\sqrt{y}-16y\sqrt{x}-16y\sqrt{y}}}{9x-16y}$
Es el momento de sacar factor común por agrupación de términos.
$\hspace{1cm}=\dfrac{{9x(\sqrt{x}+\sqrt{y})-16y(\sqrt{x}+\sqrt{y})}}{9x-16y}$
Ahora se saca factor común y se simplifica.
$\hspace{1cm}=\dfrac{{{\color{Red}\bcancel {{\color{black}(9x-16y)}}}(\sqrt{x}+\sqrt{y})}}{{\color{Red}\bcancel {{\color{black}9x-16y}}}}$
Observa la diferencia de cuadrados en el denominador, se resuelve y se aplica la propiedad distributiva en el numerador.
$\hspace{3cm}=\dfrac{a^4-2}{(\sqrt{a^4-1}-1)}\cdot\dfrac{(\sqrt{a^4-1}+1)}{(\sqrt{a^4-1}+1)}$
$\hspace{3cm}=\dfrac{(a^4-2)(\sqrt{a^4-1}+1)}{(\sqrt{a^4-1})^2-(1)^2}$
$\hspace{3cm}=\dfrac{(a^4-2)(\sqrt{a^4-1}+1)}{a^4-1-1}$
$\hspace{3cm}=\dfrac{{\color{Red}\bcancel {{\color{black}(a^4-2)}}}(\sqrt{a^4-1}+1)}{{\color{Red}\bcancel {{\color{black}a^4-2}}}}$
Después de una ardua labor aprendiendo a racionalizar numeradores y denominadores de expresiones algebraicas, es tiempo de disfrutar de un juego, diseñado por Ceferino A.Ceferino A., es un autor de la red GeoGebra, que publicó la escena interactiva "Expresiones algebraicas.". En la escena interactiva podrás aprender a pasar del lenguaje verbal al matemático expresiones que serán de utilidad para la solución de problemas en contexto de la vida cotidiana.
El reto es encestar el mayor número de balones, con el menor número de fallas.
Te puedes relajar, tratando de sacar el coche rojo de la zona de aparcamiento del puzle Rush Hour..., el puzle es una escena interactiva de un rompecabezas diseñada por Juan Guillermo Rivera Berrío y José R. Galo Sánchez.Juan Guillermo Rivera Berrío y José R. Galo Sánchez., son autores de la red Descartes, que publicaron la escena interactiva "Saca el coche de la zona de aparcamiento.", que hace honor a su nombre.
En la siguiente escena interactiva, diseñada por José Luis Abreu Leon, podrás realizar una prueba de conocimiento, sin limite de tiempo que te permitirá poner en practica los conocimientos adquiridos sobre operaciones con polinomios. Si requieres hacer uso de la calculadora, podrás utilizar la de Descartes, haciendo clic sobre la imagen. 
En la siguiente escena interactiva, diseñada por Miguel Angel Cabezón OchoaMiguel Angel Cabezón Ochoa, es un autor de la Red Descartes., podrás practicar los diferentes casos de factorización, con gran variedad de ejercicios resueltos paso a paso.

Eudoxo demostró que el volumen de una pirámide es la tercera parte del de un prisma de su misma base?
Y que Arquímedes fue uno de los matemáticos más grandes de la antigüedad?
Para saber más sobre éstos y otros personajes resuelve el puzle que nos presenta Juan Guillermo Rivera Berrío.Juan Guillermo Rivera Berrío, es un autor de la red Descartes que publicó la escena interactiva "Descubre los personajes."
La ecuación más básica en álgebra es la ecuación lineal y se define como $mx+b=0$, donde $m=\not 0$, luego, si
$mx+b=0$, $\;\;entonces \;\;x=-\dfrac{b}{m}$
Ecuación de la línea recta
Se define la pendiente $"m"$, como la razón de cambio vertical (eje de $"y"$) con respecto a la horizontal (eje de $"x"$), por un desplazamiento sobre la recta de izquierda a derecha.
$m=\dfrac {\Delta y}{\Delta x}=\dfrac {y_{2}-y_{1}}{x_{2}-x_{1}}$
Ecuación de la línea recta dados dos puntos
La ecuación de la línea recta dados los puntos $P_{1}(x_{1},y_{1}) \wedge P_{2}(x_{2},y_{2})$, se determina por la siguiente ecuación:
$\dfrac {y-y_{1}}{x-x_{1}}=\dfrac {y_{2}-y_{1}}{x_{2}-x_{1}}$
Se debe tener en cuenta que si $y_{2}-y_{1}=0$, la pendiente es igual a cero, por lo tanto no existe pendiente y se trata de una recta horizontal. Por otro lado si $x_{2}-x_{1}=0$, la recta no esta definida.
En la siguiente escena interactiva, diseñada por Juan Guillermo. Rivera Berrío y otros, podrás realizar los ejercicios que se proponen a continuación y luego verificar el resultado en la escena interactiva, sólo necesitas ingresar los puntos dados. Si requieres hacer uso de la calculadora, puedes utilizar la de Descartes, haciendo clic sobre la imagen. 
Analizando la escena interactiva anterior y luego de realizar los ejercicios propuestos, se puede concluir que es posible hallar la ecuación de la línea recta, dados un punto y la pendiente. Observa también que $\dfrac {y-y_{1}}{x-x_{1}}=\dfrac {y_{2}-y_{1}}{x_{2}-x_{1}}$ y que $m=\dfrac {y_{2}-y_{1}}{x_{2}-x_{1}}$, luego:
Ecuación de la línea recta dados un punto y la pendiente
$\dfrac {y-y_{1}}{x-x_{1}}=m$
De la ecuación anterior podemos despejar $y$ y se obtiene:
$y=m(x-x_{1})+y_{1}$
Finalmente se tiene que tener en cuenta que:
Para resolver ecuaciones, se debe tener en cuenta lo siguiente que al pasar un término o un coeficiente de un lado al otro de la igualdad, la operación cambia.
$\bullet\hspace{0.2cm}$Lo que esta sumando pasa a restar.
$\bullet\hspace{0.2cm}$Lo que esta restando pasa a sumar.
$\bullet\hspace{0.2cm}$Lo que esta multiplicando pasa a dividir y
$\bullet\hspace{0.2cm}$Lo que esta dividiendo pasa a multiplicar.
 Ejemplos de ecuaciones lineales
Ejemplos de ecuaciones lineales$6x-2x=5+7$
$4x=12$
$x=\dfrac{12}{4}$
$\color{brown}x=3$
Aplicamos la propiedad distributiva a ambos lados de la igualdad y se reducen los términos semejantes.
${\color{Red}\bcancel {{\color{black}24x^2}}}+26x-8={\color{Red}\bcancel {{\color{black}24x^2}}}+14x-3$
$26x-14x=-3+8$
$12x=5$
$\color{brown}x=\dfrac{5}{12}$
$4(13 + 2x)=3(4x + 1)$
$52+4x=12x+3$
$52-3=12x-4x$
$8x=49$, luego $\color{brown}x=\dfrac{9}{8}$
Son ecuaciones polinomiales de segundo grado, que puede escribirse en su forma estándar de la siguiente manera:
Muchos problemas sobre objetos en movimiento, implican ecuaciones cuadráticas.
 Ejemplos de ecuación cuadrática
Ejemplos de ecuación cuadráticaSolución:
Dado que el globo llega al suelo, su altura será $s=0$, por lo tanto, la ecuación quedará:
$$\color{brown}0=16t^2-48t-64$$Como podemos observar la ecuación resultante es divisible por 16 y quedaría:
$$\frac{16t^2}{16}-\frac{48t}{16}-\frac{64}{16}=t^s-3t-4=0$$Tomando $t^2-3t-4=0$, podemos factorizar el trinomio de la forma $ax^{2}+bx+c=0,\; \;\text{con}\; a=\not 0$ para hallar los posibles valores de $t$.
$$\left(t-4\right)\cdot\left(t+1\right)=0$$Ahora: $\left(t-4\right)=0$, luego $t=4$. El valor de $t$ para el factor $\left(t+1\right)$ no se tiene en cuenta por ser negativo.
R/. El globo tarda 4 segundos para llegar al suelo.
Si una ecuación cuadrática tiene la forma especial $\color{brown}x^2=d,\; \; \text{con}\ d=\not 0$, lo podemos resolver igualando a cero, esto es $x^2-d=0$. Se puede observar que es una diferencia de cuadrados y se resuelve como el producto de la suma por la diferencia de sus raíces cuadrados.
$$\left(x+\sqrt d\right)\cdot\left(x-\sqrt d\right)=0$$Esto indica que tiene dos soluciones $x=\sqrt{d}\vee x=-\sqrt{d}$.
También se pude resolver sacando raíz cuadrada a cada uno de los términos de la ecuación, teniendo en cuenta que cuando se trata de raíz cuadrada se tienen dos soluciones, una con valores positivos y otra con valores negativos.
Esto es, $\sqrt{x^2}=\pm\sqrt{d}$, luego $x=\pm\sqrt{d}$ que coincide con la respuesta anterior.
Despejamos la $x$, $x^2=\frac{6}{2}=3$; luego $x=\pm\sqrt{3}$.
El conjunto solución es $\left\{-\sqrt{3},\;\sqrt{3}\right\}$
Despejando la $y$, quedaría:
$$\color{black}\begin{aligned} \sqrt{\left(y-3\right)^2} &= \pm\sqrt5\\ &= \pm\sqrt5 \\ &= 3\pm\sqrt5 \end{aligned}$$El conjunto solución es $\color{brown}\left\{3-5,\ 3+\sqrt5\right\}$
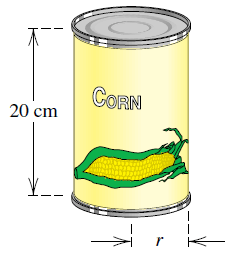
Se toma sólo el valor positivo, ya que el radio no puede ser negativo.
Para obtener los posibles valores de $x$, debemos utilizar el método de completar cuadrados, que vimos anteriormente.
Procedimiento
Se resta el término $\left(\frac{b}{2a}\right)^2$ para que la ecuación no se afecte, observemos que, si se resuelve la ecuación anterior se conserva la ecuación inicial (sólo a manera de prueba)
Recuerden que para solucionar el cuadrado de un binomio se debe proceder de la siguiente forma:
$$\color{brown}{(a\pm b)}^2={(a)}^2\pm2\left(a\right)\cdot\left(b\right)+{(b)}^2$$Para el ejercicio que estamos resolviendo, esto sería:
$$\left(x\right)^2+2\cdot\left(x\right)\cdot\left(\cfrac{b}{2a}\right)+\left(\cfrac{b}{2a}\right)^2-\left(\cfrac{b}{2a}\right)^2=-\cfrac{c}{a}\ \longrightarrow x^2+\cfrac{b}{a}x=-\cfrac{c}{a}$$Se puede observar que la ecuación no se altera y que $2\cdot\left(x\right)\cdot\left(\frac{b}{2a}\right)=\frac{b}{a}x$
Luego de completar el cuadrado, pasamos el término $-\left(\frac{b}{2a}\right)^2$ a la derecha:
$$\left(x+\cfrac{b}{2a}\right)^2=\left(\cfrac{b}{2a}\right)^2-\cfrac{c}{a}$$Hacemos la suma en los términos de la derecha, donde el M.C.D es $4a^2$, quedando así:
$$\left(x+\cfrac{b}{2a}\right)^2=\cfrac{b^2-4ac}{4a^2}$$Sacamos raíz cuadrada a cada lado de la ecuación
$$\sqrt{\left(x+\cfrac{b}{2a}\right)^2}=\pm\sqrt{\cfrac{b^2-4ac}{4a^2}}$$Aplicamos propiedades de los radicales
$$x+\cfrac{b}{2a}=\pm\cfrac{\sqrt{b^2-4ac}}{2a}$$Despejamos la $x$
$$x=-\cfrac{b}{2a}\pm\cfrac{\sqrt{b^2-4ac}}{2a}$$Hacemos una suma de fraccionarios de igual denominador y se obtiene la fórmula de la ecuación cuadrática
Como se dijo anteriormente la ecuación cuadrática sirve para solucionar muchos problemas sobre objetos en movimiento y hallar factores (factorizaciones) que no tienen soluciones en los enteros.
El término $\color{brown}\sqrt{b^2-4ac}$ de la ecuación cuadrática se conoce como el discriminante y es el que determina las posibles soluciones de la ecuación cuadrática.

 Ejemplos con ecuación cuadrática
Ejemplos con ecuación cuadráticael suelo después de t segundos está dada por $h=-16t^2+120t$. ¿Cuánto tiempo demora el cohete en obtener una altura de 200 pies?
$16t^2-120t+h=0$, pero sabemos que la altura que obtendrá en un tiempo $t$, será de 200 pies, luego:
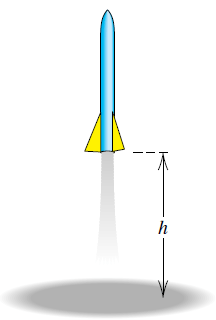
Si hacemos uso del discriminate, nos daremos cuenta que $b^2-4ac>0$,lo que indica que tiene dos soluciones en los reales.
$$b^2-4ac=\left(-120\right)^2-4\cdot\left(16\right)\cdot\left(1\right)=1600$$Utilizamos la fórmula de la ecuación cuadrática $x=-\cfrac{b\pm\sqrt{b^2-4ac}}{2a},\;\;\;\ \text{con}\; a=\not 0$ y reemplazamos.
$$t=-\cfrac{b\pm\sqrt{b^2-4ac}}{2a}$$Donde: $a=16,\:\; b=-120\;\wedge\; c=200$
$$\color{black}\begin{aligned} t &= -\cfrac{-120\pm\sqrt{\left(-120\right)^2-4\cdot\left(16\right)\cdot\left(200\right)}}{2\cdot\left(16\right)} \end{aligned}$$Por lo tanto, el cohete está a 200 pies sobre el suelo en los siguientes tiempos: $\color{brown}2.5\wedge 5\;\text{segundos}$.
Las dos respuestas obedecen a que a los $2.5$ segundos el cohete va subiendo y por efectos de la gravedad asciende a su altura máxima y empieza a descender y a los $5$ segundos pasa nuevamente para la altura de 200 pies.
Reemplazamos en la ecuación cuadrática
$$\color{brown}x=-\frac{b\pm\sqrt{b^2-4ac}}{2a},\;\;\;\text{con}\; a=\not 0$$ $$\color{black}\begin{aligned} x &=-\frac{-24\pm\sqrt{\left(-24\right)^2-4\cdot\left(9\right)\cdot\left(16\right)}}{2\cdot\left(9\right)},\;\;\;\text{con}\; a=\not 0 \end{aligned}$$En este caso como el discriminante es igual a cero, sólo se tienen una respuesta.
En este caso, observe que el discriminante es menor que cero, $\left(-1\right)^2-4\cdot\left(1\right)\left(1\right)=-3$, por lo tanto, no tiene solución en los reales.
A continuación se explica la definición de los números imaginarios y las operaciones con los complejos.
Son aquellas raíces que no tienen solución en los reales, es decir que el discriminante es menor que cero.
Se denota por $\color{brown}i$ y tiene la siguiente propiedad:
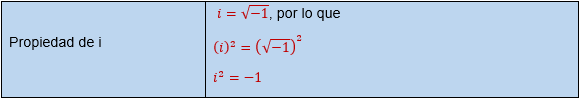
 Ejemplos de números imaginarios
Ejemplos de números imaginariosSon aquellos que están formados por una parte real y una parte imaginaria, por lo regular la parte real se separa de la imaginaria y va siempre a la izquierda. Esto es, un número complejo se define como $\color{brown}a+bi$, donde $a$ y $b$ son reales e $i$ es la parte imaginaria.
Propiedades de los complejos

Se aplican las propiedades de los (distributiva, asociativa, etc.), teniendo presente la parte imaginaria.
En la siguiente escena interactiva, diseñada por María José García CebrianMaría José García Cebrian es una autora de la red Descartes, que publicó el libro Los números complejos, del cual seleccionaremos algunas escenas interactivas en el resto de esta obra., encontrarás la definición de la conjugada de un número complejo y su inverso.
Para interactuar con la escena interactiva, modifica los valores de la parte real e imaginaria del número complejo, pulsando las flechas arriba y abajo, luego presiona "dibujar" para que puedas visualizar el resultado.
Puedes realizar el mismo procedimiento para obtener los resultados de la conjugada y el opuesto de un número complejo.
Como se pudo observar en la escena interactiva anterior, para obtener la conjugada de un número complejo, se cambia el signo a la parte imaginaria.
Igualdad de números complejos:
Suma de números complejos: Se suma la parte real y la parte imaginaria.
Resta de números complejos: Se resta la parte real y la parte imaginaria
 Ejemplo de suma y resta de complejos
Ejemplo de suma y resta de complejosSea: $Z_1= \left( 2 + 5i \right) \; y \; Z_2 = \left( 6 + 3i \right)$. Hallar:
Solución
En la siguiente escena interactiva, diseñada por María José García Cebrian, puedes interactuar realizando los ejemplos anteriores y pulsar el botón "dibujar", para obtener una representación gráfica de las respuestas.
Producto de números complejos: Se aplica la propiedad distributiva y se suman los términos semejantes, teniendo en cuenta que la parte real debe quedar a la izquierda y la parte imaginaria a la derecha.
Tener en cuenta que $i^2 = -1$
$$\left( a + bi\right) \; \left( c + di\right) = ac + adi + bci + bdi^2$$ $$\left( a + bi\right) \; \left( c + di\right) = ac + adi + bci + bd\left(-1\right)$$ $$\left( a + bi\right) \; \left( c + di\right) = ac + adi + bci - bd$$Para comprobar la definición anterior, utiliza la escena interactiva diseñada por María José García Cebrian.
En la escena interactiva, te puedes dar cuenta que:
$\bullet\hspace{0.3cm}$Para la parte real se resta el producto vertical de las dos columnas.
$\bullet\hspace{0.3cm}$Para la parte imaginaria se suma el producto en cruz de las dos columnas (el producto de la diagonal principal más el producto de la diagonal secundaria.
 Ejemplo de producto de complejos
Ejemplo de producto de complejosAnaliza el siguiente ejemplo y comprueba la respuesta en la escena interactiva.
$\left( 2+4i\right)\;\left( 2-i \right)= $ $8 + 6i$
$\left( 3+2i\right)\;\left( -1+3i \right) = $$-9 + 7i$
$\left( -2-i\right)\;\left( -3+3i \right) = $$9 - 3i$
Realiza los siguientes ejercicios de producto de complejos y comprueba la respuesta en la escena interactiva.
División de números complejos: Se debe tener en cuenta racionalizar el denominador, es decir; multiplicar numerador y denominador por la conjugada del denominador
$\dfrac{( a + bi )}{( c + di )},\;con\;( c + di )=\not 0$
 Ejemplo de división de números complejos
Ejemplo de división de números complejos$\;\;Z_2$ = $\left( 5 +3 i\right)$
$\;\;Z_2$ = $\left( 5 - 3 i\right)$
Para el numerador:
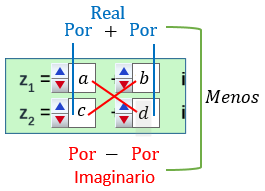
Para el denominador:
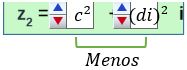
Siguiendo las indicaciones:
Ahora separamos el denominador y simplificamos.
$$\dfrac {Z_1}{Z_2}=\dfrac {26}{34}-\dfrac{2i}{34}$$Ahora separamos el denominador y simplificamos.
$$\dfrac {Z_1}{Z_2} =\dfrac {26}{34}+\dfrac{2i}{34}$$También se puede multiplicar el numerador y el denominador por la conjugada y aplicar la propiedad distributiva.
$$\begin{aligned} \dfrac {Z_1}{Z_2} &= \dfrac {(4 + 2i)}{(5 +3 i)}\cdot\dfrac {(5 -3 i)}{(5 -3 i)}\\[15pt] &= \dfrac {[(4\times5)-(4\times3i)+(2i\times5)-(2i\times3i)]}{(5 +3 i)(5 -3 i)} \\[15pt] &= \dfrac {[20-12i+10i-6i^2]}{[5^2 -(3 i)^2]}=\dfrac {[20-12i+10i-6(-1)]}{[25 -3^2 i^2]} \\[15pt] &=\dfrac {[20-2i+6]}{[25 -9(-1)]}=\dfrac {26-2i}{[25 +9]} \\[15pt] \end{aligned}$$Utilizando la siguiente escena interactiva, diseñada por María José García Cebrian puedes comprobar los resultados de los procedimientos explicados en los dos ejemplos anteriores. Si deseas, puedes plantear nuevos ejercicios en la escena interactiva y realizarlos en tu cuaderno, confronta tus conocimientos. ¡Ánimo!
Realiza los siguientes ejercicios de cociente de complejos y comprueba la respuesta en la escena interactiva anterior.
Si $P(x)=2x^3+x^2-13x+6$ , como el primer término del polinomio es diferente de 1, los ceros racionales de $P$ son de la forma de descomposición de factores.
Posible cero racional de:
$P=\dfrac{(Factores \;del \;t\text{é}rmino\; constante)}{(Factores \;del \;coeficiente\; principal)}$. El término constante es $6$ y el coeficiente principal es $2$, por lo tanto, posible cero racional de $P=\dfrac{(Factores\; de \;6)}{(Factores \;de \;2)}$.
Ahora, los factores de $6$ son $6:±1,±2,±3,±6$ y los factores de $2$ son $±1,±2$. Así los posibles ceros racionales de $P$ son: $±\dfrac{1}{1},±\dfrac{2}{1},±\dfrac{3}{1},±\dfrac{6}{1},±\dfrac{1}{2},±\dfrac{2}{2},±\dfrac{3}{2},±\dfrac{6}{2}$.
Resumiendo, nos queda $±1,±2,±3,±6,±\dfrac{1}{2},±\dfrac{3}{2}$.
Para comprobar los posibles ceros de $P(x)$, reemplazamos cada uno
de los factores anteriores para ver cual hace $P(x)=0$.
$P(1)=2(1)^3+(1)^2-13(1)+6=2+1-13+6=4$, no es un cero de $P(x)$.
$P(-1)=2(-1)^3+(-1)^2-13(-1)+6=-2+1+13+6=18$, no es un cero de $P(x)$.
$P(2)=2(2)^3+(2)^2-13(2)+6=16+4-26+6=0$, es un cero de $P(x)$.
$(x-2)$ es el primer factor de $P(x)$. Ahora resolvemos en la misma forma que se hizo con la división sintética.
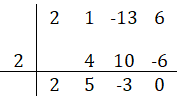
El cociente $Q(x)$, sería $2x^2+5x-3$ y con residuo $R(x)=0$
Ahora factorizamos el trinomio de la forma $ax^2+bx+c$, quedando finalmente los factores de P(x) de la siguiente forma:
$P(x)=2x^3+x^2-13x+6=\color{brown}(x-2)(2x-1)(x+3)$
En las siguientes escenas interactivas, diseñadas por Miguel Angel Cabezón OchoaMiguel Angel Cabezón Ochoa, es un autor de la red Descartes, que publicó la escena interactiva "Descomposición en factores"., podrás analizar los ejemplos propuestos sobre factores de un polinomio.
Como complemento a la explicación y al a la escena interactiva anterior, puedes analizar el siguiente video de Julio Alberto Ríos Ríos Gallego, donde se explica el paso a paso para la solución de una factorización por el método de evaluación.
Cuando se resuelven ecuaciones que tienen expresiones exponenciales, con variables en los exponentes, es usual utilizar los logaritmos a cada lado de la ecuación y convertirlas en factores, que facilitan su solución. Los logaritmos tienen aplicación en todos los campos del saber, especialmente en la química, la biología, la física y la ingeniería.
Los logaritmos con base $b=10$ se llaman logaritmos en base 10 o comunes y los logaritmos en base $b=e$ se llaman logaritmos naturales o neperianos.
Se acostumbra escribir el logaritmo natural como:
Donde: $B=Base$, $P=Potencia$ y $E=Exponente$.
Podemos convertir logaritmos en potencias de la siguiente forma:
Observen que, en el ejemplo, el logaritmo en base $10$ de $100$ es $2$, si y sólo si la $B=10$, elevada al exponente $E=2$, es igual a la potencia $P=100$.
 Ejemplos de logaritmos
Ejemplos de logaritmosConvertir los logaritmos en potencias.
Si lo expresamos en forma de potencia, nos quedaría:
$$10^2=x$$Si lo expresamos en forma de potencia, nos quedaría:
$$2^4=x$$Si lo expresamos en forma de potencia, nos quedaría:
$$3^y=2187$$La igualdad se cumple, si y sólo si $y=7$, dado que las bases de ambos lados de la igualdad son iguales a $3$.
 Ejemplos con propiedades de logaritmos
Ejemplos con propiedades de logaritmosPara su solución, se aplican las propiedades de las potencias, radicales y logaritmos.
Las ecuaciones exponenciales, tienen múltiples aplicaciones en la vida cotidiana, desde determinar el tamaño poblacional hasta los fenómenos físicos como la aceleración, velocidad y densidad.
Como ejemplos de su utilización, se pueden mencionar el crecimiento de la cantidad de personas infectadas con determinada bacteria, la disminución de la carga de un condensador, la escala de Ritcher, la magnitud de un terremoto, entre otras.
Las funciones logarítmicas, como inversas las exponenciales son utilizadas para comparara fenómenos inversos a las ecuaciones exponenciales. Como ejemplos de aplicación se pueden tener en cuenta su utilización en la economía, para determinar el valor
futuro de un depósito en un banco después de determinado tiempo y a una tasa de interés determinada, en investigaciones policiales para determinar el tiempo estimado de muerte de una persona, al medir la temperatura del cuerpo, del ambiente, de la habitación donde fue hallado, en la medicina para determinar el contenido de una determinada sustancia en el cuerpo, después de "t" tiempo de haberla ingerido.
Para resolver ecuaciones exponenciales y logarítmicas, se recomienda:
$\bullet\hspace{0.2cm}$ Reescriba una expresión exponencial como expresión logarítmica.
$\bullet\hspace{0.2cm}$ Reescriba una expresión logarítmica como expresión exponencial..
$\bullet\hspace{0.2cm}$ Use las propiedades uno a uno de $b^x$ y $log_b x$..
$\bullet\hspace{0.2cm}$ Para las ecuaciones de la forma $a^{x}_1=b^{x}_2$ , donde $a=\not b$, obtenga el logaritmo natural de ambos lados de la igualdad y simplifique usando las leyes de los logaritmos.
A continuación se resolverán algunos ejemplos de ecuaciones exponenciales y logarítmicas, para que te familiarices con los procedimientos que se deben realizar en su solución, utilizando las propiedades de las potencias y los logaritmos.
 Ejemplos de ecuaciones exponenciales y logarítmicas
Ejemplos de ecuaciones exponenciales y logarítmicasRecuerden que, para los logaritmos decimales la base es $10$ y por lo general se omite, mientras que, para los logaritmos naturales o neperianos, la base es e número Euler $e$.
Aplicamos logaritmos a lado y lado de la igualdad, y como la base es "e", se infiere que se trata de logaritmos neperianos.
$$ln_e e^{10k}=ln_e 7$$ $$10k\cdot ln_e e=ln_e 7$$Recordemos que el $log_{10} 10=1\wedge ln_e e=1$, se pueden omitir sus bases, ya que se entiende que si es $ln$, la base $e$ y si es $log$, la base es $10$.
$$10k\left(1\right)=ln 7$$Entonces $2^5=x$, por lo que $\color{brown}x=32$
Para solucionar la ecuación es conveniente convertir $8^{x+1}$ en base 2, de la siguiente forma:
$2^{x-3}=\left(2^3 \right)^{x+1}$, aplicando la propiedad de potencia de una potencia,
$2^{x-3}=2^{3x+3}$, ahora; si las bases son iguales, los exponentes tienen que ser iguales.
$2=2$, entonces $x-3=3x+3$. Despejando la $x$, nos queda:
$$x-3x=3+3$$ $$-2x=6$$Para que profundices en tus conocimientos, observa con detenimiento el siguiente video realizado por Julio Alberto Ríos Gallego "Julio Profe" Julio Alberto Ríos Gallego "Julio Profe" es un autor de la red YouTube, que publicó el video "Ecuaciones exponenciales - Ejercicio 3"., en el cual se explica la solución de una ecuación exponencial, paso a paso, tal como se hizo en los ejemplos anteriores.
Si lo resolvemos aplicando logaritmos a ambos lados de la igualdad, nos quedaría:
$$2^{x-3}=2^{3x+3}$$ $$\left(x-3\right) log 2=\left(3x+3\right) log 2$$Si, $log\;2=log\;2$, entonces,
$$x-3=3x+3$$ $$2x=-6$$Para que profundices en tus conocimientos, observa con detenimiento el siguiente video realizado por Julio Alberto Ríos Gallego "Julio Profe" Julio Alberto Ríos Gallego "Julio Profe" es un autor de la red YouTube, que publicó el video "Ecuaciones exponenciales - Ejercicio 4"., en el cual se explica la solución de una ecuación exponencial, paso a paso, tal como se hizo en los ejemplos anteriores.
Se saca logaritmo en ambos lados de la igualdad.
$$E\cdot log b=log P$$ $$\color{brown}E =\cfrac{log P} {log b}$$Como $E=log_b P, \text{podemos concluir que } \color{brown}log_B P=\cfrac{log_a P}{log_a b}$
Lo anterior es lo que se conoce como "Teorema del cambio de base".
Recuerda que puedes resolver la diferencia de fraccionarios, de la siguiente forma:
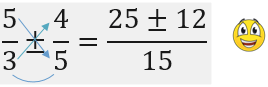
Es un trinomio de la forma $ax^2+bx+c$, lo resolvemos por la formula general.
$$\color{black}\begin{aligned} 5^x&= \cfrac{-\left(-6\right)±\sqrt{\left(-6\right)^2-4\cdot \left(1\right)\cdot \left(-1\right)}}{2\cdot \left(1\right)}\\ &= \cfrac{6±\sqrt{36+4}}{2}\\ &= \cfrac{6±\sqrt{40}}{2}\\ &= \cfrac{6±\sqrt{2^2 \cdot 10}}{2}\\ &= \cfrac{6±2\sqrt{10}}{2} \end{aligned}$$Se simplifica.
$$5^x=3±\sqrt{10}$$Se toma como solución $3+\sqrt{10}$ porque $3-\sqrt{10} < 0 \wedge 5^x > 0$
Aplicamos logaritmo a cada lado de la igualdad.
$$log 5^x=log \left(3+\sqrt{10}\right)$$Se despeja la $x$.
Observen el lado izquierdo de la igualdad es una suma de logaritmos y por propiedad, es el logaritmo del producto.
$$ln \left[2\cdot \left(4x-1\right)\right]=ln \left(2x+5\right)$$Ahora, si $ln =ln$, entonces:
$$\left[2\cdot \left(4x-1\right)\right]=\left(2x+5\right)$$Resolvemos:
$$8x-2=2x+5$$ $$8x-2x=5+2$$ $$6x=7$$ $$x=\cfrac{7}{6}$$Como la base es $e$, utilizamos $ln$ en ambos lados de la igualdad,
$$ln e^{2x}=ln 3^{x-4}$$ $$2x\cdot ln e =\left(x-4\right)\cdot ln3$$ $$2x=\left(x-4\right)\cdot ln e$$Recuerda que $ln_e e=1$
$$2x=x\cdot ln 3-4\cdot ln 3$$ $$2x-x\cdot ln 3 =-4\cdot ln 3$$Sacamos factor común $x$
$$x\left(2-ln3 \right)=-4\cdot ln 3$$Despejamos $x$
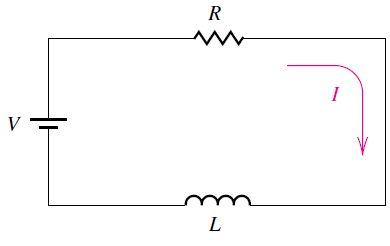
Solución:
$$I=20e^{-Rt/L}$$Despejaremos $t$ aplicando logaritmos, pero antes pasamos el 20 a dividir.
$$\cfrac{I}{20}=e^{-\frac{Rt}{L}}$$ $$ln\cfrac{I}{20}=lne^{-\frac{Rt}{L}}$$ $$ln\cfrac{I}{20}=-\cfrac{Rt}{L} ln e$$Sabemos que $ln_e e=1$
Despejamos $t$.
$\bullet\hspace{0.2cm}$¿Cuál es la temperatura del pastel 6 minutos después?
$\bullet\hspace{0.2cm}$¿En cuánto tiempo la temperatura del pastel será de 80 °F?
Solución:
$\bullet\hspace{0.2cm}$¿Cuál es la temperatura del pastel 6 minutos después?
Dado que:
$$T_0= 350 °F$$ $$T_m= 75 °F$$ $$T_1=300 °F$$Reemplazamos en $T_t=T_m+\left(T_0-T_m \right)\cdot e^{kt}$
Sabemos que la temperatura en un minuto es:
$$T_1=300 °F$$ $$300=75+\left(350-75\right)\cdot e^k$$ $$300-75=\left(350-75\right)\cdot e^k$$ $$225=275\cdot e^k$$ $$\cfrac{225}{275}=e^k$$Simplificamos, ya que la fracción es divisible por 25.
$$\cfrac{9}{11}=e^k$$Utilizamos logaritmos para despejar la k en cada lado de la igualdad.
$$ln\cfrac{9}{11}=ln e^k$$Como conocemos el valor aproximado de $k$ y sabemos que:
$T\left(t\right)=75+275 e^{kt}$, hallaremos $T\left(6\right)$
$\bullet\hspace{0.2cm}$¿En cuánto tiempo la temperatura del pastel será de 80 °F?
Sabemos que:
Despejamos $t$, utilizando logaritmos.
De acuerdo con el número de soluciones los sistemas de ecuaciones pueden ser:
Compatibles: Con solución.
Compatible determinado: Solución única.
Compatible indeterminado: Más de una solución lo que equivale a infinitas soluciones.
Incompatibles: Sin solución.
En la siguiente escena interactiva diseñada por María José García CebrianMaría José García Cebrian, es autora de la Red Descartes, que publicó el libro interactivo "Matrices, Determinantes y Sistemas de ecuaciones"., podrás observar algunos ejemplos propuestos, donde se explica cada uno de los sistemas de ecuaciones, de acuerdo con el número de soluciones.
Existen varios métodos para solucionar ecuaciones lineales 2x2 y 3x3, a continuación se explican cada uno de ellos.
 Ejemplo de solución de ecuaciones lineales 2x2-Método Gráfico
Ejemplo de solución de ecuaciones lineales 2x2-Método GráficoA un parqueadero ingresan 9 vehículos, entre bicicletas y triciclos, si se sabe que la suma las llantas es 21. Cuántas bicicletas y triciclos hay en el parqueadero?.
Consiste en representar gráficamente las ecuaciones de las rectas y el punto de intercepción será la solución.
Lo primero que se debe hacer es definir las variables para las incógnitas del problema que se plantea.
$x=$Cantidad de bicicletas
$y=$Cantidad de triciclos
Ahora se plantean las ecuaciones, de la forma $ax+by=c$
$x+y=9$
$2x+3y=21$
Se debe hacer una tabla de valores para $x\wedge y$, preferiblemente hallar los cortes con los ejes coordenados y se unen los puntos.
Ecuación 1.
| $\hspace{0.5cm}x\hspace{0.5cm}$ | $\hspace{0.5cm}y\hspace{0.5cm}$ |
| 0 | 9 |
| 9 | 0 |
Ecuación 2.
| $\hspace{0.5cm}x\hspace{0.5cm}$ | $\hspace{0.5cm}y\hspace{0.5cm}$ |
| 0 | 7 |
| $\dfrac{21}{2}$ | 0 |
Una vez se tenga la tabla de valores para $x\wedge y$, se procede a realizar la gráfica y el punto de intercepción es la solución del sistema de ecuaciones lineales 2x2.
Si la gráfica se hizo correctamente, se debe obtener lo siguiente:
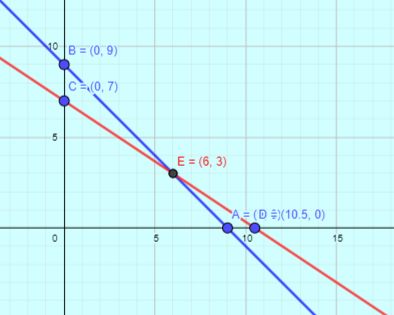
Observa que la solución es el punto de intercepción $\color{brown}E=(6,3)$
En la siguiente escena interactiva, puedes reemplazar los valores de la tabla de las ecuaciones 1 y 2 para confrontar el resultado. No olvides dar enter al ingresar cada par ordenado.
Los puntos A y B pertenecen a la primera ecuación, C y D pertenecen a la segunda y los debes reemplazar en la parte derecha de la escena interactiva, donde dice "Definición:".
Si después de dar "enter", para cada punto, la escena conserva los puntos anteriores, basta con hacer clic izquierdo sostenido y mover un poco la escena.
Para que puedas confrontar los resultados obtenidos y con el ánimo de facilitar el proceso de aprendizaje, una vez tengas definidas las ecuaciones de la forma $\color{brown}ax+by=c$ en el planteamiento del problema o en la búsqueda de solución a un sistema de ecuaciones, puedes reemplazar los coeficientes en la siguiente escena interactiva para obtener el resultado.
A continuación se presentan 7 ejercicios de sistemas de ecuaciones lineales 2x2, para que las soluciones y luego confrontes los resultados en la escena interactiva anterior.
Para solucionar el punto 5, te sugiero hacer un cambio de variable, es decir, $a=\dfrac{1}{x}\wedge b=\dfrac{1}{y}$. Cuando tengas los resultados de $a\wedge b$, reemplazas en el cambio de variable anterior, para obtener $x\wedge y$
Como su nombre lo indica, se trata de sustituir la variable de una ecuación en la otra.
Pasos para solucionar ecuaciones 2x2 por SUSTISUCIÓN
 Ejemplo de solución de ecuaciones lineales 2x2-Sustitución
Ejemplo de solución de ecuaciones lineales 2x2-SustituciónCuál es el área de un rectángulo sabiendo que su perímetro mide 16 cm y que su base es el triple de la altura?
Sea:
$y=$ La altura
$x=$ La base
En la siguiente figura, se muestra el planteamiento del problema.
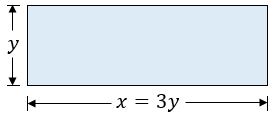
Ahora se plantea la ecuaciones.
$$2x+2y=16\tag{1}$$
$$x=3y\tag{2}$$
Como se sabe que $x=3y$, se reemplaza en la (1)
$2(3y)+2y=16$
$6y+2y=16$
$8y=16$
$\color{brown}y=2$
Ahora se reemplaza el valor de $"y"$ en la (2)
$x=3(2)$, $\color{brown}x=6$
Como su nombre lo indica, se trata de igualar las variables de ambas ecuaciones.
Pasos para solucionar ecuaciones 2x2 por IGUALACIÓN
 Ejemplo de solución de ecuaciones lineales 2x2-Igualación
Ejemplo de solución de ecuaciones lineales 2x2-IgualaciónCon dos camiones cuyas capacidades de carga son de 3 y 4 toneladas respectivamente, se hicieron en total 23 viajes para transportar 80 toneladas de madera. ¿Cuántos viajes realizó cada camión?
Lo primero que se debe hacer es plantear el sistema de ecuaciones.
Sea:
$x=$ Viajes del Camión 1.
$y=$ Viajes del Camión 2.
Luego:
$$x+y=23\tag{1})$$ $$3x+4y=80\tag{2})$$Se despeja $x$ en la ecuación (1), pudo haberse elegido la $y$.
$$x=23-y$$Se despeja la misma variable $x$ en la ecuación (2)
$$x=\dfrac{80-4y}{3}$$Se igualan las dos variables despejadas en las ecuaciones 1 y 2.
$$23-y=\dfrac{80-4y}{3}$$Se realizan las operaciones para hallar el valor de $y$.
$$3(23-y)=80-4y$$ $$69-3y=80-4y$$ $$4y-3y=80-69$$ $$\color{brown}y=11$$Por simple analogía, se puede concluir que los viajes del camión 1 son 12, ya que entre los dos realizaron 23 viajes, o simplemente se reemplaza el valor encontrado en una de las dos ecuaciones despejadas; esto es:
Respuesta: Realizaron 12 y 11 viajes respectivamente.
Como su nombre lo indica, se trata de reducir o eliminar una de las variables .
Pasos para solucionar ecuaciones 2x2 por REDUCCIÓN
 Ejemplo de solución de ecuaciones lineales 2x2-Reducción
Ejemplo de solución de ecuaciones lineales 2x2-ReducciónEn una fábrica tienen máquinas de tipo A y máquinas de tipo B. La semana pasada se dio mantenimiento a 5 máquinas de tipo A y a 4 del tipo B por un costo de $3405.
La semana anterior se pagó $3135 por dar mantenimiento a 3 máquinas de tipo A y 5 de tipo B. Suponiendo que el costo de mantenimiento no ha variado, ¿Cuál es el costo de mantenimiento de las máquinas de cada tipo?
Solución
Sea:
$x=$ Costo del mantenimiento de la máquina tipo A
$y=$ Costo del mantenimiento de la máquina tipo B
Se plantean las ecuaciones.
$$5x+4y=3405\tag{1}$$ $$3x+5y=3135\tag{2}$$Se elige cual de las dos variables se desea eliminar, para el ejemplo elegiremos la $x$, por lo que se tiene que multiplicar la primera ecuación por $(-3)$ y la segunda por $(5)$.
$$\left( -3\right) \ldots \ldots 5x+4y=3405\ldots \ldots{\color{Red}\bcancel {{\color{black}-15x}}}-12y=-10215$$ $$\hspace{0.2cm}\left( 5\right) \ldots \ldots 3x+5y=3135\ldots \ldots\hspace{0.4cm}\underline{{\color{Red}\bcancel {{\color{black}15x}}}+25y=\hspace{0.3cm}15675}$$ $\hspace{6.9cm}13y=\hspace{0.5cm}5460$ $$y=\dfrac{5460}{13}$$ $$\color{brown}y=420$$Reemplazamos la variable "$y$" en la ecuación 1 o 2, para el ejemplo lo haremos en la 1.
$$5x+4(420)=3405$$ $$5x=3405-1680$$ $$5x=1725$$ $$x=\dfrac{1725}{5}$$ $$\color{brown}x=345$$Respuesta:$\hspace{0.3cm}$El mantenimiento de las máquina tipo "A" es de $\$345$ y la tipo "B" es de $\$420$ cada una.
Con la siguiente escena interactiva, diseñada por María José García Cebrian, podrás recordar lo visto hasta el momento sobre solución de ecuaciones 2x2 por los métodos de sustitución, igualación y reducción.
Pasos para solucionar ecuaciones 2x2 por CRAMER
 Ejemplo de solución de ecuaciones lineales 2x2-Por Cramer o determinantes
Ejemplo de solución de ecuaciones lineales 2x2-Por Cramer o determinantesEl perímetro de un rectángulo es de 40 metros. Si se duplica el largo del rectángulo y se aumenta en 6 metros el ancho, el perímetro queda en 76 metros. ¿Cuáles son las medidas originales del rectángulo y cuáles las medidas del rectángulo agrandado?
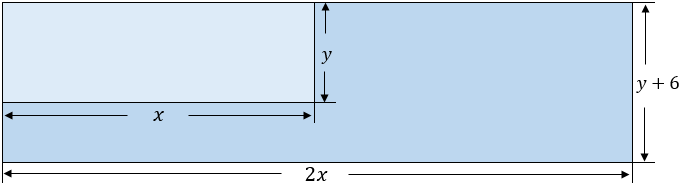
Sea:
$x=\hspace{0.2cm}\text{Largo}\\[8pt] y=\hspace{0.2cm}\text{Ancho}$Se plantean la ecuaciones.
$$2x+2y=40\tag{1}$$ $$2(2x)+2(y+6)=76$$ $$4x+2y+12=76$$ $$4x+2y=64\tag{2}$$El determinante del sistema ($D_s$), se obtiene del producto de la diagonal principal $\color{blue}\searrow$, $\color{blue}\left(C_{1x}\right)\cdot\left(\color{blue}C_{2y}\right)$, que va en el primer paréntesis y el producto de la diagonal secundaria $\color{red}\nearrow$, $\color{red}\left(C_{2x}\right)\cdot\left(\color{red}C_{1y}\right)$, que va en el segundo paréntesis como se muestra en la siguiente matriz. Recuerda la matriz la conforman los coeficientes de las variables del sistema de ecuaciones.
$$D_s=\begin{bmatrix} \color{blue}C_{1x} & \color{red} C_{1y} \\ \color{red} C_{2x} & \color{blue}C_{2y} \end{bmatrix}=\color{blue}(\hspace{2cm})\color{black}-\color{red}(\hspace{2cm})$$En lo posible reducir las ecuaciones, para este ejemplo en particular, ambas ecuaciones son divisibles por dos (2), esto es:
$$\cfrac{2x}{2}+\cfrac{2y}{2}=\cfrac{40}{2}\tag{2}$$ $$x+y=20\tag{1}$$En la matriz, obtendremos los siguiente:
$$D_s=\begin{bmatrix} \color{blue}1 & \color{red} 1 \\ \color{red} 2 & \color{blue} 1 \end{bmatrix}=\color{blue}(\hspace{1cm}1\hspace{1cm})\color{black}-\color{red}(\hspace{1cm}2\hspace{1cm})$$ $$D_s=-1$$NO olvides que debes incluir los signos de los coeficientes en la matriz, y de igual forma realizar las operaciones de los signos en el producto.
Para hallar el determinante de $x$ ($D_x$), en la fila de los coeficientes de las $x$ se ubican los términos independientes.
$$ D_x=\begin{bmatrix} \color{blue}T_{1I} & \color{red} C_{1y} \\ \color{red} T_{2I} & \color{blue}C_{2y} \end{bmatrix}=\color{blue}(\hspace{2cm})\color{black}-\color{red}(\hspace{2cm})$$El procedimiento es el mismo anterior.
$$ D_x=\begin{bmatrix} \color{blue}20 & \color{red} 1 \\ \color{red} 32 & \color{blue} 1 \end{bmatrix}=\color{blue}(\hspace{1cm}20\hspace{1cm})\color{black}-\color{red}(\hspace{1cm}32\hspace{1cm})$$ $$D_x=-12$$Recuerda que $x=\dfrac{D_x}{D_s}$
$$x=\dfrac{D_x}{D_s}=\dfrac{-12}{-1}$$Conociendo el valor de $x$, puedes reemplazar en alguna de las dos ecuaciones, para hallar la otra variable, esto es:
$$2(12)+2y=40$$ $$2y=40-24$$ $$2y=16$$ $$y=\dfrac{16}{2}$$ $$\color{brown}y=8$$Como practica, terminaremos el ejemplo por el método de determinantes, para lo cual hallaremos el determinante de $y$. Recuerda que el término independiente, ocupa la columna de los coeficientes de la variable $y$.
$$ D_y=\begin{bmatrix} \color{blue}1 & \color{red} 20 \\ \color{red} 2 & \color{blue} 32 \end{bmatrix}=\color{blue}(\hspace{1cm}32\hspace{1cm})\color{black}-\color{red}(\hspace{1cm}40\hspace{1cm})$$ $$D_x=-8$$Recuerda que $y=\dfrac{D_y}{D_s}$
$$y=\dfrac{D_y}{D_s}=\dfrac{-8}{-1}$$ $$\color{brown}y=8$$Con la escena interactiva se pretende que aprendas a formar las matrices para la solución de sistemas de ecuaciones lineales 2x2, en ella encontrarás una cantidad de  , que irás convirtiendo en
, que irás convirtiendo en  en la medida que vayas avanzando en la solución.
en la medida que vayas avanzando en la solución.
Puedes verificar las respuestas obtenidas, solucionando los ejercicios por los métodos que se explicaron en las páginas anteriores.
Con lo que aprendiste en esta escena interactiva, puedes solucionar en tu cuaderno los ejemplos propuesto en la siguiente escena interactiva, diseñada por María José García Cebrian, en la cual podrás observar diferentes ejemplos propuestos sobre solución de ecuaciones 2x2 por el método de determinantes o Cramer. ¡Inténtalo!
Se utilizan los mismos métodos estudiados para resolver ecuaciones 2x2, pero no se recomienda el gráfico, por ser en tres dimensiones (tres variables). Para explicar los métodos de solución de ecuaciones 3x3, plantearemos los siguientes ejemplos.
 Ejemplo de solución de ecuaciones lineales 3x3-Por Sustitución
Ejemplo de solución de ecuaciones lineales 3x3-Por SustituciónHay un número de tres cifras que suman 15. El número de centenas más el de unidades, es el doble de las decenas y el numero original más 594, invierte las cifras del número.
Como no sabemos los valores que pueden tomar los números, los llamaremos:
$$x=Centenas$$ $$y=Decenas$$ $$z=Unidades$$Ahora se plantean las ecuaciones.
$$x+y+z=15\tag{1}$$ $$x+z=2y\tag{2}$$ $$100x+10y+z+594=x+10y+100z\tag{3}$$Se organiza la ecuación (3) y se divide por $99$.
$$99x-99z=-594\tag{3}$$Se divide por 99
$$\cfrac{99}{99}x-\cfrac{99}{99}z=-\cfrac{594}{99}\tag{3}$$ $$x-z=-6\tag{3}$$Se despeja una variable en la ecuación (1), en este caso se despejará la $x$.
Se reemplaza en la ecuación (2), para obtener la ecuación (4)
$$x+z=2y\tag{2}$$ $$\left(15-y-z\right)+z=2y$$ $$15-y-z+z=2y$$ $$15-y=2y$$ $$15=3y$$ $$y=\cfrac{15}{3}$$ $$\color{brown}y=5\tag{4}$$Se reemplaza en la ecuación (3), para obtener la ecuación (5)
$$x-z=-6\tag{3}$$ $$\left(15-y-z\right)-z=-6$$ $$15-y-z-z=-6$$ $$-y-2z=-6-15$$ $$-y-2z=-21$$Se multiplica por menos uno (-1).
En este momento se tendrán las ecuaciones (4) y (5) en dos variables (2x2). Se haría el mismo proceso, se despeja en una ecuación y se reemplaza en la otra, pero dado que en la ecuación (4), ya se obtuvo el valor de la variable $y$, simplemente se reemplaza en la ecuación (5).
$$(5)+2z=21$$ $$2z=21-5$$ $$2z=16$$ $$z=\cfrac{16}{2}$$ $$\color{brown}z=8$$Por simple deducción, se puede determinar el valor de la variable restante, ya que en el planteamiento del problema, dice que los tres números suman $15$, luego, si ya conocemos que $y=5$, $z=8$, "$x$" tiene que valer $2$.
$$x=15-(13)$$ $$\color{brown}x=2$$Para comprobarlo, puedes reemplazar los valores de las variables encontradas, en la ecuación (1)
$$x+y+z=15\tag{1}$$ $$x+(5)+(8)=15$$ Ejemplo de solución de ecuaciones lineales 3x3-Por Igualación
Ejemplo de solución de ecuaciones lineales 3x3-Por IgualaciónEn la figura se muestra el diagrama de un circuito eléctrico que contiene tres resistores, una batería de 6 volts y una batería de 12 volts. Se puede demostrar, usando las leyes de Kirchhoff, que las tres corrientes, $I_1, I_2 \hspace{0.1cm}e \hspace{0.1cm}I_3$ son soluciones del siguiente sistema de ecuaciones:
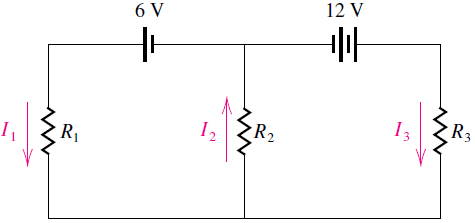 $\hspace{0.2cm}\begin{cases}I_1-I_2+I_3=0\\ R_1I_1+R_2I_2=6\\R_2I_2+R_3I_3=12\end{cases}$
$\hspace{0.2cm}\begin{cases}I_1-I_2+I_3=0\\ R_1I_1+R_2I_2=6\\R_2I_2+R_3I_3=12\end{cases}$
Encuentre las tres corrientes si:
$\bullet\hspace{0.2cm}R_1=R_2=R_3=3\hspace{0.1cm}ohms$.
Solución
Inicialmente se debe reemplazar los valores de $R$ en las ecuaciones (2) y (3).
$$I_1-I_2+I_3=0\tag{1}$$ $$\left(3\right)I_1+\left(3\right)I_2=6\tag{2}$$ $$\left(3\right)I_2+\left(3\right)I_3=12\tag{3}$$Se pueden simplificar las ecuaciones (2) y (3)
$$I_1-I_2+I_3=0\tag{1}$$ $$I_1+I_2=2\tag{2}$$ $$I_2+I_3=4\tag{3}$$Despejamos una variable en ecuación (1), despejamos la misma variable en la ecuación (2) y la reemplazamos en la ecuación (2).
$$I_1-I_2+I_3=0\tag{1}$$ $$I_1=I_2-I_3$$ $$I_1+I_2=2\tag{2}$$ $$I_1=2-I_2$$Se igualan las variable despejadas en las ecuaciones (1) y (2), para obtener la ecuación (4).
Despejamos la misma variable despejada en ecuación (1) , en la ecuación (3) , igualamos la variable despejada en las ecuaciones (1) y (3) para obtener la ecuación (5). Dado que la ecuación (3) ya es de 2x2 y en las mismas variables de la ecuación (4), se tomará como la ecuación (5):
$$I_2+I_3=4\tag{5}$$Despejamos la misma variable en las ecuaciones (5) y (5) e igualamos. Para el ejemplo que se está solucionando es más fácil despejar $I_3$.
$$2I_2-I_3=2\tag{4}$$ $$I_3=2I_2-2$$ $$I_2+I_3=4\tag{5}$$ $$I_3=4-I_2$$Igualamos
$$2I_2-2=4-I_2$$ $$3I_2=6$$ $$\color{brown}I_2=2$$Reemplazamos en la ecuación (4) o (5), despejada.
$$I_3=(2)(2)-2$$Se reemplazan los valores encontrados, en la ecuación (1) despejada.
$$I_1=I_2-I_3$$ $$I_1=2-2$$ $$\color{brown}I_1=0$$ Ejemplo de solución de ecuaciones lineales 3x3-Por Reducción
Ejemplo de solución de ecuaciones lineales 3x3-Por ReducciónEn la figura se muestra el diagrama de un circuito eléctrico que contiene tres resistores, una batería de 6 volts y una batería de 12 volts. Se puede demostrar, usando las leyes de Kirchhoff, que las tres
corrientes, $I_1, I_2 \hspace{0.1cm}e \hspace{0.1cm}I_3$ son soluciones del siguiente sistema de ecuaciones:

Encuentre las tres corrientes si:
$\bullet\hspace{0.2cm}R_1=4\hspace{0.1cm}ohms,\hspace{0.1cm}R_2=1\hspace{0.1cm}ohms,\hspace{0.1cm}R_3=4\hspace{0.1cm}ohms$.
Solución
Inicialmente se debe reemplazar los valores de $R$ en las ecuaciones (2) y (3).
$$I_1-I_2+I_3=0\tag{1}$$ $$\left(4\right)I_1+\left(1\right)I_2=6\tag{2}$$ $$\left(1\right)I_2+\left(4\right)I_3=12\tag{3}$$Eliminamos una variable en las ecuaciones (1) y (2), para obtener la ecuación (4). Como se puede observar, lo más conveniente es eliminar $I_1$ para que quede 2x2, con las mismas variables de la ecuación (3). Para lograrlo, se multiplica la ecuación (1) por menos 4 (-4).
$$\hspace{0.1cm}-4{\color{Red}\bcancel {{\color{black}I_1}}}+4I_2-4I_3=0\tag{1}$$ $$\underline{\hspace{0.2cm}{\color{Red}\bcancel {{\color{black}4I_1}}}\hspace{0.2cm}+I_2\hspace{1cm}=6\tag{2}}$$ $$\hspace{1.2 cm}5I_2\hspace{0.1cm}-4I_3=6\tag{4}$$Como la ecuación (3), esta en términos de $I_2$ e $I_3$, la podemos tomar como la ecuación (5) y eliminar $I_3$.
Conociendo el valor de $I_2$, puedes sustituirlo en la ecuación (4) o (5) y hallarás $I_3$.
$$I_2+4I_3=12\tag{5}$$ $$3+4I_3=12$$ $$4I_3=9$$ $$\color{brown}I_3=\cfrac{9}{4}$$Como práctica de aprendizaje, eliminaremos $I_2$, multiplicando la ecuación (5) por menos 5 (-5),
$$\hspace{0.2 cm}{\color{Red}\bcancel {{\color{black}5I_2}}}\hspace{0.2 cm}-4I_3=\hspace{0.4 cm}6\tag{4}$$ $$\underline{{\color{Red}\bcancel {{\color{black}-5I_2}}}-20I_3=-60\tag{5}}$$ $$\hspace{0.8 cm}-24I_3=-54$$ $$\hspace{0.8 cm}24I_3=54$$ $$I_3=\cfrac{54}{24}$$Conociendo los valores de $I_2$ e $I_3$, podemos reemplazar en la ecuación (1), para hallar $I_1$.
$$I_1=3-\cfrac{9}{4}=\cfrac{12}{4}-\cfrac{9}{4}$$ $$I_1=\cfrac{12}{4}-\cfrac{9}{4}$$ $$\color{brown}I_1=\cfrac{3}{4}$$
 Ejemplo de solución de ecuaciones lineales 3x3-Por Cramer
Ejemplo de solución de ecuaciones lineales 3x3-Por CramerHay tres cadenas que pesan 450, 610 y 950 onzas, cada una de ellas formada por eslabones de tres tamaños diferentes. Cada cadena tiene 10 eslabones pequeños y también tienen 20, 30 y 40 eslabones de tamaño mediano, así como 30, 40 y 70 eslabones grandes, respectivamente. Encuentre los pesos de los eslabones pequeños, medianos y grandes.
Solución: Se deben definir las variables.
P = Eslabón pequeño
M = Eslabón mediano
G = Eslabón grande
Se plantean las ecuaciones
$$10P+20M+30G=450\tag{1}$$ $$10P+30M+40G=610\tag{2}$$ $$10P+40M+70G=950\tag{3}$$Para facilitar las operaciones, se pueden simplificar todas las ecuaciones dividiendo por diez (10)
$$P+2M+3G=45\tag{1}$$ $$P+3M+4G=61\tag{2}$$ $$P+4M+7G=95\tag{3}$$El determinante del sistema ($D_s$), se obtiene de los productos de las diagonales principales $\color{blue}\searrow$, que va en el primer paréntesis y los productos de las diagonales secundarias $\color{red}\nearrow$, que va en el segundo paréntesis como se muestra en la siguiente matriz. Recuerda la matriz la conforman los coeficientes de las variables del sistema de ecuaciones.
Para el caso de los determinantes de un sistema de ecuaciones de 3x3, se deben multiplicar tres valores, por lo que se hace necesario ampliar la matriz. Cuando se habla de ampliar la matriz, se puede hacer de
forma horizontal (como se muestra a continuación) o vertical, repitiendo las dos primeras columnas o las dos primeras filas (en caso que se opte por la vertical).
Diagonales principales:
$D_S=\begin{bmatrix} \color{blue}C_{1x} & \color{blue} C_{1y} & \color{blue} C_{1z}&\color{black}C_{1x} & \color{black} C_{1y}\\ \color{black} C_{2x} & \color{blue}C_{2y}& \color{blue}C_{2z}&\color{blue} C_{2x} & \color{black}C_{2y}\\ \color{black} C_{3x} & \color{black}C_{3y}& \color{blue}C_{3z}& \color{blue} C_{3x} & \color{blue}C_{3y} \end{bmatrix}=\color{blue}(\hspace{0.6cm})\color{black}-\color{red}(\hspace{0.6cm})$Diagonales secundarias:
$D_S=\begin{bmatrix} \color{black}C_{1x} & \color{black} C_{1y} & \color{red} C_{1z}&\color{red}C_{1x} & \color{red} C_{1y}\\ \color{black} C_{2x} & \color{red}C_{2y}& \color{red}C_{2z}&\color{red} C_{2x} & \color{black}C_{2y}\\ \color{red} C_{3x} & \color{red}C_{3y}& \color{red}C_{3z}& \color{black} C_{3x} & \color{black}C_{3y} \end{bmatrix}=\color{blue}(\hspace{0.6cm})\color{black}-\color{red}(\hspace{0.6cm})$Teniendo en cuenta lo anterior podemos construir el determinante del sistema
Diagonales principales:
$D_S=\begin{bmatrix} \color{blue}1 & \color{blue} 2 & \color{blue} 3&\color{black}1 & \color{black} 2\\ \color{black} 1& \color{blue}3& \color{blue}4&\color{blue} 1 & \color{black}3\\ \color{black} 1 & \color{black}4& \color{blue}7& \color{blue} 1 & \color{blue}4 \end{bmatrix}=\color{blue}(21+8+12)\color{black}-\color{red}(\hspace{0.6cm})$Diagonales secundarias:
$D_S=\begin{bmatrix} \color{black}1 & \color{black} 2 & \color{red} 3&\color{red}1 & \color{red} 2\\ \color{black} 1 & \color{red}3& \color{red}4&\color{red} 1 & \color{black}3\\ \color{red} 1 & \color{red}4& \color{red}7& \color{black} 1 & \color{black}4 \end{bmatrix}=\color{blue}(\hspace{0.6cm})\color{black}-\color{red}(9+16+14)$Para una mayor comprensión, se realizaron las operaciones de las diagonales principales y secundarias por separado, pero se deben hacer en la misma matriz.
$D_S=\begin{bmatrix} \color{blue}1 & \color{blue} 2 & \color{blue} 3&\color{black}1 & \color{black} 2\\ \color{black} 1& \color{blue}3& \color{blue}4&\color{blue} 1 & \color{black}3\\ \color{black} 1 & \color{black}4& \color{blue}7& \color{blue} 1 & \color{blue}4 \end{bmatrix}=\color{blue}(21+8+12)\color{black}-\color{red}(9+16+14)$
$$D_S=\color{blue}(41)\color{black}-\color{red}(39)$$
$$D_S=2$$Para hallar el determinante de las $x$, el espacio de los coeficientes de las $x$, $C_x$ lo ocupan los términos independientes y se procede de igual forma que en el procedimiento anterior.
Diagonales principales:
$D_x=\begin{bmatrix} \color{blue}T_{I1} & \color{blue} C_{1y} & \color{blue} C_{1z}&\color{black}T_{I1} & \color{black} C_{1y}\\ \color{black} T_{I2} & \color{blue}C_{2y}& \color{blue}C_{2z}&\color{blue} T_{I2} & \color{black}C_{2y}\\ \color{black} T_{I3} & \color{black}C_{3y}& \color{blue}C_{3z}& \color{blue} T_{I3} & \color{blue}C_{3y} \end{bmatrix}=\color{blue}(\hspace{0.6cm})\color{black}-\color{red}(\hspace{0.6cm})$Diagonales secundarias:
$D_x=\begin{bmatrix} \color{black}T_{I1} & \color{black} C_{1y} & \color{red} C_{1z}&\color{red}T_{I1} & \color{red} C_{1y}\\ \color{black} T_{I2} & \color{red}C_{2y}& \color{red}C_{2z}&\color{red} T_{I2} & \color{black}C_{2y}\\ \color{red} T_{I3} & \color{red}C_{3y}& \color{red}C_{3z}& \color{black} T_{I3} & \color{black}C_{3y} \end{bmatrix}=\color{blue}(\hspace{0.6cm})\color{black}-\color{red}(\hspace{0.6cm})$Recuerda que:$\hspace{0.4cm} P=\cfrac{D_P}{D_S}$
$$P=\frac{8}{2}$$ $$\color{brown}P=4$$Para hallar el determinante de las $y$, el espacio de los coeficientes de las $y$, $C_y$ lo ocupan los términos independientes y se procede de igual forma que en el procedimiento anterior.
Diagonales principales:
$D_y=\begin{bmatrix} \color{blue}C_{1x} & \color{blue} T_{I1} & \color{blue} C_{1z}&\color{black}C_{1x} & \color{black} T_{I1}\\ \color{black} C_{2x} & \color{blue}T_{I2}& \color{blue}C_{2z}&\color{blue} C_{2x} & \color{black}T_{I2}\\ \color{black} C_{3x} & \color{black}T_{I3}& \color{blue}C_{3z}& \color{blue} C_{3x} & \color{blue}T_{I3} \end{bmatrix}=\color{blue}(\hspace{0.6cm})\color{black}-\color{red}(\hspace{0.6cm})$Diagonales secundarias:
$D_y=\begin{bmatrix} \color{black}C_{1x} & \color{black} T_{I1} & \color{red} C_{1z}&\color{red}C_{1x} & \color{red} T_{I1}\\ \color{black} C_{2x} & \color{red}T_{I2}& \color{red}C_{2z}&\color{red} C_{2x} & \color{black}T_{I2}\\ \color{red} C_{3x} & \color{red}T_{I3}& \color{red}C_{3z}& \color{black} C_{3x} & \color{black}T_{I3} \end{bmatrix}=\color{blue}(\hspace{0.6cm})\color{black}-\color{red}(\hspace{0.6cm})$Recuerda que:$\hspace{0.4cm} M=\cfrac{D_M}{D_S}$
$$M=\frac{14}{2}$$ $$\color{brown}M=7$$Para hallar el determinante de las $z$, el espacio de los coeficientes de las $z$, $C_z$ lo ocupan los términos independientes y se procede de igual forma que en el procedimiento anterior.
Diagonales principales:
$D_z=\begin{bmatrix} \color{blue}C_{1x} & \color{blue} C_{1y} & \color{blue} T_{I1}&\color{black}C_{1x} & \color{black} C_{1y}\\ \color{black} C_{2x} & \color{blue}C_{2y}& \color{blue}T_{I2}&\color{blue} C_{2x} & \color{black}C_{2y}\\ \color{black} C_{3x} & \color{black}C_{3y}& \color{blue}T_{I3}& \color{blue} C_{3x} & \color{blue}C_{3y} \end{bmatrix}=\color{blue}(\hspace{0.6cm})\color{black}-\color{red}(\hspace{0.6cm})$Diagonales secundarias:
$D_z=\begin{bmatrix} \color{black}C_{1x} & \color{black} C_{1y} & \color{red} T_{I1}&\color{red}C_{1x} & \color{red} C_{1y}\\ \color{black} C_{2x} & \color{red}C_{2y}& \color{red}T_{I2}&\color{red} C_{2x} & \color{black}C_{2y}\\ \color{red} C_{3x} & \color{red}C_{3y}& \color{red}T_{I3}& \color{black} C_{3x} & \color{black}C_{3y} \end{bmatrix}=\color{blue}(\hspace{0.6cm})\color{black}-\color{red}(\hspace{0.6cm})$Recuerda que:$\hspace{0.4cm} G=\cfrac{D_G}{D_S}$
$$G=\frac{18}{2}$$ $$\color{brown}G=9$$NOTA:$\hspace{0.2 cm}$Cuando se resuelven problemas de ecuaciones, se puede utilizar cualquiera de los métodos o su combinación. En el ejemplo anterior, al hallar dos incógnitas se podía haber reemplazado los valores hallados, en las ecuaciones originales para evitar el proceso del último determinante.
A continuación se presentan 7 ejercicios de sistemas de ecuaciones lineales 3x3, para que las soluciones por el método adecuado.
Son aquellos sistemas de ecuaciones, donde una o ambas nos son lineales (de primer grado) presentan al menos una de un grado superior.
Generalmente se resuelven por el método de sustitución, en algunos casos, cuando ambas sean cuadráticas es posible que sea más sencillo utilizar el método de igualación o reducción.
Podemos encontrar los siguientes casos:
En este caso se utilizará el método de sustitución, realizando el procedimiento que se indicó anteriormente.
 Ejemplo de solución de una ecuación lineal y otra NO lineal
Ejemplo de solución de una ecuación lineal y otra NO linealLo primero es organizar las ecuaciones, si es el caso.
Despejamos una variable en la ecuación lineal, la que consideres más fácil
$$x=y-3$$Reemplazamos en la ecuación (2)
$$\left(y-3\right)^2+y^2=5$$Solucionamos el cuadrado de un binomio que se nos presenta al lado derecho de la igualdad y realizamos las operaciones e igualamos a cero para factorizar.
Recordemos que $\left(a-b\right)^2=a^2-2ab+b^2$
$$y^2-6y+9+y^2=5$$ $$2y^2-6y+4=0$$Dividimos por 2 y simplificamos
$$\cfrac{2y^2}{2}-\cfrac{6y}{2}+\cfrac{4}{2}=\cfrac{0}{2}$$ $$y^2-3y+2=0$$En caso de que sea posible, se factoriza o si no se utiliza la fórmula general
$$\left(y-2\right)\cdot\left(y-1\right)=0$$Igualamos cada factor a cero para obtener:
$$\hspace{0.2cm}\begin{cases}y_1=2\\ y_2=1\end{cases}$$Reemplazamos cada valor en la ecuación (1) despejada $x=y-3$ , para obtener:
$$\hspace{0.2cm}\begin{cases}x_1=-1\\ x_2=-2\end{cases}$$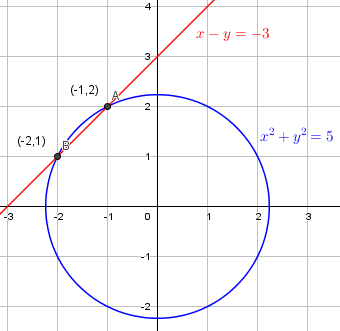
Podemos utilizar el método de reducción, en caso de que ambas ecuaciones sean cuadráticas.
 Ejemplo de solución de ambas ecuaciones son NO lineales.
Ejemplo de solución de ambas ecuaciones son NO lineales.Si utilizamos el método de reducción, podemos eliminar $y^2$
$$\hspace{0.1cm}x^2+{\color{Red}\bcancel {{\color{black}y^2}}}=41\tag{1}$$ $$\underline{\hspace{0.1cm}x^2\hspace{0.0cm}-\hspace{0.0cm}{\color{Red}\bcancel {{\color{black}y^2}}}\hspace{0cm}=9\tag{2}}$$ $$\hspace{0.1 cm}2x^2\hspace{0.8 cm}=50$$ $$x^2=25$$ $$x=\pm\sqrt{25}$$ $$\hspace{0.2cm}\begin{cases}x_1=5\\ x_2=-5\end{cases}$$Ahora eliminemos $x^2$, multiplicando la ecuación (2) por -1
$$\hspace{0.1cm}{\color{Red}\bcancel {{\color{black}x^2}}}+y^2=41\tag{1}$$ $$\underline{\hspace{0.1cm}-{\color{Red}\bcancel {{\color{black}x^2}}}\hspace{0.0cm}+\hspace{0.0cm}y^2\hspace{0cm}=-9\tag{2}}$$ $$\hspace{0.8 cm}2y^2\hspace{0.1 cm}=32$$ $$y^2=16$$ $$y=\pm\sqrt{16}$$ $$\hspace{0.2cm}\begin{cases}y_1=4\\ y_2=-4\end{cases}$$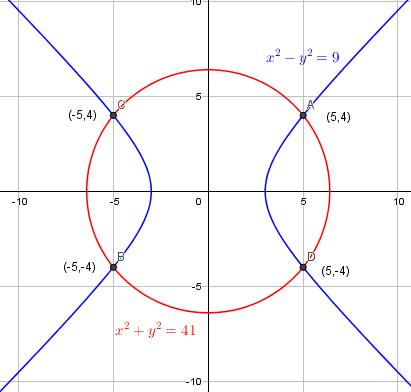
Podemos utilizar el método que más se facilite.
 Ejemplo de solución de una ecuación lineal y una irracional.
Ejemplo de solución de una ecuación lineal y una irracional.NOTA:$\hspace{0.2 cm}$Eliminar el radical en la ecuación (1) y luego utilizar el método adecuado. Se debe tener en cuenta que, al tratarse de un radical, se obtienen dos respuestas, una negativa y otra positiva. En el ejemplo se plantea la respuesta positiva, signo que precede la raíz.
$$\color{red}2\sqrt {x+1}=y+1\color{black}\tag{1}$$ $$\left(2\sqrt {x+1}\right)^2=\left(y+1\right)^2$$ $$4\left(x+1\right)=y^2+2y+1$$ $$4x+4=y^2+2y+1$$ $$y^2-4x+2y=3\tag{1}$$Ahora podemos eliminar la nueva ecuación (1) con la (2), multiplicando la segunda por 2.
$$\hspace{0.1cm}y^2+{\color{Red}\bcancel {{\color{black}4x}}}+2y=3\tag{1}$$ $$\underline{\hspace{0.5cm}-{\color{Red}\bcancel {{\color{black}4x}}}\hspace{0.0cm}-\hspace{0.0cm}6y\hspace{0cm}=2\tag{2}}$$ $$\hspace{0.8 cm}y^2\hspace{0.1 cm}-4y=5$$Igualamos a cero para tratar de factorizar
$$y^2-4y-5= 0$$Factorizamos
$$\left(y-5\right)\cdot\left(y+1\right)=0$$ $$\hspace{0.2cm}\begin{cases}y_1=5\\ y_2=-1\end{cases}$$Despejamos la $x$ en la ecuación (2) y reemplazamos $y_1$, ya que $y_2$ no aplica para este ejemplo
$$\color{blue}2x-3y=1\tag{2}$$ $$x_1=\cfrac{1+3y_1}{2}$$ $$x_1=\cfrac{1+3\cdot\left(5\right)}{2}$$ $$x_1=\cfrac{1+15}{2}$$ $$x_1=\cfrac{16}{2}$$ $$x_1=8$$ $$\hspace{0.2cm}\begin{cases}x_1=8\\ y_1=5\end{cases}$$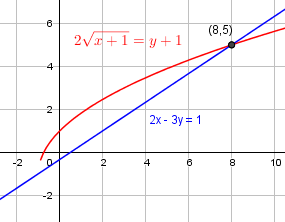
A continuación se presentan 7 ejercicios de sistemas de ecuaciones NO lineales, para que las soluciones por cualquier de los métodos vistos anteriormente.
En las siguientes escenas interactivas, adaptadas de Juan Guillermo Rivera, podrás resolver los ejercicios planteados sobre factorización y ecuaciones, para pongas a prueba tus conocimientos.
En cada escena interactiva dispones de 60 minutos para realizar los ejercicios e ir eligiendo la respuesta correcta en el cuestionario. Al finalizar tendrás la posibilidad de ingresar tu nombre y enviar las respuestas a tu docente ingresando su correo en el espacio destinado para ello.
Al solucionar los ejercicios propuestos en las escenas interactivas, estarás en capacidad de resolver los ejercicios propuestos para el capítulo 3.
Opción 1. Factorización y ecuaciones.
Opción 2. Factorización y ecuaciones.
Opción 3. Factorización y ecuaciones.
Cuando se suman dos fracciones algebraicas propias, es decir, que el grado de $P(x)< Q(x)$, tales que:
Con $Q(x)\wedge S(x)$, diferentes de cero, al sumarlas se combinan sus términos por medio del común denominador.
En algunos procedimientos del estudio de cálculo integral, se requiere invertir este proceso y volver a las expresiones racionales iniciales.
Este proceso se conoce como fracciones parciales.
El proceso de obtener $\dfrac{P(x)}{Q(x)}+\dfrac{R(x)}{S(x)}$, a partir de $\dfrac{P(x)\cdot{S(x)}+Q(x)\cdot{R(x)}}{Q(x)\cdot{S(x)}}$, se denomina descomposición en fracciones parciales.
Para facilitar su comprensión, analizaremos el siguiente ejemplo:
$$\cfrac{3}{x+2}+\cfrac{4}{x-3}$$Cuando se realiza la suma de los polinomios, se obtiene:
$$\color{black}\begin{aligned} \cfrac{3}{x+2}+\cfrac{4}{x-3}&=\cfrac{3\left(x-3\right)+4\left(x+2\right)}{\left(x+2\right)\left(x-3\right)}\\ &=\cfrac{3x-9+4x+8}{x^2-x-6}\\ &=\cfrac{7x-1}{x^2-x-6} \\ \end{aligned}$$En el ejemplo anterior se sumaron fraccionarios para llegar a una expresión racional, hay ocasiones donde es necesario invertir el proceso de sumar fraccionarios. Para ver cómo funciona en general el método de fracciones parciales, trabajaremos sobre una función racional.
$f(x)=\cfrac{P(x)}{Q(x)}$, Donde $P(x)\wedge Q(x)$ son polinomios.Vamos a descomponer el resultado del ejemplo en sus fracciones parciales, para ello, inicialmente se factoriza el denominador.
$$\color{black}\begin{aligned} \cfrac{7x-1}{x^2-x-6}&= \cfrac{7x-1}{\left(x+2\right)\left(x-3\right)}\\ &= \cfrac{A}{x+2}+ \cfrac{B}{x-3}\\ &= \cfrac{A\left(x-3\right)+B\left(x+2\right)}{\left(x+2\right)\left(x-3\right)}\\ \end{aligned}$$Se han incluido las variables $A\wedge B$, para separar el numerador en fracciones parciales. Esta ecuación es válida para todo valor de $x$ excepto para $x=-2\wedge x=3$
Luego, se puede observar que:
$$\cfrac{7x-1}{x^2-x-6}=\cfrac{A\left(x-3\right)+B\left(x+2\right)}{\left(x+2\right)\left(x-3\right)}$$Lo que implica que:
$${7x-1}=A\left(x-3\right)+B\left(x+2\right)$$Se aplica la propiedad distributiva en el término de la derecha y se agrupan saca factor común, donde sea necesario.
$$\color{black}\begin{aligned} 7x-1 &= Ax-3A+Bx+2B\\ &= x\left(A+B\right) -\left(3A-2B\right)\\ \end{aligned}$$ $\hspace{1.1cm}\color{brown}\underline{\color{brown}\hspace{0.3cm}Igual\hspace{0.5cm}}\\$ $\hspace{1cm}\color{brown}\downarrow\hspace{1.5cm}\downarrow$$\hspace{1cm}$7$x-$1$ = \left(\color{brown}A+B\right)x -\left(\color{blue}3A-2B\right)$
$\hspace{1.7cm}\color{blue}\uparrow\underline{\color{blue}\hspace{0.9cm}Igual\hspace{0.9cm}}\hspace{0.0cm}\uparrow\\$Quiere decir que:
$$\color{brown}A+B=7\tag{1}$$ $$\color{blue}3A-2B=1\tag{2}$$Se solución el sistema de ecuaciones 2x2 por uno de los métodos que se vieron anteriormente. En este caso se utilizará el método de eliminación, dado que la variable $B$ esta positiva en la ecuación (1) y negativa en la (2).
Conociendo el valor de $A$, podemos reemplazar en la ecuación (1) o (2).
$$A+B=7\tag{1}$$ $$\left(3\right)+B=7$$ $$B=7-3$$ $$B=4$$Reemplazamos en:
$$\color{black}\begin{aligned} \cfrac{7x-1}{x^2-x-6}&= \cfrac{A}{x+2}+ \cfrac{B}{x-3}\\ &= \cfrac{3}{x+2}+ \cfrac{4}{x-3}\\ \end{aligned}$$De esta forma se ha llegado a la suma inicial de polinomios racionales del ejemplo planteado.
Existen cuatro casos de fracciones parciales, los cuales dependen de los factores resultantes de factorizar el denominador.
En este caso se escribe:
Donde $A_1,A_2,\ldots,A_n$ son constantes a determinar.
 Ejemplos de fracciones parciales - Caso 1.
Ejemplos de fracciones parciales - Caso 1.Como los factores del denominador son lineales y ninguno se repite es caso 1. Se escribe la fracción parcial de la siguiente forma:
$$\color{black}\begin{aligned} \cfrac{4x^2+13x-9}{x^3+2x^2-3x} &= \cfrac{A}{x}+\cfrac{B}{\left(x+3\right)}+\cfrac{C}{\left(x-1\right)}\\ \end{aligned}$$Se realiza la suma de fraccionarios del lado derecho de la ecuación.
$$\color{black}\begin{aligned} \cfrac{4x^2+13x-9}{x^3+2x^2-3x} &= \cfrac{\left(x+3\right)\left(x-1\right)A+x\left(x-1\right)B+x\left(x+3\right)C}{x\left(x+3\right)\left(x-1\right)} \end{aligned}$$ ${4x^2+13x-9}= {\left(x+3\right)\left(x-1\right)A+x\left(x-1\right)B+x\left(x+3\right)C}$Esta ecuación es válida para todos los valores de $x$. Se aplica la propiedad distributiva al lado derecho de la ecuación.
$4x^2+13x-9= \left(x^2+2x-3\right)A+\left(x^2-x\right)B+\left(x^2+3x\right)C$Se aplica nuevamente la propiedad distributiva, agrupan términos semejantes, se saca factor común y se comparan los términos de la igualdad.
$$\color{black}\begin{aligned} 4x^2+13x-9&= Ax^2+2Ax-3A+x^2B-xB+x^2C+3Cx\\ &= x^2\left(A+B+C\right)+x\left(2A-B+3C\right)-3A\\ \end{aligned}$$ $\hspace{1.1cm}\color{brown}\underline{\color{brown}\hspace{1.8cm}Igual\hspace{0.5cm}}\\$ $\hspace{1cm}\color{brown}\downarrow\hspace{3cm}\downarrow$ $\hspace{-2.4cm}\color{blue}\underline{\color{blue}\hspace{2.8cm}Igual\hspace{1.5cm}}\\$ $\hspace{1.9cm}\color{blue}\downarrow\hspace{5cm}\downarrow$$\hspace{1cm}$4$x^2+$13$x-$9$ = \left(\color{brown}A+B+C\right)x^2 +\left(\color{blue}2A-B+3C\right)x-\color{green}3A$
$\hspace{2.7cm}\color{green}\uparrow\underline{\color{green}\hspace{3.2cm}Igual\hspace{1.9cm}}\hspace{0.0cm}\uparrow\\$Se tiene un sistema de ecuaciones 3x3, en el que la ecuación (3) nos muestra que $A=3$.
Se reemplazará este valor en las ecuaciones (1) y (2) para obtener las ecuaciones (4) y (5).
$$\color{brown}A+B+C=4\tag{1}$$ $$\color{blue}2A-B+3C=13\tag{2}$$ $$\color{black}3+B+C=4$$ $$\color{black}B+C=1\tag{4}$$ $$\color{black}2(3)-B+3C=13$$ $$\color{black}6-B+3C=13$$ $$\color{black}-B+3C=7\tag{5}$$Se puede eliminar la $B$ en las ecuaciones (5) y (6), ya que una es positiva y la otra es negativa.
$$\hspace{0.1cm}{\color{Red}\bcancel {{\color{black}B}}}+C=1$$ $$\underline{\hspace{0.1cm}{\color{Red}\bcancel {{\color{black}B}}}+3C=7}$$ $$\hspace{0.8 cm}4C\hspace{0.3 cm}=8$$Conociendo las variables $A\wedge C$, se reemplazan en la ecuación (4) o (5), para obtener el valor de $B$.
$$\color{black}B+C=1\tag{4}$$ $$\color{black}B+2=1$$ $$\color{black}B=-1$$Ahora se reemplaza en:
$$\color{black}\begin{aligned} \cfrac{4x^2+13x-9}{x^3+2x^2-3x} = \cfrac{A}{x}+\cfrac{B}{\left(x+3\right)}+\cfrac{C}{\left(x-1\right)}\\ \end{aligned}$$ $$\color{black}\begin{aligned} \cfrac{4x^2+13x-9}{x^3+2x^2-3x} &= \cfrac{3}{x}+\cfrac{-1}{\left(x+3\right)}+\cfrac{2}{\left(x-1\right)}\\ \end{aligned}$$Como la ecuación,
${4x^2+13x-9}= {\left(x+3\right)\left(x-1\right)A+x\left(x-1\right)B+x\left(x+3\right)C}$, es válida para todos los valores de $x$ y sabiendo que el denominador del ejemplo inicial, luego de ser factorizado es:${x\left(x+3\right)\left(x-1\right)}$, hay unaforma alternativa para hallar $A,B \wedge C$, en lugar de igualar los coeficientes y usar un sistema de ecuaciones 3x3, se utilizan los valores críticos $x=0, x=-3\wedge x=1$ para simplificar la solución.
Para $x=0$, $\hspace{0.1cm}$se elimina $B\wedge C$
$4\left(0\right)^2+13\left(0\right)-9=\left(0+3\right)\left(0-1\right)A\\ -9=-3A\\ A=3\\$Para $x=-3$, $\hspace{0.1cm}$se elimina $A\wedge C$
${4\left(-3\right)^2+13\left(-3\right)-9}=+(-3)\left(-3-1\right)B\\ {36-39-9}=-3\left(-4\right)B\\ {-12}=12B\\ {B}=-1$Para $x=1$, $\hspace{0.1cm}$se elimina $A\wedge B$
${4\left(1\right)^2+13\left(1\right)-9}=1\left(1+3\right)C\\ {4+13-9}=1\left(4\right)C\\ {8}=4C\\ {C}=2$Se factoriza el denominador.
$$\color{black}\begin{aligned} \cfrac{2x+1}{x^2+2x-3} = \cfrac{2x+1}{\left(x-1\right)\left(x+3\right)}\\ \end{aligned}$$Como los factores del denominador son lineales y ninguno se repite es caso 1.
Se escribe la fracción parcial de la siguiente forma:
$$\color{black}\begin{aligned} \cfrac{2x+1}{x^2+2x-3} = \cfrac{A}{\left(x-1\right)}+\cfrac{B}{\left(x+3\right)}\\ \end{aligned}$$Se realiza la suma de fraccionarios del lado derecho de la ecuación, se aplica la propiedad distributiva y se hacen las operaciones de términos semejantes.
$$\color{black}\begin{aligned} \cfrac{2x+1}{x^2+2x-3} &= \cfrac{A\left(x+3\right)+B\left(x-1\right)}{\left(x-1\right)\left(x+3\right)}\\ &=\cfrac{Ax+3A+Bx-B}{\left(x-1\right)\left(x+3\right)}\\ &=\cfrac{\left(A+B\right)x+\left(3A-B\right)}{\left(x-1\right)\left(x+3\right)}\\ \end{aligned}$$La ecuación ${\color{brown}2\color{black}x+\color{blue}1}=\left(\color{brown}A+B\right)x+\left(\color{blue}3A-B\right)$, es válida para todos los valores de $x$.
Se comparan los coeficientes y el término independiente para hallar las ecuaciones.
$\hspace{0.2cm}\begin{cases}\color{brown}A+B=2\\\color{blue} 3A-B=1\end{cases}$Al sumar las ecuaciones se deduce que $4A=3$, luego, $A=\cfrac{3}{4}$ y
Reemplazando en $\cfrac{2x+1}{x^2+2x-3} = \cfrac{A}{\left(x-1\right)}+\cfrac{B}{\left(x+3\right)}$, se obtiene:
Puedes comprobar el resultado, realizando las operaciones del lado derecho de la ecuación.
En este caso se escribe:
 Ejemplos de fracciones parciales - Caso 2.
Ejemplos de fracciones parciales - Caso 2.Podemos ver que el término es lineal pero está repetido dos veces, por lo cual corresponde a una fracción parcial del caso 2, para resolverlo primero se coloca el término lineal $x$, luego el término repetido elevado a la potencia uno y luego elevado al cuadrado. La descomposición en fracciones se escribe de la siguiente forma:
$$\color{black}\begin{aligned} \cfrac{x^2+10x-36}{x^3-6x^2+3x} &= \cfrac{A}{x}+\cfrac{B}{\left(x-3\right)}+\cfrac{C}{\left(x-3\right)^2}\\ \end{aligned}$$Se realiza la suma de fraccionarios del lado derecho de la ecuación.
$$\color{black}\begin{aligned} \cfrac{x^2+10x-36}{x^3-6x^2+3x} &= \cfrac{A\left(x-3\right)^2+Bx\left(x-3\right)+Cx}{x\left(x-3\right)^2}\\ \end{aligned}$$La ecuación, ${x^2+10x-36}={A\left(x-3\right)^2+Bx\left(x-3\right)+Cx}$ es válida para todos los valores de $x$.
Para $x=0$, $\hspace{0.1cm}$se elimina $B\wedge C$
$\left(0\right)^2+10\left(0\right)-36 = {A\left(0-3\right)^2}\\ -36 = 9A\\ A = -4$Para $x=3$, $\hspace{0.1cm}$se elimina $A\wedge B$
$\left(3\right)^2+10\left(3\right)-36 = C\left(3\right)\\ 9+30-36 = 3C\\ 3 = 3C\\ C = 1$Para encontrar la $B$, es necesario hacer uso de las ecuaciones, y para ello se tienen que resolver el lado derecho de la ecuación
${x^2+10x-36}={A\left(x-3\right)^2+Bx\left(x-3\right)+Cx}$ ${x^2+10x-36}={A\left(x^2-6x+9\right)+Bx^2-3Bx+Cx}$ ${x^2+10x-36}={Ax^2-6Ax+9A+Bx^2-3Bx+Cx}$Se saca factor común por agrupación de términos.
${x^2+10x-36}=\left(A+B\right)x^2+\left(-6A-3B+C\right)x+9A$ $\hspace{1.1cm}\color{brown}\underline{\color{brown}\hspace{1.5cm}Igual\hspace{0.3cm}}\\$ $\hspace{1cm}\color{brown}\downarrow\hspace{2.5cm}\downarrow$ $\hspace{-1.9cm}\color{blue}\underline{\color{blue}\hspace{2.3cm}Igual\hspace{1.5cm}}\\$ $\hspace{1.9cm}\color{blue}\downarrow\hspace{4.5cm}\downarrow$$\hspace{1cm}$1$x^2+$10$x-$36 $ = \left(\color{brown}A+B\right)x^2 +\left(\color{blue}-6A-3B+C\right)x+\color{green}9A$
$\hspace{2.8cm}\color{green}\uparrow\underline{\color{green}\hspace{3.0cm}Igual\hspace{1.9cm}}\hspace{0.0cm}\uparrow\\$Ecuaciones:
$\hspace{0.2cm}\begin{cases}\color{brown}A+B=1\\\color{blue} -6A-3B+C=10\\\color{green}9A=-36\end{cases}$$A+B=1$, se reemplaza el valor de $A$
$-4+B=1\\ B=5$Ahora se reemplaza en:$\hspace{0.1cm}\cfrac{x^2+10x-36}{x^3-6x^2+3x} = \cfrac{A}{x}+\cfrac{B}{\left(x-3\right)}+\cfrac{C}{\left(x-3\right)^2}$
$$\color{black}\begin{aligned} \cfrac{x^2+10x-36}{x^3-6x^2+3x} &= \cfrac{-4}{x}+\cfrac{5}{\left(x-3\right)}+\cfrac{1}{\left(x-3\right)^2}\\ \end{aligned}$$Solución:
$$\color{black}\begin{aligned} \cfrac{6x-1}{2x^4-x^3} &= \cfrac{6x-1}{x^3\left(2x-1\right)}\\ &=\cfrac{6x-1}{x^3\left(2x-1\right)}\tag{1}\\ \end{aligned}$$Se separa en fracciones parciales.
$\hspace{4cm}$Caso 2$\hspace{1.1cm}$Caso 1
$$\cfrac{6x-1}{2x^4-x^3} = \overbrace{\cfrac{A}{x}+\cfrac{B}{x^2}+\cfrac{C}{x^3}}+\overbrace{\cfrac{D}{\left(2x-1\right)}}\tag{2}$$Se suma el lado derecho de la ecuación (2).
Se aplica la propiedad distributiva.
$${6x-1}={2Ax^3-Ax^2+2Bx^2-Bx+2Cx-C+Dx^3}$$Se saca factor común por agrupación de términos.
$${6x-1}=\left(\color{brown}2A+D\right)x^3+\left(\color{blue}-A+2B\right)x^2+\left(-B+2C\right)x-C$$ $\hspace{8.5cm}\left(4\right)$Se puede observar que los ceros de los factores del denominador en la ecuación (1), son $x=0\vee x=\cfrac{1}{2}$, al igualar $x^3\left(2x-1\right)$ a cero.
$x^3\left(2x-1\right)=0$Reemplazamos estos valores en la ecuación (3).
Para $x=0$, se cancela la $A,B\wedge D$, quedando:
$${0-1}={C\left(-1\right)}$$ $$-1=-C$$ $$C=1$$Para $x=\cfrac{1}{2}$, se cancela la $A,B\wedge C$, quedando:
$$6\left(\cfrac{1}{2}\right)-1=D\left(\cfrac{1}{2}\right)^3$$ $$3-1=\cfrac{D}{8}$$ $$2=\cfrac{D}{8}$$ $$D=16$$Como el denominador de la ecuación (1), sólo tiene dos ceros distintos, para encontrar $A\wedge B$ igualamos los coeficientes correspondientes a $x^3\wedge x^2$ en la ecuación (4), para hallar:
$\hspace{0.2cm}\begin{cases}\color{brown}2A+D=0\\\color{blue} -A+2B=0\end{cases}$reemplazamos el valor de $D$, hallado anteriormente.
$$2A+16=0$$ $$2A=-16$$ $$A=-8$$Conociendo el valor de $A$, se reemplaza en la segunda ecuación de la llave.
Reemplazamos los valores obtenidos $A=-8,B=-4, C=1 \wedge D=16$, en la ecuación (2) del presente ejemplo.
$\hspace{4.4cm}$Caso 2$\hspace{1.1cm}$Caso 1
$$\cfrac{6x-1}{2x^4-x^3} = \overbrace{\cfrac{A}{x}+\cfrac{B}{x^2}+\cfrac{C}{x^3}}+\overbrace{\cfrac{D}{\left(2x-1\right)}}\tag{2}$$ $$\color{black}\begin{aligned} \cfrac{6x-1}{2x^4-x^3} = \cfrac{-8}{x}+\cfrac{-4}{x^2}+\cfrac{1}{x^3}+\cfrac{16}{\left(2x-1\right)}\\ \end{aligned}$$En la siguiente escena interactiva diseñada por Juan Guillermo Rivera y José Román GaloJuan Guillermo Rivera y José Román Galo, son autores de la red Descartes, que publicaron el libro interactivo "Integrando con Paco".,podrás practicar solucionando los ejercicios propuestos y tendrás la posibilidad de ampliar tus conocimiento con un lenguaje amigable.
Al factor cuadrático $ax^2+bx+c$ del denominador le corresponde la fracción parcial de la forma:
 Ejemplos de fracciones parciales - Caso 3.
Ejemplos de fracciones parciales - Caso 3.Se factoriza el denominador.
$$\color{black}\begin{aligned} \cfrac{4+5x^2}{x^3+4x} = \cfrac{4+5x^2}{x\left(x^2+4\right)} \end{aligned}$$Como los factores del denominador son uno lineal y otro cuadrático y ninguno se repite es el caso 1 y caso 3. Se escribe la fracción parcial de la siguiente forma:
$\hspace{3.9cm}$Caso 1$\hspace{0.6cm}$Caso 3
$$\color{black}\begin{aligned} \cfrac{4+5x^2}{x^3+4x} &= \overbrace\cfrac{A}{x}+\overbrace\cfrac{Bx}{\left(x^2+4\right)}\tag{1}\\ \end{aligned}$$Se realiza la suma de fraccionarios del lado derecho de la ecuación
$$\color{black}\begin{aligned} \cfrac{4+5x^2}{x^3+4x} = \cfrac{A\left(x^2+4\right)+Bx\left(x\right)}{x\left(x^2+4\right)} \end{aligned}$$ $$4+5x^2={A\left(x^2+4\right)+Bx\left(x\right)}\tag{2}$$La ecuación (2) es válida para todos los valores de $x$. Se aplica la propiedad distributiva al lado derecho.
$$4+5x^2={Ax^2+4A+Bx^2}$$Se saca factor común y se comparan los términos de la igualdad.
$$4+5x^2={x^2\left(A+B\right)+4A}$$ $\hspace{3.05cm}\color{brown}\underline{\color{brown}\hspace{0.5cm}Igual\hspace{0.5cm}}\\$ $\hspace{3cm}\color{brown}\downarrow\hspace{1.6cm}\downarrow$$\hspace{3cm}$5$x^2+$4$ = \left(\color{brown}A+B\right)x^2 +$4A
$\hspace{3.8cm}\color{blue}\uparrow\underline{\color{blue}\hspace{1cm}Igual\hspace{0.4cm}}\hspace{0.0cm}\uparrow\\$$\hspace{0.2cm}\begin{cases}\color{brown}A+B=5\\\color{blue} 4A=4\end{cases}$
Despejando la $A$, se obtiene que $A=1\wedge B=4$
Se reemplaza $A\wedge B$ en la ecuación (1)
$$\color{black}\begin{aligned} \cfrac{4+5x^2}{x^3+4x} &= \cfrac{A}{x}+\cfrac{Bx}{\left(x^2+4\right)}\tag{1} \end{aligned}$$Solución
Se factoriza el denominador.
$$\color{black}\begin{aligned} \cfrac{4x}{x^4+2x^3+4x^2+2x+3}&= \cfrac{4x}{x^4+2x^3+3x^2+x^2+2x+3}\\ &=\cfrac{4x}{x^2\left(x^2+2x+3\right)+x^2+2x+3}\\ &=\cfrac{4x}{\left(x^2+2x+3\right)\left(x^2+1\right)} \end{aligned}$$ $$\cfrac{4x}{x^4+2x^3+4x^2+2x+3}=\cfrac{4x}{\left(x^2+1\right)\left(x^2+2x+3\right)}$$En este caso los factores del denominador son cuadráticos y ninguno se repite es el caso 3. Se escribe la fracción parcial de la siguiente forma:
$$\color{black}\begin{aligned} \cfrac{4x}{x^4+2x^3+4x^2+2x+3} &=\cfrac{Ax+B}{\left(x^2+1\right)}+\cfrac{Cx+D}{\left(x^2+2x+3\right)}\tag{1}\\ \end{aligned}$$Se realiza la suma de fraccionarios del lado derecho de la ecuación (1)
$$\cfrac{\left(Ax+B\right)\left(x^2+2x+3\right)+\left(Cx+D\right)\left(x^2+1\right)}{\left(x^2+1\right)\left(x^2+2x+3\right)}$$Luego:
$${4x}={\left(Ax+B\right)\left(x^2+2x+3\right)+\left(Cx+D\right)\left(x^2+1\right)}$$Se aplica la propiedad distributiva
${4x}=Ax^3+2Ax^2+3Ax+Bx^2+2Bx+3B+Cx^3+Cx+Dx^2+D$Ordenando la expresión de mayor a menor, se obtiene:
${4x}=Ax^3+Cx^3+2Ax^2+Bx^2+Dx^2+3Ax+2Bx+Cx+3B+D$Se saca factor común y se comparan los coeficientes y el término independiente, para obtener las ecuaciones.
${4x}=\left(A+C\right)x^3+\left(2A+B+D\right)x^2+3\left(3A+2B+C\right)x+\left(3B+D\right)$$\hspace{0.2cm}\begin{cases}\color{black}A+C=0\\\color{black} 2A+B+D=0\\\color{black} 3A+2B+C=4\\\color{black} 3B+D=0\end{cases}$
Despejando "$A$" en la primera ecuación y "$D$" en la cuarta ecuación, se obtiene:
$A=-C$
$D=-3B$
Reemplazando en la tercera y cuarta ecuación respectivamente, se obtiene:
$\hspace{0.2cm}\begin{cases}\color{black}-2C-2B=0\\\color{black} -2C+2B=4\end{cases}$Al eliminar $B$ en las ecuaciones anteriores, se obtiene $C=-1$
Conociendo $C$, se obtiene $A=1$, con $A\wedge C$, se obtiene $B=1$ y recuerda que $D=-3B$, luego $D=-3$
Resumiendo:
$\hspace{0.2cm}\begin{cases}\color{black}A=1\\\color{black} B=1\\\color{black}C=-1\\\color{black}D=-3\end{cases}$Para hallar la solución final, se reemplazan estos valores en la ecuación (1)
$$\color{black}\begin{aligned} \cfrac{4x}{x^4+2x^3+4x^2+2x+3} &=\cfrac{Ax+B}{\left(x^2+1\right)}+\cfrac{Cx+D}{\left(x^2+2x+3\right)}\tag{1}\\ \end{aligned}$$ $$\color{black}\begin{aligned} \cfrac{4x}{x^4+2x^3+4x^2+2x+3} &=\cfrac{\left(1\right)x+\left(1\right)}{\left(x^2+1\right)}+\cfrac{\left(-1\right)x+\left(-3\right)}{\left(x^2+2x+3\right)}\\ &=\cfrac{\left(x+1\right)}{\left(x^2+1\right)}-\cfrac{\left(x+3\right)}{\left(x^2+2x+3\right)} \end{aligned}$$En el video realizado por cctmexicocctmexico son autores de la red YouTube, que publicaron el video "Ejemplos de Fracciones Parciales"., vas a repasar los conceptos de los tres casos de descomposición en fracciones parciales
explicados anteriormente y podrás ver la utilidad en la solución de integrales.
Entonces el factor $\left(ax^2+bx+c\right)^n$ le corresponde la suma de las siguientes $_n$ fracciones parciales:
 Ejemplos de fracciones parciales - Caso 4.
Ejemplos de fracciones parciales - Caso 4.Solución:
$$\color{black}\begin{aligned} \cfrac{x^3-4x}{x^4+2x^2+1} =\cfrac{x^3-4x}{\left(x^2+1\right)^2} \end{aligned}$$En este caso los factores del denominador son lineales y cuadráticos y algunos se repiten, es el caso 4. Se escribe la fracción parcial de la siguiente forma:
$$\cfrac{x^3-4x}{x^4+2x^2+1} =\cfrac{Ax+B}{\left(x^2+1\right)}+\cfrac{Cx+D}{\left(x^2+1\right)^2}\tag{1}$$Se suman los fraccionarios de la parte derecha de la ecuación (1).
$$\cfrac{x^3-4x}{x^4+2x^2+1} =\cfrac{\left(Ax+B\right)\left(x^2+1\right)+\left(Cx+D\right)}{\left(x^2+1\right)^2}$$Se aplica la propiedad distributiva al numerador de la parte derecha de la ecuación anterior.
$$\color{black}\begin{aligned} \cfrac{x^3-4x}{x^4+2x^2+1} &=\cfrac{Ax^3+Ax+Bx^2+B+Cx+D}{\left(x^2+1\right)^2}\\ &=\cfrac{Ax^3+Bx^2+Ax+Cx+\left(B+D\right)}{\left(x^2+1\right)^2}\\ &=\cfrac{Ax^3+Bx^2+\left(A+C\right)x+\left(B+D\right)}{\left(x^2+1\right)^2} \end{aligned}$$ $$x^3-4x=Ax^3+Bx^2+\left(A+C\right)x+\left(B+D\right)$$Se arman las ecuaciones.
$\hspace{0.2cm}\begin{cases}\color{black}A=1\\\color{black} B=0\\\color{black} A+C=-4\\\color{black} B+D=0\end{cases}$Solucionando las ecuaciones se tiene que:
$\hspace{0.2cm}\begin{cases}\color{black}A=1\\\color{black} B=0\\\color{black} C=-5\\\color{black} D=0\end{cases}$Se reemplazan los valores anteriores en la ecuación (1)
Solución:
Los factores del denominador son cuadráticos y se repiten, es el caso 4. Se escribe la fracción parcial de la siguiente forma:
$$\cfrac{x^2}{\left(x^2+4\right)^2} =\cfrac{Ax+B}{\left(x^2+4\right)}+\cfrac{Cx+D}{\left(x^2+4\right)^2}\tag{1}$$Se suman los fraccionarios de la parte derecha de la ecuación (1).
$$\cfrac{x^2}{\left(x^2+4\right)^2} =\cfrac{\left(Ax+B\right)\left(x^2+4\right)+\left(Cx+D\right)}{\left(x^2+4\right)^2}$$Se aplica la propiedad distributiva al numerador de la parte derecha de la ecuación anterior.
Se arman las ecuaciones.
$\hspace{0.2cm}\begin{cases}\color{black}A=0\\\color{black} B=1\\\color{black} 4A+C=0\\\color{black} 4B+D=0\end{cases}$Solucionando las ecuaciones se tiene que:
$\hspace{0.2cm}\begin{cases}\color{black}A=0\\\color{black} B=1\\\color{black} C=0\\\color{black} D=-4\end{cases}$Se reemplazan los valores anteriores en la ecuación (1)
$$\cfrac{x^2}{\left(x^2+4\right)^2} =\cfrac{Ax+B}{\left(x^2+4\right)}+\cfrac{Cx+D}{\left(x^2+4\right)^2}\tag{1}$$A continuación encontrarás 10 ejercicios propuestos con su respectiva respuesta, para que confrontes tus resultados.

Se atribuye a Gauss las primeras demostraciones del "Teorema Fundamental del álgebra", presentada en su tesis doctoral (1799) y que dicho trabajo presentó algunos errores muy controversiales, siendo motivo de discusión por mucho tiempo. Sabías que muchos matemáticos, entre ellos: D’Alembert, Lagrange, Laplace, Euler, etc., trataron de justificar dicho resultado?. Fue hasta 1814, cuando el matemático sueco, de padres franceses, Jean Robert Argand, tuvo la dicha de celebrar el reconocimiento general por presentar una demostración correcta de dicho teorema. $P\left(z\right)=a_{n}z^n+a_{n-1}z^{n-1}+\ldots+a_{1}z+a_{0}$
En la recta numérica (sección 1.11), se definió las relaciones de orden como “mayor que” y “menor que”, “mayor o igual que” y “menor o igual que” y vimos cómo interpretarlas en la recta de los números reales. Es el momento de solucionar sistemas de inecuaciones.
Para resolver inecuaciones lineales, se procede como en las ecuaciones pero se tiene en cuenta que al multiplicar por $-1$, cambio el signo de la desigualdad.
En el video realizado por Julio Alberto Ríos Gallego "Julio Profe"Julio Profe es un autor de la red YouTube, que publicó el video "Desigualdades lineales"., podrás aprender a solucionar inecuaciones lineales en el cual se explica el proceso para solucionar inecuaciones lineales, que será utilidad en la solución de ejercicios posteriores.
 Ejemplos de inecuaciones lineales
Ejemplos de inecuaciones linealesComo se trata de despejar el valor de la x, las pasamos al lado izquierdo de la desigualad.
$$8x-5x<16-4$$ $$3x<12$$Dividimos por 3 y simplificamos.
$$\cfrac{3x}{3}<\cfrac{12}{3}$$Como la $x$ quedo negativa, es necesario multiplicar toda la desigualdad por menos 1 y no olvidar cambiar el signo de la desigualdad.
$$\left(-1\right)\left(-x≤\cfrac{2}{3}\right)$$En ocasiones se presentan inecuaciones simultáneas, es decir, que la variable $x$, se encuentra en medio de dos signos de desigualdad.
En estos casos se procede de la siguiente manera:
Como se trata de una inecuación simultánea, se debe dejar la variable en medio de las desigualdades, teniendo en cuenta pasar los términos a cada lado de las desigualdades, haciendo el cambio de signo.
$$-7-\color{red}1\color{black}≤2x<\color{black}19-\color{red}1$$ $$-8≤2x<18$$Como el 2 está multiplicando a la x, dividimos toda la desigualdad por 2.
Recordemos que el resultado lo podemos expresar en forma de desigualdad y en forma de intervalo.
En forma de intervalo sería: $[-4,9)$
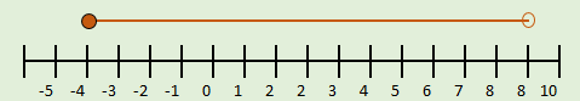
Solución: Sea $x$=Ventas y 8%$=\cfrac{8}{100}$
Sabemos que le pagan $\$ 15.000 $ al año más una comisión de 8%, como el ingreso anual esta entre $\$23.000$ y $\$27.000$, se debe expresar de la siguiente forma:
$$23000≤15000+\cfrac{8}{100} x≤27000$$Pasamos el $15000$ a cada lado de la desigualdad, con signo contrario.
Para eliminar el factor $\cfrac{8}{100}$, se debe multiplicar por su inverso, es decir, $\cfrac{100}{8}$.
$$\left(\cfrac{100}{8}\right)\cdot 8000≤\left(\cfrac{100}{8}\right)\cdot \cfrac{8}{100} x≤12000\cdot \left(\cfrac{100}{8}\right)$$Se simplifica.
Las ventas anuales deben estar entre $\$100.000$ y $\$150.000$, para que las ventas mensuales, más las comisiones se mantengan entre $\$23.000$ y $\$27.000$
En la solución, se deben tener en cuenta sus propiedades.
Si $a$ denota un número real positivo, entonces:
En la siguiente tabla se resumen los diferentes casos para la solución de inecuaciones con valor absoluto.
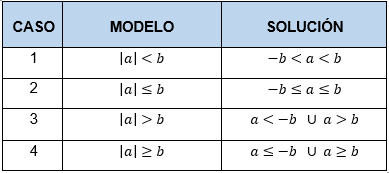
 Ejemplos de inecuaciones con valor absoluto
Ejemplos de inecuaciones con valor absolutoEl conjunto solución es el intervalo abierto $\color{brown}\left(2,\cfrac{8}{3}\right)$.
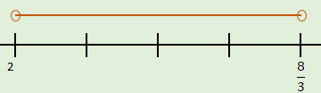
Es una inecuación que corresponde al modelo del caso 2.
$$-12≤3x-6≤12$$ $$-12+6≤3x≤12+6$$ $$-6≤3x≤18$$El conjunto solución es el intervalo cerrado $\color{brown}\left[-2,6\right]$
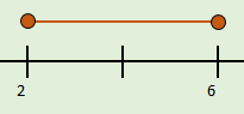
Es una inecuación que corresponde al modelo del caso 3.
$$3+x<-7 \cup 3+x>7$$ $$x<-7-3 \cup x>7-3$$El conjunto solución es el intervalo abierto $\color{brown}\left(-\infty,-10\right) \cup\left(4,\infty\right)$
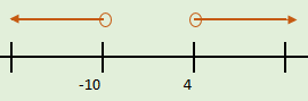
Es una inecuación que corresponde al modelo del caso 4.
$$4-\cfrac{1}{2} x≤-7\hspace{0.2cm} \cup \hspace{0.2cm} 4-\cfrac{1}{2} x≥7$$ $$-\cfrac{1}{2} x≤-7-4\hspace{0.2cm} \cup \hspace{0.2cm} -\cfrac{1}{2} x≥7-4$$ $$-\cfrac{1}{2} x≤-11\hspace{0.2cm} \cup \hspace{0.2cm} -\cfrac{1}{2} x≥3$$ $$-x≤-22\hspace{0.2cm} \cup \hspace{0.2cm} -x≥6$$Multiplicamos por -1 ambas desigualdades, teniendo en cuenta el cambio de la dirección de la desigualdad.
El conjunto solución es el intervalo $\color{brown}\left(-\infty,-6\right]\hspace{0.2cm} \cup \hspace{0.2cm}\left[22,\infty\right)$
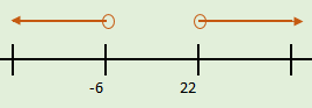
En el video realizado por Julio Alberto Ríos Gallego "Julio Profe"Julio Profe es un autor de la red YouTube, que publicó el video "Desigualdades con valor absoluto"., podrás aprender a solucionar inecuaciones con valor absoluto en el cual se explica su proceso y será utilidad en la solución de ejercicios posteriores.
Son inecuaciones donde la variable hace parte del numerador y del denominador.
Para solucionar un sistema de inecuaciones racionales, se debe:
$\bullet\hspace{0.3cm}$Se pasan todos los términos al lado izquierdo de la desigualdad y se realizan las operaciones.
$\bullet\hspace{0.3cm}$Factorizar el numerador y el denominador.
$\bullet\hspace{0.3cm}$Buscar los puntos críticos tanto del numerado como del denominar, igualando a cero los factores obtenidos anteriormente.
$\bullet\hspace{0.3cm}$Evaluar los puntos críticos en los intervalos anterior y posterior para determinar que signo tienen los factores en cada intervalo.
$\bullet\hspace{0.3cm}$Determinar el conjunto solución, de acuerdo al planteamiento de la inecuación.
 Ejemplo de Inecuaciones racionales
Ejemplo de Inecuaciones racionalesSe hace la suma de fraccionarios.
$$\hspace{0.1cm}\cfrac{x+4}{x-2}-\cfrac{3}{1}≥0$$ $$\hspace{0.1cm}\cfrac{\left(1\right)\left(x+4\right)-\left(3\right)\left(x-2\right)}{x-2}≥0$$ $$\hspace{0.1cm}\cfrac{x+4-3x+6}{x-2}≥0$$Se suman términos semejantes.
$$\hspace{0.1cm}\cfrac{-2x+10}{x-2}≥0$$En este caso no se requiere factorizar el numerador y el denominador, sólo es necesario encontrar los puntos críticos para cada uno de ellos.
Puntos críticos$\hspace{0.1cm}\begin{cases}Numerador\left(N\right):-2x+10\\\color{black} \hspace{0.2cm}Denominador\left(D\right): x-2\end{cases}$
Puntos críticos$\hspace{0.1cm}\begin{cases}\left(N\right):x=5\\\color{black}\left(D\right): x=2\end{cases}$
Como se puede observar, los puntos críticos son el 2 para el denominador el 5 para numerador.
Se ubican los puntos críticos en la recta numérica y se reemplaza la variable $"x"$ de la inecuación, por valores antes y después del punto, para determinar su signo.
Los puntos críticos en el denominador, significan que son intervalos abiertos en los mismos.
Para $x=1$:
$$\cfrac{-2\left(1\right)+10}{1-2}=\frac{-1+10}{1-2}=\cfrac{+9}{-1}=\cfrac{\left(+\right)}{\left(-\right)}$$Sólo nos interesa el signo y como el numerador es positivo $\left(+\right)$ y el denominador es negativo $\left(-\right)$, el signo es $\left(-\right)$ ya que $\left(+\right)\cdot\left(-\right)=\left(-\right)$
$$\cfrac{\left(+\right)}{\left(-\right)}=\left(-\right)$$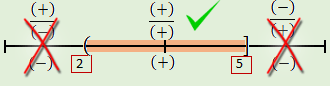
Si observamos, la inecuación nos plantea los valores que hagan que la fracción sea $≥$ que cero y dado que los números negativos son menores que cero, el intervalo $x<2$ no son solución para la inecuación.
Realizando el procedimiento anterior para los demás intervalos que estén antes y después del punto críticos se determina que:
Para $x=3$, que es un valor que esta en el intervalo $\left(3,5\right)$.
$$\cfrac{\left(+\right)}{\left(+\right)}=\left(+\right)$$Como la inecuación nos plantea los valores que hagan que la fracción sea $≥0$ y dado que los números positivos son mayores que cero, el intervalo $2<x<5$ es solución para la inecuación.
Para $x=6$, que es un valor que esta en el intervalo $\left(5,\infty\right)$.
$$\cfrac{\left(-\right)}{\left(+\right)}=\left(-\right)$$El intervalo es negativo, por tanto no es solución para la inecuación.
El conjunto solución es el intervalo $\color{brown}\left(-2,5\right]$, es abierto a la izquierda porque el 2 no se puede incluir, ya que haría el denominador cero y la división por cero es infinita.
Lo primero que se debe hacer es la suma de fraccionarios.
$$\cfrac{1}{1}+\cfrac{2}{x+1}-\cfrac{2}{x}<0$$El mcm es $x\cdot\left(x+1\right)$.
$$\cfrac{x\cdot\left(x+1\right)+2\cdot\left(x\right)-2\cdot\left(x+1\right)}{x\cdot\left(x+1\right)}<0$$Sumamos términos semejantes.
$$\cfrac{x^2+x-2}{x\cdot\left(x+1\right)}<0$$Puntos críticos$\hspace{0.1cm}\begin{cases}Numerador\left(N\right):x+2=0\wedge x-1=0\\\color{black} \hspace{0.2cm}Denominador\left(D\right): x=0\wedge x+1=0\end{cases}$
Puntos críticos$\hspace{0.1cm}\begin{cases}\left(N\right):x=-2\wedge x=1\\\color{black}\left(D\right): x=0 \wedge x=-1\end{cases}$

El conjunto solución es el intervalo:
En el video realizado por Julio Alberto Ríos Gallego "Julio Profe"Julio Profe es un autor de la red YouTube, que publicó el video "Desigualdades racionales"., podrás aprender a solucionar inecuaciones racionales en el cual se explica su proceso y será utilidad en la solución de ejercicios posteriores.
Son inecuaciones con presencia de trinomios de la forma $x^2+bx+c$ o que se solucionan con la utilización de la fórmula general.
 Ejemplo de Inecuaciones cuadráticas
Ejemplo de Inecuaciones cuadráticasLo primero que se tiene que identificar son las posibles restricciones que se presenten en la inecuación.
En este caso, obsérvese que la inecuación tiene que cumplir con 2 condiciones.
Que $4x^2-9x+2≥0$, ya que la $\sqrt{\textsf{Números\; negativos}} = \textsf{Imaginarios} \left(i\right)$ y que $\sqrt{4x^2-9x+2}≥2x+1$.
Valores Críticos: $4x-1=0\wedge x-2=0$, por lo que $x=\cfrac{1}{4}\hspace{0.1cm}\wedge\hspace{0.1cm} x=2$
Por lo que tenemos que solucionar las dos restricciones en forma independiente y luego la solución será la intersección entre las dos soluciones.
Para la primera restricción: $4x^2-9x+2≥0$
$\centerdot\hspace{0.3cm}$ Lo primero es factorizar $\left(4x-1\right)\cdot\left(x-2\right)<0$
$\centerdot\hspace{0.3cm}$Ya tenemos 2 factores, ahora lo que sigue es hallar los valores críticos, igualando a cero y obtener la solución.
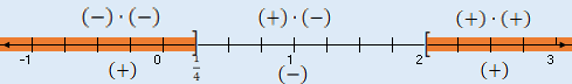
El conjunto solución es el intervalo:
$\left(-\infty,\cfrac{1}{4}\right]\hspace{0.1cm}\cup\hspace{0.1cm}\left[2,\infty\right)$Para la primera restricción: $\sqrt{4x^2-9x+2}<2x+1$
$\centerdot\hspace{0.3cm}$Es necesario eliminar el radical, elevando al cuadrado cada lado de la desigualdad.
En el lado izquierdo de la desigualdad, simplemente se saca del radical y en el lado derecho es el cuadrado de un binomio.
Llevamos la desigualdad a cero, pasando los términos del lado derecho al izquierdo.
$$4x^2-9x+2-4x^2-4x-1<0$$ $$-13x+1<0$$Como la $x$ quedó negativa, multiplicamos toda la desigualdad por menos y cambiamos de signo.
$$13x>1, \text{luego}\hspace{0.2cm}x=\cfrac{1}{13}$$
El conjunto solución es el intervalo $\left(\cfrac{1}{13},\infty\right)$.La solución total es la intersección entre los resultados de las dos restricciones.
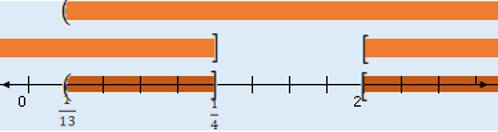
El conjunto solución es el intervalo:
La trigonometría es una subdivisión de las matemáticas encargada de calcular los elementos de los diferentes triángulos, estudiando la relación entre sus ángulos y sus lados.
Según Zill, Dennis. (2012), “…Los rudimentos de la trigonometría se remontan al trabajo de matemáticos griegos, egipcios, indios, árabes y chinos. La palabra trigonometría se deriva de dos vocablos griegos: trigon, que significa triángulo, y metro, que significa medida. Por tanto, el nombre trigonometría hace alusión a las diversas relaciones entre los ángulos de un triángulo y sus lados.”
Se forma por dos semirrectas que tienen un extremo en común llamado vértice. Una de las semirrectas será el lado inicial y la otra el lado terminal, como se muestra en la Figura 2. Ángulo (Zill, $3^{a}$ edición).
Cuando el ángulo se ubica en el plano cartesiano y tiene como lado inicial el eje positivo de las $x$, con vértice en el origen, se dice que el ángulo está en posición normal o estándar. Figura 3. Posición normal (Zill, $3^{a}$ edición).
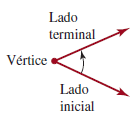
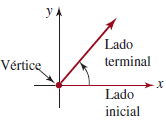
Los ángulos se miden en grados o en radianes, con las siguientes
equivalencias.
Figura 4. Ángulo de 360 grados (Zill, $3^{a}$ edición).
 Ejemplos de conversión de ángulos
Ejemplos de conversión de ángulosSon aquellos ángulos en posición normal que tienen los mismos lados terminales. Por ejemplo, los ángulos $0^{\circ},0^{\circ}+360^{\circ} \wedge 0^{\circ}-360^{\circ}$, los cuales tienen las mismas razones trigonométricas.
Figura 5. Ángulos coterminales (Zill, $3^{a}$ edición).
 Ejemplos de ángulos coterminales
Ejemplos de ángulos coterminalesHallar un ángulo coterminal a $30^{\circ},37^{\circ},45^{\circ},53^{\circ},\wedge 60^{\circ}$, tanto positivo como negativo.
En la siguiente tabla, se resume la solución.
Es el recorrido a lo largo de la curva formada desde la parte final del lado inicial de un ángulo, hasta la parte final de su lado terminal.
Cuando se realice el cálculo de la longitud de arco, se debe tener en cuenta que el ángulo este en radianes, es decir, si se presenta en grados, se debe hacer la conversión.
$L=\theta\cdot r,\theta=\cfrac{L}{r},r=\cfrac{L}{\theta}$
El circulo unitario se encuentra centrado en el origen, $r=1$. La ecuación de la circunferencia $x^2+y^2=r^2$ da origen a la ecuación del circulo unitario, dado que $r=1$, luego dicha ecuación será:
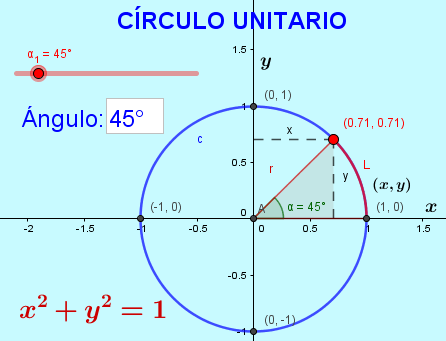
La ecuación anterior es de gran utilidad cuando se desea determinar si un punto $P\left(P_x,P_y\right)$, pertenece al círculo unitario.
 Ejemplos círculo unitario
Ejemplos círculo unitarioLas coordenadas de un punto en el plano cartesiano, están determinadas por el par ordenado $P \left(x, y\right)$.
Para que el punto $P \left(x, y\right)$, pertenezca al círculo unitario tiene que cumplir con la ecuación del círculo unitario $\color{brown}x^2+y^2=1$, luego:
$$\left(\cfrac{\sqrt{3}}{3}\right)^2+\left(\cfrac{\sqrt{6}}{3}\right)^2=1$$ $$\cfrac{\left(\sqrt{3}\right)^2}{3^2}+\cfrac{\left(\sqrt{6}\right)^2}{3^2}=1$$Observen que ha quedado una suma de fraccionarios homogéneos.
$$\cfrac{3+6}{9}=1$$ $$\cfrac{{\color{Red}\bcancel {{\color{black}9}}}}{{\color{Red}\bcancel {{\color{black}9}}}}=1$$ $$1=1$$Con el resultado anterior, podemos afirmar que el punto $P\left(\cfrac{\sqrt{3}}{3} ,\cfrac{\sqrt{6}}{3}\right)$, pertenece al círculo unitario.
Nota: El signo $\pm$ indica la existencia de dos puntos que pertenecen al círculo unitario, $P_1\left(\cfrac{\sqrt{3}}{2} ,\cfrac{1}{2}\right)$ ubicado en el primer (I) cuadrante y $P_2\left(-\cfrac{\sqrt{3}}{2} ,\cfrac{1}{2}\right)$, ubicado en el segundo (II) cuadrante.
En la siguiente escena interactiva, al utilizar el deslizador "Ángulo" podrás podrás observar que al desplazarte en una rango comprendido entre $0^{\circ}\wedge 360^{\circ}$, el lado terminal del ángulo siempre se mantiene sobre el círculo.
Puedes utilizar la calculadora, haciendo clic sobre la imagen  , para verificar si los siguientes puntos pertenecen al circulo unitario y determina en que cuadrante se encuentran y que ángulo forman (aproximar con dos decimales).
, para verificar si los siguientes puntos pertenecen al circulo unitario y determina en que cuadrante se encuentran y que ángulo forman (aproximar con dos decimales).
Para facilitar su comprensión, vamos a determinar, si el punto $P(0.71 , 0.71)$ pertenece al círculo unitario.
Recuerda que un punto $P(x , y)$, pertenece al círculo unitario si satisface la ecuación: $\;\color{brown}x^2+y^2=1$
Solución:
$$x^2+y^2=1$$ $$\left(0.71\right)^2+\left(0.71\right)^2=1$$ $$0.5+0.5=1$$ $$1=1$$Como se puede observar se cumple con la ecuación, por lo tanto el punto $P(0.71 , 0.71)$ pertenece al círculo unitario.
Ahora, si vamos a la escena interactiva y ubicamos el deslizador en radio 1 y el punto $P(0.71 , 0.71)$ (haciendo uso del deslizador "Ángulo".), se puede encontrar el valor del ángulo y el cuadrante al cual pertenece.
Haciendo lo anterior en la escena interactiva, te darás cuenta que:
$\bullet\hspace{0.2cm}$Se trata de un círculo de $r=1$
$\bullet\hspace{0.2cm}$Corresponde a un ángulo de $45^{\circ}$
$\bullet\hspace{0.2cm}$El ángulo pertenece al primer cuadrante.
En la siguiente imagen, obtenida de la escena interactiva se aprecian los resultados.
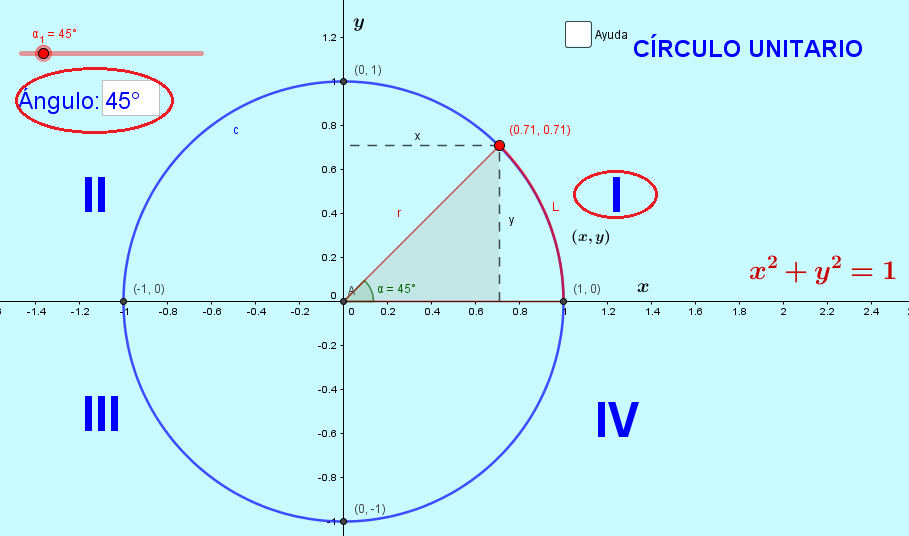
Determinar si el punto $P(1.41 , 1.41)$ pertenece al círculo unitario.
Solución:
$$x^2+y^2=1$$ $$\left(1.41\right)^2+\left(1.41\right)^2=1$$ $$1.98+1.98=1$$ $$3.98=1$$Como se puede observar NO se cumple con la ecuación, por lo tanto el punto $P(1.41 , 1.41)$ NO pertenece al círculo unitario.
Lo que si se puede inferir es que es un círculo cuyo radio $r\approx 2$.
Son aquellos que sumados son iguales al valor del ángulo de $90^{\circ}$, es decir; el ángulo complementario de $30^{\circ}$, será el de $60^{\circ}$, dado que: $90^{\circ}-30^{\circ}=60^{\circ}$
$$\color{brown}90^{\circ}-\theta$$
Son aquellos que sumados son iguales son iguales al ángulo llano $\left(180^{\circ}\right)$, es decir; el ángulo suplementario de $135^{\circ}$, será el de $45^{\circ}$, dado que: $180^{\circ}-135^{\circ}=45^{\circ}$
$$\color{brown}180^{\circ}-\theta$$
Con la ayuda de la siguiente escena interactiva, calcula los ángulos complementarios y suplementarios que se solicitan a continuación.
En el video realizado por José Maria Martín RizaldosJosé Maria Martín Rizaldos es un autor de la red YouTube, que publicó el video "Ángulos complementarios y suplementarios"., en el cual se explica el proceso para el cálculo de ángulos complementarios y suplementarios, podrás aprender a realizar diferentes ejercicios que serán de utilidad posteriormente.
Ángulo de ELEVACIÓN: Es el ángulo desde la horizontal hacia un objeto que está en la parte de superior del observador.
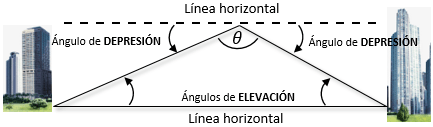
Ángulo de DEPRESIÓN: Es el ángulo desde la horizontal hacia un objeto que está en la parte de inferior del observador.
En la siguiente escena interactiva, diseñada por Juan Guillermo Rivera, podrás observar y comprender la definición de ángulo de elevación, sólo basta con presionar el botón de "Regresar" y "Animar".
En la siguiente escena interactiva, diseñada por Juan Guillermo Rivera, aprenderás a calcular el ángulo de elevación con diferentes ejemplos propuestos.
Siendo así:
En la siguiente escena interactiva, podrás analizar la definición del teorema de Pitágoras, desplazando el ponto "$A$", en dirección vertical o el punto "$C$" en dirección horizontal, observando el comportamiento de las áreas de los polígonos que rodean el triángulo rectángulo y la definición propia del teorema.
En la medida en que interactúes con la escena, te darás cuenta que el teorema de Pitágoras se aplica a triángulos rectángulos y si observas los ángulos internos del triángulo, te darás cuenta que suman $180^{\circ}$ grados.
 Ejemplos Teorema de Pitágoras
Ejemplos Teorema de PitágorasLo primero que se debe hacer es construir el dibujo de lo que se plantea en el ejercicio.
Por el teorema de Pitágoras $H^2=CO^2+CA^2$, luego:
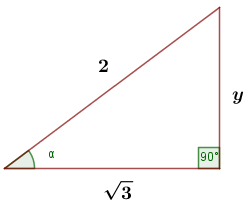
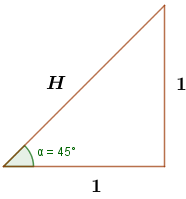
opuesto $1$ y el adyacente es $1$.
$H^2=1^2+1^2\\ H^2=1+1\\ H^2=2\\ H=\pm\sqrt{2}$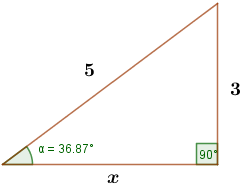
A continuación se proponen algunos ejercicios para que pongas a prueba tus conocimientos sobre el círculo unitario y el teorema de Pitágoras.
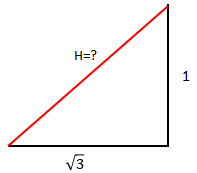
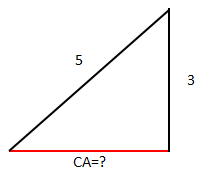
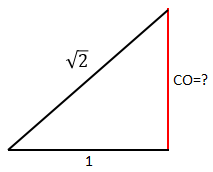
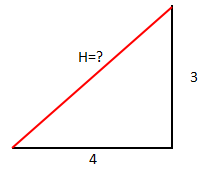
Se definen comúnmente como el cociente entre los lados del triángulo o el cociente entre sus lados y la hipotenusa, asociados al ángulo que forman.
Las razones trigonométricas del seno, coseno y tangente, así como sus inversa, se definen en triángulos rectángulos, es decir que tienen un ángulo recto $90^{\circ}$, en los cuales se puede aplicar el teorema de Pitágoras para obtener magnitudes de lados desconocidos.
En la imagen, podrás observar la relación existente entre los catetos y la hipotenusa de cada una de las razones trigonométricas, siendo:
O = Cateto Opuesto
A = Cateto Adyacente
H = Hipotenusa
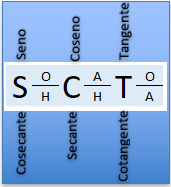
Los lados (catetos) de los triángulos rectángulos cambian de nombre, dependiendo del ángulo agudo que se considere. En el siguiente escena interactiva se muestra el cambio, dependiendo del ángulo en que concentres la atención.
En la siguiente escena interactiva diseñada por Juan Guillermo RiveraJuan Guillermo Rivera, es un autor de la red Descartes, que publicó "Discursos de trigonometría"., podrás aprender a identificar los lados de un triángulo
rectángulo, cambiando de ángulo para que observes el nombre de los lados, según el ángulo que se elija.
Teniendo como referencia al ángulo "$\alpha$" de la escena interactiva anterior y utilizando la sigla 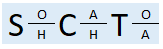 , sus razones trigonométricas serán:
, sus razones trigonométricas serán:
Con la siguiente escena interactiva, podrás interactuar y familiarizarte con los lados de los triángulos rectángulos, dependiendo del ángulo agudo que se elija.
Son aquellos ángulos que su lado terminal coincide con los ejes coordenados. Recordemos que un par ordenado tiene componentes en los ejes $x\; e \;y\; (x, y)$, y que los ángulos cuadrantales son $0^{\circ}, 90^{\circ},180^{\circ},270^{\circ} \;\text{y} \;360^{\circ}$, así como todos los que se formen sobre los ejes al girar $n$-vueltas.
Haciendo uso de la escena interactiva del "círculo unitario", analizaremos las razones trigonométricas de los ángulos cuadrantales.
Como puedes observar, al llevar el deslizador a cada uno de los ángulos cuadrantales, las razones trigonométricas coinciden con el punto $P$ de coordenadas $\left(x,y\right)$. Observa la siguiente imagen.
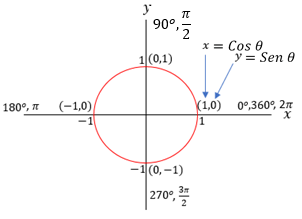
En la escena interactiva, ingresa los ángulos $0^{\circ}, 90^{\circ},180^{\circ},270^{\circ}$ y $360^{\circ}$ en la casilla "Ángulo" de la imagen superior y verifica los resultados.
De la imagen y de la escena interactiva, podemos deducir que:
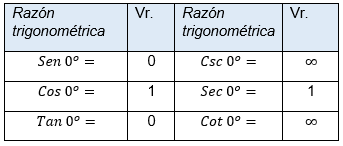
Las razones trigonométricas $Csc \;0^{\circ} \text{\;\;y} \;\;Cot \;0^{\circ}$, son $\infty$, dado que $Csc \;0^{\circ}=\cfrac{1}{Sen \;0^{\circ}}$ y $Cot \;0^{\circ}=\cfrac{1}{Tan \;0^{\circ}}\;\;$ por lo que la división por cero es infinito.
Como actividad de trabajo individual, con la ayuda de la escena interactiva y de la sigla 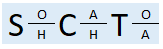 , pueden calcular las razones trigonométricas de los demás ángulos cuadrantales.
, pueden calcular las razones trigonométricas de los demás ángulos cuadrantales.
Siempre que se hable de Coseno, pensemos en la coordenada (abscisa) $\;\;"x"$, ya que $x=Cos\;\alpha$ y cuando se hable de Seno, se piensa en la coordenada (ordenada) $"y"\;$, debido a que $y=Sen\;\alpha$.
Teniendo en cuenta lo anterior, podemos tomar como referencia la siguiente gráfica, ya que la “$x$” y la “$y$” son positivas (+) en el primer cuadrante, por tanto, las razones trigonométricas de todos los
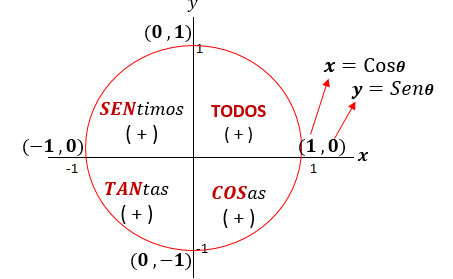
ángulos que se encuentren en este cuadrante, también lo serán. Así mismo, en el segundo cuadrante sólo el eje “$y$”, es positivo (+) y como ya se dijo, la “$y=Sen\;\alpha$", por tanta la razón $Sen\;\alpha$, es la única positiva, las demás son negativas. De la misma manera se puede analizar los signos de las funciones trigonométricas en el tercer y cuarto cuadrante, sien do la tangente positiva (+) en el tercer (III) cuadrante y el coseno positivo (+) en el cuarto (IV).
Es el ángulo agudo que representa un ángulo de cualquier medida, con los signos del cuadrante correspondiente.
En la siguiente escena interactiva "Ángulos equivalentes y signos de las razones trigonométricas", podrá encontrar los ángulos equivalentes para los ángulos agudos que ingrese en la casilla de entrada $\alpha$.
Nota: Se recomienda que se tome como referente el ángulo que se forme con el eje de las abscisas ($x$).
 Ejemplos de ángulo de referencia y equivalentes.
Ejemplos de ángulo de referencia y equivalentes.Solución:
Para a:
Observa que el ángulo de 30°, se encuentra en el primer (I) cuadrante, se ingresa el ángulo en la casilla de entrada $\alpha$ de la escena interactiva y se toman los valores del punto $P\left(x,y\right)$, teniendo en cuenta que $x=Cos\;\alpha \wedge\;y=Sen\;\alpha$. Siendo así:
Para b.
Como se trata de un ángulo de $135^{\circ}$, lo primero es ubicar en que cuadrante se encuentra y cual es su ángulo de referencia en el primer cuadrante. No se debe olvidar que son las mismas razones trigonométricas, pero con los signos del cuadrante al cual pertenece.
Observa que $135^{\circ}$ está en el segundo cuadrante, lo que quiere decir que su ángulo de referencia es $180^{\circ}-135^{\circ}=45^{\circ}$, luego:
Como se trata de un ángulo de $240^{\circ}$, se encuentra en el tercer cuadrante y su ángulo de referencia en el primer cuadrante es $240^{\circ}-180^{\circ}=60^{\circ}$, porque sobrepasa el eje de las $x$. No olvidar los signos, luego:
Como se trata de un ángulo de $330^{\circ}$, se encuentra en el cuarto cuadrante y su ángulo de referencia en el primer cuadrante es $360^{\circ}-330^{\circ}=30^{\circ}$, porque está por debajo del eje de las $x$ del giro completo. No olvidar los signos.
Si ingresaste en la escena interactiva $\alpha=30^{\circ}$, te diste cuenta que las razones trigonométricas de $30^{\circ}\wedge330^{\circ}$, sólo cambia el signo del seno, por estar en el cuarto cuadrante y allí, la "$y$" es negativa. Observa la siguiente imagen, tomada de la escena interactiva.
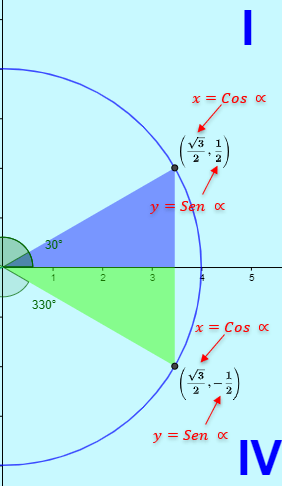
$180^{\circ}-135^{\circ}=\color{brown}45^{\circ}$, el ángulo de referencia para el primer (I) cuadrante es $45^{\circ}$, significa que las razones trigonométricas de $135^{\circ}$ son las mismas del ángulo de $45^{\circ}$,
$\hspace{0.8cm}$pero con los signos del segundo (II) cuadrante.
$\hspace{0.4cm}\text{b.}\hspace{0.2cm}240^{\circ}$está en el tercer (III) cuadrante, observa que esta después $\hspace{0.9cm}$ del ángulo llano ($180^{\circ}$), por lo tanto, para hallar el ángulo de $\hspace{0.9cm}$ referencia para el primer (I) cuadrante, se le debe restar ($180^{\circ}$) $\hspace{0.9cm}$ al ángulo dado.
$$240^{\circ}-180^{\circ}=\color{brown}60^{\circ}$$$\hspace{0.4cm}\text{c.}\hspace{0.2cm}330^{\circ}$ está en el tercer (IV) cuadrante, observa que esta antes $\hspace{0.9cm}$ del ángulo de giro ($360^{\circ}$), por lo tanto, para hallar el ángulo de $\hspace{0.8cm}$ referencia para el primer (I) cuadrante, se le debe restar a
$\hspace{0.9cm}$($360^{\circ}$) el ángulo dado.
NOTA: No pueden olvidar que se buscan las razones trigonométricas del ángulo de referencia, pero con los signos del cuadrante al que corresponde al ángulo que dieron inicialmente.
En el video realizado por Abel Esteban Ortega LunaAbel Esteban Ortega Luna es un autor de la red YouTube, que publicó el video "Razones trigonométricas en triángulo rectángulo"., en el cual se explica el proceso para el cálculo de las razones trigonométricas en triángulos rectángulos.
podrás aprender a realizar diferentes ejercicios que serán de utilidad para la solución de problemas en contexto.
En la siguiente escena interactiva encontrarás las razones trigonométricas del seno, coseno y tangente para que visualices los cambios en la medida que desplaces el lado terminal (punto rojo) del triángulo rectángulo, pasando por todo el círculo unitario.
En la siguiente escena interactiva diseñada por Juan Guillermo RiveraJuan Guillermo Rivera, es un autor de la red Descartes, que publicó "Discursos de trigonometría"., podrás aprender a identificar los lados de un triángulo rectángulo, cambiando de ángulo para que observes el nombre de los lados, según el ángulo que se elija.
En la siguiente escena interactiva, podrás aprender a calcular las razones trigonométricas de los ángulos notables "con la mano", numera los dedos desde el dedo meñique, iniciando en cero, hasta el dedo pulgar que sería el $4$ y representa $90^{\circ}$. El seno lo calculas en el sentido de las manecillas del reloj, es decir, desde el dedo pulgar hacia el meñique, siempre sacando raíz cuadrada al número que le corresponde a cada dedo y dividiendo por $2$. Para el coseno, haces lo mismo pero en sentido anti horario, partiendo del dedo meñique hacia el dedo pulgar y los numeras de mayor a menor, es decir $4$, $3$, $2$, $1$.
La escena interactiva diseñada por phet.colorado.eduphet.colorado.edu, son autores de la red Descartes que publicaron la escena interactiva "Tour trigonométrico"., te permitirá hacer un recorrido por las gráficas del seno, coseno y tangente y encontrarás las razones trigonométricas de los ángulos cuadrantales y los ángulos notables.
 Ejemplos de aplicación con triángulos rectángulos
Ejemplos de aplicación con triángulos rectángulosSolución.
En la gráfica siguiente plantea la situación problema.
Para solucionar ejercicios de este tipo, puedes utilizar el teorema de Pitágoras o las razones trigonométricas.
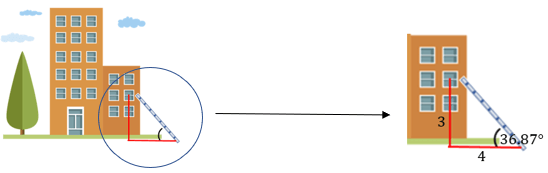
Por Pitágoras: Debes recordar el Teorema de Pitágoras
$$H^2=CO^2+CA^2$$Para efectos de la respuesta, sólo es válida la respuesta positiva $\left(+\right)$, ya que la escalera no esta en dirección bajo tierra.
Por razones trigonométricas: Podemos utilizar alguna de las razones trigonométricas que involucren la hipotenusa $\left(H\right)$.
$$Sen\left(36.87^{\circ}\right)=\cfrac{CO}{H}=\cfrac{3}{H}\\[15pt] Sen\left(36.87^{\circ}\right)=\cfrac{3}{H}\\[15pt] \left(H\right)Sen\left(36.87^{\circ}\right)=3\\[15pt] H=\cfrac{3}{Sen\left(36.87^{\circ}\right)}\\[15pt] H=\cfrac{3}{0.6}$$ $$\color{brown}H=5$$Solución: Lo primero y bien importante, es hacer una gráfica de lo que nos están planteando.
Se deben plantear ecuaciones que involucren los lados que nos están pidiendo, por lo que la más conveniente es la $Tan\;30^{\circ}$ y $Tan\; 60^{\circ}$
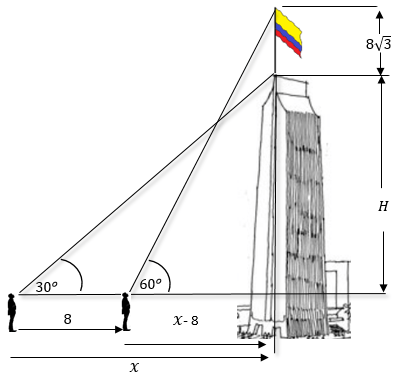
Ahora reemplazamos los valores que se puedan, por el momento la tangente de los ángulos. Se recomienda dejar los valores indicados.
Despejamos la “$x$” o la “$H$” en las ecuaciones (1) y (2), en este ejemplo es más conveniente despejar la “$x$” e igualamos las variables
despejadas.
En la ecuación (1):
$$\cfrac{1}{\sqrt{3}}=\cfrac{H}{x}$$ $$x=\sqrt{3}\cdot H\tag{3}$$En la ecuación (2).
$$\cfrac{\sqrt{3}}{1}=\cfrac{H+8\sqrt{3}}{x-8}$$ $$x-8=\cfrac{H+8\sqrt{3}}{\sqrt{3}}$$ $$x=\cfrac{H+8\sqrt{3}}{\sqrt{3}}+8\tag{4}$$Ahora igualamos las ecuaciones (3) y (4)
$$\sqrt{3}\cdot H=\cfrac{H+8\sqrt{3}}{\sqrt{3}}+8$$ $$3H=H+8\sqrt{3}+ 8\sqrt{3}$$ $$2H=16\sqrt{3}$$ $$\color{brown}H=8\sqrt{3}$$Conociendo la “$H$”, podemos encontrar la “$x$”, reemplazando en la ecuación (3) o (4)
La altura total del edificio es igual a la suma de la estatura de la persona, más la “$H$” encontrada.
$$\text{Altura Edificio}= \sqrt{3}+8\sqrt{3}$$El video realizado por Julio Alberto Ríos Gallego "Julio Profe""Julio Profe" es un autor de la red YouTube, que publicó el video "Problema 3 de trigonometría en triángulos rectángulos"., te servirá para facilitar el entendimiento de la aplicación de las razones trigonométricas, en la solución de problemas en contexto.
Son aquellos triángulos en los que ninguno de sus ángulos es recto, por lo que no se pueden resolver utilizando las identidades Pitagóricas y las identidades trigonométricas.
Para la solución de triángulos oblicuángulos en ejercicios propuestos en este contexto, se debe hacer uso de la Ley del seno y de la Ley del Coseno.
Esta ley, establece la relación existente entre un ángulo determinado y su lado opuesto.
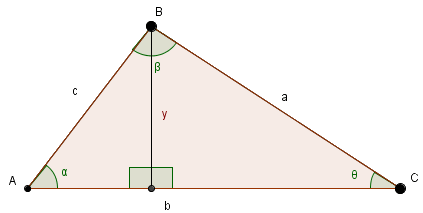
Como los ángulos $\alpha,\beta \wedge \theta$, no son rectos; es necesarios tratar de obtener ángulos rectos en el triángulo $ABC$. Par ello, se trazará una línea imaginaria desde el vértice $B$ a la intersección de la perpendicular con el lado "$b$" y lo llamaremos "$y$".
El $Sen\;\alpha=\cfrac{y}{c}$, si se despeja la "$y$" nos queda:
$$y=c\cdot Sen\;\alpha\tag{1}$$El $Sen\;\theta=\cfrac{y}{a}$, si se despeja la "$y$" nos queda:
$$y=a\cdot Sen\;\theta\tag{2}$$Ahora igualamos las ecuaciones (1) y (2)
$$c\cdot Sen\;\alpha=a\cdot Sen\;\theta$$Reescribiendo de forma equivalente, nos queda:
$$\cfrac{a}{Sen\;\alpha}=\cfrac{c}{Sen\;\theta}$$Si $\cfrac{a}{Sen\;\alpha}=\cfrac{c}{Sen\;\theta}$, se deduce que $\cfrac{b}{Sen\;\beta}$
En conclusión la ley del seno queda de la siguiente forma:
Se recomienda utilizar esta fórmula cuando los interrogantes sean los lados, ya que es más fácil para despejar las incógnitas.
De forma equivalente, se puede escribir la ley del seno como:
Se recomienda utilizar esta fórmula cuando los interrogantes sean los ángulos, ya que es más fácil para despejarlos.
Establece la relación entre los lados que conforman al ángulo y su lado opuesto.
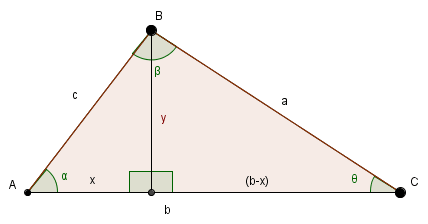
Utilizando el Teorema de Pitágoras:
$$c^2=x^2+y^2\tag{1}$$ $$a^2=y^2+\left(b-x\right)^2\tag{2}$$Resolviendo el cuadrado de un binomio en $\left(b-x\right)^2$ en la ecuación (2) , nos queda:
Reemplazamos el valor de $\left(x^2+y^2\right)$ de la ecuación (1), en la (2).
$$a^2=b^2+c^2-2bx\tag{3}$$Ahora,
$$Cos\;\alpha=\cfrac{x}{c}\tag{4}$$Despejando la $x$ en la ecuación (4) y reemplazando el la (3), se obtiene:
$$x=c\cdot Cos\;\alpha$$ $$a^2=b^2+c^2-2b\cdot c\cdot Cos\;\alpha$$Se puede observar que:
$\bullet\hspace{0.2cm}$El lado opuesto al ángulo $\color{brown}\alpha$, es “$\color{brown}a$” y lo conforman los lados $\color{brown}b \wedge c$
$\bullet\hspace{0.2cm}$El lado opuesto al ángulo $\color{brown}\theta$, es “$\color{brown}c$” y lo conforman los lados $\color{brown}a\wedge b$.
$\bullet\hspace{0.2cm}$El lado opuesto al ángulo $\color{brown}\beta$, es “$\color{brown}b$” y lo conforman los lados $\color{brown}a \wedge c$.
Si queremos hallar $\color{brown}b^2$, observen que los lados que conforman el ángulo $\color{brown}\beta$, son $\color{brown}a \wedge c$, por lo tanto:
Si queremos hallar "$\color{brown}c^2$", observen que los lados que conforman el ángulo $\color{brown}\theta$, son $\color{brown}a\wedge b$, por lo tanto:
Para concluir, la ley del coseno se resume en:
Ley del Coseno:
$$a^2=b^2+c^2-2bc\cdot Cos\;\alpha\\[8pt]b^2=a^2+c^2-2ac\cdot Cos\;\beta\\[8pt]c^2=a^2+b^2-2ab\cdot Cos\;\theta$$ Ejemplos de la ley del Seno y la le del Coseno
Ejemplos de la ley del Seno y la le del CosenoSolución:
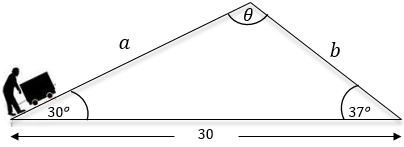
Hacer una gráfica del problema
Recordar que los ángulos internos de un triángulo,
suman $180^{\circ}$, por lo que $\theta=180^{\circ}-30^{\circ}-37^{\circ}$
$$θ=113^{\circ}$$Sabiendo que $\;\theta=113^{\circ}$, se procede aplicar la ley del Seno.
Despejamos $a$:
Despejamos $b$:
Determine:
$\bullet\hspace{0.2cm}$Las distancias rectas desde el avión a cada una de las ciudades en ese momento si la separación entre ambas es de $8.45$ Km.
$\bullet\hspace{0.2cm}$La altura del avión.
$\theta=180^{\circ}-10.2^{\circ}-8.7^{\circ}$
$\theta=161.1^{\circ}$
Sabiendo que $\;\theta=161.1^{\circ}$, se procede aplicar la ley del Seno.
Despejamos $a$:
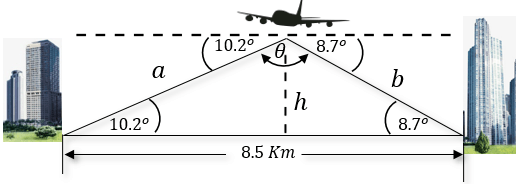
Ahora:
$$\cfrac{8.5}{Sen\;161.1^{\circ}}=\cfrac{b}{Sen\;10.2^{\circ}}$$Despejamos $b$:
$$b=\cfrac{8.5\cdot Sen\;10.2^{\circ}}{Sen\;161.1^{\circ}}\\[8pt] b=4.65$$Para hallar la altura ($h$) del avión, podemos utilizar las razones trigonométricas.
$$Sen\;8.7^{\circ}=\cfrac{h}{b}\\[8pt] Sen\;8.7^{\circ}=\cfrac{h}{4.65}\\[8pt] h=4.65\cdot Sen\;8.7^{\circ}\\[8pt] h=0.70 \;\text{Km}$$El ciclista $A$, parte en dirección noreste a una velocidad de $50 \frac{Km}{h}$
El ciclista $B$, parte en dirección sureste a una velocidad de $40\frac{Km}{h}$
Si se sabe que el ángulo que los separa es de $60^{\circ}$, al cabo de 2.5 horas que distancia los separa?.
Solución:
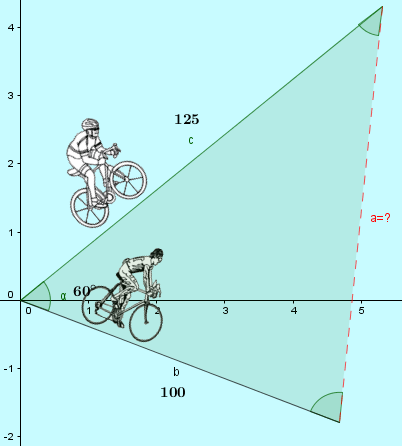
Luego de tener la gráfica de que nos plantean en el ejercicio, es importante analizar los datos. El ciclista “A” parte a una velocidad constante de $50 \;\frac{Km}{h}$, quiere decir que en $2.5$ horas a recorrido $125 Km \left(50 \times 2.5\right)$.
El ciclista “B” parte a una velocidad constante de $40 \;\frac{Km}{h}$, quiere decir que en $2.5$ horas a recorrido $100 Km \left(40 \times 2.5\right)$. Como se solicita la distancia entre los ciclistas al cabo de $2.5$ horas, con un ángulo de separación de $60^{\circ}$, es necesario aplicar la ley del coseno.
Debes recordar que $\;\color{blue}a^2=b^2+c^2-2bc\cdot Cos\;\alpha$.
Reemplazamos los datos que se indican en la gráfica.
$$\color{black}\begin{aligned} D^2 &=125^2+100^2-2\left(125\right)\left(100\right)\cdot Cos\;60^{\circ}\\ &=25.625-{\color{Red}\bcancel {{\color{black}25.000}}}\cdot\cfrac{1}{{\color{Red}\bcancel {{\color{black}2}}}}\\ &= 25.625-12.500\\ &=13.125\\ D &=\pm\sqrt{13.125}\\ &=\pm 114,56 \end{aligned}$$Para la respuesta sólo se toma la parte positiva.
En la siguiente escena interactiva, puedes ingresar la información suministrada en el problema, para que verifiques el resultado.
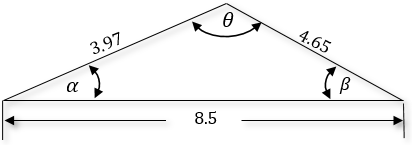
Dado que se tienen los lados, es necesario utilizar la ley del coseno, al menos para encontrar uno de los ángulos
Debes recordar que $\;\color{blue}a^2=b^2+c^2-2bc\cdot Cos\;\alpha$.
$4.65^2=3.97^2+8.5^2-2\left(3.97\right)\left(8.5\right)\cdot Cos\;\alpha\\[8pt] 21.62=15.76+72.25-67.49\cdot Cos\;α\\[8pt] 21.62=88.01-67.49\cdot Cos\;\alpha$Despejamos $Cos\;\alpha$
$67.49\cdot Cos\;\alpha=88.01-21.62\\[8pt] 67.49\cdot Cos\;\alpha=66.39\\[8pt] Cos\;\alpha=\cfrac{66.39}{67.49}\\[8pt] Cos\;\alpha=0.9837\\[8pt] \alpha=Cos^{-1}\left(0.984\right)\\[8pt] \color{brown}\alpha=10.26$Como ya se conoce el ángulo $\alpha$, podemos utilizar la ley del seno para hallar el ángulo $\theta$.
$\cfrac{Sen\;\beta}{3.97}=\cfrac{Sen\;\alpha}{4.65}$Reemplazamos $\alpha$ y despejamos $Sen\;\beta$
$Sen\;\beta=\cfrac{3.97\cdot Sen\;\left(\alpha\right)}{4.65}\\[8pt] Sen\;\beta=\cfrac{3.97\cdot Sen\;\left(10.26\right)}{4.65}\\[8pt] Sen\;\beta=0.152\\[8pt] \beta=Sen^{-1}\left(0.152\right)\\[8pt] \color{brown}\beta=8.74$Teniendo $\alpha\wedge\beta$ y recordando que los ángulos internos de un triángulo suman $180^{\circ}$, podemos encontrar $\theta$.
$\theta=180^{\circ}-10.26^{\circ}-8.74^{\circ}\\[8pt] \color{brown}\theta=161^{\circ}$En la siguiente escena interactiva se presentan cinco ejercicios de la ley del coseno, donde debes calcular la distancia recorrida por el ciclista en cada uno de los casos. Ingresa la información suministrada y verifica los resultados.
Retomamos lo aprendido con el circulo unitario y el teorema de Pitágoras.

Recordemos que la ecuación del círculo unitario es $x^2+y^2=1$, de la cual sacamos conclusiones importantes como:
$Sen\;\alpha=\cfrac{y}{r}=\cfrac{y}{1}=y$, en la que se concluyó que siempre que se mencionen valores en "$y$", se relacionan con el Seno.
$Cos\;\alpha=\cfrac{x}{r}=\cfrac{x}{1}=x$, en la que se concluyó que siempre que se mencionen valores en "$x$", se relacionan con el Coseno.
$Tan\;\alpha=\cfrac{y}{x}=\cfrac{Sen\;\alpha}{Cos\;\alpha}$
Con lo anterior y conociendo que la ecuación del círculo unitario es $x^2+y^2=1$, podemos reemplazar las "$x$" por el coseno y las "$y$" por el seno.
Reemplazando en la ecuación (1), se obtiene:
$$\left(Cos\;\alpha\right)^2+\left(Sen\;\alpha\right)^2=1$$Por lo general esta identidad trigonométrica se encuentra como:
Si se divide la ecuación (1), por $x^2$, se obtiene:
$$x^2+y^2=1\tag{1}$$ $$\cfrac{\color{Red}\bcancel {{\color{black}{x^2}}}}{\color{Red}\bcancel {{\color{black}{x^2}}}}+\cfrac{y^2}{x^2}=\cfrac{1}{x^2}$$Teniendo en cuenta que $Tan\;\alpha=\cfrac{y}{x}$ y que $Cos\;\alpha=x$, de la que se puede concluir que $\cfrac{1}{x}=Sec\;\alpha$, que es la inversa del Coseno, se obtiene:
$$1+\cfrac{Sen^2\:\alpha}{Cos^2\;\alpha}=\cfrac{1}{Cos^2\;\alpha}$$Si se divide la ecuación (1), por $y^2$, se obtiene:
Teniendo en cuenta que $Tan\;\alpha=\cfrac{y}{x}$, entonces $\cfrac{x}{y}=Cot\;\alpha$, que es la inversa de la $Tan\,\alpha$ y que $Sen\;\alpha=y$, de la que se puede concluir que $\cfrac{1}{y}=Csc\;\alpha$, que es la inversa del Seno, se obtiene:
$$\cfrac{x^2}{y^2}+\cfrac{\color{Red}\bcancel {{\color{black}{y^2}}}}{\color{Red}\bcancel {{\color{black}{y^2}}}}=\cfrac{1}{y^2}$$ $$\cfrac{Cos^2\;\alpha}{Sen^2\;\alpha}+1=\cfrac{1}{Sen^2\;\alpha}$$En la siguiente escena interactiva, podrás analizar el paso a paso de la demostración de las identidades trigonométricas de ángulos suma y resta.
Para ello debes identificar el triángulo $\color{orange}\bigtriangleup BOC$ de color naranja y encontrar las razones trigonométricas de seno y coseno. Debes realizar el mismo procedimiento para el triángulo $\color{blue}\bigtriangleup BOC$ de color Azul y el triángulo $\color{red}\bigtriangleup BOC$ de color rojo.
Luego de analizar la escena, podrás concluir que:
A partir de estas dos identidades trigonométricas, se puede calcular $Tan\;\left(\alpha\pm\beta\right)$
En este caso debed reemplazar:
$$Sen\;\left(\alpha\pm\beta\right)$$ $$Cos\;\left(\alpha\pm\beta\right)$$Para encontrar la formula de $Sen\;2\alpha$, en la formula $Sen\;\left(\alpha + \beta\right)=Sen\;\alpha\cdot Cos\;\beta + Cos\;\alpha\cdot Sen\;\beta$, haremos $\alpha=\beta$. Reemplazando nos queda:
Para encontrar la formula de $Cos\;\left(2\;\alpha\right)$, en la fórmula $Cos\;\left(\alpha+\beta\right)=Cos\;\alpha\cdot Cos\;\beta-Sen\;\alpha\cdot Sen\;\beta$, haremos $\alpha=\beta$. Reemplazando nos queda:
$Cos\;\left(\alpha+\alpha\right)=Cos\;\alpha\cdot Cos\;\alpha - Sen\;\alpha\cdot Sen\;\alpha.$Para encontrar la formula de $Tan\;\left(2\;\alpha\right)$, se reemplaza $Sen\;\left(2\,\alpha\right)\;\text{,}\; Cos\;\left(2\,\alpha\right)$ y se divide por $Cos^2\alpha$. Reemplazando y dividiendo, nos queda:
$$\color{black}\begin{aligned} Tan\;\left(2\;\alpha\right)&= \cfrac{Sen\;\left(2\,\alpha\right)}{Cos\;\left(2\,\alpha\right)} \end{aligned}$$ $$=\dfrac {\dfrac {2\cdot Sen\;\alpha\cdot Cos\;\alpha}{Cos^{2}\alpha}}{\dfrac {Cos^2\;\alpha - Sen^2\;\alpha}{Cos^{2}\alpha}}$$ $$=\dfrac {\dfrac {2\cdot Sen\;\alpha\cdot {\color{Red}\bcancel {{\color{black}Cos\;\alpha}}}}{Cos^{{\color{Red}\bcancel {{\color{black}2}}}}\alpha}}{\dfrac {{\color{Red}\bcancel {{\color{black}Cos^2\;\alpha}}}}{{\color{Red}\bcancel {{\color{black}Cos^{2}\alpha}}}} - \dfrac{Sen^2\;\alpha}{Cos^{2}\alpha}}$$En la fórmula $Cos\;\left(2\,\alpha\right)=Cos^2\;\alpha - Sen^2\;\alpha$, expresaremos $Cos\;\left(2\,\alpha\right)$ en términos de $Sen\;\alpha$, haciendo uso de la identidad pitagórica $\;\color{blue}Sen^2\;\alpha+Cos^2\;\alpha=1$, despejamos $Cos^2\;\alpha$.
$$Cos^2\;\alpha=1-Sen^2\;\alpha$$Reemplazamos en,
$$\color{black}\begin{aligned} Cos\;\left(2\,\alpha\right) &= Cos^2\;\alpha - Sen^2\;\alpha\\ &= 1-Sen^2\;\alpha - Sen^2\;\alpha\\ &= 1 - 2Sen^2\;\alpha \end{aligned}$$Despejamos $Sen\;\alpha$
$$\color{back}\begin{aligned} 2Sen^2\;\alpha &= 1 - Cos\;\left(2\,\alpha\right)\\ \end{aligned}$$ $$Sen^2\;\alpha = \dfrac{1 - Cos\;\left(2\,\alpha\right)}{2}$$ $$Sen\;\alpha = \sqrt{\dfrac{1 - Cos\;\left(2\,\alpha\right)}{2}}$$Hacemos un cambio de variable, $\;\alpha=\dfrac{\alpha}{2}$ y reemplazamos.
En la fórmula $Cos\;\left(2\,\alpha\right)=Cos^2\;\alpha - Sen^2\;\alpha$, expresaremos $Sen\;\left(2\,\alpha\right)$ en términos de $Cos\;\alpha$, haciendo uso de la identidad pitagórica $\;\color{blue}Sen^2\;\alpha+Cos^2\;\alpha=1$, despejamos $Cos^2\;\alpha$.
$$Sen^2\;\alpha=1-Cos^2\;\alpha$$Reemplazamos en,
$$\color{black}\begin{aligned} Cos\;\left(2\,\alpha\right) &= Cos^2\;\alpha - Sen^2\;\alpha\\ &= Cos^2\;\alpha -\left(1-Cos^2\;\alpha\right)\\ &= 2Cos^2\;\alpha - 1 \end{aligned}$$Despejamos $Cos\;\alpha$
$$\color{back}\begin{aligned} 2Cos^2\;\alpha &= 1 + Cos\;\left(2\,\alpha\right)\\ \end{aligned}$$ $$\color{black}\begin{aligned} Cos^2\;\alpha &= \dfrac{1 + Cos\;\left(2\,\alpha\right)}{2}\\ \end{aligned}$$ $$Cos\;\alpha = \sqrt{\dfrac{1 + Cos\;\left(2\,\alpha\right)}{2}}$$Hacemos un cambio de variable, $\;\alpha=\dfrac{\alpha}{2}$ y reemplazamos.
Con base en las identidades de seno y coseno de ángulos medios, hallamos la $Tan\left(\cfrac{\alpha}{2}\right)$.
$$\color{black}\begin{aligned} Tan\left(\cfrac{\alpha}{2}\right) &= \dfrac{Sen\;\left(\dfrac{\alpha}{2}\right)}{Cos\;\left(\dfrac{\alpha}{2}\right)}\\[25pt] &= \dfrac{\sqrt{\dfrac{1 - Cos\;\alpha}{2}}}{\sqrt{\dfrac{1 + Cos\;\alpha}{2}}} \end{aligned}$$Utilizando las propiedades de las potencias, se puedes expresar con un sólo radical.
$$\color{black}\begin{aligned} Tan\left(\cfrac{\alpha}{2}\right) &= \sqrt{\dfrac{\dfrac{1 - Cos\;\alpha}{{\color{Red}\bcancel {{\color{black}2}}}}}{\dfrac{1 + Cos\;\alpha}{{\color{Red}\bcancel {{\color{black}2}}}}}}\\[25pt] &=\sqrt{\dfrac{1 - Cos\;\alpha}{1 + Cos\;\alpha}} \end{aligned}$$En la siguiente escena interactiva, se presenta un resumen de los ángulos notables y cuadrantales, con la ayuda de la entrada ángulo "$\alpha$" o utilizando podrás ingresar el valor para el ángulo que desees analizar, además puedes seleccionar las casillas de control, para que recuerdes las formulas vistas en el capítulo y que serán de utilidad en la solución de identidades y ecuaciones trigonométricas.
Recuerda en un punto $P\left(x,y\right)$, las "$x$" corresponden a las razones trigonométricas del coseno y las "$y$" corresponden a las razones trigonométricas del seno.
Para realizar la demostración de una identidad trigonométrica, puedes hacer lo siguiente:
$\bullet\hspace{0.2cm}$Convertir el primer término (derecha) en el segundo término (izquierda).
$\bullet\hspace{0.2cm}$Convertir el segundo término (izquierda) en el primer término (derecha).
$\bullet\hspace{0.2cm}$Convertir los dos términos a la par, hasta llegar a una igualdad.
Siguiendo los siguiente criterios:
En los siguientes ejemplos, se aplican las identidades trigonométricas para realizar las demostración de las identidades trigonométricas propuestas.
 Ejemplos demostración de identidades
Ejemplos demostración de identidades Comprobar las siguientes identidades.
Multiplicamos por la conjugada del numerador.
$$\color{black}\begin{aligned} \cfrac{1-Sen\;\alpha}{Cos\;\alpha}=& \cfrac{Cos\;\alpha}{1+Sen\;\alpha}\\[15pt] \cfrac{1-Sen\;\alpha}{Cos\;\alpha}\cdot\cfrac{1+Sen\;\alpha}{1+Sen\;\alpha}=&\\[15pt] \cfrac{1^2-Sen^{2}\alpha}{Cos^{2}\alpha\cdot\left({1+Sen\;\alpha}\right)}=& \end{aligned}$$Se utiliza la identidad trigonométrica Pitagórica $Cos\;^{2}\alpha +Cos\;^{2}\alpha=1$, se despeja $Cos\;^{2}\alpha$ y se reemplaza
$$Cos\;^{2}\alpha=1-Cos\;^{2}\alpha$$ $$\color{black}\begin{aligned} \cfrac{Cos^{{\color{Red}\bcancel {{\color{black}2}}}}\alpha}{{\color{Red}\bcancel {{\color{black}Cos\;\alpha}}}\cdot\left({1+Sen\;\alpha}\right)}=&\cfrac{Cos\;\alpha}{1+Sen\;\alpha}\\[15pt] \end{aligned}$$Se resuelven los dos cuadrados de un binomio.
$$\color{black}\begin{aligned} \left(Sen\;\alpha+Cos\;\alpha\right)^2+\left(Sen\;\alpha-Cos\;\alpha\right)^2=& 2 \end{aligned}$$Para solucionar esta identidad, lo más conveniente es separar el denominador para cada término de la suma que se tiene en el numerador.
Observa y analiza detenidamente el video realizado por Julio Alberto Ríos Gallego "Julio Profe""Julio Profe" es un autor de la red YouTube, que publicó el video "Demostración de identidades trigonométricas - ejercicio 3"., en el cual se explica la demostración de identidades trigonométricas, paso a paso, que te ayudará a fortalecer los conocimientos.
adquiridos en los ejemplos anteriores y que serán la base para resolver los ejercicios propuestos a continuación.
Es una ecuación que tiene expresiones trigonométricas. Si una ecuación trigonométrica no es identidad, con frecuencia hallamos soluciones mediante el uso de técnicas semejantes a las empleadas para ecuaciones algebraicas. La principal diferencia es que, de la ecuación trigonométrica primero despejamos $Sen\;x$, $Cos\;u$, etcétera y luego hallamos valores de $x \vee u$ que satisfagan la ecuación.
Lo que significa que si $Sen\;30^{\circ}=\cfrac{1}{2}$, en caso de tener una ecuación $Sen\;x=\cfrac{1}{2}$, para encontrar el valor de $x$ se debe calcular:
$$Sen^{-1}\left(\cfrac{1}{2}\right)=x$$ $$\hspace{0.2cm}x=\begin{cases}\color{black}30^{\circ}\\\color{black} \cfrac{\pi}{6}\end{cases}$$Para dar la respuesta final, se deben buscar todos los ángulos que cumplan esta condición, lo que quiere decir que si no se limita un rango, es necesario girar infinitas veces sobre el vértice del ángulo, siendo NV=Número de vueltas o giros. Esto es:
$$\hspace{0.2cm}x=\begin{cases}\color{black}30^{\circ}+NV\left(360^{\circ}\right)=\cfrac{\pi}{6}+NV\left(2\pi\right)\\\color{black} 150^{\circ}+NV\left(360^{\circ}\right)=\cfrac{5\pi}{6}+NV\left(2\pi\right)\end{cases}$$Observa y analiza detenidamente el video “Ecuaciones trigonométricas - ejercicio 3 (parte 1 de 2)”, realizado por Julio Alberto Ríos Gallego "Julio Profe", en el cual presenta la solución, paso a paso una ecuación trigonométrica, que te servirá de base para entender los siguientes ejemplos propuestos.
 Ejemplos de ecuaciones trigonométricas
Ejemplos de ecuaciones trigonométricasPara facilitar las respuestas y si se trata de ángulos notables o cuadrantales, te recomiendo utilizar la siguiente escena interactiva que te presenta un resumen de las fórmulas y los resultados de los ángulos en los diferentes cuadrantes, con sus signos respectivos. Esta escena es la misma utilizada en la sección anterior.
Lo primero que debes hacer es buscar el triángulo rectángulo, cuyo uno de sus lados sea $\sqrt{3}$. Puedes hacer uso de la escena interactiva.
Se trata del triángulo rectángulo de $30^{\circ}$.
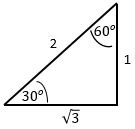
Conociendo esto, podemos dividir toda la ecuación por dos (2) y reescribir la ecuación como:
Reemplazamos $\cfrac{\sqrt{3}}{2}$ y $\cfrac{1}{2}$, por su equivalencia en el triángulo rectángulo.
$$Cos\;30^{\circ}\cdot Sen\;x+Sen\;30^{\circ}\cdot Cos\;x=\cfrac{1}{2}$$Observen que se tiene la identidad de trigonométricas de ángulos suma y resta.
Reemplazamos.
$$Sen\;\left(30^{\circ}+x\right)=Sen\;30^{\circ}\cdot Cos\;x + Cos\;30^{\circ}\cdot Sen\;x=\cfrac{1}{2}$$ $$Sen\left(30^{\circ}+x\right)=\cfrac{1}{2}$$Podemos hacer un cambio de variable, sea $a=30^{\circ}+x$.
Reescribimos:
$$Sen\;\left(a\right)=\cfrac{1}{2}$$El seno es positivo y $a=30^{\circ}$, esto significa que el ángulo está en el primer (I) cuadrante y su equivalente $a=150^{\circ}$ está en el segundo (II) cuadrante.
$$a=\hspace{0.2cm}\begin{cases}\color{black}30^{\circ}\\\color{black} 150^{\circ}\end{cases}$$Luego:
$$30^{\circ}+x=\hspace{0.2cm}\begin{cases}\color{black}30^{\circ}\\\color{black} 150^{\circ}\end{cases}$$Para el ángulo de $30^{\circ}$:
$$30^{\circ}+x=30^{\circ}$$ $$x=30^{\circ}-30^{\circ}$$ $$x=0^{\circ}\vee 360^{\circ}$$Para el ángulo de $150^{\circ}$:
$$30^{\circ}+x=150^{\circ}$$ $$x=150^{\circ}-30^{\circ}$$ $$x=120^{\circ}$$Utilizamos la fórmula de ángulos dobles:
Sacamos factor común
$$Sen\;x\left(2Cos\;x- 1\right)=0$$Se iguala cada factor a cero
$$Sen\;x=0$$ $$x=Sen^{-1}\left(0\right)$$ $$\hspace{0.2cm}\color{black}x=\begin{cases}0^{\circ}+NV\left(360^{\circ}\right)=0+NV\left(2\pi\right)\\\color{black}360^{\circ}+NV\left(360^{\circ}\right)=2\pi+NV\left(2\pi\right)\end{cases}$$La respuesta final sería:
Observa que $\;2x+60^{\circ}$ , es el doble de $\;x+30^{\circ}$. Se puede sacar factor común entre $2x+60^{\circ}\wedge x+30^{\circ}$.
Para mayor facilidad se hace un cambio de variable, sea $\;a=x+30^{\circ}$. Se reescribe la ecuación:
Se utiliza la formula de ángulos dobles.
Se saca factor común y se iguala cada factor a cero.
$$Sen\;α\left(2\cdot Cos\;α+1\right)=0$$Para $\;Sen\;α=0$:
$$Sen\;α=0$$ $$a=Sen^{-1}\left(0\right)$$ $$\hspace{0.2cm}\color{black}a=\begin{cases}0^{\circ}+NV\left(360^{\circ}\right)=0+NV\left(2\pi\right)\\\color{black}360^{\circ}+NV\left(360^{\circ}\right)=2\pi+NV\left(2\pi\right)\end{cases}$$Para $\;2\cdot Cos\;α+1=0$:
$$Cos\;α=-\cfrac{1}{2}$$ $$a=Cos^{-1}\left(-\cfrac{1}{2}\right)$$Ahora se hace el cambio de variable, para cada uno de los valores de $\color{brown}\;a=x+30^{\circ}$.
Para $a=0^{\circ}$:
$$\;0^{\circ}=x+30^{\circ}$$ $$\;x=-30^{\circ}$$Para $a=360^{\circ}$:
$$\;360^{\circ}=x+30^{\circ}$$ $$\;x=330^{\circ}$$Para $a=120^{\circ}$:
$$\;120^{\circ}=x+30^{\circ}$$ $$\;x=90^{\circ}$$Para $a=240^{\circ}$:
$$\;240^{\circ}=x+30^{\circ}$$ $$\;x=210^{\circ}$$La respuesta final sería:
En las siguientes escenas interactivas, adaptadas de Juan Guillermo Rivera, podrás resolver los ejercicios planteados sobre inecuaciones y problemas de trigonometría, para pongas a prueba tus conocimientos.
En cada escena interactiva dispones de 45 minutos para realizar los ejercicios e ir eligiendo la respuesta correcta en el cuestionario. Al finalizar tendrás la posibilidad de ingresar tu nombre y enviar las respuestas a tu docente ingresando su correo en el espacio destinado para ello.
Al solucionar los ejercicios propuestos en las escenas interactivas, estarás en capacidad de resolver los ejercicios propuestos para el capítulo 5.
Opción 1. Inecuaciones y trigonometría.
Opción 2. Inecuaciones y trigonometría.
Opción 3. Inecuaciones y trigonometría.