La fórmula más bella.
Pedro Roses Amat
Red Educativa Digital Descartes
Fondo Editorial RED Descartes

Córdoba (España)
2022.
Título de la obra: La fórmula más bella
Primera edición junio 2022
Autor: Pedro Roses Amat
Ingeniero de Caminos, Canales y Puertos
rosesamat.pedro@gmail.com
Código JavaScript para el libro: Joel Espinosa Longi, IMATE, UNAM.
Recursos interactivos: DescartesJS y GeoGebra
Recursos GeoGebra con la colaboración de Bernat Ancochea Millet.
Fuentes: Lato y UbuntuMono
Fórmulas matemáticas: $\KaTeX$
Red Educativa Digital Descartes
Córdoba (España)
descartes@proyectodescartes.org
https://proyectodescartes.org
Proyecto iCartesiLibri
https://proyectodescartes.org/iCartesiLibri/index.htm
https://prometeo.matem.unam.mx/recursos/VariosNiveles/iCartesiLibri/
ISBN: 978-84-18834-41-7
En 1988, los lectores de la revista The Mathematical Intelligencer votaron la fórmula de Euler como «la más bella fórmula matemática de la historia». En total, Euler fue el responsable de tres de las cinco primeras fórmulas del resultado de la encuesta.
The Mathematical Intelligencer es una revista matemática cuyo objetivo es disertar sobre matemáticas en un tono coloquial y didáctico, alejado del tono técnico y especializado más común entre este tipo de revistas. Fue fundada por los matemáticos Bruce Chandler y Harold Edwards Jr. Empezó a publicarse en 1979.
Este libro es un recorrido por el siglo más brillante de las matemáticas, desde la publicación de la primera tabla de logaritmos por Napier en 1614, hasta la “Introductio in analysin infinitorum” de Euler en 1745, donde aparece por primera vez la identidad que da título a este libro. La identidad, tal como la escribió Euler por primera vez, tenía este aspecto:
$$e^{\sqrt-1\ π}=-1 $$Euler, 45 años más tarde, emplea $i$ como símbolo de la unidad imaginaria y la expresión queda de esta forma:
$$e^{iπ}=-1$$Hoy en día, esta identidad se acostumbra a expresar tal como lo hemos hecho en la portada, para hacer aparecer el $0$ y el $1$, los elementos neutros de la suma y la multiplicación y de esta forma reunir en una única expresión cinco de los números más relevantes de las matemáticas.
$$e^{iπ}+1=0$$La unidad imaginaria $i$ establece un puente entre la geometría, representada por $π$, el análisis, representado por $e$ y las operaciones aritméticas más básicas, representadas por el $0$ y el $1$. Antes de su descubrimiento no se sospechaba una relación tan sencilla entre todos ellos.
La belleza que se atribuye a esta fórmula no se fundamenta en los símbolos que intervienen, ni en su grafismo que ha ido variando en el tiempo. Es una forma de belleza que no estamos acostumbrados a reconocer y valorar, pero que nos descubre la profunda armonía de las matemáticas con la naturaleza.
Las tablas de logaritmos son, hoy en día, algo verdaderamente anticuado pero sin ellos no existiría la “Spira mirabilis”, la espiral maravillosa, omnipresente en la naturaleza. ¿No son bellos los logaritmos?
Si Newton descubre las leyes que nos explican el movimiento de los planetas y de las estrellas, ¿podemos decir que sus fórmulas son tan bellas como el cielo que describen?
Describir el lenguaje de las cosas y alcanzar la comprensión de sus símbolos fue el empeño de los personajes de nuestro libro y, gracias a su prodigiosa intuición, la belleza está hoy más cerca de nuestro alcance.
El siglo XVII en Europa es un siglo de pestes y guerras que provocaron grandes hambrunas y un gran retroceso de la población. En este contexto de profunda crisis social y económica, el siglo nos dejara en herencia el arte barroco y lo que hoy reconocemos como el primer gran estilo musical europeo, con músicos como Johan Sebastián Bach, Georg Friedrich Handel, o Antonio Vivaldi.
El siglo XVII es también el siglo de oro de las matemáticas, que avanzan en estos 100 años, pese a las circunstancias sociales adversas, más de lo que los griegos habían producido en un milenio. Esto se explica, en parte, por la difusión de la educación en Europa y por el intercambio de información entre los matemáticos de Inglaterra, Francia Alemania, Italia… que estimularon nuevos esfuerzos, pero también, y sobre todo por la aparición de personalidades geniales e irrepetibles.
Los principales matemáticos del siglo son muy conocidos. Citados por orden cronológico, Descartes (René Descartes, 1596-1650 ) es el primero de ellos. Contemporáneo suyo es Fermat (Pierre de Fermat, 1607-1665), Príncipe de las Matemáticas. A ambos se debe la introducción del álgebra para la resolución de problemas geométricos, lo que dará lugar a lo que hoy llamamos geometría analítica.
La figura cumbre de esta época es sin duda Newton (Isaac Newton,1643-1727). Sus aportaciones a la física y a la matemática han sido la base sobre la que se ha construido la ciencia hasta el siglo XX. La invención, independiente y prácticamente simultánea, del cálculo diferencial e integral por Newton y Leibniz (Gottfried Leibniz, 1646-1716) es la aportación más importante a las matemáticas de este siglo.

Euler (Leonhard Paul Euler,1707-1783) nació al inicio del siglo XVIII. La música de su tiempo es la de Johan Emanuel Bach, hijo de Johan Sebastián Bach, porque es seguro que no llego a escuchar a Mozart, cincuenta años más joven.
En España, la muerte en 1700 sin descendencia de Carlos II es el final del largo declive de los Austrias y el preludio de la guerra de sucesión. Francia se convierte en la potencia dominante en Europa. Es el siglo de la ilustración y de la enciclopedia de Voltaire, que acabará trágicamente con el cataclismo de la revolución Francesa y las guerras Napoleónicas.
Euler es sin duda el matemático más original de su siglo y el más prolífico de todos los tiempos, que pertenece a la generación de matemáticos que se ocuparon del desarrollo del Cálculo, pues aunque Newton y Leibniz habían puesto las bases, quedaba mucho por hacer. Junto con Euler, destacan en esta labor diferentes miembros de la saga Bernoulli, un caso singular en la historia de matemáticos de primer nivel pertenecientes todos ellos a la misma familia. Euler fue discípulo de Johan y compañero de clase y amigo de Jean y Daniel Bernoulli.
La productividad matemática de Euler es increíble. Sus principales campos de interés fueron el cálculo infinitesimal, las ecuaciones diferenciales, la geometría analítica de curvas y superficies, la teoría de números, las series y el cálculo de variaciones aplicando todo ello a los problemas de la física en los que se ocupó. Difícilmente podemos encontrar una materia alejada de sus intereses científicos.
En particular, aquí resaltamos su labor de sistematización y divulgación del Cálculo infinitesimal recién “inventado”. Sus libros “Introductio in analysin infinitorum” (1745), de cálculo diferencial “Institutiones Calculi Differentialis “(1765) y de cálculo integral, “Institutiones Calculi Integralis” (1768-1770) son los primeros que dan forma a lo que hoy entendemos como matemáticas “clásicas” y se convierten en los libros de referencia para la divulgación y el aprendizaje de lo que, desde entonces, se llamara análisis.
La identidad de Euler establece una relación entre cinco números. El “$0$” el “$1$” y otros tres representados por letras $π$, $i$ y $e$. La elección de estas letras para designar estos números “especiales” se debe a Euler que las fue incorporando progresivamente a la notación de sus escritos.
La geometría clásica conocía perfectamente que el resultado de la división de la longitud de una circunferencia y su diámetro, o del área de un círculo y el cuadrado de su radio, era una constante “inconmensurable”, es decir, no podía expresarse mediante una fracción, porque no existe una unidad de medida común para la longitud de la circunferencia y su radio. En consecuencia, el resultado de esta división se desarrolla en un número infinito de números decimales. La letra $π$ para designar abreviadamente esta constante, la usa por primera vez, en 1706, William Jones (1675-1749), pero cuando Euler la utiliza en la “Introductio” se generaliza su uso a partir de 1748.
El caso de $i$ es muy diferente. Aparece, bajo la forma de $\small{\sqrt{-1}}$, en Italia, al intentar Rafael Bombelli resolver, en 1572, ecuaciones de tercer grado.
Dado que se pueden aplicar a $\small{\sqrt{-1}}$ las reglas del álgebra, $\small{\sqrt{-1}}$ es aceptado como número, con una componente de misterio, puesto que no se alcanza a entender su significado. Euler en una fecha tardía, para simplificar la notación, llama $i$ a este número cuyo cuadrado es $-1$. El número $i$ esta al margen de los números reales y no será identificado como la “unidad imaginaria” hasta la definición por Gauss, en 1831, de los números complejos.
Como vemos, tanto $π$ como $i$, tienen una historia que merece ser protagonista de un libro como este, pero en nuestro caso nos vamos a centrar en la historia del número $e$.
El número $e$, es un perfecto desconocido a principios de siglo XVII y se convierte, a partir de su descubrimiento, en el número más omnipresente de las matemáticas. Decimos “descubrimiento” porque $e$ no fue buscado activamente, su aparición es en cierto modo una sorpresa. Una sorpresa, como la del caminante que llega inesperadamente a un cruce de caminos que no esta en el mapa.
El mapa de las matemáticas del siglo XVII puede recorrerse en varias direcciones. Una de las direcciones principales es el camino hacia la progresiva definición del concepto de función.
Al inicio de este periodo el concepto de función no estaba identificado en el campo matemático. La palabra “función” aparece publicada por primera vez en un artículo de Leibniz de 1692 en la que da también la primera definición del concepto.
Las curvas algebraicas de Descartes, definidas como el lugar geométrico de los puntos del plano que satisfacen una ecuación de dos variables, son la primera aproximación de lo que acabará siendo una función.
Newton, requiere de las matemáticas para sustentar su descripción del movimiento no uniforme y su teoría de la gravitación universal y en general para la descripción de la naturaleza.
Para describir la naturaleza Newton tiene la certera intuición de que las leyes de la física no solo dependen de magnitudes “fluentes”, es decir, que varían en función de otras, sino también de sus “fluxiones” que son sus variaciones “instantáneas”. De esta manera establece un vinculo entre la evolución del concepto de función y la invención del cálculo.
La invención del cálculo es el segundo eje que define el avance de las matemáticas del siglo con la introducción de los infinitesimales y de las series infinitas que recurren a razonamientos basados en el infinito , ya sea por la división de los problemas en elementos “infinitamente pequeños” o por obtener resultados finitos de “sumas infinitas”, lo que en principio parece algo difícil de ejecutar, o al menos de acabar de ejecutar, en un tiempo finito.
Cuando Newton publica el teorema del binomio, generalización del procedimiento que empleamos para multiplicar binomios de exponentes enteros, para los casos de exponente negativo o fraccionario, obtiene una expresión algebraica que se desarrolla en infinitos términos. Por este camino, aparecen en el mapa las funciones trigonométricas definidas mediante series infinitas. El teorema del binomio pasa a ocupar un lugar central en la definición de nuevas funciones. Leibniz llama a estas funciones, de infinitos términos, trascendentes.
En la “Introductio”, Euler estudia la función exponencial y su relación con la logarítmica y obtiene el desarrollo en una serie infinita de ambas funciones, completando así el catálogo de funciones trascendentes elementales.
Como hemos dicho $e$ es un cruce de caminos: la función exponencial en base $e$, $\small{y = e^x}$, adquiere la propiedad especial de ser igual a su derivada. Los logaritmos en base e resultan ser los logaritmos naturales, que se obtienen integrando la hipérbola $x \cdot y=1$.
Y entonces, en el capítulo siguiente de la “Introductio”, se precipita el final de nuestra historia.
Euler partiendo de las fórmulas conocidas por la geometría clásica para el seno y el coseno de la suma de ángulos, es capaz de ver que las relaciones trigonométricas de la antigüedad y el recién descubierto número $e$ se entrelazan en una expresión sencilla, insospechada. El número oculto durante siglos de historia aparece sin hacer ruido y trae de la mano la fórmula más bella. Nada de esto estaba en la hoja de ruta. La ciencia no solo avanza con esfuerzo e imaginación, también con fortuna.
Vamos a exponer nuestro historia desde el punto de vista de los protagonistas, intentando resaltar sus grandes dosis de intuición e imaginación, asociadas a una capacidad de cálculo asombrosa, si tenemos en cuenta los medios de los que disponían. Al situarnos en este punto de vista subjetivo podemos decir que nuestra narración se asemeja en parte a una novela.
El orden cronológico del texto produce una falsa apariencia de objetividad, porque es muy difícil establecer la prioridad de muchas aportaciones clave. La atribución de los avances es, en cierta medida, una convención, que la perspectiva histórica ha ido consolidando. Hay que tener en cuenta que en la época la difusión de los avances era muy lenta y en gran parte basada en correspondencia privada entre los protagonistas. El ejemplo más extremo de esto lo tenemos en el caso de Fermat, cuyas escritos se publicaron por su hijo después de su muerte.
Además de ser cronológico y en cierta medida subjetivo, nuestro relato no tiene la pretensión de ser históricamente exhaustivo. No podemos describir todos los avances de esta época, sino que nos centramos en las contribuciones que llevan a la fórmula que da título al libro.
En conclusión, nuestro libro no es un libro de texto. Nuestro objetivo es una presentación intuitiva de los problemas y hacerlos comprensibles para lectores con conocimientos matemáticos básicos.
Para conseguir este objetivo de claridad nos ayudamos de las ilustraciones dinámicas de GeoGebra, que nos dan la oportunidad de visualizar las funciones y los conceptos. Nuestra ventaja es que gran parte del contenido se refiere a funciones que pueden ser representadas como curvas en el plano.
En los libros de texto el orden de la exposición esta subordinado a la definición progresiva y rigurosa de los conceptos y no coincide con la cronológica que nosotros seguimos. Para ayudar a relacionar ambas visiones, intercalamos en el texto notas que exponen conocimientos anteriores a la época o nos orientan hacia el futuro, lo que nos permite apreciar en cada caso la relevancia de las aportaciones que describimos.
La formación y evolución del concepto de función lo desarrollamos al margen del texto principal en cinco apuntes que se corresponden con la progresiva aproximación al concepto actual.
Una advertencia final. Sócrates le decía a Agatón en el banquete:
Viendo como otro pinta no nos haremos pintores, solo nos podremos contagiar de su pasión creativa, de la ilusión por adquirir su habilidad.
Del mismo modo, para el aprendizaje de las matemáticas, es una gran error creer que leyendo un texto y su primera comprensión podemos prescindir del esfuerzo personal imprescindible para dominar la materia. Nuestra intención es introducir al lector y al estudiante en lo que se consideran, a nuestro juicio injustamente, asuntos de difícil comprensión, pero el resultado, si se quiere dominar la materia, será siempre insuficiente, si no se apoya en el esfuerzo personal y en la práctica.
Al inicio del siglo XVII dos matemáticos, Napier y Descartes, con la publicación de una sola obra cada uno de ellos, impulsan decisivamente el desarrollo de las matemáticas de su tiempo. Son dos obras de diferente calado, pero igualmente innovadoras, porque introducen ideas originales que abren caminos inexplorados hasta la fecha. Mientras que la invención de los logaritmos es un idea práctica, de utilidad inmediata, la propuesta de Descartes es la propuesta de un filosofo y se dirige al fundamento mismo de las matemáticas provocando un verdadero cataclismo. Dos chispas de genialidad que inician la explosión de nuevas ideas que vendrán detrás.
 John Napier publica en 1614 “Mirifici logarithmorum canonis descriptio” (descripción del maravilloso canon de los logaritmos), la primera tabla de logaritmos, a cuyo cálculo consagró veinte años de su vida. Los logaritmos nacen como una tabla de multiplicar para ayudar en los cálculos astronómicos y se convertirán, en un corto espacio de tiempo, en una de las funciones centrales de las matemáticas.
John Napier publica en 1614 “Mirifici logarithmorum canonis descriptio” (descripción del maravilloso canon de los logaritmos), la primera tabla de logaritmos, a cuyo cálculo consagró veinte años de su vida. Los logaritmos nacen como una tabla de multiplicar para ayudar en los cálculos astronómicos y se convertirán, en un corto espacio de tiempo, en una de las funciones centrales de las matemáticas.
 La segunda chispa genial es “La Géométrie” de René Descartes de 1637, que es uno de los apéndices de su obra filosófica ”El discurso del Método” (Discours de la méthode pour bien conduire la raison, et chercher la vérité dans les sciences). Descartes propone en “La Géométrie” la resolución de los problemas geométricos mediante el álgebra y la identificación de las curvas con las ecuaciones algebraicas que las describen. Asistimos al nacimiento de la Geometría Algebraica, es decir, el enfoque mediante el álgebra de los problemas geométricos.
La segunda chispa genial es “La Géométrie” de René Descartes de 1637, que es uno de los apéndices de su obra filosófica ”El discurso del Método” (Discours de la méthode pour bien conduire la raison, et chercher la vérité dans les sciences). Descartes propone en “La Géométrie” la resolución de los problemas geométricos mediante el álgebra y la identificación de las curvas con las ecuaciones algebraicas que las describen. Asistimos al nacimiento de la Geometría Algebraica, es decir, el enfoque mediante el álgebra de los problemas geométricos.
Descartes desencadena una verdadera revolución al establecer el álgebra como la disciplina matemática principal por encima de la geometría, que desde Euclides, era el ejemplo de método científico, construido sobre axiomas, postulados y demostraciones. El álgebra carece en ese momento de la solidez necesaria para soportar este rol y en consecuencia la revolución algebraica socava esta tradición milenaria de rigor, en el momento en que la matemáticas se ven obligadas a avanzar y ser útiles para responder a los requerimientos de las ciencias y en particular de la física. Como consecuencia de esto:
Este es el encanto del siglo de oro de las matemáticas. Su espíritu contrasta con la manera como se nos presentan hoy académicamente, en su versión “corregida”, que se alcanzará más de un siglo después de la mano de Cauchy (Augustin-Louis Cauchy, 1789-1857), Kart Weierstrass (1815-1897), y Bernhard Riemann (1826-1866), entre otros muchos, que se ocuparan de la formulación rigurosa de los avances que vamos a describir.
La aritmética elemental nos enseña que:
$$ a^{{x+y}}= a^{x} \cdot \: a^{y} $$
y esta propiedad de la multiplicación de potencias de un número establece una correspondencia entre la serie aritmética de los exponentes y la serie geométrica de los valores de las potencias de $a$.
Si tenemos un número cualquiera $N$ podemos calcular la $x$ para que $\small{a^{x}=\: N}$. Lo mismo para $S$, obtenemos un valor $\small{a^{y}=\: S}$.
Luego sustituyendo: $ a^{x+y}= a^{x} \cdot \: a^{y} = N\cdot \: S $
Veamos un ejemplo:
| $2^x$ | x |
|---|---|
| 1 | 0 |
| 2 | 1 |
| 4 | 2 |
| 8 | 3 |
| 16 | 4 |
| 32 | 5 |
| 64 | 6 |
| 128 | 7 |
| 256 | 8 |
| 512 | 9 |
| .... | n |
Hagamos una tabla con una columna para cada una de las series, para el caso en el que $\small{{a= 2}}$
Para multiplicar dos números de la primera columna, buscamos su correspondiente en la segunda y los sumamos. Buscando en la segunda columna el número suma, obtenemos el resultado de la multiplicación en la primera columna.
Si tenemos una tabla de dos columnas ya calculada de los valores de $\small{N=a^x}$, con $N$ en la primera columna y el valor de $x$ en la segunda, para multiplicar $N · S$ hacemos como en el ejemplo anterior, buscamos en la primera columna el número $N$ y obtenemos $x$. Buscamos el número $S$ y obtenemos $y$. Sumamos $x+y$ y buscamos en la segunda columna hasta encontrar en la primera columna el resultado de $S · N$.
Hemos reducido una multiplicación a una suma, pero nos queda calcular todos los valores de la tabla. Si queremos ofrecer una tabla en la que los números estén representados y espaciados entre si de forma uniforme para conseguir el resultado deseado, necesitamos recurrir a exponentes racionales y extender la operación definida para números naturales a un espectro de números más amplio o a elegir una base muy próxima a $1$.
Las reglas del álgebra permiten la generalización a exponentes fraccionarios puesto que sabemos que $a^{1\over n}=\sqrt[n]{a}$. Para exponentes negativos resulta $\,a^{-n}= {1\over{\normalsize{a^n}}}$, puesto que $a^n \, a^{-n} = a^n \,{ 1\over{\normalsize{a^n}}} =\small{1} = \small{a^0}$.
No existe, en este momento, una definición para números irracionales de infinitos decimales, aunque se puede suponer que podemos acotar su valor entre dos números racionales próximos.
El interés en los logaritmos obedece a un objetivo práctico concreto, simplificar los cálculos, especialmente la multiplicación y la división.
Su aparición es anterior a las primeras aproximaciones al concepto de función, por lo que los esfuerzos de sus inventores se orientan hacia la obtención de tablas cada vez más precisas, sin atender a su estudio como función ni a su relación con la exponencial, a pesar de que ambas se relacionan directamente como operaciones inversas.
Nada parece señalar que van a convertirse, como veremos a lo largo de nuestro relato, en funciones estrechamente vinculadas a la invención y evolución del cálculo.
Desde su introducción, las tablas de logaritmos han sido extraordinariamente útiles hasta fechas muy cercanas.
En el siglo XIX los ingenieros de la revolución industrial utilizaron un instrumento que se conoce como regla de cálculo, que consiste en una regla graduada con una escala logarítmica, para ejecutar cálculos rutinarios.

Regla de cálculo FABER CASTELL 67/54r Addiator de 1957.
Al final del siglo XX, las calculadoras de sobremesa y los ordenadores se han encargado de hacer el trabajo de forma rápida y segura dejando obsoletas las reglas de cálculo.

Texas Instruments fue pionera en los circuitos integrados para calculadoras y suministró el conjunto de chips para Canon Pocketronic de 1970, una de las primeras calculadoras portátiles.
| $(1-10^7)^x$ | x |
|---|---|
| 1 | 0 |
| 0,9999999 | 1 |
| 0,9999998 | 2 |
| 0,9999997 | 3 |
| 0,9999996 | 4 |
| 0,9999995 | 5 |
| 0,9999994 | 6 |
| 0,9999993 | 7 |
| ..... | ..... |
| 0,9999990 | 10 |
| ..... | ..... |
| 0,9999900 | 100 |
| ..... | ..... |
| 03678794 | $10^7$ |
Napier es el primero en ponerse manos a la obra y publica la primera tabla de logaritmos. También es el inventor de la palabra logaritmo, componiendo las palabras griegas logos (razón) y arithmos (número).
La tabla de logaritmos de Napier tuvo un éxito inmediato y, junto con otras tablas semejantes, empezó a usarse de forma generalizada, para ayudar a los astrónomos en sus farragosos cálculos y a los marinos a situarse en alta mar.
Napier propuso para sus tablas una base un poco inferior a 1, igual a:
$ \bigg(1-{\large {1\over 10^7}}\bigg)=\small{0,9999999}$
para que los valores calculados con exponentes sucesivos, resultaran próximos. El cálculo de sus tablas consiste, por tanto, en multiplicar repetidamente $\small{0,9999999}$ por si mismo.
Napier multiplica el resultado por $\small{10^7}$ para eliminar los decimales, con lo que finalmente sus logaritmos responden a la expresión $ 10^7{(1-{\large {1\over 10^7}})}^x$, donde $x$ es el logaritmo de $y$.
El logaritmo de $\small{10^7}$ es 0, y el de $ 10^7\bigg(1-{\large {1\over 10^7}}\bigg)=\small{9.999.999}$, es $1$.
La diferencia más notable entre los logaritmos de Napier y los “actuales” consiste en que, al multiplicar los logaritmos por $\small{10^7}$, la fórmula habitual para la multiplicación resulta alterada.
Si:
${L_1=log\: N_1} \:\:\Lrarr \:\:{N_1=10^{7}(1-10^{-7})^{L_1}}$
${L_2=log\: N_2} \:\:\Lrarr \:\:{N_2=10^{7}(1-10^{-7})^{L_2}}$ ,
Resulta que:
${N_1\cdot N_2= 10^7.10^7 (1-10^{-7})^{(L_1+L_2)}}$
y por tanto la suma de los logaritmos no sera el logaritmo de ${\small N_1\cdot N_2}$ sino el de $\;\large{{ N_1 \cdot N_2}\over{10^7}}$.
Análogamente si, $\;{\small L=log\;N}$, entonces, $\;{\small n \cdot L}= {\large{log \:N^{n}}\over {10^{7(n-1)}}}$.
Estas diferencias no son demasiado importantes pues solo suponen el corrimiento de la coma decimal , según los casos.
John Briggs (1617) se da cuenta de las ventajas de utilizar como base de los Logaritmos el número 10 porque era uno de los impulsores de la notación decimal que, en esos años, muchos matemáticos están proponiendo, para unificar la escritura de los números enteros y de los fraccionarios y también para unificar el sistema de pesos y medidas. El uso de la coma, que hoy nos parece natural para separar las potencias de 10 positivas y negativas, en la época representó un gran avance práctico, generalizando para los números racionales los procedimientos de cálculo de las operaciones básicas.
El sistema decimal para las unidades físicas de longitud, superficie y volumen tardará aún en imponerse, hasta la famosa adopción del metro en Paris, por 17 países en 1875.
En base 10, al mover la coma decimal de un número a izquierda o derecha, el logaritmo de ese número disminuye o aumenta en la unidad. (Multiplicar por diez es sumar al $log N$ el $log 10$, que es $1$ en base $10$).
Calculando logaritmos para los números entre $1$ y $10$, ($log_{10} 1=0$ a $log_{10} 10=1$) tenemos toda la tabla completa sumando al logaritmo la potencia de $10$ correspondiente.
Por ejemplo, si hemos calculado, $log_{10}\:\small{1,2}\: =\: \small{0,07918}$,
el $log_{10}\:\small{12}$ sera: $\small{1,07918}$
$log_{10}\:\small{12}= log_{10} \small{(1,2 \cdot10)}= log_{10}\small{1,2}+ log_{10}\small{10}= log_{10}\small{1,2}\:+\small{1} $
y el de $log_{10}\:\small{120}$ sera: $\small{2,07918}$
$log_{10}\:\small{120}= log_{10} \small{(12 \cdot 10)}= log_{10}\small{12}\:+\: log_{10}\small{10}= log_{10}\small{12}\:+\:\small{1} $
| x | $log_{10}x$ | |
|---|---|---|
| $10^{\large 1\over2}$ | 3,16227766 | 0,5 |
| $10^{\large 1\over4}$ | 1,77827941 | 0,25 |
| $10^{\large 1\over8}$ | 1,3335214 | 0,125 |
| $10^{\large 1\over16}$ | 1,15478198 | 0,0625 |
| $10^{\large 1\over32}$ | 1,07460782 | 0,03125 |
| ..... | ..... | ..... |
Briggs calcula su tabla empezando por la raíz cuadrada de $10$, ($10^{1\over 2}= \small{3,162277}$), es decir, obtiene el número cuyo logaritmo es $1\over 2$.
En el siguiente paso, calcula la raíz cuadrada del número anterior,
$\small{3,162277}^{1\over2}= {(\small{10}^{1\over2})}^{1\over2}= \small{10}^{1\over4}=\small{1,77828}$
y por lo tanto, ${1\over4}$ es el log10 de 1,77828.
Por este procedimiento obtiene una primera tabla, extrayendo sucesivamente la raíz cuadrada del resultado anterior. Una vez calculada esta primera tabla de números decrecientes, puede obtener los logaritmos que corresponden a sus potencias. De esta manera obtiene el logaritmo de nuevos números, completando la tabla para valores entre $0$ y $10$. Este proceso puede seguirse en la figura 2.1.
En el primer paso obtenemos el logaritmo de $0,5$ calculando la raíz cuadrada de $10$ y obtenemos $3,1623…$. En el siguiente paso, calculamos la raíz cuadrada del número anterior, y su $\small{log_{10}}$ será por tanto $\small{3,16277^{0,5} = (10^{0,5} )^{0,5} = 10^{0,25}= 1,77828}$. Luego $\small{Log_{10} 1,77828 = 0,25}$
Al obtener los logaritmos de un número por el procedimiento anterior, podemos calcular seguidamente los logaritmos de sus potencias, puesto que al multiplicar un número por si mismo sucesivamente, el logaritmo del producto es un múltiplo de su logaritmo.
En el paso $n=2$, obteniendo el número que corresponde a log $0,25$, podemos obtener fácilmente el correspondiente a los logaritmos $0,5$ y $0,75$.
En el paso $3$, obteniendo el número que corresponde a $log 0,125$, podemos obtener fácilmente el correspondiente a los logaritmos $0,125$, $0,250$, $0,375$, $0,5$, $0,625$, $0,750$, $0,875$.
Mover el deslizador “n” para cada paso, extraer la raíz cuadrada de un número más próximo a $1$ y su logaritmo que en cada paso se reduce a la mitad. Moviendo a cada paso el deslizador “r” obtenemos los logaritmos de las potencias de la última raíz cuadrada obtenida .
Se expresa la fórmula de conversión de logaritmos de diferente base. Podemos comprobar que ${log_b\;b = 1}$ para cualquier base. También comprobamos que el cociente entre los logaritmos de un número cualquiera en dos base diferentes es una constante.
$$ {log_a {x}\over {log_b {x}}} = K$$Con estas dos propiedades de la función podemos escribir:
$${log_a {x}\over {log_b {x}}} = K = {log_a {b}\over {log_b {b}}} = log_a {b}$$Y por lo tanto:
$$\displaystyle {log_a{x}=log_b{x} .log_a{b}}$$Que es la fórmula que nos permite obtener el logaritmo de un número en cualquier base conociendo su logaritmo en otra.
Se expresa la propiedad base de los logaritmos para multiplicar números sumando sus logaritmos. Podemos comprobar deslizando sobre los puntos A y B la propiedad fundamental de los logaritmos $log (A·B) = log A + log B$.
Escalas logarítmicas.
Los logaritmos nos ofrecen la oportunidad de representar gráficamente números que cubren una gama muy grande de valores, mediante lo que se conoce como una “escala logarítmica”, que utiliza el logaritmo de un número en lugar de su magnitud. Por ejemplo, la sucesión 10, 100, 1000, 10000, … esta formada por elementos de un rango de magnitud muy diferente, aunque entre ellos existe una relación muy simple, pues forman una progresión geométrica. En una escala logarítmica de base 10 resultan equidistantes, pues su logaritmo se diferencia en una unidad.
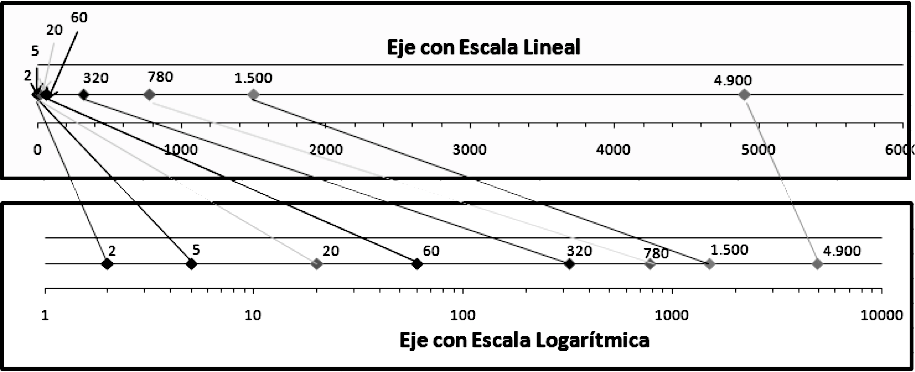
Las gráficas que utilizan escalas logarítmicas son de dos tipos. Las semi-logarítmicas, en las que solo se utiliza la escala logarítmica para uno de los ejes y las graficas de escalas logarítmicas para ambos ejes.
Si representamos una función exponencial en una escala logarítmica o semi-logarítmica obtenemos una recta.
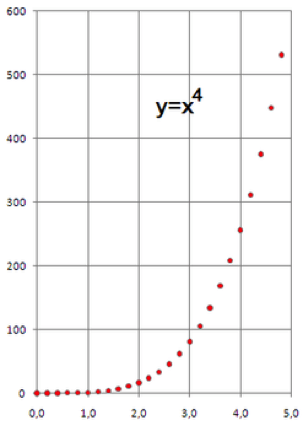
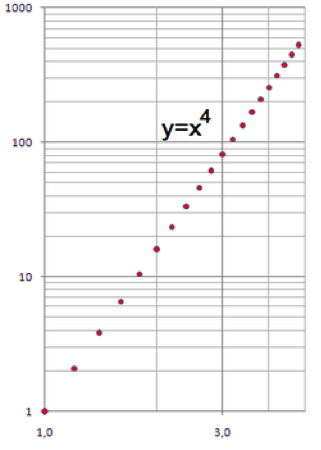
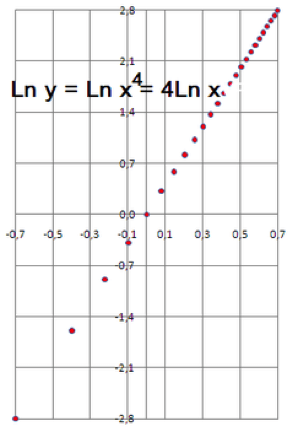
Observando detenidamente el grafico resultante, a escala logarítmica y semi-logarítmica, podemos apreciar la diferente distribución de los valores de la función tomados $a$ intervalos uniformes de $x$, lo que nos orienta sobre la conveniencia de una escala u otra según la muestra de datos a representar.
A titulo ilustrativo adjuntamos un grafico de la evolución de la población mundial en escala logarítmica, tanto para representar el tiempo como el número de habitantes, para un intervalo de 10 000 años y desde 3 M de habitantes hasta 7 000M.
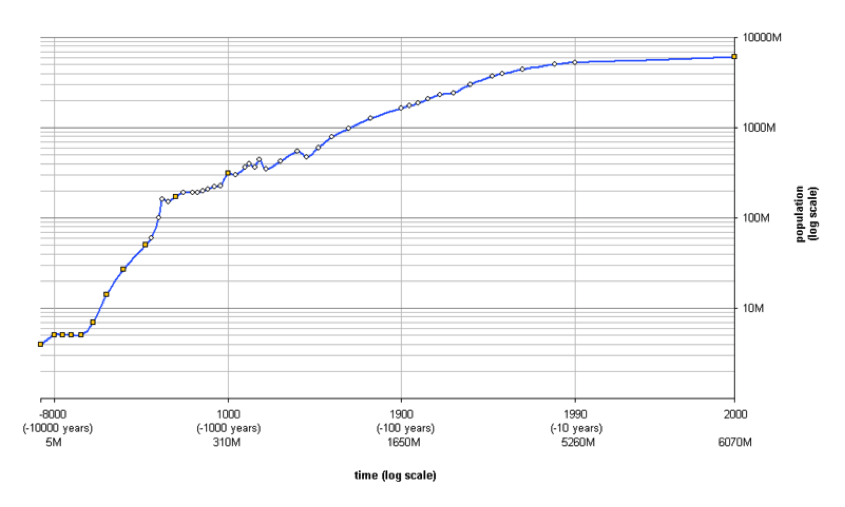
Las escalas logarítmicas se utilizan con frecuencia para la medición de fenómenos físicos. Por ejemplo, la escala de decibelios, que es la unidad de medida de la intensidad sonora, es una escala basada en logaritmos en base 10. También la escala sísmica de Richter es una escala logarítmica de base diez.
El origen de las funciones trigonométricas.
Las relaciones trigonométricas tienen su origen en la geometría clásica. Los griegos, para el estudio de la circunferencia y de los polígonos inscritos en ella, definen la cuerda y la flecha que corresponden a un determinado arco de circunferencia. La medida del arco es la del ángulo central de circunferencia que lo abarca.
Cuerdas y flechas también aparecen al estudiar las proporciones del triángulo, lo que hoy llamamos trigonometría. Por razones prácticas en trigonometría en lugar de trabajar con la cuerda completa se utiliza la “semicuerda del arco ” que es lo que hoy llamamos seno. ¿De donde viene este nombre? pues parece, que viene de las traducciones latinas de los textos griegos. La cuerda de un círculo, se denomina en latín “inscripta corda” o simplemente “inscripta”. La mitad de dicha cuerda se llama “semis inscríptae”. Su abreviatura era “s. ins.” , que terminó simplificada como sins. Para asemejarla a una palabra conocida del latín se la denominó sinus y de ahí nuestro seno.
La relación entre la cuerda de un arco y el seno de un ángulo es pues muy sencilla. El seno es la semicuerda del ángulo doble.
$$\small{seno \:α = (Cuerda \:2\:α )/2}$$Podemos ver con ayuda de un círculo que el seno de uno de los ángulos no rectos de un triángulo rectángulo es la relación entre el lado opuesto al ángulo y la hipotenusa del triángulo. El coseno es la proporción entre el lado contiguo y la hipotenusa. Se llama tangente del ángulo al cociente del lado opuesto entre el lado contiguo. Para el círculo de radio unidad, al ser la hipotenusa igual al radio y por tanto = 1, seno y coseno coinciden con las coordenadas del punto sobre el círculo que define el semi-arco.
Las funciones trigonométricas se relacionan entre sí de manera que pueden obtenerse todas ellas a partir del seno o del coseno. Las relaciones entre las funciones trigonométricas se llaman “identidades trigonométricas”. La más conocida es la que relaciona seno y coseno, que resulta evidente aplicando el teorema de Pitágoras al triángulo rectángulo que hemos construido sobre el círculo unidad.
${ sen^2 {x}+ cos^2 {x} = 1}$
También es fácil deducir que la tangente de un ángulo es igual al cociente entre su seno y su coseno.
$$\small{{tg \:x} ={{sen \: x}\over {cos \: x}}}$$El número π
La geometría del círculo es perfectamente conocida por los griegos y en los “Elementos”, Euclides (325 a.C.) afirma y demuestra que la proporción entre el área de un circulo y el cuadrado de su radio es una constante. Desde los primeros intentos para calcular su valor los geómetras griegos se dieron cuenta que estaban ante un número “inconmensurable”, es decir, para el que no podían establecer una unidad de medida exacta. No podían expresarlo como una fracción.
Una de las primeras aproximaciones al valor de π la da Arquímedes, (287 a.C.), inscribiendo en el círculo un polígono regular y calculando su longitud. El valor de π queda establecido entre 3,1408450704 y 3,1428571142.
$$ 3 {{10}\over{71}}\:< π <\:3{{1}\over{7}}$$Este procedimiento de cálculo fue llevado al extremo por Ludolph van Ceulen que calculo el valor de π con 35 decimales exactas en 1610, utilizando un polígono de $2^{62}$ lados. Dedicó toda su vida a ello y, en reconocimiento a su esfuerzo, en su tumba figura el valor de π con 35 decimales exactos.
Newton abandonara el método tradicional de cálculo de π y se planteará aproximar su valor mediante series infinitas, con el objetivo de buscar aproximaciones mucho más precisas, que requieran un esfuerzo de cálculo menor.
La obtención de π mediante una suma infinita implica su definición como número irracional, pero la demostración matemática definitiva es de Adrien Marie Legendre (1752-1833) en 1794.
En 1882, el matemático Ferdinand Lindeman demostró que el número π es un tipo de número irracional especial, que no es algebraico, es decir, no puede obtenerse con un número finito de pasos a partir de números enteros y las cinco operaciones permitidas, (suma, resta, multiplicación, división y extracción de raíz cuadrada ). A ese tipo de números se les llama números trascendentes.
Las tablas trigonométricas.

Astrolabio.
Suspendido de su anilla se mantiene vertical por su propio peso. El círculo graduado nos da la altura sobre el horizonte de una estrella.
Sus divisiones son de 5 minutos de grado.
Las razones trigonométricas son de aplicación en muchos campos. En la construcción, el trazado de caminos y levantamientos topográficos etc.… También, en un campo tan diferente como la astronomía, las razones trigonométricas son esenciales. Las aparatos para la medición de ángulos se “gradúan” dividiendo el círculo completo en 360 partes o grados sexagesimales.
Para obtener los valores de las funciones trigonométricas en grados no había más remedio que medir sobre las figuras geométricas y calcular tablas con sus valores para diferentes ángulos, lo que es un método de escasa precisión. Otra manera de calcular tablas es a partir de valores conocidos que corresponden a ángulos particulares y a partir de ellos ir interpolando el resto de la tabla, basándose en las fórmulas trigonométricas deducidas gráficamente por los matemáticos griegos, para los valores de seno y coseno de la suma de dos ángulos.
$sen (a+b) = sen\,a \; cos\,b + sen\,b \; cos\,a \\ cos (a+b) = cos\,a \; cos\,b - sen\,a \; sen\,b$
Que se convierten, haciendo $a = b$, para el ángulo doble, en:
$sen 2a = 2 (sen a cos a)$
$cos 2a = cos^2 a - sen^2 a$
Partiendo de los valores conocidos para determinados casos particulares, por ejemplo seno de $45º = \sqrt{2}/2$, podemos obtener el seno de $22,5º$. Por diferencias entre el de $45º$ y el de $30º$ podemos obtener el de $15º$ y con la fórmula del seno del ángulo doble el seno de $7,5º$. Procediendo de esta manera Ptolomeo (100 d.C.), es el primero en tabular las cuerdas de los arcos de circunferencia, lo que a nuestros efectos es una tabla de senos.
En 1637 Descartes publica “El discurso del método“ (Discours de la méthode pour bien conduire la raison, et chercher la vérité dans les sciences ) que es una de las primeras obras de la filosofía moderna. "El discurso del método" es un libro de una ambición singular porque rebasa el planteamiento filosófico y Descartes intenta desarrollar la aplicación práctica de sus ideas en tres apéndices, “Geometrie”, “Dioptrique” y “les Meteores”.
Descartes propone para la filosofía, para el estudio de la naturaleza y para la física, el método de las matemáticas que consiste, según él, en seguir unas reglas claras.
En definitiva, desde nuestro punto de vista, sus propuestas son de lo más sensatas, es difícil de entender que en su época causaran revuelo. Pero la traducción de sus ideas a principios filosóficos representan un cataclismo en la filosofía occidental dominada por los escolásticos, de tradición Aristotélica.
El punto de partida de cualquier construcción filosófica, para excluir cualquier duda de acuerdo con el primer principio, es “Cogito ergo sum”, pienso luego existo. Es superior la certeza de las ideas que la que podemos depositar en la realidad. Descartes esta en el origen de las corrientes filosóficas “idealistas” que defienden la prioridad de las ideas sobre la experiencia de los sentidos y las matemáticas como ideas divinas que se aplican al mundo real.
El discurso del Método fue, en sus sucesivas reediciones, publicado sin sus apéndices, que tuvieron un éxito desigual. La “Dioptrique” sobre la reflexión y refracción de la luz y “les Meteores” sobre el medio natural, fueron rápidamente superados por el avance de la ciencia empírica y olvidados. El dedicado a la geometría adquirió vida independiente y se convirtió pronto en uno de los libros más influyentes de las matemáticas.
La “Geometrie” es la aplicación del método científico cartesiano a las matemáticas. El sujeto escogido es la geometría clásica que era entonces la disciplina matemática central cuya solidez interna estaba fuera de dudas. Sin embargo, para Descartes era un ejemplo de los métodos antiguos que había que renovar.
Las etapas centrales del método cartesiano, que hemos citado antes son:
La primera etapa se corresponde con lo que los matemáticos de la época llamaban “análisis” y la segunda con lo que entendían como “Síntesis”.
Descartes divide el análisis para la Geometría en dos pasos:
A partir de aquí hay que efectuar la síntesis y para ello utilizamos un lenguaje simbólico que nos permite detallar la relación entre los datos y las incógnitas y expresarla en ecuaciones. Descartes confía en “mecanizar el razonamiento” y definir un lenguaje matemático universal.
Planteadas las ecuaciones, la síntesis consiste en:
El álgebra es el instrumento intermediario que permite manipular los datos obtenidos de la geometría y obtener la solución que deberá traducirse nuevamente en una figura geométrica.
Las ecuaciones algebraicas son “el esqueleto” de la síntesis que deja a descubierto como se ha obtenido la solución. Este detalle es esencial porque define la nueva geometría.
Descartes critica a los geómetras clásicos precisamente por exponer sus resultados ocultando el proceso de síntesis. Los clásicos construyen caso a caso y las soluciones aparecen por la intuición o la genialidad del geómetra que no revela sus “trucos”. La nueva geometría no obliga a esfuerzos de la imaginación sino a aplicar formulas mecánicamente.
La “Geometrie” establece la relación entre la construcción de figuras geométricas y sus ecuaciones algebraicas y el éxito en este empeño ha difuminado el límite entre ambas materias, geometría y álgebra. Asistimos al nacimiento de la Geometría algebraica, fusión de dos ramas de las matemáticas, pero no podemos perder de vista que detrás de ello Descartes establece la supremacía del análisis y, en consecuencia, el álgebra pasara a ser la disciplina matemática principal.
A cada segmento se le asigna una magnitud, por comparación con la unidad de medida definida para cada ocasión. Esta premisa es frontalmente contraria a la geometría clásica que no aceptaba identificar la longitud de las líneas con números ya que algunas magnitudes se consideraban “inconmensurables”, no eran divisibles por ninguna unidad de medida, o lo que es lo mismo, no pueden expresarse como una fracción de números enteros.
Descartes ignora este problema al asignar a “todos” lo segmentos una magnitud, lo que implica aceptar la existencia de los “inconmensurables” como números. En la imagen hoy corriente, según la cual suponemos todos los números ordenados sobre una recta de menor a mayor, los “inconmensurables” no son un corte o discontinuidad, a estos números les corresponde un punto de la recta real. Descartes no se detiene en este problema, pero acierta pasándolo por alto y aceptando lo que unos años más tarde serán los números “irracionales” de infinitas números decimales. Por otra parte, resulta curioso que para Descartes los números negativos fueran “falsos”, por la incapacidad de imaginar segmentos de longitud negativa.
Esta construcción es la que aparece en la “geometrie” como demostración de que las operaciones algebraicas pueden traducirse gráficamente.
En este caso se trata de la conocida fórmula para las raíces de una ecuación de segundo grado. Al no considerar magnitudes negativas Descartes se ve obligado a ejecutar diferentes construcciones según el signo de los coeficientes de la ecuación.
La suma y su inversa, la resta, la multiplicación y la división, la exponencial, como un caso particular de multiplicación y la extracción de raíces, son las operaciones del álgebra. Descartes demuestra que estas operaciones pueden efectuarse y son equivalentes a construcciones geométricas, donde los números son sustituidos por segmentos.
Descartes introduce para las operaciones símbolos abstractos semejantes a los actuales, salvo para el signo “igual”, para el que utiliza el símbolo "$\small{\infty}$" .
A cada segmento se le asigna, como nombre o identificador, una letra minúscula si se trata de una magnitud conocida y una letra del final del abecedario (... $x$, $y$, $z$) si es desconocida.
En el álgebra geométrica clásica, multiplicando una magnitud por otra se obtiene un área (un cuadrado en el caso de dos magnitudes iguales) y en el caso de tres obtenemos un volumen (un cubo en el caso de tres magnitudes iguales). Para Descartes las sucesivas potencias de una magnitud son a su vez magnitudes de la misma naturaleza. De esta manera se aceptan en la geometría potencias de orden superior a tres que carecían de sentido para los clásicos y se abandona el principio de homogeneidad, que obligaba a tratar separadamente las magnitudes según fueran líneas, superficies o volúmenes. Para Descartes todas las magnitudes son de la misma naturaleza y se expresan según la longitud del segmento que las representa. Este criterio es un punto esencial de ruptura con la tradición del álgebra geométrica clásica.
Para Descartes las curvas se definen por el movimiento de un punto sobre el plano y clasifica las curvas según la exactitud con la que puede ser definido ese movimiento.
No hay motivo para excluir de la geometría las curvas más complejas si pueden imaginarse descritas por un movimiento continuo o de varios movimientos sucesivos, siempre que cada uno de ellos venga determinado por los precedentes y nos permita un conocimiento exacto de su medida. Las curvas que cumplen esta condición son las curvas algebraicas, es decir, que se definen mediante una ecuación en la que intervienen las operaciones definidas en el álgebra.
Propone también, abandonar la premisa de la geometría clásica sobre la obligación de usar únicamente regla y compas para el dibujo de curvas:
Cuando a una expresión algebraica se le añade una segunda variable, obtenemos una curva como lugar geométrico de los puntos cuyas referencias a dos rectas predefinidas cumplen con esa expresión. La magnitud de esas “referencias” son las coordenadas del punto. En definitiva una curva plana queda descrita por una ecuación algebraica de dos variables, con independencia del grado con el que figuren sus variables.
Mediante esta regla deslizante, Descartes muestra como las curvas algebraicas pueden obtenerse a partir de otras más simples. En este caso la curva resultante del movimiento de la regla es un grado superior a la curva que se utiliza de base.
Descartes clasifica las curvas en “clases” según el grado de la ecuación que las describe.
Hoy llamamos “coordenadas Cartesianas” a los sistemas de referencia basados en ejes ortogonales, aunque Descartes no impone este requisito a las rectas de referencia y utiliza en cada caso las que considera más adecuadas. La dirección para las coordenadas crecientes tampoco es en todos los casos hacia la derecha y hacia arriba como estamos acostumbrados a ver hoy.
En consecuencia a su rechazo a los números negativos, sus coordenadas son siempre positivas y por la tanto no existe el tramo negativo de los ejes de coordenadas.
La adopción de un sistema de ejes ortogonales como referencia se impuso rápidamente. En las obras de Newton aparecen los ejes $X$ e $Y$ en mayúsculas, tal como los conocemos hoy, con su parte positiva y negativa a partir del punto de cruce de ambos que recibe el nombre de origen de coordenadas.
Los sistemas de referencia se multiplicaron, de manera que Newton llegó a identificar siete maneras de referenciar un punto en el plano. Coordenadas oblicuas, diferentes tipos de coordenadas polares e incluso sistemas basados en la distancia a dos puntos fijos en el plano, etc.
Pero finalmente el sistema de referencia por excelencia se basa en ejes ortogonales, y en reconocimiento a Descartes, las coordenadas y las ecuaciones referidas a ellas se denominan Cartesianas.
Descartes es el primero en proponer un método algebraico para obtener la tangente a una curva. Su método consiste en trazar una circunferencia con centro en el eje $x$, y calculando algebraicamente la intersección de esta circunferencia con la curva propuesta, resolviendo el sistema de ecuaciones formado por la ecuación de la curva y de la circunferencia. Se obtienen así dos puntos de intersección que corresponden a las raíces del sistema. Descartes razona que en el caso de que la circunferencia sea tangente a la curva, ambos puntos de corte coincidirán y por tanto la ecuación planteada tendrá únicamente una raíz doble y será de la forma $A(x-x_1)^2$. Igualando ambas ecuaciones obtiene la solución buscada.
El método de Descartes es correcto pero bastante poco eficiente para el caso más general, por lo que fue superado inmediatamente.
Los problemas del álgebra en la época de Descartes.
La prioridad del álgebra sobre la geometría era para los contemporáneos de Descartes muy difícil de aceptar. La geometría era un ejemplo de rigor, construida sobre la base de postulados y teoremas que le daban una coherencia extraordinaria. El álgebra, por el contrario, tenía pendiente de resolver muchas dificultades para encajar el resultado de las cuatro operaciones básicas dentro del perímetro de los números conocidos.
El resultado de la suma de números naturales es siempre otro número natural. Pero si contemplamos la resta, nos encontramos con que el resultado de una resta de números naturales puede no ser otro número natural. Es posible que resulte un número negativo. Aunque parezca extraño muchos matemáticos se opusieron a la extensión de la idea de número para incluir entre ellos a los negativos.
Consecuente con su criterio de correspondencia entre números y segmentos Descartes rechaza los números negativos, por la imposibilidad de imaginar longitudes, áreas o volúmenes negativos. No se puede hacer intervenir en las construcciones geométricas segmentos de magnitud negativa. En consecuencia, a-b es diferente a a+b, puesto que solo considera valores de a y b positivos y las dos expresiones se corresponden con dos construcciones geométricas diferentes, suma y resta, a tratar separadamente. (Si aceptamos números negativos, a+b, puede ser a+(-b) y según las reglas del álgebra se convierte en a-b). Para Descartes,
Si incluimos la división de números naturales, nos vemos obligados también a ampliar nuevamente el concepto de número a los que resultan de expresiones fraccionarias. Las fracciones se usaban desde la antigüedad pero se manejaban independientemente de los enteros y naturales al no estar integrados en el sistema de notación decimal. ( Se decía por ejemplo 1 y ½ en lugar de 1,5 ).
Simón Stevin, en 1585 publica “De Thiende” (El décimo), donde explica “como efectuar con una facilidad insospechada, los cálculos necesarios en la vida diaria por medio de enteros sin fracciones”. En su “Rhabdologia" de 1617, Napier se refiere a la aritmética decimal de Stevin y propone el punto o una coma como signo de separación decimal.
A partir del momento que se impuso la expresión de los números mediante fracciones decimales y se generalizó el empleo de la coma para separar la parte entera de la decimal, estos números pasaron a ser los “números racionales” que se suman a los naturales y los enteros.
Mientras los números enteros representan magnitudes discontinuas, los racionales forman un continuo, de manera que entre dos números racionales siempre podemos encontrar otro de valor intermedio.
Como este proceso se puede repetir, intuimos que entre dos números racionales hay infinitos números racionales. Si lo expresamos en notación decimal, los números racionales pueden tener un número infinito de decimales, pero el desarrollo decimal de cualquier número racional (expresión de la división de dos números enteros) siempre presenta un bloque de números que se repite.
La geometría clásica griega sabía que la relación entre el diámetro y el perímetro de una circunferencia era constante y que no existe una unidad común que nos permita medir tanto la circunferencia como su diámetro. Otros ejemplos sencillos de números que presentan esta dificultad son $\sqrt{2}$, que es la longitud de la diagonal de un cuadrado de lado $1$ o $\sqrt{3}$, que es la diagonal del cubo de lado 1.
Los griegos llamaron a estos números “inconmensurables” y hoy los llamamos números irracionales, porque en contraposición a los racionales, se desarrollan en un número infinito de cifras decimales sin pautas de repetición.
Todos estos números pueden obtenerse gráficamente con regla y compas, la diagonal del cuadrado o del cubo, incluso el número áureo, pero no se les puede asignar, un número “exacto”. Esta falta de correspondencia entre segmentos y números, era una señal de la superioridad de la geometría sobre el álgebra.
Los números con un número infinito de decimales con periodo de repetición (racionales), junto con los que teniendo un número infinito de decimales no presentan esta pauta (irracionales) forman el conjunto de los números reales.
Los números reales se representan formando parte de una recta, la recta real. La recta real contiene todos los números reales que a su vez contienen como un caso particular los racionales, los enteros y los naturales. Cada una de las generalizaciones del concepto de número ha respetado las categorías precedentes formando una unidad coherente.
La formación del concepto de función.
Al iniciarse el siglo XVII, el concepto de función aun no está identificado y se va a ir perfilando en paralelo al desarrollo del cálculo infinitesimal, pero el concepto moderno de función tardara un siglo más en concretarse.
Está claro que en el periodo que nos ocupa solo nos corresponde describir el primer capítulo de esta historia, desde la aparición del concepto hasta su definición por Euler en la “Introductio”, tratado “fundacional” del análisis.
Curvas o funciones
La primera aproximación al concepto de función se produce fuera del campo de las matemáticas y tiene su origen en las observaciones del movimiento, al estudiar las trayectorias de los sólidos “en función” del tiempo. Galileo expresa este concepto, para los cuerpos en caída libre o para la trayectoria de las balas de cañón, pero sin incorporar el lenguaje simbólico del álgebra.
En el campo matemático, las curvas algebraicas de Descartes, definidas como el lugar geométrico de los puntos del plano que satisfacen una ecuación de dos variables, son la primera aproximación a una función. Descartes imagina las curvas generadas por el movimiento “preciso y exacto” de un punto. Para Fermat “las expresiones algebraicas de dos variables representan una curva en el plano”.
Solo se conciben como objeto matemático las curvas definidas mediante una expresión algebraica. Muchas otras curvas conocidas eran consideradas mecánicas, “expulsadas” de la geometría por la incapacidad de describirlas mediante una fórmula.
En este apartado entran curvas estudiadas por desde antiguo, como las espirales, las cicloides, la cuadratriz, etc… que también se interpretan a partir de un movimiento, pero que involucran ángulos y longitudes de arco. El problema radica que en ese momento, las funciones trigonométricas no son más que valores tabulados, con más o menos decimales, que no pueden considerarse valores “exactos”.
No podemos identificar el concepto de curva y el de función, porque no todas las curvas son funciones válidas, como veremos más adelante, pero en sentido contrario si es cierto que la gráfica de una función que relaciona dos variables puede representarse en el plano como una curva.
Continuar con : la formación del concepto de función-II-
A principio del siglo XVII, no existía una organización matemática de tipo profesional que soportase la difusión de los avances científicos. Durante la primera mitad de este periodo hubo un personaje que, a título individual, sirvió de central de información matemática gracias a sus amplios contactos por correspondencia. Se trata del fraile Marin de Mersenne (1588-1648). Descartes, Fermat, Roverbal, Torricelli, y otros muchos mantenían habitualmente correspondencia con Mersenne que se encargaba de la difusión de las novedades entre ellos.
La aplicación del álgebra a la geometría, como consecuencia del impulso de Descartes, se orienta a la búsqueda de soluciones a cuatro tipos de problemas que se plantean en ese momento como independientes. El primero es la “rectificación de curvas” que consiste esencialmente en la obtención de la longitud de una curva y sus tangentes. Por otra parte, la “cuadratura de curvas”, que consiste en calcular el área encerrada por una curva, entre las rectas verticales que pasan por dos puntos $a$ y $b$ y el eje $X$. El tercer problema es lo que hoy conocemos como la obtención de los máximos y mínimos relativos de una curva y por último, el cuarto problema, el estudio del movimiento de velocidad no uniforme.
Los cuatro problemas enunciados se estudian independientemente, sin sospechar que todos ellos están relacionados.
En conjunto, esta generación de matemáticos establece las bases para el posterior desarrollo del cálculo diferencial y obtienen pruebas sobre la naturaleza inversa del problema de la tangente y de la cuadratura para determinadas curvas, pero no las valoran adecuadamente ni toman conciencia de la generalidad de los resultados que van obteniendo para problemas particulares.
Descartes fue probablemente el pensador más importante de su época, pero sus aportaciones a la matemática no son más que un episodio de su vida dedicada a la filosofía y a la ciencia en general, que le dieron una gran difusión y el reconocimiento general.
 Fermat es una personalidad opuesta. Estudió derecho en Toulouse, ejerció como abogado ocupando diferentes cargos públicos y cultivaba la matemática en su tiempo libre. Contemporáneo y rival de Descartes, su obra se conoce mediante la difusión de su correspondencia a través Mersenne, incluso antes de que se publicara la Geometrie, pero la publicación de su "Varia opera matemática" no llega hasta 1679, después de su muerte. Este retraso favoreció la impresión general de que la geometría analítica había sido únicamente atribuible a Descartes, privándole del merecido reconocimiento en este campo.
Fermat es una personalidad opuesta. Estudió derecho en Toulouse, ejerció como abogado ocupando diferentes cargos públicos y cultivaba la matemática en su tiempo libre. Contemporáneo y rival de Descartes, su obra se conoce mediante la difusión de su correspondencia a través Mersenne, incluso antes de que se publicara la Geometrie, pero la publicación de su "Varia opera matemática" no llega hasta 1679, después de su muerte. Este retraso favoreció la impresión general de que la geometría analítica había sido únicamente atribuible a Descartes, privándole del merecido reconocimiento en este campo.
Pero el interés de Fermat por las matemáticas es muy amplio y con aportaciones muy significativas en muchos ámbitos, por lo que su figura es valorada como la de uno de los grandes matemáticos de la historia. Su nombre se asocia hoy a la teoría de números y al “último teorema de Fermat”.
Fermat poseía una edición de la Arithmetica de Diofanto y escribió un comentario, de hecho, un acertijo, en el margen de cada problema. Uno por uno han sido resueltos por personalidades como Leibniz, Newton, etc.
Solo quedó sin resolver el acertijo que propuso debajo del problema VIII, que trata sobre escribir un número cuadrado como suma de dos cuadrados (es decir, encontrar ternas pitagóricas). Ahí, Fermat escribió:
El intento por resolver su teorema ha movilizado grandes esfuerzos desde entonces. Su enunciado ha figurado entre los grandes problemas matemáticos sin resolver, hasta que en 1995 fue resuelto por Andrew Wiles.
Aunque Descartes ya había planteado un método de obtención de la tangente a una curva de forma analítica, Fermat es el primero que enfoca el problema introduciendo “magnitudes infinitamente pequeñas”. Su planteamiento es innovador porque se adelanta 50 años a Newton en el tratamiento de las cantidades “infinitesimales” que utiliza en su razonamiento.
Infinitesimal, número infinitamente pequeño pero diferente de cero.
La pendiente de una recta, se mide por la tangente del ángulo que forma con la horizontal. En geometría elemental la tangente de un ángulo se define como la relación entre el lado opuesto y el contiguo de uno de los ángulos no rectos de un triángulo rectángulo.
Dada una curva de la que queramos hallar la tangente en un punto, Fermat establece la semejanza de dos triángulos rectángulos, el que la tangente de la curva forma con el eje horizontal y el triángulo formado por el punto en el que queremos hallar la tangente, un punto de la curva distante $Δx$ y la horizontal en el punto de tangencia.
Definimos dos triángulos rectángulos. El primero de base $TQ$, esta formado por la tangente a la curva, el eje $X$ y su perpendicular que pasa por el punto $A$ donde queremos obtener la tangente. La hipotenusa del segundo triángulo es un tramo de la tangente a partir de $A$ y sus catetos son $∆x$ y $f(x+∆x)-f(x)$. Fermat observa que al disminuir $∆x$ los dos triángulos tienden a hacerse semejantes y podemos plantear:
$$ {\frac{TQ}{f(x)}} = {{∆x}\over{f(x+∆x)-f(x)}}$$
$$ TQ = {{∆x \:f(x)}\over{f(x+∆x)-f(x)}}$$
$$ TQ = {{∆x \:x^2}\over{f(x+∆x)- x^2}}$$
$$ TQ = {{∆x \:x^2}\over{x^2+∆x^2+2 x ∆x- x^2}}$$
Simplificando, dividiendo arriba y abajo por $∆x$, resulta si hacemos $∆x=0$:
$$ TQ = {{x^2}\over{2x}}={ x\over {2}}$$
Luego en el punto a, la pendiente de la tangente a la curva $\small{ y= ax^2}$ es:
$${\frac{f(x)}{TQ}}={\frac{a^2}{\Large \frac{a}{2}}}=2\:a$$
El mismo razonamiento para exponentes mayores le lleva a la fórmula general para la pendiente de funciones del tipo $\small{ y=x^n}$, resultando ser:
$$n \:x^{(n-1)}$$
Para las funciones $y=x^n$, la pendiente de la tangente en un punto $x_1$ es:
$n\;{x_1}^{n-1}$
El mismo procedimiento utilizado para obtener la tangente, le sirve a Fermat para identificar los máximos y mínimos de una función. En el entorno de un máximo o de un mínimo de la función dos puntos, a un lado y otro del punto que buscamos, separados por $Δx$, tienen la misma ordenada, es decir, $f(a+Δ x)- f(a)= 0$ y por tanto la tangente, en el punto en el que la función es máxima o mínima, es horizontal (pendiente $0$).
Fermat para las cuadraturas vuelve a ser el primero en proponer un procedimiento analítico para funciones exponenciales $\small{y = x^n}$. Divide el área bajo la curva hasta la abscisa $x$, en pequeñas rebanadas $Δx$ que resultan de dividir $x$ por $k$, siendo $k$ un número que haremos crecer para que las rebanadas sean cada vez más delgadas.
En la imagen, para $\small{y=x^3}$, dividimos la distancia $x=20$ en 5 rebanadas de 4 unidades de ancho.
El área de la primera rebanada bajo $\small{y=x^3}$ será $\large{ {20\over 5}({20\over 4})^3} $. El área de la segunda será $ \large {20\over 5}({{2\;20}\over 5})^3 $ y así sucesivamente hasta la rebanada 5.
En el cuadro calculamos la suma del área de las 5 rebanadas.
| Rebanada | $∆x=x/5$ | $k ∆x$ | $f(k ∆x)$ | Área |
|---|---|---|---|---|
| 1 | 4 | 4 | 64 | 256 |
| 2 | 4 | 8 | 512 | 2.048 |
| 3 | 4 | 12 | 1.728 | 6.912 |
| 4 | 4 | 16 | 4.096 | 16.389 |
| 5 | 4 | 20 | 8.000 | 32.000 |
| Total | 57.600 |
$$ {x\over k}\:({x\over k})^n + {x\over k}\:({2x\over k})^n +{x\over k}\:({3x\over k})^n +{x\over k}\:({4x\over k})^n +{x\over k}\:({5x\over k})^n =57.600$$
El resultado obtenido es superior al área bajo la función, pero podemos observar en la figura, que incrementando $k$ el resultado disminuye progresivamente. Si generalizamos para $k$ rebanadas la expresión anterior resulta:
$$ {x\over k}\:({x\over k})^n + {x\over k}\:({2x\over k})^n +{x\over k}\:({3x\over k})^n + ...+{x\over k}\:({kx\over k})^n $$
que podemos poner de la forma:
$$ ( 1+2^n+3^n+...+k^n)\:({x\over k})^{n+1}$$
$$ {{ 1+2^n+3^n+...+k^n}\over k^{n+1}} \: x^{x+1}$$
Para sumar la serie de potencias de enteros, establecemos la siguiente desigualdad:
$${ 1+2^n+3^n+...+k^n }\ge {k^{n+1}\over 1+n}\ge { 1+2^n+3^n+...+(k-1)^n}$$
Con lo que se puede acotar el valor del coeficiente de $x^{(n+1)}$ a:
$${{ 1+2^n+3^n+...+k^n}\over{k^{n+1}}}\ge {1\over {1+n}} \ge {{ 1+2^n+3^n+...+(k-1)^n}\over{k^{n+1}}}$$
Para valores de k cada vez más grandes, el cociente de la suma de potencias dividido por $\small{ k^{n+1}}$ se aproxima cada vez más a ${1\over{1+n}}$. Obtiene así la cuadratura del área bajo las curvas de ecuación $\small{y=x^n}$.
Para las funciones $\small{y=x^n}$, el área bajo la curva, de $0$ a $x$, es: $\Large{{x^{n+1}}\over{n+1}}$
La intuición de Fermat le lleva a proponer para la diferenciación y la integración una aproximación totalmente correcta aunque limitada a las funciones del tipo $y=x^n $. Sorprende que obteniendo resultados tan simétricos en ambos problemas no se planteara la relación entre ambos.
Si calculamos la suma de n términos de la serie:
$${{ 1+2^n+3^n+...+k^n}\over{k^{n+1}}}$$
para $n=4$ y $n=9$, y para valores de $k=10$ y $k=60$, es decir, una división entre $10$ y $60$ intervalos, podemos ver que la aproximación a $\frac{1}{n+1}$ es bastante lenta y que solo a partir de dividir en 60 rectángulos, obtenemos dos decimales correctos.
| n=4 | k=10 | k=20 | k=30 | k=40 | k=50 | k=60 |
|---|---|---|---|---|---|---|
| 0,2533 | 0,2258 | 0,2170 | 0,2127 | 0,2101 | 0,2084 |
| n=9 | k=10 | k=20 | k=30 | k=40 | k=50 | k=60 |
|---|---|---|---|---|---|---|
| 0,1574 | 0,1269 | 0,1175 | 0,1130 | 0,1103 | 0,1085 |
Grégoire de Saint Vincent (Opus geometricum, 1647) estudiando la cuadratura de la hipérbola equilátera $y · x=1$ llega a la conclusión de que si tomamos a lo largo del eje $X$ puntos, de manera que los intervalos que determinan van creciendo en progresión geométrica, las áreas definidas bajo la hipérbola por dos puntos consecutivos son iguales. Según crece la abscisa geométricamente, el área contenida crece aritméticamente.
Si a partir de $x=1$, tomamos puntos $A$, $B$, $C$, ···, tales que las áreas delimitadas entre ellos y la hipérbola sean iguales, se cumple :
Área $1-B$ = $2$ Area $1-A$.
Área $1-C$ = $3$ Area $1-A$.
....
Área $1-N$ = $n$ Area $1-A$.
Y comprobamos que los puntos que hemos seleccionado están en una progresión geométrica en base $A$:
$\small{B = A^2,\; C = A^3,\cdot \cdot\cdot ,\; N = A^n }$
y por lo tanto, podemos poner:
$log\;B = 2\;log\;A$, $log\;C = 3\;log\;A$, …, $log\;N = n\;log\;A$.
En definitiva el logaritmo de un número N es proporcional al área bajo la hipérbola desde $1$ a $N$. El descubrimiento de esta relación entre la función logarítmica y la hipérbola equilátera es una aportación temprana al problema de las cuadraturas, pero Saint Vincent no supo ponerla en un contexto más general.
A partir de un punto $A$ situamos los puntos $B$, $C$ y $D$ de modo que sus abscisas estén en progresión geométrica de razón$= r$.
Trazando rectas verticales que pasan por los puntos definidos podemos observar que cortan a la curva logarítmica definiendo los puntos $A_1$, $B_1$, $C_1$ y $D_1$ sobre el eje $Y$, separados por una distancia igual para todos ellos.
Podemos comprobar que quedan definidas bajo la hipérbola, entre los puntos seleccionados, áreas iguales. Estas áreas no varían de magnitud al modificar la base de la función logarítmica,(moviendo el deslizador b).
Situando el punto $A$ en $1$, movemos el deslizador “r”, para posicionar el punto $B$. Moviendo el deslizador de la base de la función logarítmica para que $y(B_1)=1$. Podemos comprobar que la base obtenida es igual a $x(B)$, como corresponde por la propiedad de la función logarítmica, ya que $log_b \; b = 1$, para todo $b$.
¿Podemos situar B de tal forma que el área bajo la hipérbola sea igual a $1$? En esta base, resulta que el coeficiente de proporcionalidad entre áreas y logaritmos es $1$.
Nikolaus Mercator (Logarithmo-technica -1668) es capaz de obtener, de la relación entre la hipérbola equilátera y los logaritmos, observada por de Saint Vincent, resultados sorprendentes.
La hipérbola equilátera $\large{{x\over y}} \small =1$, se hace infinita en $x=0$. Para evitar esta singularidad, Mercator desplaza la hipérbola en una unidad, sustituyendo $x$ por $x+1$ y convirtiendo su ecuación en $y=\large{{1\over{1+x}}}$ .
Aplicando el método de la división larga a $\large{1\over {1+x}}$, obtenemos como resultado.
$$ {1\over {1+x}} = 1-x+x^2-x^3+x^4- \cdot \cdot \cdot $$
Que continúa indefinidamente alternando el signo de los términos pares e impares. Esta es la primera transformación de una función en una serie de potencias, lo que luego llamaremos desarrollo en serie.
Siguiendo la idea de Saint Vincent de que la curva logarítmica es proporcional a la cuadratura de la hipérbola, aplica la fórmula de la cuadratura, conocida para las potencias de $x$, a cada término de la serie, para obtener una nueva serie que identifica como $log (x+1)$. Esta serie se conoce como serie de Mercator:
$$ log(1+x) = x- {x^2\over 2}+ {x^3\over 3} -{x^4\over 4} + \cdot \cdot \cdot$$
Para estos logaritmos el coeficiente de proporcionalidad entre las áreas y los logaritmos es $1$, por lo que Mercator llama a sus logaritmos "logaritmos hiperbólicos".
En álgebra, la división larga de polinomios es un algoritmo que permite dividir un polinomio entre otro polinomio que no sea nulo, generalizando el procedimiento que utilizamos habitualmente para la división entre dos números.
Podemos ver, moviendo el deslizador, como vamos ejecutando la división larga de $1$ entre $1+x$.
Del mismo modo, podemos empezar la división de $1$ entre $1+x$ por $x^{-1}$ , que multiplicado por $1+x$ nos da $1+x^1$. en este caso el siguiente término es $-x^2$ , y la serie completa resultaría ser $x^{-1 }- x^{-2}+x^{-3}-x^{-4} + …$. que también es un desarrollo en serie válido para $\displaystyle1\over{1+x}$.
Por el mismo procedimiento podemos abordar la división larga de $1/1+x^2$ con el resultado de $1-x^2+x^4-x^6+x^8 - \cdots $ o, alternativamente, $ x^{-2}-x^{-4}+x^{-6}- \cdots $
La serie de Mercator es una aproximación de los logaritmos en un entorno centrado en el origen de coordenadas que no puede dar ninguna explicación de por qué los resultados solo son válidos para valores entre $-1$ y $1$.
No mover los deslizadores ka, kb, kc de los valores iniciales $1$, $1$, $0$. La función $1/x$ toma valor infinito en $0$ y nos es imposible desarrollarla en este punto.
Mercator trabaja con la serie $1/(1+x)$, como equivalente a $1/x$, sustituyendo $x$ por $x+1$, es decir, desplazando la función de manera que para $x=0$ tome el valor $1$.
Hacemos clic en “Mostrar hipérbola”
La función $y=1/(1+x)$ es una hipérbola equilátera de asíntotas el eje $x$ y la recta $x=-1$.
El cambio de variable permite dividir el numerador $1$ entre el denominador $1+x$, operando como hemos explicado anteriormente, por división larga, obteniendo así la serie:
$$\displaystyle {1\over{1+x}}={1-x+x^2-x^3+x^4 + \cdot \cdot \cdot}$$Hacer clic en “desarrollo en serie”
En la hoja de trabajo podemos observar que para $x=1$ la serie toma alternativamente valor $1$ y $0$, según sea el exponente del último término del desarrollo par o impar. El valor de la función en ese punto es $1/1+1=1/2$, luego el desarrollo en serie fracasa para los valores de $x$ fuera del entorno $(-1, 1)$, no siendo válida ni para $1$ ni para $-1$.
Hacer clic en “serie integrada”
Aplicamos término a término, a la serie obtenida las fórmulas para la cuadratura de Fermat y obtenemos las áreas bajo la hipérbola que identificamos con $Log (1+x)$,
$$ Log( x+1) = x- {x^2\over{2}}+ {x^3\over{3}}-…$$Para obtener el valor la base de la función logarítmica obtenida, hacemos clic en “mostrar función logarítmica” y ajustamos el valor de a su valor con el deslizador. El valor de $a$ que obtenemos es aproximadamente $2,72$.
Movimiento del deslizador $k_a$
Moviendo $k_a$, desarrollamos la función $\displaystyle{y}={k_a\over {1+x}}$ y obtenemos una serie integrada de valor:
$$log(1+x) =k_a ({x- {x^2\over 2}+ {x^3\over 3} -{x^4\over 4} + ...})$$Para obtener el valor de la base de la función logarítmica debemos ajustar el deslizador a. Por ejemplo para $k_a=1,4$, la función logarítmica integral será:
$$log_2{(1+x)} = 1,4 ({x- {x^2\over 2}+ {x^3\over 3} -{x^4\over 4} + ...})$$Movimiento del deslizador $k_b$
Si movemos $k_b$ el efecto obtenido es una traslación de la hipérbola según el eje $x$.
La ecuación de la hipérbola pasa a ser ${y} = {\Large {{k_a}\over{k_b+x}}}$.
Podemos observar dos consecuencias.
1- La ampliación del entorno de validez de la serie obtenida que pasa a ser $-k_b \lt x \lt k_b $.
2- Modificando $k_c$ ajustamos el desarrollo de la serie integrada a la función logarítmica que se desplaza manteniendo la base obtenida para $k_b=1$.
Mercator se adelanta al desarrollo del Cálculo y a la justificación de las propiedades de estos logaritmos por Euler, que lo hará 50 años más tarde. También adelanta, para un caso particular, la metodología que llevará al desarrollo en serie de funciones. Para ello asume como válido identificar una función con su desarrollo en serie de potencias y supone que se puede obtener la cuadratura de una función mediante la cuadratura término a término de su desarrollo en serie.
Es un claro ejemplo claro de intuición, que obtiene resultados correctos, difícilmente interpretables con los conocimientos de su tiempo, adelantados a la construcción teórica que los sustenta.
La cuadratura de curvas también se aborda, durante la primera mitad de este siglo, desde una perspectiva en continuidad con la tradición geométrica clásica.
Kepler, cuando compraba vino para la celebración de la boda con su segunda esposa, se sorprendió al observar el método del bodeguero para medir el volumen de vino que consistía en introducir una vara por la boca central del tonel hasta el extremo inferior de una de sus tapas circulares.
 Kepler se pregunta como una sola medida lineal puede dar resultados exactos para calcular un volumen y a partir de sus reflexiones sobre este incidente, publica en 1615 un libro, titulado "Nova Stereometria doliorum vinariorum" ("Nueva estereometría, ó cálculo de volúmenes, de barriles de vino"), con los resultados de su estudio. (¡Kepler no solo se ocupaba de los planetas!).
Kepler se pregunta como una sola medida lineal puede dar resultados exactos para calcular un volumen y a partir de sus reflexiones sobre este incidente, publica en 1615 un libro, titulado "Nova Stereometria doliorum vinariorum" ("Nueva estereometría, ó cálculo de volúmenes, de barriles de vino"), con los resultados de su estudio. (¡Kepler no solo se ocupaba de los planetas!).
Kepler se propone calcular el volumen de los toneles asimilando su forma a la que se obtiene por la rotación de rectas o de segmentos de curvas cónicas (Círculos, elipses, parábolas e hipérbolas) alrededor de un eje. Procede al cálculo mediante la descomposición del volumen en rebanadas cilíndricas cada vez más finas, reinterpretando el método de exhaución clásico.
Kepler también trató de determinar las mejores proporciones de estos sólidos de cara a maximizar su volumen y esto le llevó a considerar varios problemas de optimización que resultaron ser contribuciones muy interesantes al desarrollo del cálculo diferencial. Su método de aproximación fue absolutamente numérico, calculando los valores para las diferentes proporciones y tabulando los resultados.
Así, llegó a la conclusión de que, para valores próximos al valor máximo, las desviaciones en el volumen eran pequeñas. Para tranquilidad de los consumidores, las mediciones de los toneleros eran suficientemente exactas para barriles austriacos, donde se construían manteniendo determinadas proporciones, aunque no era aplicable a Renania, la zona del Rhin de donde era Kepler, donde los barriles se construían mucho más alargados.
El libro de Kepler anterior a la algebraización de la geometría y anterior a las aproximaciones de Fermat al estudio de los problemas de máximos y mínimos, tuvo una gran difusión y puso el foco sobre el tipo de problemas en los que se ocuparían, 30 años más tarde, los “indivisibilistas”.
El método de exhaución de Eudoxo de Cnido
El método de exhaución o de agotamiento (Termino no aceptado por la academia, que deriva de la raíz “exhausto”, de la que también deriva exhaustivo, que si es aceptado) es un procedimiento ideado por Eudoxo (337 a.C.), discípulo de Platón, para aproximar superficies o volúmenes a partir de la comparación con una figura conocida previamente, descomponiendo ambas figuras en elementos que se relacionan uno a uno. Al repetir el cálculo, en cada paso tomando elementos mas pequeños, se pueden comparar los resultados obtenidos hasta alcanzar la exactitud requerida.
Eudoxo por este procedimiento obtuvo el volumen de pirámides y conos, demostrando que se corresponden a un tercio del prisma o cilindro de su misma altura. Arquímedes (287 a.C.) utilizó este método para aproximar la longitud de la circunferencia inscribiendo en ella un polígono regular, incrementado el número de lados en cada paso del cálculo. También obtuvo el volumen de la esfera por comparación con el volumen del cilindro de base igual al círculo mayor de la esfera y altura igual a su diámetro.
Bonaventura Cavalieri, (1598-1647), Discípulo de Galileo, publica en 1645 “Geometria indivisibilibus Continuorum” donde descompone las figuras planas en líneas paralelas y los volúmenes en rebanadas planas. Los indivisibilistas mantienen que, una línea esta hecha de puntos, un plano esta hecho de líneas y un solido puede descomponerse en áreas planas como hojas de un libro.
Cavalieri llega mediante su razonamiento geométrico a un resultado correcto para obtener la cuadratura de las funciones del tipo $y=x^n$. (Para valores de $n$ enteros e inferiores a $9$).
Mediante razonamientos sobre indivisibles Cavalieri logra otros resultados relevantes, como por ejemplo, la trasformación de la parábola$\small {x^2= ay}$ en la espiral de Arquímedes de radio proporcional al giro.
Hoy, a Cavalieri, lo recordamos básicamente por su teorema sobre el volumen de dos sólidos.
“Si dos sólidos tienen igual altura y si las secciones por planos paralelos a las bases a la misma distancia de ellas están siempre en una razón dada, el volumen de los dos sólidos también esta en esta relación”.
Gilles de Roberval (1602-1675) en 1634, dibujando la trayectoria de un punto sobre una circunferencia que rueda sin deslizar sobre una recta, obtiene el área bajo la cicloide, dibuja por primera vez la función seno y obtiene su área.
Representando la función $\displaystyle{y=x^n}$ podemos dibujar en azul el rectángulo de base $x$ y altura $\displaystyle {x^n}$ por lo tanto de área $\displaystyle{x^{n+1}}$. El área bajo la función podemos “cuadrarla” en el rectángulo marrón y comprobamos la relación de ambas superficies al variar n con el deslizador.
Para $n=1$,
quedan definidos dos triángulos y la superficie del triángulo inferior es evidentemente $\displaystyle {{x^2}\over2}$.
Para $n=2$,
la curva es una parábola $\displaystyle y=x^2$ y la relación entre las superficies es $1/3$.
Los valores del seno se obtienen lógicamente en función del arco de la circunferencia generatriz de la cicloide. La representación del seno como una curva, es un pequeño paso que prepara el camino para su incorporación al catálogo de funciones.
A pesar de estos esfuerzos y éxitos parciales, la aproximación geométrica a los problemas de los indivisibles se demostró incapaz de seguir el ritmo del avance mediante el enfoque algebraico. Sus resultados, orientados a resolver problemas de cuadraturas, nos parecen anecdóticos desde la perspectiva actual.
La formación del concepto de función (II)
Nuevas curvas.
Mientras las curvas mecánicas quedan arrinconadas en la geometría, los “indivisibilistas” aportan dos curvas que van a dar lugar a funciones centrales en las matemáticas.
Hemos visto como Roberval dibuja la curva trigonométrica del seno en función del arco de la circunferencia generatriz de la cicloide.
También la relación de los logaritmos con la cuadratura de la hipérbola equilátera, lleva a representar como una curva lo que eran tablas de valores orientadas al cálculo.
Tenemos pues nuevas curvas, con una gran precisión en cuanto a número de decimales, pero definidas por puntos, es decir, sin una expresión analítica para su representación. Evidentemente, ya sabemos que no existe para estas curvas una expresión algebraica y la expresión en forma de serie infinita de Mercator para los logaritmos tampoco es muy satisfactoria, pues sus resultados solo son correctos para valores de $x$ entre $-1$ y $1$.
En nuestra historia la representación gráfica de estas funciones aportan un avance fundamental, acercando la trigonometría y los logaritmos a un enfoque funcional, al dotarles de una representación gráfica. Este salto convierte unas tablas numéricas, útiles exclusivamente para la ejecución de cálculos, en candidatas a funciones matemáticas, en espera de su mayoría de edad.
Continuar con: la formación del concepto de función -III-
Volver a -I-
La frase “enanos de pie sobre los hombros de gigantes” se deriva de la mitología griega: El gigante ciego Orión, llevó a su sirviente Cedalión sobre sus hombros para que fuera como sus ojos y le guiara al encuentro de Helio, el sol, para curarse. Actualmente, esta frase se atribuye mayoritariamente a Newton, que en una carta de 1675 a Robert Hooke dice: "Si he visto más lejos, es poniéndome sobre los hombros de Gigantes".
 El sentido de esta metáfora es bastante evidente y se puede entender como el reconocimiento de Newton a los matemáticos que se ocuparon de los problemas de tangentes y de áreas antes que él y que, indudablemente, contribuyeron a la invención del cálculo. Morris Kline lo expresa magistralmente:
El sentido de esta metáfora es bastante evidente y se puede entender como el reconocimiento de Newton a los matemáticos que se ocuparon de los problemas de tangentes y de áreas antes que él y que, indudablemente, contribuyeron a la invención del cálculo. Morris Kline lo expresa magistralmente:
“Los grandes avances en las matemáticas y en las ciencias se construyen casi siempre sobre el trabajo de muchos hombres que aportan sus contribuciones poco a poco. De vez en cuando un hombre da el paso definitivo.
Lo suficientemente lúcido para distinguir las ideas valiosas de la confusión de las sugerencias y pronunciamientos.
Lo suficientemente imaginativo para encajar las piezas en una nueva explicación.
Lo suficientemente audaz para construir un plan maestro.
En el caso del cálculo ese fue Isaac Newton”El pensamiento matemático, de la antigüedad a nuestros días. Morris Kline. Alianza editorial, 1992. pag.471
Newton, entre 1666 y 1669 desarrolla las ideas fundamentales y expone por primera vez una visión completa del Cálculo infinitesimal en el “Método de las fluxiones y series infinitas”Newton en Methodus fluxionorum et serierum infinitarum (1671), proporciona su explicación más extensa sobre el cálculo de fluxiones que ya había esbozado en “De analysi per aequationes número terminorum infinitas” de 1669, (Sobre el análisis por medio de ecuaciones con un número infinito de términos) donde publica por primera vez sus resultados. (Methodus fluxionum et serierum infinitorum), escrito en 1671, y no publicado hasta 1736, nueve años después de su muerte.
Leibniz descubrió el cálculo unos años más tarde que Newton, entre 1675 y 1676, pero publicó sus descubrimientos antes, entre 1684 y 1686 La primera exposición del cálculo diferencial de Leibniz de 1684 en su obra “Nova methodus pro maximis et minimis, itemque tangentibus, qua nec irrationales quantitates moratur” (Un nuevo método para máximos y mínimos, también para tangentes, que no se ve obstruido por las cantidades fraccionarias ni irracionales).
 Los escritos de Leibniz, de difícil lectura, encontraron en los hermanos Bernoulli unos interpretes extraordinariamente competentes y entusiastas, gracias a los cuales, el cálculo de Leibniz se impuso mayoritariamente en Europa continental, mientras que los matemáticos ingleses defendieron la prioridad de Newton en la invención. Hoy en día se tiene como cierto, que ambos trabajaron de forma independiente y sus contribuciones a la creación de esta nueva rama de las matemáticas, vistas con perspectiva histórica, se complementan.
Los escritos de Leibniz, de difícil lectura, encontraron en los hermanos Bernoulli unos interpretes extraordinariamente competentes y entusiastas, gracias a los cuales, el cálculo de Leibniz se impuso mayoritariamente en Europa continental, mientras que los matemáticos ingleses defendieron la prioridad de Newton en la invención. Hoy en día se tiene como cierto, que ambos trabajaron de forma independiente y sus contribuciones a la creación de esta nueva rama de las matemáticas, vistas con perspectiva histórica, se complementan.
Newton habla de la fluxión de una cantidad variable a lo que hoy llamamos diferencial de esa variable. El cálculo de la “razón última” entre la fluxión de dos variables es lo que hoy llamamos calcular su derivada y cálculo diferencial el procedimiento para obtenerla.
El teorema del binomio es la aportación más temprana de Newton al cálculo.
Newton no aporta ninguna demostración al teorema del Binomio porque probablemente no lo considera necesario. Para Newton se trata de un ejercicio de interpolación, desarrollado en la época que comenzaba sus estudios de matemáticas, para extender las reglas conocidas del álgebra para $\small{{(a+b)}^n}$, al caso de n negativo y racional.
Desarrollar $\small{{(a+b)}^n}$ es un problema sencillo de álgebra si n es un número entero. Por ejemplo para $n=2$ tenemos el desarrollo que todos conocemos: $\small{a^2+ x^2 + 2a\:x}$. Para obtener el desarrollo de $\small{{(a+b)}^n}$ siendo $n$ un número entero positivo, basta repetir la operación y agrupar los términos de la misma potencia de $x$. Si desarrollamos $\small{{(1+x)}^n}$, para $n=3$ y $n=4$, resulta:
$1$
$1+x$
$1+2x+x^2$
$1+3x+3x^2+x^3$
$1+4x+6x^2+4x^3+1x^4$
Comprobamos que los coeficientes se ordenan según el triángulo de Pascal, una regla mnemotécnica que nos permite obtener fácilmente los coeficientes para los sucesivos valores de $\small{{(1+x)}^n}$.
Podemos calcular los diez primeros términos del desarrollo del binomio $(a+x)^n$ para cualquier valor de $a$ y $n$.
Para coeficientes $n$ enteros, la serie obtenida es evidentemente finita, pero para exponentes fraccionarios y negativos se hace infinita, porque el numerador de los coeficientes nunca se anula.
Activando las casillas correspondientes tenemos los desarrollos para ${(a+x^2)}^n$ y ${(a-x^2)}^n$ que se obtienen sustituyendo $x$ por $x^2$ o $-x^2$ en el desarrollo anterior.
Por ejemplo, la ecuación de una circunferencia $x^2 + y^2 =r^2$, se convierte en $y= {(r^2 -x^2})^{1\over 2}$ que podemos desarrollar por el binomio $(a=r^2,\quad n={ 1\over 2})$ y sustituir en el desarrollo $x$ por $-x$. También la función $y=1/(1+x)$, que representa una hipérbola equilátera, se puede escribir $y = (1+x)^{-1}$ y desarrollar por el binomio $(a=1, n=-1)$.
El triángulo de Pascal se obtiene añadiendo filas, cuyo primer y último elemento son un $1$ y los intermedios se obtienen sumando los dos elementos más próximos de la fila anterior.
$1$
$1 \quad 1$
$1 \quad 2 \quad 1$
$1 \quad 3 \quad 3 \quad 1$
$1 \quad 4 \quad 6 \quad 4 \quad 1$
$1 \quad 5 \quad 10 \quad 10 \quad 5\quad 1$
Siguiendo esta regla mnemotécnica podemos obtener la fila número $n$ sin calcular todo el desarrollo. La fila $n$, esta formada por la sucesión:
$$1,\:n,\:\frac{n(n-1)}{1 \cdot 2}, \:\frac{n(n-1)(n-2)}{1 \cdot 2 \cdot 3},\:\frac{n(n-1)(n-2)(n-3)}{1 \cdot 2 \cdot 3 \cdot 4},....$$
Los términos $\large{ {n(n-1)(n-2)(n-3)...(n-(m-1))}\over {(m+1)!}}$ , se escriben actualmente como ${\binom{ n}{m}}$ y se leen, "$n$ sobre $m$"
$$\begin{aligned}\binom{n}{0}&=\small 1 \\ \binom{n}{1}&=\small n \\ \binom{n}{2} &={ \frac{n(n-1)}{1 \cdot 2}}\\ \binom{n}{3}&={ \frac{n(n-1)(n-2)}{1\cdot 2 \cdot 3}} \\ &.......\\ \binom{n}{n}&= \small 1 \end{aligned}$$
Luego podemos escribir el desarrollo que se obtiene para la fila $n$ de la pirámide de Pascal:
$${(a+x)}^n=a^n+\binom{n}{1}\:a^{n-1}x+\binom{n}{2}\:a^{n-2}x^2+...+\binom{n}{n}\:x^n $$
Esta expresión nos lleva a los resultados conocidos para $n$ positivo pero para $n$ negativo o racional nos conduce a una serie de infinitos términos. Este “pequeño detalle” no preocupa a Newton que opera con las series resultantes como si se tratara de un polinomio finito y opera con ellos según las reglas aritméticas habituales para suma, resta, multiplicación y división. Una vez deducida la fórmula para elevar un binomio, a una potencia negativa o racional, su validez se basa en que los resultados obtenidos son consistentes y correctos en los casos en los que se emplea.
El teorema del binomio va a tener un papel protagonista en el desarrollo del cálculo. Newton adquiere la certeza de que el análisis mediante series infinitas tiene la misma consistencia interna que el álgebra de cantidades finitas y que esta regido por las mismas leyes generales. Las series infinitas se convierten de este modo, para Newton, en una forma alternativa de representar una función.
Podemos comprobar que el desarrollo por el binomio de $1+x$ para $n=-1$ coincide con el obtenido por división larga por Mercator. Para el caso $\small{y={(1-x^2)}^{1\over2}}$, que es la la ecuación de una semicircunferencia de radio $1$ se obtiene:
$$y = 1- {1\over2}x^2-{1\over8}x^4 -{1\over16}x^6-....$$
Si multiplicamos esta serie por si misma, obtenemos $\small{(1-x)^2}$.
Newton se basa en en teorema del binomio, recién descubierto, para desarrollar la ecuación de la circunferencia en una serie infinita e integrarla término a término, como había hecho Mercator para la función logarítmica.
Podemos interpretar este desarrollo de Newton como un ejercicio de comprobación de las bases del Cálculo y de la validez de las series de potencias para aproximar funciones.
Newton parte de la ecuación de la circunferencia de radio $1/2$ con centro en $x=1/2$. El área del sector circular con ángulo central de $60º$, es $1/6$ de la del círculo y por tanto igual a: $\large{{π \:{r^2}\over 6} = {π\over24}}$.
Este área se compone del área del triángulo $ABC$ y de la integral de la circunferencia desde $0$ a $1/4$ ya que $1/4$ es la $x$ del punto $B$, al ser el ángulo central del sector $60º$.
Área del triángulo $ABC$: $$ {1\over2} \cdot \:{1\over4} \cdot \:{\lbrack { {1\over4} \cdot (1-{1\over4}) }\rbrack}^{\normalsize{1\over2}}\:= {1\over8} \cdot {({3\over{16}})}^{\normalsize{1\over2}}\:={{3^{\normalsize{1\over2}}}\over{32}}\tag{1}$$
Área de la circunferencia:
La ecuación de la circunferencia es: $ (x-{1\over 2})^2 + y^2 = {1\over4}$
que despejando resulta: $y=x^{\normalsize{1\over2}} (1-x)^{\normalsize{1\over2}}$
Desarrollamos por el binomio ${(1-x)}^{\normalsize{1\over2}}$ y multiplicamos la serie obtenida por $x^{\normalsize{1\over2}}$ y obtenemos:
$$y=x^{1\over2}( 1-0,5 x-0,125x^2-0,05625x^3-0,039062x^4 $$ $$-0,02734x^5-0,0205x^6- \cdot\cdot\cdot)$$e integramos término a término:
$$ y={2\over3}x^ {\large{3\over2}}- {2\over5}(0,5)x^{\large{5\over2}}- {2\over7}0,125 x^{\large{7\over2}}- {2\over9}0,05625x^{\large{9\over2}}- {2\over{11}}0,039062x^{\large{{11}\over2}} - \cdot\cdot\cdot$$Para los 5 primeros términos, para un valor de $x=1/4$ obtenemos.
$$y = 0,0767737720\tag{2}$$
Sustituyendo los valores obtenidos en (1) y (2) para obtener la expresión del área del sector circular cuyo valor sabemos es $π/24$.
$${π\over24} = {{3^{\normalsize{1\over2}}}\over{32}}+ 0,0767737720$$Despejando $π$
$$π = 24\:({{3^{\normalsize{1\over2}}}\over{32}}+ 0,0767737720)= 3,1416074$$Con solo cinco términos de la serie, Newton obtiene 3 decimales exactas y una diferencia con el valor de $π$ $\small{(3,141592654…..)}$ de $\small{0,000014751…}$
Si la inspiración de los primeros trabajos sobre el cálculo fue geométrica, para Newton el estímulo viene de la física. Cuando un punto $A$ se mueve a lo largo de una curva, su abscisa $x$, o su ordenada $y$, o cualquier otra cantidad variable relativa a la curva, aumenta o disminuye, cambia: fluye. A estas cantidades que fluyen las llamó “fluentes” y a sus velocidades de cambio, a sus variaciones instantáneas con respecto al tiempo, las llamó “fluxiones”. De esta manera el cálculo de “fluxiones” esta fundamentado en un concepto natural como es el del cambio y el objeto del mismo es obtener las tasas de ese cambio, intuyendo que las leyes que rigen la física pueden formularse a partir de ellas.
Newton parte de una función del tipo $y=f(t)$, que representa la distancia recorrida por una partícula en función del tiempo transcurrido. La fluxión de $y$ es el espacio recorrido en un instante y la razón de las fluxiones de $f(t)$ y de $t$ es equivalente a hablar de la velocidad de la partícula en ese instante.
De forma general una partícula no se mueve con velocidad uniforme, por lo que es fácil averiguar cual es la velocidad media en un intervalo, pero lo que buscamos es calcular la velocidad en cada instante de ese intervalo. Si dividimos el intervalo considerado en pequeños periodos de tiempo el espacio recorrido es diferente en cada uno de ellos y su velocidad media en el intervalo también.
Veamos por ejemplo la función $y=t^3$, en metros y segundos, y analicemos como se comporta en el intervalo de tiempo entre $0$ y $5$ segundos. Su velocidad media en los $5$ segundos es de $25 m/s$. Hacemos una tabla con la velocidades medias en intervalos de un segundo:
| Intervalo t=1 segundo |
y al inicio m |
y al final m |
$\dot{y}$ | velocidad en el intervalo $({\dot{y}\over t}) = m/s$ |
|---|---|---|---|---|
| 0-1 | 0 | 1 | 1 | 1 |
| 1-2 | 1 | 8 | 7 | 7 |
| 2-3 | 8 | 27 | 19 | 19 |
| 3-4 | 27 | 64 | 37 | 37 |
| 4-5 | 64 | 125 | 71 | 71 |
Queda claro que la velocidad en cada intervalo, el cociente entre la variación (fluxión) del espacio y la variación (fluxión) del tiempo, cambia desde valores inferiores a la velocidad media en el conjunto del intervalo hasta finalizar en $71m/s$, casi el triple del valor medio. ($125/5 =25m/s$). Pero si hacemos la misma tabla para valores de la fluxión de y para intervalos más pequeños, por ejemplo de una décima de segundo, entre el segundo 4 y el 5 obtenemos:
| Intervalo t=0,1 segundo |
y al inicio m |
y al final m |
$\dot{y}$ | velocidad en el intervalo $({\dot{y}\over t}) = m/s$ |
|---|---|---|---|---|
| 4,0 -4,1 | 64,000 | 68,921 | 4,921 | 49,21 |
| 4,1- 4,2 | 68,921 | 74,088 | 5,167 | 51,67 |
| 4,2 - 4,3 | 74,088 | 79,507 | 5,419 | 54,19 |
| 4,3 - 4,4 | 79,507 | 85,184 | 5,677 | 56,77 |
| 4,4 - 4,5 | 85,184 | 91,125 | 5,941 | 59,41 |
| 4,5 - 4,6 | 91,125 | 97,336 | 6,211 | 62,11 |
| 4,6 - 4,7 | 97,336 | 103,823 | 6,487 | 64,87 |
| 4,7- 4,8 | 103,823 | 110,792 | 6,769 | 67,69 |
| 4,8 - 4,9 | 110,792 | 117,649 | 7,057 | 70,57 |
| 4,9 - 5,0 | 117,649 | 125,000 | 7,351 | 73,51 |
La fluxión de y es igual a:
$$\dot{y}=f(t_i+\dot{t})-f(t_i)$$
Reproducimos gráficamente los cálculos que hemos hecho para las tablas de la velocidad media e instantánea.
La función que hemos escogido $f(t)$, $y = x^3$crece muy rápido por lo que hemos deformado la cuadrícula que representa en el eje $x$ los segundos transcurridos y en el eje $y$ la distancia recorrida.
Tomamos un punto $A$ y otro $B$ separado de $A$ por el intervalo $h$ que controlamos con el deslizador y trazamos la recta que los une. Su pendiente nos señala la velocidad media entre $A$ y $B$. Al mover el deslizador, disminuyendo $h$, $B$ se acerca a $A$ y la recta que los une se convierte en la tangente en $A$ y su pendiente es la velocidad instantánea en ese instante.
Podemos mover el punto $A$ sobre la curva e ir obteniendo los resultados de las tablas numéricas que hemos calculado para el intervalo entre el segundo 4 y 5.
Si construimos una curva con los valores de la tangente en cada punto obtenemos la derivada de $y = x^3$que es la parábola $y=3x^2$ en trazo negro.
Podemos ver que la fluxión de $y$ en el instante $4,9$ es de $7,351 m$ para un valor de la fluxión de $t$ de $0,1 s$. La relación entre la fluxión de $y$ respecto de $t$ (la velocidad media entre $4,9$ y $5 s$) ha pasado de ser $71m/s$ a $73,51 m/s$.
Y si dividimos nuevamente el intervalo de la décima de segundo entre las centésimas 4, 9 y 5, rehaciendo los cálculos tenemos:
| Intervalo t=0,01 segundo |
y al inicio m |
y al final m |
$\large{\dot{y}}$ | velocidad en el intervalo $({\.{y}\over t}) = m/s$ |
|---|---|---|---|---|
| 4,90 -4,91 | 117,649 | 118,370771 | 0,721771 | 72,1771 |
| 4,91- 4,92 | 118,370771 | 119,095488 | 0,724717 | 72,4717 |
| 4,92 -4,93 | 119,095488 | 119,823157 | 0,727669 | 72,7669 |
| 4,93-4,94 | 119,823157 | 120,553784 | 0,730627 | 73,0627 |
| 4,94 -4,95 | 120,553784 | 121,287375 | 0,733591 | 73,3591 |
| 4,95-4,96 | 121,287375 | 122,023936 | 0,736561 | 73,6561 |
| 4,96 -4,97 | 122,023936 | 122,763473 | 0,739537 | 73,9537 |
| 4,97- 4,98 | 122,763473 | 123,505992 | 0,742519 | 74,2519 |
| 4,98 -4,99 | 123,505992 | 124,251499 | 0,745507 | 74,5507 |
| 4,99 - 5,00 | 124,251499 | 125,000000 | 0,748501 | 74,8501 |
Ahora la velocidad en 5 ya es de $74,8501 m/s$.
Cada vez que disminuimos el intervalo, el valor calculado de la velocidad en el segundo 5 aumenta. ¿Hasta que valor?
La velocidad en cada instante es igual al cociente de la fluxión de "$y$" respecto de la de "$t$" por lo que obtenemos:
$$v={{{(t+\.{t})}^3-{t^3}}\over\.{t}}$$
$$ v= {{(t^3+3\:t^2\.{t}+3\:t\:{\.t}^2+{\.t}^{\:3})-t^3}\over {\.t}}= 3\:t^2+3\:t\:{\.t}+{\.t}^{\:2}$$
y como $ \.{t}$ es cada vez más pequeño, acercándose a $0$, despreciamos los términos segundo y tercero que van a resultar cada vez más pequeños y obtenemos.
$$v=3t^2$$
Particularizando para $t=5 seg$ el resultado exacto es $75 m/seg$, que es la velocidad instantánea al final del tramo.
La interpretación cinemática de la fluxión del espacio recorrido por una partícula en relación al tiempo, es la velocidad instantánea en ese punto. La aguja del tablero del coche que indica la velocidad, nos da el valor de la razón de cambio entre las fluxiones en cada instante, la velocidad instantánea. La velocidad media es el resultado de agregar la velocidad instantánea de cada uno de los puntos de un recorrido.
Pero, ¿existe la velocidad instantánea? o más bien, la velocidad instantánea es un concepto teórico. Cualquier medición de velocidad que hagamos se referirá a un intervalo de tiempo, por pequeño que sea, y nunca obtendremos una velocidad instantánea mediante una medición.
La velocidad instantánea no es una velocidad en el sentido que nos define la física. Hemos dado un paso que tiene todo el aspecto de haber sido poco riguroso.
Hemos estudiado el caso de una función $y=f(t)$. Podemos aplicar el cálculo de fluxiones al caso de una curva de ecuación $f(x, y)= 0$. Si ponemos la curva en forma paramétrica en función de $t$, de acuerdo con la visión de Newton imaginamos la curva como un punto en movimiento:
$$\small{y=f_1(t)\quad \quad x=f_2(t)}$$y calculamos para cada función la razón del cambio respecto de $t$:
$${{\.{y}}\over{\.{t}}}\quad \quad {{\.{x}}\over{\.{t}}}$$Según lo que hemos visto anteriormente, los cocientes nos definen la velocidad instantánea en la dirección de cada eje de coordenadas.
Puesto que nos referimos al mismo instante, $\:\.{t}$ tiene el mismo valor en ambos casos y podemos simplificar la fracción:
$${\displaystyle{ {\dot{y} }\over{\dot{t}} } \over\displaystyle{ {\dot{x}}\over{\dot{t}} }}={{\dot{y}}\over{\dot{x}}}$$Una vez tenemos el cociente de fluxiones, hay que calcular la "razón última" entre ellas. Newton explica así el proceso de cálculo:
La razón entre las fluxiones es el cambio relativo de una variable con respecto a otra. Cuando la variable independiente era el tiempo, el cambio relativo del espacio respecto del tiempo nos daba la velocidad instantánea. En el caso de una curva, una función $f(x y)= 0$, el cambio relativo nos proporciona el valor de la pendiente en ese punto de la tangente a la curva.
Podemos observar como construimos la representación de la función derivada a partir de la secante que pasa por dos puntos $A$ y $B$ distantes entre sí $Δx$, y trasladamos el valor de la pendiente de la secante, obteniendo un “escalón” horizontal de ancho $Δx$. Al disminuir $Δx$, la función derivada se dibuja con más precisión. Es la visión de Leibniz que interpreta una función como una sucesión de escalones de ancho $dx$ y de altura $dy$, que al hacerse $dx$ cada vez más pequeño se suaviza y se convierte en una línea continua.
También podemos observar que la relación entre una función y su derivada sigue unas determinada reglas.
Por ejemplo. Cuando la función pasa por un máximo, la derivada se hace $0$. Geométricamente podemos decir que la tangente en ese punto es horizontal. Antes de un máximo, la función es creciente y la pendiente de su tangente es positiva. Rebasado el máximo la pendiente se vuelve negativa y la función decrece.
El mismo razonamiento, en sentido contrario, se puede hacer para los puntos en que la función sea mínima.
Lo que Newton llama “fluxiones”, para Leibniz son diferenciales o infinitesimales. El cálculo de Leibniz obtiene sus resultados mediante la manipulación de estos infinitesimales.
Una curva es una sucesión de tramos rectos, “infinitamente pequeños”, pequeños tramos que se corresponden con la hipotenusa del triángulo de diferenciales. Esto permite identificar la derivada, que es el cociente de diferenciales, $\large {dy \over dx} $, como la pendiente de la recta tangente en el punto en el que calculamos la derivada. Es exactamente el razonamiento que hemos visto en Fermat, con diferente notación. Como vemos, la derivada tiene una interpretación geométrica sencilla, que es muy útil para plantear y resolver problemas.
Leibniz utilizaba el símbolo $Δ$ para expresar la diferencia de las variables para puntos próximos. El cociente de incrementos $Δy/Δx$, siendo $Δx$ la variación de $x$. La variación de $y$ es, $Δy = f(x+ Δx)-f(x)$, y resulta:
$${{Δy}\over{Δx}}= {{f(x+Δx)-f(x)} \over{Δx}} $$
$Δy$ y $Δx$ se transforman en $dy$ y $dx$ cuando $Δx$ se hace “infinitamente pequeño”, sin ser $0$, pero "más pequeño que cualquier número real positivo".
Así, $dy$ y $dx$ se corresponden con lo que Newton escribía como $\.y$ o $\.x$. La notación de Leibniz se ha impuesto como la estándar del cálculo, porque tiene la ventaja de ser más expresiva y resumir el proceso del cálculo como cociente de diferenciales y probablemente también, porque es tipográficamente más clara, evitando erratas de impresión.
Newton y Leibniz llegan al mismo punto, que intuitivamente es muy claro y que da resultados prácticos, pero no lo demuestran con rigor porque un cociente de diferenciales o de fluxiones no es únicamente una división de incrementos. Falta explicar cómo podemos ir obteniendo valores finitos de la función, al dividir por una cantidad que decimos que es cada vez más pequeña. Si el $dx = Δx$ se hace $0$ en el denominador, obtenemos $0/0$ que es un valor indeterminado. Luego estamos ante una fórmula que funciona para valores tan pequeños como queramos de $Δx$, pero no parece que sea así para $Δx =0$.
A pesar de este comportamiento especial de los diferenciales, el Cálculo opera con ellos como si fueran números ordinarios. No es de extrañar que para los contemporáneos de Newton y Leibniz los diferenciales tuvieran un aire mágico.
La crítica a la fundamentación del cálculo estaba justificada en parte y se nutrió de la incapacidad de Newton y Leibniz de clarificar sus conceptos básicos. En realidad, estaban introduciendo conceptos radicalmente nuevos que requerían de unos cimientos propios que tardaran más de un siglo en llegar.
Infinito actual e infinito potencial
En la Metafísica de Aristóteles los entes pueden estar en acto, es decir, existir, estar completos en presente, o en potencia, que requieren completarse para devenir actuales. Así, cuando cualificamos una entidad como infinita, nos podemos referir a un “infinito actual” o a un “infinito potencial”. Un número potencialmente infinito es el que tiene la capacidad de crecer indefinidamente para convertirse en infinito.
Los infinitésimos de los inventores del cálculo son infinitésimos actuales porque son números que son más pequeños que cualquier número, pero no son $0$ y siendo números reales, siguen las reglas del álgebra. Aceptar un infinito actual, incluso imaginarlo es difícil. Para Aristóteles el infinito actual es un atributo divino.
Leibniz, ante las dificultades de definición, admite que los infinitesimales no son “magnitudes ordinarias”, sino objetos ideales que resultan útiles porque permiten obtener resultados correctos.
Hemos visto como Newton, en uno de sus intentos para explicar el procedimiento para obtener lo que llama razones últimas, utiliza un lenguaje en el camino de describir un infinito potencial.
La derivación o diferenciación es una nueva operación que se aplica a funciones mediante la cual se obtiene una función “derivada” de la función “primitiva”. Esta operación podemos repetirla sobre la función derivada y obtenemos la segunda derivada de la función primitiva.
La derivada de una función $f$ se indica como $f^{\prime}$ y su valor en $x$, $f^{\prime}(x)$.
$$y^{\prime}=f^{\prime}(x) = {{dy}\over{dx}}$$
Análogamente la derivada segunda se indica como:
$$y^{\prime\prime}= f^{\prime\prime}(x) = {{dy^{\prime}}\over{dx}}$$
y así sucesivamente las de orden superior. Para las derivadas de orden superior a tres, la notación más habitual es escribir $\small{f^{(n)}}$, siendo $n$, entre paréntesis, el orden de la derivada.
Si consideramos la velocidad instantánea obtenida en el anterior cálculo como “fluente”, es decir, magnitud sujeta a variación, también podemos obtener la fluxión de la velocidad instantánea con el tiempo, en este caso sería la aceleración instantánea (en el caso de un movimiento rectilíneo), de modo que constatamos que podemos aplicar el cálculo de fluxiones a una función y obtener sucesivamente fluxiones de primer orden, segundo orden, etc.
En el caso de que obtengamos una constante, como resultado en alguno de los sucesivos cálculos, el proceso se detiene, puesto que un cantidad constante no puede considerarse fluyente y su fluxión es $0$.
Queda por discutir que condiciones debe cumplir una función para ser derivable, es decir, si la derivación es posible para todas las funciones y para todos sus puntos.
Si nos atenemos a la interpretación geométrica de la derivada, para que exista la derivada de una función en un punto, debe ser posible trazar una tangente a la curva en ese punto. Determinadas funciones presentan puntos singulares en los que no es posible trazar una tangente. Si seguimos con la interpretación gráfica, las funciones derivables son aquellas que se llaman “localmente lineales” concepto que expresa que si ampliamos la gráfica de la función en el entorno de un punto, su gráfica se suaviza y se aproxima cada vez más a la tangente.
Esto no se da cuando estamos en un punto “anguloso”, que sigue apreciándose al ampliar la gráfica de la función.
Otros puntos en el que tampoco es derivable una función son los de tangente vertical, en los que la pendiente se hace infinita.
Este análisis, sobre los requisitos de una función para ser derivable, requiere una maduración del concepto de función que no se da en la época. Las propiedades de las funciones se asociaban a ellas globalmente y no existía el análisis de sus propiedades locales, es decir, de las que se refieren a sus puntos singulares.
Una vez resuelta, mediante la derivación, la obtención de la tasa de cambio entre las variables de una función, se plantea el problema inverso que consiste en obtener, si es posible, una función de la que se conoce su derivada.
Seguimos con el ejemplo sobre la velocidad de una partícula que se mueve de acuerdo con la ecuación $\small{y=f(t)=t^3}$, siendo $y$ el espacio recorrido y $t$ el tiempo. Hemos obtenido la derivada de esta función, $\small {y=3\:t^2}$, que geométricamente se interpreta como la pendiente de la tangente de la función $\small{y=t^3}$ y cinemáticamente es el valor de lo que hemos llamado velocidad instantánea.
De forma semejante a como hicimos para la derivada, podemos construir el siguiente cuadro de valores de la función derivada, refiriéndonos a periodos de $1$ segundo en el intervalo de $0$ a $5$ segundos y calcular el espacio recorrido a esta velocidad en el periodo.
Si nos atenemos a la interpretación física, multiplicando una velocidad, suponiendo constante la velocidad instantánea en ese intervalo, por el tiempo en el que se mantiene obtenemos el espacio recorrido.
| Intervalo t=1 segundo |
y al inicio m |
y al final m |
Espació recorrido inicial y final |
|
|---|---|---|---|---|
| 0-1 | 0 | 3 | 0 | 3 |
| 1-2 | 3 | 12 | 3 | 12 |
| 2-3 | 12 | 27 | 12 | 27 |
| 3-4 | 27 | 48 | 27 | 48 |
| 4-5 | 48 | 75 | 48 | 75 |
| Área 0-5 | 90 | 165 | ||
Si repetimos el cálculo para intervalos de tiempo más cortos obtendremos los resultados que resumimos en el cuadro siguiente:
| Intervalo en segundos |
Espacio recorrido inicial y final |
|
|---|---|---|
| 1 | 90 | 165 |
| 0,1 | 121,275 | 128,775 |
| 0,01 | 124,62525 | 125,3725 |
El cálculo que hacemos es equivalente a obtener una aproximación del área bajo la curva $\small{y=3\:x^2}$ mediante la suma de rectángulos de base el intervalo de tiempo definido y altura el valor de $\small{y=3\:x^2}$ al inicio o al final del intervalo. Podemos ver que el área calculada mediante la suma de rectángulos nos lleva, al disminuir el intervalo, a un valor que se aproxima progresivamente al del espacio recorrido en el intervalo, es decir, $y=t^3$, para $t=5$ que es $125$ metros. El área bajo la derivada de una función nos devuelve la función inicial.
Este resultado coincide plenamente con el obtenido analíticamente por Fermat para la obtención de la tangente y la cuadratura de curvas exponenciales. Para curvas del tipo, $\small{y= a x^n}$, Fermat ha demostrado que el área bajo la curva es:
$$y=\frac{a\:x^{n+1}}{n+1}$$
cuya derivada nos devuelve la función original.
Fermat no presta atención a esta relación entre ambas fórmulas, y tampoco lo hicieron ninguno de los matemáticos que los estudiaron posteriormente.
Hemos de comprender que esta conexión se plantea para una familia de funciones en particular y las fórmulas proceden de la resolución de problemas diferentes, la tangente y el área bajo una curva, con metodología diferente y esto puede explicar que no se atribuyera una validez general a la coincidencia de los resultados .
También hemos visto que la relación descubierta por Saint Vincent, entre la hipérbola equilátera y la curva logarítmica, apuntaba a relacionar un problema con otro, como hizo Mercator, pero en este caso la función logarítmica aun no estaba suficientemente estudiada.
Para demostrar la relación entre el problema del cálculo de las áreas y las fluxiones, Newton plantea construir una curva $f(x)$ de manera que el área que encierra con el eje $X$ varía según $A(x)$, que llamaremos función de áreas de $f(x)$.
A partir de la expresión de la variación de la función de áreas cuando nos desplazamos de $A(x)$ a un punto próximo $A(x+dx)$, podemos poner:
$A(x)+f(x) dx= A(x+dx)$
Que nos conduce directamente al cociente incremental de $A(x)$, cuya "razón última" es lo que hemos llamado $A'$, derivada de $A(x)$.
$$f(x)=\frac{A(x+dx)-A(x)}{dx}$$
Las áreas contenidas bajo una curva $f(x)$ pueden obtenerse invirtiendo el proceso de derivación, es decir, obteniendo una función $A(x)$ cuya derivada sea precisamente $f(x)$.
Newton llama a esta operación, que nos permite obtener una función a partir de su derivada o fluxión el método inverso de las fluxiones.
Inicio de la demostración.
Si la función de áreas $A(x)$ es una función exponencial, del tipo $\small{a\:x^m}$, con exponente m entero o fraccionario, si incrementamos $x$ en $dx$ podemos establecer la igualdad,
$A(x)+f(x) dx= A(x+dx) = a(x+dx)^m$
Desarrollando por el binomio el segundo término obtenemos:
$$A(x)\:+\:f(x)\:dx\:=\:a\:x^m+a\:m\:x^{m-1}dx+\frac{a\:(m^2-m)}{2}x^{m-2}dx^2+...$$
y restando a cada lado la función inicial:
$$f(x)\:dx\:=\:a\:m\:x^{m-1}dx+\frac{a\:(m^2-m)}{2}x^{m-2}dx^2+...$$
Dividiendo por $dx$, cuando el diferencial se hace igual a $0$, desaparecen los términos con $dx$ y obtenemos:
$$f(x)\:=\:a\:m\:x^{m-1}$$
El resultado nos demuestra que $f(x)$ es la derivada de $A(x)$,
$$A'(x)\:=\:a\:m\:x^{m-1}=f(x)$$
Final de la demostración.
A pesar de tratarse, como en el caso de Fermat, de una demostración para un tipo particular de funciones, $f(x)$ y su función de áreas, se ponen en relación directamente en una sola demostración, cuando en el caso de Fermat la similitud suponía relacionar resultados obtenidos en diferentes problemas. El teorema del binomio toma protagonismo convirtiendo definitivamente las series infinitas en el corazón del cálculo.
A la operación inversa a la derivación, Leibniz le puso el nombre de Integración, considerablemente más práctico que “método inverso de las fluxiones” de Newton. La función obtenida por la integración de $f(x)$, es la “primitiva” de la función, a la que hemos llamado al inicio “función de áreas” y que llamaremos en adelante $P(x)$. (Por la $P$ de primitiva).
A diferencia del caso de la derivación donde el resultado de la operación es único, para la integración esto no es así, porque todas las funciones que se diferencian solo en un término constante, tienen la misma derivada. Si:
Partimos de una función $y=f(x)$ dibujada en violeta. Para cada punto obtenemos el valor de la tangente, que se corresponde al valor de la derivada en ese punto, y construimos la línea verde, que representa $y'= f '(x)$, es decir, la función derivada de $f(x)$.
Moviendo los puntos con el deslizador comprobamos que la construcción es correcta. Cuando la función es creciente la tangente es positiva y se transforma en negativa al decrecer. El máximo de la función se corresponde con $y'=0$.
Activando la casilla de anti derivada: Si obtenemos $f(x)$ a partir de $f‘(x)$, calculando la función cuya derivada se corresponda con la función verde y situamos $M$ en el origen, $y(M) =0$, comprobamos que el área verde se corresponde con la ordenada del punto $L$. Es decir, el área bajo una curva se puede obtener calculando su “anti derivada”. Para acotar el área bajo una curva tenemos que definir un punto de origen y un punto final. En este caso nuestro origen es el punto $M$ situado en $x=0$ y el área verde se calcula desde $x=0$ a $x=x(L)$.
Si movemos el punto $M$, el área se calcula desde $x(M)$ a $x(L)$ y comprobamos que su valor se corresponde con la diferencia entre las ordenadas de $L$ y $M$.
Es evidente la propiedad aditiva de las áreas, es decir, el área entre $M$ y $L$ es igual al área hasta $L$ menos el área hasta $M$.
$y = P(x)+ C, \Lrarr y'= P'(x) + 0 = P'(x)$
La constante $C$ es lo que se llama constante de integración. Mediante la integración de $f(x)$ hemos obtenido una nueva función $P(x)$ que nos define como varía el área bajo ella, salvo en una constante.
Esta indeterminación tiene lógica. En el caso de la función derivada, solo necesitamos concretar un valor de $x$, para identificar el punto en el que queremos obtener la pendiente de la tangente. Para obtener la magnitud del área bajo una curva necesitamos especificar un intervalo, es decir, dos valores de $x$ para la función integral. Es lo mismo que decir que, el valor del área en un punto depende del punto desde donde empecemos a contar.
El segundo teorema del cálculo afirma que, la integral interpretada como un área, es decir, una magnitud asociada a un intervalo de la curva, se obtiene como la diferencia de valor de la función primitiva en los puntos extremos del intervalo de cálculo. La magnitud obtenida se llama Integral definida.
Si $P(x)$ es integrable en el intervalo $[a,b]$, para un punto $c$ que pertenece a ese intervalo, podemos afirmar que la áreas cumplen:
$A(c,b)= A(a,b) - A(a,c)$
La función primitiva se puede diferenciar de la función de áreas en la constante de integración, por lo tanto el área en $B$ y en $C$ la podemos expresar como: $A(a,b) = P(b)+C$ y, $A(a,c) = P(c)+C$. Sustituyendo:
$A(c,b)=P(b)+C-P(c)+C \\ A (c,b)=P(b)-P(c)$
Es decir, la constante de integración no interviene cuando calculamos el área bajo una curva entre dos puntos:
Si $f(x)=P'(x)$, el área bajo $f(x)$ entre $c$ y $b$ es $P(b)-P(c)$.
Hemos visto como el problema de las áreas bajo una curva queda resuelto según el teorema general del cálculo obteniendo su anti derivada. Es sin duda la manera más sencilla de obtener el área bajo una curva una vez conocida su ecuación.
Hemos visto también como Fermat procedía mediante la suma de rectángulos de base infinitesimal y de altura dada por la ecuación de la curva. Tenemos pues dos aproximaciones al cálculo del área bajo una curva. El método “revolucionario” mediante la obtención de la anti derivada y el método “clásico-geométrico” de obtención de las sumas de los rectángulos infinitesimales. Obviamente ambos métodos nos deberían conducir al mismo resultado y curiosamente en este punto Newton y Leibniz optan por priorizar aproximaciones diferentes. Leibniz opta por definir la integral como la suma de áreas infinitesimales.
El área bajo una curva se obtiene dividiendo el intervalo de integración en pequeños elementos $Δx$. Para cada uno de estos elementos, la función toma un valor y puede aproximarse el area del rectángulo de base $Δx$, tomando un valor de la función en el intervalo $Δx$. La integral definida es la suma de estas áreas, cuando la base de los rectángulos $Δx$ disminuye, y se confunde con $dx$. La integral es pues una suma de infinitos términos, lo que en principio parece algo difícil de ejecutar, o al menos de acabar de ejecutar en un tiempo finito. (La suma no esta definida para un número infinito de sumandos).
Esta interpretación de la integrales es igual a la planteada por Fermat y recuerda la idea de los indivisibles de Cavalieri y su descomposición de un área en líneas de grosor infinitesimal. La imprecisión del concepto de infinitesimal nos vuelve a llevar a un terreno intuitivamente correcto pero con una fundamentación endeble.
Si consideramos un incremento de $x$ pequeño ($Δx$), podemos calcular el área de un rectángulo de base $Δx$ y altura $f(x)$, o un rectángulo de base $Δx$ y altura $f(x+Δt)$. El área bajo la curva para $Δx$ es una cantidad entre el primer valor y el segundo. Podemos deducir dos cosas:
Podemos comprobar la propiedad aditiva de la integral definida moviendo los límites de integración con el deslizador.
Si movemos el límite superior de integración vamos obteniendo un valor del área bajo la curva que trasladamos al punto de color. Al mover el deslizador nuestro punto va describiendo un recorrido que representa la función integral.
El símbolo elegido por Leibniz para la integración, con su forma de $S$, quiere expresar el sumatorio de elementos en los que se basa su concepto de integral, para el cálculo de la magnitud del área bajo la curva en ese intervalo $[a,b]$:
$${\int}_{a}^b f(x) \:dx$$
que según el teorema general del cálculo es igual a $P(b)-P(a)$.
Para designar una primitiva de $f(x)$ emplea:
$$P(x)={\int}_{c}^x f(t) \:dt$$
Lo que esta notación nos dice es que la variable $x$ de la función primitiva se corresponde con el extremo del intervalo de integración, es decir, que $P(x)$ es el valor del área bajo $f(t)$, desde $t=c$, hasta $t=x$.
Por esta razón hemos puesto $t$ en lugar de $x$, diferenciando el valor de la variable en el intervalo y su valor en el extremo del intervalo de integración.
Si suprimimos la concreción del intervalo de integración y añadimos la constante de integración nos queda la notación para una función primitiva:
$$ {\int} f(x) \:dx=\:P(x)+C$$
$$ {\int} f(x) \:dx=\:{\int}_{c}^x f(t) \:dt+C$$
A pesar de utilizar el mismo símbolo de la integral definida estas expresiones tienen un significado muy diferente.
El segundo teorema del cálculo nos define áreas de signo positivo y negativo según lo sea $P(b) - P(a)$. Si el intervalo de integración es $b > a$, las áreas sobre el eje $X$ (y positivas) son positivas y bajo el eje $X$ negativas. En caso contrario, es decir, el intervalo de integración se define de derecha a izquierda, las áreas sobre el eje $X$ (y positivas) son negativas y las áreas bajo el eje $X$ (y negativas) son positivas.
Para calcular correctamente el área bajo una curva es necesario tener en cuenta esta regla sobre los signos, para no sumar algebraicamente áreas positivas y negativas. En el intervalo de integración la curva no debe cambiar de signo si queremos obtener un resultado que se corresponda con la magnitud del área desde el punto de vista geométrico. Por este motivo el procedimiento habitual para el cálculo de áreas comienza con la obtención de las raíces de la función a integrar, eligiendo estos valores de $x$ como extremos de los intervalos de integración, podemos calcular por separado las áreas positivas y negativas del intervalo. Para obtener un resultado geométricamente correcto sumaremos su valor absoluto.
Para el cálculo de una integral definida solo en casos singulares podemos obtener una expresión de la suma de áreas de base $Δx$ que nos permita el cálculo exacto de su valor. Para algunas funciones este procedimiento puede ser muy laborioso y en algunos casos incluso imposible.
El método alternativo para calcular la integral definida consiste en aplicar métodos numéricos. La integración numérica es un procedimiento de aproximaciones sucesivas, calculando en cada paso una suma de áreas, obteniendo una sucesión de valores que se aproximan progresivamente al valor de la integral, deteniendo el cálculo cuando dos aproximaciones sucesivas difieran en valor absoluto en una cantidad menor que el error que asumimos para la aproximación. Estamos ante una ejecución muy laboriosa y de resultados que pueden ser poco precisos. (hemos visto antes, al hablar de Fermat, que necesitábamos 60 divisiones para obtener dos decimales correctas de $\small{y=x^4}$ y de $\small{y=x^9}$.
A pesar de ello, esta aproximación al cálculo de la integral definida es hoy en día, con la potencia de cálculo de los ordenadores, una estrategia abordable. El problema se traslada entonces a la búsqueda de un algoritmo para optimizar los cálculos que aproximen el resultado final de forma lo más rápida y eficiente posible.
El método de Simpson (Thomas Simpson 1710-1761) consiste en dividir el intervalo a integrar en un número par de segmentos y calcular el área de dos de estos intervalos, sustituyendo la función a integrar por una parábola que pasa por los puntos $f(A)$, $f((A+B)/2)$ y $f(B)$ siendo $A$ y $B$ los extremos de los dos segmentos consecutivos.
El método de Simpson es una buena forma de calcular la integral definida, porque con su aplicación se requieren menos cálculos para la misma precisión, y se obtiene mucho más rápidamente el resultado.
Para obtener la fórmula de Simpson vamos calcular el área bajo una parábola a partir del área del triángulo inscrito, con vértices en lo que hemos llamado $f(A)$, $f(B)$ y en el punto medio $f((A+B)/2)=f(C)$. El área contenida bajo la parábola es $4/3$ del área de este triángulo inscrito según un teorema clásico de Arquímedes que Kepler conocía perfectamente. El área del triángulo se puede calcular conociendo sus tres lados, (fórmula de Herón) por lo que el problema queda resuelto haciendo las operaciones y simplificando. Área = $4/3$ Área del triángulo inscrito + Área $ABED$.
Área del triángulo inscrito $ACB = x(C) [y(A)-y(B)] + x(A)[y(B)-y(C)] + x(B) [y(C)-y(A)]$
Área $ABED = [x(B)-x(A)] [y(A)+y(B)]/2$.
Y efectuando las operaciones resulta:
Área = $[x(B) - x(A)] [y (A) + 4 y(C) + y (B)] / 6$.
Podemos comprobar que el resultado resulta válido sean cuales sean los tres puntos sobre la parábola.
Por último, podemos comprobar que la fórmula de Simpson se aproxima al resultado de forma más eficiente que el cálculo mediante rectángulos. También calculamos una aproximación mediante una recta en lugar de la parábola de Simpson. Como era de esperar su resultado, mediante trapecios, es una media del cálculo con rectángulos superiores e inferiores.
La formación del concepto de función (III)
las funciones de la física.
La palabra función apareció publicada por vez primera en un artículo de Leibniz de 1692. La idea esta ligada, en su nacimiento, al tratamiento de los problemas geométricos con el lenguaje del Cálculo.
El acercamiento del Cálculo a los problemas de la física impulsa una gran evolución del concepto de función. Para Newton, el concepto de función se independiza de la geometría y en consecuencia se vuelve mucho más abstracto.
Una función expresa la dependencia de unas magnitudes con otras y el Cálculo describe como varían estas magnitudes instantáneamente.
Es fácil ver, que el nivel de abstracción alcanzado permitirá generalizar el concepto, no solo a funciones de tres variables, que pueden imaginarse en el espacio tridimensional, sino a funciones de n variables sin posible representación gráfica.
Al identificar la diferenciación y la integración como operaciones que se aplican a las funciones y que las transforman en otras nuevas se desvincula finalmente a las funciones de su representación geométrica o física. La funciones, ellas mismas, son objetos que se transforman en otros, mediante las operaciones del Cálculo.
Estas operaciones abren la puerta a la definición y manipulación de nuevas funciones. Por ejemplo hemos visto como los logaritmos pueden definirse como una función primitiva de la hipérbola. Del mismo modo veremos que las funciones trigonométricas se definen a partir del Cálculo mediante integración del área bajo el círculo unidad.
Continuar con la formación del concepto de función -IV-
Volver a -II-
Las herramientas del Cálculo son decisivas para la definición de nuevas funciones y un gran impulso para el avance del concepto mismo de función.
Para iniciar este panorama de nuevas funciones, estudiamos la conversión de las tablas logarítmicas en una función a partir de la relación descubierta desde los inicios del cálculo entre “la cuadratura” del área bajo la hipérbola de ecuación $\small{y \cdot x = 1}$ , y los logaritmos.
Entre las primeras funciones en concretarse están las funciones trigonométricas, vinculadas al círculo, mediante la integración de la ecuación de la circunferencia.
También presentamos las funciones hiperbólicas, que surgen repitiendo casi exactamente el procedimiento utilizado para las trigonométricas sustituyendo la ecuación de la circunferencia, $\small{x^2+y^2=1}$, por la de la hipérbola equilátera, $\small{x^2-y^2=1}$, que se diferencian exclusivamente en un signo.
Si interpretamos, a la luz del teorema fundamental del cálculo, el resultado de Saint Vincent sobre la proporcionalidad entre el área definida bajo la hipérbola $x·y=1$ desde $1$ hasta $x$ con los logaritmos, queda establecido que podemos definir una función que llamaremos logarítmica como:
$${log_a {x}}=k_a\: {\int_{1}^{x}}{{1\over{t}}}dt,\quad para \:x > 1$$
Para $x<1$ el área, según el teorema fundamental del cálculo será negativa, por lo que podemos extender la definición de la función para todos $x>0$, pero no para $x=0$, ya que para este valor la función se hace infinita. Como hemos visto al presentar las tablas de logaritmos en el apartado 2.1, los logaritmos de diferente base mantienen, para todo $x>0$, una proporción constante:
$$\frac{log_a{x}}{log_b{x}}=k\tag{5.1}$$
Este coeficiente de proporcionalidad, es el mismo para todo $x$ y por lo tanto, podemos calcularlo conociendo el logaritmo en dos bases diferentes de cualquier valor particular de $x$.
Esto significa que existe una función logarítmica, que llamaremos logaritmo natural, para la que reservamos la notación especial $ln (x)$, que nos puede servir como unidad de medida, para comparar funciones logarítmicas de diferente base.
Los logaritmos naturales son aquellos para los que $k=1$ y se cumple:
$${ln\: {x}}={\int_{1}^{x}}{{ 1\over{t}}}dt,\quad para\: x > 0$$
Las ordenadas de la función ln se corresponden exactamente con el área bajo la hipérbola $x · y =1$, lo que justifica que también se llame a estos logaritmos hiperbólicos.
Queda por averiguar cual es la base de estos logaritmos en particular. Teniendo en cuenta que para los logaritmos siempre se cumple que el logaritmo de su base es igual a $1$, ($\small{log_a{a} =1}$), la base de los logaritmos naturales será igual al valor de $x$ para el que el área bajo la hipérbola sea igual a $1$. Es decir, el valor que buscamos es aquel para el que se cumple:
$$ 1={\int_{1}^{x}}{{ 1\over {t}}}\:dt$$
Si en la expresión (5.1) hacemos:
$$\frac{log_a{x}}{ln\:{x}}=k$$
Según el convenio de signos para la integral definida, la función logarítmica para valores de $x>1$ es positiva y para valores de $x$ entre $0$ y $1$ es negativa. La función no esta definida para $x=0$. Al acercarse a $0$ los valores de la función logarítmica de cualquier base tienden a $-\infty $. Todas las funciones logarítmicas cortan el eje $x$ en $x=1$, puesto que cualquier número elevado a $0$ resulta ser $1$.
y por lo tanto:
$${\frac{log_a{a}}{ln\:{a}}}=k_a={\frac{1}{ln\:{a}}}$$
Con lo que la definición inicial se convierte en:
$${log_a \:{x}}={\frac{1}{Ln\:{a}}\:{\int_{1}^{x}}{1\over{t}}}dt\quad para\: x > 0 $$
Si hacemos una tabla de las derivadas de la potencias de $x^n$, con todos los valores posibles de $n$, vemos que falta una función cuya derivada sea $x^{-1}$ para completar la tabla con todos los exponentes enteros de $x$ (positivos y negativos).
| Función | Derivada |
|---|---|
| k xn | k n xn-1 |
| k x1 | k x0 |
| logax | ka x-1 |
| k x-1 | -k x-2 |
| k n x-n | -k n x(n-1) |
Con la derivada de la función logarítmica completamos la tabla con el único caso en el que la función $x^n$ no se obtiene como derivada de otra potencia de $x$, aunque aun nos queda por determinar el factor de proporcionalidad $k_a$.
A tener en cuenta que al estar definida la función logarítmica solo para valores de $x$ positivos, la integral de la hipérbola solo es válida para su rama positiva. Esta dificultad se salva asignando como integral para valores negativos de $x$, $log_a |x|$.
Consecuencia directa de su definición como función, podemos concluir que la derivada de una función logarítmica es, para los valores del dominio definido para la función ($x>0$):
[5.2]
$${log'_a{x}}=\frac{1}{ln\:{a}}\:{1\over{x}}$$
y para los logaritmos naturales:
[5.3]
$${ln'{x}}={1\over{x}}$$
Esta definición de la función logarítmica es válida para valores reales de $x$, mejorando la definición inicial de los logaritmos como operación inversa de la exponencial, que solo contemplaba valores de $x$ naturales y racionales.
Hemos visto que expresar las razones trigonométricas en función de su ángulo central en grados es una decisión basada en su utilidad para construir aparatos de medición sencillos, pero totalmente arbitraria desde el punto de vista matemático. Como en el caso de los logaritmos nos encontramos con la dificultad adicional de que los grados están definidos para valores racionales, por lo que la definición es insuficiente si queremos definir funciones válidas para todo los números reales.
Para convertir las razones trigonométricas en funciones de variable real, es conveniente abordar una nueva definición de la magnitud del ángulo central. Probablemente la utilidad de esta nueva definición se puso de manifiesto en los diferentes estudios sobre la cicloide, pero su impulso definitivo se debe a la aparición del Cálculo que aporta los recursos para abordar el problema.
Newton y Leibniz, definen la magnitud del ángulo en función de la longitud del arco abarcado por el sector circular que se forma trazando una circunferencia con centro en su vértice.
La conversión de unidades de grados sexagesimales a radianes es por tanto:
$2 π x°/360 = π x°/180 = x^r$
siendo $x^r$ la medida del ángulo en radianes y $x°$ su medida en grados sexagesimales. La unidad de medida de la longitud del arco abarcado es el radio de la circunferencia trazada. El resultado así obtenido es la medida del ángulo en radianes.
El cambio de grados a radianes, supone modificar la escala del eje $X$ para las funciones trigonométricas de manera que su periodo pasa de $360$ unidades a $2π$. Es decir, la gráfica de las funciones sufre una deformación, haciéndose mucho más “proporcionada”.
Si situamos un punto $A$ sobre el círculo unidad, seno $α$ y coseno $α$ coinciden con las coordenadas del punto $A$, tomando el ángulo a partir del eje $x$ en sentido contrario a las agujas del reloj.
Moviendo el punto $A$ sobre el círculo de radio unidad, el coseno del ángulo central en grados, se corresponde con la magnitud del segmento $OB$ y el seno se corresponde con la magnitud del segmento $AB$.
Es obvio ver que la magnitud del ángulo, medida en radianes, resulta independiente del radio de la circunferencia sobre la que se mida, por lo que a partir de ahora, trabajaremos sobre la circunferencia de radio unidad.
La ventaja de utilizar radianes, como variable independiente de las funciones trigonométricas, es que el arco equivale al doble del área del sector circular de radio $r=1$ que abarca, (Para el círculo completo, el área del círculo es $π$ y la longitud de la circunferencia es $2π$), y el área del sector definido podemos calcularla integrando la ecuación de la circunferencia.
El nombre de radianes para la unidad de medida angular, no empieza a utilizarse hasta 1873, en una pregunta de examen formulada por James Thomson en el Queen's College de Belfast.
Las funciones trigonométricas clásicas son funciones derivadas del círculo y por ello nos referimos a ellas frecuentemente como funciones circulares. Una vez adoptada la unidad de medida angular en radianes, podemos definir con precisión las funciones circulares apoyándonos en los instrumentos con los que el Cálculo nos ha dotado. Vamos a ver en detalle el caso de las funciones coseno y seno, porque a partir de ellas quedan definidas todas las funciones circulares aplicando las identidades trigonométricas.
Para el coseno tenemos que para cualquier valor $x$ en radianes del arco abarcado entre $0$ y $π$, $cos(x)$ esta comprendido en $[-1,1]$. La circunferencia unidad corta al eje $X$ en los extremos de $[-1,1]$, por lo tanto cualquier punto sobre ese diámetro de la circunferencia corresponde a un valor de $cos(x)$.
Para cada abscisa $x$, punto $B$, le asignamos el valor del arco definido entre el punto $x=1$ y el punto $A$ de la circunferencia unidad, de abscisa igual a $x$. El punto $(x, y=arco(A))$ para los valores de $x$ entre $-1$ y $1$ describe una función que llamamos arco coseno de $x$.
Para $x=cos$ (arco $ODA$), el área del sector circular se puede obtener como suma del triángulo ($OBA$) y del área bajo el arco de circunferencia ($ADB$), que obtenemos integrando la circunferencia de $x$ hasta $1$.
$${Área[ODA] = {\frac{x\sqrt{1-x^2}}{2}}+{{{\int_{x}^{1}}}\sqrt{1-x^2}} dx}$$
$2$ Área de ($ODA$) = arco($ODA$) = $arcos(x)$
La función arco coseno queda definida para valores de arco entre $0$ y $π$, puesto que hemos utilizado la función que define el semicírculo de ordenadas positivas. La tabla de valores de esta función podemos comprobar que es como sigue:
| x | arcos (x) |
|---|---|
| 1 | 0 |
| 0 | π/2 |
| -1 | π |
Definición de coseno como función inversa del arcocoseno
Funciones inversas
Para el caso de funciones de dos variables que nos ocupa, podemos decir que dos funciones son inversas una de otra, ($\small{f^{-1}}$ inversa de $f$), cuando introduciendo en la segunda, el resultado obtenido en la primera para cualquier valor de $x$, nos devuelve el valor inicial. Si $f(a)= b$, la función inversa, evaluada para $b$, nos retorna a ($\small{f^{-1}b= a}$). La condición necesaria para que la función $f(x)$ tenga inversa es que $\small{f(a) \not =f(b)}$, si $\small{a\not = b}$. Esta condición puede interpretarse gráficamente como que ninguna recta horizontal corta a la gráfica de $f(x)$ en más de un punto.
Las gráficas de funciones inversas son simétricas respecto la diagonal del primer cuadrante, es decir, se obtienen una de otra sustituyendo la $x$ por la $y$.
La función coseno es la inversa de la función arcocoseno que acabamos de definir.
$y = arccos (x) =$ arco $ODA$.
coseno (arco $ODA$) $= cos(y)= x$.
| y=arco | cos (y)=x |
|---|---|
| 0 | 1 |
| π/2 | 0 |
| π | -1 |
La definición de la función $sen (x)$
Del mismo modo que hemos hecho para el coseno, podemos plantear para el seno la misma estrategia de cálculo y obtendremos en primer lugar la función inversa del seno que llamaremos arcoseno.
Para cualquier valor $x$ en radianes del arco abarcado entre $0$ y $π$, $sen(x)$ esta comprendido en $[-1,1]$. La circunferencia unidad corta al eje $X$ en los extremos de $[-1,1]$, por lo tanto cualquier punto sobre ese diámetro de la circunferencia corresponde a un valor de $sen(x)$.
A diferencia del caso del coseno a cada abscisa $x$, punto $B$, le asignamos el valor del arco complementario de $α$ que es $π/2-α$
El punto $(x, y=arco(A))$ para los valores de $x$ entre $-1$ y $1$ describe una función que llamamos arcoseno de $x$.
Para calcular la función seno tenemos que calcular el arco abarcado $ODC$, $x= sen (arco ODC)$. El seno de $ODC$ es igual, por las propiedades del ángulo complementario a $OA$ y por lo tanto $OA = x$. El sector circular $ODC$ es igual al sector $OBI$, que podemos calcular por la integral del círculo de $0$ a $x$ restando el área del triángulo $OAB$.
$$Área [OBI]= {{{\int_{0}^{x}}}\sqrt{(1-r^2)}dr}\:-\: {x\over{2}}\sqrt{(1-r^2)}$$
$2$ Área ($OBI$) = arco ($ODC$) $= arcsen (OA) =arcsen (x)$
La tabla de valores de la función arcoseno es como sigue:
| x | arcosen (x) |
|---|---|
| 0 | 0 |
| 1 | π/2 |
| 0 | π |
Definición de seno como función inversa de arcoseno
La función seno es la inversa de la función arcoseno que acabamos de definir.
$arcsen (x)=arco ODC = y$
$sen (arco ODC) = sen (y)=x$
La tabla de valores de esta función es como sigue:
| y=arco | sen (y) |
|---|---|
| 0 | 0 |
| π/2 | 1 |
| π | 0 |
Definidas las funciones $sen \; x$ y $cos \; x$ para el intervalo entre $0$ y $π$, nos queda definir estas funciones para todos los valores de la recta real.
En primer lugar para el intervalo entre $π$ y $2π$ podemos repetir el proceso con la rama negativa de la circunferencia.
Obtenidos los valores entre $0$ y $2π$, las funciones seno y coseno son periódicas, siendo su valor entre $2kπ$ y $2(k+1)π$, para cualquier $k$ entero, positivo o negativo, igual al de la función entre $0$ y $2π$.
Completado este proceso, quedan definidas las funciones trigonométricas para todo valor de $x$.
Las funciones hiperbólicas se definen asociando a un punto sobre la hipérbola dos funciones, el seno hiperbólico y el coseno hiperbólico, cuyo valor depende del área ($OAB$) comprendida entre, la recta que une el origen de coordenadas con el punto elegido, el eje $x$ y la hipérbola, mediante las siguientes ecuaciones .
Para el seno hiperbólico:
$$\small{\begin{aligned}x&= 2\: Área \:(OAB)\\ y &= y\:(A)\end{aligned}}$$
$\small{{senh \:(2 \:Área\: OAB)}} {\normalsize =y ={(x^2-1)}^{(1/2)}}$
Para el coseno hiperbólico:
$$\small{\begin{aligned}x&= 2 \:Área \:(OAB) \\y &= x\:(A)\end{aligned}}$$
$\small{cosh \:(2\: Área\: OAB) =x}$
De esta definición se deduce directamente, sumando el cuadrado de ambas definiciones, la ecuación fundamental:
$cosh^2 (2$ Área $OAB) -senh^2 (2$ Área $OAB) =1$
Del mismo modo que hemos procedido para las funciones circulares, el área concernida en la definición de las funciones hiperbólicas se puede obtener mediante cálculo integral, como diferencia entre el área del triángulo $OCA$ y la integral de la hipérbola entre $B=1$ y $x(A)$.
$$\small{Área (OAB)}= {x\over{2}}{\sqrt{x^2-1}}-{{\int_{1}^{x}}}{\sqrt{x^2-1}} dx$$
Podemos observar que la función $senh \; x$ es una función impar, continuamente creciente de derivada siempre positiva. Su valor para $x=0$ es $0$, siendo este punto un punto de inflexión.
La función $cosh$ es una función par, simétrica respecto al eje $Y$. Tiene un mínimo en $x=0$, tomando en ese punto el valor $1$.
Para obtener la derivada de la función seno empezamos por calcular el cociente incremental y obtenemos :
$${\frac{sen (x+∆x)-sen\:x}{∆x}}$$
Aplicamos ahora, para $sen (x+∆x)$ la fórmula del seno de la suma de ángulos que hemos visto en el capitula anterior,
$$sen \:(a+b)=sen \:a \:cos\: b\:+\:sen\: b\: cos\: a$$
$$sen \:(x+∆x)=sen \:x \:cos \:∆x\:+\:sen \:∆x \: cos\:x$$
Sustituyendo en la expresión del cociente incremental:
$${\frac{sen \:x\: cos\:∆x+sen\:∆x\:cos\: x -sen\:x}{∆x}}=$$
$${\frac{sen \:x \:cos\: ∆x-sen\: x}{∆x}}+{\frac{cos\: x \:sen \:∆x}{∆x}=}$$
$${sen \:x {\frac{cos \:x-1}{∆x}}}+{cos\: x {\frac{sen \:∆x}{∆x}}}$$
El término $\large{\frac{cos\: x-1}{∆x}}$ se hace $0$ al aproximarse $∆x$ a $0$, ya que $cos \; 0 =1$, lo que anula el numerador.
El término $\large{\frac{sen\: ∆x}{∆x}}$ se aproxima a $1$, al tender $∆x$ a $0$. La razón última de la expresión anterior es:
$sen^{\prime} x = cos \;x$
Para la derivada de coseno procedemos del mismo modo:
$$\small{{\frac{cos( x+∆x)-cos\: x}{∆x}}}$$
Utilizando la fórmula del coseno de la suma de ángulos,
$cos (x+∆x)=cos \: x \; cos \: ∆x - sen \: x \: sen \: ∆x$
sustituyendo en el cociente anterior tenemos:
$$\small{{\frac{cos \:x\: cos\:∆x-sen\:∆x\:sen\: x -cos\:x}{∆x}}=}$$
$$\small{{\frac{cos \:x \:cos\: ∆x-cos\: x}{∆x}}-{\frac{sen\: x \:sen \:∆x}{∆x}}=}$$
$$\small{{cos \:x {\frac{cos \:x-1}{∆x}}}-{sen\: x {\frac{sen \:∆x}{∆x}}}}$$
Como hemos visto antes la primera fracción tiende a $0$ y la segunda a $1$, con lo que el resultado es:
$cos' \: x = -sen \: x$
Para las funciones hiperbólicas teniendo en cuenta que las fórmulas para la suma de ángulos es para el $senh$ idéntica a la trigonométrica,
$senh (a+b) = senh \: a \: cosh \: b + senh \: b \: cosh \: a$
podemos deducir fácilmente que:
$senh' \: x = cosh \: x$
Para el coseno hiperbólico, la fórmula de la suma de ángulos varía en un signo respecto de su equivalente trigonométrica:
$cosh (a+b) = cosh \: a \: cosh \: b + senh \: a \: senh \: b$
y podemos deducir fácilmente que:
$cosh' \: x = senh \: x$
Hemos visto hasta aquí como obtener la derivada de una función. Para extender el procedimiento de derivación, vamos a ver las reglas para derivar funciones compuestas por la suma, la diferencia, el producto y la división de dos funciones, que llamamos $f(x)$ y $g(x)$.
La regla para derivar una suma de funciones es muy simple:
$(f(x)+ g(x) )' = f(x)' + g(x)'$
Esta regla es fácilmente demostrable aplicando la definición de derivada:
$$\frac{(f(x+∆x)+g(x+∆x)- (f(x)+g(x))}{∆x}$$
que es evidentemente igual a:
$${\frac{(f(x+∆x)-f(x))}{∆x}}+{\frac{(g(x+∆x)-g(x))}{∆x}}$$
La demostración para la diferencia es inmediata, siguiendo los pasos de la anterior demostración para la suma de funciones.
Para el producto de funciones la regla de derivación es también muy simple y fácil de demostrar.
$(f(x) · g(x))' = f ‘(x) · g(x)+ f(x) · g ‘(x)$
Si aplicamos esta regla al producto de una función por una constante obtenemos que:
$(a f(x))' = a f'(x)$
Resumiendo, la derivada se comporta linealmente respecto de la suma de funciones y a su multiplicación por una constante.
$(a f(x)+b g(x) )' = a f'(x) + b g'(x)$
Inicio de la demostración.
Aplicando el procedimiento de cálculo de la derivada a $f(x)·g(x)$ obtenemos:
$${\frac{f(x+∆x)\cdot g(x+∆x)-f(x) \cdot g(x)}{∆x}}$$
sumando y restando $g(x) \cdot f(x+∆x)$
$${g(x){\frac{f(x+∆x)-f(x)}{∆x}}}+{f(x+∆x){\frac{g(x+∆x)-g(x)}{∆x}}}$$
$$=g(x)\cdot f'(x)+f(x) \cdot g'(x)$$
lo que confirma la regla de derivación de un producto.
Final de la demostración.
Ejemplos de la regla del producto
Derivada de un producto de polinomios:
$${\frac{ d(x^2+1) (x^3-1)}{dx}}=2x(x^3-1)+(x^2+1)3x^2$$
Derivada de un producto de funciones:
$y=x sen (x), \Lrarr y' = sen (x)+x cos(x)$
$y= sen(x) cos(x), \;\Lrarr \small{y'= cos^2 (x)-sen^2(x)}$
La regla para la derivada de un cociente de funciones es la siguiente:
$$\left({\frac{f(x)}{g(x)}}\right)'={\frac{g(x)\cdot f'(x)-f(x)\cdot g'(x)}{g(x)^2}}$$
Inicio de la demostración.
Aplicando la definición de derivada a $1/g(x)$ tenemos el siguiente cociente de diferencias:
$${\frac{{\displaystyle\frac{1}{g(x+∆x)}}-{\displaystyle\frac{1}{g(x)}}}{∆x}}={\frac{(-1)(g(x+∆x)-g(x))}{∆x}}{\frac{1}{g(x)}}{\frac{1}{g(x+∆x)}}$$
Al tender h a cero esta expresión se convierte en :
$$\frac{-g'(x)}{g(x)^2}$$
Si aplicamos la fórmula del producto a $(f(x) · 1/g(x))'$ obtenemos la expresión que queremos demostrar.
Final de la demostración.
Si aplicamos la fórmula del cociente a:
$$tg \:x=( \frac{sen \:x}{cos\:x}) $$
obtenemos:
$$tg' \:x=\frac{cos^2\:x+sen^2\:x}{cos^2\:x}=\frac{1}{cos^2\:x}$$
Otra propiedad de las derivadas es la regla de la cadena que se aplica para el caso funciones compuestas, es decir,
$z= f (g(x))$
Donde $z=f(y)$, $y=g(x)$
La regla de la cadena establece que:
[5.4]
$z'= f'(g(x)) · g'(x)$
La regla de la cadena es un ejemplo excelente para demostrar la utilidad de la notación de Leibniz para las derivadas, ya que la expresión (5.4) escrita con la notación de Leibniz toma la apariencia de una identidad algebraica trivial.
$${\frac{dz}{dx}}={\frac{dz}{dy}}{\frac{dy}{dx}}$$
Si se interpreta literalmente, esta expresión sugiere que las derivadas se comportan como si fueran fracciones, lo que carece de sentido puesto que no lo son, aunque su origen sea un cociente de incrementos.
A pesar de ello la expresión ilustra la regla de la cadena y muestra como las tasas de cambio se multiplican en el caso de funciones compuestas. Operando algebraicamente con los diferenciales estamos aplicando la regla de la cadena de una forma nemotécnica y automática.
Ejemplo de aplicación de la regla de la cadena
El volumen de una esfera aumenta en función de su radio. Si conocemos la variación del radio con el tiempo, la tasa de variación del volumen con el tiempo será el producto de las tasas de variación del volumen respecto de su radio y de la variación del radio en relación al tiempo.
$${\frac{dV}{dt}}={\frac{dV}{dr}}{\frac{dr}{dt}}$$
Siendo V el volumen $\small{(V= {\large{\frac{4}{3}}} π r^3)}$,
$${\frac{dV}{dr}}=4πr^2$$
Si la tasa de variación del Radio es de $3 cm/s$, entonces:
$${\frac{dV}{dt}}=12π\:r^2 \:(cm/s)$$
La derivación implícita consiste en derivar una ecuación del tipo $f(x, y)=0$, sin necesidad de resolverla en "$y$" (sin despejar la $y$), utilizando la regla de la cadena. Esto supone que tenemos que derivar “$y$” como lo que es, una función de $x$. La derivada de $y$ es obviamente $y'$, pero la derivada de $y^2$ es, $2y · y'$. Por la misma razón, a los términos en "$x · y$", se les aplica la regla del producto, por lo que para $x · y$, la derivada resulta, $y+x ·y'$.
Las derivación nos ha llevado a discutir sobre el valor finito de la “razón última” de diferenciales. Hemos visto las dificultades teóricas que representa la introducción de los infinitesimales. Hemos visto también como la integración equivale a la cuadratura de una curva y que para obtenerla nos encontramos con el reto de obtener una suma de infinitos sumandos.
Pero no va a detenerse aquí el dialogo de las matemáticas con el infinito, porque las series van a formar una parte inseparable del Cálculo con el que comparten una fecha de nacimiento común y plantean los mismos problemas para su fundamentación teórica.
Para Euler, la suma de una serie se obtiene cuando los primeros infinitos términos nos dan un valor finito y si continuamos sumando infinitos términos a partir de ese punto, la suma de esos términos adicionales es un infinitesimal. Es decir, la suma obtenida mediante infinitos términos no admite crecimiento.
Pero esta definición de suma no aclara que significa una suma de $∞$ sumandos, ni existe una idea precisa de los requisitos a cumplir por una serie para ser sumable. Por ejemplo, hemos obtenido por división larga:
$$\small{\frac{1}{1+x}=1-x+x^2-x^3+x^4- ...}$$que para $x=1$ resulta:
$$\small{\frac{1}{1+x}=1-1+1-1+1-1+ ...}$$Esta serie suma alternativamente $1$ o $0$ según el número de términos considerados. Para Leibniz y para Euler esta serie suma $1/2$ porque la función toma ese valor para $x=1$, pero esta claro que adjudicar este valor a la suma de la serie es una arbitrariedad.
Queda claro que el manejo de series plantea dificultades pero los resultados de seguir adelante, sin detenerse en casos particulares, llevará a los inventores del cálculo a éxitos espectaculares. La fundamentación rigurosa del cálculo tiene aún que esperar.
Cuando nos referimos a series tenemos que distinguir si nos referimos a series numéricas o por el contrario nos referimos a series cuyos términos son funciones. Nos vamos a centrar en el estudio de un tipo especial de series de funciones, en la cual sus términos son potencias enteras de x.
La primera serie de este tipo la hemos visto, obtenida por Mercator, para aproximar la función logarítmica.
Vamos a ver como Newton redefine las funciones trigonométricas mediante desarrollos en serie de potencias, y como posteriormente, MacLaurin y Taylor obtienen una fórmula general para desarrollar una función, basada en sus derivadas sucesivas. Las series obtenidas se llaman desarrollos en serie de MacLaurin o de Taylor en su honor.
Si conseguimos sustituir una función por su desarrollo en serie de potencias podemos obtener ventajas muy importantes.
La primera es aproximar la función, de manera que su valor en un punto se corresponda con la suma de los términos de la serie para ese punto.
Una segunda utilidad, muy importante, es derivar o integrar una función derivando o integrando término a término su desarrollo. Así, una función difícil de manejar puede derivarse e integrarse fácilmente aplicando las fórmulas elementales para las potencias de x.
Una sucesión es un conjunto de elementos que podemos ordenar según la secuencia de los números naturales.
Una sucesión se construye a partir de lo que llamamos término general, que es una expresión que incorpora una variable $n$, que variando a partir de $1$, es la regla para calcular los sucesivos elementos. Esto lo expresamos llamando al término general $a_n$, sustituyendo $n$ por cualquier número natural, obtenemos el elemento que ocupa el lugar $n$ en la sucesión.
$$\lbrack {a_n}\rbrack$$Por ejemplo si el término general es $1/n$, el término que ocupa el lugar $10$ en la sucesión es $1/10$.
Los términos de una sucesión sin esa regla que le da coherencia podrían adoptar valores arbitrarios y por lo tanto carecería de sentido y de utilidad. Dicho de otro modo, toda sucesión se autodefine de manera que conociendo $n-1$ términos podemos deducir el término $n$ que le sigue.
Una serie infinita es la suma de una sucesión de infinitos elementos. Representamos una serie con un símbolo que llamamos sumatorio $Σ$ y la serie entonces queda como:
$$\small{{\sum_{n=1}^\infty}{a_n}}$$siendo n es un número entero positivo y esta expresión se lee, suma de $a_n,$ para $n$ de $1$ a $∞$. Este índice $n$ se llama variable muda porque desaparece al sumar la serie.
La suma de una serie infinita es el valor que se corresponde con la suma de sus infinitos términos. Las series cuya suma es finita se llaman convergentes y en caso contrario divergentes.
Si la suma de infinitos términos debe dar un resultado finito es evidente que el término general, al incrementarse n, debe ser cada vez más próximo a $0$. Si no es así, la suma de sucesivos términos crecerá indefinidamente. Esta condición es necesaria, pero no suficiente. Por ejemplo, podemos comprobar en el gráfico siguiente ”Suma de series numéricas”, que la serie,
$$\sum_{\substack{n=1}}^\infty{\frac{1}{\sqrt{n}}}$$cuyo término general tiende a $0$, es divergente, evidenciando que esta condición es necesaria para la convergencia pero no siempre suficiente.
De entre las series, distinguimos entre aquellas en las que todos sus términos tienen el mismo signo y las que lo alternan. Estas series con alternancia de signos pueden analizarse en valor absoluto. Una serie es absolutamente convergente cuando la serie de sus términos en valor absoluto converge. La convergencia absoluta de una serie implica la convergencia de la serie original.
La suma de series numéricas.
La suma de series numéricas es desde antiguo un “deporte” matemático resultado de la curiosidad de calcular la suma de las diferentes sucesiones que se ponían de moda. Existen sucesiones que se suman desde la época clásica y otras que se han planteado como un desafío y que se ha tardado siglos en resolver.
Por ejemplo, es claro que la suma de la sucesión de los números naturales nos da un valor infinito. Pero, ¿cuál es la suma de la sucesión de los inversos de los números naturales? $1 + 1/2 + 1/3+1/4+ …$, también es infinita, como lo es la de los inversos de los números primos.
La suma de los inversos de las potencias de $2$ resulta ser:
$$1+{1\over2}+{1\over4}+{1\over8}+...=2$$Existen dos tipos de series fácilmente sumables.
Las series geométricas son aquellas para las que existe un factor constante que multiplica dos términos consecutivos. Este factor es la razón de la serie geométrica.
$$\sum_{\substack{0}}^n{a\:r^n}$$Los $n$ primeros términos de una serie geométrica suman:
$$\sum_{\substack{0}}^n{a\:r^n}= a\:\frac{\:1-r^{r-1}}{1-r}$$si $r < 1$ la serie converge y podemos obtener la suma de todos sus infinitos términos.
$$\sum_{\substack{0}}^\infty {a\:r^n}={a\over{1-r}}$$Una serie telescópica es aquella cuyas sumas parciales poseen un número fijo de términos por cancelación entre términos sucesivos. Como ejemplo podemos poner la serie de Mengoli (Pietro Mengoli,1626-1686):
$$\sum_{\substack{1}}^n{\frac{1}{n\:(n+1)}}=\sum_{\substack{1}}^n{({1\over n}-{1\over {n+1}})}$$que podemos comprobar que resulta:
$$\lim_{n\rarr\infty}(1-{1\over {n+1}})$$Para el cálculo del área por debajo de la gráfica de $x^n$ , hemos visto que el procedimiento de Fermat lleva a la suma de una serie de potencias de grado $n$:
$$1+{2^n}+{3^n}+{4^n}+...+{k^n}$$Las sumas de potencias de cualquier orden fue estudiado y finalmente solucionado por Jacob Bernoulli en 1690. La fórmula general de Bernoulli que involucra lo que se laman “números de Bernoulli”, es la siguiente:
Siendo Bi los números de Bernoulli.
Para n=1.
$$\sum_{\substack{1}}^n {k}= 1+2+3+....+k= {{n^2}\over2} + {n\over 2}$$para n=2.
$$\sum_{\substack{1}}^n {k^2}= 1^2+2^2+3^2+....+k^2= {{n^3}\over3} + {n^2\over 2}+{n\over 6}$$para n=3.
$$\sum_{\substack{1}}^n {k^3}= 1^3+2^3+3^3+....+k^3= {{n^4}\over4} + {n^3\over 2}+{n^2\over 4}$$Para saber más sobre los números de Bernoulli podéis consultar esta página de Wikipedia
El problema de Basilea
Pietro Mengoli, planteó en 1650, el problema de obtener la suma de los inversos de los cuadrados de los números naturales . Euler lo resolvió en 1735 cuando tenía veintiocho años, obteniendo un resultado que sorprende por involucrar a π.
$$\frac{π^2}{6}={\sum_{0}^∞}\:\frac{1}{n^2}$$Euler residía en esa época en Basilea, de ahí el nombre que se le ha dado desde entonces al problema, que supuso para Euler el reconocimiento por la elite matemática de su época.
La demostración de este resultado , la veremos en detalle en el anexo 3.
Las series de funciones son una generalización de las series numéricas, cuando sus elementos son funciones, es decir, su término general ${a_n = f_n(x)}$, es una función definida para un conjunto común de valores de $x$.
Podemos definir del mismo modo que hemos hecho para las sucesiones en general, las series de funciones como:
$$\small{{\sum_{n=0}^\infty}{a_n}\: f_n(x)}$$Las series de potencias son un tipo particular de series de funciones, cuando sus términos son potencias enteras de $x$.
$$\small{f(x)={\sum_{0}^\infty {a_n}{ x^n}}= a_0+a_1x+a_2 x^2+a_3 x^3+... }$$o de una forma más general:
Euler en el capítulo 4 de la “Introductio” considera que la expresión analítica más general para expresar una función es una serie infinita de potencias.
Hemos visto dos maneras de obtener una serie como desarrollo de una función. Mediante la división larga y también mediante el teorema del binomio.
Las series de potencias se manejan con mucha libertad y se asume para ellas un comportamiento semejante al de un polinomio “muy largo” y se aplican entre series las operaciones algebraicas de suma, resta, multiplicación y división, como si lo fueran.
Hoy sabemos que las serie de potencias tienen un comportamiento más “amistoso” que las series de funciones en general y que pueden ser derivadas e integradas término a término, lo que no es válido, en general, para cualquier serie de funciones.
Un desarrollo en serie de potencias de $x$, tal como la hemos descrito es una función de una variable, en este caso la $x$.
Para cada valor de $x$ la función se convierte en una serie numérica. Si la serie es convergente, el valor de la función en ese punto es igual a la suma de los infinitos términos de la serie en la que se desarrolla.
Al aplicar los criterios de convergencia a una serie de potencias cuyo término general depende de $x$, nos podemos encontrar que la serie solo es convergente para determinado rango de valores de $x$.
Analizamos diferentes términos generales y su dependencia de $x$ para tender a $0$, que es el criterio necesario para su convergencia.
El intervalo de convergencia, para las series más generales del tipo $\small{\sum_{\substack{0}}^\infty{a_n {(x-c)}^n } }$ esta siempre centrado en $c$ y se define como $|x-c|< r$. Este intervalo, $r$, en el que la serie converge se llama radio de convergencia de la serie y puede ser abierto o cerrado según incluya o no alguno de los valores extremos del intervalo $(-r, r)$.
El de $\large{\frac{1}{1+x^2}}$ es una de las primeras funciones para la que se obtiene su desarrollo en serie y, como el de $\large{\frac{1}{1+x}}$, se consigue mediante división larga. Este desarrollo se conoce como serie de Gregory.
$1/(1+x^2)$ por división larga nos da:
$$y=1-x^2+x^4-x^6+x^8-...+(-1)^n x^{2n}$$En la representación gráfica de la función y la serie, podemos observar que la serie solo se ajusta a la función en un radio de $|x| < 1$.
¿Qué obstáculo impide que deje de converger para $|x|≥1$?
No hay respuesta (de momento…) a este comportamiento, como no la teníamos para $1/(1+x)$ donde la función se hacia infinita en $x=-1$.
Si analizamos el valor de la función y de la serie para $x=1$ vemos, como en el caso de $\displaystyle{1\over{1+x}}$, que para la función obtenemos $\displaystyle{1\over 2}$ y haciendo $x=1$ en la serie obtenemos:
$$y=1-1+1-1+1-1+...$$que toma valor $+1$ o $-1$ según el número de términos que se consideren. En la representación gráfica se observa muy bien esta alternancia comparando las gráficas de la serie con número par e impar de términos. Además se puede ver en la gráfica como para valores mayores a 1 la serie tiende alternativamente a más menos infinito.
Newton propuso para valores “grandes” de $x$ la serie:
$$y=x^{-2}-x^{-4}+x^{-6}-x^{-8}+...$$que se ajusta a la función para valores fuera del entorno $|x| ≤1$.
Podemos obtener la integral de la función $1\over{{x^2}+1}$, mediante el método gráfico que hemos empleado para ilustrar el significado de la integral definida. La función integral que dibujamos es una de las funciones trigonométricas básicas que estudiaremos más adelante. Ahora lo que nos interesa es ver como la integración término a término de la serie para valores “pequeños” y de la serie para valores “grandes” se ajustan a la integral dibujada para $1\over{{x^2}+1}$.
La integral de la serie para valores “grandes” requiere de una constante de integración diferente para los valores positivos ($π/2$) y negativos ($- π/2$).
La relación de las funciones trigonométricas con el círculo unidad, que hemos descrito en 5.2, da la pista a Newton para su desarrollo en serie. El procedimiento consiste en calcular en primer lugar el desarrollo de las funciones inversas, arcocoseno y arcoseno, para posteriormente invertir las series obtenidas.
Una vez tenemos claro la igualdad que tenemos que calcular (apartado 5.2.1),
$arccos (x) = {{x\sqrt{1-x^2}}}+{2{\Large\int_{x}^{1}}\sqrt{1-x^2}} dx$
Solo nos queda ir paso a paso obteniendo cada uno de los términos de la ecuación. Desarrollando por el binomio la ecuación de la circunferencia $\small{(1-x^2)^{1\over2}}$ obtenemos:
$y= 1- 1/2\: x^2 -1/8 \:x^4 - 3/48 \:x^6 - 15/384 \:x^8 -105/3840 \:x^{10} - 945/46080 \:x^{12} - 135135/10321920 \:x^{14} - \cdots $
Integramos término a término obtenemos el área del círculo entre $0$ y $x$. Para obtener el área entre $x$ y $1$, restamos la serie obtenida del valor del área entre $0$ y $1$, que es $π/4$.
$y = π/4 - (x - 1/6 \:x^3 -1/40 \:x^5 - 3/336 \:x^7 - 15/3.456 \:x^9 -105/42.240 \:x^{11} - 945/599.040\: x{13} - 135135/154.828.800 \:x^{15} - \cdots $ (1)
Multiplicando por $x$ y dividiendo por $2$ la serie del desarrollo por el binomio de la circunferencia, obtenemos el área del triángulo:
$y=1/2 \:x- 1/4\: x^3 -1/16 \:x^5 - 3/96 \:x^7 - 15/768 \:x^9 -105/7680 \:x^{11} - 945/92.160 \:x^{13} - 135135/20.643.840 \:x^{15} -\cdots $ (2)
Para obtener el desarrollo de la función $arccos (x)$, sumamos (1) y (2) y multiplicamos por $2$ para pasar del área calculada a la longitud del arco.
$y/2 = π/4 - 1/2 \:x + (1/6-1/4) \:x^3 +(1/40-1/16) \:x^5 + (3/336-3/96) \:x^7 + (15/3.456-17/768)\: x^9 +(105/42.240- 105/7680) \:x^{11} + (945/599.040-945/92.168)\: x^{13} + (135135/154.828.800- 135135/20.643.840)\: x^{15}+ \cdots $
Simplificando, obtenemos el desarrollo de $arccos (x)$:
$y = π/2 - x-1/6 \:x^3 -3/40 \:x^5 -1/22,4\: x^7-1/32,91 \:x^9- 1/44,7\: x^{11} -1/57,63 \:x^{13} - 1/71,6\: x^{15}+\cdots $
En este caso debemos calcular:
$arcosen (x) = {{{\int_{0}^{x}}}\sqrt{(1-r^2)}dr}\:-\: {x\over{2}}\sqrt{(1-r^2)}$
Desarrollando por el binomio la ecuación de la circunferencia $\small{(1-x^2)^{1\over2}}$ obtenemos:
$y= 1- 1/2 x^2 -1/8 x^4 - 3/48 x^6 - 15/384 x^8 -105/3840 x^{10} - 945/46080 x^{12} - 135135/10321920 x^{14} -\cdots $
Integrando término a término obtenemos el área del sector circular entre $0$ y $x$.
$y = x - 1/6 x3 -1/40 x5 - 3/336 x7 - 15/3.456 x9 -105/42.240 x11 - 945/599.040 x13 - 135135/154.828.800 x15 -\cdots$
Multiplicando el desarrollo de la circunferencia por $x$ y dividiendo por $2$, obtenemos el área del triángulo:
$y=1/2 x- 1/4 x^3 -1/16 x^5 - 3/96 x^7 - 15/768 x^9 -105/7680 x^{11} - 945/92.160 x^{13} - 135135/20.643.840 x^{15} - \cdots $
Para obtener el desarrollo de la función $arcsen (x)$, restamos del área del triángulo el área del sector circular y multiplicamos por $2$.
$y/2 = 1/2 x + (1/6-1/4) x^3 +(1/40-1/16) x^5 + (3/336-3/96) x^7 + (15/3.456-17/768) x^9 +(105/42.240- 105/7680) x^{11} + (945/599.040-945/92.168) x^{13} + (135135/154.828.800- 135135/20.643.840) x^{15}+ \cdots $
Simplificando, obtenemos el desarrollo de $arcsen (x)$:
$y = x+1/6 x^3 +3/40 x^5 +1/22,4 x^7+1/32,91 x^9+ 1/44,7 x^{11} +1/57,63 x^{13} + 1/71,6 x^{15}+ \cdots +(2n)! /4^n(n!)^2 (2n+1)\: x^{2n+1}$
Las funciones seno y coseno son la inversa de las funciones obtenidas. Es decir, tenemos una serie:
$$y=a_0+a_1x+a_2x^2+a_3x^3+….$$
y queremos obtener la función inversa, es decir,
$$x=A_0+A_1y+A_2y^2+A_3y^3+...$$
La idea es simple y geométricamente su interpretación es sencilla, se trata de obtener una función simétrica respecto la recta x=y.
Sustituimos en (1) las x por la expresión (2) y obtenemos:
$y=a_0+a_1{(A_0+A_1y+A_2y^2+A_3y^3+...)}+a_2{(A_0+A_1y+A_2y^2+A_3y^3+...)}^2+a_3{(A_0+A_1y+A_2y^2+A_3y^3+...)}^3+ \cdots $
Desarrollamos la expresión e igualamos los coeficientes obtenidos para cada potencia de y con el coeficiente correspondiente de (2).
Obtenidos los desarrollos en serie de $arcosen (x)$ y $arcocos (x)$, nos queda invertir estas series para obtener las de $sen \; x$ y $cos \; x$.
Invertir una serie es teóricamente sencillo, pero algebraicamente es un trabajo muy engorroso que implica una capacidad de cálculo muy grande. No lo encontraremos en nuestros libros de texto. Nosotros lo resolvemos en la siguiente hoja de trabajo con la ayuda de una hoja de cálculo. Increíblemente Newton y Leibniz lo afrontaron y nos dieron el resultado correcto para muchas series, trabajando con lápiz y papel!
Inversión de arco seno para obtener sen x
Invirtiendo la serie del arcoseno obtenemos:
$${y = x-0,16666 x^3+0,0083333 x^5-0,000198413 x^7+…}$$
Que se puede poner como:
$$y={x\over{1!}}-{x^3\over{3!}}+{x^5\over{5!}}-{x^7\over{7!}}+ \cdots { { {(-1)} ^ {n+1} {x ^ {2n+1} } }\over {(2n+1)!} }$$
Inversión de arcocoseno para obtener $cos \; x$
Podemos seguir la inversión de arcocoseno en la figura 6.8 y obtenemos:
$$y=1-{x^2\over2!}+{x^4\over4!}-{x^6\over6!}+{x^8\over8!}+ \cdots { { {(-1)} ^ {n} {x ^ {2n} } }\over {(2n)!} }$$
Hemos obtenido arcocoseno:
$y = π/2 - x-1/6 x^3 -3/40 x^5 -1/22,4 x^7-1/32,91 x^9- 1/44,7 x^{11} -1/57,63 x^{13} - 1/71,6 x^{15}+ \cdots $
Pasamos $π/2$ restando de la $y$, obtenemos la inversión de la serie, sabiendo que la $x$ es ahora la inversa de $y-π/2$, es decir, $x-π/2$. Luego, la serie obtenida esta desplazada según el eje $x$, $π/2$:
$$y-π/2 = -x + 1/3!\; x^3 - 1/5!\; x^5 + 1/7!\; x^7 - \cdots $$
Sustituyendo en el desarrollo, $x$ por $x-π/2$, obtenemos haciendo las operaciones:
$$y=1-{x^2\over2!}+{x^4\over4!}-{x^6\over6!}+{x^8\over8!}+ \cdots { { {(-1)} ^ {n} {x ^ {2n} } }\over {(2n)!} }$$
Vamos a resumir en una tabla los desarrollos en serie de las funciones trigonométricas y obtener también los desarrollos de sus funciones derivadas.
$tg \; x = sen \; x/cos \; x= sen \; x · 1/cos \; x$.
Listamos junto a cada función trigonométrica su derivada. Obtenemos su desarrollo en serie simplemente derivando término a término los desarrollos de la tabla anterior. Podemos con paciencia comprobar que obtendríamos el mismo resultado calculando su desarrollo directamente.
Para la derivada de la tangente, que ya sabemos que es $\large{{\frac{1}{cos^2\:x}} }$, obtenemos el cuadrado la serie de cos x:
$$cos^2 x =1- {x^2}+{1\over{3}}{x^4}-{{2}\over{45}}{ x^6}+{{1}\over{315}} {x^8}+ \cdots $$
y dividiendo $1$ entre $cos^2 \; x$ obtenemos a continuación:
$${\frac{1}{cos^2 x}}=1+ {x^2}+{2\over{3}}{x^4}+{{17}\over{45}}{ x^6}+{{62}\over{315}} {x^8}+ \cdots $$
que resulta ser igual a la serie que se obtiene derivando término a término la serie de la tangente.
Para arcoseno y arcocoseno podemos desarrollar por el binomio la circunferencia unidad $\small{(1-x^2)^{1/2}}$ y calcular después $\large{\frac{1}{(1-x^2)^{1/2}}}$ con la misma hoja de cálculo que hemos usado anteriormente (Figura 4.3).
Derivando la serie obtenida para arcotangente obtenemos la de su derivada, que resulta ser la que hemos obtenido en el apartado 6.2, por division larga, para $\large{\frac{1}{1+x^2}}$ .
| Función | Desarrollo en el entorno de 0 | Radio de convergencia |
|---|---|---|
| sen x | $\displaystyle{y={x\over{1!}}-{x^3\over{3!}}+{x^5\over{5!}}-{x^7\over{7!}}+\cdots { { {(-1)} ^ {n} {x ^ {2n+1} } }\over {(2n+1)!} }}$ | Para todo x |
| cos x | $\displaystyle{y=1-{x^2\over2!}+{x^4\over4!}-{x^6\over6!}+{x^8\over8!}+ \cdots{ { {(-1)} ^ {n} {x ^ {2n} } }\over {(2n)!}} }$ | Para todo x |
| tg x | $\displaystyle{y=x+{1\over{3}} {x^3}+{2\over{15}}{x^5}+{{17}\over{315}}{ x^7}+{{62}\over{2835}} {x^9}+ \cdots}$ | (-π/2, π/2) |
| arcsen x | $\displaystyle{y=x+{1\over{6}} {x^3}+{3\over{40}}{x^5}+{{1}\over{22,4}}{ x^7}+{{1}\over{32,91}} {x^9}+ \cdots}$ | (-1 +1) |
| arccos x | $\displaystyle{y= {π\over{2}} -x- {1\over{6}} {x^3}-{3\over{40}}{x^5}-{{1}\over{22,4}}{ x^7}-{{1}\over{32,91}} {x^9}+ \cdots}$ | (-1 +1) |
| arctg x | $\displaystyle{y=x-{1\over{3}} {x^3}+{1\over{5}}{x^5}-{{1}\over{7}}{ x^7}+{{1}\over{9}} {x^9}+ \cdots}$ | (-1 +1) |
| sinh x | $\displaystyle{y={x\over{1!}}+{x^3\over{3!}}+{x^5\over{5!}}+{x^7\over{7!}}+ \cdots {{x ^ {2n+1}}\over{(2n+1)!}}}$ | |
| cosh x | $\displaystyle{y=1+{x^2\over2!}+{x^4\over4!}+{x^6\over6!}+{x^8\over8!}+\cdots { {x ^ {2n}} \over {(2n)!} }}$ |
| Función | Derivada | Desarrollo en el entorno de 0 |
|---|---|---|
| tg x | $\displaystyle{1\over{cos^{2}x}}$ | $\displaystyle{y=1+{x^2}+{2\over{3}}{x^4}+{{17}\over{45}}{ x^6}+{{62}\over{315}} {x^8}+ \cdots}$ |
| arcsen x | $\displaystyle{1\over{(1-x^2)^{1\over2}}}$ | $\displaystyle{y=1+{1\over{2}}{x^2}+{15\over{40}}{x^4}+{{7}\over{22,4}}{ x^6}+{{9}\over{32,91}} {x^8}+{{11}\over{4,7}} {x^{10}}\cdots}$ |
| arccos x | $\displaystyle{1\over{(1-x^2)^{1\over2}}}$ | $\displaystyle{y=-1-{1\over{2}}{x^2}-{15\over{40}}{x^4}-{{7}\over{22,4}}{ x^6}-{{9}\over{32,91}} {x^8}-{{11}\over{4,7}} {x^{10}}\cdots}$ |
| arctg x | $\displaystyle{1\over {(1+x^2)}}$ | $\displaystyle{y= 1-{x^2}+{x^4}-{ x^6}+ {x^8}- {x^{10}}+ \cdots + {-1}^n x^{2n}}$ |
Hemos visto como se obtienen desarrollos en serie por dos procedimientos diferentes pero no disponemos de un método general para hacerlo. MacLaurin se da cuenta de que si escribimos la igualdad entre la función y su desarrollo, $f(x)= a_0+ a_1 x + a_2 x^2 +a_3 x^3 +\cdots $ podemos calcular los coeficientes derivando la función sucesivamente, y haciendo $x=0$, obtenemos:
$\small{f (0)= a_0}$
$\small{f ' (x)= a_1 + 2 a_2 x +3 a_3 x^2 +\cdots }$ luego: $\small{{f ' (0) = a_1}}$
$\small{f '' (x)= 2 a_2 +6 a_3 x + \cdots }$ luego: $\small{{f '' (0) = 2 a_2}}$
$\small{f '''(x)= 6 a_3 +\cdots }$ luego: $\small{{f '''(0) = 6 a_3}}$
y por tanto sustituyendo los coeficientes, el desarrollo se convierte en:
$$f(x)=f(0)+ f'(0) x+{f''(0)\over{2!}}{x^2}+{f'''(0)\over{3!}}{x^3}+⋯+ $$
Este desarrollo se conoce como serie de MacLaurin y nos permite desarrollar en serie una función en el entorno de $x=0$, siempre que la función sea sucesivamente derivable. Los desarrollos para $x=0$ se dice que son centrados en $0$.
Con un cambio de variable $t = x-a$ obtenemos el desarrollo centrado en $a$, que es el que se atribuye a Taylor, publicado en 1715. Para $a=0$ ambos desarrollos coinciden. También podemos comprobar que los desarrollos obtenidos por la fórmula de Taylor coinciden exactamente con los que hemos calculado previamente para las funciones trigonométricas partiendo del desarrollo del binomio.
Con la casilla de control seleccionamos la función que queremos representar y su desarrollo en serie. Con el deslizador controlamos el punto en el que se centra el desarrollo.
Para calcular el desarrollo de Taylor derivamos n veces la función seno y coseno obteniendo para seno de $x: f' =cos x$, $f''= -senx$, $f'''= -cos x$, $f''''=sen x$ volviendo a repetirse la secuencia a partir de $f'''''$.
Para $cos x$ obtenemos: $f' = -sen x$, $f''= -cos x$, $f'''=sen x$, $f''''= cos x$ volviendo a repetirse la secuencia a partir de $f'''''$.
Resulta por tanto, que para obtener el desarrollo requerimos los valores de $sen x$ y $cos x$ para el punto en el que se centra el desarrollo.
Cuando las series de Taylor se centran en $0$ coinciden exactamente con las calculadas analíticamente en el apartado 6.4.
Podemos comprobar como los desarrollos de Taylor de seno y coseno aumentan su entorno de convergencia al aumentar el número de términos de la serie y comprobamos por tanto que convergen para todos los valores del eje $x$.
Obtenido el desarrollo en serie de una función podemos calcular su valor para cada $x$. El procedimiento más sencillo de hacerlo es sumar un número suficiente de términos para obtener una buena aproximación a la función en ese punto. Este enfoque nos lleva a la necesidad de medir esa proximidad al resultado “exacto”, para dar por bueno el resultado o continuar sumando términos.
Si llamamos al desarrollo de Taylor con n términos como $\small{P_{n,a} (x)}$, (Polinomio de $n$ términos centrado en $a$), podemos decir que:
$$f(x)= P_{n,a}(x)+ R_{n,a} (x)$$
Es decir, que sumando una cierta cantidad al polinomio de $n$ términos obtenemos exactamente el valor de la función en $a$. A este valor le llamamos “resto”.
Podemos suponer que el resto tenga la forma que correspondería al término $n+1$ del desarrollo en serie, sustituyendo en la derivada $n+1$ de ${\small{f (x)}}$ en $a$, es decir, $\small{f^{(n+1)'} (a)}$, por un valor $t$ que haga que el resto tome el valor que cumple la igualdad anterior.
$$f(x)= P_{n,a}(x)+ f^{(n+1)}(t) \frac{\;(x-a)^{n+1}} {(n+1)!}$$
Evidentemente no conocemos cual es el valor de $t$, pero podemos con un poco de ingenio acotar el valor del resto para que el error se mantenga bajo un determinado valor.
Veamos por ejemplo como proceder para el desarrollo de seno $x$. El término general del desarrollo de seno $x$ es,
$$sen ^{(2n+1)}(x){ { {(-1)} ^ {n} {x ^ {2n+1} } }\over {(2n+1)!} }$$
Luego el resto, escogiendo un término par para que sea positivo, vale:
$$ sen ^{(2n+2)}(t){ { {x ^ {2n+2} } }\over {(2n+2)!} }$$
Y sabemos que el valor de la derivada de seno siempre será $≤ 1$, puesto que la función seno y coseno están acotadas entre $-1$ y $1$. Luego:
$$ \big \vert sen ^{(2n+2)}(t){ { {x ^ {2n+2} } }\over {(2n+2)!} }\big \vert ≤ { { {x ^ {2n+2} } }\over {(2n+2)!} }$$
$\large{{ {x ^ {2n+2} } }\over {(2n+2)!}}$, puede hacerse tan pequeño como queramos para $n+2$ suficientemente grande (lo grande que tenga que ser depende de $x$).
Si por ejemplo, queremos calcular seno $x$, para $x=2$, con un error menor de $\small{10^{-4}}$, podemos utilizar el polinomio de Taylor $\small{P_{2n+1, 0}(2)+R}$ donde:
$$R ≤ {{2^{2n+2}}\over{(2n+2)!}}< 10^{-4}$$
esta desigualdad se cumple para $n=5$, luego.
$${sen (x)={x\over{1!}}-{x^3\over{3!}}+{x^5\over{5!}}-{x^7\over{7!}}+{x^9\over{9!}}-{x^{11}\over{11!}}}+R$$ siendo $R ≤ 10^{-4}$
En azul representamos la gráfica de la función $ln \; x$ y su desarrollo en serie centrado en el punto $x=x(A)$. Con el deslizador podemos modificar el número de términos del desarrollo desde $1$ hasta $10$. Presentamos la gráfica del desarrollo en serie de $n$ términos y en línea discontinua el de orden inmediatamente inferior, $n-1$. De este modo podemos ver como se agregan sucesivamente términos, representados en rojo, al desarrollo de orden $n$.
Nos interesa señalar varias cuestiones para evaluar la aproximación del desarrollo en serie a la función en el punto $x=x(C)$.
En primer lugar, constatamos que el radio de convergencia del desarrollo de Taylor es simétrico respecto de $x=x(A)$, ya que la función no esta definida para $x=0$, ni para valores negativos de $x$. El radio de convergencia lo representamos en color marrón.
En la segunda pantalla gráfica representamos en rojo el valor de los sucesivos términos del desarrollo para $x=x(C)$, (de $1$ a $10$) y, en azul, la suma parcial de la serie de Taylor de los términos desde $1$ a $n$. En azul se señala el valor de la función $ln \; x$ en $x=x(C)$.
Podemos observar, que la serie de Taylor converge hacia el valor de la función en ese punto si $C$ se mantiene dentro del radio de convergencia. En ese caso los términos del desarrollo, al crecer $n$, se aproximan a $0$.
Fuera del radio de convergencia, vemos como la serie es divergente y los sucesivos términos, al crecer $n$, no disminuyen en valor absoluto.
Para obtener el desarrollo de Taylor de una función, son necesarias dos condiciones:
La formación del concepto de función (IV)
Las funciones trascendentes.
Las series infinitas representan otro momento clave para la evolución del concepto de función. El Cálculo, que maneja series de potencias, no tiene reparos en identificar una serie infinita con una función.
La antigua clasificación entre funciones algebraicas y mecánicas se transforma, según la nomenclatura de Leibniz, en algebraicas y trascendentes que se diferencian porque las segundas se desarrollan en un número infinito de términos.
Se da así, el paso definitivo para interpretar las funciones trigonométricas como funciones y para la definición de nuevas funciones a partir de la integración, como es el caso de los logaritmos hiperbólicos a partir de $1/(1+x)$.
Por otra parte, al comprobar la posibilidad de desarrollar en serie cualquier función, comprendemos por qué no todas las curvas son funciones válidas. Un desarrollo en serie nos devuelve un único valor de y para cada $x$, por lo tanto la gráfica de una función no puede tener bucles. Una recta vertical puede cortar una curva en varios puntos, pero solo en uno a la gráfica de una función.
Una ecuación de la forma $f(x,y)=0$ define una curva, pero no siempre podemos interpretar esta curva como una función, puesto que puede haber más de un valor de y para algún valor de $x$.
Un ejemplo de ecuación implícita es la que define un círculo, $\small{x^2+y^2=r^2}$. Si despejamos la y obtenemos $\small{y= ±\sqrt{(r^2-x^2)}}$. Es decir, la ecuación implícita se descompone en dos ramas y cada una de ellas corresponde a una función diferente.
El teorema de la función implícita, que se estudia en cálculo avanzado, establece las condiciones suficientes para que una ecuación implícita de varias variables pueda definir una función de una o varias variables respecto de las demás.
Continuar con la formación del concepto de función -V-
Volver a -III-
Euler, antes de publicar sus libros sobre cálculo diferencial e integral, en 1745, publica la “Introductio in analysin infinitorum”.
La “Introductio” consta de dos volúmenes, el primero dedicado al estudio de las funciones elementales, y el segundo a la geometría de las curvas. En el capítulo octavo del primer volumen, aparece por primera vez la identidad a la que hemos dado el título honorífico de “la fórmula más bella”. Su aparición en la “Introductio” es la meta a la que encaminamos nuestra historia.
Como parece desprenderse de la cita de su carta a D'Alambert, Euler ya tenía preparados sus dos volúmenes sobre el cálculo y en la “Introductio”, probablemente, presenta resultados ya conocidos que desarrolla utilizando recursos “exclusivamente” algebraicos.
Vamos a ver como Euler obtiene en la ”Introductio” los desarrollos en serie de las funciones exponencial y logarítmica en el capítulo séptimo del primer volumen. Como él mismo nos advierte, su enfoque es diferente al habitual del cálculo y se basa en el teorema del binomio como una regla “avanzada” del álgebra y en su concepción de los infinitesimales como “entes” a los que se aplican las reglas del álgebra.
Euler presupone una aritmética capaz de operar con números infinitamente pequeños e infinitamente grandes.
Los infinitesimales son “entes” singulares porque, sumados o multiplicados por una cantidad finita continúan siendo infinitamente pequeños. Sin embargo, del producto entre un número que se hace grande indefinidamente y un infinitesimal, podemos obtener un número finito.
La división entre infinitésimos puede ser un número finito. Si $n · 0 =0$ para cualquier $n$, Euler concluye que $n=0/0$ es una razón arbitraria, que puede ser finita.
Un infinitésimo elevado a un exponente natural es un infinitésimo de orden superior, por tanto se puede igualar a cero.
Todas estas reglas las hemos empleado desde que hemos visto las primeras demostraciones de Fermat y se han ido aplicando por todos los creadores del Cálculo.
La definición de función en la “Introductio” (V)
Euler, en los primeros capítulos de la “Introductio”, propone eliminar toda referencia a la geometría en el análisis. Para lograr este objetivo, introduce el concepto de cantidad abstracta para definir las variables y a partir de este concepto, define su noción de función.
En el prólogo de “Instituciones calculi differentialis” (1755) dice Euler:
En la primera definición nos encontramos con la palabra “analítica'. Euler tenía en mente que una expresión analítica es una expresión compuesta de magnitudes relacionadas mediante operaciones algebraicas (es decir, la adición, la resta, la multiplicación, la división, la exponenciación y la extracción de raíces ) o trascendentes (como la exponencial, el logaritmo y “otras que aporta el cálculo integral en abundancia”). Las funciones se dividen en algebraicas y trascendentes según consten de un número finito o infinito de operaciones elementales. Euler considera que la expresión analítica más general para una función es una serie infinita y toda función es desarrollable en forma de serie de potencias.
Para Euler, una función es continua si se encuentra definida por una única expresión analítica. La continuidad es una propiedad intrínseca de cada función y esto implica que es una propiedad global y no referida a puntos concretos o a tramos como la definimos hoy. Este concepto de continuidad, separa a Euler de la moderna concepción de función.
Euler revisará el concepto de función de la "Introductio" unos años más tarde como consecuencia de su participación y contribuciones en el debate de la cuerda vibrante.
Continuar con la definición moderna de función
Volver a -IV-
Euler vuelve al planteamiento original que dio lugar a la invención de los logaritmos, es decir, poner en valor la relación de la función logarítmica y la exponencial como funciones inversas. A cada función logarítmica le corresponde una función inversa del tipo $y= a^x$, que llamamos función exponencial.
Euler inicia su aproximación desarrollando directamente en serie la función exponencial en lugar de partir de la función logarítmica, definida mediante el cálculo como integral de la hipérbola.
A diferencia de las funciones logarítmicas, las funciones exponenciales están definidas para todo valor de $x$. También podemos comprobar que son siempre positivas y crecientes para valores de la base $a > 1$. Para valores de la base menores que $1$ la función exponencial es decreciente. En todos los casos la función exponencial corta al eje $Y$ en $y=1$ puesto que cualquier número elevado a $0$ resulta ser igual a $1$.
Como hemos dicho, Euler se propone obtener una serie infinita para la función exponencial. Para obtener este desarrollo procede de la siguiente manera:
Si $ϵ$ es un infinitesimal, $a^ϵ$ es un poco mayor que $1$, ($a^0=1$), y se puede escribir, para algún $k>0$:
$$a^\epsilon=1+k\epsilon$$
Si $x$ es una cantidad finita positiva, que resulta de multiplicar $ϵ$ por un número $N$ suficientemente grande, podemos poner:
$$a^x= a^{ N\epsilon}={(a^{\epsilon})}^N={(1+k\epsilon)}^N$$
Para establecer esta igualdad Euler aplica con una gran destreza los principios del álgebra de los infinitesimales. La originalidad de este planteamiento supone un alarde de imaginación y de seguridad en su razonamiento insuperables.
A partir de aquí, Euler desarrolla esta expresión por el teorema del binomio y obtiene:
[7.1]
Principio de la demostración.
$ a^x={(1+k\epsilon)}^N =1+N(k\epsilon) +{\large{\frac{N(N-1)}{2}}}{(k\epsilon)}^2 +$
$${+{\frac{N(N-1)(N-2)}{3!}}{(k\epsilon)}^3+{\frac{N(N-1)(N-2)(N-3)}{4!}}{(k\epsilon)}^4+....}$$
Recordemos que, $x= N \cdot \epsilon $, sustituimos:
$a^x={(1+k{\large{x\over{N}})}}^N=1+(kx)$
$${+{\frac{\textcolor{red}{(N-1)}}{2\textcolor{red}{N}}}{k^2}{x^2}+{\frac{\textcolor{red}{(N-1)}\textcolor{green}{(N-2)}}{2\textcolor{red}{N}3\textcolor{green}{N}}}{k^3}{x^3}+{\frac{\textcolor{red}{(N-1)}\textcolor{green}{(N-2)}\textcolor{blue}{(N-3)}}{2\textcolor{red}{N}3\textcolor{green}{N}4\textcolor{blue}{N}}}{k^4}{x^4}+....}$$
Al tender $N$ a $∞$ resulta,
$$\textcolor{red}{{\frac{(N-1)}{N}}=1}$$
$$\textcolor{green}{{\frac{(N-2)}{N}}=1}$$
$$\textcolor{blue}{{\frac{(N-3)}{N}}=1}$$
Simplificando obtenemos el desarrollo anterior.
Final de la demostración.
Euler ha obtenido el desarrollo en serie de $\small{a^x}$ y de forma simultánea, tenemos el binomio que ha dado lugar a la serie, y que es una sucesión de funciones para cada valor de $N$.
Al definir las sucesiones hemos aceptado que sus términos pueden ser numéricos o funciones. El término de la sucesión que resulta cuando $N$ se hace suficientemente grande también define $a^x$.
Euler aplica para desarrollar la función logarítmica un procedimiento semejante al de la exponencial. Partiendo del mismo punto,
$a^ω= 1+k ω$
$ω =log_a (1+k ω)$
luego, multiplicando por $N$.
$N · ω =log_a (1+k ω)^N$
si hacemos,
$(1+k ω)^N =1+x$.
tomando logaritmos a ambos lados de la igualdad,
$N ·ω =log_a (1+x)$
Como tenemos, $(1+k ω)^N =1+x$.
$${(1+k ω)={(1+x)}^{1\over{N}}}$$
$${k ω={(1+x)}^{1\over{N}}-1}$$
[7.2]
multiplicando por $N$ cada miembro,
$${Nω={N\over{k}}[{{(1+x)}^{1\over{N}}-1}]=log_a(1+x)}$$
y con un cambio de variable de $x$ por $x+1$,
$${log_a(x)={N\over{k}}{({x}^{\normalsize{1\over{N}}}-1)}}$$
Desarrollando en serie $ \small{{(1+x)}}^{1\over{N}}$ obtenemos.
$${N{(1+x)}^{1\over{N}}-N=x-{\frac{x^2}{2}}+{\frac{x^3}{3}}-{\frac{x^4}{4}}+...}$$
Inicio de la demostración.
$ {(1+x)}^{1\over{N}}=$
$$\small{1+{1\over{N}}(x)+{\frac{1\textcolor{red}{(N-1)}}{N\textcolor{red}{2N}}}{(x)}^2+{\frac{1\textcolor{red}{(N-1)}\textcolor{green}{(2N-1)}}{N\textcolor{red}{2N}\textcolor{green}{3N}}}{(x)}^3+{\frac{1\textcolor{red}{(N-1)}\textcolor{green}{(N-2)}\textcolor{blue}{(N-3)}}{N\textcolor{red}{2N}\textcolor{green}{3N}\textcolor{blue}{4N}}}{(x)}^4+....}$$
Al tender $n$ a $∞$ resulta que.
$$\textcolor{red}{{\frac{(N-1)}{2N}}={1\over{2}}}$$
$$\textcolor{green}{{\frac{(2N-1)}{3N}}={2\over{3}}}$$
$$\textcolor{blue}{{\frac{(3N-1)}{4N}}={3\over{4}}}$$
Sustituyendo y multiplicando por $N$ obtenemos:
$$N{{(1+x)}^{1\over{N}}=N+x-{\frac{x^2}{\textcolor{red}2}}+{\frac{\textcolor{green}{2}x^3}{\textcolor{red}{2}.\textcolor{green}{3}}}-{\frac{\textcolor{green}{2}.\textcolor{blue}{3}x^4}{\textcolor{red}{2}.\textcolor{green}{3}.\textcolor{blue}{4}}}+...}$$
Final de la demostración.
[7.3]
y obtenemos el desarrollo en serie de la función logarítmica volviendo a la expresión inicial [7.2]:
$${log_a(1+x)={1\over{k}}(x-{\frac{x^2}{2}}+{\frac{x^3}{3}}-{\frac{x^4}{4}}+...)}$$
La función exponencial y logarítmica son inversas
Podemos comprobar que la función logarítmica es inversa de la exponencial. Sustituyendo $x$ por $y$ en la expresión de los logaritmos, $x=log_a (y)$, obtenemos:
$${a^x=a^{{log_a(y)}}=y}$$Efectuando la misma sustitución en las expresiones obtenidas para ambas funciones resulta:
$${a^x={ {\Large\lbrack}1+ {\frac{ kN(y^{1\over{N}}-1) }{kN}}{\Large \rbrack}}^N = [y^{1\over {N}}]^N=y}$$
Obtenido el desarrollo en serie de la función exponencial podemos observar que la base elegida, no es necesariamente un número natural o entero, sino que la propia definición de la función nos conduce a aceptar como base cualquier número real. Haciendo $x=1$ en el desarrollo en serie obtenido para la función exponencial, podemos obtener el valor de a que corresponde a cada valor de $k$.
$${a={(1+{{k}\over{N}})}^N=1+k+{\frac{1}{2!}}{k^2}+{\frac{1}{3!}}{k^3}+{\frac{1}{4!}}{k^4}+....}$$
por ejemplo, para $a = 10$, $k$ es un número entre $2,3$ y $2,31$. Para $a= 2$, $k$ esta entre $0,69$ y $0,7$. Aplicando un procedimiento inverso, dando valores exactos a $k$, obtenemos para $k=1$ un valor de a de aproximadamente $2,72$. Euler bautiza este número de infinitas cifras decimales como $e$:
$${e={(1+{{1}\over{N}})}^N=1+1+{\frac{1}{2!}}+{\frac{1}{3!}}+{\frac{1}{4!}}+....}$$
$e$ puede obtenerse,según resulta de su definición, de dos maneras equivalentes, como valor de una suma infinita y como valor límite de una sucesión, aunque como vemos en el cálculo adjunto ambas difieren bastante en su velocidad para acercarse al valor límite.
Este número $e$, resulta ser también la base de los logaritmos naturales que, en el estudio de la función logarítmica como función de áreas de la hipérbola, (apartado 5.1) hemos identificado como el valor de $x$ para que el área definida por la integral sea exactamente $1$.
$$\int_{1}^{x}{1\over{x}}\small{dx=1}$$Representamos $(1+1/n)^n$ para $x=n$ para comprobar que al crecer $n$ la función se aproxima a un límite que identificamos como $e$.
| n | (1+1/n)n |
|---|---|
| 1 | 2,00000 |
| 10 | 2,59374 |
| 50 | 2,69159 |
| 100 | 2,70481 |
| 1000 | 2,71692 |
| 10.000 | 2,71815 |
| 100.000 | 2,71827 |
| 1000.000 | 2,71828 |
| 10.000.000 | 2,71828 |
Podemos comprobar que es más eficiente el cálculo mediante su desarrollo en serie, que a partir de la suma de los primeros doce términos nos da: $2,718281828$.
Una historia paralela de $e$.
Euler, como discípulo de Bernoulli, conocía el estudio sobre el interés compuesto de Jacques Bernoulli de 1683 donde aparecía la expresión $(1+1/n)^n$.
Si se invierte una Unidad Monetaria (que abreviaremos en lo sucesivo como UM) con un interés del 100% anual y se pagan los intereses una vez al año, se obtendrán 2 UM al final del año. Si se pagan los intereses 2 veces al año, dividiendo el interés entre 2, la cantidad obtenida es 1 UM multiplicado por 1,5 dos veces, es decir, 1 UM x 1,502 = 2,25 UM. Si dividimos el año en 4 períodos (trimestres), al igual que la tasa de interés, se obtienen 1 UM x 1,254 = 2,4414... En caso de pagos mensuales el monto asciende a 1 UM x = 2,61303...UM.
Por tanto, cada vez que se aumenta la cantidad de períodos de pago en un factor de $n$ y se reduce la tasa de interés en el período, en un factor de $1/n$, el total de unidades monetarias obtenidas estará dado por la siguiente expresión: $(1+1/n)^n$ y se obtiene un resultado que se acerca progresivamente a un valor sin llegar a alcanzarlo.
El número e esta por tanto presente en las finanzas y aparece en la fórmula del interés continuo, que es el valor límite del interés que se obtiene al disminuir indefinidamente el periodo de pago.
La fórmula del interés continuo es:
Capital final = Capital inicial $· e^{i n}$
Siendo $i$ la tasa de interés para un periodo y $n$ el número de periodos que transcurren en el plazo de la inversión.
Por ejemplo, si sobre mil euros nos ofrecen 12% anual, el capital a final del año será 1 120€. Si nos pagan mensualmente los intereses, al 1% mensual, el capital final resultara ser $1000 e^{0,01*12} =1 130€$. Atentos pues a como nos aplican los intereses en nuestro banco, puesto que el periodo de cálculo afecta al resultado final. En lenguaje bancario, el 13% es la Tasa Anual Equivalente (TAE) del interés del 12%, pagado mensualmente.
Con seguridad, Bernoulli no reconoció ninguna conexión entre su trabajo y los logaritmos. Euler es el primero en establecer esta relación y utilizar la letra $e$ para identificar este número.
En efecto, para $k=1$, el valor de la base de la función exponencial es $e$, y la serie obtenida como desarrollo de la función logarítmica en [7.3], resulta ser igual a la serie de Mercator.
$${{N[{{(1+x)}^{1\over{N}}-1}]=log_a(1+x)=(x-{\frac{x^2}{2}}+{\frac{x^3}{3}}-{\frac{x^4}{4}}+...)}}$$con lo que podemos afirmar que:
En consecuencia, la exponencial $e^x$ es la función inversa de la función logarítmica natural, lo que la convierte en la función exponencial por excelencia y justifica que para distinguirla entre las demás funciones del mismo tipo, se la conozca como exponencial natural.
Los logaritmos naturales también se suelen llamar neperianos, que es un reconocimiento a Napier como inventor, pero no implica una correspondencia exacta entre ellos, aunque podemos ver que si existe una cierta similitud.
Los logaritmos neperianos se definen como.
$$N=10^7(1-10^-7)^L$$
Haciendo $N_1= {\frac{N}{10^7}}$ y $L_1= {\frac{L}{10^7}}$ podemos poner,
$$N_1={{{\Large\lbrack}{(1-10^{-7})}}^{10^7}}{\Large\rbrack}^{L_1}$$
siendo $\small{{(1-10^{-7})}^{10^7}=(0,999999)^{10^7}=0,3678794.. }$,
casi igual a: $\;\large{{1\over{e}}} \approx \small{0,3687969}$

$$L_1=log_{\large{1\over{e}}}N_1$$
$\frac{L}{10^7}=log_{\large{1\over{e}}}(\frac{N}{10^7})$, es decir: $L=10^7 log_{\large{1\over{e}}}(\frac{N}{10^7})$
Los logaritmos naturales en base $1/e$, se corresponden casi exactamente, con los logaritmos neperianos, si dividimos $N$ por $10^7$ y multiplicamos el logaritmo obtenido por $10^7$.
La derivada de las funciones exponenciales, son proporcionales a la función original, como podemos comprobar derivando la serie obtenida para $a^x$,
$${ a^x=1+kx+{\frac{1}{2!}}{k^2}{x^2}+{\frac{1}{3!}}{k^3}{x^3}+{\frac{1}{4!}}{k^4}{x^4}+....}$$
cuya derivada es:
$${ (a^x)'=k(1+kx+{\frac{1}{2!}}{k^2}{x^2}+{\frac{1}{3!}}{k^3}{x^3}+{\frac{1}{4!}}{k^4}{x^4}+....)=k\: a^x}$$
Como consecuencia de que la función exponencial y la logarítmica son inversas podemos poner:
$$y= a^x\:=\:e^{\small{(ln\:a)x}} $$
Si derivamos esta expresión obtenemos:
$$y'= ln\:a\:(e^{\small{(ln\:a)x}} \:) =ln\:a\:a^x $$
luego, podemos identificar $k$ con $ln \; a$.
$$y'=(a^x)'= a^x \:ln\:a$$
Inicio de la demostración aplicando la definición de derivada.
Si aplicamos las reglas para la derivación a la función exponencial , resulta:
$${\frac{a^{x+∆x}-a^x}{∆x}}$$
que es igual a,
$${\frac{a^{x}\:a^{∆x}-a^x}{∆x}}$$
luego,
$$ a^x({\frac{a^{∆x}-1}{∆x}})$$
Podemos poner en lugar de $Δx$, $1/N$ cuando $N$ tiende a $\small{\infty}$, sustituyendo, obtenemos para el paréntesis el valor: $N(a^{1\over{N}}-1)$, que es por definición $ln (a)$. Luego:
$$y'=a^x\:ln(a)$$
Fin de la demostración.
La función exponencial natural tiene la propiedad de ser igual a su derivada.
Si $y'=y \:ln(a)$, para el caso de $a=e$, obtenemos $y'=e^x$, es decir, $y'=y$.
La especial propiedad de la función exponencial en base $e$ es observable fácilmente, porque obtenemos la serie inicial, si derivamos el desarrollo en serie de la función término a término,
Esta propiedad, convierte a la exponencial natural, en opinión de muchos, en la función más importante en matemáticas.
La propiedad de la función exponencial, en base $e$, de ser igual a su derivada también es válida para sus derivadas sucesivas. Esta propiedad nos permite obtener de forma muy sencilla su desarrollo en serie siguiendo la fórmula de Taylor, porque la función y todas sus derivadas son iguales a $1$ para $x=0$.
$f(x)= f'(x)= f''(x)= f'''(x) =\cdot \cdot \cdot= 1$
Al definir la función logarítmica como la función de áreas de la hipérbola equilátera, hemos visto que la derivada de la función es siempre la hipérbola $1/x$. También hemos identificado el coeficiente de esta proporción, que hemos llamado $k_a$:
$$k_a={\frac{1}{ln \:a}}$$
Una vez identificado e como la base de los logaritmos naturales, podemos redefinir $k_a$ como:
$$k_a={\frac{log_a x}{ln \:x}}={\frac{1}{ln \:a}}={\frac{log_a\:e}{1}}$$
y resulta:
$$y'= log'_a\: x={1\over{ln\:a}}{1\over x}={1\over{x}}log_a\:e$$
Este resultado también podemos obtenerlo aplicando a la función logarítmica la definición de derivada y ejecutando los cálculos tal como mostramos a continuación.
Inicio de la demostración aplicando la definición de derivada.
Aplicando las reglas para la derivación obtenemos:
$${\frac{log_a(x+∆x)-log_a x}{∆x}}$$
que por las propiedades de los logaritmos podemos poner:
$${\frac{log_a{\frac{(x+∆x)}{x}}}{∆x}}$$
Simplificando,
$$log_a{(1+{{∆x}\over{x}})}^{\large{1\over{∆x}}}$$
Si multiplicamos el exponente por $\small{1}= \large{{x\over x}}$
$$log_a{(1+{{∆x}\over{x}})}^{\large{x\over{x\:∆x}}}$$
$${1\over{x}}log_a{(1+{{∆x}\over{x}})}^{\large{x\over{∆x}}}$$
Manejando adecuadamente el resultado obtenido,
$${(1+{{∆x}\over{x}})}^{\large{x\over{∆x}}}$$
es equivalente a:
$${(1+{{1}\over{x\over{∆x}}})}^{\large{x\over{∆x}}}$$
que podemos poner como ${(1+{1\over{n}})}^n$ siendo $\small{n=}\large{x\over ∆x}$ .
Cuando $Δx$ se hace pequeño, $n$ aumenta, por lo tanto podemos concluir que la expresión de la derivada es:
$$y'= {1\over{x}}log_a ({1+{1\over{n}}})^n$$
para $n$ tendiendo a infinito, resulta según la definición obtenida de $e$:
$$y'= {1\over{x}}log_a\:e$$
Fin de la demostración.
Representación de la función exponencial $a^x$ y su función derivada. Con el deslizador movemos la base de la función y observamos que la función y su derivada coincidan cuando el deslizador nos da el valor de $e$.
Representación de la función logarítmica y su derivada. Con el deslizador modificamos la base de la función logarítmica.
Se calcula el área bajo la hipérbola equilátera $y = 1/x$ desde $1$ a $x$ igual a la base de la función logarítmica, que es lo mismo que la intersección con la horizontal de abscisa $= 1$.
Podemos comprobar que cuando la derivada coincide con la hipérbola $y = 1/x$, el área resaltada tiene valor $1$ y el deslizador nos señala e como base de la función logarítmica.
Crecimiento y decrecimiento exponencial.
Cuando el número $e$ aparece en las ecuaciones para describir fenómenos de crecimiento o decrecimiento decimos que varían exponencialmente. Existen muchos fenómenos naturales de crecimiento o decrecimiento exponencial, como por ejemplo la desintegración del carbono 14 o el crecimiento de poblaciones de bacterias en ausencia de factores que limiten el crecimiento.
La fórmula general de estos fenómenos es:
$P(t) = P(0) e^{kt}
La población en un instante $t$, se obtiene multiplicando la población en el instante $0$ por el factor ${e^{kt}}$ en el que $k$ se denomina constante de crecimiento.
Si derivamos esta función de crecimiento obtenemos:
$$y'={\frac{d\:P(0)\:e^{kt}}{dt}}=kP(0)\: e^{kt}=ky$$El crecimiento en el periodo $t$ de la población es proporcional a la población en ese momento $t$
Si en laboratorio unas bacterias crecen exponencialmente con una constante de crecimiento $k=0,41$ en un periodo de una hora, si la población en el instante $0$ es $1000$, a las cinco horas la población será:
$$P(5)=1000\:e^{0,41.5}=1000 \:e^{2,05}=7.768$$El tiempo que una población tarda en duplicarse:
$$2P=P e^{kt}$$ $$2=e^{kt}$$Luego, el tiempo de duplicación es:
$$t=\frac{ln 2}{k}$$El carbono 14
El $C^{14}$ está en una proporción en la atmosfera de $R$ atm = $10^{-12}$ (ratio en la atmosfera) respecto del $C^{12}$
El $C^{14}$ es radioactivo y se desintegra exponencialmente con una $k$ de $0,000121$ por año. A partir de la fecha en que un organismo vivo deja de respirar, la desintegración del $C^{14}$ hace variar el Ratio del $C^{14}$ respecto del $R$ atm en la atmosfera original. Si una muestra tiene con un ratio del 15% del $R$ atm resulta:
$$R_{atm}\:e^{-0,000121t}=0,15\: R_{atm}$$ $$e^{-0,000121t}=0,15 $$ $$-0,000121t=ln (0,15) $$$t = 15.700$ años.
$i$, el primer número imaginario de la historia.
Si cualquier número real puede expresarse algebraicamente, la afirmación inversa no es cierta. De antiguo son conocidas expresiones algebraicas que no tienen su solución entre los números conocidos. Para Descartes,
Tal como están definidas las operaciones, el cuadrado de un número positivo es otro número positivo. También el cuadrado de un número negativo es un número positivo. En consecuencia al extraer la raíz de un número positivo podemos dar por válidos dos resultados, uno positivo y otro negativo, pero no podemos extraer la raíz cuadrada de un número negativo, puesto que no hay ningún número real cuyo cuadrado sea negativo. Las raíces de números negativos aparecen al intentar resolver expresiones polinómicas de segundo grado del tipo $\small{a\:x^2+b\:x+c =0}$, cuyas dos soluciones se obtienen por la conocida fórmula:
En el caso de que el discriminante sea negativo, (Se llama discriminante al término $\small{ b^2-4ac} $ que esta afectado por la raíz cuadrada), no podemos obtener la raíz cuadrada de un número negativo, y por lo tanto, un número real como solución. Si dibujamos la función, una parábola, podemos observar que, el caso del discriminante negativo se corresponde con el hecho de que la curva no corta el eje $x$ y por lo tanto, desde un punto de vista gráfico, se confirma que no existe solución en este caso.
En el siglo XVI, en la Italia del renacimiento, surge el interés por la resolución de las ecuaciones de tercer y cuarto grado, que se convierten en protagonistas de los duelos matemáticos que se celebraban entre matemáticos, intercambiando listas de problemas a resolver por el rival. En uno de estos duelos, Antonio Maria Fior, que conocía soluciones para algunas cúbicas incompletas heredadas de su maestro, Scipione del Ferro (1465-1526), reta a Nicolo Tartaglia (1500-1557) un matemático competente y de gran prestigio en ese momento, a resolver una lista de problemas basados precisamente en la resolución de ecuaciones cúbicas.
Tartaglia, resuelve la ecuación general de tercer grado y comparte su fórmula con Cardano (1501-1576), bajo el solemne juramento de no revelar el secreto hasta su muerte. Unos años más tarde, en 1545, con la escusa de haber tenido acceso a los documentos de Scipione del Ferro, publica la solución de la ecuación cúbica en “Ars magna”, donde expone además la solución para las cuárticas.
La solución que desde entonces se conoce como “fórmula de Cardano”, transcrita a notación moderna es, para la ecuación $x^3+p\:x+\:q=\:0$ :
$$ x=\big({-q\over2}+{1\over2}\sqrt{({q^2}+{4\:p^3\over27}})\big)^ {\large {1\over3}}+ \big({-q\over2}-{1\over2}\sqrt{({q^2}+{4\:p^3\over27}})\big)^{\large{1\over3}}$$Como en el caso de las ecuaciones de segundo grado, la expresión bajo la raíz cuadrada se llama discriminante, que en este caso es:
$${({q^2}+4\;{p^3\over27})}$$Representando la función para los diferentes valores de $p$ y $q$, podemos ver que la fórmula de Cardano obtiene la raíz de la ecuación cuando el discriminante es positivo. Cuando los coeficientes dan un valor negativo al discriminante, la fórmula de Cardano fracasa.
Lo que ocurre para las cúbicas es diferente de lo que hemos visto para los polinomios de segundo grado. En el caso de discriminante negativo, el gráfico de la función delata raíces reales y la gráfica de la ecuación corta el eje $x$ en tres puntos.
Cardano detecta este problema pero no puede entender que sentido tiene su fórmula en este caso. Por ejemplo, si aplicamos la fórmula al caso de $\small{ x^3-15\:x-4=0}$
$$x={(\textcolor{red}{2+(-121)^{\large{1\over2}}}})^{\large {1\over3}}+{(\textcolor{blue}{2-(-121)^{\large {1\over2}}}})^{\large{1\over3}}$$y queda la raíz cuadrada de un número negativo ($-121$) que impide obtener una solución. Pero por otra parte es fácil comprobar que existe una raíz de valor $x=4$.
La solución del enigma se debe a Rafael Bombelli que en 1572 realiza estos cálculos sustituyendo $-121^{\:\large{1\over2}}$ por su valor ${11 \:(-1)}^{\large{1\over2}}$ , resultando:
$$x={\textcolor{red}{(2+11\:( -1)^{\large{1\over2}}}})^{\large{1\over3}} + {{(\textcolor{blue}{2- 11\:(-1)}^{\large{1\over2}}}})^{\large{1\over3}}\tag {1}$$y para resolver la raíz cúbica, establece una relación entre el radicando de las dos raíces cúbicas, para lo que necesita obtener un par de números, $a$ y una $b$, que cumplan las igualdades siguientes,
$${\textcolor{green}{(a + b\:(-1)^{\large{1\over2}})^3}} =\textcolor{red} {2+11\:( -1)^{\large{1\over2}}}$$ $${\textcolor{green}{(a - b\:(-1)^{\large{1\over2}})^3}}= \textcolor{blue}{2- 11\:( -1)^{\large{1\over2}}}$$De esta manera, sustituir en la fórmula de Cardano, el término $b\:(-1)^{\large{1\over2}}$ se anula con $-b\:(-1)^{\large{1\over2}}$ y el resultado es $2 a$.
Si sabemos que el resultado es $4$, entonces $a= 2$. El único valor posible para $b$ es $1$.
$${(2+(-1)^{\large{1\over2}}})^3 =2+ 11 \:(-1)^{\large{1\over2}}$$podemos sustituir la primera raíz cubica de ($1$) por.
$${(\textcolor{green}{(2+(-1)^{\large{1\over2}})^3})}^{\large{1\over3}} =2+(-1)^{\large{1\over2}}$$y del mismo modo la segunda raíz cubica por.
$${(\textcolor{green}{(2-(-1)^{\large{1\over2}})^3})}^{\large{1\over3}} =2-(-1)^{\large{1\over2}}$$El resultado es:
$$(2+(-1)^{\large{1\over2}}) + (2-(-1)^{\large{1\over2}})=4$$Es decir, al sumar los dos radicandos desaparece $\small{\sqrt{-1}}$ y el problema es salvable sin entrar a discutir el significado de $\small{\sqrt{-1}}$ y siguiendo las reglas del álgebra para obtener la solución. De alguna manera, suponiendo que las raíces cuadradas de $-1$ tienen sentido obtenemos un resultado correcto.
La solución de Bombelli no tiene ningún valor práctico, puesto que para llegar a la solución debemos conocer la raíz previamente, lo cual no es precisamente el caso más general. Su manejo de $\small{\sqrt{-1}}$, es el primer paso para su aceptación como número, aunque su encaje con los “números” tradicionales no va a ser inmediata.
La $\small{\sqrt{-1}}$, permanece en el misterio durante los dos siglos siguientes. Ya hemos visto la opinión de Descartes sobre las raíces “falsas”.
Para Leibniz, los números imaginarios.
El símbolo $i$
Euler rescata del olvido a $\small{\sqrt{-1}}$ en la “Introductio”, donde aparece como una de las claves para la obtención de la “fórmula más bella”. Euler es consciente que $\small{\sqrt{-1}}$, no es una operación válida, porque la raíz cuadrada solo esta definida para números positivos. Por este motivo, unos años más tarde, prefiere introducir $\small{\sqrt{-1}}$ como un nuevo número, al que llama $i$, y que define como $i^2=-1$.
Hay que esperar hasta el siglo XIX para la definición por Gauss de una nueva categoría de números, que se llamarán números complejos, y de los que el número $i$ será la “unidad imaginaria”. A partir de su introducción los números complejos adquieren el protagonismo que les corresponde y darán el salto a las ecuaciones de la física, demostrando que también forman parte del lenguaje de la naturaleza.
La fórmula de Cardano, para los casos de discriminante negativo, puede resolverse operando de acuerdo con el álgebra de los números complejos, y se obtienen correctamente las raíces de la ecuación de tercer grado. (Ver la solución de la ecuación de Cardano en el anexo sobre números complejos, figura 9.11)
En el siguiente capítulo de la "Introductio", Cantidades trascendentes derivadas del círculo, Euler aborda la definición de las funciones trigonométricas y también aquí opta por un camino original. Euler observa que la identidad básica de la trigonometría,
$$cos^2 x+sen^2 x=1$$
Puede descomponerse, con la ayuda del número $i$, en factores de la forma:
$(cos\: x + i sen\: x) \:(cos \:x - i sen \:x) = 1$
La introducción de $i$, tiene para Euler un sentido puramente algebraico, para aprovechar las propiedades de las potencias sucesivas del número $i$,
$\begin{aligned}(ix)^2 & =-x^2 \\ (ix)^3 & =-x^2 \cdot ix=-ix^3 \\ (ix)^4 & =-ix^3 \cdot ix=x^4\\ (ix)^5 & =x^4 \cdot ix=ix^5\\ (ix)^6 & =ix^5 \cdot ix=-x^6 \end{aligned}$
Repitiéndose la secuencia $-1, -i, 1, i, -1 …$. Indefinidamente al incrementarse el exponente.
Esta descomposición en factores, con la inclusión del número $i$, permite que la alternancia de signos se corresponda con la propia de las funciones trigonométricas.
$\small{(cos \;x + i \;sen\; x) (cos\; y + i \;sen\; y)} =$
$\small{cos \;y \;\;cos \;x - sen \;y \;\;sen\; x + i\;(cos\; y \;\;sen \;x + sen\; y \;\;cos \;x)}$
Teniendo en cuenta la fórmula de la suma de ángulos,
$\small{cos\;y\;\; cos\; x\; -\; sen \;y \;\;sen \;x = cos\;(y+x)}$
$\small{cos\;y\;\; sen\; x\; +\; sen \;y \;\;cos \;x = sen\;(y+x)}$
obtiene:
$\small{(cos \;x + i \;sen\; x) (cos\; y + i \;sen\; y) = cos\;(y+x)+i\;sen\;(y+x)}$
Repitiendo la multiplicación por un nuevo factor,
$\small{(cos \;(x+y) + i \;sen\; (x+y)) (cos\; z + i \;sen\; z) =}$
$\small{cos\;(y+x+z)+i\;sen\;(y+x+z)}$
y por inducción:
$\small{(cos \;x + i \;sen \;x)^n = cos\;(nx) + i \;sen \;(nx)}$,
del mismo modo podemos obtener,
$\small{(cos \;x - i \;sen \;x)^n = cos\;(nx) + i \;sen \;(nx)}$,
Estas fórmulas ya habían sido publicadas por De Moivre en 1707 y eran conocidas por Euler.
Sumando y restando las fórmulas de De Moivre para seno y coseno obtenemos:
$$\small{cos \:n \:x ={\frac{{(cos x + i \:sen x)}^n + {(cos x - i \:sen x)}^n} {2}}}$$ $$\small{sen \:n \:x ={\frac{{(cos x + i \:sen x)}^n - {(cos x - i \:sen x)}^n} {2}}}$$Euler interviene con su habilidad para manejar los infinitesimales y propone, $n · x = z$, para $n$ muy grande y $x$ muy pequeño, cuyo producto es un número finito $z$. Sustituimos en la fórmula $n · x$ por $z$ y simplificando, teniendo en cuenta que, $x= z/n$, y que para $x$ muy pequeño podemos sustituir $sen \; x$ por $x$ y $cos \; x$ por $1$.
Efectuando las operaciones, resulta:
$$\small{cos\: z}={\frac{ {(1+i{\normalsize{z\over{n}}})}^n + {(1-i{\normalsize{z\over{n}}})}^n }{\small{2i}}}$$ $$\small{sen\: z}={\frac{ {(1+i{\normalsize{z\over{n}}})}^n - {(1-i{\normalsize{z\over{n}}})}^n }{\small{2i}}}$$Puesto que sabemos que:
$$\small{e^z={(1+{z\over{n}})}^n}$$Las anteriores expresiones quedan, como:
Este resultado nos viene a decir que las funciones trigonométricas pueden obtenerse a partir de la función exponencial, de una forma misteriosa, porque no sabemos muy bien que significa $e^{ix}$, ya que la función exponencial no la hemos definido para exponentes imaginarios. Esta conexión entre las funciones trigonométricas y la exponencial nunca pudo imaginarse cuando se definieron estas funciones.
Sumando $cos \; x$ y $sen \; x$, obtenemos:
y restando :
Esta fórmula se conoce como fórmula de Euler, aunque es un título que no detenta en exclusiva pues existen otras “fórmulas de Euler” que compiten con ella.
Estamos ante una fórmula cuyo sentido pleno se obtiene aplicada a los números complejos, pero los números complejos aun tardarán un siglo en aparecer en la escena matemática. Esta fórmula adquirirá una gran importancia en la integración de determinadas funciones trigonométricas aprovechando que la integral de $e^{ix}$ es inmediata.
Una vez descubierta la relación entre las funciones trigonométricas y la exponencial, advertimos que se podría haber sospechado esta conexión.
La pista a seguir es la simetría de la ecuación de la circunferencia con la de las hipérbolas que obtenemos sustituyendo en su ecuación $x$ por $ix$ o multiplicando por $i$. De la circunferencia partimos para obtener integrando las funciones trigonométricas, y podemos relacionar la hipérbola con la exponencial a través de su inversa, la función logarítmica.
Para obtener las funciones trigonométricas hemos partido de la integral del área bajo la circunferencia unidad, $y= (1-x^2)^{1\over2}$. Cambiando el signo del paréntesis, o sustituyendo por $ix$, obtenemos una hipérbola,$y= (1+x^2)^{1\over2}$, simétrica respecto del eje $Y$, tangente a la circunferencia de radio $1$ en $y=1$. Multiplicando la ecuación de la circunferencia por $i$, obtenemos otra hipérbola, $y= (x^2-1)^{1\over2}$, también tangente al círculo en el punto $x=1$ y simétrica respecto del eje $X$.
Por otra parte las funciones logarítmicas las hemos obtenido mediante la integral de la hipérbola $y={1\over{(x ln a)}}$, que es una hipérbola girada 45º respecto de cualquiera de las anteriores y que coincide con ellas para $ln(a) =2$. Para este valor la función logarítmica tiene por ecuación $y={1\over{2 x}}$, y su simétrica, la exponencial $y= e^{2x} = {(e^x)}^2$.
Una fórmula es una igualdad que establece una relación entre constantes y variables que siempre debe cumplirse. Dando valores particulares a las variables de una fórmula, obtenemos lo que se conoce como una identidad. Vamos a concretar la fórmula de Euler para algunos valores particulares de $x$.
La primera de ellas, la identidad que estamos persiguiendo desde el inicio de nuestro libro, a la que nos hemos referido de forma un tanto impropia como “fórmula” de Euler.
Particularizando la expresión $e^{ix} = cos(x)+ i\:sen(x)$, para $x=π$, se obtiene:
$$e^{iπ}=-1$$y de ahí la presentación como:
$$e^{iπ}+1=0$$Un segundo resultado interesante de la fórmula de Euler es que permite descubrir la naturaleza de los logaritmos de los números negativos. Podemos poner la identidad anterior como:
$$\small{ln (-1) = π \:i}$$Entonces para cualquier número negativo.
Euler demuestra que el logaritmo de un número negativo es un número con una componente imaginaria, que en el futuro se llamaran números complejos. Además, como es evidente que se cumple:
$$\small{e^{i(x+2kπ)} = cos\:(x)+ i \:sen\:(x)}$$podemos poner:
$$\small{ln\:(-a)= ln \:a +2kπ \:i}$$con lo que se demuestra que existen infinitos logaritmos para un mismo número negativo.
Por último, la fórmula de Euler también nos permite obtener otra identidad interesante. Particularizando $e^{ix} = cos(x)+ i sen(x)$ para $x=π/2$, resulta:
$$\small{e^{{-iπ/2}}=i}$$luego:
$$\small{i^{i}={(e^{-iπ/2})}^{i}=e^{π/2}}$$Con lo que obtenemos un resultado sorprendente, ya que elevando $i$ a un número imaginario obtenemos un número real.
La relación entre las funciones exponencial y las hiperbólicas, se puede deducir de forma similar a como lo hemos hecho para las trigonométricas y en este caso no involucrarán a $i$.
La fórmula de Euler equivalente para las funciones hiperbólicas es:
$$\small{e^{x}=cosh\: x+ senh\: x }$$ $$\small{e^{-x}=senh \:x- cosh\: x} $$Sumando ambas expresiones tenemos:
$$\small{cosh\:x ={\frac{e^{x}-e^{-x}}{2}}\quad \quad senh \:x ={\frac{e^{x}+e^{-x}}{2}}}$$Al iniciar nuestro relato hemos definido este siglo como el de la rotura de las reglas de las matemáticas antiguas, que avanzaban progresando sobre la base de demostraciones basadas en esquemas lógicos sencillos, como el silogismo, la inducción, ...
La explosión de nuevas ideas y conceptos lleva a la necesidad de plantear una manera de consolidar los avances de una manera completamente diferente. Además de constatar su utilidad para la descripción de los fenómenos físicos y su aplicación a casos particulares, uno de las garantías para confirmar un resultado es comprobar su consistencia cuando se obtiene por diferentes vías.
Si revisamos lo que hemos ido describiendo en una secuencia temporal, podremos comprobar que existe diversidad de demostraciones que aportan evidencia de certeza a los resultados.
Esta habilidad para compatibilizar diferentes aproximaciones da coherencia al universo matemático de Euler y le proporciona la perspectiva necesaria para ofrecer una nueva visión del Cálculo. Así interpretamos el objetivo de la “Introductio” de ofrecer una sistematización de desarrollos ya conocidos previamente, sin utilizar los métodos del cálculo diferencial e integral.
La identificación de e es la pieza clave del puente que Euler establece a través de la exponencial, entre las funciones trascendentes y las funciones trigonométricas. El número e aparece bajo tres formas diferentes. La primera como valor límite de la sucesión ${(1+{1\over{n}})}^n$ , la segunda como desarrollo en serie, y una vez identificados los logaritmos hiperbólicos con los logaritmos en base e, mediante la integral definida de la hipérbola equilátera.
$$\small{\int_{1}^{e}{1\over{x}}dx=1}$$Tres definiciones para un único valor de $e$.
La definición de Euler de las funciones exponencial y logarítmica se basa en su habilidad con el “álgebra de los infinitesimales” para formular ambas funciones en forma de binomio, y obtener sus desarrollos en serie. Euler obtiene una conexión entre, la sucesión de funciones que obtiene al desarrollar el binomio para valores de n enteros, con los n primeros términos de su serie de Taylor. Al crecer n hacia valores “grandes”, la serie de funciones converge a la función exponencial y su serie de Taylor se hace infinita.
Las expresiones obtenidas para estas funciones confirman su definición como funciones inversas.
$$\small{a^x={(1+{{kx}\over{N}})}^N}$$ $$\small{log_a(x)={N\over{k}}{({x}^{1\over{N}}-1)}}$$Para las funciones trigonométricas, Euler prescinde en la “Introductio” de los desarrollos en serie obtenidos por Newton a partir de la integración de la ecuación de la circunferencia. Su punto de partida son las fórmulas clásicas para el seno y el coseno de la suma de ángulos, a partir de las cuales obtiene la fórmula De Moivre y a partir de ella la definición de $e^{ix}$ en función de seno y coseno de $x$, y escribir:
$$\small{e^{ix} = cos\:x+ i \:sen\:x}$$Este resultado se hubiera podido obtener igualmente a partir del Cálculo, que es el procedimiento de demostración habitual hoy en día. Una vez establecida la propiedad de $e^x$ de que todas sus derivadas son iguales a la función original, es inmediato obtener su desarrollo de Taylor y observar su relación con los desarrollos ya conocidos para $sen \; x$ y $cos \; x$, obtenidos mediante la integración de la circunferencia.
$$\small{\begin{aligned} e^x & =1+{\frac{x}{1!}}+{\frac{x^2}{2!}}+{\frac{x^3}{3!}}+{\frac{x^4}{4!}}+{\frac{x^5}{5!}}+{\frac{x^6}{6!}}+{\frac{x^7}{7!}}+...\\ sen\:x & =\qquad\textcolor{red}{{\frac{x}{1!}}\qquad-{\frac{x^3}{3!}}\qquad+{\frac{x^5}{5!}}\qquad-{\frac{x^7}{7!}}}+...\\ cos\:x & =\textcolor{blue}{1\qquad\:\:{-\frac{x^2}{2!}}\qquad+{\frac{x^4}{4!}}\qquad-{\frac{x^6}{6!}}}+...\end{aligned}}$$Sustituyendo en los desarrollos en serie de $e^x$ y de $sen \; x$, $x$ por $ix$, obtiene:
$$\small{\begin{aligned} e^x & =1+{\frac{ix}{1!}}-{\frac{x^2}{2!}}-{\frac{ix^3}{3!}}+{\frac{x^4}{4!}}+{\frac{ix^5}{5!}}-{\frac{ix^6}{6!}}+{\frac{ix^7}{7!}}+...\\ sen\:x & =\qquad\textcolor{red}{{\frac{ix}{1!}}\qquad-{\frac{ix^3}{3!}}\qquad+{\frac{ix^5}{5!}}\qquad-{\frac{ix^7}{7!}}}+...\\ cos\:x & =\textcolor{blue}{1\qquad\:\:{-\frac{x^2}{2!}}\qquad+{\frac{x^4}{4!}}\qquad-{\frac{x^6}{6!}}}+...\end{aligned}}$$Podemos extraer $i$ en el desarrollo de $sen \; x$ y resulta:
$$\small{sen(ix)=i\:sen(x)}$$Con lo que finalmente:
$$\small{e^{ix} = \textcolor{blue}{cos x}+ \textcolor{red}{i\: sen x}}$$Obteniendo la fórmula de Euler por este procedimiento, mediante la suma de desarrollos en serie, se observa claramente el papel de $i$ para alternar, en el sentido adecuado, el signo de los diferentes sumandos.
Descartes tuvo un sueño, Napier una obsesión, Fermat invento los infinitesimales, Newton y Leibniz hicieron posible el “invento del siglo”, pero finalmente, Euler ilumina la escena. Percibimos esta capacidad, solo al alcance de los grandes, cuando estamos comentando unas pocas páginas, del conjunto de miles, de su monumental obra.
Euler tenía todo a su alcance para obtener estos resultados mediante el Cálculo, pero su opción de abrir una nueva vía de demostración nos confirma la superioridad de su punto de vista, que le permitía abordar los problemas desde diferentes aproximaciones y dotar al Cálculo, recién descubierto, de una gran solidez.
El progreso de las matemáticas no se detiene. Hemos seguido la pista durante un siglo al número e pero, al acabar el relato, queda por explicar el final para muchos de los hilos de debate que han ido apareciendo y que quedan abiertos al futuro. Hacemos un inventario de cómo se fueron resolviendo en el tiempo, ordenados según su fecha de resolución, referida a la de publicación de la “Introductio” en 1745, poniendo de manifiesto indirectamente la genialidad de su formulación prematura.
+2 - 1747 - La definición moderna de función.
Los matemáticos empezaron a aplicar el cálculo infinitesimal para resolver problemas de la física. Hemos visto que en su origen el cálculo se ocupa de problemas de cuadraturas que quedan resueltos mediante funciones elementales. La resolución de problemas más complicados lleva a plantear las primeras ecuaciones diferenciales. El problema del péndulo, la ecuación de la cuerda flexible suspendida y sometida a su propio peso, o los primeros estudios sobre elasticidad aplicados a la deformación de vigas. En la lógica evolución aparecen problemas que requieren el estudio de ecuaciones de segundo grado y en derivadas parciales.
Jean Le Rond d'Alambert en 1746, plantea el problema de la cuerda vibrante “una cuerda tensa que se hace vibrar”, como la de los instrumentos musicales. Pocos meses después Euler escribe un artículo “Sobre la oscilación de cuerdas” en la que sostiene la conveniencia de aceptar como soluciones válidas configuraciones del estado inicial de la cuerda lo más generales posibles, en concreto propone admitir funciones definidas “a trozos”. En terminología de Euler funciones discontinuas, aunque hoy las definimos como continuas con derivadas discontinuas. Por ejemplo, al tensar una cuerda pulsando un punto intermedio, podemos imaginar el estado inicial de la curva como la composición de dos tramos rectos que se unen en el punto donde pinzamos la cuerda para hacerla vibrar.
Euler introduce así un nuevo tipo de funciones, que superan lo propuesto por él mismo en la “Introductió” muy poco tiempo antes.
Esta nueva definición de función se consolidará a partir de los estudios sobre el calor de Fourier (otra vez la física señalando el camino a los avances matemáticos).
El estado inicial del “calor” de una barra metálica es más arbitrario que el de la cuerda vibrante y no requiere de ninguna ley de continuidad. Fourier consigue desarrollar funciones muy arbitrarias, definidas por tramos, en series de funciones trigonométricas, y demuestra que por más arbitraria que parezca la función definida, la serie trigonométrica obtenida converge a los valores de dicha función.
De allí que Fourier exprese una idea verdaderamente revolucionaria:
Podemos imaginar una función como una «máquina» o caja negra, que transforma los valores u objetos de «entrada» en los valores u objetos de «salida». La única restricción para esta caja negra es que para cada valor de entrada asigne un único valor de salida. Los valores de entrada, sobre los que se aplica la función son el “dominio” de la función y los valores de salida la “imagen” de la función.
Una función puede definirse por varios procedimientos. En general, la definición se obtiene por la regla o método que permite calcular la imagen a partir de los valores de la variable de entrada.
+76 - 1821 - El fin de los infinitesimales.
Durante el siglo XVIII, la búsqueda de fundamento para los infinitesimales estuvo siempre presente entre los matemáticos, pero los primeros resultados sólidos deben esperar al siglo XIX, a lo que a veces se llama la “época del rigor”, en la que los matemáticos se inclinaron por la introducción de la teoría de límites en el análisis.
 A partir de la publicación por Cauchy en 1821 de su "Curso de análisis", se precisa el concepto de función, de límite y de continuidad, tomando el concepto de límite como punto de partida del análisis y eliminando de la idea de función toda referencia a una expresión formal, algebraica o no, para fundarla sobre la noción de correspondencia introducida por Fourier.
A partir de la publicación por Cauchy en 1821 de su "Curso de análisis", se precisa el concepto de función, de límite y de continuidad, tomando el concepto de límite como punto de partida del análisis y eliminando de la idea de función toda referencia a una expresión formal, algebraica o no, para fundarla sobre la noción de correspondencia introducida por Fourier.
Karl Weierstrass (1815 1897), profesor desde 1856 y durante treinta años, de la Universidad de Berlín es también considerado el "padre del análisis moderno". A él se deben las definiciones de continuidad, límite y derivada de una función, que siguen vigentes en la actualidad.
Con la teoría de límites se logra eliminar las dificultades en el manejo del infinito por el cálculo diferencial e integral de Leibniz y Newton, definiendo la derivada como límite de un cociente y la integral como límite de unas sumas parciales. Los infinitésimos, como cantidades infinitamente pequeñas diferentes de $0$, se abandonan y se sustituyen por un proceso potencialmente infinito de aproximación. En definitiva, se introduce en el análisis una nueva operación, que llamamos “paso al límite”. Esta operación asociada a la suma, permite sumar infinitos sumandos y asociada a la división nos permite resolver la indeterminación de su resultado cuando el divisor es $0$.
La teoría de límites esta muy enraizada en nuestra manera de razonar y en el lenguaje natural, de manera que es difícil imaginar desde nuestra perspectiva, la dificultades que los matemáticos tuvieron para justificar los conceptos que dieron inicialmente forma al Cálculo.
El paso al límite.
Una sucesión puede definirse para un número finito de valores de $n$, o bien puede entenderse definida para cualquier número natural. A estas sucesiones las llamamos infinitas puesto que, por muy grande que tomemos el valor de $n$, siempre podremos concebir uno mayor. El infinito que resulta de esta operación reiterativa e ilimitada, es decir, de una recursividad interminable, es lo que se llama “infinito potencial”. Esta noción de infinito es a la que se apela para la definición moderna de límite. Las sucesiones cuyo término general se aproxima a un valor dado “$L$” al crecer $n$ hacia infinito, se dice que tienen por límite ese valor (También se dice que tiende hacia “$L$” o convergen hacia “$L$”). La definición de límite que usamos actualmente se expresa así:
Una sucesión converge hacia $L$, si para todo $ε > 0$, existe un número natural $N$ tal que, para todo $n> N$ se cumple que: $|a_n -L|<ε$
Entonces se dice que la sucesión tiende a $L$ o que tiene el límite $L$, cuando $n$ tiende a infinito: $$\lim_{n\rarr\infty} a_n= L$$
Para definir una aproximación debemos disponer de una unidad de medida que nos indique la distancia a ese límite. La unidad de medida que establecemos es $ε$. Esta unidad no necesitamos definirla como sucede con las unidades que se aplican a la física. En la definición de límite, tenemos libertad para definir $ε$ tan pequeño como queramos, pero sea cual sea su valor, debe existir un número $N$ a partir del cual la distancia al límite sea menor que $ε$.
Una sucesión converge si y solo si la diferencia en valor absoluto entre dos términos cualesquiera $a_m$ y $a_n$, para $m$ y $m > N$, tiende a $0$. $$\lim_{n,m\rarr\infty}\vert a_m - a_n \vert = 0$$
La derivada como límite. Con la teoría de límites se logra fundamentar el cálculo diferencial e integral resolviendo los problemas de justificación teórica originales. La derivada resulta definida utilizando el concepto de límite de la siguiente manera:
La función $f(x)$ es diferenciable en “$x$” si existe el límite:
$$ \small{{dy\over dx} =\lim_{Δx\rarr 0}{Δy\over Δx}= \lim_{Δx\rarr 0}{{f(x+Δx)-f(x)}\over dx}}$$Es decir, el cociente de incrementos cuando $Δx$ tiende a $0$, converge en $f'(x)= dy/dx$.
Este enfoque evita la discusión sobre la naturaleza de los infinitesimales. $Δx$ es simplemente una variable respecto de la cual se efectúa la operación de paso al límite.
Las suma de series infinitas. Una serie es la suma de una sucesión de infinitos elementos. Representamos una serie con un símbolo que llamamos sumatorio $Σ$ y la serie entonces queda como:
$$\sum_{\substack{n=0}}^\infty{a_n}$$siendo $n$ es un número entero y esta expresión se lee, suma de $a_n$, para $n$ de $0$ a $\small{\infty}$.
Como no existe definida una suma de infinitos elementos, podemos considerar la suma de sus $n$ primeros términos que llamaremos $S_n$. De esta manera a partir de la serie obtenemos una sucesión. Si existe un límite para esa sucesión $S_n$, cuando $n$ tiende a infinito, a ese límite le llamamos suma de la serie.
$$S\:=\lim_{n\rarr\infty}S_n$$Las series para los que existe un límite finito para su suma se dice que convergen hacia ese valor y en caso contrario se dice que son divergentes. Para que una serie converja debe de cumplir varias condiciones. La primera condición es que el término general sea cada vez más pequeño, es decir, se aproxime a $0$ al aumentar $n$. Esta condición no es sin embargo suficiente.
Debemos hacer una comprobación adicional para asegurarnos de la convergencia de una serie. Existen diferentes maneras de hacerlo, una de ellas es que el cociente del valor absoluto de los coeficientes de dos términos consecutivos sea menor que $1$. Cuando el límite es $1$ no podemos asegurar la convergencia.
Para profundizar el la teoría de límites, consultar el capítulo IV de Cálculo diferencial e integral Módulo II en iCartesiLibri.
+86 -1831- Los números imaginarios.
La introducción el número i en las matemáticas deja el camino abierto para la aparición de una nueva categoría de números, que no sospechábamos.
 Gauss (“Theoria residuorum bicuadraticorm”, 1831), define los “números complejos” como pares ordenados de números reales, que tienen una componente real y otra imaginaria. Un número complejo “$z$” es de la forma $z=x+iy$, es decir, “$z$” es una pareja de números reales, siendo “$x$” la componente real e “$y$” la componente imaginaria.
Gauss (“Theoria residuorum bicuadraticorm”, 1831), define los “números complejos” como pares ordenados de números reales, que tienen una componente real y otra imaginaria. Un número complejo “$z$” es de la forma $z=x+iy$, es decir, “$z$” es una pareja de números reales, siendo “$x$” la componente real e “$y$” la componente imaginaria.
Hasta la aparición de los números complejos todos los números estaban alineados en la recta de los números reales. Caspar Wessel en 1799 y Jean-Robert Argand en 1806, fueron los primeros en representar los números complejos en un plano, el plano complejo, con un eje real y el eje vertical representando la componente imaginaria, siendo el punto $(0,1)$ del plano la representación de la unidad imaginaria $i$.
Gauss también demuestra el teorema general del álgebra, según el cual, las raíces de un polinomio con coeficientes complejos son números complejos. De este modo se cierra la posibilidad de que aparezca un nuevo tipo de números como había pasado con los números reales. Los polinomios con coeficientes reales tienen raíces que pueden ser reales o imaginarias. Los números imaginarios son los números más “generales” que existen. Si a los matemáticos les fue difícil aceptar números negativos, con infinitos decimales... los números imaginarios son el último reto para comprender lo que es un número. El club de los números no admite más socios, naturales, enteros, racionales, irracionales, reales e imaginarios.
Podemos interpretar una función de variable compleja como una correspondencia que se representa visualmente utilizando dos planos, uno para la variable independiente $z_1=x_1+i\:y_1$, que llamamos plano “cartesiano” y otro plano $z_2=u_2+i\:v_2$ para la variable dependiente. Este plano se llama habitualmente plano de Gauss.
La función de variable compleja es una transformación de las líneas del plano “cartesiano” en otras figuras en el plano de “Gauss”. La función $e^{ix}$, siendo $x$ un número real, la parte real la función $e^{ix}$ es $cos(x)$ y la parte imaginaria $sen(x)$, por lo que los puntos de la recta real se transforman en una circunferencia de radio unidad en el plano de Gauss.
Tenemos un punto $A$ sobre el eje $y$ en la primera ventana que podemos mover con el deslizador. En la segunda ventana vemos la transformación del punto $A$ en $z1$ por la función $e^{ix}$ sobre el círculo unidad.
En esta segunda pantalla representamos los puntos con su componente real sobre el eje $x$ y su componente imaginaria sobre el eje $y$.
Si activamos la segunda casilla de control obtenemos también el punto $z_2$ que es el transformado de $A$ por $e^{ix}$.
Podemos ver el movimiento de los puntos $z_1$ y $z_2$ simétricamente al eje real.
Activando la casilla de control 3 obtenemos la suma de $z_1$ y $z_2$ como suma de dos vectores. (Sumando su componente real y su componente imaginaria separadamente). El vector rojo resultante vemos que solo tiene componente real y comprobamos que se cumple la identidad de Euler, $\displaystyle{{cos x} = \frac {e^{ix} + e^{-ix}} {2}}$, trasladando a la primera ventana la mitad del valor obtenido sobre el eje real del plano de Gauss, como valor de $y=cos \; x$.
i en las ecuaciones de la física
Hay otra manera de entender la función $\small{e^{ix}= cos \:x + i \:sen \:x}$, al margen de la representación habitual de las funciones de variable compleja, descomponiendo la función por una parte en, $\small{y =cos \:x}$, y por otra en $\small{z=i \:sen \:x}$. De este modo, podemos representar la función en dos planos perpendiculares, siendo el eje $Z$, perpendicular a $X$ e $Y$, el eje de la componente imaginaria de la función.
La composición de movimientos ondulatorios perpendiculares permite interpretar diferentes fenómenos físicos. En las ecuaciones de Maxwell, que describen el electromagnetismo, y en la ecuación de onda, que explica el comportamiento de las partículas subatómicas, aparece i. Lo que ha nacido imaginario, como “seres anfibios a medio camino de la existencia y la no existencia” (Leibniz), resulta estar en lo más profundo del comportamiento de la realidad. La física de hoy aprovecha la especulación matemática 250 años avanzada a su tiempo.
Para cada $x$, podemos dibujar un punto de la componente real $y = cos\; x$ y otro de la componente imaginaria $z=sen\; x$. El conjunto de estos dos puntos nos dibuja una espiral de generatriz circular que se proyecta en el plano $(y, z)$ como la circunferencia $e^{ix}$.
Estamos superponiendo las funciones seno y coseno que ondulan en planos perpendiculares y la presencia de $i$ es la responsable de este giro de $90º$.
+ 109 -1854- La integral de Riemann.
 La integral de Riemann, creada por Bernhard Riemann en un artículo publicado en 1854, fue la primera definición rigurosa de la integral de una función en un intervalo.
La integral de Riemann, creada por Bernhard Riemann en un artículo publicado en 1854, fue la primera definición rigurosa de la integral de una función en un intervalo.
La integral de Riemann de una función de variable real se denota usualmente de la siguiente forma:
$$\small{\int_{a}^{b}f(x)dx}$$Necesitamos definir cuatro conceptos:
• La partición de un intervalo, $[a, b]$ es un conjunto finito de puntos, $\small{P[(x_1=a), x_2, \cdot \cdot \cdot (x_n=b)]}$ con $\small{x_i > x_{i-1}}$ para valores de $i$ desde $1$ a $n$
• La norma de una partición es la amplitud del intervalo mayor.
• Para una función $f$ en $[a, b]$, tomando una partición $P$ de ese intervalo, llamamos suma de Riemann a la suma:
$$\small{S(P,f)=\sum_{k=1}^{n}f(t_k)(x_k-x_{k-1})}\quad para,\quad x_{(k-1)}≤\;t_k≤\:x_k$$• Una función $f$ acotada en un intervalo $[a, b]$ se dice que es integrable Riemann en ese intervalo, si existe un número $I$ tal que para todo número real positivo $ε$, existe una $δ$ positiva tal que, si $P$ es una partición de $[a, b]$ cuya norma es $< δ$, entonces:
$$\small{{\big\vert}\small{ S(P,f)\:-\:I}{\big\vert}< ε}$$En otras palabras, la integral es el límite de la suma de Riemann cuando la norma de la partición tiende a $0$.
Por razones prácticas, la partición del intervalo total suele suponerse compuesta de intervalos de igual magnitud $\frac{x_b-x_a} {N}$, que al tender $N$ a $\small{\infty}$, podemos identificar como $dx$.
La notación de Leibniz sobrevive a la introducción de la definición de la integral como límite de sumas de Riemann,
$$\small{{\int_{a}^{b}f(x)\:dx}=\lim\limits_{dx \rarr 0}\sum_{x_i=a}^{x_i=n}\:f(x_i)dx_i}$$Originalmente $\small{\int_{a}^{b}f(x)dx}$ representaba la suma del área de rectángulos infinitesimales y se ha convertido en una abreviatura que asume la integral como límite de una sucesión de sumas. El cálculo de una integral definida consiste en calcular y obtener el límite de esa sucesión.
Si para la diferenciación, necesitábamos ejecutar un “paso al límite”, la operación inversa nos vuelve a llevar a un problema parecido. Para la derivación se trata del valor límite de una división, aquí estamos ante el valor límite de una suma de $n$ sumandos, cuando $n$ se hace suficientemente grande.
+ 221 -1966- El análisis no estándar.
En 1966, Abraham Robinson publica Non-Standard Análisis, donde presenta el análisis no estándar como una teoría de los infinitesimales, que bien puede considerarse su renacimiento dentro de las matemáticas “rigurosas”.
En su "Prefacio", Robinson dice lo siguiente:
Robinson construye una extensión de los números reales, que llama el campo hiperreal, que incluye los números finitos, los infinitesimales y los infinitos, y demuestra que para el campo hiperreal son válidas todas las fórmulas del campo real. Para la recta hiperreal todo número real ordinario finito esta rodeado de los que están infinitesimalmente próximos a él y forman el átomo del número real.
Las ideas intuitivas de los creadores del cálculo.
Hallar la tangente a una curva es el problema más elemental resuelto por el cálculo. Exponemos aquí el caso de una curva de la que no podemos obtener su ecuación explícita.
Para el folium de Descartes de ecuación $\small{x^3+y^3=3xy}$, derivamos, aplicando al término $3yx$ la regla del producto:
$$\small{3x^2+3y^2 y'= 3y+3xy'}$$Despejando $y'$ obtenemos.
$$\small{y'=\frac{x^2-y}{x-y^2}}$$Sustituyendo $x$ e $y$ por las coordenadas del punto obtenemos la pendiente de la tangente en ese punto.
La longitud de una curva, también esta a nuestro alcance puesto que observando el triángulo formado por los diferenciales en un punto, podemos afirmar que la hipotenusa del triángulo, es la longitud de la curva en ese tramo infinitesimal, y por Pitágoras, $\small{ds=\sqrt{(dx^2+dy^2 )}}$. Dividiendo por dx obtenemos:
$$\small{\frac{ds}{dx}=\sqrt {1+y'^2}}$$La longitud de la curva es la integral,
$$\small{S=\int_{a}^{b} \sqrt{1+y'^2}dx}$$entre los dos puntos que definen el tramo. Obtener la longitud de una curva supone, por tanto, ejecutar una integral que, frecuentemente, no es inmediata, ni fácil de obtener. En este supuesto, tenemos dos alternativas a mano. La primera desarrollar en serie la función a integrar, para integrar a continuación término a término y la segunda obtener la integral definida mediante un método de aproximación numérica, con la fórmula de Simpson, por ejemplo.
Longitud de la parábola
Si tenemos una parábola de ecuación $y =\large{{x^2 }\over 2}$ , queremos obtener la longitud de la curva entre $x=0$ y $x=a$,
$$\small{y'=x}$$ $$\small{S=\int_{0}^{a} \sqrt{1+x^2}dx}$$Esta integral es bastante difícil de ejecutar. Una primitiva de la función resulta ser:
$$\small{- {1\over 2}ln (-x+\sqrt{{x^2}+1})+{1\over 2} x \sqrt{{x^2}+1}}$$Para $x=0$, esta expresión es $0$, por lo tanto, la integral definida entre $0$ y a toma el valor:
$$\small{- {1\over 2}ln (-a+\sqrt{{a^2}+1})+{a\over 2} \sqrt{{a^2}+1}}$$Longitud de la hipérbola
Hipérbola de ecuación $y={\large{1\over x}}$, desde $x=1$ a $x=a$. Su derivada es: ${y'=-\large{{1\over{x^2}}}}$
$$\small{S=\int_{1}^{a} \sqrt{1+x^{-4}}dx}$$En este caso la función a integrar se hace infinita en $0$. Su desarrollo en serie centrado en $0$ no es viable. Optamos en este caso por el cálculo de la integral definida por métodos numéricos.
Longitud de la función logarítmica
Curva logarítmica de ecuación $y= ln x$, desde $x=1$ a $x=a$,cuya derivada es: $y'=\large{{1\over x}}$.
$$\small{S=\int_{1}^{a} \sqrt{1+x^{-2}}dx}$$Es un caso semejante al de la hipérbola por no estar definida la función en $0$.
Resolvemos el problema clásico de obtener el rectángulo de área máxima inscrito en un triángulo, que puede convertirse en obtener el cilindro de volumen máximo inscrita en un cono. El cálculo de tangentes y el de máximos y mínimos son problemas íntimamente relacionados. Obtenida la tangente, una función alcanza un máximo o un mínimo en los puntos en los que su tangente es horizontal, de pendiente igual a $0$.
Para resolver el problema, obtenemos en primer lugar el área del rectángulo inscrito en función el punto de contacto con el triángulo. Obtenemos el máximo de esta función derivando la expresión obtenida e igualando a $0$.
Para distinguir entre un máximo o un mínimo, debemos averiguar si la función es creciente o decreciente en el entorno de el punto obtenido. Para ello obtenemos la segunda derivada en el punto que investigamos.
También resolvemos analíticamente el problema planteado por Kepler sobre el volumen de los barriles de vino, reducido al cálculo del volumen máximo de un tonel cilíndrico, cuya diagonal desde su boca superior hasta su base sea dada, variando el diámetro de su base circular.
"$d$" es la longitud medida por la vara del comerciante y "$r$" el radio de la base del cilindro.
Los cilindros de diferente base para una misma longitud de la vara diagonal están inscritos en un círculo de radio igual a "$d$".
Fijando "$d$" podemos observar la variación del volumen en función de "$r$".
Dibujada en rojo la función del volumen y superpuesta en línea discontinua su derivada.
Hemos obtenido la tangente a una curva en un punto. Nos queda definida, en ese punto, la recta perpendicular a la tangente que llamamos normal a la curva. Es posible trazar una circunferencia con centro en un punto cualquiera de la normal y de radio igual a la distancia del punto elegido y el punto de tangencia. De este modo podemos ver que hay muchos círculos tangentes a una curva en un punto.
De entre todas estas circunferencias, con centro sobre la normal a la curva buscamos identificar una que fue llamada «circulum osculans» («círculo que besa») por Leibniz. La inversa del radio de esta circunferencia lo llamamos curvatura. De acuerdo al concepto intuitivo, en los puntos de mayor curvatura el círculo “osculador” tiene un radio menor. Para una recta, la curvatura es $0$ y el círculo “osculador”, de radio infinito, se confunde con la propia recta.
Para calcular la curvatura en un punto de una curva, ponemos atención a la variación de la pendiente de la tangente, al mover el punto de tangencia un ds sobre la curva.
La curvatura la definimos como:
$$\small{K_p=\frac{dα}{ds}}$$y podemos poner:
$$\small{\frac{dα}{ds}={\frac{dα}{dx}}{\frac{dx}{ds}}=\frac{dα}{dx} \frac{1}{\large{\frac{ds}{dx}}}}$$Sabemos que $tg \; α = y'$ y por lo tanto, $α =arctg (y')$, por lo que derivando y aplicando la regla de la cadena:
Por otra parte sabemos de $\small{ ds=\sqrt{dx^2+dy^2}}$ por lo que.
$$\small{\frac{ds}{dx}=\sqrt{dx^2+dy^2}}$$Efectuando las operaciones obtenemos la fórmula de la curvatura:
$$\small{\frac{dα}{ds}=\frac{1}{1+y'^2} y'' \frac{1}{\sqrt{1+y'^2}}}$$Simplificando:
$$\small{k_p=\frac{y''}{{(1+y'^2)}^{3/2}}}$$El radio de curvatura es el inverso de la curvatura obtenida.
La obtención de la curvatura es un cálculo que solo requiere obtener la derivada primera y segunda de la función.
La ecuación del péndulo simple se debe a Christian Huygens. Hacia el año 1673, construyó el primer reloj de péndulo, basándose en el isocronismo de las oscilaciones que sus ecuaciones demostraban, dando el primer paso importante para la medición del tiempo con precisión.
El isocronismo es una propiedad del movimiento armónico simple, que es un movimiento periódico de vaivén, en el que un cuerpo oscila de un lado al otro de su posición de equilibrio, en una dirección determinada, y en intervalos de tiempo iguales.
Esta propiedad, en la que se basa el reloj de Huygens, fue observada por Galileo, hacia el año 1581 en la catedral de Pisa, cuando la amplitud de las oscilaciones se iba reduciendo, permanecía sensiblemente constante su duración.
Un día en que asistía, algo distraído sin duda, a una ceremonia religiosa, fijó su mirada en una lámpara de bronce, obra maestra de Benvenuto Cellini, que, suspendida de una larga cuerda, oscilaba con lentitud ante el altar. Quizás, con los ojos fijos en aquel metrónomo improvisado, unió su voz a la de los celebrantes; la lámpara se detuvo poco a poco y, atento Galileo a sus últimos movimientos, observó que marcaba siempre el mismo compás.J. Bertrand: Galileo y sus trabajos
Un ejemplo es el caso de un cuerpo colgado de un muelle, oscilando arriba y abajo. El objeto oscila alrededor de la posición de equilibrio cuando se le separa de ella y se le deja en libertad. Para el caso de un objeto suspendido de un muelle podemos poner:
$$\small{m \frac{d^2 x}{dt^2}= -kx}$$Siendo $m$ la masa del objeto y $k$ el coeficiente de elasticidad del muelle. Haciendo $ω^2=\large{{k\over m}}$ resulta la ecuación:
$$\small{\frac{d^2 x}{dt^2}= -ω^2 x}$$Para obtener las ecuaciones del péndulo podemos plantear el equilibrio de fuerzas que actúan sobre él, descomponiendo el peso de la masa suspendida, en una componente en el sentido del hilo y en otra perpendicular a él y por tanto tangente al círculo que describe el péndulo.
$$\small{F_t\:=\:-mg \:sen\:θ=m \:a_t }$$La aceleración tangencial del péndulo podemos convertirla en aceleración angular, expresada en función del ángulo y de la longitud del péndulo ($L$).
$$\small{a_t\: = \:L \:θ”}$$La ecuación del movimiento resulta, sustituyendo en la ecuación de equilibrio:
$$\small{ - m\:g\: sen\:θ =m L\:θ” \:\:\:,\:\:\: θ”=\frac{g}{L} sen\:θ}$$Esta ecuación no es la de una función armónica, por la presencia de $sen\; θ$, en el lugar de $θ$, en la ecuación del movimiento, a diferencia de la ecuación del cuerpo suspendido del muelle elástico.
La resolución de esta ecuación diferencial no esta al nivel de este libro, pero podemos obtener una solución aproximada, transformando la ecuación del péndulo en la de un movimiento armónico, considerando oscilaciones para las que se puede aceptar que $sen\; θ = θ$.
$$\small{θ”= -{g\over L}\:θ }$$Haciendo $ω^2=\Large{{g\over L}}$ resulta la ecuación:
$$\small{θ”= - w^2 \:θ }$$La solución general de este tipo de ecuaciones es:
$$\small{θ=A\: cos\: (ωt)\:+\:B\:sen\:(ωt)}$$Los coeficientes $A$ y $B$ se determinan a partir de las condiciones iniciales del movimiento. Habitualmente el péndulo se separa $θ$ de la posición de equilibrio y se suelta, por lo que para $t=0$, $θ_0=A$.
La velocidad angular será $0$ en el instante inicial, luego:
$$\small{\frac{dθ}{dt}θ=w (-A\: sen\: (ωt)\:+\:B\:cos\:(ωt))}$$Luego para $\large{\frac{dθ}{dt}=0}$, resulta $B=0$, con lo que la ecuación del movimiento queda:
El periodo del movimiento, el tiempo que tarda en completar una oscilación es:
El periodo del péndulo simple es independiente de la masa suspendida y, también, de la amplitud de las oscilaciones, siempre que éstas sean suficientemente pequeñas como para que la aproximación $sen\; θ ≈ θ$ sea aceptable. Para amplitudes menores de $10º$ la corrección es menor del $0,2$%.
El periodo depende de la longitud del péndulo, de manera que al aumentar la longitud aumenta el periodo. Por ejemplo el péndulo de Foucault del museo de la ciencia de Barcelona de $23,9 m$ de longitud oscila en un periodo de casi $10 s$.
La ecuación del movimiento del péndulo general es bastante más compleja, y confirma que la amplitud es sinodal para pequeñas oscilaciones pero deja de serlo al aumentar. El periodo no depende de la masa suspendida pero aumenta al incrementarse la amplitud, de acuerdo con la expresión:
$$ \small{T≈T_0 \:(1+{{θ^2}\over 16})}$$La catenaria es la curva que forma una cadena o una cuerda, perfectamente flexible, suspendida entre dos puntos sometida únicamente a su propio peso.
Suspendemos la cuerda flexible entre dos puntos situados a la misma altura sobre el eje de coordenadas $X$. La tensión de la cuerda en cada punto sigue la dirección de la tangente de su deformada. Obtenemos la ecuación de la catenaria planteando las ecuaciones de equilibrio. En primer lugar constatamos que el esfuerzo en dirección vertical es el mismo en cada punto de fijación y su magnitud es la mitad del peso de la cuerda.
Si estudiamos el equilibrio de un elemento , de longitud “$s$” a partir del punto central de la cuerda, podemos descomponer el peso del tramo de cuerda en sentido horizontal, siendo $p$ su peso por unidad de longitud, y en sentido vertical conociendo el ángulo que forma la tangente a la cuerda con la horizontal en este punto.
$$\small{T\: cos \:α=\:T_0} \;\;y,\;\;\small{T \:sen \:α=\:p\: s}$$Dividiendo ambas ecuaciones obtenemos:
$$\small{tg \:α=\:\frac{dy}{dx}=\:{{(p \:s)}\over{T_0 }}}$$Puesto que el valor de la derivada de la curva es el de la tangente. La derivada segunda será, sustituyendo $ds$ por su valor en relación a $dx$ y $dy$:
$$\small{\frac{d^2 y}{dx^2 }= \frac{p}{T_0} \frac{ds}{dx}\:=\frac{p}{T_0}\sqrt{1+{(\frac{dy}{dx})}^2} }$$Si llamamos $v$ a $dy/dx$, la expresión anterior es:
$$\small{\frac{dv}{dx}={\frac{p}{T_0}}\sqrt{1+{(dv)^2}}}$$ $$\small{\frac{dv}{\sqrt{1+{(dv)}^2}}=\frac{p}{T_0}dx}$$Integrando la ecuación, desde el punto medio $x=a$ hasta $x$, teniendo en cuenta que para $x=a$, la tangente es horizontal y por tanto $dy/dx=0$.
$$\small{\int{\frac{dv}{\sqrt{1+v^2}}}=\int_a^x {\frac{p}{T_0}dx}}$$ $$\small{arc\: senh\:v= \frac{p}{T_0}(x-a)}$$cuya inversa es:
$$\small{v=\frac{dy}{dx}=senh\:(\frac{p}{T_0}(x-a))}$$Integrando de nuevo en el intervalo entre $a$ y $x$ cada uno de los términos, puesto que para $x=a$, y es igual $a-h$,
$$\small{\int_{a}^x{y'}dx=y+h}$$y el primer miembro es:
$$\small{\int_a^x{senh\:(\frac{p}{T_0}(x-a))=\frac{T_0}{p}cosh\:(\frac{p}{T_0}(x-a))-\frac{T_0}{p}}}$$con lo que resulta la igualdad:
$$\small{y+h=\frac{T_0}{p}cosh\:(\frac{p}{T_0}(x-a))-\frac{T_0}{p}}$$Sabemos que para $x=0$, $y=0$, por lo que:
Sustituyendo queda la ecuación:
La longitud del cable suspendido es:
$$\small{L=\int{ds}=\int_0^{2a}{\sqrt{1+(\frac{dy}{dx})^2}dx}=\int_0^{2a}{cosh\:(\frac{p}{T_0}(x-a))dx}}$$Para definir la catenaria podemos partir de una longitud ($L$) de cable y una distancia ($2a$) entre anclajes, o calcular la longitud de cable necesaria para salvar una distancia, con un valor de descenso ($h$) fijado. En el primer caso debemos resolver la ecuación obtenida para la longitud de la cuerda que podemos poner en la forma:
$$L\frac{p}{2T_0} = sinh (\frac{p}{T_0} a)$$Cuya solución podemos obtener gráficamente, haciendo $\frac{p}{T_0} =x$, mediante la intersección de la recta $\frac{L}{2} x =y$, la gráfica de $sinh (x a)=y$, obteniendo así
$$T_0=\frac{x}{p}$$Una vez obtenida $T_0$ podemos completar la ecuación de la catenaria.
Para el segundo caso podemos seguir una estrategia semejante a partir de la ecuación obtenida para $h$.
Con el deslizador podemos controlar la longitud de la cuerda suspendida. Fijada una longitud, podemos observar que modificando la distancia $OA$, controlamos el ángulo de la fuerza de tracción con la horizontal para sostener la cuerda. Esta observación se corresponde con nuestra experiencia: si extendemos una cuerda de longitud dada entre dos puntos el esfuerzo horizontal para sostenerla varía al aumentar la distancia. (la cuerda esta más tirante).
Al hablar de Gauss hemos introducido brevemente los números complejos. Vamos a continuación a desarrollar un poco más la teoría para introducir al lector en el estudio de esta materia.
Recomendamos el documento Análisis complejo de Juan Carlos Ponce Campuzano disponible en este enlace
La generalización del álgebra a un nuevo tipo de números obliga a definir las operaciones, (suma, multiplicación… ) de manera que sean compatibles con esas mismas operaciones definidas para los números conocidos hasta ahora, es decir, los números reales.
La suma de dos números complejos, $z_1= x_1+i\:y_1\: $ y $\:z_2 = x_2 +i y_2$ se define como:
Situados en un plano de ejes $X$ e $Y$, los tres números $z_1 \:,\: z_2 \:y\: z_3$ forman con el origen de coordenadas un romboide siendo la diagonal del mismo la línea que une el origen con $z_3$. Vemos que si $z_1 \:y\: z_2$ son reales, $y_1=0 \:\:e\:\: y_2=0$ , y por tanto $z_1+z_2 = x_1+x_2$.
Definimos la multiplicación del siguiente modo,
que también es una operación válida para los números reales, resultando.
$z_1\:z_2 = x_1 \cdot x_2$ , cuando $y_1=0 \:\:e \:\:y_2=0$.
Cuando operamos con números complejos sin componente imaginaria, $z_1= x_1+ 0\:i$, lo escribimos como $z_1= x_1$ . Del mismo modo cuando operamos con números imaginarios puros, $z_1= 0+i\:y_1 = i\:y_1 $. Cuando $y_1 =1$ tenemos la unidad imaginaria $i$. Si aplicamos las reglas de la multiplicación a la unidad imaginaria, $\small{z= 0+i}$ , para multiplicarla por si misma , obtenemos:
$$\small{i^2 = i \cdot i = (0+i 1) (0 +i 1) = (0 - 1) + i (0 + 0)= -1}$$Hemos obtenido una definición de i sin tener que recurrir a la expresión con la que aparece por primera vez en la historia $\small{\sqrt{-1}}$ y que vulnera claramente las reglas de las operaciones con números reales y la sustituimos por $i^2=-1$ que es una expresión válida para números complejos. $\small{{(0+i)}^2= (-1+i\:0)}$.
Una manera alternativa de definir los números complejos es mediante coordenada polares, es decir, identificando cada punto del plano por su distancia al origen y el ángulo que forma la recta, que pasa por el punto y el origen de coordenadas, con el eje $x$. A la distancia se le llama módulo y al ángulo formado con el eje $x$ argumento. En coordenadas polares podemos interpretar mejor la multiplicación de dos números complejos observando que el producto de dos números complejos es otro número complejo que tiene por módulo el producto de los módulos y de argumento la suma de los argumentos de los factores. También podemos ver que si sumamos $2π$ al argumento de un número complejo volvemos a obtener el mismo número, que ocupa en el plano de Gauss el mismo punto. Para $z = a+i b$,
$$\small{|z|=\sqrt{a^2+b^2}}$$ $$\small{arg(z)= arctg \frac{b}{a}=θ+ 2π k}$$Las operaciones con números complejos se pueden visualizar fácilmente si utilizamos una notación vectorial para designar los puntos $z_i = x_i +i \; y_i$, representando cada punto por su modulo, que es la distancia entre $(0, 0)$ y $(x_i, y_i)$, de valor $\sqrt {{x_i}^2+{y_i}^2}$ y el ángulo que forma el modulo con el eje $x$.
La suma de números complejos se comporta como la suma de vectores. La multiplicación de números complejos resulta ser otro número complejo cuyo modulo es el producto de los módulos y su ángulo con el eje $x$ es la suma de los ángulos de los factores.
Con la notación en polares, hemos visto que de la multiplicación de un número complejo por otro resulta un número complejo, cuyo módulo es el producto de los módulos y su argumento la suma de los argumentos de los factores.
Moviendo el deslizador obtenemos las raíces de orden $n$ del número $A$. Podemos observar la distribución de las raíces sobre un círculo, de centro en el origen de coordenadas y radio el módulo de las raíces.
Para elevar un número complejo a una potencia $n$, podemos poner:
$$\small{|z^n|= |z|^n}$$ $$\small{arg(z^n)=n\:arg(z)=nϕ=n (ϕ+ 2π k)}$$La operación inversa, la raíz n de un número complejo se obtiene análogamente.
$$|\sqrt[n] {z}|= \sqrt[n] {|z|}$$ $$\small{arg(\sqrt[n]{z})= arg{\frac{z}{n}} = {\frac{ϕ}{n}} ={\frac{(ϕ+ 2π k)}{n}}}$$Al ser $k$ un número entero positivo existe infinitas raíces de un número complejo. De entre ellas, las $n$ primeras, con argumento entre $-π$ y $+π$.
Hemos visto que la fórmula de Cardano para resolver ecuaciones cúbicas, en el caso de discriminante negativo, fracasaba en la identificación de las raíces reales, al aparecer en su resolución números complejos.
Hemos visto la solución de Bombelli para el caso particular de la ecuación $x^3-15x-4=0$.
Si aplicamos a los números complejos, que aparecen en el caso de discriminante negativo, las reglas de las operaciones con números complejos, obtenemos tres raíces reales. Cada una de las raíces cúbicas de la fórmula nos da como resultado tres números complejos, que resultan ser conjugados dos a dos. (Números que difieren en el signo de su componente imaginaria). La suma de estos conjugados nos devuelve las tres raíces reales de la ecuación cúbica.
En la figura superponemos la función cúbica en el plano de Gauss donde hacemos las operaciones con los números complejos y comprobamos el resultado sobre el eje real, donde nos aparecen las raíces de la ecuación.
Si aceptamos como variable independiente de una función un número complejo, por el teorema general del álgebra sabemos que obtendremos como resultado otro número complejo, puesto que los números complejos son un conjunto de números cerrado. En consecuencia, podemos descomponer una función de variable compleja en dos funciones, una para la parte real y otra para la parte imaginaria. Normalmente se escribe, siendo $z$ la variable compleja $\:\small{z=x+i \:y}$,
$$\small{f(z)=u\:(x,y)\:+\:i\:v\:(x,y)}$$Es decir, la funciones “parte real” y “parte imaginaria” son funciones de dos variables independientes, por lo que para representarlas gráficamente debemos recurrir a dibujar cada una de ellas como una superficie en un espacio de tres dimensiones. A pesar de ello es difícil interpretar una función utilizando estas gráficas.
La fórmula de Euler para variable compleja
Hemos visto como la función $e^{ix}$ se puede representar como una transformación del plano real al plano imaginario de Gauss.
Podemos generalizar la fórmula de Euler fácilmente si sustituimos la $x$ (un número real) por $z$ (un número complejo) y aplicamos las propiedades básicas de la función exponencial:
$$\small{e^z=e^{x+iz}=e^x\:(cos\:y+i\:sen\:y)= (e^x cos\:y)+\:i(e^x sen\:y)}$$Es decir, la función nos trasforma un número complejo $\small{z=x+i\:y}$ en $\small{z_1=x_1+i\:y_1}$ en el que $\small{x_1 =e^x cos \:y \:\: siendo\:\: y_1 = e^x sen \:y}$.
La ventana 1 representa el plano $xy$ cartesiano. La ventana 2 representa el plano de Gauss, con la componente real según el eje $x$ y la componente imaginaria según el eje vertical.
Podemos visualizar como la función $e^{x+iy} = e^x (cos y + i sen y)$, transforma un punto $A (x,y)$ en la primera ventana en un punto, $z_1$ en el plano complejo y las líneas rectas de colores se transforman en diferentes figuras. Moviendo $A$ con el cursor desplazamos las rectas de colores.
Las rectas verticales en rojo se transforman en circunferencias y las rectas horizontales azules se transforman en rectas que pasan por el origen de coordenadas. Las rectas verdes que pasan por el origen de coordenadas se transforman en espirales.
Deslizar los puntos $C$, $D$ y $E$ sobre sus rectas y observar el recorrido sobre las figuras del plano imaginario del punto transformado.
Al hablar de la suma de series numéricas hemos explicado que en muchos casos la dificultad de su cálculo supone un verdadero desafío. La resolución por Euler del caso de la serie de los inversos de los cuadrados de los números naturales se aparta de la línea argumental de nuestro libro, pero la tratamos en este anexo porque es muy ilustrativa de la libertad con la que Euler maneja las series infinitas y también nos ilustra sobre la importancia de su obra.
El punto de partida es el desarrollo en serie de sen x :
$$\small{{sen\:x}=x\:- \frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}...}$$Suponiendo que la función, desarrollada en serie, se comporta como un polinomio podemos establecer su igualdad con el producto de monomios $(x-x_i)$, siendo $x_i$ cada una de sus raíces. Puesto que sen $n.π = 0$ para todos los infinitos valores de $n = ±1,±2,...$, resulta un producto infinito.
$$\small{sen x = K x (x-π)(x+π)(x-2π)(x+2π)(x-3π)(x+3π)...}$$Y efectuando el producto de los binomios dos a dos:
$$\small{sen x = K x (x^2-π^2)(x^2-4π^2)(x^2-9π^2)...}$$ $$\small{x\:- \frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}...=K x(x^2-π^2)(x^2-4π^2)(x^2-9π^2)...}$$Dividiendo por $x$:
$$\small{1\:- \frac{x^2}{3!}+\frac{x^4}{5!}-\frac{x^6}{7!}...=K (x^2-π^2)(x^2-4π^2)(x^2-9π^2)...}$$Haciendo $x=0$, resulta: $\small{1\:=K (-π^2)(-4π^2)(-9π^2)...}$
Si dividimos los dos términos de la igualdad anterior por esta última:
$$\small{1\:- \frac{x^2}{3!}+\frac{x^4}{5!}-\frac{x^6}{7!}...=(1-\frac{x^2}{π^2})(1-\frac{x^2}{4π^2})(1-\frac{x^2}{9π^2})...}$$Igualando los coeficientes del termino en $x^2$.
$$\small{-\frac{1}{3!} = -\;(\frac{1}{π^2}+\frac{1}{4π^2}+\frac{1}{9π^2}....)=-\frac{1}{π^2}{\sum_{0}^∞}\:\:\frac{1}{n^2}}$$Con lo que obtenemos un resultado en el que interviene inesperadamente $π$.
$$\small{\frac{π^2}{6}={\sum_{1}^∞}\:\frac{1}{n^2}}$$Esta serie, no puede interpretarse como un procedimiento para calcular el valor de $π$, porque hace falta un número muy grande de términos para obtener una buena aproximación.
Si la “fórmula más bella” nos ha descubierto un puente entre la exponencial y las funciones trigonométricas, el problema de Basilea también abre el camino a la conexión entre disciplinas matemáticas, desbordando el análisis para adentrase en la teoría de números. La actual teoría de los números primos se inicia con la igualdad demostrada por Euler que vincula un producto, en el que intervienen infinitos números primos ($p$), con la serie de las potencias ($s>1$) de los recíprocos de los números naturales ($n$).
$$\small{\prod\frac{1}{1-p^s} ={\sum_{1}^∞}\:\frac{1}{n^s}}$$Riemann plantea, en 1859, una generalización de la serie de los inversos de los números naturales, considerando como exponentes números complejos.
$$\zeta(s)={\sum_{1}^∞}\:\frac{1}{n^s}$$Esta función, que se conoce como función “Zeta de Riemann”, converge para exponentes cuya componente real sea estrictamente superior a $1$ y, para $s=2$, coincide con la serie de Basilea.
En el caso de exponentes cuya parte real es inferior a $1$, la función $Z$ de Riemann no es la suma de la serie, tal como se entiende habitualmente la suma de una serie, sino de su “extensión analítica”.
Riemann avanzó una conjetura sobre las propiedades de la función $\zeta (s)$ cuya demostración se ha convertido en uno de los "siete problemas matemáticos del milenio" por los que la fundación "Clay Mathematics Institute" de Massachusetts ofrece un premio de un millón de dólares a quien lo resuelva. La hipótesis de Riemann continúa sin demostración hoy en día.
En el canal YouTube “3 blue 1 Brown”, canal de divulgación con muchos videos interesantes, podemos encontrar ¿porqué esta Pi aquí? , donde se plantea una construcción que justifica geométricamente el resultado de Euler.
Etapa 1- Situamos sobre el eje $Y$, un punto de coordenadas $A = (0, 2/π)$ y trazamos una circunferencia de centro en $A$, que pase por el origen de coordenadas. En el diámetro de la circunferencia situamos dos puntos $F$ y $G$ cuya distancia al origen es, aplicando el teorema inverso de Pitágoras:
$$\frac{1}{h^2}=\frac{1}{a^2}+\frac{1}{b^2}$$Siendo $h$ la altura del triángulo rectángulo y $a$, $b$ los catetos. Podemos poner entonces, puesto que la hipotenusa es igual al diámetro de la circunferencia:
$$\frac{π^2}{4}=\frac{1}{a^2}+\frac{1}{b^2}$$Siendo $a$ y $b$ la distancia de $F$ y $G$ al origen de coordenadas.
Etapa 2- Si construimos una circunferencia de diámetro doble, tangente al eje $X$, trasladamos los puntos obtenidos en la circunferencia anterior a la nueva, mediante el procedimiento que se puede seguir en la figura. Sobre la nueva circunferencia los puntos resultan duplicados, pero la suma del cuadrado de la inversa de sus distancias al origen, de todos ellos resulta inalterada.
Podemos comprobar este resultado aplicando el teorema de Pitágoras a cada uno de los triángulos formados por los nuevos puntos, en el extremo del diámetro de la nueva circunferencia, y el origen de coordenadas.
Etapa 3- Repetimos proceso para una nueva circunferencia de diámetro doble del anterior.
Al aumentar el diámetro de la circunferencia el número de puntos uniformemente distribuidos sobre el perímetro se incrementa. Podemos continuar indefinidamente la generación de nuevos puntos duplicando en cada paso el diámetro de la circunferencia.
Una recta es, en el límite, una circunferencia de radio infinito. Si observamos, los puntos sobre la circunferencia, al crecer su diámetro, se aproximan a los números impares, positivos y negativos situados sobre el eje $X$. Establecida esta correspondencia entre los números naturales de la recta real y los de la circunferencia, podemos poner:
$$\frac{π^2}{4}=\frac{1}{1^2}+\frac{1}{(-1)^2}+\frac{1}{3^2}+\frac{1}{(-3)^2}+\frac{1}{5^2}+\frac{1}{(-5)^2}...$$puesto que hemos visto anteriormente que la suma de los inversos del cuadrado de las distancias al origen de coordenadas se mantiene constante al crecer el diámetro de la circunferencia.
Como solo nos interesa la suma de los enteros impares positivos resulta:
$$\frac{π^2}{8}=\frac{1}{1^2}+\frac{1}{3^2}+\frac{1}{5^2}+\frac{1}{7^2}...$$Aun no hemos obtenido el resultado final puesto que nos falta el cuadrado de los inversos de los números pares. De la observación atenta de la construcción podemos concluir que la suma de los números pares es $π^2/12$, cuya mitad (solo de los números pares positivos) es $π^2/24$. La suma de las fracciones para los números pares y los impares, es el resultado obtenido Euler.
Capítulo 2 - Chispas de genialidad
Figura 2.1 Cálculo de logaritmos en base $10$
Figura 2.2 Logaritmo del producto de dos números
Figura 2.3 Cambio de base de logaritmos
Figura 2.4 Resolución gráfica de ecuaciones de segundo grado
Figura 2.5 Regla trazadora de Descartes
Figura 2.6 Trazado de tangentes por el método del círculo
Capítulo 3 - Precursores del cálculo
Figura 3.1 La tangente de Fermat
Figura 3.2 Áreas bajo la hipérbola
Figura 3.3 División larga de $1/1+x$
Figura 3.4 Serie de Mercator
Figura 3.5 La fórmula de Cavalieri
Figura 3.6 La primera representación gráfica de la función seno
Capítulo 4 - A hombros de gigantes
Figura 4.1 Desarrollos en serie por la fórmula del binomio
Figura 4.2 Multiplicación de series
Figura 4.3 División de series
Figura 4.4 Desarrollo del cálculo de $π$ por Newton
Figura 4.5 Cálculo de la fluxión de $y=x^3$
Figura 4.6 Interpretación geométrica de la derivada
Figura 4.7 Cálculo de la distancia recorrida
Figura 4.8 La función de áreas
Figura 4.9 Teorema fundamental del Cálculo
Figura 4.10 Interpretación de la integral definida
Figura 4.11 Cálculo del área en el intervalo $AB$
Figura 4.12 La fórmula de Simpson
Capítulo 5 - Las nuevas funciones
Figura 5.1 La función logarítmica
Figura 5.2 Grados sexagesimales y radianes
Figura 5.3 Definición de arco coseno
Figura 5.4 Cálculo de arco coseno
Figura 5.5 Definición de arco seno
Figura 5.6 Cálculo de arco seno
Figura 5.7 La definición de las funciones hiperbólicas
Figura 5.8 La derivada de la función seno
Figura 5.9 Breve catálogo de funciones derivadas
Figura 5.10 Derivación implícita
Capítulo 6 - Infinitos sumandos
Figura 6.1 Sucesión de funciones
Figura 6.2 Series de potencias
Figura 6.3 Valor límite del término general de una serie
Figura 6.4 Desarrollo en serie de $1/1+x2$
Figura 6.5 Desarrollo en serie de la función arco coseno
Figura 6.6 Desarrollo en serie de la función arco seno
Figura 6.7 Inversión de series
Figura 6.8 Inversión de arco coseno
Figura 6.9 Desarrollo de Taylor de $sen\; x$
Figura 6.10 Resto de Taylor de $e^x$
Capítulo 7 - La fórmula más bella
Figura 7.1 La gráfica de la función exponencial y logarítmica
Figura 7.2 Funciones de Euler
Figura 7.3 Diferentes definiciones de $e$
Figura 7.6 Derivada de las funciones logarítmica y exponencial
Figura 7.7 Simetrías
Figura 7.8 Simetrías hiperbólicas
Capítulo 8 - Euler no escribía sin sentido
Figura 8.1 $e^{ix}$ en el plano de Gauss
Figura 8.2 $i$ en las ecuaciones de la física
Figura 8.3 La integral de Riemann
Capítulo 9 Anexo 1- Problemas resueltos de geometría analítica
Figura 9.1 La tangente al folium de Descartes
Figura 9.2 Ejemplos de cálculo de longitud de una curva
Figura 9.3 Rectángulo de área máxima inscrito en un triángulo
Figura 9.4 El tonel de Kepler
Figura 9.5 Ejemplos de evolutas
Figura 9.6 Péndulo simple
Figura 9.7 La catenaria
Figura 9.8 Familias de catenarias
Capítulo 9 Anexo 2- Los números complejos
Figura 9.9 Operaciones con números complejos
Figura 9.10 Raíces de un número complejo
Figura 9.11 Raíces complejas de la ecuación de tercer grado
Figura 9.12 Representación 3D de una función de variable compleja
Figura 9.13 Representación de $e^z$
Capítulo 9 Anexo 3- El problema de Basilea
Figura 9.14 El producto de Euler y la función zeta
Figura 9.15 Resolución gráfica del problema de Basilea
Libros de Historia de las matemáticas
Libros de texto para consulta
Libros de texto para consulta en iCartesiLibri
Figuras GeoGebra