Juguemos con el Tangram.
¡Actividad 1!
Hablemos de las figuras planas, para ello, hagamos referencia a las piezas que forman el Tangram.
¡Piensa!... Responde las preguntas a continuación:
- ¿Cómo se clasifican las figuras del Tangram? ¿que tipo de polígonos son?, defina cada polígono.
- ¿Qué relación hay entre los lados de algunas piezas del Tangram? ¿Idetificamos alguna medida como referencia?
- ¿Cómo determinar el perímetro y área de cada figura, será posible?
¡Actividad 2!
Secuencias utilizando las piezas del Tangram Chino.
¡Piensa!... Responde las preguntas a continuación:
- Utilzando dos piezas, ¿que figuras geométricas se forman?, dibuja las figuras que se forman.
- Ahora, con el mismo proceso de la pregunta anterior, utiliza 3, 4, 5, 6 y 7 piezas del tangram. Encuentra la secuencia para cada figura, si es posible.
(Utiliza como ayuda la escena interactiva)
Tangram Chino
¡Actividad 3!
Construcción de poligonos con las piezas del Tangram Chino.
¡Piensa!... Responde las preguntas a continuación:
- Construir triángulos y cuadrados utilizando solo 2, 3 y 4 piezas del tangram respectivamente.
- Construir un rectángulo con tres triángulos, 2 pequeños y el mediano. ¿Se puede hacer utilizando otras piezas?
- Construir un romboide con dos piezas. ¿Puedes construir uno con tres piezas? ¿Y otro con cuatro?
- Utilizar dos piezas para formar un trapecio. Añade otra pieza y forma otro trapecio. ¿Se puede con más piezas?
- Realizar con todas las piezas polígonos de cuatro lados.
- Utilizando el cuadrado y los dos triángulos pequeños, construir polígonos. Señala qué polígonos son cóncavos y cuáles convexos.
- Utilizando todas la piezas del Tangram construye la figuras:
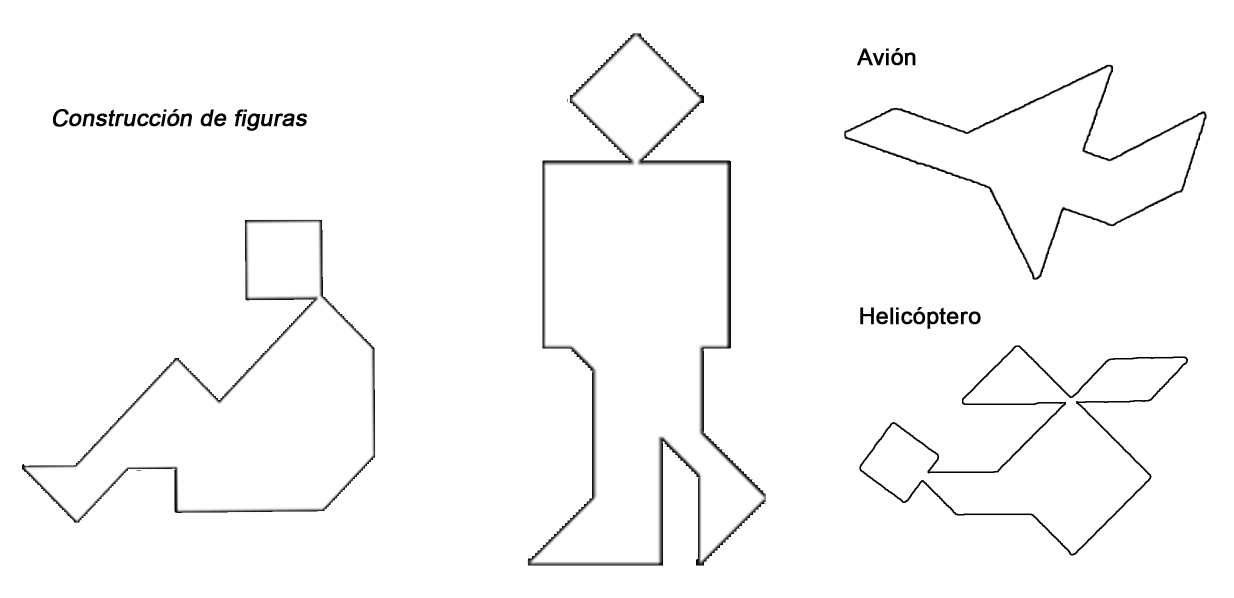
¡Actividad 4!
Áreas y perimetros.
¡Piensa!... Responde las preguntas a continuación:
- Utilzando dos piezas, ¿que figuras geométricas se forman?, dibuja las figuras que se forman.
- Construye un trapecio isósceles. Debes dar por lo menos dos posibilidades.
- Construye trapecio rectángulo. ¿Cuánto mide la altura? (Dos posibilidades).
- Construye un rectángulo cuya área sea el doble de la de la pieza cuadrada.
- Construye un triángulo isósceles (con más de una pieza del Tangram). Tres posibilidades.
- Construye un pentágono y un hexágono (no regular).
