NORMA PATRICIA APODACA ALVAREZ
UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO
Córdoba (España)
2022
Título de la obra:
Funciones
Autora:
Norma Patricia Apodaca Alvarez
Código JavaScript para el libro: Joel Espinosa Longi, IMATE, UNAM.
Recursos interactivos: DescartesJS
Fuentes: SourceSansPro, SourceSerifPro y UbuntuMono
Red Educativa Digital Descartes
Córdoba (España)
descartes@proyectodescartes.org
https://proyectodescartes.org
Proyecto iCartesiLibri
https://proyectodescartes.org/iCartesiLibri/index.htm
https://prometeo.matem.unam.mx/recursos/VariosNiveles/iCartesiLibri/
ISBN: 978-84-18834-56-1
El contenido de esta obra está bajo una licencia:
Creative Commons (Atribución-No Comercial-Compartir Igual).


Un elemento fundamental en Matemáticas lo constituyen las funciones, concepto en el que se ha basado el desarrollo de otras áreas de este campo del conocimiento, entre las cuales se puede mencionar el Análisis Matemático.
El objetivo de este libro es introducir el tema, de manera que al terminarlo se tenga una visión general del mismo y de su utilidad.
De inicio, se hace referencia a nociones generales sobre funciones y matemáticas.
Dada la relación existente entre los conceptos de función y conjunto, se incorporan las nociones básicas sobre conjuntos:
Asimismo, se incluye la definición conjuntista de función.
Como el dominio y el codominio de las funciones de una variable real están en los números reales, se consideró pertinente incluir un capítulo sobre ellos, presentando de manera breve datos sobre:
Ya entrando en el tópico del libro, se expone el concepto de función, presentando su:
A continuación se explica la función de una variable real, indicando su clasificación y propiedades:
También se introduce el criterio de la recta vertical mediante el cual, de manera visual, se puede verificar si una relación es una función de variable real o no.
Enseguida se describen sus diferentes tipos:
Finalmente, se dan algunos ejemplos de sus aplicaciones en la vida cotidiana.
Para una mejor comprensión de las funciones de una variable real, a partir del quinto capítulo se incluyen escenas interactivas, creadas con la herramienta de autor DescartesJS, que tienen controles mediante los cuales se pueden manipular las opciones o parámetros pertinentes. Dichos controles se muestran en la parte inferior, en forma de pulsadores.
Estas escenas se pueden desplegar en una ventana aparte, mediante el símbolo que se encuentra en la esquina superior derecha.
Asimismo, cabe indicar que las imágenes pueden ampliarse pulsando sobre las mismas.
Para terminar el libro, en Fuentes se incluyen referencias de consulta y del origen de las imágenes empleadas.

Proveniente del latín, generalmente se emplea para hacer referencia a un proceso, cuyos pasos llevan a la consecución de un objetivo determinado.

Este término es usado en varios ámbitos, por ejemplo para indicar:
Cotidianamente es empleada en varias disciplinas: Biología, Computación, Ingeniería, Lingüística, Matemáticas, Música, Química, Sociología; con un significado específico para cada una. Así, en Ingeniería se refiere a una acción determinada que un sistema puede realizar, en tanto que en Música, describe la relación de un acorde a un centro tonal.
Este libro está enfocado a dar respuesta a las preguntas:
Antes de entrar en materia, convendría plantearse:
¿Qué son las Matemáticas o la Matemática?
La palabra matemática proviene del griego μαθηματικά (mathēmatiká), que quiere decir lo que se aprende, y que a su vez se origina en el vocablo perteneciente al griego antiguo μάθημα (máthēma), que significa campo de estudio o instrucción.

En general, se emplea más en su forma plural, matemáticas, que viene del latín mathematĭca, basado a su vez en la forma plural del griego, τα μαθηματικά (ta mathēmatiká), que se refiere a todas las cosas matemáticas.
Este término ya era utilizado en el siglo VI a. C. por los pitagóricos, seguidores del pitagorismo, movimiento filosófico-religioso fundado por Pitágoras de Samos.

Sin embargo, su significado más técnico y reducido de estudio matemático, por requerir un esfuerzo de aprendizaje, se dio en la época de Aristóteles (siglo IV a. C.).

Es probable que, en la literatura científica moderna, se extendiera el uso de esta palabra a partir del siglo XV, pasando del latín a las lenguas romances.
Esta disciplina se define como la ciencia formal y exacta que, con base en los principios de la Lógica, estudia tanto las propiedades como las relaciones existentes entre entes abstractos, refiriéndose por tales a números, símbolos y figuras geométricas.
Es ciencia, considerando esa palabra en su acepción de campo de conocimiento.
Es formal ya que sus objetos de estudio son abstractos, no reales.
Es exacta porque en sus procesos de razonamiento no hay lugar para la interpretación, la subjetividad o la duda.
Su método consiste en el análisis de dichos entes abstractos, generando tanto hipótesis como conjeturas, y realizando deducciones rigurosas con el fin de alcanzar el conocimiento matemático.

Tiene tres pares de elementos básicos:
Sin embargo, hay quienes consideran que más que una ciencia, con su objeto y su método, debe entenderse como un lenguaje formal, seguro y eficiente que permite comprender la naturaleza.

La evolución de esta disciplina ha estado basada en contar, calcular y medir, así como en estudiar sistemáticamente la forma y movimiento de los objetos físicos.
Cabe mencionar que hasta antes de los babilonios y los egipcios, alrededor del año 3000 a. C., no se dieron mayores avances en esta área del conocimiento.
En realidad, puede decirse que las Matemáticas Modernas comenzaron aproximadamente en el siglo XVII, en los inicios del Cálculo con la utilización, aún no del todo precisa, de dos conceptos: variable y función, que son característicos de ellas.
El hecho de que en una parte considerable de la Teoría Matemática se hallen involucradas dos colecciones de objetos relacionados, ha conducido a la noción de función, y consecuentemente a la elaborada rama de las matemáticas conocida como Teoría de Funciones.
Si bien, desde sus inicios esta disciplina tuvo un enfoque práctico, pues se trataba de resolver cuestiones como la división de un terreno, hoy se tienen dos vertientes: Matemáticas Puras y Matemáticas Aplicadas.
La primeras se desarrollan desde el punto de vista de la investigación, generando conocimiento nuevo.
En tanto que las segundas se emplean para la solución de problemas del día a día, y se utilizan en varios campos, entre ellos:
Por ejemplo, el análisis de las redes sociales se basa en la Teoría de Gráficas.
Tanto el Álgebra Lineal como la Probabilidad son elementos básicos para el algoritmo empleado por los buscadores en Internet.
La Teoría de Juegos, la Probabilidad, el Cálculo, los Sistemas no Lineales y Caóticos, se utilizan en Psicología.
Para el área financiera son importantes y el Análisis, la Probabilidad y el Movimiento Browniano.
En la Criptografía son usadas la Teoría de los Campos Finitos, la Combinatoria, la Probabilidad y la Teoría de Retículas.
Así, las Matemáticas se hallan presentes en diversas actividades del quehacer humano.


Como se indicó en el Prefacio, se incluye este tema, de manera breve, debido a la relación que existe entre las nociones de conjunto y función. Asimismo, esto permite introducir al final del capítulo la definición conjuntista de función.
Por lo que respecta a su etimología, la palabra conjunto tiene su origen en el latín coniunctus, cuyo significado es estar unido, contiguo o combinado con algo.

En general, es empleada para designar a una agrupación de cosas o personas que tienen algo en común, como un:
Según sea su conformación, un conjunto puede ser: finito, infinito, unitario, vacío, homogéneo, heterogéneo. Entre los conjuntos finitos se encuentra el de los meses del año, y entre los conjuntos infinitos está el de los números.
De acuerdo a la definición de Georg Ferdinand Ludwig Philipp Cantor, un conjunto es: “una colección en un todo, de determinados y distintos objetos de nuestra percepción o nuestro pensamiento, llamados los elementos del conjunto”.

Dichos elementos tienen características similares, carácter individual y son únicos. Pueden ser concretos o abstractos. Entre los primeros se tienen personas, animales, muebles. En tanto, que entre los segundos están números, letras, colores, figuras.

En caso de que los elementos deban satisfacer más de una condición, se utilizan los conectivos disyunción (letra $o$) y conjunción (letra $y$).
Un ejemplo es el conjunto de libros escritos en español o en inglés, cuyos elementos deben cumplir las dos condiciones:

Se conoce como subconjunto a aquel conjunto que se halla incluido dentro de otro más amplio. Así, si el conjunto $B$ está contenido en el conjunto $A$, entonces $B$ es un subconjunto de $A$.
Considerando que $A$ sea el conjunto de las letras del alfabeto y $B$ sea el conjunto de las vocales, se tiene que $B$ es subconjunto de $A$.
Para denotar un conjunto se usan por lo general letras mayúsculas, en tanto que sus elementos pueden ser representados por letras minúsculas, dígitos, nombre o característica, escritos entre los símbolos $\{ \}$ y separados por comas, como se muestra en la imagen a continuación.

Se tienen dos maneras para describir un conjunto: por extensión y por comprensión, como se ilustra en la siguiente imagen.

En el primer caso, se escriben uno a uno todos los elementos del conjunto. Si el conjunto tiene muchos elementos, pueden utilizarse puntos suspensivos, como en el caso del conjunto $B$.
En el segundo, sólo se menciona una característica común a todos sus elementos, como se indica en el conjunto $D$, y que se lee: “el conjunto $D$ está formado por elementos $d$ tales que $d$ es un libro”, o bien como en el conjunto $E$ donde se indica que sus elementos son aquéllos en los que la condición $G(e)$ es verdadera.
Para representar de forma gráfica a los conjuntos se utilizan los Diagramas de Venn, en los que se muestran los elementos del conjunto dentro de una línea cerrada.
Llevan el nombre de su creador John Venn, matemático y lógico británico, quien en julio de 1880, los presentó en la revista Philosophical Magazine and Journal of Science, bajo el título de On the Diagrammatic and Mechanical Representation of Propositions and Reasonings (De la representación mecánica y diagramática de proposiciones y razonamientos). Trabajo de gran repercusión en el campo de la Lógica Formal.

Estos diagramas permiten una comprobación de la validez o invalidez de un silogismo.
Al paso del tiempo, y con el surgimiento de la Teoría de Conjuntos, se les consideró adecuados para visualizar, tanto los conjuntos como sus operaciones básicas.
Así, se tienen dos tipos de diagramas de Venn:
En general, el universo de que se trate se representa mediante un rectángulo, y para los conjuntos se utilizan círculos u óvalos.
En el primer tipo, los elementos se colocan dentro de la forma del conjunto si pertenecen a él, de no ser así se ponen fuera, como se puede apreciar en la imagen superior derecha.
Permiten identificar de manera visual:
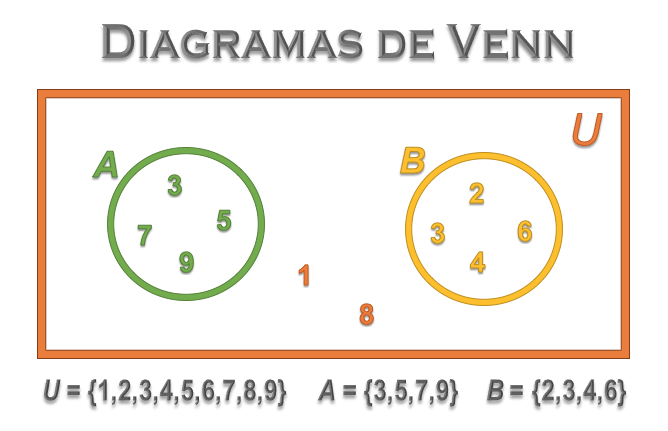
Los del segundo tipo, se emplean para visualizar las operaciones entre conjuntos, y suelen utilizarse colores.
En el caso de que se trate de dos conjuntos, se tiene el código de dos colores, que en un sistema binario puede asociarse al primer color el valor 0 y al segundo el valor 1, con lo que los resultados de las operaciones pueden digitalizarse.
Como ejemplo, en la imagen a continuación se muestra la intersección de los conjuntos $A$ y $B$.
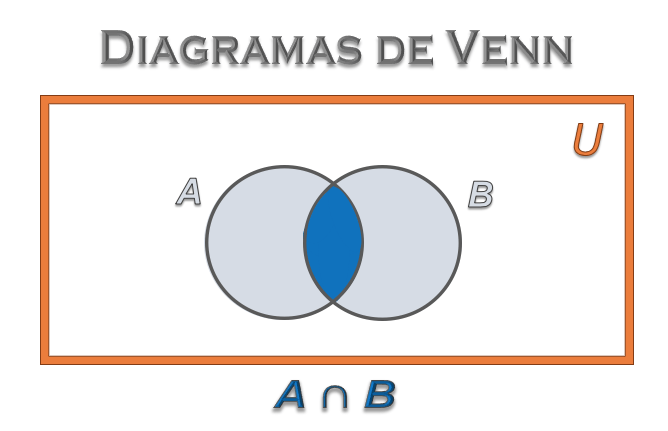
Se consideran tres relaciones básicas entre conjuntos: pertenencia, igualdad e inclusión, esquematizadas en la imagen de la derecha para los conjuntos A, B y C mostrados en ella.
La pertenencia de un objeto a un conjunto dado, siempre está bien definida por medio de alguna propiedad que todos sus elementos poseen.
Para indicar que un objeto $a$ pertenece al conjunto $A$, la notación utilizada es $a ∈ A$.
En tanto que para señalar que no pertenece a él, se emplea $a ∉ A$.
La igualdad entre conjuntos se da si y sólo si están formados por los mismos elementos. También se le conoce como principio de extensionalidad, y establece que un conjunto es definido sólo por sus elementos.
Se escribe como $A = B$. Para indicar que ambos conjuntos son diferentes se emplea $A ≠ B$.
La inclusión dice que si un conjunto $A$ es igual al conjunto $B$ o es una subcolección de éste, sus elementos son un subconjunto de $B$, y se denota como $A ⊆ B$.
En caso contrario: $A ⊈ B$. Si se considera un tercer conjunto $C$ del cual $B$ es un subconjunto, entonces $A$ es también un subconjunto de $C$.

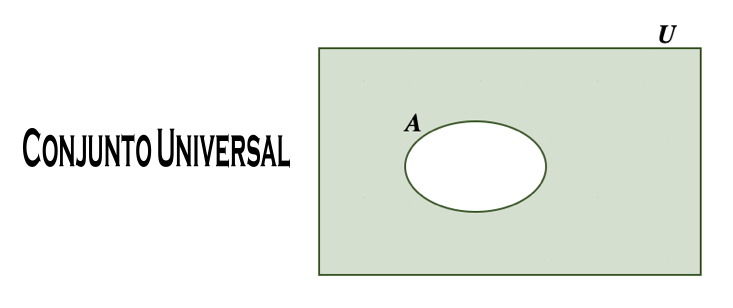
Existen dos conjuntos de mención especial: el conjunto universal y el conjunto vacío. El primero, como su nombre lo indica, consta de todos los elementos de estudio en el contexto de que se trate. Como ejemplos de conjunto universal se pueden citar:
Así, se establece una clara distinción entre sus elementos y los conjuntos formados por dichos elementos, que son subconjuntos del conjunto universal. Se denota por la letra U, y tiene las siguientes propiedades:
El segundo, es único y no tiene elementos. Su símbolo es la letra $∅$. Sus propiedades son:
Al estudio de las operaciones básicas que pueden realizarse con conjuntos, se le conoce como Álgebra de Conjuntos. Estas operaciones son:
Las operaciones de unión, intersección, diferencia y complemento, tienen similaridad tanto con el Álgebra de Boole, como con los conectores lógicos de la Lógica Proposicional.
Además, la unión y la intersección son conmutativas y asociativas.
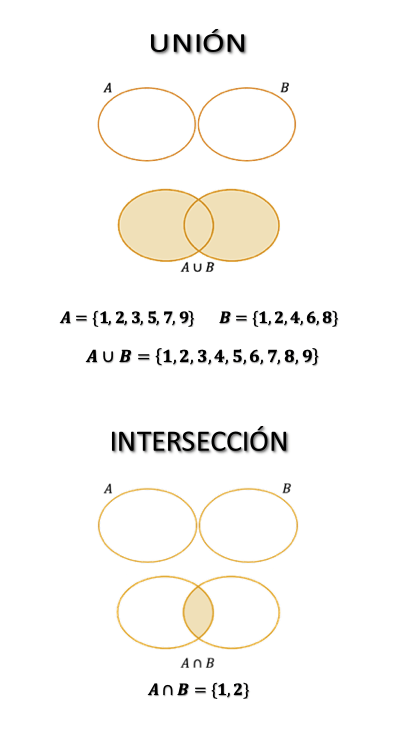
La unión de dos conjuntos $A$ y $B$, resulta en un tercer conjunto $C$ que contiene todos los elementos de ambos conjuntos.
En el caso de que haya un elemento repetido, forma parte de la unión sólo una vez.
Así, un elemento $x$ pertenece al conjunto $C$, si y sólo si pertenece al conjunto $A$ o al conjunto $B$.
Para representarla se utiliza el símbolo $∪$, denominado copa:
$C=A∪B$.
Esta operación puede realizarse sobre dos o más conjuntos.
Si se trata de tres conjuntos $A$, $B$, y $C$, cuya unión es el conjunto $D$, un elemento $x$ pertenece al conjunto $D$, si y sólo si pertenece al conjunto $A$ o al conjunto $B$ o al conjunto $C$.
La intersección de dos conjuntos $A$ y $B$ , es el conjunto cuyos elementos son comunes a $A$ y a $B$.
Se denota como $A∩B$.
La diferencia entre dos conjuntos $A$ y $B$, es el conjunto que contiene aquellos elementos de $A$ que no pertenecen a $B$.
Su representación es: $A∖B$.
La diferencia simétrica entre dos conjuntos $A$ y $B$, es el conjunto formado por los elementos de $A$ y $B$ que no son comunes.
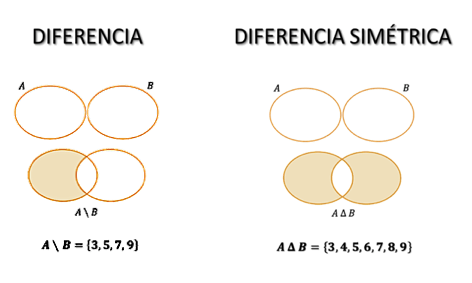
El complemento de un conjunto $A$ , es el conjunto de todos los elementos que no pertenecen a $A$, y se representa como: $A^C$.
Por ejemplo, si se considera al conjunto $U$ formado por las letras del alfabeto, y al conjunto $A$ conteniendo las vocales, $A^C$ sería el conjunto constituido por las consonantes.
El conjunto vacío es el complemento del conjunto universal y viceversa.
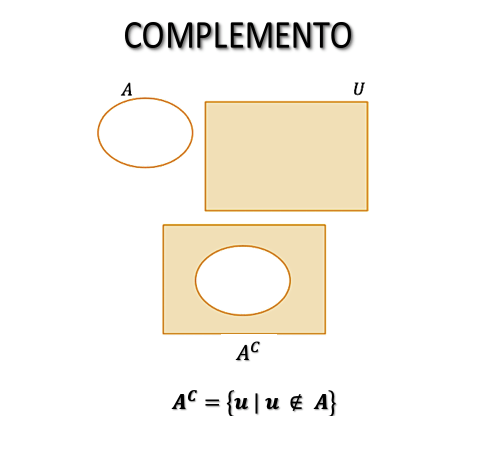
El resultado del producto cartesiano de dos conjuntos $A$ y $B$, es el conjunto formado por todos los pares ordenados $(a,b)$, cuyo primer elemento pertenece al conjunto $A$ y el segundo al conjunto $B$, como puede apreciarse en la imagen inferior.
Se denota como $A×B$.
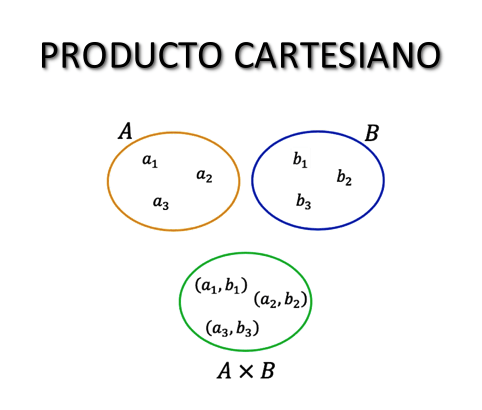
En el sentido matemático, una función es una correspondencia entre dos conjuntos $A$ y $B$, de manera que a cada elemento de $A$ le corresponda un único elemento de $B$, con la restricción de que $B$ sea diferente del conjunto vacío.
En la imagen siguiente se presenta un ejemplo que ilustra esta correspondencia biunívoca.
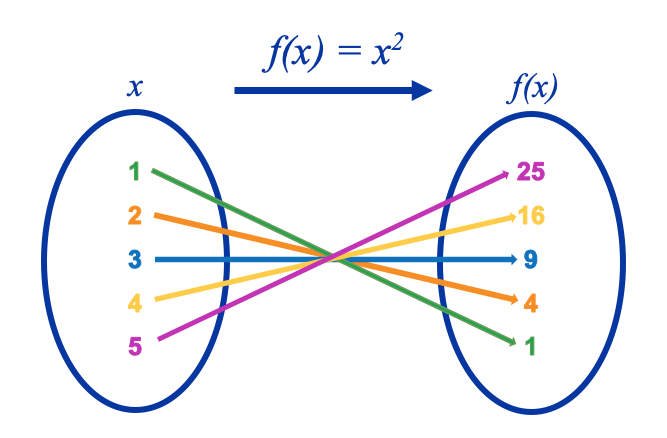
El conjunto $A$ se refiere a la variable independiente y se le denomina dominio de la función. Ésta es la parte esencial que determina la función. Como puede verse en el ejemplo anterior, $x$ es la variable independiente.
En tanto que el conjunto $B$ representa a la variable dependiente, como su nombre lo indica, su valor depende de la variable independiente, y se le llama codominio de la función $f(x)$.
En caso de que el dominio de una función no se especifique, se asume que éste incluye a todos los números reales para los que dicha función tenga sentido.
Así, considerando que si la función es:
En lo que respecta a la variable dependiente en la salida, hay que distinguir entre:
De lo anterior se desprende que el rango es un subconjunto del codominio.


La palabra número, de origen latino, significa asignar, tomar o ditribuir.

En Matemáticas indica una cantidad en relación con su unidad, y representa por lo general:
El desarrollo de este concepto se dio de manera lenta a lo largo del tiempo, conforme a la evolución de la mente humana en su proceso de abstracción natural.
Es una noción que existe desde tiempos remotos. Inició con la necesidad de contar del hombre primitivo, acción que se formalizó mediante sistemas de numeración en las civilizaciones de la Antigüedad. Se considera que algunos de ellos existieron antes del surgimiento de la escritura.
Ya en dichas culturas, tenían forma de medir tanto longitudes como áreas comparándolas con una unidad, lo que dio lugar a la noción intuitiva de número fraccionario.
A través de los siglos, el concepto de número tuvo varias adecuaciones en las diferentes culturas, llegando al que ahora tenemos: una abstracción que representa una cantidad, una magnitud.
El origen de los números reales se remonta al uso de fracciones comunes en la civilización egipcia, alrededor del año 1000 a.C.

Posteriormente, se dio un avance en el concepto con los aportes de los griegos, en particular con el surgimiento de la existencia de los números irracionales.
En los siglos XVI y XVII con el desarrollo del Cálculo, se hizo evidente la necesidad de tener una definición formal y rigurosa del concepto de número real.
Finalmente hacia principios del siglo XIX, se da la definición actual.
Los denominados números reales son aquellos que corresponden a un punto en la recta real, como puede observarse en la siguiente imagen.
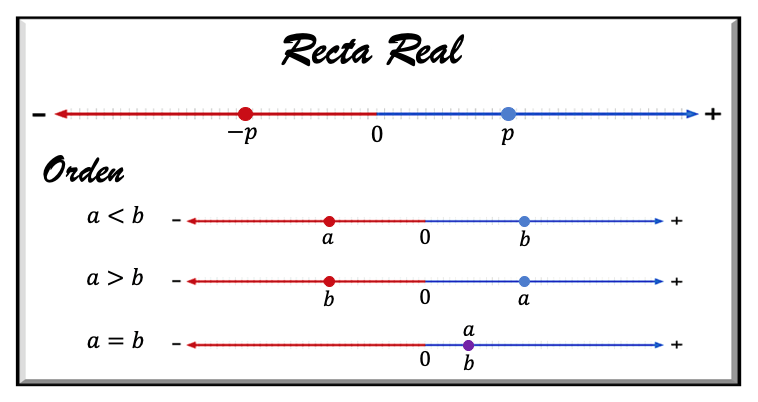
Se sitúan en ella de tal manera, que en cada tramo hay una cantidad infinita de ellos. Pueden expresarse con decimales infinitos o finitos, periódicos o no periódicos.
Forman un conjunto que se denota por la letra $ℝ$, y se encuentra entre los extremos infinitos, lo que se expresa como:
Así, éste es un conjunto infinito y continuo.
Sus elementos cumplen con una condición que garantiza una correspondencia biunívoca, esto es uno a uno, entre ellos y los del conjunto de puntos en la recta o eje. Dicha condición es conocida como axioma de completitud.
Su clasificación parte de los denominados números complejos denotados por la letra $\Complex$, y que se dividen en reales ($\R$) e imaginarios ($\mathbb I$ o $i\R$).
A su vez, los reales se subdividen en racionales e irracionales.
Los racionales forman el conjunto al pertenecen todos los números que pueden formularse como el cociente de dos números enteros:
$$\frac{a}{b}$$
donde:
$a$ es el numerador.
$b$ es el denominador distinto de cero.
Dado que este conjunto de números se refiere al cociente, es representado por la letra $\mathbb Q$ (Quotient).
Comprende a los enteros ($\mathbb Z$) y a los fraccionarios. El primer grupo lo forman los números naturales (uno, primos y compuestos), el cero y los enteros negativos. El segundo se subdivide en fracciones propias e impropias.
Un número racional admite una expansión finita o periódica.
Los irracionales corresponden valores que no pueden representarse como un número racional. Su expresión decimal no es exacta ni periódica. Se trata de un decimal infinito y aperiódico, por ello no se pueden expresar como la razón de dos números enteros.
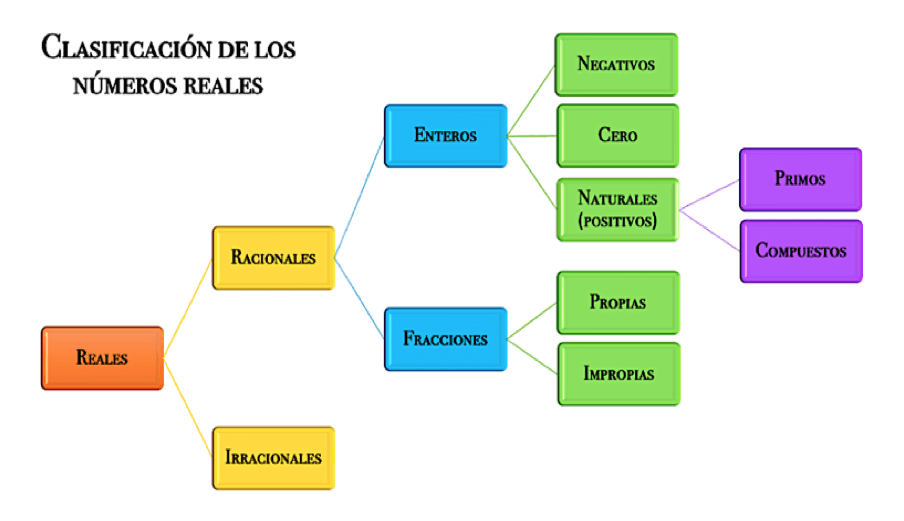
Los números reales también se subdividen en algebraicos y trascendentes. Los primeros pueden ser racionales o irracionales, en tanto que los segundos sólo comprenden a los irracionales.
Como ejemplos de los trascendentes se pueden citar los números $π$, $e$ y $ϕ$ (áureo).
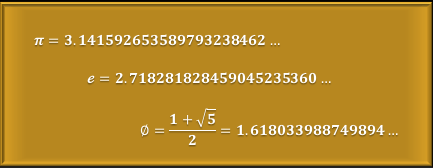
Es cerrada, por lo que su resultado será también un número real, de manera que si $a, b ∈ \mathbb R$ entonces: $$(a+b) ∈ \mathbb R$$
Es conmutativa, por lo que: $$a+b = b+a$$
Es asociativa, esto es: $$(a+b)+c = a+(b+c)$$
Si uno de los sumandos es cero, el resultado es igual al otro: $$a+0 = a$$
Para cada número real existe uno que es simétrico, tal que: $$a+(-a) = 0$$
Es cerrada, de ahí que si $a, b ∈ \mathbb R$, entonces: $$a×b ∈ \mathbb R$$
Es conmutativa, así que: $$a×b = b×a$$
Es asociativa, es decir: $$(a×b)×c = a×(b×c)$$
Existe un elemento neutro: $1$, de forma que: $$a×1 = a$$
Para cada número real que sea diferente de cero, existe otro que se denomina el inverso multiplicativo, tal que: $$a×a^{-1}= 1$$
Si $a, b, c ∈ \mathbb R$, entonces: $$a(b+c) = (a×b)+(a×c)$$

A continuación se presenta un breve panorama histórico del surgimiento y desarrollo del concepto de función, desde la Antigüedad hasta el siglo XX.

En Matemáticas, al igual que en otras disciplinas, algunas nociones surgen inicialmente como ideas intuitivas, y así sucedió con este concepto.
Tiene su origen, como otros, en el interés del hombre por comprender el mundo en el que habita, y que lo lleva a examinar con suma atención todo lo que lo rodea.
Se fue gestando a través de los siglos, pasando por diversas precisiones, generalizaciones y depuraciones, hasta llegar a la definición que se acepta en la actualidad, relacionada con el concepto de conjunto, incluida en el Capítulo 2 (página 45).
Las primeras referencias aparecen en las civilizaciones de la Antigüedad. Si bien, no se conocía entonces el concepto abstracto de función, sí se han encontrado indicios de la utilización de lo que podría considerarse funciones particulares.
En general, dichas referencias estaban dadas en forma de tablas. De manera que, podría pensarse en una definición de función para la época como una tabla de correspondencia.
Así, en algunos escritos encontrados en Babilonia, aparecen funciones tabuladas con las que se pretendía, por medio de métodos cuantitativos, predecir fenómenos astronómicos de repetición periódica, tales como movimientos lunares y planetarios.
Un ejemplo es la Tablilla de Venus de Ammisaduqa, de escritura cuneiforme, que data del siglo VII a. C. y es copia de un texto babilonio de unos mil años atrás. En ella se hallan registrados veintiún años de observaciones astronómicas del planeta Venus, correspondientes al siglo XVII a.C. y realizadas durante el reinado de Ammi-Saduqa, rey de Babilonia y cuarto sucesor de Hammurabi.


Asimismo, en la civilización egipcia hay ejemplos como el Papiro Rhind, que data de mediados del siglo XVI a. C., y es conocido también como Papiro de Ahmes por haber sido redactado por el escriba del mismo nombre.

Éste es considerado como el primer tratado de Matemáticas que se conserva.
En la Antigua Grecia surgieron las proporciones y los primeros intentos de cálculo infinitesimal.
Durante esta época Euclides de Alejandría, recupera y aplica a problemas concretos la Teoría de las proporciones de Eudoxo de Cnido, anticipando con el uso de razones una noción temprana de funcionalidad.
Así, en el Libro V de los Elementos, su obra cumbre, la tercera definición establece que "Una razón es determinada relación con respecto a su tamaño entre dos magnitudes homogéneas".

También en este período, la idea de dependencia entre cantidades aparece claramente señalada, en las investigaciones de Arquímedes de Siracusa. Esta noción puede apreciarse en sus obras:

Es en esta época cuando se establecen las bases para la definición del concepto de función.
A finales del siglo XIII y durante la primera mitad del siglo XIV, hubo gran interés por el estudio del movimiento de los cuerpos, tanto en Oxford como en París, siendo de gran importancia los trabajos de Thomas Bradwardine y Nicole d'Oresme.
El primero, formaba parte de los Mertonianos, un grupo de académicos del Merton College de Oxford ligados a la Orden Franciscana, en el marco de la Escolástica tardía, conocidos también como los Calculadores.
Bradwardine centró su actividad en encontrar las leyes de la dinámica. Así, en su obra Tractatus de proportionibus velocitatum in motibus (Tratado de las razones entre las velocidades de los móviles), publicada en 1328, aborda el concepto de función potencia, tratando de conocer la manera en que la velocidad de un cuerpo en movimiento es dependiente de las fuerzas que actúan sobre él.
El impulso que dio a la idea, de que la única forma de enteder las leyes naturales es expresarlas en una formulación matemática, es considerado como su mayor aportación a la ciencia.

Nicole d'Oresme, de la Universidad de París, introdujo un método para representar de manera gráfica las velocidades del movimiento uniformemente acelerado.
Sus principales contribuciones matemáticas, se hallan en su Tractatus de configurationibus qualitatum et motuum (Tratado de las cualidades y los movimientos), en el que utiliza coordinadas rectangulares y las figuras geométricas resultantes para distinguir entre distribuciones uniformes y no uniformes de varias cantidades.
Fue el primero en concebir la noción de potencias fraccionarias.
En su obra Algorismus Proportium (Algoritmo de las razones) explora las reglas para manipular las funciones potencia.
Se considera que la primera aproximación al concepto de función, se debe a Nicole d'Oresme por la descripción que hizo de las leyes de la naturaleza como relaciones de dependencia entre dos magnitudes.
Enl siglo XVII surge la Física Moderna. Destacan en él los trabajos de Galileo Galilei, René Descartes, Isaac Newton y Gottfried Wilhelm Leibniz.
Las investigaciones realizadas por Galileo sobre el movimiento, revelan que tenía un claro entendimiento de la relación existente entre las variables, y por ende, del concepto de función. Una de las relaciones estudiadas por él fue $n → n^2$, con la que se demuestra que hay tantos números naturales como cuadrados perfectos.
La contribución más relevante de Descartes a las Matemáticas fue la introducción de la Geometría Analítica. Su obra más famosa es el Discurso del método, publicado en 1637, en la que incluye un breve tratado, La Géométrie (La Geometría). En éste, detalla la aplicación de métodos algebraicos a la resolución de problemas geométricos, mostrando así el camino para la introducción de la noción de función.
Por su parte, Newton a finales de 1665 introdujo el concepto de fluxión, definido como la velocidad con la que una variable "fluye", esto es varía con el tiempo. Es entonces cuando descubre la reciprocidad de las operaciones de integración y derivación, lo que lo lleva a aproximarse al concepto de función.
Leibniz empleó la palabra función por primera vez en 1673, aunque no en el sentido que tiene actualmente, en su obra Methodus Tangentium Inversa Sen de fontionibus. Con ella representaba la dependencia de cantidades geométricas en la forma de una curva. También acuñó los términos constante, variable y parámetro.

Durante el siglo XVIII surge el concepto de función, tal como se le conoce actualmente, siendo uno de los principales intereses de la investigación matemática el desarrollo del Cálculo, disciplina muy relacionada con la noción de función. A este respecto, las contribuciones de Johann Bernoulli, Leonhard Paul Euler y Marie-Jean-Antoine Nicolas de Caritat, marqués de Condorcet fueron significativas para la definición de este concepto.
A Bernoulli se debe la primera definición, que aparece en un artículo publicado en Acta Eroditorum: Aquí denotamos por función de una variable una cantidad compuesta, de una o varias maneras, de esta cantidad variable y constantes.. Dando así, a la idea de función de Leibniz un carácter más abstracto.
En 1748, Euler la modifica, precisando así el concepto: Una función de cantidad variable es una expresión analítica formada de cualquier manera por esa cantidad variable y por números ó cantidades constantes. Ésta es la primera definición del concepto de función dada por él en su obra Introductor in Analysi Infinitorum.
Un tiempo después, en su libro Institutiones calculi differentialis de 1755, da una segunda definición más general de función: Algunas cantidades en verdad dependen de otras, si al ser combinadas las últimas, las primeras también sufren cambio, y entonces las primeras se llaman funciones de las últimas. Una cantidad puede ser determinada por otras, así si $x$ denota una cantidad variable, entonces todas las cantidades que dependen de $x$ en cualquier forma están determinadas por $x$ y se les llama funciones de $x$.
Posteriormente, Condorcet retomando esta segunda definición indica: asumo que tengo un cierto número de cantidades $x$, $y$, $z$,… y para cada valor definido de $x,$ $y,$ $z,$…, $F$ tiene uno o más valores definidos correspondientes a ellos; yo digo que $F$ es una función de $x,$ $y,$ $z,$…".
Él considera que no se necesita una expresión explícita, una fórmula analítica o una ecuación para definir una función, noción que se extendió en el siglo XIX.

A finales del siglo, los trabajos de Joseph-Louis de Lagrange tienen un rol muy importante en el desarrollo de las bases tanto del análisis como de la elaboración de la Teoría de Funciones.
En su obra Théorie des fonctions analytiques (Teoría de funciones analíticas), publicada en 1797, presenta una definición muy general: Llamamos función de una o varias cantidades a toda expresión de cálculo en la cual estas cantidades entran de cualquier manera, mezcladas o no, con otras cantidades que consideramos como valores dados e invariables, mientras que las cantidades de la función pueden recibir todos los valores posibles. Así, en las funciones no consideramos más que las cantidades que suponemos variables, sin ninguna consideración a las constantes que pueden estar mezcladas.
En el siglo XIX, los trabajos de Jean Baptiste Joseph Fourier, Johann Peter Gustav Lejeune Dirichlet, Georg Friedrich Bernhard Riemann y Karl Theodor Wilhelm Weierstrass contribuyeron a formalizar el concepto de función.
Derivado de sus investigaciones, en 1815 Fourier establece que: En general, la función $f(x)$ representa una sucesión de valores u ordenadas cada uno de los cuales es arbitrario. Dados una infinidad de valores de la abscisa $x$, hay un número igual de ordenadas $f(x)$.
Dirichlet es considerado el primero en formular el concepto moderno de función, al expresarlo de manera muy general como: $y = f(x)$ de una variable independiente en un intervalo $a$ < $x$ < $b$.
En 1837 propuso la definición de función como una correspondencia cualquiera entre dos conjuntos de números, que relaciona a cada número del primer conjunto con un único número del segundo.
Al respecto, se le atribuyen las siguientes frases registradas ese mismo año:

Su trabajo sobre funciones discontinuas, lo lleva a ser el primero en dar un ejemplo de éstas: una función definida en un intervalo $[0,1]$ y que es discontinua en todos sus puntos, como se muestra en la siguiente figura. Se le conoce como la función de Dirichlet.

A Riemann se le considera el fundador de la Teoría Moderna de Funciones.
En 1850 presenta la tesis Grundlagen Fur eine allgemeine Theorie der Functionem einer veranderlichen complexe Grosse (Fundamentos para una teoría general de las funciones de una variable compleja), en la que indica que una función viene definida por sus puntos singulares y los valores en los límites.
En ese mismo año, define la continuidad de una función $f(z)$ de la manera siguiente: La función $f(z)$ es continua en un intervalo, si cuando $z$ recorre de un manera continua todos los valores comprendidos entre dos valores fijos, la función $f(z)$ varía igualmente de una manera continua
Fue él quien hizo la primera distinción entre las nociones de continuidad y diferenciación.
En 1858, precisa la definición de función: Se dirá que $y$ es función de $x$ si a todo valor de $x$ corresponde un valor bien determinado de $y$ cualquiera que sea la forma de la relación que une a $x$ y a $y$.
Por su parte, Weierstrass hace aportaciones, en 1841, sobre la Teoría de Funciones Analíticas, planteando la Teoría de Funciones basada en el desarrollo de series de potencias de las funciones analíticas.
En 1881, en su artículo Remarques sur qualques points de la théorie des fonctions analítiques (Observaciones sobre algunos puntos de la teoría de funciones analíticas), presenta sus ideas relativas a la relación intuitiva entre continuidad y derivabilidad.También establece criterios de convergencia de series, formalizando así el concepto de límite, y puso los fundamentos del conjunto de los números reales.

Durante el siglo XX, el concepto de función se:
En esta época destacan, para su evolución, las contribuciones que derivan de los trabajos de tres matemáticos franceses: Édouard Jean-Baptiste Goursat, Henri León Lebesgue y Maurice René Fréchet.
En 1923, Goursat define una función de la forma siguiente: Se dice que $y$ es una función de $x$ si a cada valor de $x$ le corresponde un único valor de $y$. Esta correspondencia se indica mediante la ecuación $y = ƒ(x)$.
Lebesgue, expresa su acuerdo en que existe una función cuando hay correspondencia entre $y$, y los números $x_1$, $x_2$, $x_3$,...,$x_n$, sin preocuparse del procedimiento que sirve para establecer esta correspondencia.
Después, Fréchet en su tesis Généralisation d’un Théorème de Weierstrass (Generalización de un Teorema de Weierstrass), expone que: Supongamos que damos una cierta categoría (elementos cualesquiera, números, superficies, etc.) en la cual se sabe discernir los diferentes elementos. Podemos decir que $Vx$ es una función (operación funcional), uniforme en un conjunto $E$ de elementos de $c,$ si a todo elemento $A$ de $E$ le corresponde un número bien determinado $Vx$.

Una función $f$ indica una relación de dependencia de una variable con respecto a otra, por ejemplo:
A dicha relación se le conoce como regla de correspondencia o regla de transformación, y es la que determina a la función $f$.
Esto se puede esquematizar con una caja, que tiene una entrada y una salida. En la primera está la variable independiente $x$, la caja representa la transformación dada por la regla de correspondencia, y en la salida se tiene a la variable dependiente $f(x)$.

En caso de que se desee calcular el área de un círculo, $x$ se refiere al radio y $f(x)$ al área, la regla de correspondencia se expresa como:
$$f(x) = π x^2$$La notación $f(x)$ fue utilizada por primera vez por Leonhard Paul Euler en su artículo Additamentum ad dissertationem de infinitis curvis eiusdem generis, que fue presentado en 1734 y publicado en 1740.
De esta manera se indica que la función $f$ depende de la variable $x$, y se lee “$f$ de $x$”, o bien, “la función $f$ de $x$”. Así, se facilita identificar:
Por ejemplo, en la función:
$$f(x)=2x+5$$se puede apreciar con claridad que:
El dominio de la función $f:X→Y$ se define como: $$D_f = \{x ∈ X :∃ ∈ Y : f(x) = y\}$$
El dominio y el codominio de la función $f$ se denotan, de forma abreviada, como sigue:
$$f: \mathbb R → \mathbb R$$ $$f: X → Y$$La relación entre un elemento $x$ del conjunto $X$ (dominio) y su único correspondiente $f(x)$ del conjunto $Y$ (codominio), se expresa: $$x → f(x)$$
Una función puede representarse de cinco formas:
Dependerá del tipo de función que se pretenda representar, la elección de cada una de ellas.
La imagen de la derecha, ilustra las cinco maneras para la función:
$$f(x)=(x+1)^2-3x+1 \;\;\;\;\;\;\;\;\;\;\;\; D_f=\{1,2,3,4,5\}$$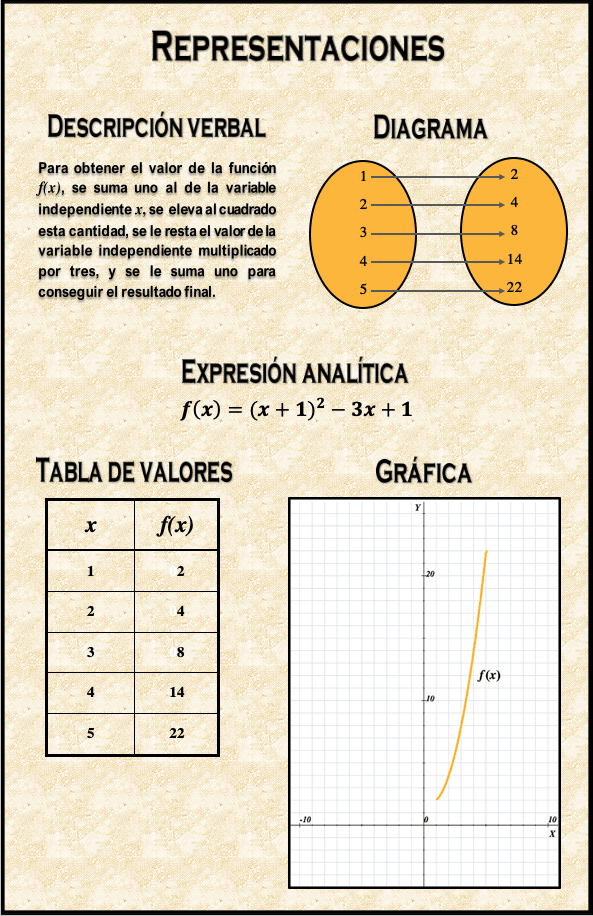
A continuación se detallan estas representaciones.
Consiste en exponer mediante lenguaje común, sin necesidad de simbología especializada, la relación existente entre los elementos de entrada y los de salida de la función.
Es una manera que permite dar una explicación general y cualitativa de la función de que se trate.
Fue sugerida por Gustav Dirichlet, para separar el concepto de función de fórmulas concretas.
Un ejemplo de ella se encuentra en la Función de Dirichlet. Cabe mencionar que una de sus características es que no es posible graficarla.
Por medio de la utilización de un diagrama, se obtiene una clara y rápida visualización de la función que se desea analizar.
Su aplicación es muy similar a la de los diagramas de Venn respecto a los conjuntos.
Es empleada generalmente para trabajar con conjuntos finitos.
Con este tipo de representación se indica, ya sea de manera explícita o implícita, la regla de correspondencia, a través de una fórmula matemática.
Conviene utilizarla para funciones en las que otras representaciones no resultan del todo adecuadas.
Mediante esta forma, se genera una tabla de valores con los de la variable independiente $x$, y los correspondientes de la dependiente $f(x)$.
Es muy usada en situaciones cotidianas, por ejemplo para señalar porcentajes.
Dependiendo de la función, puede tomarse como el punto de partida para pasar a la representación gráfica.
De esta manera, se plasma en el plano cartesiano la gráfica formada con todos los pares de puntos $(x, f(x))$, tales que $x ∈ D_f$, visualizando así las características globales de la función, lo que la hace muy popular.

Se dice que una función $f(x)$ es de una variable real si a cada número real del dominio ($\textbf{D}$), corresponde un único número real del rango. Su expresión formal es:
$$f: \textbf{D}_f ⊂ \mathbb R → \mathbb R \\ x⟼y = f(x)$$
donde:
$f$ es la función (regla de correspondencia) de $\mathbb R$ en $\mathbb R$.
$\textbf{D}_f$ es el dominio de la función $f$.
$\mathbb R$ es el codominio de la función.
$x$ es la variable independiente.
$y = f(x)$ es la variable dependiente (imagen de $x$).
Conviene recordar que la imagen de la función es muy importante, aunque no se encuentre explícitamente en la definición, y que de manera formal se representa como:
$$\textbf{Im}_f = y ∈ \mathbb R │ ∃ x ∈ \textbf{D}_f, f(x) = y$$En algunos casos, podría ser útil restringir el dominio de la función a un subconjunto de los números reales cuando:
Una forma de determinar visualmente si una relación es una función de variable real, es el criterio de la recta vertical. También se le conoce como regla de la recta vertical.
Consiste en trazar rectas paralelas al eje de las ordenadas, sobre la gráfica de la curva de que se trate, y dado que en una función de variable real, a cada valor de la variable independiente le corresponde sólo uno de la variable dependiente, si alguna de ellas la interseca en más de un punto, implica que dicha curva no es una función.
De esta manera, se puede verificar que a cada par $(x,y)$ de la curva, le corresponda en el plano cartesiano un único punto $P$ tal que:
$$P(x,y) = P(x,f(x))$$En la escena interactiva se presentan algunos ejemplos de la aplicación de este criterio.
Para desplazar la recta sobre la curva, basta pulsar el control $x$ o introducir un valor dentro del campo del mismo, seguido de la tecla Intro. Para ver un efecto de deslizamiento en la recta debe mantenerse oprimido el pulsador $x$.
La función $f$ está acotada superiormente si existe un número real $M$, denominado cota superior, tal que:
$$f(x) ≤ M, ∀x ∈ \textbf{D}_f$$Cualquier otro número real $M' > M$, es también cota superior de $f$. A la menor de ellas se le llama supremo.
La función $f$ está acotada inferiormente si existe un número real $m$, llamado cota inferior, tal que:
$$f(x) ≥ m, ∀x ∈ \textbf{D}_f$$Cualquier otro número real $m' < m$, es también cota inferior de $f$. A la mayor de ellas se le llama ínfimo.
La función $f$ está acotada si tiene cota superior y cota inferior, de manera que:
$$∃m, M / m ≤ f(x) ≤ M, ∀x ∈ \textbf{D}_f$$En la escena interactiva se presentan ejemplos de funciones con alguna cota.
Geométricamente se dice que una función $f(x)$, cuya gráfica sea una curva continua en el intervalo $[i,i']$ es cóncava en dicho intervalo si dados dos puntos $(x,x')$ cualesquiera de la gráfica, el segmento que los une queda por encima de la curva.
En caso de que el segmento referido quede por debajo de la curva, $f(x)$ es convexa.
Dado que con cierta frecuencia se definen estos dos conceptos con el criterio exactamente contrario, es habitual que se hable de funciones cóncava hacia arriba y cóncava hacia abajo, siendo la segunda la que aquí se ha presentado como convexa.
Los puntos en los que $f(x)$ cambia su concavidad por convexidad, y viceversa, se conocen como puntos de inflexión (pi).
En la escena interactiva de presentan ejemplos de esta propiedad.
Se dice que una función $f(x)$ es continua, si puede representarse en todo su dominio por medio de un trazo continuo, en caso contrario se dice que dicha función es discontinua.
En la escena interactiva se presentan dos ejemplos.
Se dice que una función $f(x)$ es par, si para cualquier $x$ del dominio se verifica que:
$$f(x) = f(-x)$$Esto quiere decir que ni su valor ni su signo cambian al sustituir $x$ por $-x$.
Una función $f(x)$ es impar, si se comprueba que para cualquier $x$ del dominio:
$$f(x) = -f(-x)$$Como se puede observar en la escena interactiva, las funciones pares son simétricas con respecto al eje $Y$, en tanto que las impares lo son con respecto al origen.
Se refiere al crecimiento o decrecimiento de una función $f$, analizándola sobre el eje $X$, de izquierda a derecha, y expresando los intervalos del eje $X$ en los que crece o decrece. Así, en un intervalo $I[i,i']$ la función $f$ es:
Geométricamente, como puede verse en el interactivo, la curva:
Las funciones periódicas son aquellas en las que sus valores se repiten siempre cada intervalo determinado del eje $X$. Dicho intervalo se conoce como el período de la función.
Esto es:
$$f(x+p) = f(x+2p) = ... = f(x+np)$$En la escena interactiva se presentan dos ejemplos.
Una función es simétrica, respecto al eje $Y$, si a la abscisa $x > 0$ le corresponde la misma ordenada que a la abscisa $x < 0$, esto es:
$$f(x)=f(-x)$$También se encuentra la simetría con respecto al origen, donde:
$$f(x) = -f(-x)$$Como se indicó en el Prefacio, se tienen cinco tipos de función de una variable real:
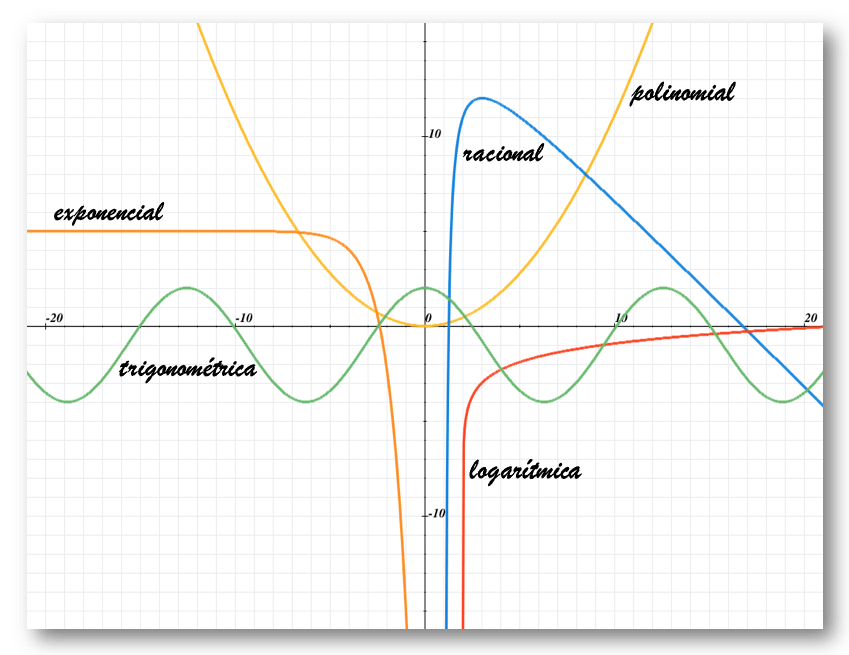
En los siguientes capítulos se encuentra la descripción de cada uno de ellos, y se incluyen las escenas interactivas mencionadas en el Prefacio, que permiten visualizar, de manera clara, los cambios que se dan en las representaciones gráficas al variar sus parámetros.
Asimismo, al final de cada capítulo hay un interactivo en el que se puede experimentar, introduciendo en el campo de texto las funciones que se desee graficar.

Las funciones polinomiales, denominadas también polinómicas, tienen su dominio en los números reales.
Su definición, como su nombre lo indica, viene dada por un polinomio, esto es:
$$f(x) = a_nx^n + a_{n-1}x^{n-1} + ⋯ + a_2 x^2 + a_1 x + a_0$$
donde:
$a_i ≠ 0$
$a_i$ son constantes reales.
$n$ es un entero positivo.
De ellas puede decirse que:
Se clasifican según el grado del polinomio, que corresponde al mayor exponente de la variable independiente: grado cero, grado uno, grado dos, … grado $n$.
En este capítulo se describen las que corresponden a los primeros cinco grados.
De acuerdo al grado de la función, su rango es:
Asimismo, conviene recordar que dado que se trata de polinomios, su grado indica el número de raíces del mismo, y que éstas son de tres tipos: positivas, negativas y complejas.
En la sección de funciones polinomiales de grado 2, se presentan varios ejemplos en una escena interactiva.
La función de polinomial de grado cero, es un caso particular de las funciones polinomiales. Tiene la forma:
$$f(x) = a$$donde $a$ es una constante, y por ello se le conoce como función constante.
Como puede observarse en la escena interactiva, su representación gráfica es una recta paralela al eje $X$, que interseca al eje $Y$ en el punto $(0, a)$. Variando el valor de la constante en la escena interactiva, ya sea introduciéndolo directamente en el campo de texto, seguido de la tecla Intro, o mediante el pulsador en la zona inferior, puede verse el desplazamiento de la recta de ordenada $a$.
A la función polinomial de grado uno también se le denomina polinomial lineal.
Su expresión algebraica es:
$$f(x) = mx+n$$
donde:
$x$ es la variable independiente.
$m$ es el coeficiente de la variable o pendiente de la recta.
$n$ es el término dependiente u ordenada, e indica el punto en el que la recta cruza al eje $Y$.
Se representa gráficamente como una recta inclinada.
Desde el punto de vista geométrico, a mayor pendiente mayor inclinación de la recta, y viceversa.
En la escena interactiva, variando el valor de $m$ puede observarse que si:
La función es estrictamente creciente si $m > 0$. En caso contrario, si $m < 0$, la función es estrictamente decreciente.
En tanto que, cuando $m = 1$ y $n = 0$, se trata de la función identidad.
En la escena interactiva, variando el valor del pulsador, se pueden ver las gráficas correspondientes.
También se utiliza la letra $b$ para designar al término dependiente, de manera que la función se escribe: $$f(x) = mx+b$$
Otra forma, menos usual, sería: $$f(x) = ax+b$$
Para trazar su gráfica se tienen los métodos:
Esta función, también conocida como función cuadrática, consta de tres términos:
Como puede apreciarse en la imagen de la derecha, este tipo de función se clasifica en:
A su vez, las incompletas se denominan:
Si la función consta sólo del término cuadrático, el vértice $V(v_x, v_y)$ se halla en el punto $(0, c)$ y el eje de simetría es el de las ordenadas.
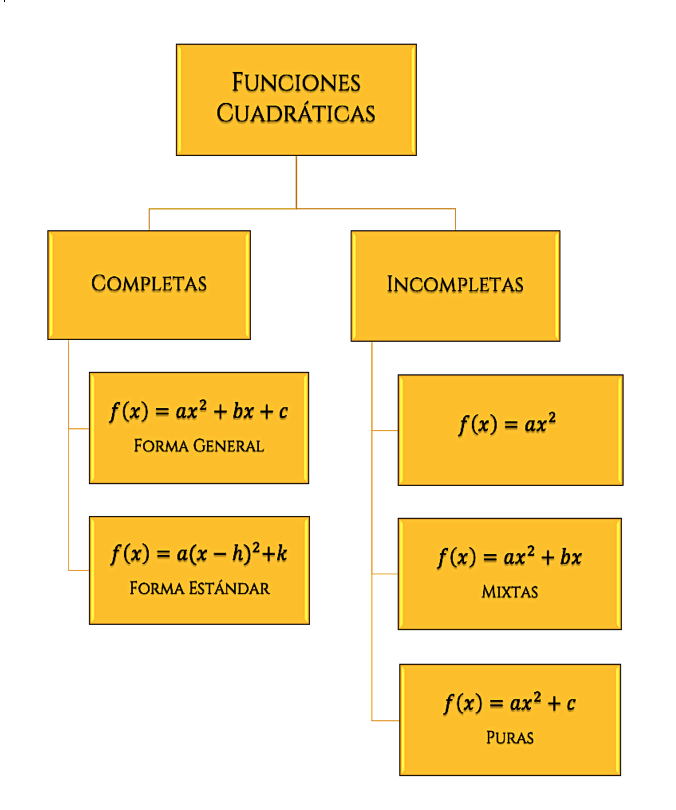
Su representación gráfica es una parábola vertical, que puede cortar al eje de las abscisas en uno, dos o en ningún punto, conforme al número de raíces reales de la función.
Conviene recordar, que las raíces de la función son los valores que satisfacen la ecuación cuadrática generada al igualar la función a cero.
Así, dada la función: $$f(x)=ax^2+bx+c$$
Se tiene la ecuación: $$ ax^2+bx+c=0$$
Cuyas soluciones están dadas por:
Los valores de $x_1$ y $x_2$ corresponden a las raíces reales de $f(x)$.
En la escena interactiva de la derecha se presentan varios ejemplos, en ellos se puede observar también que la parábola interseca al eje de las ordenadas en el punto $p (0, c)$
La función polinomial de grado dos o polinomial cuadrática tiene la forma general:
$f(x) = ax^2 + bx + c$
donde:
$a, b, c$ son los coeficientes (constantes).
$a ≠ 0$ es la condición esencial.
$ax^2$ es el término cuadrático.
$bx$ es el término lineal.
$c$ es el término independiente.
Como ya se indicó, su gráfica es una parábola vertical, cuyo eje de simetría (recta dorada en la escena interactiva) es paralelo al eje $Y$ y se calcula mediante:
$x = -b / 2a$
Las coordenadas del vértice $V$ están dadas por:
$v_x = -b / 2a$$v_y = (-b^2 + 4ac) / 4a$
Variando, en el interactivo, el valor del coeficiente $a$, se observa que:
La forma estándar de la función cuadrática es:
$$f(x) = a(x-h)^2 + k$$
donde:
$a$ es el coeficiente principal.
$a≠0$ es la condición esencial.
$h$ y $k$ son las coordenadas del vértice $V$.
El utilizar esta expresión, permite visualizar mejor las modificaciones dadas en la gráfica por la variación de los coeficientes, ya que en ella se indican de manera explícita tanto el vértice, como la abertura de la parábola.
Cambiando los valores de $a$, $h$ y $k$ en la escena interactiva, se puede observar directamente en la gráfica que cuando:
A la función polinomial de grado tres se le llama también polinomial cúbica.
Su forma general es:
$$f(x) = ax^3 + bx^2 + cx + d$$
donde:
$a$, $b$, $c$ y $d$ son los coeficientes (constantes).
$a ≠ 0$ es la condición esencial.
$ax^3$ es el término cúbico.
$bx^2$ es el término cuadrático.
$cx$ es el término lineal.
$d$ es el término independiente.
La gráfica de la función cúbica puede tener entre uno y tres puntos de corte en el eje $X$, pero siempre interseca al eje $Y$ en el punto $(0, d)$.
Esto puede observarse al variar los coeficientes en la escena interactiva, en la que inicialmente la gráfica interseca al eje de las abscisas en tres puntos y al eje de las ordenadas en el punto $(0, 0)$.
La función polinomial de grado cuatro es conocida asimismo como polinomial cuártica.
Su forma general es:
$$f(x) = ax^4 + b^3 + cx^2 + dx + e$$
donde:
$a$, $b$, $c$ y $d$ son los coeficientes (constantes).
$a ≠ 0$ es la condición esencial.
$ax^4$ es el término a la cuarta potencia.
$bx^3$ es el término cúbico.
$cx^2$ es el término cuadrático.
$dx$ es el término lineal.
$e$ es el término independiente.
Variando los coeficientes en la escena interactiva, pueden observarse los cambios en la gráfica.
En el campo de texto FUNCIÓN POLINOMIAL de la escena interactiva, introduce alguna función de las presentadas en este capítulo, y observa cómo se comporta la gráfica correspondiente al variar los parámetros.
La notación para escribir la función es:
^ para la potencia de la variable independiente,
$/$ para la división,
$()$ para agrupar los términos que así lo requieran,
Intro para terminar.
Por ejemplo, la función:
$$5x^3 + 2x^2 + 4$$debe escribirse:
5x^3+2x^2+4
Como su nombre lo indica, la función racional se refiere a una razón o cociente, irreductible, de dos polinomios. Tiene la forma general:
$$f(x) = \frac{P(x)}{Q(x)}$$
donde:
$P(x)$ y $Q(x)$ son polinomios.
$x$ es la variable independiente.
$Q(x) ≠ 0$ es condición esencial.
Su dominio es el conjunto de $\mathbb R$, exceptuando los valores de $x$ que anulan a $Q(x)$, éstos son conocidos como valores excluidos, ceros o raíces de la función. Formalmente se expresa como:
$$f : \textbf{D}_f = \mathbb{R} - x ∈ \mathbb{R} | Q(x) = 0$$Para cada uno de ellos hay una asíntota vertical cuando $x$ toma dicho valor, esto es, si $a$ es una raíz de $f(x)$, entonces la función tiene una asíntota vertical en $x=a$. Si el grado de:
Existen tres casos particulares de las funciones racionales: de proporcionalidad inversa, de proporcionalidad inversa trasladada y homográfica.
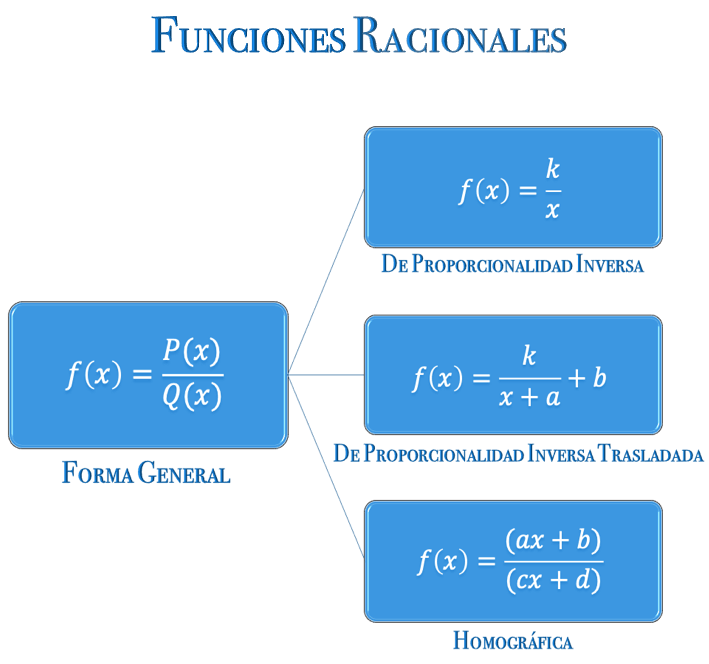
Desde el punto de vista gráfico, este tipo de función adopta diversas formas, como se puede apreciar en los ejemplos presentados en la escena interactiva.
Como puede observarse, para funciones racionales de primer grado, la gráfica es la correspondiente a una hipérbola.
La función racional de proporcionalidad inversa, se llama así debido a que relaciona dos magnitudes inversamente proporcionales.
Es la forma más sencilla de las funciones racionales, y se define como:
$$f(x) = \frac{k}{x}$$
donde:
$k$ es la constante de proporcionalidad.
Tanto su dominio como su rango están en el conjunto de los números reales, con excepción del cero.
Su gráfica es una hipérbola, cuyas asíntotas se hallan en los ejes $X$ y $Y$.
En la escena interactiva, se puede notar que, si:
Como su nombre lo indica, la función racional de proporcionalidad inversa trasladada es una función racional de proporcionalidad inversa desplazada.
El desplazamiento oblicuo se da con la forma general:
$$f(x) = \frac{k}{x+m}+n$$
donde:
$k$ es la constante de proporcionalidad.
$m$ y $n$ son las constantes de traslación.
Las expresiones particulares de traslación son:
Al variar el valor de los parámetros, en la escena interactiva, se ven dichos desplazamientos. Así, si
La función racional homográfica o racional lineal, se caracteriza porque $P(x)$ y $Q(x)$ son polinomios de grado uno:
$$f(x) = \frac{ax+b}{cx+d}$$
donde:
$x$ es la variable independiente.
$a$, $b$, $c$ y $d$ son los parámetros de la función.
Existe sólo un valor excluido, para encontrarlo se tiene que resolver la ecuación obtenida al hacer:
$$cx+d=0$$Este valor es la solución de la ecuación y también se le conoce como cero o raíz del polinomio.
La asíntotas vertical y horizontal están dadas por:
$$x = \frac{-d}{c}$$ $$y = \frac{a}{c}$$Como puede observarse en la escena interactiva, si:
En la escena interactiva, introduce alguna función de las descritas en este capítulo en el campo de texto FUNCIÓN RACIONAL y observa la forma de su gráfica.
Al escribir la función hay que utilizar:
^ para la potencia de la variable independiente,
$/$ para la división,
$()$ para agrupar los términos que así lo requieran,
Intro para terminar.
Por ejemplo, la función
$$\frac{3}{(x+1)(x-2)}$$debe escribirse:
3/((x+1)(x-2))
La función exponencial se denomina así debido a que la variable independiente se halla en la posición del exponente. Se define de la siguiente manera:
Así, se dice que $a^x$ es una función exponencial de base $a$ y exponente $x$. El valor $a=1$ se excluye porque con éste, se tendría la función constante $f(x) = 1^x = 1$.
Con las restricciones $a>0$ y $a≠1$, su dominio es el conjunto de los números reales y su rango el de los números reales positivos.

Las más importantes, y las que tienen mayor aplicación, son aquellas en las que $a=10$ o $a=e$.
Esta última es llamada función exponencial natural:
$$f(x) = e^x$$Conviene recordar aquí que el número $e$ es uno de los números irracionales y trascendentes más importantes en Matemáticas. Su valor truncado a sus primeras cifras decimales es:
Es conocido como número de Euler porque Leonhard Paul Euler fue quien le identificó con la letra $e$, y con sus aportaciones dio un tratamiento definitivo a las ideas preexistetes sobre esta constante.
En 1748, Euler publicó su obra Introductio in analysin infinitorum (Introducción al análisis del infinito), en la que mostró el valor de $e$, aproximándolo a 18 cifras decimales, como la serie:
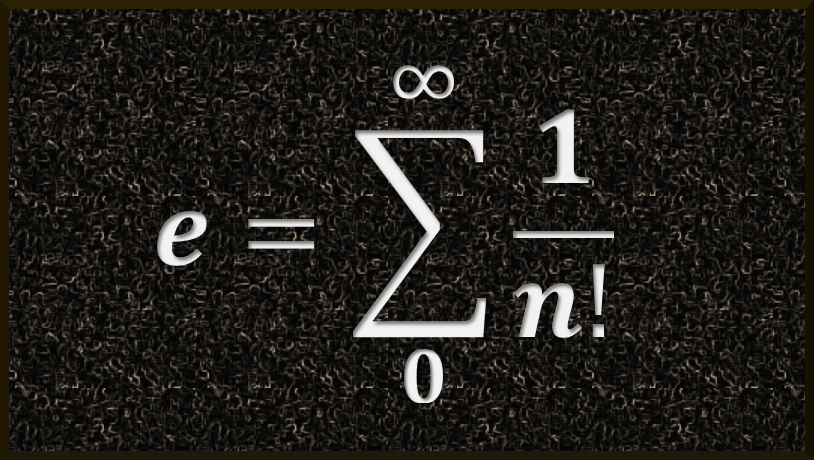
También se le define como el límite de la sucesión $(1+({1}/{n}))^n$.
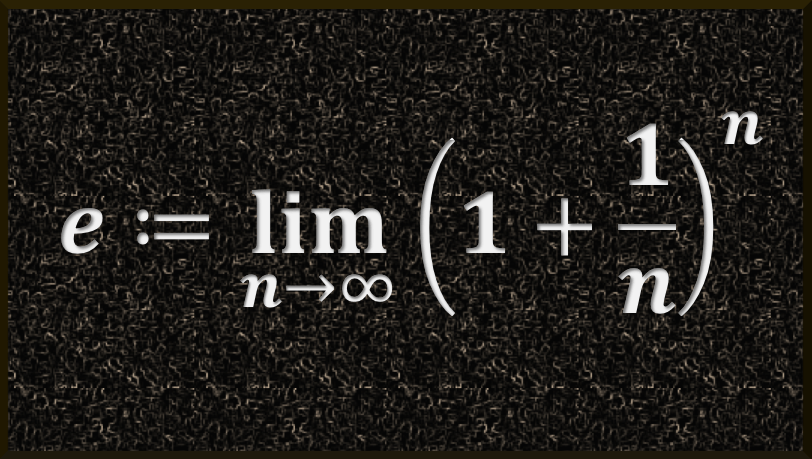
Asimismo, se le denomina constante de Napier, debido a que fue John Napier de Merchiston el primero en reconocerlo y utilizarlo.

Como puede verse en la escena interactiva, las gráficas de las funciones exponenciales tienen las siguientes propiedades:
También puede observarse que las gráficas de las funciones:
son simétricas respecto al eje $OY$.
Lo mismo aplica en el caso de la función exponencial natural:
Al utilizarlas, conviene tener en cuenta las leyes de los exponentes:
Mediante la adición de algunos parámetros se pueden transformar, a la función resultante se le denomina función de forma exponencial. Las traslaciones se hacen con las constantes $b$ (horizontal) y $c$ (vertical):
$$f(x) = a^{x+b} + c$$En la escena interactiva se presentan algunos de estos casos, observa los cambios en las gráficas.
En la escena interactiva, introduce alguna función de las descritas en este capítulo en el campo de texto FUNCIÓN EXPONENCIAL y observa la forma y características de su gráfica.
Al escribir la función hay que utilizar:
^ para la potencia de la base,
$/$ para la división,
$()$ para agrupar los términos que así lo requieran,
Intro para terminar.
Por ejemplo, la función:
$$f(x) = (\frac{3}{4})^x$$debe escribirse:
(3/4)^x
Dado que la función logarítmica, como su nombre lo indica, está basada en el concepto de logaritmo, es pertinente incluir algunos comentarios al respecto.
Este concepto surgió a principios del siglo XVII, de los estudios realizados por John Napier de Merchiston, orientados a encontrar métodos eficientes de cálculo, siendo ésta su contribución más importante a las Matemáticas. En particular, su objetivo era simplificar los difíciles cálculos astronómicos. Su trabajo sobre este tema quedó plasmado en sus obras:
En un principio utilizó el término números artificiales para designarlos. Posteriormente creó su nombre actual.

El logaritmo se define de la siguiente manera:
$$log_a x = y ⇔ a^y = x; x, a >0; a≠1$$La forma general de este tipo de función es:
$$f(x) = log_a (x)$$
donde:
$a$ es la base.
$a > 0$ y $a ≠ 1$ es condición esencial.
$x$ es la variable independiente.
Así, se dice que $f(x)$ es igual al logaritmo base $a$ de $x$.
Las bases que se utilizan más frecuentemente son aquellas en las que $a = 10$ o $a = e$, por lo que son las descritas en esta sección.
La primera es la función logarítmica de base 10, cuya expresión es:
$$f(x) = log_(10)(x)$$La segunda se denomina función logarítmica natural y se escribe:
$$f(x) = ln(x)$$De la definición de logaritmo enunciada, se desprende que la función logarítmica es la inversa de la función exponencial, por lo que el dominio de la primera es el rango de la segunda y viceversa.
Como se puede observar en la escena interactiva de la derecha, sus gráficas son simétricas respecto a la recta:
$$y = x$$Como puede verse en la escena interactiva, las gráficas de las funciones logarítmicas tienen las siguientes propiedades:
Asimismo, puede observarse la simetría que, con respecto al eje $OX$, presentan las gráficas de las funciones:
Lo mismo sucede en el caso de la función logarítmica natural.
Al utilizarlas, conviene tener en cuenta las siguientes propiedades de los logaritmos:
Estas funciones pueden transformarse mediante algunos parámetros, y a la función resultante se le conoce como función de forma logarítmica. Para hacer una traslación, se añade la constante $b$ (vertical) y/o $c$ (horizontal):
$$f(x) = log_a (x+b) + c$$Con la constante $k$ se cambia la rapidez con que la función crece o decrece:
$$f(x) = klog_a (x)$$En la escena interactiva se presentan algunos de estos casos, observa los cambios en las gráficas.
En la escena interactiva de la derecha, introduce alguna función de las presentadas en este capítulo en el campo de texto FUNCIÓN LOGARÍTMICA y observa la forma de su gráfica.
Al escribir la función hay que utilizar:
$log10(x)$ para las de base decimal.
$log(x)$ para las de base $e$.
$/$ para la división,
$()$ para agrupar los términos que así lo requieran,
Intro para terminar.
Por ejemplo, la función:
$$f(x) = log_{10}(x)$$debe escribirse:
log10(x)
En las funciones trigonométricas a cada número real de la variable independiente $x$, se le asocia el valor de la razón trigonométrica del ángulo cuya medida, en radianes, es $x$.
En general, se definen como el cociente entre dos lados de un triángulo rectángulo vinculados a sus ángulos, como se muestra en la imagen de la siguiente sección.
Las funciones trigonométricas son las que se listan a continuación, note que entre paréntesis se indica su abreviatura:
Cabe mencionar que existen también las: funciones trigonométricas inversas y las funciones trigonométricas hiperbólicas. Sin embargo, su descripción no forma parte del material a desarrollar en este libro.
Basta indicar que las primeras, llamadas también funciones arco, como su nombre lo indica, son las inversas de las seis trigonométricas, y permiten determinar un ángulo partiendo de las relaciones angulares de las mismas.
Las funciones inversas existen sólo para ciertos intervalos del dominio de las funciones trigonométricas, estando éstos establecidos debidamente para cada una.
En tanto que la definición de las funciones trigonométricas hiperbólicas, está basada en la función exponencial.
La imagen que sigue muestra las relaciones angulares de acuerdo a la definición general de las funciones trigonométricas.
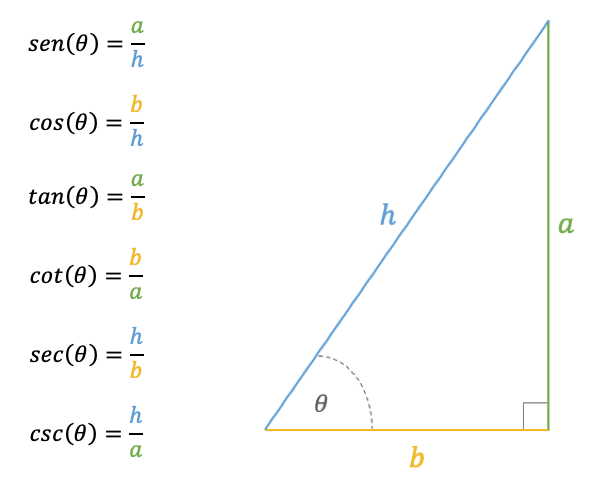
Como puede apreciarse en ella:
Las funciones trigonométricas son funciones periódicas.
En las primeras cuatro el período es igual a $2π$, en tanto que en las dos últimas es igual a $π$.
Así, se tiene que:
A continuación se describen las propiedades de cada una de estas funciones.
En la función seno a cada número real de la variable independiente $x$ se asocia el valor del seno del ángulo cuya medida, en radianes, es dicha variable: $f(x) = sen\;x$
Tiene las siguientes propiedades:
En la función coseno a cada número real de la variable independiente $x$ se asocia el valor del coseno del ángulo cuya medida, en radianes, es dicha variable: $f(x) = cos\;x$
Tiene las siguientes propiedades:
En la función tangente a cada número real de la variable independiente $x$ se asocia el valor de la tangente del ángulo cuya medida, en radianes, es dicha variable: $f(x) = tan\;x$, recordando que $tan\;x = \frac{sen\;x}{cos\;x}$.
Tiene las siguientes propiedades:
En la función cotangente a cada número real de la variable independiente $x$ se asocia el valor de la cotangente del ángulo cuya medida, en radianes, es dicha variable: $f(x) = cot\;x$, recordando que $cot\;x = \frac{cos\;x}{sen\;x}$
Tiene las siguientes propiedades:
En la función secante a cada número real de la variable independiente $x$ se asocia el valor de la secante del ángulo cuya medida, en radianes, es dicha variable: $f(x) = sec\;x$, recordando que $sec\;x = \frac{1}{cos\;x}$
Tiene las siguientes propiedades:
En la función cosecante a cada número real de la variable independiente $x$ se asocia el valor de la cosecante del ángulo cuya medida, en radianes, es dicha variable: $f(x) = csc\;x$, recordando que $csc\;x = \frac{1}{sen\;x}$
Tiene las siguientes propiedades:
Las funciones trigonométricas tienen tres parámetros fundamentales:
La amplitud sirve para modificar el tamaño de la función.
Con la frecuencia se puede cambiar el grado de repetición.
La fase permite el desplazamiento de la función. Para adelantarla se utiliza el signo $+$, y hay un corrimiento hacia la izquierda. Para atrasarla se emplea el signo $-$, y el deslizamiento es a la derecha.
Así, considerando que $A≠0$ y $k≠0$, estas funciones pueden escribirse como:
$f(x) = A \; sen(kx+α)$
$f(x) = A \; cos(kx+α)$
$f(x) = A \; tan(kx+α)$
$f(x) = A \; cot(kx+α)$
$f(x) = A \; sec(kx+α)$
$f(x) = A \; csc(kx+α)$
En la escena interactiva se presentan algunos ejemplos, que permiten observar la manera en que estos parámetros afectan la gráfica de la función.
En la escena interactiva de la derecha, introduce alguna función de las descritas en este capítulo en el campo de texto FUNCIÓN TRIGONOMÉTRICA, y observa la forma de su gráfica.
Al escribir la función hay que utilizar:
^ para la potencia de la variable independiente,
$/$ para la división,
$()$ para agrupar los términos que así lo requieran,
Intro para terminar.
Por ejemplo, la función
$$f(x) = 5 cos(2x+7)$$debe escribirse:
5cos(2x+7)
La importancia de las funciones de una variable real, radica en la gran utilidad que presentan para diversos aspectos de la vida cotidiana. A continuación se mencionan algunos ejemplos, por tipo de función.
Las funciones polinomiales, en general, son muy útiles para analizar y resolver situaciones prácticas, mediante el desarrollo de modelos que las describan, tales como:
En particular, las que se emplean comúnmente para modelar diversos fenómenos reales, son las funciones de grado dos.
Las funciones racionales son utilizadas para interpolar resultados de funciones más complejas como son:
Las funciones exponenciales tienen gran aplicación en diversas disciplinas, entre las que se encuentran:
Entre los fenómenos de comportamiento exponencial están:
Las funciones logarítmicas se emplean para:
En tanto que las funciones trigonométricas son relevantes especialmente en las siguientes disciplinas:
Particularmente las de seno y coseno, son muy útiles para analizar fenómenos periódicos como son:
