Física - Volumen II
INTERACTIVO
José Gregorio Doria Andrade
Juan Guillermo Rivera Berrío
Institución Universitaria Pascual Bravo
Red Educativa Digital Descartes
Fondo Editorial RED Descartes

Córdoba (España)
2022
Título de la obra:
Física - Volumen II
Segunda edición
Autor:
José Gregorio Doria Andrade
Juan Guillermo Rivera Berrío
Obra derivada del libro (University Physics - Volume I)
Samuel J. Ling (Truman State University)
Jeff Sanny (Loyola Marymount University)
Bill Moebs
Código JavaScript para el libro: Joel Espinosa Longi, IMATE, UNAM.
Recursos interactivos: DescartesJS
Diseño de cubierta: Margarita Patiño Jaramillo
Fuentes: Livvic y UbuntuMono
Fórmulas matemáticas: $\KaTeX$
Red Educativa Digital Descartes
Córdoba (España)
descartes@proyectodescartes.org
https://proyectodescartes.org
Proyecto iCartesiLibri
https://proyectodescartes.org/iCartesiLibri/index.htm
https://prometeo.matem.unam.mx/recursos/VariosNiveles/iCartesiLibri/
ISBN Obra completa: 978-84-18834-39-4
ISBN Volumen II: 978-958-56858-5-7
Esta obra está bajo una licencia Creative Commons 4.0 internacional: Reconocimiento-No Comercial-Compartir Igual.
Este libro digital interactivo se ha diseñado con fundamento en la filosofía del Proyecto Descartes: "Trabajando altruistamente por la comunidad educativa de la aldea global", que sólo busca desarrollar contenidos educativos para el provecho de la comunidad académica, esperando únicamente como retribución el uso y difusión de estos contenidos. El contenido del libro, al igual que los objetos interactivos se han diseñado de tal forma que se puedan leer en ordenadores y dispositivos móviles sin necesidad de instalar ningún programa o plugin. El libro se puede descargar para su uso en local sin dependencia con la red, a excepción de los ocho vídeos incluidos en el texto.
El contenido del libro se basa en un recurso de OpenStax, organización sin fines de lucro de la Universidad de Rice, cuya misión, similar a la nuestra, es mejorar el acceso de los estudiantes a la educación. El libro ha sido desarrollado para cumplir con el alcance y la secuencia de la mayoría de los cursos de física universitarios y proporciona una base para una carrera en matemáticas, ciencias o ingeniería.
Este segundo volumen del libro de texto de Física Universitaria se adhiere al alcance y la secuencia de los cursos de física universitaria. Se ha trabajado para hacer que la física sea interesante y accesible para los estudiantes, manteniendo el rigor matemático inherente a la materia. Con este objetivo en mente, el contenido de este libro de texto ha sido desarrollado y organizado para proporcionar una progresión lógica de conceptos fundamentales a más avanzados, basándose en lo que los alumnos ya han aprendido y enfatizando las conexiones entre los temas y entre la teoría y las aplicaciones. El objetivo de cada sección es permitir que los estudiantes no solo reconozcan conceptos, sino que trabajen con ellos de manera que sean útiles en cursos posteriores y carreras futuras. La organización y las características pedagógicas fueron desarrolladas y revisadas con comentarios de educadores de ciencias dedicados al proyecto.
A lo largo del libro encontrarás derivaciones de conceptos que presentan ideas y técnicas clásicas, así como también aplicaciones y métodos modernos. La mayoría de los capítulos comienzan con observaciones o experimentos que colocan el material en un contexto de experiencia física. Las presentaciones y explicaciones se basan en años de experiencia en el aula por parte de profesores de física de larga data, que luchan por un equilibrio de claridad y rigor que ha demostrado ser exitoso con sus alumnos. Las figuras históricas clave y los experimentos se discuten en el texto principal, manteniendo un enfoque en el desarrollo de la intuición física. Las ideas clave, las definiciones y las ecuaciones se destacan en el texto.
Los ejemplos y las imágenes de apertura de capítulos a menudo incluyen aplicaciones contemporáneas de la vida cotidiana o de la ciencia y la ingeniería modernas con las que los estudiantes se pueden relacionar, desde teléfonos inteligentes hasta Internet y dispositivos GPS.
El texto original, desarrollado por Ling S., Sanny J. y Moebs B., ha sido publicado en versiones html y pdf. Esta obra derivada, en español y como libro interactivo, creada por Doria J. & Rivera J.G., presenta las siguientes aportaciones: traducción al español, diseño en formato flipbook, incorporación de 56 objetos interactivos de aprendizaje, 36 de ellos diseñados con el editor DescartesJS, y ocho vídeos. Para evitar, al máximo, la dependencia con la conectividad en la red, las expresiones matemáticas se han construido recurriendo al diseño de algunas clases en la hoja de estilos (style.css) y, en algunos casos, al editor DescartesJS.
Se ha conservado la propuesta pedagógica en los ejemplos presentados en cada uno de los capítulos, los cuales incluyen: formulación del problema, estrategia de solución, solución, explicación o sentido de los resultados obtenidos y, en la mayoría de los ejemplos, un problema propuesto, denominado "Comprueba tu aprendizaje". Al final de cada capítulo se han incluido tanto los problemas propuestos como las respuestas.

En capítulos anteriores, describimos el movimiento (cinemática) y cómo cambiar el movimiento (dinámica), y definimos conceptos importantes, como la energía para los objetos que se pueden considerar como masas puntuales. Las masas puntuales, por definición, no tienen forma y, por lo tanto, solo pueden experimentar un movimiento de traslación. Sin embargo, sabemos por la vida cotidiana que el movimiento de rotación también es muy importante y que muchos objetos que se mueven tienen tanto la traslación como la rotación.
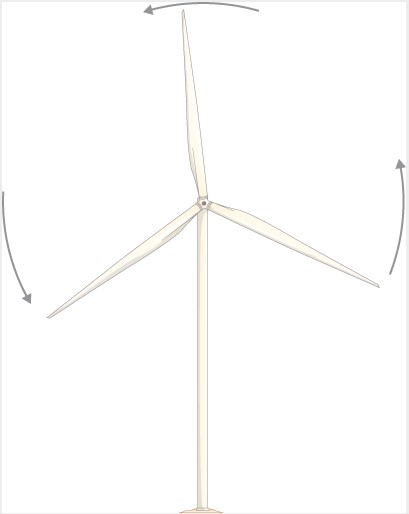
Las turbinas eólicas en la imagen de apertura de nuestro capítulo son un excelente ejemplo de cómo el movimiento rotacional impacta nuestras vidas diarias, a medida que el mercado de fuentes de energía limpia continúa creciendo.
Comenzamos a tratar el movimiento rotacional en este capítulo, comenzando con la rotación del eje fijo. La rotación del eje fijo describe la rotación alrededor de un eje fijo de un cuerpo rígido; es decir, un objeto que no se deforma cuando se mueve. Mostraremos cómo aplicar todas las ideas que hemos desarrollado hasta este momento sobre el movimiento de traslación a un objeto que gira alrededor de un eje fijo. En el próximo capítulo, extendemos estas ideas a un movimiento rotacional más complejo, que incluye objetos que giran y se trasladan, y objetos que no tienen un eje de rotación fijo.
Hasta ahora en este texto, hemos estudiado principalmente el movimiento traslacional, incluidas las variables que lo describen: desplazamiento, velocidad y aceleración. Ahora, expandimos nuestra descripción de movimiento a rotación, específicamente, movimiento de rotación sobre un eje fijo. Encontraremos que el movimiento de rotación se describe mediante un conjunto de variables relacionadas similares a las que utilizamos en el movimiento traslacional.
El movimiento circular uniforme (discutido anteriormente) es un movimiento en círculo a velocidad constante. Aunque este es el caso más simple de movimiento rotacional, es muy útil para muchas situaciones, y lo usamos aquí para introducir variables rotativas.
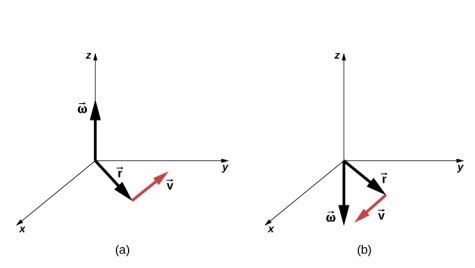
En la , mostramos una partícula moviéndose en un círculo. El sistema de coordenadas es fijo y sirve como un marco de referencia para definir la posición de la partícula. Su vector de posición desde el origen del círculo hasta la partícula barre el ángulo $θ$, que aumenta en la dirección contraria a las agujas del reloj a medida que la partícula se mueve a lo largo de su trayectoria circular.
El ángulo $θ$ se llama la posición angular de la partícula. A medida que la partícula se mueve en su trayectoria circular, también traza una longitud de arco $s$.
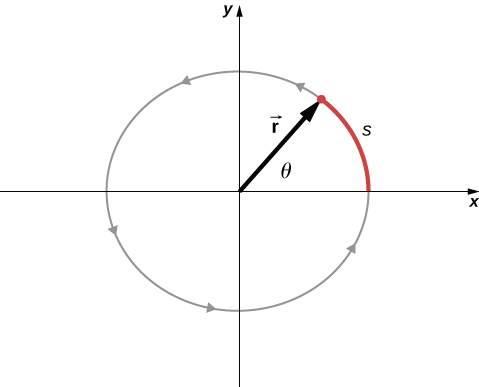
El ángulo está relacionado con el radio del círculo y la longitud del arco.
El ángulo $θ$, la posición angular de la partícula a lo largo de su trayectoria, tiene unidades de radianes ($rad$). Hay $2π$ radianes en $360°$. Tenga en cuenta que la medida de radianes es una relación de medidas de longitud, y por lo tanto es una cantidad adimensional. A medida que la partícula se mueve a lo largo de su trayectoria circular, su posición angular cambia y sufre desplazamientos angulares $Δθ$.
Podemos asignar vectores a las cantidades en la Ecuación 1.1. El ángulo $\overrightarrow{θ}$ es un vector fuera de la página en la . El vector de posición angular $\overrightarrow{\bold{r}}$ y la longitud del arco $\overrightarrow{\bold{s}}$ se encuentran en el plano de la página. Estos tres vectores están relacionados entre sí por
Es decir, la longitud del arco es el producto cruz entre el vector $\overrightarrow{θ}$ y el vector $\overrightarrow{\bold{r}}$, como se muestra en la .
La velocidad angular instantánea se define como el límite en el cual $Δt \to 0$ en la velocidad angular promedio.
$$ω = \lim_{Δt \to 0} \frac{Δθ}{Δt} = \frac{dθ}{dt}$$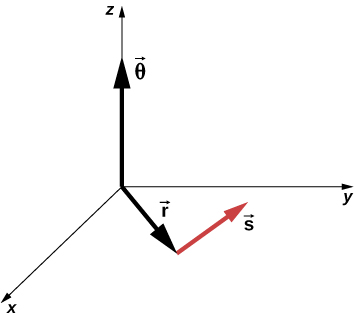
El ángulo está relacionado con el radio del círculo y la longitud del arco donde $θ$ es el ángulo de rotación (). Las unidades de velocidad angular son radianes por segundo ($rad/s$). La velocidad angular también se puede denominar velocidad de rotación en radianes por segundo. En muchas situaciones, se nos da la velocidad de rotación en $revoluciones/s$ o $ciclos/s$. Para encontrar la velocidad angular, debemos multiplicar revoluciones por segundo, ya que hay $2π$ radianes en una revolución completa. Como la dirección de un ángulo positivo en un círculo es en sentido antihorario, tomamos rotaciones en sentido antihorario como positivas y rotaciones en sentido horario como negativas.
Podemos ver cómo la velocidad angular se relaciona con la velocidad tangencial de la partícula al diferenciar la ecuación 1.1 con respecto al tiempo. Reescribimos la Ecuación 1.1 como
Tomando la derivada con respecto al tiempo y observando que el radio $r$ es una constante, tenemos
$$\frac{ds}{dt} = \frac{d(rθ)}{dt} = \frac{θdr}{dt} + \frac{rdθ}{dt} = \frac{rdθ}{dt}$$donde $\frac{θdr}{dt}=0$. Aquí $\frac{ds}{dt}$ es justamente la velocidad tangencial $v_t$ de la partícula (). Por lo tanto, al usar la Ecuación 1.2, llegamos a
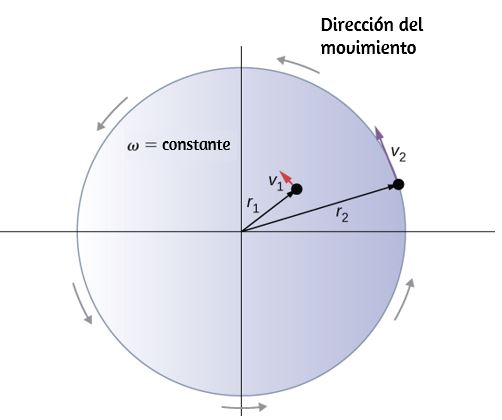
Es decir, la velocidad tangencial de la partícula es su velocidad angular multiplicada por el radio del círculo. A partir de la ecuación 1.4, vemos que la velocidad tangencial de la partícula aumenta con su distancia desde el eje de rotación para una velocidad angular constante. Este efecto se muestra en la . Dos partículas se colocan en diferentes radios en un disco giratorio con una velocidad angular constante. A medida que el disco gira, la velocidad tangencial aumenta linealmente con el radio del eje de rotación.
En la , vemos que $v_1 = r_1 ω_1$ y $v_2 = r_2 ω_2$. Pero el disco tiene una velocidad angular constante, por lo que $ω_1 = ω_2$. Esto significa que $\frac{v_1}{r_1} = \frac{v_2}{r_2}$ o $v_2 = (\frac{r_2}{r_1}) v_1$, por lo tanto, $r_2 \gt r_1$, $v_2 \gt v_1$.
Hasta ahora, hemos discutido la magnitud de la velocidad angular, que es una cantidad escalar, y se define como el cambio en la posición angular con respecto al tiempo $ω = dθ / dt$. El vector $\overrightarrow{\bold{w}}$ es el vector relacionado con la velocidad angular y los puntos a lo largo del eje de rotación.
En el siguiente interactivo, diseñado por Andrew Duffy, puedes...
Esto es útil porque cuando un cuerpo rígido está girando, queremos saber tanto el eje de rotación como la dirección en que el cuerpo gira alrededor del eje, en sentido horario o antihorario. La velocidad angular $\overrightarrow{\bold{w}}$ nos da esta información. La velocidad angular $\overrightarrow{\bold{w}}$ tiene una dirección determinada por lo que se llama una regla de la mano derecha. La regla de la mano derecha es tal que los dedos de la mano derecha se envuelven en sentido antihorario desde el eje $x$ (la dirección en la que $θ$ aumenta) hacia el eje $y$, su pulgar apunta en la dirección del eje $z$ positivo ().
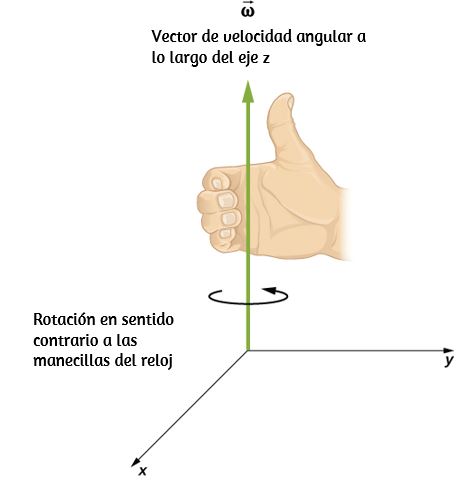
Una velocidad angular $\overrightarrow{\bold{w}}$ que apunte hacia el eje $z$ positivo, por lo tanto, corresponde a una rotación en contra a las manecillas del reloj, donde la velocidad angular $\overrightarrow{\bold{w}}$ apunta a lo largo del eje $z$ negativo que corresponde a una rotación en el sentido de las agujas del reloj.
Podemos verificar la regla de la mano derecha usando la expresión del vector $\overrightarrow{\bold{s}} = \overrightarrow{θ} × \overrightarrow{\bold{r}}$. Ecuación 1.4. Si diferenciamos esta ecuación con respecto al tiempo, encontramos
$$\frac{d \overrightarrow{\bold{s}}}{dt} = \frac{d}{dt}(\overrightarrow{θ} × \overrightarrow{\bold{r}}) = \left(\frac{d \overrightarrow{θ}}{dt} × \overrightarrow{\bold{r}} \right) + \left(\overrightarrow{θ} × \frac{d \overrightarrow{\bold{r}}}{dt} \right) = \frac{d \overrightarrow{θ}}{dt} × \overrightarrow{\bold{r}}$$Como $\overrightarrow{\bold{r}}$ es constante, el término $(\overrightarrow{θ} × \frac{d \overrightarrow{\bold{r}}}{dt}) = 0$. Ya que $\overrightarrow{\bold{v}} = \frac{d \overrightarrow{\bold{r}}}{dt}$ es la velocidad tangencial y $\overrightarrow{\bold{w}} = \frac{d \overrightarrow{θ}}{dt}$ es la velocidad angular, así tenemos que:
Es decir, la velocidad tangencial es el producto cruzado entre velocidad angular y el vector posición angular como se muestra en la . De la parte (a) de esta figura, vemos que con la velocidad angular en la dirección $z$ positiva, la rotación en el plano $xy$ es en sentido antihorario. En la parte (b), la velocidad angular está en la dirección negativa, dando una rotación en el sentido de las agujas del reloj en el plano $xy$.
Ejemplo 1.1
Rotación de un volante
Un volante gira de tal manera que barre un ángulo a la velocidad de $θ = ωt = (45 rad/s)t$. La rueda gira hacia la izquierda cuando se ve en el plano de la página.
(a) ¿Cuál es la velocidad angular del volante?
(b) ¿Qué dirección tiene la velocidad angular?
(c) ¿Cuántos radianes gira el volante en $30 s$?
(d) ¿Cuál es la velocidad tangencial de un punto en el volante a $10 cm$ del eje de rotación?
Estrategia
La forma funcional de la posición angular de la rueda voladora se da en los problemas $θ (t) = ωt$, así que tomando la derivada con respecto al tiempo, podemos encontrar la velocidad angular. Usamos la regla de la mano derecha para encontrar la velocidad angular. Para encontrar el desplazamiento angular del volante durante $30 s$, buscamos el desplazamiento angular $Δθ$, donde el cambio en la posición angular está entre $0$ y $30 s$. Para encontrar la velocidad tangencial de un punto a una distancia del eje de rotación, multiplicamos su distancia por la velocidad angular del volante.
Solución
a. $ω = \frac{dθ}{dt} = 45 rad / s$. Vemos que la velocidad angular es una constante.
b. Con la regla de la mano derecha, curvamos los dedos en la dirección de rotación, que está en sentido antihorario en el plano de la página, y el pulgar apunta en la dirección de la velocidad angular, que está fuera de la página.
c. $Δθ = θ(30 s) - θ(0 s) = 45(30s) - 45(0s) = 1350 rad$.
d. $v_t = rω = (0.1 m)(45rad/s) = 4.5 m/s$.
Significado
En $30 s$, el volante ha girado alrededor de $215$, si dividimos el desplazamiento angular por $2π$. Un volante masivo se puede utilizar para almacenar energía de esta manera y las pérdidas debidas a la fricción son mínimas. Una investigación reciente ha considerado los cojinetes superconductores en los que descansa el volante, con cero pérdida de energía debido a la fricción.
Aceleración angular
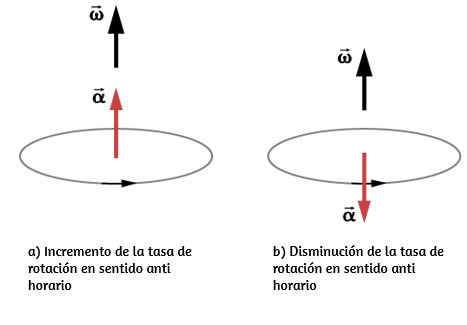
Acabamos de analizar la velocidad angular para un movimiento circular uniforme, pero no todo el movimiento es uniforme. Imagine a un patinador de hielo girando con los brazos extendidos; cuando tira de sus brazos hacia adentro, su velocidad angular aumenta, o piense en que el disco duro de una computadora se desacelere a medida que disminuye la velocidad angular. Exploraremos estas situaciones más adelante, pero ya podemos ver la necesidad de definir una aceleración angular para describir situaciones donde $ω$ cambia. Cuanto más rápido sea el cambio en $ω$, mayor será la aceleración angular. Definimos la aceleración angular instantánea $α$ como la derivada de la velocidad angular con respecto al tiempo:
donde hemos tomado el límite de la aceleración angular promedio $α = \frac{Δw}{Δt}$ cuando $Δt \to 0$
Las unidades de aceleración angular son $(rad/s^2)$. De la misma manera que definimos el vector asociado con la velocidad angular $\overrightarrow{\bold{w}}$, podemos definir $\overrightarrow{α}$, el vector asociado con la aceleración angular (). Si la velocidad angular está a lo largo del eje $z$ positivo, como en la , y $\frac{dw}{dt}$ es positivo, entonces la aceleración angular $\overrightarrow{α}$ es positiva y apunta a lo largo del eje $+z$. De manera similar, si la velocidad angular $\overrightarrow{\bold{w}}$ está a lo largo del eje $z$ positivo y $\frac{dw}{dt}$ es negativo, entonces la aceleración angular es negativa y apunta a lo largo del eje $+z$.
Podemos expresar el vector de aceleración tangencial como un producto cruzado de la aceleración angular y el vector de posición. Esta expresión se puede encontrar tomando la derivada de tiempo de $\overrightarrow{\bold{v}} = \overrightarrow{\bold{w}} × \overrightarrow{\bold{r}}$ y se deja como un ejercicio:
Las relaciones de vectoriales para la aceleración angular y la aceleración tangencial se muestran en la .
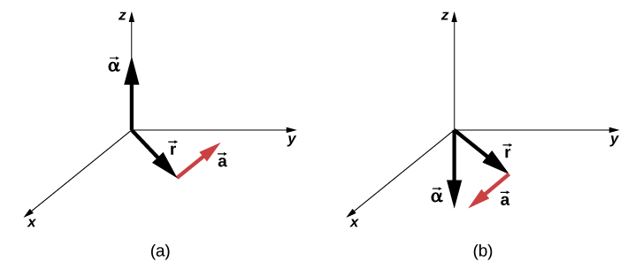
Podemos relacionar la aceleración tangencial de un punto en un cuerpo giratorio a una distancia del eje de rotación de la misma manera que relacionamos la velocidad tangencial con la velocidad angular. Si diferenciamos la ecuación 1.7 con respecto al tiempo, observando que el radio $r$ es constante, obtenemos
Por lo tanto, la aceleración tangencial $a$ es el radio multiplicado por la aceleración angular. La ecuación 1.4 y la ecuación 1.8 son importantes para la discusión del movimiento de rotación (ver Momento angular). Vamos a aplicar estas ideas al análisis de algunos escenarios simples de rotación de eje fijo. Antes de hacerlo, presentamos una estrategia de resolución de problemas que se puede aplicar a la cinemática rotacional: la descripción del movimiento rotacional.
Estrategia de resolución de problemas: cinemática rotacional
1. Examine la situación para determinar que la cinemática rotacional (movimiento de rotación) está involucrada.
2. Identifique exactamente qué debe determinarse en el problema (identifique las incógnitas). Un boceto de la situación es útil.
3. Haga una lista completa de lo que se da o se puede deducir del problema tal como se establece (identifique los conocimientos).
4. Resuelve la ecuación o ecuaciones apropiadas para la cantidad que se determinará (lo desconocido). Puede ser útil pensar en términos de un análogo traslacional, porque a estas alturas ya está familiarizado con las ecuaciones del movimiento traslacional.
5. Sustituya los valores conocidos junto con sus unidades en la ecuación apropiada y obtenga soluciones numéricas completas con unidades. Asegúrese de usar unidades de radianes para ángulos.
6. Verifique su respuesta para ver si es razonable: ¿tiene sentido su respuesta?
Ahora apliquemos esta estrategia de resolución de problemas a algunos ejemplos específicos.
Ejemplo 1.2
Una rueda de bicicleta giratoria
Un mecánico de bicicletas monta una bicicleta en el soporte de reparación e inicia la rotación de la rueda trasera desde el reposo hasta una velocidad angular final de $250 rpm$ en $5.00 s$. (a) Calcule la aceleración angular promedio en $rad / s^2$. (b) Si ahora golpea los frenos, causando una aceleración angular de $-87.3 rad / s^2$, ¿cuánto tiempo demora la rueda en detenerse?
Estrategia
La aceleración angular promedio se puede encontrar directamente desde su definición $\={α} = \dfrac{w_f - w_i}{Δt}$ dado que la velocidad angular final y el tiempo se dan.
Vemos que $w_f - w_i = 250 rev/s$ y $Δt$ es $5.00 s$. Para la parte (b), conocemos la aceleración angular y la velocidad angular inicial. Podemos encontrar el tiempo de parada usando la definición de aceleración angular promedio y resolviendo para $Δt$, produciendo $Δt = \frac{Δw}{α}$.
Solución
a. Ingresando información conocida en la definición de aceleración angular, obtenemos:
$$\={α} = \frac{Δw}{Δt} = \frac{250rpm}{5.00s}$$Como $Δω$ está en revoluciones por minuto ($rpm$) y queremos las unidades estándar de $rad / s^2$ para la aceleración angular, necesitamos convertir de $rpm$ a $rad / s$:
$Δw= 250 \frac{rev}{min} \cdot \frac{2π}{rev} \cdot \frac{1min}{60s} =26.2 \frac{rad}{s}$. Ingresando esta cantidad en la expresión para $α$, obtenemos.
$$α = \frac{Δw}{Δt} = \frac{26.2rad/s}{5.00s} = 5.24rad/s^2$$b. Aquí la velocidad angular disminuye de $26.2 rad / s$ ($250 rpm$) a cero, de modo que $Δω$ es $-26.2 rad / s$, y $α$ se da como $-87.3 rad / s^2$.
Así, $Δt = \dfrac{-26.2rad/s}{-87.3rad/s^2} = 0.300s$
Significado
Tenga en cuenta que la aceleración angular a medida que el mecánico hace girar la rueda es pequeña y positiva; toma $5 s$ para producir una velocidad angular apreciable. Cuando golpea el freno, la aceleración angular es grande y negativa. La velocidad angular rápidamente va a cero.
 Comprueba tu aprendizaje 1.1
Comprueba tu aprendizaje 1.1
(a) ¿Cuál es la aceleración angular promedio?
(b) ¿Cuál es la aceleración angular instantánea en cualquier momento durante los primeros $20 s$?

Ejemplo 1.3
Turbina eólica
Una turbina eólica () en un parque eólico se está cerrando para su mantenimiento. La turbina tarda $30 s$ en pasar de su velocidad angular operativa a una parada completa en la cual la función de velocidad angular es:
$$ω (t) = [(ts^{-1} - 30.0)^2 / 100.0] rad / s$$Si la turbina de la gira hacia la izquierda mirando hacia la página, (a) ¿cuáles son las direcciones de los vectores de aceleración y velocidad angular? (b) ¿Cuál es la aceleración angular promedio? (c) ¿Cuál es la aceleración angular instantánea en $t = 0.0, 15.0, 30.0s$?
Estrategia
a. Nos da el sentido de rotación de la turbina, que está en sentido antihorario en el plano de la página.
Usando la regla de la mano derecha (), podemos establecer las direcciones de los vectores de velocidad angular y aceleración.
b. Calculamos las velocidades angulares inicial y final para obtener la aceleración angular promedio.
c. Se nos da la forma funcional de la velocidad angular, por lo que podemos encontrar la forma funcional de la función de aceleración angular tomando su derivada con respecto al tiempo.
Solución
a. Dado que la turbina está girando en sentido antihorario, la velocidad angular $\overrightarrow{\bold{w}}$ señala fuera de la página. Pero dado que la velocidad angular está disminuyendo, la aceleración angular $\overrightarrow{α}$ apunta a la página, en el sentido opuesto a la velocidad angular.
b. La velocidad angular inicial de la turbina, configuración $t = 0$, es $ω = 9.0rad / s$. La velocidad angular final es cero, por lo que la aceleración angular promedio es
$$\={α} \frac{Δw}{Δt} = \frac{w - w_0}{t - t_0} = \frac{0 - 9.0 rad/s}{30.0 - 0 s} = -0.3rad/s^2$$c. Tomando la derivada de la velocidad angular con respecto al tiempo da:
$$α = \frac{dω}{dt} = (t-30)/50.0 rad/s^2$$ $α(0,0s) = -0.6rad/s^2$, $α(15,0s) = -0.3 rad/s^2$ y $α(30,0s)= 0 rad/s^2$Significado
De los cálculos de (a) y (b) encontramos que la aceleración angular $α$ y la aceleración angular promedio $α$ son negativas. La turbina tiene una aceleración angular en el sentido opuesto a su velocidad angular.
Ahora tenemos un vocabulario básico para discutir la cinemática rotacional de eje fijo y las relaciones entre variables rotacionales. Discutimos más definiciones y conexiones en la siguiente sección.

En la sección anterior, definimos las variables de rotación del desplazamiento angular, la velocidad angular y la aceleración angular. En esta sección, trabajamos con estas definiciones para derivar relaciones entre estas variables y usamos estas relaciones para analizar el movimiento de rotación de un cuerpo rígido alrededor de un eje fijo bajo una aceleración angular constante. Este análisis forma la base de la cinemática rotacional. Si la aceleración angular es constante, las ecuaciones de la cinemática rotacional se simplifican, similar a las ecuaciones de la cinemática lineal tratadas en Movimiento a lo largo de una Línea recta y Movimiento en dos y tres dimensiones. Entonces podemos usar este conjunto simplificado de ecuaciones para describir muchas aplicaciones en física e ingeniería donde la aceleración angular del sistema es constante. La cinemática rotacional es también un prerrequisito para la discusión de la dinámica rotacional más adelante en este capítulo.

Utilizando nuestra intuición, podemos comenzar a ver cómo las cantidades de rotación $θ$, $ω$, $α$ y $t$ se relacionan entre sí. Por ejemplo, vimos en la sección anterior que si un volante tiene una aceleración angular en la misma dirección que su vector de velocidad angular, su velocidad angular aumenta con el tiempo y también aumenta su desplazamiento angular. Por el contrario, si la aceleración angular es opuesta al vector de velocidad angular, su velocidad angular disminuye con el tiempo. Podemos describir estas situaciones físicas y muchas otras con un conjunto consistente de ecuaciones cinemáticas rotativas bajo una constante aceleración angular. El método para investigar el movimiento rotacional de esta manera se denomina cinemática del movimiento rotacional.
Para comenzar, notamos que si el sistema está girando bajo una aceleración constante, entonces la velocidad angular promedio sigue una relación simple porque la velocidad angular aumenta linealmente con el tiempo. La velocidad angular promedio es solo la mitad de la suma de los valores inicial y final:
A partir de la definición de la velocidad angular promedio, podemos encontrar una ecuación que relaciona la posición angular, la velocidad angular promedio y el tiempo:
$\={w}= \frac{Δθ}{Δt}$. Resolviendo para $θ$, tenemos:
donde hemos establecido $t_0 = 0$. Esta ecuación puede ser muy útil si conocemos la velocidad angular promedio del sistema. Entonces podríamos encontrar el desplazamiento angular en un período de tiempo dado. A continuación, encontramos una ecuación que relaciona $ω$, $α$ y $t$. Para determinar esta ecuación, comenzamos con la definición de aceleración angular:
$$α = \frac{dω}{dt}$$Reorganizamos esto para obtener $αdt = dω$ y luego integramos ambos lados de esta ecuación desde los valores iniciales hasta los valores finales, es decir, desde $t_0$ a $t$ y $ω_0$, $t_0$, $ω_f$. En un movimiento de rotación uniforme, la aceleración angular es constante por lo que se puede extraer de la integral, produciendo dos integrales definidas
$$α \int_{t_0}^t dt' = \int_{w_0}^{w_f} dθ$$Asumiendo que $t_0 = 0$, tenemos
$$αt = w_f - w_0$$Reordenando lo anterior obtenemos:
donde $ω_0$ es la velocidad angular inicial. La ecuación 1.11 es la contraparte rotacional de la ecuación de la cinemática lineal $v_f = v_0 + at$. Con la ecuación 1.11, podemos encontrar la velocidad angular de un objeto en cualquier momento especificado $t$ dada la velocidad angular inicial y la aceleración angular.
Hagamos ahora un tratamiento similar comenzando con la ecuación $ω = \frac{dθ}{dt}$. Lo reorganizamos para obtener $ωdt = dθ$ e integramos ambos lados de los valores iniciales a los valores finales de nuevo, teniendo en cuenta que la aceleración angular es constante y no tiene dependencia del tiempo. Sin embargo, esta vez, la velocidad angular no es constante (en general), por lo que sustituimos en lo que derivamos anteriormente:
$$\begin{split} \int_{t_0}^{t_f} w_0 dt + \int_{t_0}^{t_f} αt dt &= \int_{θ_0}^{θ_f} dθ = \left[w_0t' + α \left(\frac{(t')^2}{2}\right) \right]_{t_0}^{t_f} \\ &= w_0 + α \left( \frac{t^2}{2} \right) = θ_f - θ_0 \end{split}$$donde hemos establecido que $t_0 = 0$. Ahora reorganizamos para obtener
La ecuación 1.12 es la contraparte de rotación de la ecuación de la cinemática lineal encontrada en Movimiento a lo largo de una línea recta para la posición en función del tiempo. Esta ecuación nos da la posición angular de un cuerpo rígido giratorio en cualquier momento t dadas las condiciones iniciales (posición angular inicial y velocidad angular inicial) y la aceleración angular.Podemos encontrar una ecuación que sea independiente del tiempo resolviendo para t en la ecuación 1.11 y sustituyéndolo por la ecuación 1.12. La ecuación 1.12 se convierte
$$θ_f = θ_0 + w_0 \left(\frac{w_f - w_0}{α} \right) + \frac{1}{2} α \left(\frac{w_f - w_0}{α} \right)^2$$o
La ecuación 1.10 y la ecuación 1.13 describe la rotación del eje fijo para la aceleración constante y se resumen en la
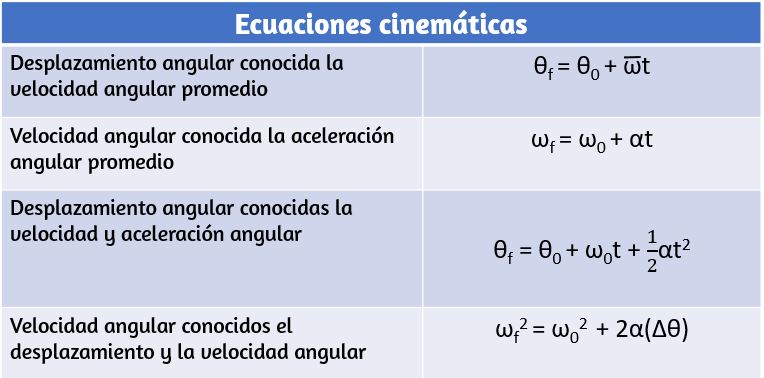
Ahora podemos aplicar las relaciones cinemáticas, clave para el movimiento rotatorio a algunos ejemplos simples para tener una idea de cómo las ecuaciones se pueden aplicar a las situaciones cotidianas.
Ejemplo 1.4
Cálculo de la aceleración de un carrete de pesca
Un pescador de aguas profundas engancha un gran pez que nada desde el bote, tirando de la cuerda de pescar de su carrete de pesca. Todo el sistema está inicialmente en reposo, y la línea de pesca se desenrolla del carrete a un radio de $4.50 cm$ desde su eje de rotación. Al carrete se le da una aceleración angular de $110rad / s^2$ por $2.00 s$ ().
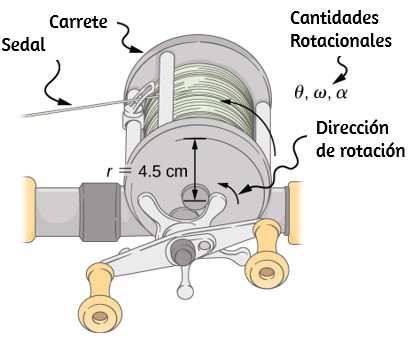
(a) ¿Cuál es la velocidad angular final del carrete después de $2 s$?
(b) ¿Cuántas revoluciones hace el carrete?
Estrategia
Identifique los conocimientos y compare con las ecuaciones cinemáticas para la aceleración constante. Busque la ecuación apropiada que se pueda resolver para lo desconocido, usando los conocimientos que se dan en la descripción del problema.
Solución
a) Nos dan $α$ y $t$ y queremos determinar $ω$. La ecuación más directa para usar es $w_f = w_0 + αt$, ya que todos los términos son conocidos además de la variable desconocida que estamos buscando. Se nos da que $w_0 = 0$ (comienza desde el reposo), entonces
$$w_f = 0 + 110 \frac{rad}{s^2} (2.00s) = 220 \frac{rad}{s}$$b) Se nos pide que encontremos el número de revoluciones. Debido a que $1rev = 2π rad$, podemos encontrar el número de revoluciones encontrando $θ$ en radianes. Nos dan $α$ y $t$, y sabemos que $w_0$ es cero, entonces podemos obtener $θ$ usando
$$θ_f = θ_0 + w_0 t + \frac{1}{2}αt^2$$ $$θ_f = 0 + 0 + (0.500) \left(110 \frac{rad}{s^2} \right)(2s)^2 = 220 rad$$La conversión de radianes a revoluciones da
Número de revoluciones $= (220rad) \dfrac{1rev}{2π rad} = 35.0 rev$
Significado
Este ejemplo ilustra que las relaciones entre cantidades rotacionales son altamente análogas a aquellas entre cantidades lineales. Las respuestas a las preguntas son realistas. Después de desenrollar durante dos segundos, se encuentra que el carrete gira a $220 rad / s$, que es $2100 rpm$.
En el ejemplo anterior, consideramos un carrete de pesca con una aceleración angular positiva. Ahora consideremos qué sucede con una aceleración angular negativa.
Ejemplo 1.5
Cálculo de la duración cuando el carrete de pesca disminuye y se detiene. Ahora el pescador aplica un freno al carrete giratorio, logrando una aceleración angular de $-300rad/s^2$. ¿Cuánto tiempo demora el carrete en detenerse?
Estrategia
Se nos pide que encontremos el tiempo t para que el carrete se detenga. Las condiciones iniciales y finales son diferentes a las del problema anterior, que involucró el mismo carrete de pesca. Ahora vemos que la velocidad angular inicial es $w_0 = 220rad/s$ y la velocidad angular final $ω$ es cero. La aceleración angular se da como $α = -300rad/s^2$. Al examinar las ecuaciones disponibles, vemos todas las cantidades pero $t$ se conocen en $w_f = w_0 + αt$, por lo que es más fácil usar esta ecuación.
Solución
La ecuación establece $$w_f = w_0 + αt$$
Resolvemos la ecuación algebraicamente para $t$ y luego sustituimos los valores conocidos como de costumbre, produciendo
$$t = \frac{w_f - w_0}{α} = \frac{0 - 220.0 rad/s}{-300.0 rad/s^2} = 0.733s$$Explicación
Tenga en cuenta que se debe tener cuidado con los signos que indican las direcciones de varias cantidades. Además, tenga en cuenta que el tiempo para detener el carrete es
bastante pequeño porque la aceleración es bastante grande. Las líneas de pesca a veces se rompen debido a las aceleraciones involucradas, y los pescadores a menudo dejan que los peces naden por un tiempo antes de aplicar los frenos en el carrete. Un pez cansado es más lento, requiere una aceleración más pequeña.

 Comprueba tu aprendizaje 1.2
Comprueba tu aprendizaje 1.2
Ejemplo 1.6
Aceleración angular de una hélice
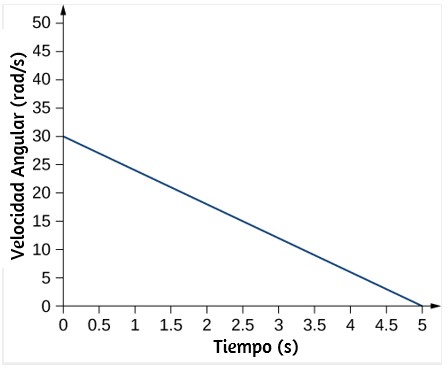
La muestra un gráfico de la velocidad angular de una hélice en un avión en función del tiempo. Su velocidad angular comienza en 30 rad/s y cae linealmente a 0 rad/s en el transcurso de 5 segundos. (a) Encuentre la aceleración angular del objeto y verifique el resultado usando las ecuaciones cinemáticas. (b) Encuentre el ángulo a través del cual gira la hélice durante estos 5 segundos y verifique su resultado usando las ecuaciones cinemáticas.
Estrategia
a) Dado que la velocidad angular varía linealmente con el tiempo, sabemos que la aceleración angular es constante y no depende de la variable de tiempo. La aceleración angular es la pendiente del gráfico de velocidad angular vs. tiempo, $α = \frac{dω}{dt}$. Para calcular la pendiente, leemos directamente de la , y vemos que $w_0 = 30rad / s$ en $t = 0 s$ y $w_f = 0 rad/s$ en $t = 5 s$. Entonces, podemos verificar el resultado usando $w = w_0 + αt$.
b) Usamos la ecuación $w = \frac{dθ}{dt}$; dado que la derivada en el tiempo del ángulo es la velocidad angular, podemos encontrar el desplazamiento angular integrando la velocidad angular, que de la figura significa tomar el área bajo el gráfico de velocidad angular. En otras palabras:
$$\int_{θ_0}^{θ_f} dθ = θ_f - θ_0 = \int {t_0}^{t_f} w(t)dt$$Luego usamos las ecuaciones cinemáticas para la aceleración constante para verificar el resultado.
Solución
a) Calculando la pendiente, obtenemos
$$α = \frac{w - w_0}{t - t_0} = \frac{(0 - 30.0)rad/s}{(5.0 -0)s} = -6.0 rad/s^2$$Vemos que esta es exactamente la Ecuación 1.11 con una pequeña reorganización de los términos
b) Podemos encontrar el área debajo de la curva calculando el área del triángulo rectángulo, como se muestra en la
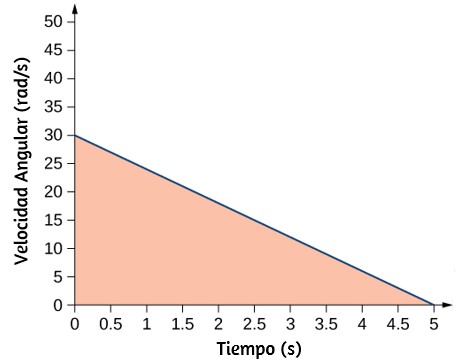
$Δθ =$ área (triángulo)
$$Δθ = \frac{1}{2}(30rad/s)(5s)= 75 rad$$Verificamos la solución usando la Ecuación 1.12:
$$θ_f = θ_0 + w_0 t + \frac{1}{2} αt^2$$Asumiendo que $θ_0 = 0$, tenemos
$$\begin{split} θ_f &= (30.0rad/s)(5s)+ \frac{1}{2} (-6.0rad/s^2)(5.0rad/s)^2 \\ &= 150.0 - 75.0 = 75.0 rad \end{split}$$Esto verifica la solución encontrada al encontrar el área debajo de la curva.
Explicación
Vemos en la parte (b) que existen enfoques alternativos para analizar la rotación del eje fijo con aceleración constante. Comenzamos con un enfoque gráfico y verificamos la solución utilizando las ecuaciones cinemáticas de rotación. Como $α = \frac{dω}{dt}$, podríamos hacer el mismo análisis gráfico en una curva de aceleración angular vs. tiempo. El área bajo una curva $α$-vs-$t$ nos da el cambio en la velocidad angular. Como la aceleración angular es constante en esta sección, este es un ejercicio directo.
En la rotación del eje fijo se presentan otras variables que trabajaremos en los próximos apartados. Por ahora, te presentamos la siguiente escena interactiva diseñada por Denis Radin, la cual hemos modificado para incorporar dos piezas adicionales. Con el puntero del ratón rota las hélices o la turbina y observa cómo la inercia juega un papel importante en la rotación.
Te sugerimos interactuar con la escena en una ventana ampliada.
En esta sección, relacionamos cada una de las variables de rotación con las variables de traslación definidas en Movimiento a lo largo de una línea recta y Movimiento en dos y tres dimensiones. Esto completará nuestra capacidad de describir rotaciones de cuerpo rígido.
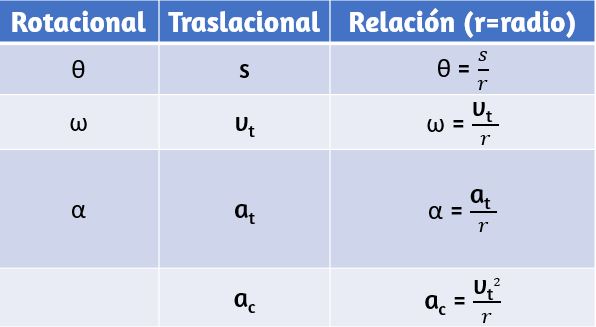
En variables de rotación, presentamos variables angulares. Si comparamos las definiciones de rotación con las definiciones de variables cinemáticas lineales del movimiento a lo largo de la línea recta y el movimiento en dos y tres dimensiones, encontramos que hay un mapeo de las variables lineales con las rotacionales. La posición lineal, la velocidad y la aceleración tienen sus equivalentes rotativos, como podemos ver cuando los escribimos uno al lado del otro como se muestra en la siguiente .
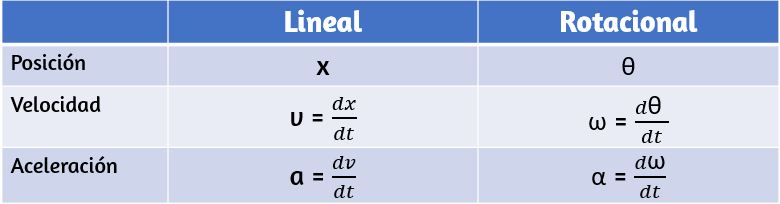
Comparemos las variables lineales y rotacionales individualmente. La variable lineal de posición tiene unidades físicas de metros, mientras que la variable de posición angular tiene unidades adimensionales de radianes, como se puede ver en la definición de $θ = sr$, que es la relación de dos longitudes. La velocidad lineal tiene unidades de $m/s$, y su contraparte, la velocidad angular, tiene unidades de $rad/s$. En Variables de rotación, vimos en el caso del movimiento circular que la velocidad tangencial lineal de una partícula a un radio $r$ del eje de rotación está relacionada con la velocidad angular por la relación $v_t = rω$. Esto también podría aplicarse a puntos en un cuerpo rígido que gira alrededor de un eje fijo. Aquí, consideramos solo movimiento circular. En movimientos circulares, uniformes y no uniformes, existe una aceleración centrípeta (Movimiento en Dos y Tres Dimensiones). El vector de aceleración centrípeta apunta hacia adentro desde la partícula que ejecuta el movimiento circular hacia el eje de rotación. La derivación de la magnitud de la aceleración centrípeta se da en movimiento en dos y tres dimensiones. A partir de esa derivación, se encontró que la magnitud de la aceleración centrípeta era:
donde $r$ es el radio del círculo. Por lo tanto, en un movimiento circular uniforme cuando la velocidad angular es constante y la aceleración angular es cero, tenemos una aceleración lineal, es decir, aceleración centrípeta, ya que la velocidad tangencial en la ecuación 1.14 es una constante. Si el movimiento circular no uniforme está presente, el sistema rotativo tiene una aceleración angular, y tenemos tanto una aceleración centrípeta lineal que está cambiando (por que $v_t$ está cambiando) como una aceleración tangencial lineal.
Estas relaciones se muestran en la donde mostramos las aceleraciones centrípeta y tangencial para el movimiento circular uniforme y no uniforme.
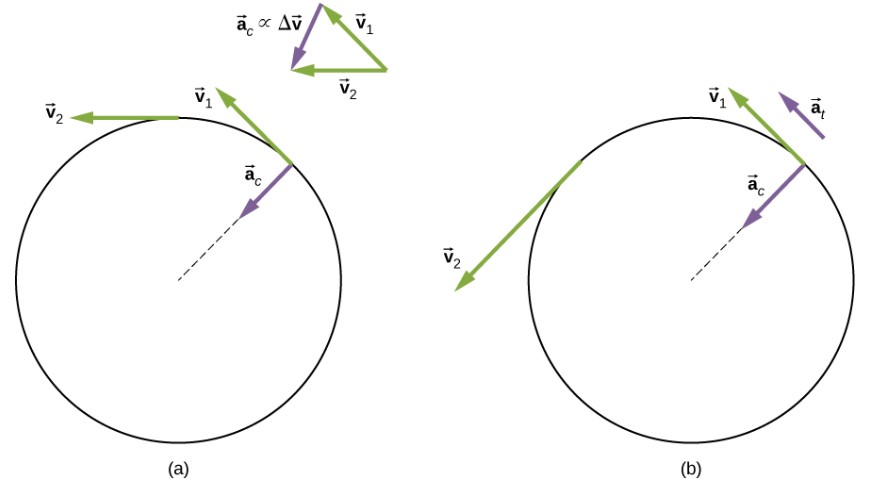
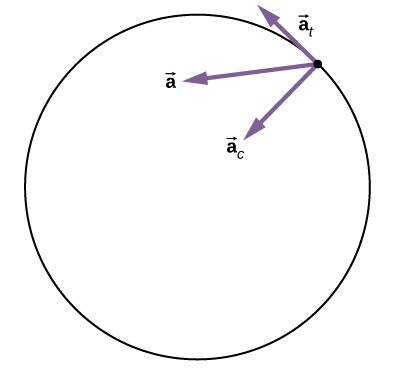
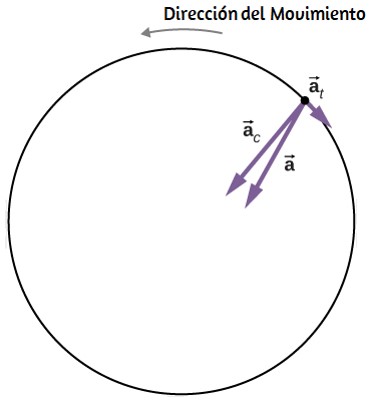
La aceleración centrípeta se debe al cambio en la dirección de la velocidad tangencial, mientras que la aceleración tangencial se debe a cualquier cambio en la magnitud de la velocidad tangencial. Los vectores de aceleración tangencial y centrípeta $\overrightarrow{\bold{a}}_t$ y $\overrightarrow{\bold{a}}_c$ son siempre perpendiculares entre sí, como se ve en la . Para completar esta descripción, podemos asignar un vector de aceleración lineal total a un punto en un cuerpo rígido giratorio o una partícula que ejecuta un movimiento circular a un radio $r$ desde un eje fijo. El vector de aceleración lineal total $\overrightarrow{\bold{a}}$ es la suma vectorial de las aceleraciones centrípeta y tangencial.
El vector de aceleración lineal total en el caso del movimiento circular no uniforme apunta en un ángulo entre los vectores de aceleración tangencial y centrípeta, como se muestra en la . Desde $\overrightarrow{\bold{a}}_c ⊥ \overrightarrow{\bold{a}}_t$, la magnitud de la aceleración lineal total es:
Ten en cuenta que si la aceleración angular es cero, la aceleración lineal total es igual a la aceleración centrípeta.
La muestra la aceleración lineal total, tangencial y centrípeta.
En la siguiente escena interactiva, diseñada por Andrew Duffy, puedes observar una comparación de la aceleración constante en cinemática rotacional y de una dimensión.
En la anterior escena, puedes comparar el movimiento de una bola, que está influenciada solo por la gravedad, con la de un disco, que tiene una aceleración angular constante dirigida hacia la izquierda. Puedes ver el diagrama de movimiento de la bola, con la posición marcada a intervalos de $0,5 s$. También puedes ver el diagrama de movimiento del disco, con la posición marcada a intervalos de $0,5 s$. Luego, puedes ver gráficos de la posición, velocidad y aceleración de la bola, todo en función del tiempo, o gráficos de la posición angular, velocidad angular y aceleración angular del disco, también en función del tiempo.
Podemos ver dos relaciones entre el movimiento rotacional y traslacional.
1. En términos generales, las ecuaciones cinemáticas lineales tienen sus equivalentes rotacionales. La enumera las cuatro ecuaciones cinemáticas lineales y la correspondiente contraparte rotacional.

Los dos conjuntos de ecuaciones se parecen entre sí, pero describen dos situaciones físicas diferentes, es decir, rotación y traslación.
2. La segunda correspondencia tiene que ver con relacionar variables lineales y rotacionales en el caso especial de movimiento circular. Esto se muestra en la , donde en la tercera columna, hemos enumerado la ecuación de conexión que relaciona la variable lineal con la variable de rotación. Las variables de rotación de velocidad angular y aceleración tienen subíndices que indican su definición en movimiento circular.
Ejemplo 1.7
Aceleración lineal de una centrífuga
Una centrífuga tiene un radio de $20 cm$ y acelera desde una velocidad máxima de rotación de $10.000 rpm$ hasta descansar en $30$ segundos bajo una aceleración angular constante. Está girando en sentido antihorario. ¿Cuál es la magnitud de la aceleración total de un punto en la punta de la centrífuga en $t = 29.0s$? ¿Cuál es la dirección del vector de aceleración total?
Estrategia
Con la información dada, podemos calcular la aceleración angular, que luego nos permitirá encontrar la aceleración tangencial. Podemos encontrar la aceleración centrípeta en $t = 0$ calculando la velocidad tangencial en este momento. Con las magnitudes de las aceleraciones, podemos calcular la aceleración lineal total. A partir de la descripción de la rotación en el problema, podemos dibujar la dirección del vector de aceleración total.
Solución
La aceleración angular es
$$α = \frac{w - w_0}{t} = \frac{0 - (1.0x10^4) 2π/60.0s (rad/s)}{30.0s} = -34.9 rad/s^2$$Por lo tanto, la aceleración tangencial es:
$$a_t = rα = 0.2m (-34.9 rad/s^2) = -7.0 m/s^2$$La velocidad angular en $t = 29.0s$ es:
$$w = w_0 + αt = 1.0 × 10^4(\frac{2π}{60.0s})+ (-34.9 rad/s^2)(29.0s)$$ $$w = 1047.2 rad/s - 1012.71 rad/s = 35.1 rad/s$$Por lo tanto, la velocidad tangencial en $t = 29.0s$ es:
$$v_t = rw = 0.2m (35.1rad/s)= 7.0 m/s$$Ahora podemos calcular la aceleración centrípeta en $t = 29.0s$
$$a_c= \frac{v^2 }{r} = \frac{(7.0 m/s)^2}{0.2 m}= 245.1 m/s^2$$ $$a = \sqrt{x^2}$$Dado que la centrífuga tiene una aceleración angular negativa, se está desacelerando. El vector de aceleración total es como se muestra en la . El ángulo con respecto al vector de aceleración centrípeta es:
$$θ = tan^{-1} \frac{-7.0}{245.0} = -1.6º$$El signo negativo significa que el vector de aceleración total está en ángulo hacia la dirección de las agujas del reloj.
Explicación
En la , vemos que el vector de aceleración tangencial es opuesto a la dirección de rotación. La magnitud de la aceleración tangencial es mucho menor que la aceleración centrípeta, por lo que el vector de aceleración lineal total formará un ángulo muy pequeño con respecto al vector de aceleración centrípeta.
 Comprueba tu aprendizaje 1.3
Comprueba tu aprendizaje 1.3
Hasta ahora en este capítulo, hemos estado trabajando con la cinemática rotacional: la descripción del movimiento para un cuerpo rígido giratorio con un eje de rotación fijo. En esta sección, definimos dos nuevas cantidades que son útiles para analizar propiedades de objetos rotativos: momento de inercia y energía cinética rotacional. Con estas propiedades definidas, tendremos dos herramientas importantes que necesitamos para analizar la dinámica rotacional.
Cualquier objeto en movimiento tiene energía cinética. Sabemos cómo calcular esto para un cuerpo sometido a movimiento de traslación, pero ¿qué tal si un cuerpo rígido sufre rotación?. Esto puede parecer complicado porque cada punto en el cuerpo rígido tiene una velocidad diferente. Sin embargo, podemos hacer uso de la velocidad angular, que es la misma para todo el cuerpo rígido, para expresar la energía cinética de un objeto giratorio. La muestra un ejemplo de un cuerpo giratorio muy enérgico: una muela eléctrica propulsada por un motor. Las chispas están volando, y el ruido y la vibración se generan cuando la piedra de afilar hace su trabajo. Este sistema tiene una energía considerable, en parte en forma de calor, luz, sonido y vibración. Sin embargo, la mayor parte de esta energía está en forma de energía cinética de rotación.
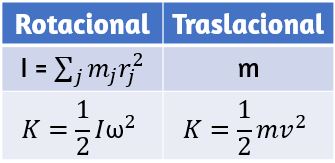
La energía en movimiento rotacional no es una nueva forma de energía; más bien, es la energía asociada con el movimiento de rotación, lo mismo que la energía cinética en el movimiento de traslación. Sin embargo, debido a que la energía cinética viene dada por $K = \frac{1}{2} \, m \, v^2$, y la velocidad es una cantidad diferente para cada punto de un cuerpo giratorio alrededor de un eje, tiene sentido encontrar una forma de escribir energía cinética en términos de la variable $ω$, que es el mismo para todos los puntos en un cuerpo giratorio rígido.

Para una sola partícula que gira alrededor de un eje fijo, esto es fácil de calcular. Podemos relacionar la velocidad angular con la magnitud de la velocidad de traslación usando la relación $v_t = ωr$, donde $r$ es la distancia de la partícula desde el eje de rotación y $v_t$ es su velocidad tangencial. Sustituyendo en la ecuación por energía cinética, encontramos:
$$K = \frac{1}{2} m v^2 = \frac{1}{2} m (wr)^2 = \frac{1}{2} (mr^2)w^2$$En el caso de un cuerpo giratorio rígido, podemos dividir cualquier cuerpo en un gran número de masas más pequeñas, cada una con una masa $m_j$ y distancia al eje de rotación $r_j$, de modo que la masa total del cuerpo sea igual a la suma de las masas individuales $M = \sum m_j$.
Cada masa más pequeña tiene velocidad tangencial $v_j$, donde hemos soltado el subíndice $t$ por el momento. La energía cinética total del cuerpo giratorio rígido es:
$$K = \sum \frac{1}{2} m_j v^2_j = \sum \frac{1}{2}m_j(r_jω_j)^2$$y dado que $ω_j = ω$ para todas las masas,
Las unidades de la ecuación 1.16 son joules ($J$). La ecuación en esta forma es completa, pero incómoda; necesitamos encontrar una manera de generalizarlo.
Si comparamos la ecuación 1.16 con la forma en que escribimos la energía cinética en trabajo y energía cinética, ($\frac{1}{2} mv^2$), esto sugiere que tenemos una nueva variable de rotación para agregar a nuestra lista de nuestras relaciones entre las variables de rotación y traslacional. La cantidad $\sum m_jr_j^2$ es la contraparte de la masa en la ecuación de la energía cinética de rotación. Este es un nuevo término importante para el movimiento de rotación. Esta cantidad se denomina momento de inercia $I$, con unidades de $kg m^2$:
Por ahora, dejamos la expresión en forma de suma, que representa el momento de inercia de un sistema de partículas puntuales que giran alrededor de un eje fijo. Observamos que el momento de inercia de una sola partícula puntual alrededor de un eje fijo es simplemente $mr^2$, siendo r la distancia desde la partícula puntual al eje de rotación. En la siguiente sección, exploramos la forma integral de esta ecuación, que puede usarse para calcular el momento de inercia de algunos cuerpos rígidos de forma regular.
El momento de inercia es la medida cuantitativa de la inercia rotacional, al igual que en el movimiento traslacional, y la masa es la medida cuantitativa de la inercia lineal; es decir, cuanto más masivo es un objeto, más inercia tiene y mayor es su resistencia para cambiar en velocidad lineal. De manera similar, cuanto mayor es el momento de inercia de un cuerpo rígido o sistema de partículas, mayor es su resistencia al cambio en la velocidad angular alrededor de un eje de rotación fijo. Es interesante ver cómo el momento de inercia varía con $r$, la distancia al eje de rotación de las partículas de masa en la ecuación 1.17. Los cuerpos rígidos y los sistemas de partículas con más masa concentrada a una mayor distancia del eje de rotación tienen mayores momentos de inercia que los cuerpos y sistemas de la misma masa, pero concentrados cerca del eje de rotación. De esta manera, podemos ver que un cilindro hueco tiene más inercia rotacional que un cilindro sólido de la misma masa cuando gira alrededor de un eje a través del centro. Sustituyendo la ecuación 1.17 en la ecuación 10.16, la expresión de la energía cinética de un cuerpo rígido giratorio se convierte en:
Vemos a partir de esta ecuación que la energía cinética de un cuerpo rígido giratorio es directamente proporcional al momento de inercia y al cuadrado de la velocidad angular. Esto se explota en dispositivos de almacenamiento de energía de volante, que están diseñados para almacenar grandes cantidades de energía cinética de rotación. Muchos fabricantes de automóviles ahora están probando dispositivos de almacenamiento de energía volante en sus automóviles, como el volante, o el sistema de recuperación de energía cinética, que se muestra en la .
Las cantidades rotacionales y de traslación para la energía cinética y la inercia se resumen en la .

Ejemplo 1.8
Momento de inercia de un sistema de partículas
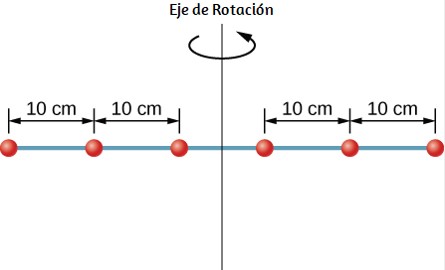
Seis arandelas pequeñas están espaciadas a $10 cm$ de distancia en una varilla de masa despreciable y de $0,5 m$ de longitud. La masa de cada arandela es de $20 g$. La barra gira alrededor de un eje ubicado a $25 cm$, como se muestra en la . (a) ¿Cuál es el momento de inercia del sistema? (b) Si se quitan las dos arandelas más cercanas al eje, ¿cuál es el momento de inercia de las cuatro arandelas restantes? (c) Si el sistema con seis arandelas gira a $5 rev/s$, ¿cuál es su energía cinética de rotación?.
Estrategia
a) Usamos la definición de momento de inercia para un sistema de partículas y realizamos la suma para evaluar esta cantidad. Las masas son todas iguales, así que podemos tirar esa cantidad delante del símbolo de suma.
b) Hacemos un cálculo similar.
c) Insertamos el resultado de (a) en la expresión de energía cinética de rotación
Solución
a)
$$\begin{split} I &= \sum m_jr_j^2 \\ &= (0.02 kg)(2×(0.25 m)^2 + 2×(0.15 m)^2 + 2×(0.05 m)^2) \\ &= 0.0035 kg \cdot m^2 \end{split}$$b)
$$\begin{split} I &= \sum m_jr_j^2 \\ &= (0.02 kg)(2×(0.25 m)^2 + 2×(0.15 m)^2 \\ &= 0.0034 kg \cdot m^2 \end{split}$$c)
$$K = \frac{1}{2}Iω^2 = 12(0.0035 kg \cdot m ^2)(5.0×2π rad/s)^2 = 1.73 J$$Explicación
Podemos ver las contribuciones individuales al momento de inercia. Las masas cercanas al eje de rotación tienen una contribución muy pequeña. Cuando los quitamos, tuvo un efecto muy pequeño en el momento de inercia.
En la siguiente escena interactiva, diseñada por Juan Guillermo Rivera Berrío, presentamos una simulación del problema anterior, en la cual puedes cambiar la separación de las arandelas, quitar o poner las arandelas más cercanas al eje y detener o reanudar la rotación.
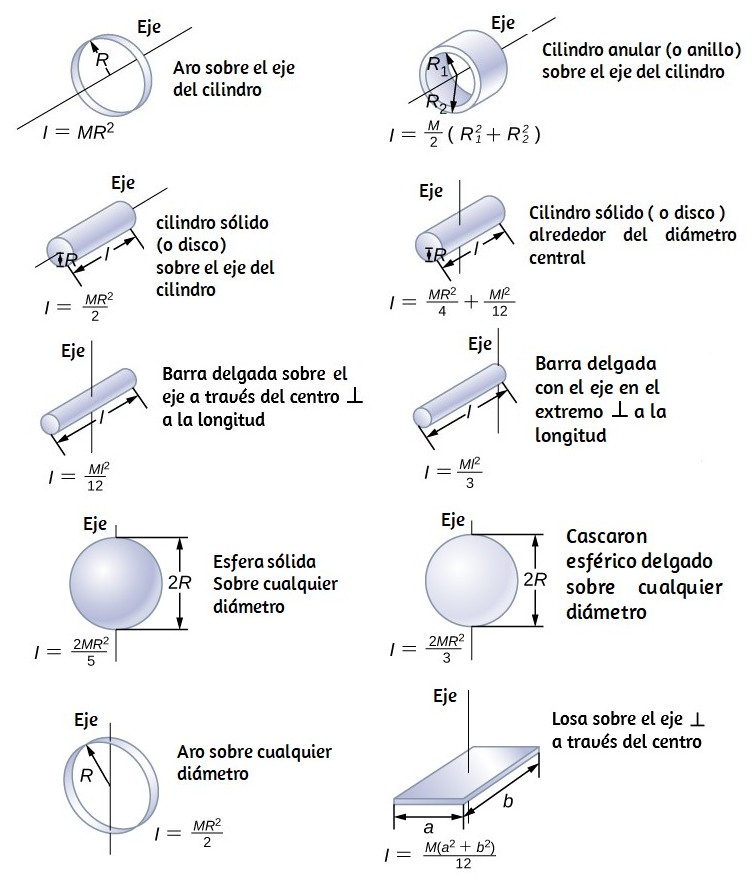
En la siguiente sección, generalizamos la ecuación de suma para partículas puntuales y desarrollamos un método para calcular momentos de inercia para cuerpos rígidos. Por ahora, sin embargo, la da valores de inercia rotacional para formas de objetos comunes alrededor de ejes especificados.
Ahora apliquemos las ideas de la energía cinética rotacional y el momento de la tabla de inercia para tener una idea de la energía asociada con unos pocos objetos rotativos. Los siguientes ejemplos también lo ayudarán a sentirse cómodo usando estas ecuaciones. Primero, veamos una estrategia general de resolución de problemas para la energía rotacional.
Estrategia de resolución de problemas: energía rotacional
1. Determine que la energía o el trabajo está involucrado en la rotación.
2. Determine el sistema de interés. Un boceto generalmente ayuda.
3. Analice la situación para determinar los tipos de trabajo y energía involucrados.
4. Si no hay pérdidas de energía debido a la fricción y otras fuerzas no conservativas, la energía mecánica se conserva, es decir: $K_i + U_i = K_f + U_f$
5. Si hay fuerzas no conservativas presentes, la energía mecánica no se conserva y otras formas de energía, como el calor y la luz, pueden entrar o salir del sistema. Determine cuáles son y calcúlelos según sea necesario.
6. Eliminar términos siempre que sea posible para simplificar el álgebra.
7. Evalúe la solución numérica para ver si tiene sentido en la situación física presentada en la redacción del problema.
Ejemplo 1.9
Cálculo de las energías de los helicópteros
Un pequeño helicóptero de rescate típico tiene cuatro hélices: cada una tiene $4.00 m$ de largo y una masa de $50.0 kg$, . Las hélices se pueden aproximar como barras delgadas que giran alrededor de un extremo de un eje perpendicular a su longitud. El helicóptero tiene una masa total cargada de $1000 kg$. (a) Calcule la energía cinética de rotación en las hélices cuando giran a $300 rpm$. (b) Calcule la energía cinética de traslación del helicóptero cuando vuela a $20.0 m / s$, y compárelo con la energía de rotación en las hélices.

Estrategia
Las energías cinéticas de rotación y traslación se pueden calcular a partir de sus definiciones. La redacción del problema proporciona todas las constantes necesarias para evaluar las expresiones de las energías cinéticas de rotación y translación.
Solución
a. La energía cinética de rotación es: $$K = \frac{1}{2}Iω^2$$
Debemos convertir la velocidad angular en radianes por segundo y calcular el momento de inercia antes de que podamos encontrar $K$. La velocidad angular $ω$ es:
$$ω = \frac{300 rev}{1.00 min} \frac{2π rad}{1 rev}\frac{1.00 min}{60.0s} = 31.4 rad/s$$El momento de inercia de una hélice es el de una varilla delgada que gira alrededor de su extremo, enumerada en la . El momento total $I$ es cuatro veces este momento de inercia porque hay cuatro hélices. Así,
$$I = 4\frac{Ml^2}{3}= 4×\frac{(50.0 kg)(4.00 m)^2}{3} = 1067.0 k \cdot gm^2$$Ingresando $ω$ y $I$ en la expresión de la energía cinética de rotación da
$$K = 0.5(1067 kg \cdot m^2)(31.4 rad/s)^2 = 5.26×105 J$$b. Ingresando los valores dados en la ecuación para la energía cinética de la traducción, obtenemos:
$$K = \frac{1}{2}mv^2 = (0.5)(1000.0 kg)(20.0 m/s)^2 = 2.00×10^5J$$Para comparar energías cinéticas, tomamos la proporción de energía cinética de traslación a energía cinética de rotación. Esta relación es:
$$\frac{2.00×10^5J}{5.26×10^5J} = 0.380$$Explicación
La relación de energía de traslacional y la energía cinética de rotación es solo $0.380$. Esta relación nos dice que la mayor parte de la energía cinética del helicóptero está en sus hélices giratorias.
Ejemplo 1.10
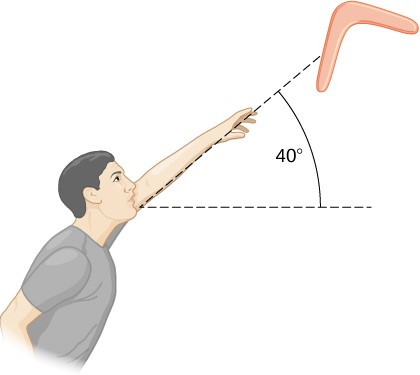
Energía en un Boomerang
Una persona arroja un boomerang al aire con una velocidad de $30.0 m / s$ en un ángulo de $40.0°$ con respecto a la horizontal . Tiene una masa de $1.0 kg$ y está girando a $10.0 rev / s$. El momento de inercia del boomerang se da como $I = \frac{1}{12}mL^2$ donde $L = 0.7m$. (a) ¿Cuál es la energía total del boomerang cuando sale de la mano? (b) ¿Qué tan alto va el bumerang desde la elevación de la mano, despreciando la resistencia del aire?
Estrategia
Usamos las definiciones de energía cinética rotacional y lineal para encontrar la energía total del sistema. El problema indica que debemos despreciar la resistencia del aire, por lo que no debemos preocuparnos por la pérdida de energía. En la parte (b), usamos la conservación de energía mecánica para encontrar la altura máxima del boomerang.
Solución
a. Momento de inercia:
$$I = \frac{1}{12}mL^2 = \frac{1}{12}(1.0 kg)(0.7 m)^2 = 0.041 kg \cdot m^2$$Velocidad angular:
$$ω = (10.0rev/s)(2π)= 62.83 rad/s$$La energía cinética de rotación es por lo tanto
$$K_R = \frac{1}{2}(0.041 kg \cdot m^2)(62.83 rad/s)^2 = 80.93 J$$La energía cinética de traslación es:
$$K_T = \frac{1}{2}mv^2=\frac{1}{2}(1.0 kg)(30.0 m/s)^2= 450.0 J$$Por lo tanto, la energía total en el boomerang es:
$$K_{\textsf{total}} = K_R + K_T = 80.93 + 450.0 = 530.93 J$$b. Usamos la conservación de energía mecánica. Como el boomerang se lanza con un ángulo, necesitamos escribir las energías totales del sistema en términos de sus energías cinéticas lineales usando la velocidad en las direcciones $x$ e $y$. La energía total cuando el boomerang sale de la mano es:
$$E_{\textsf{Antes}} = \frac{1}{2}mv^2_x + \frac{1}{2}mv^2_y + \frac{1}{2}Iω^2$$La energía total a la altura máxima es:
$$E_{\textsf{Final}} = \frac{1}{2}mv^2_x + \frac{1}{2}Iω^2 + mgh$$Por conservación de la energía mecánica, $E_{\textsf{Antes}} = E_{\textsf{Final}}$, entonces tenemos, después de cancelar los términos semejante
$$\frac{1}{2}mv^2_y = mgh$$Dado que $v_y = 30.0 m/s(sen40°) = 19.28 m/s$, encontramos
$$h = \frac{ (19.28 m/s)^2}{2(9.8 m/s^2)} = 18.97 m$$Explicación
En la parte (b), la solución demuestra cómo la conservación de energía es un método alternativo para resolver un problema que normalmente se resolvería utilizando la cinemática. En ausencia de resistencia al aire, la energía cinética de rotación no era un factor en la solución para la altura máxima.
 Comprueba tu aprendizaje 1.4
Comprueba tu aprendizaje 1.4
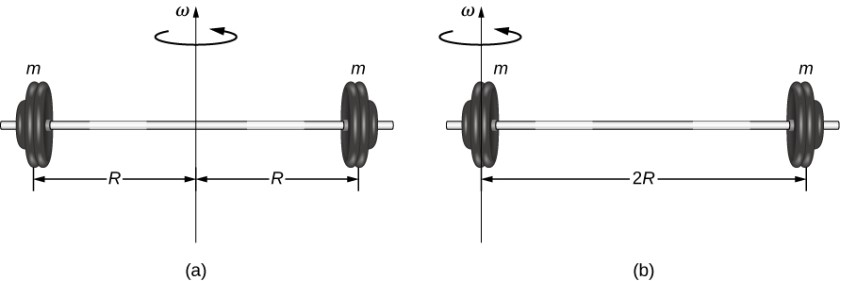
Definimos el momento de inercia $I$ de un objeto como $I = \sum m_ir^2_i$ para todas las masas de puntos que componen el objeto. Como $r$ es la distancia al eje de rotación de cada masa que forma el objeto, el momento de inercia para cualquier objeto depende del eje elegido. Para ver esto, tomemos un ejemplo simple de dos masas al final de una varilla sin masa (insignificantemente pequeña) y calculemos el momento de inercia alrededor de dos ejes diferentes. En este caso, la suma sobre las masas es simple porque las dos masas al final de la barra se pueden aproximar como masas puntuales, y la suma, por lo tanto, tiene solo dos términos.
En el caso del eje en el centro de la barra, cada una de las dos masas $m$ está a una distancia $R$ lejos del eje, dando un momento de inercia de $$I_1 = mR^2 + mR^2 = 2mR^2$$
En el caso del eje al final de la barra, que pasa por una de las masas, el momento de inercia es
$$I_2 = m(0)^2 + m(2R)^2 = 4mR^2$$A partir de este resultado, podemos concluir que es dos veces más difícil rotar la barra con respecto al extremo que sobre su centro.
En este ejemplo, tuvimos dos masas puntuales y la suma fue simple de calcular. Sin embargo, para tratar con objetos que no son puntuales, debemos pensar cuidadosamente sobre cada uno de los términos en la ecuación. La ecuación nos pide que sumemos cada "porción de masa" a cierta distancia del eje de rotación. Pero, ¿qué significa exactamente cada "porción de masa"? Recordemos que en nuestra derivación de esta ecuación, cada porción de masa tenía la misma magnitud de velocidad, lo que significa que toda la porción tenía que tener una sola distancia r con respecto al eje de rotación. Sin embargo, esto no es posible a menos que tomemos una porción de masa infinitesimalmente pequeña, como se muestra en la .
La necesidad de usar una cantidad de masa infinitamente pequeña dm sugiere que podemos escribir el momento de inercia evaluando una integral sobre masas infinitesimales en lugar de hacer una suma discreta sobre masas finitas:
$I = \sum m_ir_i^2$ se convierte $I = \int r^2dm$ $(1.19)$
Esto, de hecho, es la forma que necesitamos para generalizar la ecuación para formas complejas. Lo mejor es trabajar con ejemplos específicos en detalle para tener una idea de cómo calcular el momento de inercia para formas específicas. Este es el enfoque de la mayor parte del resto de esta sección.
Una varilla delgada y uniforme con un eje a través del centro
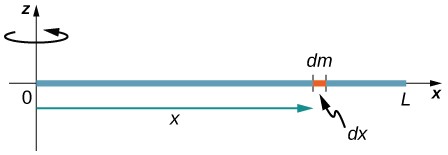
Considere una varilla delgada uniforme (densidad y forma) de masa $M$ y longitud $L$, como se muestra en la . Queremos una varilla delgada para que podamos asumir que el área de la sección transversal de la varilla es pequeña y la varilla puede considerarse como una cadena de masas a lo largo de una línea recta unidimensional. En este ejemplo, el eje de rotación es perpendicular a la varilla y pasa por el punto medio para simplificar. Nuestra tarea es calcular el momento de inercia sobre este eje. Orientamos los ejes para que el eje $z$ sea el eje de rotación y el eje $x$ pase a lo largo de la varilla, como se muestra en la figura. Esta es una opción conveniente porque podemos integrarnos a lo largo del eje $x$.
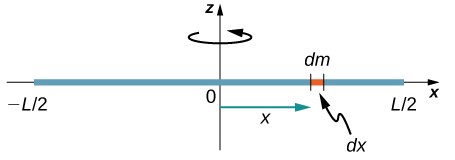
Definimos $dm$ como un pequeño elemento de masa que forma la barra. El momento de inercia es una integral sobre la distribución de masa. Sin embargo, sabemos cómo integrar sobre el espacio, no sobre la masa. Por lo tanto, necesitamos encontrar una manera de relacionar las variables masivas con las espaciales. Hacemos esto usando la densidad de masa lineal $λ$ del objeto, que es la masa por unidad de longitud. Dado que la densidad de masa de este objeto es uniforme, podemos escribir
$λ = \dfrac{m}{l}$ ó $m=λ l$
Si tomamos el diferencial de cada lado de esta ecuación, encontramos
$$dm = d(λl) = λ(dl)$$ya que $λ$ es constante. Elegimos orientar la varilla a lo largo del eje $x$ para mayor comodidad; aquí es donde esa elección se vuelve muy útil. Tenga en cuenta que una pieza de la barra $dl$ se encuentra completamente a lo largo del eje $x$ y tiene una longitud $dx$; de hecho, $dl = dx$ en esta situación. Por lo tanto, podemos escribir $dm = λ (dx),$ que nos da una variable de integración que sabemos cómo manejar. La distancia de cada pieza de masa $dm$ desde el eje viene dada por la variable $x$, como se muestra en la figura. Juntando todo esto, obtenemos
$$I = \int r^2dm = \int x^2dm = \int x^2λdx$$El último paso es tener cuidado con nuestros límites de integración.
La varilla se extiende desde $x = -L/2$ a $x = L/2$, ya que el eje está en el centro de la varilla en $x = 0$. Esto nos da
A continuación, calculamos el momento de inercia para la misma varilla delgada uniforme pero con una elección de eje diferente para que podamos comparar los resultados. Es de esperar que el momento de inercia sea más pequeño en torno a un eje a través del centro de masa que el eje de punto final, tal como lo fue para el ejemplo de barra al comienzo de esta sección. Esto sucede porque más masa se distribuye más lejos del eje de rotación.
Una varilla delgada uniforme con eje en el extremo
Ahora considere la misma varilla delgada uniforme de masa $M$ y longitud $L$, pero esta vez movemos el eje de rotación hasta el final de la varilla. Deseamos encontrar el momento de inercia sobre este nuevo eje . La cantidad dm se define nuevamente como un pequeño elemento de masa que forma la varilla. Al igual que antes, obtenemos
$$I = \int r^2dm = \int x^2dm = \int x^2λdx$$Sin embargo, esta vez tenemos diferentes límites de integración. La varilla se extiende desde $x = 0$ hasta $x = L$, ya que el eje está al final de la varilla en $x = 0$. Por lo tanto, encontramos
$$\begin{split} I = \int_0^L x^2λdx &= λ \left(\frac{1}{3}\right)[(L)^3-(0)^3] \\ &= λ \left(\frac{1}{3}\right)L^3 = \frac{M}{L} \left(\frac{1}{3}\right)L^3 = \frac{1}{3}ML^2 \end{split}$$Tenga en cuenta que la inercia de rotación de la varilla alrededor de su punto final es mayor que la inercia rotacional alrededor de su centro (consistente con el ejemplo de la barra) por un factor de cuatro.
El Teorema de los Ejes Paralelos
La similitud entre el proceso de encontrar el momento de inercia de una varilla alrededor de un eje a través de su centro y alrededor de un eje hasta su final es llamativa, y sugiere que podría haber un método más simple para determinar el momento de inercia de una varilla sobre cualquier eje paralelo al eje a través del centro de masa. Tal eje se llama eje paralelo. Hay un teorema para esto, llamado el teorema del eje paralelo, que aquí indicamos pero no derivamos en este texto.
Teorema de los ejes paralelos
Sea $m$ la masa de un objeto y d la distancia desde un eje a través del centro de masa del objeto a un nuevo eje. Entonces tenemos
$$I_{\textsf{eje paralelo}} = I_{\textsf{centro de masa}} + md^2 \tag{1.20}$$Vamos a aplicar esto a los ejemplos de varillas resueltos anteriormente:
$$\begin{split} I &= I_{\textsf{centro de masa}} + md^2 \\ &= \frac{1}{12} m L^2 + m \left(\frac{L}{2}\right)^2 = \left(\frac{1}{12}+\frac{1}{4}\right) m L^2 = \frac{1}{3} m L^2 \end{split}$$Este resultado concuerda con nuestro cálculo más extenso hecho arriba. Esta es una ecuación útil que aplicamos en algunos de los ejemplos y problemas.
 Comprueba tu aprendizaje 1.5
Comprueba tu aprendizaje 1.5
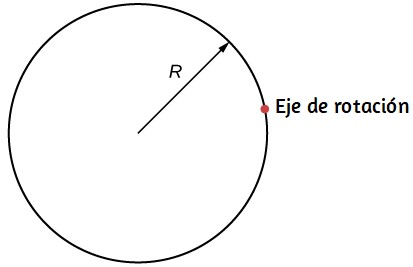
¿Cuál es el momento de inercia de un cilindro de radio $R$ y masa $m$ alrededor de un eje a través de un punto en la superficie, como se muestra a continuación?
Un disco delgado uniforme alrededor de un eje a través del centro
Integrar para encontrar el momento de inercia de un objeto bidimensional es un poco más complicado, pero una forma que se suele hacer en este nivel de estudio: un disco delgado y uniforme alrededor de un eje que atraviesa su centro
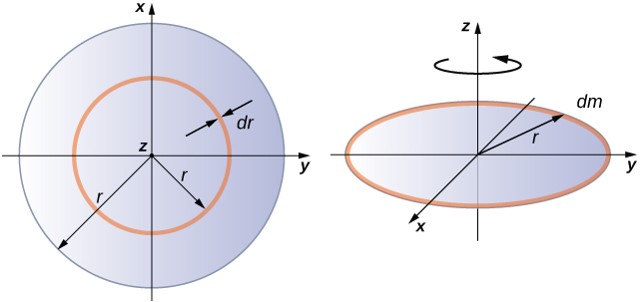
Como el disco es delgado, podemos tomar la masa distribuida por completo en el plano $xy$. Nuevamente comenzamos con la relación de la densidad de masa superficial, que es la masa por área de superficie unitaria. Como es uniforme, la densidad de masa superficial σ es constante:
$σ = \dfrac{m}{A}$ o $σA = m$, así que $dm = σ(dA)$
Ahora usamos una simplificación para el área. Se puede pensar que el área está formada por una serie de anillos delgados, donde cada anillo es un incremento en masa dm de radio r equidistante del eje, como se muestra en la parte (b) de la figura.
El área infinitesimal de cada anillo $dA$ está dada por la longitud de cada anillo ($2πr$) multiplicado por el ancho infinitesimal de cada anillo $dr$:
$A = πr^2$, $dA = d(πr^2) = πdr^2 = 2πrdr$
El área completa del disco se compone de la adición de todos los anillos delgados con un radio de $0$ a $R$. Este rango de radio se convierte en nuestros límites de integración para $dr$, es decir, integramos de $r = 0$ a $r = R$. Juntando todo esto, tenemos
$$I = \int_{0}^{R} r^2σ(2πr)dr = 2πσ \int_{0}^{R} r^3dr = 2πσ \left(\frac{R^4}{4} - 0 \right)$$ $$I = 2π \frac{m}{A} \left(\frac{R^4}{4} \right) = 2π \frac{m}{πR^2} \left(\frac{R^4}{4} \right) = \frac{1}{2}mR^2$$Ten en cuenta que esto concuerda con el valor dado en la .
Cálculo del momento de inercia para objetos compuestos
Ahora considera un objeto compuesto como el de la , que representa un disco delgado al final de una varilla delgada. Esto no se puede integrar fácilmente para encontrar el momento de inercia porque no es un objeto de forma uniforme. Sin embargo, si volvemos a la definición inicial del momento de inercia como una sumatoria, podemos razonar que el momento de inercia de un objeto compuesto se puede encontrar a partir de la suma de cada parte del objeto:
Es importante observar que los momentos de inercia de los objetos en la ecuación 1.21 se refieren a un eje común. En el caso de este objeto, sería una barra de longitud $L$ girando alrededor de su extremo, y un disco delgado de radio $R$ girando alrededor de un eje desplazado fuera del centro por una distancia $L + R$, donde $R$ es el radio de la disco. Vamos a definir la masa de la barra por $m_T$ y la masa del disco por $m_d$.
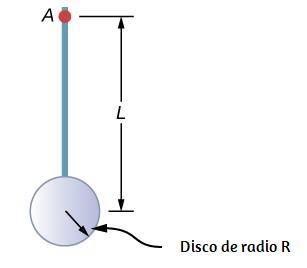
El momento de inercia de la varilla es simplemente $\frac{1}{3}m_TL^2$, pero tenemos que usar el teorema de eje paralelo para encontrar el momento de inercia del disco alrededor del eje que se muestra. El momento de inercia del disco alrededor de su centro es $\frac{1}{2}m_dR^2$ y aplicamos el teorema del eje paralelo $I_{\textsf{eje paralelo}} = I_{\textsf{centro de masa}} + md^2$ para encontrar
$$I_{\textsf{eje paralelo}} = \frac{1}{2}m_dR^2 + m_d(L+R)^2$$Añadiendo el momento de inercia de la varilla más el momento de inercia del disco con un eje de rotación desplazado, encontramos que el momento de inercia para el objeto compuesto es
$$I_{\textsf{total}} = \frac{1}{3}m_TL^2 + \frac{1}{2}m_dR^2 + m_d(L+R)^2$$Aplicación de cálculos de momento de inercia para resolver problemas
Ahora examinemos algunas aplicaciones prácticas de los cálculos del momento de inercia.
Ejemplo 1.11
Persona en un tiovivo
Un niño de $25 kg$ se encuentra a una distancia $r = 1.0 m$ del eje de un carrusel giratorio . El tiovivo se puede aproximar como un disco sólido uniforme con una masa de $500 kg$ y un radio de $2.0 m$. Encuentra el momento de inercia de este sistema.
Estrategia
Este problema implica el cálculo de un momento de inercia. Se nos da la masa y la distancia al eje de rotación del niño, así como la masa y el radio del tiovivo.
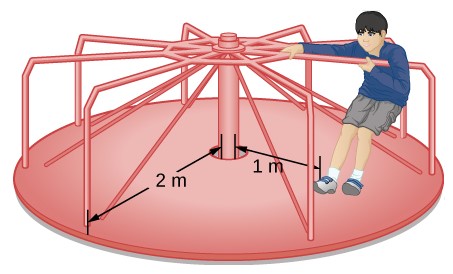
Como la masa y el tamaño del niño son mucho más pequeños que el tiovivo, podemos aproximar al niño como una masa de puntos. La notación que usamos es
$$m_c = 25 kg, \;\;\; r_c = 1.0 m, \;\;\; m_m = 500 kg, \;\;\; r_m = 2.0 m$$Nuestro objetivo es encontrar $I_{\textsf{total}} = \sum_i I_i$
Solución
Para el niño, $I_c = m_cr^2$, y para el tiovivo, $I_m = 12m_mr^2$. Por lo tanto
$$I_{\textsf{total}} = 25(1)^2 + \frac{1}{2}(500)(2)^2 = 25 + 1000 = 1025 kg \cdot m^2$$Explicación
El valor debe estar cerca del momento de inercia del tiovivo por sí solo porque tiene mucha más masa distribuida desde el eje que el niño.
Ejemplo 1.12
Varilla y esfera sólida
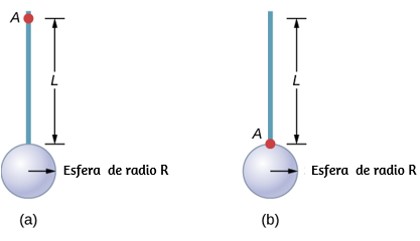
Encuentre el momento de inercia de la varilla y la combinación de esfera sólida alrededor de los dos ejes, como se muestra a continuación. La barra tiene una longitud de $0,5 m$ y una masa de $2,0 kg$. El radio de la esfera es de $20.0 cm$ y tiene una masa de $1.0 kg$.
Estrategia
Como tenemos un objeto compuesto en ambos casos, podemos usar el teorema del eje paralelo para encontrar el momento de inercia sobre cada eje. En (a), el centro de masa de la esfera se encuentra a una distancia $L + R$ del eje de rotación. En (b), el centro de masa de la esfera se encuentra a una distancia $R$ del eje de rotación. En ambos casos, el momento de inercia de la varilla es alrededor de un eje en un extremo. Consulte la para conocer los momentos de inercia de los objetos individuales.
a) $I_{\textsf{total}} = \sum_i I_i = I_{\textsf{barra}} + I_{\textsf{esfera}}$;
$I_{\textsf{esfera}} = I_{\textsf{centro de masa}} + m_{\textsf{esfera}}(L+R)^2 = \frac{2}{5}m_{\textsf{esfera}}R^2 + m_{\textsf{esfera}}(L+R)^2$;
$I_{\textsf{total}} = \frac{1}{3}(2.0 kg)(0.5 m)^2 + \frac{2}{5}(1.0 kg)(0.2 m)^2 + (1.0 kg)(0.5 m+0.2 m)^2$;
$I_{\textsf{total}} = (0.167 + 0.016 + 0.490) kg \cdot m^2 = 0.673 kg \cdot m^2$.
b) $I_{\textsf{esfera}} = \frac{2}{5}m_{\textsf{esfera}}R^2 + m_{\textsf{esfera}}R^2$;
$I_{\textsf{total}} = I_{\textsf{barra}} + I_{\textsf{esfera}} = \frac{1}{3}m_{\textsf{barra}}L^2 + \frac{2}{5}m_{\textsf{esfera}}R^2 + m_{\textsf{esfera}}R^2$;
$I_{\textsf{total}} = \frac{1}{3}(2.0 kg)(0.5 m)^2+\frac{2}{5}(1.0 kg)(0.2 m)^2 + (1.0 kg)(0.2 m)^2$;
$I_{\textsf{total}} = (0.167 + 0.016 + 0.04) kg \cdot m^2 = 0.223 kg \cdot m^2$.
Explicación
El uso del teorema del eje paralelo facilita el cálculo del momento de inercia de los objetos compuestos. Vemos que el momento de inercia es mayor en (a) que (b). Esto se debe a que el eje de rotación está más cerca del centro de masa del sistema en (b). La simple analogía es la de una varilla. El momento de inercia en un extremo es de $\frac{1}{3} ml^2$, pero el momento de inercia a través del centro de masa a lo largo de su longitud es de $\frac{1}{12} ml^2$.
Ejemplo 1.13
Velocidad angular de un péndulo.
Un péndulo en forma de varilla (), se libera en un ángulo de $30°$. Tiene una longitud de $30 cm$ y una masa de $300 g$. ¿Cuál es su velocidad angular en su punto más bajo?
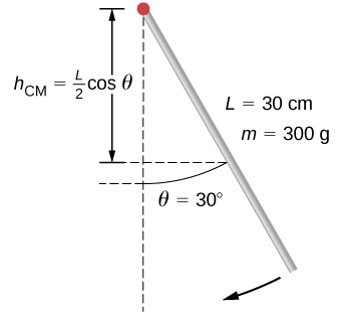
Estrategia
Usa la conservación de la energía para resolver el problema. En el punto de liberación, el péndulo tiene energía potencial gravitacional, que se determina a partir de la altura del centro de masa por encima de su punto más bajo en el columpio. En la parte inferior de la oscilación, toda la energía potencial gravitatoria se convierte en energía cinética de rotación.
Solución
El cambio en la energía potencial es igual al cambio en la energía cinética de rotación $ΔU+ΔK=0$.
En la parte superior del péndulo $U = mgh_{\textsf{CM}} = mgL^2(cosθ)$. En la parte inferior del péndulo, $U = mgL^2$.
En la parte superior del péndulo, la energía cinética de rotación es $K = 0$. En la parte inferior del péndulo, $K = \frac{1}{2}Iω^2$. Por lo tanto:
$$ΔU+ΔK = 0 → \left(mg\frac{L}{2}(1 - cosθ)- 0 \right) + \left(0 - \frac{1}{2}Iω^2 \right) = 0$$ $$\frac{1}{2}Iω^2 = mgL^2(1-cosθ)$$Resolviendo para $ω$, tenemos
Insertando los valores numéricos, obtenemos
$$w = \sqrt{9.8m/s^2 \frac{3}{0.3m} (1-cos30)} = 3.6 rad/s$$Péndulo con soporte móvil - Interactivo
Presentamos una escena interactiva, diseñada por Wolfgang Christian, en la que puedes incluir los datos del ejemplo anterior y observar el comportamiento del pénduloCuando ejecutes esta simulación en una tableta o teléfono inteligente, configura los parámetros y luego presione el botón Reproducir. Cuando ejecutes esta simulación en un ordenador, asegúrate de desmarcar "Acelerómetro", luego configura los parámetros y presiona el botón Reproducir..
Esta simulación muestra una masa $m = 1$ que se entrega desde una barra de longitud $L$ que cuelga de un punto de soporte móvil. El movimiento del punto de soporte es el movimiento del dispositivo móvil o el movimiento del control deslizante cuando se selecciona la opción "sin sensor". También hay una fuerza de fricción (fricción) viscosa a baja velocidad $F_{\textsf{drag}} = -Dv$ que es proporcional a la velocidad $v$ y al coeficiente de amortiguación $D$. La configuración del arrastre no cero es útil para amortiguar el movimiento transitorio al realizar observaciones.
Practica para la masa del péndulo con $θ = \{0°, 30°, 45°, 90° 180°\}$ sin fricción y con $ω = 0$. Ten en cuenta que la posición angular se ingresa usando radianes, no grados, en la simulación.
¿Cómo cambiará el comportamiento del péndulo si $ω = 3.6$ (resultado del ejemplo anterior)?
Ingresa una velocidad angular inicial mayor y observa el movimiento.
Hasta ahora hemos definido muchas variables que son equivalentes rotativos a sus contrapartes traslacionales. Consideremos cuál debe ser la contraparte de la fuerza. Dado que las fuerzas cambian el movimiento de traslación de los objetos, la contraparte rotacional debe estar relacionada con el cambio del movimiento de rotación de un objeto sobre un eje. Llamamos a este par de contraparte rotacional: torque.
En la vida cotidiana, rotamos objetos sobre un eje todo el tiempo, por lo que intuitivamente ya sabemos mucho sobre el torque. Considera, por ejemplo, cómo rotamos una puerta para abrirla. Primero, sabemos que una puerta se abre lentamente si nos acercamos demasiado a sus bisagras; es más eficiente rotar una puerta para abrirla si nos alejamos de las bisagras. Segundo, sabemos que debemos empujar perpendicularmente al plano de la puerta; si empujamos en paralelo al plano de la puerta, no podemos rotarlo. En tercer lugar, cuanto mayor es la fuerza, más eficaz es para abrir la puerta; cuanto más empuje, más rápidamente se abre la puerta. El primer punto implica que cuanto más se aplica la fuerza desde el eje de rotación, mayor es la aceleración angular; el segundo implica que la efectividad depende del ángulo al que se aplica la fuerza; el tercero implica que la magnitud de la fuerza también debe ser parte de la ecuación. Ten en cuenta que para la rotación en un plano, el par tiene dos direcciones posibles.
El par de torsión es en sentido horario o antihorario en relación con el punto de pivote elegido. La muestra rotaciones en sentido antihorario.
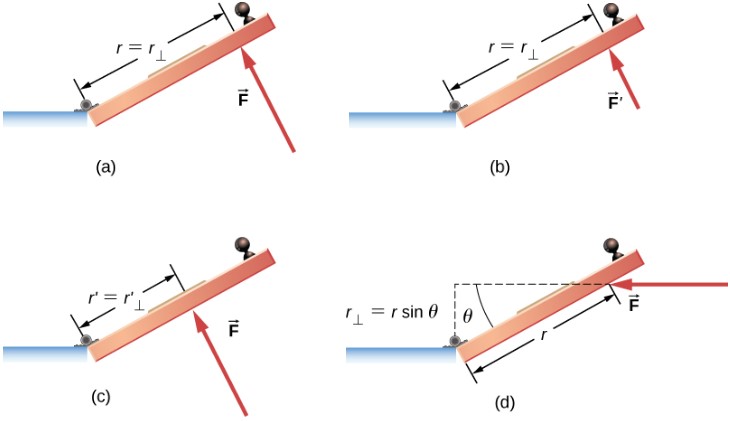
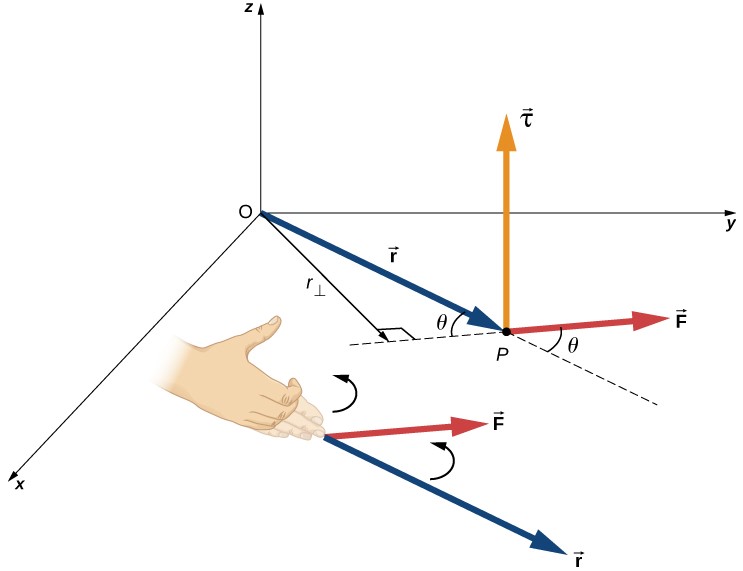
A partir de la definición del producto cruz, el par $\overrightarrow{τ}$ es perpendicular al plano que contiene $\overrightarrow{\bold{r}}$ y $\overrightarrow{\bold{F}}$ y tiene magnitud $|\overrightarrow{τ}| = |\overrightarrow{\bold{r}} × \overrightarrow{\bold{F}}| = rsenθ$ donde $θ$ es el ángulo entre los vectores $\overrightarrow{\bold{r}}$ y $\overrightarrow{\bold{F}}$. La unidad del torque en el SI es newtons por metros, generalmente escrito como $N \cdot m$. La cantidad $r⊥ = rsenθ$ es la distancia perpendicular de $O$ a la línea determinada por el vector $\overrightarrow{\bold{F}}$ y se llama brazo de palanca. Ten en cuenta que cuanto mayor es el brazo de palanca, mayor es la magnitud del par o torque. En términos del brazo de palanca, la magnitud del torque es
El producto cruz $\overrightarrow{\bold{r}} × \overrightarrow{\bold{F}}$ también nos dice el signo del torque. En la , el producto cruz $\overrightarrow{\bold{r}} × \overrightarrow{\bold{F}}$ está a lo largo del eje $z$ positivo, que por convención es un par positivo. Si $\overrightarrow{\bold{r}} × \overrightarrow{\bold{F}}$ está a lo largo del eje $z$ negativo, esto produce un par negativo.
Si consideramos un disco que puede girar libremente alrededor de un eje a través del centro, como se muestra en la podemos ver cómo el ángulo entre el radio $\overrightarrow{\bold{r}}$ y la fuerza $\overrightarrow{\bold{F}}$ afecta la magnitud del torque. Si el ángulo es cero, el par es cero; si el ángulo es de $90°$ el par es máximo. El torque en la es positivo porque la dirección del torque por la regla de la mano derecha está fuera de la página a lo largo del eje $z$ positivo. El disco gira en sentido antihorario debido al par, en la misma dirección que una aceleración angular positiva.
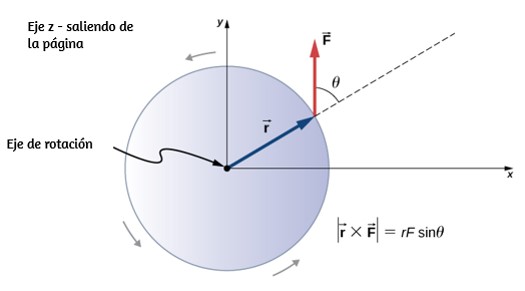
Se puede calcular cualquier cantidad de pares sobre un eje dado. Los pares o torques individuales se suman para producir un par neto alrededor del eje. Cuando se asigna el signo apropiado (positivo o negativo) a las magnitudes de los pares individuales sobre un eje específico, el par neto alrededor del eje es la suma de los pares individuales:
Cálculo del par neto para cuerpos rígidos en un eje fijo
En los siguientes ejemplos, calculamos el par tanto de forma abstracta como aplicada a un cuerpo rígido. Primero presentamos una estrategia de resolución de problemas.
Estrategia de resolución de problemas: Encontrar el par neto
1. Elige un sistema de coordenadas con el punto de pivote o el eje de rotación como el origen del sistema de coordenadas seleccionado.
2. Determina el ángulo entre el brazo de palanca $\overrightarrow{\bold{r}}$ y el vector de fuerza.
3. Toma el producto cruz de $\overrightarrow{\bold{r}}$ y $\overrightarrow{\bold{F}}$ para determinar si el torque es positivo o negativo sobre el eje o punto de pivote.
4. Evalúa la magnitud del torque usando $r⊥F$.
5. Asigna el signo apropiado, positivo o negativo, a la magnitud.
6. Suma los pares para encontrar el par neto.
Ejemplo 1.14
Calculando el torque
En la se muestran cuatro fuerzas en ubicaciones y orientaciones particulares con respecto a un sistema de coordenadas $xy$ dado. Encuentra el torque debido a cada fuerza sobre el origen, luego usa tus resultados para encontrar el torque neto sobre el origen.
Estrategia
Este problema requiere calcular el torque. Todas las cantidades conocidas -fuerzas con direcciones y brazos de palanca- se dan en la figura. El objetivo es hallar cada torque individual y el torque neto sumando los pares individuales. Ten cuidado de asignar el signo correcto a cada torque usando el producto cruz de $\overrightarrow{\bold{r}}$ y el vector fuerza $\overrightarrow{\bold{F}}$.
Solución
Utiliza $|\overrightarrow{τ} | = r⊥F = rFsenθ$ para encontrar la magnitud y $\overrightarrow{τ} = \overrightarrow{\bold{r}} × \overrightarrow{\bold{F}}$ para determinar el signo del torque.
El par de la fuerza $40 N$ en el primer cuadrante viene dado por $(4)(40)sen90° = 160 N \cdot m$.
El producto cruz de $\overrightarrow{\bold{r}}$ y $\overrightarrow{\bold{F}}$ está fuera de la página, positivo.
El par de la fuerza $20 N$ en el tercer cuadrante está dado por $-(3)(20)sen90° = -60 N \cdot m$.
El producto cruz de $\overrightarrow{\bold{r}}$ y $\overrightarrow{\bold{F}}$ está dentro de la página, por lo que es negativo.
El par de la fuerza $30 N$ en el tercer cuadrante viene dado por $(5)(30)sen53° = 120N \cdot m$.
El producto cruz de $\overrightarrow{\bold{r}}$ y $\overrightarrow{\bold{F}}$ está fuera de la página, positivo.
El par de la fuerza $20 N$ en el segundo cuadrante está dado por $(1)(20)sen30° = 10N \cdot m$.
El producto cruz de $\overrightarrow{\bold{r}}$ y $\overrightarrow{\bold{F}}$ está fuera de la página.
El par neto es, por lo tanto,
$$τ_{\textsf{neto}} = \sum_i |\overrightarrow{\bold{τ}}_i| = 160 - 60 + 120 + 10 = 230 N \cdot m$$Explicación
Ten en cuenta que cada fuerza que actúa en el sentido contrario a las agujas del reloj tiene un par positivo, mientras que cada fuerza que actúa en el sentido de las agujas del reloj tiene un par negativo. El torque es mayor cuando la distancia, la fuerza o los componentes perpendiculares son mayores.
Practica con el cálculo de torques en las siguiente escena, diseñada por Juan Guillermo Rivera Berrío. Trata, al menos, de estimar el signo del torque.
Ejemplo 1.15
Cálculo de par en un cuerpo rígido
La muestra varias fuerzas que actúan en diferentes ubicaciones y ángulos en un volante. Tenemos $||\overrightarrow{\bold{F}}_1|| = 20N$, $||\overrightarrow{\bold{F}}_2|| = 30N$, $||\overrightarrow{\bold{F}}_3|| = 30N$, y $r = 0.5 m$. Encuentra el torque neto en el volante alrededor de un eje a través del centro.
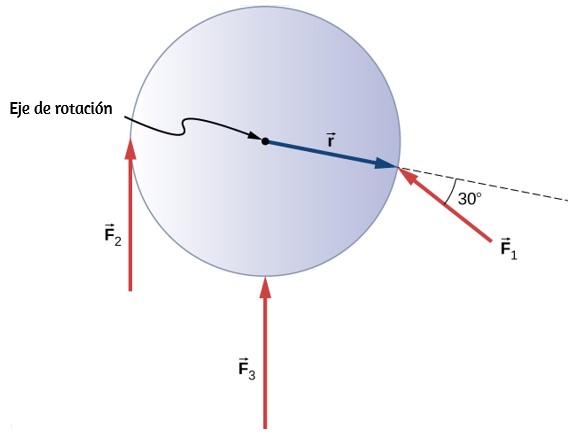
Estrategia
Calculamos cada torque de forma individual, utilizando el producto cruz, y determinamos el signo del torque. Luego sumamos los torques para encontrar el torque neto.
Solución
Comenzamos con $\overrightarrow{\bold{F}}_1$. Si observamos la vemos que $\overrightarrow{\bold{F}}_1$ forma un ángulo de $90° + 60°$ con el vector de radio $\overrightarrow{\bold{r}}$. Tomando el producto cruz, vemos que está fuera de la página y, por lo tanto, es positivo. También vemos esto al calcular su magnitud:
$$|\overrightarrow{\bold{τ}}_1| = r F_1 sen150° = 0.5m(20 N)(0.5) = 5.0 N \cdot m$$A continuación, observamos $\overrightarrow{\bold{F}}_2$. El ángulo entre $\overrightarrow{\bold{F}}_2$ y $\overrightarrow{\bold{r}}$ es $90°$ y el producto cruz está hacia dentro de la página, por lo que el torque es negativo. Su valor es
$$|\overrightarrow{\bold{τ}}_2| = -r F_2 sen90° = -0.5m(30 N) = -15.0N \cdot m$$Cuando evaluamos el torque debido a $\overrightarrow{\bold{F}}_3$, vemos que el ángulo que hace con $\overrightarrow{\bold{r}}$ es cero, entonces $\overrightarrow{\bold{r}} × \overrightarrow{\bold{F}}_3 = 0$. Por lo tanto, $\overrightarrow{\bold{F}}_3$ no produce ningún torque en el volante. Evaluamos la suma de los pares:
$$τ_{\textsf{neto}} = \sum_i |\overrightarrow{\bold{τ}}_i| = 5 - 15 = -10N \cdot m$$Explicación
El eje de rotación está en el centro de la masa del volante. Como el volante está en un eje fijo, no es libre de trasladar. Si estuviera en una superficie sin fricción y no se fijara en su lugar, $\overrightarrow{\bold{F}}_3$ haría que el volante se traslade, así como también $\overrightarrow{\bold{F}}_1$. Su movimiento sería una combinación de traslación y rotación.
 Comprueba tu aprendizaje
Comprueba tu aprendizaje
Un gran barco oceánico encalla cerca de la costa, similar al destino del Costa Concordia, y se encuentra en un ángulo como se muestra a continuación. Las cuadrillas de salvamento deben aplicar un par de torsión para enderezar la nave para el transporte. Una fuerza de $5.0 × 10^5 N$ que actúa en el punto $A$ se debe aplicar a la derecha del barco. ¿Cuál es el torque sobre el punto de contacto de la nave con el suelo ().
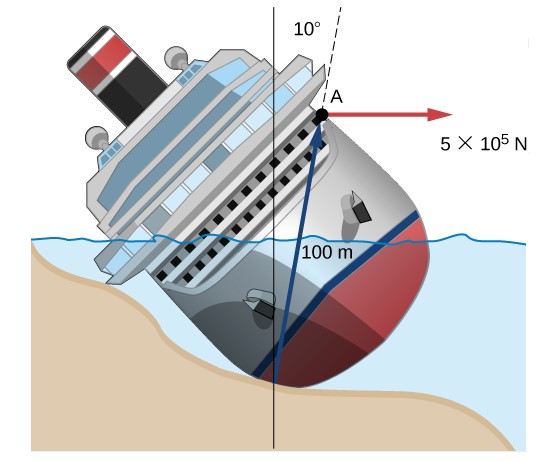
Hasta ahora, hemos encontrado muchas contrapartes a los términos de traslación utilizados en este texto, más recientemente, el torque, el análogo de rotación a la fuerza. Esto plantea la pregunta: ¿Existe una ecuación análoga a la segunda ley de Newton, $\sum \overrightarrow{\bold{F}} = m \overrightarrow{\bold{a}}$, ¿qué implica el par y el movimiento de rotación? Para investigar esto, comenzamos con la segunda ley de Newton para una sola partícula que gira alrededor de un eje y ejecuta un movimiento circular. Ejerzamos una fuerza $\overrightarrow{\bold{F}}$ en una masa de punto m que está a una distancia $r$ de un punto de pivote (). La partícula está obligada a moverse en una trayectoria circular con un radio fijo y la fuerza es tangente al círculo. Aplicamos la segunda ley de Newton para determinar la magnitud de la aceleración $a = F/m$ en la dirección de $\overrightarrow{\bold{F}}$.
Recuerda que la magnitud de la aceleración tangencial es proporcional a la magnitud de la aceleración angular $a = rα$. Sustituyendo esta expresión en la segunda ley de Newton, obtenemos: $F = mrα$
Multiplica ambos lados de esta ecuación por $r$; $rF = mr^2α$
Ten en cuenta que el lado izquierdo de esta ecuación es el par sobre el eje de rotación, donde $r$ es el brazo de palanca y $F$ es la fuerza, perpendicular a $r$.
Recuerda que el momento de inercia para una partícula puntual es $I = mr^2$. El torque aplicado perpendicularmente a la masa de punto en la es por lo tanto
$$τ = Iα$$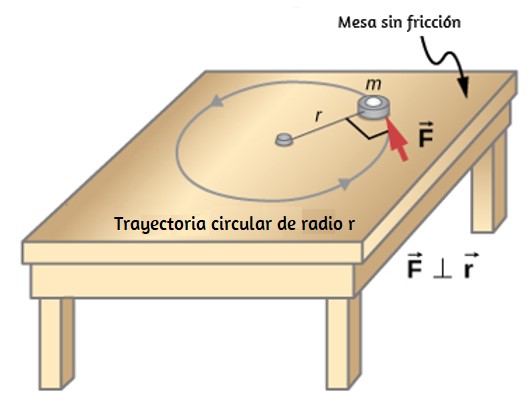
El torque en la partícula es igual al momento de inercia alrededor del eje de rotación multiplicado por la aceleración angular. Podemos generalizar esta ecuación a un cuerpo rígido que gira alrededor de un eje fijo.
La segunda ley de rotación de Newton
Si más de un torque actúa sobre un cuerpo rígido alrededor de un eje fijo, entonces la suma de los torques es igual al momento de inercia multiplicado por la aceleración angular
$$\sum_i τ_i = Iα \tag{1.25}$$El término Iα es una cantidad escalar y puede ser positivo o negativo (en sentido antihorario o en el sentido de las agujas del reloj) según el signo del torque neto. Recuerde la convención de que la aceleración angular en sentido antihorario es positiva. Por lo tanto, si un cuerpo rígido está girando en el sentido de las agujas del reloj y experimenta un par positivo (en sentido antihorario), la aceleración angular es positiva.
La ecuación 1.25 es la segunda ley de rotación de Newton y nos dice cómo relacionar torque, momento de inercia y cinemática rotacional. Esto se llama la ecuación para la dinámica rotacional. Con esta ecuación, podemos resolver una clase completa de problemas que involucran fuerza y rotación. Tiene sentido que la relación de cuánta fuerza se necesita para rotar un cuerpo incluiría el momento de inercia, ya que esa es la cantidad que nos dice qué tan fácil o difícil es cambiar el movimiento de rotación de un objeto.
Derivando la segunda ley de Newton para la rotación en forma de vector
Como antes, cuando encontramos la aceleración angular, también podemos encontrar el vector de par. La segunda ley $\sum \overrightarrow{\bold{F}} = m \overrightarrow{\bold{a}}$ nos dice la relación entre la fuerza neta y cómo cambiar el movimiento de traslación de un objeto. Tenemos un equivalente de rotación vectorial de esta ecuación, que se puede encontrar usando la Ecuación 1.7 y la . La ecuación 1.7 relaciona la aceleración angular con la posición y los vectores de aceleración tangencial:
$$\overrightarrow{\bold{a}} = \overrightarrow{α} × \overrightarrow{\bold{r}}$$Formamos el producto cruz de esta ecuación con $\overrightarrow{\bold{r}}$ y usamos una identidad de producto cruz (ten en cuenta que $\overrightarrow{\bold{r}} \cdot \overrightarrow{α} = 0$):
Ahora formamos el producto cruzado de la segunda ley de Newton con el vector de posición $\overrightarrow{\bold{r}}$,
$$\sum (\overrightarrow{\bold{r}} × \overrightarrow{\bold{F}}) = \overrightarrow{\bold{r}} ×(m \overrightarrow{\bold{a}}) = m \overrightarrow{\bold{r}} × \overrightarrow{\bold{a}} = mr^2 \overrightarrow{α}$$Identificando el primer término a la izquierda como la suma de los pares, y $mr^2$ como el momento de inercia, llegando a la segunda ley de rotación de Newton en forma vectorial:
Esta ecuación es exactamente la ecuación 1.25 pero con el torque y la aceleración angular como vectores. Un punto importante es que el vector de torque está en la misma dirección que la aceleración angular.
Aplicando la ecuación de dinámica rotacional
Antes de aplicar la ecuación de dinámica rotacional a algunas situaciones cotidianas, repasemos una estrategia general de resolución de problemas para usar con esta categoría de problemas.
Estrategia de resolución de problemas: dinámica rotacional
1. Examina la situación para determinar que el torque y la masa están involucrados en la rotación. Dibuja un esbozo cuidadoso de la situación.
2. Determina el sistema de interés.
3. Dibuja un diagrama de cuerpo libre. Es decir, dibujar y etiquetar todas las fuerzas externas que actúan sobre el sistema de interés.
4. Identifica el punto de pivote. Si el objeto está en equilibrio, debe estar en equilibrio para todos los puntos pivote posibles: elige el que simplifique más tu trabajo.
5. Aplica $\sum_i τ_i = Iα$, el equivalente de rotación de la segunda ley de Newton, para resolver el problema. Se debe tener cuidado de usar el momento correcto de inercia y considerar el torque alrededor del punto de rotación.
6. Como siempre, verifica la solución para ver si es razonable.
Ejemplo 1.16
Cálculo del efecto de la distribución de masa en un tiovivo
Considera al padre empujando un carrusel de patio de recreo en la . Él ejerce una fuerza de $250 N$ en el borde del carrusel de $50.0 kg$, que tiene un radio de $1.50 m$. Calcula la aceleración angular producida (a) cuando nadie está en el tiovivo y (b) cuando un niño de $18.0 kg$ se encuentra a $1.25 m$ del centro. Considera que el tiovivo es un disco uniforme con una fricción insignificante.
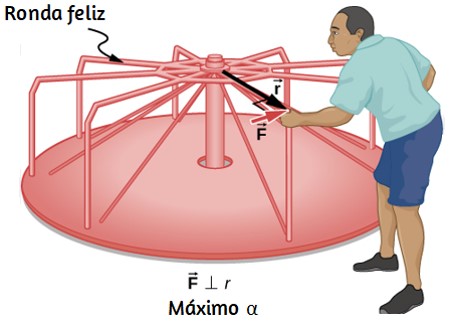
Estrategia
El torque neto está dado directamente por la expresión $\sum_i τ_i = Iα$, para hallar $α$, primero
debemos calcular el torque neto $τ$ (que es el mismo en ambos casos) y el momento de inercia $I$ (que es mayor en el segundo caso).
Solución
a. El momento de inercia de un disco sólido alrededor de este eje se da en la para ser
$$\frac{1}{2}MR^2$$Tenemos $M = 50.0 kg$ y $R = 1.50 m$, entonces
$$I = (0.500)(50.0 kg)(1.50 m)^2 = 56.25 kg \cdot m^2$$Para encontrar el torque neto, observamos que la fuerza aplicada es perpendicular al radio y la fricción es insignificante, por lo que
$$τ = rFsenθ = (1.50 m)(250.0 N) = 375.0 N \cdot m$$Ahora, después de que sustituimos los valores conocidos, encontramos que la aceleración angular es
$$α = \frac{τ}{I} = \frac{375.0 N \cdot m }{56.25 kg \cdot m^2} = 6.67 rad/s^2$$b. Esperamos que la aceleración angular para el sistema sea menor en esta parte porque el momento de inercia es mayor cuando el niño está en el tiovivo.
Para encontrar el momento total de inercia $I$, primero encontramos el momento de inercia $I_c$ del niño al aproximar al niño como una masa puntual a una distancia de $1.25 m$ del eje. Entonces
$$I_c = mR^2 = (18.0 kg)(1.25 m)^2 = 28.13 kg \cdot m^2$$El momento total de inercia es la suma de los momentos de inercia del tiovivo y el niño (sobre el mismo eje):
$$I = 28.13 kg \cdot m^2 + 56.25 kg \cdot m^2 = 84.38 kg \cdot m^2$$Al sustituir los valores conocidos en la ecuación para $α$ da
$$α = \frac{τ}{I} = \frac{375.0 Nm}{84.38 kg \cdot m^2} = 4.44 rad/s^2$$Explicación
La aceleración angular es menor cuando el niño está en el tiovivo que cuando el tiovivo está vacío, como se esperaba. Las aceleraciones angulares encontradas son bastante grandes, en parte debido al hecho de que la fricción se consideró insignificante. Si, por ejemplo, el padre siguió presionando perpendicularmente durante $2.00 s$, le daría al carrusel una velocidad angular de $13.3 rad/s$ cuando está vacía, pero solo $8.89 rad/s$ cuando el niño está sobre ella.
En términos de revoluciones por segundo, estas velocidades angulares son $2.12 rev/s$ y $1.41 rev/s$, respectivamente. El padre terminaría corriendo a unos $50 km/h$ en el primer caso.
 Comprueba tu aprendizaje
Comprueba tu aprendizaje
Las aspas del ventilador en un motor a reacción tienen un momento de inercia de $30.0 kgm^2$. En $10 s$, giran en sentido antihorario desde el reposo hasta una velocidad de rotación de $20 rev/s$. (a) ¿Qué torque se debe aplicar a las cuchillas para lograr esta aceleración angular? (b) ¿Cuál es el par de torsión requerido para que las paletas del ventilador giren a $20 rev/s$ a un reposo en $20 s$?
En la siguiente escena interactiva, arrastra el disco desde diferentes puntos y verifica que el movimiento se facilita cuando el torque se aplica en los extremos.
En el capítulo anterior, hemos abordado ampliamente la cinemática y la dinámica para rotar cuerpos rígidos alrededor de un eje fijo. En esta sección final, definimos el trabajo y la potencia dentro del contexto de rotación sobre un eje fijo, que tiene aplicaciones tanto para la física como para la ingeniería. La discusión sobre el trabajo y la potencia hace que nuestro tratamiento del movimiento rotacional sea casi completo, con la excepción del movimiento giratorio y el momento angular, que se analizan en otro capítulo. Comenzamos esta sección con un tratamiento del teorema del trabajo y la energía para la rotación.
Ahora que hemos determinado cómo calcular la energía cinética para cuerpos rígidos rotativos, podemos proceder con una discusión del trabajo realizado en un cuerpo rígido que gira alrededor de un eje fijo. La muestra un cuerpo rígido que ha girado en un ángulo $dθ$ desde $A$ hasta $B$ bajo la influencia de una fuerza $\overrightarrow{\bold{F}}$. La fuerza externa $\overrightarrow{\bold{F}}$ se aplica al punto $P$, cuya posición es $\overrightarrow{\bold{r}}$, y el cuerpo rígido se ve obligado a girar alrededor de un eje fijo que es perpendicular a la página y pasa por $O$. El eje de rotación es fijo, por lo que el vector $\overrightarrow{\bold{r}}$ se mueve un círculo de radio $r$, y el vector $d \overrightarrow{\bold{s}}$ es perpendicular a $\overrightarrow{\bold{r}}$.
De la Ecuación 1.2, tenemos
$$\overrightarrow{\bold{s}} = \overrightarrow{θ} × \overrightarrow{\bold{r}}$$ $$d \overrightarrow{\bold{s}} = d (\overrightarrow{θ} × \overrightarrow{\bold{r}}) = d \overrightarrow{θ} × \overrightarrow{\bold{r}} + d \overrightarrow{\bold{r}} × \overrightarrow{θ} = d \overrightarrow{θ} × \overrightarrow{\bold{r}}$$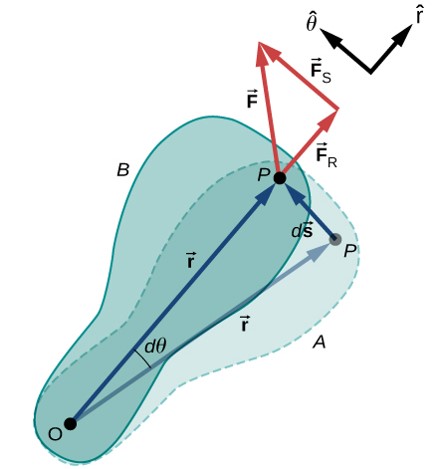
Ten en cuenta que $d\overrightarrow{\bold{r}}$ es cero porque $\overrightarrow{\bold{r}}$ está fijo en el cuerpo rígido desde el origen $O$ hasta el punto $P$. Usando la definición de trabajo, obtenemos
$$W = \int \sum \overrightarrow{\bold{F}} \cdot d \overrightarrow{\bold{s}} = \int \sum \overrightarrow{\bold{F}} \cdot (d\overrightarrow{θ} × \overrightarrow{\bold{r}}) = \int d \overrightarrow{θ} \cdot (\overrightarrow{\bold{r}} × \sum \overrightarrow{\bold{F}})$$donde usamos la identidad $\overrightarrow{\bold{a}} \cdot (\overrightarrow{\bold{b}} × \overrightarrow{\bold{c}}) = \overrightarrow{\bold{b}} \cdot (\overrightarrow{\bold{c}} × \overrightarrow{\bold{a}})$. Teniendo en cuenta que $(\overrightarrow{\bold{r}} × \sum \overrightarrow{\bold{F}}) = \sum \overrightarrow{τ}$, llegamos a la expresión del trabajo de rotación realizado en un cuerpo rígido:
El trabajo total realizado en un cuerpo rígido es la suma de los torques integrados en el ángulo a través del cual gira el cuerpo. El trabajo incremental es
donde hemos tomado el producto de puntos en la Ecuación 1.27, dejando solo torsiones a lo largo del eje de rotación. En un cuerpo rígido, todas las partículas giran en el mismo ángulo; por lo tanto, el trabajo de cada fuerza externa es igual al torque por el ángulo incremental común $dθ$. La cantidad ($\sum_i τ_i$) es el par neto en el cuerpo debido a fuerzas externas.
De manera similar, encontramos la energía cinética de un cuerpo rígido que gira alrededor de un eje fijo al sumar la energía cinética de cada partícula que forma el cuerpo rígido. Como el teorema de trabajo y energía $W_i = ΔK_i$ es válido para cada partícula, es válido para la suma de las partículas y el cuerpo entero.
Teorema del trabajo-energía para la rotación
El teorema del trabajo-energía para un cuerpo rígido que gira alrededor de un eje fijo es
$$W_{AB} = K_B - K_A \tag{1.29}$$donde
$$K = \frac{1}{2}Iω^2$$y el trabajo de rotación realizado por una fuerza neta que rota un cuerpo desde el punto $A$ al punto $B$ es
Proporcionamos una estrategia para usar esta ecuación al analizar el movimiento rotacional.
Estrategia de resolución de problemas: Teorema de trabajo-energía para el movimiento de rotación
Veamos dos ejemplos y usemos el teorema del trabajo-energía para analizar el movimiento rotacional.
Ejemplo 1.17
Trabajo rotativo y energía
Un torque de $12.0 N \cdot m$ se aplica a un volante que gira alrededor de un eje fijo y tiene un momento de inercia de $30.0 kg \cdot m^2$. Si el volante está inicialmente en reposo, ¿cuál es su velocidad angular después de haber girado ocho revoluciones?
Estrategia
Aplicamos el teorema del trabajo-energía. Sabemos por la descripción del problema cuál es el torque y el desplazamiento angular del volante. Entonces podemos encontrar la velocidad angular final.
Solución
El volante gira a través de ocho revoluciones, que son $16π$ radianes. El trabajo realizado por el torque, que es constante y por lo tanto puede salir de la integral en la Ecuación 1.30, es
$$W_{AB} = τ(θ_B - θ_A)$$Aplicamos el teorema del trabajo-energía:
$$W_{AB} = τ(θ_B - θ_A) = \frac{1}{2}Iω^2_B - \frac{1}{2}Iω^2_A$$Con $τ = 12.0 N \cdot m$, $θ_B - θ_A = 16.0 πrad$, $I = 30.0 kg \cdot m^2$, y $ω_A = 0,$
$$12.0 N \cdot m(16.0πrad) = \frac{1}{2}(30.0 k \cdot gm^2)(ω^2_B) - 0$$Por lo tanto, $ω_B = 6.3 rad/s$
Esta es la velocidad angular del volante después de ocho revoluciones.
Explicación
El teorema del trabajo-energía proporciona una manera eficiente de analizar el movimiento de rotación, conectando el torque con la energía cinética de rotación.
Ejemplo 1.18
Trabajo de rotación: una polea
Una cuerda enrollada alrededor de la polea en la se tira con una fuerza constante hacia abajo $F$ de magnitud $50 N$. El radio $R$ y el momento de inercia $I$ de la polea son $0.10 m$ y $2.5 × 10^{-3} kg \cdot m^2,$ respectivamente. Si la cuerda no se desliza, ¿cuál es la velocidad angular de la polea después de que se haya desenrollado $1.0 m$ de cuerda? Supongamos que la polea comienza desde el reposo.
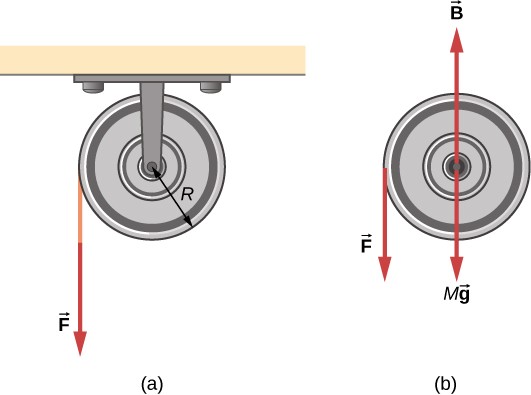
Estrategia
Al observar el diagrama de cuerpo libre, vemos que ni $\overrightarrow{\bold{B}}$, la fuerza en los cojinetes de la polea, ni el peso de la polea $M \overrightarrow{\bold{g}}$, ejercen un torque alrededor del eje de rotación $y$, por lo tanto, no influyen en la rotación de la polea. A medida que la polea gira en un ángulo $θ$, $\overrightarrow{\bold{F}}$ actúa a través de una distancia $d$, tal que $d = Rθ$.
Solución
Dado que el torque debido a $\overrightarrow{\bold{F}}$ tiene una magnitud $τ = RF$, tenemos
$$W = τθ = (FR)θ = Fd$$Si la fuerza sobre la cuerda actúa a una distancia de $1.0 m$, tenemos, desde el teorema del trabajo-energía,
$$W_{AB} = K_B - K_B$$ $$Fd = \frac{1}{2}Iω^2 - 0$$ $$(50.0 N)(1.0 m)= \frac{1}{2}(2.5×10^{-3} kg \cdot m^2)ω^2$$Resolviendo para $ω$, obtenemos
$$ω = 200.0 rad/s$$La potencia siempre surge en la discusión de aplicaciones en ingeniería y física. La potencia para el movimiento de rotación es igual de importante que la potencia en el movimiento lineal y se puede derivar de manera similar a la del movimiento lineal cuando la fuerza es una constante.
La potencia lineal cuando la fuerza es una constante es $P = \overrightarrow{\bold{F}} \cdot \overrightarrow{\bold{v}}$. Si el torque neto es constante sobre el desplazamiento angular, la ecuación 1.25 se simplifica y el torque neto se puede sacar de la integral. En la siguiente discusión, asumimos que el torque neto es constante. Podemos aplicar la definición de potencia derivada de la potencia al movimiento de rotación. Desde el trabajo y la energía cinética, la potencia instantánea (o solo potencia) se define como la tasa de trabajo,
$$P = \frac{dW}{dt}$$Si tenemos un torque neto constante, la ecuación 1.25 se convierte en $W = τθ$ y la potencia es
$$P = \frac{dW}{dt}t = \frac{d}{dt}(τθ)= τ\frac{dθ}{dt}$$ó
Ejemplo 1.19
Torque en una hélice de barco
Un motor de bote que opera a $9.0 × 10^4 W$ está funcionando a $300 rev/min$. ¿Cuál es el par en el eje de la hélice?
Estrategia
Nos dan la velocidad de rotación en $rev/min$ y el consumo de energía, por lo que podemos calcular fácilmente el torque.
Solución
$$300.0 rev/min = 31.4 rad/s$$ $$τ = \frac{P}{ω} = \frac{9.0×10^4 N \cdot m/s}{31.4 rad/s = 2864.8 N \cdot m}$$Explicación
Es importante tener en cuenta que el radián es una unidad adimensional porque su definición es la relación de dos longitudes. Por lo tanto, no aparece en la solución.
 Comprueba tu aprendizaje
Comprueba tu aprendizaje
Se aplica un torque constante de $500 kN \cdot m$ a un aerogenerador para mantenerlo girando a $6 rad/s$. ¿Cuál es la potencia requerida para mantener la turbina girando?
Las magnitudes de rotación y su análogo lineal se resumen en tres tablas. La resume las variables de rotación para el movimiento circular alrededor de un eje fijo con sus análogos lineales y la ecuación de conexión, excepto la aceleración centrípeta, que se mantiene por sí misma. La resume las ecuaciones cinemáticas de rotación y traslación. La resume las ecuaciones de dinámica rotacional con sus análogos lineales.
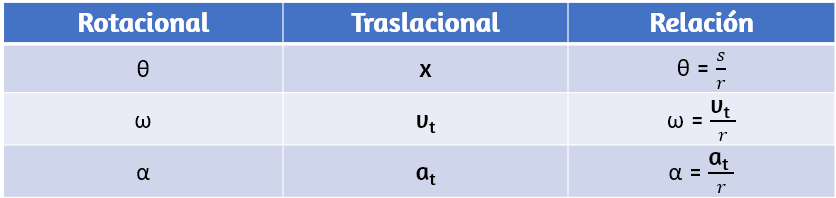

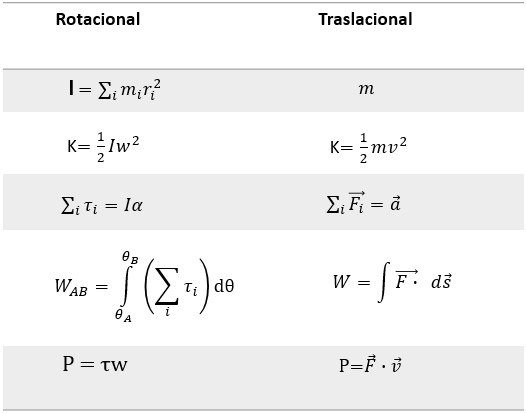

El momento angular es la contraparte rotacional del momento lineal. Cualquier objeto masivo que gira alrededor de un eje tiene un momento angular, incluyendo volantes giratorios, planetas, estrellas, huracanes, tornados, remolinos, y así sucesivamente. El helicóptero que se muestra en la imagen de apertura del capítulo se puede utilizar para ilustrar el concepto de momento angular. Las paletas de elevación giran alrededor de un eje vertical a través del cuerpo principal y llevan un momento angular. El cuerpo del helicóptero tiende a rotar en el sentido opuesto para conservar el momento angular. Los pequeños rotores en la cola del avión proporcionan un contra empuje contra el cuerpo para evitar que esto suceda, y el helicóptero se estabiliza.
El concepto de conservación del momento angular se analiza más adelante en este capítulo. En la parte principal de este capítulo, exploramos las complejidades del momento angular de cuerpos rígidos, como una parte superior, y también de partículas puntuales y sistemas de partículas. Pero para ser completo, comenzamos con una discusión sobre el movimiento continuo, que se basa en los conceptos del capítulo anterior.
El movimiento de rodadura es la combinación común de movimiento rotacional y de traslación que vemos en todas partes, todos los días. Piensa en las diferentes situaciones de las ruedas que se mueven en un automóvil a lo largo de una carretera, o las ruedas de un avión que aterriza en una pista, o las ruedas de un explorador robótico en otro planeta. Comprender las fuerzas y pares que intervienen en el balanceo del movimiento es un factor crucial en muchos tipos diferentes de situaciones.
La gente ha observado movimientos de rodadura sin deslizamientos desde la invención de la rueda. Por ejemplo, podemos ver la interacción de los neumáticos de un automóvil y la superficie de la carretera. Si el conductor presiona el acelerador hacia el piso, de modo que las llantas giren sin que el automóvil avance, debe existir una fricción cinética entre las ruedas y la superficie de la carretera. Si el conductor presiona el acelerador lentamente, haciendo que el automóvil avance, las llantas ruedan sin deslizarse. Es sorprendente para la mayoría de las personas que, de hecho, la parte inferior de la rueda está en reposo con respecto al suelo, lo que indica que debe haber fricción estática entre las llantas y la superficie de la carretera.
En la , la bicicleta está en movimiento con el ciclista en posición vertical. Los neumáticos tienen contacto con la superficie de la carretera y, aunque están rodando, los fondos de los neumáticos se deforman levemente, no resbalan y están en reposo con respecto a la superficie de la carretera durante un período de tiempo medible. Debe haber una fricción estática entre el neumático y la superficie de la carretera para que así sea.

Para analizar el movimiento rodante sin deslizamiento, primero derivamos las variables lineales de velocidad y aceleración del centro de masa de la rueda en términos de las variables angulares que describen el movimiento de la rueda. La situación se muestra en la .
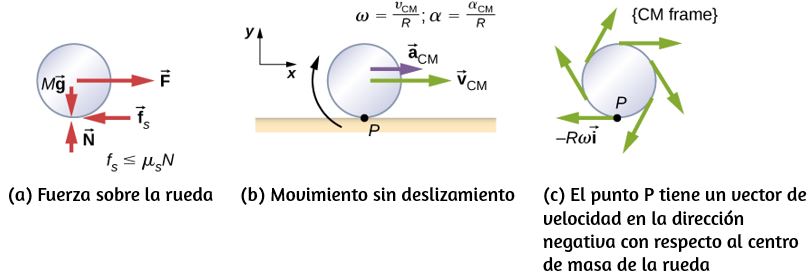
En la (a), vemos los vectores de fuerza implicados en la prevención de deslizamiento de la rueda. En (b), el punto $P$ que toca la superficie está en reposo con relación a la superficie. En relación con el centro de masa, el punto $P$ tiene la velocidad $-Rω \^{i}$, donde $R$ es el radio de la rueda y $ω$ es la velocidad angular de la rueda sobre su eje. Dado que la rueda está rodando, la velocidad de $P$ con respecto a la superficie es su velocidad con respecto al centro de masa más la velocidad del centro de masa con respecto a la superficie:
$$\overrightarrow{\bold{v}}_P = -Rω \^{i} + v_{\textsf{CM}} \^{i}$$Como la velocidad de $P$ con respecto a la superficie es cero, $v_P = 0$, entonces
Por lo tanto, la velocidad del centro de masa de la rueda es su radio multiplicado por la velocidad angular alrededor de su eje. Mostramos la correspondencia de la variable lineal en el lado izquierdo de la ecuación con la variable angular en el lado derecho de la ecuación. Esto se hace a continuación para la aceleración lineal; pero antes, practica con la siguiente escena interactiva diseñada por Juan Guillermo Rivera Berrío.
En la escena se describe el movimiento de rodadura de una rueda como una combinación de traslación y rotación.
Cuando la rueda está rodando, la velocidad de cualquier punto en la rueda es igual a la suma de las velocidades debidas a la rotación y la traslación por separado. Las velocidades debidas a la rotación durante el movimiento de balanceo se pueden visualizar más fácilmente al imaginar que estás mirando la rueda mientras corre a tu lado a una velocidad igual a la velocidad de su centro de masa.
Las velocidades de la parte superior, central e inferior de la rueda se encuentran sumando la velocidad del centro de masa a la velocidad debido a la rotación:
$v_{\textsf{sup}} = v_{\textsf{CM}} + v_{\textsf{CM}} = 2v_{\textsf{CM}}$,
$v_{\textsf{med}} = v_{\textsf{CM}} + 0 = v_{\textsf{CM}}$,
$v_{\textsf{inf}} = v_{\textsf{CM}} - v_{\textsf{CM}} = 0$ (https://www.wiley.com)La escena interactiva fue diseñada con fundamento en la presentada por Wiley College, denominada "Rolling Motion of a Wheel".
Retornando a nuestra discusión anterior, si diferenciamos la Ecuación 2.1 en el lado izquierdo de la ecuación, obtenemos una expresión para la aceleración lineal del centro de masa. En el lado derecho de la ecuación, $R$ es una constante y desde $α = \frac{dω}{dt}$, tenemos
Además, podemos encontrar la distancia que recorre la rueda en términos de variables angulares consultando la .
A medida que la rueda de la bicicleta rueda del punto $A$ al punto $B$, su superficie exterior se mapea en el suelo exactamente por la distancia recorrida, que es $d_{\textsf{CM}}$. Vemos en la que la longitud de la superficie exterior que se dibuja en el suelo es la longitud del arco $Rθ$. Igualando las dos distancias, obtenemos
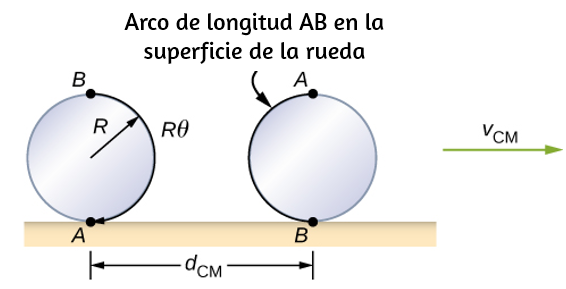
Ejemplo 2.1
Rodando en un plano inclinado
Un cilindro sólido rueda por un plano inclinado sin deslizarse, comenzando desde el reposo. Tiene masa $m$ y radio $r$.
(a) ¿Cuál es su aceleración?
(b) ¿Qué condición debe cumplir el coeficiente de fricción estática $μ_S$ para que el cilindro no se deslice?
Estrategia
Dibuja un boceto y un diagrama de cuerpo libre, y elige un sistema de coordenadas. Colocamos $x$ en la dirección descendente del plano y $y$ hacia arriba perpendicularmente al plano. Identifica las fuerzas involucradas. Estas son la fuerza normal, la fuerza de la gravedad y la fuerza debida a la fricción. Escribe las leyes de Newton en las direcciones $x$ e $y$, y la ley de Newton para la rotación, y luego halla la aceleración y la fuerza debidas a la fricción.
Solución
a. El diagrama y el boceto de cuerpo libre se muestran en la , que incluyen la fuerza normal, los componentes del peso y la fuerza de fricción estática. Apenas hay suficiente fricción para mantener el cilindro rodando sin resbalar. Como no hay deslizamiento, la magnitud de la fuerza de fricción es menor o igual a $μ_SN$.
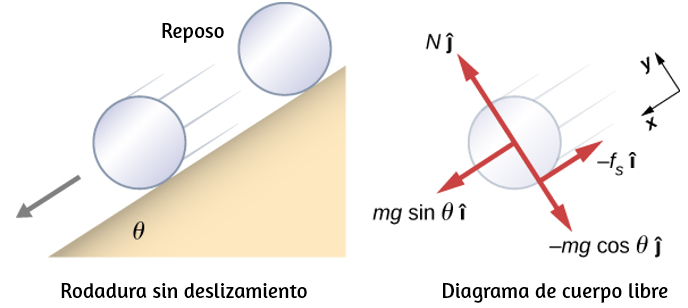
Escribiendo las leyes de Newton en las direcciones $x$ e $y$, tenemos
$$\sum F_x = ma_x; \;\;\; \sum F_y = ma_y$$Sustituyendo en del diagrama de cuerpo libre,
$mgsenθ - f_S = m(a_{\textsf{CM}})_x$,
$N - mgcosθ = 0$
$f_S ≤ μ_SN$
entonces podemos hallar la aceleración lineal del centro de masa a partir de estas ecuaciones:
$$(a_{\textsf{CM}})_x = g(senθ - μ_Scosθ).$$Sin embargo, es útil expresar la aceleración lineal en términos del momento de inercia. Para esto, escribimos la segunda ley de Newton para la rotación,
$$\sum τ_{\textsf{CM}} = I_{\textsf{CM}}α$$Los torques (pares) se calculan sobre el eje a través del centro de masa del cilindro. El único torque (par) distinto de cero es proporcionado por la fuerza de fricción.
Tenemos, entonces
$$f_Sr = I_{\textsf{CM}}α$$Finalmente, la aceleración lineal está relacionada con la aceleración angular por
$$(a_{\textsf{CM}})_x = rα$$Estas ecuaciones se pueden usar para hallar $a_{\textsf{CM}}$, $α$, y $f_S$ en términos del momento de inercia, donde hemos descartado el subíndice $x$. Escribimos $a_{\textsf{CM}}$ en términos del componente vertical de la gravedad y la fuerza de fricción, y realizamos las siguientes sustituciones.
$$a_{\textsf{CM}} = gsenθ - f_S/m$$ $$f_S = \frac{I_{\textsf{CM}}α}{r} = \frac{I_{\textsf{CM}}a_{\textsf{CM}}}{r^2}$$De esto obtenemos
$$\begin{split} a_{\textsf{CM}} &= gsenθ - \frac{I_{\textsf{CM}}a_{\textsf{CM}}}{mr^2} \\ &= \frac{mgsenθ}{m + (I_{\textsf{CM}}/r^2)} \end{split}$$Ten en cuenta que este resultado es independiente del coeficiente de fricción estática, $μ_S$.
Como tenemos un cilindro sólido, de la , tenemos $I_{\textsf{CM}} = mr^2/2$ y
$$a_{\textsf{CM}} = \frac{mgsenθ}{m + (m^2/2r^2)} = \frac{2}{3}gsenθ$$Por lo tanto, obtenemos
$$α = \frac{a_{\textsf{CM}}}{r} = \frac{2}{3r}gsenθ$$b. Como no se produce deslizamiento, $f_S ≤ μ_SN$. Resolviendo para la fuerza de fricción,
Sustituyendo esta expresión en la condición de no deslizamiento, y observando que $N = mgcosθ$, tenemos
$$\frac{mgI_{\textsf{CM}}senθ}{mr^2 + I_{\textsf{CM}}} ≤ μ_Smgcosθ$$o $$μ_S ≥ \frac{tan θ}{1 + (2mr^2/mr^2)} = \frac{1}{3}tanθ$$
Explicación
La aceleración lineal es linealmente proporcional a $senθ$. Por lo tanto, cuanto mayor es el ángulo de la inclinación, mayor es la aceleración lineal, como cabría esperar. La aceleración angular, sin embargo, es linealmente proporcional a $senθ$ e inversamente proporcional al radio del cilindro. Por lo tanto, cuanto mayor es el radio, menor es la aceleración angular.
Para que no se produzca deslizamiento, el coeficiente de fricción estática debe ser mayor o igual que $(1/3)tanθ$. Por lo tanto, cuanto mayor sea el ángulo de inclinación, mayor será el coeficiente de fricción estática para evitar que el cilindro se deslice.
 Comprueba tu aprendizaje 2.1
Comprueba tu aprendizaje 2.1
Vale la pena repetir la ecuación derivada en este ejemplo para la aceleración de un objeto que rueda sin deslizarse:
Esta es una ecuación muy útil para resolver problemas que implican rodar sin resbalar.
Observa que la aceleración es menor que la de un objeto deslizándose por un plano sin fricción sin rotación. La aceleración también será diferente para dos cilindros giratorios con diferentes inercias rotacionales.
En el caso del movimiento de rodadura con deslizamiento, debemos usar el coeficiente de fricción cinética, que da lugar a la fuerza de fricción cinética ya que la fricción estática no está presente. La situación se muestra en la . En el caso de deslizamiento, $v_{\textsf{CM}} - Rω ≠ 0$, porque el punto $P$ en la rueda no está en reposo en la superficie, y $v_P ≠ 0$. Por lo tanto, $ω ≠ \frac{v_{\textsf{CM}}}{R}$, $α ≠ \frac{a_{\textsf{CM}}}{R}$.
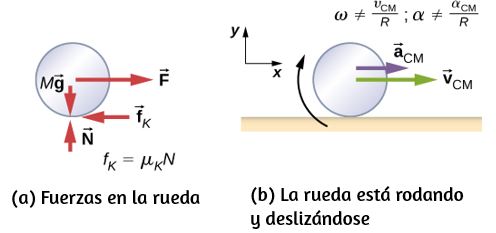
Ejemplo 2.2
Desplazamiento en un plano inclinado con deslizamiento
Un cilindro sólido rueda desde un plano inclinado y se desliza (). Tiene masa $m$ y radio $r$. (a) ¿Cuál es su aceleración lineal? (b) ¿Cuál es su aceleración angular alrededor de un eje a través del centro de masa?
Estrategia
Dibuja un boceto y un diagrama de cuerpo libre que muestre las fuerzas involucradas. El diagrama de cuerpo libre es similar al caso de antideslizamiento, excepto por la fuerza de fricción, que es cinética en lugar de estática. Usa la segunda ley de Newton para hallar la aceleración en la dirección $x$. Usa la segunda ley de rotación de Newton para hallar la aceleración angular.
Solución
La suma de las fuerzas en la dirección y es cero, por lo que la fuerza de fricción es ahora $f_k = μ_kN = μ_kmgcosθ$.
La segunda ley de Newton en la dirección $x$ se convierte en
$$\sum F_x = ma_x$$ $$mgsenθ - μ_kmgcosθ = m(a_{\textsf{CM}})_x$$ $$(a_{\textsf{CM}})_x = g(senθ - μ_kcosθ)$$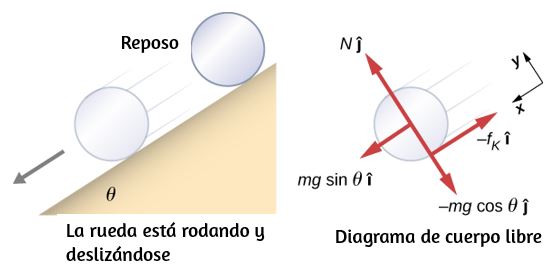
La fuerza de fricción proporciona el único torque (par) sobre el eje a través del centro de masa, por lo que la segunda ley de rotación de Newton se convierte en
$$\sum τ_{\textsf{CM}} = I_{\textsf{CM}}α \\ f_kr = I_{\textsf{CM}}α = \frac{1}{2}mr^2α$$Resolviendo para $α$, tenemos $$α = \frac{2f_k}{mr} = \frac{2μ_kgcosθ}{r}$$
Explicación
Escribimos las aceleraciones lineales y angulares en términos del coeficiente de fricción cinética. La aceleración lineal es la misma que la encontrada para un objeto que se desliza por un plano inclinado con fricción cinética. La aceleración angular alrededor del eje de rotación es linealmente proporcional a la fuerza normal, que depende del coseno del ángulo de inclinación. Como $θ → 90°$, esta fuerza tiende a cero, y, por lo tanto, la aceleración angular tiende a cero.
En el capítulo anterior, introdujimos la energía cinética de rotación. Cualquier objeto rodante lleva energía cinética de rotación, así como energía cinética de traslación y energía potencial si el sistema lo requiere. Incluyendo la energía potencial gravitacional, la energía mecánica total de un objeto rodando es
$$E_T = \frac{1}{2}mv_{\textsf{CM}}^2 + \frac{1}{2}I_{\textsf{CM}}^2ω^2 + mgh$$En ausencia de fuerzas no conservativas que extraigan la energía del sistema en forma de calor, la energía total de un objeto rodante sin deslizamiento se conserva y es constante durante todo el movimiento. Los ejemplos en los que no se conserva la energía son un objeto rodante que se desliza, la producción de calor como resultado de la fricción cinética y un objeto rodante que encuentra resistencia al aire.
Puedes preguntar por qué un objeto rodante que no se desliza conserva energía, ya que la fuerza de fricción estática no es conservadora. La respuesta se puede encontrar haciendo referencia a la .
El punto $P$ en contacto con la superficie está en reposo con respecto a la superficie. Por lo tanto, su desplazamiento infinitesimal $d \overrightarrow{\bold{r}}$ con respecto a la superficie es cero, y el trabajo incremental hecho por la fuerza de fricción estática es cero. Podemos aplicar la conservación de la energía a nuestro estudio del movimiento de rotación para sacar algunos resultados interesantes.
Ejemplo 2.3
Curiosity Rover
El rover Curiosity, que se muestra en la , se desplegó en Marte el 6 de agosto de 2012. Las ruedas del rover tienen un radio de $25 cm$. Supongamos que los astronautas llegan a Marte en el año 2050 y encuentran al Curiosity ahora inoperativa en el costado de una cuenca. Mientras están desmantelando el rover, un astronauta accidentalmente pierde un agarre en una de las ruedas, que rueda sin deslizarse hacia abajo en el fondo de la cuenca a $25$ metros abajo. Si la rueda tiene una masa de $5 kg$, ¿cuál es su velocidad en la parte inferior de la cuenca?
Estrategia
Usamos la conservación de la energía mecánica para analizar el problema. En la cima de la colina, la rueda está en reposo y solo tiene energía potencial. En el fondo de la cuenca, la rueda tiene energía cinética de rotación y de traslación, que debe ser igual a la energía potencial inicial mediante la conservación de la energía. Como la rueda del rover rueda sin deslizarse, utilizamos la relación $v_{\textsf{CM}} = rω$ para relacionar las variables de traslación con las variables de rotación en la ecuación de conservación de energía. Entonces resolvemos la velocidad. En la , vemos que un cilindro hueco es una buena aproximación para la rueda, por lo que podemos utilizar este momento de inercia para simplificar el cálculo.

Solución
La energía en la parte superior de la cuenca equivale a la energía en la parte inferior:
$$mgh = \frac{1}{2}mv_{\textsf{CM}}^2 + \frac{1}{2}I_{\textsf{CM}}^2ω^2$$Las cantidades conocidas son $I_{\textsf{CM}} = mr^2$, $r = 0.25 m$, y $h = 25.0 m$.
Reescribimos la ecuación de conservación de energía eliminando $ω$ usando $ω = \frac{v_{\textsf{CM}}}{r}$. Tenemos, entonces:
$$mgh = \frac{1}{2}mv_{\textsf{CM}}^2 + \frac{1}{2}mr^2\frac{v_{\textsf{CM}}^2}{r^2}$$o
$$gh = \frac{1}{2}v_{\textsf{CM}}^2 + \frac{1}{2}v_{\textsf{CM}}^2 → v_{\textsf{CM}} = \sqrt{gh}$$En Marte, la aceleración de la gravedad es de $3.71 m/s^2$, lo que da la magnitud de la velocidad en el fondo de la cuenca como
$$v_{\textsf{CM}} = \sqrt{(3.71 m/s^2) \, 25.0 m}$$Explicación
Este es un resultado bastante preciso teniendo en cuenta que Marte tiene muy poca atmósfera, y la pérdida de energía debido a la resistencia del aire sería mínima. El resultado también supone que el terreno es liso, de modo que la rueda no se topará con rocas y baches a lo largo del camino.
Además, en este ejemplo, la energía cinética, o energía del movimiento, se comparte por igual entre el movimiento lineal y rotacional. Si miramos los momentos de inercia en la , vemos que el cilindro hueco tiene el mayor momento de inercia para un radio y masa dados. Si las ruedas del rover fueran sólidas y se aproximaran mediante cilindros sólidos, por ejemplo, habría más energía cinética en el movimiento lineal que en el movimiento rotatorio. Esto daría a la rueda una mayor velocidad lineal que la aproximación de cilindro hueco. Por lo tanto, el cilindro sólido llegaría al fondo del tanque más rápido que el cilindro hueco.
Una simulación para los dos cilindros (sólido y hueco), la presentamos a continuación, la cual fue diseñada por Juan Guillermo Rivera Berrío. Puedes cambiar el valor del ángulo de inclinación.
Por otra parte, en el siguiente apartado, estudiaremos la naturaleza vectorial del momento angular, cómo hallar el momento angular total y el torque sobre un origen designado de un sistema de partículas, el momento angular de un cuerpo rígido que gira alrededor de un eje fijo, el torque en un cuerpo rígido que gira alrededor de un eje fijo y la utilización de la conservación del momento angular en el análisis de objetos que cambian su velocidad de rotación.
¿Por qué la Tierra sigue girando? ¿Qué la hizo girar para empezar? ¿Por qué la atracción gravitacional de la Tierra no atrae a la Luna hacia la Tierra? ¿Y cómo un patinador de hielo puede girar cada vez más rápido simplemente tirando de sus brazos? ¿Por qué no tiene que ejercer un torque para girar más rápido?
Preguntas como estas tienen respuestas basadas en el momento angular, el análogo de rotación al momento lineal. En este capítulo, primero definimos y luego exploramos el momento angular desde una variedad de puntos de vista. Primero, sin embargo, investigamos el momento angular de una sola partícula. Esto nos permite desarrollar un momento angular para un sistema de partículas y para un cuerpo rígido que es cilíndricamente simétrico.
La muestra una partícula en una posición $\overrightarrow{\bold{r}}$ con un momento lineal $\overrightarrow{\bold{p}} = m \overrightarrow{\bold{v}}$ con respecto al origen. Incluso si la partícula no está girando sobre el origen, aún podemos definir un momento angular en términos del vector de posición y el momento lineal.
Momento angular de una particula
El momento angular $\overrightarrow{\bold{l}}$ de una partícula se define como el producto cruzado de $\overrightarrow{\bold{r}}$ y $\overrightarrow{\bold{p}}$, y es perpendicular al plano que contiene $\overrightarrow{\bold{r}}$ y $\overrightarrow{\bold{p}}$:
$$\overrightarrow{\bold{l}} = \overrightarrow{\bold{r}} × \overrightarrow{\bold{p}} \tag{2.5}$$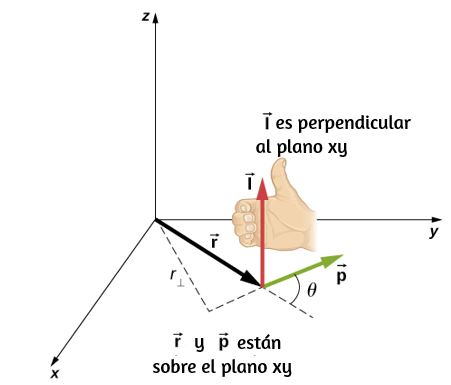
La intención de elegir la dirección del momento angular para que sea perpendicular al plano que contiene $\overrightarrow{\bold{r}}$ y $\overrightarrow{\bold{p}}$ es similar a elegir la dirección del torque para que sea perpendicular al plano de $\overrightarrow{\bold{r}}$ y $\overrightarrow{\bold{F}}$, como se explica en el capítulo I. La magnitud del momento angular se encuentra a partir de la definición del producto cruz,
$$\overrightarrow{\bold{l}} = rpsenθ$$donde $θ$ es el ángulo entre $\overrightarrow{\bold{r}}$ y $\overrightarrow{\bold{p}}$. Las unidades de momento angular son $kg \cdot m^2/s$.
Al igual que con la definición de torque, podemos definir un brazo de palanca $r⊥$ que es la distancia perpendicular desde el vector de momento $\overrightarrow{\bold{p}}$ al origen, $r⊥ = rsenθ$. Con esta definición, la magnitud del momento angular se vuelve
$$l = r⊥p = r⊥mv$$Vemos que si la dirección de $\overrightarrow{\bold{p}}$ es tal que pasa por el origen, entonces $θ = 0$, y el momento angular es cero porque el brazo de palanca es cero. A este respecto, la magnitud del momento angular depende de la elección del origen.
Si tomamos la derivada temporal del momento angular, llegamos a una expresión para el torque en la partícula:
$$\frac{d\overrightarrow{\bold{l}}}{dt} = \frac{d\overrightarrow{\bold{r}}}{dt} × \overrightarrow{\bold{p}} + \overrightarrow{\bold{r}} × \frac{d\overrightarrow{\bold{p}}}{dt} = \overrightarrow{\bold{v}} × m\overrightarrow{\bold{v}} + \overrightarrow{\bold{r}} × \frac{d\overrightarrow{\bold{p}}}{dt} = \overrightarrow{\bold{r}}\frac{d\overrightarrow{\bold{p}}}{dt}$$Aquí hemos utilizado la definición de $\overrightarrow{\bold{p}}$ y el hecho de que un vector cruz en sí mismo es cero. De la segunda ley de Newton, $\frac{d\overrightarrow{\bold{p}}}{dt} = \sum \overrightarrow{\bold{F}}$, la fuerza neta que actúa sobre la partícula, y la definición del torque neto, podemos escribir
Observa la similitud con el resultado lineal de la segunda ley de Newton, $\frac{d \overrightarrow{\bold{p}}}{dt} = \sum \overrightarrow{\bold{F}}$.
La siguiente estrategia de resolución de problemas puede servir como una guía para calcular el momento angular de una partícula.
Estrategia de resolución de problemas: momento angular de una partícula
1. Elige un sistema de coordenadas sobre el cual se calculará el momento angular.
2. Escribe el vector $\overrightarrow{\bold{r}}$ de la partícula en la notación de vector unitario.
3. Escribe el vector de momento lineal de la partícula en la notación de vector unitario.
4. Toma el producto cruz $\overrightarrow{\bold{l}} = \overrightarrow{\bold{r}} × \overrightarrow{\bold{p}}$ y usa la regla de la mano derecha para establecer la dirección del vector de momento angular.
5. Observa si hay una dependencia de tiempo en la expresión del vector de momento angular. Si existe, entonces existe un torque sobre el origen, y debes usar $\frac{d \overrightarrow{\bold{l}}}{dt} = \sum \overrightarrow{τ}$ para calcular el torque. Si no hay dependencia del tiempo en la expresión del momento angular, entonces el torque neto es cero.
Ejemplo 2.4
Momento angular y torque en un meteorito
Un meteorito entra en la atmósfera de la Tierra () y es observado por alguien en el suelo antes de que se incendie en la atmósfera. El vector $\overrightarrow{\bold{r}} = 25km\^{i} + 25km\^{j}$ da la posición del meteoro con respecto al observador. En el instante en que el observador ve el meteoro, tiene un momento lineal $\overrightarrow{\bold{p}} = 15.0kg (-2.0 km/s\^{j})$, y se está acelerando a una constante de $2.0 m/s^2(-\^{j})$ a lo largo de su trayectoria, que para nuestros propósitos puede ser tomado como una línea recta.
(a) ¿Cuál es el momento angular del meteoro sobre el origen, que está en la ubicación del observador?
(b) ¿Cuál es el torque en el meteoro sobre el origen?
Estrategia
Hallamos la aceleración en componentes $x$ e $y$ usamos las ecuaciones cinemáticas para expresar la velocidad en función de la aceleración y el tiempo. Insertamos estas expresiones en el momento lineal y luego calculamos el momento angular usando el producto cruz.
Dado que los vectores de posición y momento están en el plano $xy$, esperamos que el vector de momento angular esté a lo largo del eje $z$. Para encontrar el torque, tomamos la derivada de tiempo del momento angular.
Solución
El meteoro está entrando a la atmósfera de la Tierra en un ángulo de $90.0°$ por debajo de la horizontal, por lo que los componentes de la aceleración en las direcciones $x$ e $y$ son
$$a_x = 0, a_y = -2.0 m/s^2$$Escribimos las velocidades usando las ecuaciones cinemáticas.
$$v_x = 0, v_y = -2.0 × 10^3 m/s - (2.0 m/s^2)t$$a. El momento angular es
$$\begin{split} \overrightarrow{\bold{l}} &= \overrightarrow{\bold{r}} × \overrightarrow{\bold{r}} = (25.0km\^{i} + 25.0km\^{j}) × 15.0 kg(0\^{i} + v_y\^{j}) \\ &= 15.0 kg[25.0 km(v_y)\^{k}] \\ &= 15.0 kg[2.50 × 10^4 m(-2.0 × 10^3 m/s - (2.0 m/s^2)t)\^{k}] \end{split}$$En $t = 0$, el momento angular del meteoro sobre el origen es
Este es el instante en que el observador ve el meteoro.
b. Para encontrar el torque, tomamos la derivada de tiempo del momento angular. Tomando la derivada de tiempo de $\overrightarrow{\bold{l}}$ en función del tiempo, que es la segunda ecuación inmediatamente anterior, tenemos
$$\frac{d\overrightarrow{\bold{l}}}{dt} = -15.0 kg(2.50 × 10^4 m)(2.0 m/s^2)\^{k}$$Luego, ya que, $\frac{d\overrightarrow{\bold{l}}}{dt} = \sum \overrightarrow{τ}$, obtenemos
$$\sum \overrightarrow{τ} = -7.5 × 10^5 N \cdot m\^{k}$$Las unidades de torque se dan como newton-metro, que no deben confundirse con julios. Como comprobación, notamos que el brazo de palanca es la componente $x$ del vector $\overrightarrow{\bold{r}}$ en la ya que es perpendicular a la fuerza que actúa sobre el meteoro, que está a lo largo de su trayectoria. Según la segunda ley de Newton, esta fuerza es
$$\overrightarrow{\bold{F}} = ma(-\^{j}) = 15.0 kg(2.0 m/s^2)(-\^{j}) = 30.0 kg \cdot m/s^2(-\^{j})$$El brazo de la palanca es
$$\overrightarrow{\bold{r}}⊥ = 2.5 × 10^4 m\^{i}$$Por lo tanto, el torque es
Explicación
Dado que el meteoro está acelerando hacia la Tierra, su radio y su vector de velocidad están cambiando. Por lo tanto, dado que $\overrightarrow{\bold{l}} = \overrightarrow{\bold{r}} × \overrightarrow{\bold{p}}$, el momento angular está cambiando en función del tiempo. Sin embargo, el torque en el meteoro sobre el origen es constante, porque el brazo de palanca $\overrightarrow{\bold{r}}⊥$ y la fuerza en el meteoro son constantes. Este ejemplo es importante porque ilustra que el momento angular depende de la elección del origen sobre el que se calcula. Los métodos utilizados en este ejemplo también son importantes para desarrollar el momento angular para un sistema de partículas y para un cuerpo rígido.
 Comprueba tu aprendizaje 2.2
Comprueba tu aprendizaje 2.2
Un protón que gira en espiral alrededor de un campo magnético ejecuta un movimiento circular en el plano del papel, como se muestra a continuación. La trayectoria circular tiene un radio de $0,4 m$ y el protón tiene una velocidad de $4,0 × 10^6 m/s$. ¿Cuál es el momento angular del protón sobre el origen?

El momento angular de un sistema de partículas es importante en muchas disciplinas científicas, una de ellas es la astronomía. Considere una galaxia espiral, una isla giratoria de estrellas como nuestra propia Vía Láctea. Las estrellas individuales pueden tratarse como partículas puntuales, cada una de las cuales tiene su propio momento angular. La suma del vector de los momentos angulares individuales da el momento angular total de la galaxia. En esta sección, desarrollamos las herramientas con las cuales podemos calcular el momento angular total de un sistema de partículas.
En la sección anterior, presentamos el momento angular de una partícula individual sobre un origen designado. La expresión de este momento angular es $\overrightarrow{\bold{l}} = \overrightarrow{\bold{r}} × \overrightarrow{\bold{p}}$, donde el vector $\overrightarrow{\bold{r}}$ está desde el origen hasta la partícula, y $\overrightarrow{\bold{p}}$ es el momento lineal de la partícula. Si tenemos un sistema de $N$ partículas, cada una con un vector de posición del origen dado por $\overrightarrow{\bold{r}}_i$ y cada una con un momento $\overrightarrow{\bold{p}}_i$, entonces el momento angular total del sistema de partículas sobre el origen es la suma del vector de los momentos angulares individuales sobre el origen. Es decir,
De forma similar, si la partícula $i$ está sujeta a un torque neto $\overrightarrow{\bold{τ}}_i$ sobre el origen, entonces podemos encontrar el torque neto sobre el origen debido al sistema de partículas al diferenciar la ecuación 2.7:
La suma de los torques individuales produce un torque externo neto en el sistema, que designamos $\sum \overrightarrow{\bold{τ}}_i$. Así,
La ecuación 2.8 establece que la tasa de cambio del momento angular total de un sistema es igual al torque externo neto que actúa en el sistema cuando ambas cantidades se miden con respecto a un origen dado. La ecuación 2.8 se puede aplicar a cualquier sistema que tenga un momento angular neto, incluidos los cuerpos rígidos, como se analiza en la siguiente sección.
Ejemplo 2.5
Momentum angular de tres partículas
Con referencia a la (a), determina el momento angular total debido a las tres partículas sobre el origen. (b) ¿Cuál es la tasa de cambio del momento angular?
Estrategia
Escribe la posición y los vectores de momento para las tres partículas. Calcula los momentos angulares individuales y súmalos como vectores para encontrar el momento angular total. Luego haz lo mismo para los torques.
Solución
a. Partícula 1: $\overrightarrow{\bold{r}}_1 = -2.0 m\^{i} + 1.0 m\^{j}$, $\overrightarrow{\bold{p}}_1 = 2.0 kg (4.0 m/s\^{j}) = 8.0 kg \cdot m/s\^{j}$, $\overrightarrow{\bold{l}}_1 = \overrightarrow{\bold{r}}_1 × \overrightarrow{\bold{p}}_1 = -16.0 kg \cdot m^2/s\^{k}$.
Partícula 2: $\overrightarrow{\bold{r}}_2 = 4.0 m\^{i} + 1.0 m\^{j}$, $\overrightarrow{\bold{p}}_2 = 4.0 kg(5.0 m/s\^{i}) = 20.0 kg \cdot m/s\^{i}$, $\overrightarrow{\bold{l}}_2 = \overrightarrow{\bold{r}}_2 × \overrightarrow{\bold{p}}_2 = -20.0 kg \cdot m^2/s\^{k}$.
Partícula 3: $\overrightarrow{\bold{r}}_3 = 2.0 m\^{i} - 2.0 m\^{j}$, $\overrightarrow{\bold{p}}_3 = 1.0 kg(3.0 m/s\^{i}) = 3.0 kg \cdot m/s\^{i}$, $\overrightarrow{\bold{l}}_3 = \overrightarrow{\bold{r}}_3 × \overrightarrow{\bold{p}}_3 = 6.0kg \cdot m^2/s\^{k}$.
Sumamos los momentos angulares individuales para encontrar el total sobre el origen:
$$\overrightarrow{\bold{l}}_T = \overrightarrow{\bold{l}}_1 + \overrightarrow{\bold{l}}_2 + \overrightarrow{\bold{l}}_3 = -30kg \cdot m^2/s\^{k}$$b. Las fuerzas individuales y los brazos de palanca son
$$\overrightarrow{\bold{r}}_1⊥ = 1.0 m\^{j}, \overrightarrow{\bold{F}}_1 = -6.0 N\^{i}, \overrightarrow{τ}_1 = 6.0 N \cdot m\^{k}$$ $$\overrightarrow{\bold{r}}_2⊥ = 4.0 m\^{i}, \overrightarrow{\bold{F}}_2 = 10.0 N\^{j}, \overrightarrow{τ}_2 = 40.0 N \cdot m\^{k}$$ $$\overrightarrow{\bold{r}}_3⊥ = 2.0 m\^{i}, \overrightarrow{\bold{F}}_3 = -8.0 N\^{j}, \overrightarrow{τ}_3 = -16.0 N \cdot m\^{k}$$Por lo tanto
$$\sum_i \overrightarrow{\bold{τ}}_i = \overrightarrow{\bold{τ}}_1 + \overrightarrow{\bold{τ}}_2 + \overrightarrow{\bold{τ}}_3 = 30 N \cdot m\^{k}$$Explicación
Este ejemplo ilustra el principio de superposición para el momento angular y el torque de un sistema de partículas. Se debe tener cuidado al evaluar los vectores de radio $\overrightarrow{\bold{r}}_i$ de las partículas para calcular los momentos angulares, y los brazos de palanca, $\overrightarrow{\bold{r}}_1⊥$ para calcular los torques, ya que son cantidades completamente diferentes.
En la siguiente escena interactiva, diseñada por Juan Guillermo Rivera Berrío, puedes practicar el ejemplo anterior para diferentes posiciones y valores del momento angular. Copia los datos y resuelve el ejercicio, luego escribe tu resultado en el cuadro de texto para verificarlo.
Hemos investigado el momento angular de una sola partícula, que hemos generalizado a un sistema de partículas. Ahora podemos usar los principios discutidos en la sección anterior para desarrollar el concepto del momento angular de un cuerpo rígido. Los objetos celestes, como los planetas, tienen un momento angular debido a su giro y órbitas alrededor de las estrellas. En ingeniería, todo lo que gira alrededor de un eje transporta momento angular, como volantes, hélices y piezas giratorias en los motores. El conocimiento de los momentos angulares de estos objetos es crucial para el diseño del sistema en el que forman parte.
Para hallar el momento angular de un cuerpo rígido, modelamos un cuerpo rígido formado por pequeños segmentos de masa, $Δm_i$. En la , un cuerpo rígido está obligado a girar alrededor del eje $z$ con una velocidad angular $ω$. Todos los segmentos de masa que componen el cuerpo rígido experimentan un movimiento circular alrededor del eje $z$ con la misma velocidad angular. La parte (a) de la figura muestra el segmento de masa $Δm_i$ con el vector de posición $\overrightarrow{\bold{r}}_i$ desde el origen y el radio $R_i$ con respecto al eje $z$. La magnitud de su velocidad tangencial es $v_i = R_iω$. Debido a que los vectores $\overrightarrow{\bold{v}}_i$ y $\overrightarrow{\bold{r}}_i$ son perpendiculares entre sí, la magnitud del momento angular de este segmento de masa es
$$l_i = r_i(Δmv_i)sen90°$$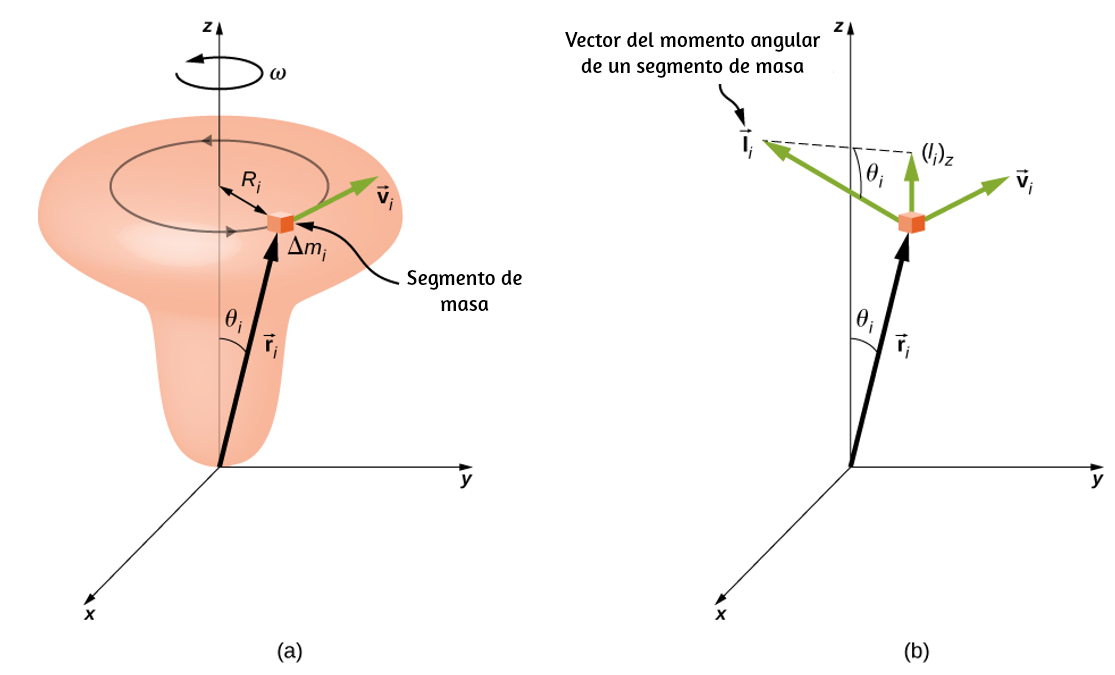
Usando la regla de la mano derecha, el vector de momento angular apunta en la dirección que se muestra en la parte (b). La suma de los momentos angulares de todos los segmentos de masa contiene componentes tanto a lo largo como perpendiculares al eje de rotación.
Cada segmento de masa tiene una componente perpendicular del momento angular que será cancelada por la componente perpendicular de un segmento de masa idéntico en el lado opuesto del cuerpo rígido, porque es cilíndricamente simétrico. Por lo tanto, el componente a lo largo del eje de rotación es el único componente que da un valor distinto de cero cuando se suma a todos los segmentos de masa. De la parte (b), el componente de $\overrightarrow{\bold{l}}_i$ a lo largo del eje de rotación es
$$\begin{split} (l_i)_z &= l_isenθ_i = (r_iΔm_iv_i)senθ_i \\ &= (r_isenθ_i)(Δm_iv_i) = R_iΔm_iv_i \end{split}$$El momento angular neto del cuerpo rígido a lo largo del eje de rotación es
La suma $\sum Δm_i(R_i)^2$ es simplemente el momento de inercia $I$ del cuerpo rígido alrededor del eje de rotación. Para un aro delgado que gira alrededor de un eje perpendicular al plano del aro, todos los $R_i$ son iguales a $R$, por lo que la suma se reduce a $R^2 \sum Δm_i = mR^2$, que es el momento de inercia de un aro delgado que se ve en la . Por lo tanto, la magnitud del momento angular a lo largo del eje de rotación de un cuerpo rígido que gira con una velocidad angular $ω$ alrededor del eje es
Esta ecuación es análoga a la magnitud del momento lineal $p = mv$. La dirección del vector de momento angular se dirige a lo largo del eje de rotación dado por la regla de la mano derecha.
Ejemplo 2.6
Momento angular de un brazo de robot
Un brazo robótico en un explorador de Marte como Curiosity que se muestra en la tiene $1.0 m$ de largo y tiene pinzas en el extremo libre para recoger rocas.
La masa del brazo es de $2,0$ kg y la masa del fórceps es de $1,0 kg$ (Ver la ). El brazo del robot y las pinzas se mueven desde el reposo a $ω = 0.1π rad/s$ en $0.1 s$. Gira hacia abajo y recoge una roca de Marte que tiene una masa de $1,5 kg$. El eje de rotación es el punto donde el brazo del robot se conecta al rover.
(a) ¿Cuál es el momento angular del brazo del robot por sí mismo sobre el eje de rotación después de $0.1$ s cuando el brazo ha dejado de acelerar?
(b) ¿Cuál es el momento angular del brazo del robot cuando tiene la roca de Marte en su fórceps y está girando hacia arriba?
(c) Cuando el brazo no tiene una roca en el fórceps, ¿cuál es el torque sobre el punto donde el brazo se conecta al rover cuando está acelerando desde el reposo hasta su velocidad angular final?
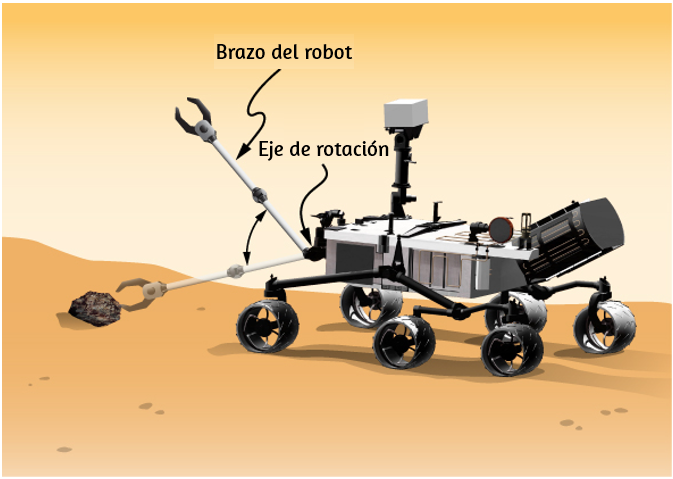
Estrategia
Usamos la Ecuación 2.9 para encontrar el momento angular en las diversas configuraciones. Cuando el brazo está girando hacia abajo, la regla de la mano derecha da el vector de momento angular dirigido fuera de la página, que llamaremos la dirección $z$ positiva. Cuando el brazo está girando hacia arriba, la regla de la mano derecha proporciona la dirección del vector de momento angular en la página o en la dirección $z$ negativa. El momento de inercia es la suma de los momentos individuales de inercia. El brazo se puede aproximar con una barra sólida, y las pinzas y la roca de Marte se pueden aproximar como masas puntuales ubicadas a una distancia de $1 m$ del origen. Para la parte (c), usamos la segunda ley de movimiento de Newton para la rotación para encontrar el torque en el brazo del robot.
Solución
a. Escribiendo los momentos individuales de inercia, tenemos
Brazo del robot: $I_R = \frac{1}{3}m_Rr^2 = \frac{1}{3}(2.00 kg)(1.00 m)^2 = \frac{2}{3}kg \cdot m^2$.
Fórceps: $I_F = m_Fr^2 = (1.0 kg)(1.0 m)^2 = 1.0 kg \cdot m^2$.
Roca de Marte: $I_{MR} = m_{MR}r^2 = (1.5 kg)(1.0 m)^2 = 1.5 kg \cdot m^2$.
Por lo tanto, sin la roca de Marte, el momento total de inercia es
$$I_{\textsf{total}} = I_R + I_F = 1.67 kg \cdot m^2$$y la magnitud del momento angular es
$$L = Iω = 1.67 kg \cdot m^2(0.1π rad/s) = 0.17π kg \cdot m^2/s$$El vector de momento angular se dirige fuera de la página en la dirección $\^{k}$ ya que el brazo del robot está girando en sentido antihorario.
b. Debemos incluir la roca de Marte en el cálculo del momento de inercia, por lo que tenemos
$$I_{\textsf{total}} = I_R + I_F + I_{MR} = 3.17 kg \cdot m^2$$y
$$L = Iω = 3.17 kg \cdot m^2(0.1π rad/s) = 0.32π kg \cdot m^2/s$$Ahora el vector de momento angular se dirige a la página en la dirección $-\^{k}$, por la regla de la mano derecha, ya que el brazo del robot ahora está girando en el sentido de las agujas del reloj.
c. Encontramos el torque cuando el brazo no tiene la roca tomando la derivada del momento angular usando la Ecuación 2.8
$$\frac{d \overrightarrow{\bold{L}}}{dt} = \sum τ$$Pero como $L = Iω$, y entendiendo que la dirección del momento angular y los vectores de torque están a lo largo del eje de rotación, podemos suprimir la notación vectorial y encontrar
$$\frac{dL}{dt} = \frac{d(Iω)}{dt} = I\frac{dω}{dt} = Iα = \sum τ$$que es la segunda ley de Newton para la rotación. Dado que $α = \dfrac{0.1π rad/s}{0.1 s} = π rad/s^2$, podemos calcular el torque neto:
$$\sum τ = Iα = 1.67 kg \cdot m^2(π rad/s^2) = 1.67π N \cdot m$$Explicación
El momento angular en (a) es menor que el de (b) debido al hecho de que el momento de inercia en (b) es mayor que (a), mientras que la velocidad angular es la misma.
 Comprueba tu aprendizaje 2.3
Comprueba tu aprendizaje 2.3
Hasta ahora, hemos analizado el momento angular de los sistemas compuestos por partículas puntuales y cuerpos rígidos. También hemos analizado los torques involucrados, usando la expresión que relaciona el par neto externo con el cambio en el momento angular (Ecuación 2.8). Los ejemplos de sistemas que obedecen esta ecuación incluyen un neumático de bicicleta que gira libremente que se ralentiza con el tiempo debido al par provocado por la fricción o la ralentización de la rotación de la Tierra durante millones de años debido a las fuerzas de fricción ejercidas sobre las deformaciones de las mareas.
Sin embargo, supongamos que no existe un torque externo neto en el sistema, $\sum \overrightarrow{τ} = 0$. En este caso, la Ecuación 2.8 se convierte en la ley de conservación del momento angular.
Ley de conservación del momento angular
El momento angular de un sistema de partículas alrededor de un punto en un marco de referencia inercial fijo se conserva si no hay un torque externo neto alrededor de ese punto:
$$\frac{d\overrightarrow{\bold{L}}}{dt} = 0 \tag{2.10}$$ o $$\overrightarrow{\bold{L}} = \overrightarrow{\bold{l}}_1 + \overrightarrow{\bold{l}}_2 + \overrightarrow{\bold{l}}_3 + ⋅⋅⋅ + \overrightarrow{\bold{l}}_N = constante \tag{2.11}$$Tenga en cuenta que el momento angular total $\overrightarrow{\bold{L}}$ es conservado. Cualquiera de los momentos angulares individuales puede cambiar siempre que su suma permanezca constante. Esta ley es análoga al momento lineal que se conserva cuando la fuerza externa en un sistema es cero.
Como ejemplo de conservación del momento angular, la muestra una patinadora sobre hielo ejecutando un giro. El torque neto en ella es muy cercano a cero porque hay relativamente poca fricción entre sus patines y el hielo. Además, la fricción se ejerce muy cerca del punto de pivote. Ambos $|\overrightarrow{\bold{F}}|$ y $|\overrightarrow{\bold{r}}|$ son pequeños, entonces $|\overrightarrow{τ}|$ es despreciable. En consecuencia, ella puede girar durante bastante tiempo. También puede aumentar su velocidad de giro tirando de sus brazos y piernas. ¿Por qué tira de sus brazos y piernas para aumentar su velocidad de giro? La respuesta es que su momento angular es constante, por lo que
$$L' = L$$o
$$I'ω' = Iω$$donde las cantidades a la izquierda (prima) se refieren a las condiciones después de que ella ha jalado a sus brazos y reducido su momento de inercia. Como $I'$ es más pequeño, la velocidad angular $ω'$ debe aumentar para mantener constante el momento angular.
Es interesante ver cómo la energía cinética de rotación de la patinadora cambia cuando empuja sus brazos hacia adentro. Su energía de rotación inicial es
$$K_{\textsf{rot}} = \frac{1}{2}Iω^2$$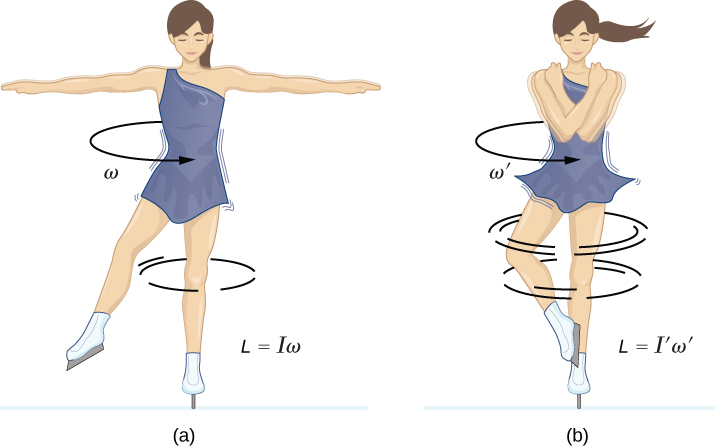
mientras que su energía de rotación final es
$$K'_{\textsf{rot}} = \frac{1}{2}I'(ω')^2$$Como $I'ω' = Iω$, podemos sustituir a $ω'$ y encontrar
$$K'_{\textsf{rot}} = \frac{1}{2}I'(ω')^2 = \frac{1}{2}I' \left(\frac{I}{I'}ω \right)^2 = \frac{1}{2}Iω^2 \left(\frac{I}{I'} \right) = K_{\textsf{rot}} \left(\frac{I}{I'} \right)$$En la siguiente imagen animada, observa cómo la patinadora Natalia Kanounnikov rompe el record mundial en 2010, al girar $308 RPM$.

Debido a que su momento de inercia ha disminuido, $I' < I$, su energía cinética de rotación final ha aumentado. La fuente de esta energía cinética giratoria adicional es el trabajo requerido para tirar de sus brazos hacia adentro. Ten en cuenta que los brazos de la patinadora no se mueven en un círculo perfecto, sino que se mueven en espiral hacia adentro. Este trabajo causa un aumento en la energía cinética de rotación, mientras que su momento angular permanece constante. Como ella está en un entorno sin fricciones, no escapa energía del sistema.
Por lo tanto, si extendiera sus brazos a sus posiciones originales, rotaría a su velocidad angular original y su energía cinética volvería a su valor original.
El sistema solar es otro ejemplo de cómo funciona la conservación del momento angular en nuestro universo. Nuestro sistema solar nació de una enorme nube de gas y polvo que inicialmente tenía energía de rotación.
Las fuerzas gravitacionales causaron que la nube se contrajera, y la velocidad de rotación aumentó como resultado de la conservación del momento angular ().
Continuamos nuestra discusión con un ejemplo que tiene aplicaciones para la ingeniería.
Ejemplo 2.7
Volantes acoplados
Un volante gira sin fricción a una velocidad angular $ω_0 = 600 rev/min$ en un eje vertical sin fricción de insignificante inercia rotacional. Se deja caer un segundo volante, que está en reposo y tiene un momento de inercia tres veces mayor que el del volante giratorio (). Debido a que existe fricción entre las superficies, los volantes alcanzan rápidamente la misma velocidad de rotación, después de lo cual giran juntos. (a) Usa la ley de conservación del momento angular para determinar la velocidad angular $ω$ de la combinación. (b) ¿Qué fracción de la energía cinética inicial se pierde en el acoplamiento de los volantes?
Estrategia
La parte (a) es fácil de resolver para la velocidad angular del sistema acoplado. Usamos el resultado de (a) para comparar las energías cinéticas inicial y final del sistema en la parte (b).
Solución
a. No hay torques externos que actúen en el sistema.
La fuerza debida a la fricción produce un torque interno, que no afecta el momento angular del sistema. Por lo tanto, la conservación del momento angular da
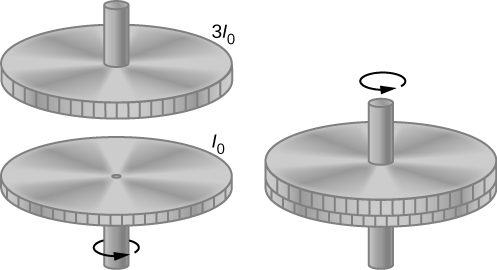
b. Antes del contacto, solo un volante está girando. La energía cinética de rotación de este volante es la energía cinética de rotación inicial del sistema, $\frac{1}{2}I_0ω_0^2$. La energía cinética final es $\frac{1}{2}(4I_0)ω^2 = \frac{1}{2}(4I_0)(ω_0/4)^2 = \frac{1}{8}I_0ω_0^2$. Por lo tanto, la relación de la energía cinética final a la energía cinética inicial es
$$\frac{(1/8)I_0ω_0^2}{(1/2)I_0ω_0^2} = \frac{1}{4}$$Por lo tanto, $3/4$ de la energía cinética inicial se pierde al acoplar los dos volantes.
Explicación
Dado que la inercia rotacional del sistema aumentó, la velocidad angular disminuyó, como se esperaba de la ley de conservación del momento angular. En este ejemplo, vemos que la energía cinética final del sistema ha disminuido, ya que la energía se pierde al acoplar los volantes. Compara esto con el ejemplo de la patinadora en la que hace un trabajo para llevar sus brazos hacia adentro y agregar energía cinética de rotación.
 Comprueba tu aprendizaje 2.4
Comprueba tu aprendizaje 2.4
Ejemplo 2.8
Desmontar de una Barra Alta
Un gimnasta de $80.0 kg$ se desmonta de una barra alta. Él comienza el desmontaje en extensión completa, luego se pliega para completar un número de revoluciones antes de aterrizar. Su momento de inercia cuando está completamente extendido se puede aproximar como una vara de $1,8 m$ de longitud y cuando se coloca una vara de la mitad de esa longitud. Si su tasa de rotación en extensión completa es $1.0 rev/s$, y él ingresa en la posición de relleno cuando su centro de masa está a $3.0 m$ de altura moviéndose horizontalmente al piso, ¿cuántas revoluciones puede ejecutar si sale de la curvatura a una altura de $1.8 m$? (Observa la ).
Estrategia
Utilizando la conservación del momento angular, podemos encontrar su índice de rotación cuando está plegado. Usando las ecuaciones de la cinemática, podemos encontrar el intervalo de tiempo desde una altura de $3.0 m$ hasta $1.8 m$. Como se mueve horizontalmente con respecto al suelo, las ecuaciones de caída libre se simplifican. Esto permitirá que se calcule el número de revoluciones que se pueden ejecutar. Como usamos una razón, podemos mantener las unidades como $rev/s$ y no necesitamos convertirlas a $radianes/s$.
Solución
El momento de inercia en extensión completa es $I_0 = \frac{1}{12}mL^2 = \frac{1}{12}80.0 kg(1.8 m)^2 = 21.6 kg \cdot m^2$
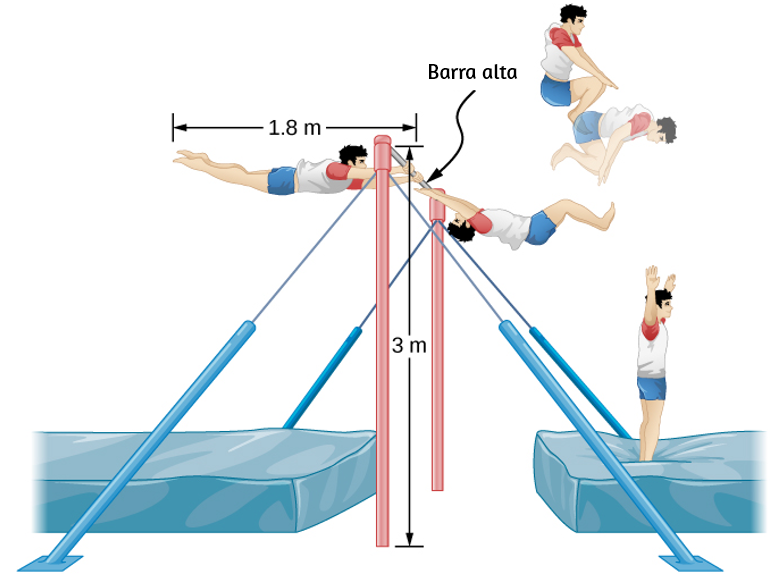
El momento de inercia en posición plegada es $I_p = \frac{1}{12}mL_p^2 = \frac{1}{12}80.0 kg(0.9 m)^2 = 5.4 kg \cdot m^2$
La conservación del momento angular:
$$I_pω_p = I_0ω_0 → ω_p = \frac{I_0ω_0}{I_p} = \frac{21.6 kg \cdot m^2(1.0 rev/s)}{5.4 kg \cdot m^2} = 4.0 rev/s$$El intervalo de tiempo en el plegado:
$$t = \sqrt{2h/g} = \sqrt{2(3.0 -1.8)m/(9.8 m/s)} = 0.5 s$$En $0.5 s$, podrá ejecutar dos revoluciones a $4.0 rev/s$.
Explicación
Observa que la cantidad de revoluciones que puede completar dependerá de cuánto tiempo esté en el aire. En el problema, él está saliendo de la barra alta horizontalmente al suelo. También podría salir en un ángulo con respecto al suelo, dándole más o menos tiempo en el aire dependiendo del ángulo, positivo o negativo, con respecto al suelo. Los gimnastas deben tener esto en cuenta cuando están ejecutando sus desmontajes.
Ejemplo 2.9
Conservación del momento angular de una colisión
Una bala de masa $m = 2.0 g$ se mueve horizontalmente con una velocidad de $500.0 m/s$. La bala impacta y se incrusta en el borde de un disco sólido de masa $M = 3.2 kg$ y $radio R = 0.5 m$. El cilindro puede girar libremente alrededor de su eje e inicialmente está en reposo (). ¿Cuál es la velocidad angular del disco inmediatamente después de incrustar la bala?
Estrategia
Para el sistema de la bala y el cilindro, ningún torque externo actúa a lo largo del eje vertical a través del centro del disco. Por lo tanto, el momento angular a lo largo de este eje se conserva. El momento angular inicial de la bala es $mvR$, que se toma alrededor del eje de rotación del disco en el momento anterior a la colisión. El momento angular inicial del cilindro es cero. Por lo tanto, el momento angular neto del sistema es $mvR$. Dado que se conserva el momento angular, el momento angular inicial del sistema es igual al momento angular de la bala incrustado en el disco inmediatamente después del impacto.
Solución
El momento angular inicial del sistema es
$$L_i = mvR$$El momento de inercia del sistema con la bala incrustada en el disco es
$$I = mR^2 + \frac{1}{2}MR^2 = (m + M/2)R^2$$El momento angular final del sistema es
$$L_i = Iω_f$$Por lo tanto, mediante la conservación del momento angular, $L_i = L_i$ y
$$mvR = (m + M/2)R^2ω_f$$resolviendo para $ω_f$
$$ω_f = \frac{mvR}{(m + M/2)R^2} = \frac{(2.0 × 10^{-3} kg)(500.0 m/s)}{(2.0 × 10^{-3} kg + 1.6 kg)(0.50 m)}$$Explicación
El sistema está compuesto de una partícula puntual y un cuerpo rígido. Se debe tener cuidado al formular el momento angular antes y después de la colisión. Justo antes del impacto, el momento angular de la bala se toma alrededor del eje de rotación del disco.
La muestra un giroscopio, definido como un disco giratorio en el que el eje de rotación puede asumir cualquier orientación. Al girar, la orientación del eje de giro no se ve afectada por la orientación del cuerpo que la encierra. El cuerpo o vehículo que rodea el giroscopio se puede mover de un lugar a otro y la orientación del eje de giro seguirá siendo la misma. Esto hace que los giroscopios sean muy útiles en la navegación, especialmente cuando no se pueden usar brújulas magnéticas, como en las naves espaciales tripuladas y no tripuladas, misiles balísticos intercontinentales, vehículos aéreos no tripulados y satélites como el Telescopio Espacial Hubble.

Ilustramos la precesión de un giroscopio con un ejemplo en las siguientes dos figuras. Si la parte superior se coloca sobre una superficie plana cerca de la superficie de la Tierra en un ángulo respecto a la vertical y no gira, se caerá, debido a la fuerza de la gravedad produciendo un torque que actúa sobre su centro de masa. Esto se muestra en la (a).
Sin embargo, si la parte superior está girando sobre su eje, en lugar de caer debido a este torque, precede sobre la vertical, que se muestra en la parte (b) de la figura. Esto se debe al torque en el centro de masa, que proporciona el cambio en el momento angular.
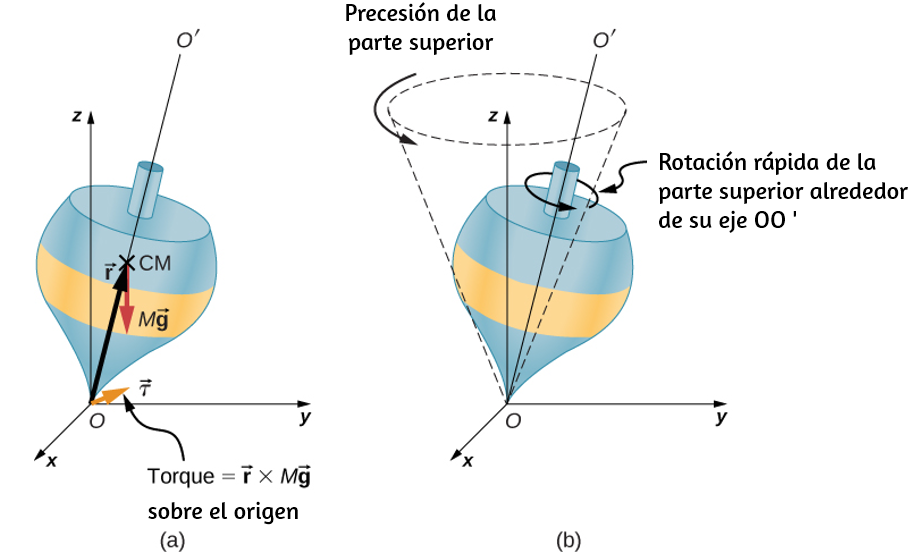
La muestra las fuerzas que actúan sobre un trompo giratorio. El torque producido es perpendicular al vector de momento angular. Esto cambia la dirección del vector de momento angular $\overrightarrow{\bold{L}}$ según $d \overrightarrow{\bold{L}} = \overrightarrow{τ} dt$, pero no su magnitud.
La parte superior precede alrededor de un eje vertical, ya que el torque es siempre horizontal y perpendicular a $\overrightarrow{\bold{L}}$. Si la parte superior no está girando, adquiere un momento angular en la dirección del torque, y gira alrededor de un eje horizontal, cayendo justo como cabría esperar.
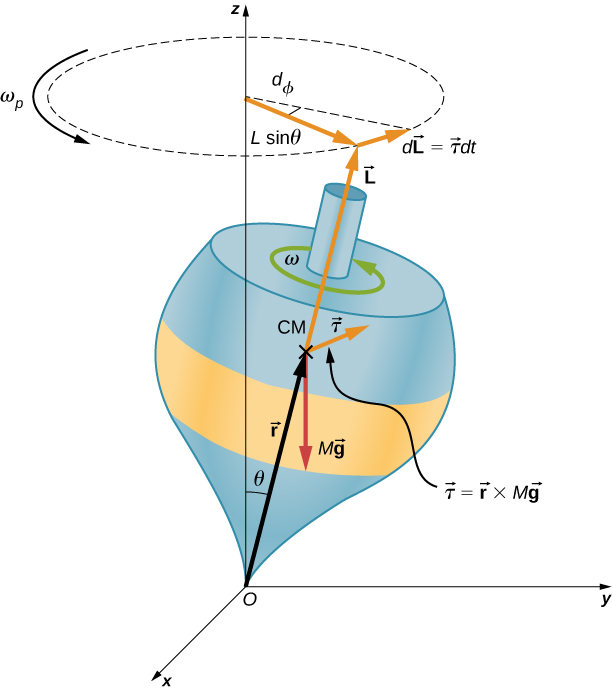
Podemos experimentar este fenómeno de primera mano sujetando una rueda giratoria de bicicleta e intentando girarla alrededor de un eje perpendicular al eje de giro. Como se muestra en la , la persona aplica fuerzas perpendiculares al eje de giro en un intento de girar la rueda, pero en su lugar, el eje de la rueda comienza a cambiar de dirección hacia la izquierda debido al torque aplicado.
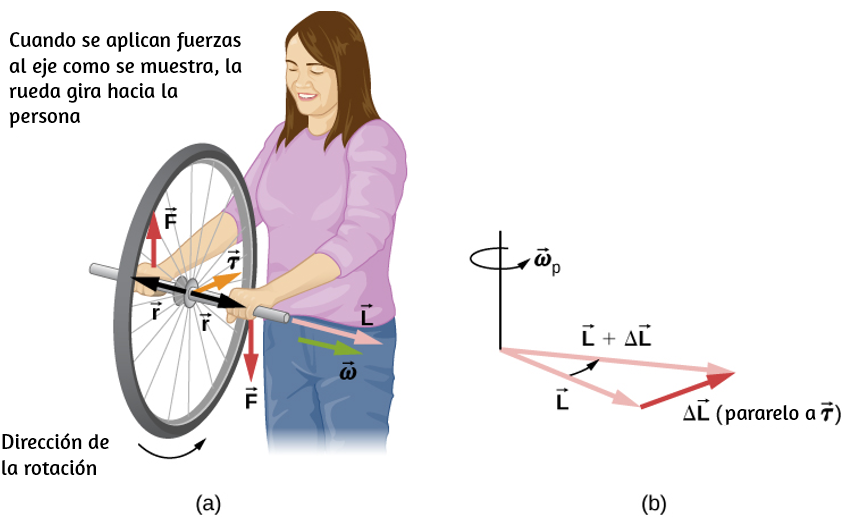
Todos sabemos lo fácil que es para una bicicleta volcarse cuando te sientas en reposo. Pero al andar en bicicleta a un buen ritmo, inclinarla implica cambiar el vector de momento angular de las ruedas giratorias.
En la siguiente escena interactiva, diseñada por Joseph Stephen, se presenta un simulador que muestra cómo funciona la precesión giroscópica. En este simulador, ni las medidas de entrada ni las resultantes son válidas y pueden usarse solo con fines educativos. Observa algunas imágenes resultantes de la interacción con el simulador:
Con clic sostenido, puedes mover el giroscopio. Con la rueda del ratón puedes hacer zoom a la escena.
Cuando coloques un disco giratorio en una caja, como un reproductor de Blu-Ray, intenta moverlo. Es fácil trasladar la caja en una dirección dada pero es difícil girarla sobre un eje perpendicular al eje del disco giratorio, ya que estamos aplicando un par de torsión en la caja que hará que el vector de momento angular del disco giratorio preceda.
Podemos calcular la tasa de precesión de la parte superior en la , en la que la magnitud del torque es
$$τ = rMgsenθ$$Entonces, $$dL = rMgsenθdt$$
El ángulo por el que la parte superior pasa a precesión en el tiempo dt es
$$dφ = \frac{dL}{Lsenθ} = \frac{rMgsenθ}{Lsenθ}dt = \frac{rMg}{L}dt$$La velocidad angular de precesión es $ω_{P } = dφ/dt$ y de esta ecuación vemos que
$$ω_{P } = \frac{rMg}{L}$$ya que $L = Iω$
En esta derivación, supusimos que $ω_P << ω$, es decir, que la velocidad angular de precesión es mucho menor que la velocidad angular del disco del giroscopio.
La velocidad angular de precesión agrega un componente pequeño al momento angular a lo largo del eje $z$. Esto se ve en una ligera sacudida hacia arriba y hacia abajo a medida que el giroscopio avanza, lo que se conoce como nutación.
La Tierra misma actúa como un gigantesco giroscopio. Su momento angular es a lo largo de su eje y actualmente apunta a Polaris, la estrella polar. Pero la Tierra está precesando lentamente (una vez en aproximadamente 26,000 años) debido al torque del Sol y la Luna en su forma no esférica.
Ejemplo 2.10
Período de Precesión
Un giroscopio gira con su punta en el suelo y gira con una resistencia a la fricción despreciable. El disco del giroscopio tiene una masa de $0.3 kg$ y está girando a $20 rev/s$. Su centro de masa está a $5.0 cm$ del pivote y el radio del disco es $5.0 cm$. ¿Cuál es el período de precesión del giroscopio?
Estrategia
Usamos la Ecuación 2.12 para hallar la velocidad angular de precesión del giroscopio. Esto nos permite encontrar el período de precesión.
Solución
El momento de inercia del disco es
$$I = \frac{1}{2}mr^2 = \frac{1}{2}(0.30 kg)(0.05 m)^2 = 3.75 × 10^{-4}kg \cdot m^2$$La velocidad angular del disco es
$$20.0 rev/s = 20.0(2π) rad/s = 125.66 rad/s$$Ahora podemos sustituir en la Ecuación 21.12. La velocidad angular precesional es
$$ω_{P } = \frac{rMg}{Iω} = \frac{(0.05 m)(0.3 kg)(9.8 m/s^2)}{(3.75 × 10^{-4} kg \cdot m^2)(125.66 rad/s)} = 3.12 rad/s$$El período precesional del giroscopio es
$$T_P = \frac{2π}{3.12 rad/s} = 2.0 s$$Explicación
La frecuencia angular precesional del giroscopio, $3.12 rad/s$, o aproximadamente $0.5 rev/s$, es mucho menor que la velocidad angular $20 rev/s$ del disco del giroscopio. Por lo tanto, no esperamos que surja un componente grande del momento angular debido a la precesión, y la ecuación 2.12 es una buena aproximación de la velocidad angular en precesión.
 Comprueba tu aprendizaje 2.5
Comprueba tu aprendizaje 2.5
Antes de proponerte algunos problemas a resolver, relájate con el siguiente juego, diseñado por James O'Toole. Presiona enter (con el ratón en el juego) y con las teclas del desplazamiento, trata de bajar el pajarito.

En capítulos anteriores, aprendiste sobre las fuerzas y las leyes de Newton para el movimiento traslacional. Luego estudiaste los pares y el movimiento de rotación de un cuerpo sobre un eje fijo de rotación. También aprendiste que el equilibrio estático significa que no hay movimiento en absoluto y que el equilibrio dinámico significa movimiento sin aceleración.
En este capítulo, combinamos las condiciones para el equilibrio de traslación estático y el equilibrio rotacional estático para describir situaciones típicas de cualquier tipo de construcción.
¿Qué tipo de cable soportará un puente colgante? ¿Qué tipo de fundación apoyará un edificio de oficinas? ¿Funcionará correctamente este brazo protésico? Estos son ejemplos de preguntas que los ingenieros contemporáneos deben ser capaces de responder.
Las propiedades elásticas de los materiales son especialmente importantes en aplicaciones de ingeniería, incluida la bioingeniería. Por ejemplo, los materiales que se pueden estirar o comprimir y luego regresar a su forma o posición original son buenos amortiguadores. En este capítulo, aprenderás sobre algunas aplicaciones que combinan el equilibrio con la elasticidad para construir estructuras reales que perduren.
Decimos que un cuerpo rígido está enequilibrio cuando tanto su aceleración lineal como angular son cero con respecto a un marco de referencia inercial. Esto significa que un cuerpo en equilibrio puede estar en movimiento, pero si es así, sus velocidades lineales y angulares deben ser constantes. Decimos que un cuerpo rígido está en equilibrio estático cuando está en reposo en nuestro marco de referencia seleccionado. Ten en cuenta que la distinción entre el estado de reposo y un estado de movimiento uniforme es artificial, es decir, un objeto puede estar en reposo en nuestro marco de referencia seleccionado, pero para un observador que se mueve a velocidad constante en relación con nuestro marco, el mismo objeto parece estar en movimiento uniforme con velocidad constante. Como el movimiento es relativo, lo que está en equilibrio estático para nosotros está en equilibrio dinámico con el observador en movimiento, y viceversa. Dado que las leyes de la física son idénticas para todos los marcos de referencia inerciales, en un marco de referencia inercial, no hay distinción entre el equilibrio estático y el equilibrio.
De acuerdo con la segunda ley del movimiento de Newton, la aceleración lineal de un cuerpo rígido es causada por una fuerza neta que actúa sobre él, o
Aquí, la suma es de todas las fuerzas externas que actúan sobre el cuerpo, donde $m$ es su masa y $\overrightarrow{\bold{a}}_{\textsf{CM}}$ es la aceleración lineal de su centro de masa. En equilibrio, la aceleración lineal es cero. Si establecemos la aceleración en cero en la ecuación 3.1, obtenemos la siguiente ecuación:
Primera condición de equilibrio
La primera condición de equilibrio para el equilibrio estático de un cuerpo rígido se expresa en el equilibrio traslacional:
$$\sum_k \overrightarrow{\bold{F}}_k = \overrightarrow{\bold{0}} \tag{3.2}$$La primera condición de equilibrio, la Ecuación 3.2, es la condición de equilibrio para las fuerzas, que encontramos al estudiar las aplicaciones de las leyes de Newton.
Esta ecuación vectorial es equivalente a las siguientes tres ecuaciones escalares para los componentes de la fuerza neta:
$$\sum_k F_{kx} = 0, \;\;\; \sum_k F_{ky} = 0, \;\;\; \sum_k F_{kz} = 0 \tag{3.3}$$Análogamente a la Ecuación 3.1, podemos afirmar que la aceleración rotacional $\overrightarrow{α}$ de un cuerpo rígido alrededor de un eje fijo de rotación es causada por el torque neto que actúa sobre el cuerpo, o
Aquí $I$ es la inercia rotacional del cuerpo en rotación alrededor de este eje y la suma está sobre todos los torques $\overrightarrow{τ}_k$ de las fuerzas externas en la ecuación 3.2. En equilibrio, la aceleración rotacional es cero. Al poner a cero el lado derecho de la Ecuación 3.4, obtenemos la segunda condición de equilibrio:
Segunda condición de equilibrio
La segunda condición de equilibrio para el equilibrio estático de un cuerpo rígido expresa el equilibrio rotacional:
$$\sum_k \overrightarrow{τ}_k = \overrightarrow{\bold{0}} \tag{3.5}$$La segunda condición de equilibrio, la Ecuación 3.5, es la condición de equilibrio para los torques que encontramos cuando estudiamos la dinámica rotacional. Vale la pena señalar que esta ecuación para el equilibrio es generalmente válida para el equilibrio rotacional sobre cualquier eje de rotación (fijo o no). De nuevo, esta ecuación vectorial es equivalente a tres ecuaciones escalares para los componentes del vector del torque neto:
$$\sum_k τ_{kx} = 0, \sum_k τ_{ky} = 0, \sum_k τ_{kz} = 0 \tag{3.6}$$La segunda condición de equilibrio significa que, en equilibrio, no existe un torque externo neto para causar rotación alrededor de ningún eje.
La primera y la segunda condición de equilibrio se establecen en un marco de referencia particular. La primera condición implica solo fuerzas y, por lo tanto, es independiente del origen del marco de referencia. Sin embargo, la segunda condición implica un torque, que se define como un producto cruz, $\overrightarrow{τ}_k = \overrightarrow{\bold{r}}_k × \overrightarrow{\bold{F}}_k$, donde el vector de posición $\overrightarrow{\bold{r}}_k$ con respecto al eje de rotación del punto donde se aplica la fuerza entra en la ecuación. Por lo tanto, el torque depende de la ubicación del eje en el marco de referencia. Sin embargo, cuando las condiciones de equilibrio de rotación y traslación se mantienen simultáneamente en un marco de referencia, también se mantienen en cualquier otro marco de referencia inercial, de modo que el torque neto alrededor de cualquier eje de rotación sigue siendo cero. La explicación de esto es bastante sencilla.
Supongamos que el vector $\overrightarrow{\bold{r}}$ es la posición del origen de un nuevo marco inercial de referencia $S'$ en el antiguo marco inercial de referencia $S$. De nuestro estudio del movimiento relativo, sabemos que en el nuevo marco de referencia $S'$, el vector de posición $\overrightarrow{\bold{r'}}_k$ del punto donde se aplica la fuerza $\overrightarrow{\bold{F}}_k$ se relaciona con $\overrightarrow{\bold{r}}_k$ a través de la ecuación $$\overrightarrow{\bold{r'}}_k = \overrightarrow{\bold{r}}_k - \overrightarrow{\bold{r}}_k$$
Ahora, podemos sumar todos los pares $\overrightarrow{τ}_k = \overrightarrow{\bold{r'}}_k × \overrightarrow{\bold{F}}_k$ de todas las fuerzas externas en un nuevo marco de referencia, $S'$:
$$\begin{split} \sum_k \overrightarrow{τ'}_k &= \sum_k \overrightarrow{\bold{r'}}_k × \overrightarrow{\bold{F}}_k = \sum_k (\overrightarrow{\bold{r}}_k - \overrightarrow{\bold{r}}) × \overrightarrow{\bold{F}}_k \\ &= \sum_k \overrightarrow{\bold{r}}_k × \overrightarrow{\bold{F}}_k - \sum_k \overrightarrow{\bold{r}}_k × \overrightarrow{\bold{F}}_k \\ &= \sum_k \overrightarrow{τ}_k - \overrightarrow{\bold{r}} × \overrightarrow{\bold{F}}_k = \overrightarrow{\bold{0}} \end{split}$$En el último paso de esta cadena de razonamiento, utilizamos el hecho de que en equilibrio en el antiguo marco de referencia, $S$, el primer término desaparece debido a la Ecuación 3.5 y el segundo término desaparece debido a la Ecuación 3.2. Por lo tanto, vemos que el torque neto en cualquier marco inercial de referencia $S'$ es cero, siempre que ambas condiciones para el equilibrio se mantengan en un marco inercial de referencia $S$.
La implicación práctica de esto es que al aplicar las condiciones de equilibrio para un cuerpo rígido, somos libres de elegir cualquier punto como el origen del marco de referencia. Nuestra elección del marco de referencia está dictada por las características físicas del problema que estamos resolviendo. En un marco de referencia, la forma matemática de las condiciones de equilibrio puede ser bastante complicada, mientras que en otro marco, las mismas condiciones pueden tener una forma matemática más simple que sea fácil de resolver. El origen de un marco de referencia seleccionado se llama punto de pivote.
En el caso más general, las condiciones de equilibrio se expresan mediante las seis ecuaciones escalares (Ecuación 3.3 y Ecuación 3.6). Para problemas de equilibrio planar con rotación alrededor de un eje fijo, que consideramos en este capítulo, podemos reducir el número de ecuaciones a tres. El procedimiento estándar es adoptar un marco de referencia donde el eje $z$ es el eje de rotación. Con esta elección de eje, el torque neto tiene solo un componente $z$, todas las fuerzas que tienen pares de torsión distintos de cero se encuentran en el plano $xy,$ y por lo tanto las contribuciones al torque neto provienen solo de los componentes $x$ e $y$ de las conexiones externas. Por lo tanto, para problemas planos con el eje de rotación perpendicular al plano $xy$, tenemos las siguientes tres condiciones de equilibrio para fuerzas y pares: $$F_{1x} + F_{2x} + ⋅⋅⋅ + F_{Nx} = 0 \tag{3.7}$$
donde la suma es sobre todas las $N$ fuerzas externas que actúan sobre el cuerpo y sobre sus torques. En la Ecuación 3.9, simplificamos la notación descartando el subíndice $z$, pero entendemos aquí que la sumatoria es sobre todas las contribuciones a lo largo del eje $z$, que es el eje de rotación. En la ecuación 3.9, la componente $z$ del torque $\overrightarrow{τ}_k$ de la fuerza $\overrightarrow{\bold{F}}_k$ es $$τ_k = r_kF_ksenθ \tag{3.10}$$
donde $r_k$ es la longitud del brazo de palanca de la fuerza y $F_k$ es la magnitud de la fuerza. El ángulo $θ$ es el ángulo entre los vectores $\overrightarrow{\bold{r}}_k$ y $\overrightarrow{\bold{F}}_k$, que se mide desde el vector $\overrightarrow{\bold{r}}_k$ hasta el vector $\overrightarrow{\bold{F}}_k$ en el sentido antihorario ().
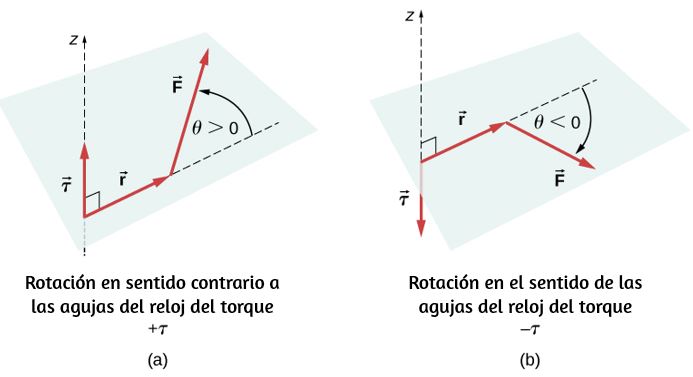
Al usar la Ecuación 3.10, a menudo calculamos la magnitud del torque y asignamos su sentido como positivo ($+$) o negativo ($-$), dependiendo de la dirección de rotación causada solo por este torque. En la ecuación 3.9, el torque neto es la suma de los términos, con cada término calculado a partir de la ecuación 3.10, y cada término debe tener el sentido correcto. De manera similar, en la Ecuación 3.7, asignamos el signo $+$ para forzar los componentes en la dirección $+ x$ y el signo $-$ a los componentes en la dirección $- x$. La misma regla se debe seguir consistentemente en la ecuación 3.8, al calcular los componentes de fuerza a lo largo del eje $y$.
En la siguiente escena interactiva, diseñada por Juan Guillermo Rivera Berrío, podrás comprender la regla de la mano derecha, también conocida como regla del sacacorchos, la cual es útil para determinar sentidos vectoriales, tanto de movimientos vectoriales lineales como de tipo rotacional. Explora la escena y cambia los valores del ángulo entre los vectores para entender el método.
A continuación, en otra escena de Juan Guillermo Rivera Berrío, puedes interactuar con dos fuerzas actuando en un cuadrado rígido en dos dimensiones. En todo momento, se satisfacen las condiciones de equilibrio estático dadas por la Ecuación 3.7 a la Ecuación 3.9. Puedes variar las magnitudes de las fuerzas y sus brazos de palanca y observar el efecto que estos cambios tienen en el cuadrado (la idea original de la escena, es de John Evans).
En muchas situaciones de equilibrio, una de las fuerzas que actúa sobre el cuerpo es su peso. En los diagramas de cuerpo libre, el vector de peso está unido al centro de gravedad del cuerpo. Para todos los propósitos prácticos, el centro de gravedad es idéntico al centro de masa.
Solo en situaciones en las que un cuerpo tiene una gran extensión espacial de modo que el campo gravitacional no es uniforme en todo su volumen, el centro de gravedad y el centro de masa se encuentran en diferentes puntos. Sin embargo, en situaciones prácticas, incluso objetos tan grandes como edificios o cruceros se encuentran en un campo gravitatorio uniforme en la superficie de la Tierra, donde la aceleración debida a la gravedad tiene una magnitud constante de $g = 9.8 m/s^2$. En estas situaciones, el centro de gravedad es idéntico al centro de masa. Por lo tanto, a lo largo de este capítulo, usamos el centro de masa (CM) como el punto donde se adjunta el vector de peso. Recuerda que el CM tiene un significado físico especial: cuando se aplica una fuerza externa a un cuerpo exactamente en su CM, el cuerpo como un todo se somete a un movimiento de traslación y dicha fuerza no causa rotación.
Cuando el CM se encuentra fuera del eje de rotación, se produce un torque gravitacional neto en un objeto. El torque gravitacional es el par causado por el peso. Este par gravitacional puede girar el objeto si no hay soporte presente para equilibrarlo. La magnitud del torque gravitacional depende de qué tan lejos del pivote esté ubicado el CM. Por ejemplo, en el caso de un camión basculante (), el pivote está ubicado en la línea donde los neumáticos hacen contacto con la superficie de la carretera. Si el CM está ubicado muy por encima de la superficie de la carretera, el torque gravitacional puede ser lo suficientemente grande como para voltear el camión. Los automóviles de pasajeros con un CM de poca altura, cerca del pavimento, son más resistentes a vuelcos que los camiones.
Si inclinas una caja para que un borde permanezca en contacto con la base debajo de ella, entonces un borde de la base de soporte se convierte en un pivote. Mientras el centro de gravedad de la caja permanezca sobre la base del soporte, el torque gravitacional hace que la caja vuelva a su posición original de equilibrio estable. Cuando el centro de gravedad se mueve fuera de la base de soporte, el torque gravitacional gira la caja en la dirección opuesta, y la caja se da vuelta. Observa esta situación y para experimenta con posiciones estables e inestables de una caja en la siguiente escena interactiva diseñada por Juan Guillermo Rivera Berrío.
Ejemplo 3.1
Centro de gravedad de un automóvil
Un automóvil de pasajeros con una distancia entre ejes de $2,5 m$ tiene el $52$% de su peso en las ruedas delanteras en terreno llano, como se ilustra en la . ¿Dónde está ubicado el CM de este automóvil con respecto al eje trasero?
Estrategia
No sabemos el peso $w$ del automóvil. Todo lo que sabemos es que cuando el automóvil descansa sobre una superficie nivelada, $0.52w$ empuja hacia abajo sobre la superficie en los puntos de contacto de las ruedas delanteras y $0.48w$ empuja hacia abajo sobre la superficie en los puntos de contacto de las ruedas traseras.
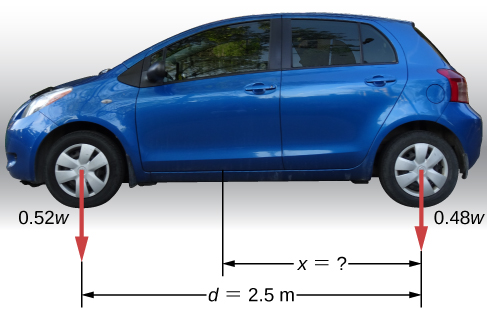
Además, los puntos de contacto están separados el uno del otro por la distancia $d = 2.5 m$. En estos puntos de contacto, el automóvil experimenta fuerzas de reacción normales con magnitudes $F_F = 0.52w$ y $F_R = 0.48w$ en los ejes delantero y trasero, respectivamente. También sabemos que el automóvil es un ejemplo de un cuerpo rígido en equilibrio cuyo peso completo $w$ actúa en su CM. El CM está ubicado en algún lugar entre los puntos donde actúan las fuerzas de reacción normales, en algún lugar a una distancia $x$ desde el punto donde actúa $F_R$. Nuestra tarea es encontrar $x$. Por lo tanto, identificamos tres fuerzas que actúan sobre el cuerpo (el automóvil), y podemos dibujar un diagrama de cuerpo libre para el cuerpo rígido extendido, como se muestra en la .
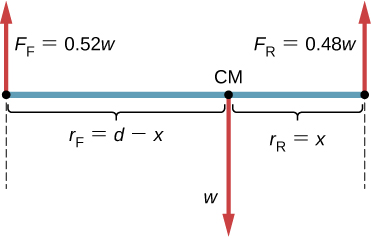
Estamos casi listos para anotar las condiciones de equilibrio de la Ecuación 3.7 a la Ecuación 3.9 para el automóvil, pero primero debemos decidir sobre el marco de referencia.
Supongamos que elegimos el eje $x$ a lo largo de la longitud del auto, el eje $y$ vertical y el eje $z$ perpendicular a este plano $xy$. Con esta opción solo necesitamos escribir la Ecuación 3.7 y la Ecuación 3.9 porque todos los componentes $y$ son idénticamente cero. Ahora tenemos que decidir sobre la ubicación del punto de pivote. Podemos elegir cualquier punto como la ubicación del eje de rotación (eje $z$). Supongamos que colocamos el eje de rotación en CM, como se indica en el diagrama de cuerpo libre para el automóvil. En este punto, estamos listos para escribir las condiciones de equilibrio para el automóvil.
Solución
Cada condición de equilibrio contiene solo tres términos porque hay $N = 3$ fuerzas que actúan sobre el automóvil. La primera condición de equilibrio, la Ecuación 3.7, dice
$$+F_F - w + F_R = 0 \tag{3.11}$$Esta condición se cumple trivialmente porque cuando sustituimos los datos, la ecuación 3.11 se convierte en $+ 0.52w - w + 0.48w = 0$. La segunda condición de equilibrio, Ecuación 3.9, dice
$$τ_F + τ_w + τ_R = 0 \tag{3.12}$$donde $τ_F$ es el torque de la fuerza $F_F$, $τ_w$ es el torque gravitacional de la fuerza $w$, y $τ_R$ es el torque de la fuerza $F_R$. Cuando el pivote está ubicado en CM, el torque gravitacional es idénticamente cero porque el brazo de palanca del peso con respecto a un eje que pasa a través de CM es cero. Las líneas de acción de ambas fuerzas de reacción normales son perpendiculares a sus brazos de palanca, por lo que en la ecuación 3.10, tenemos $|senθ| = 1$ para ambas fuerzas.
Del diagrama de cuerpo libre, leemos que el torque $τ_F$ causa rotación en el sentido de las agujas del reloj alrededor del pivote en CM, por lo que su sentido es negativo; y el torque $τ_R$ causa una rotación en sentido antihorario alrededor del pivote en CM, por lo que su sentido es positivo. Con esta información, escribimos la segunda condición de equilibrio como
$$-R_FF_F + r_RF_R = 0 \tag{3.13}$$Con la ayuda del diagrama de cuerpo libre, identificamos las magnitudes de fuerza $F_R = 0.48w$ y $F_F = 0.52w$, y sus correspondientes brazos de palanca $r_R = x$ y $r_F = d - x$. Ahora podemos escribir la segunda condición de equilibrio, la Ecuación 3.13, explícitamente en términos de la distancia desconocida $x$:
$$-0.52(d - x)w + 0.48xw = 0 \tag{3.14}$$Aquí el peso $w$ se cancela y podemos resolver la ecuación para la posición desconocida $x$ del CM. La respuesta es $x = 0.52d = 0.52(2.5 m) = 1.3 m$.
Elegir el pivote en la posición del eje delantero no cambia el resultado. El diagrama de cuerpo libre para esta ubicación de pivote se presenta en la .
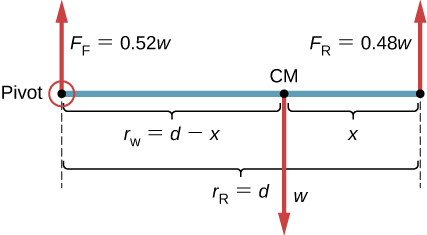
Para esta elección del punto de pivote, la segunda condición de equilibrio es
$$-R_ww + r_RF_R = 0 \tag{3.15}$$Cuando sustituimos las cantidades indicadas en el diagrama, obtenemos
$$-(d - x)w + 0.48dw = 0 \tag{3.16}$$La respuesta obtenida al resolver la Ecuación 3.13 es, nuevamente, $x = 0.52d = 1.3 m$.
Explicación
Este ejemplo muestra que cuando resolvemos problemas de equilibrio estático, somos libres de elegir la ubicación del pivote. Para diferentes opciones del punto de pivote tenemos diferentes conjuntos de condiciones de equilibrio para resolver. Sin embargo, todas las opciones conducen a la misma solución al problema.
 Comprueba tu aprendizaje 3.1
Comprueba tu aprendizaje 3.1
 Comprueba tu aprendizaje 3.2
Comprueba tu aprendizaje 3.2
Un caso especial de equilibrio estático ocurre cuando todas las fuerzas externas en un objeto actúan a lo largo del eje de rotación o cuando la extensión espacial del objeto puede ser ignorada. En tal caso, el objeto puede tratarse efectivamente como una masa puntual. En este caso especial, no debemos preocuparnos por la segunda condición de equilibrio, Ecuación 3.9, porque todos los torques son cero y la primera condición de equilibrio (por fuerzas) es la única condición que debe cumplirse. El diagrama de cuerpo libre y la estrategia de resolución de problemas para este caso especial fueron delineados en el capítulo sobre las Leyes de Newton y sus Aplicaciones. Verás una situación de equilibrio típica que implica solo la primera condición de equilibrio en el siguiente ejemplo.
Ejemplo 3.2
Una tensión de ruptura
Una pequeña cubeta de masa $42.0 g$ es soportada por dos cadenas, como se muestra en la . La tensión máxima que la cuerda puede soportar es de $2.80 N$. La masa se agrega gradualmente a la bandeja hasta que se rompa una de las cuerdas. ¿Qué cuerda es? ¿Cuánta masa se debe agregar para que esto ocurra?
Estrategia
Este sistema mecánico que consiste en cuerdas, masas y la bandeja está en equilibrio estático. Específicamente, el nudo que ata las cuerdas a la bandeja está en equilibrio estático. El nudo se puede tratar como un punto; por lo tanto, solo necesitamos la primera condición de equilibrio. Las tres fuerzas que tiran al nudo son la tensión $\overrightarrow{\bold{T}}_1$ en la cuerda de $5.0 cm$, la tensión $\overrightarrow{\bold{T}}_2$ en la cuerda de $10.0 cm$, y el peso $\overrightarrow{\bold{w}}$ de la bandeja que contiene las masas. Adoptamos un sistema de coordenadas rectangulares con el eje $y$ apuntando opuesto a la dirección de la gravedad y dibujamos el diagrama de cuerpo libre para el nudo (observa la , las cuerdas forman dos lados de un triángulo rectángulo. Podemos usar el teorema de Pitágoras para resolver este triángulo, que se muestra en la , y encontrar el seno y el coseno de los ángulos $α_1$ y $α_2$.
Entonces podemos hallar las tensiones en sus componentes rectangulares, sustituir en la primera condición de equilibrio (Ecuación 3.7 y Ecuación 3.8) y hallar las tensiones en las cuerdas. La cuerda con una mayor tensión se romperá primero.
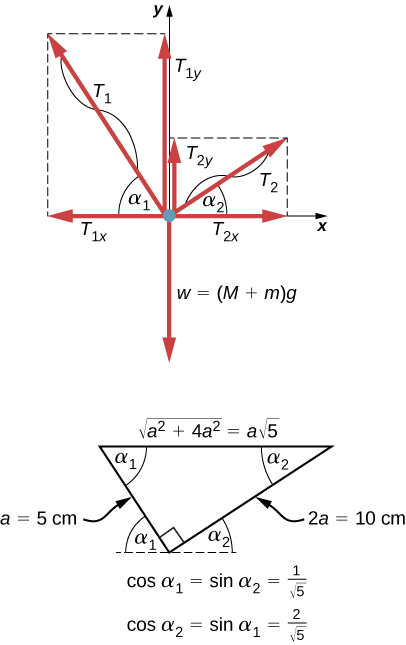
Solución
El peso $w$ que tira del nudo se debe a la masa $M$ de la bandeja y la masa $m$ añadida a la bandeja, o $w = (M + m)g$. Con la ayuda del diagrama de cuerpo libre de la , podemos establecer las condiciones de equilibrio para el nudo:
en la dirección $x, -T_{1x} + T_{2x} = 0$
en la dirección $y, +T_{1y} + T_{2y} - w = 0$
Del diagrama de cuerpo libre, las magnitudes de los componentes en estas ecuaciones son
$$T_{1x} = T_1cosα_1 = T_1/\sqrt{5}, T_{1y} = T_1senα_1 = 2T_1/\sqrt{5}$$ $$T_{2x} = T_2cosα_2 = 2T_2/\sqrt{5}, T_{2y} = T_2senα_2 = T_2/\sqrt{5}$$Sustituimos estos componentes en las condiciones de equilibrio y simplificamos. Luego obtenemos dos ecuaciones de equilibrio para las tensiones:
En dirección $x, T_1 = 2T_2$
En dirección $y, 2T_1/\sqrt{5} + T_2/\sqrt{5} = (M + m)g$
La ecuación de equilibrio para la dirección x nos dice que la tensión $T_1$ en la cuerda de $5,0 cm$ es el doble de la tensión $T_2$ en la cuerda de $10,0 cm$. Por lo tanto, la cadena más corta se romperá.
Cuando usamos la primera ecuación para eliminar $T_2$ de la segunda ecuación, obtenemos la relación entre la masa $m$ en la bandeja y la tensión $T_1$ en la cadena más corta: $$2.5T_1/\sqrt{5} = (M + m)g$$
La cuerda se rompe cuando la tensión alcanza el valor crítico de $T_1 = 2.80 N$. La ecuación anterior se puede resolver para la masa crítica $m$ que rompe la cadena:
$$m = \frac{2.5}{\sqrt{5}} \frac{T_1}{g} - M = \frac{2.5}{\sqrt{5}} \frac{2.80 N}{9.8 m/s^2} - 0.042 kg = 0.277 kg = 277.0 g$$Explicación
Supongamos que el sistema mecánico considerado en este ejemplo está unido a un techo dentro de un elevador que sube. Siempre que el elevador se mueva hacia arriba a una velocidad constante, el resultado permanece igual porque el peso $w$ no cambia. Si el elevador se mueve hacia arriba con aceleración, la masa crítica es más pequeña porque el peso de $M + m$ aumenta por un peso aparente debido a la aceleración del elevador. Aún así, en todos los casos, la cadena más corta se rompe primero.
En la siguiente escena interactiva, diseñada por Walter Fendt observa tres pesos que están conectados por cuerdas sobre poleas y unidos en un nudo. Puedes experimentar con los pesos para ver cómo afectan la posición de equilibrio del nudo y, al mismo tiempo, ver la representación del diagrama vectorial de la primera condición de equilibrio en funcionamiento.
En esta escena interactiva se simula un experimento simple sobre el equilibrio de tres fuerzas: los pesos se suspenden de tres cuerdas atadas. Dos de las cuerdas corren sobre poleas sin fricción. Las tres fuerzas que actúan sobre el nudo (flechas de colores) están en equilibrio.
Puedes elegir fuerzas de $1 N$ a $10 N$ en los campos de entrada.
¡Observa que cada fuerza debe ser más pequeña que la suma de las otras dos fuerzas! Es posible variar las posiciones de las dos poleas arrastrándolas con el ratón. El paralelogramo de fuerzas que se dirigen a la parte superior izquierda y derecha (rojo y azul, respectivamente) se dibujará si seleccionas la opción correspondiente. En la parte inferior derecha puede leer los ángulos de estas dos fuerzas con respecto a la vertical.
Todos los ejemplos en este capítulo son problemas planarios. En consecuencia, utilizamos condiciones de equilibrio en la forma de la Ecuación 3.7 a la Ecuación 3.9. Introdujimos una estrategia de resolución de problemas en el Ejemplo 3.1 para ilustrar el significado físico de las condiciones de equilibrio. Ahora generalizamos esta estrategia en una lista de pasos a seguir cuando resolvemos problemas de equilibrio estático para cuerpos rígidos extendidos. Procedemos en cinco pasos prácticos.
Estrategia de resolución de problemas: equilibrio estático
1. Identifica el objeto a analizar. Para algunos sistemas en equilibrio, puede ser necesario considerar más de un objeto. Identifica todas las fuerzas que actúan sobre el objeto. Identifica las preguntas que necesitas responder. Identifica la información dada en el problema. En problemas realistas, cierta información clave puede estar implícita en la situación en lugar de proporcionarse de manera explícita.
2. Configura un diagrama de cuerpo libre para el objeto. (a) Elige el marco de referencia $xy$ para el problema. Dibuja un diagrama de cuerpo libre para el objeto, que incluya solo las fuerzas que actúan sobre él.
Cuando sea adecuado, representa las fuerzas en términos de sus componentes en el marco de referencia elegido. Al hacer esto para cada fuerza, tacha la fuerza original para que no incluya erróneamente la misma fuerza dos veces en las ecuaciones. Etiqueta todas las fuerzas; lo necesitarás para los cálculos correctos de las fuerzas netas en las direcciones $x$ e $y$. Para una fuerza desconocida, la dirección debe asignarse arbitrariamente; piensa en ello como una "dirección de trabajo" o una "dirección sospechada". La dirección correcta está determinada por el signo que obtienes en la solución final. Un signo más ($+$) significa que la dirección de trabajo es la dirección real. Un signo menos ($-$) significa que la dirección real es opuesta a la dirección de trabajo asumida. (b) Elige la ubicación del eje de rotación; en otras palabras, elige el punto de pivote con respecto al cual calcularás torques de fuerzas actuantes. En el diagrama de cuerpo libre, indica la ubicación del pivote y los brazos de palanca de las fuerzas actuantes; lo necesitarás para cálculos de torques correctos. En la selección del pivote, ten en cuenta que el pivote se puede colocar en cualquier lugar que desees, pero el principio rector es que la mejor opción simplificará tanto como sea posible el cálculo del torque neto a lo largo del eje de rotación.
3. Configura las ecuaciones de equilibrio para el objeto. (a) Usa el diagrama de cuerpo libre para escribir una condición de equilibrio correcta con la ecuación 3.7 para componentes de fuerza en la dirección $x$. (b) Usa el diagrama de cuerpo libre para escribir una condición de equilibrio correcta con la ecuación 3.11 para componentes de fuerza en la dirección $y$. (c) Usa el diagrama de cuerpo libre para escribir una condición de equilibrio correcta con la ecuación 3.9 para torques a lo largo del eje de rotación. Usa la ecuación 3.10 para evaluar las magnitudes y los sentidos del torque.
4. Simplifica y resuelve el sistema de ecuaciones de equilibrio para obtener cantidades desconocidas. En este punto, tu trabajo solo requiere álgebra. Ten en cuenta que el número de ecuaciones debe ser el mismo que el número de incógnitas. Si el número de incógnitas es mayor que el número de ecuaciones, el problema no se puede resolver.
5. Evalúa las expresiones de las cantidades desconocidas que obtuviste en tu solución. Tus respuestas finales deben tener valores numéricos correctos y unidades físicas correctas. Si no lo hacen, utiliza los pasos anteriores para rastrear un error hasta su origen y corregirlo. Además, puedes verificar independientemente tus respuestas numéricas desplazando el pivote a una ubicación diferente y resolviendo el problema nuevamente, que es lo que hicimos en el Ejemplo 3.1.
Observa que la creación de un diagrama de cuerpo libre para un problema de equilibrio de cuerpo rígido es el componente más importante en el proceso de solución. Sin la configuración correcta y un diagrama correcto, no podrás anotar las condiciones correctas para el equilibrio. También ten en cuenta que un diagrama de cuerpo libre para un cuerpo rígido extendido que puede experimentar movimiento rotacional es diferente de un diagrama de cuerpo libre para un cuerpo que experimenta solo movimiento traslacional (como vimos en los capítulos sobre las leyes de movimiento de Newton).
En la dinámica traslacional, un cuerpo se representa como su CM, donde todas las fuerzas del cuerpo están unidas y no aparecen torques. Esto no es válido en la dinámica rotacional, donde un cuerpo rígido extendido no puede ser representado por un solo punto. La razón de esto es que al analizar la rotación, debemos identificar los torques que actúan sobre el cuerpo, y el torque depende tanto de la fuerza actuante como de su brazo de palanca. Aquí, el diagrama de cuerpo libre para un cuerpo rígido extendido nos ayuda a identificar torques externos.
Ejemplo 3.3
El Equilibrio de Torque
Tres masas se unen a una viga de madera uniforme, como se muestra en la . La masa de la viga es de $150.0 g$ y las masas a la izquierda del fulcro son $m_1 = 50.0 g$ y $m_2 = 75.0 g$. Encuentra la masa $m_3$ que equilibra el sistema cuando está conectado en el extremo derecho de la palanca, y la fuerza de reacción normal en el fulcro cuando el sistema está equilibrado.
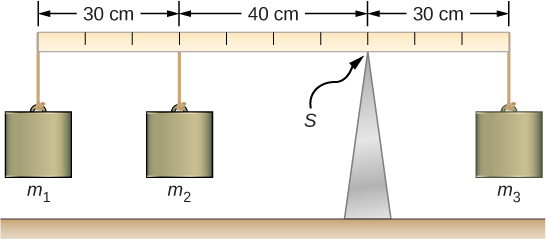
Estrategia
Para la disposición que se muestra en la figura, identificamos las siguientes cinco fuerzas que actúan en la viga:
$w_1 = m_1g$ es el peso de la masa $m_1$; $w_2 = m_2g$ es el peso de la masa $m_2$;
$w = mg$ es el peso de la viga; $w_3 = m_3g$ es el peso de la masa desconocida $m_3$;
$F_S$ es la fuerza de reacción normal en el punto de soporte $S$.
Elegimos un marco de referencia donde la dirección del eje y es la dirección de la gravedad, la dirección del eje $x$ está a lo largo de la viga y el eje de rotación (el eje $z$) es perpendicular al eje $x$ y pasa a través del punto de soporte $S$. En otras palabras, elegimos el pivote en el punto donde la viga toca el soporte. Esta es una opción natural para el pivote porque este punto no se mueve cuando gira la viga. Ahora estamos listos para configurar el diagrama de cuerpo libre para la viga. Indicamos el pivote y unimos cinco vectores que representan las cinco fuerzas a lo largo de la línea que representa la viga de madera, ubicando las fuerzas con respecto al pivote ().
En esta etapa, podemos identificar los brazos de palanca de las cinco fuerzas dada la información provista en el problema. Para las tres masas colgantes, el problema es explícito sobre su ubicación a lo largo de la viga, pero la información sobre la ubicación del peso $w$ se da implícitamente. La palabra clave aquí es "uniforme". Sabemos por nuestros estudios previos que el CM de una viga uniforme se encuentra en su punto medio, por lo que aquí es donde se adjunta el peso $w$, en la marca de $50 cm$.
Solución
Con la y la como referencia, comenzamos por encontrar los brazos de palanca de las cinco fuerzas que actúan sobre la viga:
$r_1 = 30.0 cm + 40.0 cm = 70.0 cm$
$r_2 = 40.0 cm$
$r = 50.0 cm - 30.0 cm = 20.0 cm$
$r_S = 0.0 cm$ (porque $F_S$ está conectado al pivote)
$r_3 = 30.0 cm$
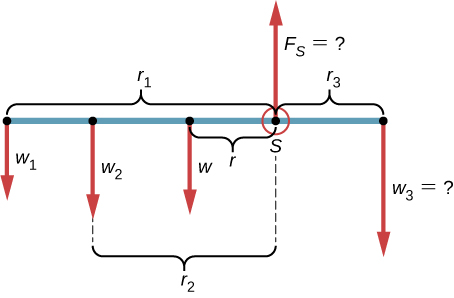
Ahora podemos encontrar los cinco torques con respecto al pivote elegido:
$τ_1 = +r_1w_1sen90° = +r_1m_1g$ (rotación en sentido antihorario, sentido positivo)
$τ_2 = +r_2w_2sen90° = +r_2m_2g$ (rotación en sentido antihorario, sentido positivo)
$τ = + rwsen90° = +rmg$ (torque gravitacional)
$τ_S = +r_SF_Ssenθ_S = 0$ (porque $r_S = 0 cm$)
$τ_3 = -r_3w_3sen90° = -r_3m_3g$ (rotación en el sentido de las agujas del reloj, sentido negativo)
La segunda condición de equilibrio (ecuación para los torques) para la viga es
$$τ_1 + τ_2 + τ + τ_S + τ_S = 0$$Al sustituir los valores de torque en esta ecuación, podemos omitir los torques que dan contribuciones cero. De esta manera, la segunda condición de equilibrio es
$$+ r_1m_1g + r_2m_2g + rmg - r_3m_3g = 0 \tag{3.17}$$Seleccionando la dirección $+ y$ para que sea paralela a $\overrightarrow{\bold{F}}_S$, la primera condición de equilibrio para la viga es
$$- W_1 - w_2 - w + F_S - w_3 = 0$$Sustituyendo las fuerzas, la primera condición de equilibrio se vuelve
$$- M_1g - m_2g - mg + F_S - m_3g = 0 \tag{3.18}$$Resolvemos estas ecuaciones simultáneamente para los valores desconocidos $m3$ y $FS$. En la ecuación 12.17, cancelamos el factor $g$ y reorganizamos los términos para obtener
$$r_3m_3 = r_1m_1 + r_2m_2 + rm$$Para obtener $m_3$ dividimos ambos lados por $r_3$, entonces tenemos
$$m_3 = \frac{r_1}{r_3}m_1 + \frac{r_2}{r_3}m_2 + \frac{r}{r_3}m \tag{3.19}$$ $$= \frac{70}{30}(50.0 g) + \frac{40}{30}(75.0 g) + \frac{20}{30}(150.0 g) = 316\frac{2}{3}g ≃ 317 g$$Para encontrar la fuerza de reacción normal, reorganizamos los términos en la Ecuación 3.18, convirtiendo gramos a kilogramos:
$$F_S = (m_1 + m_2 + m + m_3)g \tag{3.20}$$ $$= (50.0 + 75.0 + 150.0 + 316.7)×10^{-3}kg × 9.8 m/s^2 = 5.8N.$$Explicación
Observa que la ecuación 3.17 es independiente del valor de $g$. Por lo tanto, el balance de torque se puede usar para medir la masa, ya que las variaciones en los valores de $g$ en la superficie de la Tierra no afectan estas mediciones.
 Comprueba tu aprendizaje 3.3
Comprueba tu aprendizaje 3.3
En la siguiente escena interactiva de PhET Simulaciones, practica con una viga similar al ejemplo anterior, disponiendo objetos de diferentes masas en el balancín. Predice cómo los cambios en las posiciones de las masas en el tablón afectará el movimiento de la viga. Utiliza las ecuaciones para resolver los acertijos sobre equilibrio.
En el siguiente ejemplo, mostramos cómo usar la primera condición de equilibrio (ecuación para fuerzas) en la forma vectorial dada por la Ecuación 3.7 y la Ecuación 3.8. Presentamos esta solución para ilustrar la importancia de una elección adecuada del marco de referencia. Aunque todos los marcos de referencia inerciales son equivalentes y las soluciones numéricas obtenidas en un marco son las mismas que en cualquier otro, una elección inadecuada del marco de referencia puede hacer que la solución sea bastante larga y complicada, mientras que una elección inteligente del marco de referencia simplifica la solución. Mostramos esto en la solución equivalente al mismo problema. Este ejemplo particular ilustra una aplicación del equilibrio estático a la biomecánica.
Ejemplo 3.4
Fuerzas en el antebrazo
Un levantador de pesas tiene un peso de $50.0 lb$ (equivalente a $222.4 N$) con su antebrazo, como se muestra en la . Su antebrazo está posicionado en $β = 60°$ con respecto a su brazo superior. El antebrazo se apoya en una contracción del músculo bíceps, lo que provoca un torque alrededor del codo. Suponiendo que la tensión en el bíceps actúa a lo largo de la dirección vertical dada por la gravedad, ¿qué tensión debe ejercer el músculo para mantener el antebrazo en la posición que se muestra? ¿Cuál es la fuerza sobre la articulación del codo? Supón que el peso del antebrazo es insignificante. Da tus respuestas finales en unidades del SI.
Estrategia
Identificamos tres fuerzas que actúan sobre el antebrazo: la fuerza desconocida $\overrightarrow{\bold{F}}$ en el codo; la tensión desconocida $\overrightarrow{\bold{T}}_M$ en el músculo; y el peso $\overrightarrow{\bold{w}}$ con una magnitud $w = 50 lb$.
Adoptamos el marco de referencia con el eje $x$ a lo largo del antebrazo y el pivote en el codo. La dirección vertical es la dirección del peso, que es la misma que la dirección del brazo superior. El eje $x$ forma un ángulo $β = 60°$ con la vertical. El eje $y$ es perpendicular al eje $x$. Ahora configuramos el diagrama de cuerpo libre para el antebrazo. Primero, dibujamos los ejes, el pivote y los tres vectores que representan las tres fuerzas identificadas. Luego ubicamos el ángulo $β$ y representamos cada fuerza por sus componentes $x$ e $y$, recordando tachar el vector de fuerza original para evitar el doble conteo. Finalmente, etiquetamos las fuerzas y sus brazos de palanca. El diagrama de cuerpo libre para el antebrazo se muestra en la .
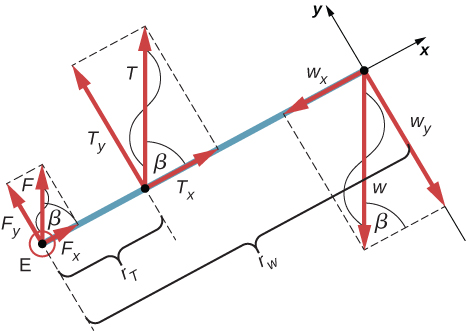
En este punto, estamos listos para establecer las condiciones de equilibrio para el antebrazo. Cada fuerza tiene componentes $x$ e $y$; por lo tanto, tenemos dos ecuaciones para la primera condición de equilibrio, una ecuación para cada componente de la fuerza neta que actúa sobre el antebrazo.
Observa que en nuestro marco de referencia, las contribuciones a la segunda condición de equilibrio (para torques) provienen únicamente de los componentes y de las fuerzas porque los componentes $x$ de las fuerzas son todos paralelos a sus brazos de palanca, por lo que para cualquiera de ellos tenemos $senθ = 0$ en la ecuación 3.10. Para los componentes $y$ tenemos $θ = ± 90°$ en la ecuación 3.10. También nota que el torque de la fuerza en el codo es cero porque esta fuerza está unida al pivote. Entonces, la contribución al torque neto proviene solo de los torques de $T_y$ y de $w_y$.
Solución
Vemos en el diagrama de cuerpo libre que el componente $x$ de la fuerza neta satisface la ecuación
$$+F_x + T_x - w_x = 0 \tag{3.21}$$y el componente $y$ de la fuerza neta satisface
$$+F_y + T_y - w_y = 0 \tag{3.22}$$La ecuación 3.21 y la ecuación 3.22 son dos ecuaciones de la primera condición de equilibrio (para las fuerzas). A continuación, leemos del diagrama de cuerpo libre que el torque neto a lo largo del eje de rotación es
$$+r_TT_y - r_ww_y = 0 \tag{3.23}$$La ecuación 3.23 es la segunda condición de equilibrio (para torques) para el antebrazo. El diagrama de cuerpo libre muestra que los brazos de palanca son $r_T = 1.5$ pulgadas y $r_w = 13.0$ pulgadas. En este punto, no necesitamos convertir pulgadas en unidades del SI, ya que mientras estas unidades sean consistentes en la Ecuación 3.23, se cancelan. Usando nuevamente el diagrama de cuerpo libre, encontramos las magnitudes de las fuerzas componentes:
$$F_x = Fcosβ = Fcos60° = F/2 \\ T_x = Tcosβ = Tcos60° = T/2 \\ w_x = wcosβ = wcos60° = w/2 \\ F_y = Fsenβ = Fsen60° = F\sqrt{3}/2 \\ T_y = Tsenβ = Tsen60° = T\sqrt{3}/2 \\ w_y = wsenβ = wsen60° = w\sqrt{3}/2$$Sustituimos estas magnitudes en la Ecuación 3.21, la Ecuación 3.22 y la Ecuación 3.23 para obtener, respectivamente,
$$F/2 + T/2 -w/2 = 0$$ $$F\sqrt{2}/2 + T\sqrt{3}/2 - w\sqrt{3}/2 = 0$$ $$r_TT\sqrt{3}/2 - r_ww\sqrt{3}/2 = 0$$Cuando simplificamos estas ecuaciones, vemos que nos quedan solo dos ecuaciones independientes para las dos magnitudes de fuerza desconocidas, $F$ y $T$, porque la ecuación 3.21 para el componente $x$ es equivalente a la ecuación 3.22 para el componente $y$. De esta manera, obtenemos la primera condición de equilibrio para las fuerzas
$$F + T - w = 0 \tag{3.24}$$y la segunda condición de equilibrio para torques $$r_TT - r_ww = 0 \tag{3.25}$$
La magnitud de la tensión en el músculo se obtiene al resolver la Ecuación 3.25:
$$T = \frac{r_w}{r_T}w = \frac{13.0}{1.5}(50 lb) = 4.33\frac{1}{3} lb ≅ 433.3 lb$$La fuerza en el codo se obtiene al resolver la Ecuación 3.24:
$$F = w - T = 50.0 lb - 433.3 lb = -383.3 lb$$El signo negativo en la ecuación nos dice que la fuerza real en el codo es antiparalela a la dirección de trabajo adoptada para dibujar el diagrama de cuerpo libre. En la respuesta final, convertimos las fuerzas en unidades de fuerza del SI. La respuesta es
$F = 383.3 lb = 383.3(4.448 N) = 1705 N$ hacia abajo
$T = 433.3 lb = 433.3(4.448 N) = 1927 N$ hacia arriba.
Explicación
Hay dos cuestiones importantes que vale la pena mencionar. La primera se refiere a la conversión en unidades del SI, lo que se puede hacer al final de la solución siempre que conservemos la coherencia en las unidades. El segundo problema importante se refiere a las articulaciones de bisagra, como el codo. En el análisis inicial de un problema, siempre se debe asumir que las articulaciones de bisagras ejercen una fuerza en una dirección arbitraria, y luego se debe resolver para todos los componentes de una fuerza de bisagra de forma independiente. En este ejemplo, la fuerza del codo pasa a ser vertical porque el problema asume que la tensión del bíceps también es vertical. Tal simplificación, sin embargo, no es una regla general.
Solución equivalente
Supongamos que adoptamos un marco de referencia con la dirección del eje $y$ a lo largo del peso de $50 lb$ y el pivote colocado en el codo.
En este marco, las tres fuerzas tienen solo componentes $y$, por lo que tenemos una sola ecuación para la primera condición de equilibrio (para las fuerzas). Dibujamos el diagrama de cuerpo libre para el antebrazo como se muestra en la , indicando el pivote, las fuerzas actuantes y sus brazos de palanca con respecto al pivote, y los ángulos $θ_T$ y $θ_w$ que las fuerzas $\overrightarrow{\bold{T}}_M$ y $\overrightarrow{\bold{w}}$ (respectivamente) hacen con sus brazos de palanca. En la definición de torque dada por la ecuación 3.10, el ángulo $θ_T$ es el ángulo de dirección del vector $\overrightarrow{\bold{T}}_M$, contado en sentido antihorario desde la dirección radial del brazo de palanca que siempre apunta hacia fuera del pivote. Según la misma convención, el ángulo $θ_w$ se mide en sentido antihorario desde la dirección radial del brazo de palanca hasta el vector $\overrightarrow{\bold{w}}$. Hecho de esta manera, los torques distintos de cero se calculan más fácilmente al sustituir directamente en la ecuación 3.10 de la siguiente manera:
$$τ_T = r_TTsenθ_T = r_TTsenβ = r_TTsen60° = +r_TT\sqrt{3}/2$$ $$τ_w = r_wwsenθ_w = r_wwsen(β + 180°) = -r_wsenβ = = -r_ww\sqrt{3}/2$$La segunda condición de equilibrio, $τ_T + τ_w = 0$, se puede escribir ahora como
$$r_TT\sqrt{3}/2 - r_ww\sqrt{3}/2 = 0 \tag{3.26}$$Del diagrama de cuerpo libre, la primera condición de equilibrio (para fuerzas) es
$$-F + T - w = 0 \tag{3.27}$$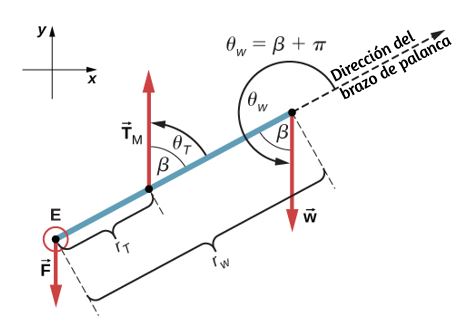
La ecuación 3.26 es idéntica a la ecuación 3.25 y da el resultado $T = 433.3 lb$. Da la ecuación 3.27 obtenemos
$$F = T - w = 433,3 lb - 50,0 lb = 383,3 lb$$Vemos que estas respuestas son idénticas a nuestras respuestas anteriores, pero la segunda opción para el marco de referencia conduce a una solución equivalente que es más simple y más rápida porque no requiere que las fuerzas se resuelvan en sus componentes rectangulares.
 Comprueba tu aprendizaje 3.4
Comprueba tu aprendizaje 3.4
Ejemplo 3.5
Una escalera que descansa contra una pared
Una escalera uniforme de $L = 5.0 m$ de largo y peso $400.0 N$, descansa contra una pared vertical resbaladiza, como se muestra en la . El ángulo de inclinación entre la escalera y el piso áspero es $β = 53°$. Encuentra las fuerzas de reacción del piso y de la pared en la escalera y el coeficiente de fricción estática $μ_s$ en la interfaz de la escalera con el piso que evita que la escalera se deslice.
Estrategia
Podemos identificar cuatro fuerzas que actúan en la escalera. La primera fuerza es la fuerza de reacción normal $N$ del piso en la dirección vertical ascendente. La segunda fuerza es la fuerza de fricción estática $f = μ_sN$ dirigida horizontalmente a lo largo del piso hacia la pared; esta fuerza evita que la escalera se deslice. Estas dos fuerzas actúan sobre la escalera en su punto de contacto con el piso. La tercera fuerza es el peso $w$ de la escalera, unida a su CM ubicada a medio camino entre sus extremos. La cuarta fuerza es la fuerza de reacción normal $F$ de la pared en la dirección horizontal alejada de la pared, unida al punto de contacto con la pared.
No hay otras fuerzas porque la pared es resbaladiza, lo que significa que no hay fricción entre la pared y la escalera. En base a este análisis, adoptamos el marco de referencia con el eje $y$ en la dirección vertical (paralelo a la pared) y el eje $x$ en la dirección horizontal (paralelo al piso). En este marco, cada fuerza tiene un componente horizontal o un componente vertical, pero no ambos, lo que simplifica la solución. Seleccionamos el pivote en el punto de contacto con el piso. En el diagrama de cuerpo libre para la escalera, indicamos el pivote, las cuatro fuerzas y sus brazos de palanca, y los ángulos entre los brazos de palanca y las fuerzas, como se muestra en la . Con nuestra elección de la ubicación del pivote, no existe torque desde la fuerza de reacción normal $N$ o desde la fricción estática $f$ porque ambas actúan en el pivote.
Solución
Del diagrama de cuerpo libre, la fuerza neta en la dirección $x$ es
$$+f - F = 0 \tag{3.28}$$la fuerza neta en la dirección $y$ es
$$+N - w = 0 \tag{3.29}$$y el torque neto a lo largo del eje de rotación en el punto de pivote es
$$τ_w + τ_F = 0 \tag{3.30}$$donde $τ_w$ es el torque del peso $w$ y $τ_F$ es el torque de la reacción $F$. Del diagrama de cuerpo libre, identificamos que el brazo de palanca de la reacción en la pared es $r_F = L = 5.0 m$ y el brazo de palanca de el peso es $r_w = L/2 = 2.5 m$. Con la ayuda del diagrama de cuerpo libre, identificamos los ángulos que se usarán en la ecuación 3.10 para torques: $θ_F = 180° - β$ para el torque de la fuerza de reacción con la pared, y $θ_w = 180° + (90° - β)$ para el torque debido al peso. Ahora estamos listos para usar la Ecuación 3.10 para calcular torques:
$$\begin{split} τ_w = r_wwsenθ_w &= r_wwsen(180° + 90° - β) \\ &= -\frac{L}{2}wsen(90° - β) = -\frac{L}{2}wcosβ \end{split}$$ $$τ_F = r_FFsenθ_F = r_FFsen(180° - β) = LFsenβ.$$Sustituimos los torques por la ecuación 3.30 y hallamos $F$:
$$-\frac{L}{2}wcosβ + LFsenβ = 0$$ $$F = \frac{w}{2}cotβ = \frac{400.0 N}{2}cot53° = 150.7N \tag{3.31}$$Obtenemos la fuerza de reacción normal con el piso resolviendo la Ecuación 3.29: $N = w = 400.0 N$. La magnitud de la fricción se obtiene al resolver la Ecuación 3.28: $f = F = 150.7 N$. El coeficiente de fricción estática es $μ_s = f/N = 150.7/400.0 = 0.377$.
La fuerza neta en la escalera en el punto de contacto con el piso es la suma vectorial de la reacción normal del piso y las fuerzas de fricción estáticas:
Su magnitud es
$$F_{\textsf{Piso}} = \sqrt{f^2 + N^2} = \sqrt{150.7^2 + 400.0^2} N = 427.4 N$$y su dirección es
$φ = tan^{-1}(N/f) = tan^{-1}(400.0/150.7) = 69.3°$ sobre el piso
Deberíamos enfatizar aquí dos observaciones generales de uso práctico. Primero, observa que cuando elegimos un punto de pivote, no hay expectativa de que el sistema realmente pivoteará alrededor del punto elegido. La escalera en este ejemplo no gira en absoluto, sino que se apoya firmemente en el piso; no obstante, su punto de contacto con el piso es una buena opción para el pivote. Segundo, observa que cuando usamos la Ecuación 3.10 para el cálculo de torques individuales, no necesitamos resolver las fuerzas en sus componentes normales y paralelos con respecto a la dirección del brazo de palanca, y no necesitamos considerar el sentido del torque. Siempre que el ángulo en la Ecuación 3.10 esté correctamente identificado -con la ayuda de un diagrama de cuerpo libre- como el ángulo medido en sentido antihorario desde la dirección del brazo de palanca hasta la dirección del vector de fuerza, la Ecuación 3.10 da la magnitud y el sentido del torque. Esto se debe a que el torque es el producto vectorial del vector palanca-brazo cruzado con el vector de fuerza, y la ecuación 3.10 expresa el componente rectangular de este producto vectorial a lo largo del eje de rotación.
Explicación
Este resultado es independiente de la longitud de la escalera porque L se cancela en la segunda condición de equilibrio (Ecuación 3.31). No importa qué tan larga o corta sea la escalera, siempre y cuando su peso sea de $400 N$ y el ángulo con el piso sea de $53°$, nuestros resultados se mantienen. Pero la escalera se deslizará si el torque neto se vuelve negativo en la ecuación 3.31. Esto sucede en algunos ángulos cuando el coeficiente de fricción estática no es lo suficientemente grande como para evitar que la escalera se deslice.
 Comprueba tu aprendizaje 3.5
Comprueba tu aprendizaje 3.5
Ejemplo 3.6
Fuerzas en las bisagras de una puerta
Una puerta basculante que pesa $w = 400.0 N$ es soportada por las bisagras $A$ y $B$ de modo que la puerta puede balancearse alrededor de un eje vertical que pasa a través de las bisagras (). La puerta tiene un ancho $b = 1.00 m$, y la lámina de la puerta tiene una densidad de masa uniforme. Las bisagras se colocan simétricamente en el borde de la puerta de tal forma que el peso de la puerta se distribuye uniformemente entre ellas. Las bisagras están separadas por una distancia $a = 2.00 m$. Encuentra las fuerzas en las bisagras cuando la puerta está medio abierta.
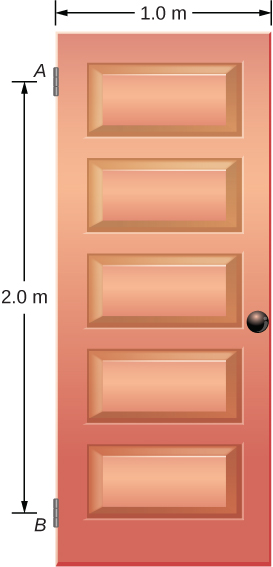
Estrategia
Las fuerzas que la puerta ejerce sobre sus bisagras se pueden encontrar simplemente invirtiendo las direcciones de las fuerzas que ejercen las bisagras sobre la puerta.
Por lo tanto, nuestra tarea es encontrar las fuerzas de las bisagras en la puerta. Tres fuerzas actúan sobre la lámina de la puerta: una fuerza desconocida $\overrightarrow{\bold{A}}$ de la bisagra $A$, una fuerza desconocida $\overrightarrow{\bold{B}}$ de la bisagra $B$, y el peso conocido $\overrightarrow{\bold{w}}$ unido al centro de masa de la lámina de la puerta. El CM está ubicado en el centro geométrico de la puerta porque la lámina tiene una densidad de masa uniforme. Adoptamos un marco rectangular de referencia con el eje largo de la dirección de la gravedad y el eje $x$ en el plano de la placa, como se muestra en el panel (a) de la , y hallamos todas las fuerzas en sus componentes rectangulares.
De esta manera, tenemos cuatro fuerzas con componentes desconocidos: dos componentes de la fuerza $\overrightarrow{\bold{A}}$ ($A_x$ y $A_y$) y dos componentes de la fuerza $\overrightarrow{\bold{B}}$ ($B_x$ y $B_y$). En el diagrama de cuerpo libre, representamos las dos fuerzas en las bisagras por sus componentes vectoriales, cuyas orientaciones asumidas son arbitrarias. Debido a que hay cuatro incógnitas $(A_x, B_x, A_y y B_y)$, debemos configurar cuatro ecuaciones independientes. Una ecuación es la condición de equilibrio para las fuerzas en la dirección $x$. La segunda ecuación es la condición de equilibrio para las fuerzas en la dirección $y$. La tercera ecuación es la condición de equilibrio para torques en rotación sobre una bisagra. Debido a que el peso se distribuye uniformemente entre las bisagras, tenemos la cuarta ecuación, $A_y = B_y$.
Para establecer las condiciones de equilibrio, dibujamos un diagrama de cuerpo libre y elegimos el punto de pivote en la bisagra superior, como se muestra en el panel (b) de la . Finalmente, resolvemos las ecuaciones para los componentes de fuerza desconocidos y encontramos las fuerzas.
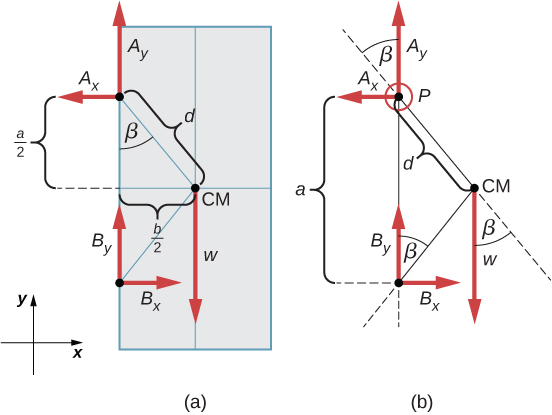
Solución
Del diagrama de cuerpo libre para la puerta tenemos la primera condición de equilibrio para las fuerzas:
En dirección $x: -A_x + B_x = 0 → A_x = B_x$
En dirección $x: +A_y +B_y - w = 0 → A_y = B_y = \frac{w}{2} = \frac{400.0 N}{2} = 200.0N$.
Seleccionamos el pivote en el punto $P$ (bisagra superior, según el diagrama de cuerpo libre) y escribimos la segunda condición de equilibrio para los torques en rotación alrededor del punto $P$:
pivote en $P$: $$τ_w + τ_{Bx} + τ_{By} = 0 \tag{3.32}$$
Usamos el diagrama de cuerpo libre para encontrar todos los términos en esta ecuación:
$$τ_w = dwsen(-β) = -dwsenβ = -dw\frac{b/2}{d} = -w\frac{b}{2}$$ $$τ_{Bx} = aB_xsen90° = +aBx_x$$ $$τ_{By} = aB_ysen180° = 0$$Al evaluar $senβ$, utilizamos la geometría del triángulo que se muestra en la parte (a) de la figura. Ahora sustituimos estos torques en la Ecuación 3.32 y calculamos $B_x$:
pivote en $P$: $$-w\frac{b}{2} + aB_x = 0 → B_x = w\frac{b}{2a} = (400.0 N) \frac{1}{2 \cdot 2} = 100.0 N$$
Por lo tanto, las magnitudes de las fuerzas del componente horizontal son $A_x = B_x = 100.0 N$. Las fuerzas en la puerta son
en la bisagra superior: $\overrightarrow{\bold{F}}_{A\textsf{ sobre la puerta}} = -100.0 N\^{i} + 200.0 N\^{j}$
en la bisagra inferior: $\overrightarrow{\bold{F}}_{B\textsf{ sobre la puerta}} = +100.0 N\^{i} + 200.0 N\^{j}$
Las fuerzas en las bisagras se encuentran en la tercera ley de Newton como
en la bisagra superior: $\overrightarrow{\bold{F}}_{\textsf{la puerta sobre }A} = 100.0 N\^{i} - 200.0 N\^{j}$
en la bisagra inferior: $\overrightarrow{\bold{F}}_{\textsf{la puerta sobre }B} = -100.0 N\^{i} - 200.0 N\^{j}$
Explicación
Ten en cuenta que si el problema se formuló sin suponer que el peso se distribuye por igual entre las dos bisagras, no podríamos resolverlo porque el número de incógnitas sería mayor que el número de ecuaciones que expresan condiciones de equilibrio.
 Comprueba tu aprendizaje 3.6
Comprueba tu aprendizaje 3.6
 Comprueba tu aprendizaje 3.7
Comprueba tu aprendizaje 3.7
Una persona de $50 kg$ se encuentra a $1.5 m$ de distancia de un extremo de un andamio uniforme de $6.0 m$ de largo con una masa de $70.0 kg$. Encuentra las tensiones en las dos cuerdas verticales que sostienen el andamio.
 Comprueba tu aprendizaje 3.8
Comprueba tu aprendizaje 3.8
Un aviso de $400.0 N$ cuelga del extremo de un puntal uniforme. El puntal mide $4.0 m$ de largo y pesa $600.0 N$. El puntal es sostenido por una bisagra en la pared y por un cable cuyo otro extremo está atado a la pared en un punto $3.0 m$ por encima del extremo izquierdo del puntal. Encuentra la tensión en el cable de soporte y la fuerza de la bisagra en el puntal.
Un modelo de un cuerpo rígido es un ejemplo idealizado de un objeto que no se deforma bajo las acciones de fuerzas externas. Es muy útil cuando se analizan sistemas mecánicos, y muchos objetos físicos son de hecho rígidos en gran medida. El grado en que un objeto puede percibirse como rígido depende de las propiedades físicas del material del que está hecho. Por ejemplo, una pelota de ping-pong hecha de plástico es frágil, y una pelota de tenis hecha de caucho es elástica cuando actúa sobre fuerzas de aplastamiento. Sin embargo, bajo otras circunstancias, tanto una pelota de ping-pong como una de tenis pueden rebotar bien como cuerpos rígidos. Del mismo modo, alguien que diseña extremidades protésicas puede ser capaz de aproximarse a la mecánica de las extremidades humanas modelándolas como cuerpos rígidos; sin embargo, la combinación real de huesos y tejidos es un medio elástico.
Para el resto de este capítulo, pasamos de la consideración de las fuerzas que afectan el movimiento de un objeto a aquellas que afectan la forma de un objeto. Un cambio de forma debido a la aplicación de una fuerza se conoce como una deformación. Incluso se sabe que fuerzas muy pequeñas causan cierta deformación. La deformación es experimentada por objetos o medios físicos bajo la acción de fuerzas externas, por ejemplo, ésta puede aplastar, apretar, rasgar, retorcer, esquilar o separar los objetos. En el lenguaje de la física, dos términos describen las fuerzas sobre los objetos sometidos a deformación: esfuerzo y deformación.
El esfuerzo es una cantidad que describe la magnitud de las fuerzas que causan la deformación. El esfuerzo generalmente se define como la fuerza por unidad de área. Cuando las fuerzas tiran de un objeto y causan su alargamiento, como el estiramiento de una banda elástica, llamamos a este esfuerzo un esfuerzo de tensión o tracción. Cuando las fuerzas causan la compresión de un objeto, lo llamamos esfuerzo de compresión.
Cuando un objeto se aprieta desde todos los lados, como un submarino en las profundidades de un océano, llamamos a este tipo de esfuerzo un esfuerzo masivo (o esfuerzo volumétrico). En otras situaciones, las fuerzas actuantes pueden no ser ni extensibles ni compresivas, y aún así producir una deformación notable. Por ejemplo, supón que sostienes un libro apretadamente entre las palmas de las manos, luego con una mano presionas y tiras de la cubierta frontal alejándola de ti, mientras con la otra mano presionas y tiras de la cubierta posterior hacia ti. En tal caso, cuando las fuerzas de deformación actúan tangencialmente a la superficie del objeto, las llamamos fuerzas de cizalla y el esfuerzo que provocan se denomina esfuerzo de cizalladura o cortante.
La unidad de esfuerzo en el SI es el pascal ($Pa$). Cuando un newton de fuerza presiona sobre un área de superficie unitaria de un metro cuadrado, el esfuerzo resultante es un pascal:
Un pascal $= 1.0 Pa = \dfrac{1.0 N}{1.0 m^2}$
En el sistema británico de unidades, la unidad de esfuerzo es '$psi$', que significa 'libra por pulgada cuadrada' ($lb/in^2$). Otra unidad que se utiliza a menudo para el esfuerzo es la $atm$ (atmósfera). Los factores de conversión son
$$1 psi = 6895 Pa \; \textsf{ y } \; 1Pa = 1.450 × 10^{-4}psi$$ $$1 atm = 1.013 × 10^5 Pa = 14.7 psi$$Un objeto o un medio bajo esfuerzo se deforma. La cantidad que describe esta deformación se llama esfuerzo. La deformación se da como un cambio fraccionario en la longitud (bajo esfuerzo de tracción) o el volumen (bajo esfuerzo en masa) o la geometría (bajo esfuerzo de cizalladura).
Por lo tanto, la deformación es un número adimensional. La deformación bajo un esfuerzo de tracción se denomina deformación por tracción, la deformación bajo el esfuerzo masivo se denomina deformación volumétrica y la causada por el esfuerzo cortante se denomina deformación por cizalladura.
Cuanto mayor es el esfuerzo, mayor es la deformación; sin embargo, la relación entre la deformación y el esfuerzo no necesita ser lineal. Solo cuando el esfuerzo es suficientemente bajo se produce la deformación en proporción directa con el valor del esfuerzo. La constante de proporcionalidad en esta relación se llama módulo elástico. En el límite lineal de los valores de bajo esfuerzo, la relación general entre el esfuerzo y la deformación es
$$\textsf{Esfuerzo = (módulo \; elástico) × deformación} \tag{3.33}$$Como podemos ver en el análisis dimensional de esta relación, el módulo elástico tiene la misma unidad física que el esfuerzo porque la deformación es adimensional.
También podemos ver a partir de la Ecuación 3.33 que cuando un objeto se caracteriza por un gran valor de módulo elástico, el efecto del esfuerzo es pequeño. Por otro lado, un pequeño módulo elástico significa que el esfuerzo produce una notable deformación. Por ejemplo, un esfuerzo en una banda de caucho produce una deformación mayor que el mismo esfuerzo en una banda de acero de las mismas dimensiones porque el módulo elástico para el caucho es dos órdenes de magnitud menor que el módulo elástico para el acero.
El módulo elástico para el esfuerzo de tracción se llama módulo de Young; que para el esfuerzo masivo se llama módulo volumétrico; y que para el esfuerzo cortante se llama módulo de corte. Ten en cuenta que la relación entre el esfuerzo y la tensión es una relación observada y medida en el laboratorio.
Los módulos elásticos para diversos materiales se miden bajo diversas condiciones físicas, como la variación de temperatura, y se recogen en tablas de datos de ingeniería para referencia (). Estas tablas son referencias valiosas para la industria y para cualquier persona involucrada en ingeniería o construcción. En la siguiente sección, discutiremos las relaciones esfuerzo-deformación más allá del límite lineal representado por la ecuación 3.33, en el rango completo de valores de esfuerzo hasta un punto de fractura. En el resto de esta sección, estudiamos el límite lineal expresado por la Ecuación 3.33.
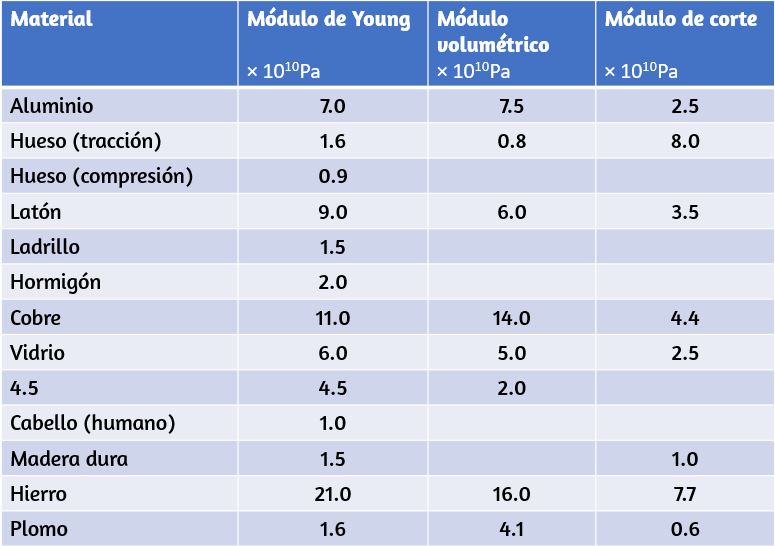
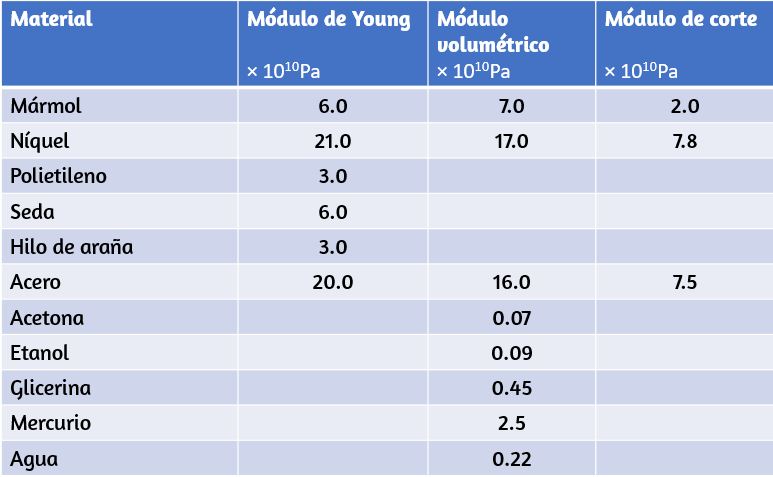
La tracción o compresión ocurren cuando dos fuerzas antiparalelas de igual magnitud actúan sobre un objeto a lo largo de solo una de sus dimensiones, de tal forma que el objeto no se mueve. Una forma de visualizar tal situación se ilustra en la . Un segmento de varilla se estira o se aprieta mediante un par de fuerzas que actúan a lo largo de su longitud y son perpendiculares a su sección transversal. El efecto neto de tales fuerzas es que la barra cambia su longitud desde la longitud original $L_0$ que tenía antes de que aparecieran las fuerzas, a una nueva longitud $L$ que tiene bajo la acción de las fuerzas.
Este cambio en la longitud $ΔL = L - L_0$ puede ser o elongación (cuando $L$ es más grande que la longitud original $L_0$) o contracción (cuando $L$ es más pequeño que la longitud original $L_0$). El esfuerzo y la deformación a tracción ocurren cuando las fuerzas están estirando un objeto, causando su elongación, y el cambio de longitud $ΔL$ es positivo. El esfuerzo y la deformación de compresión se producen cuando las fuerzas se contraen con un objeto, lo que provoca su acortamiento, y el cambio de longitud $ΔL$ es negativo.
En cualquiera de estas situaciones, definimos el esfuerzo como la relación entre la fuerza de deformación $F⊥$ y el área de sección transversal $A$ del objeto que se está deformando. El símbolo $F⊥$ que reservamos para la fuerza de deformación significa que esta fuerza actúa perpendicularmente a la sección transversal del objeto. Las fuerzas que actúan en paralelo a la sección transversal no cambian la longitud de un objeto. La definición del esfuerzo de tracción es
$$\textsf{Esfuerzo de tracción} = \frac{F⊥}{A} \tag{3.34}$$La deformación a tracción es la medida de la deformación de un objeto bajo esfuerzo de tracción y se define como el cambio fraccional de la longitud del objeto cuando el objeto experimenta deformación a tracción
$$\textsf{Deformación a tracción} = \frac{ΔL}{L_0} \tag{3.35}$$El esfuerzo y la deformación compresiva se definen con las mismas fórmulas, las ecuaciones 3.34 y 3.35, respectivamente. La única diferencia con respecto a la situación de tracción es que para el esfuerzo de compresión y la deformación, tomamos valores absolutos de los lados derechos en la Ecuación 3.34 y la Ecuación 3.35.
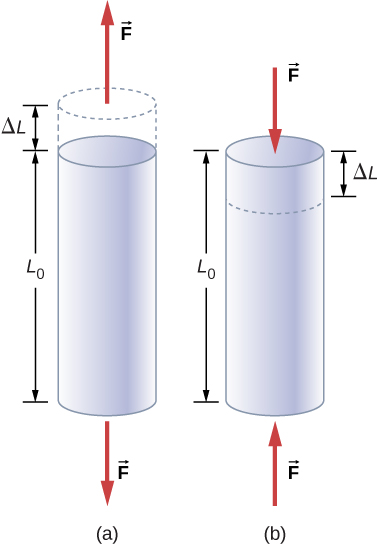
El módulo $Y$ de Young es el módulo elástico cuando la deformación es causada por el esfuerzo de tracción o de compresión, y se define mediante la ecuación 3.33. Al dividir esta ecuación por la deformación a tracción, obtenemos la expresión del módulo de Young:
$$Y = \frac{\textsf{Esfuerzo a tracción}}{\textsf{Deformación a tracción}} = \frac{F⊥/A}{ΔL/L_0} = \frac{F⊥}{A}\frac{L_0}{ΔL} \tag{3.36}$$Ejemplo 3.7
Esfuerzo de compresión en un pilar
Una escultura con un peso de $10.000 N$ descansa sobre una superficie horizontal en la parte superior de un pilar vertical de $6.0 m$ de altura (). El área transversal del pilar es de $0.20 m^2$ y está hecho de granito con una densidad de masa de $2700 kg/m^3$. Encuentra el esfuerzo de compresión en la sección transversal ubicada a $3,0 m$ por debajo de la parte superior del pilar y el valor de la deformación de compresión del segmento superior de $3,0 m$ del pilar.
Estrategia
Primero, encontramos el peso de la sección superior de $3,0 m$ de largo del pilar. La fuerza normal que actúa en la sección transversal ubicada a $3.0 m$ hacia abajo desde la parte superior es la suma del peso del pilar y el peso de la escultura. Una vez que tenemos la fuerza normal, usamos la ecuación 3.34 para encontrar el esfuerzo. Para encontrar la deformación a compresión, encontramos el valor del módulo de Young para granito en la y reemplazamos en la ecuación 3.36.

Solución
El volumen del segmento del pilar con altura $h = 3.0 m$ y área de sección transversal $A = 0.20 m^2$ es
$$V = Ah = (0.20 m^2)(3.0 m) =0.6 0m^3$$Con la densidad del granito $ρ = 2.7 × 10^3 kg/m^3$, la masa del segmento del pilar es
$$m = ρV = (2.7 × 10^3 kg/m^3)(0.60 m^3) = 1.60 × 10^3 kg$$El peso del segmento del pilar es
$$w_p = mg = (1,60 × 10^3 kg)(9,80 m/s^2) = 1,568 × 10^4 N$$El peso de la escultura es $w_s = 1.0 × 10^4 N$, por lo que la fuerza normal en la superficie de la sección transversal ubicada a $3.0 m$ por debajo de la escultura es
$$F⊥ = w_p + w_s = (1.568 + 1.0) × 10^4 N = 2.568 × 10^4 N$$Por lo tanto, el esfuerzo es
$$\textsf{Esfuerzo} = \frac{F⊥}{A} = \frac{2.568 × 10^4 N}{0.20 m^2} = 1.284× 10^5 Pa = 128.4 kPa$$El módulo de Young para granito es $Y = 4.5 × 10^{10} Pa = 4.5 × 10^7 kPa$. Por lo tanto, la deformación a compresión en esta posición es
$$\textsf{Deformación} = \frac{\textsf{Esfuerzo}}{Y} = \frac{128.4 kPa}{4.5 × 10^7 kPa} = 2.85 × 10^{-6}$$Explicación
Observa que la fuerza normal que actúa en el área de la sección transversal del pilar no es constante a lo largo de su longitud, sino que varía desde su valor más pequeño en la parte superior hasta su valor más grande en la parte inferior del pilar. Por lo tanto, si el pilar tiene un área transversal uniforme a lo largo de su longitud, la deformación es mayor en su base.
 Comprueba tu aprendizaje 3.9
Comprueba tu aprendizaje 3.9
Ejemplo 3.8
Estirando una barra
Una barra de acero de $2,0 m$ de longitud tiene un área de sección transversal de $0,30 cm^2$. La varilla es parte de un soporte vertical que sostiene una plataforma pesada de $550 kg$ que cuelga unida al extremo inferior de la varilla. Ignorando el peso de la varilla, ¿cuál es el esfuerzo a tracción en la varilla y el alargamiento de la varilla bajo ese esfuerzo?
Estrategia
Primero calculamos el esfuerzo a tracción en la varilla bajo el peso de la plataforma de acuerdo con la Ecuación 3.34.
Luego invertimos la ecuación 3.36 para encontrar el alargamiento de la varilla, usando $L_0 = 2.0 m$. De la , el módulo de Young para el acero es $Y = 2.0 × 10^{11} Pa$.
Solución
La sustitución de valores numéricos en las ecuaciones nos da
Explicación
De forma similar a como en el ejemplo de la columna, la deformación a tracción en este ejemplo no es uniforme a lo largo de la longitud de la barra. A diferencia del ejemplo anterior, sin embargo, si se tiene en cuenta el peso de la varilla, el esfuerzo en la varilla es mayor en la parte superior y más pequeño en la parte inferior de la varilla donde está fijado el equipo.
 Comprueba tu aprendizaje 3.10
Comprueba tu aprendizaje 3.10
Los objetos a menudo pueden experimentar tanto esfuerzo de compresión como de tracción simultáneamente (). Un ejemplo es un estante largo cargado con libros pesados que se pliega entre los soportes finales bajo el peso de los libros. La superficie superior del estante está sometida a esfuerzo de compresión y la superficie inferior del estante a esfuerzo de tracción. De manera similar, los entrepaños largos y pesados se comban por su propio peso. En la construcción de edificios modernos, tales deformaciones a flexión pueden eliminarse casi por completo con el uso de vigas I ().
Cuando te sumerges en el agua, sientes una fuerza que presiona todas las partes de tu cuerpo desde todas las direcciones. Lo que estás experimentando es un esfuerzo masivo o volumétrico, o en otras palabras, presión.

El esfuerzo masivo siempre tiende a disminuir el volumen encerrado por la superficie de un objeto sumergido. Las fuerzas de este "apretar" son siempre perpendiculares a la superficie sumergida (). El efecto de estas fuerzas es disminuir el volumen del objeto sumergido en una cantidad $ΔV$ en comparación con el volumen $V_0$ del objeto. Este tipo de deformación se denomina deformación volumétrica y se describe por un cambio en el volumen relativo al volumen original:
$$\textsf{Esfuerzo volumétrico} = \frac{ΔV}{V_0} \tag{3.37}$$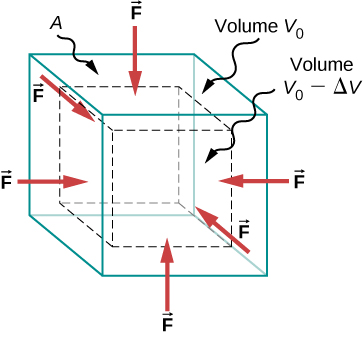
La deformación volumétrica es consecuencia del esfuerzo masivo, que es una fuerza $F⊥$ normal a una superficie que presiona en el área de la superficie de la unidad $A$ de un objeto sumergido. Este tipo de cantidad física, o presión $p$, se define como
Estudiaremos la presión en fluidos con mayor detalle en el siguiente capítulo. Una característica importante de la presión es que es una cantidad escalar y no tiene una dirección particular; es decir, la presión actúa por igual en todas las direcciones posibles.
Cuando sumerges tu mano en agua, sientes la misma cantidad de presión que actúa en la superficie superior de la mano que en la superficie inferior, en la superficie lateral o en la superficie de la piel entre los dedos. Lo que estás percibiendo en este caso es un aumento de la presión $Δp$ sobre lo que estás acostumbrado a sentir cuando tu mano no está sumergida en agua. Lo que sientes cuando tu mano no está sumergida en el agua es la presión normal $p_0$ de una atmósfera, que sirve como punto de referencia. El esfuerzo masivo es este aumento de la presión, o $Δp$, sobre el nivel normal, $p_0$.
Cuando aumenta el esfuerzo masivo, la deformación volumétrica aumenta en respuesta, de acuerdo con la Ecuación 3.33. La constante de proporcionalidad en esta relación se llama módulo volumétrico, $B$, o
El signo menos que aparece en la ecuación 3.39 es la coherencia, para garantizar que B sea una cantidad positiva. Ten en cuenta que el signo menos ($-$) es necesario porque un aumento $Δp$ en la presión (una cantidad positiva) siempre causa una disminución $ΔV$ en el volumen, y la disminución en el volumen es una cantidad negativa. El recíproco del módulo volumétrico se denomina compresibilidad $k$, o
El término "compresibilidad" se usa en relación con fluidos (gases y líquidos). La compresibilidad describe el cambio en el volumen de un fluido por unidad de aumento de presión.
Los fluidos caracterizados por una gran compresibilidad son relativamente fáciles de comprimir. Por ejemplo, la compresibilidad del agua es $4.64 × 10^{-5} atm$ y la compresibilidad de la acetona es $1.45 × 10^{-4} atm$. Esto significa que bajo un aumento de $1.0 atm$ en la presión, la disminución relativa en el volumen es aproximadamente tres veces más grande para la acetona que para el agua.
Ejemplo 3.9
Prensa hidráulica
En una prensa hidráulica (), un volumen de $250$ litros de aceite está sujeto a un aumento de presión de $2300 psi$. Si la compresibilidad del aceite es $2.0 × 10^{-5}/atm$, encuentra la deformación volumétrica y la disminución absoluta en el volumen de aceite cuando la prensa está funcionando.
Estrategia
Debemos invertir la ecuación 3.40 para encontrar la deformación del volumen. Primero, convertimos el aumento de presión de $psi$ a $atm$, $Δp = 2300 psi = 2300/14.7 atm ≈ 160 atm$, e identificamos $V_0 = 250 L$.
Solución
Sustituyendo valores en la ecuación, tenemos
La solución es:
$$ΔV = 0.0032V_0 = 0.0032(250 L) = 0.78 L$$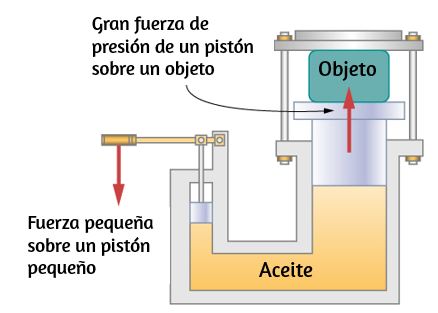
Explicación
Ten en cuenta que dado que la compresibilidad del agua es $2,32$ veces mayor que la del aceite, si la sustancia de trabajo en la prensa hidráulica de este problema se cambiara por agua, la deformación general y el cambio de volumen serían $2,32$ veces más grandes.
 Comprueba tu aprendizaje 3.11
Comprueba tu aprendizaje 3.11
Los conceptos de deformación y esfuerzo cortante se refieren únicamente a objetos o materiales sólidos. Los edificios y las placas tectónicas son ejemplos de objetos que pueden estar sujetos a esfuerzos de corte. En general, estos conceptos no se aplican a los fluidos.
La deformación por corte se produce cuando dos fuerzas antiparalelas de igual magnitud se aplican tangencialmente a superficies opuestas de un objeto sólido, sin causar deformación en la dirección transversal a la línea de fuerza, como en el ejemplo típico de esfuerzo de corte ilustrado en la . La deformación por cizallamiento o corte se caracteriza por un desplazamiento gradual $x$ de las capas en la dirección tangente a las fuerzas de acción. Esta gradación en $Δx$ ocurre en la dirección transversal a lo largo de alguna distancia $L_0$. La deformación por cortante se define por la relación del mayor desplazamiento $Δx$ a la distancia transversal $L_0$
$$\textsf{Deformación por cortante} = \frac{Δx}{L_0} \tag{3.41}$$La deformación por cortante es causada por el esfuerzo de corte. El esfuerzo cortante se debe a fuerzas que actúan paralelas a la superficie. Usamos el símbolo $F_∥$ para tales fuerzas. La magnitud $F_∥$ por área de superficie $A$ donde se aplica la fuerza de corte es la medida del esfuerzo cortante.
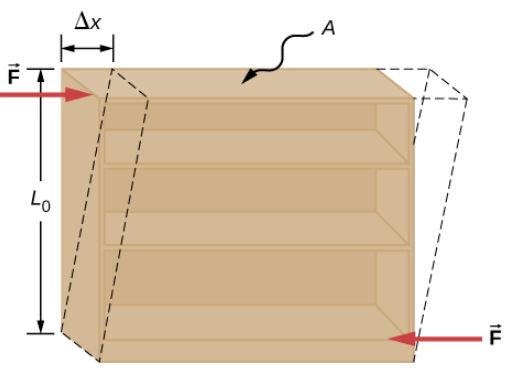
El módulo de cizalladura o de corte es la constante de proporcionalidad en la ecuación 3.33 y se define por la relación de esfuerzo a deformación. El módulo de corte es comúnmente denotado por $S$:
Ejemplo 3.10
Un viejo estante
Una persona de limpieza trata de mover una estantería pesada y vieja sobre un piso alfombrado presionando tangencialmente la superficie del estante superior. Sin embargo, el único efecto notable de este esfuerzo es similar al observado en la , y desaparece cuando la persona deja de presionar. La librería tiene $180.0$ cm de alto y $90.0 cm$ de ancho con cuatro estantes de $30.0 cm$ de profundidad, todos parcialmente cargados de libros. El peso total de la librería y los libros es de $600.0 N$. Si la persona le da a la repisa superior un empuje de $50.0 N$ que desplaza la repisa superior horizontalmente por $15.0 cm$ con respecto a la repisa inferior inmóvil, encuentra el módulo de corte de la librería.
Estrategia
Las únicas piezas de información relevante son las dimensiones físicas de la librería, el valor de la fuerza tangencial y el desplazamiento que causa esta fuerza. Identificamos $F_∥ = 50.0N$, $Δx = 15.0 cm$, $L_0 = 180.0 cm$, y $A = (30.0 cm)(90.0 cm) = 2700.0 cm^2$, y usamos la Ecuación 3.43 para calcular el módulo de corte.
Solución
Sustituyendo los datos en las ecuaciones, obtenemos para el módulo de corte:
También podemos encontrar el esfuerzo de de corte y la deformación:
$$\frac{F_∥}{A} = \frac{50.0 N}{2700.0 cm^2} = \frac{5}{27} kPa = 185.2 Pa$$ $$\frac{Δx}{L_0} = \frac{15 cm}{180 cm} = \frac{1}{12} = 0.083$$Explicación
Si la persona en este ejemplo le dio un empujón suave a la estantería, podría suceder que la cizalla inducida la colapsara. Gran parte del mismo mecanismo de corte es responsable de las fallas de diques llenos de tierra; y, en general, por deslizamientos.
 Comprueba tu aprendizaje 3.12
Comprueba tu aprendizaje 3.12
Los esfuerzos cortantes también se presentan por la acción de una carga axial en un plano inclinado, tal como se indica en la siguiente escena interactiva, diseñada por Juan Guillermo Rivera Berrío.
Nos referimos a la constante de proporcionalidad entre el esfuerzo y la deformación como el módulo elástico. Pero, ¿por qué lo llamamos así? ¿Qué significa que un objeto sea elástico y cómo describimos su comportamiento?
La elasticidad es la tendencia de los objetos y materiales sólidos a volver a su forma original después de que se eliminan las fuerzas externas (carga) que causan una deformación. Un objeto es elástico cuando vuelve a su tamaño y forma originales cuando la carga ya no está presente. Las razones físicas del comportamiento elástico varían entre los materiales y dependen de la estructura microscópica del material. Por ejemplo, la elasticidad de los polímeros y cauchos es causada por el estiramiento de las cadenas de polímeros bajo una fuerza aplicada. En contraste, la elasticidad de los metales es causada por el cambio de tamaño y la remodelación de las celdas cristalinas de las redes (que son las estructuras materiales de los metales) bajo la acción de fuerzas aplicadas externamente.
Los dos parámetros que determinan la elasticidad de un material son su módulo de elasticidad y su límite elástico. Un alto módulo elástico es típico de los materiales que son difíciles de deformar; en otras palabras, materiales que requieren una carga alta para lograr una deformación significativa. Un ejemplo es una banda de acero. Un módulo de elasticidad bajo es típico de los materiales que se deforman fácilmente bajo una carga; por ejemplo, una goma elástica. Si el esfuerzo bajo una carga se vuelve demasiado alta, entonces cuando se retira la carga, el material ya no vuelve a su forma y tamaño original, sino que se relaja a una forma y tamaño diferentes: el material se deforma permanentemente. El límite elástico es el valor del esfuerzo más allá del cual el material ya no se comporta elásticamente, sino que se deforma permanentemente.
Nuestra percepción de un material elástico depende tanto de su límite elástico como de su módulo elástico. Por ejemplo, todos los cauchos se caracterizan por un módulo elástico bajo y un límite elástico alto; Por lo tanto, es fácil estirarlos y el estiramiento es notablemente grande. Entre los materiales con límites elásticos idénticos, el más elástico es el que tiene el módulo elástico más bajo.
Cuando la carga aumenta desde cero, el esfuerzo resultante es directamente proporcional a la deformación dada por la Ecuación 12.33, pero solo cuando el esfuerzo no excede algún valor límite. Para valores de esfuerzo dentro de este límite lineal, podemos describir el comportamiento elástico en analogía con la ley de Hooke para un resorte. Según la ley de Hooke, el valor de estiramiento de un resorte bajo una fuerza aplicada es directamente proporcional a la magnitud de la fuerza. Por el contrario, la fuerza de respuesta del resorte a un estiramiento aplicado es directamente proporcional al estiramiento. De la misma manera, la deformación de un material bajo una carga es directamente proporcional a la carga y, a la inversa, el esfuerzo resultante es directamente proporcional a la deformación. El límite de linealidad (o el límite de proporcionalidad) es el mayor valor de esfuerzo más allá del cual el esfuerzo ya no es proporcional a la deformación. Más allá del límite de linealidad, la relación entre el esfuerzo y la deformación ya no es lineal. Cuando el esfuerzo se hace más grande que el límite de la linealidad pero aún dentro del límite de elasticidad, el comportamiento sigue siendo elástico, pero la relación entre el esfuerzo y la deformación se vuelve no lineal.
Para esfuerzos más allá del límite elástico, un material exhibe un comportamiento plástico. Esto significa que el material se deforma irreversiblemente y no vuelve a su forma y tamaño originales, incluso cuando se retira la carga. Cuando el esfuerzo aumenta gradualmente más allá del límite elástico, el material sufre una deformación plástica. Los materiales parecidos al caucho muestran un aumento de la deformación a medida que aumenta el esfuerzo, lo que significa que se vuelven más difíciles de estirar y, eventualmente, alcanzan un punto de fractura donde se rompen. Los materiales dúctiles, como los metales, muestran una disminución gradual del esfuerzo a medida que aumenta la deformación, lo que significa que se vuelven más fáciles de deformar a medida que los valores de esfuerzo-deformación se acercan al punto de ruptura. Los mecanismos microscópicos responsables de la plasticidad de los materiales son diferentes para diferentes materiales.
Podemos graficar la relación entre el esfuerzo y la deformación en un diagrama de esfuerzo-deformación. Cada material tiene su propia curva característica de esfuerzo-deformación. En la se muestra un diagrama típico de esfuerzo-deformación para un metal dúctil bajo carga. En esta figura, la deformación es una elongación fraccionada (no dibujada a escala). Cuando la carga aumenta gradualmente, el comportamiento lineal (línea roja) que comienza en el punto sin carga (el origen) termina en el límite de linealidad en el punto $H$. Para mayores aumentos de carga más allá del punto $H$, la relación esfuerzo-deformación es no lineal. Pero sigue siendo elástico. En la figura, esta región no lineal se ve entre los puntos $H$ y $E$. Las cargas cada vez más grandes llevan el esfuerzo al límite E de elasticidad, donde el comportamiento elástico termina y comienza la deformación plástica. Más allá del límite de elasticidad, cuando se elimina la carga, por ejemplo, en $P$, el material se relaja a una nueva forma y tamaño a lo largo de la línea verde. Esto quiere decir que el material se deforma permanentemente y no vuelve a su forma y tamaño iniciales cuando el esfuerzo se vuelve cero.
El valor del esfuerzo en el punto de fractura se denomina esfuerzo de rotura (o tensión final). Los materiales con propiedades elásticas similares, como dos metales, pueden tener esfuerzos de rotura muy diferentes. Por ejemplo, el esfuerzo máximo para el aluminio es de $2.2 × 10^8 Pa$ y para el acero puede ser tan alta como $20.0 × 10^8 Pa$, dependiendo del tipo de acero. Podemos hacer una estimación rápida, basada en la ecuación 12.34, de que para las barras con un área de sección transversal de 1 en 2, la carga de rotura para una barra de aluminio es de $3.2 × 10^4 lb$, y la carga de rotura para una barra de acero es aproximadamente nueve veces mayor.
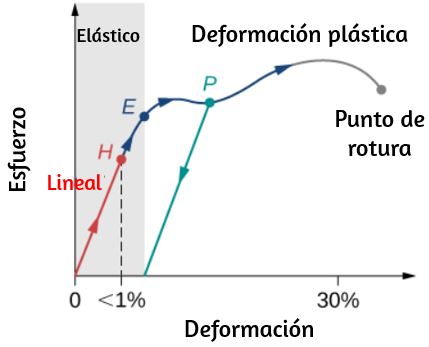
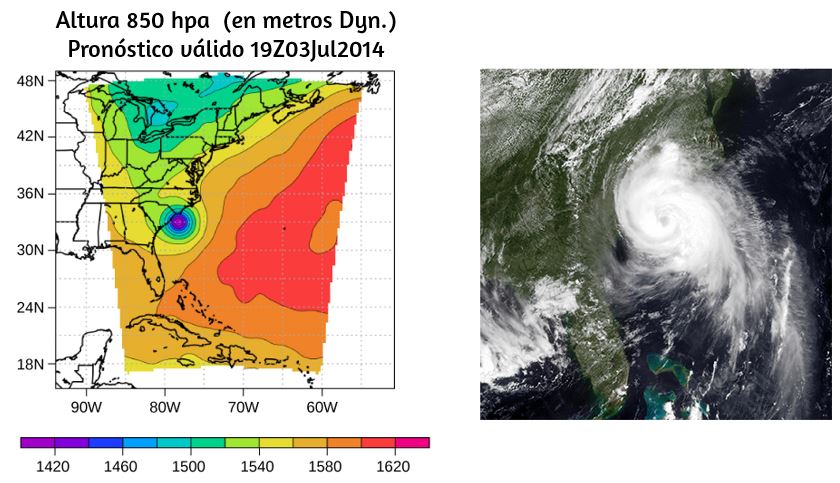
Imagínate caminando por una playa en la costa este de los Estados Unidos. El aire huele a sal de mar y el sol calienta tu cuerpo. De repente, una alerta aparece en tu teléfono celular. Una depresión tropical se ha convertido en un huracán. La presión atmosférica ha caído hasta casi un $15$% por debajo del promedio.
Como resultado, los pronosticadores esperan lluvias torrenciales, vientos de más de $100 mph$ y daños de millones de dólares. Mientras se prepara para evacuar, se pregunta: ¿Cómo puede una caída tan pequeña en la presión provocar un cambio tan severo en el clima?
La presión es un fenómeno físico que es responsable de mucho más que el clima. Los cambios en la presión hacen que los oídos se "salten" durante el despegue en un avión. Los cambios en la presión también pueden hacer que los buceadores sufran un trastorno a veces fatal conocido como "curvas", que se produce cuando el nitrógeno disuelto en el agua del cuerpo a profundidades extremas vuelve a un estado gaseoso en el cuerpo cuando el buceador emerge. La presión se encuentra en el corazón de los fenómenos llamados flotabilidad, que hacen que los globos de aire caliente se eleven y los barcos floten. Antes de que podamos comprender completamente el papel que juega la presión en estos fenómenos, debemos discutir los estados de la materia y el concepto de densidad.
La materia comúnmente existe son los sólidos, líquidos o gases; estos estados son conocidos como las tres fases comunes de la materia. Veremos cada una de estas fases en detalle en esta sección.
Los sólidos son rígidos y tienen formas específicas y volúmenes definidos. Los átomos o moléculas en un sólido están muy cerca entre sí, y hay una fuerza significativa entre estas moléculas. Los sólidos tomarán una forma determinada por la naturaleza. De estas fuerzas entre las moléculas.
Aunque los sólidos verdaderos no son incompresibles, requiere una gran fuerza. Para cambiar la forma de un sólido, en algunos casos, la fuerza entre las moléculas puede hacer que las moléculas se organicen en una red como se muestra en la . La estructura de esta red tridimensional se representa como moléculas conectadas por uniones rígidas (modeladas como resortes rígidos), que permiten una libertad limitada para el movimiento. Incluso una gran fuerza produce solo un pequeño desplazamiento en los átomos o moléculas de la red, y el sólido mantiene su forma. Los sólidos también resisten las fuerzas de cizallamiento. (Las fuerzas de cizallamiento son fuerzas aplicadas tangencialmente a una superficie, como se describe en Equilibrio estático y Elasticidad).
Los líquidos y los gases se consideran fluidos porque dan lugar a fuerzas de cizallamiento, mientras que los sólidos los resisten. Al igual que los sólidos, las moléculas en un líquido están unidas a moléculas vecinas, pero poseen muchos menos de estos enlaces. Las moléculas en un líquido no están bloqueadas en su lugar y pueden moverse una con respecto a la otra. La distancia entre las moléculas es similar a las distancias en un sólido, por lo que los líquidos tienen volúmenes definidos, pero la forma de un líquido cambia, dependiendo de la forma de su recipiente. Los gases no están unidos a los átomos vecinos y pueden tener grandes separaciones entre moléculas. Los gases no tienen formas específicas ni volúmenes definidos, ya que sus moléculas se mueven para llenar el recipiente en el que se encuentran . Los líquidos se deforman fácilmente cuando están esforzados y no vuelven a su forma original una vez que se elimina la fuerza. Esto ocurre porque los átomos o las moléculas en un líquido son libres de deslizarse alrededor de sus vecinos. Es decir, los líquidos fluyen (por lo que son un tipo de fluido), con las moléculas unidas por atracción mutua.
Cuando un líquido se coloca en un recipiente sin tapa, permanece en el contenedor. Debido a que los átomos están muy compactos, los líquidos, como los sólidos, resisten la compresión; una fuerza extremadamente grande será necesaria para cambiar el volumen de un líquido. En contraste, los átomos en los gases están separados por grandes distancias, y las fuerzas entre los átomos en un gas son por lo tanto muy débiles, Excepto cuando los átomos chocan entre sí. Esto hace que los gases sean relativamente fáciles de comprimir y les permite fluir (lo que los hace fluidos). Cuando se colocan en un recipiente abierto, los gases, a diferencia de los líquidos, escaparán. En este capítulo, generalmente nos referimos tanto a los gases como a los líquidos simplemente como fluidos, haciendo una distinción entre ellos solo cuando se comportan de manera diferente. Existe otra fase de la materia, el plasma, que existe a temperaturas muy altas.
A altas temperaturas, las moléculas pueden disociarse en átomos y los átomos disociarse en electrones (con cargas negativas) y protones (con cargas positivas), formando un plasma. El plasma no se analizará en profundidad en este capítulo porque el plasma tiene propiedades muy diferentes de las otras tres fases comunes de la materia, discutidas en este capítulo, debido a la fuerte fuerza eléctrica entre las cargas.
Supongamos que un bloque de latón y un bloque de madera tienen exactamente la misma masa. Si ambos bloques se caen en un tanque de agua, ¿Por qué la madera flota y el bronce se hunde? . Esto ocurre porque el latón tiene una mayor densidad que el agua, mientras que la madera tiene una menor densidad que el agua.

La densidad es una característica importante de las sustancias. Es crucial, por ejemplo, para determinar si un objeto se hunde o flota en un fluido.
Densidad
La densidad media de una sustancia u objeto se define como su masa por unidad de volumen
$$ρ = \frac{m}{V} \tag{4.1}$$donde la letra griega $ρ$ (rho) es el símbolo de densidad, $m$ es la masa y $V$ es el volumen.
La unidad de densidad del SI es $kg/m^3$. La enumera algunos valores representativos. La unidad de densidad $cgs$ es el gramo por centímetro cúbico, $g / cm^3$, donde
$$1 g/cm^3 = 1000 kg/m^3$$El sistema métrico se diseñó originalmente para que el agua tuviera una densidad de $1 g / cm^3$, equivalente a $10^3 kg / m^3$. Así, la unidad de masa básica, el kilogramo, se diseñó por primera vez para ser la masa de $1000 ml$ de agua, que tiene un volumen de $1000 cm^3$.
Como puede ver al examinar la , la densidad de un objeto puede ayudar a identificar su composición. La densidad del oro, por ejemplo, es aproximadamente $2,5$ veces la densidad del hierro, que es aproximadamente $2,5$ veces la densidad del aluminio. La densidad también revela algo sobre la fase de la materia y su estructura. Observe que las densidades de líquidos y sólidos son más o menos comparables, en concordancia con el hecho de que sus átomos están en contacto cercano.
Las densidades de los gases son mucho menores que las de los líquidos y los sólidos, porque los átomos en los gases están separados por grandes cantidades de espacio vacío. Los gases se muestran para una temperatura estándar de $0.0 °C$ y una presión estándar de $101.3 kPa$, y existe una fuerte dependencia de las densidades de temperatura y presión. Las densidades de sólidos y líquidos mostrados se dan para la temperatura estándar de $0.0 °C$ y las densidades de sólidos y líquidos dependen de la temperatura. La densidad de sólidos y líquidos normalmente aumenta al disminuir la temperatura.
La muestra la densidad del agua en varias fases y temperatura. La densidad del agua aumenta con la disminución temperatura, alcanzando un máximo a $4.0°C$, y luego disminuye a medida que la temperatura cae por debajo de $4.0°C$. Este comportamiento de la densidad del agua explica por qué el hielo se forma en la parte superior de un cuerpo de agua.
La densidad de una sustancia no es necesariamente constante en todo el volumen de una sustancia. Si la densidad es constante en toda la sustancia, se dice que la sustancia es una sustancia homogénea. Una barra de hierro sólida es un ejemplo de una sustancia homogénea. La densidad es constante en todo momento, y la densidad de cualquier muestra de la sustancia es la misma que su densidad promedio. Si la densidad de una sustancia no fuera constante, se dice que la sustancia es una sustancia heterogénea. Un trozo de queso suizo es un ejemplo de un material heterogéneo que contiene tanto el queso sólido como los huecos llenos de gas. La densidad en una ubicación específica dentro de un material heterogéneo se llama densidad local, y se da en función de la ubicación, $ρ = ρ (x, y, z)$ ()
La densidad local se puede obtener mediante un proceso limitante, basado en la densidad promedio en un volumen pequeño alrededor del punto en cuestión, tomando el límite donde el tamaño del volumen se acerca a cero,
donde $ρ$ es la densidad, $m$ es la masa y $V$ es el volumen. Dado que los gases son libres de expandirse y contraerse, las densidades de los gases varían considerablemente con la temperatura, mientras que las densidades de los líquidos varían poco con la temperatura. Por lo tanto, las densidades de los líquidos a menudo se tratan como constantes, con la densidad igual a la densidad promedio. La densidad es una propiedad dimensional; por lo tanto, al comparar las densidades de dos sustancias, las unidades deben tomarse en consideración.
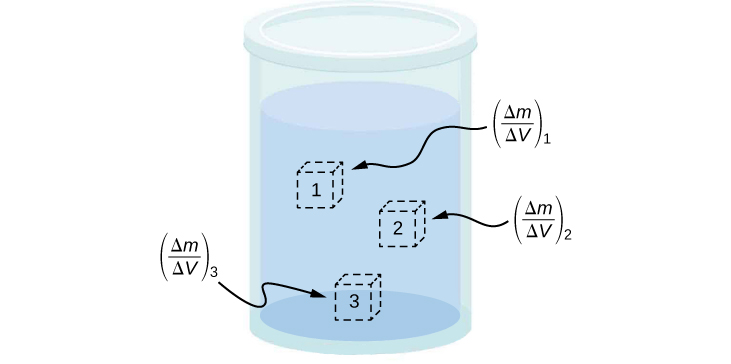
Por esta razón, una cantidad más conveniente y sin dimensiones llamada gravedad específica se utiliza a menudo para comparar densidades. La gravedad específica se define como la relación de la densidad del material a la densidad del agua a $4.0°C$ y una atmósfera de presión, que es $1000 kg /m^3$:
$$\textsf{Gravedad específica} = \frac{\textsf{Densidad del material}}{\textsf{Densidad del agua}}$$La comparación usa agua porque la densidad del agua es de $1 g / cm^3$, que originalmente se usó para definir el kilogramo. La gravedad específica, al no tener dimensiones, proporciona una comparación fácil entre los materiales sin tener que preocuparse por la unidad de densidad.
Por ejemplo, la densidad del aluminio es $2.7$ en $g / cm^3 (2700 en kg / m^3)$, pero su peso específico es $2.7$, independientemente de la unidad de densidad. La gravedad específica es una cantidad particularmente útil con respecto a la flotabilidad, que veremos más adelante en este capítulo.
Sin duda ha escuchado la palabra "presión" utilizada en relación con la sangre (presión arterial alta o baja) y en relación con el clima (sistemas meteorológicos de alta y baja presión). Estos son solo dos de los muchos ejemplos de presión en fluidos. (Recuerde que introdujimos la idea de la presión en el equilibrio estático y la elasticidad, en el contexto de la tensión y la tensión en masa).
Presión
La presión ($p$) se define como la fuerza normal $F$ por unidad de área $A$ sobre la cual se aplica la fuerza, o
$$P = \frac{F}{A} \tag{4.3}$$Para definir la presión en un punto específico, la presión se define como la fuerza $dF$ ejercida por un fluido sobre un elemento infinitesimal del área $dA$ que contiene el punto, dando como resultado $P = \frac{dF}{dA}$.
Una fuerza dada puede tener un efecto significativamente diferente, dependiendo del área sobre la cual se ejerce la fuerza.
Por ejemplo, una fuerza aplicada a un área de $1 mm^2$ tiene una presión que es $100$ veces mayor que la fuerza aplicada a un área de $1 cm^2$.
Es por eso que una aguja afilada puede atravesar la piel cuando se ejerce una pequeña fuerza, pero la aplicación de la misma fuerza con un dedo no pincha la piel .
Tenga en cuenta que aunque la fuerza es un vector, la presión es un escalar. La presión es una cantidad escalar porque se define como proporcional a la magnitud de la fuerza que actúa perpendicular al área de la superficie.
La unidad SI para la presión es el pascal ($Pa$), que lleva el nombre del matemático y físico francés Blaise Pascal (1623-1662), donde
$$1Pa = 1N/m^2$$Otras unidades se utilizan para la presión, que veremos más adelante en el capítulo.
La presión se define para todos los estados de la materia, pero es particularmente importante cuando se habla de fluidos. Una característica importante de los fluidos es que no existe una resistencia significativa al componente de una fuerza aplicada en paralelo a la superficie de un fluido. Las moléculas del fluido simplemente fluyen para acomodar la fuerza horizontal. Una fuerza aplicada perpendicular a la superficie comprime o expande el fluido. Si intenta comprimir un fluido, encontrará que se desarrolla una fuerza de reacción en cada punto dentro del fluido en dirección hacia afuera, equilibrando la fuerza aplicada sobre las moléculas en el límite.
Considere un fluido de densidad constante como se muestra en la . La presión en el fondo del recipiente se debe a la presión de la atmósfera ($p_0$) más la presión debida al peso del fluido. La presión debida al fluido es igual al peso del fluido dividido por el área. El peso del fluido es igual a su masa multiplicada por la aceleración debida a la gravedad.
Como la densidad es constante, el peso se puede calcular utilizando la densidad:
$$ w = mg = ρVg = ρAhg$$La presión en el fondo del contenedor es, por lo tanto, igual a la presión atmosférica agregada al peso del fluido dividido por el área. Por tanto la ecuación de la presión a una profundidad para un fluido de densidad constante es:
$$ p = p_0 + \frac{ρAhg}{A}= p_0 + ρhg$$
Presión a una profundidad para un fluido de densidad constante
La presión a una profundidad en un fluido de densidad constante es igual a la presión de la atmósfera más la presión debida a el peso del fluido, o
$$p = p_0 + ρhg \tag{4.4}$$Donde $p$ es la presión a una profundidad particular, $p_0$ es la presión de la atmósfera, $ρ$ es la densidad del fluido, $g$ es la aceleración debida a la gravedad, y $h$ es la profundidad.

Ejemplo 4.1
Considere la presión y la fuerza que actúa sobre la presa que retiene un reservorio de agua . Supongamos que la presa tiene $500 m$ de ancho y el agua tiene una profundidad de $80.0 m$ en la presa, como se ilustra a continuación. (a) ¿Cuál es la presión promedio en la presa debido al agua? (b) Calcule la fuerza ejercida contra la presa.
La presión promedio $p$ debido al peso del agua es la presión a la profundidad promedio $h$ de $40.0 m$, ya que la presión aumenta linealmente con la profundidad.
La fuerza ejercida sobre la presa por el agua es la presión promedio por el área de contacto, $F = pA$.
a. La presión media debida al peso de un fluido es
$$p = hρg \tag{4.5}$$Ingresando la densidad del agua de la Tabla 4.1 y tomando $h$ como la profundidad promedio de $40.0 m$, obtenemos
$$\begin{split} p &= (40.0 m) \left(10^3\frac{kg}{m^3} \right) \left(9.8\frac{m}{s^2} \right) \\ &= 3.92x10^5\frac{N}{m^2} = 392 kPa \end{split}$$b. Ya hemos encontrado el valor para $p$. Entonces, el área de la presa es
$$A = 80.0 m × 500 m = 4.00 × 10^4m^2$$así que
$$\begin{split} F &= (3.92 × 10^5 N/m^2)(4.00 × 10^4 m^2) \\ &= 1.57 × 10^{10}N \end{split}$$Explicación
Aunque esta fuerza parece grande, es pequeña en comparación con el peso de $1.96 × 10^{13}N$ del agua en el depósito. De hecho, es sólo el $0.0800\%$ del peso.
 Comprueba tu aprendizaje 4.1
Comprueba tu aprendizaje 4.1
Si el reservorio en el Ejemplo 4.1 cubriera dos veces el área, pero se mantuviera a la misma profundidad, ¿sería necesario rediseñar la presa?
Un fluido estático es un fluido que no está en movimiento. En cualquier punto dentro de un fluido estático, la presión en todos los lados debe ser igual; de lo contrario, el fluido en ese punto reaccionaría a una fuerza neta y aceleraría. La presión en cualquier punto de un fluido estático depende solo de la profundidad en ese punto. Como se discutió, la presión en un fluido cerca la Tierra varía con la profundidad debido al peso del fluido por encima de un nivel particular.
En los ejemplos anteriores, asumimos que la densidad es constante y la densidad media del fluido para ser una buena representación de la densidad. Esta es una aproximación razonable para líquidos como el agua, donde se requieren grandes fuerzas para comprimir el líquido o cambiar el volumen. En una piscina, por ejemplo, la densidad es aproximadamente constante y el agua en el fondo se comprime muy poco por el peso de la agua encima, sin embargo, viajar a la atmósfera es una situación muy diferente. La densidad del aire comienza a cambiar significativamente solo una corta distancia sobre la superficie de la Tierra. Para obtener una fórmula para la variación de la presión con la profundidad en un tanque que contiene un fluido de densidad ρ en la superficie de la Tierra, debemos comenzar con el supuesto de que la densidad del fluido no es constante.
El fluido ubicado en niveles más profundos está sujeto a más fuerza que el fluido más cercano a la superficie debido al peso del fluido que se encuentra sobre él. Por lo tanto, la presión calculada a una profundidad dada es diferente de la presión calculada utilizando una densidad constante. Imagine un elemento delgado de fluido a una profundidad $h$, como se muestra en la . El elemento tiene un área transversal $A$ y una altura $y$. Las fuerzas que actúan sobre el elemento se deben a las presiones $p(y)$ arriba y $p_y + Δy$ debajo de él. El peso del elemento en sí también se muestra en el diagrama de cuerpo libre.
Dado que el elemento de fluido entre $y - y + Δy$ no está acelerando, las fuerzas están equilibradas. Usando un eje $y$.
Orientados hacia arriba, encontramos la siguiente ecuación para el componente $y$:
$$p(y + Δy )A - p(y)A - gΔm = 0 (Δy > 0) \tag{4.6}$$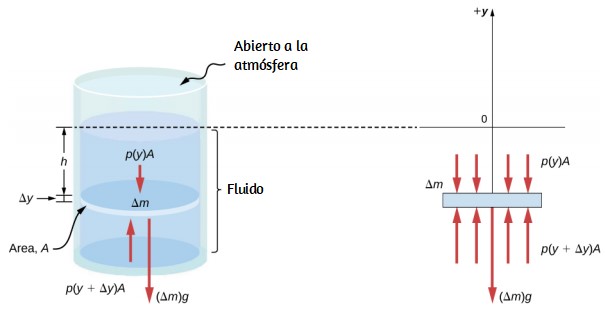
Tenga en cuenta que si el elemento tuviera una componente de aceleración distinto de cero y, el lado derecho no sería cero, sino la masa multiplicada por la aceleración y la masa del elemento puede ser escrita en términos de la densidad del fluido y el volumen de los elementos:
$$Δm = |ρAΔy| = -ρAΔy (Δy > 0)$$Poniendo esta expresión para $Δm$ en la Ecuación 4.6 y luego dividiendo ambos lados por $AΔy$, encontramos
$$\frac{p(y + Δy) - p(y)}{Δy} = -ρg \tag{4.7}$$Tomando el límite del elemento infinitesimalmente delgado $Δy → 0$, obtenemos la siguiente ecuación diferencial, que da la variación de la presión en un fluido:
Esta ecuación nos dice que la tasa de cambio de presión en un fluido es proporcional a la densidad del fluido. La solución de esta ecuación depende de si la densidad ρ es constante o cambia con la profundidad; es decir, la función $ρ(y)$.
Si el alcance de la profundidad que se está analizando no es demasiado grande, podemos asumir que la densidad es constante. Pero si el rango de profundidad es lo suficientemente grande como para que la densidad varíe de forma apreciable, como en el caso de la atmósfera, hay un cambio significativo en densidad con profundidad. En ese caso, no podemos utilizar la aproximación de una densidad constante.
Usemos la Ecuación 4.9 para elaborar una fórmula para la presión a una profundidad h de la superficie en un tanque de un líquido como el agua, donde la densidad del líquido puede ser tomada como constante.
Necesitamos integrar la Ecuación 4.9 de $y = 0$, donde la presión es la presión atmosférica $(p_0), a y = -h$, que es la coordenada de la profundidad:
$$\int_{p_0}^{p} dp = -\int_0^h ρgdy \tag{4.9}$$ $$p - p_0 = ρgh$$ $$p = p_0 + ρgh$$Por lo tanto, la presión a una profundidad de fluido en la superficie de la Tierra es igual a la presión atmosférica más ρgh si la densidad de la el fluido es constante en la altura, como encontramos anteriormente. Tenga en cuenta que la presión en un fluido depende sólo de la profundidad de la superficie y no de la forma del recipiente. Así, en un recipiente en el que un fluido puede moverse libremente en varias partes, el líquido se mantiene al mismo nivel en todas las partes, independientemente de las forma, como se muestra en la .

El cambio en la presión atmosférica con la altura es de particular interés. Asumiendo que la temperatura del aire sea constante, y que la ley de gas ideal de la termodinámica describa la atmósfera a una buena aproximación, podemos encontrar la variación de presión atmosférica con la altura, cuando la temperatura es constante. (Discutiremos la ley del gas ideal en un capítulo posterior, pero asuma que usted tiene alguna familiaridad con él desde la escuela secundaria y la química.) Sea $p(y)$ la presión atmosférica en la altura $y$. La densidad $ρ$ a $y$, la temperatura $T$ en la escala de Kelvin ($K$), y la masa m de una molécula de aire se relacionan con el absoluto presión por la ley de gas ideal, en la forma
$$p = ρ\frac{k_B T}{m}(atmósfera) \tag{4.10}$$donde $k_B$ es la constante de Boltzmann, que tiene un valor de $1,38 × 10^{-23} J/K$. Es posible que haya encontrado la ley del gas ideal en la forma $pV = nRT$, donde $n$ es el número de moles y $R$ es la constante del gas. Aquí, la misma ley ha sido escrita en una forma diferente, usando la densidad $ρ$ en lugar del volumen $V$. Por lo tanto, si la presión $p$ cambia con la altura, también lo hace la densidad $ρ$. Usando la densidad de la ley de gas ideal, la tasa de variación de la presión con la altura se da como sigue
$$\frac{dp}{dy}= -p \left(\frac{mg}{ k_BT} \right)$$donde se han recogido cantidades constantes dentro de los paréntesis. Reemplazando estas constantes con un solo símbolo $α$, la ecuación parece mucho más simple:
Esto da la solución $$p(y) = p_0exp(-αy)$$
Así, la presión atmosférica cae exponencialmente con la altura, ya que el eje $y$ está apuntando hacia arriba desde el suelo e y tiene valores positivos en la atmósfera sobre el nivel del mar. Las caídas de presión se multiplican por $1/e$ cuando la altura es $1/α$, lo que nos da una interpretación física de $α$:
La constante $1/α$ es una escala de longitud que caracteriza la forma en que la presión varía con la altura y que a menudo se conoce como la altura de la escala de presión. Podemos obtener un valor aproximado de $α$ utilizando la masa de una molécula de nitrógeno como aproximación de una molécula de aire. A temperatura $27°C$, o $300 K$, nos encontramos con
$$α = -\frac{mg}{k_b T} = \frac{4.8 × 10^{-26} kg}{1.38 × 10^{-23} J/K}$$Por lo tanto, por cada $8800$ metros, la presión del aire cae en un factor $1/e$, o aproximadamente un tercio de su valor. Esto nos da solo una estimación aproximada de la situación real, ya que hemos asumido una temperatura constante y una $g$ constante a distancias tan grandes de la Tierra, ninguna de las cuales es correcta en realidad.
La presión del fluido no tiene dirección, siendo una cantidad escalar, mientras que las fuerzas debidas a la presión tienen direcciones bien definidas: Se ejercen siempre perpendicularmente a cualquier superficie. La razón es que los fluidos no pueden soportar o ejercer fuerzas de cizallamiento. Así, en un fluido estático encerrado en un tanque, la fuerza ejercida sobre las paredes del tanque se ejerce perpendicularmente a la superficie interior. Asimismo, la presión se ejerce perpendicularmente a las superficies de cualquier objeto dentro del fluido. La ilustra la presión ejercida por el aire en las paredes de un neumático y por el agua en el cuerpo de un nadador.
En el siguiente interactivo, diseñado por Valentina Muñoz Porras, puedes comparar el efecto de la variación de las magnitudes masa y volumen, en la densidad de cuerpos sólidos y líquidos. Con la manipulación de estas variables mediante controles en el interactivo, podrás inferir que la densidad es directamente proporcional a la masa e inversamente proporcional al volumen.
En la sección anterior, derivamos una fórmula para calcular la variación en la presión de un fluido en equilibrio hidrostático. Resulta que este es un cálculo muy útil. Las mediciones de la presión son importantes en la vida diaria, así como en las aplicaciones científicas y de ingeniería. En esta sección, discutimos diferentes maneras en que la presión puede ser reportada y medida.
Supongamos que el manómetro de un tanque de buceo lleno lee $3000 psi$, lo que equivale aproximadamente a $207$ atmósferas. Cuando la válvula el aire comienza a salir porque la presión dentro del tanque es mayor que la presión atmosférica fuera del tanque. tanque. El aire continúa escapando del tanque hasta que la presión dentro del tanque es igual a la presión de la atmósfera exterior. el tanque. En este punto, el manómetro en el tanque lee cero, aunque la presión dentro del tanque sea de 1 la misma que la presión de aire fuera del tanque. La mayoría de los manómetros, como el del tanque de buceo, están calibrados para leer cero a presión atmosférica. Lecturas de presión de estos manómetros se denomina presión manométrica, que es la presión relativa a la presión atmosférica. Cuando la presión dentro del tanque es mayor que la presión atmosférica, el medidor reporta un valor positivo. Algunos manómetros están diseñados para medir la presión negativa. Por ejemplo, muchos experimentos de física deben llevarse a cabo en un cámara de vacío, una cámara rígida desde la que se bombea parte del aire. La presión dentro de la cámara de vacío es menor que la presión atmosférica, por lo que el manómetro de la cámara lee un valor negativo. A diferencia de la presión manométrica, la presión absoluta representa la presión atmosférica, que en efecto se suma a la presión de cualquier fluido no encerrado en un recipiente rígido
Presión absoluta
La presión absoluta, o presión total, es la suma de la presión manométrica y la presión atmosférica:
$$p_{\textsf{abs}} = p_g + p_{\textsf{atm}} \tag{4.11}$$donde $p_{\textsf{abs}}$ es presión absoluta, $p_g$ es presión manométrica y $p_{\textsf{atm}}$ es presión atmosférica.
Por ejemplo, si un medidor de aire lee $34 psi$, entonces la presión absoluta es $34 psi$ más $14.7 psi$ ("$p_{\textsf{atm}}$ en $psi$"), o $48.7 psi$ (equivalente a $336 kPa$). En la mayoría de los casos, la presión absoluta en los fluidos no puede ser negativa. Los fluidos empujan en lugar de tirar, por lo que la presión absoluta más pequeña en un fluido es cero (una presión absoluta negativa es un tirón). Por lo tanto, la presión manométrica más pequeña posible es $p_g = -p_{\textsf{atm}}$ (lo que hace que $p_{\textsf{abs}}$ sea cero). No existe un límite teórico para el tamaño de la presión manométrica.
Una gran cantidad de dispositivos se utilizan para medir la presión, desde medidores de presión de neumáticos hasta monitores de presión arterial. Muchos otros tipos de manómetros se utilizan comúnmente para probar la presión de los fluidos, como los manómetros mecánicos. Exploraremos algunos de ellos en esta sección. Cualquier propiedad que cambie con la presión de una manera conocida puede ser utilizada para construir un manómetro. Algunos de los tipos más comunes incluyen los medidores de tensión, que utilizan el cambio en la forma de un material con presión; los medidores de presión de capacitancia, que utilizan el cambio en la capacitancia eléctrica debido al cambio de forma con la presión; los medidores de presión piezoeléctricos, que generan una diferencia de voltaje a través de un material piezoeléctrico bajo una diferencia de presión entre los dos lados; y los medidores de iones, que miden la presión por medio de moléculas ionizantes en cámaras altamente evacuadas. Diferentes manómetros son útiles en diferentes rangos de presión y bajo diferentes situaciones físicas.

Una de las clases más importantes de manómetros aplica la propiedad de que la presión debido al peso de un fluido de la densidad constante viene dada por $p = hρg$. El tubo en forma de U mostrado en la es un ejemplo de un manómetro; en parte (a), ambos lados del tubo están abiertos a la atmósfera, lo que permite que la presión atmosférica empuje hacia abajo en cada lado por igual, de manera que la presión atmosférica se mantenga constante que sus efectos cancelan. Un manómetro con un solo lado abierto a la atmósfera es un dispositivo ideal para medir presiones de manómetro. La presión manométrica es $p_g = hρg$ y se obtiene midiendo $h$.
Por ejemplo, supongamos que un lado del tubo en U está conectado a alguna de las siguientes conexiones fuente de presión, como el globo en la parte (b) de la figura o el frasco de maní envasado al vacío que se muestra en la parte (c), $p_{\textsf{abs}}$ es menor que la presión atmosférica.
En ambos casos, $p_{\textsf{abs}}$ difiere de la presión atmosférica en una cantidad $h_{ρg}$, donde $ρ$ es la densidad del fluido en el manómetro. En la parte (b), los $p_{\textsf{abs}}$ pueden soportar una columna de fluido de altura $h$, por lo que deben ejercer una presión $h_{ρg}$ mayor que la presión atmosférica (la presión del medidor es positiva). En la parte (c), la presión atmosférica puede soportar una columna de fluido de altura $h$, por lo que pabs es menor que la presión atmosférica en una cantidad $h_{ρg}$ (la presión manométrica $p_g$ es negativa).
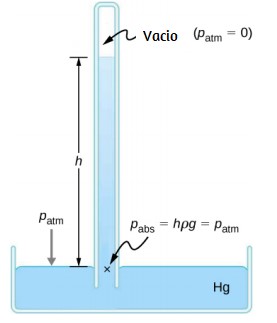
Los manómetros suelen utilizar un tubo en forma de U de un fluido (a menudo mercurio) para medir la presión. Un barómetro () es un dispositivo que típicamente utiliza una sola columna de mercurio para medir la presión atmosférica. El barómetro, inventado por el matemático y físico italiano Evangelista Torricelli (1608-1647) en 1643, está construido con un tubo de vidrio cerrado en un extremo y lleno de mercurio. El tubo se invierte y se coloca en una piscina de mercurio. Este dispositivo mide presión atmosférica, en lugar de la presión manométrica, porque hay un vacío casi puro por encima del mercurio en el tubo. La altura del mercurio es tal que $hρg = p_{\textsf{atm}}$. Cuando la presión atmosférica varía, el mercurio sube o baja.
Los meteorólogos monitorean de cerca los cambios en la presión atmosférica (a menudo reportados como presión barométrica), ya que el aumento del mercurio típicamente indica una mejora en el clima y la caída del mercurio indica un deterioro en el clima. El barómetro también sirve como altímetro, ya que la presión atmosférica media varía con la altitud. Los barómetros y manómetros de mercurio son tan común que las unidades de $mm \, Hg$ se cotizan a menudo para la presión atmosférica y la presión arterial.
Ejemplo 4.2
Un tubo en U con ambos extremos abiertos se llena con un líquido de densidad $ρ_1$ a una altura $h$ en ambos lados . Un líquido de densidad $ρ_2 < ρ_1$ se vierte en un lado y el Líquido 2 se asienta sobre el Líquido 1.
Las alturas de los dos lados son diferentes. La altura hasta la parte superior del Líquido 2 desde la interfaz es $h_2$ y la altura hasta la parte superior del Líquido 1 desde el nivel de la interfaz es $h_1$. Derivar una fórmula para la diferencia de altura.
Estrategia
La presión en los puntos a la misma altura en los dos lados de un tubo en U debe ser la misma mientras los dos puntos estén en el mismo líquido. Por lo tanto, consideramos dos puntos al mismo nivel en los dos brazos del tubo: Un punto es la interfaz en el lado del Líquido 2 y el otro es un punto en el brazo con Líquido 1 que está al mismo nivel que la interfaz en el otro brazo. La presión en cada punto se debe a la presión atmosférica más el peso del líquido sobre ella.
$$\textsf{Presión lateral con Líquido 1} = p_0 + ρ_1gh_1$$ $$\textsf{Presión lateral con Líquido 2} = p_0 + ρ_2gh_2$$Solución
Como los dos puntos están en el Líquido 1 y están a la misma altura, la presión en los dos puntos debe ser la misma. Por lo tanto, tenemos
$$p_0 + ρ_1 gh_1 = p_0 + ρ_2gh_2$$Por lo tanto
$$ ρ_1h_1 = ρ_2h_2$$Esto significa que la diferencia de alturas en los dos lados del tubo en U es
$$ h_2- h_1 =(1 - \frac{p_1 }{p_2})h_2$$El resultado tiene sentido si fijamos $p_2 = p_1$, lo que da $h_2 = h_1$. Si los dos lados tienen la misma densidad, tienen la misma altura.
 Comprueba tu aprendizaje 4.2
Comprueba tu aprendizaje 4.2
El mercurio es una sustancia peligrosa. ¿Por qué se supone que el mercurio se utiliza normalmente en los barómetros en lugar de un fluido más seguro como el agua?
En la siguiente escena interactiva, diseñada por Fu-Kwun Hwang, Fremont Teng y Loo Kang Wee, puedes cambiar las alturas y densidades de los tres líquidos y observar el cambio en las alturas manométricas.
De los mismos autores, en la siguiente escena puedes interactuar con dos medidores de presión:
Como se indicó anteriormente, la unidad SI para presión es el pascal ($Pa$), donde
$$1 Pa = 1 N/m^2$$Además del pascal, muchas otras unidades de presión son de uso común (). En meteorología, la presión atmosférica se describe a menudo en la unidad de milibares ($mb$), donde
$$1000 mb = 1 × 10^5Pa$$El milibar es una unidad conveniente para los meteorólogos porque la presión atmosférica promedio a nivel del mar en la Tierra es $1.013 × 10^5 Pa = 1013 mb = 1 atm$.

Usando las ecuaciones derivadas cuando se considera la presión a una profundidad en un fluido, la presión también se puede medir como milímetros o pulgadas de mercurio.
La presión en la parte inferior de una columna de mercurio de $760 mm$ a $0°C$ en un contenedor donde se evacua la parte superior es igual a la presión atmosférica.
Por lo tanto, $760 mm Hg$ también se utiliza en lugar de $1$ atmósfera de presión. En los laboratorios de física de vacío, los científicos a menudo usan otra unidad llamada torr, llamada así por Torricelli, quien, como acabamos de ver, inventó el manómetro de mercurio para medir la presión. Un $torr$ es igual a una presión de $1 mm Hg$.
En 1653, el filósofo y científico francés Blaise Pascal publicó su Tratado sobre el Equilibrio de los Líquidos, en el cual discutió los principios de los fluidos estáticos. Un fluido estático es un fluido que no está en movimiento. Cuando un fluido no está fluyendo, decimos que el está en equilibrio estático. Si el fluido es agua, decimos que está en equilibrio hidrostático. Para un fluido en equilibrio estático, la fuerza neta en cualquier parte del fluido debe ser cero; de lo contrario, el fluido comenzará a fluir.
Las observaciones de Pascal proporcionan los cimientos de la hidráulica, una de las más importantes, la evolución de la tecnología mecánica moderna. Pascal observó que un cambio en la presión aplicada a un fluido encerrado es transmitido sin disminuir a través del fluido y a las paredes de su contenedor. Debido a esto, a menudo sabemos más sobre presión que otras cantidades físicas en los fluidos. Además, el principio de Pascal implica que la presión total en un fluido es el suma de las presiones de diferentes fuentes. Un buen ejemplo es que el fluido en una profundidad depende de la profundidad del fluido y la presión de la atmósfera.
El principio de Pascal (también conocido como ley de Pascal) establece que cuando se aplica un cambio en la presión a un fluido cerrado, se transmite sin disminuir a todas las porciones del fluido y a las paredes de su recipiente.
En un fluido cerrado, dado que los átomos del fluido pueden moverse libremente, transmiten presión a todas las partes del fluido ya las paredes del recipiente. Cualquier cambio en la presión se transmite sin disminuir. Tenga en cuenta que este principio no dice que la presión sea la misma en todos los puntos de un fluido, lo cual no es cierto, ya que la presión en un fluido cerca de la Tierra varía con la altura. Más bien, este principio se aplica al cambio de presión. Supongamos que colocas agua en un contenedor cilíndrico de altura $H$ y área de sección transversal $A$ que tiene un pistón móvil de masa $m$ . Al añadir peso $Mg$ en la parte superior del pistón aumenta la presión en la parte superior en $Mg / A$, ya que el peso adicional también actúa sobre el área $A$ de la tapa:
Según el principio de Pascal, la presión en todos los puntos del agua cambia en la misma cantidad, $Mg / A$. Así, la presión. En la parte inferior también aumenta por $Mg / A$. La presión en el fondo del contenedor es igual a la suma de la Presión atmosférica , la presión debida al fluido y la presión suministrada por la masa. El cambio de presión en la parte inferior de la contenedor debido a la masa es
$$Δp_{\textsf{fondo}} = \frac{Mg}{A}$$Dado que los cambios de presión son los mismos en todo el fluido, ya no necesitamos subíndices para designar el cambio de presión para la parte superior o inferior:
$$Δp = Δp_{\textsf{parte superior}} = Δp_{\textsf{fondo}} = Δp_{\textsf{en todos lados}}$$El barril de Pascal es una gran demostración del principio de Pascal. Mire una simulación (https://openstaxcollege.org/l/21pascalbarrel) del experimento de Pascal en 1646, en el que demostró los efectos del cambio de presión en un fluido.
Los sistemas hidráulicos se utilizan para operar frenos automotrices, gatos hidráulicos y muchos otros sistemas mecánicos .
Podemos derivar una relación entre las fuerzas en este simple sistema hidráulico aplicando el principio de Pascal. Primero, tenga en cuenta que los dos pistones en el sistema están a la misma altura, por lo que no hay diferencia en la presión debido a una diferencia en la profundidad. La presión debida a la $F_1$ que actúa en el área $A_1$ es simplemente
$p_1 = \frac{F_1}{A_1}$, como se define y $p = \frac{F}{A}$
Según el principio de Pascal, esta presión se transmite sin disminuir a través del fluido y a todas las paredes del contenedor. Así, en el otro pistón se siente una presión $p_2$ igual a $p_1$. Es decir, $p_1 = p_2$. Sin embargo, como $p_2 = \frac{F_2}{A_2}$ vemos que
La ecuación anterior relaciona las fuerza sobree un área cualquiera en un sistema hidráulico, siempre que los pistones estén a la misma altura vertical y que la fricción en el sistema sea insignificante. Los sistemas hidráulicos pueden aumentar o disminuir la fuerza aplicada sobre ellos. Para aumentar la fuerza, la presión se aplica a un área más grande. Por ejemplo, si se aplica una fuerza de 100 N al cilindro izquierdo en la y el cilindro derecho tiene un área cinco veces mayor, entonces la fuerza de salida es de $500 N$. Los sistemas hidráulicos son análogos a las palancas simples, pero tienen la ventaja de que la presión se puede enviar a través de líneas tortuosamente curvas a varios lugares a la vez. El gato hidráulico es un sistema hidráulico de este tipo. Un gato hidráulico se utiliza para levantar cargas pesadas, como las que utilizan los mecánicos de automóviles para levantar un automóvil. Consiste en un fluido incompresible en un tubo en U provisto de un pistón móvil en cada lado. Un lado del tubo en U es más estrecho que el otro. Una pequeña fuerza aplicada sobre un área pequeña puede equilibrar un área mucho más grande. fuerza en el otro lado sobre un área mayor ().
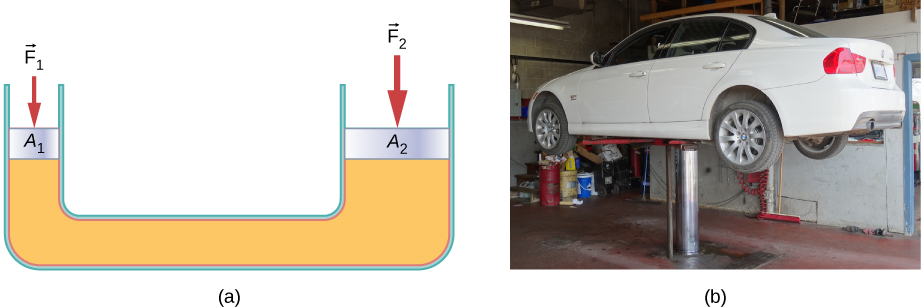
Desde el principio de Pascal, se puede demostrar que la fuerza necesaria para levantar el auto es menor que el peso del auto:
$$F_1 = \frac{A_1}{A_2}F_2$$donde $F_1$ es la fuerza aplicada para levantar el carro, $A_1$ es el área de la sección transversal del pistón más pequeño, $A_2$ es el área de la sección transversal del pistón más grande y $F_2$ es el peso del carro.
Ejemplo 4.3
Considere el sistema hidráulico del automóvil que se muestra en la .
Supongamos que se aplica una fuerza de $100 N$ al pedal del freno, que actúa sobre el cilindro del pedal a través de una palanca. Una fuerza de $500 N$ se ejerce sobre el cilindro del pedal. La presión creada en el cilindro del pedal se transmite a los cilindros de las cuatro ruedas. El cilindro de pedal tiene un diámetro de $0,500 cm$ y cada cilindro de rueda tiene un diámetro de $2,50 cm$. Calcule el magnitud de la fuerza $F_2$ creado en cada uno de los cilindros de rueda.
Estrategia
Si la fuerza $F_1$ se aplica al cilindro de pedal. Las secciones transversales $A_1$ y $A_2$ pueden calcularse a partir de sus diámetros dados. Entonces podemos usar la siguiente relación para encontrar la fuerza $F_2$ $$\frac{F_1}{A_1} = \frac{F_2}{A_2}$$
Manipular esta ecuación algebraicamente para obtener $F_2$ en un lado y sustituir valores conocidos.
Solución
El principio de Pascal aplicado a los sistemas hidráulicos viene dado por
$$\frac{F_1}{A_1} = \frac{F_2}{A_2}$$ $$F_2= \frac{A_2}{A_1}F_1 = \frac{πr_2 ^2}{πr_1^2} = F_1$$ $$ = \frac{(1.25 cm)^2}{ (0.250 cm)^2} x 500 N = 1.25 × 10^4N$$Explicación
Este valor es la fuerza ejercida por cada uno de los cilindros de las cuatro ruedas. Tenga en cuenta que podemos añadir tantos cilindros de rueda como sea posible como queramos. Si cada uno de ellos tiene un diámetro de $2,50 cm$, cada uno de ellos ejercerá $1,25 × 10^4 N$.
Un sistema hidráulico simple, en forma de ejemplo de una máquina simple, puede aumentar la fuerza pero no puede hacer más trabajo del que se hace en ella. El trabajo son tiempos de fuerza distancia se movió, y el cilindro de la rueda se mueve a través de una distancia menor que el cilindro del pedal. Además, cuantas más ruedas se añadan, menor será la distancia que cada uno recorra. Muchos sistemas hidráulicos, como los frenos eléctricos y los de las excavadoras tienen una bomba motorizada que realmente hace la mayor parte del trabajo en el sistema.
 Comprueba tu aprendizaje 4.4
Comprueba tu aprendizaje 4.4
Cuando se colocan en un fluido, algunos objetos flotan debido a una fuerza flotante. ¿De dónde viene esta fuerza flotante? ¿Por qué algunas cosas flotan y otras no? ¿Los objetos que se hunden reciben algún tipo de soporte del líquido? ¿Su cuerpo es impulsado por la atmósfera, o sólo se ven afectados los globos de helio ()?
Las respuestas a todas estas preguntas, y muchas otras, se basan en el hecho de que la presión aumenta con la profundidad en un fluido. Esto significa que la fuerza ascendente en la parte inferior de un objeto en un fluido es mayor que la fuerza descendente en la parte superior del objeto.

Hay una fuerza ascendente, o fuerza de flotación, sobre cualquier objeto en cualquier fluido . Si la fuerza de flotación es mayor que el peso del objeto, el objeto sube a la superficie y flota. Si la fuerza de flotación es menor que el peso del objeto, el objeto se hunde. Si la fuerza de flotación es igual al peso del objeto, éste puede permanecer suspendido en su profundidad actual. La fuerza de flotación siempre está presente, ya sea que el objeto flote, se hunda o esté suspendido en un fluido.
La fuerza de flotación es la fuerza ascendente sobre cualquier objeto en cualquier fluido.
¿Qué tan grande es la fuerza de flotación? Para responder a esta pregunta, piense en lo que sucede cuando se extrae un objeto sumergido de un fluido, como en la . Si el objeto no estuviera en el fluido, el espacio que ocupaba el objeto se llenaría con un fluido con un peso $w_{fl}$. Este peso es soportado por el fluido circundante, por lo que la fuerza de flotación debe ser igual al peso del fluido desplazado por el objeto.
Principio de Arquímedes
La fuerza de flotación sobre un objeto es igual al peso del fluido que desplaza. En forma de ecuación, el principio de Arquímedes es
$$F_B = w_{fl}$$donde $F_B$ es la fuerza de flotación y $w_{fl}$ es el peso del fluido desplazado por el objeto.
Este principio lleva el nombre del matemático e inventor griego Arquímedes (287-212 A.C.), quien declaró lo siguiente mucho antes de que los conceptos de fuerza estuvieran bien establecidos. El principio de Arquímedes se refiere a la fuerza de flotación que resulta cuando un cuerpo se sumerge en un fluido, ya sea parcial o totalmente. La fuerza que proporciona la presión de un líquido actúa sobre un cuerpo perpendicular a la superficie del cuerpo. En otras palabras, la fuerza debida a la presión en la parte inferior está apuntando hacia arriba, mientras que en la parte superior, la fuerza debida a la presión está apuntando hacia abajo; las fuerzas debidas a las presiones a los lados están apuntando hacia el cuerpo. Debido a que la parte inferior del cuerpo está a una profundidad mayor que la parte superior del cuerpo, la presión en la parte inferior del cuerpo es mayor. que la presión en la parte superior, como se muestra en la . Por lo tanto, una fuerza ascendente neta actúa sobre el cuerpo. Esta fuerza ascendente es la fuerza de flotación, o simplemente de flotación.
La exclamación "Eureka" (que significa "lo encontré") a menudo ha sido atribuida a Arquímedes al hacer el descubrimiento que llevaría al principio de Arquímedes.
Como hemos visto, la fuerza de flotación es la fuerza hacia arriba ejercida sobre un objeto por un fluido cuando el objeto está parcial o totalmente sumergido en el fluido. En este caso hay un bloque que cuelga de una balanza. El bloque se puede bajar al fluido (usa el control deslizante "Porcentaje de bloque sumergido"). Esto hace que la lectura de la escala de resorte cambie, ¿por qué? La lectura de la balanza de resorte muestra el peso aparente del bloque; esto es solo igual al peso real del bloque cuando el bloque está completamente fuera del fluido. Investiga de qué depende la fuerza de flotación (y de qué no depende). Observa que la simulación establece que $g$ es de $10 m/s^2$. Dados los límites de los controles deslizantes en la simulación, ¿cuál es la mayor fuerza de flotación que se puede lograr aquí?
En la siguiente escena interactiva, diseñada por Andrew Duffy, se ilustra el concepto de peso aparente, así como la fuerza de flotación. También puede mostrar una escala debajo del contenedor de líquido. Es interesante ver qué sucede con la lectura de la escala a medida que el bloque desciende (o se elimina) del fluido.
Si tiras un trozo de arcilla en agua, se hundirá. Pero si moldeas el mismo trozo de arcilla en la forma de un bote, flotará. Debido a su forma, el barco de arcilla desplaza más agua que el bulto y experimenta una mayor fuerza de flotación, a pesar de que su masa es la misma. Lo mismo ocurre con los buques de acero. La densidad media de un objeto es lo que finalmente determina si flota. Si la densidad media de un objeto es menor que del fluido circundante, flotará.
La razón es que el fluido, al tener una densidad más alta, contiene más masa y por lo tanto más peso en el mismo volumen. La fuerza de flotación, que es igual al peso del fluido desplazado, es por lo tanto mayor que la fuerza de flotación que el peso del objeto. Del mismo modo, un objeto más denso que el líquido se hundirá.
El grado en que un objeto flotante se sumerge depende de cómo se compara la densidad del objeto con la densidad del fluido. En la , por ejemplo, el buque descargado tiene una densidad menor y menos de él está sumergido en comparación con el mismo buque cargado. Podemos derivar una expresión cuantitativa para la fracción sumergida considerando la densidad. La fracción sumergida es la relación entre el volumen sumergido y el volumen del objeto, o bien
$$\textsf{fracción sumergida} = \frac{V_{\textsf{sub}}}{V_{\textsf{obj}}} = \frac{V_{fl}}{V_{\textsf{obj}}}$$El volumen sumergido es igual al volumen de fluido desplazado, que llamamos $V_{fl}$. Ahora podemos obtener la relación entre las densidades, sustituyendo $ρ = \frac{m}{V}$ en la expresión. Esto da
$$\frac{V_{\textsf{sub}}}{V_{\textsf{obj}}} = \frac{m_{fl}/ρ_{fl}}{m_{\textsf{obj}} /ρ_{\textsf{obj}}}$$donde $ρ_{\textsf{obj}}$ es la densidad media del objeto y $ρ_{fl}$ es la densidad del fluido. Puesto que el objeto flota, su masa y la del fluido desplazado son iguales, por lo que se cancelan de la ecuación, quedando
$$\textsf{fracción sumergida} = \frac{ρ_{\textsf{obj}}}{ρ_{fl}}$$Esta relación la podemos usar para medir densidades.

Ejemplo 4.4
Supongamos que una mujer de $60,0 kg$ flota en agua dulce con el $97,0%$ de su volumen sumergido cuando sus pulmones están llenos de aire. ¿Cuál es su densidad media?
Estrategia
Podemos encontrar la densidad de la mujer resolviendo la ecuación
$$\textsf{fracción sumergida} = \frac{V_{\textsf{obj}}}{V_{fl}}$$para la densidad del objeto. Esto da como resultado
$$ρ_{\textsf{obj}} = ρ_{\textsf{persona}} = (\textsf{fracción sumergida}) \cdot ρ_f$$Conocemos tanto la fracción sumergida como la densidad del agua, por lo que podemos calcular la densidad de la mujer.
Solución
Introduciendo los valores conocidos en la expresión de su densidad, obtenemos
$$ρ_{\textsf{persona}}= 0.970 (10^3\frac{kg}{m^3})$$Explicación
La densidad de la mujer es menor que la densidad del fluido. Esperamos esto porque ella flota
Numerosos objetos o sustancias de baja densidad flotan en fluidos de alta densidad: aceite sobre agua, un globo aerostático en la atmósfera, un pedazo de corcho sobre vino, un iceberg en agua salada y cera caliente en una "lámpara de lava", por nombrar algunos. Un ejemplo menos obvio son las cadenas montañosas que flotan en la corteza de mayor densidad y el manto debajo de ellas. Incluso la Tierra aparentemente sólida tiene características fluidas.
En la página siguiente, presentamos una unidad interactiva, tomada del Proyecto @prende.mx, el cual es una iniciativa de la Secretaría de Educación Pública del gobierno mejicano a través de la cual busca la introducción de las TIC en la Educación y contribuir, mediante el uso y aprovechamiento de la computadora personal, a la mejora de las condiciones de estudio de los estudiantes. Desde este recurso podrás complementar el estudio de la flotabilidad de líquidos y su papel en el orden como éstos se acomodan en un recipiente, la flotabilidad de objetos en general en función de su densidad específica respecto al líquido que los contiene y una explicación mas detallada de la razón por la cual flotan objetos masivos tales como barcos, además de una introducción al principio de Arquímedes.
La unidad didáctica cuenta con cuatro apartados. En el primero se presenta un vídeo con diferentes líquidos y, obviamente, diferentes densidades. El segundo, permite comprender la importancia de la densidad en lo flotación de cuerpos. El tercer apartado, profundiza en el tema de la flotación, incluyendo densidades y forma del cuerpo flotante. Finalmente, podrás confrontar lo aprendido en una prueba.
Una de las técnicas más comunes para determinar la densidad se muestra en la .
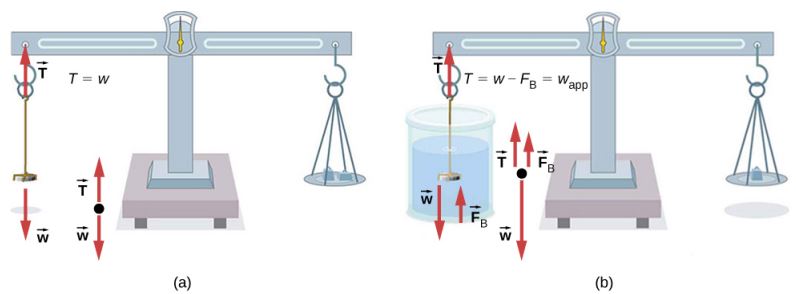
Un objeto, aquí una moneda, se pesa en el aire y luego se pesa de nuevo mientras está sumergido en un líquido. La densidad de la moneda, una indicación de su autenticidad, puede calcularse si se conoce la densidad del fluido. Podemos utilizar esta misma técnica para determinar la densidad del fluido si se conoce la densidad de la moneda. Todos estos cálculos se basan en el principio de Arquímedes, que establece que la fuerza de flotación sobre el objeto es igual al peso del fluido desplazado. Esto, a su vez, significa que el objeto parece pesar menos cuando está sumergido; lo llamamos medir el peso aparente del objeto. El objeto sufre una pérdida de peso aparente igual al peso del fluido desplazado.
Alternativamente, en las balanzas que miden la masa, el objeto sufre una pérdida aparente de masa igual a la masa de fluido desplazada. Es decir, la pérdida de peso aparente es igual al peso del fluido desplazado, o la pérdida de masa aparente es igual a la masa del fluido desplazado.
La primera parte de este capítulo trata de la estática de los fluidos, el estudio de los fluidos en reposo. El resto de este capítulo trata de los fluidos la dinámica, el estudio de los fluidos en movimiento. Incluso las formas más básicas de movimiento fluido pueden ser bastante complejas. Por esta razón, limitamos nuestra investigación a fluidos ideales en muchos de los ejemplos. Un fluido ideal es un fluido con una viscosidad insignificante. La viscosidad es una medida de la fricción interna en un fluido; la examinamos con más detalle en Viscosidad y Turbulencia. En algunos ejemplos, examinamos un fluido incompresible - uno para el cual se requiere una fuerza extremadamente grande para cambiar el ya que la densidad en un fluido incompresible es constante en todo momento.
Los vectores de velocidad se utilizan a menudo para ilustrar el movimiento de fluidos en aplicaciones como la meteorología. Por ejemplo, el viento, el movimiento fluido del aire en la atmósfera, se puede representar mediante vectores que indican la velocidad y la dirección del viento en cualquier punto del mapa. La muestra los vectores de velocidad que describen los vientos durante el huracán Arthur en 2014. Otro método para representar el movimiento de fluidos es una línea de corriente. Una línea de corriente representa la trayectoria de un pequeño volumen de fluido como fluye. La velocidad es siempre tangencial a la línea de corriente.
La velocidad es siempre tangencial a la línea de corriente. Los diagramas de la utilizan líneas de corriente para ilustrar dos ejemplos de fluidos que se mueven a través de una tubería.
El primer fluido muestra un flujo laminar (a veces descrito como un flujo constante), representado por líneas de corriente paralelas y suaves. Tenga en cuenta que en el ejemplo que se muestra en la parte (a), la velocidad del fluido es mayor en el centro y disminuye cerca de las paredes de la tubería debido a la viscosidad del fluido y la fricción entre las paredes de la tubería y el fluido. Este es un caso especial de flujo laminar, donde la fricción entre la tubería y el fluido es alta, lo que se conoce como condiciones de frontera sin deslizamiento.
El segundo diagrama representa un flujo turbulento, en el que las líneas de corriente son irregulares y cambian con el tiempo. En el flujo turbulento, las trayectorias del flujo de fluido son irregulares a medida que diferentes partes del fluido se mezclan o forman pequeñas regiones circulares que se asemejan a remolinos. Esto puede ocurrir cuando la velocidad del fluido alcanza una cierta velocidad crítica.
El volumen de fluido que pasa por una ubicación determinada a través de un área durante un período de tiempo se denomina caudal $Q$, o más precisamente, caudal. En símbolos, esto se escribe como
donde $V$ es el volumen y $t$ es el tiempo transcurrido. En la , el volumen del cilindro es $Ax$, por lo que el caudal es
La unidad del SI para el caudal es $m^3/s$, pero otras unidades para $Q$ son de uso común, como litros por minuto ($L/min$). Ten en cuenta que un litro ($L$) es $1/1000$ de un metro cúbico o $1000$ centímetros cúbicos ($10^{-3}m^3$ o $10^3cm^3$).
El caudal y la velocidad están relacionados, pero son cantidades físicas muy diferentes. Para dejar clara la distinción, considera la tasa de flujo de un río. Cuanto mayor sea la velocidad del agua, mayor será el caudal del río. Pero el caudal también depende del tamaño y la forma del río. Un rápido arroyo de montaña transporta mucha menos agua que el río Amazonas en Brasil, por ejemplo. La ilustra el caudal volumétrico. El caudal volumétrico es $Q = \frac{dV}{dt} = Av$, donde $A$ es el área de la sección transversal de la tubería y $v$ es la magnitud de la velocidad.
La relación precisa entre el caudal $Q$ y la velocidad media $v$ es
$$Q = Av$$donde $A$ es el área de la sección transversal y v es la velocidad promedio. La relación nos dice que la tasa de flujo es directamente proporcional tanto a la velocidad promedio del fluido como al área de sección transversal de un río, tubería u otro conducto. Cuanto más grande sea el conducto, mayor será su área de sección transversal. La ilustra cómo se obtiene esta relación. El cilindro sombreado tiene un volumen $V = Ad$, que fluye más allá del punto $P$ en un tiempo $t$. Dividiendo ambos lados de esta relación por $t$, obtenemos:
$$\frac{V}{t} = \frac{A}{t}$$Notamos que $Q = V/t$ y la velocidad promedio es $v = d/t$. Así, la ecuación se convierte en $Q = Av$.
La muestra un fluido incompresible que fluye a lo largo de una tubería de radio decreciente. Debido a que el fluido es incompresible, la misma cantidad de fluido debe fluir más allá de cualquier punto del tubo en un momento dado para garantizar la continuidad del flujo. El flujo es continuo porque no hay fuentes ni sumideros que agreguen o eliminen masa, por lo que la masa que fluye hacia la tubería debe ser igual a la masa que fluye hacia afuera de la tubería. En este caso, debido a que el área de la sección transversal de la tubería disminuye, la velocidad necesariamente debe aumentar. Esta lógica se puede ampliar para decir que el caudal debe ser el mismo en todos los puntos a lo largo de la tubería. En particular, para los puntos 1 y 2 arbitrarios,
Esto se denomina ecuación de continuidad y es válido para cualquier fluido incompresible (con densidad constante). Las consecuencias de la ecuación de continuidad se pueden observar cuando el agua fluye de una manguera a una boquilla rociadora estrecha: emerge a gran velocidad, que es el propósito de la boquilla. A la inversa, cuando un río desemboca en un extremo de un embalse, el agua se ralentiza considerablemente, tal vez recuperando velocidad cuando abandona el otro extremo del embalse. En otras palabras, la velocidad aumenta cuando el área de la sección transversal disminuye, y la velocidad disminuye cuando el área de la sección transversal aumenta.
Como los líquidos son esencialmente incompresibles, la ecuación de continuidad es válida para todos los líquidos. Sin embargo, los gases son compresibles, por lo que la ecuación debe aplicarse con precaución a los gases si están sujetos a compresión o expansión.
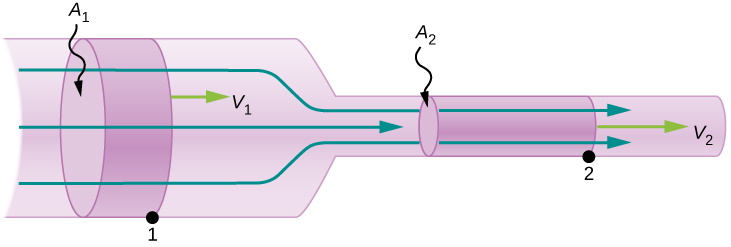
Ejemplo 4.5
Cálculo de la velocidad del fluido a través de una boquilla
Una boquilla con un diámetro de $0.500 cm$ está conectada a una manguera de jardín con un radio de $0.900 cm$. El caudal a través de la manguera y la boquilla es de $0.500 l/s$. Calcula la velocidad del agua (a) en la manguera y (b) en la boquilla.
Estrategia
Podemos usar la relación entre el caudal y la velocidad para encontrar ambas velocidades. Usamos el subíndice 1 para la manguera y 2 para la boquilla.
Solución
a. Resolvemos la ecuación de caudal para la velocidad y utilizamos $πr_1^2$ para el área de la sección transversal de la manguera, obteniendo
$$v = \frac{Q}{A} = \frac{Q}{πr_1^2}$$Sustituyendo los valores y utilizando la conversión apropiada de unidades, obtenemos.
$$v = \frac{(0.500 L/s)(10^{-3} m^3/L)}{3.14(9.00 × 10^{-3} m)^2} = 1.96 m/s$$b. Podríamos repetir este cálculo para encontrar la velocidad en la boquilla $v_2$, pero usamos la ecuación de continuidad para dar una idea algo diferente. Los estados de la ecuación
$$A_1v_1 = A_2v_2$$Hallando $v_2$ y sustituyendo $πr^2$ por los resultados del área de la sección transversal
$$v_2 = \frac{A_1}{A_2}v_1 = \frac{π r_1^2}{π r_2^2} = \frac{r_1^2}{r_2^2}v_1$$Sustituyendo los valores conocidos
$$v_2 = \frac{(0.900 cm)^2}{(0.250 cm)^2}1.96 m/s = 25.5m/s$$Explicación
Una velocidad de $1.96 m/s$ es la adecuada para el agua que sale de una manguera sin boquilla. La boquilla produce una corriente considerablemente más rápida simplemente restringiendo el flujo a un tubo más estrecho.
La solución a la última parte del ejemplo muestra que la velocidad es inversamente proporcional al cuadrado del radio del tubo, lo que genera grandes efectos cuando el radio varía. Podemos apagar una vela a cierta distancia, por ejemplo, frunciendo los labios, mientras que soplar una vela con la boca abierta es bastante ineficaz.
Conservación de masas
La velocidad de flujo de un fluido también se puede describir mediante la velocidad de flujo másico o la velocidad de flujo másica. Esta es la velocidad a la que una masa del fluido se mueve más allá de un punto. Consulte una vez más la , pero esta vez considere la masa en el volumen sombreado. La masa se puede determinar a partir de la densidad y el volumen:
$$ m = ρV = ρAx$$El caudal másico es entonces:
$$ \frac{dm}{ dt } = \frac{d}{dt}(ρAx) = ρA \frac{dx}{dt} = ρAv$$donde $ρ$ es la densidad, $A$ es el área de la sección transversal, y $v$ es la magnitud de la velocidad. El caudal másico es una cantidad importante en la dinámica de fluidos y se puede utilizar para resolver muchos problemas. Considere la , el tubo en la figura comienza en la entrada con un área de sección transversal de $A_1$ y se contrae en una salida con un área de sección transversal más pequeña de $A_2$. La masa de fluido que entra en la tubería debe ser igual a la masa de fluido que sale de la tubería. Por esta razón, la velocidad en la salida $(v_2$) es mayor que la velocidad de la entrada $(v_1)$. Al utilizar el hecho de que la masa de fluido que entra en la tubería debe ser igual a la masa de fluido que sale de la tubería, podemos encontrar una relación entre la velocidad y el área de la sección transversal tomando la tasa de cambio de la masa y la masa afuera:
La ecuación 4.15 también se conoce como la ecuación de continuidad en forma general. Si la densidad del fluido permanece constante a través de la constricción, -es decir, el fluido es incompresible- entonces la densidad se cancela de la ecuación de continuidad,
$$A_1v_1 = A_2v_2$$La ecuación anterior muestra que la tasa de flujo volumétrico en la tubería es igual a la tasa de flujo volumétrico fuera de la tubería.
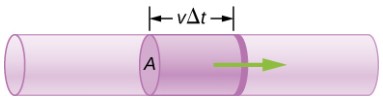
Como mostramos en la , cuando un fluido fluye hacia un canal más estrecho, su velocidad aumenta. Esto significa que su energía cinética también aumenta. El aumento de la energía cinética proviene del trabajo neto realizado en el fluido para empujarlo hacia el canal. Además, si el fluido cambia de posición vertical, el trabajo se realiza en el fluido por la fuerza gravitacional. Una diferencia de presión ocurre cuando el canal se estrecha. Esta diferencia de presión resulta en una fuerza neta sobre el fluido porque la presión multiplicada por el área es igual a la fuerza, y esta fuerza neta sí funciona. Recordar el teorema de trabajo y energía,
$$W_{\textsf{net}} =\frac{1}{2}mv^2 -\frac{1}{2}mv_0^2$$El trabajo neto realizado aumenta la energía cinética del fluido. Como resultado, la presión cae en un fluido que se mueve rápidamente, ya sea o no no el fluido está confinado a un tubo.
Hay muchos ejemplos comunes de caída de presión en fluidos que se mueven rápidamente. Por ejemplo, las cortinas de ducha tienen un desagradable hábito de abultarse en la cabina de ducha cuando la ducha está abierta. La razón es que la corriente de alta velocidad de el agua y el aire crean una región de menor presión dentro de la ducha, mientras que la presión en el otro lado permanece en el presión atmosférica estándar.
Esta diferencia de presión resulta en una fuerza neta, empujando la cortina hacia adentro. De manera similar, cuando un automóvil pasa por un camión en la carretera, los dos vehículos parecen acercarse el uno al otro.
La razón es la misma: la alta velocidad del aire entre el coche y el camión crea una región de menor presión entre los vehículos, y son empujados juntos por una mayor presión en el exterior . Este efecto se observó ya a mediados del siglo XIX, cuando se encontró que los trenes que pasaban en direcciones opuestas se inclinaban uno hacia el otro.
La aplicación del principio de conservación de la energía al flujo laminar sin fricción conduce a una relación muy útil entre presión y velocidad de flujo en un fluido. Esta relación se denomina ecuación de Bernoulli, en honor a Daniel Bernoulli (1700-1782), quien publicó sus estudios sobre el movimiento fluido en su libro Hydrodynamica (1738). Considere un fluido incompresible que fluye a través de una tubería que tiene un diámetro y una altura variables, como se muestra en la . Los subíndices 1 y 2 de la figura denotan dos ubicaciones a lo largo de la tubería e ilustran las relaciones entre las áreas de la tubería. A, la velocidad del flujo v, la altura desde el suelo y, y la presión p en cada punto. Suponemos aquí que la densidad en los dos puntos es la misma -por lo tanto, la densidad es denotada por ρ sin subíndices- y dado que el fluido en incompresible, los volúmenes sombreados deben ser iguales.
También asumimos que no hay fuerzas viscosas en el fluido, por lo que se conservará la energía de cualquier parte del fluido. Para derivar la ecuación de Bernoulli, primero calculamos el trabajo que se hizo sobre el fluido:
$$dW = F_1dx_1 - F_2dx_2$$ $$dW = p_11 A_1dx_1 - p_2 A_2dx_2 = p _1dV - p_2dV = (p_1 - p_2)dV$$
El trabajo realizado se debió a la fuerza conservadora de la gravedad y al cambio en la energía cinética del fluido. El cambio en la energía cinética del fluido es igual a $$dK =\frac{1}{2}m_2v_2^2 - \frac{1}{2}m_1v_1^2 = \frac{1}{2}ρdV(v_2^2 - v_1^2)$$
El cambio en la energía potencial es $$dU = mgy_2 - mgy_1 = ρdVg(y_2 - y_1)$$
La ecuación de energía se convierte entonces en
$$dW = dK + dU$$ $$(p_1 - p_2)dV = \frac{1}{2}ρdV (v_2^2 - v_1^2)+ ρdVg(y_2 - y_1)$$ $$(p_1 - p_2)= \frac{1}{2}ρd(v_2^2 - v_1^2)+ ρdg(y_2 - y_1)$$Reorganizando la ecuación anterior nos da la ecuación de Bernoulli:
$$p_1 +\frac{1}{2}ρv_1^2 + ρgy_1 = p_2 +\frac{1}{2}ρv_2^2 + ρgy_2$$Esta relación indica que la energía mecánica de cualquier parte del fluido cambia como resultado del trabajo realizado por el fluido externo a esa parte, debido a la variación de la presión a lo largo del camino. Dado que los dos puntos fueron elegidos arbitrariamente, podemos escribir la ecuación de Bernoulli de manera más general como un principio de conservación a lo largo de la corriente.
Una nota especial debe hacerse aquí del hecho de que en una situación dinámica, las presiones a la misma altura en diferentes partes del fluido pueden ser diferentes si tienen diferentes velocidades de flujo.
Ecuación de Bernoulli
Para un fluido incompresible y sin fricción, la combinación de presión y la suma de las densidades de energía cinética y potencial es constante no solo a lo largo del tiempo, sino también a lo largo de una línea de corriente:
$$p +\frac{1}{2}ρv^2 + ρgy = \textsf{constante} \tag{4.16}$$De acuerdo con la ecuación de Bernoulli, si seguimos un pequeño volumen de fluido a lo largo de su trayectoria, varias cantidades en la suma pueden cambiar, pero el total permanece constante. La ecuación de Bernoulli es, de hecho, es una expresión conveniente de conservación de energía para un fluido incompresible en ausencia de fricción. La forma general de la ecuación de Bernoulli tiene tres términos, y es de amplia aplicación. Para entenderlo mejor, déjanos considere algunas situaciones específicas que simplifican e ilustran su uso y significado.
Primero considere la situación muy simple donde el fluido es estático, es decir, $v_1 = v_2 = 0$. La ecuación de Bernoulli en ese caso es $$p_1 + ρgh_1 = p_2 + ρgh_2$$
Podemos simplificar aún más la ecuación estableciendo $h_2 = 0$.
(Se puede elegir cualquier altura para una altura de referencia de cero, como se hace a menudo para otras situaciones que involucran fuerza gravitacional, haciendo que todas las demás alturas sean relativas). En este caso, obtenemos $$p_2 = p_1 + ρgh_1$$
Esta ecuación nos dice que, en los fluidos estáticos, la presión aumenta con la profundidad. A medida que avanzamos del punto 1 al punto 2 en el fluido, la profundidad aumenta en $h_1$ y, en consecuencia, $p_2$ es mayor que $p_1$ en una cantidad $ρgh_1$. En el caso más simple, $p_1$ es cero en la parte superior del fluido, y obtenemos la relación familiar $p = ρgh$. (Recuerde que $p = ρgh$ y $ΔUg = -mgh$). Por lo tanto, la ecuación de Bernoulli confirma el hecho de que el cambio de presión debido al peso de un fluido es ρgh. Aunque introducimos la ecuación de Bernoulli para el movimiento de fluidos, incluye mucho de lo que estudiamos anteriormente para fluidos estáticos.
Supongamos que un fluido se está movimiento pero su profundidad es constante, es decir, $h_1 = h_2$. Bajo esta condición, la ecuación de Bernoulli se convierte en
$$p_1 +\frac{1}{2}ρv_1^2 = p_2 +\frac{1}{2}ρv_2^2$$Las situaciones en las que el fluido fluye a una profundidad constante son tan comunes que esta ecuación también suele denominarse Principio de Bernoulli, que es simplemente la ecuación de Bernoulli para fluidos a una profundidad constante. (Tenga en cuenta nuevamente que esto se aplica a un pequeño volumen de fluido a medida que lo seguimos a lo largo de su trayectoria). El principio de Bernoulli refuerza el hecho de que la presión disminuye a medida que aumenta la velocidad en un fluido en movimiento: si $v_2$ es mayor que $v_1$ en la ecuación, entonces $p_2$ debe ser menor que $p_1$ para mantener la igualdad.
Ejemplo 4.6
En el Ejemplo 4.5, encontramos que la velocidad del agua en una manguera que aumentó de $1.96 m/s$ a $25.5 m/s$ desde la manguera hasta la boquilla. Calcule la presión en la manguera, dado que la presión absoluta en la boquilla es $1.01 × 10^5 N/m^2$ (atmosférica, como debe ser) y suponiendo un flujo a nivel y sin fricción.
Estrategia
El flujo de nivel significa profundidad constante, por lo que se aplica el principio de Bernoulli. Usamos el subíndice 1 para los valores en la manguera y 2 para los que están en la boquilla. Por lo tanto, se nos pide que encontremos $p_1$.
Solución
Resolviendo el principio de Bernoulli para los rendimientos de $p_1$.
$$p_1 = p_2 +\frac{1}{2}ρv_2^2 -\frac{1}{2}ρv_1^2 = p_2 +\frac{1}{2}ρ(v_2^2 - v_1^2)$$Sustituyendo los valores conocidos de presión reducida en fluidos de alta velocidad para mover las cosas. Con una presión más alta en el exterior, el fluido de alta velocidad fuerza a otros fluidos a entrar en la corriente. Este proceso se llama arrastre. Los dispositivos de arrastre se han utilizado desde la antigüedad como bombas para elevar el agua a pequeñas alturas, como es necesario para drenar pantanos, campos u otras áreas bajas. En la se muestran algunos otros dispositivos que utilizan el concepto de arrastre.
$$\begin{split} p_1 &= 1.01 × 10^5N/m^2+\frac{1}{2}(10^3kg/m^3)[(25.5 m/s)^2 - (1.96 m/s)^2] \\ &= 4.24 × 10^5 N/m^2 \end{split}$$Explicación
Esta presión absoluta en la manguera es mayor que en la boquilla, como se esperaba, ya que $v$ es mayor en la boquilla. La presión $p_2$ en la boquilla debe ser atmosférica, ya que el agua sale a la atmósfera sin que se produzcan otros cambios en las condiciones.
Se producen muchos dispositivos y situaciones en los que el fluido fluye a una altura constante y, por lo tanto, puede analizarse con el principio de Bernoulli.
Arrastre
La gente lleva mucho tiempo poniendo en práctica el principio de Bernoulli utilizando una presión reducida en fluidos de alta velocidad para mover las cosas. acerca de. Con una presión más alta en el exterior, el fluido de alta velocidad fuerza a otros fluidos a entrar en la corriente. Este proceso es llamado arrastre.
Los dispositivos de arrastre se han utilizado desde la antigüedad como bombas para elevar el agua a pequeñas alturas, como se describe a continuación necesario para drenar pantanos, campos u otras áreas bajas. Algunos otros dispositivos que utilizan el concepto de arrastre son que se muestra en la
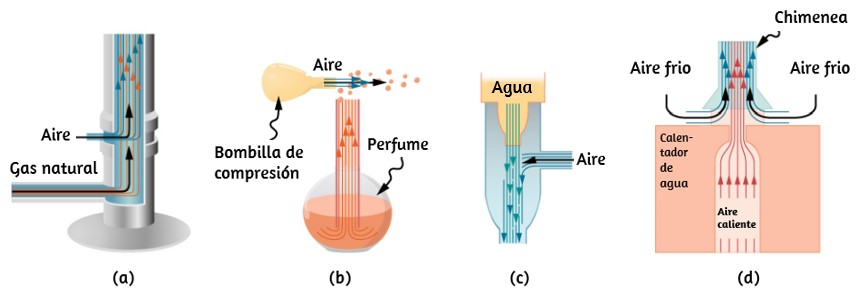
La muestra dos dispositivos que aplican el principio de Bernoulli para medir la velocidad del fluido. El manómetro en la parte (a) está conectado a dos tubos que son lo suficientemente pequeños como para no perturbar apreciablemente el flujo.
El tubo que mira hacia el fluido que viene crea un punto muerto con velocidad cero ($v_1 = 0$) delante de él, mientras que el fluido que pasa por el otro tubo tiene velocidad $v_2$. Esto significa que el principio de Bernoulli, tal y como se establece en
$$p_1 +\frac{1}{2}ρv_1^2 = p_2 +\frac{1}{2}ρv_2^2$$se convierte en $$p_1 = p_2 +\frac{1}{2}ρv_2^2$$
Así, la presión $p_2$ sobre la segunda abertura se reduce en $\frac{1}{2}ρv_2^2$, de modo que el fluido en el manómetro sube en $h$ en el lado conectado a la segunda abertura, donde
$$h ∝ \frac{1}{2}ρv_2^2$$(Recordemos que el símbolo $∝$ significa "proporcional a"). Resolviendo para $v_2$, vemos que $$v_2 ∝ \sqrt{h}$$
La parte (b) muestra una versión de este dispositivo que es de uso común para medir varias velocidades de fluidos; tales dispositivos se utilizan frecuentemente como indicadores de velocidad del aire en aeronaves.
Todas las aplicaciones precedentes de la ecuación de Bernoulli implicaban la simplificación de las condiciones, como la altura o la presión constantes. El siguiente ejemplo es una aplicación más general de la ecuación de Bernoulli en la que la presión, la velocidad y la altura cambian.
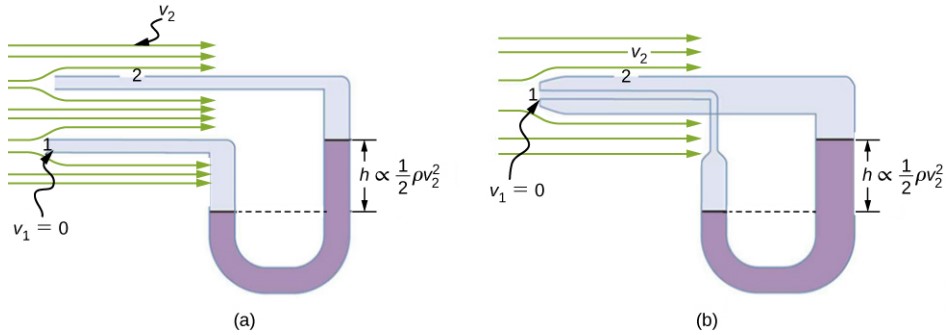
Ejemplo 4.7
Las mangueras utilizadas en los grandes incendios estructurales tienen un diámetro interior de $6,40 cm$ . Supongamos que una manguera de este tipo transporta un caudal de $40,0 L/s$, a partir de una presión manométrica de $1,62×10^6 N/m^2$. La manguera sube $10,0 m$ a lo largo de una escalera hasta una boquilla con un diámetro interior de $3,00 cm$. ¿Cuál es la presión en la boquilla?
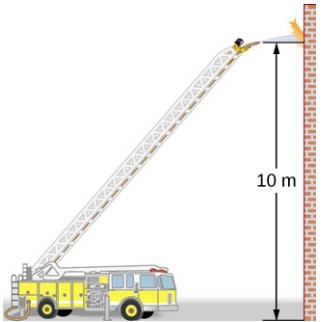
Estrategia
Debemos usar la ecuación de Bernoulli para resolver la presión, ya que la profundidad no es constante.
Solución
La ecuación de Bernoulli es
$$p1 +\frac{1}{2}ρv_1^2 + ρgh_1 = p_2 +\frac{2}{2}ρv_2^2 + ρgh_2$$donde los subíndices 1 y 2 se refieren a las condiciones iniciales a nivel del suelo y a las condiciones finales dentro de la boquilla, respectivamente. Primero debemos encontrar las velocidades $v_1$ y $v_2$. Como $Q = A_1 v_1$, obtenemos
$$v_1 = \frac{Q}{A_1} = \frac{40.0 × 10^{-3} m^3/s}{π (3.20 × 10^{-2} m)^2}$$Del mismo modo, encontramos
$$v_2 = 56.6 m/s$$Esta velocidad bastante grande es útil para alcanzar el fuego. Ahora, tomando $h_1$ como cero, resolvemos la ecuación de Bernoulli para $p_2$
$$p_2 = p_1 +\frac{1}{2}ρ(v_1^2 - v_2^2) - ρgh_2$$Sustituyendo valores conocidos por rendimientos
$p^2 = 1.62 × 106 N/m^2 +12(1000 kg/m^3)[(12.4 m/s)^2 - \\ \;\;\;\;\;\;\;\; (56.6 m/s)^2]- (1000 kg/m^3)(9.80 m/s^2)(10.0 m) = 0$
Explicación
Este valor es una presión manométrica, ya que la presión inicial se dio como presión manométrica. Así, la presión de la boquilla es igual a la presión atmosférica, ya que el agua sale a la atmósfera sin cambios en sus condiciones.
En las aplicaciones de las Leyes de Newton, se introdujo el concepto de fricción, vimos que un objeto que se deslizaba a través de la con una velocidad inicial y sin que la fuerza aplicada se detenga debido a la fuerza de fricción. La fricción depende de los tipos de en contacto y es proporcional a la fuerza norma También discutimos la resistencia al arrastre y al aire en ese mismo capítulo. Explicamos que a bajas velocidades, la resistencia es proporcional a la velocidad, mientras que a altas velocidades, la resistencia es proporcional a las velocidad al cuadrado. En este apartado se presentan las fuerzas de fricción que actúan sobre los fluidos en movimiento. Por ejemplo, un fluido que fluye a través de un tubo está sujeto a resistencia, un tipo de fricción, entre el fluido y las paredes. La fricción también se produce entre el diferentes capas de fluido. Estas fuerzas resistivas afectan la forma en que el fluido fluye a través de la tubería.
Cuando te sirves un vaso de jugo, el líquido fluye libre y rápidamente. Pero si usted vierte jarabe de arce en sus panqueques, ese líquido fluye lentamente y se pega a la jarra. La diferencia es la fricción de los fluidos, tanto dentro del propio fluido como entre el fluido y su entorno. A esta propiedad de los fluidos la llamamos viscosidad. El jugo tiene baja viscosidad, mientras que el jarabe tiene alta viscosidad. La definición precisa de la viscosidad se basa en el flujo laminar o no turbulento. La muestra esquemáticamente cómo el flujo laminar y el turbulento difieren. Cuando el flujo es laminar, las capas fluyen sin mezclarse. Cuando el flujo es turbulento, las capas se mezclan, y velocidades significativas ocurren en direcciones diferentes a la dirección general del flujo.
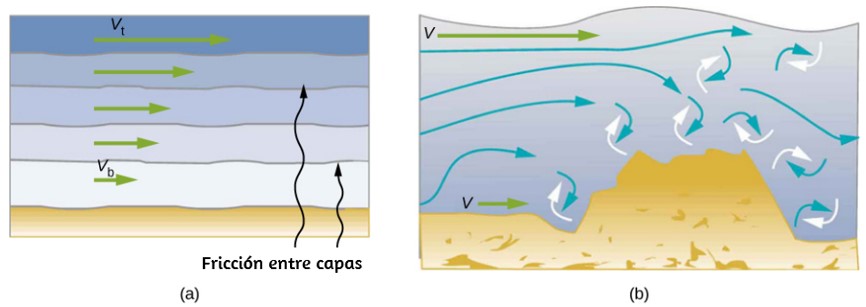
Turbulencia es un flujo de fluido en el que las capas se mezclan a través de remolinos y remolinos. Tiene dos causas principales. Primero, cualquier obstrucción o esquina aguda, como en un grifo, crea turbulencia al impartir velocidades perpendiculares al flujo. Segundo, las altas velocidades causan turbulencia. El arrastre entre capas adyacentes de fluido y entre el fluido y sus alrededores puede formar remolinos y remolinos si la velocidad es lo suficientemente grande. En la , la velocidad del humo que se acelera alcanza el punto en que comienza a girar debido a la resistencia entre el humo y el aire circundante.

La muestra cómo se mide la viscosidad de un fluido. El fluido a medir se coloca entre dos placas paralelas. La placa inferior se mantiene fija, mientras que la placa superior se mueve hacia la derecha, arrastrando el fluido con ella. La capa (o lámina) de fluido en contacto con cualquiera de las dos placas no se mueve en relación con la placa, por lo que la capa superior se mueve a la velocidad v mientras que la capa inferior permanece en reposo.
Cada capa sucesiva de arriba hacia abajo ejerce una fuerza sobre la que está debajo, intentando arrastrarla, produciendo una variación continua en la velocidad de $v$ a $0$ como se muestra. Se tiene cuidado de asegurar que el flujo sea laminar, es decir, que las capas no se mezclen. El movimiento en la figura es como un movimiento de cizallamiento continuo. Los fluidos tienen cero resistencia al cizallamiento, pero la velocidad a la que se cortan está relacionada con los mismos factores geométricos $A$ y $L$ que la deformación por cizallamiento de los sólidos.
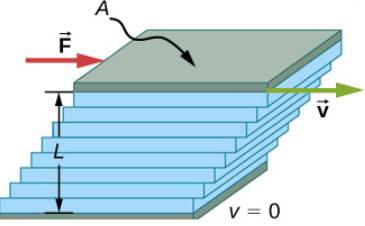
En el diagrama, el fluido está inicialmente en reposo. La capa de fluido en contacto con la placa móvil se acelera y comienza a moverse debido a la fricción interna entre la placa móvil y el fluido. La siguiente capa está en contacto con la capa en movimiento; como hay fricción interna entre las dos capas, también se acelera, y así sucesivamente a través de la profundidad del fluido. También hay fricción interna entre la placa estacionaria y la capa más baja de fluido, junto a la placa de la estación. La fuerza es necesaria para mantener la placa en movimiento a una velocidad constante debido a la fricción interna.
Se requiere una fuerza $F$ para mantener la placa superior en la moviéndose a una velocidad constante $v$, y los experimentos han demostrado que esta fuerza depende de cuatro factores. Primero, $F$ es directamente proporcional a $v$ (hasta que la velocidad es tan alta que ocurre la turbulencia - entonces se necesita una fuerza mucho mayor, y tiene una dependencia más complicada de $v$). En segundo lugar, $F$ es proporcional a la zona $A$ de la placa. Esta relación parece razonable, ya que $A$ es directamente proporcional a la cantidad de fluido que se mueve. Tercero, $F$ es inversamente proporcional a la distancia entre las placas $L$. Esta relación también es razonable; $L$ es como un brazo de palanca, y cuanto mayor es el brazo de palanca, menor es la fuerza que se necesita. En cuarto lugar, $F$ es directamente proporcional a la coeficiente de viscosidad, $η$ Cuanto mayor sea la viscosidad, mayor será la fuerza requerida. Estas dependencias se combinan en la ecuación
$$F = η\frac{vA}{L}$$Esta ecuación nos da una definición práctica de la viscosidad del fluido $η$. La solución para $η$ ofrece
que define la viscosidad en términos de cómo se mide.
La unidad de viscosidad SI es
$$Nm/[(m/s)m^2] = [ N/m^2] o Pa \cdot s$$La enumera los coeficientes de viscosidad para varios fluidos. La viscosidad varía de un fluido a otro en varios órdenes de magnitud. Como es de esperar, las viscosidades de son mucho menores que los de los líquidos, y estas viscosidades a menudo dependen de la temperatura.
Posterior a la tabla, podrás practicar con una escena interactiva, diseñada por Andrew Duffy, en la cual puedes usar varios tipos de fluidos y observar cómo cambia la velocidad de una bola cuando cae dentro del fluido. Ten en cuenta que el número entre paréntesis al lado de cada fluido o cada material de la bola es la gravedad específica.
Las viscosidades tienen valores en la simulación en unidades pascales segundos ($Pa\,s$), así: Agua: $0.001$, Aceite de oliva: $0.08$, Glicerina: $1.4$, y el fluido "Ninguno" tiene una viscosidad de cero y una densidad de cero. Simplemente no se lo digas a Aristóteles.
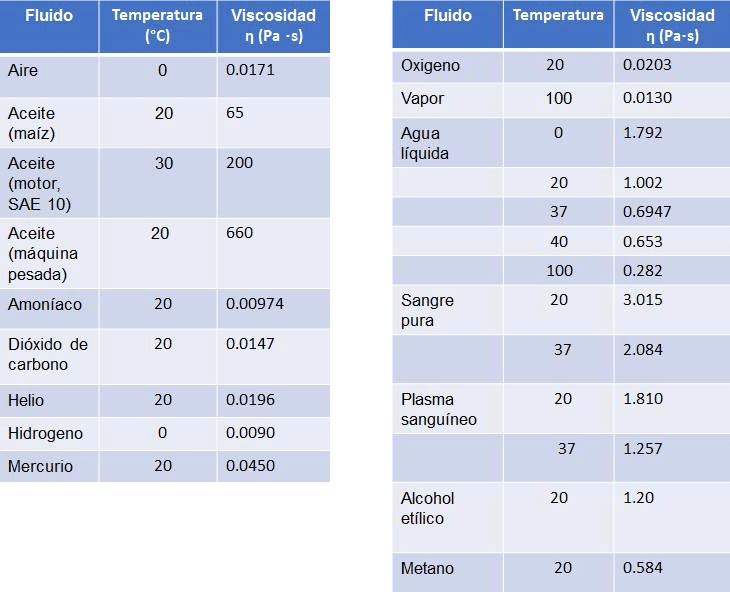
¿Qué causa el flujo?. La respuesta, como es lógico, es una diferencia de presión. De hecho, existe una relación muy simple entre el flujo horizontal y la presión. El caudal $Q$ está en la dirección de alta a baja presión. Cuanto mayor sea la diferencia de presión entre dos puntos, mayor será el caudal. Esta relación puede expresarse de la siguiente manera
$$Q = \frac{p_2 - p_1}{R}$$donde $p_1$ y $p_2$ son las presiones en dos puntos, como en cada extremo de un tubo, y $R$ es la resistencia al flujo. La resistencia $R$ incluye todo, excepto la presión, que afecta al caudal. Por ejemplo, $R$ es mayor para un tubo largo que para uno corto. Cuanto mayor es la viscosidad de un fluido, mayor es el valor de $R$. La turbulencia aumenta enormemente $R$, mientras que el aumento del diámetro de un tubo disminuye $R$. Si la viscosidad es cero, el fluido no tiene fricción y la resistencia al flujo también es cero. Comparando el flujo sin fricción en un tubo con el flujo viscoso, como en la , vemos que para un fluido viscoso, la velocidad es mayor en la mitad del flujo debido a la resistencia en el límites. Podemos ver el efecto de la viscosidad en una llama de quemador Bunsen [parte (c)], aunque la viscosidad del gas natural es pequeño.
Esta ecuación se llama la ley de Poiseuille para la resistencia, que debe su nombre al científico francés J. L. Poiseuille (1799-1869), que lo derivó en un intento de entender el flujo de sangre a través del cuerpo. Examinemos la expresión de Poiseuille para $R$ para ver si tiene sentido intuitivo. Vemos que la resistencia es directamente proporcional tanto a la viscosidad del fluido $η$ como a la longitud $l$ de un tubo. Después de todo, ambos afectan directamente la cantidad de fricción mayor es, mayor es la resistencia y menor el caudal.
El radio $r$ de un tubo afecta al resistencia, lo cual tiene sentido, ya que cuanto mayor sea el radio, mayor será el flujo (todos los demás factores quedan igual). Pero es sorprendente que $r$ se eleve a la cuarta potencia en la ley de Poiseuille.
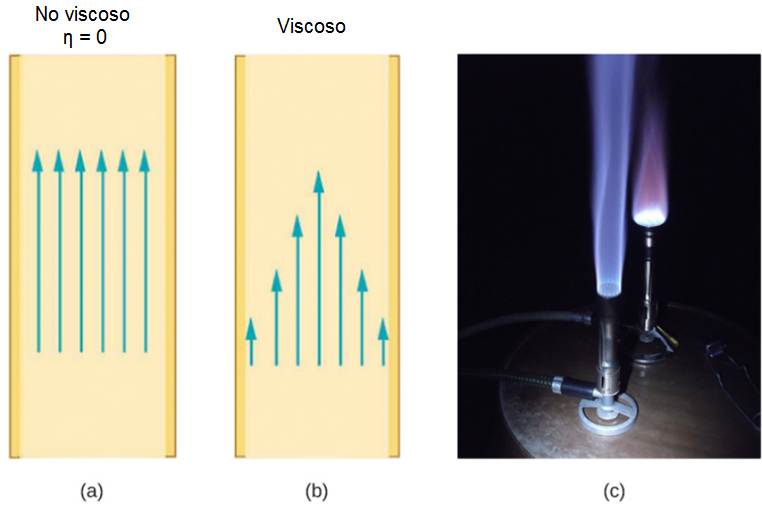
La resistencia $R$ al flujo laminar de un fluido incompresible con viscosidad $η$ a través de un tubo horizontal de radio uniforme $r$ y la longitud $l$, está dada por
Este exponente significa que cualquier cambio en el radio de un tubo tiene un efecto muy grande en la resistencia. Por ejemplo, doblar el radio de un tubo disminuye la resistencia de la siguiente manera un factor de $2^4 = 16$.
Tomados en conjunto nos queda,
$$Q = \frac{p_2 - p_1}{R} y R = \frac{8ηl}{π r^4}$$dando así la siguiente expresión para el caudal:
Esta ecuación describe el flujo laminar a través de un tubo. A veces se le llama la ley de Poiseuille para el flujo laminar, o simplemente la ley de Poiseuille .
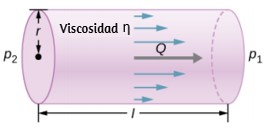
Ejemplo 4.18
Se está diseñando un sistema de aire acondicionado para suministrar aire a una presión manométrica de $0,054 Pa$ a una temperatura de $20°C$. El aire es enviado a través de un conducto redondo y aislado con un diámetro de $18,00 cm$. El conducto tiene una longitud de $20$ metros y está abierto en una habitación a una presión atmosférica de $101,30 kPa$. La habitación tiene una longitud de $12$ metros, un ancho de $6$ metros y una altura de $3$ metros. (a) ¿Cuál es la tasa de flujo volumétrico a través de la tubería, suponiendo flujo laminar? (b) Calcule el tiempo necesario para reemplazar completamente el aire de la habitación. (c) Los constructores deciden ahorrar dinero utilizando un conducto con un diámetro de $9,00 cm$. ¿Cuál es el nuevo caudal?
Estrategia
Asumiendo el flujo laminar, la ley de Poiseuille establece que
$$Q = \frac{(p_2 - p_1)π r^4}{8ηl} = \frac{dV}{dt}$$Necesitamos comparar el radio de la arteria antes y después de la reducción del caudal. Nótese que se nos da el diámetro del conducto, por lo que debemos dividirlo por dos para obtener el radio.
Solución
a. Suponiendo una diferencia de presión constante y utilizando la viscosidad $η = 0.0181 mPa \cdot s$,
b. Asumiendo flujo constante
$$\begin{split} Q &= \frac{dV}{dt} ≈ \frac{∆V}{∆t} → ∆t = \frac{∆V}{Q} \\ &= \frac{(12 m)(6 m)(3 m)}{3.84 × 10^{-3}m^3/s} \end{split}$$ $$∆t = 5.63 × 10^4s = 15.63 hr$$c. Usando el flujo laminar, la ley de Poiseuille produce
$$Q = \frac{(0.054 Pa)(3.14)(0.045 m)^4 }{8(0.0181× 10^{-3}Pa \cdot s(20 m)} = 2.40 ×10^{-4}\frac{m^3}{s}$$De este modo, el radio del conducto disminuye a la mitad, lo que reduce el caudal al $6,25$% del valor original.
Explicación
En general, asumiendo el flujo laminar, disminuir el radio tiene un efecto más dramático que cambiar la longitud. Si la longitud aumenta y todas las demás variables permanecen constantes, el caudal disminuye:
$$\frac{Q_A}{Q_B} = \frac{l_B}{l_A}$$Donde
$$l_A = \frac{(p_2 - p_1)π r^4}{8ηl_A}$$Al cortar el radio a la mitad se reduce el caudal a una dieciseisava parte del caudal original.
La presión del agua en los hogares es a veces más baja de lo normal durante las épocas de uso intenso, como los días calurosos de verano. La caída de presión ocurre en la tubería principal de agua antes de que llegue a los hogares individuales. Consideremos el flujo a través de la tubería principal de agua como se ilustra en la . Podemos entender por qué la presión $p_1$ a la casa disminuye durante los momentos de uso intensivo, reorganizando la ecuación para la tasa de flujo:
$$Q = \frac{p_2 - p_1}{R}$$ $$p_2 - p_1 = RQ$$En este caso, $p_2$ es la presión en las obras hidráulicas y $R$ es la resistencia de la tubería principal de agua. En tiempos de uso intensivo, el caudal $Q$ es grande. Esto significa que $p_2 - p_1$ también debe ser grande. Por lo tanto, $p1$ debe disminuir. Es correcto pensar que el flujo y la resistencia causan una caída de presión de $p_2$ a $p_1$. La ecuación $p_2 - p_1 = RQ$ es válido tanto para el laminar como para el flujos turbulentos.
También podemos utilizar $p_2 - p_1 = RQ$ para analizar las caídas de presión que se producen en sistemas más complejos en los que el radio del tubo no es el mismo en todas partes. La resistencia es mucho mayor en lugares estrechos. Para caudal $Q$ dado, la caída de presión es mayor donde el tubo es más estrecho. Así es como los grifos de agua controlan el flujo. Además, $R$ se incrementa enormemente por la turbulencia, y una constricción que crea turbulencia reduce enormemente la presión río abajo. La placa en una arteria reduce la presión y, por lo tanto, el flujo, tanto por su resistencia como por la turbulencia que crea.
Un indicador llamado el número de Reynolds $N_R$ puede revelar si el flujo es laminar o turbulento. Para el flujo en un tubo de diámetro uniforme, el número de Reynolds se define como
donde $ρ$ es la densidad del fluido, $v$ su velocidad, $η$ su viscosidad, y $r$ el radio del tubo. El número de Reynolds es un número sin dimensión. Los experimentos han revelado que la $N_R$ está relacionada con el inicio de la turbulencia. Para $N_R$ por debajo de aproximadamente $2000$, el flujo es laminar. Para $N_R$ por encima de $3000$, el flujo es turbulento.
Para valores de $N_R$ entre $2000$ y $3000$, el flujo es inestable, es decir, puede ser laminar, pero pequeñas obstrucciones y la rugosidad de la superficie puede hacerla turbulenta, y puede oscilar al azar entre laminar y turbulenta. De hecho, el de un fluido con un número de Reynolds entre $2000$ y $3000$ es un buen ejemplo de comportamiento caótico. Se define un sistema caótico cuando su comportamiento es tan sensible a algún factor que es extremadamente difícil de predecir. Es difícil, pero no lo es imposible, predecir si el flujo es turbulento o no cuando el número de Reynold de un fluido cae dentro de este rango debido a que extremadamente dependencia sensible de factores como la rugosidad y las obstrucciones de la naturaleza del flujo. Una pequeña variación en un factor tiene un efecto exagerado (o no lineal) sobre el flujo.
Ejemplo 4.9
En el ejemplo 4.8, encontramos que el caudal volumétrico de un sistema de aire acondicionado es $Q = 3,84 × 10^{-3} m^3/s$. Este cálculo asumió el flujo laminar. (a) ¿Fue una buena suposición? (b) ¿A qué velocidad se produciría el flujo? se vuelven turbulentos?
Estrategia
Para determinar si el flujo de aire a través del sistema de aire acondicionado es laminar, primero necesitamos encontrar la velocidad, que se puede encontrar por
$$Q = Av = π r^2v$$Entonces podemos calcular el número de Reynold, usando la ecuación de abajo, y determinar si cae en el rango para flujo laminar
$$N_R = \frac{2ρvr}{η}$$Solución
a. Usando los valores dados:
$$v = \frac{Q}{π r^2} = \frac{3.84 × 10^{-3}m^3/s}{3.14(0.09m)^2} = 0.15 m/s$$ $$N_R = \frac{2ρvr}{η}$$ $$N_R = \frac{2 (1.23kg \cdot m^{-3})(0.15 m/s)(0.09m)}{0.0181 × 10^{-3} Pa \cdot s}$$Dado que el número de Reynolds es $1835 \lt 2000$, el flujo es laminar y no turbulento. La suposición de que el flujo era laminar es válida.
b. Para encontrar la velocidad máxima del aire y para mantener el flujo laminar, considere el número de Reynold
$$N_R = \frac{2ρvr}{η} ≤ 2000$$Explicación
Cuando se transfiere un fluido de un punto a otro, es deseable limitar la turbulencia. La turbulencia resulta un desperdicio de energía, ya que parte de la energía destinada a mover el fluido se disipa cuando se forman remolinos. En este caso, el aire. El sistema de acondicionado será menos eficiente una vez que la velocidad supere los $0,16 m/s$, ya que este es el punto en el que la turbulencia comenzará a ocurrir.
Otra aplicación del principio de Bernoulli se muestra en la siguiente escena interactiva, tomada de las simulaciones de Boston University:
Comenzamos el estudio de las oscilaciones con sistemas simples de péndulos y resortes. Aunque estos sistemas pueden parecer bastante básicos, los conceptos involucrados tienen muchas aplicaciones de la vida real. Por ejemplo, el edificio Comcast en Filadelfia, Pensilvania, tiene una altura de aproximadamente $305$ metros ($1000$ pies).
A medida que los edificios se construyen más altos, pueden actuar como péndulos físicos invertidos, con los pisos superiores oscilantes debido a la actividad sísmica y los vientos fluctuantes. En el edificio Comcast, se utiliza un amortiguador de masa sintonizada para reducir las oscilaciones. Instalado en la parte superior del edificio hay un amortiguador de masa de columna de líquido sintonizado, que consiste en un depósito de agua de $300,000$ galones. Este tanque en forma de U permite que el agua oscile libremente a una frecuencia que coincida con la frecuencia natural del edificio. La amortiguación se proporciona ajustando los niveles de turbulencia en el agua en movimiento usando baffles o deflectores.
Cuando se toca una cuerda de guitarra, el sonido resultante tiene un tono estable y dura mucho tiempo (). La cuerda vibra alrededor de una posición de equilibrio, y una oscilación se completa cuando la cuerda comienza desde la posición inicial, viaja a una de las posiciones extremas, luego a la otra posición extrema, y regresa a su posición inicial. Definimos el movimiento periódico como cualquier movimiento que se repita a intervalos regulares de tiempo, como lo muestra la cuerda de la guitarra o cuando un niño se balancea en un columpio. En esta sección, estudiamos las características básicas de las oscilaciones y su descripción matemática.
En ausencia de fricción, el tiempo para completar una oscilación permanece constante y se denomina período ($T$). Sus unidades suelen ser segundos, pero pueden ser cualquier unidad de tiempo conveniente. La palabra "período" se refiere al tiempo para algún evento, ya sea repetitivo o no, pero en este capítulo trataremos principalmente en movimientos periódicos, lo que es por definición repetitivo.

Un concepto estrechamente relacionado con el período es la frecuencia de un evento. La frecuencia ($f$) se define como el número de eventos por unidad de tiempo. Para movimientos periódicos, la frecuencia es el número de oscilaciones por unidad de tiempo. La relación entre frecuencia y período es
La unidad del SI para la frecuencia es el hercio ($Hz$) y se define como un ciclo por segundo:
$1 Hz = \dfrac{ciclo}{seg}$ o $1 Hz = \dfrac{1}{seg} = 1 s^{-1}$
Un ciclo es una oscilación completa.
Ejemplo 5.1
Determinación de la frecuencia de un ultrasonido
Los profesionales de la medicina utilizan las máquinas de ultrasonido para hacer imágenes y examinar los órganos internos del cuerpo. Una máquina de ultrasonido emite ondas sonoras de alta frecuencia, que se reflejan en los órganos, y una computadora recibe las ondas, usándolas para crear una imagen. Podemos usar las fórmulas presentadas en este módulo para determinar la frecuencia, según lo que sabemos acerca de las oscilaciones. Considera un dispositivo de imágenes médicas que produce ultrasonido al oscilar con un período de $0.400 μs$. ¿Cuál es la frecuencia de esta oscilación?
Estrategia
Se da el período ($T$) y se nos pide que encontremos la frecuencia ($f$).
Solución
Sustituye $0.400 μs$ por $T$ en $f = \dfrac{1}{T} → f = \dfrac{1}{0.400 × 10^{-6} s}$
encontramos que
$$f = 2,50 × 10^{-6} Hz$$Explicación
Esta frecuencia de sonido es mucho más alta que la frecuencia más alta que los humanos pueden escuchar (el rango de audición humana es de $20 Hz$ a $20,000 Hz$); Por eso, se llama ultrasonido. Las oscilaciones apropiadas a esta frecuencia generan un ultrasonido utilizado para diagnósticos médicos no invasivos, como las observaciones de un feto en el útero.
Un tipo muy común de movimiento periódico se llama movimiento armónico simple (MAS). Un sistema que oscila con MAS se llama un oscilador armónico simple.
Movimiento armónico simple
En el movimiento armónico simple, la aceleración del sistema, y por lo tanto la fuerza neta, es proporcional al desplazamiento y actúa en la dirección opuesta al desplazamiento.
Un buen ejemplo de MAS es un objeto con masa $m$ unida a un resorte en una superficie sin fricción, como se muestra en la . El objeto oscila alrededor de la posición de equilibrio, y la fuerza neta sobre el objeto es igual a la fuerza proporcionada por el resorte. Esta fuerza obedece a la ley de Hooke $F_s = -kx$, como se discutió anteriormente.
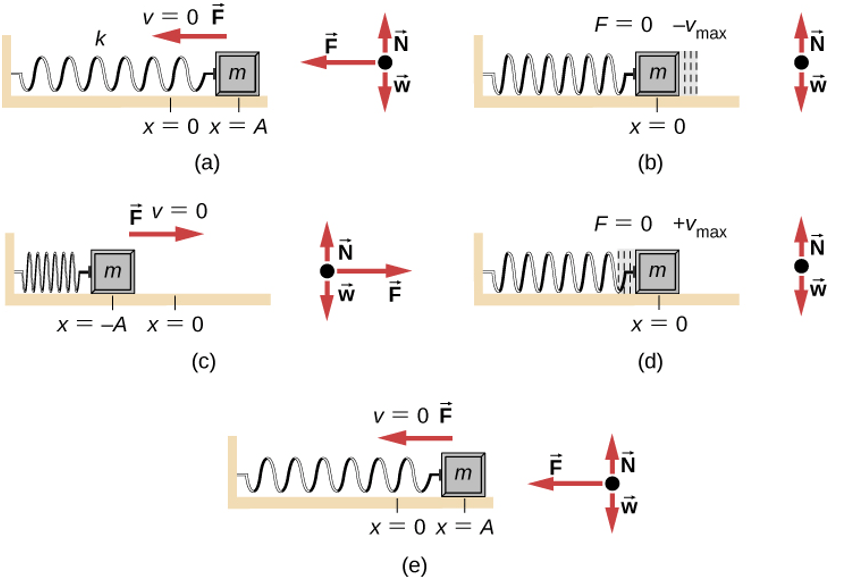
Si la ley de Hooke puede describir la fuerza neta y no hay amortiguación (desaceleración debido a la fricción u otras fuerzas no conservadoras), entonces un oscilador armónico simple oscila con igual desplazamiento en ambos lados de la posición de equilibrio, como se muestra para un objeto en un resorte en la . El desplazamiento máximo desde el equilibrio se llama amplitud ($A$). Las unidades de amplitud y desplazamiento son las mismas pero dependen del tipo de oscilación. Para el objeto en el resorte, las unidades de amplitud y desplazamiento son metros.
En la siguiente escena interactiva, diseñada por Wolfgang Christian y Francisco Esquembre, muestra la dinámica de una bola unida a un resorte ideal.
El resorte se estira inicialmente y la bola tiene una velocidad inicial cero. La posición inicial de la bola se puede cambiar haciendo clic y arrastrando la bola cuando la simulación está en pausa.
¿Qué tiene de importante el MAS? Por un lado, el período $T$ y la frecuencia $f$ de un oscilador armónico simple son independientes de la amplitud. La cuerda de una guitarra, por ejemplo, oscila con la misma frecuencia si se toca con suavidad o con fuerza.
Dos factores importantes afectan el período de un oscilador armónico simple. El período está relacionado con la rigidez del sistema. Un objeto muy rígido tiene una gran fuerza constante ($k$), lo que hace que el sistema tenga un período más pequeño. Por ejemplo, puedes ajustar la rigidez de un trampolín: cuanto más rígido es, más vibra y más corto es su período. El período también depende de la masa del sistema oscilante. Cuanto más masivo es el sistema, más largo es el período. Por ejemplo, una persona pesada en un trampolín salta y baja más lentamente que una ligera. De hecho, la masa m y la constante de fuerza k son los únicos factores que afectan el período y la frecuencia de un MAS. Para derivar una ecuación para el período y la frecuencia, primero debemos definir y analizar las ecuaciones de movimiento. Ten en cuenta que la constante de fuerza a veces se denomina constante del resorte.
Considera un bloque unido a un resorte en una mesa sin fricción (). La posición de equilibrio (la posición donde el resorte no está estirado ni comprimido) se marca como $x = 0$. En la posición de equilibrio, la fuerza neta es cero.
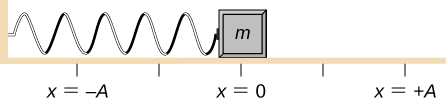
El trabajo se realiza en el bloque para sacarlo a una posición de $x = + A$, y luego se libera del reposo. La posición $x$ máxima (A) se denomina amplitud del movimiento. El bloque comienza a oscilar en un MAS entre $x = + A$ y $x = -A$, donde $A$ es la amplitud del movimiento y $T$ es el período de la oscilación. El período es el tiempo para una oscilación. La muestra una gráfica de la posición del bloque en función del tiempo. Cuando se grafica la posición en función del tiempo, está claro que los datos se pueden modelar mediante una función coseno con una amplitud $A$ y un período $T$. La función coseno $cosθ$ se repite cada múltiplo de $2π$, mientras que el movimiento del bloque se repite cada período $T$. Sin embargo, la función cos ($2πTt$) repite todos los múltiplos enteros del período. El máximo de la función coseno es uno, por lo que es necesario multiplicar la función coseno por la amplitud $A$.
Recuerda que la frecuencia angular es igual a $ω = \frac{dθ}{dt}$. En este caso, el período es constante, por lo que la frecuencia angular se define como $2π$ dividida por el período, $ω = \frac{2π}{T}$.
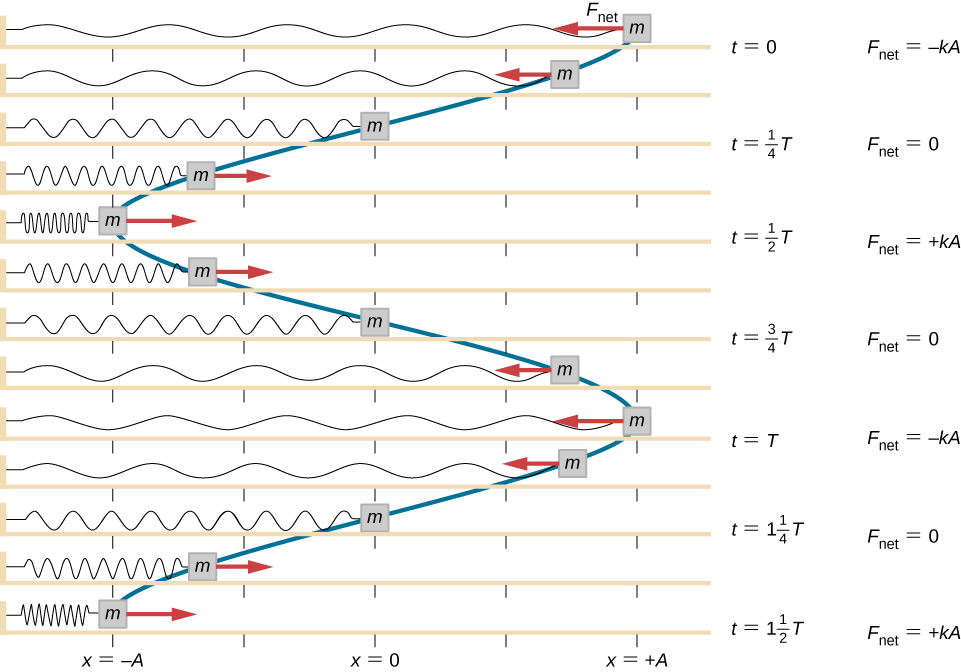
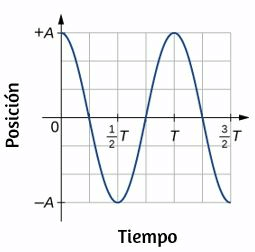
La ecuación para la posición en función del tiempo $x(t) = Acos(ωt)$ es buena para modelar datos, donde la posición del bloque en el tiempo inicial $t = 0.00 s$ está en la amplitud $A$ y la velocidad inicial es cero. A menudo, cuando se toman datos experimentales, la posición de la masa en el tiempo inicial $t = 0.00 s$ no es igual a la amplitud y la velocidad inicial no es cero. Considera $10$ segundos de datos recolectados por un estudiante en el laboratorio, como se muestra en la
Los datos de la aún pueden modelarse con una función periódica, como una función de coseno, pero la función se desplaza hacia la derecha. Este cambio se conoce como cambio de fase y generalmente se representa con la letra griega phi ($φ$). La ecuación de la posición en función del tiempo para un bloque en un resorte se convierte en $$x(t) = Acos (ωt + φ)$$
Esta es la ecuación generalizada para el MAS donde $t$ es el tiempo medido en segundos, $ω$ es la frecuencia angular con unidades de segundos inversos, $A$ es la amplitud medida en metros o centímetros y $φ$ es el cambio de fase medido en radianes (). Se debe tener en cuenta que debido a que las funciones seno y coseno solo se diferencian por un cambio de fase, este movimiento podría modelarse utilizando la función coseno o seno.
La velocidad de la masa en un resorte, que oscila en un MAS, se puede encontrar tomando la derivada de la ecuación de posición:
$$\begin{split} v(t) &= \frac{dx}{dt} = \frac{d}{dt}(Acos(ωt + φ)) \\ &= -Aωsen(ωt + φ) = -v_{\textsf{max}}sen(ωt + φ) \end{split}$$
Debido a que la función sinusoidal oscila entre $–1$ y $+1$, la velocidad máxima es la amplitud por la frecuencia angular, $v_{\textsf{max}} = Aω$. La velocidad máxima se produce en la posición de equilibrio ($x = 0$) cuando la masa se está moviendo hacia $x = +A$. La velocidad máxima en la dirección negativa se alcanza en la posición de equilibrio ($x = 0$) cuando la masa se está moviendo hacia $x = -A$ y es igual a $-v_{\textsf{max}}$.
La aceleración de la masa en el resorte se puede encontrar tomando la derivada con respecto al tiempo de la velocidad:
$$\begin{split} a(t) &= \frac{dv}{dt} = \frac{d}{dt}(-Aωsen(ωt + φ)) \\ &= -Aω^2cos(ωt + φ) = -a_{\textsf{max}}cos(ωt + φ) \end{split}$$La aceleración máxima es $a_{\textsf{max}} = Aω^2$. La aceleración máxima ocurre en la posición ($x = -A$), y la aceleración en la posición ($x = -A$) es igual a $-a_{\textsf{max}}$.
En resumen, el movimiento oscilatorio de un bloque en un resorte se puede modelar con las siguientes ecuaciones de movimiento:
Aquí, $A$ es la amplitud del movimiento, $T$ es el período, $φ$ es el desplazamiento de fase y $ω = 2πT = 2πf$ es la frecuencia angular del movimiento del bloque.
Ejemplo 5.2
Determinación de las ecuaciones de movimiento para un bloque y un resorte
Se coloca un bloque de $2.00 kg$ en una superficie sin fricción. Un resorte con una constante de fuerza $k = 32.00 N/m$ está unido al bloque, y el extremo opuesto del resorte está unido a la pared. El resorte puede ser comprimido o extendido. La posición de equilibrio está marcada como $x = 0.00 m$. El trabajo se realiza en el bloque, sacándolo a $x = + 0.02 m$. El bloque se libera del reposo y oscila entre $x = +0.02 m$ y $x = -0.02 m$. El periodo del movimiento es de $1.57 s$. Determinar las ecuaciones de movimiento.
Estrategia
Primero encontramos la frecuencia angular. El cambio de fase es cero, $φ = 0.00 rad$, porque el bloque se libera del reposo en $x = A = +0.02 m$. Una vez que se encuentra la frecuencia angular, podemos determinar la velocidad máxima y la aceleración máxima.
Solución
La frecuencia angular se puede encontrar y utilizar para encontrar la velocidad máxima y la aceleración máxima:
$$ω = \frac{2π}{1.57} = 4.00 s^{- 1}$$ $$v_{\textsf{max}} = Aω = 0.02 m(4.00 s^{- 1}) = 0.0 8m/s$$ $$a_{\textsf{max}} = Aω^2 = 0.0 2m (4.00 s^{- 1})^2 = 0.32 m/s^2$$Todo lo que queda es completar las ecuaciones de movimiento:
Explicación
La posición, la velocidad y la aceleración se pueden encontrar en cualquier momento. Es importante recordar que al usar estas ecuaciones, tu calculadora debe estar en modo radianes.
Una característica interesante del MAS de un objeto unido a un resorte es que la frecuencia angular, y por lo tanto el período y la frecuencia del movimiento, dependen solo de la masa y la constante de fuerza, y no de otros factores como la amplitud del movimiento. Podemos usar las ecuaciones de movimiento y la segunda ley de Newton ($\overrightarrow{\bold{F}}_{\textsf{net}} = m \overrightarrow{\bold{a}}$) para encontrar las ecuaciones para la frecuencia angular, la frecuencia y el período.
Considera el bloque en un resorte en una superficie sin fricción. Hay tres fuerzas en la masa: el peso, la fuerza normal y la fuerza debida al resorte. Las dos únicas fuerzas que actúan perpendiculares a la superficie son el peso y la fuerza normal, que tienen magnitudes iguales y direcciones opuestas, y por lo tanto suman cero. La única fuerza que actúa paralela a la superficie es la fuerza debida al resorte, por lo que la fuerza neta debe ser igual a la fuerza del resorte:
$$F_x = -kx$$ $$ma = -kx$$Sustituyendo las ecuaciones de movimiento por $x$ y $a$, nos da
$$-Aω^2cos(ωt + φ) = -\frac{k}{m}Acos(ωt + φ)$$Cancelando términos semejantes y resolviendo para la frecuencia angular
La frecuencia angular depende solo de la constante de fuerza y la masa, y no de la amplitud. La frecuencia angular se define como $ω = 2π/T$, que produce una ecuación para el período del movimiento:
El período también depende solo de la masa y la constante de fuerza. Cuanto mayor es la masa, más largo es el período. Cuanto más rígido es el resorte, más corto es el período. La frecuencia es
Cuando un resorte se cuelga verticalmente y un bloque se une y se pone en movimiento, el bloque oscila en MAS. En este caso, no hay una fuerza normal, y el efecto neto de la fuerza de la gravedad es cambiar la posición de equilibrio. Considera la . Dos fuerzas actúan sobre el bloque: el peso y la fuerza del resorte. El peso es constante y la fuerza del resorte cambia a medida que cambia la longitud del resorte.
Cuando el bloque alcanza la posición de equilibrio, como se ve en la , la fuerza del resorte es igual al peso del bloque, $F_{\textsf{net}} = F_s - mg = 0$, donde
$$-k(-Δy) = mg$$De la figura, el cambio en la posición es $Δy = y_0 - y_1$ y como $-k(-Δy) = mg$, tenemos
$$k(y_0 - y_1) - mg = 0$$Si el bloque se desplaza y se libera, oscilará alrededor de la nueva posición de equilibrio. Como se muestra en la , si la posición del bloque se registra como una función del tiempo, el movimiento es una función periódica.
Si el bloque se desplaza a una posición y, la fuerza neta se convierte en $F_{\textsf{net}} = k(y - y_0) - mg = 0$. Pero encontramos que en la posición de equilibrio, $mg = kΔy = ky_0 - ky_1$. Sustituyendo el peso en los campos de la ecuación.
$$F_{\textsf{net}} = ky - ky_0 -(ky_0 - ky_1) = -k(y - y_1)$$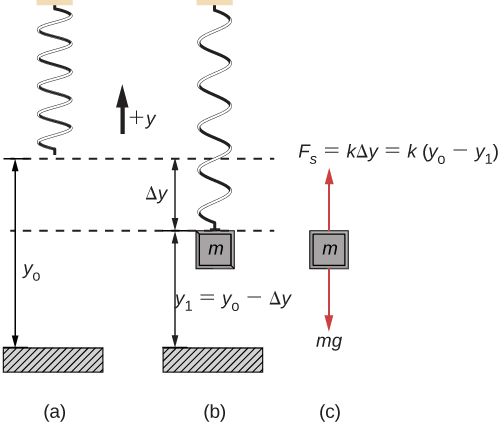
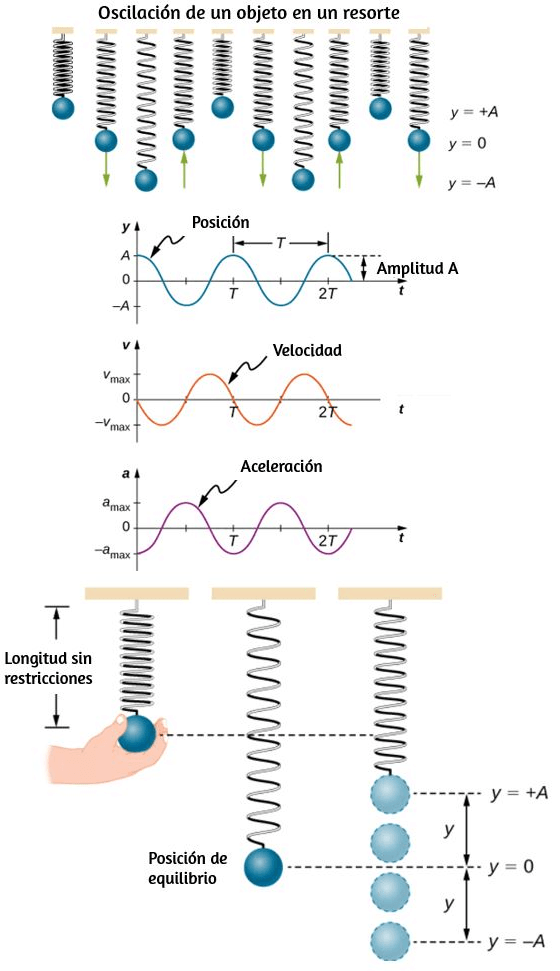
Recuerda que $y_1$ es solo la posición de equilibrio y que cualquier posición se puede configurar para que sea el punto $y = 0.00 m$. Así que vamos a configurar $y_1$ a $y = 0.00 m$. La fuerza neta se convierte entonces en
$$F_{\textsf{net}} = -ky$$ $$m \frac{d^2y}{dt^2} = -ky$$Esto es justo lo que encontramos anteriormente para una masa deslizante horizontal en un resorte. La fuerza de gravedad constante solo sirvió para cambiar la ubicación de equilibrio de la masa. Por lo tanto, la solución debe ser de la misma forma que para un bloque en un resorte horizontal, $y(t) = Acos(ωt + φ)$. Las ecuaciones para la velocidad y la aceleración también tienen la misma forma que para el caso horizontal. Ten en cuenta que la inclusión del cambio de fase significa que el movimiento puede modelarse usando una función de coseno o seno, ya que estas dos funciones solo difieren en un cambio de fase.
Para terminar este apartado, presentamos un discurso interactivo de DescartesJSUn discurso interactivo DescartesJS es un entorno de edición de textos y fórmulas en el que se puede incluir los objetos interactivos cartesianos; es decir, es un entorno que incluye textos, gráficas bi y tridimensionales, vectores, controles gráficos, campos de texto, aleatoriedad, corrección automática, etcétera., en el cual puedes practicar con la determinación de la frecuencia en funciones seno y coseno, a través de un resorte animado.
Para estudiar la energía de un oscilador armónico simple, debemos considerar todas las formas de energía. Considera el ejemplo de un bloque unido a un resorte, colocado sobre una superficie sin fricción, que oscila en el MAS. La energía potencial almacenada en la deformación del resorte es
$$U = \frac{1}{2}kx^2$$En un oscilador armónico simple, la energía oscila entre la energía cinética de la masa $K = \frac{1}{2}mv^2$ y la energía potencial $U = \frac{1}{2}kx^2$ almacenada en el resorte. En el MAS del sistema de masa y resorte, no hay fuerzas disipativas, por lo que la energía total es la suma de la energía potencial y la energía cinética. En esta sección, consideramos la conservación de la energía del sistema. Los conceptos examinados son válidos para todos los osciladores armónicos simples, incluidos aquellos en los que la fuerza gravitatoria desempeña un papel.
Considera la , que muestra un bloque oscilante unido a un resorte. En el caso del MAS no amortiguado, la energía oscila de un lado a otro entre la cinética y el potencial, yendo completamente de una forma de energía a otra a medida que el sistema oscila. Entonces, para el ejemplo simple de un objeto en una superficie sin fricción unida a un resorte, el movimiento comienza con toda la energía almacenada en el resorte como energía potencial elástica. Cuando el objeto comienza a moverse, la energía potencial elástica se convierte en energía cinética, convirtiéndose en energía completamente cinética en la posición de equilibrio. La energía se convierte de nuevo en energía potencial elástica por el resorte cuando se estira o se comprime. La velocidad se vuelve cero cuando la energía cinética se convierte completamente, y este ciclo se repite. Comprender la conservación de la energía en estos ciclos proporcionará una visión adicional aquí y en aplicaciones posteriores de MAS, como los circuitos alternos.
Considera la , que muestra la energía en puntos específicos del movimiento periódico. Mientras se mantiene constante, la energía oscila entre la energía cinética del bloque y la energía potencial almacenada en el resorte:
$$E_{\textsf{total}} = U + K = \frac{1}{2}kx^2 + \frac{1}{2}mv^2$$El movimiento del bloque en un resorte en el MAS se define por la posición $x(t) = Acos (ωt + φ)$ con una velocidad de $v(t) = -Aωsen(ωt + φ)$. Usando estas ecuaciones, la identidad trigonométrica $cos^2θ + sen^2θ = 1$ y $ω = \sqrt{k/m}$, podemos encontrar la energía total del sistema:
$$\begin{split} E_{\textsf{total}} &= \frac{1}{2} kA^2 cos^2(ωt + φ) + \frac{1}{2} mA^2ω^2 sen^2(ωt + φ) \\ &= \frac{1}{2} kA^2 cos^2(ωt + φ) + \frac{1}{2} mA^2 \left(\frac{k}{m}\right) sen^2(ωt + φ) \\ &= \frac{1}{2} kA^2 cos^2(ωt + φ) + \frac{1}{2} kA^2 sen^2(ωt + φ) \\ &= \frac{1}{2} kA^2 (cos^2(ωt + φ) + sen^2(ωt + φ)) \\ &= \frac{1}{2} kA^2 \end{split}$$La energía total del sistema de un bloque y un resorte es igual a la suma de la energía potencial almacenada en el resorte más la energía cinética del bloque y es proporcional al cuadrado de la amplitud $E_{\textsf{total}} = (1/2)kA^2$. La energía total del sistema es constante.
Una mirada más cercana a la energía del sistema muestra que la energía cinética oscila como una función seno-cuadrada, mientras que la energía potencial oscila como una función coseno-cuadrado. Sin embargo, la energía total para el sistema es constante y es proporcional a la amplitud al cuadrado.
La muestra una gráfica de las energías potencial, cinética y total del sistema de bloque y resorte en función del tiempo. También se grafican la posición y la velocidad en función del tiempo. Antes del tiempo $t = 0.0 s$, el bloque se une al resorte y se coloca en la posición de equilibrio. El trabajo se realiza en el bloque aplicando una fuerza externa, sacándolo a una posición de $x = +A$. El sistema ahora tiene energía potencial almacenada en el resorte. En el momento $t = 0.00 s$, la posición del bloque es igual a la amplitud, la energía potencial almacenada en el resorte es igual a $U = \frac{1}{2}kA^2$, y la fuerza en el bloque es máxima y apunta en la dirección $x$ negativa ($F_S = -kA$). La velocidad y la energía cinética del bloque son cero en el tiempo $t = 0.00 s$. En el momento $t = 0.00 s$, el bloque se libera del reposo.
En la siguiente escena interactiva, diseñada por Francisco Esquembre y Loo Kang, muestra el movimiento armónico simple configurado como un sistema de masa de resorte horizontal donde el movimiento oscilatorio se encuentra bajo una fuerza de retardo proporcional a la cantidad de desplazamiento desde una posición de equilibrio. El interactivo permite observar el modelo, la gráfica de energías u otras variables o ambas.
Para simplificar, se asume que la reacción de los resortes a un desplazamiento $dx$ desde el punto de equilibrio sigue la Ley de Hooke, $F(dx) = -kdx$, donde $k$ es una constante que depende de las características físicas del resorte.
Acabamos de considerar la energía del MAS como una función del tiempo. Otra vista interesante del oscilador armónico simple es considerar la energía como una función de
la posición. La muestra un gráfico de la energía en función de la posición de un sistema que experimenta MAS.
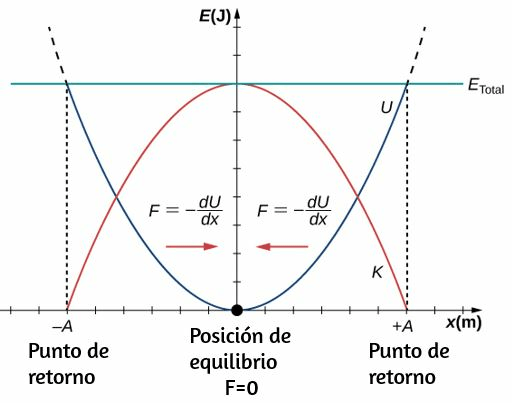
La curva de energía potencial en la se asemeja a un cuenco. Cuando una canica se coloca en un tazón, se asienta en la posición de equilibrio en el punto más bajo del tazón ($x = 0$). Esto sucede porque una fuerza de restauración apunta hacia el punto de equilibrio. Este punto de equilibrio se refiere a veces como un punto fijo. Cuando la canica se desplaza a una posición diferente ($x = +A$), la canica oscila alrededor de la posición de equilibrio. Mirando hacia atrás en el gráfico de energía potencial, la fuerza se puede encontrar al observar la pendiente del gráfico de energía potencial ($F = -\frac{dU}{dx}$). Dado que la fuerza a cada lado del punto fijo apunta hacia el punto de equilibrio, el punto de equilibrio se llama un punto de equilibrio estable. Los puntos $x = A$ y $x = -A$ se denominan puntos de giro.
La estabilidad es un concepto importante. Si un punto de equilibrio es estable, una ligera perturbación de un objeto que se encuentra inicialmente en el punto de equilibrio estable hará que el objeto oscile alrededor de ese punto. El punto de equilibrio estable se produce porque la fuerza de cada lado se dirige hacia él. Para un punto de equilibrio inestable, si el objeto se altera ligeramente, no regresa al punto de equilibrio.
Considere la canica en el ejemplo de la taza. Si el tazón está boca arriba, la canica, si se altera ligeramente, oscilará alrededor del punto de equilibrio estable. Si el tazón se da vuelta, la canica se puede equilibrar en la parte superior, en el punto de equilibrio donde la fuerza neta es cero. Sin embargo, si la canica se altera ligeramente, no regresará al punto de equilibrio, sino que rodará fuera del recipiente. La razón es que la fuerza a ambos lados del punto de equilibrio se dirige lejos de ese punto. Este punto es un punto de equilibrio inestable. La muestra tres condiciones. El primero es un punto de equilibrio estable (a), el segundo es un punto de equilibrio inestable (b) y el último es también un punto de equilibrio inestable (c), porque la fuerza en un solo lado apunta hacia el punto de equilibrio.
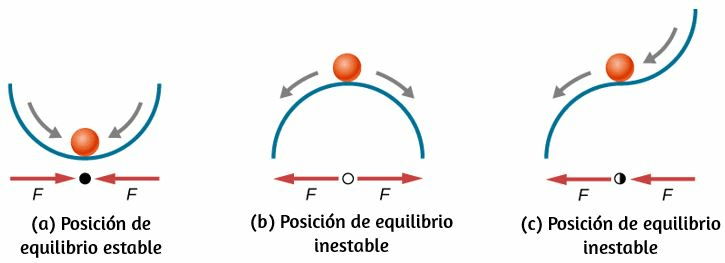
El proceso de determinar si un punto de equilibrio es estable o inestable puede formalizarse. Considera las curvas de energía potencial que se muestran en la . La fuerza se puede encontrar analizando la pendiente de la gráfica. La fuerza es $F = -\frac{dU}{dx}$. En (a), el punto fijo es $x = 0.00 m$. Cuando $x<0.00 m$, la fuerza es positiva. Cuando $x>0.00 m$, la fuerza es negativa. Este es un punto estable. En (b), el punto fijo es $x = 0.00 m$. Cuando $x<0.00 m$, la fuerza es negativa. Cuando $x>0.00 m$, la fuerza también es negativa. Este es un punto inestable.
Una aplicación práctica del concepto de puntos de equilibrio estables es la fuerza entre dos átomos neutros en una molécula. Si dos moléculas están muy cerca, separadas por unos pocos diámetros atómicos, pueden experimentar una fuerza atractiva. Si las moléculas se mueven lo suficientemente cerca como para que las capas de electrones de los otros electrones se superpongan, la fuerza entre las moléculas se vuelve repulsiva. La fuerza atractiva entre los dos átomos puede hacer que los átomos formen una molécula. La fuerza entre las dos moléculas no es una fuerza lineal y no se puede modelar simplemente como dos masas separadas por un resorte, pero los átomos de la molécula pueden oscilar alrededor de un punto de equilibrio cuando se desplazan una pequeña cantidad de la posición de equilibrio. Los átomos oscilan debido a la fuerza atractiva y la fuerza repulsiva entre los dos átomos.
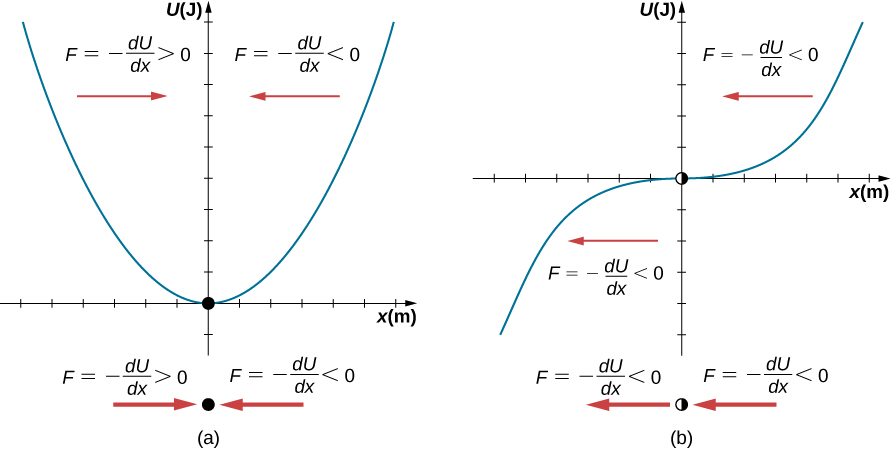
Considera un ejemplo de la interacción entre dos átomos conocida como la interacción de van Der Waals. Está más allá del alcance de este capítulo discutir en profundidad las interacciones de los dos átomos, pero las oscilaciones de los átomos pueden examinarse considerando un ejemplo de un modelo de la energía potencial del sistema. Una sugerencia para modelar la energía potencial de esta molécula es con el potencial de Lennard-Jones 6-12:
$$U(x) = 4ε[(σ/x)^{12} - (σ/x)^6]$$Una gráfica de esta función se muestra en la . Los dos parámetros $ε$ y $σ$ se encuentran experimentalmente.
En el gráfico, puedes ver que hay un pozo de energía potencial, que tiene algunas similitudes con el pozo de energía potencial de la función de energía potencial del oscilador armónico simple descrito en la . El potencial de Lennard-Jones tiene un punto de equilibrio estable donde la energía potencial es mínima y la fuerza a cada lado de los puntos de equilibrio apunta hacia el punto de equilibrio. Ten en cuenta que, a diferencia del oscilador armónico simple, el potencial de Lennard-Jones no es simétrico. Esto se debe al hecho de que la fuerza entre los átomos no es una fuerza de la ley de Hooke y no es lineal. Los átomos aún pueden oscilar alrededor de la posición de equilibrio $x_{\textsf{min}}$ porque cuando $x<x_{\textsf{min}}$, la fuerza es positiva; cuando $x>x_{\textsf{min}}$, la fuerza es negativa. Observa que cuando $x$ se acerca a cero, la pendiente es bastante pronunciada y negativa, lo que significa que la fuerza es grande y positiva. Esto sugiere que se necesita una gran fuerza para tratar de juntar los átomos. A medida que $x$ se hace cada vez más grande, la pendiente se vuelve menos pronunciada y la fuerza es menor y negativa. Esto sugiere que si se les da una energía lo suficientemente grande, los átomos se pueden separar.
Si estás interesado en esta interacción, encuentra la fuerza entre las moléculas tomando la derivada de la función de energía potencial. Verás inmediatamente que la fuerza no se parece a la fuerza de la ley de Hooke ($F = -kx$), pero si está familiarizado con el teorema del binomio:
$$(1 + x)^n = 1 + nx + \frac{n(n - 1)}{2!}x^2 + \frac{n(n - 1)(n -2)}{3!}x^3 + ...$$La fuerza puede ser aproximada por una fuerza de ley de Hooke.
Volviendo al sistema de un bloque y un resorte en la , una vez que el bloque se libera del reposo, comienza a moverse en la dirección negativa hacia la posición de equilibrio. La energía potencial disminuye y la magnitud de la velocidad y la energía cinética aumentan. En el momento $t = T/4$, el bloque alcanza la posición de equilibrio $x = 0.00 m$, donde la fuerza en el bloque y la energía potencial son cero. En la posición de equilibrio, el bloque alcanza una velocidad negativa con una magnitud igual a la velocidad máxima $v = -Aω$. La energía cinética es máxima e igual a $K = \frac{1}{2}mv^2 = \frac{1}{2}mA^2ω^2 = \frac{1}{2}kA^2$. En este punto, la fuerza en el bloque es cero, pero el impulso lleva el bloque y continúa en la dirección negativa hacia $x = -A$. A medida que el bloque continúa moviéndose, la fuerza sobre él actúa en la dirección positiva y la magnitud de la velocidad y la energía cinética disminuyen. La energía potencial aumenta a medida que el resorte se comprime. En el tiempo $t = T/2$, el bloque alcanza $x = -A$. Aquí la velocidad y la energía cinética son iguales a cero. La fuerza en el bloque es $F = +kA$ y la energía potencial almacenada en el resorte es $U = \frac{1}{2}kA^2$. Durante las oscilaciones, la energía total es constante e igual a la suma de la energía potencial y la energía cinética del sistema,
La ecuación de la energía asociada con el MAS se puede resolver para encontrar la magnitud de la velocidad en cualquier posición:
La energía en un oscilador armónico simple es proporcional al cuadrado de la amplitud. Al considerar muchas formas de oscilaciones, encontrarás la energía proporcional a la amplitud al cuadrado.
 Comprueba tu aprendizaje 5.1
Comprueba tu aprendizaje 5.1
 Comprueba tu aprendizaje 5.2
Comprueba tu aprendizaje 5.2
Una forma fácil de modelar el MAS es considerando un movimiento circular uniforme. La .
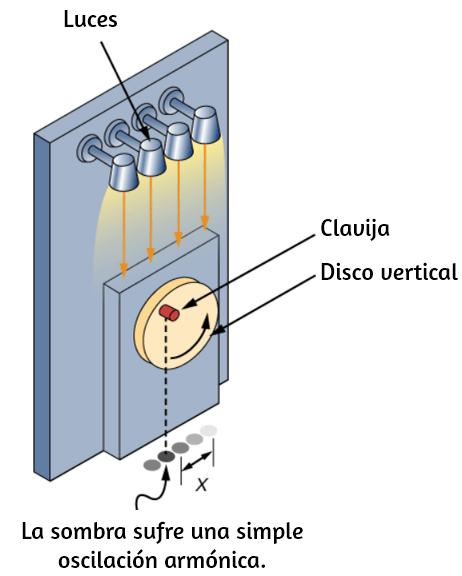
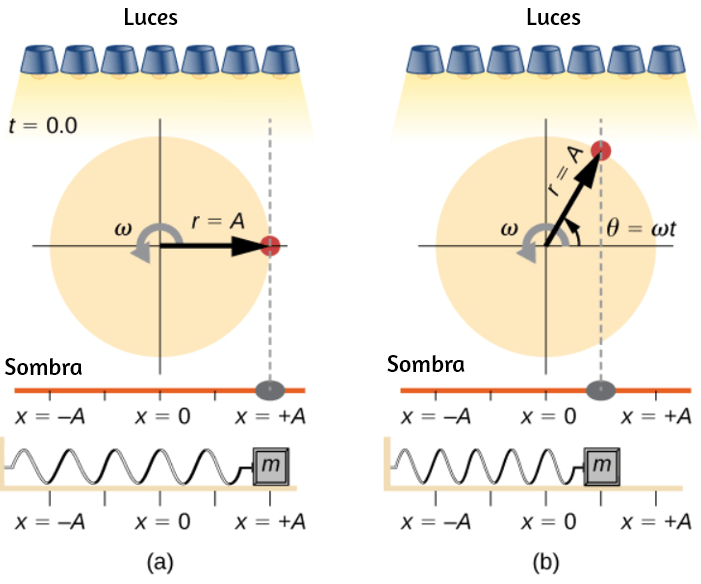
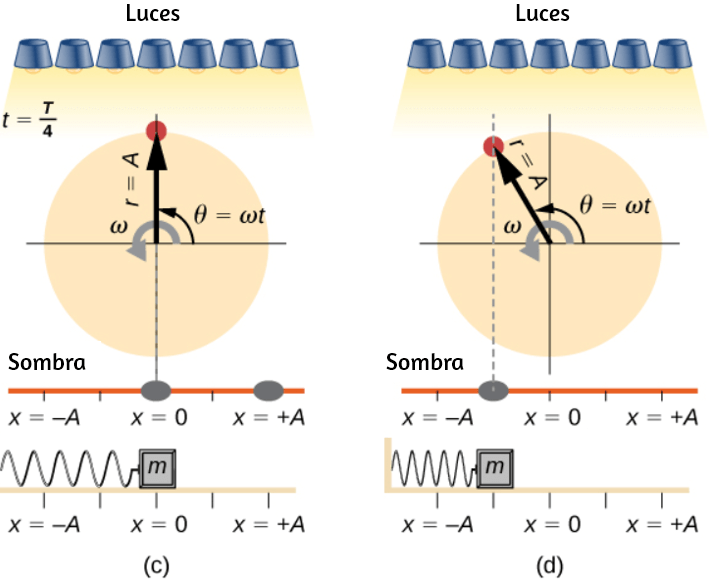
Si el disco gira a la frecuencia angular adecuada, la sombra sigue el bloque. La posición de la sombra se puede modelar con la ecuación:
Recuerda que el bloque unido al resorte no se mueve a una velocidad constante. ¿Con qué frecuencia debe girar la rueda para tener la sombra de la clavija siempre en el bloque? El disco debe girar a una frecuencia angular constante igual a $2π$ veces la frecuencia de oscilación ($ω = 2πf$).
La muestra la relación básica entre el movimiento circular uniforme y el MAS. La clavija se encuentra en la punta del radio, una distancia $A$ desde el centro del disco. El eje $x$ está definido por una línea trazada paralela al suelo, que corta el disco por la mitad. El eje $y$ (no mostrado) se define por una línea perpendicular al suelo, cortando el disco en una mitad izquierda y una mitad derecha. El centro del disco es el punto ($x = 0$, $y = 0$). La proyección de la posición de la clavija sobre el eje $x$ fijo da la posición de la sombra, que sufre el MAS análogo al sistema del bloque y el resorte. En el momento que se muestra en la figura, la proyección tiene la posición $x$ y se mueve hacia la izquierda con la velocidad $v$. La velocidad tangencial de la clavija alrededor del círculo es igual a $v_{\textsf{max}}$ del bloque en el resorte. El componente $x$ de la velocidad es igual a la velocidad del bloque en el resorte.
Podemos usar la para analizar la velocidad de la sombra a medida que gira el disco. La clavija se mueve en un círculo con una velocidad de $v_{\textsf{max}} = Aω$. La sombra se mueve con una velocidad igual a la componente de la velocidad de la clavija que es paralela a la superficie donde se produce la sombra:
De ello se deduce que la aceleración es
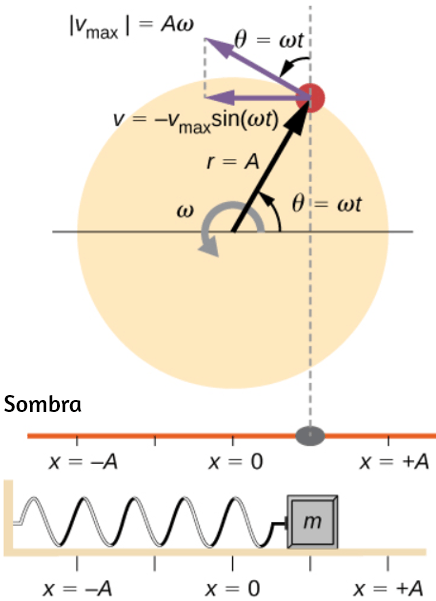
 Comprueba tu aprendizaje 5.3
Comprueba tu aprendizaje 5.3
En la siguiente escena interactiva, diseñada por Fu-Kwun Hwang, muestra cómo el movimiento armónico simple puede considerarse en algunos casos como la proyección unidimensional del movimiento circular uniforme. Si un objeto se mueve con velocidad angular $ω$ alrededor de un círculo de radio $A$ centrado en el origen del plano $x - y$, entonces su movimiento a lo largo de cada coordenada es un movimiento armónico simple con amplitud $A$ y frecuencia angular $ω$.
Algunas preguntas y respuestas planteadas por Fu-Kwun Hwang:
P1: dado que, un movimiento circular puede ser descrito por $x = Acos(ωt)$ e $y = Asen(ωt)$ ¿cuál es la ecuación-modelo del componente y que puede describir el movimiento de un movimiento circular uniforme?
R1: $y = Asen(ωt)$
P2: Cuando el componente $x$ del movimiento circular se modela con $x = Acos(ωt)$ e $y = Asen(ωt)$ sugiere una ecuación modelo para $y$.
R2: $y = Acos(ωt)$ para la posición superior o $y = -Acos(ωt)$ para la posición inferior.
P3: explica por qué los modelos para proyecciones $x$ e $y$ de un movimiento circular uniforme es ¿un movimiento armónico simple?
R3: tanto $x = Acos(ωt)$ como $y = Asen(ωt)$ siguen la relación de definición de un MAS como ecuaciones diferenciales ordinarias de $\frac{d^2x}{dt^2} = -ω^2x y \frac{d^2y}{dt^2} = -ω^2y$ respectivamente.
Un péndulo simple se define por tener una masa puntual, también conocido como el péndulo bob, que se suspende de una cadena de longitud L con masa insignificante (). Aquí, las únicas fuerzas que actúan sobre el bob son la fuerza de la gravedad (es decir, el peso del bob) y la tensión de la cuerda. Se supone que la masa de la cuerda es despreciable en comparación con la masa del bob.
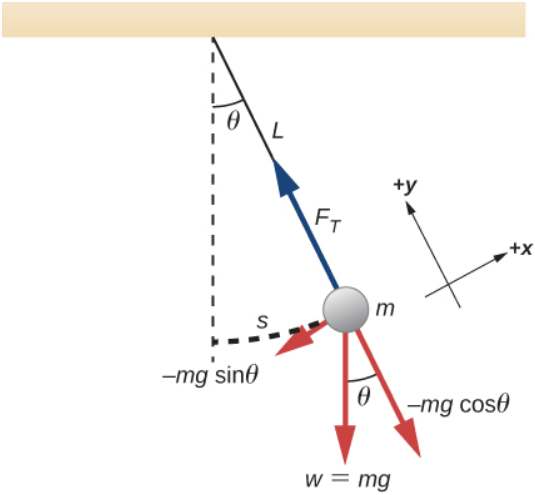
Observa el péndulo simple en la siguiente escena interactiva, diseñada por Christian Wolfgang
Considera el torque en el péndulo. La fuerza que proporciona el torque de restauración es el componente del peso del péndulo que actúa a lo largo de la longitud del arco. El torque es la longitud de la cuerda $L$ por el componente de la fuerza neta que es perpendicular al radio del arco. El signo menos indica que el torque actúa en la dirección opuesta al desplazamiento angular:
$$τ = -L(mgsenθ)$$ $$Iα = -L(mgsenθ)$$ $$I\frac{d^2θ}{dt^2} = -L(mgsenθ)$$ $$mL^2\frac{d^2θ}{dt^2} = -L(mgsenθ)$$ $$\frac{d^2θ}{dt^2} = -\frac{g}{L}senθ$$La solución a esta ecuación diferencial implica el cálculo avanzado, y está más allá del alcance de este texto. Pero ten en cuenta que para ángulos pequeños (menos de $15$ grados), $senθ$ y $θ$ difieren en menos de $1$%, por lo que podemos usar la aproximación de ángulo pequeño $senθ ≈ θ$. El ángulo $θ$ describe la posición del péndulo. Usando la aproximación de ángulo pequeño da una solución aproximada para ángulos pequeños,
Debido a que esta ecuación tiene la misma forma que la ecuación para el MAS, la solución es fácil de encontrar. La frecuencia angular es
Y el período es
El período de un péndulo simple depende de su longitud y la aceleración debida a la gravedad. El período es completamente independiente de otros factores, como la masa y el desplazamiento máximo. Al igual que con los osciladores armónicos simples, el período $T$ para un péndulo es casi independiente de la amplitud, especialmente si $θ$ es menor que aproximadamente $15°$. Incluso los relojes de péndulo simples pueden ajustarse con precisión y seguir siendo precisos.
Nota la dependencia de $T$ en $g$. Si se conoce con precisión la longitud de un péndulo, en realidad se puede utilizar para medir la aceleración debida a la gravedad, como en el siguiente ejemplo.
Ejemplo 5.3
Medición de la aceleración debida a la gravedad en el período de un péndulo
¿Cuál es la aceleración debida a la gravedad en una región donde un péndulo simple que tiene una longitud de $75.000 cm$ tiene un período de $1.7357 s$?
Estrategia
Se nos pide que encontremos $g$ dado el período $T$ y la longitud $L$ de un péndulo. Podemos resolver $T = 2π\sqrt{L/g}$, suponiendo solo que el ángulo de desviación es menor que $15°$.
Solución
Explicación
Este método para determinar $g$ puede ser muy preciso, por lo que la longitud y el período se dan a cinco dígitos en este ejemplo. Para que la precisión de la aproximación $senθ ≈ θ$ sea mejor que la precisión de la longitud y el período del péndulo, el ángulo de desplazamiento máximo debe mantenerse por debajo de aproximadamente $0,5°$.
 Comprueba tu aprendizaje 5.4
Comprueba tu aprendizaje 5.4
Cualquier objeto puede oscilar como un péndulo. Considera una taza de café colgada de un gancho en la despensa. Si la taza es golpeada, oscila de un lado a otro como un péndulo hasta que las oscilaciones se extinguen. Hemos descrito un péndulo simple como una masa puntual y una cuerda. Un péndulo físico es cualquier objeto cuyas oscilaciones son similares a las del péndulo simple, pero no puede modelarse como una masa puntual en una cuerda, y la distribución de masa debe incluirse en la ecuación de movimiento.
En cuanto al péndulo simple, la fuerza restauradora del péndulo físico es la fuerza de la gravedad. Con el péndulo simple, la fuerza de gravedad actúa sobre el centro del péndulo. En el caso del péndulo físico, la fuerza de gravedad actúa sobre el centro de masa (CM) de un objeto. El objeto oscila alrededor de un punto $O$. Considera un objeto de una forma genérica como se muestra en la .
Cuando un péndulo físico cuelga de un punto pero puede girar libremente, gira debido al torque aplicado en el CM, producido por el componente del peso del objeto que actúa tangente al movimiento del CM. Tomando la dirección contraria a las manecillas del reloj como positiva, la componente de la fuerza gravitacional que actúa tangente al movimiento es $-mgsenθ$. El signo menos es el resultado de la fuerza restauradora que actúa en la dirección opuesta al ángulo creciente. Recuerda que el torque es igual a $\overrightarrow{τ} = \overrightarrow{\bold{r}} × \overrightarrow{\bold{F}}$. La magnitud del torque es igual a la longitud del brazo del radio por la componente tangencial de la fuerza aplicada, $|τ| = rFsenθ$. Aquí, la longitud $L$ del brazo del radio es la distancia entre el punto de rotación y el CM.
Para analizar el movimiento, comienza con el torque neto. Al igual que el péndulo simple, considera solo ángulos pequeños para que $senθ ≈ θ$. Recuerda que el torque neto es igual al momento de inercia $I = \int r^2dm$ veces la aceleración angular $α$, donde $α = \dfrac{d^2θ}{dt^2}$:
$$Iα = τ_{\textsf{net}} = L(-mg)senθ$$Usando la aproximación de ángulo pequeño y reorganizando:
$$Iα = -L(mg)θ$$ $$I\frac{d^2θ}{dt^2} = -L(mg)θ$$ $$\frac{d^2θ}{dt^2} = - \left(\frac{mgL}{I} \right)θ$$Una vez más, la ecuación dice que la segunda derivada de la posición (en este caso, el ángulo) es igual a menos una constante ($-mgL/I$) multiplicada por la posición. La solución es
$$θ(t) = θcos(ωt + φ),$$donde $θ$ es el desplazamiento angular máximo. La frecuencia angular es
El período es por lo tanto
Ten en cuenta que para un péndulo simple, el momento de inercia es $I = \int r^2dm = mL^2$ y el período se reduce a $T = 2π\sqrt{L/g}$
Ejemplo 5.4
Reduciendo el balanceo de un rascacielos
En condiciones extremas, los rascacielos pueden oscilar hasta dos metros con una frecuencia de hasta $20.00 Hz$ debido a los vientos fuertes o la actividad sísmica. Varias compañías han desarrollado péndulos físicos que se colocan en la parte superior de los rascacielos. Cuando el rascacielos se balancea hacia la derecha, el péndulo gira hacia la izquierda, reduciendo el balanceo. Suponiendo que las oscilaciones tienen una frecuencia de $0,50 Hz$, diseña un péndulo que consiste en una viga larga, de densidad constante, con una masa de $100$ toneladas métricas y un punto de pivote en un extremo de la viga. ¿Cuál debería ser la longitud de la viga?
Estrategia
Se nos pide que encontremos la longitud del péndulo físico con una masa conocida. Primero tenemos que encontrar el momento de inercia de la viga. Luego podemos usar la ecuación para el período de un péndulo físico para encontrar la longitud.
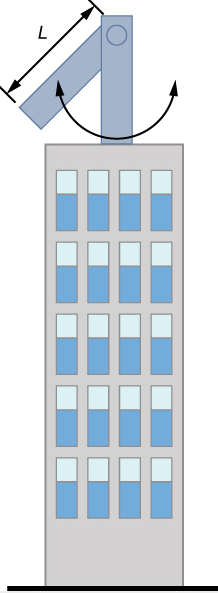
Solución
1. Encuentra el momento de inercia para el CM.
2. Usa el teorema de los ejes paralelos para encontrar el momento de inercia sobre el punto de rotación:
$$I = I_{\textsf{CM}} + \frac{L^2}{4}M = \frac{1}{12}ML^2 + \frac{1}{4}ML^2 = \frac{1}{3}ML^2$$El período de un péndulo físico tiene un período de $T = 2π\sqrt{I/mgL}$. Usa el momento de inercia para hallar la longitud $L$:
$$T = 2π\sqrt{I/mgL} = 2π\sqrt{(1/3)ML^2/MgL} = 2π\sqrt{L/3g}$$ $$L = 3g(\frac{T}{2π})^2 = 3(9.8\frac{m}{s^2})(\frac{2s}{2π})^2 = 2.98 m$$Explicación
Hay muchas formas de reducir las oscilaciones, incluida la modificación de la forma de los rascacielos, el uso de múltiples péndulos físicos y el uso de amortiguadores de masa afinada.
Un péndulo torsional consiste en un cuerpo rígido suspendido por un alambre o resorte ligero (). Cuando el cuerpo está torcido en un ángulo pequeño máximo ($θ$) y se libera del reposo, el cuerpo oscila entre ($θ = +θ$) y ($θ = -θ$). El torque de restauración es suministrado por el corte de la cuerda o cable.
El torque de restauración se puede modelar como proporcional al ángulo:
$$τ = -κθ$$La variable kappa ($κ$) se conoce como la constante de torsión del cable o cuerda. El signo menos muestra que el torque de restauración actúa en dirección opuesta al aumento del desplazamiento angular. El torque neto es igual al momento de inercia multiplicado por la aceleración angular:
$$I\frac{d^2θ}{dt^2} = -κθ$$ $$\frac{d^2θ}{dt^2} = -\frac{κ}{I}θ$$Esta ecuación dice que la segunda derivada de la posición con respecto al tiempo (en este caso, el ángulo) es igual a una constante negativa por la posición. Esto se ve muy similar a la ecuación de movimiento para el MAS $\frac{d^2x}{dt^2} = -\frac{k}{m}x$, donde se encontró que el período es $T = 2π\sqrt{I/κ}$. Por lo tanto, el período del péndulo torsional se puede encontrar usando
Las unidades para la constante de torsión son $[κ] = N-m = (kgm/s^2)m = kgm^2/s^2$ y las unidades para el momento de inercia son $[I] = kg-m^2$, que muestran que la unidad para el período es la segunda.
Ejemplo 5.5
Medición de la constante de torsión de una cuerda
Una varilla tiene una longitud $l = 0,30 m$ y una masa de $4,00 kg$. Una cuerda está unida al CM de la varilla y el sistema se cuelga del techo (). La varilla se desplaza $10$ grados desde la posición de equilibrio y se libera del reposo. La varilla oscila con un periodo de $0,5 s$. ¿Cuál es la constante de torsión $κ$?
Estrategia
Se nos pide que encontremos la constante de torsión de la cuerda. Primero tenemos que encontrar el momento de inercia.
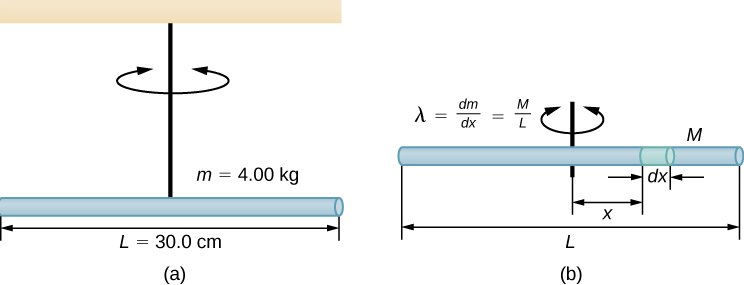
Solución
1. Encuentra el momento de inercia para el CM:
$$\begin{split} I_{\textsf{CM}} &= \int x^2 dm = \int_{-L/2}^{L/2} s^2 λdx = λ [x^3/3]_{-L/2}^{L/2} \\ &= λ \frac{2L^3}{24} = (M/L) \frac{2L^3}{24} = \frac{1}{12}ML^2 \end{split}$$Calcula la constante de torsión usando la ecuación para el período:
$$T = 2π\sqrt{I/κ}$$ $$κ = I(2π/T)^2 = \left(\frac{1}{12} \right)ML^2(2π/T)^2$$ $$\frac{1}{2}(4.00 kg)(0.30 m)^2(2π/0.50 s)^2 = 4.73 N \cdot m$$Explicación
Al igual que la constante de fuerza del sistema de un bloque y un resorte, cuanto mayor es la constante de torsión, más corto es el período.
Para terminar este apartado, presentamos dos escenas interactivas. La primera, diseñada por Walter Fendt, muestra dos péndulos acoplados por un resorte que tiene una pequeña constante de resorte (acoplamiento débil). Para tales sistemas, es característico que la energía de la oscilación se mueva permanentemente de un sistema parcial a otro.
El botón "Restablecer" lleva el sistema a su posición inicial. Puedes iniciar o detener y continuar la simulación con el otro botón. Si eliges la opción "Cámara lenta", el movimiento será diez veces más lento. Es posible cambiar las posiciones iniciales de los dos péndulos utilizando los campos de texto correspondientes. Un ángulo positivo (negativo) significa un alargamiento hacia el lado derecho (izquierdo).
La segunda escena interactiva es tomada de las simulaciones Phet, la cual permite interactuar con uno o dos péndulos y analizar el período, la masa del péndulo, la fuerza de gravedad y la amplitud de la oscilación. Observa la energía en el sistema en tiempo real y cambia la cantidad de fricción. Mide el período usando el temporizador o cronómetro. Utiliza el péndulo para encontrar el valor de $g$ en el Planeta X. Observa el comportamiento armónico a gran amplitud.
En el mundo real, las oscilaciones rara vez siguen el verdadero MAS. La fricción de algún tipo generalmente actúa para amortiguar el movimiento, por lo que se desvanece o necesita más fuerza para continuar. En esta sección, examinamos algunos ejemplos de movimiento armónico amortiguado y veremos cómo modificar las ecuaciones de movimiento para describir este caso más general.
Una cuerda de guitarra deja de oscilar unos segundos después de ser pulsada. Para mantener el swing en un columpio en el patio de recreo, debes seguir empujando (). Aunque a menudo podemos hacer que la fricción y otras fuerzas no conservativas sean pequeñas o insignificantes, es raro el movimiento completamente sin amortiguación. De hecho, es posible que incluso deseemos amortiguar las oscilaciones, como con los amortiguadores de automóviles.

La muestra una masa $m$ unida a un resorte con una constante de fuerza $k$. La masa se eleva a una posición $A_0$, la amplitud inicial, y luego se libera. La masa oscila alrededor de la posición de equilibrio en un fluido con viscosidad, pero la amplitud disminuye para cada oscilación. Para un sistema que tiene una pequeña cantidad de amortiguación, el período y la frecuencia son constantes y son casi los mismos que para el MAS, pero la amplitud disminuye gradualmente como se muestra. Esto ocurre porque la fuerza de amortiguación no conservadora elimina la energía del sistema, generalmente en forma de energía térmica.
Considera las fuerzas que actúan sobre la masa. Ten en cuenta que la única contribución del peso es cambiar la posición de equilibrio, como se explicó anteriormente en este capítulo. Por lo tanto, la fuerza neta es igual a la fuerza del resorte y la fuerza de amortiguación ($F_A$). Si la magnitud de la velocidad es pequeña, lo que significa que la masa oscila lentamente, la fuerza de amortiguación es proporcional a la velocidad y actúa en contra de la dirección del movimiento ($F_A = -bv$). La fuerza neta sobre la masa es por lo tanto $$ma = -bv - kx$$
Escribiendo esto como una ecuación diferencial en $x$, obtenemos
Para determinar la solución a esta ecuación, considera la gráfica de posición frente al tiempo que se muestra en la . La curva se asemeja a una curva de coseno que oscila en la envolvente de una función exponencial $A_0e^{-αt}$ donde $α = \frac{b}{2m}$.
La solución es
Se deja como un ejercicio para probar que esta es, de hecho, la solución. Para probar que es la solución correcta, toma la primera y segunda derivadas con respecto al tiempo y sustitúyelas en la Ecuación 5.23. Se encuentra que la ecuación 5.24 es la solución. $$ω = \sqrt{\frac{k}{m} - \left(\frac{b}{2m}\right)^2}$$
Recuerda que la frecuencia angular de una masa que experimenta MAS es igual a la raíz cuadrada de la constante de fuerza dividida por la masa. Esto se conoce a menudo como la frecuencia angular natural, que se representa como
La frecuencia angular para el movimiento armónico amortiguado se convierte en
Recuerda que cuando comenzamos esta descripción del movimiento armónico amortiguado, afirmamos que la amortiguación debe ser pequeña. Dos preguntas vienen a la mente. ¿Por qué debe ser pequeña la amortiguación? ¿Y qué pequeño es pequeño? Si aumentas gradualmente la cantidad de amortiguación en un sistema, el período y la frecuencia comienzan a verse afectados, porque la amortiguación se opone y, por lo tanto, frena el movimiento hacia adelante y hacia atrás (la fuerza neta es menor en ambas direcciones). Si hay una amortiguación muy grande, el sistema ni siquiera oscila, se mueve lentamente hacia el equilibrio. La frecuencia angular es
$$ω = \sqrt{\frac{k}{m} - \left(\frac{b}{2m}\right)^2}$$A medida que $b$ aumenta, $k/m - (b/2m)^2$ se vuelve más pequeño y finalmente llega a cero cuando $b = \sqrt{4mk}$. Si $b$ se hace más grande $k/m - (b/2m)^2$ se convierte en un número negativo y la frecuencia angular sería un número complejo.
La muestra el desplazamiento de un oscilador armónico para diferentes cantidades de amortiguación.
Cuando la constante de amortiguación es pequeña, $b < \sqrt{4mk}$, el sistema oscila mientras que la amplitud del movimiento decae exponencialmente. Se dice que este sistema es subamortiguado, como en la curva (a). Muchos sistemas no están en buen estado y oscilan mientras que la amplitud disminuye exponencialmente, como la masa que oscila en un resorte. La amortiguación puede ser bastante pequeña, pero finalmente la masa se detiene. Si la constante de amortiguación es $b = \sqrt{4mk}$, se dice que el sistema está amortiguado críticamente, como en la curva (b). Un ejemplo de un sistema críticamente amortiguado son los amortiguadores en un automóvil.
Es ventajoso que las oscilaciones disminuyan lo más rápido posible. Aquí, el sistema no oscila, pero se aproxima asintóticamente a la condición de equilibrio lo más rápido posible. La curva (c) en la representa un sistema sobreamortiguado donde $b > \sqrt{4mk}$. Un sistema sobreamortiguado se aproximará al equilibrio durante un período de tiempo más largo.
A menudo se desea una amortiguación crítica, porque un sistema de este tipo vuelve al equilibrio rápidamente y también permanece en equilibrio. Además, una fuerza constante aplicada a un sistema críticamente amortiguado mueve el sistema a una nueva posición de equilibrio en el menor tiempo posible sin sobrepasar u oscilar sobre la nueva posición.
 Comprueba tu aprendizaje 5.5
Comprueba tu aprendizaje 5.5
El resorte de la suspensión de un automóvil se amortigua críticamente de modo que cuando un automóvil pasa por encima de un bache, el pasajero en el automóvil recupera el equilibrio de manera rápida y sin problemas. En la siguiente escena interactiva, diseñada por Loo Kang, puedes verificar los factores que afectan el coeficiente de amortiguamiento $b$.
Siéntate frente a un piano en algún momento y cántale una breve nota en voz alta con los amortiguadores fuera de sus cuerdas (). Te volverá a cantar la misma nota: las cuerdas, que tienen las mismas frecuencias que tu voz, están resonando en respuesta a las fuerzas de las ondas de sonido que les enviaste. Este es un buen ejemplo del hecho de que los objetos, en este caso, las cuerdas de piano, pueden forzarse a oscilar y oscilar más fácilmente a su frecuencia natural. En esta sección, exploraremos brevemente la aplicación de una fuerza motriz periódica que actúa sobre un oscilador armónico simple. La fuerza motriz pone energía en el sistema a una cierta frecuencia, no necesariamente la misma que la frecuencia natural del sistema. Recuerda que la frecuencia natural es la frecuencia a la que un sistema oscilaría si no hubiera fuerza motriz ni de amortiguación.

La mayoría de nosotros hemos jugado con juguetes que involucran un objeto apoyado en una banda elástica, algo como la bola de remo suspendida de un dedo en la . Imagina que el dedo en la figura es tu dedo. Al principio, mantienes el dedo firme y la pelota rebota hacia arriba y hacia abajo con una pequeña cantidad de amortiguación. Si mueves el dedo hacia arriba y hacia abajo lentamente, la bola sigue sin rebotar mucho por sí misma.
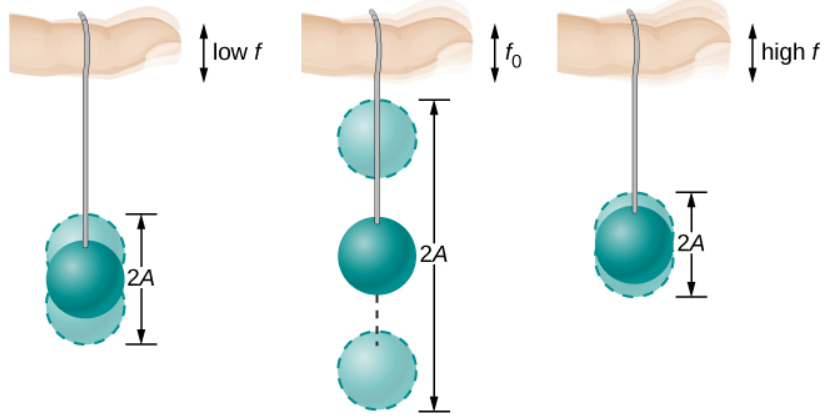
A medida que aumenta la frecuencia con la que mueves el dedo hacia arriba y hacia abajo, la bola responde oscilando a medida que aumenta la amplitud. Cuando manejas la pelota a su frecuencia natural, las oscilaciones de la pelota aumentan en amplitud con cada oscilación durante el tiempo que la impulsas. El fenómeno de conducir un sistema con una frecuencia igual a su frecuencia natural se llama resonancia. Se dice que un sistema que está siendo accionado a su frecuencia natural resuena. A medida que la frecuencia de conducción se vuelve progresivamente más alta que la frecuencia resonante o natural, la amplitud de las oscilaciones se hace más pequeña hasta que las oscilaciones casi desaparecen, y tu dedo simplemente se mueve hacia arriba y hacia abajo con poco efecto en la bola.
Considera un experimento simple. Conecta una masa m a un resorte en un fluido viscoso, similar al aparato descrito en el oscilador armónico amortiguado. Esta vez, en lugar de fijar el extremo libre del resorte, conecta el extremo libre a un disco impulsado por un motor de velocidad variable. El motor gira con una frecuencia de conducción angular de $ω$. El disco giratorio proporciona energía al sistema por el trabajo realizado por la fuerza impulsora ($F_d = F_0sen(ωt)$). El aparato experimental se muestra en la .
Usando la segunda ley de Newton ($\overrightarrow{\bold{F}}_{\textsf{net}} = m \overrightarrow{\bold{a}}$), podemos analizar el movimiento de la masa. La ecuación resultante es similar a la ecuación de fuerza para el oscilador armónico amortiguado, con la adición de la fuerza motriz:
Cuando un oscilador es forzado con una fuerza motriz periódica, el movimiento puede parecer caótico. Los movimientos del oscilador se conocen como transitorios. Después de que los transitorios se extinguen, el oscilador alcanza un estado estable, donde el movimiento es periódico. Después de algún tiempo, la solución de estado estable a esta ecuación diferencial es
Una vez más, queda como un ejercicio para demostrar que esta ecuación es una solución. Tomar la primera y la segunda derivada de $x(t)$ y sustituirlas en la ecuación de fuerza muestra que $x(t) = Asen(ωt + φ)$ es una solución siempre que la amplitud sea igual a
Donde $ω_0 = \sqrt{k/m}$ es la frecuencia angular natural del sistema de la masa y el resorte.
Recuerda que la frecuencia angular, y por lo tanto la frecuencia, se puede ajustar. Mirando el denominador de la ecuación para la amplitud, cuando la frecuencia de conducción es mucho más pequeña, o mucho más grande que la frecuencia natural, el cuadrado de la diferencia de las dos frecuencias angulares ($A_{\textsf{max}} = F_0/bω$). La muestra un gráfico de la amplitud de un oscilador armónico amortiguado en función de la frecuencia de la fuerza periódica que lo impulsa.
Cada una de las tres curvas en el gráfico representa una cantidad diferente de amortiguación. Las tres curvas alcanzan su punto máximo en el punto donde la frecuencia de la fuerza motriz es igual a la frecuencia natural del oscilador armónico. El pico más alto, o la mayor respuesta, es para la menor cantidad de amortiguación, ya que la fuerza de amortiguación elimina menos energía. Ten en cuenta que, dado que la amplitud aumenta a medida que disminuye la amortiguación, lleve esto al límite donde no hay amortiguación ($b=0$), la amplitud se vuelve infinita.
Ten en cuenta que una fuerza motriz de pequeña amplitud puede producir una respuesta de gran amplitud. Este fenómeno se conoce como resonancia. Un ejemplo común de resonancia es un padre que empuja a un niño pequeño en un columpio. Cuando el niño quiere ir más alto, el padre no se mueve hacia atrás y luego, al comenzar a correr, golpea al niño, aplicando una gran fuerza en un corto intervalo. En cambio, el padre aplica pequeños empujes al niño con la frecuencia justa, y la amplitud de los cambios del niño aumenta.
Es interesante observar que los anchos de las curvas de resonancia que se muestran en la dependen de la amortiguación: cuanto menor es la amortiguación, más estrecha es la resonancia. La consecuencia es que si deseas que un oscilador accionado resuene a una frecuencia muy específica, necesitas la menor amortiguación posible.
Por ejemplo, una radio tiene un circuito que se utiliza para elegir una estación de radio en particular. En este caso, el oscilador forzado amortiguado consiste en una resistencia, un condensador y un inductor. El circuito está "sintonizado" para elegir una estación de radio en particular. Aquí es deseable que la curva de resonancia sea muy estrecha, para seleccionar la frecuencia exacta de la estación de radio elegida. La estrechez del gráfico y la capacidad de seleccionar una cierta frecuencia se conoce como la calidad del sistema.
La calidad se define como la extensión de la frecuencia angular, o, de manera equivalente, la extensión en la frecuencia, a la mitad de la amplitud máxima, dividida por la frecuencia natural ($Q = \frac{Δω}{ω_0}$) como se muestra en la . Para una pequeña amortiguación, la calidad es aproximadamente igual a $Q ≈ \frac{2b}{m}$.
Estas características de los osciladores armónicos accionados se aplican a una gran variedad de sistemas. Por ejemplo, la resonancia magnética (RM) es una herramienta de diagnóstico médico ampliamente utilizada en la cual los núcleos atómicos (en su mayoría núcleos de hidrógeno o protones) se hacen resonar por las ondas de radio entrantes (del orden de $100 MHz$). En todos estos casos, la eficiencia de la transferencia de energía de la fuerza motriz al oscilador es mejor en resonancia. La muestra una fotografía de un famoso ejemplo (el puente Tacoma Narrows) de los efectos destructivos de una oscilación armónica impulsada. El puente Millennium en Londres se cerró durante un corto período de tiempo por el mismo motivo mientras se realizaban las inspecciones. Las observaciones conducen a modificaciones en el puente antes de la reapertura.

 Comprueba tu aprendizaje 5.6
Comprueba tu aprendizaje 5.6
La siguiente escena interactiva, diseñada por Loo Kang, permite diseñar varios modelos de oscilaciones forzadas. En la siguiente página hemos dejado algunos ejemplos explicados por Loo Kang.
Terminamos este capítulo con una escena interactiva tomada de las simulaciones Phet de la Universidad de Colorado.
Se trata de la simulación Masas y resortes, en la que puedes colgar las masas de los resortes y ajustar la constante del resorte y la amortiguación. Transportar el laboratorio a diferentes planetas, o ralentizar el tiempo.

En este capítulo, estudiaremos la física del movimiento de las ondas. Nos concentramos en las ondas mecánicas, que son perturbaciones que se mueven a través de un medio como el aire o el agua. Al igual que el movimiento armónico simple estudiado en el capítulo anterior, la energía transferida a través del medio es proporcional a la amplitud al cuadrado. Las ondas de agua superficial en el océano son ondas transversales en las que la energía de la onda se desplaza horizontalmente mientras el agua oscila hacia arriba y hacia abajo debido a cierta fuerza restauradora. En la imagen de arriba, una boya se usa para convertir el asombroso poder de las olas del océano en electricidad. El movimiento hacia arriba y hacia abajo de la boya generada cuando las ondas pasan se convierte en un movimiento de rotación que convierte un rotor en un generador eléctrico.
El generador carga baterías, que a su vez se utilizan para proporcionar una fuente de energía constante para el usuario final. Este modelo fue probado con éxito por la Marina de los EE. UU. En un proyecto para proporcionar energía a las redes de seguridad costeras y fue capaz de proporcionar una potencia promedio de $350 W$. La boya sobrevivió el difícil entorno marino, incluida la operación frente a la costa de Nueva Jersey a través del huracán Irene en 2011.
Los conceptos presentados en este capítulo serán la base de muchos temas interesantes, desde la transmisión de información hasta los conceptos de mecánica cuántica.
Vimos en Oscilaciones que el movimiento oscilatorio es un tipo importante de comportamiento que puede usarse para modelar una amplia gama de fenómenos físicos. El movimiento oscilatorio también es importante porque las oscilaciones pueden generar ondas, que son de fundamental importancia en la física. Muchos de los términos y ecuaciones que estudiamos en el capítulo sobre oscilaciones se aplican igualmente al movimiento ondulatorio ().
Una onda es una perturbación que se propaga, o se mueve desde el lugar donde fue creada. Hay tres tipos básicos de ondas: ondas mecánicas, ondas electromagnéticas y ondas de materia.
Las ondas mecánicas básicas se rigen por las leyes de Newton y requieren un medio.

Un medio es la sustancia a través de la cual se propagan las ondas mecánicas, y el medio produce una fuerza de restauración elástica cuando se deforma. Las ondas mecánicas transfieren energía y momento, sin transferir masa. Algunos ejemplos de ondas mecánicas son ondas de agua, ondas de sonido y ondas sísmicas. El medio para las ondas de agua es el agua; Para las ondas de sonido, el medio suele ser el aire (las ondas de sonido también pueden viajar en otros medios; lo veremos con más detalle en el capítulo de Sonido). En el caso de las ondas de agua superficial, la perturbación se produce en la superficie del agua, tal vez creada por una roca lanzada a un estanque o por una nadador salpicando la superficie repetidamente.
Para las ondas de sonido, la perturbación es un cambio en la presión del aire, tal vez creado por el cono oscilante dentro de un altavoz o un diapasón vibrador. En ambos casos, la perturbación es la oscilación de las moléculas del fluido. En ondas mecánicas, la energía y el momento se transfieren con el movimiento de la onda, mientras que la masa oscila alrededor de un punto de equilibrio. Los terremotos generan ondas sísmicas a partir de varios tipos de perturbaciones, incluida la perturbación de la superficie de la Tierra y las perturbaciones de presión debajo de la superficie. Las ondas sísmicas viajan a través de los sólidos y líquidos que forman la Tierra. En este capítulo, nos centraremos en las ondas mecánicas.
Las ondas electromagnéticas están asociadas con oscilaciones en campos eléctricos y magnéticos y no requieren un medio. Los ejemplos incluyen rayos gamma, rayos X, ondas ultravioletas, luz visible, ondas infrarrojas, microondas y ondas de radio. Las ondas electromagnéticas pueden viajar a través del vacío a la velocidad de la luz, $v = c = 2.99792458×10^8 m/s$. Por ejemplo, la luz de estrellas distantes viaja a través del vacío del espacio y llega a la Tierra. Las ondas electromagnéticas tienen algunas características que son similares a las ondas mecánicas.
Las ondas de materia son una parte central de la rama de la física conocida como mecánica cuántica. Estas ondas están asociadas con protones, electrones, neutrones y otras partículas fundamentales que se encuentran en la naturaleza. La teoría de que todos los tipos de materia tienen propiedades de onda fue propuesta por primera vez por Louis de Broglie en 1924.
Las ondas mecánicas muestran características comunes a todas las ondas, como la amplitud, la longitud de onda, el período, la frecuencia y la energía. Todas las características de onda se pueden describir mediante un pequeño conjunto de principios subyacentes.
Las ondas mecánicas más simples se repiten durante varios ciclos y se asocian con un movimiento armónico simple. Estas simples ondas armónicas se pueden modelar usando una combinación de funciones seno y coseno. Por ejemplo, considera la onda de agua superficial simplificada que se mueve a través de la superficie del agua como se ilustra en la , las olas hacen que una gaviota se mueva hacia arriba y hacia abajo en un simple movimiento armónico a medida que las crestas de las olas y los valles (picos y valles) pasan por debajo del ave. La cresta es el punto más alto de la onda, y el canal es la parte más baja de la onda. El tiempo para una oscilación completa del movimiento hacia arriba y hacia abajo es el período T de la onda. La frecuencia de la onda es el número de ondas que pasan a través de un punto por unidad de tiempo y es igual a $f = 1/T$. El período se puede expresar utilizando cualquier unidad de tiempo conveniente, pero generalmente se mide en segundos; La frecuencia generalmente se mide en hercios ($Hz$), donde $1Hz = 1 s^{-1}.$
La longitud de la onda se denomina longitud de onda y está representada por la letra griega lambda ($λ$), que se mide en cualquier unidad de longitud conveniente, como un centímetro o metro. La longitud de onda se puede medir entre dos puntos similares a lo largo del medio que tienen la misma altura y la misma pendiente. En la , la longitud de onda se muestra medida entre dos crestas. Como se indicó anteriormente, el período de la onda es igual al tiempo para una oscilación, pero también es igual al tiempo para que una longitud de onda pase por un punto a lo largo de la trayectoria de la onda.
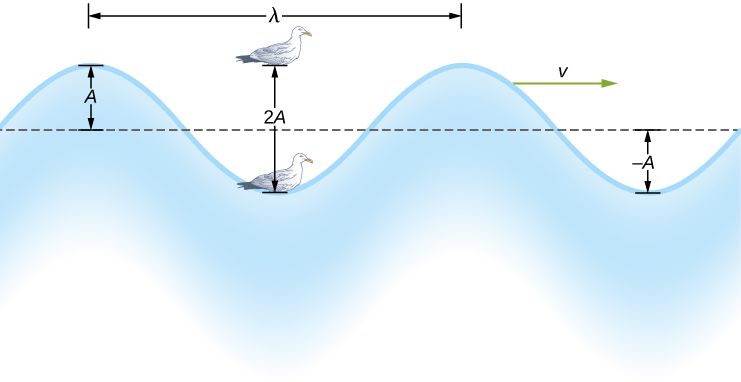
La amplitud de la onda ($A$) es una medida del desplazamiento máximo del medio desde su posición de equilibrio. En la figura, la posición de equilibrio está indicada por la línea de puntos, que es la altura del agua si no hubiera olas que se movieran a través de ella. En este caso, la onda es simétrica, la cresta de la onda es una distancia $+A$ por encima de la posición de equilibrio, y el canal es una distancia $-A$ por debajo de la posición de equilibrio. Las unidades para la amplitud pueden ser centímetros o metros, o cualquier unidad conveniente de distancia.
La onda de agua en la figura se mueve a través del medio con una velocidad de propagación $\overrightarrow{\bold{v}}$. La magnitud de la velocidad de la onda es la distancia que la onda recorre en un tiempo determinado, que es una longitud de onda en el tiempo de un período, y la velocidad de la onda es la magnitud de la velocidad de la onda. En forma de ecuación, esto es
Esta relación fundamental es válida para todo tipo de ondas. Para las ondas de agua, $v$ es la velocidad de una onda de superficie; para el sonido, $v$ es la velocidad del sonido; y para la luz visible, $v$ es la velocidad de la luz.
Hemos visto que una onda mecánica simple consiste en una perturbación periódica que se propaga de un lugar a otro a través de un medio. En la (a), la onda se propaga en la dirección horizontal, mientras que el medio se altera en la dirección vertical. Tal onda se llama onda transversal. En una onda transversal, la onda puede propagarse en cualquier dirección, pero la perturbación del medio es perpendicular a la dirección de propagación. Por contraste, en una onda longitudinal u onda compresiva, la perturbación es paralela a la dirección de propagación. La (b) muestra un ejemplo de una onda longitudinal. El tamaño de la perturbación es su amplitud $A$ y es completamente independiente de la velocidad de propagación $v$.
En la (b) a (g) muestra instantáneas del resorte tomadas con un cuarto de período de tiempo, en algún momento después del final del resorte se oscila hacia atrás y hacia adelante en la dirección $x$ a una frecuencia constante. La perturbación de la onda se ve como las compresiones y las expansiones del resorte. Ten en cuenta que el punto azul oscila alrededor de su posición de equilibrio a una distancia $A$, a medida que la onda longitudinal se mueve en la dirección $x$ positiva con una velocidad constante. La distancia A es la amplitud de la onda. La posición $y$ del punto no cambia cuando la onda se mueve a través del resorte. La longitud de onda se mide en la parte (d). La longitud de onda depende de la velocidad de la onda y la frecuencia de la fuerza impulsora.
En la siguiente escena interactiva tomada de las simulaciones Phet de la Universidad de Colorado (Onda en una cuerda), explora el mundo de las ondas. Incluso observa la cuerda vibrar en cámara lenta. Mueve el extremo de la cuerda y crea ondas, o ajusta la frecuencia y amplitud de un oscilador. Haz la onda manual o usa la opción de oscilación.
Las ondas pueden ser transversales, longitudinales o una combinación de las dos. Ejemplos de ondas transversales son las ondas en instrumentos de cuerda u ondas superficiales en el agua, como las ondas que se mueven en un estanque. Las ondas sonoras en el aire y el agua son longitudinales. Con las ondas de sonido, las perturbaciones son variaciones periódicas de la presión que se transmiten en los fluidos. Los fluidos no tienen una fuerza de corte apreciable, y por esta razón, las ondas de sonido en ellos son ondas longitudinales.
El sonido en sólidos puede tener componentes longitudinales y transversales, como los de una onda sísmica. Los terremotos generan ondas sísmicas bajo la superficie de la Tierra con componentes tanto longitudinales como transversales (llamadas ondas compresionales o $P$ y ondas de corte o $S$, respectivamente). Los componentes de las ondas sísmicas tienen características individuales importantes: se propagan a diferentes velocidades, por ejemplo. Los terremotos también tienen ondas superficiales que son similares a las ondas superficiales en el agua. Las olas del océano también tienen componentes transversales y longitudinales.
Ejemplo 6.1
Onda en un resorte
Un estudiante toma una cuerda de $30.00 m$ de largo y une un extremo a la pared en el laboratorio de física. El estudiante luego sostiene el extremo libre de la cuerda, manteniendo la tensión constante en la cuerda. Luego, el estudiante comienza a enviar ondas por la cadena moviendo el extremo de la cadena hacia arriba y hacia abajo con una frecuencia de $2.00 Hz$. El desplazamiento máximo del final de la cuerda es de $20.00 cm$. La primera onda golpea la pared del laboratorio $6,00 s$ después de su creación. (a) ¿Cuál es la velocidad de la onda? (b) ¿Cuál es el período de la onda? (c) ¿Cuál es la longitud de onda?
Estrategia
a. La velocidad de la onda se puede obtener dividiendo la distancia recorrida por el tiempo.
b. El período de la onda es el inverso de la frecuencia de la fuerza impulsora.
c. La longitud de onda se puede encontrar a partir de la velocidad y el período $v = λ/T$.
Solución
a. La primera onda recorrió $30.00 m$ en $6.00 s$:
$$v = \frac{30.00 m}{6.00 s} = 5.00 m/s$$b. El período es igual al inverso de la frecuencia:
$$T = \frac{1}{f} = \frac{1}{2 s^{-1}} = 0.50s$$c. La longitud de onda es igual a la velocidad por el período:
$$λ = vT = 5.00 \frac{ m}{s}(0.50s) = 2.50 m$$Explicación
La frecuencia de la onda producida por una fuerza impulsora oscilante es igual a la frecuencia de la fuerza impulsora.
 Comprueba tu aprendizaje 6.1
Comprueba tu aprendizaje 6.1
Ejemplo 6.2
Características de una onda
Una onda mecánica transversal se propaga en la dirección $x$ positiva a través de un resorte (como se muestra en la muestra la altura del resorte ($y$) frente a la posición ($x$), donde el eje $x$ apunta en la dirección de propagación. La figura muestra la altura del resorte frente a la posición $x$ en $t = 0.00 s$ como una línea de puntos y la onda en $t = 3.00 s$ como una línea continua.
(a) Determina la longitud de onda y la amplitud de la onda.
(b) Encuentra la velocidad de propagación de la onda.
(c) Calcula el período y la frecuencia de la onda.
Estrategia
a. La amplitud y la longitud de onda se pueden determinar a partir de la gráfica.
b. Dado que la velocidad es constante, la velocidad de la onda se puede encontrar al dividir la distancia recorrida por la onda por el tiempo que tomó la onda para recorrer la distancia.
c. El período se puede encontrar desde $v = \dfrac{λ}{T}$ y la frecuencia desde $f = \dfrac{1}{T}$.
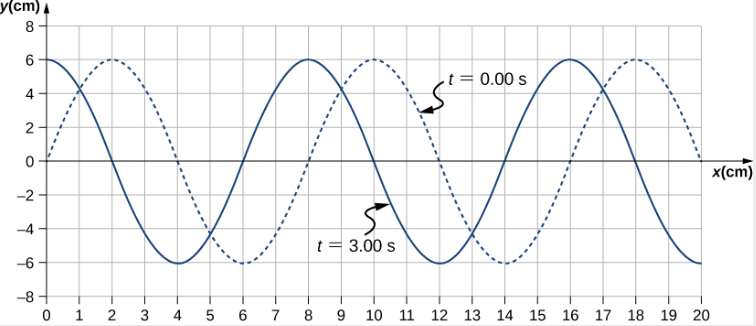
Solución
a. Lee la longitud de onda de la gráfica, mirando la flecha púrpura en la . Lee la amplitud mirando la flecha verde. La longitud de onda es $λ = 8.00 cm$ y la amplitud es $A = 6.00 cm$.
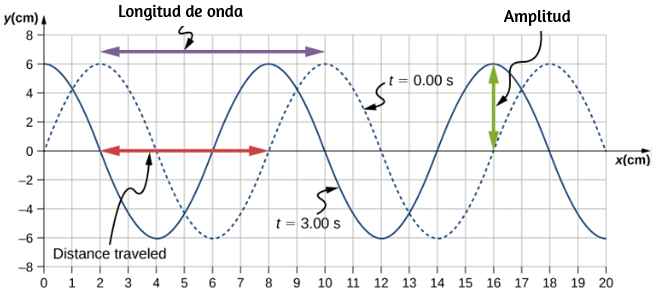
b. La distancia que la onda recorrió desde el tiempo $t = 0.00 s$ hasta el tiempo $t = 3.00 s$ se puede ver en la gráfica. Considera la flecha roja, que muestra la distancia que se ha movido la cresta en $3 s$. La distancia es de $8.00 cm - 2.00 cm = 6.00cm$. La velocidad es
c. El período es $T = \frac{λ}{v} = \frac{8.00 cm}{2.00 cm/s} = 4.00s$ y la frecuencia es $f = \frac{1}{T} = 14.00 s = 0.25 Hz$.
Explicación
Ten en cuenta que la longitud de onda se puede encontrar utilizando cualquiera de los dos puntos idénticos sucesivos que se repiten, con la misma altura y pendiente. Debes elegir dos puntos que sean los más convenientes. El desplazamiento también se puede encontrar utilizando cualquier punto conveniente.
 Comprueba tu aprendizaje 6.2
Comprueba tu aprendizaje 6.2
En la sección anterior, describimos las ondas periódicas por sus características de longitud de onda, período, amplitud y velocidad de onda. Las ondas también pueden describirse por el movimiento de las partículas del medio a través del cual se mueven las ondas. La posición de las partículas del medio se puede modelar matemáticamente como funciones de onda, que se pueden usar para encontrar la posición, la velocidad y la aceleración de las partículas del medio en cualquier momento.
Un pulso se puede describir como una onda que consiste en una sola perturbación que se mueve a través del medio con una amplitud constante. El pulso se mueve como un patrón que mantiene su forma a medida que se propaga con una velocidad de onda constante. Debido a que la velocidad de onda es constante, la distancia a la que se mueve el pulso en un tiempo $Δt$ es igual a $ΔX = vΔt$ ().
Considera una cuerda mantenida en tensión constante $F_T$ donde un extremo es fijo y el extremo libre oscila entre $y = +A$ y $y = -A$, por un dispositivo mecánico a una frecuencia constante. La muestra las instantáneas de la onda en un intervalo de un octavo de un período, comenzando después de un período ($t = T$).
Observa que cada punto de selección en la cuerda (marcado por puntos de colores) oscila hacia arriba y hacia abajo en un movimiento armónico simple, entre $y = +A$ y $y = -A$, con un período $T$. La onda en la cuerda es sinusoidal y se traslada en la dirección $x$ positiva a medida que avanza el tiempo.
En este punto, es útil recordar de tu estudio del álgebra que si $f(x)$ es alguna función, entonces $f(x - d)$ es la misma función trasladada en la dirección $x$ positiva en una distancia $d$. La función $f(x + d)$ es la misma función trasladada en la dirección $x$ negativa en una distancia $d$. Queremos definir una función de onda que proporcione la posición $y$ de cada segmento de la cuerda para cada posición $x$ a lo largo de la cuerda para cada tiempo $t$.
Mirando la primera instantánea en la , la posición $y$ de la cuerda entre $x = 0$ y $x = λ$ puede modelarse como una función senoidal. Esta onda se propaga por la cuerda una longitud de onda en un período, como se ve en la última instantánea. Por lo tanto, la onda se mueve con una velocidad de onda constante de $v = λ/T$.
Recuerda que una función sinusoidal es una función del ángulo $θ$, que oscila entre $+1$ y $-1$, y que se repite cada $2π$ radianes (). Sin embargo, la posición y del medio, o la función de onda, oscila entre $+A$ y $-A$, y repite cada longitud de onda $λ$.
Para construir nuestro modelo de onda usando una función periódica, considere la relación del ángulo y la posición,
$$\frac{θ}{x} = \frac{2π}{λ}$$ $$θ = \frac{2π}{λ}x$$Usando $θ = \frac{2π}{λ}x$ y multiplicando la función seno por la amplitud $A$, ahora podemos modelar la posición $y$ de la cuerda como una función de la posición $x$:
$$y(x) = Asen \left(\frac{2π}{λ}x \right)$$La onda en la cuerda se desplaza en la dirección $x$ positiva con una velocidad constante $v$, y se mueve una distancia $vt$ en un tiempo $t$. La función de onda ahora se puede definir por
$$y(x, t) = Asen \left(\frac{2π}{λ}(x - vt) \right)$$A menudo es conveniente reescribir esta función de onda en una forma más compacta. Multiplicando a través de la relación $\frac{2π}{λ}$ conduce a la ecuación
$$y(x, t) = Asen \left(\frac{2π}{λ}x - \frac{2π}{λ}vt \right)$$El valor $\frac{2π}{λ}$ se define como el número de onda. El símbolo para el número de onda es $k$ y tiene unidades de metros inversos, $m^{-1}$:
Recuerde que la frecuencia angular se define como $\frac{2π}{λ}$. El segundo término de la función de onda se convierte en
$$\frac{2π}{λ}vt = \frac{2π}{λ} \left(\frac{λ}{T} \right)t = ωt$$La función de onda para una onda armónica simple en una cuerda se reduce a
$$y(x,t) = Asen(kx ± ωt),$$donde $A$ es la amplitud, $k =\frac{2π}{λ}$ es el número de onda, $ω = \frac{2π}{T}$ es la frecuencia angular, el signo menos es para las ondas que se mueven en la dirección $x$ positiva, y el signo más es para las ondas que se mueven en la dirección $x$ negativa.
La velocidad de la onda es igual a
Piensa de nuevo en nuestra discusión sobre una masa en un resorte, cuando la posición de la masa se modeló como $x(t) = Acos(ωt + φ)$. El ángulo $φ$ es un cambio de fase, agregado para permitir el hecho de que la masa puede tener condiciones iniciales distintas de $x = +A$ y $v = 0$. Por razones similares, la fase inicial se agrega a la función de onda. La función de onda que modela una onda sinusoidal, permitiendo un cambio de fase inicial $φ$, es
El valor
se conoce como la fase de la onda, donde $φ$ es la fase inicial de la función de onda. Si el término temporal $ωt$ es negativo o positivo depende de la dirección de la onda. Primero considera el signo menos para una onda con una fase inicial igual a cero ($φ = 0$). La fase de la onda sería ($kx - ωt$). Considera seguir un punto en una onda, como una cresta. Se producirá una cresta cuando $sen(kx - ωt) = 1.00$, es decir, cuando $kx - ωt = nπ + \frac{π}{2}$, para cualquier valor integral de $n$. Por ejemplo, una cresta en particular ocurre en $kx - ωt = \frac{π}{2}$. A medida que la onda se mueve, el tiempo aumenta y $x$ también debe aumentar para mantener la fase igual a $\frac{π}{2}$. Por lo tanto, el signo menos es para una onda que se mueve en la dirección $x$ positiva. Usando el signo más, $kx + ωt = \frac{π}{2}$. A medida que aumenta el tiempo, $x$ debe disminuir para mantener la fase igual a $\frac{π}{2}$. El signo más se utiliza para las ondas que se mueven en la dirección $x$ negativa. En resumen, $y(x, t) = Asen(kx - ωt + φ)$ modela una onda que se mueve en la dirección $x$ positiva y $y(x, t) = Asen(kx + ωt + φ)$ modela una onda que se mueve en la dirección $x$ negativa.
La ecuación 6.4 se conoce como una función de onda armónica simple. Una función de onda es cualquier función tal que $f(x, t) = f(x - vt)$. Más adelante en este capítulo, veremos que es una solución a la ecuación de onda lineal. Ten en cuenta que $y(x, t) = Acos(kx + ωt + φ')$ funciona igual de bien porque corresponde a un cambio de fase diferente $φ' = φ - \frac{π}{2}$.
Estrategia de resolución de problemas: encontrar las características de una onda sinusoidal
1. Para hallar la amplitud, longitud de onda, período y frecuencia de una onda sinusoidal, escribe la función de onda en la forma $y(x, t) = Asen(kx - ωt + φ)$.
2. La amplitud se puede leer directamente de la ecuación y es igual a $A$.
3. El período de la onda se puede derivar de la frecuencia angular $(T = 2π/ω)$.
4. La frecuencia se puede encontrar usando $f = 1/T$.
5. La longitud de onda se puede encontrar usando el número de onda $(λ = 2π/k)$.
Ejemplo 6.3
Características de una onda viajera en una cuerda
Una onda transversal en una cuerda tensa se modela con la función de onda $$y(x, t) = Asen(kx - ωt) = 0.2 m sen(6.28 m^{-1}x - 1.57 s^{-1}t)$$
Encuentra la amplitud, longitud de onda, período y velocidad de la onda.
Estrategia
Todas estas características de la onda se pueden encontrar a partir de las constantes incluidas en la ecuación o de combinaciones simples de estas constantes.
Solución
1. La amplitud, el número de onda y la frecuencia angular se pueden leer directamente de la ecuación de onda:
$$y(x, t) = Asen(kx - ωt) = 0.2 m sen(6.28 m^{-1}x - 1.57 s^{-1}t)$$ $$(A = 0.2 m; k = 6.28 m^{-1}; ω = 1.57 s^{-1})$$2. El número de onda se puede usar para encontrar la longitud de onda:
$$k = \frac{2π}{λ}$$ $$λ = \frac{2π}{k} = \frac{2π}{6.28 m^{-1}} = 1.0 m$$3. El período de la onda se puede encontrar usando la frecuencia angular:
$$ω = \frac{2π}{T}$$ $$T = \frac{2π}{ω} = \frac{2π}{1.57 s^{-1}} = 4 s$$La velocidad de la onda se puede encontrar utilizando el número de onda y la frecuencia angular. La dirección de la onda se puede determinar considerando el signo de $kx ± ωt$: un signo negativo sugiere que la onda se está moviendo en la dirección $x$ positiva:
$$|v| = \frac{ω}{k} = \frac{1.57 s^{-1}}{6.28 m^{-1}} = 0.25 m/s$$Explicación
Todas las características de la onda están contenidas en la función de onda. Ten en cuenta que la velocidad de la onda es la velocidad en la dirección paralela al movimiento de la onda. El trazado de la altura del medio $y$ versus la posición $x$ para dos veces $t = 0.00 s$ y $t = 0.80 s$ puede proporcionar una visualización gráfica de la onda ().
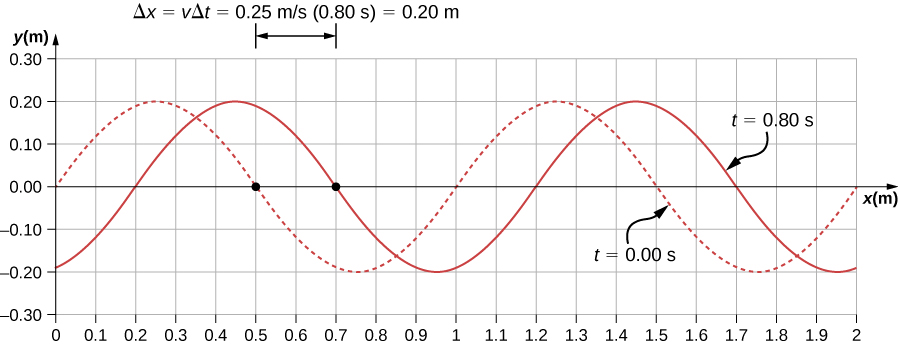
Hay una segunda velocidad en el movimiento. En este ejemplo, la onda es transversal, moviéndose horizontalmente a medida que el medio oscila hacia arriba y hacia abajo perpendicular a la dirección del movimiento. El gráfico en la muestra el movimiento del medio en el punto $x = 0.60 m$ en función del tiempo. Observa que el medio de la onda oscila hacia arriba y hacia abajo entre $y = + 0.20 m$ y $y = -0.20 m$ cada período de $4.0$ segundos.
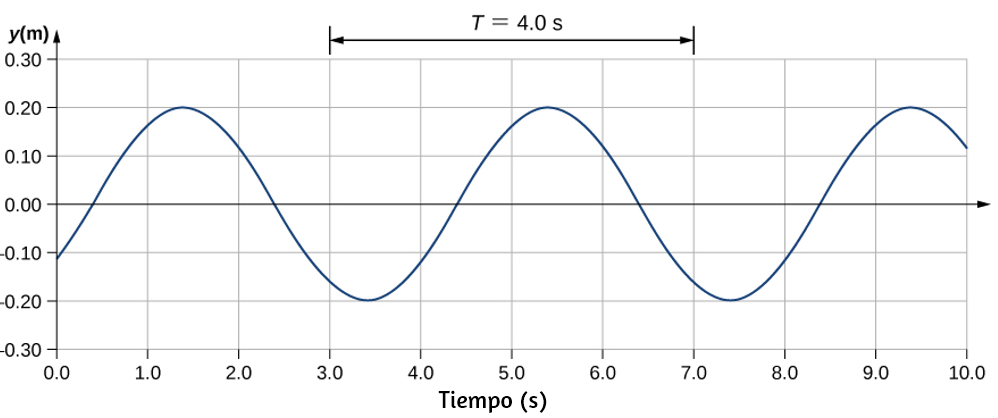
 Comprueba tu aprendizaje 6.3
Comprueba tu aprendizaje 6.3
Como se ve en el Ejemplo 6.4, la velocidad de la onda es constante y representa la velocidad de la onda a medida que se propaga a través del medio, no la velocidad de las partículas que forman el medio. Las partículas del medio oscilan alrededor de una posición de equilibrio a medida que la onda se propaga a través del medio. En el caso de la onda transversal que se propaga en la dirección $x$, las partículas oscilan hacia arriba y hacia abajo en la dirección $y$, perpendicular al movimiento de la onda. La velocidad de las partículas del medio no es constante, lo que significa que hay una aceleración. La velocidad del medio, que es perpendicular a la velocidad de la onda en una onda transversal, se puede encontrar tomando la derivada parcial de la ecuación de posición con respecto al tiempo. La derivada parcial se encuentra al tomar la derivada de la función, tratando todas las variables como constantes, excepto la variable en cuestión. En el caso de la derivada parcial con respecto al tiempo $t$, la posición $x$ se trata como una constante. Aunque esto puede sonar extraño si no lo has visto antes, el objetivo de este ejercicio es encontrar la velocidad transversal en un punto, por lo que en este sentido, la posición $x$ no está cambiando. Tenemos
$$y(x, t) = Asen(kx - ωt + φ)$$ $$v_y(x, t) = \frac{∂y(x, t)}{∂t} = \frac{∂}{∂t}(Asen(kx - ωt + φ))$$ $$v_y(x, t) = -Aωcos(kx - ωt + φ)$$ $$v_y(x, t) = -v_{y\textsf{ max}}cos(kx - ωt + φ)$$La magnitud de la aceleración máxima es $|a_{y\textsf{ max}}| = Aω^2$. Las partículas del medio, o los elementos de masa, oscilan en un movimiento armónico simple para una onda mecánica.
Acabamos de determinar la velocidad del medio en una posición $x$ tomando la derivada parcial, con respecto al tiempo, de la posición $y$. Para una onda transversal, esta velocidad es perpendicular a la dirección de propagación de la onda. Encontramos la aceleración al tomar la derivada parcial, con respecto al tiempo, de la velocidad, que es la segunda derivada del tiempo de la posición:
$$\begin{split} a_y(x, t) &= \frac{∂^2y(x, t)}{∂t^2} = \frac{∂^2}{∂t^2}(Asen(kx - ωt + φ)) \\ &= -Aω^2sen(kx - ωt + φ) \end{split}$$Ahora considera las derivadas parciales con respecto a la otra variable, la posición $x$, manteniendo como constante el tiempo. La primera derivada es la pendiente de la onda en un punto $x$ en un tiempo $t$, $$\begin{split} \textsf{pendiente} &= \frac{∂y(x, t)}{∂t} = \frac{∂}{∂t}(Asen(kx - ωt + φ)) \\ &= Akcos(kx - ωt + φ) \end{split}$$
La segunda derivada parcial expresa cómo cambia la pendiente de la onda con respecto a la posición; en otras palabras, la curvatura de la onda, donde $$\begin{split} \textsf{curvatura} &= \frac{∂^2y(x, t)}{∂x^2} = \frac{∂^2}{∂x^2}(Asen(kx - ωt + φ)) \\ &= -Ak^2sen(kx - ωt + φ) \end{split}$$
La relación de la aceleración y la curvatura conduce a una relación muy importante en la física conocida como la ecuación de onda lineal. Tomando la relación y usando la ecuación $v = ω/k$ se obtiene la ecuación de onda lineal (también conocida simplemente como la ecuación de onda o la ecuación de una cuerda vibrante),
La ecuación 6.6 es la ecuación de onda lineal, que es una de las ecuaciones más importantes en física e ingeniería. La derivamos aquí para una onda transversal, pero es igualmente importante cuando se investigan ondas longitudinales. Esta relación también se derivó utilizando una onda sinusoidal, pero describe con éxito cualquier onda o pulso que tenga la forma $y(x, t) = f(x ± vt)$. Estas ondas se producen debido a una fuerza de restauración lineal del medio, por lo tanto, el nombre de ecuación de onda lineal. Cualquier función de onda que satisfaga esta ecuación es una función de onda lineal.
Un aspecto interesante de la ecuación de onda lineal es que si dos funciones de onda son soluciones individuales a la ecuación de onda lineal, entonces la suma de las dos funciones de onda lineal es también una solución a la ecuación de onda. Considera dos ondas transversales que se propagan a lo largo del eje $x$, ocupando el mismo medio. Supongamos que las ondas individuales se pueden modelar con las funciones de onda $y_1(x, t) = f(x ± vt)$ e $y_2(x, t) = g(x ± vt)$, que son soluciones a las ecuaciones de onda lineales y son por lo tanto funciones de onda lineales. La suma de las funciones de onda es la función de onda.
Considera la ecuación de onda lineal:
$$\frac{∂^2(f + g)}{∂x^2} = \frac{1}{v^2}\frac{∂^2(f + g)}{∂t^2}$$ $$\frac{∂^2f}{∂x^2} + \frac{∂^2g}{∂x^2} = \frac{1}{v^2} \left(\frac{∂^2f}{∂t^2} + \frac{∂^2g}{∂t^2} \right)$$Esto ha demostrado que si se agregan algebraicamente dos funciones de onda lineales, la función de onda resultante también es lineal. Esta función de onda modela el desplazamiento del medio de la onda resultante en cada posición a lo largo del eje $x$. Si dos ondas lineales ocupan el mismo medio, se dice que interfieren. Si estas ondas se pueden modelar con una función de onda lineal, estas funciones de onda se suman para formar la ecuación de onda de la onda que resulta de la interferencia de las ondas individuales. El desplazamiento del medio en cada punto de la onda resultante es la suma algebraica de los desplazamientos debidos a las ondas individuales.
Llevando este análisis un paso más allá, si las funciones de onda $y_1(x, t) = f(x ± vt)$ e $y_2(x, t) = g(x ± vt)$ son soluciones a la ecuación de onda lineal, entonces $Ay_1(x, t) + By_2(x, y)$, donde $A$ y $B$ son constantes, también es una solución a la ecuación de onda lineal. Esta propiedad es conocida como el principio de superposición.
Ejemplo6.4
Interferencia de ondas en una cuerda
Considera una cuerda muy larga sostenida por dos estudiantes, uno en cada extremo. El estudiante $A$ oscila el final de la cadena produciendo una onda modelada con la función de onda $y_1(x, t) = Asin (kx - ωt)$ y el estudiante $B$ oscila la cadena produciendo el doble de frecuencia, moviéndose en la dirección opuesta. Ambas ondas se mueven a la misma velocidad $v = ω/k$. Las dos ondas interfieren para formar una onda resultante cuya función de onda es $y_{R1}(x, t) = y_1(x, t) + y_2(x, t)$. Encuentra la velocidad de la onda resultante usando la ecuación de onda lineal
Estrategia
Primero, escribe la función de onda para la onda creada por el segundo estudiante. Ten en cuenta que la frecuencia angular de la segunda onda es el doble de la frecuencia de la primera onda ($2ω$), y como la velocidad de las dos ondas es la misma, el número de onda de la segunda onda es el doble que la de la primera onda ($2k$). Luego, escribe la ecuación de onda para la función de onda resultante, que es la suma de las dos funciones de onda individuales. Luego encuentra la segunda derivada parcial con respecto a la posición y la segunda derivada parcial con respecto al tiempo. Usa la ecuación de onda lineal para encontrar la velocidad de la onda resultante.
Solución
1. Escribe la función de onda de la segunda onda: $y_1(x, t) = Asen (2kx + 2ωt)$.
2. Escribe la función de onda resultante:
$$y_R(x, t) = y_1(x, t) + y(x, t) = Asen(kx - ωt) + Asen(2kx + 2ωt)$$3. Halla las derivadas parciales:
$$\frac{∂y_R(x, t)}{∂x} = -Akcos(kx - ωt) + 2Akcos(2kx + 2ωt)$$ $$\frac{∂^2y_R(x, t)}{∂x^2} = -Ak^2sen(kx - ωt) - 4Ak^2sen(2kx + 2ωt)$$ $$\frac{∂y_R(x, t)}{∂t} = -Aωcos(kx - ωt) + 2Aωcos(2kx + 2ωt)$$ $$\frac{∂^2y_R(x, t)}{∂t^2} = -Aω^2sen(kx - ωt) - 4Aω^2sen(2kx + 2ωt)$$4. Usa la ecuación de onda para encontrar la velocidad de la onda resultante:
$$\frac{∂^2y(x, t)}{∂x^2} = \frac{1}{v^2}\frac{∂^2y(x, t)}{∂t^2}$$$-Ak^2sen(kx-ωt) - 4Ak^2sen(2kx+2ωt) = \dfrac{1}{v^2}(-Aω^2sen(kx-ωt) - 4Aω^2sen(2kx+2ωt))$
$k^2(-Asen(kx-ωt) - 4Asen(2kx+2ωt)) = \dfrac{ω^2}{v^2}(-Asen(kx-ωt) - 4Asen(2kx+2ωt))$
Explicación
La velocidad de la onda resultante es igual a la velocidad de las ondas originales ($v = ω/k$). Mostraremos en la siguiente sección que la velocidad de una onda armónica simple en una cuerda depende de la tensión en la cuerda y de la masa por longitud de la cuerda. Por esta razón, no es sorprendente que las ondas componentes, así como la onda resultante, viajen a la misma velocidad.
 Comprueba tu aprendizaje 6.4
Comprueba tu aprendizaje 6.4
Cualquier perturbación que cumpla con la ecuación de onda puede propagarse como una onda que se mueve a lo largo del eje $x$ con una velocidad de onda $v$. Funciona igualmente bien para ondas en una cuerda, ondas de sonido y ondas electromagnéticas. Esta ecuación es extremadamente útil. Por ejemplo, se puede usar para mostrar que las ondas electromagnéticas se mueven a la velocidad de la luz.
En la siguiente escena, diseñada por Andreu Glasmann, Wolfgang Christian y Mario Belloni, practica con el principio de superposición.
La velocidad de una onda depende de las características del medio. Por ejemplo, en el caso de una guitarra, las cuerdas vibran para producir el sonido. La velocidad de las ondas en las cuerdas y la longitud de onda determinan la frecuencia del sonido producido. Las cuerdas de una guitarra tienen diferentes grosores, pero pueden estar hechas de material similar. Tienen diferentes densidades lineales, donde la densidad lineal se define como la masa por longitud,
En este capítulo, consideramos solo una cuerda con una densidad lineal constante. Si la densidad lineal es constante, entonces la masa ($Δm$) de una pequeña cuerda ($Δx$) es $Δm = μΔx$. Por ejemplo, si la cuerda tiene una longitud de $2.00 m$ y una masa de $0.06 kg$, entonces la densidad lineal es $μ = \frac{0.06 kg}{2.00 m} = 0.03 \frac{kg}{m}$. Si se corta una sección de $1.00 mm$ de la cuerda, la masa de la longitud de $1.00 mm$ es $Δm = μΔx = (0.03 \frac{kg}{m}) 0.001 m = 3.00 × 10^{-5} kg$. La guitarra también tiene un método para cambiar la tensión de las cuerdas. La tensión de las cuerdas se ajusta girando los husillos, llamados clavijas de afinación, alrededor de las cuales se envuelven las cuerdas. Para la guitarra, la densidad lineal de la cuerda y la tensión en la cuerda determinan la velocidad de las ondas en la cuerda y la frecuencia del sonido producido es proporcional a la velocidad de la onda.
Para ver cómo la velocidad de una onda en una cuerda depende de la tensión y la densidad lineal, considera un pulso enviado por una cuerda tensa (). Cuando la cuerda tensa está en reposo en la posición de equilibrio, la tensión en la cuerda $F_T$ es constante. Considera un pequeño elemento de la cuerda con una masa igual a $Δm = μΔx$. El elemento de masa está en reposo y en equilibrio, y la fuerza de tensión de cada lado del elemento de masa es igual y opuesta.
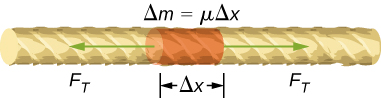
Si pulsa una cuerda bajo tensión, una onda transversal se mueve en la dirección $x$ positiva, como se muestra en la . El elemento de masa es pequeño pero se amplía en la figura para hacerlo visible. El pequeño elemento de masa oscila perpendicularmente al movimiento de la onda como resultado de la fuerza restauradora proporcionada por la cuerda y no se mueve en la dirección $x$. La tensión $F_T$ en la cuerda, que actúa en la dirección $x$ positiva y negativa, es aproximadamente constante y es independiente de la posición y el tiempo.
Supongamos que la inclinación de la cuerda desplazada con respecto al eje horizontal es pequeña. La fuerza neta sobre el elemento de la cuerda, que actúa paralela a la cuerda, es la suma de la tensión en la cuerda y la fuerza de restauración.
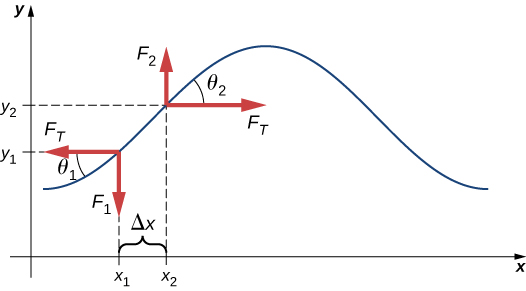
La componente $x$ de la fuerza de tensión se cancelan, por lo que la fuerza neta es igual a la suma de las componentes $y$ de la fuerza. La magnitud de la componente $x$ de la fuerza es igual a la fuerza horizontal de tensión de la cuerda $F_T$ como se muestra en la . Para obtener la componente $y$ de la fuerza, ten en cuenta que $tanθ_1 = \frac{-F_1}{F_T} y tanθ_2 = \frac{F_2}{F_T}$. El valor de $tanθ$ es igual a la pendiente de una función en un punto, que es igual a la derivada parcial de $y$ con respecto a $x$ en ese punto. Por lo tanto, $\frac{F_1}{F_T}$ es igual a la pendiente negativa de la cuerda en $x_1$ y $\frac{F_2}{F_T}$ es igual a la pendiente de la cuerda en $x_2$:
$$\frac{F_1}{F_t} = - \left( \frac{∂y}{∂x} \right)_{x_1} \;\; \textsf{y} \;\; \frac{F_2}{F_t} = - \left( \frac{∂y}{∂x} \right)_{x_2}$$La fuerza neta en el pequeño elemento, puede escribirse como:
$$F_{\textsf{net}} = F_1 + F_2 = F_T \left[ \left( \frac{∂y}{∂x} \right)_{x_2} - \left( \frac{∂y}{∂x} \right)_{x_1} \right]$$Usando la segunda ley de Newton, la fuerza neta es igual a la masa multiplicada por la aceleración. La densidad lineal de la cuerda μ es la masa por longitud de la cuerda, y la masa de la porción de la cuerda es $μΔx$,
$$F_T \left[ \left( \frac{∂y}{∂x} \right)_{x_2} - \left( \frac{∂y}{∂x} \right)_{x_1} \right] = Δma,$$ $$F_T \left[ \left( \frac{∂y}{∂x} \right)_{x_2} - \left( \frac{∂y}{∂x} \right)_{x_1} \right] = μΔx\frac{∂^2y}{∂t^2},$$Dividiendo por $F_TΔx$ y tomando el límite cuando $Δx$ se acerca a cero,
$$\frac{\left[ \left( \dfrac{∂y}{∂x} \right)_{x_2} - \left( \dfrac{∂y}{∂x} \right)_{x_1} \right]}{Δx} = \frac{μ}{F_T} \frac{∂^2y}{∂t^2}$$ $$\lim_{Δx \to 0} \frac{\left[ \left( \dfrac{∂y}{∂x} \right)_{x_2} - \left( \dfrac{∂y}{∂x} \right)_{x_1} \right]}{Δx} = \frac{μ}{F_T} \frac{∂^2y}{∂t^2}$$ $$\frac{∂^2y}{∂x^2} = \frac{μ}{F_T}\frac{∂^2y}{∂t^2}$$Recordemos que la ecuación de onda lineal es
Por lo tanto,
Resolviendo para $v$, vemos que la velocidad de la onda en una cuerda depende de la tensión y la densidad lineal.
Velocidad de una onda en una cuerda bajo tensión
La velocidad de un pulso u onda en una cuerda bajo tensión se puede encontrar con la ecuación
$$|v| = \sqrt{F_T}{μ} \tag{6.8}$$donde $F_T$ es la tensión en la cuerda y $μ$ es la masa por longitud de la cuerda.
Ejemplo 6.5
La velocidad de onda de un muelle de guitarra
En una guitarra de seis cuerdas, la cuerda alta $E$ tiene una densidad lineal de $μ_{\textsf{alta E}} = 3.09 × 10^{-4} kg / m$ y la cuerda baja $E$ tiene una densidad lineal de $μ_{\textsf{baja E}} = 5.78 × 10^{-3} kg / m$. (a) Si se tira de la cuerda alta $E$, produciendo una onda en la cuerda, ¿cuál es la velocidad de la onda si la tensión de la cuerda es $56.40 N$? (b) La densidad lineal de la cadena $E$ baja es aproximadamente $20$ veces mayor que la de la cadena $E$ alta. Para que las ondas viajen a través de la cadena $E$ baja a la misma velocidad de onda que la $E$ alta, ¿la tensión debería ser mayor o menor que la cadena $E$ alta? ¿Cuál sería la tensión aproximada? (c) Calcula la tensión de la cuerda $E$ baja necesaria para la misma velocidad de onda.
Estrategia
a. La velocidad de la onda se puede encontrar a partir de la densidad lineal y la tensión $\sqrt{F_T/μ}$
b. De la ecuación $\sqrt{F_T/μ}$, si la densidad lineal aumenta en un factor de casi $20$, la tensión debería aumentarse en un factor de $20$.
c. Conociendo la velocidad y la densidad lineal, la ecuación de velocidad se puede resolver para la fuerza de tensión $F_T = μv^2$.
Solución
a. Usa la ecuación de velocidad para encontrar la velocidad:
$$v = \sqrt{\frac{F_T}{μ}} = \sqrt{\frac{56.40N}{3.09 \times 10^{-4} kg/m}} = 427.23 m/s$$b. La tensión tendría que aumentarse en un factor de aproximadamente $20$. La tensión sería ligeramente menor que $1128 N$.
c. Usa la ecuación de velocidad para encontrar la tensión real:
$$F_T = μv^2 = 5.78×10^{-3} kg/m(427.23 m/s)^2 = 1055.00 N$$Esta solución está dentro del $7$% de la aproximación.
Explicación
Las notas estándar de las seis cuerdas ($E$ alta, $B$, $G$, $D$, $A$, $E$ baja) están sintonizadas para vibrar en las frecuencias fundamentales $(329.63 Hz$, $246.94Hz$, $196.00Hz$, $146.83Hz$, $110.00Hz$ y $82.41Hz$) cuando se pulsan. Las frecuencias dependen de la velocidad de las ondas en la cuerda y la longitud de onda. Las seis cuerdas tienen diferentes densidades lineales y se "sintonizan" al cambiar las tensiones en las cuerdas. Veremos, más adelante, que la longitud de onda depende de la longitud de las cuerdas y las condiciones de los límites. Para tocar otras notas que no sean las fundamentales, las longitudes de las cuerdas se cambian presionando las cuerdas.
 Comprueba tu aprendizaje 6.5
Comprueba tu aprendizaje 6.5
La velocidad de una onda en una cuerda depende de la raíz cuadrada de la tensión dividida por la masa por longitud, la densidad lineal. En general, la velocidad de una onda a través de un medio depende de la propiedad elástica del medio y de la propiedad inercial del medio.
$$|v| = \sqrt{\frac{\textsf{propiedad elástica}}{\textsf{propiedad inercial}}}$$La propiedad elástica describe la tendencia de las partículas del medio a volver a su posición inicial cuando están perturbadas. La propiedad inercial describe la tendencia de la partícula a resistir los cambios en la velocidad. La velocidad de una onda longitudinal a través de un líquido o gas depende de la densidad del fluido y del módulo de volumen del fluido,
Aquí el módulo de volumen se define como $B = -\frac{ΔP}{Δv/v_0}$, donde $ΔP$ es el cambio en la presión y el denominador es la relación entre el cambio en el volumen y el volumen inicial, y $ρ ≡ mV$ es la masa por unidad de volumen. Por ejemplo, el sonido es una onda mecánica que viaja a través de un fluido o un sólido. La velocidad del sonido en el aire con una presión atmosférica de $1.013 × 10^5 Pa$ y una temperatura de $20°C$ es de $≈ 343.00 m/s$. Debido a que la densidad depende de la temperatura, la velocidad del sonido en el aire depende de la temperatura del aire.
Todas las ondas transportan energía, y algunas veces esto se puede observar directamente. Los terremotos pueden tirar ciudades enteras al suelo, realizando el trabajo de miles de bolas de demolición (). Los sonidos fuertes pueden pulverizar las células nerviosas en el oído interno, causando pérdida de audición permanente. El ultrasonido se utiliza para el tratamiento de las distensiones musculares con calor. Un rayo láser puede quemar una malignidad. Las olas del agua estropean las playas.
En esta sección, examinamos la expresión cuantitativa de la energía en ondas. Esto será de fundamental importancia en las discusiones posteriores sobre las ondas, desde el sonido a la luz hasta la mecánica cuántica.
La cantidad de energía en una onda está relacionada con su amplitud y su frecuencia. Los terremotos de gran amplitud producen grandes desplazamientos del terreno. Los sonidos fuertes tienen amplitudes de alta presión y provienen de vibraciones de una fuente de mayor amplitud que los sonidos suaves. Los grandes rompeolas rompen la orilla más que los pequeños.

Considera el ejemplo de la gaviota y la ola de agua al principio del capítulo (). El trabajo se realiza en la gaviota por la ola a medida que la gaviota se mueve hacia arriba, cambiando su energía potencial. Cuanto mayor sea la amplitud, mayor será la elevación de la gaviota por la ola y mayor será el cambio en la energía potencial.
La energía de la onda depende tanto de la amplitud como de la frecuencia. Si se considera que la energía de cada longitud de onda es un paquete discreto de energía, una onda de alta frecuencia entregará más de estos paquetes por unidad de tiempo que una onda de baja frecuencia.
Veremos que la tasa promedio de transferencia de energía en ondas mecánicas es proporcional tanto al cuadrado de la amplitud como al cuadrado de la frecuencia. Si dos ondas mecánicas tienen amplitudes iguales, pero una onda tiene una frecuencia igual a dos veces la frecuencia de la otra, la onda de mayor frecuencia tendrá una tasa de transferencia de energía un factor cuatro veces mayor que la tasa de transferencia de energía del onda de baja frecuencia. Cabe señalar que aunque la tasa de transporte de energía es proporcional tanto al cuadrado de la amplitud como al cuadrado de la frecuencia en ondas mecánicas, la tasa de transferencia de energía en las ondas electromagnéticas es proporcional al cuadrado de la amplitud, pero independiente de la frecuencia.

Considera una onda sinusoidal en una cuerda producida por un vibrador de cuerdas, como se muestra en la . A medida que la energía se propaga a lo largo de la cuerda, cada elemento de masa de la cuerda se mueve hacia arriba y hacia abajo a la misma frecuencia que la onda. Cada elemento de masa de la cuerda puede modelarse como un simple oscilador armónico. Como la cadena tiene una densidad lineal constante $μ = \frac{Δm}{Δx}$, cada elemento de masa de la cadena tiene la masa $Δm = μΔx$.
La energía mecánica total de la onda es la suma de su energía cinética y energía potencial. La energía cinética $K = \frac{1}{2}mv^2$ de cada elemento de masa de la cadena de longitud $Δx$ es $ΔK = \frac{1}{2}(Δm)v_y^2$, ya que el elemento de masa oscila perpendicularmente a la dirección del movimiento de la onda. Usando la densidad de masa lineal constante, la energía cinética de cada elemento de masa de la cuerda con longitud $Δx$ es
$$ΔK = \frac{1}{2}(μΔx)v_y^2$$Se puede formar una ecuación diferencial al permitir que la longitud del elemento de masa de la cuerda se aproxime a cero,
$$dK = \lim_{Δx \to 0} \frac{1}{2}(μΔx)v_y^2 = \frac{1}{2}(μdx)v_y^2$$Dado que la onda es una onda sinusoidal con una frecuencia angular $ω$, la posición de cada elemento de masa se puede modelar como $y(x, t) = Asen(kx - ωt)$. Cada elemento de masa de la cuerda oscila con una velocidad $v_y = \frac{∂y(x, t)}{∂t} = -Aωcos(kx - ωt)$. La energía cinética de cada elemento de masa de la cuerda se convierte en
$$dK = \frac{1}{2}(μdx)(-Aωcos(kx - ωt))^2$$ $$dK = \frac{1}{2}(μdx)A^2ω^2cos^2(kx - ωt)$$La onda puede ser muy larga, consistente en muchas longitudes de onda. Para estandarizar la energía, considera la energía cinética asociada con una longitud de onda de la onda. Esta energía cinética se puede integrar en la longitud de onda para encontrar la energía asociada con cada longitud de onda:
$$dK = \frac{1}{2}(μdx) A^2 ω^2 cos^2 (kx),$$ $$\int_0^{Kλ} dK = \int_0^λ \frac{1}{2} μ A^2 ω^2 cos^2 (kx)dx = \frac{1}{2} μ A^2 ω^2 \int_0^λ cos^2 (kx)dx,$$También hay energía potencial asociada a la onda. Al igual que la masa que oscila en un resorte, hay una fuerza restauradora conservadora que, cuando el elemento de masa se desplaza de la posición de equilibrio, hace que el elemento de masa regrese a la posición de equilibrio. La energía potencial del elemento de masa se puede encontrar considerando la fuerza de restauración lineal de la cuerda, En el capítulo anterior, vimos que la energía potencial almacenada en un resorte con una fuerza de restauración lineal es igual a $U = (1/2)k_sx^2$, donde la posición de equilibrio es definido como $x = 0.00 m$. Cuando una masa unida al resorte oscila en un movimiento armónico simple, la frecuencia angular es igual a $ω = \sqrt{k_s/m}$. Como cada elemento de masa oscila en un movimiento armónico simple, la constante del resorte es igual a $k_s = Δmω^2$. La energía potencial del elemento masa es igual a
$$ΔU = \frac{1}{2}k_sx^2 = \frac{1}{2}Δmω^2x^2$$Ten en cuenta que $k_s$ es la constante de resorte y no el número de onda $k = 2π/λ$. Esta ecuación se puede usar para encontrar la energía en una longitud de onda. Al integrar en la longitud de onda, podemos calcular la energía potencial en una longitud de onda:
$$dU = \frac{1}{2} k_s x^2 = \frac{1}{2} μω^2x^2dx,$$ $$U_λ = \frac{1}{2} μω^2 A^2 \int_0^λ cos^2 (kx)dx = \frac{1}{4} μ A^2 ω^2 λ$$La energía potencial asociada con una longitud de onda es igual a la energía cinética asociada con una longitud de onda.
La energía total asociada con una longitud de onda es la suma de la energía potencial y la energía cinética:
$$E_λ = U_{λ} + K_{λ},$$ $$E_{λ} = \frac{1}{4}μA^2ω^2λ + \frac{1}{2}μA^4ω^2λ = \frac{1}{2}μA^2ω^2λ$$La potencia promediada en el tiempo de una onda mecánica sinusoidal, que es la tasa promedio de transferencia de energía asociada con una onda a medida que pasa un punto, se puede encontrar al tomar la energía total asociada a la onda dividida por el tiempo que se tarda en transferir la energía. Si la velocidad de la onda sinusoidal es constante, el tiempo para que una longitud de onda pase por un punto es igual al período de la onda, que también es constante. Para una onda mecánica sinusoidal, la potencia promediada en el tiempo es, por lo tanto, la energía asociada con una longitud de onda dividida por el período de la onda. La longitud de onda de la onda dividida por el período es igual a la velocidad de la onda,
Observa que esta ecuación para la potencia promediada en el tiempo de una onda mecánica sinusoidal muestra que la potencia es proporcional al cuadrado de la amplitud de la onda y al cuadrado de la frecuencia angular de la onda. Recuerda que la frecuencia angular es igual a $ω = 2πf$, por lo que la potencia de una onda mecánica es igual al cuadrado de la amplitud y al cuadrado de la frecuencia de la onda.
Ejemplo 6.6
Potencia suministrada por un vibrador de cuerdas
Considera una cuerda de dos metros de largo con una masa de $70.00 g$ unida a un vibrador de cuerda como se ilustra en la . La tensión en la cuerda es de $90.0 N$. Cuando el vibrador de cuerda se enciende, oscila con una frecuencia de $60 Hz$ y produce una onda sinusoidal en la cuerda con una amplitud de $4.00 cm$ y una velocidad de onda constante ¿Cuál es la potencia promediada en el tiempo suministrada a la onda por el vibrador de cuerda?
Estrategia
La potencia suministrada a la onda debe ser igual a la potencia promediada en el tiempo de la onda en la cuerda. Sabemos la masa de la cuerda ($m_s$), la longitud de la cuerda ($L_s$) y la tensión ($F_T$) en la cuerda. La velocidad de la onda en la cuerda se puede derivar de la densidad de masa lineal y la tensión. La cuerda oscila con la misma frecuencia que el vibrador de cuerdas, desde donde podemos encontrar la frecuencia angular.
Solución
1. Comienza con la ecuación de la potencia promediada en el tiempo de una onda sinusoidal en una cuerda:
$$P = \frac{1}{2}μA^2ω^2v$$La amplitud está dada, por lo que necesitamos calcular la densidad de masa lineal de la cuerda, la frecuencia angular de la onda en la cuerda y la velocidad de la onda en la cuerda.
2. Necesitamos calcular la densidad lineal para encontrar la velocidad de onda:
$$μ = \frac{m_s}{L_s} = \frac{0.070 kg}{2.00 m} = 0.035 kg/m$$3. La velocidad de onda se puede encontrar utilizando la densidad de masa lineal y la tensión de la cuerda:
$$v = \sqrt{\frac{F_T}{μ}} = \sqrt{\frac{90.0 N}{0.035 kg/m}} = 50.71 m/s$$4. La frecuencia angular se puede encontrar a partir de la frecuencia:
$$ω = 2πf = 2π(60 s^{-1}) = 376.80 s^{-1}$$5. Calcula la potencia promediada en el tiempo:
$$\begin{split} P &= \frac{1}{2}μA^2ω^2v = 12(0.035 kg/m)(0.040 m)^2(376.80 s^{-1})^2(50.71 m/s) \\ &= 201.59 W \end{split}$$Explicación
La potencia promediada en el tiempo de una onda sinusoidal es proporcional al cuadrado de la amplitud de la onda y al cuadrado de la frecuencia angular de la onda. Esto es cierto para la mayoría de las ondas mecánicas. Si la frecuencia angular o la amplitud de la onda se duplicaran, la potencia aumentaría en un factor de cuatro. La potencia promediada en el tiempo de la onda en una cuerda también es proporcional a la velocidad de la onda sinusoidal en la cuerda. Si la velocidad se duplicara, al aumentar la tensión en un factor de cuatro, la potencia también se duplicaría.
 Comprueba tu aprendizaje 6.6
Comprueba tu aprendizaje 6.6
Las ecuaciones para la energía de la onda y la potencia promediada en el tiempo se derivaron para una onda sinusoidal en una cuerda. En general, la energía de una onda mecánica y la potencia son proporcionales a la amplitud al cuadrado y a la frecuencia angular al cuadrado (y, por lo tanto, a la frecuencia al cuadrado).
Otra característica importante de las ondas es la intensidad de las ondas. Las ondas también se pueden concentrar o extender. Las ondas de un terremoto, por ejemplo, se extienden sobre un área más grande a medida que se alejan de una fuente, por lo que causan menos daño cuanto más se alejan de la fuente. Cambiar el área que cubren las ondas tiene efectos importantes. Todos estos factores pertinentes se incluyen en la definición de intensidad ($I$) como potencia por unidad de área:
donde $P$ es la potencia transportada por la onda a través del área $A$. La definición de intensidad es válida para cualquier energía en tránsito, incluida la transportada por ondas. La unidad del SI para intensidad es vatios por metro cuadrado ($W/m^2$). Muchas ondas son ondas esféricas que salen de una fuente como una esfera.
Por ejemplo, un altavoz de sonido montado en un poste sobre el suelo puede producir ondas de sonido que se alejan de la fuente como una onda esférica. Las ondas de sonido se discuten con más detalle en el siguiente capítulo, pero en general, cuanto más lejos estés del hablante, menos intenso será el sonido que escuche. A medida que una onda esférica sale de una fuente, el área de superficie de la onda aumenta a medida que aumenta el radio ($A = 4πr^2$). La intensidad para una onda esférica es por lo tanto
Si no hay fuerzas disipativas, la energía permanecerá constante a medida que la onda esférica se aleja de la fuente, pero la intensidad disminuirá a medida que aumenta el área de la superficie.
En el caso de la onda circular bidimensional, la onda se mueve hacia afuera, aumentando la circunferencia de la onda a medida que aumenta el radio del círculo. Si arrojas una piedra en un estanque, la ondulación de la superficie se mueve como una onda circular. A medida que la onda se aleja de la fuente, la amplitud disminuye. La energía de la onda se extiende alrededor de una circunferencia más grande y la amplitud disminuye proporcionalmente a $\frac{1}{r}$, que también es igual en el caso de una onda esférica, ya que la intensidad es proporcional a la amplitud al cuadrado.
En la siguiente escena interactiva, diseñada para las simulaciones Phet, podrás hacer ondas circulares con un grifo que gotea, con paralantes o con un láser. Puedes ver las ondas de agua, sonido y luz moverse y ver cómo se relacionan. Todas pueden ser representadas por una onda circular o sinusoidal. También puedes generar interferencias, como preludio al siguiente apartado.
Retomaremos esta escena en otros apartados, dada la variedad de prácticas que incorpora, útiles para contrastar la teoría ondulatoria.
Hasta ahora, hemos estado estudiando ondas mecánicas que se propagan continuamente a través de un medio, pero no hemos discutido qué sucede cuando las ondas encuentran el límite del medio o qué sucede cuando una onda encuentra otra onda que se propaga a través del mismo medio. Las ondas interactúan con los límites del medio, y toda o parte de la onda puede reflejarse. Por ejemplo, cuando te paras a cierta distancia de un acantilado rígido y gritas, puedes escuchar las ondas de sonido reflejadas en la superficie rígida como un eco. Las ondas también pueden interactuar con otras ondas que se propagan en el mismo medio.
Si arrojas dos rocas en un estanque a cierta distancia entre sí, las ondulaciones circulares que resultan de las dos piedras parecen pasar una a la otra a medida que se propagan desde donde las piedras entraron en el agua o, usando la escena interactiva anterior, seleccionar dos fuentes y observar el fenómeno que se genera. Este fenómeno se conoce como interferencia. En esta sección, examinamos qué sucede con las ondas que se encuentran con el límite de un medio u otra onda que se propaga en el mismo medio. Veremos que su comportamiento es bastante diferente del comportamiento de las partículas y los cuerpos rígidos. Más adelante, cuando estudiemos la física moderna, veremos que solo en la escala de los átomos vemos similitudes en las propiedades de las ondas y las partículas.
Cuando una onda se propaga a través de un medio, se refleja cuando se encuentra con el límite del medio. La ola antes de golpear el límite se conoce como la onda incidente. La onda después de encontrar el límite se conoce como la onda reflejada. La forma en que se refleja la onda en el límite del medio depende de las condiciones del límite; las ondas reaccionarán de manera diferente si el límite del medio se fija en su lugar o se puede mover libremente (). Existe una condición de límite fijo cuando el medio en un límite se fija en su lugar por lo que no se puede mover. Existe una condición de límite libre cuando el medio en el límite se puede mover libremente.
La parte (a) de la muestra una condición de límite fijo. Aquí, un extremo de la cuerda se fija a una pared, de modo que el final de la cuerda se fija en su lugar y el medio (la cuerda) en el límite no se puede mover. Cuando la onda se refleja, la amplitud de la forma reflejada es exactamente la misma que la amplitud de la onda incidente, pero la onda reflejada se refleja $180°$ ($π \; rad$) fuera de fase con respecto a la onda incidente.
El cambio de fase se puede explicar usando la tercera ley de Newton: recuerda que esta ley establece que cuando el objeto $A$ ejerce una fuerza sobre el objeto $B$, entonces el objeto $B$ ejerce una fuerza opuesta e igual sobre el objeto $A$. Cuando la onda incidente se encuentra con la pared, la cuerda ejerce una fuerza hacia arriba en la pared y la pared reacciona ejerciendo una fuerza igual y opuesta en la cuerda. La reflexión en un límite fijo se invierte. Ten en cuenta que la figura muestra una cresta de la onda incidente reflejada como un canal. Si la onda incidente fuera un canal, la onda reflejada sería una cresta.
La parte (b) de la figura muestra una condición de contorno libre. Aquí, un extremo de la cuerda está atado a un anillo sólido de masa despreciable en un polo sin fricción, por lo que el extremo de la cuerda queda libre para moverse hacia arriba y hacia abajo. A medida que la onda incidente se encuentra con el límite del medio, también se refleja. En el caso de una condición de contorno libre, la onda reflejada está en fase con respecto a la onda incidente. En este caso, la onda encuentra el límite libre aplicando una fuerza hacia arriba en el anillo, acelerando el anillo hacia arriba. El anillo viaja hasta la altura máxima igual a la amplitud de la onda y luego acelera hacia la posición de equilibrio debido a la tensión en la cuerda. La figura muestra la cresta de una onda incidente que se refleja en la fase con respecto a la onda incidente como una cresta. Si la onda incidente fuera un canal, la onda reflejada también sería un canal. La amplitud de la onda reflejada sería igual a la amplitud de la onda incidente.
En algunas situaciones, el límite del medio no es fijo ni libre. Considera la (a), donde una cuerda de baja densidad de masa lineal está unida a una cuerda de mayor densidad de masa lineal. En este caso, la onda reflejada está fuera de fase con respecto a la onda incidente. También hay una onda transmitida que está en fase con respecto a la onda incidente. Tanto la onda incidente como la reflejada tienen amplitudes menores que la amplitud de la onda incidente. Si la tensión es la misma en ambas cuerdas, la velocidad de la onda es mayor en la cuerda con la densidad de masa lineal más baja.
La parte (b) de la figura muestra que una cuerda de alta densidad de masa lineal está unida a una cuerda de una densidad lineal más baja. En este caso, la onda reflejada está en fase con respecto a la onda incidente. También hay una onda transmitida que está en fase con respecto a la onda incidente. Tanto la onda incidente como la reflejada tienen amplitudes menores que la amplitud de la onda incidente.
Aquí puedes observar que si la tensión es la misma en ambas cuerdas, la velocidad de la onda es mayor en la cuerda con la densidad de masa lineal más baja.
La mayoría de las ondas no parecen muy simples. Las ondas complejas son más interesantes, incluso hermosas, pero parecen formidables. Las ondas mecánicas más interesantes consisten en una combinación de dos o más ondas viajeras que se propagan en el mismo medio. El principio de superposición se puede utilizar para analizar la combinación de ondas.
Considera dos pulsos simples de la misma amplitud que se mueven uno hacia el otro en el mismo medio, como se muestra en la . Eventualmente, las ondas se superponen, produciendo una onda que tiene el doble de amplitud, y luego continúan sin verse afectadas por el encuentro. Se dice que los pulsos interfieren, y este fenómeno se conoce como interferencia.
Para analizar la interferencia de dos o más ondas, utilizamos el principio de superposición. Para las ondas mecánicas, el principio de superposición establece que si dos o más ondas viajeras se combinan en el mismo punto, la posición resultante del elemento de masa del medio, en ese punto, es la suma algebraica de la posición debida a las ondas individuales. Esta propiedad es exhibida por muchas ondas observadas, tales como ondas en una cuerda, ondas de sonido y ondas de agua de una superficie. Las ondas electromagnéticas también obedecen al principio de superposición, pero los campos eléctrico y magnético de la onda combinada se agregan en lugar del desplazamiento del medio. Las ondas que obedecen al principio de superposición son ondas lineales; Las ondas que no obedecen al principio de superposición se denominan ondas no lineales.
El principio de superposición se puede entender considerando la ecuación de onda lineal. En Matemáticas de una onda, definimos una onda lineal como una onda cuya representación matemática obedece a la ecuación de onda lineal. Para una onda transversal en una cuerda con una fuerza de restauración elástica, la ecuación de onda lineal es
$$\frac{∂^2y(x, t)}{∂x^2} = \frac{1}{v^2}\frac{∂^2y(x, t)}{part;t^2}$$
Cualquier función de onda $y(x, t) = y(x ± vt)$, donde el argumento de la función es lineal ($x ± vt$) es una solución a la ecuación de onda lineal y es una función de onda lineal. Si las funciones de onda $y_1(x, t)$ y $y_2(x, t)$ son soluciones a la ecuación de onda lineal, la suma de las dos funciones $y_1(x, t) + y_2(x, t)$ también es una solución a la ecuación lineal de onda. Las ondas mecánicas que obedecen a la superposición están normalmente restringidas a ondas con amplitudes que son pequeñas con respecto a sus longitudes de onda. Si la amplitud es demasiado grande, el medio se distorsiona más allá de la región donde la fuerza restauradora del medio es lineal.
Las ondas pueden interferir constructiva o destructivamente. La muestra dos ondas sinusoidales idénticas que llegan al mismo punto exactamente en fase. La (a) y (b) muestra las dos ondas individuales, la parte (c) muestra la onda resultante que resulta de la suma algebraica de las dos ondas lineales. Las crestas de las dos ondas están alineadas con precisión, al igual que los canales. Esta superposición produce interferencia constructiva. Debido a que las perturbaciones se suman, la interferencia constructiva produce una onda que tiene el doble de amplitud que las ondas individuales, pero tiene la misma longitud de onda.
La muestra dos ondas idénticas que llegan exactamente $180°$ fuera de fase, lo que produce interferencia destructiva. La (a) y (b) muestra las ondas individuales, y la parte (c) muestra la superposición de las dos ondas. Debido a que los canales de una onda agregan la cresta de la otra onda, la amplitud resultante es cero para la interferencia destructiva: las ondas se cancelan por completo.
Posterior a las dos gráficas (6.20 y 6.21), presentamos una escena interactiva diseñada por Loo Kang y Wolfgang Christian, en la cual puedes practicar con un modelo de superposición de dos ondas. El modelo muestra cómo el principio de superposición da lugar a fenómenos de onda, como las ondas estacionarias y los latidos. Puedes ingresar funciones de onda de valor real y observar tanto las funciones dependientes del tiempo como su superposición. Con la configuración inicial, con sólo hacer clic en el botón de reproducción, podrás recrear las gráficas 6.20 y 6.21.
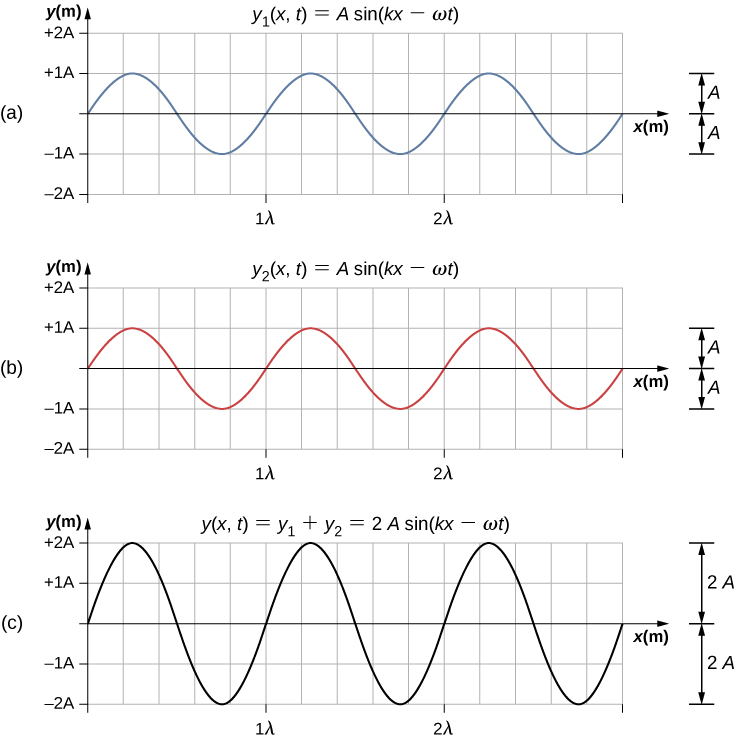
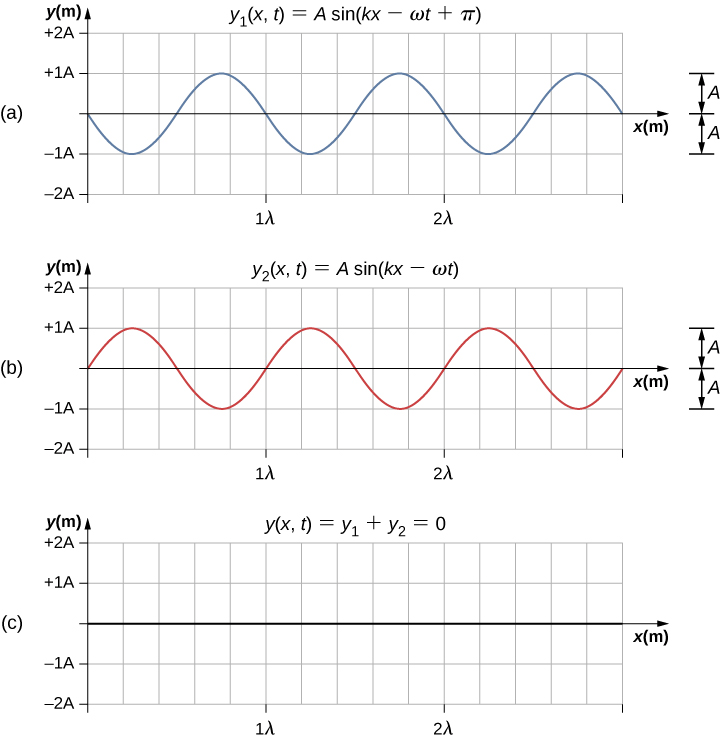
Cuando las ondas lineales interfieren, la onda resultante es solo la suma algebraica de las ondas individuales como se establece en el principio de superposición. La muestra dos ondas (roja y azul) y la onda resultante (negra). La onda resultante es la suma algebraica de las dos ondas individuales.
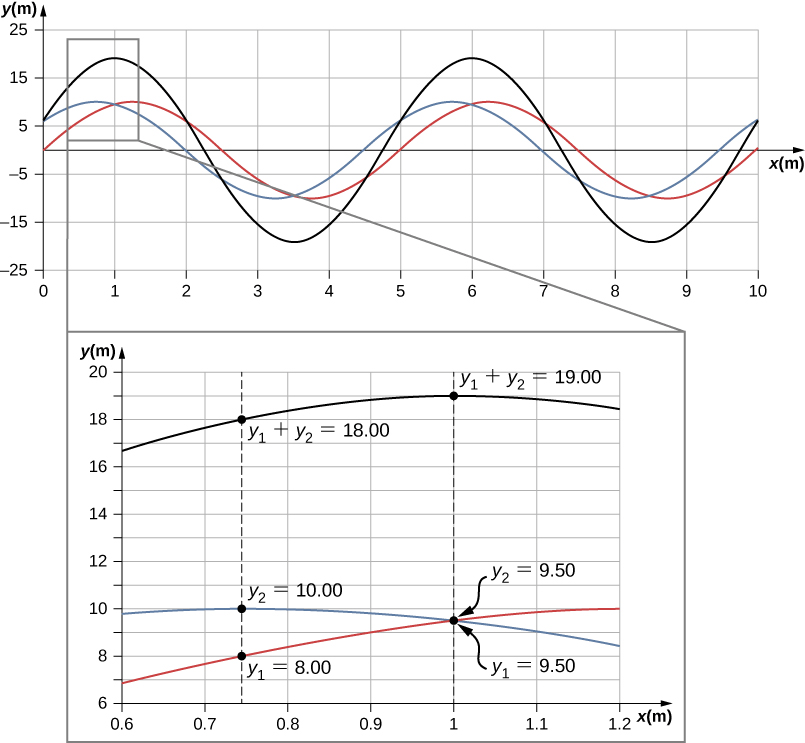
La superposición de la mayoría de las ondas produce una combinación de interferencia constructiva y destructiva, y puede variar de un lugar a otro y de un momento a otro. El sonido de un estéreo, por ejemplo, puede ser alto en un lugar y tranquilo en otro. La intensidad de sonido variable significa que las ondas de sonido se agregan parcialmente de manera constructiva y parcialmente destructiva en diferentes ubicaciones. Un estéreo tiene al menos dos altavoces que crean ondas de sonido, y las ondas pueden reflejarse desde las paredes. Todas estas ondas interfieren, y la onda resultante es la superposición de las ondas.
Hemos mostrado varios ejemplos de la superposición de ondas que son similares. La ilustra un ejemplo de la superposición de dos ondas diferentes. Aquí nuevamente, las perturbaciones se suman, produciendo una onda resultante.
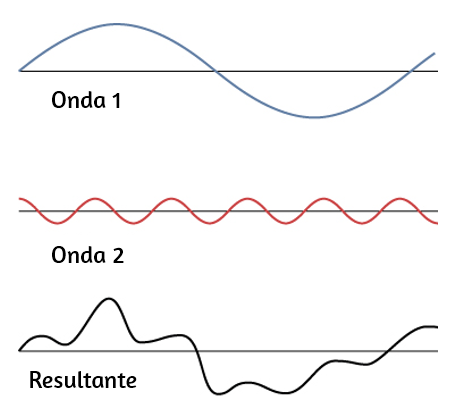
A veces, cuando dos o más ondas mecánicas interfieren, el patrón producido por la onda resultante puede ser rico en complejidad, algunos sin ningún patrón fácilmente discernible. Por ejemplo, trazar la onda de sonido de tu música favorita puede parecer bastante complejo y es la superposición de las ondas de sonido individuales de muchos instrumentos; es la complejidad lo que hace que la música sea interesante y valga la pena escucharla. En otras ocasiones, las ondas pueden interferir y producir fenómenos interesantes, que son complejos en su apariencia y, sin embargo, hermosos en la simplicidad del principio físico de superposición, que formó la onda resultante. Un ejemplo es el fenómeno conocido como ondas estacionarias, producido por dos ondas idénticas que se mueven en diferentes direcciones. Veremos más de cerca este fenómeno en la siguiente sección.
Muchos ejemplos en física consisten en dos ondas sinusoidales que son idénticas en amplitud, número de onda y frecuencia angular, pero difieren en un cambio de fase:
$$y_1(x, t) = Asen(kx - ωt + φ), y_2(x, t) = Asen (kx - ωt)$$Cuando estas dos ondas existen en el mismo medio, la onda resultante de la superposición de las dos ondas individuales es la suma de las dos ondas individuales:
La onda resultante se puede entender mejor usando la identidad trigonométrica:
$$senu + senv = 2sen \left(\frac{u + v}{2} \right) cos \left(\frac{u - v}{2} \right)$$donde $u = kx - ωt + φ$ y $v = kx - ωt$. La onda resultante se convierte en
Esta ecuación generalmente se escribe como
La onda resultante tiene el mismo número de onda y frecuencia angular, una amplitud de $A_R = [2Acos(2)]$, y un desplazamiento de fase igual a la mitad del cambio de fase original. En la se muestran ejemplos de ondas que difieren solo en un cambio de fase. Las ondas roja y azul tienen cada una la misma amplitud, número de onda y frecuencia angular, y difieren solo en un cambio de fase. Por lo tanto, tienen el mismo período, longitud de onda y frecuencia. La onda verde es el resultado de la superposición de las dos ondas. Cuando las dos ondas tienen una diferencia de fase de cero, las ondas están en fase, y la onda resultante tiene el mismo número de onda y frecuencia angular, y una amplitud igual al doble de las amplitudes individuales (parte (a)). Esto es una interferencia constructiva. Si la diferencia de fase es de $180°$, las ondas interfieren en la interferencia destructiva (parte (c)). La onda resultante tiene una amplitud de cero. Cualquier otra diferencia de fase da como resultado una onda con el mismo número de onda y frecuencia angular que las dos ondas incidentes, pero con un desplazamiento de fase de $φ/2$ y una amplitud igual a $2Acos(φ/2)$. Los ejemplos se muestran en las partes (b) y (d).
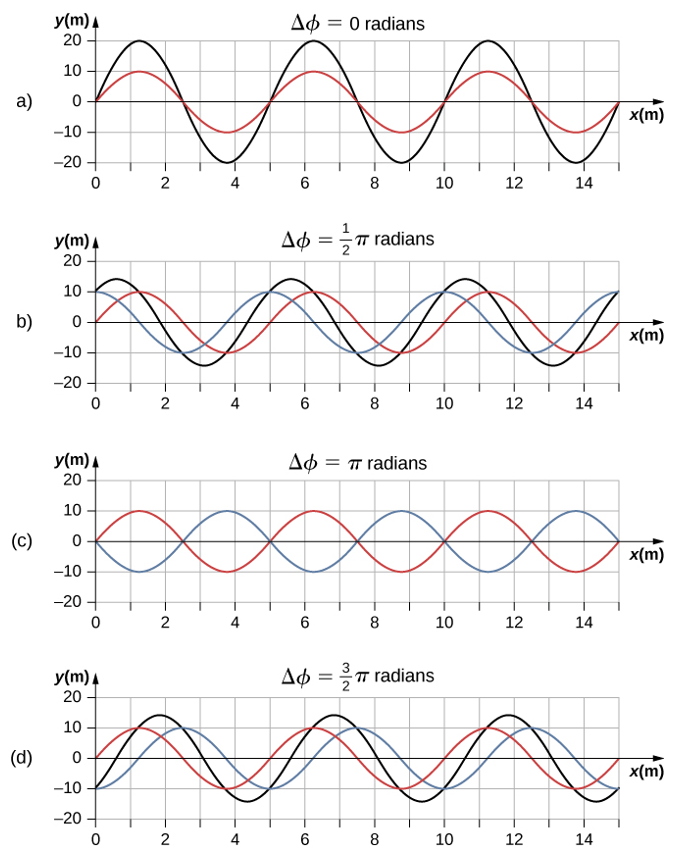
A lo largo de este capítulo, hemos estado estudiando ondas viajeras, o ondas que transportan energía de un lugar a otro. Bajo ciertas condiciones, las olas pueden rebotar hacia adelante y hacia atrás a través de una región en particular, quedando efectivamente estacionarias. Estas se llaman ondas estacionarias. Otro efecto relacionado se conoce como resonancia. En el capítulo de Oscilaciones, definimos la resonancia como un fenómeno en el que una fuerza motriz de pequeña amplitud podría producir un movimiento de gran amplitud. Piensa en un niño en un columpio, que puede modelarse como un péndulo físico. Los impulsos de amplitud relativamente pequeña por parte de un padre pueden producir oscilaciones de gran amplitud. A veces, esta resonancia es buena, por ejemplo, al producir música con un instrumento de cuerda. En otros momentos, los efectos pueden ser devastadores, como el colapso de un edificio durante un terremoto. Por otra parte, las ondas estacionarias de amplitud relativamente grande se producen por la superposición de ondas de amplitud más pequeña.
A veces las ondas no parecen moverse; más bien, simplemente vibran en su lugar. Por ejemplo, puedes ver ondas inmóviles en la superficie de un vaso de leche en un refrigerador. Las vibraciones del motor del refrigerador crean ondas en la leche que oscilan hacia arriba y hacia abajo pero que no parecen moverse a través de la superficie. La muestra un experimento que puedes probar en casa. Toma un tazón de leche y colóquelo en un ventilador de caja común. Las vibraciones del ventilador producirán ondas estacionarias circulares en la leche. Las ondas son visibles en la foto debido al reflejo de una lámpara. Estas ondas están formadas por la superposición de dos o más ondas viajeras, como se ilustra en la para dos ondas idénticas que se mueven en direcciones opuestas.
Las ondas se mueven una a la otra con sus disturbios añadiéndose a medida que pasan. Si las dos ondas tienen la misma amplitud y longitud de onda, entonces alternan entre interferencia constructiva y destructiva. El resultado se parece a una onda que permanece en su lugar y, por lo tanto, se llama onda estacionaria.

Considera dos ondas idénticas que se mueven en direcciones opuestas. La primera onda tiene una función de onda de $y_1(x, t) = Asen(kx - ωt)$ y la segunda onda tiene una función de onda $y_2(x, t) = Asen(kx + ωt)$. Las ondas interfieren y forman una onda resultante.
$$\begin{split} y(x, t) &= y_1(x, t) + y_2(x, t), y (x, t) \\ &= Asen(kx - ωt) + Asen(kx + ωt) \end{split}$$Esto se puede simplificar utilizando la identidad trigonométrica.
$$sen(α ± β) = senαcosβ ± cosαsenβ,$$donde $α = kx$ y $β = ωt$, dándonos
$$\begin{split} y(x, t) &= A[sen(kx)cos(ωt) - cos(kx)sen(ωt) \\ &+ sen(kx)cos(ωt) - cos(kx)sen (ωt)] \end{split}$$lo que simplifica a
Observa que la onda resultante es una onda sinusoidal que es una función solo de la posición, multiplicada por una función de coseno que es una función solo del tiempo. Los gráficos de $y(x, t)$ en función de $x$ para varios tiempos se muestran en la . La onda roja se mueve en la dirección $x$ negativa, la onda azul se mueve en la dirección $x$ positiva y la onda negra es la suma de las dos ondas. A medida que las ondas rojas y azules se mueven entre sí, se mueven dentro y fuera de la interferencia constructiva y la interferencia destructiva.
Inicialmente, en el tiempo $t = 0$, las dos ondas están en fase, y el resultado es una onda que es el doble de la amplitud de las ondas individuales. Las ondas también están en fase en el momento $t = T/2$. De hecho, las ondas están en fase en cualquier múltiplo entero de la mitad de un período:
$t = n\frac{T}{2}$, donde $n = 0,1,2,3...$ (en fase)
En otros momentos, las dos ondas están $180°$ (radios $π$) fuera de fase, y la onda resultante es igual a cero. Esto sucede en
$t = \frac{1}{4}T, \frac{3}{4}T, \frac{5}{4}T, ..., \frac{n}{4}T$, donde $n = 1,3,5 ...$ (en fase)
Observa que algunas posiciones $x$ de la onda resultante siempre son cero, sin importar cuál sea la relación de fase. Estas posiciones se llaman nodos. ¿Dónde ocurren los nodos? Considera la solución a la suma de las dos ondas.
$$y(x, t) = [2Asen(kx)]cos(ωt)$$Encontrar las posiciones donde la función seno es igual a cero proporciona las posiciones de los nodos.
También hay posiciones donde $y$ oscila entre $y = ± A$. Estos son los antinodos. Podemos encontrarlos considerando qué valores de $x$ resultan en $sen (kx) = ± 1$.
Lo que resulta es una onda estacionaria como se muestra en la , que muestra instantáneas de la onda resultante de dos ondas idénticas que se mueven en direcciones opuestas. La onda resultante parece ser una onda sinusoidal con nodos en múltiplos enteros de medias longitudes de onda. Los antinodos oscilan entre $y = ± 2A$ debido al término coseno, $cos(ωt)$, que oscila entre $± 1$. La onda resultante parece estar parada, sin movimiento aparente en la dirección $x$, aunque está compuesta por una función de onda que se mueve en la positiva, mientras que la segunda onda se mueve en la dirección $x$ negativa. La muestra varias instantáneas de la onda resultante. Los nodos están marcados con puntos rojos, mientras que los antinodos están marcados con puntos azules.
En la siguiente escena interactiva, diseñada por Andrew Duffy, puedes interactuar con diferentes valores de $n$, los cuales determinan el número de nodos en la onda estacionaria. Un ejercicio interesante es usar los botones paso adelante y atrás, para obtener una onda estacionaria de amplitud cero.
Un ejemplo común de ondas estacionarias son las ondas producidas por instrumentos musicales de cuerda. Cuando se tira de la cuerda, los pulsos viajan a lo largo de la cuerda en direcciones opuestas. Los extremos de las cuerdas están fijos en su lugar, por lo que aparecen nodos en los extremos de las cuerdas: las condiciones de contorno del sistema, que regulan las frecuencias resonantes en las cuerdas. La resonancia producida en un instrumento de cuerda se puede modelar en un laboratorio de física utilizando el aparato que se muestra en la
La configuración del laboratorio muestra una cuerda unida a un vibrador de cadena, que oscila la cuerda con una frecuencia ajustable $f$. El otro extremo de la cuerda pasa sobre una polea sin fricción y está atado a una masa colgante. La magnitud de la tensión en la cuerda es igual al peso de la masa colgante. La cadena tiene una densidad lineal constante (masa por longitud) $μ$ y la velocidad a la que una onda se desplaza por la cadena es igual a $v = \sqrt{\frac{F_T}{μ}} = \sqrt{\frac{mg}{μ}}$ (ecuación 6.7). Las condiciones de contorno simétricas (un nodo en cada extremo) dictan las posibles frecuencias que pueden excitar las ondas estacionarias.
Comenzando desde una frecuencia de cero y aumentando lentamente la frecuencia, el primer modo n = 1 aparece como se muestra en la . El primer modo, también denominado modo fundamental o primer armónico, muestra que se ha formado la mitad de la longitud de onda, por lo que la longitud de onda es igual al doble de la longitud entre los nodos $λ_1 = 2L$. La frecuencia fundamental, o la primera frecuencia armónica, que controla este modo es $f_1 = \dfrac{v}{λ_1} = \dfrac{v}{2L}$
donde la velocidad de la onda es $v = \sqrt{\frac{F_T}{μ}}$. Mantener la tensión constante y aumentar la frecuencia conduce al segundo armónico o al modo $n = 2$. Este modo es una longitud de onda completa $λ_2 = L$ y la frecuencia es el doble de la frecuencia fundamental:
$f_2 = \frac{v}{λ_2} = \frac{v}{L} = 2f_1$
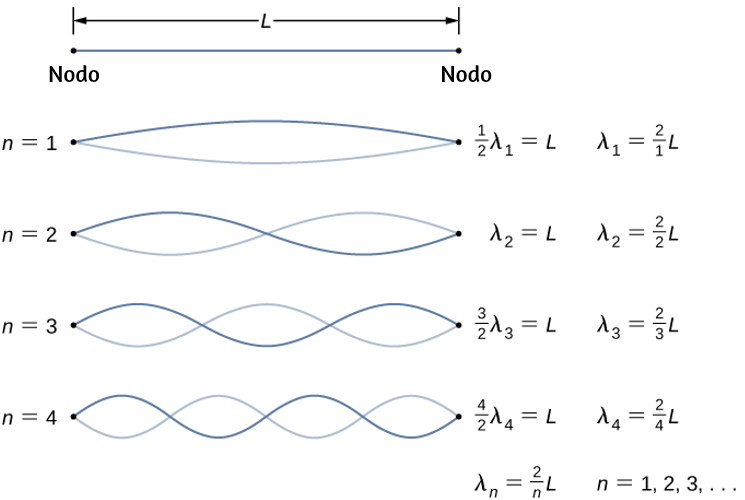
Practica, nuevamente, con la última escena interactiva, en la que puedes observar hasta seis modos de vibración o armónicos. Los siguientes dos modos, o los armónicos tercero y cuarto, tienen longitudes de onda de $λ_3 = \frac{3}{3}L$ y $λ_4 = \frac{3}{4}L$, controladas por frecuencias de $f_3 = \frac{3v}{2L} = 3f_1$ y $f_4 = \frac{4v}{2L} = 4f_1$. Todas las frecuencias por encima de la frecuencia $f_1$ se conocen como sobretonos. Las ecuaciones para la longitud de onda y la frecuencia se pueden resumir como:
Los patrones de onda estacionaria que son posibles para una cuerda, los primeros cuatro de los cuales se muestran en la , se conocen como los modos normales, con frecuencias conocidas como las frecuencias normales. En resumen, la primera frecuencia para producir un modo normal se denomina frecuencia fundamental (o primer armónico). Cualquier frecuencia por encima de la frecuencia fundamental son armónicos. La segunda frecuencia del modo normal $n = 2$ de la cadena es el primer sobretono (o segundo armónico). La frecuencia del modo normal $n = 3$ es el segundo sobretono (o tercer armónico) y así sucesivamente.
Las soluciones que se muestran como la Ecuación 6.15 y la Ecuación 6.16 son para una cuerda con la condición de contorno de un nodo en cada extremo. Cuando la condición de frontera en cualquiera de los lados es la misma, se dice que el sistema tiene condiciones de frontera simétricas. La ecuación 6.15 y la ecuación 6.16 son buenas para cualquier condición de frontera simétrica, es decir, nodos en ambos extremos o antinodos en ambos extremos.
Ejemplo 6.7
Ondas estacionarias en una cuerda
Considera una cuerda de $L = 2.00m$. conectada a un vibrador de cuerda de frecuencia ajustable como se muestra en la . Las ondas producidas por el vibrador viajan por la cuerda y son reflejadas por la condición de límite fijo en la polea. La cuerda, que tiene una densidad de masa lineal de $μ = 0,006 kg/m$, se pasa sobre una polea sin fricción de una masa despreciable, y la tensión es proporcionada por una masa colgante de $2,00 kg$. (a) ¿Cuál es la velocidad de las ondas en la cuerda? (b) Dibuja un boceto de los tres primeros modos normales de las ondas estacionarias que se pueden producir en la cuerda y etiquételas con la longitud de onda. (c) Enumera las frecuencias a las que se debe sintonizar el vibrador de cuerda para producir los primeros tres modos normales de las ondas estacionarias.
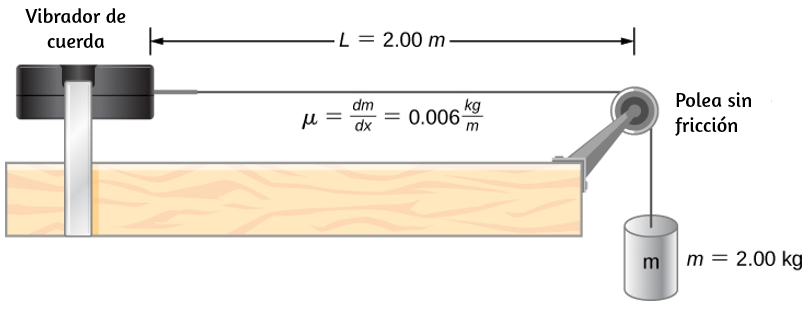
Estrategia
a. La velocidad de la onda se puede encontrar usando $v = \sqrt{\frac{F_T}{μ}}$. La tensión es proporcionada por el peso de la masa colgante.
b. Las ondas estacionarias dependerán de las condiciones de contorno. Debe haber un nodo en cada extremo. El primer modo será la mitad de una onda. El segundo se puede encontrar agregando una media longitud de onda. Esa es la longitud más corta que resultará en un nodo en los límites. Por ejemplo, agregar un cuarto de una longitud de onda resultará en un antinodo en el límite y no es un modo que satisfaga las condiciones del límite. Esto se muestra en la .
c. Dado que la velocidad de la onda es la longitud de onda multiplicada por la frecuencia, la frecuencia es la velocidad de la onda dividida por la longitud de onda.
Solución
a. Comienza con la velocidad de una onda en una cuerda. La tensión es igual al peso de la masa colgante. La densidad de masa lineal y la masa de la masa colgante se dan:
$$v = \sqrt{\frac{F_T}{μ}} = \sqrt{\frac{mg}{μ}} = \sqrt{\frac{2 kg(9.8 m/s)}{0.06 kg/m}} = 57.15 m/s$$b. El primer modo normal que tiene un nodo en cada extremo es una longitud de onda media. Los siguientes dos modos se encuentran agregando la mitad de una longitud de onda.
c. Las frecuencias de los tres primeros modos se encuentran usando $f = \frac{v_w}{λ}$.
$$f_1 = \frac{v_w}{λ_1} = \frac{57.15 m/s}{4.00 m} = 14.29 Hz$$ $$f_2 = \frac{v_w}{λ_2} = \frac{57.15 m/s}{2.00 m} = 28.58 Hz$$ $$f_3 = \frac{v_w}{λ_3} = \frac{57.15 m/s}{1.333 m} = 42.87 Hz$$Explicación
Los tres modos en este ejemplo fueron producidos manteniendo la tensión en la cuerda y ajustando la frecuencia de conducción. Mantener la tensión constante en la cuerda da como resultado una velocidad constante. Los mismos modos podrían haberse producido manteniendo la frecuencia constante y ajustando la velocidad de la onda en la cuerda (cambiando la masa colgante).
En el siguiente Comprueba tu aprendizaje, las condiciones de contorno libre pueden parecer difíciles de visualizar. ¿Cómo puede haber un sistema que oscile libremente en cada extremo? En la se muestran dos configuraciones posibles de barras metálicas (que se muestran en rojo) unidas a dos soportes (que se muestran en azul). En la parte (a), la varilla se apoya en los extremos y hay condiciones de frontera fijas en ambos extremos. Dada la frecuencia adecuada, la varilla puede activarse en resonancia con una longitud de onda igual a la longitud de la varilla, con nodos en cada extremo.
 Comprueba tu aprendizaje 6.7
Comprueba tu aprendizaje 6.7
Las ecuaciones para las longitudes de onda y las frecuencias de los modos de una onda producida en una cuerda:
$$λ_n = \frac{2}{n}L, \; \textsf{con} \; n = 1,2,3,4,5,...$$ $$f_n = n\frac{v}{2L}, \; \textsf{con} \; n = 1,2,3,4,5,...$$se derivaron considerando una onda en una cuerda donde había condiciones de límites simétricas de un nodo en cada extremo. Estos modos resultaron de dos ondas sinusoidales con características idénticas, excepto que se movían en direcciones opuestas, confinadas a una región $L$ con nodos requeridos en ambos extremos. ¿Funcionarán las mismas ecuaciones si hubiera condiciones de contorno simétricas con antinodos en cada extremo? ¿Cómo serían los modos normales para un medio que podía oscilar libremente en cada extremo? No te preocupes, por ahora, si no puedes imaginar un medio así, solo considera dos funciones de onda sinusoidal en una región de longitud $L$, con antinodos en cada extremo.
En la parte (b) de la , la varilla se apoya en las posiciones de un cuarto de la longitud de cada extremo de la varilla, y hay condiciones de frontera libre en ambos extremos. Dada la frecuencia adecuada, esta varilla también puede activarse en resonancia con una longitud de onda igual a la longitud de la varilla, pero hay antinodos en cada extremo. Si tienes problemas para visualizar la longitud de onda en esta figura, recuerda que la longitud de onda puede medirse entre los dos puntos idénticos más cercanos y, además, puedes considerar .
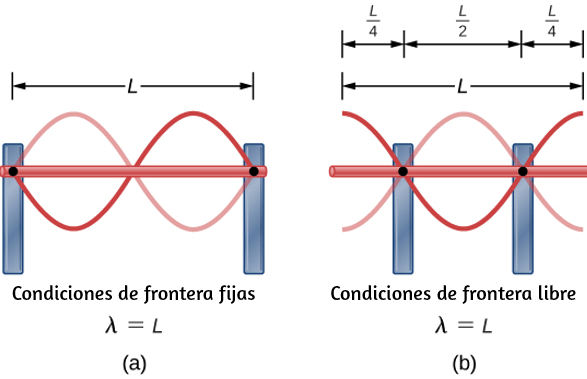
Tenga en cuenta que el estudio de las ondas estacionarias puede llegar a ser bastante complejo. En la (a), se muestra el modo $n = 2$ de la onda estacionaria, y da como resultado una longitud de onda igual a $L$. En esta configuración, el modo $n = 1$
también habría sido posible con una onda estacionaria igual a $2L$ ¿Es posible obtener el modo $n = 1$ para la configuración que se muestra en la parte (b)? La respuesta es no. En esta configuración, hay condiciones adicionales establecidas más allá de las condiciones de contorno. Dado que la varilla se monta en un punto de un cuarto de la longitud de cada lado, debe existir un nodo allí, y esto limita los posibles modos de ondas estacionarias que se pueden crear. Lo dejamos como un ejercicio para que el lector considere si otros modos de ondas estacionarias son posibles.
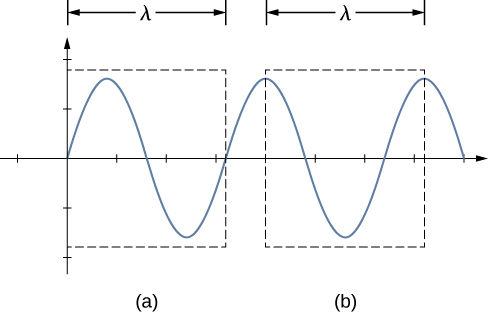
Debe observarse que cuando un sistema se acciona a una frecuencia que no hace que el sistema resuene, pueden producirse vibraciones, pero la amplitud de las vibraciones será mucho menor que la amplitud en la resonancia.
Un campo de la ingeniería mecánica utiliza el sonido producido por las partes vibrantes de sistemas mecánicos complejos para solucionar problemas con los sistemas. Supongamos que una parte en un automóvil está resonando en la frecuencia del motor del automóvil, causando vibraciones no deseadas en el automóvil. Esto puede hacer que el motor falle prematuramente. Los ingenieros usan micrófonos para grabar el sonido producido por el motor, luego usan una técnica llamada análisis de Fourier para encontrar frecuencias de sonido producidas con grandes amplitudes y luego miran la lista de piezas del automóvil para encontrar una parte que resuene en esa frecuencia. La solución puede ser tan simple como cambiar la composición del material utilizado o cambiar la longitud de la parte en cuestión.
Hay otros numerosos ejemplos de resonancia en ondas estacionarias en el mundo físico. El aire en un tubo, como el que se encuentra en un instrumento musical como una flauta, puede forzarse en resonancia y producir un sonido agradable, como discutiremos en el capítulo de Sonido.
En otras ocasiones, la resonancia puede causar problemas graves. Una mirada más cercana a los terremotos proporciona evidencia de las condiciones apropiadas para la resonancia, las ondas estacionarias y las interferencias constructivas y destructivas. Un edificio puede vibrar durante varios segundos con una frecuencia de conducción igual a la frecuencia natural de vibración del edificio, produciendo una resonancia que hace que un edificio se derrumbe, mientras que los edificios vecinos no lo hacen. A menudo, los edificios de cierta altura son devastados, mientras que otros edificios más altos permanecen intactos.
La altura del edificio coincide con la condición para configurar una onda estacionaria para esa altura en particular. La extensión del techo también es importante. A menudo se ve que los gimnasios, los supermercados y las iglesias sufren daños cuando las casas individuales sufren mucho menos daños. Los techos con grandes áreas de superficie soportadas solo en los bordes resuenan en las frecuencias de los terremotos, lo que hace que se colapsen. A medida que las ondas sísmicas viajan a lo largo de la superficie de la Tierra y se reflejan en rocas más densas, se producen interferencias constructivas en ciertos puntos. A menudo, las áreas más cercanas al epicentro no se dañan, mientras que las áreas más alejadas se dañan.
Un ejemplo de resonancia mecánica, muy utilizado en ingeniería, fue el colapso del puente colgante de Tacoma Narrows, en el estado de Washington: "El fenómeno de resonancia longitudinal, hacia que el puente se deformara en esa dirección. Literalmente los coches galopaban sobre el asfalto como barquitos sobre las olas del mar, se movían de arriba abajo" (http://eldilemadehamlet.blogspot.com/).

Terminamos este capítulo con otra escena interactiva, diseñada por Andrew Duffy, sobre ondas estacionarias en una tubería.

El sonido es un ejemplo de una onda mecánica, específicamente, una onda de presión: las ondas de sonido viajan por el aire y otros medios como oscilaciones de las moléculas. La audición humana normal abarca una impresionante gama de frecuencias de $20 Hz$ a $20 kHz$. Los sonidos por debajo de $20 Hz$ se llaman infrasonidos, mientras que los que están por encima de $20 kHz$ se llaman ultrasonidos. Algunos animales, como el murciélago que se muestra en la , pueden escuchar sonidos en el rango ultrasónico.
Muchos de los conceptos tratados en el capítulo de Ondas también tienen aplicaciones en el estudio del sonido. Por ejemplo, cuando una onda de sonido encuentra una interfaz entre dos medios con diferentes velocidades de onda, se produce la reflexión y la transmisión de la onda.
La ecografía tiene muchos usos en ciencia, ingeniería y medicina. El ultrasonido se usa para pruebas no destructivas en ingeniería, como las pruebas del espesor del recubrimiento en metal. En medicina, las ondas sonoras son mucho menos destructivas que los rayos X y pueden usarse para obtener imágenes del feto en el útero de una madre sin peligro para el feto o la madre. Más adelante en este capítulo, analizaremos el efecto Doppler, que se puede usar para determinar la velocidad de la sangre en las arterias o la velocidad del viento en los sistemas meteorológicos.
El fenómeno físico del sonido es una perturbación de la materia que se transmite desde su origen hacia el exterior. Oír es la percepción del sonido, así como ver es la percepción de la luz visible. En la escala atómica, el sonido es una perturbación de los átomos que está mucho más ordenada que sus movimientos térmicos. En muchos casos, el sonido es una onda periódica, y los átomos experimentan un movimiento armónico simple. Por lo tanto, las ondas de sonido pueden inducir oscilaciones y efectos de resonancia ().
Un altavoz produce una onda de sonido al oscilar un cono, causando vibraciones de las moléculas de aire. En la , un altavoz vibra a una frecuencia y amplitud constantes, produciendo vibraciones en las moléculas de aire circundantes. A medida que el altavoz oscila hacia adelante y hacia atrás, transfiere energía al aire, principalmente como energía térmica.
Sin embargo, una pequeña parte de la energía del altavoz se concentra en comprimir y expandir el aire circundante, creando presiones locales ligeramente más altas y más bajas. Estas compresiones (regiones de alta presión) y rarefacciones (regiones de baja presión) se mueven hacia afuera como ondas de presión longitudinales que tienen la misma frecuencia que el altavoz: son la perturbación que es una onda de sonido (las ondas de sonido en el aire y en la mayoría de los fluidos son longitudinales, porque los fluidos casi no tienen resistencia al corte. En los sólidos, las ondas de sonido pueden ser tanto transversales como longitudinales).
La (a) muestra las compresiones y rarefacciones, y también muestra un gráfico de la presión manométrica en función de la distancia desde un altavoz. A medida que el hablante se mueve en la dirección $x$ positiva, empuja las moléculas de aire, desplazándolas de sus posiciones de equilibrio.
A medida que el hablante se mueve en la dirección $x$ negativa, las moléculas de aire retroceden hacia sus posiciones de equilibrio debido a una fuerza restauradora. Las moléculas de aire oscilan en un movimiento armónico simple sobre sus posiciones de equilibrio, como se muestra en la parte (b). Observa que las ondas de sonido en el aire son longitudinales, y en la figura, la onda se propaga en la dirección $x$ positiva y las moléculas oscilan paralelas a la dirección en que se propaga la onda.
Modelos que describen el sonido
El sonido puede modelarse como una onda de presión considerando el cambio en la presión de la presión promedio,
$$ΔP = ΔP_{\textsf{max}}sen(kx ± ωt + φ) \tag{7.1}$$Esta ecuación es similar a las ecuaciones de onda periódicas observadas en el capítulo de Ondas, donde $ΔP$ es el cambio en la presión, $ΔP_{\textsf{max}}$ es el cambio máximo en la presión, $k = \frac{2π}{λ}$ es el número de onda, $ω = \frac{2π}{T} = \frac{2π}{f}$ es la frecuencia angular, y $φ$ es la fase inicial. La velocidad de onda se puede determinar a partir de $v = \frac{ω}{k} = \frac{λ}{T}$. Las ondas de sonido también se pueden modelar en términos del desplazamiento de las moléculas de aire.
El desplazamiento de las moléculas de aire se puede modelar usando una función coseno:
$$s(x, t) = s_{\textsf{max}}cos(kx ± ωt + φ) \tag{7.2}$$En esta ecuación, $s$ es el desplazamiento y $s_{\textsf{max}}$ es el desplazamiento máximo.
No se muestra en la figura la amplitud de una onda de sonido a medida que disminuye con la distancia desde su fuente, porque la energía de la onda se extiende sobre un área cada vez más grande. La intensidad disminuye a medida que se aleja del hablante, como se explicó en el capítulo de Ondas. La energía también es absorbida por los objetos y convertida en energía térmica por la viscosidad del aire. Además, durante cada compresión, un poco de calor se transfiere al aire; durante cada rarefacción, incluso menos transferencias de calor del aire, y estas transferencias de calor reducen la perturbación organizada en movimientos térmicos aleatorios. Si la transferencia de calor de la compresión a la rarefacción es significativa, depende de cuán alejados estén, es decir, depende de la longitud de onda. La longitud de onda, la frecuencia, la amplitud y la velocidad de propagación son características importantes para el sonido, como lo son para todas las ondas.
El sonido, como todas las ondas, viaja a una cierta velocidad y tiene las propiedades de frecuencia y longitud de onda. Puede observar evidencia directa de la velocidad del sonido mientras ves una exhibición de fuegos artificiales (). Observas el destello de una explosión mucho antes de escuchar su sonido y posiblemente sientas la onda de presión, lo que implica que el sonido viaja a una velocidad finita y que es mucho más lento que la luz.
La diferencia entre la velocidad de la luz y la velocidad del sonido también se puede experimentar durante una tormenta eléctrica. El destello de la iluminación se ve a menudo antes del trueno. Es posible que hayas escuchado que si cuentas la cantidad de segundos entre el flash y el sonido, puedes estimar la distancia a la fuente.
Cada cinco segundos se convierte en aproximadamente una milla. La velocidad de cualquier onda está relacionada con su frecuencia y longitud de onda por
donde $v$ es la velocidad de la onda, $f$ es su frecuencia y $λ$ es su longitud de onda. Recuerda que la longitud de onda es la longitud de la onda medida entre puntos idénticos secuenciales. Por ejemplo, para una onda de agua superficial o una onda sinusoidal en una cuerda, la longitud de onda se puede medir entre dos puntos secuenciales convenientes con la misma altura y pendiente, como entre dos crestas secuenciales o dos depresiones secuenciales.

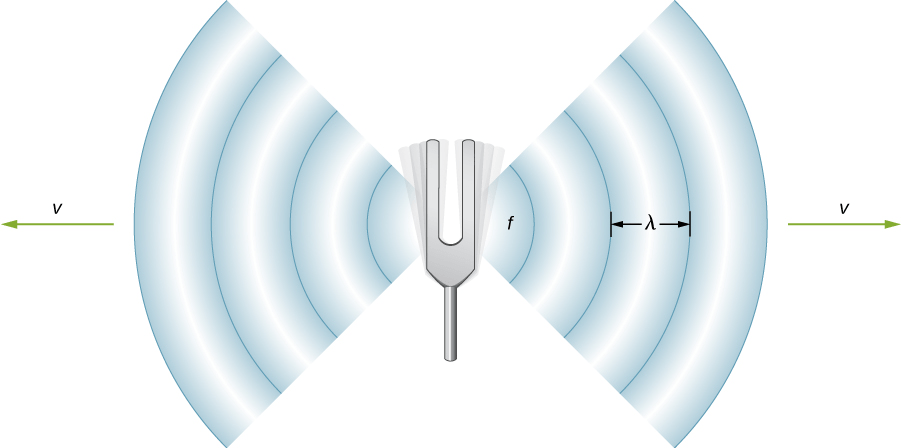
De manera similar, la longitud de onda de una onda de sonido es la distancia entre partes idénticas secuenciales de una onda, por ejemplo, entre compresiones secuenciales (). La frecuencia es la misma que la de la fuente y es el número de ondas que pasan un punto por unidad de tiempo.
En la siguiente escena, diseñada por Andreu Glasmann, Wolfgang Christian, Mario Belloni y lookang, se muestra al vista molecular de una onda de sonido:
La tabla 7.1 muestra que la velocidad del sonido varía mucho en diferentes medios. La velocidad del sonido en un medio depende de la rapidez con la que se pueda transferir la energía vibratoria a través del medio. Por esta razón, la derivación de la velocidad del sonido en un medio depende del medio y del estado del medio. En general, la ecuación de la velocidad de una onda mecánica en un medio depende de la raíz cuadrada de la fuerza restauradora, o la propiedad elástica, dividida por la propiedad inercial,
$$v = \sqrt{\frac{\textsf{propiedad elástica}}{\textsf{propiedad inercial}}}$$Además, las ondas de sonido satisfacen la ecuación de onda,
$$\frac{∂^2(x, t)}{∂x^2} = \frac{1}{v^2} \frac{∂^2(x, t)}{∂t^2}$$Recuerde de Ondas que la velocidad de una onda en una cuerda es igual a $v = \sqrt{\frac{F_T}{μ}}$, donde la fuerza restauradora es la tensión en $F_T$ la cuerda y la densidad lineal $μ$ es la propiedad inercial.
En un fluido, la velocidad del sonido depende del módulo volumétrico y la densidad,
La velocidad del sonido en un sólido depende del módulo de Young del medio y la densidad,
En un gas ideal (ver la teoría cinética de los gases), la ecuación de la velocidad del sonido es
donde $γ$ es el índice adiabático, $R = 8.31 J/mol \cdot K$ es la constante de gas, $T_K$ es la temperatura absoluta en kelvins y $M$ es la masa molecular. En general, cuanto más rígido (o menos compresible) sea el medio, más rápida será la velocidad del sonido.
Esta observación es análoga al hecho de que la frecuencia del movimiento armónico simple es directamente proporcional a la rigidez del objeto oscilante, medida por $k$, la constante del resorte. Cuanto mayor sea la densidad de un medio, más lenta será la velocidad del sonido. Esta observación es análoga al hecho de que la frecuencia de un movimiento armónico simple es inversamente proporcional a $m$, la masa del objeto oscilante. La velocidad del sonido en el aire es baja, porque el aire es fácilmente compresible. Debido a que los líquidos y los sólidos son relativamente rígidos y muy difíciles de comprimir, la velocidad del sonido en tales medios es generalmente mayor que en los gases.
Debido a que la velocidad del sonido depende de la densidad del material y la densidad depende de la temperatura, existe una relación entre la temperatura en un medio dado y la velocidad del sonido en el medio. Para el aire a nivel del mar, la velocidad del sonido viene dada por
donde la temperatura en la primera ecuación (indicada como $T_C$) es en grados Celsius y la temperatura en la segunda ecuación (indicada como $T_K$) está en grados kelvins. La velocidad del sonido en los gases está relacionada con la velocidad promedio de las partículas en el gas, $v_{rms} = \sqrt{3k_BT/m}$, donde $k_B$ es la constante de Boltzmann $(1.38 × 10^{-23} J/K)$ y $m$ es la masa de cada partícula en el gas. Ten en cuenta que $v$ se refiere a la velocidad de la propagación coherente de una perturbación (la onda), mientras que $v_{rms}$ describe las velocidades de las partículas en direcciones aleatorias. Por lo tanto, es razonable que la velocidad del sonido en el aire y otros gases dependa de la raíz cuadrada de la temperatura. Si bien no es despreciable, esta no es una dependencia fuerte. A $0 °C$, la velocidad del sonido es de $331 m/s$, mientras que a $20.0 °C$, es de $343 m/s$, un aumento de menos del $4$%. La muestra cómo un murciélago usa la velocidad del sonido para detectar distancias.
Como se dijo anteriormente, la velocidad del sonido en un medio depende del medio y del estado del medio. La derivación de la ecuación para la velocidad del sonido en el aire comienza con la tasa de flujo másico y la ecuación de continuidad discutida en Mecánica de fluidos.
Considera el flujo de fluido a través de una tubería con un área de sección transversal A (). La masa en un pequeño volumen de longitud $x$ de la tubería es igual a la densidad por el volumen, o $m = ρV = ρAx$. El caudal másico es
$$\frac{dm}{dt} = \frac{d}{dt}(ρV) = \frac{d}{dt}(ρAx) = ρA\frac{dx}{dt} = ρv$$La ecuación de continuidad de la Mecánica de fluidos indica que el caudal másico en un volumen debe ser igual al caudal másico fuera del volumen, $ρ_{\textsf{in}}A_{\textsf{in}}v_{\textsf{in}} = ρ_{\textsf{ext}}A_{\textsf{ext}}v_{\textsf{ext}}$.
Ahora considera una onda de sonido que se mueve a través de una parcela de aire. Una parcela de aire es un pequeño volumen de aire con límites imaginarios (). La densidad, la temperatura y la velocidad en un lado del volumen del fluido se dan como $ρ$, $T$, $v$, y en el otro lado son $ρ + dρ$, $T + dT$, $v + dv$.
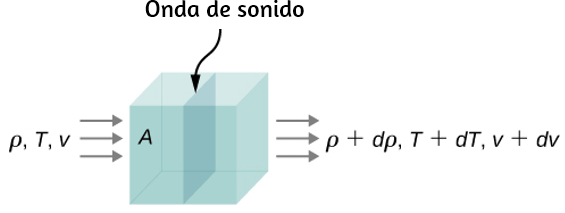
La ecuación de continuidad indica que el caudal másico que ingresa al volumen es igual al caudal másico que sale del volumen, por lo que
$$ρAv = (ρ + dρ)A(v + dv)$$Esta ecuación se puede simplificar, observando que el área se cancela y considerando que la multiplicación de dos infinitesimales es aproximadamente igual a cero: $dρ(dv) ≈ 0$,
$$ρv = (ρ + dρ)(v + dv)$$ $$ρv = ρv + ρ(dv) + (dρ)v + (dρ)(dv)$$ $$0 = ρ(dv) + (dρ)v$$ $$ρdv = -vdρ$$La fuerza neta en el volumen de fluido () es igual a la suma de las fuerzas en la cara izquierda y la cara derecha:
$$F_{\textsf{net}} = pdydz - (p + dp)dydz$$ $$F_{\textsf{net}} = pdydz - pdydz - dpdydz$$ $$F_{\textsf{net}} = -dpdydz$$ $$ma = -dpdydz$$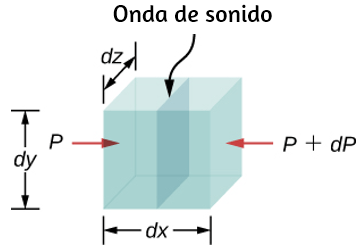
La aceleración es la fuerza dividida por la masa y la masa es igual a la densidad por el volumen, $m = ρV = ρdxdydz$. Tenemos
$$ma = -dpdydz$$ $$a = -\frac{dpdydz}{m} = - \frac{dpdydz}{ρdxdydz} = - \frac{dp}{ρdx}$$ $$\frac{dv}{dt} = -\frac{dp}{ρdx}$$ $$dv = -\frac{dp}{ρdx}dt = \frac{dp}{ρ}\frac{1}{v}$$ $$ρvdv = -dp$$De la ecuación de continuidad $ρdv = -vdρ$, obtenemos
$$ρvdv = -dp$$ $$(-vdρ)v = -dp$$ $$v = \sqrt{dp/dρ}$$Considera una onda de sonido moviéndose a través del aire. Durante el proceso de compresión y expansión del gas, no se agrega o elimina calor del sistema. Un proceso donde el calor no se agrega o elimina del sistema se conoce como sistema adiabático. Los procesos adiabáticos se tratan en detalle en La primera ley de la termodinámica, pero por ahora es suficiente decir que para un proceso adiabático, $pV^{γ} = constante$, donde $p$ es la presión, $V$ es el volumen y gamma ($γ$) es una constante. Eso depende del gas. Para el aire, $γ = 1.40$. La densidad es igual al número de moles multiplicado por la masa molar dividida por el volumen, por lo que el volumen es igual a $V = \frac{nM}{ρ}$.
El número de moles y la masa molar son constantes y se pueden absorber en la constante $p(\frac{1}{ρ})^{γ} = constante$. Tomando el logaritmo natural de ambos lados se obtiene $lnp - γlnρ = constante$. Al diferenciarse con respecto a la densidad, la ecuación se convierte en
$$lnp - γlnρ = constante$$ $$\frac{d}{dρ}(lnp - γlnρ) = \frac{1}{dρ}(constante)$$ $$\frac{1}{p}\frac{dp}{dρ} - \frac{γ}{ρ} = 0$$ $$\frac{dp}{dρ} = \frac{γp}{ρ}$$Si el aire puede considerarse un gas ideal, podemos usar la ley del gas ideal:
$$ρV = nRT = \frac{m}{M}RT$$ $$p = \frac{m}{v}\frac{RT}{M} = ρ\frac{RT}{M}$$Aquí $M$ es la masa molar del aire:
$$\frac{dp}{dρ} = \frac{γp}{ρ} = \frac{γρRT/M}{ρ} = \frac{γRT}{M}$$Dado que la velocidad del sonido es igual a $v = \sqrt{dp/ρ}d$, la velocidad es igual a
$$v = \sqrt{\frac{γRT}{M}}$$Observa que la velocidad es más rápida a temperaturas más altas y más lenta para gases más pesados. Para el aire, $γ = 1.4$, $M = 0.02897 kg/mol$ y $R = 8.31 \frac{J}{mol \cdot K}$. Si la temperatura es $T_C = 20 °C$ ($T = 293 K$), la velocidad del sonido es $v = 343 m/s$.
La ecuación para la velocidad del sonido en el aire $v = \sqrt{\frac{γRT}{M}}$ se puede simplificar para dar la ecuación para la velocidad del sonido en el aire en función de la temperatura absoluta:
$$\begin{split} v &= \sqrt{\frac{γRT}{M}} \\ &= \sqrt{\frac{γRT}{M} \frac{273K}{273K}} = \sqrt{\frac{(273 K)γR}{M}} \sqrt{\frac{T}{273K}} \\ &≈331\frac{m}{s} \sqrt{\frac{T}{273K}} \end{split}$$Una de las propiedades más importantes del sonido es que su velocidad es casi independiente de la frecuencia. Esta independencia es cierta al aire libre para sonidos en el rango audible. Si esta independencia no fuera cierta, sin duda lo notarías en la música que toca una banda de música en un estadio de fútbol, por ejemplo. Supongamos que los sonidos de alta frecuencia viajaban más rápido; entonces, cuanto más lejos estuvieras de la banda, más se retrasaría el sonido de los instrumentos de tono bajo que los de tono agudo. Pero la música de todos los instrumentos llega en cadencia independiente de la distancia, por lo que todas las frecuencias deben viajar casi a la misma velocidad. Recordar que
$$v = fλ$$En un medio dado bajo condiciones fijas, $v$ es constante, por lo que hay una relación entre $f$ y $λ$; cuanto mayor sea la frecuencia, menor será la longitud de onda ().

Ejemplo 7.1
Cálculo de longitudes de onda
Calcula las longitudes de onda de los sonidos en los extremos del rango audible, $20$ y $20,000 Hz$, en el aire a $30.0 °C$ (supón que los valores de frecuencia son precisos para dos cifras significativas).
Estrategia
Para encontrar la longitud de onda desde la frecuencia, podemos usar $v = fλ$.
Solución
1. Identificar los datos conocidos. El valor para $v$ está dado por
$$v = (331 m/s) \sqrt{\frac{T}{273 K}}$$2. Convierte la temperatura en kelvins y luego ingresa la temperatura en la ecuación
$$v = (331 m/s) \sqrt{\frac{303 K}{273 K}} = 348.7 m/s$$Resuelve la relación entre velocidad y longitud de onda para $λ$:
$$λ = \frac{v}{f}$$4. Introduce la velocidad y la frecuencia mínima para obtener la longitud de onda máxima:
Introduce la velocidad y la frecuencia máxima para hallar la longitud de onda mínima:
$$λ_{\textsf{min}} = \frac{348.7 m/s}{20,000 Hz} = 0.017 m = 1.7 cm$$Explicación
Debido a que el producto de $f$ multiplicado por $λ$ es igual a una constante, mientras más pequeña sea $f$, mayor será $λ$, y viceversa.
La velocidad del sonido puede cambiar cuando el sonido viaja de un medio a otro, pero la frecuencia generalmente permanece igual. Esto es similar a la frecuencia de una onda en una cuerda que es igual a la frecuencia de la fuerza que oscila la cuerda. Si $v$ cambia y $f$ permanece igual, entonces la longitud de onda $λ$ debe cambiar. Es decir, porque $v = fλ$, cuanto mayor es la velocidad de un sonido, mayor es su longitud de onda para una frecuencia dada.
 Comprueba tu aprendizaje 7.1
Comprueba tu aprendizaje 7.1
Aunque las ondas de sonido en un fluido son longitudinales, las ondas de sonido en un sólido viajan tanto como ondas longitudinales como ondas transversales.
Las ondas sísmicas, que son esencialmente ondas sonoras en la corteza terrestre producida por los terremotos, son un ejemplo interesante de cómo la velocidad del sonido depende de la rigidez del medio. Los terremotos producen ondas longitudinales y transversales, y estos viajan a diferentes velocidades. El módulo de volumen de granito es mayor que su módulo de corte. Por esa razón, la velocidad de las ondas longitudinales o de presión (ondas $P$) en los terremotos en granito es significativamente mayor que la velocidad de las ondas transversales o de corte (ondas $S$). Ambos tipos de ondas sísmicas viajan más lentamente en material menos rígido, como los sedimentos. Las ondas $P$ tienen velocidades de $4$ a $7 km/s$, y las ondas $S$ tienen una velocidad de $2$ a $5 km/s$, ambas más rápidas en material más rígido. La onda $P$ avanza progresivamente más lejos de la onda $S$ a medida que viajan a través de la corteza terrestre. El tiempo entre las ondas $P$ y $S$ se usa de manera rutinaria para determinar la distancia a su fuente, el epicentro del terremoto. Debido a que las ondas $S$ no pasan a través del núcleo líquido, se producen dos regiones de sombra ().
A medida que las ondas de sonido se alejan de un altavoz o se alejan del epicentro de un terremoto, su potencia por unidad de área disminuye. Esta es la razón por la que el sonido es muy alto cerca de un altavoz y se vuelve menos fuerte a medida que se aleja del altavoz. Esto también explica por qué puede haber un daño extremo en el epicentro de un terremoto, pero solo se sienten temblores en áreas alejadas del epicentro. La potencia por unidad de área se conoce como intensidad, y en la siguiente sección, discutiremos cómo la intensidad depende de la distancia desde la fuente.
En el siguiente interactivo, diseñado por José Luis Abreu León, puedes variar la amplitud, la velocidad de propagación y la frecuencia para generar ondas transversales y longitudinales.
En un bosque tranquilo, a veces puedes escuchar una sola hoja caer al suelo. Pero cuando un conductor que pasa tiene su estéreo encendido, ni siquiera puede escuchar lo que la persona que está a su lado en su automóvil está diciendo (). Todos estamos muy familiarizados con la intensidad de los sonidos y somos conscientes de que la intensidad está relacionada con la energía que vibra la fuente. La alta exposición al ruido es peligrosa para la audición, por lo que es importante que las personas que trabajan en entornos industriales usen protección auditiva. La cantidad física relevante es la intensidad del sonido, un concepto que es válido para todos los sonidos, estén o no en el rango audible.

En el capítulo de Ondas, definimos la intensidad como la potencia por unidad de área transportada por una onda. La potencia es la velocidad a la que la onda transfiere la energía. En forma de ecuación, la intensidad $I$ es
$$I = \frac{P}{A} \tag{7.8}$$donde $P$ es la potencia a través de un área $A$. La unidad del SI para $I$ es $W/m^2$. Si asumimos que la onda de sonido es esférica y que no se pierde energía en los procesos térmicos, la energía de la onda de sonido se extiende sobre un área más grande a medida que aumenta la distancia, por lo que la intensidad disminuye. El área de una esfera es $A = 4πr^2$. A medida que la onda se extiende desde $r_1$ a $r_2$, la energía también se extiende sobre un área más grande:
$$P_1 = P_2$$ $$I_14πr_1^2 = I_24πr_2^2$$La intensidad disminuye a medida que la onda sale de la fuente. En una relación cuadrada inversa, como la intensidad, al duplicar la distancia, la intensidad disminuye a un cuarto,
$$I_2 = I_1 \left(\frac{r_1}{r_2} \right)^2 = I_1 \left(\frac{r_1}{2r_1} \right)^2 = \frac{1}{4}I_1$$Generalmente, al considerar la intensidad de una onda de sonido, consideramos que la intensidad es el valor de la potencia promediado en el tiempo, denotado por $≺P≻$, dividido por el área,
La intensidad de una onda de sonido es proporcional al cambio en la presión al cuadrado e inversamente proporcional a la densidad y la velocidad. Considera una parcela de un medio inicialmente no perturbado y luego influenciado por una onda de sonido en el tiempo t, como se muestra en la .
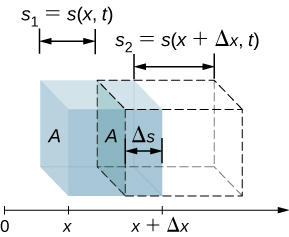
A medida que la onda de sonido se mueve a través de la parcela, la parcela se desplaza y puede expandirse o contraerse. Si $s_2 > s_1$, el volumen ha aumentado y la presión disminuye. Si $s_2 < s_1$, el volumen ha disminuido y la presión aumenta. El cambio en el volumen es
$$ΔV = AΔs = A(s_2 - s_1) = A(s(x + Δx, t) - s(x, t))$$El cambio fraccionario en el volumen es el cambio en el volumen dividido por el volumen original:
$$\frac{dV}{V} = \lim_{Δx \to 0} \frac{A[s(x + Δx,t) - s(x,t)]}{AΔx} = \frac{∂s(x, t)}{∂x}$$El cambio fraccional en el volumen está relacionado con la fluctuación de la presión por el módulo de volumen $β = -\frac{Δp(x, t)}{ dV/V}$. Recuerda que el signo menos es necesario porque el volumen está inversamente relacionado con la presión (utilizamos $p$ minúscula para la presión para distinguirla de la potencia, denotada por $P$). Por lo tanto, el cambio en la presión es $Δp(x, t) = -β\frac{dV}{V} = -β\frac{∂s(x, t)}{∂x}$. Si la onda de sonido es sinusoidal, entonces el desplazamiento como se muestra en la Ecuación 7.2 es $s(x, t) = s_{\textsf{max}}cos(kx ± ωt + φ)$ y se encuentra que la presión es
$$\begin{split} Δp(x, t) &= -β\frac{dV}{V} = -β\frac{∂s(x, t)}{∂x} \\ &= βks_{\textsf{max}}sen(kx - ωt + φ) = Δp_{\textsf{max}}sen(kx - ωt + φ) \end{split}$$La intensidad de la onda de sonido es la potencia por unidad de área, y la potencia es la fuerza multiplicada por la velocidad, $I = \frac{P}{A} = \frac{Fv}{A} = pv$. Aquí, la velocidad es la velocidad de las oscilaciones del medio, y no la velocidad de la onda de sonido. La velocidad del medio es el tiempo de cambio en el desplazamiento:
Así, la intensidad sería:
$$\begin{split} I &= Δp(x, t)v(x, t) \\ &= βks_{\textsf{max}}sen(kx - ωt + φ)[s_{\textsf{max}}ωsen(kx - ωt + φ)] \\ &= βkωs^2_{\textsf{max}}sen^2(kx - ωt + φ) \end{split}$$Para encontrar la intensidad promediada en el tiempo en un período $T = \frac{2π}{ω}$ para una posición $x$, integramos en el período, $I = \frac{βkωs^2_{\textsf{max}}}{2}$. Usando $Δp_{\textsf{max}} = βks_{\textsf{max}}$, $v = \sqrt{β/ρ}$, y $v = ω/k$, obtenemos
Es decir, la intensidad de una onda de sonido está relacionada con su amplitud al cuadrado por
Aquí, $Δp_{\textsf{max}}$ es la variación de la presión o la amplitud de la presión en unidades de pascales ($Pa$) o $N/m^2$. La energía (como energía cinética $\frac{1}{2}^2mv$) de un elemento oscilante de aire debido a una onda de sonido que viaja es proporcional a su amplitud al cuadrado. En esta ecuación, $ρ$ es la densidad del material en el que se desplaza la onda de sonido, en unidades de $kg/m^3$, y $v$ es la velocidad del sonido en el medio, en unidades de $m/s$.
La variación de presión es proporcional a la amplitud de la oscilación, por lo que varía como $(Δp)^2$. Esta relación es consistente con el hecho de que la onda de sonido es producida por alguna vibración; cuanto mayor sea la amplitud de su presión, más comprimirá el aire en el sonido que crea.
Como se indicó anteriormente en este capítulo, la audición es la percepción del sonido. El mecanismo de la audición implica algunas características físicas interesantes. La onda de sonido que incide sobre nuestro oído es una onda de presión. El oído es un transductor que convierte las ondas de sonido en impulsos nerviosos eléctricos de una manera mucho más sofisticada que un micrófono, pero de manera análoga. La muestra la anatomía del oído.
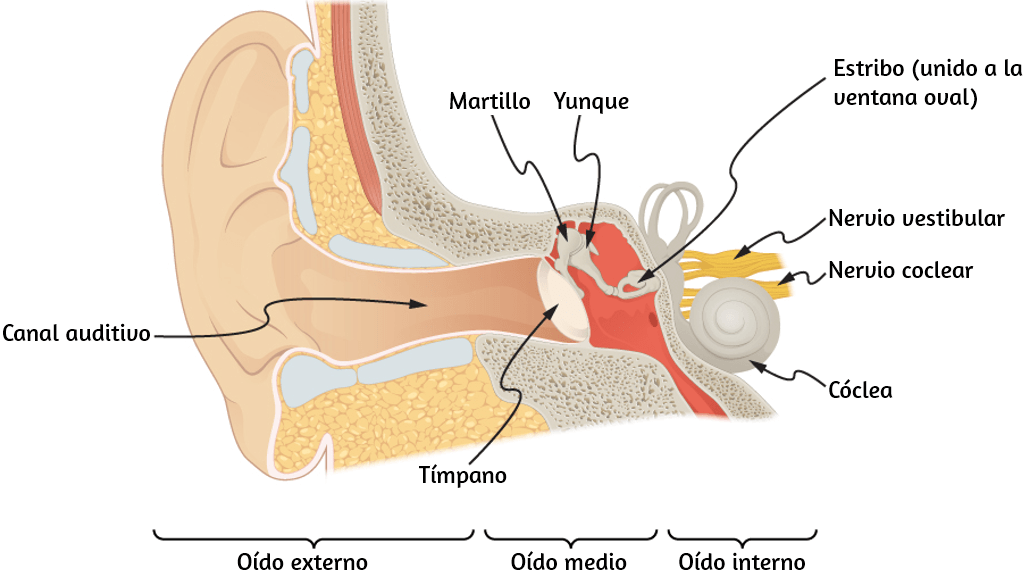
El oído externo, o canal auditivo, lleva el sonido al tímpano protegido y empotrado. La columna de aire en el canal auditivo resuena y es parcialmente responsable de la sensibilidad del oído a los sonidos en el rango de $2000–5000 Hz$. El oído medio convierte el sonido en vibraciones mecánicas y aplica estas vibraciones a la cóclea.
El rango de intensidades que el oído humano puede escuchar depende de la frecuencia del sonido, pero, en general, el rango es bastante grande. La intensidad de umbral mínima que se puede escuchar es $I_0 = 10^{-12} W/m^2$. El dolor se experimenta a intensidades de $I_{\textsf{dolor}} = 1 W/m^2$. Las mediciones de la intensidad del sonido (en unidades de $W/m^2$) son muy complicadas debido a este amplio rango de valores. Por esta razón, así como por otras razones, se propuso el concepto de nivel de intensidad de sonido.
El nivel de intensidad del sonido $β$ de un sonido, medido en decibelios, con una intensidad I en vatios por metro cuadrado, se define como
donde $I_0 = 10^{-12} W/m^2$ es una intensidad de referencia, correspondiente a la intensidad de umbral del sonido que una persona con audición normal puede percibir a una frecuencia de $1.00 kHz$. Es más común considerar los niveles de intensidad del sonido en $dB$ que en $W/m_2$. La forma en que los oídos humanos perciben el sonido se puede describir con mayor precisión mediante el logaritmo de la intensidad en lugar de hacerlo directamente por la intensidad. Debido a que $β$ se define en términos de una relación, es una cantidad sin unidades, que le indica el nivel del sonido en relación con un estándar fijo ($10^{-12} W/m^2$). Las unidades de decibelios ($dB$) se utilizan para indicar que esta relación se multiplica por $10$ en su definición. El bel, sobre el cual se basa el decibelio, lleva el nombre de Alexander Graham Bell, el inventor del teléfono.
El nivel de decibelios de un sonido que tiene una intensidad de umbral de $^{-12} W/m^2$ es $β = 0 dB$, porque $log_{10} 1 = 0$. La proporciona niveles en decibelios e intensidades en vatios por metro cuadrado para algunos sonidos familiares. El oído es sensible a una billonésima de vatio por metro cuadrado, incluso más impresionante cuando te das cuenta de que el área del tímpano es de solo $1 cm^2$, por lo que solo cae entre $10$ y $16 W$ en el umbral de audición.
Las moléculas de aire en una onda de sonido de esta intensidad vibran a una distancia de menos de un diámetro molecular, y las presiones manométricas involucradas son menores de $10^{-9} atm$.
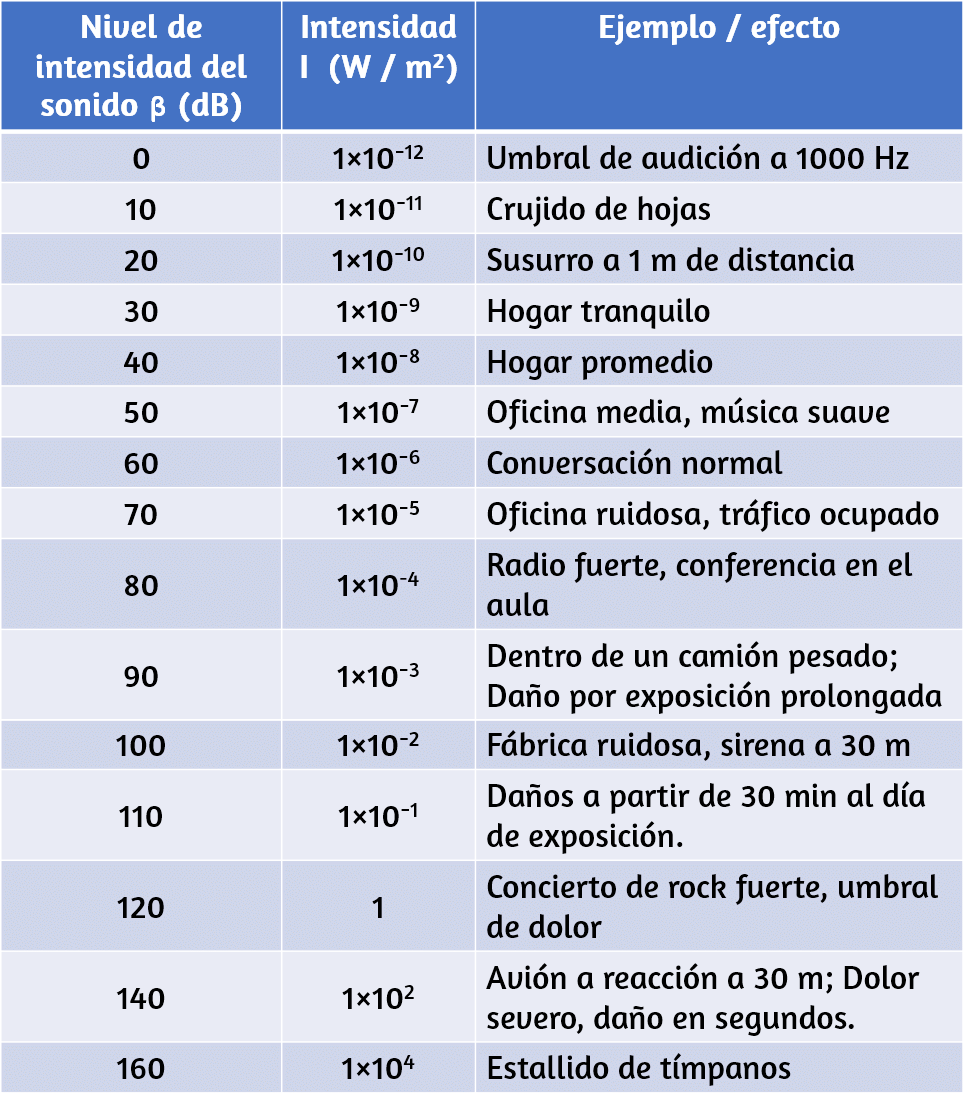
Una observación verificada fácilmente al examinar la o al usar la Ecuación 7.12 es que cada factor de $10$ en intensidad corresponde a $10 dB$. Por ejemplo, un sonido de $90 dB$ comparado con un sonido de $60 dB$ es $30 dB$ mayor, o tres factores de $10$ (es decir, $10^3$ veces). Otro ejemplo es que si un sonido es $10^7$ tan intenso como otro, es $70 dB$ más alto ().
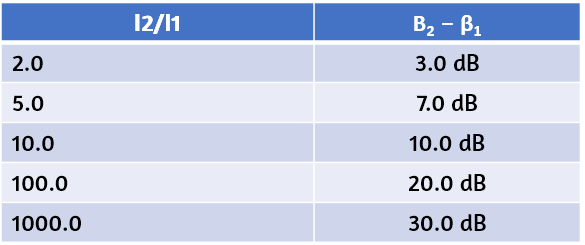
Ejemplo 7.2
Cálculo de los niveles de intensidad del sonido
Calcula el nivel de intensidad del sonido en decibelios para una onda de sonido que viaja en el aire a $0 °C$ y tiene una amplitud de presión de $0.656 Pa$.
Estrategia
Nos dan $Δp$, por lo que podemos calcular $I$ usando la ecuación $I = (Δp)^2/2ρv_w$.
Usando $I$, podemos calcular $β$ directamente de su definición en $β(dB) = 10log_{10}(I/I_0)$.
Solución
1. Identifica los datos conocidos:
El sonido viaja a $331 m/s$ en el aire a $0 °C$.
El aire tiene una densidad de $1,29 kg/m^3$ a presión atmosférica y $0 °C$.
2. Ingresa estos valores y la amplitud de presión en $I = (Δp)^2/2ρv$.
$$I = \frac{(Δp)^2}{2ρv} = \frac{(0.656 Pa)^2}{2(1.29 kg/m^3)(331 m/s)} = 5.04 × 10^{-4} W/m^2$$3. Ingresa el valor para $I$ y el valor conocido para $I_0$ en $β(dB) = 10log_{10}(I/I_0)$. Calcula para hallar el nivel de intensidad del sonido en decibelios:
$$10log_{10}(5.04 × 10^8) = 10(8.70) dB = 87 dB$$Explicación
Este sonido de $87 dB$ tiene una intensidad cinco veces mayor que un sonido de $80 dB$. Por lo tanto, un factor de intensidad de cinco corresponde a una diferencia de $7 dB$ en el nivel de intensidad del sonido. Este valor es verdadero para cualquier intensidad que difiera en un factor de cinco.
Ejemplo 7.3
Cambiando los niveles de intensidad de un sonido
Demuestra que si un sonido es dos veces más intenso que otro, tiene un nivel de sonido aproximadamente $3 dB$ más alto.
Estrategia
Tenemos en cuenta que la proporción de dos intensidades es de $2$ a $1$, y luego se nos pide que encontremos la diferencia en sus niveles de sonido en decibelios. Podemos resolver este problema usando las propiedades de los logaritmos.
Solución
1. Identificar los datos conocidos:
La relación de las dos intensidades es $2$ a $1$, o
$$\frac{I_2}{I_1} = 2.00$$Queremos mostrar que la diferencia en los niveles de sonido es de aproximadamente $3 dB$. Es decir, queremos mostrar:
$$β_2 - β_1 = 3dB$$Recuerda que
$$log_{10}b - log_{10}a = log_{10}(b/a)$$2. Usa la definición de $β$ para obtener
$$β_2 - β_1 = 10log_{10}(I_2/I_1) = 10log_{10}2.00 = 10(0.301) dB$$entonces:
$$β_2 - β_1 = 3.01 dB$$Explicación
Esto significa que los dos niveles de intensidad de sonido difieren en $3.01 dB$, o aproximadamente $3 dB$, como se anuncia. Ten en cuenta que dado que solo se proporciona la relación $I_2/I_1$ (y no las intensidades reales), este resultado es verdadero para cualquier intensidad que difiera en un factor de dos. Por ejemplo, un sonido de $56,0 dB$ es dos veces más intenso que un sonido de $53,0 dB$, un sonido de $97,0 dB$ es la mitad de intenso que un sonido de $100 dB$, y así sucesivamente.
 Comprueba tu aprendizaje 7.2
Comprueba tu aprendizaje 7.2
También se está utilizando otra escala de decibeles, llamada nivel de presión acústica, en función de la relación de la amplitud de la presión a la presión de referencia. Esta escala se usa particularmente en aplicaciones donde el sonido viaja en el agua. Tratar esta escala está fuera del alcance de este texto porque no se usa comúnmente para los sonidos en el aire, pero es importante tener en cuenta que cuando se citan los niveles de presión sonora se pueden encontrar niveles de decibeles muy diferentes.
El oído humano tiene una tremenda amplitud y sensibilidad. Nos puede dar una gran cantidad de información simple, como el tono, el volumen y la dirección. La percepción de la frecuencia se llama tono. Típicamente, los humanos tienen un excelente tono relativo y pueden discriminar entre dos sonidos si sus frecuencias difieren en $0.3$% o más.
Por ejemplo, $500.0$ y $501.5 Hz$ son notablemente diferentes. Las notas musicales son sonidos de una frecuencia particular que pueden ser producidos por la mayoría de los instrumentos y en la música occidental tienen nombres particulares, como A-sharp, C o E-flat. La percepción de intensidad se llama sonoridad. A una frecuencia dada, es posible discernir diferencias de aproximadamente $1 dB$, y se nota fácilmente un cambio de $3 dB$. Pero la sonoridad no está relacionada solo con la intensidad. La frecuencia tiene un efecto importante en la intensidad del sonido. Los sonidos cerca de los extremos de frecuencias altas y bajas del rango de audición parecen incluso menos fuertes, porque el oído es menos sensible a esas frecuencias. Cuando un violín toca la mitad C, no se puede confundir con un piano que toca la misma nota. La razón es que cada instrumento produce un conjunto distintivo de frecuencias e intensidades. Llamamos a nuestra percepción de estas combinaciones de frecuencias e intensidades el tono de calidad o, más comúnmente, el timbre del sonido. Timbre es la forma de la onda que surge de las muchas reflexiones, resonancias y superposiciones en un instrumento.
Una unidad llamada fonio se usa para expresar el volumen numéricamente. Los fonios difieren de los decibeles porque el fonio es una unidad de percepción de sonoridad, mientras que el decibelio es una unidad de intensidad física. La muestra la relación del volumen con la intensidad (o nivel de intensidad) y la frecuencia de las personas con audición normal.
Las líneas curvas son curvas de igual sonoridad. Cada curva está etiquetada con su sonoridad en fonios. Cualquier sonido a lo largo de una curva dada es percibido como igualmente alto por la persona promedio. Las curvas se determinaron teniendo un gran número de personas que compararon la sonoridad de los sonidos en diferentes frecuencias y niveles de intensidad de sonido. A una frecuencia de $1000 Hz$, los fonios se consideran numéricamente iguales a los decibelios.
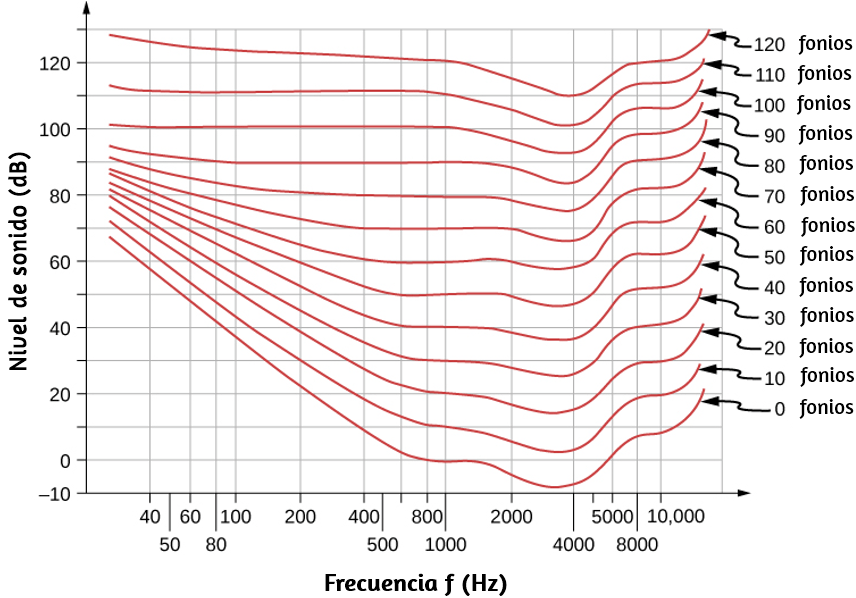
Ejemplo 7.4
Medición de la sonoridad
(a) ¿Cuál es la intensidad en fonios de un sonido de $100 Hz$ que tiene un nivel de intensidad de $80 dB$? (b) ¿Cuál es el nivel de intensidad en decibelios de un sonido de $4000 Hz$ con un volumen de $70$ fonios? (c) ¿A qué nivel de intensidad tendrá un sonido de $8000 Hz$ la misma intensidad que un sonido de $200 Hz$ a $60 dB$?
Estrategia
La gráfica de la debe estar referenciada para resolver este ejemplo. Para encontrar la intensidad de un sonido determinado, debes conocer su frecuencia y nivel de intensidad, ubicar ese punto en la cuadrícula cuadrada y luego interpolar entre las curvas de intensidad para obtener la intensidad en fonios. Una vez que se localiza ese punto, el nivel de intensidad se puede determinar a partir del eje vertical.
Solución
1. Identifica los datos conocidos: la cuadrícula cuadrada del gráfico que relaciona los fonios y los decibelios es un gráfico del nivel de intensidad en función de la frecuencia, ambas cantidades físicas: $100 Hz$ a $80 dB$ se encuentran a medio camino entre las curvas marcadas de $70$ y $80$ fonios.
Encuentra la sonoridad: $75$ fonios.
2. Identifica los datos conocidos: los valores se dan a $4000 Hz$ a $70$ fonios.
Sigue la curva de $70$ fonios hasta que alcances $4000 Hz$. En ese punto, estás por debajo de la línea de $70 dB$ a aproximadamente $67 dB$.
Encuentra el nivel de intensidad: $67 dB$.
3. Localiza l punto para un sonido de $200 Hz$ y $60 dB$.
Encuentra la intensidad: este punto se encuentra ligeramente por encima de la curva de $50$ fonios, por lo que su intensidad es de $51$ fonios.
Busca el nivel de $51$ fonios en $8000 Hz$: $63 dB$.
Explicación
Estas respuestas, al igual que toda la información extraída de la figura , tienen incertidumbres de varios fonios o varios decibeles, en parte debido a dificultades en la interpolación, pero en su mayoría relacionadas con incertidumbres en las curvas de igual sonoridad.
 Comprueba tu aprendizaje 7.3
Comprueba tu aprendizaje 7.3
En esta sección, discutimos las características del sonido y cómo escuchamos, pero ¿cómo se producen los sonidos que escuchamos? Las fuentes de sonido interesantes son los instrumentos musicales y la voz humana, y discutiremos estas fuentes. Pero antes de que podamos entender cómo los instrumentos musicales producen sonido, debemos observar los mecanismos básicos detrás de estos instrumentos. Las teorías detrás de los mecanismos utilizados por los instrumentos musicales involucran interferencia, superposición y ondas estacionarias, las cuales discutimos en la siguiente sección.
La siguiente unidad didáctica hace parte del proyecto @prende.mx, que es una iniciativa de la Secretaría de Educación Pública del gobierno mejicano a través de la cual busca la introducción de las TIC en la Educación. Dentro de este proyecto, el Instituto de Matemáticas de la Universidad Autónoma de México y el Laboratorio de Tecnologías de la Educación (LITE) han participado desarrollando unidades didácticas que han sido específicamente diseñadas para su uso en las tabletas usando la herramienta DescartesJS. La unidad didáctica, se ha titulado ¿Por qué cambia el sonido que se escucha?, que discute los conceptos asociados al tono o frecuencia.
Puedes hacer un recorrido por los cuatro apartados de la unidad (Observa, Explora, Aprende y Prueba), de tal forma que interactúes con cada una de las escenas, y puedas verificar el comportamiento de las ondas de sonidos para diferentes valores de velocidad, frecuencia y dirección de las ondas. La prueba medirá el nivel de conocimientos adquiridos. La unidad cuenta con algunas herramientas como regla, transportador y calculadora, que para las escenas no son necesarias, sólo son parte del diseño general del proyecto, útiles para otras unidades.
En el botón de créditos, puedes conocer información sobre los autores de la unidad didáctica.
Si prestaste atención al apartado Aprende, habrás notado que, mientras más rápido el oyente se acerca a la fuente de sonido, más crestas recibe en un mismo tiempo. Esto significa en que oirá una frecuencia más alta de la onda o, si se prefiere, un tono más alto, conforme se acerque más rápido a la fuente.
La interferencia es el sello distintivo de las ondas, todas las cuales exhiben una interferencia constructiva y destructiva exactamente análoga a la observada para las ondas de agua. De hecho, una forma de probar que algo "es una onda" es observar los efectos de interferencia. Como el sonido es una onda, esperamos que muestre interferencia.
En el capítulo de Ondas, discutimos la interferencia de las funciones de onda que difieren solo en un cambio de fase. Encontramos que la función de onda que resulta de la superposición de $y_1(x, t) = Asen(kx - ωt + φ)$ e $y_2(x, t) = Asen(kx - ωt)$ es
$$y(x, t) = [2Acos(φ/2)]sen(kx - ωt + φ/2)$$Una forma en que dos ondas idénticas que inicialmente están en fase se desfasan entre sí es hacer que las ondas recorran distancias diferentes; es decir, tienen diferentes longitudes de camino. Las ondas de sonido proporcionan un excelente ejemplo de un cambio de fase debido a una diferencia de trayectoria. Como hemos discutido, las ondas de sonido se pueden modelar básicamente como ondas longitudinales, donde las moléculas del medio oscilan alrededor de una posición de equilibrio, o como ondas de presión.
Cuando las ondas salen de los altavoces, se mueven hacia afuera como ondas esféricas (). Las olas interfieren; la inferencia constructiva es producida por la combinación de dos crestas o dos canales, como se muestra. La interferencia destructiva es producida por la combinación de un canal y una cresta.
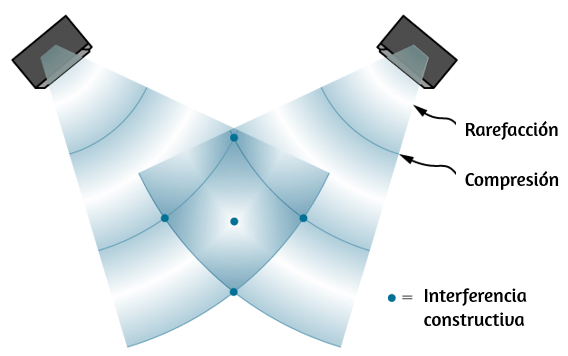
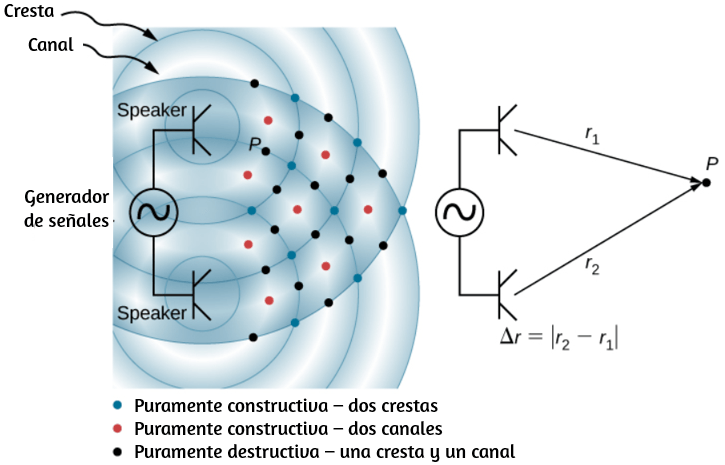
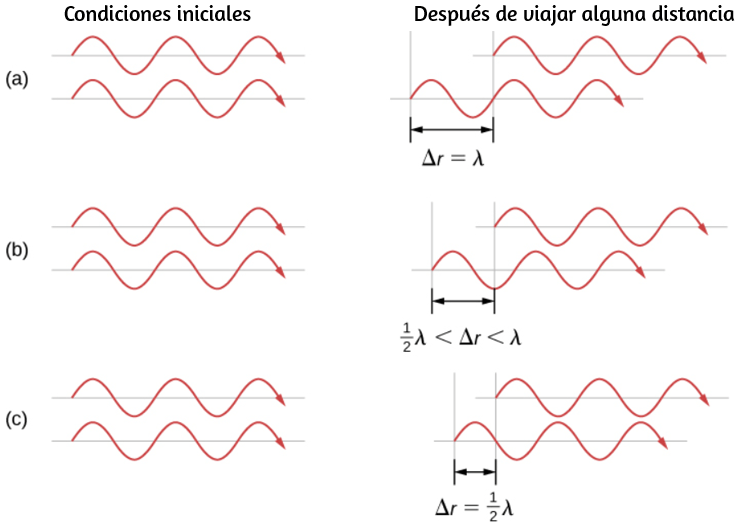
La diferencia de fase en cada punto se debe a las diferentes longitudes de trayectoria recorridas por cada onda. Cuando la diferencia en las longitudes de ruta es un múltiplo entero de una longitud de onda,
$$Δr = |r_2 - r_1| = nλ, \; \textsf{donde} \; n = 0,1,2,3,...,$$Las ondas están en fase y hay interferencia constructiva. Cuando la diferencia en la longitud de la trayectoria es un múltiplo impar de la mitad de la longitud de onda,
$$Δr = |r_2 - r_1| = n\frac{λ}{2}, \; \textsf{donde} \; n = 1,3,5,...,$$Las ondas están desfasadas $180°$ ($π rad$) y el resultado es una interferencia destructiva. Estos puntos se pueden ubicar con un medidor de intensidad de nivel de sonido.
Ejemplo 7.5
Interferencia de las ondas sonoras
Dos altavoces están separados por $5.00 m$ y están siendo controlados por un generador de señales a una frecuencia desconocida. Un estudiante con un medidor de nivel de sonido se retira horizontalmente $6.00 m$ y baja $2.00 m$, y encuentra la primera intensidad mínima, como se muestra a continuación. ¿Cuál es la frecuencia suministrada por el generador de señales? Supón que la velocidad de onda del sonido es $v = 343.00 m/s$.
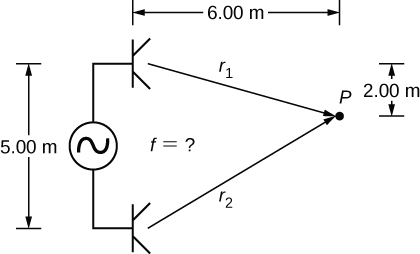
Estrategia
La velocidad de onda es igual a $v = \frac{λ}{T} = λf$. La frecuencia es entonces $f = \frac{v}{λ}$. Una intensidad mínima indica interferencia destructiva y el primer punto se produce cuando hay una diferencia de trayectoria de $Δr = λ/2$, que se puede encontrar en la geometría.
Solución
1. Encuentra la longitud del camino al punto mínimo de cada altavoz (ver figura).
$$r_1 = \sqrt{(6.00 m)^2 + (2.00 m)^2} = 6.32 m,$$ $$r_2 = \sqrt{(6.00 m)^2 + (3.00 m)^2} = 6.71 m$$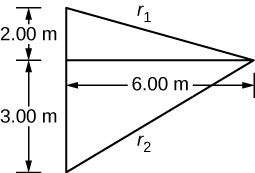
2. Usa la diferencia en la longitud de la trayectoria para encontrar la longitud de onda.
$$Δr = |r_2 - r_2| = |6.71 m - 6.32 m| = 0.39 m$$ $$λ = 2Δr = 2(0.39 m) = 0.78 m$$3. Encuentra la frecuencia.
Explicación
Si el punto $P$ fuera un punto de intensidad máxima, entonces la longitud de la trayectoria sería un múltiplo entero de la longitud de onda.
 Comprueba tu aprendizaje 7.4
Comprueba tu aprendizaje 7.4
El concepto de un cambio de fase debido a una diferencia en la longitud de la trayectoria es muy importante. Volverás a utilizar este concepto en fotones y ondas de la materia., donde analizaremos cómo Thomas Young usó este método en su famoso experimento de doble rendija para proporcionar evidencia de que la luz tiene propiedades de onda.
La muestra un uso inteligente de la interferencia de sonido para cancelar el ruido. Se han propuesto aplicaciones a gran escala de reducción activa de ruido por interferencia destructiva para compartimentos completos de pasajeros en aviones comerciales. Para obtener una interferencia destructiva, se realiza un análisis electrónico rápido y se introduce un segundo sonido $180°$ fuera de fase con el sonido original, con sus máximos y mínimos exactamente invertidos del ruido entrante.
Las ondas sonoras en los fluidos son ondas de presión y son consistentes con el principio de Pascal; es decir, las presiones de dos fuentes diferentes se suman y restan como números simples. Por lo tanto, las presiones manométricas positivas y negativas se suman a una presión mucho menor, produciendo un sonido de menor intensidad. Aunque la interferencia completamente destructiva solo es posible en las condiciones más simples, es posible reducir los niveles de ruido en $30 dB$ o más con esta técnica.
 Comprueba tu aprendizaje 7.5
Comprueba tu aprendizaje 7.5
¿Dónde más podemos observar la interferencia de sonido? Todas las resonancias de sonido, como en los instrumentos musicales, se deben a interferencias constructivas y destructivas. Solo las frecuencias resonantes interfieren constructivamente para formar ondas estacionarias, mientras que otras interfieren destructivamente y están ausentes.
Como vimos en el capítulo de Ondas, las ondas estacionarias están formadas por dos ondas que se mueven en direcciones opuestas. Cuando dos ondas sinusoidales idénticas se mueven en direcciones opuestas, las ondas pueden modelarse como
$$y_1(x, t) = Asen(kx - ωt) y y_2(x, t) = Asen(kx + ωt)$$Cuando estas dos ondas interfieren, la onda resultante es una onda estacionaria:
$$y_R(x, t) = [2Asen(kx)]cos(ωt)$$La resonancia se puede producir debido a las condiciones de contorno impuestas en una onda. En el capítulo de Ondas, demostramos que la resonancia se podía producir en una cuerda bajo tensión que tenía condiciones de contorno simétricas, específicamente, un nodo en cada extremo. Definimos un nodo como un punto fijo donde la cuerda no se movió. Encontramos que las condiciones de los límites simétricos dieron lugar a que algunas frecuencias resonaran y produjeran ondas estacionarias, mientras que otras frecuencias interfieren destructivamente. Las ondas de sonido pueden resonar en un tubo hueco, y las frecuencias de las ondas de sonido que resuenan dependen de las condiciones de contorno.
Supongamos que tenemos un tubo que está cerrado en un extremo y abierto en el otro. Si sostenemos un diapasón de sintonía vibrante cerca del extremo abierto del tubo, una onda de sonido incidente se desplaza a través del tubo y se refleja en el extremo cerrado. El sonido reflejado tiene la misma frecuencia y longitud de onda que la onda de sonido incidente, pero está viajando en la dirección opuesta. En el extremo cerrado del tubo, las moléculas de aire tienen muy poca libertad para oscilar, y surge un nodo. En el extremo abierto, las moléculas son libres de moverse, y en la frecuencia correcta, se produce un antinodo. A diferencia de las condiciones de contorno simétricas para las ondas estacionarias en la cuerda, las condiciones de contorno para un tubo abierto en un extremo y cerrado en el otro extremo son anti-simétricas: un nodo en el extremo cerrado y un antinodo en el extremo abierto.
Si el diapasón de sintonía tiene la frecuencia correcta, la columna de aire en el tubo resuena con fuerza, pero en la mayoría de las frecuencias vibra muy poco. Esta observación solo significa que la columna de aire tiene solo ciertas frecuencias naturales. Considera la frecuencia más baja que hará que el tubo resuene, produciendo un sonido fuerte. Habrá un nodo en el extremo cerrado y un antinodo en el extremo abierto, como se muestra en la .
La onda estacionaria formada en el tubo tiene un antinodo en el extremo abierto y un nodo en el extremo cerrado. La distancia desde un nodo a un antinodo es un cuarto de la longitud de onda, y esto es igual a la longitud del tubo; por lo tanto, $λ_1 = 4L$. Esta misma resonancia puede producirse por una vibración introducida en o cerca del extremo cerrado del tubo (). Es mejor considerar esto como una vibración natural de la columna de aire, independientemente de cómo se induzca.
Dado que los desplazamientos máximos de aire son posibles en el extremo abierto y ninguno en el extremo cerrado, otras longitudes de onda más cortas pueden resonar en el tubo, como la que se muestra en la . Aquí, la onda estacionaria tiene tres cuartas partes de su longitud de onda en el tubo, o $\frac{3}{4}λ_3 = L$, de modo que $λ_3 = \frac{4}{3}L$.
Continuar con este proceso revela una serie completa de sonidos de menor longitud de onda y de mayor frecuencia que resuenan en el tubo. Usamos términos específicos para las resonancias en cualquier sistema. La frecuencia de resonancia más baja se denomina fundamental, mientras que todas las frecuencias de resonancia más altas se denominan armónicos. Las frecuencias resonantes que son múltiplos integrales de la fundamental se denominan colectivamente armónicos. El fundamental es el primer armónico, el segundo armónico es el doble de la frecuencia del primer armónico, y así sucesivamente. Algunos de estos armónicos pueden no existir para un escenario dado. La muestra los armónicos fundamental y los tres primeros (o los armónicos primero, tercero, quinto y séptimo) en un tubo cerrado en un extremo.
La relación para las longitudes de onda resonantes de un tubo cerrado en un extremo es
Ahora busquemos un patrón en las frecuencias de resonancia para un tubo simple que está cerrado en un extremo. El fundamental tiene $λ = 4L$, y la frecuencia está relacionada con la longitud de onda y la velocidad del sonido según lo dado por
$$v = fλ$$Resolviendo para f en esta ecuación obtenemos
$$f = \frac{v}{λ} = \frac{v}{4L}$$donde v es la velocidad del sonido en el aire. De manera similar, el primer sobretono tiene $λ = 4L/3$ (ver ), de modo que
$$f = 3\frac{v}{4L} = 3f_1$$Debido a que $f_3 = 3f_1$, llamamos al primer armónico el tercer armónico. Continuando con este proceso, vemos un patrón que puede generalizarse en una sola expresión. Las frecuencias resonantes de un tubo cerrado en un extremo son
donde $f_1$ es el fundamental, $f_3$ es el primer sobretono, y así sucesivamente. Es interesante que las frecuencias de resonancia dependen de la velocidad del sonido y, por lo tanto, de la temperatura. Esta dependencia plantea un problema notable para los órganos en las catedrales antiguas sin calefacción, y también es la razón por la cual los músicos comúnmente ponen sus instrumentos de viento a temperatura ambiente antes de tocarlos.
Otra fuente de ondas estacionarias es un tubo que está abierto en ambos extremos. En este caso, las condiciones de contorno son simétricas: un antinodo en cada extremo. Las resonancias de los tubos abiertos en ambos extremos se pueden analizar de manera muy similar a las de los tubos cerrados en un extremo. Las columnas de aire en tubos abiertos en ambos extremos tienen desplazamientos máximos de aire en ambos extremos (). Las ondas estacionarias se forman como se muestra en la figura.
La relación para las longitudes de onda resonantes de un tubo abierto en ambos extremos es
Basado en el hecho de que un tubo abierto en ambos extremos tiene desplazamientos máximos de aire en ambos extremos, y al usar la como guía, podemos ver que las frecuencias resonantes de un tubo abierto en ambos extremos son
donde $f_1$ es el fundamental, $f_2$ es el primer armónico, $f_3$ es el segundo armónico, y así sucesivamente. Observa que un tubo abierto en ambos extremos tiene una frecuencia fundamental el doble de lo que tendría si se cerrara en un extremo. También tiene un espectro de armónicos diferente al de un tubo cerrado en un extremo.
Ten en cuenta que un tubo abierto en ambos extremos tiene condiciones de contorno simétricas, similares a las cuerdas fijas en ambos extremos discutidas en el capítulo de Ondas. Las relaciones para las longitudes de onda y las frecuencias de un instrumento de cuerda son las mismas que se dan en la ecuación 7.15 y la ecuación 7.16. La velocidad de la onda en la cuerda (en Ondas) es $v = \sqrt{\frac{F_T}{μ}}$. El aire alrededor de la cuerda vibra a la misma frecuencia que la cuerda, produciendo un sonido de la misma frecuencia. La onda de sonido se mueve a la velocidad del sonido y la longitud de onda se puede encontrar usando $v = λf$.
 Comprueba tu aprendizaje 7.6
Comprueba tu aprendizaje 7.6
 Comprueba tu aprendizaje 7.7
Comprueba tu aprendizaje 7.7
Te presentamos otra unidad didáctica interactiva del proyecto @prende.mx, llamada: el sonido atrapado en un tubo. Recorre los tres apartados y repasa algunos conceptos asociados a las ondas estacionarias.
Algunos instrumentos musicales, como vientos de madera, latón y órganos tubulares, pueden modelarse como tubos con condiciones de contorno simétricas, es decir, abiertos o cerrados en ambos extremos (). Otros instrumentos se pueden modelar como tubos con condiciones de contorno anti-simétricas, como un tubo con un extremo abierto y el otro extremo cerrado ().
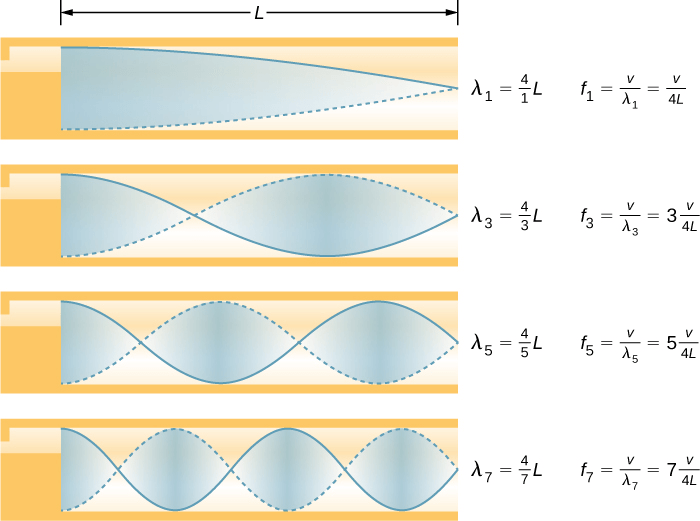
Las frecuencias resonantes son producidas por ondas longitudinales que viajan por los tubos e interfieren con las ondas reflejadas que viajan en la dirección opuesta. Un órgano de tubos se fabrica con varios tubos de longitudes fijas para producir diferentes frecuencias. Las ondas son el resultado del aire comprimido que se permite expandir en los tubos. Incluso en tubos abiertos, se produce cierta reflexión debido a las restricciones de los lados de los tubos y la presión atmosférica fuera del tubo abierto.
Los antinodos no aparecen en la abertura del tubo, sino que dependen del radio del tubo. Las ondas no se expanden completamente hasta que están fuera del extremo abierto de un tubo, y para un tubo de pared delgada, se debe agregar una corrección final. Esta corrección final es aproximadamente $0,6$ veces el radio del tubo y se debe agregar a la longitud del tubo.
Los músicos de instrumentos como la flauta o el oboe varían la longitud del tubo al abrir y cerrar los orificios para los dedos. En un trombón, cambia la longitud del tubo utilizando un tubo deslizante. Los bugles tienen una longitud fija y pueden producir solo un rango limitado de frecuencias.
El fundamental y los armónicos pueden estar presentes simultáneamente en una variedad de combinaciones. Por ejemplo, la C media en una trompeta suena distintivamente diferente de la C media en un clarinete, aunque ambos instrumentos son versiones modificadas de un tubo cerrado en un extremo. La frecuencia fundamental es la misma (y generalmente la más intensa), pero los armónicos y su combinación de intensidades son diferentes y están sujetos a la maniobra del músico. Esta mezcla es lo que le da a los diversos instrumentos musicales (y voces humanas) sus características distintivas, ya sea que tengan columnas de aire, cuerdas, cajas de resonancia o cabezas de tambor. De hecho, gran parte de nuestra habla está determinada por la conformación de la cavidad formada por la garganta y la boca, y la posición de la lengua para ajustar el fundamental y la combinación de armónicos. Por ejemplo, se puede hacer que las cavidades resonantes simples resuenen con el sonido de las vocales (). En los niños en la pubertad, la laringe crece y la forma de la cavidad resonante cambia, dando lugar a la diferencia en las frecuencias predominantes en el habla entre hombres y mujeres.
Ejemplo 7.6
Encontrar la longitud de un tubo con un Fundamental de $128 Hz$
(a) ¿Qué longitud debe tener un tubo cerrado en un extremo en un día en que la temperatura del aire es $22.0 °C$ si su frecuencia fundamental es de $128 Hz$ (C por debajo de la C media)?
(b) ¿Cuál es la frecuencia de su cuarto armónico?
Estrategia
La longitud $L$ se puede encontrar en la relación $fn = n\frac{n}{4L}$, pero primero necesitamos encontrar la velocidad del sonido $v$.
Solución
a. Identifica los datos conocidos: la frecuencia fundamental es de $128 Hz$ y la temperatura del aire es de $22.0 °C$.
Usa $f_n = n\frac{n}{4L}$ para encontrar la frecuencia fundamental ($n = 1$),
$$f_1 = \frac{n}{4L}$$Resuelve esta ecuación para la longitud,
$$L = \frac{v}{4f_1}$$Encuentra la velocidad del sonido usando $v = (331 m/s)\sqrt{T/273K}$
$$v = (331 m/s)\sqrt{295K/273K} = 344 m/s$$Introduce los valores de la velocidad del sonido y la frecuencia en la expresión para $L$.
$$L = \frac{v}{4f_1} = \frac{344 m/s}{4(128 Hz)} = 0.672 m$$b. Identifica los datos conocidos: el primer armónico tiene $n = 3$, el segundo armónico tiene $n = 5$, el tercer armónico tiene $n = 7$ y el cuarto armónico tiene $n = 9$.
$$f_9 = 9\frac{v}{4L} = 9f_1 = 1.15 kHz$$Explicación
Muchos instrumentos de viento son tubos modificados que tienen orificios para los dedos, válvulas y otros dispositivos para cambiar la longitud de la columna de aire resonante y, por lo tanto, la frecuencia de la nota tocada. Las bocinas que producen frecuencias muy bajas requieren tubos tan largos que se enrollan en bucles. Un ejemplo es la tuba. El hecho de que se produzca un sobretono en un tubo simple o en un instrumento musical depende de cómo se estimule la vibración y de los detalles de su forma. El trombón, por ejemplo, no produce su frecuencia fundamental y solo hace armónicos.
Si tienes dos tubos con la misma frecuencia fundamental, pero uno está abierto en ambos extremos y el otro cerrado en un extremo, sonarían diferente cuando se tocan porque tienen armónicos diferentes. El C medio, por ejemplo, sonaría más rico tocado en un tubo abierto, porque tiene incluso múltiplos de los fundamentales, así como impares. Un tubo cerrado solo tiene múltiplos impares.
La resonancia se produce en muchos sistemas diferentes, incluidas cuerdas, columnas de aire y átomos. Como vimos en capítulos anteriores, la resonancia es la oscilación conducida o forzada de un sistema a su frecuencia natural. En la resonancia, la energía se transfiere rápidamente al sistema oscilante, y la amplitud de sus oscilaciones aumenta hasta que el sistema ya no puede ser descrito por la ley de Hooke. Un ejemplo de esto es el sonido distorsionado producido intencionalmente en ciertos tipos de música rock.
Los instrumentos de viento utilizan la resonancia en las columnas de aire para amplificar los tonos hechos por labios o cañas vibrantes. Otros instrumentos también utilizan la resonancia de aire en formas inteligentes para amplificar el sonido.
La muestra un violín y una guitarra, ambos con cajas de resonancia pero con diferentes formas, lo que resulta en diferentes estructuras de armónicos. La cuerda vibrante crea un sonido que resuena en el cuadro de sondeo, amplificando en gran medida el sonido y creando armónicos que dan al instrumento su timbre característico.
Cuanto más compleja sea la forma de la caja de resonancia, mayor será su capacidad de resonar en un amplio rango de frecuencias. La marimba, como la que se muestra en la , usa macetas o calabazas debajo de las tablillas de madera para amplificar sus tonos. La resonancia de la olla se puede ajustar añadiendo agua.

Hemos enfatizado las aplicaciones de sonido en nuestras discusiones sobre resonancia y ondas estacionarias, pero estas ideas se aplican a cualquier sistema que tenga características de onda. Las cuerdas vibrantes, por ejemplo, realmente resuenan y tienen fundamentales y armónicos similares a los de las columnas de aire. Más sutiles son las resonancias en los átomos debido al carácter de onda de sus electrones.
Sus orbitales pueden verse como ondas estacionarias, que tienen un fundamental (estado fundamental) y armónicos (estados excitados). Es fascinante que las características de onda se apliquen a una amplia gama de sistemas físicos.

En esta otra unidad didáctica interactiva del proyecto @prende.mx, llamada: ¿Cómo detecto los sonidos graves y los agudos?, podrás analizar el efecto (conocido como difracción) por el cual el sonido da vuelta al pasar por un obstáculo y el grado en que da vuelta dependiendo de su frecuencia, y entender la razón por la cual los sonidos graves nos llegan más fácilmente que los agudos.
El estudio de la música proporciona muchos ejemplos de la superposición de ondas y la interferencia constructiva y destructiva que se produce. Muy pocos ejemplos de música consisten en una sola fuente que reproduce una sola frecuencia durante un período prolongado de tiempo. Probablemente estarás de acuerdo en que una sola frecuencia de sonido durante un período prolongado puede ser aburrida hasta el punto de irritación, similar al drone no deseado de un motor de avión o un ventilador ruidoso. La música es agradable e interesante debido a la mezcla de las frecuencias cambiantes de varios instrumentos y voces.
Un fenómeno interesante que ocurre debido a la interferencia constructiva y destructiva de dos o más frecuencias de sonido es el fenómeno de las pulsaciones. Si dos sonidos difieren en las frecuencias, las ondas de sonido se pueden modelar como
Usando la identidad trigonométrica $cosu + cosv = 2cos(\frac{u + v}{2})cos(\frac{u - v}{2})$ y considerando el punto en el espacio como $x = 0.0 m$, encontramos que el sonido resultante en un punto en el espacio, a partir de la superposición de los dos sonidos, es igual a la :
$$y(t) = 2Acos(2πf_{\textsf{prom}}t) cos2π \left(\frac{|f_2 - f_1|}{2} \right)t$$donde la frecuencia de la pulsación es
Los sintonizadores de piano pueden utilizar estas pulsaciones para afinar un piano. Se toca un diapasón y se toca una nota en el piano. A medida que el afinador de piano sintoniza la cuerda, los tiempos tienen una frecuencia más baja a medida que la frecuencia de la nota tocada se acerca a la frecuencia del diapasón.
Ejemplo 7.7
Encuentra la frecuencia de pulsación entre dos diapasones
¿Cuál es la frecuencia de pulsación producida cuando una horquilla de sintonización de una frecuencia de $256 Hz$ y una horquilla de sintonía de una frecuencia de $512 Hz$ se tocan simultáneamente?
Estrategia
La frecuencia de pulsación es la diferencia de las dos frecuencias.
Solución
Usamos $f_{\textsf{prom}} = |f_2 - f_1|$:
$$|f_2 - f_1| = (512 - 256)Hz = 256 Hz$$Explicación
La frecuencia de pulsación es el valor absoluto de la diferencia entre las dos frecuencias. Una frecuencia negativa no tendría sentido.
 Comprueba tu aprendizaje 7.9
Comprueba tu aprendizaje 7.9
El estudio de la superposición de varias ondas tiene muchas aplicaciones interesantes más allá del estudio del sonido. En capítulos posteriores, discutiremos las propiedades de onda de las partículas. Las partículas pueden modelarse como un "paquete de ondas" que resulta de la superposición de varias ondas, donde la partícula se mueve a la "velocidad de grupo" del paquete de ondas.
El sonido característico del zumbido de una motocicleta es un ejemplo del efecto Doppler. Específicamente, si estás parado en una esquina y observas una ambulancia con una sirena que suena a una velocidad constante, notarás dos cambios característicos en el sonido de la sirena. Primero, el sonido aumenta en intensidad cuando la ambulancia se acerca y disminuye en intensidad cuando se aleja, lo que se espera. Pero además, la sirena aguda cambia dramáticamente a un sonido de tono más bajo. A medida que pasa la ambulancia, la frecuencia del sonido que escucha un observador estacionario cambia de una frecuencia alta constante a una frecuencia inferior constante, aunque la sirena está produciendo una frecuencia de fuente constante. Cuanto más se acerque la ambulancia, más brusco será el cambio. Además, cuanto más rápido se mueva la ambulancia, mayor será el cambio. También escuchamos este cambio característico en la frecuencia de los automóviles, aviones y trenes que pasan.
El efecto Doppler es una alteración en la frecuencia observada de un sonido debido al movimiento de la fuente o del observador. Vive este efecto en la siguiente escena interactiva, diseñada por Julio César Domínguez Tovar:
Aunque menos familiar, este efecto se nota fácilmente para una fuente estacionaria y un observador en movimiento. Por ejemplo, si viajas en un tren por una bocina de advertencia estacionaria, escucharás que la frecuencia de la bocina cambia de alta a baja a medida que pasa.
El cambio real en la frecuencia debido al movimiento relativo de la fuente y el observador se llama cambio Doppler. El efecto Doppler y el cambio Doppler llevan el nombre del físico y matemático austriaco Christian Johann Doppler (1803–1853), quien realizó experimentos con fuentes móviles y observadores móviles. Doppler, por ejemplo, tenía músicos tocando en un vagón de tren abierto y también tocaba parado junto a las vías del tren cuando pasaba un tren. Su música se observó tanto dentro como fuera del tren, y se midieron los cambios en la frecuencia.
¿Qué causa el cambio Doppler? La ilustra las ondas de sonido emitidas por fuentes estacionarias y móviles en una masa de aire estacionaria. Cada perturbación se propaga de forma esférica desde el punto en el que se emite el sonido. Si la fuente es estacionaria, entonces todas las esferas que representan las compresiones de aire en la onda de sonido se centran en el mismo punto, y los observadores estacionarios en ambos lados escuchan la misma longitud de onda y frecuencia que la fuente (caso a). Si la fuente se está moviendo, la situación es diferente. Cada compresión del aire se mueve hacia fuera en una esfera desde el punto en el que se emitió, pero el punto de emisión se mueve. Este punto de emisión en movimiento hace que las compresiones de aire estén más juntas en un lado y más separadas en el otro. Por lo tanto, la longitud de onda es más corta en la dirección en que se mueve la fuente (a la derecha en el caso b), y más larga en la dirección opuesta (a la izquierda en el caso b). Finalmente, si los observadores se mueven, como en el caso (c), la frecuencia a la que reciben las compresiones cambia. El observador que se mueve hacia la fuente los recibe a una frecuencia más alta, y la persona que se aleja de la fuente los recibe a una frecuencia más baja.
Sabemos que la longitud de onda y la frecuencia están relacionadas por $v = fλ$, donde v es la velocidad fija del sonido. El sonido se mueve en un medio y tiene la misma velocidad v en ese medio si la fuente se está moviendo o no. Por lo tanto, $f$ multiplicado por $λ$ es una constante. Debido a que el observador de la derecha en el caso (b) recibe una longitud de onda más corta, la frecuencia que recibe debe ser mayor. De manera similar, el observador de la izquierda recibe una longitud de onda más larga y, por lo tanto, oye una frecuencia más baja. Lo mismo sucede en el caso (c). El observador recibe una frecuencia más alta que se mueve hacia la fuente, y un observador que se aleja de la fuente recibe una frecuencia más baja. En general, entonces, el movimiento relativo de la fuente y el observador uno hacia el otro aumenta la frecuencia recibida.
El movimiento relativo separado disminuye la frecuencia. Cuanto mayor sea la velocidad relativa, mayor será el efecto.
El efecto Doppler se produce no solo para el sonido, sino para cualquier onda cuando hay un movimiento relativo entre el observador y la fuente. Los cambios Doppler ocurren en la frecuencia de las ondas de sonido, luz y agua, por ejemplo. Los cambios Doppler se pueden usar para determinar la velocidad, como cuando el ultrasonido se refleja en la sangre en un diagnóstico médico. Las velocidades relativas de las estrellas y galaxias están determinadas por el cambio en las frecuencias de luz recibidas de ellas y han implicado mucho sobre los orígenes del universo. La física moderna se ha visto profundamente afectada por las observaciones de los cambios Doppler.
Considera dos observadores estacionarios $X$ e $Y$ en la , ubicados a cada lado de una fuente estacionaria. Cada observador escucha la misma frecuencia, y esa frecuencia es la frecuencia producida por la fuente estacionaria.
Ahora considere un observador estacionario $X$ con una fuente alejándose del observador con una velocidad constante $v_s < v$ (). En el momento $t = 0$, la fuente emite una onda de sonido, indicada en negro. Esta onda se mueve a la velocidad del sonido $v$. La posición de la onda de sonido en cada intervalo de tiempo del período $T_s$ se muestra como líneas de puntos. Después de un período, la fuente ha movido $Δx = v_sT_s$ y emite una segunda onda de sonido, que se mueve a la velocidad del sonido. La fuente continúa moviéndose y produciendo ondas de sonido, como lo indican los círculos numerados con $3$ y $4$. Observa que a medida que las ondas se mueven, permanecen centradas en sus respectivos puntos de origen.
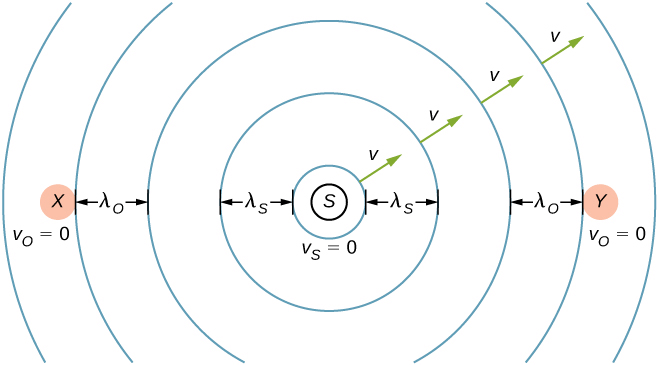
Usando el hecho de que la longitud de onda es igual a la velocidad por el período, y el período es el inverso de la frecuencia, podemos deducir la frecuencia observada:
$$λ_o = λ_s + Δx$$ $$vT_o = vT_s + v_sT_s$$ $$\frac{v}{f_o} = \frac{v}{f_s} + \frac{v_s}{f_s} = \frac{v + v_s}{f_s}$$ $$f_o = f_s \left(\frac{v}{v + v_s} \right)$$
A medida que la fuente se aleja del observador, la frecuencia observada es más baja que la frecuencia de la fuente. Ahora considera una fuente que se mueve a una velocidad constante $v_s$, moviéndose hacia un observador estacionario $Y$, que también se muestra en la .
La longitud de onda es observada por $Y$ como $λ_o = λ_s - Δx = λ_s - v_sT_s$. Una vez más, utilizando el hecho de que la longitud de onda es igual a la velocidad por el período y el período es el inverso de la frecuencia, podemos deducir la frecuencia observada:
$$λ_o = λ_s - Δx$$ $$vT_o = vT_s - v_sT_s$$ $$\frac{v}{f_o} = \frac{v}{f_s} - \frac{v_s}{f_s} = \frac{v - v_s}{f_s}$$ $$f_o = f_s \left(\frac{v}{v - v_s} \right)$$Cuando una fuente se está moviendo y el observador está parado, la frecuencia observada es
donde $f_o$ es la frecuencia observada por el observador estacionario, $f_s$ es la frecuencia producida por la fuente en movimiento, $v$ es la velocidad del sonido, $v_s$ es la velocidad constante de la fuente, y el signo superior es para la fuente que se aproxima al observador y el signo negativo es para la fuente que sale del observador.
¿Qué sucede si el observador se está moviendo y la fuente está estacionaria? Si el observador se mueve hacia la fuente estacionaria, la frecuencia observada es más alta que la frecuencia de la fuente. Si el observador se está alejando de la fuente estacionaria, la frecuencia observada es más baja que la frecuencia de la fuente.
Considera al observador $X$ en la cuando el observador se mueva hacia una fuente estacionaria con una velocidad $v_o$. La fuente emite un tono con una frecuencia constante $f_s$ y un período constante $T_s$. El observador escucha la primera onda emitida por la fuente. Si el observador estuviera estacionario, el tiempo para que pase una longitud de onda del sonido debería ser igual al período de la fuente $T_s$. Como el observador se está moviendo hacia la fuente, el tiempo para que pase una longitud de onda es menor que $T_s$ y es igual al período observado $T_o = T_s - Δt$. En el momento $t = 0$, el observador comienza al principio de una longitud de onda y se mueve hacia la segunda longitud de onda a medida que la longitud de onda se aleja de la fuente. La longitud de onda es igual a la distancia recorrida por el observador más la distancia recorrida por la onda de sonido hasta que el observador la alcanza:
Si el observador se está alejando de la fuente (), se puede encontrar la frecuencia observada:
Las ecuaciones para un observador que se mueve hacia o desde una fuente estacionaria se pueden combinar en una ecuación:
donde $f_o$ es la frecuencia observada, $f_s$ es la frecuencia de origen, $v$ es la velocidad del sonido, $v_o$ es la velocidad del observador, el signo superior es para el observador que se aproxima a la fuente y el signo inferior para el observador que se aleja de la fuente.
La ecuación 7.18 y la ecuación 7.19 se pueden resumir en una ecuación (el signo superior es para aproximarse) y se ilustra más detalladamente en la :
donde $f_o$ es la frecuencia observada, $f_s$ es la frecuencia de origen, v es la velocidad del sonido, $v_o$ es la velocidad del observador, $v_s$ es la velocidad de la fuente, el signo superior es para acercarse y el signo de abajo para salir.
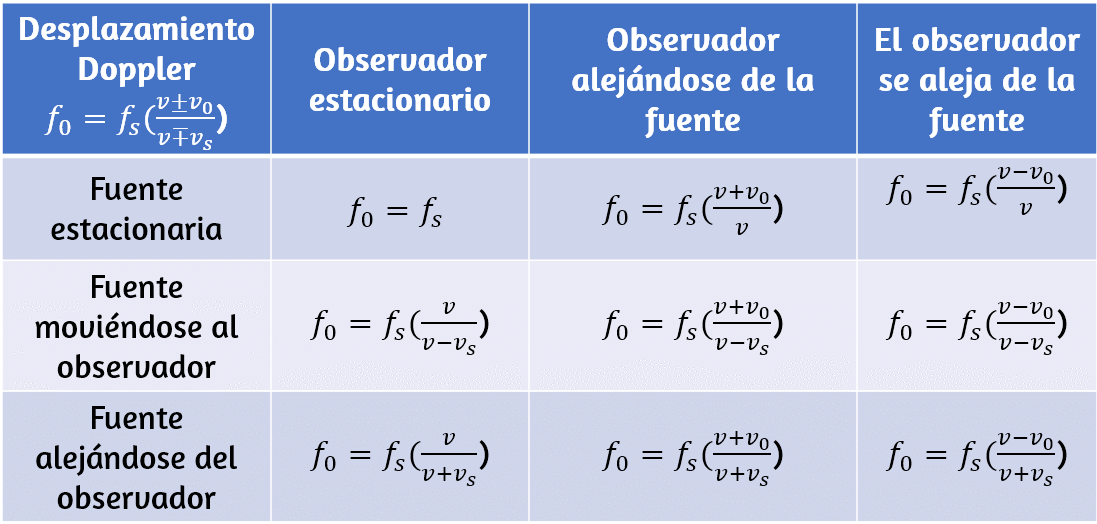
Ejemplo 7.8
Cálculo de un cambio Doppler
Supongamos que un tren que tiene una bocina de $150 Hz$ se está moviendo a $35.0 m/s$ en aire en un día cuando la velocidad del sonido es de $340 m/s$.
(a) ¿Qué frecuencias observa una persona estacionaria al costado de las vías a medida que se acerca el tren y después de que pasa?
(b) ¿Qué frecuencia observa el ingeniero del tren que viaja en el tren?
Estrategia
Para encontrar la frecuencia observada en (a), debemos usar $f_{obs} = f_s(\frac{v ± v}{v ± _s})$ porque la fuente se está moviendo. El signo menos se usa para el tren que se aproxima, y el signo más para el tren que retrocede. En (b), hay dos cambios Doppler: uno para una fuente en movimiento y otro para un observador en movimiento.
Solución
a. Introduce los valores conocidos en $f_o = f_s \left(\dfrac{v ± v}{v - _s} \right)$
$$f_o = f_s \left(\frac{v ± v}{v - _s} \right) = (150 Hz) \left(\frac{340 m/s}{340 m/s - 35.0 m/s} \right)$$Calcula la frecuencia observada por una persona estacionaria a medida que se acerca el tren:
$$f_o = (150Hz)(1.11) = 167 Hz$$Usa la misma ecuación con el signo más para encontrar la frecuencia que escucha una persona estacionada mientras el tren retrocede:
$$f_o = f_s \left(\frac{v ± v}{v + _s} \right) = (150 Hz) \left(\frac{340 m/s}{340 m/s + 35.0 m/s} \right)$$Calcula la segunda frecuencia $f_o = (150Hz)(0.907) = 136 Hz$
b. Identifica los datos conocidos:
Usa la siguiente ecuación:
$$f_0 = \left[f_s \left(\frac{v ± v_o}{v} \right)\right] \left(\frac{v}{v ± v_s} \right)$$La cantidad entre corchetes es la frecuencia desplazada por Doppler debido a un observador en movimiento. El factor a la derecha es el efecto de la fuente en movimiento.
Debido a que el ingeniero de trenes se está moviendo en la dirección hacia la bocina, debemos usar el signo más para las $v_{obs}$; sin embargo, debido a que la bocina también se está moviendo en la dirección del ingeniero, también usamos el signo más para $v_s$. Pero el tren está llevando tanto al ingeniero como a la bocina a la misma velocidad, por lo que $v_s = v_o$. Como resultado, todo menos $f_s$ se cancela, produciendo
$$f_0 = f_s$$Explicación
En el caso de que la fuente y el observador no se muevan juntos, los números calculados son válidos cuando la fuente (en este caso, el tren) está lo suficientemente lejos como para que el movimiento esté casi a lo largo de la línea que une la fuente y el observador. En ambos casos, el cambio es significativo y se nota fácilmente. Ten en cuenta que el desplazamiento es de $17.0 Hz$ hacia el movimiento y $14.0 Hz$ para el movimiento de distancia. Los turnos no son simétricos.
Para el ingeniero que viaja en el tren, podemos esperar que no haya cambios en la frecuencia porque la fuente y el observador se mueven juntos. Esto coincide con tu experiencia. Por ejemplo, no hay un cambio Doppler en la frecuencia de las conversaciones entre el conductor y el pasajero en una motocicleta. Las personas que hablan cuando un viento mueve el aire entre ellos tampoco observan ningún cambio Doppler en su conversación. El punto crucial es que la fuente y el observador no se están moviendo unos respecto a otros.
 Comprueba tu aprendizaje 7.9
Comprueba tu aprendizaje 7.9
El efecto Doppler y el cambio Doppler tienen muchas aplicaciones importantes en ciencia e ingeniería. Por ejemplo, el cambio Doppler en el ultrasonido se puede usar para medir la velocidad de la sangre, y la policía usa el cambio Doppler en el radar (un microondas) para medir las velocidades del automóvil. En meteorología, el cambio Doppler se utiliza para rastrear el movimiento de las nubes de tormenta; tal "Radar Doppler" puede dar la velocidad y la dirección de la lluvia o la nieve en los frentes climáticos. En astronomía, podemos examinar la luz emitida por galaxias distantes y determinar su velocidad en relación con la nuestra. A medida que las galaxias se alejan de nosotros, su luz se desplaza a una frecuencia más baja y, por lo tanto, a una longitud de onda más larga, el llamado desplazamiento del rojo. Dicha información de galaxias muy, muy lejos, nos ha permitido estimar la edad del universo (desde el Big Bang) en aproximadamente 14 mil millones de años.
Al analizar el efecto Doppler de una fuente en movimiento y un observador estacionario, los únicos casos que consideramos fueron los casos en que la fuente se movía a velocidades que eran menores que la velocidad del sonido. Recuerda que la frecuencia observada para una fuente en movimiento que se aproxima a un observador estacionario es $f_o = f_s(\frac{v}{v - v_s})$. A medida que la fuente se acerca a la velocidad del sonido, la frecuencia observada aumenta.
De acuerdo con la ecuación, si la fuente se mueve a la velocidad del sonido, el denominador es igual a cero, lo que implica que la frecuencia observada es infinita. Si la fuente se mueve a velocidades superiores a la velocidad del sonido, la frecuencia observada es negativa.
¿Qué podría significar esto? ¿Qué sucede cuando una fuente se acerca a la velocidad del sonido? Algunos científicos argumentaron una vez que una onda de presión tan grande resultaría de la interferencia constructiva de las ondas sonoras, que sería imposible que un avión supere la velocidad del sonido porque las presiones serían lo suficientemente grandes como para destruir el avión. Pero ahora los aviones vuelan rutinariamente más rápido que la velocidad del sonido. El 28 de julio de 1976, el capitán Eldon W. Joersz y el comandante George T. Morgan volaron un Lockheed SR-71
Blackbird #61-$7958$ a $3529,60 km/h$ ($2193,20 mi/h$), que es Mach $2.85$. El número de Mach es la velocidad de la fuente dividida por la velocidad del sonido:
Verás que ocurren fenómenos interesantes cuando una fuente se acerca y supera la velocidad del sonido.
¿Qué sucede con el sonido producido por una fuente en movimiento, como un avión a reacción, que se acerca o incluso supera la velocidad del sonido? La respuesta a esta pregunta se aplica no solo al sonido, sino también a todas las otras ondas. Supongamos que un avión se acerca directamente a ti, emitiendo un sonido de frecuencia $f_s$.
Cuanto mayor sea la velocidad en comparación con la del avión, mayor será el desplazamiento Doppler y mayor será el valor observado para $f_o$ ().
Ahora, cuando $v_s$ se acerca a la velocidad del sonido, $f_o$ se acerca al infinito, porque el denominador en $f_o = f_s(\frac{v}{v ± v_s})$ se acerca a cero. A la velocidad del sonido, este resultado significa que delante de la fuente, cada onda sucesiva interfiere con la anterior porque la fuente avanza a la velocidad del sonido. El observador los obtiene a todos en el mismo instante, por lo que la frecuencia es infinita [parte (c) de la figura].
Si la fuente excede la velocidad del sonido, el observador no recibe ningún sonido hasta que la fuente haya pasado, por lo que los sonidos de la fuente que se aproxima se mezclan con los de la fuente cuando se retira. Esta mezcla parece desordenada, pero sucede algo interesante: se crea una onda de choque ().
La interferencia constructiva a lo largo de las líneas mostradas (un cono en tres dimensiones) de ondas de sonido similares a las que llegan allí simultáneamente. Esta superposición forma una perturbación llamada explosión sónica, una interferencia constructiva del sonido creada por un objeto que se mueve más rápido que el sonido.
Dentro del cono, la interferencia es principalmente destructiva, por lo que la intensidad del sonido es mucho menor que en la onda de choque. El ángulo de la onda de choque se puede encontrar en la geometría. En el tiempo $t$, la fuente ha movido $v_st$ y la onda de sonido ha movido una distancia $vt$ y el ángulo se puede encontrar usando $senθ = \frac{vt}{v_st} = \frac{v}{v_s}$. Ten en cuenta que el número de Mach se define como $\frac{v_s}{v}$, por lo que el seno del ángulo es igual al inverso del número de Mach,
Es posible que haya oído hablar del término común "estallido supersónico" o "explosión sónica". Un error común es que la explosión sónica se produce cuando el avión rompe la barrera del sonido; es decir, acelera a una velocidad superior a la velocidad del sonido. En realidad, la explosión sónica se produce cuando la onda de choque se desplaza por el suelo.
Un avión crea dos ondas de choque, una desde su nariz y otra desde su cola (). Durante la cobertura televisiva de los aterrizajes del transbordador espacial, a menudo se oían dos explosiones distintas. Estas estaban separadas exactamente por el tiempo que tardaría la lanzadera en pasar por un punto. Los observadores en tierra a menudo no ven que la aeronave está creando la explosión sónica, ya que pasó antes de que la onda de choque los alcance, como se ve en la figura. Si el avión vuela cerca a baja altura, las presiones en la explosión sónica pueden ser destructivas y romper ventanas, así como los nervios de traqueteo. Debido a lo destructivas que pueden ser las explosiones sónicas, los vuelos supersónicos están prohibidos en áreas pobladas.
Las ondas de choque son un ejemplo de un fenómeno más amplio llamado estela de arco. Una estela de arco, como la de la , se crea cuando la fuente de onda se mueve más rápido que la velocidad de propagación de la onda. Las ondas de agua se extienden en círculos desde el punto donde se crearon, y la estela de arco es la estela familiar en forma de V, que se arrastra hacia la fuente. Una estela de arco más exótica se crea cuando una partícula subatómica viaja a través de un medio más rápido que la velocidad de la luz que viaja en ese medio (en el vacío, la velocidad máxima de la luz es $c = 3.00 × 10^8 m/s$; en el medio del agua, la velocidad de la luz es más cercana a $0.75 c$).

Si la partícula crea luz en su paso, esa luz se propaga en una cono con un ángulo indicativo de la velocidad de la partícula, como se ilustra en la . Tal estela de arco se llama radiación de Cerenkov y se observa comúnmente en la física de partículas.



Nuestra investigación de la luz gira en torno a dos preguntas de importancia fundamental: (1) ¿Cuál es la naturaleza de la luz y (2) ¿cómo se comporta la luz en diversas circunstancias? Las respuestas a estas preguntas se pueden encontrar en las ecuaciones de Maxwell, que predicen la existencia de ondas electromagnéticas y su comportamiento. Los ejemplos de luz incluyen radio y ondas infrarrojas, luz visible, radiación ultravioleta y rayos X. Curiosamente, no todos los fenómenos de la luz pueden explicarse por la teoría de Maxwell. Los experimentos realizados a principios del siglo XX mostraron que la luz tiene propiedades corpusculares o similares a las partículas. La idea de que la luz puede mostrar tanto las características de onda como de partícula se llama dualidad onda-partícula.
En este capítulo, estudiaremos las propiedades básicas de la luz. En los siguientes capítulos, investigamos el comportamiento de la luz cuando interactúa con dispositivos ópticos como espejos, lentes y aperturas.
La velocidad de la luz en un vacío $c$ es una de las constantes fundamentales de la física. Es un concepto central en la teoría de la relatividad de Einstein. A medida que se mejoró la precisión de las mediciones de la velocidad de la luz, se encontró que diferentes observadores, incluso aquellos que se mueven a grandes velocidades entre sí, miden el mismo valor para la velocidad de la luz. Sin embargo, la velocidad de la luz varía de manera precisa con el material que atraviesa. Estos hechos tienen implicaciones de gran alcance, como veremos en capítulos posteriores.
La primera medición de la velocidad de la luz fue realizada por el astrónomo danés Ole Roemer (1644–1710) en 1675. Estudió la órbita de Io, una de las cuatro lunas grandes de Júpiter, y descubrió que tuvo un período de revolución de $42.5 h$ alrededor de Júpiter. También descubrió que este valor fluctuaba unos segundos, dependiendo de la posición de la Tierra en su órbita alrededor del Sol. Roemer se dio cuenta de que esta fluctuación se debía a la velocidad finita de la luz y podía usarse para determinar $c$.
Roemer encontró el período de revolución de Io al medir el intervalo de tiempo entre los eclipses sucesivos de Júpiter. La (a) muestra las configuraciones planetarias cuando dicha medición se realiza desde la Tierra en la parte de su órbita donde se aleja de Júpiter. Cuando la Tierra está en el punto $A$, la Tierra, Júpiter e Io están alineados. La próxima vez que ocurra esta alineación, la Tierra se encuentra en el punto $B$, y la luz que lleva esa información a la Tierra debe viajar a ese punto. Como $B$ está más lejos de Júpiter que de $A$, la luz tarda más tiempo en llegar a la Tierra cuando la Tierra está en $B$.
Ahora imagina que es aproximadamente 6 meses más tarde, y los planetas están dispuestos como en la parte (b) de la figura. La medición del período de Io comienza con la Tierra en el punto $A'$ e Io eclipsada por Júpiter. El siguiente eclipse ocurre cuando la Tierra está en el punto $B'$, al que debe viajar la luz que lleva la información de este eclipse. Como $B'$ está más cerca de Júpiter que de $A'$, la luz tarda menos tiempo en llegar a la Tierra cuando está en $B'$. Este intervalo de tiempo entre los eclipses sucesivos de Io vistos en $A'$ y $B'$ es, por lo tanto, menor que el intervalo de tiempo entre los eclipses vistos en $A$ y $B$. Al medir la diferencia en estos intervalos de tiempo y con el conocimiento apropiado de la distancia entre Júpiter y Tierra, Roemer calculó que la velocidad de la luz era de $2.0 × 10^8 m/s$, que es un $33$% por debajo del valor aceptado hoy.
La primera medición terrestre exitosa de la velocidad de la luz fue realizada por Armand Fizeau (1819–1896) en 1849. Colocó una rueda dentada que podía rotarse muy rápidamente en una colina y un espejo en una segunda colina a 8 km de distancia (). Se colocó una fuente de luz intensa detrás de la rueda, de modo que cuando la rueda giró, cortó el haz de luz en una sucesión de pulsos. La velocidad de la rueda se ajustó hasta que no regresó la luz al observador ubicado detrás de la rueda. Esto solo podría suceder si la rueda girara en un ángulo correspondiente a un desplazamiento de ($n + 1/2$) dientes, mientras que los pulsos viajaban hacia el espejo y hacia atrás. Al conocer la velocidad de rotación de la rueda, el número de dientes en la rueda y la distancia al espejo, Fizeau determinó que la velocidad de la luz era de $3,15 × 10^8 m/s$, que es solo un $5$% demasiado alta.
El físico francés Jean Bernard Léon Foucault (1819–1868) modificó el aparato de Fizeau al reemplazar la rueda dentada con un espejo giratorio. En 1862, midió la velocidad de la luz en $2.98 × 10^8 m/s$, lo que está dentro del $0.6$% del valor actualmente aceptado.
Albert Michelson (1852–1931) también usó el método de Foucault en varias ocasiones para medir la velocidad de la luz. Sus primeros experimentos se realizaron en 1878; para 1926, había refinado la técnica tan bien que encontró que $c$ era $(2.99796 ± 4) × 10^8 m/s$.
Hoy en día, la velocidad de la luz es conocida con gran precisión.
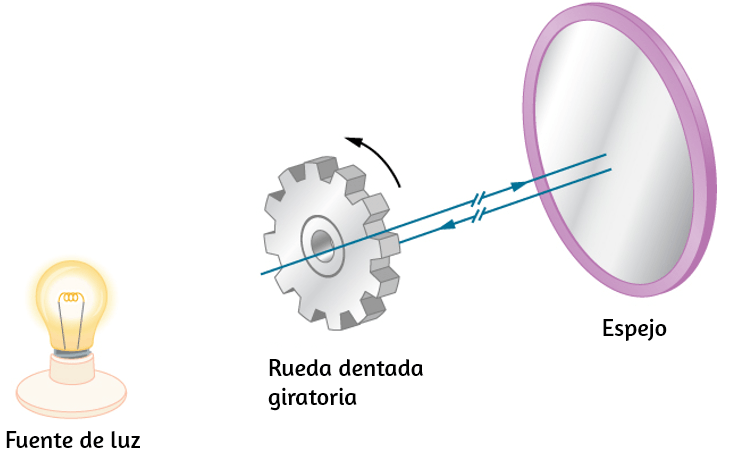
De hecho, la velocidad de la luz en el vacío $c$ es tan importante que se acepta como una de las cantidades físicas básicas y tiene el valor
donde se utiliza el valor aproximado de $3.00 × 10^8 m/s$ cuando la precisión de tres dígitos es suficiente.
La velocidad de la luz a través de la materia es menor que en el vacío, porque la luz interactúa con los átomos en un material. La velocidad de la luz depende en gran medida del tipo de material, ya que su interacción varía con diferentes átomos, celosías de cristal y otras subestructuras. Podemos definir una constante de un material que describe la velocidad de la luz en él, llamado índice de refracción $n$:
donde $v$ es la velocidad observada de la luz en el material.
Como la velocidad de la luz siempre es menor que $c$ en la materia y es igual a $c$ solo en el vacío, el índice de refracción siempre es mayor o igual que uno; es decir, $n ≥ 1$. La muestra los índices de refracción de algunas sustancias representativas. Los valores se enumeran para una longitud de onda de luz particular, porque varían ligeramente con la longitud de onda (esto puede tener efectos importantes, como los colores separados por un prisma, como veremos más adelante). Ten en cuenta que para los gases, $n$ está cerca de $1.0$. Esto parece razonable, ya que los átomos en los gases están muy separados, y la luz viaja a $c$ en el vacío entre los átomos. Es común tomar $n = 1$ para gases a menos que se necesite una gran precisión. Aunque la velocidad de la luz $v$ en un medio varía considerablemente de su valor $c$ en el vacío, sigue siendo una gran velocidad.
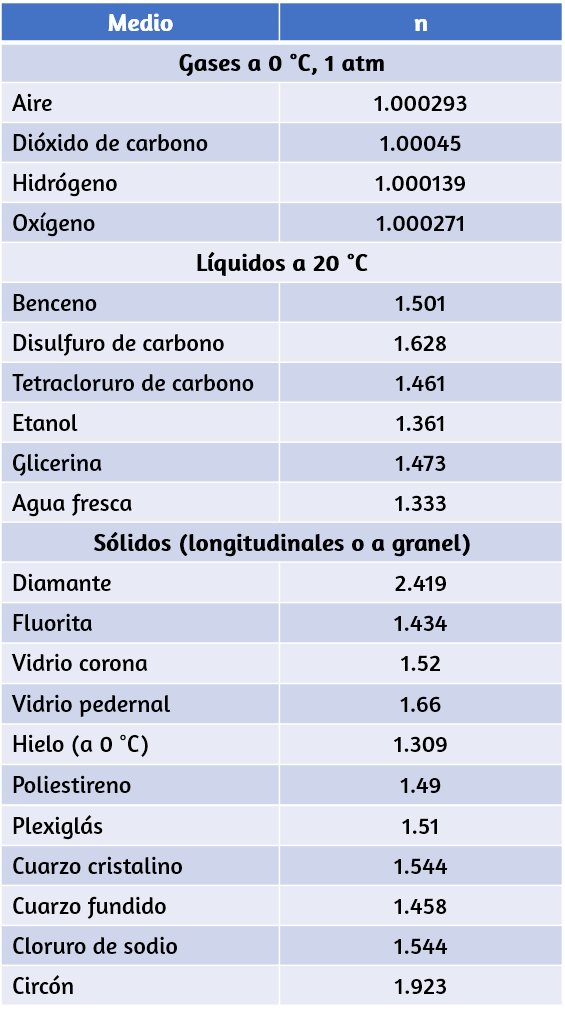
Ejemplo 8.1
La velocidad de la luz en joyería/Bisutería
Calcula la velocidad de la luz en zircon, un material usado en joyería para imitar el diamante.
Estrategia
Podemos calcular la velocidad de la luz $v$ en un material a partir del índice de refracción $n$ del material, utilizando la ecuación $n = c/v$.
Solución
Reorganizamos la ecuación $n = c/v$ para $v$, que nos da
$$v = \frac{c}{n}$$El índice de refracción para el circón se da como $1.923$ en la , y $c$ se da en la Ecuación 8.1. La introducción de estos valores en la ecuación da
$$v = \frac{3.00 × 10^8 m/s}{1.923} = 1.56 × 10^8 m/s$$Explicación
Esta velocidad es ligeramente mayor que la mitad de la velocidad de la luz en el vacío y sigue siendo alta en comparación con las velocidades que normalmente experimentamos. La única sustancia enumerada en la que tiene un mayor índice de refracción que el circón es el diamante. Veremos más adelante que el gran índice de refracción para el circón hace que brille más que el vidrio, pero menos que el diamante.
 Comprueba tu aprendizaje 8.1
Comprueba tu aprendizaje 8.1
Hay tres formas en que la luz puede viajar de una fuente a otra ubicación (). Puede venir directamente de la fuente a través del espacio vacío, como desde el Sol a la Tierra. O la luz puede viajar a través de varios medios, como el aire y el vidrio, hasta el observador. La luz también puede llegar después de ser reflejada, como por un espejo. En todos estos casos, podemos modelar el camino de la luz como una línea recta llamada rayo.
Los experimentos muestran que cuando la luz interactúa con un objeto varias veces más grande que su longitud de onda, viaja en línea recta y actúa como un rayo.
Sus características de onda no son pronunciadas en tales situaciones. Dado que la longitud de onda de la luz visible es menor que una micra (milésima de milímetro), actúa como un rayo en las muchas situaciones comunes en las que encuentra objetos más grandes que una micra. Por ejemplo, cuando la luz visible encuentra algo lo suficientemente grande como para poder observarla con ojos sin ayuda, como una moneda, actúa como un rayo, con características de onda generalmente despreciables.
En todos estos casos, podemos modelar el camino de la luz como líneas rectas. La luz puede cambiar de dirección cuando encuentra objetos (como un espejo) o al pasar de un material a otro (como cuando pasa del aire al vidrio), pero luego continúa en línea recta o como un rayo. La palabra "rayo" viene de las matemáticas y aquí significa una línea recta que se origina en algún punto. Es aceptable visualizar los rayos de luz como rayos láser. El modelo de rayo de luz describe el camino de la luz como líneas rectas.
Dado que la luz se mueve en línea recta, cambiando de dirección cuando interactúa con los materiales, su trayectoria se describe mediante la geometría y la trigonometría simple. Esta parte de la óptica, donde el aspecto del rayo de la luz domina, por lo tanto, se llama óptica geométrica. Dos leyes gobiernan cómo la luz cambia de dirección cuando interactúa con la materia. Estas son la ley de la reflexión, para situaciones en las que la luz rebota sobre la materia, y la ley de la refracción, para situaciones en las que la luz pasa a través de la materia. Examinaremos más acerca de cada una de estas leyes en las próximas secciones de este capítulo.
La ley de reflexión establece que el ángulo de reflexión es igual al ángulo de incidencia, o
La ley de reflexión se ilustra en la , que también muestra cómo se miden el ángulo de incidencia y el ángulo de reflexión en relación con el perpendicular a la superficie en el punto donde el rayo de luz incide.
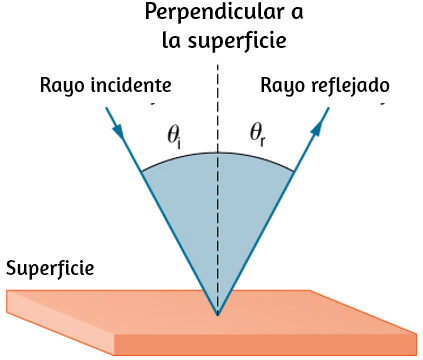
A continuación, puedes practicar con la escena interactiva, diseñada por Steven Sahyun, de la Universidad de Wisconsin - Whitewater. Ajusta el ángulo del espejo y observa qué sucede con el rayo reflejado. Determina el ángulo cuando cada observador pueda ver la luz.
Esperamos ver reflejos de superficies lisas, pero la ilustra cómo una superficie rugosa refleja la luz. Dado que la luz incide en diferentes partes de la superficie en diferentes ángulos, se refleja en muchas direcciones diferentes, o difusa. La luz difusa es lo que nos permite ver una hoja de papel desde cualquier ángulo, como se muestra en la (a). Las personas, la ropa, las hojas y las paredes tienen superficies ásperas y pueden verse desde todos los lados. Por otro lado, un espejo tiene una superficie lisa (en comparación con la longitud de onda de la luz) y refleja la luz en ángulos específicos, como se ilustra en la (b).
Cuando la Luna se refleja desde un lago, como se muestra en la (c), tiene lugar una combinación de estos efectos.

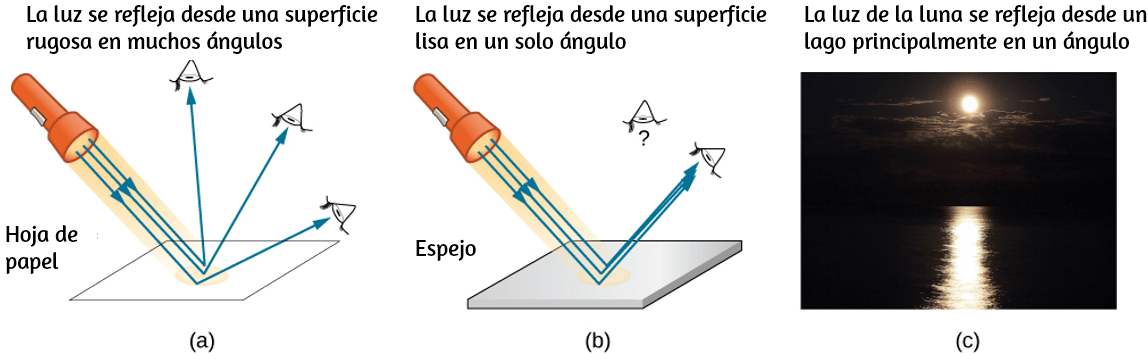
Cuando te ves en un espejo, parece que la imagen está realmente detrás del espejo (). Vemos la luz que viene de una dirección determinada por la ley de la reflexión. Los ángulos son tales que la imagen está exactamente a la misma distancia detrás del espejo cuando te paras frente al espejo. Si el espejo está en la pared de una habitación, las imágenes están detrás del espejo, lo que puede hacer que la habitación parezca más grande. Aunque estas imágenes especulares hacen que los objetos parezcan estar donde no pueden estar (como detrás de un muro sólido), las imágenes no son producto de tu imaginación. Las imágenes de espejo se pueden fotografiar y grabar en video con los instrumentos y se ven igual que con nuestros ojos (que son instrumentos ópticos en sí mismos). La forma precisa en que se forman las imágenes mediante espejos y lentes se analiza en un próximo capítulo sobre la óptica geométrica y la formación de imágenes.
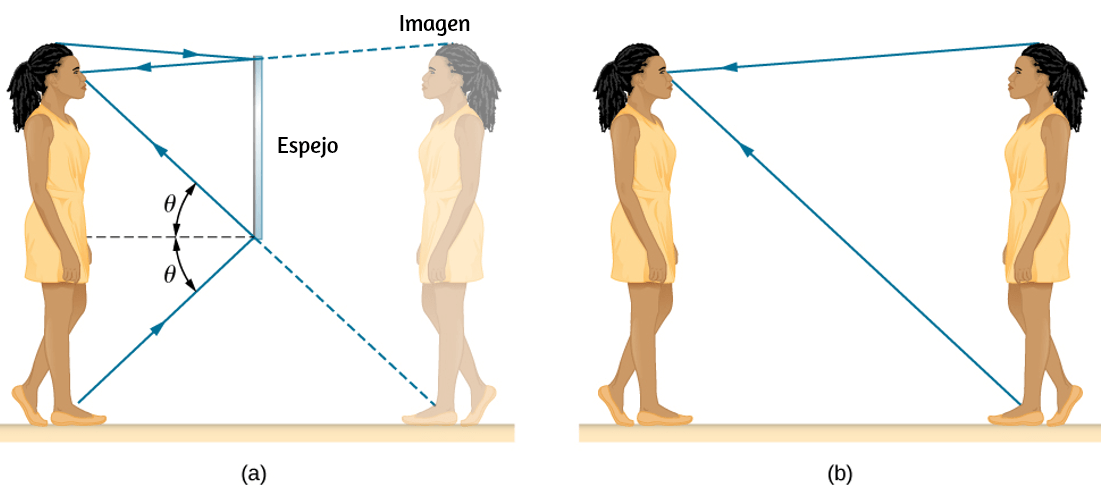
Un rayo de luz que incide sobre un objeto que consiste en dos superficies reflectantes mutuamente perpendiculares se refleja exactamente en paralelo a la dirección desde la cual vino (). Esto es cierto siempre que las superficies reflectantes son perpendiculares, y es independiente del ángulo de incidencia. Dicho objeto se llama reflector de esquina, ya que la luz rebota desde su esquina interior. Los reflectores de esquina son una subclase de retrorreflectores, todos los cuales reflejan los rayos en las direcciones de donde provienen. Aunque la geometría de la prueba es mucho más compleja, los reflectores de esquina también pueden construirse con tres superficies reflectantes mutuamente perpendiculares y son útiles en aplicaciones tridimensionales.
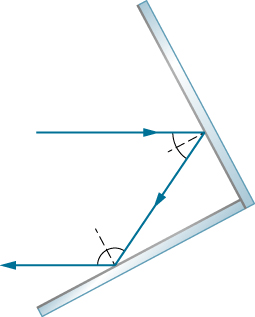
Muchos botones reflectores de bajo costo en bicicletas, automóviles y señales de advertencia tienen reflectores de esquina diseñados para devolver la luz en la dirección en la que se originó. En lugar de simplemente reflejar la luz en un ángulo amplio, la retrorreflexión garantiza una gran visibilidad si el observador y la fuente de luz están ubicados juntos, como el conductor y los faros de un automóvil. Los astronautas del Apolo colocaron un verdadero reflector de esquina en la Luna (). Las señales láser de la Tierra pueden rebotar desde ese reflector de esquina para medir la distancia que aumenta gradualmente a la Luna de unos pocos centímetros por año.
Trabajando según el mismo principio que estos reflectores ópticos, los reflectores de esquina se utilizan habitualmente como reflectores de radar () para aplicaciones de radiofrecuencia. En la mayoría de los casos, los botes pequeños hechos de fibra de vidrio o madera no reflejan fuertemente las ondas de radio emitidas por los sistemas de radar. Para hacer que estos barcos sean visibles al radar (para evitar colisiones, por ejemplo), los reflectores de radar están conectados a los barcos, generalmente en lugares altos.


Con frecuencia, puedes observar algunas cosas extrañas al mirar un tanque de peces. Por ejemplo, puedes ver que el mismo pez parece estar en dos lugares diferentes ().
Esto sucede porque la luz que viene del pez a ti cambia de dirección cuando sale del tanque, y en este caso, puedes recorrer dos caminos diferentes para llegar a tus ojos. El cambio de la dirección de un rayo de luz (vagamente llamado flexión) cuando pasa a través de sustancias de diferentes índices de refracción se denomina refracción y está relacionado con cambios en la velocidad de la luz, $v = c/n$. La refracción es responsable de una tremenda gama de fenómenos ópticos, desde la acción de las lentes hasta la transmisión de datos a través de las fibras ópticas.
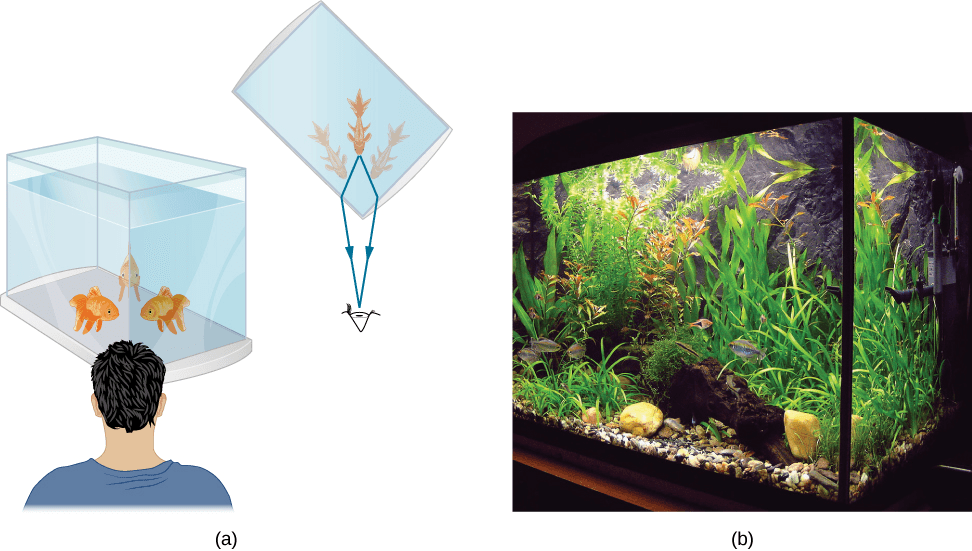
En la siguiente escena interactiva, diseñada por Daniel Monsivais Velásquez y modificada por Juan Guillermo Rivera Berrío, puedes cambiar el valor del índice de refracción, la altura del agua y las posiciones del pez y el cazador (clic sostenido sobre las imágenes) ¿Qué ocurre si $n = 1$?
La muestra cómo un rayo de luz cambia de dirección cuando pasa de un medio a otro. Como antes, los ángulos se miden en relación con un perpendicular a la superficie en el punto donde el rayo de luz lo cruza. (Parte de la luz incidente se refleja desde la superficie, pero por ahora nos concentramos en la luz que se transmite).
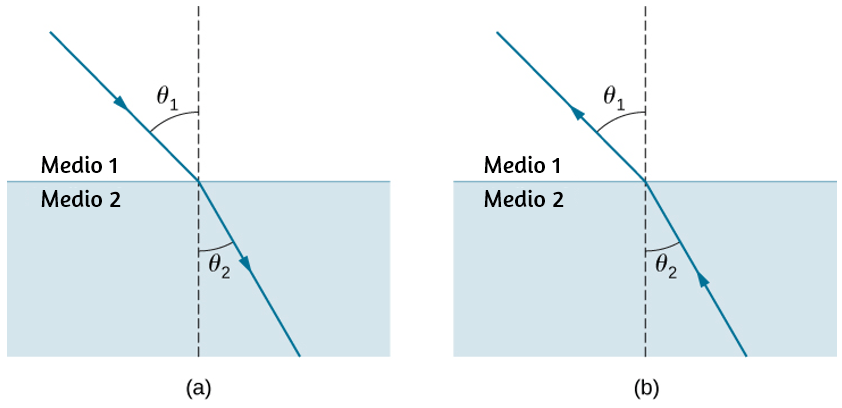
El cambio en la dirección del rayo de luz depende de los valores relativos de los índices de refracción (La propagación de la luz) de los dos medios involucrados. En las situaciones que se muestran, el medio $2$ tiene un mayor índice de refracción que el medio $1$. Ten en cuenta que, como se muestra en la (a), la dirección del rayo se acerca a la perpendicular cuando avanza desde un medio con un índice de refracción más bajo a uno con mayor índice de refracción. A la inversa, como se muestra en la (b), la dirección del rayo se aleja de la perpendicular cuando avanza desde un medio con un índice de refracción más alto a uno con un índice de refracción más bajo. El camino es exactamente reversible.
La cantidad que un rayo de luz cambia su dirección depende tanto del ángulo incidente como de la cantidad en que cambia la velocidad. Para un rayo en un ángulo de incidencia dado, un gran cambio en la velocidad provoca un gran cambio en la dirección y, por lo tanto, un gran cambio en el ángulo. La relación matemática exacta es la ley de refracción, o ley de Snell, del matemático holandés Willebrord Snell (1591–1626), quien la descubrió en 1621. La ley de refracción se expresa en forma de ecuación como
Aquí $n_1$ y $n_2$ son los índices de refracción para los medios $1$ y $2$ y $θ_1$ y $θ_2$ son los ángulos entre los rayos y la perpendicular en los medios $1$ y $2$. El rayo entrante se llama rayo incidente, el rayo saliente se llama rayo refractado, y los ángulos asociados son el ángulo incidente y el ángulo refractado, respectivamente.
Los experimentos de Snell mostraron que la ley de refracción se cumple y que un índice característico de refracción $n$ podría asignarse a un medio dado. Snell no era consciente de que la velocidad de la luz variaba en diferentes medios, un hecho clave utilizado cuando dedujimos la ley de la refracción utilizando teóricamente el principio de Huygens.
Ejemplo 8.2
Determinación del índice de refracción
Encuentra el índice de refracción para el medio $2$ en la (a), asumiendo que el medio $1$ es aire y dado que el ángulo incidente es de $30.0°$ y el ángulo de refracción es de $22.0°$.
Estrategia
El índice de refracción para el aire se toma en $1$ en la mayoría de los casos (y hasta cuatro cifras significativas, es $1.000$). Por lo tanto, $n1 = 1.00$ aquí. De la información dada, $θ_1 = 30.0°$ y $θ_2 = 22.0°$. Con esta información, lo único desconocido en la ley de Snell es $n_2$, por lo que podemos usar la ley de Snell para encontrarlo.
Solución
De la ley de Snell tenemos
$$n_1 senθ_1 = n_2 senθ_2$$ $$n_2 = n_1\frac{senθ_1}{senθ_2}$$Reemplazando los datos conocidos:
$$n_1senθ_1 = 1.00\frac{sen 30°}{sen 22°} = \frac{0.500}{0.375} = 1.33$$Explicación
Este es el índice de refracción para el agua, y Snell pudo haberlo determinado al medir los ángulos y realizar este cálculo. Entonces habría encontrado que $1.33$ era el índice apropiado de refracción para el agua en todas las demás situaciones, como cuando un rayo pasa del agua al vidrio. Hoy, podemos verificar que el índice de refracción esté relacionado con la velocidad de la luz en un medio midiendo esa velocidad directamente.
En la escena interactiva que presentamos en la página siguiente, tomada de las simulaciones Phet y denominada "Reflexión y refracción de la luz", explora la flexión de la luz entre dos medios con diferentes índices de refracción. Usa el apartado "Introducción" de la simulación y observa cómo cambiar el ángulo de flexión del aire al agua y al vidrio. Usa la herramienta del transportador para medir los ángulos y observa si puedes recrear la configuración del Ejemplo 8.2. También, usando el trasportador, confirma que el ángulo de reflexión es igual al ángulo de incidencia.
Ejemplo 8.3
Un gran cambio en la dirección
Supongamos que en una situación como la del ejemplo 8.2, la luz pasa del aire al diamante y que el ángulo incidente es de $30.0°$. Calcula el ángulo de refracción $θ_2$ en el diamante.
Estrategia
Nuevamente, el índice de refracción para el aire se toma como $n_1 = 1.00$, y se nos da $θ_2 = 30.0°$. Podemos buscar el índice de refracción para el diamante en la , encontrando $n_2 = 2.419$. La única incógnita en la ley de Snell es $θ_2$, que deseamos determinar.
Solución
Resolviendo la ley de Snell para el $senθ_2$, obtenemos:
$$senθ_2 = \frac{n_1}{n_2}senθ_1$$Ingresando los datos conocidos:
$$senθ_2 = \frac{1.00}{2.419} sen30.0° = (0.413)(0.500) = 0.207$$El ángulo, entonces, es:
$$θ_2 = sen^{-1}(0.207) = 11.9°$$Explicación
Para el mismo ángulo de incidencia de $30.0°$, el ángulo de refracción en el diamante es significativamente menor que en el agua ($11.9°$ en lugar de $22.0°$, ver Ejemplo 8.2). Esto significa que hay un cambio más grande en la dirección en el diamante. La causa de un gran cambio en la dirección es un gran cambio en el índice de refracción (o velocidad). En general, cuanto mayor sea el cambio de velocidad, mayor será el efecto sobre la dirección del rayo.
 Comprueba tu aprendizaje 8.2
Comprueba tu aprendizaje 8.2
Considera lo que sucede cuando un rayo de luz golpea la superficie entre dos materiales, como se muestra en la figura (a). Parte de la luz cruza el límite y se refracta; el resto queda reflejado. Si, como se muestra en la figura, el índice de refracción para el segundo medio es menor que para el primero, el rayo se desvía de la perpendicular. (Dado que $n_1 > n_2$, el ángulo de refracción es mayor que el ángulo de incidencia, es decir, $θ_2 > θ_1$). Ahora imagina lo que sucede a medida que aumenta el ángulo incidente. Esto hace que $θ_2$ aumente también. El mayor ángulo de refracción $θ_2$ puede ser $90°$, como se muestra en la parte (b). El ángulo crítico $θ_c$ para una combinación de materiales se define como el ángulo incidente $θ_1$ que produce un ángulo de refracción de $90°$. Es decir, $θ_c$ es el ángulo de incidencia para el cual $θ_2 = 90°$. Si el ángulo incidente $θ_1$ es mayor que el ángulo crítico, como se muestra en la (c), entonces toda la luz se refleja nuevamente en el medio 1, una condición llamada reflexión interna total (como muestra la figura, los rayos reflejados obedecen la ley de reflexión, de modo que el ángulo de reflexión es igual al ángulo de incidencia en los tres casos).
La ley de Snell establece la relación entre los ángulos y los índices de refracción. La cual es dada por
$$n_1senθ_1 = n_2senθ_2$$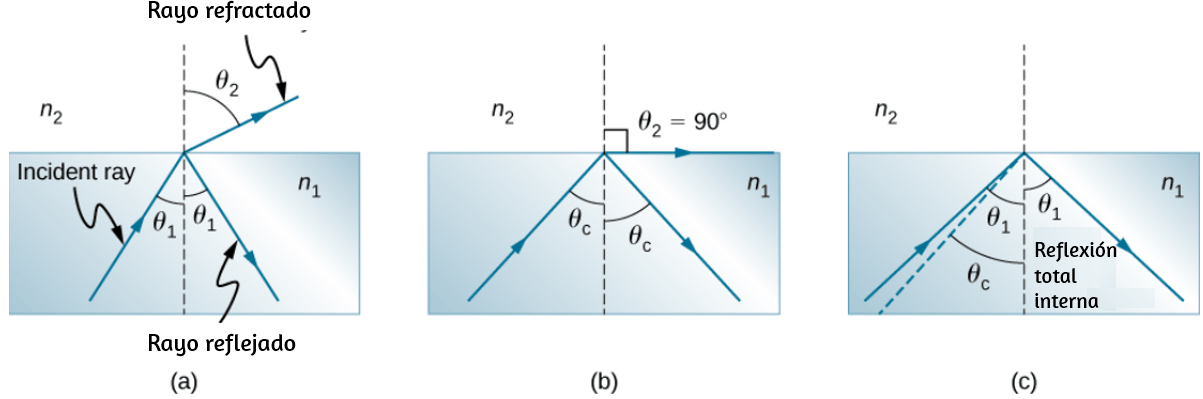
Cuando el ángulo incidente es igual al ángulo crítico ($θ_1 = θ_c$), el ángulo de refracción es $90°$ ($θ_2 = 90°$). Notando que $sen 90° = 1$, la ley de Snell en este caso se vuelve
$$n_1senθ_1 = n_2$$El ángulo crítico $θ_c$ para una combinación dada de materiales es así
La reflexión total interna se produce para cualquier ángulo incidente mayor que el ángulo crítico $θ_c$, y solo puede ocurrir cuando el segundo medio tiene un índice de refracción menor que el primero. Ten en cuenta que esta ecuación se escribe para un rayo de luz que viaja en el medio $1$ y se refleja en el medio $2$, como se muestra en la .
Ejemplo 8.4
Determinar un ángulo crítico
¿Cuál es el ángulo crítico para la luz que viaja en un tubo de poliestireno (un tipo de plástico) rodeado de aire? El índice de refracción para el poliestireno es de $1,49$.
Estrategia
El índice de refracción del aire puede tomarse en $1.00$, como antes. Por lo tanto, se cumple la condición de que el segundo medio (aire) tiene un índice de refracción menor que el primero (plástico), y podemos usar la ecuación
$$θ_c = sen^{-1}(\frac{n_2}{n_1})$$para encontrar el ángulo crítico $θ_c$, donde $n_2 = 1.00$ y $n_1 = 1.49$.
Solución
Sustituyendo los valores identificados, obtenemos:
$$θ_c = sen^{-1}(\frac{1.00}{1.49}) = sen^{-1}(0.671) = 42.2°$$Explicación
Este resultado significa que cualquier rayo de luz dentro del plástico que golpea la superficie en un ángulo mayor a $42.2°$ se refleja totalmente. Esto hace que la superficie interior del plástico transparente sea un espejo perfecto para tales rayos, sin necesidad de la plata utilizada en los espejos comunes. Las diferentes combinaciones de materiales tienen diferentes ángulos críticos, pero cualquier combinación con $n_1 > n_2$ puede producir una reflexión interna total.
El mismo cálculo que se hace aquí muestra que el ángulo crítico para un rayo que va del agua al aire es de $48.6°$, mientras que el del diamante al aire es de $24.4°$, y el del vidrio de pedernal al vidrio de corona es de $66.3°$.
 Comprueba tu aprendizaje 8.3
Comprueba tu aprendizaje 8.3
En la que abre este capítulo, la imagen de un nadador bajo el agua es capturada por una cámara que también está bajo el agua. El nadador en la mitad superior de la fotografía, aparentemente mirando hacia arriba, es, de hecho, una imagen reflejada del nadador que se encuentra debajo. La ondulación circular cerca del centro de la fotografía se encuentra realmente en la superficie del agua. El agua no perturbada que lo rodea hace una buena superficie reflectante cuando se ve desde abajo, gracias a la reflexión interna total. Sin embargo, en el borde superior de esta fotografía, los rayos desde abajo golpean la superficie con ángulos incidentes menores que el ángulo crítico, lo que permite a la cámara capturar una vista de las actividades en la plataforma de la piscina sobre el agua.
La fibra óptica es una aplicación de reflexión interna total que se usa ampliamente. En comunicaciones, se utiliza para transmitir señales de teléfono, Internet y televisión por cable. La fibra óptica emplea la transmisión de fibras de plástico o vidrio hacia abajo. Debido a que las fibras son delgadas, es probable que la luz que ingresa en uno golpee la superficie interior en un ángulo mayor que el ángulo crítico y, por lo tanto, quede totalmente reflejada ().
El índice de refracción fuera de la fibra debe ser más pequeño que el interior. De hecho, la mayoría de las fibras tienen un índice de refracción variable para permitir que se guíe más luz a lo largo de la fibra a través de la refracción interna total. Los rayos se reflejan en las esquinas como se muestra, convirtiendo las fibras en pequeños tubos de luz.
Los paquetes de fibras se pueden utilizar para transmitir una imagen sin una lente, como se ilustra en la (b). Los endoscopios se utilizan para explorar el interior del cuerpo a través de sus orificios naturales o incisiones menores. La luz se transmite a través de un haz de fibras para iluminar las partes internas, y la luz reflejada se transmite hacia afuera a través de otro haz que debe observarse.
La fibra óptica ha revolucionado las técnicas quirúrgicas y las observaciones dentro del cuerpo, con una gran cantidad de usos diagnósticos y terapéuticos médicos. Se puede realizar una cirugía, como la cirugía artroscópica en una articulación de la rodilla o el hombro, empleando herramientas de corte unidas y observadas con el endoscopio. También se pueden obtener muestras, por ejemplo, mediante el enlace de un pólipo intestinal para un examen externo. La flexibilidad del haz de fibra óptica permite a los médicos navegar por regiones pequeñas y difíciles de alcanzar en el cuerpo, como los intestinos, el corazón, los vasos sanguíneos y las articulaciones. La transmisión de un rayo láser intenso para quemar las placas obstructivas en las arterias principales, así como el suministro de luz para activar los medicamentos de quimioterapia, se está convirtiendo en algo común. De hecho, las fibras ópticas han habilitado la microcirugía y la cirugía remota, donde las incisiones son pequeñas y los dedos del cirujano no necesitan tocar el tejido enfermo.
Las fibras ópticas en haces están rodeadas por un material de revestimiento que tiene un índice de refracción más bajo que el núcleo ().
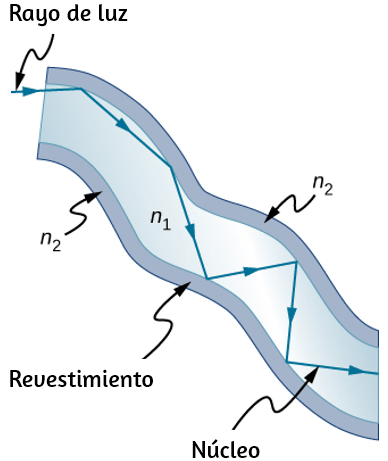
El revestimiento evita que la luz se transmita entre las fibras de un haz. Sin el revestimiento, la luz podría pasar entre las fibras en contacto, ya que sus índices de refracción son idénticos. Dado que no entra luz en el revestimiento (hay una reflexión interna total en el núcleo), ninguna puede transmitirse entre las fibras de revestimiento que están en contacto unas con otras. En cambio, la luz se propaga a lo largo de la fibra, lo que minimiza la pérdida de señal y garantiza que se forme una imagen de calidad en el otro extremo. El revestimiento y una capa protectora adicional hacen que las fibras ópticas sean duraderas y flexibles.
Se han diseñado y fabricado pequeñas lentes especiales que se pueden unir a los extremos de los haces de fibras. La luz que emerge de un haz de fibras puede enfocarse a través de una lente de este tipo, creando imágenes de un punto pequeño.
En algunos casos, el punto se puede escanear, lo que permite obtener imágenes de calidad de una región interna del cuerpo. Los filtros ópticos de minutos especiales insertados al final del haz de fibras tienen la capacidad de obtener imágenes del interior de los órganos ubicados a decenas de micrones por debajo de la superficie sin cortar la superficie, un área conocida como diagnóstico no intrusivo. Esto es particularmente útil para determinar la extensión de los cánceres en el estómago y el intestino.
En otro tipo de aplicación, las fibras ópticas se usan comúnmente para transportar señales para conversaciones telefónicas y comunicaciones por Internet. Se han colocado extensos cables de fibra óptica en el fondo del océano y bajo tierra para permitir las comunicaciones ópticas. Los sistemas de comunicación de fibra óptica ofrecen varias ventajas sobre los sistemas eléctricos (de cobre), especialmente para largas distancias. Las fibras pueden hacerse tan transparentes que la luz puede viajar muchos kilómetros antes de que se vuelva lo suficientemente oscura como para requerir una amplificación, muy superior a los conductores de cobre. Esta propiedad de las fibras ópticas se llama baja pérdida. Los láseres emiten luz con características que permiten muchas más conversaciones en una fibra de las que son posibles con señales eléctricas en un solo conductor. Esta propiedad de las fibras ópticas se llama alto ancho de banda. Las señales ópticas en una fibra no producen efectos indeseables en otras fibras adyacentes. Esta propiedad de las fibras ópticas se denomina interferencia reducida. Exploraremos las características únicas de la radiación láser en un capítulo posterior.
Los reflectores de esquina son perfectamente eficientes cuando se cumplen las condiciones para la reflexión total interna. Con materiales comunes, es fácil obtener un ángulo crítico que sea menor a $45°$.
Un uso de estos espejos perfectos es en binoculares, como se muestra en la . Otro uso es en periscopios encontrados en submarinos. La reflexión total interna, junto con un gran índice de refracción, explica por qué los diamantes brillan más que otros materiales. El ángulo crítico para una superficie de diamante a aire es de solo $24.4°$, de modo que cuando la luz entra en un diamante, tiene problemas para volver a salir (). Aunque la luz penetra libremente en el diamante, solo puede salir si forma un ángulo inferior a $24.4°$. Las facetas en los diamantes tienen la intención específica de hacer esto poco probable.
Los buenos diamantes son muy claros, de modo que la luz hace muchos reflejos internos y se concentra antes de salir, de ahí el brillo brillante (el circón es una piedra preciosa natural que tiene un índice de refracción excepcionalmente grande, pero no es tan grande como el diamante, por lo que no es tan preciado. La circonia cúbica se fabrica y tiene un índice de refracción aún mayor, aproximadamente $2.17$, pero todavía es menos que el diamante). Los colores que ves que emergen de un diamante transparente no se deben al color del diamante, que generalmente es casi incoloro. Los colores resultan de la dispersión.
Los diamantes de colores obtienen su color de los defectos estructurales de la red cristalina y la inclusión de cantidades diminutas de grafito y otros materiales. La mina Argyle en Australia Occidental produce alrededor del $90$% de los diamantes rosa, rojo, champán y coñac del mundo, mientras que alrededor del $50$% de los diamantes transparentes del mundo provienen de África central y meridional.
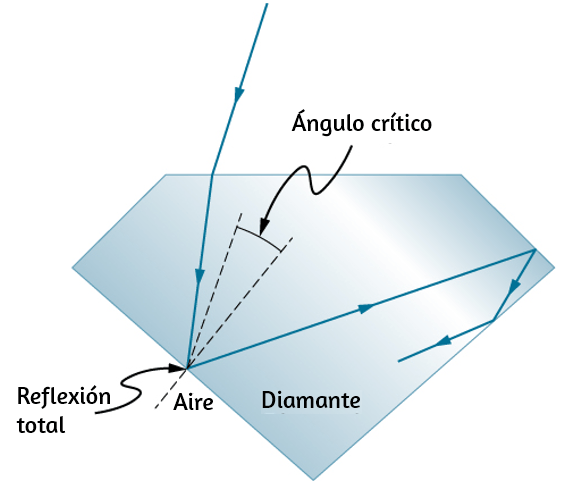
Nuevamente, en la escena de simulaciones Phet, explora la refracción y el reflejo de la luz entre dos medios con diferentes índices de refracción. Intenta hacer desaparecer el rayo refractado con total reflexión interna. Use la herramienta de transportador para medir el ángulo crítico y compare con la predicción de la Ecuación 1.5.
Todo el mundo disfruta del espectáculo de un arco iris que brilla sobre un cielo oscuro y tormentoso. ¿Cómo se rompe la luz del sol que cae sobre las gotas de lluvia en el arco iris de colores que vemos? El mismo proceso hace que la luz blanca se divida en colores mediante un prisma de vidrio transparente o un diamante ().

Vemos unos seis colores en un arco iris: rojo, naranja, amarillo, verde, azul y violeta; a veces indigo está en la lista, también. Estos colores están asociados con diferentes longitudes de onda de la luz, como se muestra en la . Cuando nuestro ojo recibe la luz de la longitud de onda pura, tendemos a ver solo uno de los seis colores, dependiendo de la longitud de onda. Los miles de otros tonos que podemos percibir en otras situaciones son la respuesta de nuestro ojo a varias mezclas de longitudes de onda. La luz blanca, en particular, es una mezcla bastante uniforme de todas las longitudes de onda visibles. La luz solar, considerada blanca, en realidad parece ser un poco amarilla, debido a su mezcla de longitudes de onda, pero contiene todas las longitudes de onda visibles. La secuencia de colores en el arco iris es la misma secuencia de los colores que se muestran en la figura. Esto implica que la luz blanca se extiende en un arco iris de acuerdo con la longitud de onda. La dispersión se define como la propagación de la luz blanca en todo su espectro de longitudes de onda. Más técnicamente, la dispersión ocurre cuando la propagación de la luz depende de la longitud de onda.
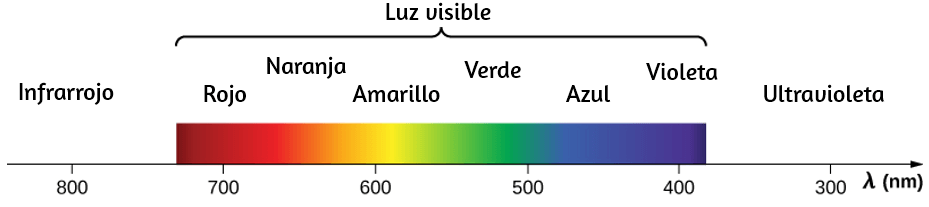
Cualquier tipo de onda puede exhibir dispersión. Por ejemplo, las ondas de sonido, todos los tipos de ondas electromagnéticas y las ondas de agua se pueden dispersar de acuerdo con la longitud de onda. La dispersión puede requerir circunstancias especiales y puede resultar en exhibiciones espectaculares como en la producción de un arco iris. Esto también es válido para el sonido, ya que todas las frecuencias normalmente viajan a la misma velocidad. Si escuchas el sonido a través de un tubo largo, como una manguera de aspiradora, puedes escucharlo dispersarse fácilmente mediante la interacción con el tubo. De hecho, la dispersión puede revelar mucho sobre lo que la onda ha encontrado que dispersa sus longitudes de onda. La dispersión de la radiación electromagnética desde el espacio exterior, por ejemplo, ha revelado mucho acerca de lo que existe entre las estrellas, el llamado medio interestelar.
En la siguiente unidad didáctica que hace parte del proyecto @prende.mx puedes explorar la luz y su espectro de colores.
La refracción es responsable de la dispersión en arco iris y muchas otras situaciones. El ángulo de refracción depende del índice de refracción, como sabemos por la ley de Snell. Sabemos que el índice de refracción $n$ depende del medio. Pero para un medio dado, $n$ también depende de la longitud de onda (). Ten en cuenta que para un medio dado, n aumenta a medida que la longitud de onda disminuye y es mayor para la luz violeta. Por lo tanto, la luz violeta se dobla más que la luz roja, como se muestra para un prisma en la .
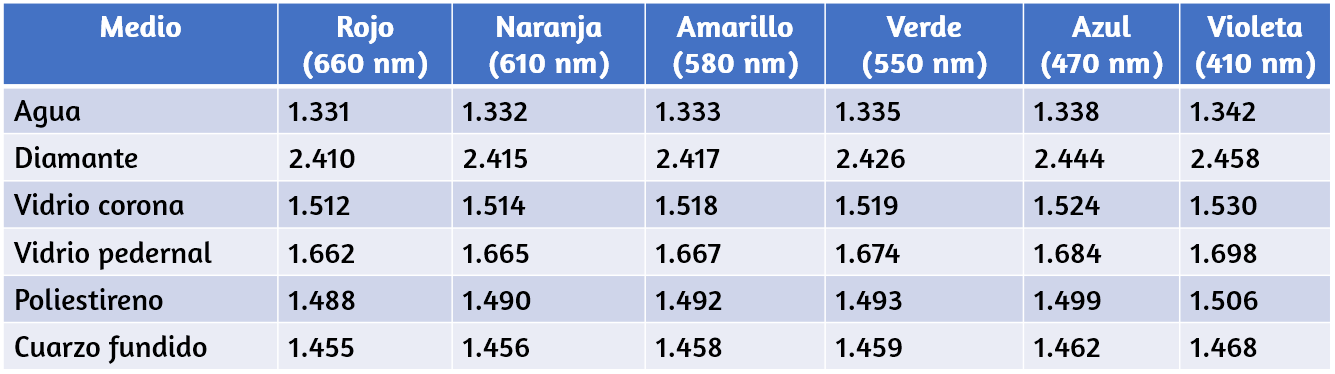
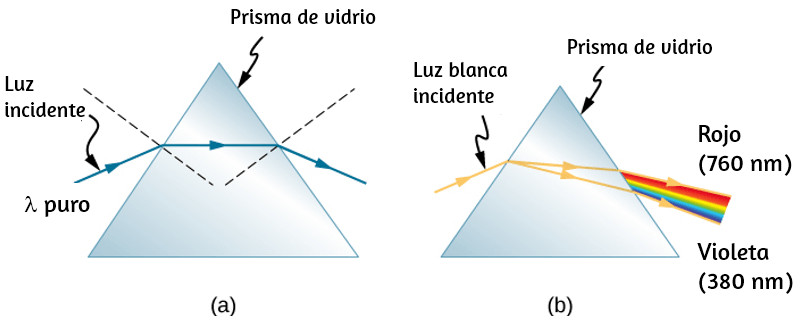
Ejemplo 8.5
Dispersión de luz blanca por un vidrio de pedernal
Un haz de luz blanca pasa del aire al vidrio de pedernal en un ángulo de incidencia de $43.2°$. ¿Cuál es el ángulo entre las partes roja ($660 nm$) y violeta ($410 nm$) de la luz refractada?
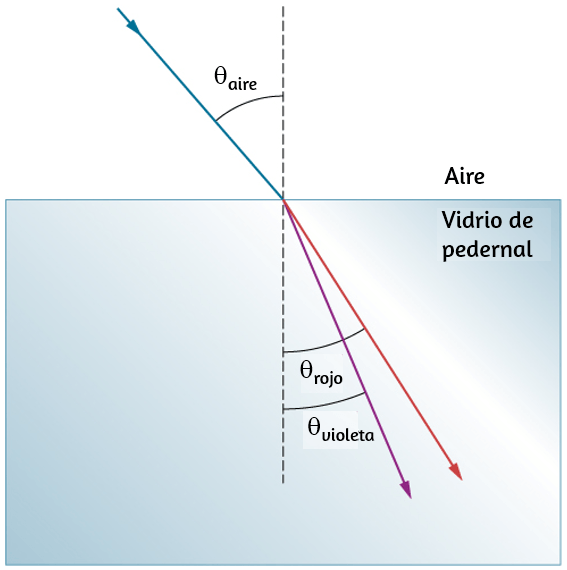
Estrategia
Los valores para los índices de refracción para vidrio de pedernal en varias longitudes de onda se enumeran en la . Usa estos valores para calcular el ángulo de refracción para cada color y luego tome la diferencia para encontrar el ángulo de dispersión.
Solución
Aplicando la ley de refracción para la parte roja del haz.
$$n_{\textsf{aire}}senθ_{\textsf{aire}} = n_{\textsf{rojo}}senθ_{\textsf{rojo}}$$Podemos hallar el ángulo de refracción así
Del mismo modo, el ángulo de incidencia para la parte violeta del haz es
La diferencia entre estos dos ángulos es
$$θ_{\textsf{rojo}} - θ_{\textsf{violeta}} = 27.0° - 26.4° = 0.6°$$Explicación
Aunque $0.6°$ puede parecer un ángulo despreciablemente pequeño, si se permite que este rayo se propague una distancia lo suficientemente larga, la dispersión de los colores se vuelve bastante notable.
 Comprueba tu aprendizaje 8.4
Comprueba tu aprendizaje 8.4
Los arco iris son producidos por una combinación de refracción y reflexión. Puede que hayas notado que solo ves un arco iris cuando apartas la vista del Sol. La luz entra en una gota de agua y se refleja desde la parte posterior de la gota (). La luz se refracta tanto a medida que entra como sale de la gota.
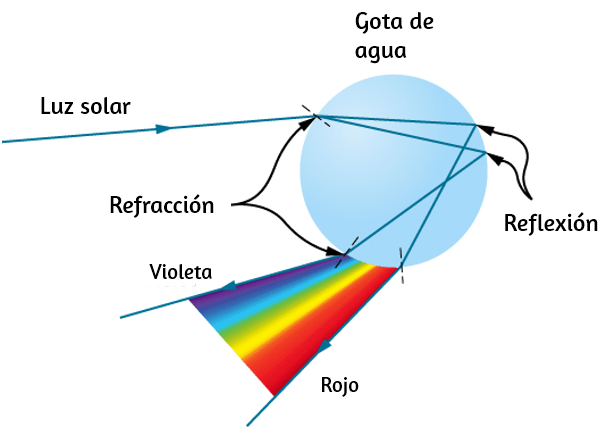
Como el índice de refracción del agua varía con la longitud de onda, la luz se dispersa y se observa un arco iris ( (a)). (No se produce dispersión en la superficie posterior, porque la ley de reflexión no depende de la longitud de onda). El arco iris real de colores visto por un observador depende de la gran cantidad de rayos que se refractan y se reflejan hacia los ojos del observador desde numerosas gotas de agua. El efecto es más espectacular cuando el fondo es oscuro, como en un clima tormentoso, pero también se puede observar en cascadas y rociadores de césped.
El arco de un arco iris proviene de la necesidad de mirar un ángulo específico en relación con la dirección del Sol, como se ilustra en la parte (b). Si se producen dos reflejos de luz dentro de la gota de agua, se produce otro arco iris "secundario". Este evento raro produce un arco que se encuentra sobre el arco iris primario, como en la parte (c), y produce colores en el orden inverso del arco iris primario, con rojo en el ángulo más bajo y violeta en el ángulo más grande.
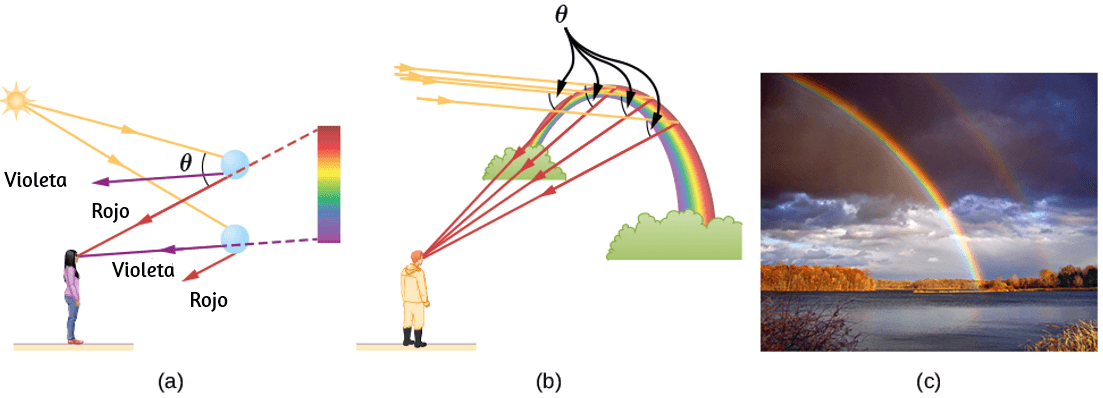
La dispersión puede producir hermosos arco iris, pero puede causar problemas en los sistemas ópticos. La luz blanca utilizada para transmitir mensajes en una fibra se dispersa, se extiende en el tiempo y eventualmente se superpone con otros mensajes. Dado que un láser produce una longitud de onda casi pura, su luz experimenta poca dispersión, una ventaja sobre la luz blanca para la transmisión de información. En contraste, la dispersión de las ondas electromagnéticas que nos llegan del espacio exterior se puede usar para determinar la cantidad de materia que atraviesan.
Para terminar este apartado, te compartimos una animación interactiva que incluye el espectro de colores, si no intervienes podrás observar la formación de un corazón, si lo haces las partículas dejan un rastro y son repelidas por el cursor. La animación fue diseñada por John Weachock
Hasta ahora, en este capítulo, hemos estado discutiendo los fenómenos ópticos utilizando el modelo de rayos de luz. Sin embargo, algunos fenómenos requieren análisis y explicaciones basadas en las características de onda de la luz. Esto es particularmente cierto cuando la longitud de onda no es despreciable en comparación con las dimensiones de un dispositivo óptico, como una hendidura en el caso de difracción. El principio de Huygens es una herramienta indispensable para este análisis.
La muestra cómo se ve una onda transversal vista desde arriba y desde el lado. Se puede imaginar una onda de luz para propagarse así, aunque en realidad no la vemos moviéndose a través del espacio. Desde arriba, vemos los frentes de las olas (o las crestas de las olas) como si estuviéramos mirando hacia abajo en las olas del océano. La vista lateral sería una gráfica del campo eléctrico o magnético. La vista desde arriba es quizás más útil en el desarrollo de conceptos sobre la óptica de onda.
El científico holandés Christiaan Huygens (1629-1695) desarrolló una técnica útil para determinar en detalle cómo y dónde se propagan las olas. A partir de una posición conocida, el principio de Huygens establece que cada punto en un frente de onda es una fuente de ondas que se extienden en la dirección hacia adelante a la misma velocidad que la propia onda.
La muestra cómo se aplica el principio de Huygens. Un frente de onda es el borde largo que se mueve, por ejemplo, con la cresta o el canal. Cada punto en el frente de onda emite una onda semicircular que se mueve a la velocidad de propagación $v$.
Podemos dibujar estas pequeñas ondas en un momento t más tarde, de modo que se hayan movido una distancia $s = vt$. El nuevo frente de onda es un plano tangente a las ondas y es donde esperaríamos que la onda fuera un tiempo $t$ más tarde. El principio de Huygens funciona para todo tipo de ondas, incluidas las ondas de agua, las ondas de sonido y las ondas de luz. Es útil no solo para describir cómo se propagan las ondas de luz, sino también para explicar las leyes de reflexión y refracción. Además, veremos que el principio de Huygens nos dice cómo y dónde interfieren los rayos de luz.
La muestra cómo un espejo refleja una onda entrante en un ángulo igual al ángulo incidente, verificando la ley de reflexión. Cuando el frente de onda golpea el espejo, las ondas se emiten primero desde la parte izquierda del espejo y luego desde la derecha. Las ondas más cercanas a la izquierda han tenido tiempo de viajar más lejos, produciendo un frente de onda que se desplaza en la dirección que se muestra.
La ley de refracción puede explicarse aplicando el principio de Huygens a un frente de onda que pasa de un medio a otro (). Cada ondita en la figura se emitió cuando el frente de onda cruzó la interfaz entre los medios. Como la velocidad de la luz es menor en el segundo medio, las ondas no viajan tan lejos en un tiempo determinado, y el nuevo frente de onda cambia de dirección como se muestra. Esto explica por qué un rayo cambia de dirección para acercarse a la perpendicular cuando la luz disminuye la velocidad. La ley de Snell se puede derivar de la geometría en la (Ejemplo 8.6).
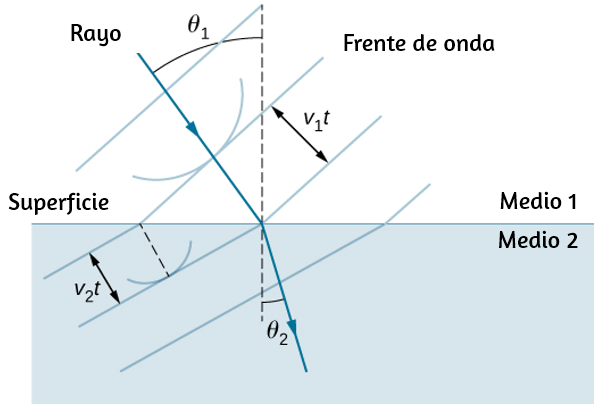
Ejemplo 8.6
Deduciendo la ley de refracción
Al examinar la geometría de los frentes de onda, deduce la ley de la refracción.
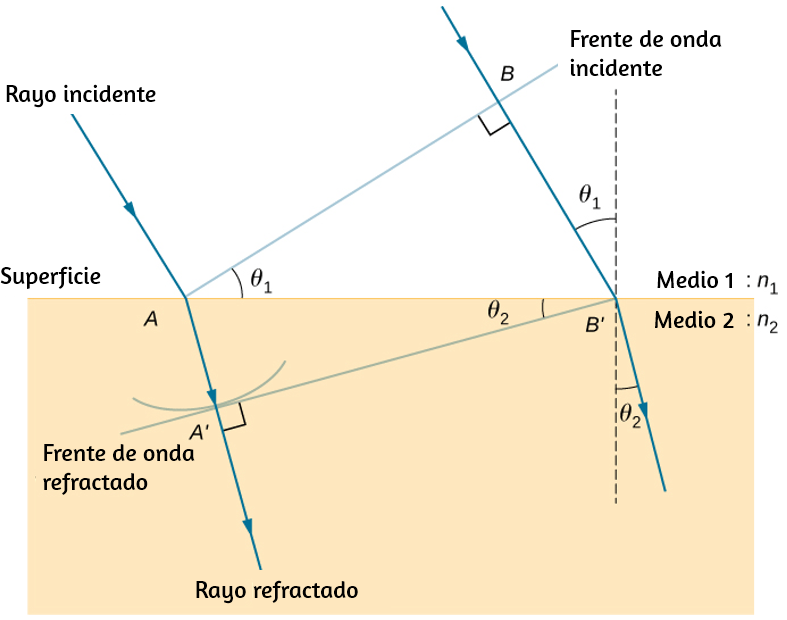
Estrategia
Considera la . Muestra el frente de la onda incidente que acaba de llegar a la superficie en el punto $A$, mientras que el punto $B$ todavía está bien dentro del medio $1$. En el tiempo $Δt$ tarda una onda de $B$ en llegar a $B'$ en la superficie a la velocidad $v_1 = c/n_1$, una ondita de $A$ viaja al medio $2$ a una distancia de $AA' = v_2Δt$, donde $v_2 = c/n_2$. Ten en cuenta que en este ejemplo, $v_2$ es más lento que $v_1$ porque $n_1 < n_2$.
El segmento en la superficie $AB'$ se comparte con el triángulo $ABB'$ dentro del medio $1$ y el triángulo $AA'B'$ dentro del medio $2$. Ten en cuenta que, desde la geometría, el ángulo $∠BAB'$ es igual al ángulo de incidencia, $θ_1$. Del mismo modo, $∠AB'A'$ es $θ_2$.
La longitud de $AB'$ se da de dos maneras:
$$AB' = \frac{BB'}{sen θ_1} = \frac{AA'}{sen θ_2}$$Invirtiendo la ecuación y sustituyendo $AA' = cΔt/n_2$ desde arriba y de manera similar $BB' = cΔt/n_1$, obtenemos
$$\frac{sen θ_1}{cΔt/n_1} = \frac{sen θ_2}{cΔt/n_2}$$La cancelación de $cΔt$ nos permite simplificar esta ecuación en la forma familiar
$$n_1sen θ_1 = n_2sen θ_2$$Explicación
Aunque la ley de la refracción fue establecida experimentalmente por Snell, su deducción aquí requiere el principio de Huygens y el entendimiento de que la velocidad de la luz es diferente en diferentes medios.
 Comprueba tu aprendizaje 8.5
Comprueba tu aprendizaje 8.5
La siguiente escena interactiva, diseñada por Walter Fendt, muestra una animación de reflexión y refracción utilizando las onditas u ondas secundarias de Huygens mientras controlas los parámetros. Asegúrate de hacer clic en "Siguiente paso" para mostrar las onditas. Se pueden ver los frentes de onda reflejados y refractados formándose.
Esta escena interactiva explica la reflexión y la refracción de las ondas según el principio de Huygens. Las explicaciones de cada uno de los pasos se proporcionan en el cuadro de texto. Cuando termines un paso, presiona el botón "Siguiente paso".
Puedes detener y continuar la simulación utilizando el botón "Pausa/Reanudar". Los tres campos de texto permiten variar el índice de refracción de ambos medios y el ángulo de incidencia. El medio con el índice de refracción más pequeño (la mayor velocidad de fase) está pintado de amarillo, el otro de azul.
¿Qué sucede cuando una ola pasa a través de una abertura, como la luz que brilla a través de una puerta abierta hacia una habitación oscura?
Para la luz, observamos una sombra nítida de la puerta en el piso de la habitación, y ninguna luz visible se dobla en las esquinas hacia otras partes de la habitación. Cuando el sonido pasa a través de una puerta, lo escuchamos en todas partes de la habitación y, por lo tanto, observamos que el sonido se propaga al pasar por tal abertura (). ¿Cuál es la diferencia entre el comportamiento de las ondas de sonido y las ondas de luz en este caso? La respuesta es que la luz tiene longitudes de onda muy cortas y actúa como un rayo. El sonido tiene longitudes de onda del orden del tamaño de la puerta y se dobla alrededor de las esquinas (para una frecuencia de $1000 Hz$, aproximadamente tres veces más pequeño que el ancho de la puerta).
Si pasamos luz a través de aberturas más pequeñas como las rendijas, podemos usar el principio de Huygens para ver que la luz se dobla como lo hace el sonido (). La flexión de una onda alrededor de los bordes de una abertura o un obstáculo se llama difracción. La difracción es una característica de la onda y ocurre para todos los tipos de ondas. Si se observa difracción para algún fenómeno, es evidencia de que el fenómeno es una onda. Por lo tanto, la difracción horizontal del rayo láser después de que pasa a través de las rendijas en la es evidencia de que la luz es una onda. Aprenderás sobre la difracción con mucho más detalle en el capítulo sobre la difracción.

Las gafas de sol polarizadas son familiares para la mayoría de nosotros. Tienen una capacidad especial para cortar el brillo de la luz reflejada por el agua o el vidrio (). Tienen esta habilidad debido a una onda característica de la luz llamada polarización. ¿Qué es la polarización? ¿Cómo se produce? ¿Cuáles son algunos de sus usos? Las respuestas a estas preguntas están relacionadas con el carácter de onda de luz.

La luz es un tipo de onda electromagnética (EM). Las ondas EM son ondas transversales que consisten en campos eléctricos y magnéticos variables que oscilan perpendicularmente a la dirección de propagación ().
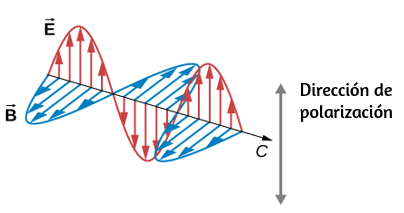
Para examinar esto más detenidamente, considera las ondas transversales en las cuerdas que se muestran en la . Las oscilaciones en una cuerda están en un plano vertical y se dice que están polarizadas verticalmente. Los de la otra cuerda están en un plano horizontal y están polarizados horizontalmente. Si se coloca una ranura vertical en la primera cuerda, las ondas pasan a través. Sin embargo, una rendija vertical bloquea las ondas polarizadas horizontalmente. Para las ondas EM, la dirección del campo eléctrico es análoga a las perturbaciones en las cuerdas.
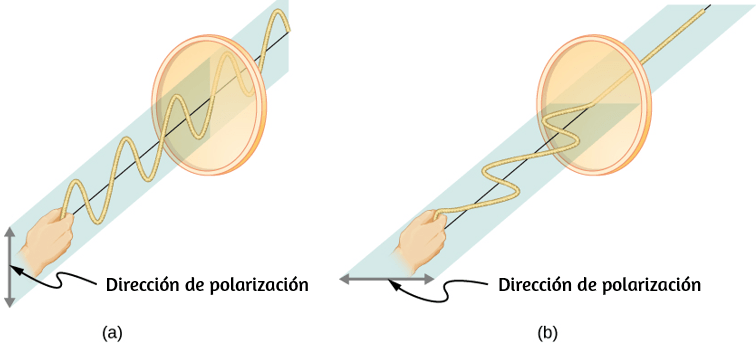
El Sol y muchas otras fuentes de luz producen ondas que tienen los campos eléctricos en direcciones aleatorias ( (a)). Se dice que dicha luz no está polarizada, porque está compuesta de muchas ondas con todas las direcciones posibles de polarización. Los materiales polaroid, que fueron inventados por el fundador de la Corporación Polaroid, Edwin Land, actúan como una rendija polarizadora para la luz, permitiendo que solo pase la polarización en una dirección. Los filtros polarizadores están compuestos por moléculas largas alineadas en una dirección. Si pensamos en las moléculas como muchas hendiduras, análogas a las de las cuerdas oscilantes, podemos entender por qué solo puede atravesar la luz con una polarización específica.
El eje de un filtro polarizador es la dirección a lo largo de la cual el filtro pasa el campo eléctrico de una onda EM.
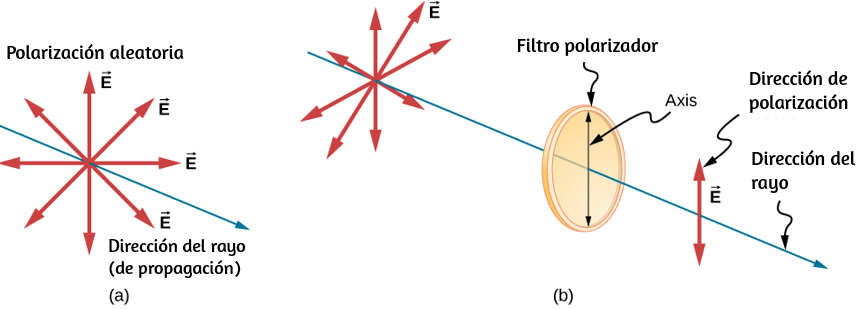
La muestra el efecto de dos filtros polarizadores en la luz originalmente no polarizada. El primer filtro polariza la luz a lo largo de su eje. Cuando los ejes del primer y segundo filtros están alineados (paralelos), toda la luz polarizada que pasa por el primer filtro también pasa por el segundo filtro. Si se gira el segundo filtro polarizador, solo se pasa la parte de la luz paralela al eje del segundo filtro.
Cuando los ejes son perpendiculares, el segundo filtro no pasa luz. Solo se pasa la componente de la onda EM paralela al eje de un filtro. Llamemos al ángulo entre la dirección de polarización y el eje de un filtro $θ$. Si el campo eléctrico tiene una amplitud $E$, entonces la parte transmitida de la onda tiene una amplitud $Ecosθ$ (). Dado que la intensidad de una onda es proporcional a su amplitud al cuadrado, la intensidad $I$ de la onda transmitida está relacionada con la onda incidente por
donde $I_0$ es la intensidad de la onda polarizada antes de pasar por el filtro. Esta ecuación es conocida como la ley de Malus.
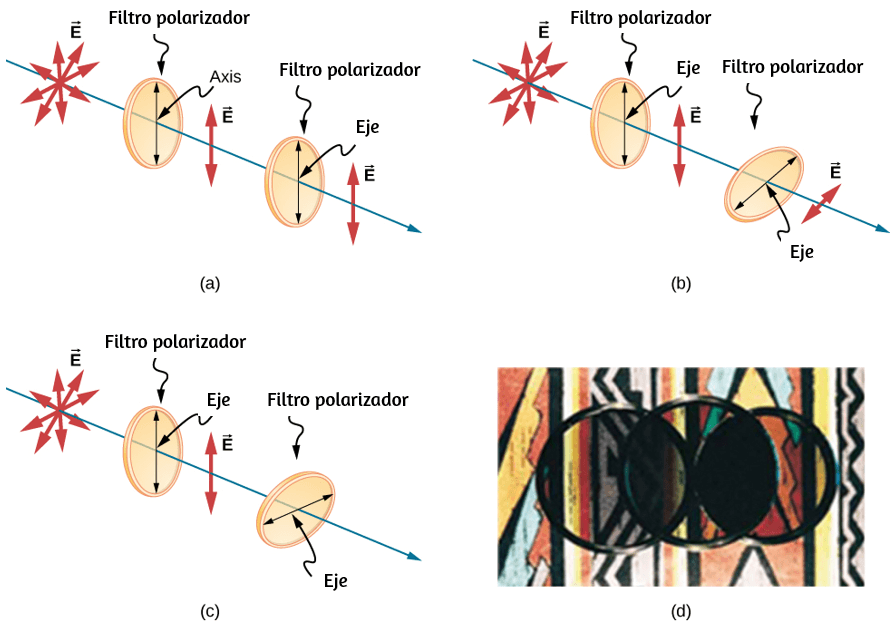
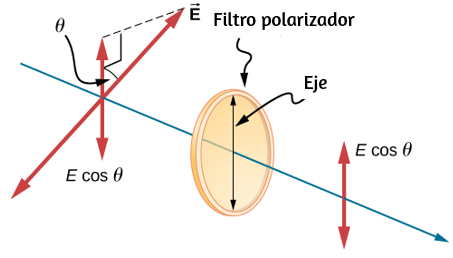
En la siguiente escena interactiva, diseñada por Andrew Duffy, puedes observar ¿Qué sucede cuando la luz polarizada con una intensidad de $800 W/m^2$ incide en un polarizador?.
La luz viaja de izquierda a derecha. Usa los controles deslizantes para ajustar la dirección de polarización de la luz y el ángulo del eje de transmisión del polarizador. El gráfico muestra la intensidad de la luz en función del ángulo del eje de transmisión del polarizador. La línea entre el disco de luz incidente y el polarizador muestra la dirección en la que está polarizada la luz incidente. La línea a la derecha del polarizador muestra la dirección en la que está polarizada la luz después de pasar a través del polarizador.
Ejemplo 8.7
Cálculo de la reducción de intensidad por un filtro polarizador
¿Qué ángulo se necesita entre la dirección de la luz polarizada y el eje de un filtro polarizador para reducir su intensidad en un $90.0$%?
Estrategia
Cuando la intensidad se reduce en un $90.0$%, es un $10.0$% o $0.100$ veces su valor original. Es decir, $I = 0.100I_0$. Usando esta información, la ecuación $I = I_0cos^2θ$ se puede usar para hallar el ángulo necesario.
Solución
Resolviendo la ecuación $I = I_0cos^2θ$ para $cosθ$ y sustituyendo con la relación entre $I$ e $I_0$, obtenemos
$$cosθ = \sqrt{\frac{I}{I_0}} = \sqrt{\frac{0.100I_0}{I}} = 0.3162$$despejando $θ$ tenemos:
$$θ = cos^{-1}0.3162 = 71.6°$$Explicación
Se necesita un ángulo bastante grande entre la dirección de polarización y el eje del filtro para reducir la intensidad a $10.0$% de su valor original. Esto parece razonable basado en la experimentación con películas polarizantes. Es interesante que, en un ángulo de $45°$, la intensidad se reduzca al $50$% de su valor original. Ten en cuenta que $71.6°$ está a $18.4°$ de la reducción de la intensidad a cero, y que en un ángulo de $18.4°$, la intensidad se reduce a $90.0$% de su valor original, lo que evidencia la simetría.
 Comprueba tu aprendizaje 8.6
Comprueba tu aprendizaje 8.6
A estas alturas, probablemente puedas adivinar que las gafas de sol polarizadas cortan el brillo de la luz reflejada, porque esa luz está polarizada. Puedes comprobarlo por ti mismo sosteniendo los anteojos de sol polarizadores frente a ti y girándolos mientras observas la luz reflejada en el agua o el vidrio. A medida que gires las gafas de sol, notarás que la luz se vuelve brillante y tenue, pero no completamente negra. Esto implica que la luz reflejada está parcialmente polarizada y no puede ser bloqueada completamente por un filtro polarizador.
La ilustra lo que sucede cuando la luz no polarizada se refleja desde una superficie. La luz polarizada verticalmente se refracta preferentemente en la superficie, por lo que la luz reflejada se deja polarizada más horizontalmente. Las razones de este fenómeno están más allá del alcance de este texto, pero una mnemotécnica conveniente para recordar esto es imaginar que la dirección de polarización es como una flecha. La polarización vertical es como una flecha perpendicular a la superficie y es más probable que se pegue y no se refleje. La polarización horizontal es como una flecha que rebota en su costado y es más probable que se refleje. Las gafas de sol con ejes verticales bloquean más luz reflejada que la luz no polarizada de otras fuentes.
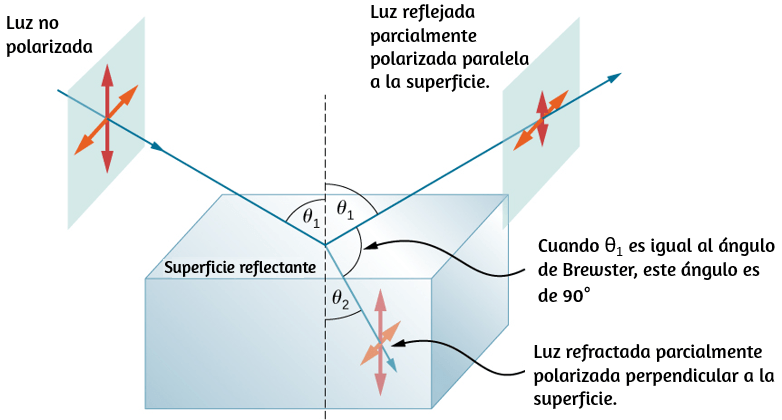
Como la parte de la luz que no se refleja se refracta, la cantidad de polarización depende de los índices de refracción de los medios involucrados. Se puede mostrar que la luz reflejada está completamente polarizada en un ángulo de reflexión $θ_b$ dado por
donde $n_1$ es el medio en el que viajan la luz incidente y reflejada y $n_2$ es el índice de refracción del medio que forma la interfaz que refleja la luz. Esta ecuación se conoce como la ley de Brewster y $θ_b$ se conoce como el ángulo de Brewster, que lleva el nombre del físico escocés del siglo XIX que los descubrió.
Ejemplo 8.8
Calculando la polarización por reflexión
(a) ¿En qué ángulo la luz que viaja en el aire se polariza completamente horizontalmente cuando se refleja en el agua? (b) en el vidrio de corona?
Estrategia
Todo lo que necesitamos para resolver estos problemas son los índices de refracción. El aire tiene $n_1 = 1.00$, el agua tiene $n_2 = 1.333$ y el vidrio de corona tiene $n_2' = 1.520$. La ecuación $tan θ_b = \frac{n_2}{n_1}$ se puede aplicar directamente para encontrar $θ_b$ en cada caso.
Solución
a. Reemplazamos las cantidades conocidas en la ecuación.
$$tan θ_b = \frac{n_2}{n_1}$$Obteniendo
$$tan θ_b = \frac{n_2}{n_1} = \frac{1.333}{1.00} = 1.333$$Despejamos el ángulo $θ_b$
$$θ_b = tan^{-1}1.333 = 53.1°$$b. Del mismo modo, para el vidrio de corona y el aire,
$$tan θ'_b = \frac{n'_2}{n_1} = \frac{1.520}{1.00} = 1.52$$Luego
$$θ'_b = tan^{-1}1.52 = 56.7°$$Explicación
La luz reflejada en estos ángulos podría estar completamente bloqueada por un buen filtro polarizador mantenido con su eje vertical. El ángulo de Brewster para el agua y el aire son similares a los del vidrio y el aire, por lo que las gafas de sol son igualmente efectivas para la luz reflejada por el agua o el vidrio en circunstancias similares. La luz que no se refleja se refracta en estos medios. Por lo tanto, en un ángulo incidente igual al ángulo de Brewster, la luz refractada está ligeramente polarizada verticalmente. No está completamente polarizado verticalmente, porque solo se refleja una pequeña fracción de la luz incidente, por lo que se refracta una cantidad significativa de luz polarizada horizontalmente.
 Comprueba tu aprendizaje 8.7
Comprueba tu aprendizaje 8.7
Los filtros polarizadores tienen un eje de polarización que actúa como una hendidura. Esta rendija pasa ondas EM (a menudo luz visible) que tienen un campo eléctrico paralelo al eje. Esto se logra con moléculas largas alineadas perpendicularmente al eje, como se muestra en la .
La ilustra cómo se absorbe el componente del campo eléctrico paralelo a las moléculas largas. Una onda EM está compuesta de campos eléctricos y magnéticos oscilantes.
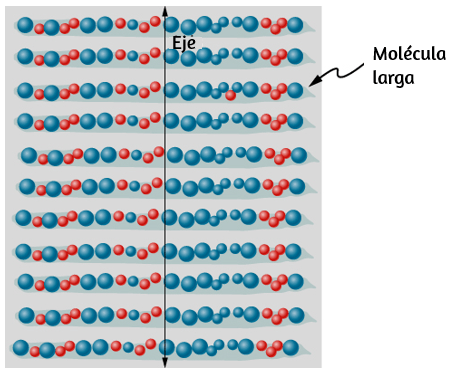
El campo eléctrico es fuerte en comparación con el campo magnético y es más efectivo para ejercer fuerza en las cargas de las moléculas. Las partículas cargadas más afectadas son los electrones, ya que las masas de electrones son pequeñas. Si se obliga a un electrón a oscilar, puede absorber energía de la onda EM. Esto reduce el campo en la onda y, por lo tanto, reduce su intensidad. En las moléculas largas, los electrones pueden oscilar más fácilmente en paralelo a la molécula que en la dirección perpendicular. Los electrones están unidos a la molécula y están más restringidos en su movimiento perpendicular a la molécula. Por lo tanto, los electrones pueden absorber ondas EM que tienen un componente de su campo eléctrico paralelo a la molécula.
Los electrones son mucho menos sensibles a los campos eléctricos perpendiculares a la molécula y permiten que estos campos pasen. Por lo tanto, el eje del filtro polarizador es perpendicular a la longitud de la molécula.
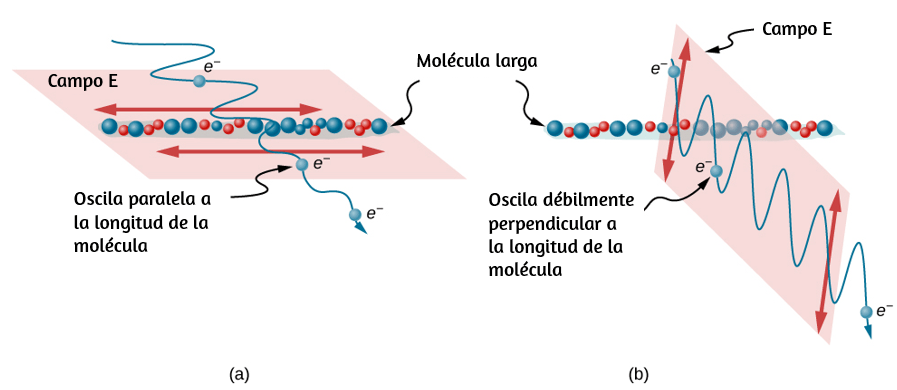
Si sostienes tus gafas de sol polarizadas frente a ti y las giras mientras miras el cielo azul, verás que el cielo se vuelve más oscuro y tenue. Esta es una clara indicación de que la luz dispersada por el aire está parcialmente polarizada. La ayuda a ilustrar cómo sucede esto. Dado que la luz es una onda EM transversal, vibra los electrones de las moléculas de aire perpendiculares a la dirección en la que está viajando. Los electrones entonces irradian como pequeñas antenas. Dado que oscilan perpendicularmente a la dirección del rayo de luz, producen radiación EM que está polarizada perpendicularmente a la dirección del rayo. Al ver la luz a lo largo de una línea perpendicular al rayo original, como en la figura, no puede haber polarización en la luz dispersada paralela al rayo original, ya que eso requeriría que el rayo original fuera una onda longitudinal.
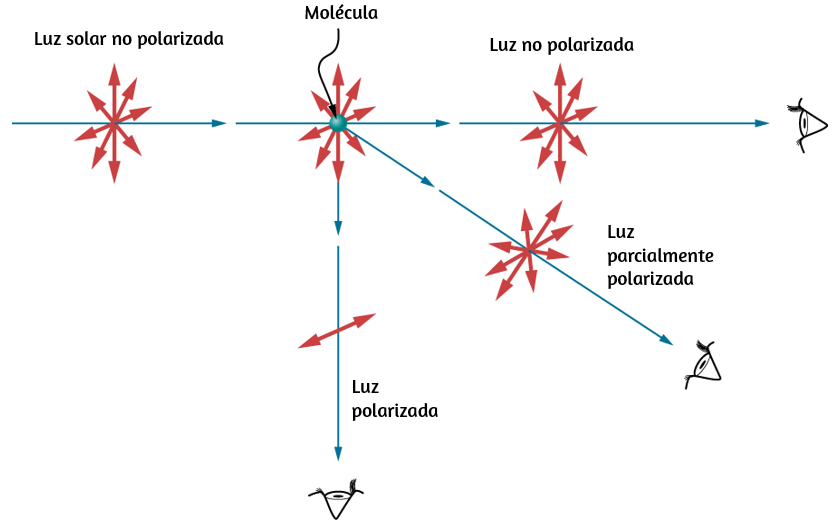
En otras direcciones, se puede proyectar un componente de la otra polarización a lo largo de la línea de visión, y la luz dispersada está solo parcialmente polarizada. Además, la dispersión múltiple puede llevar la luz a los ojos desde otras direcciones y puede contener diferentes polarizaciones.
Las fotografías del cielo pueden oscurecerse con filtros polarizadores, un truco utilizado por muchos fotógrafos para hacer que las nubes se vean más brillantes en contraste. La dispersión de otras partículas, como el humo o el polvo, también puede polarizar la luz. Detectar la polarización en ondas EM dispersas puede ser una herramienta analítica útil para determinar la fuente de dispersión.
Una gama de efectos ópticos se utilizan en gafas de sol. Además de ser polarizantes, las gafas de sol pueden tener pigmentos de colores incrustados, mientras que otras usan un revestimiento reflectivo o no reflectivo. Un desarrollo reciente son las lentes fotocromáticas, que se oscurecen a la luz del sol y se aclaran en el interior. Las lentes fotocromáticas están integradas con moléculas microcristalinas orgánicas que cambian sus propiedades cuando se exponen a los rayos UV a la luz del sol, pero se vuelven claras en la iluminación artificial sin rayos UV.
Aunque sin duda conoces las pantallas de cristal líquido (LCD) que se encuentran en los relojes, calculadoras, pantallas de computadoras, teléfonos celulares, televisores de pantalla plana y muchos otros lugares, es posible que no sepas que se basan en la polarización. Los cristales líquidos se llaman así porque sus moléculas pueden alinearse aunque estén en un líquido. Los cristales líquidos tienen la propiedad de que pueden rotar la polarización de la luz que pasa a través de ellos en $90$°. Además, esta propiedad se puede desactivar mediante la aplicación de un voltaje, como se ilustra en la . Es posible manipular esta característica rápidamente y en regiones pequeñas y bien definidas para crear los patrones de contraste que vemos en tantos dispositivos LCD.
En los televisores de pantalla plana, se genera una gran luz en la parte posterior del televisor. La luz viaja a la pantalla frontal a través de millones de pequeñas unidades llamadas píxeles (elementos de la imagen). Uno de estos se muestra en la (a) y (b). Cada unidad tiene tres celdas, con filtros rojo, azul o verde, cada una controlada de forma independiente. Cuando el voltaje a través de un cristal líquido se apaga, el cristal líquido pasa la luz a través del filtro particular. Podemos variar el contraste de la imagen variando la intensidad de la tensión aplicada al cristal líquido.
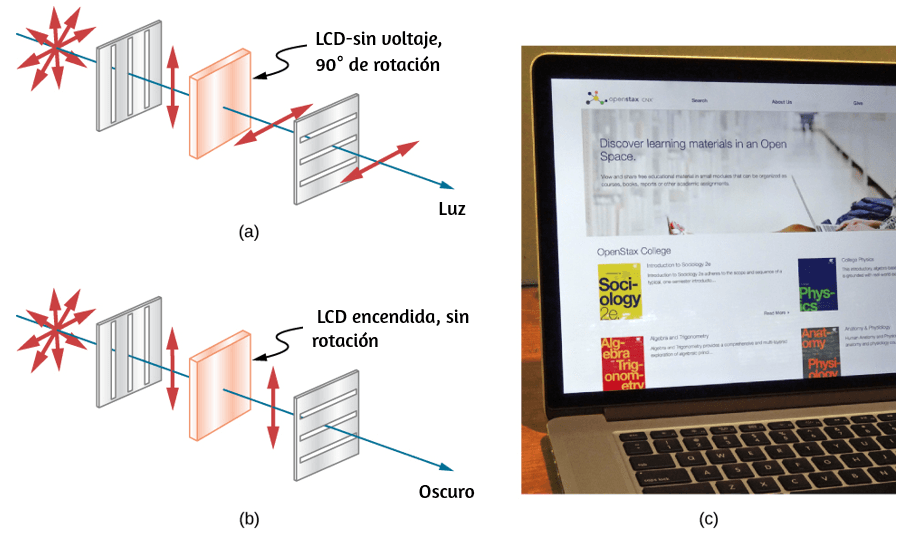
Muchos cristales y soluciones giran el plano de polarización de la luz que pasa a través de ellos. Se dice que tales sustancias son ópticamente activas. Los ejemplos incluyen agua azucarada, insulina y colágeno ().
Además de depender del tipo de sustancia, la cantidad y la dirección de rotación dependen de varios otros factores. Entre ellas se encuentra la concentración de la sustancia, la distancia que la luz recorre a través de ella y la longitud de onda de la luz. La actividad óptica se debe a la forma asimétrica de las moléculas en la sustancia, como ser helicoidal.
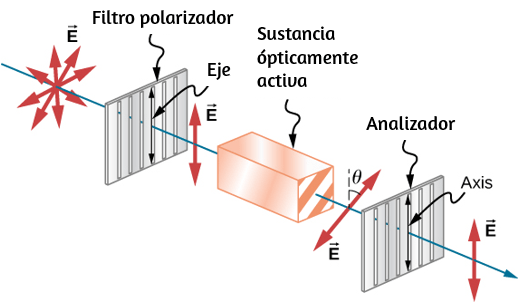
Las mediciones de la rotación de la luz polarizada que pasa a través de sustancias se pueden utilizar para medir concentraciones, una técnica estándar para los azúcares. También puede proporcionar información sobre las formas de las moléculas, como las proteínas, y los factores que afectan sus formas, como la temperatura y el pH.
El vidrio y el plástico se vuelven ópticamente activos cuando están esforzados: cuanto mayor es el esfuerzo, mayor es el efecto. El análisis de la tensión óptica en formas complicadas se puede realizar haciendo modelos de plástico de ellos y observándolos a través de filtros cruzados, como se ve en la . Es evidente que el efecto depende tanto de la longitud de onda como del esfuerzo. La dependencia de la longitud de onda también se utiliza a veces con fines artísticos.
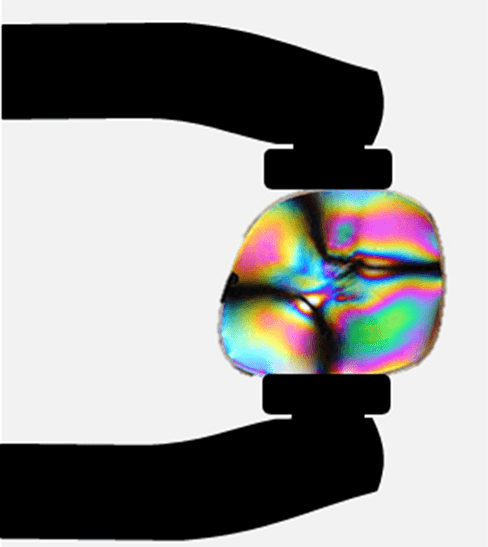
Otro fenómeno interesante asociado con la luz polarizada es la capacidad de algunos cristales para dividir un haz de luz no polarizado en dos haces polarizados. Esto ocurre porque el cristal tiene un valor para el índice de refracción de la luz polarizada pero un valor diferente para el índice de refracción de la luz polarizada en la dirección perpendicular, de modo que cada componente tiene su propio ángulo de refracción. Se dice que dichos cristales son birrefringentes y, cuando se alinean adecuadamente, surgirán dos rayos polarizados perpendiculares del cristal (). Se pueden usar cristales birrefringentes para producir haces polarizados a partir de luz no polarizada. Algunos materiales birrefringentes absorben preferentemente una de las polarizaciones. Estos materiales se denominan dicroicos y pueden producir polarización por esta absorción preferencial. Esto es fundamentalmente cómo funcionan los filtros polarizadores y otros polarizadores.
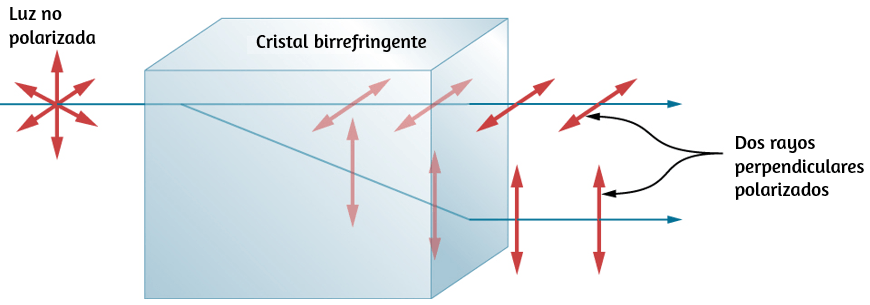

Este capítulo presenta las ideas principales de la óptica geométrica, que describen la formación de imágenes debido a la reflexión y la refracción. Se llama óptica "geométrica" porque las imágenes se pueden caracterizar mediante construcciones geométricas, como los diagramas de rayos. Hemos visto que la luz visible es una onda electromagnética; sin embargo, su naturaleza de onda se hace evidente solo cuando la luz interactúa con objetos con dimensiones comparables a la longitud de onda (aproximadamente $500 nm$ para la luz visible). Por lo tanto, las leyes de la óptica geométrica solo se aplican a la luz que interactúa con objetos mucho más grandes que la longitud de onda de la luz.
Solo tienes que mirar hasta el baño más cercano para encontrar un ejemplo de una imagen formada por un espejo. Las imágenes en un espejo plano son del mismo tamaño que el objeto, están ubicadas detrás del espejo y están orientadas en la misma dirección que el objeto (es decir, "en posición vertical").
Para entender cómo sucede esto, considera la . Dos rayos emergen del punto $P$, golpean el espejo y se reflejan en el ojo del observador. Ten en cuenta que usamos la ley de reflexión para construir los rayos reflejados.
Si los rayos reflejados se extienden hacia atrás detrás del espejo (observa las líneas discontinuas en la ), parecen originarse desde el punto $Q$. Aquí es donde se encuentra la imagen del punto $P$. Si repetimos este proceso para el punto $P'$, obtenemos su imagen en el punto $Q'$. Deberías convencerte utilizando geometría básica de que la altura de la imagen (la distancia de $Q$ a $Q'$) es la misma que la altura del objeto (la distancia de $P$ a $P'$). Al formar imágenes de todos los puntos del objeto, obtenemos una imagen vertical del objeto detrás del espejo.
Observa que los rayos reflejados le parecen al observador que vienen directamente de la imagen detrás del espejo. En realidad, estos rayos provienen de los puntos del espejo donde se reflejan. La imagen detrás del espejo se llama imagen virtual porque no se puede proyectar en una pantalla; los rayos solo parecen originarse desde un punto común detrás del espejo. Si caminas detrás del espejo, no puedes ver la imagen, porque los rayos no van allí. Sin embargo, frente al espejo, los rayos se comportan exactamente como si vinieran de detrás del espejo, de modo que es donde se encuentra la imagen virtual.
Más adelante en este capítulo, discutimos imágenes reales; una imagen real se puede proyectar en una pantalla porque los rayos atraviesan físicamente la imagen. Ciertamente puedes ver imágenes tanto reales como virtuales. La diferencia es que una imagen virtual no se puede proyectar en una pantalla, mientras que una imagen real sí.
La ley de reflexión nos dice que el ángulo de incidencia es el mismo que el ángulo de reflexión. La aplicación de esto a los triángulos $PAB$ y $QAB$ en la y el uso de la geometría básica muestra que son triángulos congruentes.
Esto significa que la distancia $PB$ desde el objeto al espejo es la misma que la distancia $BQ$ desde el espejo a la imagen. La distancia del objeto (denotado como $d_o$) es la distancia desde el espejo al objeto (o, más generalmente, desde el centro del elemento óptico que crea su imagen). De manera similar, la distancia de la imagen (denotada $d_i$) es la distancia desde el espejo a la imagen (o, más generalmente, desde el centro del elemento óptico que la crea). Si medimos distancias desde el espejo, entonces el objeto y la imagen están en direcciones opuestas, por lo que para un espejo plano, las distancias del objeto y la imagen deben tener los signos opuestos:
Un objeto extendido como el contenedor en se puede tratar como una colección de puntos, y podemos aplicar el método anterior para ubicar la imagen de cada punto en el objeto extendido, formando así la imagen extendida.
Si un objeto está situado frente a dos espejos, puedes ver imágenes en ambos espejos. Además, la imagen en el primer espejo puede actuar como un objeto para el segundo espejo, por lo que el segundo espejo puede formar una imagen de la imagen. Si los espejos se colocan paralelos entre sí y el objeto se coloca en un punto que no sea el punto medio entre ellos, este proceso de imagen de una imagen continúa sin fin, como habrás notado al estar de pie en un pasillo con espejos a cada lado. Esto se muestra en la , que muestra tres imágenes producidas por el objeto azul. Ten en cuenta que cada reflexión se invierte en la parte delantera y trasera, al igual que tirar un guante de la mano derecha de adentro hacia afuera produce un guante de la mano izquierda (esta es la razón por la que un reflejo de tu mano derecha es una mano izquierda).
Por lo tanto, los frentes y respaldos de las imágenes 1 y 2 se invierten con respecto al objeto, y el frente y el reverso de la imagen 3 se invierten con respecto a la imagen 2, que es el objeto para la imagen 3.
Es posible que hayas notado que la imagen 3 es más pequeña que el objeto, mientras que las imágenes 1 y 2 tienen el mismo tamaño que el objeto. La relación de la altura de la imagen con respecto a la altura del objeto se llama ampliación. Más se dirá acerca de la ampliación en la siguiente sección.
Las reflexiones infinitas pueden terminar. Por ejemplo, dos espejos en ángulos rectos forman tres imágenes, como se muestra en la parte (a) de la . Las imágenes 1 y 2 son el resultado de los rayos que se reflejan desde un solo espejo, pero la imagen 1,2 está formada por rayos que se reflejan en ambos espejos. Esto se muestra en el diagrama de trazado de rayos en la parte (b) de la . Para encontrar la imagen 1, 2, tienes que mirar detrás de la esquina de los dos espejos.
En la escena interactiva que presentamos en la página siguiente, tomada de las simulaciones de Boston University, puedes investigar la relación entre el ángulo del tablero y el ángulo en que el puck sale del palo de hockey. Para ello, usa el trasportador y cambia el ángulo del tablero.
La imagen en un espejo plano tiene el mismo tamaño que el objeto, está en posición vertical y está a la misma distancia detrás del espejo que el objeto que está frente al espejo. Un espejo curvo, por otro lado, puede formar imágenes que pueden ser más grandes o más pequeñas que el objeto y pueden formarse ya sea frente al espejo o detrás de él. En general, cualquier superficie curva formará una imagen, aunque algunas imágenes se distorsionan tanto como para ser irreconocibles (piensa en los espejos de las casas de recreo).
Debido a que los espejos curvos pueden crear una variedad tan rica de imágenes, se usan en muchos dispositivos ópticos que tienen muchos usos. Nos concentraremos en los espejos esféricos en su mayor parte, porque son más fáciles de fabricar que otros espejos como los parabólicos, por lo que son más comunes.
Podemos definir dos tipos generales de espejos esféricos. Si la superficie reflectante es el lado exterior de la esfera, el espejo se llama espejo convexo. Si la superficie interior es la superficie reflectante, se llama espejo cóncavo. La simetría es una de las principales características de muchos dispositivos ópticos, incluidos los espejos y las lentes. El eje de simetría de tales elementos ópticos se suele denominar eje principal o eje óptico. Para un espejo esférico, el eje óptico pasa a través del centro de curvatura del espejo y el vértice del espejo, como se muestra en la .
Considera los rayos que son paralelos al eje óptico de un espejo parabólico, como se muestra en la parte (a) de la . Siguiendo la ley de reflexión, estos rayos se reflejan para que converjan en un punto, llamado punto focal. La parte (b) de esta figura muestra un espejo esférico que es grande en comparación con su radio de curvatura.
Para este espejo, los rayos reflejados no se cruzan en el mismo punto, por lo que el espejo no tiene un punto focal bien definido. Esto se denomina aberración esférica y da como resultado una imagen borrosa de un objeto extendido.

La parte (c) muestra un espejo esférico que es pequeño en comparación con su radio de curvatura. Este espejo es una buena aproximación de un espejo parabólico, por lo que los rayos que llegan paralelos al eje óptico se reflejan en un punto focal bien definido. La distancia a lo largo del eje óptico desde el espejo hasta el punto focal se llama la distancia focal del espejo.
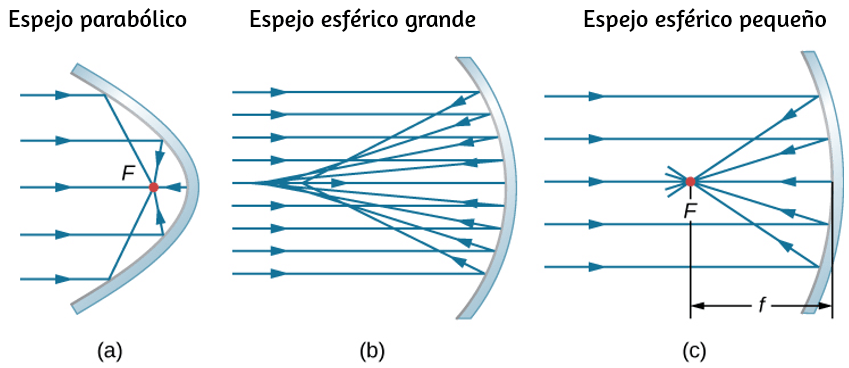
Un espejo esférico convexo también tiene un punto focal, como se muestra en la . Los rayos incidentes paralelos al eje óptico se reflejan desde el espejo y parecen originarse desde el punto F a la distancia focal f detrás del espejo. Por lo tanto, el punto focal es virtual porque en realidad no lo atraviesan los rayos reales; sólo parecen originarse de él.
¿Cómo se relaciona la longitud focal de un espejo con el radio de curvatura del espejo? La muestra un solo rayo que es reflejado por un espejo cóncavo esférico. El rayo incidente es paralelo al eje óptico. El punto en el cual el rayo reflejado cruza el eje óptico es el punto focal. Ten en cuenta que todos los rayos incidentes que son paralelos al eje óptico se reflejan a través del punto focal; solo mostramos un rayo por simplicidad.
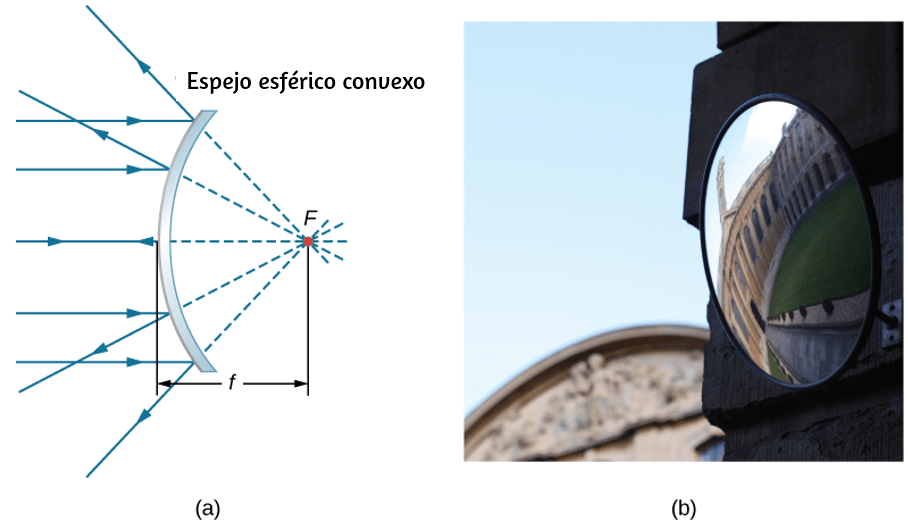
Queremos encontrar cómo la distancia focal FP (indicada por $f$) se relaciona con el radio de curvatura del espejo, $R$, cuya longitud es $R = CF + FP$. La ley de reflexión nos dice que los ángulos $OXC$ y $CXF$ son iguales, y como el rayo incidente es paralelo al eje óptico, los ángulos $OXC$ y $XCP$ también son iguales. Por lo tanto, el triángulo $CXF$ es un triángulo isósceles con $CF = FX$. Si el ángulo $θ$ es pequeño (de modo que $senθ ≈ θ$; esto se denomina “aproximación de ángulo pequeño”), entonces $FX ≈ FP$ o $CF ≈ FP.$ Insertando esto en la ecuación para el radio $R$, obtenemos
$$R = CF + FP = FP + FP = 2FP = 2f$$
En otras palabras, en la aproximación de ángulo pequeño, la distancia focal $f$ de un espejo esférico cóncavo es la mitad de su radio de curvatura, $R$:
En este capítulo, asumimos que la aproximación de ángulo pequeño (también llamada aproximación paraxial) siempre es válida. En esta aproximación, todos los rayos son rayos paraxiales, lo que significa que forman un pequeño ángulo con el eje óptico y están a una distancia mucho menor que el radio de curvatura del eje óptico. En este caso, sus ángulos $θ$ de reflexión son ángulos pequeños, entonces $senθ ≈ tanθ ≈ θ$.
Para encontrar la ubicación de una imagen formada por un espejo esférico, primero usamos el trazado de rayos, que es la técnica de dibujar rayos y usar la ley de reflexión para determinar los rayos reflejados (más adelante, para lentes, usamos la ley de refracción para determinar rayos refractados). Combinado con una geometría básica, podemos usar el trazado de rayos para encontrar el punto focal, la ubicación de la imagen y otra información sobre cómo un espejo manipula la luz. De hecho, ya usamos el trazado de rayos de arriba para ubicar el punto focal de los espejos esféricos, o la distancia de la imagen de los espejos planos. Para localizar la imagen de un objeto, debes ubicar al menos dos puntos de la imagen. La ubicación de cada punto requiere dibujar al menos dos rayos desde un punto en el objeto y construir sus rayos reflejados. El punto en el que los rayos reflejados se intersecan, ya sea en el espacio real o en el espacio virtual, es donde se encuentra el punto correspondiente de la imagen. Para facilitar el trazado de rayos, nos concentramos en cuatro rayos "principales" cuyos reflejos son fáciles de construir.
La muestra un espejo cóncavo y un espejo convexo, cada uno con un objeto en forma de flecha en frente de él. Estos son los objetos cuyas imágenes queremos localizar mediante el trazado de rayos. Para ello, dibujamos rayos desde el punto $Q$ que está en el objeto pero no en el eje óptico. Elegimos dibujar nuestro rayo desde la punta del objeto. El rayo principal $1$ va desde el punto $Q$ y viaja paralelo al eje óptico. La reflexión de este rayo debe pasar a través del punto focal, como se explicó anteriormente. Así, para el espejo cóncavo, la reflexión del rayo principal $1$ pasa por el punto focal $F$, como se muestra en la parte (b) de la figura. Para el espejo convexo, la extensión hacia atrás de la reflexión del rayo principal $1$ atraviesa el punto focal (es decir, un foco virtual).
El rayo principal $2$ viaja primero en la línea que pasa por el punto focal y luego se refleja a lo largo de una línea paralela al eje óptico. El rayo principal $3$ se desplaza hacia el centro de curvatura del espejo, por lo que golpea al espejo en una incidencia normal y se refleja de nuevo a lo largo de la línea de donde proviene. Finalmente, el rayo principal $4$ golpea el vértice del espejo y se refleja simétricamente sobre el eje óptico.
Los cuatro rayos principales se intersecan en el punto $Q'$, que es donde se encuentra la imagen del punto $Q$. Para ubicar el punto $Q'$, sería suficiente dibujar dos de estos rayos principales. Por lo tanto, somos libres de elegir cualquiera de los rayos principales que deseamos para localizar la imagen. Dibujar más de dos rayos principales a veces es útil para verificar que el trazado de rayos sea correcto.
Para ubicar completamente la imagen extendida, necesitamos ubicar un segundo punto en la imagen, para que sepamos cómo está orientada la imagen. Para ello, trazamos los rayos principales desde la base del objeto. En este caso, los cuatro rayos principales se desplazan a lo largo del eje óptico, se reflejan desde el espejo y luego vuelven a correr a lo largo del eje óptico. La dificultad es que, como estos rayos son colineales, no podemos determinar un punto único en el que se intersecan. Todo lo que sabemos es que la base de la imagen está en el eje óptico. Sin embargo, como el espejo es simétrico de arriba a abajo, no cambia la orientación vertical del objeto. Por lo tanto, debido a que el objeto es vertical, la imagen debe ser vertical. Por lo tanto, la imagen de la base del objeto está en el eje óptico directamente sobre la imagen de la punta, como se dibuja en la figura.
Para el espejo cóncavo, la imagen extendida en este caso se forma entre el punto focal y el centro de curvatura del espejo. Está invertida con respecto al objeto, es una imagen real y es más pequeña que el objeto. Si moviéramos el objeto más cerca o más lejos del espejo, las características de la imagen cambiarían.
Por ejemplo, mostramos, como un ejercicio posterior, que un objeto colocado entre un espejo cóncavo y su punto focal conduce a una imagen virtual que es vertical y más grande que el objeto. Para el espejo convexo, la imagen extendida se forma entre el punto focal y el espejo. Es vertical con respecto al objeto, es una imagen virtual y es más pequeña que el objeto.
El trazado de rayos es muy útil para los espejos. Las reglas para el trazado de rayos se resumen aquí como referencia:
Utilizamos el trazado de rayos para ilustrar cómo se forman las imágenes mediante espejos y para obtener información numérica sobre las propiedades ópticas del espejo. Si asumimos que un espejo es pequeño en comparación con su radio de curvatura, también podemos usar el álgebra y la geometría para deducir una ecuación de espejo, lo que hacemos en la siguiente sección. Combinar el trazado de rayos con la ecuación de espejo es una buena manera de analizar los sistemas de espejo.
Para un espejo plano, mostramos que la imagen formada tiene la misma altura y orientación que el objeto, y está ubicada a la misma distancia detrás del espejo que el objeto que está frente al espejo. Aunque la situación es un poco más complicada para los espejos curvos, el uso de la geometría conduce a fórmulas simples que relacionan el objeto y las distancias de la imagen con las distancias focales de los espejos cóncavos y convexos.
Considera el objeto $OP$ que se muestra en la . El centro de curvatura del espejo está etiquetado como $C$ y está a una distancia $R$ del vértice del espejo, como se indica en la figura. Las distancias de los objetos y las imágenes están etiquetadas como $d_o$ y $d_i$, y las alturas de los objetos y las imágenes están etiquetadas como $h_o$ y $h_i$, respectivamente. Debido a que los ángulos $φ$ y $φ'$ son ángulos alternos internos, sabemos que tienen la misma magnitud. Sin embargo, deben diferir en el signo si medimos ángulos desde el eje óptico, entonces $φ = -φ'$. Un escenario análogo se mantiene para los ángulos $θ$ y $θ'$. La ley de la reflexión nos dice que tienen la misma magnitud, pero sus signos deben diferir si medimos los ángulos desde el eje óptico. Por lo tanto, $θ = -θ'$. Tomando la tangente de los ángulos $θ$ y $θ'$, y usando la propiedad $tan(-θ) = -tanθ$, nos da
$$\begin{rcases} tanθ = \frac{h_o}{d_o} \\ tanθ' = -tanθ = \frac{h_i}{d_i} \end{rcases} \frac{h_o}{d_o} = -\frac{h_i}{d_i} \; \textsf{o} \; -\frac{h_o}{h_i} = \frac{d_o}{d_i} \tag{9.3}$$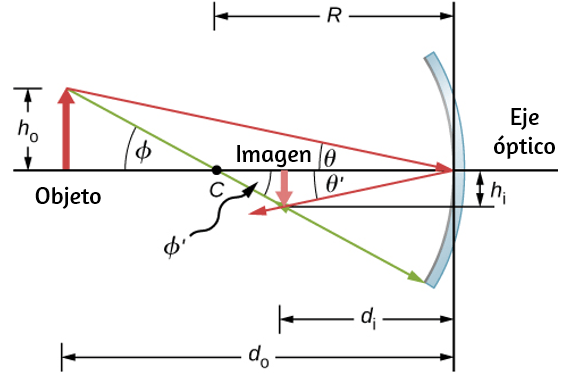
Del mismo modo, tomando la tangente de $φ$ y $φ'$, obtenemos:
$$\begin{rcases} tanϕ = \frac{h_o}{d_o-R} \\ tanϕ' = -tanϕ = \frac{h_i}{R-d_i} \end{rcases} \frac{h_o}{d_o-R} = -\frac{h_i}{R-d_i} \; \textsf{o} \; -\frac{h_o}{h_i} = \frac{d_o-R}{R-d_i}$$Combinando estos dos resultados da
$$\frac{d_o}{d_i} = \frac{d_{o - R}}{R - d_i}$$Después de un poco de álgebra, esta expresión se convierte en
$$\frac{1}{d_o} + \frac{1}{d_i} = \frac{2}{R} \tag{9.4}$$No se requiere una aproximación para este resultado, por lo que es exacto. Sin embargo, como se mencionó anteriormente, en la aproximación de ángulo pequeño, la distancia focal de un espejo esférico es la mitad del radio de curvatura del espejo, o $f = R/2$. Al insertar esto en la Ecuación 9.3 se obtiene la ecuación del espejo:
La ecuación del espejo relaciona las distancias de la imagen y el objeto con la distancia focal y solo es válida en la aproximación de ángulo pequeño. Aunque se dedujo para un espejo cóncavo, también se aplica a los espejos convexos (demostración que queda como un ejercicio). Podemos extender la ecuación del espejo al caso de un espejo plano observando que un espejo plano tiene un radio infinito de curvatura. Esto significa que el punto focal está en el infinito, por lo que la ecuación de espejo se simplifica a
$$d_o = -d_i \tag{9.6}$$que es lo mismo que la ecuación 9.1 obtenida anteriormente.
Observa que hemos sido muy cuidadosos con los signos para deducir la ecuación del espejo. Para un espejo plano, la distancia de la imagen tiene el signo opuesto de la distancia del objeto. Además, la imagen real formada por el espejo cóncavo en la está en el lado opuesto del eje óptico con respecto al objeto. En este caso, la altura de la imagen debe tener el signo opuesto de la altura del objeto. Para realizar un seguimiento de los signos de las diversas cantidades en la ecuación de espejo, ahora presentamos una convención de signos.
Usar una convención de signos consistente es muy importante en la óptica geométrica. Asigna valores positivos o negativos para las cantidades que caracterizan un sistema óptico. Comprender la convención de signos te permite describir una imagen sin construir un diagrama de rayos. Este texto utiliza la siguiente convención de signos:
Observa que la regla 1 significa que el radio de curvatura de un espejo esférico puede ser positivo o negativo. ¿Qué significa tener un radio de curvatura negativo? Esto significa simplemente que el radio de curvatura para un espejo convexo se define como negativo.
Usamos la convención de signos para interpretar mejor la deducción de la ecuación del espejo. Al deducir esta ecuación, encontramos que las alturas del objeto y la imagen están relacionadas por
$$-\frac{h_o}{h_i} = \frac{d_o}{d_i} \tag{9.7}$$Tanto el objeto como la imagen formada por el espejo en la son reales, por lo que las distancias entre el objeto y la imagen son positivas.
El punto más alto del objeto está por encima del eje óptico, por lo que la altura del objeto es positiva. Sin embargo, la imagen está debajo del eje óptico, por lo que la altura de la imagen es negativa. Por lo tanto, esta convención de signos es consistente con nuestra deducción de la ecuación del espejo.
La ecuación 9.7, de hecho, describe el aumento lineal (a menudo llamado simplemente "aumento") de la imagen en términos del objeto y las distancias de la imagen. Así definimos la ampliación adimensional $m$ de la siguiente manera:
$$m = \frac{h_i}{h_o} \tag{9.8}$$Si $m$ es positiva, la imagen está en posición vertical, y si $m$ es negativa, la imagen se invierte. Si $|m| > 1$, la imagen es más grande que el objeto, y si $|m| < 1$, la imagen es más pequeña que el objeto. Con esta definición de ampliación, obtenemos la siguiente relación entre el objeto vertical y horizontal y las distancias de la imagen:
Esta es una relación muy útil porque te permite obtener la ampliación de la imagen del objeto y las distancias de la imagen, que puedes obtener de la ecuación del espejo.
Ejemplo 9.1
Sistema de generación eléctrica solar
Una de las tecnologías solares utilizadas hoy en día para generar electricidad involucra un dispositivo (llamado colector parabólico o colector de concentración) que concentra la luz solar en una tubería ennegrecida que contiene un fluido. Este fluido calentado se bombea a un intercambiador de calor, donde la energía térmica se transfiere a otro sistema que se utiliza para generar vapor y, finalmente, genera electricidad a través de un ciclo de vapor convencional. La muestra un sistema de este tipo en el sur de California. El espejo real es un cilindro parabólico con su foco ubicado en la tubería; sin embargo, podemos aproximar el espejo exactamente como un cuarto de un cilindro circular.

a. Si queremos que los rayos del sol se enfoquen a $40.0 cm$ del espejo, ¿cuál es el radio del espejo?
b. ¿Cuál es la cantidad de luz solar concentrada en la tubería, por metro de longitud de tubería, suponiendo que la insolación (radiación solar incidente) sea de $900 W/m^2$?
Si la tubería de transporte de fluido tiene un diámetro de $2,00 cm$, ¿cuál es el aumento de temperatura del fluido por metro de tubería en un período de $1$ minuto? Supón que toda la radiación solar que incide sobre el reflector es absorbida por la tubería y que el fluido es aceite mineral.
Estrategia
Primero identifica los principios físicos involucrados. La parte (a) está relacionada con la óptica de los espejos esféricos. La parte (b) involucra un poco de matemáticas, principalmente geometría. La parte (c) requiere una comprensión del calor y la densidad.
Solución
a. El sol es el objeto, por lo que la distancia del objeto es esencialmente infinita: $d_o = ∞$. La distancia de la imagen deseada es $d_i = 40.0cm$. Usamos la ecuación del espejo para encontrar la longitud focal del espejo:
$$\frac{1}{d_o} + \frac{1}{d_i} = \frac{1}{f}$$ $$f = \left(\frac{1}{d_o} + \frac{1}{d_i} \right)^{-1}$$ $$f = \left(\frac{1}{∞} + \frac{1}{40.0 cm} \right)^{-1}$$ $$f = 40.0 cm$$Por lo tanto, el radio del espejo es $R = 2f = 80.0 cm$.
b. La insolación es de $900 W/m^2$. Debes encontrar el área transversal A del espejo cóncavo, ya que la potencia entregada es de $900 W/m^2 × A$. En este caso, el espejo se estima como un cuarto de sección de un cilindro, por lo que el área para una longitud $L$ del espejo es $A = \frac{1}{4}(2πR)L$. El área para una longitud de $1.00 m$ es entonces
$$A = \frac{π}{2}R(1.00 m) = \frac{3.14}{2}(0.800 m)(1.00 m) =1.26 m^2$$La insolación en el tramo de tubería de $1.00 m$ es entonces
$$(9.00 × 10^2 W/m^2)(1.26 m^2) = 1130W$$c. El aumento de temperatura viene dado por $Q = mcΔT$. La masa $m$ del aceite mineral en la sección de tubo de un metro es
$$\begin{split} m &= ρV = ρπ(d/2)^2(1.00 m) \\ m &= (8.00 × 10^2 kg/m^3)(3.14)(0.0100 m)^2(1.00 m) \\ &= 0.251 kg \end{split}$$Por lo tanto, el aumento de temperatura en un minuto es
$$ΔT = Q/mc$$ $$ΔT = \frac{(1130 W)(60.0 s)}{(0.251 kg)(1670 J \cdot kg/°C)} = 162 °C$$Explicación
Un conjunto de tuberías de este tipo en el desierto de California puede proporcionar una potencia térmica de $250 MW$ en un día soleado, con fluidos que alcanzan temperaturas de hasta $400 °C$. Estamos considerando solo un metro de tubería aquí e ignorando las pérdidas de calor a lo largo de la tubería.
Ejemplo 9.2
Imagen en un espejo convexo
Un queratómetro es un dispositivo que se usa para medir la curvatura de la córnea del ojo, especialmente para colocar lentes de contacto. La luz se refleja desde la córnea, que actúa como un espejo convexo, y el queratómetro mide la ampliación de la imagen. Cuanto menor sea el aumento, menor será el radio de curvatura de la córnea. Si la fuente de luz está a $12 cm$ de la córnea y el aumento de la imagen es de $0.032$, ¿cuál es el radio de curvatura de la córnea?
Estrategia
Si encuentras la distancia focal del espejo convexo formado por la córnea, entonces conoces su radio de curvatura (es el doble de la distancia focal). La distancia del objeto es $d_o = 12 cm$ y la ampliación es $m = 0.032$. Primero encuentra la distancia de la imagen $d_i$ y luego halla la distancia focal $f$.
Solución
Comienza con la ecuación para la ampliación, $m = -\frac{d_i}{d_o}$. Resolviendo para $d_i$ e insertando los valores dados, obtenemos:
$$d_i = -md_o = -(0.032)(12 cm) = -0.384 cm$$donde retuvimos una cifra significativa adicional porque este es un paso intermedio en el cálculo. Resuelve la ecuación del espejo para la distancia focal f e inserta los valores conocidos para el objeto y las distancias de la imagen. El resultado es
$$\frac{1}{d_o} + \frac{1}{d_i} = \frac{1}{f}$$ $$f = \left(\frac{1}{d_o} + \frac{1}{d_i} \right)^{-1}$$ $$f = \left(\frac{1}{12 cm} + \frac{1}{-0.384 cm} \right)^{-1}$$ $$f = -40.0 cm$$El radio de curvatura es el doble de la distancia focal, por lo que
$$R = 2f = -0.80 cm$$Explicación
La distancia focal es negativa, por lo que el enfoque es virtual, como se espera para un espejo cóncavo y un objeto real. El radio de curvatura encontrado aquí es razonable para una córnea. La distancia de la córnea a la retina en un ojo adulto es de unos $2,0 cm$. En la práctica, las córneas pueden no ser esféricas, lo que complica el trabajo de colocar lentes de contacto. Observa que la distancia de la imagen aquí es negativa, consistente con el hecho de que la imagen está detrás del espejo. Por lo tanto, la imagen es virtual porque en realidad no la atraviesan los rayos. En los problemas y ejercicios, demostrarás que, para una distancia de objeto fija, un radio de curvatura más pequeño corresponde a una ampliación más pequeña.
Estrategia de resolución de problemas: espejos esféricos
Paso 1. Primero asegúrate de que la formación de la imagen mediante un espejo esférico esté involucrada.
Paso 2. Determina si se requiere el trazado de rayos, la ecuación del espejo o ambos. Un boceto es muy útil incluso si el problema no requiere específicamente el trazado de rayos. Escribir símbolos y valores conocidos en el boceto.
Paso 3. Identifica exactamente lo que se debe determinar en el problema (identifica las incógnitas).
Paso 4. Haz una lista de lo que se da o se puede inferir del problema como se indica (identifica lo que se sabe).
Paso 5. Si se requiere el trazado de rayos, usa las reglas de trazado de rayos que aparecen cerca del comienzo de esta sección.
Paso 6. La mayoría de los problemas cuantitativos requieren el uso de la ecuación del espejo. Usa los ejemplos como guías para usar la ecuación del espejo.
Paso 7. Comprueba si la respuesta tiene sentido. ¿Los signos de la distancia del objeto, la distancia de la imagen y la distancia focal se corresponden con lo que se espera del trazado de rayos? ¿Es correcto el signo de la ampliación? ¿Son razonables las distancias de objeto e imagen?
La aproximación de ángulo pequeño es una piedra angular de la discusión anterior sobre la formación de imágenes mediante un espejo esférico. Cuando se viola esta aproximación, la imagen creada por un espejo esférico se distorsiona. Tal distorsión se llama aberración. Aquí discutimos brevemente dos tipos específicos de aberraciones: la aberración esférica y el coma.
Considera un haz amplio de rayos paralelos que inciden en un espejo esférico, como se muestra en la .
Cuanto más lejos del eje óptico golpean los rayos, peor se aproxima el espejo esférico a un espejo parabólico. Por lo tanto, estos rayos no se enfocan en el mismo punto que los rayos que están cerca del eje óptico, como se muestra en la figura. Debido a la aberración esférica, la imagen de un objeto extendido en un espejo esférico será borrosa. Las aberraciones esféricas son características de los espejos y lentes que consideramos en la siguiente sección de este capítulo (se necesitan espejos y lentes más sofisticados para eliminar las aberraciones esféricas).
Coma es similar a la aberración esférica, pero surge cuando los rayos entrantes no son paralelos al eje óptico, como se muestra en la parte (b) de la . Debido a que un espejo esférico es simétrico con respecto al eje óptico, los diversos rayos de colores en esta figura crean círculos del color correspondiente en el plano focal.
Si bien se muestra un espejo esférico en la parte (b) de la , la aberración cromática también ocurre con los espejos parabólicos: no es el resultado de una ruptura en la aproximación de ángulo pequeño. La aberración esférica, sin embargo, ocurre solo para espejos esféricos y es el resultado de una ruptura en la aproximación de ángulo pequeño. Discutiremos tanto el coma como la aberración esférica más adelante en este capítulo, en relación con los telescopios.
La siguiente escena interactiva tomada del Proyecto Telesecundaria, permite interactuar con los dos tipos de espejos esféricos (cóncavos y convexos).
En el espejo convexo, el objeto que se refleja es una flecha amarilla. La flecha se desplaza y/o cambia de tamaño al arrastrar el botón rojo mediante el ratón. De la punta de la flecha surgen tres rayos de luz, uno de los cuales se dirige al punto $C$, de color turquesa, que es el centro de curvatura del espejo. La imagen reflejada se construye mediante las reflexiones de estos rayos. El punto $F$ es el foco del espejo. Existe también la posibilidad de modificar el centro de curvatura, arrastrando el punto turquesa $C$. Esta acción produce cambios en el tamaño de la imagen reflejada.
En el espejos cóncavo, la funcionalidad es igual a la descrita para el espejo convexo, es decir, puede variarse el tamaño y posición de la flecha, así como el centro de curvatura del espejo, y observar las características de la imagen reflejada.
Cuando los rayos de luz se propagan de un medio a otro, estos rayos sufren refracción, que es cuando las ondas de luz se doblan en la interfaz entre dos medios. La superficie refractiva puede formar una imagen de manera similar a una superficie reflectante, excepto que la ley de refracción (ley de Snell) está en el centro del proceso en lugar de la ley de reflexión.
Si observas una varilla recta parcialmente sumergida en agua, parece doblarse en la superficie (). La razón detrás de este curioso efecto es que la imagen de la varilla dentro del agua se forma un poco más cerca de la superficie que la posición real de la varilla, por lo que no se alinea con la parte de la varilla que está por encima del agua. El mismo fenómeno explica por qué un pez en el agua parece estar más cerca de la superficie de lo que realmente es.
Para estudiar la formación de imágenes como resultado de la refracción, considera las siguientes preguntas:
Para ser concretos, consideramos un sistema simple que consiste en dos medios separados por una interfaz plana (). El objeto está en un medio y el observador en el otro. Por ejemplo, cuando observas un pez desde arriba de la superficie del agua, el pez está en el medio 1 (el agua) con un índice de refracción de $1.33$, y su ojo está en el medio 2 (el aire) con un índice de refracción de $1.00$, y la superficie del agua es la interfaz. La profundidad que “ves” es la altura de la imagen $h_i$ y se llama la profundidad aparente. La profundidad real del pez es la altura del objeto $h_o$.
La profundidad aparente $h_i$ depende del ángulo en el que se ve la imagen. Para una vista desde arriba (la llamada vista "normal"), podemos aproximar el ángulo de refracción $θ$ para que sea pequeño, y reemplazar el $senθ$ en la ley de Snell por $tanθ$. Con esta aproximación, puedes usar los triángulos $ΔOPR$ y $ΔOQR$ para mostrar que la profundidad aparente está dada por
La deducción de este resultado se deja como ejercicio. Por lo tanto, un pez aparece a $3/4$ de la profundidad real cuando se ve desde arriba.
Las formas esféricas de alta calidad son mucho más fáciles de fabricar que otras superficies curvas. Para estudiar la refracción en una sola superficie esférica, asumimos que el medio con la superficie esférica en un extremo continúa indefinidamente (un medio "semi-infinito").
Considera una fuente de luz puntual en el punto $P$ frente a una superficie convexa hecha de vidrio (consulta la ). Sea $R$ el radio de curvatura, $n_1$ el índice de refracción del medio en el que se encuentra el punto $P$ del objeto y $n_2$ el índice de refracción del medio con la superficie esférica. Queremos saber qué sucede como resultado de la refracción en esta interfaz.
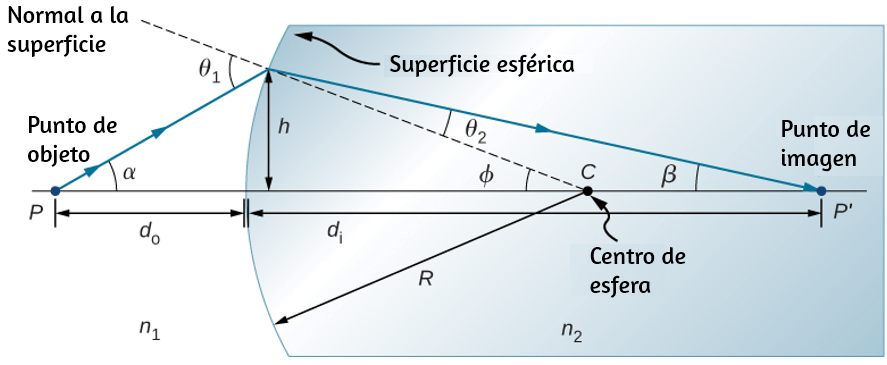
Debido a la simetría involucrada, es suficiente examinar los rayos en un solo plano. La figura muestra un rayo de luz que comienza en el punto $P$ del objeto, se refracta en la interfaz y atraviesa el punto $P$ de la imagen. Dedujimos una fórmula que relaciona la distancia del objeto $d_o$, la distancia de la imagen $d_i$ y el radio de curvatura $R$.
La aplicación de la ley de Snell al rayo que emana del punto $P$ da $n_1senθ_1 = n_2senθ_2$. Trabajamos en la aproximación de ángulo pequeño, por lo que $senθ ≈ θ$ y la ley de Snell toman la forma
$$n_1θ_1 ≈ n_2θ_2$$Desde la geometría de la figura, vemos que
$$θ_1 = α + φ, θ_2 = φ - β$$Al reemplazar estas expresiones en la ley de Snell, obtenemos:
$$n_1(α + φ) ≈ n_2(φ - β)$$Usando el diagrama, calculamos la tangente de los ángulos $α$, $β$, y $φ$:
$$tan α ≈ \frac{h}{d_o}, tan β ≈ \frac{h}{d_i}, φ ≈ \frac{h}{R}$$Nuevamente, utilizando la aproximación de ángulo pequeño, encontramos que $tan θ ≈ θ$, por lo que las relaciones anteriores se vuelven $$α ≈ \frac{h}{d_o}, β ≈ \frac{h}{d_i}, φ ≈ \frac{h}{R}$$
Al reemplazar estos ángulos en la ley de Snell, obtenemos:
$$n_1 \left(\frac{h}{d_o} + \frac{h}{R} \right) = n_2 \left(\frac{h}{R} - \frac{h}{d_i} \right)$$Podemos escribir esto más conveniente como
Si el objeto se coloca en un punto especial llamado primer foco, o el foco $F_1$ del objeto, entonces la imagen se forma en el infinito, como se muestra en la parte (a) de la .
Podemos encontrar la ubicación $f_1$ del primer foco $F_1$ al establecer $d_i = ∞$ en la ecuación anterior.
$$\frac{n_1}{f_1} + \frac{n_2}{∞} = \frac{n_2 - n_1}{R} \tag{9.12}$$ $$f_1 = \frac{n_1R}{n_2 - n_1} \tag{9.13}$$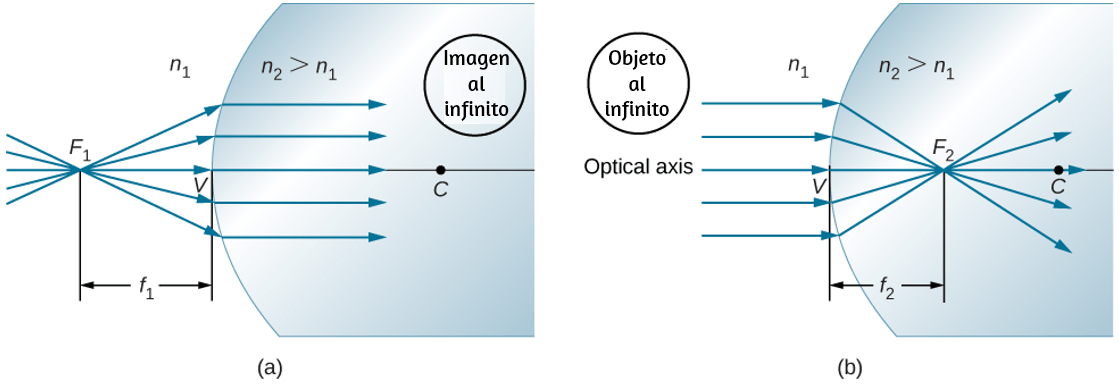
De manera similar, podemos definir un segundo foco o foco de imagen $F_2$ donde la imagen se forma para un objeto que está lejos [parte (b)]. La ubicación del segundo foco $F_2$ se obtiene a partir de la ecuación 2.11 estableciendo $d_o = ∞$:
$$\frac{n_1}{∞} + \frac{n_2}{f_2} = \frac{n_2 - n_1}{R}$$ $$f_2 = \frac{n_2R}{n_2 - n_1}$$Observa que el foco del objeto se encuentra a una distancia diferente del vértice que el foco de la imagen porque $n_1 ≠ n_2$.
Aunque dedujimos esta ecuación para la refracción en una superficie convexa, la misma expresión es válida para una superficie cóncava, siempre que usemos la siguiente convención de signos:
Las lentes se encuentran en una gran variedad de instrumentos ópticos, que van desde una simple lupa hasta la lente de zoom de una cámara y hasta el ojo. En esta sección, usamos la ley de Snell para explorar las propiedades de las lentes y cómo forman las imágenes.
La palabra "lente" deriva de la palabra latina para un grano de lenteja, cuya forma es similar a una lente convexa. Sin embargo, no todas las lentes tienen la misma forma. La muestra una variedad de diferentes formas de lentes. El vocabulario utilizado para describir las lentes es el mismo que el utilizado para los espejos esféricos: el eje de simetría de una lente se denomina eje óptico, donde este eje se intersecta con la superficie de la lente y se llama vértice de la lente, etc.
Una lente convexa o convergente tiene una forma tal que todos los rayos de luz que ingresan en paralelo a su eje óptico se intersecan (o enfocan) en un solo punto en el eje óptico en el lado opuesto de la lente, como se muestra en la parte (a) de la . Del mismo modo, una lente cóncava o divergente tiene una forma tal que todos los rayos que ingresan en paralelo a su eje óptico divergen, como se muestra en la parte (b). Para comprender con mayor precisión cómo manipula la luz una lente, observa detenidamente el rayo superior que atraviesa la lente convergente en la parte (a). Debido a que el índice de refracción de la lente es mayor que el del aire, la ley de Snell nos dice que el rayo está inclinado hacia la perpendicular a la interfaz cuando ingresa a la lente. Del mismo modo, cuando el rayo sale de la lente, se desvía de la perpendicular. El mismo razonamiento se aplica a las lentes divergentes, como se muestra en la parte (b). El efecto general es que los rayos de luz se inclinan hacia el eje óptico para una lente convergente y se alejan del eje óptico para lentes divergentes.
Para una lente convergente, el punto en el que los rayos se cruzan es el punto focal $F$ de la lente. Para una lente divergente, el punto desde el cual los rayos parecen originarse es el punto focal (virtual). La distancia desde el centro de la lente hasta su punto focal es la distancia focal $f$ de la lente.
Se considera que una lente es delgada si su grosor t es mucho menor que el radio de curvatura de ambas superficies, como se muestra en la . En este caso, se puede considerar que los rayos se doblan una vez en el centro de la lente. Para el caso dibujado en la figura, el rayo de luz 1 es paralelo al eje óptico, por lo que el rayo saliente se dobla una vez en el centro de la lente y pasa por el punto focal. Otra característica importante de las lentes delgadas es que los rayos de luz que pasan a través del centro de la lente no se desvían, como lo muestra el rayo de luz 2.
Como se señaló en la discusión inicial de la ley de Snell, los caminos de los rayos de luz son exactamente reversibles. Esto significa que la dirección de las flechas podría invertirse para todos los rayos en la . Por ejemplo, si se coloca una fuente de luz puntual en el punto focal de una lente convexa, como se muestra en la , los rayos de luz paralelos emergen del otro lado.
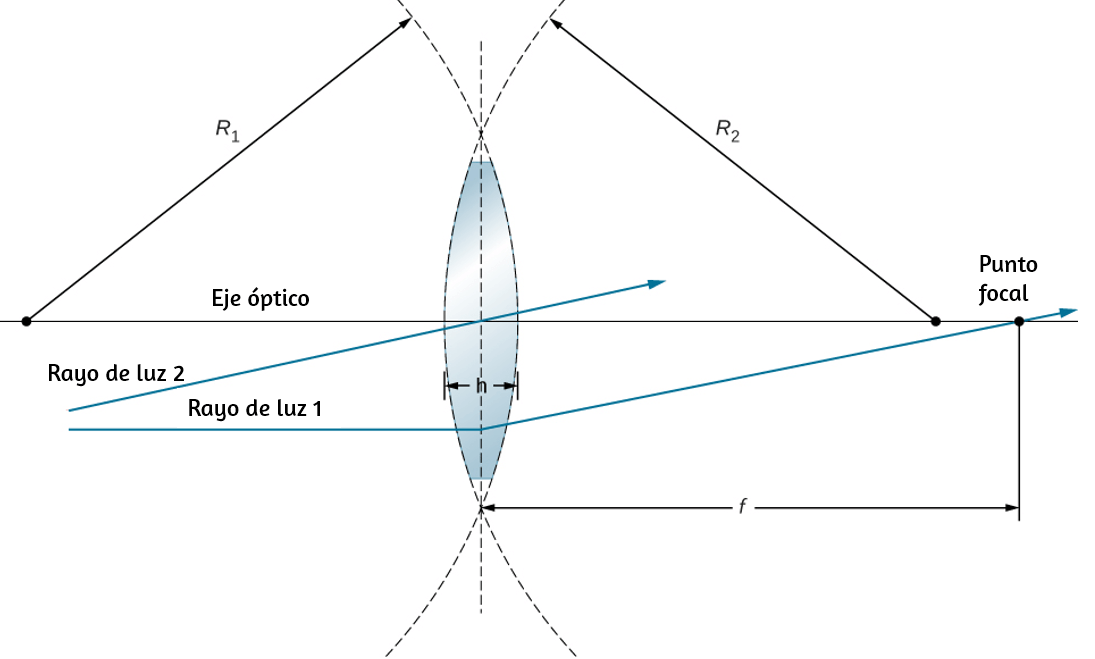
El trazado de rayos es la técnica para determinar o seguir (trazar) los caminos que toman los rayos de luz.
El trazado de rayos para lentes delgadas es muy similar a la técnica que utilizamos con espejos esféricos. En cuanto a los espejos, el trazado de rayos puede describir con precisión el funcionamiento de una lente. Las reglas para el trazado de rayos para lentes delgadas son similares a las de los espejos esféricos:
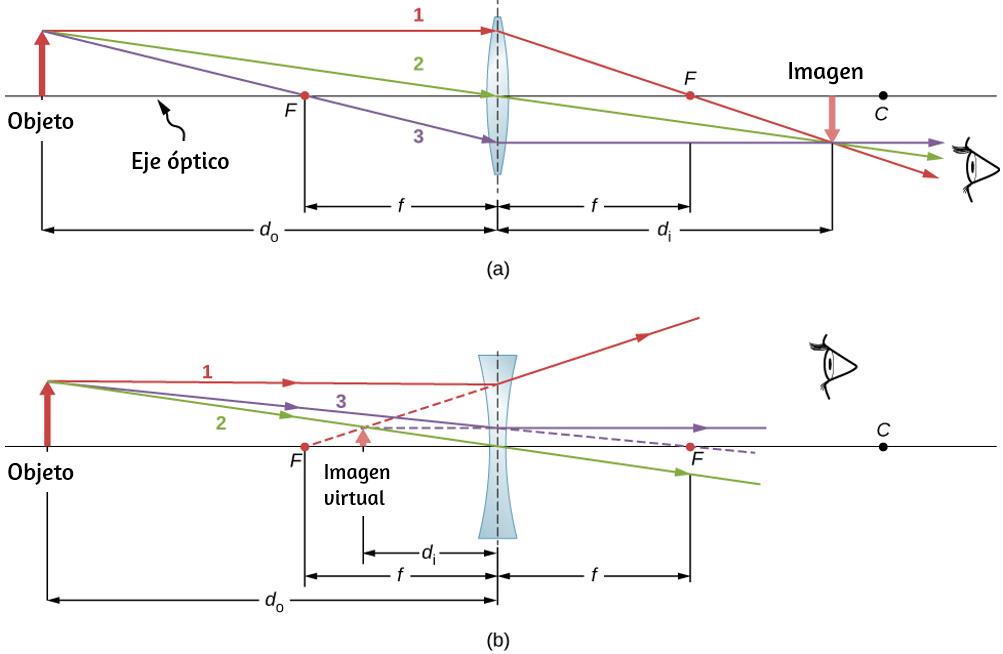
En la siguiente escena interactiva, diseñada por Andrew Duffy, puedes practicar con lentes convexas y cóncavas.
Las lentes delgadas funcionan bastante bien para la luz monocromática (es decir, la luz de una sola longitud de onda). Sin embargo, para la luz que contiene varias longitudes de onda (por ejemplo, luz blanca), las lentes funcionan menos bien. El problema es que, como aprendimos en el capítulo anterior, el índice de refracción de un material depende de la longitud de onda de la luz. Este fenómeno es responsable de muchos efectos coloridos, como el arco iris. Desafortunadamente, este fenómeno también conduce a aberraciones en las imágenes formadas por lentes. En particular, debido a que la distancia focal de la lente depende del índice de refracción, también depende de la longitud de onda de la luz incidente. Esto significa que la luz de diferentes longitudes de onda se enfocará en diferentes puntos, lo que se denomina "aberraciones cromáticas".
En particular, los bordes de una imagen de un objeto blanco se volverán de color y borrosos. Las lentes especiales llamadas dobletes son capaces de corregir las aberraciones cromáticas. Un doblete se forma pegando juntos una lente convergente y una lente divergente. La lente doblete combinada produce aberraciones cromáticas significativamente reducidas.
Usamos el trazado de rayos para investigar diferentes tipos de imágenes que pueden ser creadas por una lente. En algunas circunstancias, una lente forma una imagen real, como cuando un proyector de películas proyecta una imagen en una pantalla. En otros casos, la imagen es una imagen virtual, que no se puede proyectar en una pantalla. ¿Dónde, por ejemplo, está la imagen formada por las gafas? Utilizaremos el trazado de rayos para lentes delgadas para ilustrar cómo se forman imágenes, y luego desarrollaremos ecuaciones para analizar cuantitativamente las propiedades de las lentes delgadas.
Considera un objeto a cierta distancia de una lente convergente, como se muestra en la . Para encontrar la ubicación y el tamaño de la imagen, trazamos las rutas de los rayos de luz seleccionados que se originan desde un punto en el objeto, en este caso, la punta de la flecha. La figura muestra tres rayos de muchos rayos que emanan de la punta de la flecha. Estos tres rayos se pueden rastrear mediante el uso de las reglas de trazado de rayos indicadas anteriormente.
Los tres rayos se cruzan en un solo punto en el lado opuesto de la lente. Por lo tanto, la imagen de la punta de la flecha se encuentra en este punto. Todos los rayos que provienen de la punta de la flecha y entran en la lente se refractan y se cruzan en el punto que se muestra.
Después de ubicar la imagen de la punta de la flecha, necesitamos otro punto de la imagen para orientar la imagen completa de la flecha. Elegimos ubicar la base de la imagen de la flecha, que está en el eje óptico. Como se explicó en la sección sobre espejos esféricos, la base estará en el eje óptico justo encima de la imagen de la punta de la flecha (debido a la simetría superior-inferior de la lente). Por lo tanto, la imagen abarca el eje óptico hasta la altura (negativa) mostrada. Los rayos de otro punto de la flecha, como el centro de la flecha, se cruzan en otro punto común, completando así el resto de la imagen.
Aunque en esta figura se trazan tres rayos, solo dos son necesarios para localizar un punto de la imagen. Es mejor rastrear los rayos para los cuales existen reglas simples de trazado de rayos.
Varias distancias importantes aparecen en la figura. En cuanto a un espejo, definimos $d_o$ para ser la distancia del objeto, o la distancia de un objeto desde el centro de una lente. La distancia de la imagen $d_i$ se define como la distancia de la imagen desde el centro de una lente. La altura del objeto y la altura de la imagen se indican con $h_o$ y $h_i$, respectivamente. Las imágenes que aparecen en posición vertical en relación con el objeto tienen alturas positivas, y las que están invertidas tienen alturas negativas. Al usar las reglas del trazado de rayos y hacer un dibujo a escala con papel y lápiz, como en la , podemos describir con precisión la ubicación y el tamaño de una imagen. Pero el beneficio real del trazado de rayos está en visualizar cómo se forman las imágenes en una variedad de situaciones.
Hemos visto que los rayos paralelos al eje óptico se dirigen al punto focal de una lente convergente. En el caso de una lente divergente, salen en una dirección tal que parecen provenir del punto focal en el lado opuesto de la lente (es decir, el lado desde el cual los rayos paralelos entran en la lente). ¿Qué sucede con los rayos paralelos que no son paralelos al eje óptico ()? En el caso de una lente convergente, estos rayos no convergen en el punto focal. En su lugar, se unen en otro punto en el plano llamado plano focal. El plano focal contiene el punto focal y es perpendicular al eje óptico. Como se muestra en la figura, los rayos paralelos se enfocan donde el rayo a través del centro de la lente cruza el plano focal.
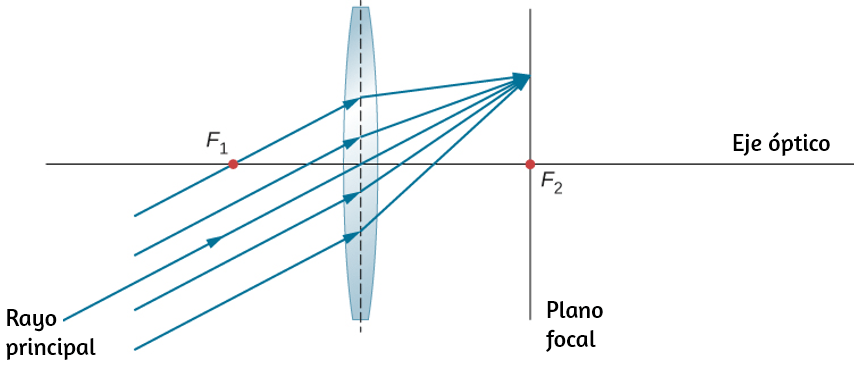
El trazado de rayos nos permite obtener una imagen cualitativa de la formación de la imagen. Para obtener información numérica, deducimos un par de ecuaciones a partir de un análisis geométrico del trazado de rayos para lentes delgadas. Estas ecuaciones, llamadas la ecuación de lente delgada y la ecuación del fabricante de lentes, nos permiten analizar cuantitativamente las lentes finas.
Considere la lente bi-convexa gruesa que se muestra en la . El índice de refracción del medio circundante es $n_1$ (si la lente está en el aire, entonces $n_1 = 1.00$) y la de la lente es $n_2$.
Los radios de curvaturas de los dos lados son $R_1$ y $R_2$. Deseamos encontrar una relación entre la distancia del objeto $d_o$, la distancia de la imagen $d_i$ y los parámetros de la lente.
Para deducir la ecuación de la lente delgada, consideramos la imagen formada por la primera superficie refractiva (es decir, la superficie izquierda) y luego utilizamos esta imagen como el objeto para la segunda superficie refractiva. En la figura, la imagen de la primera superficie de refracción es $Q'$, que se forma extendiendo hacia atrás los rayos desde el interior de la lente (estos rayos resultan de la refracción en la primera superficie). Esto se muestra por las líneas discontinuas en la figura. Observa que esta imagen es virtual porque en realidad no pasan rayos por el punto $Q'$. Para encontrar la distancia de la imagen $d'_i$ correspondiente a la imagen $Q'$, usamos la ecuación 9.11. En este caso, la distancia del objeto es $d_o$, la distancia de la imagen es $d'_i$, y el radio de curvatura es $R_1$. La inserción de éstos en la ecuación 9.3 da
$$\frac{n_1}{d_o} + \frac{n_2}{d'_i} = \frac{n_2 - n_1}{R_1} \tag{9.14}$$La imagen es virtual y está en el mismo lado que el objeto, por lo que $d'_i < 0$ y $d_o > 0$. La primera superficie es convexa hacia el objeto, entonces $R_1 > 0$.
Para encontrar la distancia del objeto para el objeto $Q$ formado por refracción desde la segunda interfaz, ten en cuenta que el papel de los índices de refracción $n_1$ y $n_2$ se intercambian en la Ecuación 9.11. En la , vemos que la distancia del objeto es $d'_o$ y la distancia de la imagen es $d_i$. El radio de curvatura es $R_2$. Insertando estas cantidades en la Ecuación 2.11 se obtiene
$$\frac{n_2}{d'_o} + \frac{n_1}{d_i} = \frac{n_1 - n_2}{R_2} \tag{9.15}$$La imagen es real y está en el lado opuesto del objeto, por lo que $d_i > 0$ y $d'_o > 0$. La segunda superficie está convexa lejos del objeto, por lo tanto, $R_2 < 0$. La ecuación 2.15 se puede simplificar observando que $d'_o = |d'_i| + t$, donde hemos tomado el valor absoluto porque $d'_i$ es un número negativo, mientras que $d'_o$ y $t$ son positivos. Podemos prescindir del valor absoluto si negamos $d'_i$, lo que da $d'_o = -d'_i + t$. Reemplazando en la ecuación 2.15, obtenemos:
$$\frac{n_2}{-d'_i + t} + \frac{n_1}{d_i} = \frac{n_1 - n_2}{R_2} \tag{9.16}$$Sumando la ecuación 9.14 y la ecuación 9.16, obtenemos
$$\frac{n_1}{d_o} + \frac{n_1}{d_i} + \frac{n_2}{d'_i} + \frac{n_2}{-d'_i + t} = (n_2 - n_1)\left( \frac{1}{R_1} - \frac{1}{R_2} \right) \tag{9.17}$$En la aproximación de lente delgada, asumimos que la lente es muy delgada en comparación con la primera distancia de la imagen, o $t << d'_i$ (o, equivalentemente, $t << R_1$ y $R_2$).
En este caso, los términos tercero y cuarto en el lado izquierdo de la Ecuación 9.17 se cancelan, dejándonos con
$$\frac{n_1}{d_o} + \frac{n_1}{d_i} = (n_2 - n_1)\left( \frac{1}{R_1} - \frac{1}{R_2} \right) $$Dividiendo por $n_1$ nos da finalmente
$$\frac{1}{d_o} + \frac{1}{d_i} = (\frac{n_2}{n_1} - 1)\left( \frac{1}{R_1} - \frac{1}{R_2} \right) \tag{9.18}$$El lado izquierdo se parece sospechosamente a la ecuación del espejo que dedujimos antes para los espejos esféricos. Como se hizo para los espejos esféricos, podemos usar el trazado de rayos y la geometría para mostrar que, para una lente delgada,
donde $f$ es la longitud focal de la lente delgada (esta deducción se deja como ejercicio). Esta es la ecuación de la lente delgada. La distancia focal de una lente delgada es la misma a la izquierda y a la derecha de la lente. Combinando la ecuación 9.18 y la ecuación 9.19 se obtiene
que se llama la ecuación del fabricante de lentes. Muestra que la distancia focal de una lente delgada depende solo del radio de curvatura y del índice de refracción de la lente y del medio circundante.
Para una lente en el aire, $n_1 = 1.0$ y $n_2 ≡ n$, por lo que la ecuación del fabricante de la lente se reduce a
$$\frac{1}{f} = (n_1 - 1)\left(\frac{1}{R_1} - \frac{1}{R_2} \right) \tag{9.21}$$Para utilizar correctamente la ecuación de lente delgada, se deben cumplir las siguientes convenciones de signos:
Al utilizar un objeto de tamaño finito en el eje óptico y el trazado de rayos, puedes demostrar que la ampliación $m$ de una imagen es
donde las tres líneas significan "se define como". Esta es exactamente la misma ecuación que obtuvimos para los espejos (ver Ecuación 9.8).
Si $m > 0$, entonces la imagen tiene la misma orientación vertical que el objeto (llamada imagen "vertical"). Si $m < 0$, entonces la imagen tiene la orientación vertical opuesta al objeto (llamada imagen "invertida").
La ecuación de la lente delgada y la ecuación del fabricante de lentes son ampliamente aplicables a situaciones que involucran lentes delgadas. Exploraremos muchas características de la formación de imágenes en los siguientes ejemplos.
Considera una lente convergente delgada. ¿Dónde se forma la imagen y qué tipo de imagen se forma cuando el objeto se acerca a la lente desde el infinito? Esto se puede ver usando la ecuación de la lente delgada para una distancia focal dada para trazar la distancia de la imagen en función de la distancia del objeto. En otras palabras, trazamos
$$d_i = \left(\frac{1}{f} - \frac{1}{d_o} \right)^{-1}$$para un valor dado de $f$. Para $f = 1 cm$, el resultado se muestra en la parte (a) de la .
Un objeto mucho más lejano que la distancia focal f de la lente debería producir una imagen cerca del plano focal, porque el segundo término en el lado derecho de la ecuación anterior se vuelve insignificante en comparación con el primer término, por lo que tenemos $d_i ≈ f$. Esto se puede ver en la gráfica de la parte (a) de la figura, que muestra que la distancia de la imagen se aproxima asintóticamente a la distancia focal de $1 cm$ para distancias de objetos más grandes.
Cuando el objeto se aproxima al plano focal, la distancia de la imagen diverge al infinito positivo. Esto se espera porque un objeto en el plano focal produce rayos paralelos que forman una imagen en el infinito (es decir, muy lejos de la lente). Cuando el objeto está más lejos que la distancia focal del objetivo, la distancia de la imagen es positiva, por lo que la imagen es real, en el lado opuesto del objetivo, e invertida (porque $m = -d_i/d_o$). Cuando el objeto está más cerca que la distancia focal desde la lente, la distancia de la imagen se vuelve negativa, lo que significa que la imagen es virtual, en el mismo lado de la lente que el objeto, y en posición vertical.
Para una lente delgada divergente de distancia focal $f = -1.0 cm$, en la parte (b) se muestra un gráfico similar de la distancia de la imagen frente a la distancia del objeto.
En este caso, la distancia de la imagen es negativa para todas las distancias de objeto positivas, lo que significa que la imagen es virtual, en el mismo lado de la lente que el objeto, y en posición vertical. Estas características también pueden verse en los diagramas de trazado de rayos (consulta la ).
Para ver un ejemplo concreto de imágenes verticales e invertidas, mira la , que muestra imágenes formadas por lentes convergentes cuando el objeto (la cara de la persona en este caso) se coloca a diferentes distancias de la lente. En la parte (a) de la figura, la cara de la persona está más alejada que la distancia focal de la lente, por lo que la imagen se invierte. En la parte (b), la cara de la persona está más cerca que una distancia focal de la lente, por lo que la imagen está vertical.

Trabaja a través de los siguientes ejemplos para comprender mejor cómo funcionan las lentes delgadas.
Estrategia de resolución de problemas: lentes
Paso 1. Determina si el trazado de rayos, la ecuación de lente delgada o ambos serían útiles. Incluso si no se utiliza el trazado de rayos, un esbozo cuidadoso siempre es muy útil. Escribe símbolos y valores en el boceto.
Paso 2. Identifica lo que se debe determinar en el problema (identifica las incógnitas).
Paso 3. Haz una lista de lo que se da o se puede inferir del problema (identifica lo que se sabe).
Paso 4. Si se requiere el trazado de rayos, usa las reglas de trazado de rayos que se enumeran cerca del comienzo de esta sección.
Paso 5. La mayoría de los problemas cuantitativos requieren el uso de la ecuación de lente delgada y/o la ecuación del fabricante de la lente. Resuelve esto para las incógnitas e inserta las cantidades dadas o utiliza ambas juntas para encontrar dos incógnitas.
Paso 6. Verifica si la respuesta es razonable. ¿Son correctos los signos? ¿Es consistente el trazado de rayos o el bosquejo con el cálculo?
Ejemplo 9.3
Usando la ecuación del fabricante de lentes
Encuentra el radio de curvatura de una lente bicóncava molida simétricamente desde un vidrio con un índice de refracción de $1.55$, de modo que su distancia focal en el aire sea de $20 cm$ (para una lente bicóncava, ambas superficies tienen el mismo radio de curvatura).
Estrategia
Usa la la ecuación del fabricante de lentes para una lente delgada:
$$\frac{1}{f} = \left(\frac{n_2}{n_1} - 1 \right) \left(\frac{1}{R_1} - \frac{1}{R_2} \right)$$donde $R_1 < 0$ y $R_2 > 0$. Como estamos haciendo una lente bicóncava simétrica, tenemos $|R_1| = |R_2|$.
Solución
Podemos determinar el radio $R$ de curvatura desde
$$\frac{1}{f} = \left(\frac{n_2}{n_1} - 1 \right) \left(-\frac{2}{R} \right)$$Resolviendo para $R$ y reemplazando $f = -20 cm$, $n_2 = 1.55$, y $n_1 = 1.00$, obtenemos:
$$R = -2f \left(\frac{n_2}{n_1} - 1 \right) = -2(-20 cm)(1.55/1.00 - 1) = 22 cm$$Ejemplo 9.4
Lentes convergentes y diferentes distancias de objetos
Encuentra la ubicación, la orientación y la ampliación de la imagen para un objeto de $3.0 cm$ de altura en cada una de las siguientes posiciones frente a una lente convexa de 10.0 cm de distancia focal. (a) $d_o = 50.0 cm$, (b) $d_o = 5.00 cm$, y (c) $d_o = 20.0 cm$.
Estrategia
Comenzamos con la ecuación de lente delgada $\frac{1}{d_i} + \frac{1}{d_o} = \frac{1}{f}$. Resuelve para la distancia de la imagen $d_i$ e inserta la distancia del objeto y la distancia focal dadas.
Solución
a. Para $d_o = 50 cm$, $f = +10cm$, obtenemos:
$$d_i = \left(\frac{1}{f} - \frac{1}{d_o} \right)^{-1}$$ $$d_i = \left(\frac{1}{10.0 cm} - \frac{1}{50.0 cm} \right)^{-1} = 12.5 cm$$La imagen es positiva, por lo que la imagen es real, está en el lado opuesto de la lente del objeto y está a $12.5 cm$ de la lente. Para encontrar la ampliación y orientación de la imagen, utiliza
La ampliación negativa significa que la imagen está invertida. Desde $|m| < 1$, la imagen es más pequeña que el objeto. El tamaño de la imagen está dado por
$$|h_i| = |m|h_o = (0.250)(3.0 cm) = 0.75 cm$$b. Para $d_o = 5.00 cm$, $f = +10cm$, obtenemos:
$$d_i = \left(\frac{1}{f} - \frac{1}{d_o} \right)^{-1}$$ $$d_i = \left(\frac{1}{10.0 cm} - \frac{1}{5.00 cm} \right)^{-1} = -10.0 cm$$La distancia de la imagen es negativa, por lo que la imagen es virtual, está en el mismo lado de la lente que el objeto y está a $10 cm$ de la lente. La ampliación y orientación de la imagen se encuentran desde
$$m = -\frac{d_i}{d_o} = -\frac{-10.0 cm}{5.00 cm} = +2.00$$La ampliación positiva significa que la imagen está vertical (es decir, tiene la misma orientación que el objeto). Desde $|m| > 0$, la imagen es más grande que el objeto. El tamaño de la imagen es
$$|h_i| = |m|h_o = (2.00)(3.0 cm) = 6.0 cm$$c. Para $d_o = 20 cm$, $f = +10cm$, obtenemos:
$$d_i = \left(\frac{1}{f} - \frac{1}{d_o} \right)^{-1}$$ $$d_i = \left(\frac{1}{10.0 cm} - \frac{1}{20.0 cm} \right)^{-1} = 20.0 cm$$La distancia de la imagen es positiva, por lo que la imagen es real, está en el lado opuesto de la lente del objeto y está a $20.0 cm$ de la lente. La ampliación es
$$m = -\frac{d_i}{d_o} = -\frac{20.0 cm}{20.0 cm} = +1.00$$La ampliación negativa significa que la imagen está invertida. Como $|m| = 1$, la imagen es del mismo tamaño que el objeto.
Al resolver problemas en la óptica geométrica, a menudo necesitamos combinar el trazado de rayos y las ecuaciones de las lentes. El siguiente ejemplo demuestra este enfoque.
Ejemplo 9.5
Elegir la longitud focal y el tipo de lente
Para proyectar una imagen de una bombilla en una pantalla a $1.50 m$ de distancia, debes elegir qué tipo de lente usar (convergente o divergente) y su distancia focal (). La distancia entre la lente y la bombilla se fija en $0,75 m$. Además, ¿cuál es la ampliación y orientación de la imagen?
Estrategia
La imagen debe ser real, por lo que elige utilizar una lente convergente. La distancia focal se puede encontrar usando la ecuación de lente delgada y hallando la distancia focal. La distancia del objeto es $d_o = 0.75 m$ y la distancia de la imagen es $d_i = 1.5 m$.
Solución
Resuelve la lente delgada para la distancia focal e inserta el objeto deseado y las distancias de la imagen:
La ampliación es
$$m = -\frac{d_i}{d_o} = -\frac{1.5 m}{0.75 m} = -2.0$$Explicación
El signo menos para la ampliación significa que la imagen está invertida. La distancia focal es positiva, como se espera para una lente convergente. El trazado de rayos se puede utilizar para verificar el cálculo (consulta la ). Como se esperaba, la imagen está invertida, es real y es más grande que el objeto.
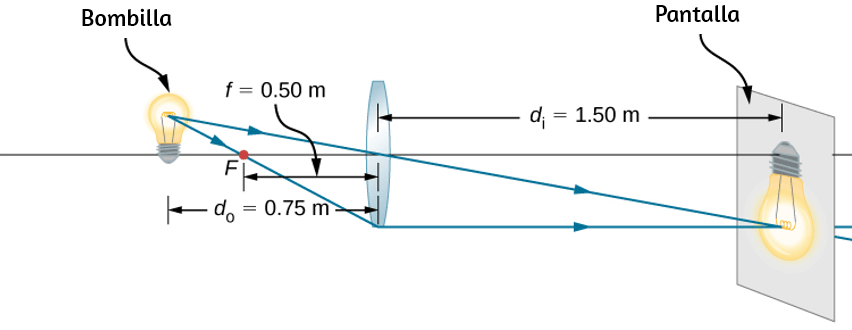
En la siguiente escena interactiva, diseñada por Fu Kwun Hwang, Fremont Teng y lookang, puedes practicar con dos lentes para formar imágenes reales o virtuales. El interactivo te permite cambiar el tipo de lente, trabajar con una o dos lentes, cambiar la posición de los focos, la distancia del objeto (flecha azul) a la lente, la altura del objeto y las posiciones de las lentes.
Desplaza los cuadrados de colores con el puntero del ratón, para realizar los cambios. También, puedes usar los controles que aparecen en cada una de las tres opciones del menú (Posición, $f1$ y $f2$, Lentes).
El ojo humano es quizás el más interesante e importante de todos los instrumentos ópticos. Nuestros ojos realizan una gran cantidad de funciones: nos permiten detectar la dirección, el movimiento, los colores y la distancia. En esta sección, exploramos la óptica geométrica del ojo.
El ojo es notable por la forma en que forma las imágenes y por la riqueza de detalles y colores que puede detectar. Sin embargo, nuestros ojos a menudo necesitan alguna corrección para alcanzar lo que se denomina visión "normal". En realidad, la visión normal debe denominarse visión "ideal" porque casi la mitad de la población humana requiere algún tipo de corrección de la vista, por lo que la necesidad de anteojos no es "anormal".
La muestra la anatomía básica del ojo. La córnea y la lente forman un sistema que, en una buena aproximación, actúa como una sola lente delgada. Para una visión clara, se debe proyectar una imagen real sobre la retina sensible a la luz, que se encuentra a una distancia fija de la lente. La lente flexible del ojo le permite ajustar el radio de curvatura de la lente para producir una imagen en la retina para objetos a diferentes distancias. El centro de la imagen cae sobre la fóvea, que tiene la mayor densidad de receptores de luz y la mayor agudeza (nitidez) en el campo visual. La apertura variable (es decir, la pupila) del ojo, junto con la adaptación química, permite que el ojo detecte las intensidades de luz desde el observable más bajo hasta $10^{10}$ veces más (sin daño). Esta es una increíble gama de detección. El procesamiento de los impulsos nerviosos visuales comienza con las interconexiones en la retina y continúa en el cerebro. El nervio óptico transmite las señales recibidas por el ojo al cerebro.
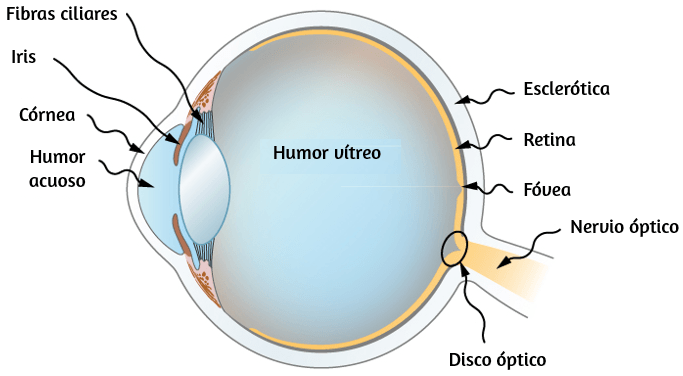
Los índices de refracción en el ojo son cruciales para su capacidad de formar imágenes. La enumera los índices de refracción relevantes para el ojo. El mayor cambio en el índice de refracción, que es donde los rayos de luz están más doblados, se produce en la interfaz aire-córnea en lugar de en la interfaz acuosa de la lente. El diagrama de rayos en la muestra la formación de imágenes por la córnea y la lente del ojo. La córnea, que es en sí misma una lente convergente con una distancia focal de aproximadamente $2,3 cm$, proporciona la mayor parte del poder de enfoque del ojo. La lente, que es una lente convergente con una longitud focal de aproximadamente $6,4 cm$, proporciona el enfoque más fino necesario para producir una imagen clara en la retina.
La córnea y la lente se pueden tratar como una sola lente delgada, aunque los rayos de luz atraviesan varias capas de material (como la córnea, el humor acuoso, varias capas de la lente y el humor vítreo), cambiando de dirección en cada interfaz. La imagen formada es muy parecida a la producida por una sola lente convexa (es decir, una imagen real invertida). Aunque las imágenes que se forman en el ojo están invertidas, el cerebro las invierte una vez más para que parezcan rectas.
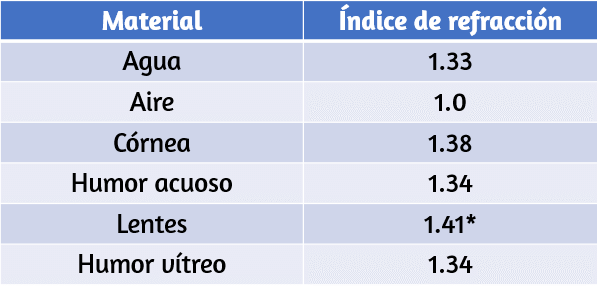
Como se señaló, la imagen debe caer precisamente en la retina para producir una visión clara, es decir, la distancia de la imagen $d_i$ debe ser igual a la distancia de la lente a la retina. Debido a que la distancia de la lente a la retina no cambia, la distancia de la imagen $d_i$ debe ser la misma para los objetos a todas las distancias. Los músculos ciliares ajustan la forma de la lente del ojo para enfocar objetos cercanos o lejanos. Al cambiar la forma de la lente del ojo, el ojo cambia la distancia focal de la lente. Este mecanismo del ojo se llama acomodación.
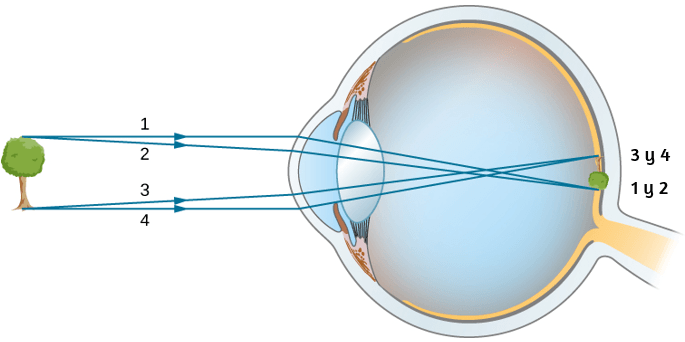
El punto más cercano al que se puede colocar un objeto para que el ojo pueda formar una imagen clara en la retina se llama el punto cercano del ojo. De manera similar, el punto lejano es la distancia más lejana a la que un objeto es claramente visible. Una persona con visión normal puede ver los objetos claramente a distancias que van desde los $25 cm$ hasta el infinito. El punto cercano aumenta con la edad, convirtiéndose en varios metros para algunas personas mayores. En este texto, consideramos que el punto cercano es de $25 cm$.
Podemos usar las ecuaciones de lente delgada para examinar cuantitativamente la formación de imágenes en el ojo. Primero, definimos la potencia óptica de una lente como
con la longitud focal $f$ dada en metros. Las unidades de potencia óptica se denominan “dioptrías” ($D$). Es decir, $1 D = \frac{1}{m}$, o $1 m^{- 1}$. Los optometristas prescriben anteojos y lentes de contacto comunes en unidades de dioptrías. Con esta definición de potencia óptica, podemos reescribir las ecuaciones de lentes delgadas como
$$P = \frac{1}{d_o} + \frac{1}{d_i} \tag{9.24}$$Trabajar con potencia óptica es conveniente porque, para dos o más lentes juntas, la potencia óptica efectiva del sistema de lentes es aproximadamente la suma de la potencia óptica de las lentes individuales:
Ejemplo 9.6
Distancia focal efectiva del ojo
La córnea y la lente ocular tienen distancias focales de $2,3$ y $6,4 cm$, respectivamente. Encuentra la longitud focal neta y la potencia óptica del ojo.
Estrategia
Las potencias ópticas de las lentes estrechamente espaciadas se agregan, por lo que $P_{\textsf{ojo}} = P_{\textsf{córnea}} + P_{\textsf{lente}}$.
Solución
Escribir la ecuación para la potencia en términos de las distancias focales
Por lo tanto, la distancia focal del ojo (córnea y lente juntas) es
$$f_{\textsf{ojo}} = 1.69 cm$$La potencia óptica del ojo es
$$P_{\textsf{ojo}} = \frac{1}{f_{\textsf{ojo}}} = \frac{1}{0.0169 m} = 59 D$$Para una visión clara, la distancia de la imagen $d_i$ debe ser igual a la distancia de la lente a la retina. La visión normal es posible para objetos a distancias de $25 cm$ hasta el infinito. El siguiente ejemplo muestra cómo calcular la distancia de la imagen para un objeto colocado en el punto cercano del ojo.
Ejemplo 9.7
Imagen de un objeto colocado en el punto cercano
La longitud focal neta de un ojo humano en particular es de $1,7 cm$. Un objeto se coloca en el punto cercano del ojo. ¿A qué distancia de la lente se forma una imagen enfocada?
Estrategia
El punto cercano está a $25 cm$ del ojo, por lo que la distancia del objeto es de $25 cm$. Determinamos la distancia de la imagen a partir de la ecuación de la lente:
$$\frac{1}{d_i} = \frac{1}{f} - \frac{1}{d_o}$$Solución
$$d_i = \left(\frac{1}{f} - \frac{1}{d_o} \right)^{-1}$$ $$d_i = \left(\frac{1}{1.7 cm} - \frac{1}{25 cm} \right)^{-1} = 1.8 cm$$Por lo tanto, la imagen se forma a 1,8 cm por detrás de la lente.
Explicación
De la fórmula de aumento, encontramos $m = -\frac{1.8 cm}{25 cm} = -0.073$. Como $m < 0$, la imagen está invertida en orientación con respecto al objeto. Del valor absoluto de $m$ vemos que la imagen es mucho más pequeña que el objeto; de hecho, es solo el $7$% del tamaño del objeto.
La necesidad de algún tipo de corrección de la visión es muy común. Los defectos típicos de la visión son fáciles de entender con la óptica geométrica, y algunos son simples de corregir. La ilustra dos defectos comunes de la visión. La miopía es la capacidad de ver objetos cercanos, mientras que los objetos distantes son borrosos. El ojo sobrepasa los rayos casi paralelos de un objeto distante, y los rayos se cruzan frente a la retina. Los rayos más divergentes de un objeto cercano convergen en la retina para una imagen clara. La distancia al objeto más lejano que se puede ver claramente se denomina punto lejano del ojo (normalmente el punto lejano es el infinito). La presbicia, o hipermetropía, es la capacidad de ver objetos lejanos claramente, mientras que los objetos cercanos están borrosos. Un ojo con visión hipermétrope no converge suficientemente los rayos de un objeto cercano para hacer que los rayos se encuentren en la retina.
Dado que el ojo miope sobrepasa los rayos de luz, la corrección para la miopía consiste en colocar una lente divergente en la parte frontal del ojo, como se muestra en la . Esto reduce la potencia óptica de un ojo que es demasiado potente (recuerda que la distancia focal de una lente divergente es negativa, por lo que su potencia óptica es negativa).
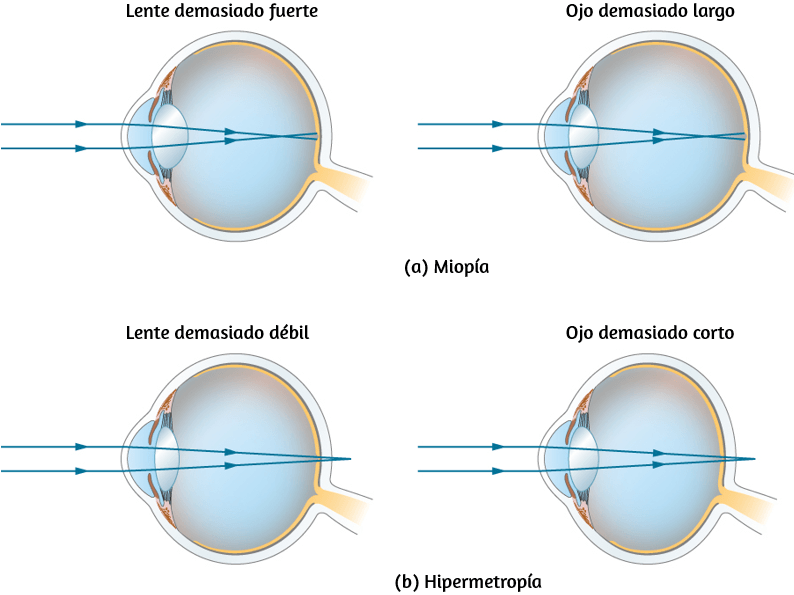
Otra forma de entender esta corrección es que una lente divergente hará que los rayos entrantes diverjan más para compensar la convergencia excesiva causada por el sistema de lentes del ojo. La imagen producida por la lente divergente sirve como objeto (óptico) para el ojo, y debido a que el ojo no puede enfocar objetos más allá de su punto lejano, la lente divergente debe formar una imagen de objetos distantes (físicos) en un punto que está más cerca que el punto lejano.
Ejemplo 9.8
Cómo corregir la miopía
¿Qué potencia óptica de la lente de anteojos se necesita para corregir la visión de una persona miope cuyo punto lejano es $30.0 cm$? Supongamos que la lente correctora está fija a $1,50 cm$ del ojo.
Estrategia
Deseas que esta persona miope pueda ver claramente los objetos distantes, lo que significa que la lente del anteojos debe producir una imagen a $30.0 cm$ del ojo para un objeto en el infinito. Una imagen de $30.0 cm$ desde el ojo será $30.0 cm - 1.50 cm = 28.5 cm$ desde la lente del anteojos. Por lo tanto, debemos tener $d_i = -28.5 cm$ cuando $d_o = ∞$. La distancia de la imagen es negativa porque está en el mismo lado de la lente del anteojos que del objeto.
Solución
Dado que $d_i$ y $d_o$ son conocidos, podemos encontrar la potencia óptica de la lente del anteojos utilizando la ecuación 9.24:
$$P = \frac{1}{d_o} + \frac{1}{d_i} = \frac{1}{∞} + \frac{1}{-0.285 m} = -3.51 D$$Explicación
La potencia óptica negativa indica una lente divergente (o cóncava), como se esperaba. Si examinas los anteojos en busca de personas miopes, encontrarás que las lentes son más delgadas en el centro. Además, si examinas una receta para anteojos para personas miopes, encontrarás que la potencia óptica prescrita es negativa y se administra en unidades de dioptrías.
La corrección de la hipermetropía consiste simplemente en utilizar el tipo opuesto de lente para la miopía (es decir, una lente convergente), como se muestra en la .
Dicha lente producirá una imagen de objetos físicos que están más cerca que el punto cercano a una distancia que se encuentra entre el punto cercano y el punto lejano, de modo que la persona pueda ver la imagen con claridad. Para determinar la potencia óptica necesaria para la corrección, debes conocer el punto cercano de la persona, como se explica en el Ejemplo 9.9.
Ejemplo 9.9
Corrección de la hipermetropía
¿Qué potencia óptica de la lente de un anteojos se necesita para permitir que una persona con visión hipermétrope, cuyo punto cercano es $1.00 m$, vea un objeto claramente a $25.0 cm$ del ojo? Supongamos que la lente correctiva está fijada a $1,5 cm$ del ojo.
Estrategia
Cuando un objeto está a $25.0 cm$ de los ojos de la persona, la lente del anteojos debe producir una imagen a $1 m$ de distancia (el punto cercano), para que la persona pueda verlo claramente. Una imagen a $1.00 m$ del ojo será de $100 cm - 1.5 cm = 98.5 cm$ desde la lente del anteojos porque la lente del anteojos está a $1.5 cm$ del ojo. Por lo tanto, $d_i = -98.5 cm$, donde el signo menos indica que la imagen está en el mismo lado de la lente que el objeto. El objeto está a $25.0 cm - 1.5 cm = 23.5 cm$ de la lente del anteojos, por lo que $d_o = 23.5 cm$.
Solución
Dado que $d_i$ y $d_o$ son conocidos, podemos encontrar la potencia óptica de la lente del anteojos utilizando la ecuación 9.24:
Explicación
La potencia óptica positiva indica una lente convergente (convexa), como se esperaba. Si examinas los anteojos de personas con visión hipermétrope, encontrarás que las lentes son más gruesas en el centro. Además, los anteojos recetados para personas con visión hipermétrope tienen una potencia óptica prescrita que es positiva.
Las cámaras son muy comunes en nuestra vida cotidiana. Entre 1825 y 1827, el inventor francés Nicéphore Niépce fotografió con éxito una imagen creada por una cámara primitiva. Desde entonces, se ha logrado un enorme progreso en el diseño de cámaras y detectores basados en cámaras.
Inicialmente, las fotografías se registraron utilizando la reacción sensible a la luz de compuestos a base de plata como el cloruro de plata o el bromuro de plata. El papel fotográfico con base de plata era de uso común hasta el advenimiento de la fotografía digital en la década de 1980, que está íntimamente conectado a los detectores de dispositivos de carga acoplada (CCD). En pocas palabras, un CCD es un chip semiconductor que graba imágenes como una matriz de píxeles pequeños, cada píxel ubicado en una "caja" en la superficie. Cada píxel es capaz de detectar la intensidad de la luz que incide sobre él. El color se pone en juego al colocar filtros de color rojo, azul y verde sobre los píxeles, lo que da como resultado imágenes digitales en color (). En su mejor resolución, un píxel CCD corresponde a un píxel de la imagen. Para reducir la resolución y el tamaño del archivo, podemos "agrupar" varios píxeles de CCD en uno, lo que resulta en una imagen más pequeña pero "pixelada".
Claramente, la electrónica es una gran parte de una cámara digital; Sin embargo, la física subyacente es la óptica básica. De hecho, las ópticas de una cámara son muy parecidas a las de una sola lente con una distancia del objeto que es significativamente mayor que la distancia focal de la lente ().
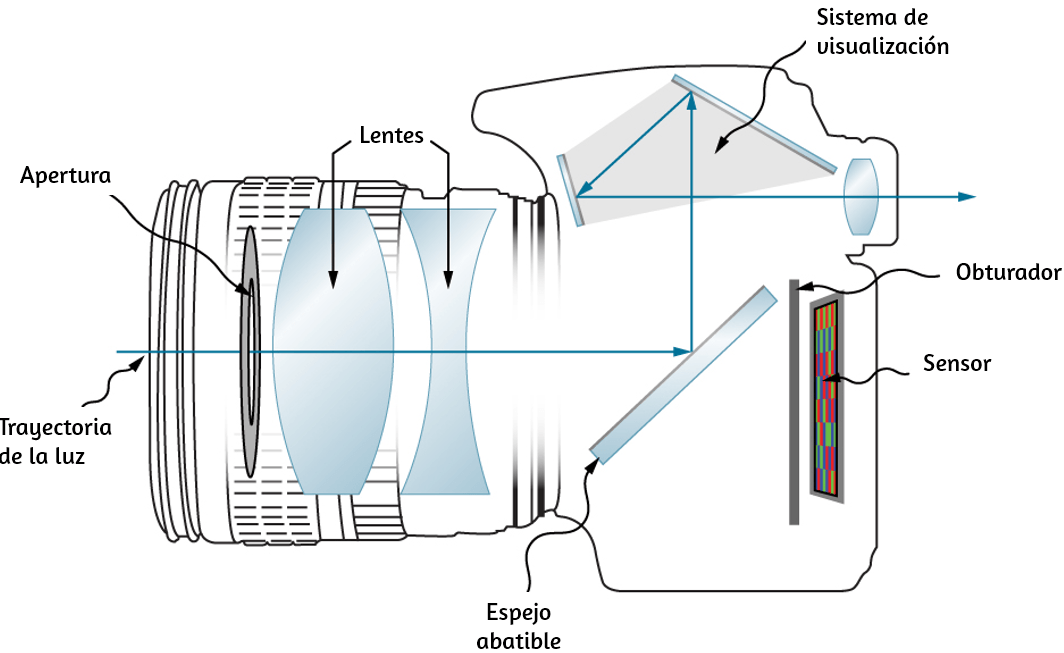
Por ejemplo, consideremos la cámara en un teléfono inteligente promedio, la cual está equipada con una lente fija de gran angular con una distancia focal de aproximadamente $4$ a $5 mm$ (esta distancia focal es aproximadamente igual al grosor del teléfono). La imagen creada por la lente se enfoca en el detector de CCD montado en el lado opuesto del teléfono. En un teléfono celular, la lente y el CCD no pueden moverse entre sí. Entonces, ¿cómo nos aseguramos de que tanto las imágenes de un objeto distante como un objeto cercano estén enfocadas?
Recuerda que un ojo humano puede adaptarse a imágenes distantes y cercanas cambiando su distancia focal. Una cámara de teléfono celular no puede hacer eso porque la distancia desde la lente hasta el detector es fija. Aquí es donde la pequeña distancia focal se vuelve importante. Supongamos que tenemos una cámara con una distancia focal de $5 mm$. ¿Cuál es la distancia de la imagen para una selfie? La distancia del objeto para una selfie (la longitud de la mano que sostiene el teléfono) es de unos $50 cm$. Usando la ecuación de lente delgada, podemos escribir
$$\frac{1}{5 mm} = \frac{1}{500 mm} + \frac{1}{d_i}$$Luego obtenemos la distancia de la imagen:
$$\frac{1}{d_i} = \frac{1}{5 mm} - \frac{1}{500 mm}$$Observa que la distancia del objeto es 100 veces mayor que la distancia focal. Podemos ver claramente que el término $1/(500 mm)$ es significativamente menor que $1/(5 mm)$, lo que significa que la distancia de la imagen es prácticamente igual a la distancia focal del objetivo. Un cálculo real nos da la distancia de la imagen $dd_i = 5.05 mm$. Este valor está muy cerca de la distancia focal del objetivo.
Consideremos ahora el caso de un objeto distante. Digamos que nos gustaría tomar una fotografía de una persona que se encuentra a unos $5 m$ de nosotros. Usando nuevamente la ecuación de lente delgada, obtenemos la distancia de imagen de $5.005 mm$. Cuanto más lejos esté el objeto de la lente, más se acercará la distancia de la imagen a la distancia focal. En el caso límite de un objeto infinitamente distante, obtenemos la distancia de la imagen exactamente igual a la distancia focal de la lente.
Como puede ver, la diferencia entre la distancia de la imagen para un selfie y la distancia de la imagen para un objeto distante es de aproximadamente $0,05 mm$ o $50$ micrones. Incluso una distancia de objeto corta, como la longitud de tu mano, es dos órdenes de magnitud mayor que la distancia focal del objetivo, lo que produce variaciones mínimas de la distancia de la imagen (la diferencia de $50$ micrones es más pequeña que el grosor de una hoja de papel promedio). Una diferencia tan pequeña puede ser acomodada fácilmente por el mismo detector, ubicado a la distancia focal de la lente. El software de análisis de imágenes puede ayudar a mejorar la calidad de la imagen. Las cámaras convencionales de apuntar y disparar a menudo usan una lente móvil para cambiar la distancia de la lente a la imagen. Las lentes complejas de las cámaras réflex más caras permiten reflejar imágenes fotográficas de excelente calidad. La óptica de estas lentes de cámara está fuera del alcance de este libro de texto.
En la siguiente escena interactiva, diseñada por Steve Ridout, puedes practicar con una cámara simulada que muestra los niveles de ruido relativo de las cámaras en función de su tamaño de apertura absoluta. El nivel de ruido se exagera para ser más visible en la pequeña ventana de la foto. El ruido es una función del tamaño del sensor, y no tiene en cuenta las diferencias en la sensibilidad del sensor. Cada escena se compone de uno o dos planos que se pueden desenfocar (difuminar) de forma independiente.
Puedes seleccionar el tipo de cámara, la foto, el foco (cercano o lejano), modo automático o manual, entre otros factores.
La escena es visible en todos los navegadores sólo en línea (on line); no obstante, en local es compatible con los navegadores Firefox y Edge.
El tamaño aparente de un objeto percibido por el ojo depende del ángulo que el objeto subtiende del ojo. Como se muestra en la , el objeto en $A$ subtiende un ángulo mayor desde el ojo que cuando está en la posición en el punto $B$. Por lo tanto, el objeto en $A$ forma una imagen más grande en la retina (ver $OA'$) que cuando está posicionado en $B$ (ver $OB'$). Por lo tanto, los objetos que subtienden los ángulos grandes del ojo parecen más grandes porque forman imágenes más grandes en la retina.
Hemos visto que, cuando un objeto se coloca dentro de una distancia focal de una lente convexa, su imagen es virtual, vertical y más grande que el objeto (consulta la parte (b) de la ), la imagen en la retina se agranda, porque la imagen producida por la lente subtiende un ángulo más grande en el ojo que el objeto. Una lente convexa utilizada para este propósito se llama una lupa o una lupa simple.
Para explicar el aumento de una lente de aumento, comparamos el ángulo subtendido por la imagen (creado por la lente) con el ángulo subtendido por el objeto (visto sin lente), como se muestra en la . Suponemos que el objeto está situado en el punto cercano del ojo, porque esta es la distancia del objeto a la que el ojo sin ayuda puede formar la imagen más grande en la retina. Compararemos las imágenes ampliadas creadas por una lente con este tamaño máximo de imagen para el ojo sin ayuda.
La ampliación de una imagen cuando es observada por el ojo es la ampliación angular $M$, que se define por la relación de la imagen del ángulo subtendido por la imagen al ángulo del objeto subtendido por el objeto:
Considera la situación mostrada en la . La lente de aumento se mantiene a una distancia del ojo, y la imagen producida por la lupa forma una distancia $L$ del ojo. Queremos calcular el aumento angular para cualquier $L$ y $ℓ$ arbitrarios. En la aproximación de ángulo pequeño, la imagen de tamaño angular de la imagen es $h_i/L$. El $θ_{\textsf{objeto}}$ de tamaño angular del objeto en el punto cercano es $θ_{\textsf{objeto}} = h_o/(25 cm)$.
El aumento angular es entonces
$$M = \frac{θ_{\textsf{imagen}}}{θ_{\textsf{objeto}}} = \frac{h_i(25 cm)}{Lh_o} \tag{9.27}$$Usando la ecuación 9.8 para la ampliación lineal
$$m = -\frac{d_i}{d_o} = \frac{h_i}{h_o}$$y la ecuación de lente delgada
$$\frac{1}{d_o} + \frac{1}{d_i} = \frac{1}{f}$$En la ecuación 9.27, llegamos a la siguiente expresión para la ampliación angular de una lente de aumento:
$$M = \left( -\frac{d_i}{d_o} \right) \left(\frac{25 cm}{L} \right)$$ $$= -d_i \left(\frac{1}{f} - \frac{1}{d_i} \right) \left(\frac{25 cm}{L} \right)$$ $$= \left(1 - \frac{d_i}{f} \right) \left(\frac{25 cm}{L} \right) \tag{9.28}$$De la parte (b) de la figura, vemos que el valor absoluto de la distancia de la imagen es $|di| = L - ℓ$. Observa que $d_i < 0$ porque la imagen es virtual, por lo que podemos prescindir del valor absoluto insertando explícitamente el signo menos: $-d_i = L - ℓ$. Al insertar esto en la Ecuación 9.28 nos da la ecuación final para la ampliación angular de una lente de aumento:
Tenga en cuenta que todas las cantidades en esta ecuación deben expresarse en centímetros. A menudo, queremos que la imagen se encuentre a una distancia cercana al punto ($L = 25 cm$) para obtener la máxima ampliación, y mantenemos la lente de aumento cerca del ojo ($ℓ = 0$). En este caso, la ecuación 9.29 quedaría así:
$$M = 1 + \frac{25 cm}{f} \tag{9.30}$$Lo que demuestra que el mayor aumento se produce para la lente con la distancia focal más corta. Además, cuando la imagen está a una distancia cercana al punto y la lente se mantiene cerca del ojo $(ℓ = 0)$, entonces $L = d_i = 25 cm$ y la Ecuación 9.27 se convierte en
$$M = \frac{h_i}{h_o} = m \tag{9.31}$$donde $m$ es el aumento lineal (Ecuación 9.32) deducido de los espejos esféricos y las lentes delgadas. Otra situación útil es cuando la imagen está en el infinito ($L = ∞$). La ecuación 9.29 toma la forma:
$$M(L = ∞) = \frac{25 cm}{f} \tag{9.32}$$La ampliación resultante es simplemente la relación de la distancia del punto cercano a la distancia focal de la lente de aumento, por lo que una lente con una distancia focal más corta da un aumento más fuerte. Aunque este aumento es menor en 1 que el aumento obtenido con la imagen en el punto cercano, proporciona las condiciones de visión más cómodas, ya que el ojo está relajado cuando se ve un objeto distante.
Al comparar la Ecuación 9.29 con la Ecuación 9.32, vemos que el rango de ampliación angular de una lente convergente dada es
Ejemplo 9.10
Ampliando un diamante
Un joyero desea inspeccionar un diamante de $3.0 mm$ de diámetro con una lupa. El diamante se mantiene en el punto cercano del joyero ($25 cm$) y el joyero sostiene la lente de aumento cerca de su ojo.
(a) ¿Cuál debe ser la longitud focal de la lente de aumento para ver una imagen del diamante de $15 mm$ de diámetro?
(b) ¿Cuál debería ser la distancia focal de la lente de aumento para obtener un aumento de 10x?
Estrategia
Necesitamos determinar el aumento requerido de la lupa. Debido a que el joyero sostiene la lente de aumento cerca de su ojo, podemos usar la Ecuación 9.30 para encontrar la longitud focal de la lente de aumento.
Solución
a. El aumento lineal requerido es la relación entre el diámetro de imagen deseado y el diámetro real del diamante (Ecuación 9.32). Debido a que el joyero sostiene la lente de aumento cerca de su ojo y la imagen se forma en su punto cercano, el aumento lineal es el mismo que el aumento angular, por lo que
$$M = m = \frac{h_i}{h_o} = \frac{15 mm}{3.0 mm} = 5.0$$La distancia focal $f$ de la lente de aumento puede calcularse resolviendo la Ecuación 9.30 para $f$, que da
b. Para obtener una imagen ampliada por un factor de diez, nuevamente resolvemos la Ecuación 9.30 para $f$, pero esta vez usamos $M = 10$. El resultado es
$$f = \frac{25 cm}{M - 1} = \frac{25 cm}{10 - 1} = 2.8 cm$$Explicación
Observa que se logra un aumento mayor utilizando una lente con una distancia focal más pequeña. Por lo tanto, necesitamos usar una lente con un radio de curvatura de menos de unos pocos centímetros y mantenerla muy cerca de nuestro ojo. Esto no es muy conveniente. Un microscopio compuesto, explorado en la siguiente sección, puede superar este inconveniente.
Los microscopios y telescopios son instrumentos importantes que han contribuido enormemente a nuestra comprensión actual de los mundos micro y macroscópico. La invención de estos dispositivos llevó a numerosos descubrimientos en disciplinas como la física, la astronomía y la biología, por nombrar algunos. En esta sección, explicamos la física básica que hace que estos instrumentos funcionen.
Aunque el ojo es maravilloso en su capacidad para ver objetos grandes y pequeños, obviamente está limitado en los detalles más pequeños que puede detectar. El deseo de ver más allá de lo que es posible a simple vista condujo al uso de instrumentos ópticos. Hemos visto que una simple lente convexa puede crear una imagen ampliada, pero es difícil obtener una gran ampliación con tal lente. Una ampliación superior a 5x es difícil sin distorsionar la imagen. Para obtener una mayor ampliación, podemos combinar la lupa simple con una o más lentes adicionales. En esta sección, examinamos los microscopios que amplían los detalles que no podemos ver a simple vista.
Los microscopios se desarrollaron por primera vez a principios del siglo XVII por fabricantes de gafas en los Países Bajos y Dinamarca. El microscopio compuesto más simple se construye a partir de dos lentes convexas (). La lente objetivo es una lente convexa de corta distancia focal (es decir, alta potencia) con un aumento típico de 5× a 100×. El ocular es una lente convexa de mayor longitud focal.
El propósito de un microscopio es crear imágenes magnificadas de objetos pequeños, y ambas lentes contribuyen a la ampliación final. Además, la imagen ampliada se produce lo suficientemente lejos del observador para poder verla fácilmente, ya que el ojo no puede enfocar objetos o imágenes que están demasiado cerca (es decir, más cerca que el punto cercano del ojo).
Para ver cómo el microscopio en la forma una imagen, considera sus dos lentes en sucesión. El objeto está justo más allá de la distancia focal $f^{\textsf{obj}}$ de la lente objetivo, produciendo una imagen real invertida que es más grande que el objeto. Esta primera imagen sirve como objeto para la segunda lente u ocular.
El ocular se coloca de manera que la primera imagen se encuentre dentro de su distancia focal $f^{\textsf{ojo}}$, de modo que pueda ampliar aún más la imagen. En cierto sentido, actúa como una lupa que magnifica la imagen intermedia producida por el objetivo. La imagen producida por el ocular es una imagen virtual ampliada. La imagen final permanece invertida pero está más alejada del observador que del objeto, lo que facilita su visualización.
El ojo ve la imagen virtual creada por el ocular, que sirve como objeto para la lente en el ojo. La imagen virtual formada por el ocular está bien fuera de la distancia focal del ojo, por lo que el ojo forma una imagen real en la retina.
El aumento del microscopio es el producto del aumento lineal $m^{\textsf{obj}}$ por el objetivo y el aumento angular $M^{\textsf{ojo}}$ por el ocular. Estos son dados por
$$m^{\textsf{obj}} = -\frac{d_i^{\textsf{obj}}}{d_o^{\textsf{obj}}} ≈ -\frac{d_i^{\textsf{obj}}}{f^{\textsf{obj}}} (\textsf{Aumento lineal por objetivo})$$ $$M^{\textsf{ojo}} = 1 + \frac{25 cm}{f^{\textsf{ojo}}} (\textsf{Aumento angular por ocular})$$Aquí, $f^{\textsf{obj}}$ y $f^{\textsf{ojo}}$ son las distancias focales del objetivo y el ocular, respectivamente. Suponemos que la imagen final se forma en el punto cercano del ojo, proporcionando la mayor ampliación. Ten en cuenta que la ampliación angular del ocular es la misma que se obtuvo anteriormente para la lupa simple. Esto no debería sorprender, porque el ocular es esencialmente una lupa, y la misma física se aplica aquí. El aumento neto $M_{\textsf{neto}}$ del microscopio compuesto es el producto del aumento lineal del objetivo y el aumento angular del ocular:
Ejemplo 9.11
Ampliación o aumento del microscopio
Calcula la ampliación de un objeto colocado a $6.20 mm$ de un microscopio compuesto que tiene un objetivo de distancia focal de $6.00 mm$ y un ocular de distancia focal de $50.0 mm$. El objetivo y el ocular están separados por $23.0 cm$.
Estrategia
Esta situación es similar a la que se muestra en la . Para encontrar la ampliación global, debemos conocer la ampliación lineal del objetivo y la ampliación angular del ocular. Podemos usar la Ecuación 9.34, pero necesitamos usar la ecuación de lente delgada para encontrar la distancia de imagen $d_i^{\textsf{obj}}$ del objetivo.
Solución
Resolviendo la ecuación de lente delgada para $d_i^{\textsf{obj}}$, obtenemos:
$$d_i^{\textsf{obj}} = \left(\frac{1}{f^{\textsf{obj}}} - \frac{1}{d_o^{\textsf{obj}}} \right)^{-1}$$ $$d_i^{\textsf{obj}} = \left(\frac{1}{6.00 mm} - \frac{1}{6.20 mm} \right)^{-1} = 186 mm = 18.6 cm$$Reemplazando este resultado en la Ecuación 9.34 junto con los valores conocidos $f^{\textsf{obj}} = 6.00 mm = 0.600 cm$ y $f^{\textsf{ojo}} = 50.0 mm = 5.00 cm$, obtenemos:
$$M_{\textsf{neto}} = -\frac{d_i^{\textsf{obj}}(f^{\textsf{ojo}} + 25 cm)}{f^{\textsf{obj}}f^{\textsf{ojo}}}$$ $$M_{\textsf{neto}} = -\frac{(18.6 cm)(5.00 cm + 25 cm)}{(0.600 cm)(5.00 cm)} = -186$$Explicación
Tanto el objetivo como el ocular contribuyen a la ampliación general, que es grande y negativa, consistente con la ).
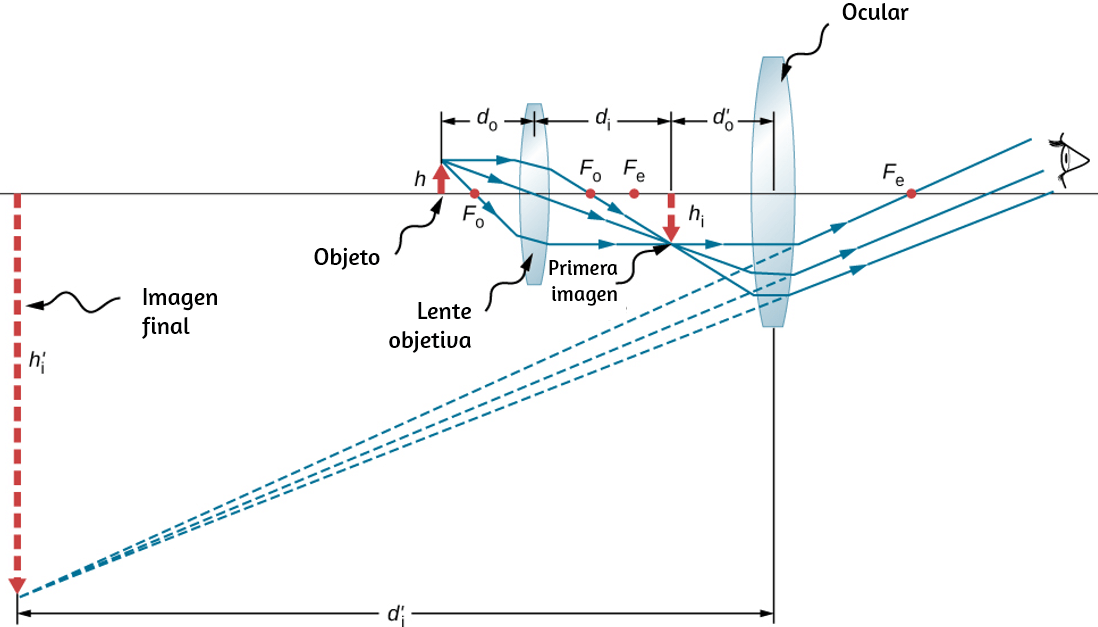
Ahora calculamos la potencia del aumento de un microscopio cuando la imagen está en el infinito, como se muestra en la , porque esto permite una visualización más relajada. La potencia del aumento del microscopio es el producto del aumento lineal del objetivo y del aumento angular $M^{\textsf{ojo}}$ del ocular. Sabemos que $m^{\textsf{obj}} = -d_i^{\textsf{obj}}/d_o^{\textsf{obj}}$ y de la ecuación de lente delgada obtenemos
$$m^{\textsf{obj}} = -\frac{d_i^{\textsf{obj}}}{d_o^{\textsf{obj}}} = 1 - \frac{d_i^{\textsf{obj}}}{f^{\textsf{obj}}} = \frac{f^{\textsf{obj}} - d_i^{\textsf{obj}}}{f^{\textsf{obj}}} \tag{9.35}$$Si la imagen final está en el infinito, entonces la imagen creada por el objetivo debe ubicarse en el punto focal del ocular. Esto se puede ver considerando la ecuación de lente delgada con $d_i = ∞$ o recordando que los rayos que pasan a través del punto focal salen de la lente en paralelo entre sí, lo que equivale a enfocar al infinito.
Para muchos microscopios, la distancia entre el punto focal del lado de la imagen del objetivo y el punto focal del lado del objeto del ocular se estandariza en $L = 16 cm$. Esta distancia se llama la longitud del tubo del microscopio. De la , vemos que $L = f^{\textsf{obj}} - d_i^{\textsf{obj}}$. Reemplazado en la ecuación 9.35, obtenemos:
$$m^{\textsf{obj}} = \frac{L}{f^{\textsf{obj}}} = 16 cm/f^{\textsf{obj}} \tag{9.36}$$Ahora debemos calcular el aumento angular del ocular con la imagen en el infinito. Para hacerlo, tomamos el radio del ángulo $θ_{\textsf{imagen}}$ subtendido por la imagen al ángulo $θ_{\textsf{objeto}}$ subtendido por el objeto en el punto cercano del ojo (esto es lo más cerca que el ojo sin ayuda puedes ver el objeto, y por lo tanto esta es la posición donde el objeto formará la imagen más grande en la retina del ojo sin ayuda). Utilizando la y trabajando en la aproximación de ángulo pequeño, tenemos $θ_{\textsf{imagen}} ≈ h_i^{\textsf{obj}}/f^{\textsf{ojo}}$ y $θ_{\textsf{objeto}} ≈ h_i^{\textsf{obj}}/ 25cm$, donde $h_i^{\textsf{obj}}$ es la altura de la imagen formada por el objetivo, que es el objeto del ocular. Así, la ampliación angular del ocular es
$$M^{\textsf{ojo}} = \frac{θ_{\textsf{imagen}}}{θ_{\textsf{objeto}}} = \frac{h_i^{\textsf{obj}}}{f^{\textsf{ojo}}}\frac{25 cm}{f^{\textsf{obj}}} = \frac{25 cm}{f^{\textsf{ojo}}} \tag{9.37}$$Por lo tanto, la potencia de aumento neta del microscopio compuesto con la imagen en el infinito es
$$M_{\textsf{neto}} = m^{\textsf{obj}}M^{\textsf{ojo}} = -\frac{(16 cm)(25 cm)}{f^{\textsf{obj}}f^{\textsf{ojo}}} \tag{9.38}$$Las distancias focales deben ser en centímetros. El signo menos indica que la imagen final está invertida. Observa que las únicas variables en la ecuación son las distancias focales del ocular y el objetivo, lo que hace que esta ecuación sea particularmente útil.
Los telescopios están diseñados para ver objetos distantes y producir una imagen que es más grande que la imagen producida a simple vista. Los telescopios reúnen mucha más luz que el ojo, lo que permite observar objetos oscuros con mayor aumento y mejor resolución. Los telescopios se inventaron alrededor de 1600, y Galileo fue el primero en usarlos para estudiar los cielos, con consecuencias monumentales. Observó las lunas de Júpiter, los cráteres y las montañas en la luna, los detalles de las manchas solares y el hecho de que la Vía Láctea está compuesta por un gran número de estrellas individuales.
La muestra un telescopio de refracción hecho de dos lentes. La primera lente, llamada objetivo, forma una imagen real dentro de la distancia focal de la segunda lente, que se llama el ocular. La imagen de la lente del objetivo sirve como objeto para el ocular, que forma una imagen virtual ampliada que es observada por el ojo. Este diseño es lo que Galileo solía usar para observar los cielos.
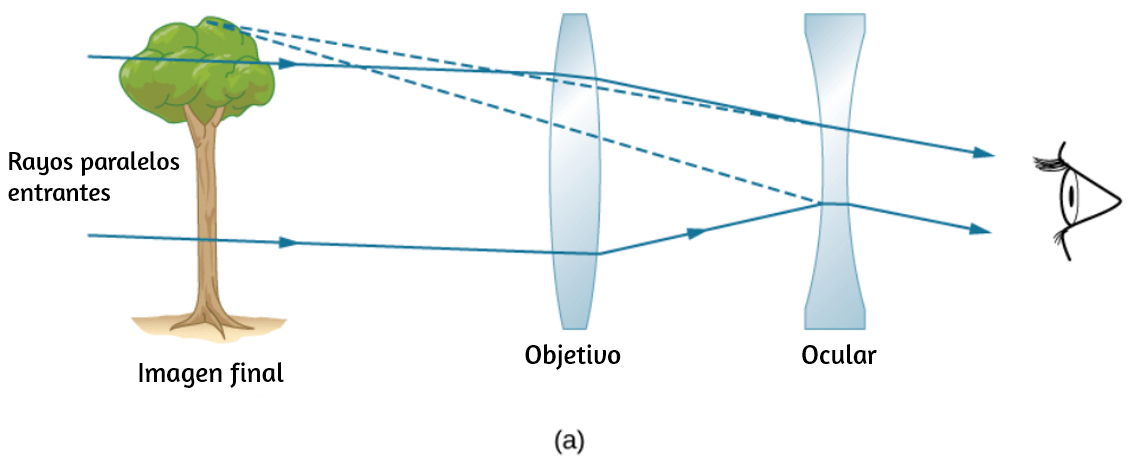
Aunque la disposición de las lentes en un telescopio de refracción es similar a la de un microscopio, existen diferencias importantes. En un telescopio, el objeto real está muy lejos y la imagen intermedia es más pequeña que el objeto. En un microscopio, el objeto real está muy cerca y la imagen intermedia es más grande que el objeto.
Tanto en el telescopio como en el microscopio, el ocular magnifica la imagen intermedia; en el telescopio, sin embargo, esta es la única ampliación.
El telescopio de dos lentes más común se muestra en la . El objeto está tan lejos del telescopio que está esencialmente en el infinito en comparación con las distancias focales de las lentes $(d_o^{\textsf{obj}} ≈ ∞)$, por lo que los rayos entrantes son esencialmente paralelos y se enfocan en el plano focal. Por lo tanto, la primera imagen se produce en $d_i^{\textsf{obj}} = f^{\textsf{obj}}$, como se muestra en la figura, y no es grande en comparación con lo que se puede ver al mirar directamente el objeto. Sin embargo, el ocular del telescopio (como el ocular del microscopio) le permite acercarse más a su punto cercano a esta primera imagen y, por lo tanto, la amplía (debido a que está cerca, subtiende un ángulo más grande del ojo y se forma una imagen más grande en su retina). En cuanto a una simple lupa, la ampliación angular de un telescopio es la proporción del ángulo subtendido por la imagen ($θ_{\textsf{imagen}}$ en la ) al ángulo subtendido por el objeto real ($θ_{\textsf{objeto}}$):
$$M = \frac{θ_{\textsf{imagen}}}{θ_{\textsf{objeto}}} \tag{9.39}$$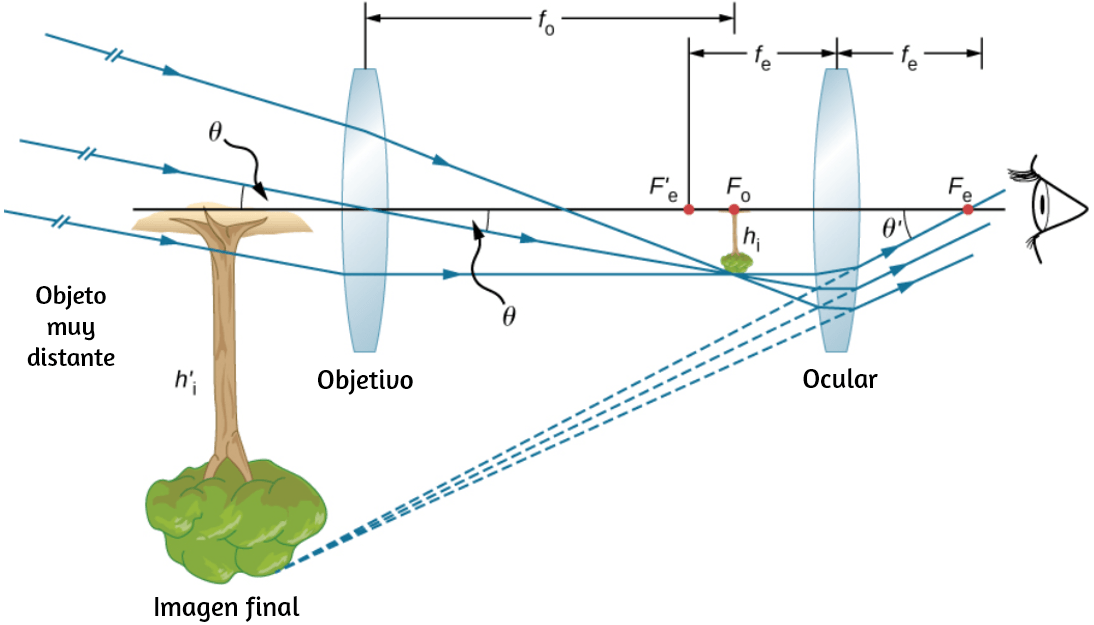
Para obtener una expresión para el aumento que involucre solo los parámetros de la lente, ten en cuenta que el plano focal de la lente objetivo se encuentra muy cerca del plano focal del ocular. Si asumimos que estos planos están superpuestos, tenemos la situación que se muestra en la .
Además, asumimos que los ángulos $θ_{\textsf{objeto}}$ y $θ_{\textsf{imagen}}$ son pequeños, de modo que la aproximación de ángulo pequeño se mantiene ($tanθ ≈ θ$). Si la imagen formada en el plano focal tiene altura $h$, entonces
$$θ_{\textsf{objeto}} ≈ tanθ = \frac{h}{f^{\textsf{obj}}}$$ $$θ_{\textsf{imagen}} ≈ tanθ = \frac{-h}{f_{\textsf{ojo}}}$$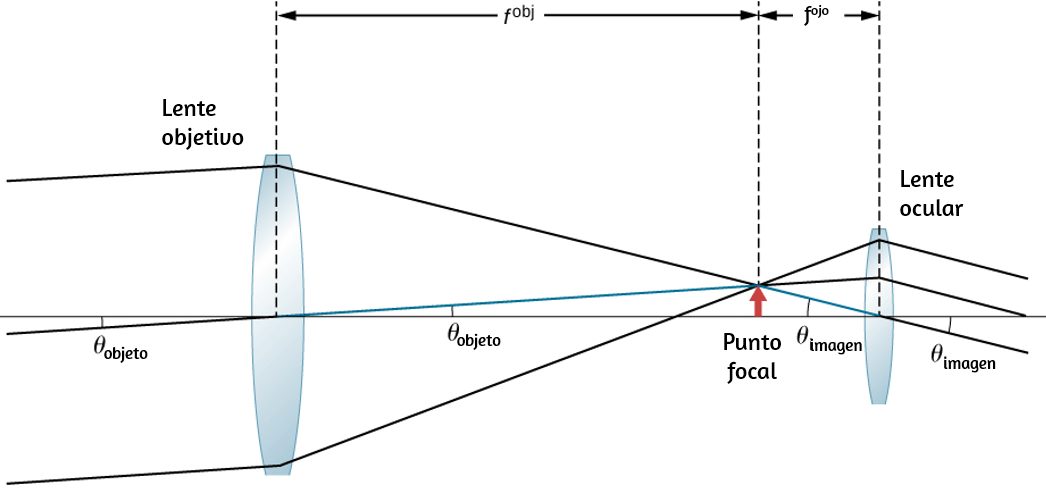
donde se introduce el signo menos porque la altura es negativa si medimos ambos ángulos en sentido contrario a las agujas del reloj. Al reemplazar estas expresiones en la ecuación 9.39, obtenemos:
$$M = \frac{-h_i}{f_{\textsf{ojo}}}\frac{f^{\textsf{obj}}}{h_i} = -\frac{f^{\textsf{obj}}}{f_{\textsf{ojo}}} \tag{9.40}$$Por lo tanto, para obtener el mayor aumento angular, es mejor tener un objetivo con una longitud focal larga y un ocular con una distancia focal corta. Cuanto mayor sea el aumento angular $M$, más grande aparecerá un objeto cuando se vea a través de un telescopio, haciendo más visibles los detalles. Los límites a los detalles observables son impuestos por muchos factores, incluyendo la calidad de la lente y la perturbación atmosférica. Los oculares típicos tienen distancias focales de $2,5 cm$ o $1,25 cm$. Si el objetivo del telescopio tiene una longitud focal de $1$ metro, estos oculares producen aumentos de 40x y 80x, respectivamente. Así, las ampliaciones angulares hacen que la imagen aparezca $40$ veces u $80$ veces más cerca que el objeto real.
El signo menos en la ampliación indica que la imagen está invertida, lo cual no es importante para observar las estrellas, pero es un problema real para otras aplicaciones, como telescopios en barcos o miras telescópicas. Si se necesita una imagen vertical, se puede usar la disposición de Galileo en la . Pero una disposición más común es usar una tercera lente convexa como un ocular, aumentando la distancia entre los dos primeros e invirtiendo la imagen una vez más, como se ve en la .
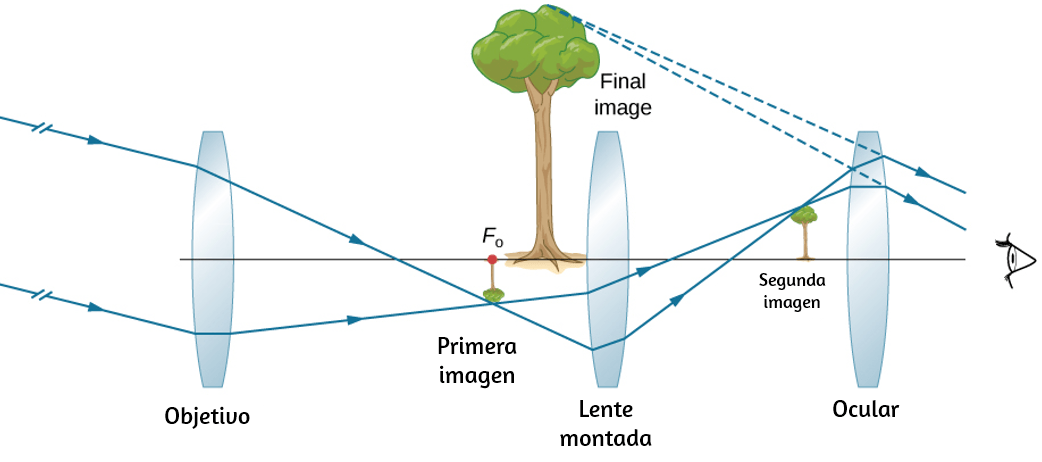
El telescopio refractor más grande del mundo es el telescopio Yerkes de 40 pulgadas de diámetro ubicado en Lake Geneva, Wisconsin () y operado por la Universidad de Chicago.
Es muy difícil y costoso construir grandes telescopios refractores. Necesita grandes lentes sin defectos, lo que en sí mismo es una tarea técnicamente exigente. Un telescopio de refracción básicamente parece un tubo con una estructura de soporte para rotarlo en diferentes direcciones. Un telescopio refractor sufre de varios problemas. La aberración de las lentes hace que la imagen sea borrosa.
Además, a medida que las lentes se vuelven más gruesas para lentes más grandes, se absorbe más luz, lo que hace que las estrellas débiles sean más difíciles de observar. Las lentes grandes también son muy pesadas y se deforman bajo su propio peso. Algunos de estos problemas con los telescopios de refracción se abordan al evitar la refracción para recoger la luz y, en su lugar, utilizar un espejo curvo en su lugar, como lo ideó Isaac Newton. Estos telescopios se llaman telescopios reflectores.

Isaac Newton diseñó el primer telescopio reflector alrededor de 1670 para resolver el problema de la aberración cromática que ocurre en todos los telescopios refractores.
En la aberración cromática, la luz de diferentes colores se refracta en cantidades ligeramente diferentes en la lente. Como resultado, aparece un arco iris alrededor de la imagen y la imagen aparece borrosa. En el telescopio reflector, los rayos de luz de una fuente distante caen sobre la superficie de un espejo cóncavo fijado en el extremo inferior del tubo. El uso de un espejo en lugar de una lente elimina la aberración cromática. El espejo cóncavo enfoca los rayos en su plano focal. El problema del diseño es cómo observar la imagen enfocada. Newton utilizó un diseño en el que la luz enfocada del espejo cóncavo se reflejaba en un lado del tubo en un ocular [ (a)]. Esta disposición es común en muchos telescopios de aficionados y se denomina diseño newtoniano.
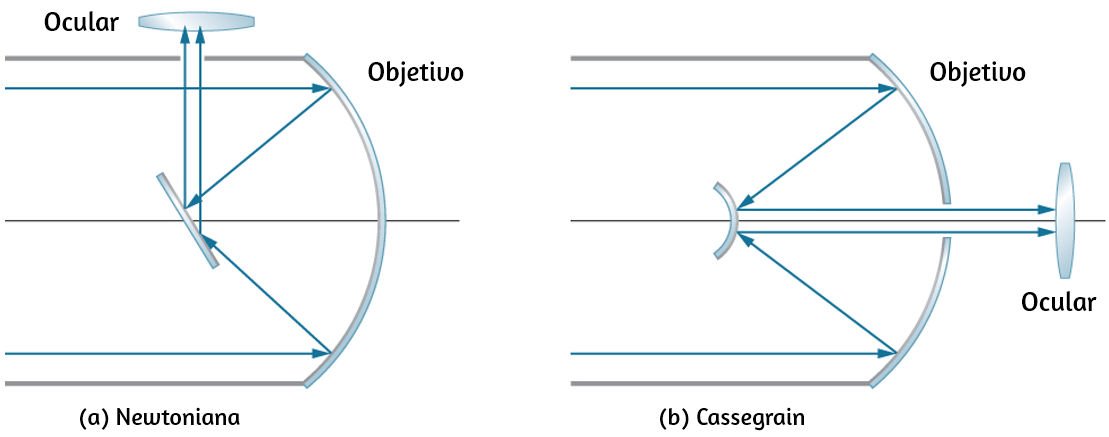
Algunos telescopios reflejan la luz hacia el centro del espejo cóncavo usando un espejo convexo. En esta disposición, el espejo cóncavo que recoge la luz tiene un orificio en la parte central [ (b)]. Entonces, la luz incide en la lente de un ocular. Esta disposición del objetivo y del ocular se denomina diseño de Cassegrain. La mayoría de los telescopios grandes, incluido el telescopio espacial Hubble, son de este diseño. También son posibles otros arreglos. En algunos telescopios, un detector de luz se coloca justo en el lugar donde la luz es enfocada por el espejo curvo.

La mayoría de los telescopios de investigación astronómica son ahora del tipo reflectante. Uno de los primeros telescopios grandes de este tipo es el telescopio Hale de $200$ pulgadas (o $5$ metros) construido en el Monte Palomar en el sur de California, que tiene un espejo de $200$ pulgadas de diámetro. Uno de los telescopios más grandes del mundo es el telescopio Keck de $10$ metros en el Observatorio Keck en la cima del volcán Mauna Kea en Hawaii. El Observatorio Keck opera dos telescopios de $10$ metros. Cada uno no es un solo espejo, sino que está formado por 36 espejos hexagonales. Además, los dos telescopios en el Keck pueden trabajar juntos, lo que aumenta su potencia a un espejo efectivo de $85$ metros. El telescopio Hubble () es otro gran telescopio reflector con un espejo primario de $2.4$ metros de diámetro. El Hubble fue puesto en órbita alrededor de la Tierra en 1990.
El aumento angular $M$ de un telescopio reflector también está dado por la Ecuación 9.36. Para un espejo esférico, la distancia focal es la mitad del radio de curvatura, por lo que hacer un espejo objetivo grande no solo ayuda al telescopio a recolectar más luz sino que también aumenta el aumento de la imagen.
En la siguiente unidad didáctica que hace parte del proyecto @prende.mx puedes explorar, nuevamente, el estudio de la refracción de la luz al pasar a medios diferentes y su aplicación en la construcción de lentes convergentes y divergentes. En esta unidad interactiva se hace una explicación amplia y, en especial, muy detallada de los microscopios.

La indicación más segura de una onda es la interferencia. Esta característica de onda es más prominente cuando la onda interactúa con un objeto que no es grande en comparación con la longitud de onda. Se observan interferencias en las ondas de agua, ondas de sonido, ondas de luz y, de hecho, todos los tipos de ondas.
Si alguna vez has visto los rojos, azules y verdes en una burbuja de jabón iluminada por el sol y te has preguntado cómo podría producirlos el agua jabonosa de color pajizo, te has topado con uno de los muchos fenómenos que solo pueden explicarse por el carácter ondulado de la luz (Ver ). Lo mismo se aplica a los colores vistos en una mancha de aceite o en la luz reflejada de un disco DVD. Estos y otros fenómenos interesantes no pueden explicarse completamente por la óptica geométrica. En estos casos, la luz interactúa con los objetos y presenta características de onda. La rama de la óptica que considera el comportamiento de la luz cuando exhibe características de onda se llama óptica de onda (a veces llamada óptica física). Es el tema de este capítulo.
El físico holandés Christiaan Huygens (1629-1695) pensó que la luz era una onda, pero Isaac Newton no lo hizo. Newton pensó que había otras explicaciones para el color, y para los efectos de interferencia y difracción que eran observables en ese momento. Debido a la tremenda reputación de Newton, su opinión prevaleció en general; el hecho de que el principio de Huygens funcionara no se consideraba evidencia directa que probara que la luz es una onda. La aceptación del carácter de onda de la luz se produjo muchos años después, en 1801, cuando el físico y médico inglés Thomas Young (1773–1829) demostró la interferencia óptica con su ahora clásico experimento de doble rendija.
Si no hubiera una sino dos fuentes de ondas, las ondas podrían interferir, como en el caso de las olas en el agua (). Si la luz es una onda electromagnética, por lo tanto, debe exhibir efectos de interferencia en circunstancias apropiadas. En el experimento de Young, la luz del sol pasaba a través de un agujero en una tabla. El haz emergente cayó en dos agujeros en una segunda tabla. La luz que emana de los dos orificios luego cayó sobre una pantalla donde se observó un patrón de puntos brillantes y oscuros. Este patrón, llamado franjas, solo puede explicarse a través de la interferencia, un fenómeno de onda.
Podemos analizar la interferencia de doble rendija con la ayuda de la , que muestra un aparato análogo al de Young. La luz de una fuente monocromática cae en una rendija $S_0.$ La luz que emana de $S_0$ incide en otras dos rendijas $S_1$ y $S_2$ que son equidistantes de $S_0.$ Luego, la luz que emana de $S_1$ y $S_2$ produce un patrón de franjas de interferencia en la pantalla. Se supone que todas las rendijas son tan estrechas que pueden considerarse fuentes puntuales secundarias para las wavelets (onditas) de Huygens (La naturaleza de la luz).
Las ranuras $S_1$ y $S_2$ están separadas por una distancia $d$ ($d ≤ 1 mm$), y la distancia entre la pantalla y las ranuras es $D$ ($≈ 1 m$), que es mucho mayor que $d$.

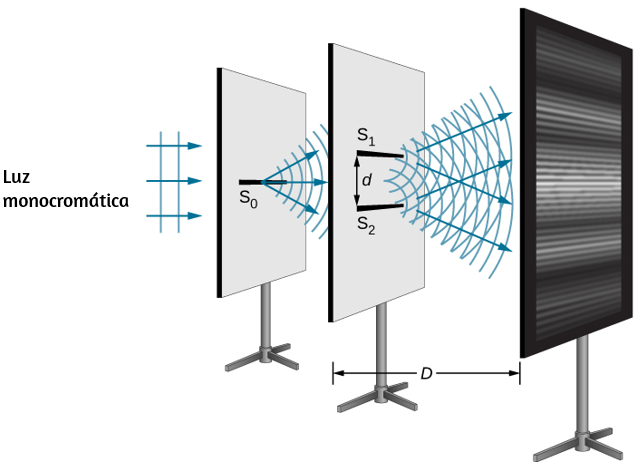
Dado que se supone que $S_0$ es una fuente puntual de luz monocromática, las wavelets secundarias de Huygens que dejan $S_1$ y $S_2$ siempre mantienen una diferencia de fase constante (cero en este caso porque $S_1$ y $S_2$ son equidistantes de $S_0$) y tienen la misma frecuencia. Se dice que las fuentes $S_1$ y $S_2$ son coherentes. Por ondas coherentes, queremos decir que las ondas están en fase o tienen una relación de fase definida.
El término incoherente significa que las ondas tienen relaciones de fase aleatorias, lo que sería el caso si $S_1$ y $S_2$ estuvieran iluminadas por dos fuentes de luz independientes, en lugar de una sola fuente $S_0$. Dos fuentes de luz independientes (que pueden ser dos áreas separadas dentro de la misma lámpara o el Sol) generalmente no emiten su luz al unísono, es decir, no de manera coherente. Además, como $S_1$ y $S_2$ están a la misma distancia de $S_0$, las amplitudes de las dos wavelets de Huygens son iguales.
Young usó la luz solar, donde cada longitud de onda forma su propio patrón, lo que hace que el efecto sea más difícil de ver. En la siguiente discusión, ilustramos el experimento de doble rendija con luz monocromática ($λ$ único) para aclarar el efecto. La muestra la interferencia constructiva pura y destructiva pura de dos ondas que tienen la misma longitud de onda y amplitud.
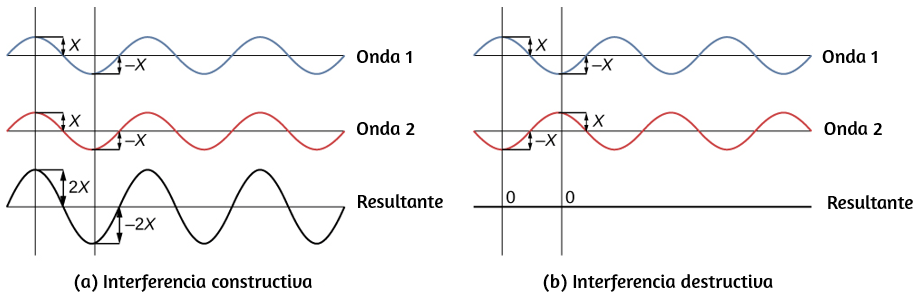
Cuando la luz pasa a través de rendijas estrechas, las rendijas actúan como fuentes de ondas coherentes y la luz se extiende como ondas semicirculares, como se muestra en la (a). La interferencia constructiva pura ocurre cuando las ondas son de cresta a cresta o de canal a canal. La interferencia destructiva pura ocurre cuando están en la cresta. La luz debe caer en una pantalla y estar dispersa en nuestros ojos para que podamos ver el patrón. Un patrón análogo para las ondas de agua se muestra en la . Tenga en cuenta que las regiones de interferencia constructiva y destructiva salen de las ranuras en ángulos bien definidos al haz original. Estos ángulos dependen de la longitud de onda y la distancia entre las rendijas, como veremos más adelante.
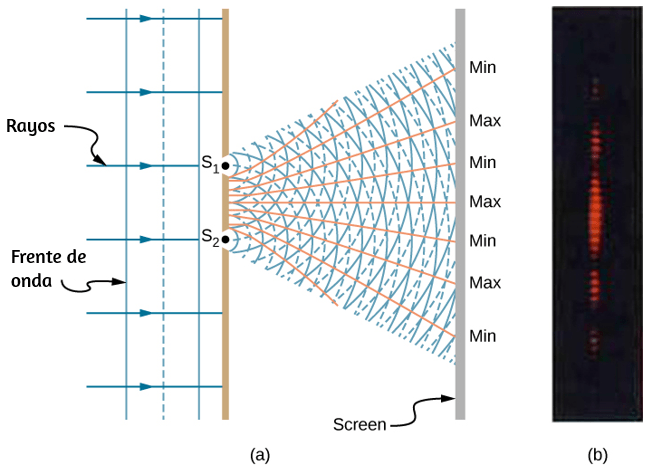
Para comprender el patrón de interferencia de doble rendija, considera cómo viajan dos ondas desde las rendijas a la pantalla (). Cada ranura es una distancia diferente de un punto dado en la pantalla. Por lo tanto, diferentes números de longitudes de onda encajan en cada camino. Las ondas comienzan desde las ranuras en fase (cresta a cresta), pero pueden terminar fuera de fase (cresta a canal) en la pantalla si las trayectorias difieren en longitud en media longitud de onda, interfiriendo destructivamente.
Si los caminos difieren en una longitud de onda completa, las ondas llegan en fase (cresta a cresta) en la pantalla, interfiriendo constructivamente. De manera más general, si la diferencia de longitud de trayectoria $Δl$ entre las dos ondas es un número de semi-integrales de longitudes de onda $[(1/2)λ, (3/2)λ, (5/2)λ, etc.]$, entonces la interferencia destructiva ocurre. De manera similar, si la diferencia de longitud del camino es un número entero de longitudes de onda ($λ, 2λ, 3λ, etc.$), entonces ocurre una interferencia constructiva. Estas condiciones se pueden expresar como ecuaciones:
$$Δl = mλ, \; \textsf{para} \; m = 0, ±1, ±2, ±3... \\ (\textsf{interferencia constructiva}) \tag{10.1}$$ $$Δl = (m + 1/2)λ, \; \textsf{para} \; m = 0, ±1, ±2, ±3... \\ (\textsf{interferencia destructiva}) \tag{10.2}$$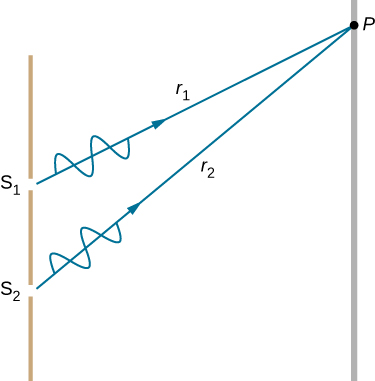
En la escena interactiva que presentamos en la página siguiente, tomada de las simulaciones Phet, puedes realizar varias actividades, entre ellas: utilizar múltiples fuentes con un espacio diferente y ver cómo cambia un patrón de interferencia, encontrar visualmente y mediante los detectores puntos de interferencia constructiva y destructiva, poner una barrera para ver cómo las ondas se mueven a través de una o dos rendijas ¿Qué clase de patrón crean las ranuras? ¿Cómo se puede cambiar este patrón? En el panel de luz, predice la ubicación de las franjas que aparecen en la pantalla utilizando $dsen(θ) = mλ$. Utiliza la cinta de medir para comprobar tus predicciones.
La (a) muestra cómo determinar la diferencia de longitud de la trayectoria $Δl$ para las ondas que viajan desde dos rendijas hasta un punto común en una pantalla. Si la pantalla está a una gran distancia en comparación con la distancia entre las rendijas, entonces el ángulo $θ$ entre la trayectoria y una línea desde las rendijas hasta la pantalla [parte (b)] es casi el mismo para cada trayectoria. En otras palabras, $r_1$ y $r_2$ son esencialmente paralelos. Las longitudes de $r_1$ y $r_2$ difieren en $Δl$, como lo indican las dos líneas discontinuas en la figura (demostraciones simples de trigonometría).
$$Δl = dsenθ \tag{10.3}$$donde $d$ es la distancia entre las rendijas. Combinando este resultado con la Ecuación 10.1, obtenemos una interferencia constructiva para una doble rendija cuando la diferencia de longitud del trayecto es un múltiplo entero de la longitud de onda, o
$$dsenθ = mλ, \; \textsf{para} \; m = 0, ±1, ±2, ±3... \\ (\textsf{interferencia constructiva}) \tag{10.4}$$De manera similar, para obtener una interferencia destructiva para una doble rendija, la diferencia de longitud de la trayectoria debe ser un múltiplo de media rendija de la longitud de onda, o
$$dsenθ = (m + \frac{1}{2})λ, \; \textsf{para} \; m = 0, ±1, ±2, ±3... \\ (\textsf{interferencia destructiva}) \tag{10.5}$$donde $λ$ es la longitud de onda de la luz, d es la distancia entre rendijas, y $θ$ es el ángulo desde la dirección original del haz, como se explicó anteriormente. Llamamos a $m$ el orden de la interferencia. Por ejemplo, $m = 4$ es la interferencia de cuarto orden.
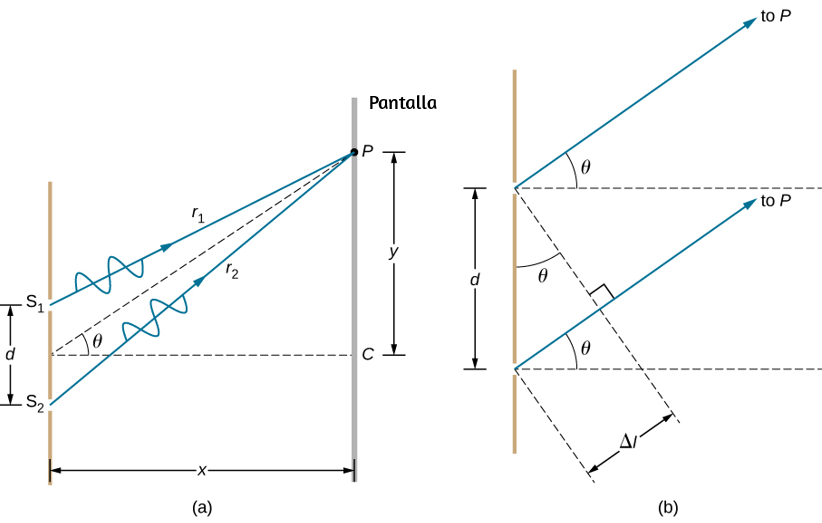
Las ecuaciones para la interferencia de doble rendija implican que se forman una serie de líneas brillantes y oscuras. Para las rendijas verticales, la luz se propaga horizontalmente a cada lado del haz incidente en un patrón llamado franjas de interferencia (). Cuanto más cerca están las rendijas, más se separan las franjas brillantes. Podemos ver esto examinando la ecuación $dsenθ = mλ$, para $m = 0, ±1, ±2, ±3…$. Para $λ$ y $m$ fijos, la $d$ más pequeña es la $θ$ más grande, ya que $senθ = mλ/d$. Esto es consistente con nuestra afirmación de que los efectos de onda son más notables cuando el objeto con el que se encuentra la onda (aquí, ranuras a una distancia d) es pequeño. La $d$ pequeña da $θ$ grande, por lo tanto, un gran efecto.
Con referencia a la parte (a) de la figura, $θ$ suele ser lo suficientemente pequeño para que $senθ ≈ tanθ ≈ y_m/D$, donde $y_m$ es la distancia desde el máximo central hasta la franja brillante $m_{ésima}$ y $D$ es la distancia entre la rendija y la pantalla. La ecuación 10.4 se puede escribir como
o
$$y_m = \frac{mλD}{d} \tag{10.6}$$Ejemplo 10.1
Encontrar una longitud de onda a partir de un patrón de interferencia
Supón que pasa la luz de un láser de He-Ne a través de dos rendijas separadas por $0.0100 mm$ y encuentras que la tercera línea brillante en una pantalla se forma en un ángulo de $10.95°$ con respecto al haz incidente. ¿Cuál es la longitud de onda de la luz?
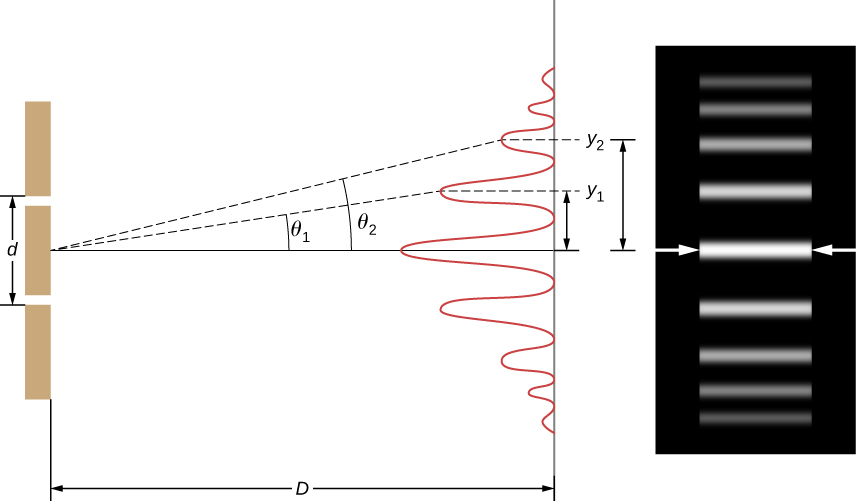
Estrategia
El fenómeno es una interferencia de dos rendijas, como se ilustra en la y la tercera línea brillante se debe a una interferencia constructiva de tercer orden, lo que significa que $m = 3$. Nos dan $d = 0.0100 mm$ y $θ = 10.95°$. La longitud de onda se puede encontrar usando la ecuación $dsenθ = mλ$ para la interferencia constructiva.
Solución
Resolviendo $dsenθ = mλ$ para la longitud de onda $λ$ da
$$λ = \frac{dsenθ}{m}$$Reemplazando los datos conocidos, obtenemos:
$$λ = \frac{(0.0100 mm)(sen 10.95°)}{3} = 6.33 × 10^{-4} mm = 633 nm$$Explicación
A tres dígitos, esta es la longitud de onda de la luz emitida por el láser común $He-Ne$. No por coincidencia, este color rojo es similar al emitido por las luces de neón. Más importante, sin embargo, es el hecho de que los patrones de interferencia pueden usarse para medir la longitud de onda. Young hizo esto para las longitudes de onda visibles. Esta técnica analítica todavía se usa ampliamente para medir espectros electromagnéticos. Para un orden dado, el ángulo para la interferencia constructiva aumenta con $λ$, de modo que se pueden obtener espectros (mediciones de intensidad en función de la longitud de onda).
Ejemplo 10.2
Cálculo del orden más alto posible
Los patrones de interferencia no tienen un número infinito de líneas, ya que hay un límite de cuán grande puede ser $m$. ¿Cuál es la interferencia constructiva de orden más alto posible con el sistema descrito en el ejemplo anterior?
Estrategia
La ecuación $dsenθ = mλ$ (para $m = 0, ±1, ±2, ±3…$) describe la interferencia constructiva de dos rendijas. Para valores fijos de $d$ y $λ$, cuanto mayor es $m$, mayor es $θ$. Sin embargo, el valor máximo que puede tener $senθ$ es $1$, para un ángulo de $90°$ (los ángulos más grandes implican que la luz retrocede y no llega a la pantalla). Veamos qué valor de $m$ corresponde a este ángulo de difracción máximo.
Solución
Despejando $m$ de la ecuación $dsenθ = mλ$ para $m$, resulta:
$$m = \frac{dsenθ}{λ}$$Tomando $senθ = 1$ y sustituyendo los valores de $d$ y $λ$, del ejemplo anterior, obtenemos:
$$m = \frac{(0.0100 mm)(1)}{633 nm} ≈ 15.8$$Por lo tanto, el entero más grande que $m$ puede ser es $15$, o $m = 15$.
Explicación
El número de franjas depende de la longitud de onda y la separación de la hendidura. El número de franjas es muy grande para grandes separaciones de hendidura. Sin embargo, recuerda que la interferencia de onda solo es prominente cuando la onda interactúa con objetos que no son grandes en comparación con la longitud de onda. Por lo tanto, si la separación de la rendija y el tamaño de las rendijas son mucho más grandes que la longitud de onda, el patrón de intensidad de la luz en la pantalla cambia, por lo que simplemente hay dos líneas brillantes emitidas por las rendijas, como se espera, cuando la luz se comporta como los rayos. También notamos que las franjas se vuelven más débiles lejos del centro. En consecuencia, no todas las 15 franjas pueden ser observables.
 Comprueba tu aprendizaje 10.1
Comprueba tu aprendizaje 10.1
En la siguiente escena interactiva, diseñada por Daniel V. Schroeder , se muestra la interferencia de ondas de dos fuentes idénticas que están separadas por una distancia variable. Las crestas de las olas se muestran en rojo y los canales en azul, con negro que indica una amplitud de onda local de cero (observa que la imagen completa se actualiza instantáneamente cuando mueves el control deslizante, ya que se dibuja utilizando una fórmula que supone una separación fija, en lugar de hacerlo a partir de una simulación de la respuesta dependiente del tiempo del medio de onda. Ten en cuenta, también, que la amplitud de onda no disminuye con la distancia desde la fuente, como lo haría para las ondas físicas).
El análisis de la interferencia de la luz que pasa a través de dos rendijas establece el marco teórico de la interferencia y nos da una visión histórica de los experimentos de Thomas Young. Sin embargo, gran parte de la aplicación moderna de la interferencia de rendijas usa no solo dos rendijas sino muchas, acercándose al infinito con propósitos prácticos. El elemento óptico clave se denomina rejilla de difracción, una herramienta importante en el análisis óptico, que analizaremos en detalle en Difracción. Aquí, comenzamos el análisis de la interferencia de múltiples rendijas tomando los resultados de nuestro análisis de la doble rendija ($N = 2$) y extendiéndolos a configuraciones con tres, cuatro y un número mucho mayor de rendijas.
La muestra el caso más simple de interferencia de múltiples rendijas, con tres rendijas, o $N = 3$. El espacio entre las ranuras es $d$, y la diferencia de longitud de la ruta entre las ranuras adyacentes es $dsenθ$, igual que en el caso de la doble rendija. Lo nuevo es que la diferencia de longitud de trayectoria para la primera y la tercera ranura es $2dsenθ$. La condición para la interferencia constructiva es la misma que para la doble rendija, es decir $dsenθ = mλ$.
Cuando se cumple esta condición, $2dsenθ$ es automáticamente un múltiplo de $λ$, por lo que los tres rayos se combinan de manera constructiva, y las franjas brillantes que ocurren aquí se llaman máximos principales. Pero, ¿qué sucede cuando la diferencia de longitud de trayectoria entre cortes adyacentes es solo $λ/2$? Podemos pensar que el primer y segundo rayo interfieren destructivamente, pero el tercer rayo permanece inalterado. En lugar de obtener una franja oscura, o un mínimo, como hicimos para la doble rendija, vemos un máximo secundario con una intensidad más baja que los máximos principales.
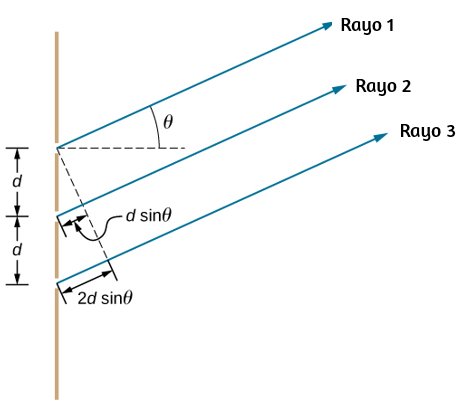
En general, para las ranuras en $N$, estos máximos secundarios ocurren cada vez que se presenta un rayo no pareado que no desaparece debido a la interferencia destructiva. Esto ocurre en $(N - 2)$ posiciones espaciadas uniformemente entre los máximos principales. La amplitud de la onda electromagnética disminuye correspondientemente a $1/N$ de la onda en los máximos principales, y la intensidad de la luz, al ser proporcional al cuadrado de la amplitud de la onda, disminuye a $1/N^2$ de la intensidad en comparación con los máximos principales . Como muestra la , una franja oscura se encuentra entre cada máximo (principal o secundario). A medida que $N$ crece y el número de franjas brillantes y oscuras aumenta, los anchos de los máximos se vuelven más estrechos debido a las franjas oscuras vecinas cercanas. Debido a que la cantidad total de energía luminosa permanece inalterada, los máximos más estrechos requieren que cada máximo alcance una intensidad correspondiente más alta.
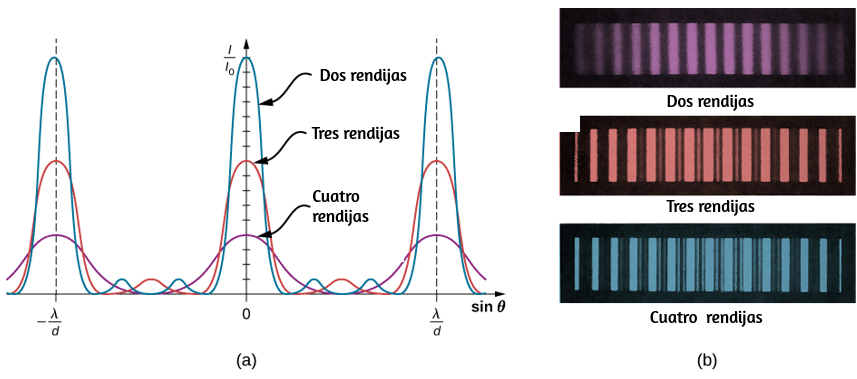
Los colores brillantes que se ven en una mancha de aceite flotando en el agua o en una burbuja de jabón iluminada por el sol son causados por la interferencia. Los colores más brillantes son los que interfieren constructivamente. Esta interferencia es entre la luz reflejada desde diferentes superficies de una película delgada; por lo tanto, el efecto se conoce como interferencia de película delgada.
Como notamos antes, los efectos de interferencia son más prominentes cuando la luz interactúa con algo que tiene un tamaño similar a su longitud de onda. Una película delgada es aquella que tiene un grosor t menor que unas pocas veces la longitud de onda de la luz, $λ$. Como el color está asociado indirectamente con $λ$ y debido a que todas las interferencias dependen de alguna manera de la relación de $λ$ con el tamaño del objeto involucrado, deberíamos esperar ver diferentes colores para diferentes espesores de una película, como en la .

¿Qué causa la interferencia de la película delgada? La muestra cómo puede interferir la luz reflejada desde las superficies superior e inferior de una película. La luz incidente se refleja solo parcialmente desde la superficie superior de la película (rayo 1). El resto entra en la película y se refleja parcialmente desde la superficie inferior.
Parte de la luz reflejada desde la superficie inferior puede emerger desde la parte superior de la película (rayo 2) e interferir con la luz reflejada desde la parte superior (rayo 1). El rayo que entra en la película viaja una distancia mayor, por lo que puede estar dentro o fuera de fase con el rayo reflejado desde la parte superior. Sin embargo, considera por un momento, nuevamente, las burbujas en la . Las burbujas son más oscuras donde son más delgadas. Además, si observas cuidadosamente una burbuja de jabón, notarás que se oscurece en el punto donde se rompe.
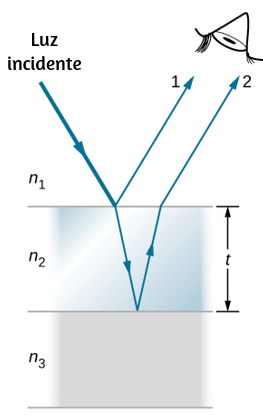
Para películas muy delgadas, la diferencia en las longitudes de trayectoria de los rayos 1 y 2 en la es despreciable, ¿por qué deberían interferir destructivamente y no constructivamente? La respuesta es que un cambio de fase puede ocurrir en la reflexión, como se discute a continuación.
Ya vimos que el reflejo de las ondas mecánicas puede implicar un cambio de fase de $180°$. Por ejemplo, una onda que viaja en una cuerda se invierte (es decir, un cambio de fase de $180°$) en la reflexión en un límite al que se ata una cuerda más pesada. Sin embargo, si la segunda cuerda es más ligera (o más precisamente, de una densidad lineal más baja), no se produce ninguna inversión. Las ondas de luz producen el mismo efecto, pero el parámetro decisivo para la luz es el índice de refracción.
Las ondas de luz experimentan un cambio de fase de $180°$ o $π$ radianes tras la reflexión en una interfaz más allá de la cual es un medio de mayor índice de refracción. No se produce ningún cambio de fase cuando se refleja desde un medio de índice de refracción más bajo (). Debido a la naturaleza periódica de las ondas, este cambio de fase o inversión es equivalente a $±λ/2$ en la distancia recorrida, o longitud de trayectoria. Tanto la longitud de la trayectoria como los índices de refracción son factores importantes en la interferencia de película delgada.
Si la película en la es una burbuja de jabón (esencialmente agua con aire en ambos lados), entonces se produce un cambio de fase de $λ/2$ para el rayo 1 pero no para el rayo 2. Por lo tanto, cuando la película es muy delgada y en la longitud de la trayectoria la diferencia entre los dos rayos es insignificante, están exactamente desfasadas y se producen interferencias destructivas en todas las longitudes de onda. Por lo tanto, la burbuja de jabón es oscura aquí. El grosor de la película en relación con la longitud de onda de la luz es el otro factor crucial en la interferencia de película delgada.
El rayo 2 en la recorre una distancia mayor que el rayo 1. Para la luz incidente perpendicular a la superficie, el rayo 2 recorre una distancia aproximadamente $2t$ más lejos que el rayo 1. Cuando esta distancia es un múltiplo integral o semi-integral de la longitud de onda en el medio ($λ_n = λ/n$, donde $λ$ es la longitud de onda en el vacío y $n$ es el índice de refracción), se producen interferencias constructivas o destructivas, dependiendo también de si hay un cambio de fase en cualquiera de los rayos.
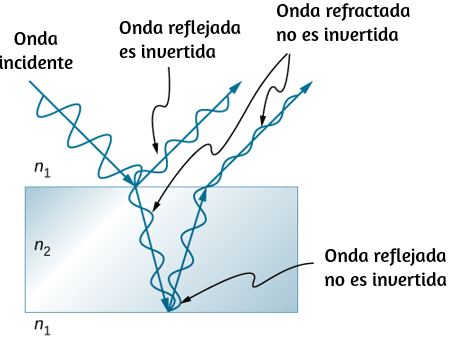
Ejemplo 10.3
Cálculo del espesor de un recubrimiento de lente no reflectante
Las cámaras sofisticadas utilizan una serie de varias lentes. La luz puede reflejarse desde las superficies de estas diferentes lentes y degradar la claridad de la imagen. Para limitar estos reflejos, las lentes están recubiertas con una capa delgada de fluoruro de magnesio, que causa una interferencia destructiva de la película delgada. ¿Qué es lo más delgado que puede ser esta película si su índice de refracción es $1.38$ y está diseñado para limitar la reflexión de la luz de $550 nm$, normalmente la longitud de onda visible más intensa? Supongamos que el índice de refracción del vidrio es $1.52$.
Estrategia
Consulta la y usa $n_1 = 1.00$ para aire, $n_2 = 1.38$ y $n_3 = 1.52$. Tanto el rayo 1 como el rayo 2 tienen un desplazamiento $λ/2$ en la reflexión. Por lo tanto, para obtener una interferencia destructiva, el rayo 2 necesita viajar media longitud de onda más lejos que el rayo 1. Para los rayos que inciden perpendicularmente, la diferencia de longitud de trayectoria es $2t$.
Solución
Para obtener la interferencia destructiva aquí, $2t = \dfrac{λ_{n2}}{2}$
donde $λ_{n2}$ es la longitud de onda en la película y está dada por $λ_{n2} = λ/n_2$. Así,
$$2t = \frac{λ/n_2}{2}$$Resolviendo para t e introduciendo los valores conocidos
$$t = \frac{λ/n_2}{4} = \frac{(500 nm)/1.38}{4} = 90.6 nm$$Explicación
Las películas como la de este ejemplo son más efectivas para producir interferencias destructivas cuando se utiliza la capa más delgada, ya que la luz en un rango más amplio de ángulos incidentes se reduce en intensidad. Estas películas se denominan recubrimientos no reflectantes; sin embargo, esta es solo una descripción aproximadamente correcta, ya que otras longitudes de onda solo se cancelan parcialmente. Los revestimientos no reflectantes también se utilizan en ventanas de automóviles y gafas de sol.
La interferencia de película delgada es más constructiva o más destructiva cuando la diferencia de longitud de trayectoria para los dos rayos es una longitud de onda integral o semi-integral. Es decir, para rayos incidentes perpendicularmente,
$$2t = λ_n, 2λ_n, 3λ_n,… o 2t = λ_n/2, 3λ_n/2, 5λ_n/2,…$$Para saber si la interferencia es constructiva o destructiva, también debes determinar si hay un cambio de fase en la reflexión. La interferencia de la película delgada depende, por lo tanto, del espesor de la película, la longitud de onda de la luz y los índices de refracción. Para incidentes de luz blanca en una película que varía en grosor, puedes observar colores de arco iris de interferencia constructiva para varias longitudes de onda a medida que varías el grosor.
Ejemplo 10.4
Burbujas de jabón
(a) ¿Cuáles son los tres espesores más pequeños de una burbuja de jabón que producen una interferencia constructiva para la luz roja con una longitud de onda de $650 nm$? El índice de refracción del jabón se considera el mismo que el del agua.
(b) ¿Qué tres espesores más pequeños dan interferencia destructiva?
Estrategia
Usa la para visualizar la burbuja, que actúa como una película delgada entre dos capas de aire. Así, $n_1 = n_3 = 1.00$ para aire, y $n_2 = 1.333$ para jabón (equivalente a agua). Hay un desplazamiento $λ/2$ para el rayo 1 reflejado desde la superficie superior de la burbuja y no hay cambio para el rayo 2 reflejado desde la superficie inferior. Para obtener una interferencia constructiva, entonces, la diferencia de longitud de la trayectoria ($2t$) debe ser un múltiplo semi-integral de la longitud de onda; los tres primeros son $λ_n/2$, $3λ_n/2$ y $5λ_n/2$. Para obtener una interferencia destructiva, la diferencia de longitud de la trayectoria debe ser un múltiplo integral de la longitud de onda; los tres primeros son $0$, $λ_n$ y $2λ_n$.
Solución
a. La interferencia constructiva ocurre aquí cuando
$$2t_c = \frac{λ_n}{2}. \frac{3λ_n}{2}, \frac{5λ_n}{2}, ..$$Así, el menor espesor constructivo $t_c$ es
$$t_c = \frac{λ_n}{4} = \frac{λ/n}{4} = \frac{(650 nm)/1.333}{4} = 122 nm$$El siguiente espesor que proporciona interferencia constructiva es $t'_c = 3λ_n/4$, de modo que
$$t'_c = 366 nm$$Finalmente, el tercer espesor que produce interferencia constructiva es $t'_c = 5λ_n/4$, de modo que
$$t'_c = 610 nm$$b. Para la interferencia destructiva, la diferencia de longitud de trayectoria aquí es un múltiplo integral de la longitud de onda. El primero ocurre para el espesor cero, ya que hay un cambio de fase en la superficie superior, es decir,
$$t_d = 0,$$el caso muy delgado (o despreciablemente delgado) discutido anteriormente. El primer espesor no nulo que produce interferencia destructiva es
$$2t'_d = λ_n$$Reemplazando con los valores conocidos, obtenemos:
$$t'_d = \frac{λ}{2} = \frac{λ/n}{2} = \frac{(650 nm)/1.333}{2} = 244 nm$$Finalmente, el tercer espesor destructivo es $2t"_d = 2λ_n$, de modo que
$$t"_d = λ_n = \frac{λ}{n} = \frac{650 nm}{1.333} = 488 nm$$Explicación
Si la burbuja se iluminara con luz roja pura, veríamos bandas brillantes y oscuras con incrementos de espesor muy uniformes. Primero sería una banda oscura con un grosor de $0$, luego brillante a $122 nm$ de espesor, luego oscura a $244 nm$, brillante a $366 nm$, oscura a $488 nm$ y brillante a $610 nm$. Si la burbuja variara suavemente en grosor, como una cuña lisa, entonces las bandas estarían espaciadas uniformemente.
 Comprueba tu aprendizaje 10.2
Comprueba tu aprendizaje 10.2
Se puede ver otro ejemplo de interferencia de película delgada cuando se separan los portaobjetos del microscopio (consulta la ). Las diapositivas son muy planas, de modo que la cuña de aire entre ellas aumenta de espesor de manera muy uniforme. Se produce un cambio de fase en la segunda superficie pero no en la primera, por lo que se forma una banda oscura donde se tocan las diapositivas. Los colores del arco iris de la interferencia constructiva se repiten, yendo de violeta a rojo una y otra vez a medida que aumenta la distancia entre las diapositivas. A medida que aumenta la capa de aire, las bandas se vuelven más difíciles de ver, porque los cambios leves en el ángulo de incidencia tienen mayores efectos en las diferencias de longitud de la trayectoria. Si se utiliza luz monocromática en lugar de luz blanca, se obtienen bandas brillantes y oscuras en lugar de repetir los colores del arco iris.
Una importante aplicación de la interferencia de película delgada se encuentra en la fabricación de instrumentos ópticos. Una lente o un espejo se puede comparar con un patrón, ya que está siendo rectificado, lo que permite que tenga una precisión de menos de una longitud de onda en toda su superficie. La ilustra el fenómeno llamado anillos de Newton, que ocurre cuando las superficies planas de dos lentes se colocan juntas (las bandas circulares se llaman anillos de Newton porque fue Isaac Newton quien las describió en detalle. Su descubrimiento se debe a Robert Hooke, Newton no creía que se debieran al carácter de onda de la luz).
Cada anillo sucesivo de un color dado indica un aumento de solo la mitad de la longitud de onda en la distancia entre la lente y el blanco, para que se pueda obtener una gran precisión. Una vez que la lente está perfecta, no aparecen anillos.
La interferencia de película delgada tiene muchas otras aplicaciones, tanto en la naturaleza como en la fabricación. Las alas de ciertas polillas y mariposas tienen colores casi iridiscentes debido a la interferencia de la película delgada. Además de la pigmentación, el color del ala se ve afectado en gran medida por la interferencia constructiva de ciertas longitudes de onda reflejadas desde su superficie recubierta con película. Algunos fabricantes de automóviles ofrecen trabajos de pintura especiales que utilizan interferencia de película delgada para producir colores que cambian con el ángulo. Esta opción costosa se basa en la variación de las diferencias de longitud de trayectoria de película delgada con el ángulo. Las funciones de seguridad en tarjetas de crédito, billetes de banco, permisos de conducir y artículos similares propensos a la falsificación utilizan interferencias de película delgada, rejillas de difracción u hologramas. Desde 1998, Australia abrió el camino con billetes de dólar impresos en polímero con una función de seguridad de rejilla de difracción, lo que dificulta la falsificación de la moneda. Otros países, como Canadá, Nueva Zelanda y Taiwán, están usando tecnologías similares, mientras que la moneda estadounidense incluye un efecto de interferencia de película delgada.
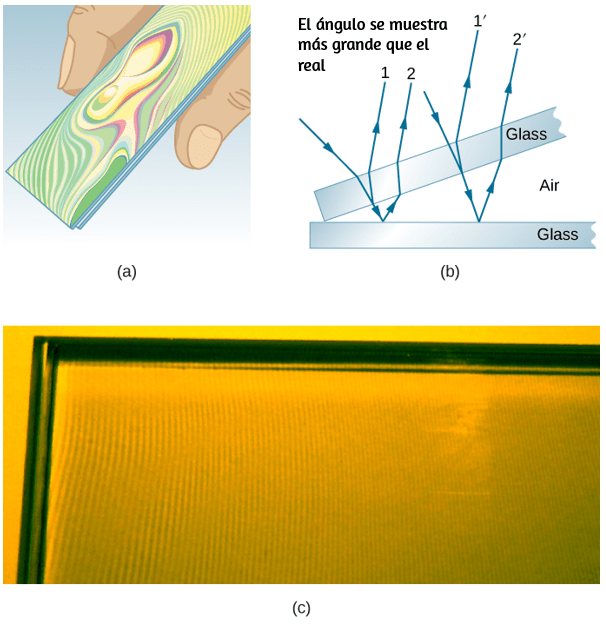

En la siguiente escena interactiva de los anillos de Newton, diseñada por Andrew Duffy, un cristal de reloj curvo se asienta sobre una pieza plana de vidrio. Una delgada película de aire se encuentra entre los dos: la película delgada tiene un espesor que es cero donde las dos piezas de vidrio se tocan y aumenta gradualmente a medida que se aleja de ese punto. La luz de una sola longitud de onda brilla desde arriba. La luz que se refleja desde las superficies superior e inferior de la película delgada interfiere, lo que lleva a un patrón de ojo de buey, como vemos a la izquierda (la vista desde arriba). A la derecha está la vista lateral. Ten en cuenta que el grosor de la película delgada no se muestra a la misma escala que la longitud de onda de las dos ondas reflejadas; esas ondas muestran la interferencia, que puede ser constructiva o destructiva.
Andrew Duffy y Logan Scheiner nos presentan otra escena interactiva de interferencia de película delgada, en la cual la onda incidente se muestra en la parte superior. La onda que se refleja en la superficie frontal de la película se mueve debajo de ella, por lo que podemos verla fácilmente sin que esté encima de la onda incidente. La onda que se refleja en la superficie posterior de la película se mueve aún más abajo. Mira la interferencia que se produce entre las dos ondas reflejadas que viajan hacia la izquierda en el primer medio.
Podemos comenzar nuestro análisis pensando en la diferencia de longitud de camino que se produce para las dos ondas. Una onda simplemente rebota en la película, mientras que la otra pasa a través de la película, se refleja y viaja a través de la película nuevamente antes de emerger de nuevo al primer medio.
Si el espesor de la película es t, la segunda ola recorre una distancia adicional de $2t$ en comparación con la primera onda. La diferencia de longitud de la trayectoria, en otras palabras, es $2t$.
Los autores proponen las siguientes actividades:
El interferómetro de Michelson (inventado por el físico estadounidense Albert A. Michelson, 1852–1931) es un instrumento de precisión que produce franjas de interferencia al dividir un haz de luz en dos partes y luego combinarlas después de que hayan recorrido diferentes caminos ópticos. La muestra el interferómetro y la trayectoria de un haz de luz desde un punto en la fuente $S$ extendida, que es una placa de vidrio esmerilado que difunde la luz de una lámpara monocromática de longitud de onda $λ_0.$ El haz golpea el espejo plateado $M$, donde la mitad se refleja hacia un lado y la mitad atraviesa el espejo. La luz reflejada viaja hacia el espejo plano móvil $M_1$, donde se refleja hacia el observador a través de $M$. La mitad transmitida del haz original es reflejada hacia atrás por el espejo estacionario $M_2$ y luego hacia el observador por $M$.
Debido a que ambos haces se originan desde el mismo punto en la fuente, son coherentes y, por lo tanto, interfieren. Observa por la que un haz pasa por $M$ tres veces y la otra solo una vez. Para garantizar que ambos haces atraviesen el mismo espesor del vidrio, se coloca una placa compensadora $C$ de vidrio transparente en el brazo que contiene $M_2$. Esta placa es un duplicado de $M$ (sin plateado) y generalmente se corta del mismo vidrio utilizado para producir $M$. Con el compensador en su lugar, cualquier diferencia de fase entre los dos haces se debe únicamente a la diferencia en las distancias que viaje.
La diferencia de trayectoria de los dos haces cuando se recombinan es $2d_1 - 2d_2$, donde $d_1$ es la distancia entre $M$ y $M_1$, y $d_2$ es la distancia entre $M$ y $M_2$. Supongamos que esta diferencia de ruta es un número entero de longitudes de onda $mλ_0$. Luego, se produce una interferencia constructiva y se ve una imagen brillante del punto en la fuente en el observador.
Ahora, la luz de cualquier otro punto en la fuente cuyos dos haces tienen esta misma diferencia de trayectoria también sufre una interferencia constructiva y produce una imagen brillante. La colección de estas imágenes de puntos es una franja brillante que corresponde a una diferencia de trayectoria de $mλ_0$ (). Cuando $M_1$ se mueve una distancia $d = λ_0/2$, esta diferencia de trayectoria cambia en $λ_0$, y cada borde se mueve a la posición previamente ocupada por un borde adyacente. En consecuencia, al contar el número de franjas que pasan por un punto dado a medida que se mueve $M_1$, un observador puede medir desplazamientos diminutos que son exactos a una fracción de una longitud de onda, como lo muestra la relación
$$Δd = m\frac{λ_0}{2} \tag{10.6}$$
Ejemplo 10.5
Mediciones de distancia precisas por el interferómetro de Michelson
Se utiliza una luz láser roja de $630 nm$ de longitud de onda en un interferómetro de Michelson. Mientras se mantiene fijo el espejo $M_1$, se mueve el espejo $M_2$. Se encuentra que las franjas se mueven más allá de una cruz fija en el visor. Encuentra la distancia a la que se mueve el espejo $M_2$ para que una sola franja se mueva más allá de la línea de referencia.
Estrategia
Consulta la para la geometría. Utilizamos el resultado de la condición de interferencia del interferómetro de Michelson para encontrar la distancia recorrida, $Δd$.
Solución
Para una luz láser roja de $630 nm$ y para cada cruce de franjas ($m = 1$), la distancia recorrida por $M_2$ si mantiene $M_1$ fija es
$$Δd = m\frac{λ_0}{2} = 1 × \frac{630 nm}{2} = 315 nm = 0.315 μm$$Explicación
Una aplicación importante de esta medida es la definición del medidor estándar. La longitud del medidor estándar una vez se definió como el desplazamiento del espejo en un interferómetro de Michelson que corresponde a $1,650,763.73$ longitudes de onda de la franja particular de criptón-86 en un tubo de descarga de gas.
Ejemplo 10.6
Medición del índice de refracción de un gas
En un brazo de un interferómetro de Michelson, se coloca una cámara de vidrio con accesorios para evacuar el interior y colocar gases en él. El espacio interior del contenedor es de $2 cm$ de ancho. Inicialmente, el contenedor está vacío. A medida que el gas entra lentamente en la cámara, observas que las franjas oscuras se mueven más allá de una línea de referencia en el campo de observación. En el momento en que la cámara se llene hasta la presión deseada, habrá contado $122$ franjas que se moverán más allá de la línea de referencia. La longitud de onda de la luz utilizada es de $632.8 nm$. ¿Cuál es el índice de refracción de este gas?
Estrategia
Los $m = 122$ franjas observadas componen la diferencia entre el número de longitudes de onda que caben dentro de la cámara vacía (vacío) y el número de longitudes de onda que caben dentro de la misma cámara cuando se llena con gas. La longitud de onda en la cámara llena es más corta en un factor de $n$, el índice de refracción.
Solución
El rayo se desplaza una distancia $t = 2 cm$ hacia la derecha a través de la cámara de vidrio y otra distancia $t$ hacia la izquierda al reflexionar. El recorrido total es $L = 2t$.
Cuando está vacío, el número de longitudes de onda que caben en esta cámara es
$$N_0 = \frac{L}{λ_0} = \frac{2t}{λ_0}$$donde $λ_0 = 632.8 nm$ es la longitud de onda en el vacío de la luz utilizada. En cualquier otro medio, la longitud de onda es $λ = λ_0/n$ y el número de longitudes de onda que caben en la cámara llena de gas es
$$N = \frac{L}{λ} = \frac{2t}{λ_0/n}$$El número de franjas observadas en la transición es
$$m = N - N_0$$ $$m = \frac{2t}{λ_0/n} - \frac{2t}{λ_0}$$Despejando desde $(n - 1)$, obtenemos:
$$n - 1 = m \left(\frac{λ_0}{2t} \right) = 122 \left(\frac{632.8 × 10^{-9} m}{2(2 × 10^{-2} m)} \right) = 0.0019$$Entonces, $n = 1.0019$.
Explicación
Los índices de refracción para los gases son tan cercanos a los del vacío, que normalmente los consideramos iguales a $1$. La diferencia entre $1$ y $1.0019$ es tan pequeña que medirla requiere una técnica correspondientemente sensible, como la interferometría. No podemos, por ejemplo, esperar medir este valor utilizando técnicas basadas simplemente en la ley de Snell.
 Comprueba tu aprendizaje 10.3
Comprueba tu aprendizaje 10.3
Estrategia de resolución de problemas: la óptica de onda
Paso 1. Examina la situación para determinar que la interferencia está involucrada. Identifica si las rendijas, las películas delgadas o los interferómetros se consideran en el problema.
Paso 2. Si hay rendijas involucradas, ten en cuenta que las rejillas de difracción y las rendijas dobles producen patrones de interferencia muy similares, pero que las rejillas tienen máximos más estrechos (más afilados). Los patrones de una sola rendijas se caracterizan por un máximo central grande y máximos más pequeños a los lados.
Paso 3. Si se trata de una interferencia de película delgada o un interferómetro, toma nota de la diferencia de longitud de la trayectoria entre los dos rayos que interfieren. Asegúrate de utilizar la longitud de onda en el medio involucrado, ya que difiere de la longitud de onda en el vacío. Ten en cuenta también que hay un desplazamiento de fase $λ/2$ adicional cuando la luz se refleja en un medio con un mayor índice de refracción.
Paso 4. Identifica exactamente lo que se debe determinar en el problema (identifica las incógnitas). Una lista escrita es útil. Dibuja un diagrama de la situación. Etiquetar el diagrama es útil.
Paso 5. Haz una lista de lo que se da o se puede inferir del problema como se indica (identifica lo que se sabe).
Paso 6. Resuelve la ecuación apropiada para la cantidad a determinar (lo desconocido) e ingresa los datos conocidos. Las rendijas, rejillas y el límite de Rayleigh involucran ecuaciones.
Paso 7. Para la interferencia de película delgada, tienes una interferencia constructiva para un cambio total que es un número integral de longitudes de onda. Tienes una interferencia destructiva para un cambio total de un número de semi-integrales de longitudes de onda. Siempre ten en cuenta que la cresta a cresta es constructiva, mientras que la cresta a canal es destructiva.
Paso 8. Verifica si la respuesta es razonable: ¿Tiene sentido? Los ángulos en los patrones de interferencia no pueden ser superiores a $90°$, por ejemplo.


Imagina pasar un haz de luz monocromática a través de una abertura estrecha, una rendija un poco más ancha que la longitud de onda de la luz. En lugar de una simple sombra de la rendija en la pantalla, verás que aparece un patrón de interferencia, aunque solo haya una rendija.
En el capítulo sobre interferencias, vimos que necesitas dos fuentes de ondas para que se produzcan interferencias. ¿Cómo puede haber un patrón de interferencia cuando solo tenemos una ranura? En La naturaleza de la luz, aprendimos que, debido al principio de Huygens, podemos imaginar un frente de onda equivalente a infinitas fuentes puntuales de ondas. Por lo tanto, una onda de una rendija puede comportarse no como una onda sino como un número infinito de fuentes puntuales.
Estas ondas pueden interferir entre sí, dando como resultado un patrón de interferencia sin la presencia de una segunda rendija. Este fenómeno se llama difracción.
Otra forma de ver esto es reconocer que una ranura tiene un ancho pequeño pero finito. En el capítulo anterior, consideramos implícitamente las rendijas como objetos con posiciones pero sin tamaño. Los anchos de las rendijas se consideraron despreciables. Cuando las rendijas tienen anchos finitos, cada punto a lo largo de la abertura puede considerarse una fuente puntual de luz, una base del principio de Huygens. Debido a que los instrumentos ópticos del mundo real deben tener aperturas finitas (de lo contrario, la luz no puede entrar), la difracción juega un papel importante en la forma en que interpretamos la salida de estos instrumentos ópticos. Por ejemplo, la difracción limita nuestra capacidad para hallar imágenes u objetos. Este es un problema que estudiaremos más adelante en este capítulo.
Después de pasar a través de una abertura estrecha (rendija), una onda que se propaga en una dirección específica tiende a extenderse. Por ejemplo, las ondas de sonido que entran en una habitación a través de una puerta abierta pueden escucharse incluso si el oyente está en una parte de la habitación donde la geometría de la propagación de rayos indica que solo debe haber silencio. De manera similar, las olas oceánicas que pasan por una abertura en un rompeolas pueden extenderse por toda la bahía (). La propagación y la flexión del sonido y las ondas del océano son dos ejemplos de difracción, que es la flexión de una onda alrededor de los bordes de una abertura o un obstáculo, un fenómeno que presentan todos los tipos de ondas.

La difracción de las ondas de sonido es evidente para nosotros porque las longitudes de onda en la región audible son aproximadamente del mismo tamaño que los objetos que encuentran, una condición que debe cumplirse para que los efectos de la difracción se observen fácilmente. Dado que las longitudes de onda de la luz visible varían de aproximadamente $390$ a $770 nm$, la mayoría de los objetos no difractan la luz significativamente. Sin embargo, ocurren situaciones en las que las aberturas son lo suficientemente pequeñas como para que la difracción de la luz sea observable. Por ejemplo, si colocas tus dedos medio e índice juntos y miras a través de la abertura hacia una bombilla, puedes ver un patrón de difracción bastante claro, que consiste en líneas claras y oscuras que van paralelas a tus dedos.
La luz que pasa a través de una sola rendija forma un patrón de difracción algo diferente de los formados por rendijas dobles o rejillas de difracción, que analizamos en el capítulo sobre interferencia. La muestra un patrón de difracción de un solo corte. Ten en cuenta que el máximo central es más grande que el máximo en ambos lados y que la intensidad disminuye rápidamente en ambos lados. Por el contrario, una rejilla de difracción produce líneas espaciadas uniformemente que se atenúan lentamente a cada lado del centro.
El análisis de la difracción de una sola rendija se ilustra en la . Aquí, la luz llega a la rendija, iluminándola uniformemente y está en fase a lo ancho. Luego consideramos que la luz se propaga hacia adelante desde diferentes partes de la misma rendija. De acuerdo con el principio de Huygens, cada parte del frente de onda en la rendija emite wavelets, como discutimos en el capítulo sobre la naturaleza de la luz. Estos son como rayos que comienzan en fase y se dirigen en todas direcciones (cada rayo es perpendicular al frente de onda de una wavelet). Suponiendo que la pantalla está muy lejos en comparación con el tamaño de la rendija, los rayos que se dirigen hacia un destino común son casi paralelos. Cuando viajan en línea recta, como en la parte (a) de la figura, permanecen en fase y observamos un máximo central. Sin embargo, cuando los rayos viajan en un ángulo con respecto a la dirección original del haz, cada rayo se desplaza a una distancia diferente de una ubicación común, y pueden llegar dentro o fuera de la fase. En la parte (b), el rayo desde la parte inferior recorre una distancia de una longitud de onda $λ$ más lejos que el rayo desde la parte superior. Por lo tanto, un rayo desde el centro recorre una distancia $λ/2$ menor que la del borde inferior de la rendija, llega fuera de fase e interfiere destructivamente. Un rayo ligeramente por encima del centro y otro ligeramente por encima del fondo también se cancelan entre sí. De hecho, cada rayo de la rendija interfiere destructivamente con otro rayo. En otras palabras, una cancelación por pares de todos los rayos se traduce en un mínimo oscuro de intensidad en este ángulo. Por simetría, otro mínimo ocurre en el mismo ángulo a la derecha de la dirección del incidente (hacia la parte inferior de la figura) de la luz.
En el ángulo mayor que se muestra en la parte (c), las longitudes de la trayectoria difieren en $3λ/2$ para los rayos desde la parte superior e inferior de la rendija. Un rayo recorre una distancia $λ$ diferente del rayo desde la parte inferior y llega en fase, interfiriendo constructivamente. Dos rayos, cada uno ligeramente por encima de esos dos, también se agregan constructivamente.
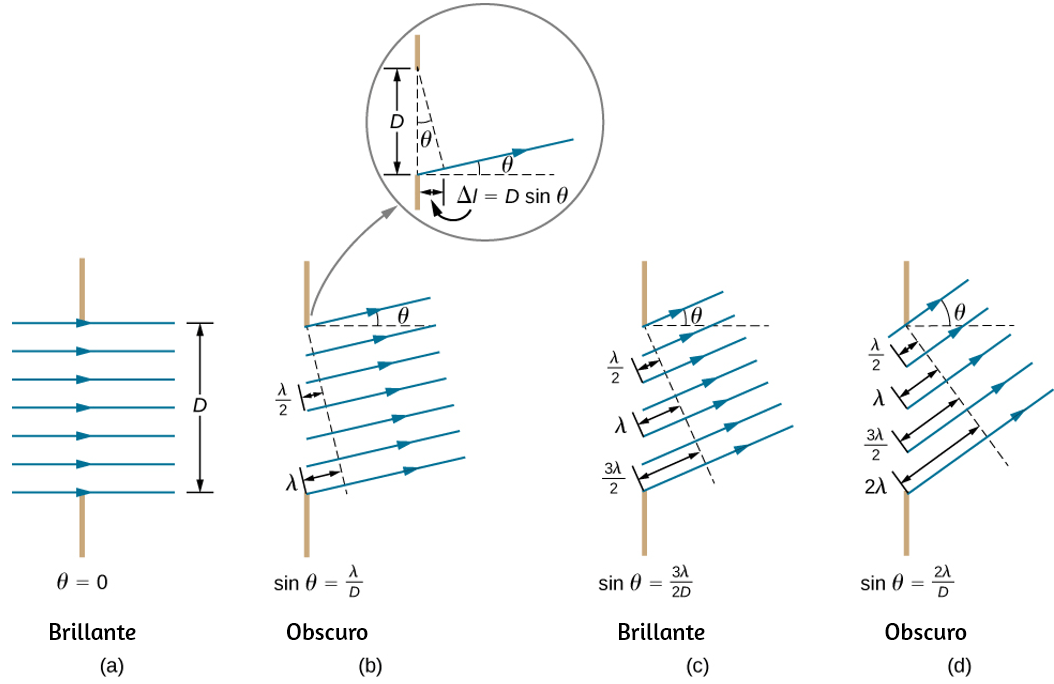
La mayoría de los rayos de la rendija tienen otro para interferir constructivamente, y se produce un máximo de intensidad en este ángulo. Sin embargo, no todos los rayos interfieren constructivamente en esta situación, por lo que el máximo no es tan intenso como el máximo central. Finalmente, en la parte (d), el ángulo mostrado es lo suficientemente grande como para producir un segundo mínimo. Como se ve en la figura, la diferencia en la longitud del recorrido para los rayos desde cualquier lado de la rendija es $Dsenθ$, y vemos que se obtiene un mínimo destructivo cuando esta distancia es un múltiplo integral de la longitud de onda.
Por lo tanto, para obtener interferencia destructiva para una sola rendija,
donde $D$ es el ancho de la ranura, $λ$ es la longitud de onda de la luz, $θ$ es el ángulo relativo a la dirección original de la luz, y m es el orden del mínimo. La muestra un gráfico de intensidad para la interferencia de una sola rendija, y es evidente que los máximos a cada lado del máximo central son mucho menos intensos y no tan anchos. Este efecto se explora en la difracción de doble rendija.
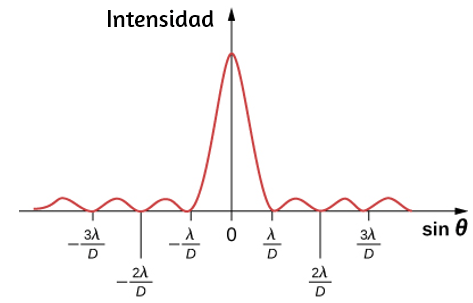
Ejemplo 10.1
Cálculo de la difracción de una sola rendija
La luz visible de longitud de onda de $550 nm$ cae sobre una sola rendija y produce su segundo mínimo de difracción en un ángulo de $45.0°$ con respecto a la dirección incidente de la luz, como se muestra en la (a) ¿Cuál es el ancho de la rendija? (b) ¿En qué ángulo se produce el primer mínimo?
Estrategia
A partir de la información dada, y asumiendo que la pantalla está lejos de la rendija, podemos usar la ecuación $Dsenθ = mλ$ primero para encontrar $D$, y nuevamente para encontrar el ángulo para el primer mínimo $θ_1$.
Solución
a. Se nos da que $λ = 550 nm$, $m = 2$, y $θ_2 = 45.0°$. Resolviendo la ecuación $Dsenθ = mλ$ para $D$ y sustituyendo los valores conocidos se obtiene
$$D = \frac{mλ}{senθ_2} = \frac{2(550 nm)}{sin45.0°} = \frac{1100 × 10^{-9} m}{0.707} = 1.56 × 10^{-6} m$$b. Resolviendo la ecuación $Dsenθ = mλ$ para $senθ_1$ y sustituyendo los valores conocidos, obtenemos:
$$senθ_1 = \frac{mλ}{D} = \frac{1(550 × 10^{-9} m)}{1.56 × 10^{-6} m}$$Así, el ángulo $θ_1$ es
$$θ_1 = sen^{-1}0.354 = 20.7°$$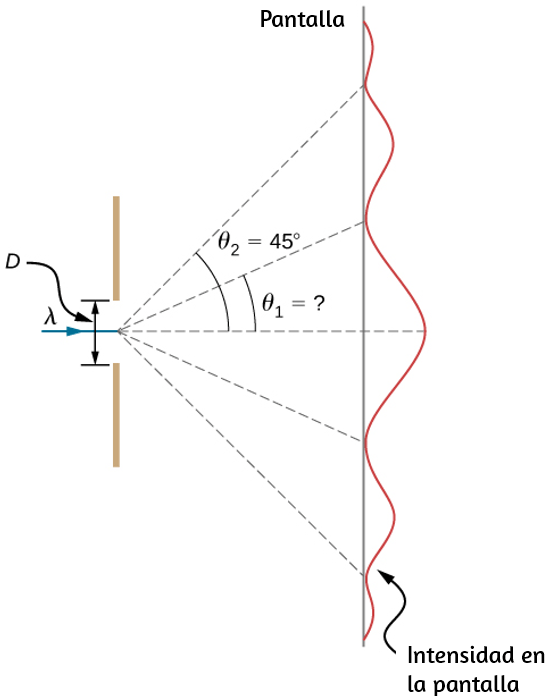
Explicación
Vemos que la rendija es estrecha (es solo unas pocas veces mayor que la longitud de onda de la luz). Esto es consistente con el hecho de que la luz debe interactuar con un objeto de tamaño comparable a su longitud de onda para exhibir efectos de onda significativos como este patrón de difracción de una sola rendija. También vemos que el máximo central se extiende $20.7°$ a cada lado del haz original, para un ancho de aproximadamente $41°$. El ángulo entre el primer y segundo mínimo es de solo $24°$ ($45.0° - 20.7°$). Por lo tanto, el segundo máximo es solo la mitad de ancho que el máximo central.
 Comprueba tu aprendizaje 11.1
Comprueba tu aprendizaje 11.1
La siguiente escena interactiva, diseñada por Daniel V. Schroeder, muestra la difracción de ondas por una sola rendija. El ancho de la abertura es controlado por el control deslizante. Inicialmente, las ondas se muestran en blanco y negro (escala de grises), y tanto los picos como los valles son blancos. El negro indica una amplitud cero. Alternativamente, puedes cambiar a un esquema de color rojo y azul, en el que las crestas de las ondas se muestran en rojo y los valles en azul, con el negro aún indicando una amplitud cero. Tenga en cuenta que la amplitud de la onda no disminuye con la distancia desde la fuente, como lo haría para las ondas físicas.
Para calcular la intensidad del patrón de difracción, seguimos el método del fasor utilizado para los cálculos con circuitos de CA en circuitos de corriente alterna. Si consideramos que hay fuentes $N$ Huygens a través de la rendija que se muestra en la , con cada fuente separada por una distancia $D/N$ de sus vecinos adyacentes, la diferencia de trayectoria entre las ondas de las fuentes adyacentes que llegan al punto arbitrario $P$ en la pantalla es $(D/N)senθ$. Esta distancia es equivalente a una diferencia de fase de $(2πD/λN)senθ$. El diagrama de fasores para las ondas que llegan al punto cuya posición angular es $θ$ se muestra en la .
La amplitud del fasor para cada wavelet de Huygens es $ΔE_0$, la amplitud del fasor resultante es $E$, y la diferencia de fase entre las wavelets desde la primera y la última fuente es
$$φ = (2π/λ)Dsenθ$$Con $N → ∞$, el diagrama fasor se aproxima a un arco circular de longitud $NΔE_0$ y radio $r$. Dado que la longitud del arco es $NΔE_0$ para cualquier $φ$, el radio $r$ del arco debe disminuir a medida que $φ$ aumenta (o de manera equivalente, ya que los fasores forman espirales más firmes).
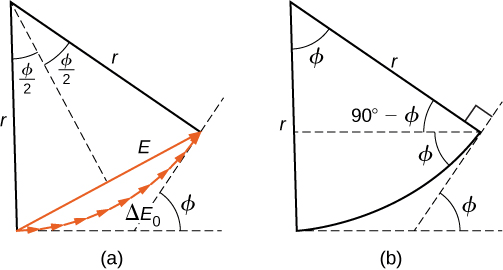
El diagrama de fasores para $φ = 0$ (el centro del patrón de difracción) se muestra en la (a) usando $N = 30$.
En este caso, los fasores se colocan de extremo a extremo en una línea recta de longitud $NΔE_0$, el radio $r$ va al infinito y la resultante tiene su valor máximo $E = NΔE_0$. La intensidad de la luz se puede obtener utilizando la relación $I = \frac{1}{2}cε_0E^2$ de Ondas electromagnéticas. La intensidad del máximo es entonces.
$$I_0 = \frac{1}{2}cε_0(NΔE_0)^2 = \frac{1}{2μ_0c}(NΔE_0)^2$$donde $ε_0 = 1/μ_0c^2$. Los diagramas de fasores para los dos primeros ceros del patrón de difracción se muestran en las partes (b) y (d) de la figura. En ambos casos, los fasores se suman a cero, después de rotar a través de $φ = 2π rad$ para $m = 1$ y $4π rad$ para $m = 2$.
Los siguientes dos máximos más allá de los máximos centrales están representados por los diagramas fasoriales de las partes (c) y (e). En la parte (c), los fasores han girado a través de $φ = 3π rad$ y han formado un fasor resultante de magnitud $E_1$. La longitud del arco formado por los fasores es $NΔE_0$. Como esto corresponde a $1.5$ rotaciones alrededor de un círculo de diámetro $E_1$, tenemos
$$\frac{3}{2}πE_1 ≈ NΔE_0$$ $$E_1 = \frac{2NΔE_0}{3π}$$Además, $I_1 = \dfrac{1}{2μ_0c}E_1^2 = \dfrac{4(NΔE_0)^2}{(9π)(2μ_0)^2} ≈ 0.045I_0$
Donde, $I_0 = \dfrac{(NΔE_0)^2}{2μ_0c}$
En la parte (e), los fasores han girado a través de $φ = 5π rad$, correspondientes a $2.5$ rotaciones alrededor de un círculo de diámetro $E_2$ y longitud de arco $NΔE_0$. Esto resulta en $I_2 ≈ 0.016I_0$. La prueba se deja como un ejercicio para el estudiante.
Estos dos máximos corresponden en realidad a valores de $φ$ ligeramente menores que $3π rad$ y $5π rad$. Como la longitud total del arco del diagrama fasorial es siempre $NΔE_0$, el radio del arco disminuye a medida que aumenta. Como resultado, $E_1$ y $E_2$ resultan ser un poco más grandes para los arcos que no se han curvado completamente a través de $3π rad$ y $5π rad$, respectivamente. Los valores exactos de $φ$ para los máximos se investigan en el Ejercicio 11.1. Al resolver ese problema, encontrarás que son menos que, pero muy cerca de, $φ = 3π, 5π, 7π, ... rad$.
Para calcular la intensidad en un punto arbitrario $P$ en la pantalla, volvemos al diagrama de fasores de la . Dado que el arco subtiende un ángulo en el centro del círculo,
$$NΔE_0 = rφ$$y
$$sen \left(\frac{φ}{2} \right) = \frac{E}{2r}$$donde $E$ es la amplitud del campo resultante. Resolviendo la segunda ecuación para $E$ y luego sustituyendo $r$ de la primera ecuación, encontramos
$$E = 2rsen\frac{φ}{2} = 2\frac{NΔE_0}{φ}sen\frac{φ}{2}$$Ahora definiendo
obtenemos
Esta ecuación relaciona la amplitud del campo resultante en cualquier punto del patrón de difracción con la amplitud $NΔE_0$ en el máximo central. La intensidad es proporcional al cuadrado de la amplitud, por lo que
donde $I_0 = (NΔE_0)^2/2μ_0c$ es la intensidad en el centro del patrón.
Para el máximo central, $φ = 0$, $β$ también es cero y vemos en la regla de l’Hôpital que $\lim_{β \to 0}(senβ/β) = 1$, por lo que $\lim_{φ \to 0}I = I_0$. Para el siguiente máximo, $φ = 3π rad$, tenemos $β = 3π/2 rad$ y cuando se sustituye en la Ecuación 11.4, se obtiene
$$I_1 = I_0 \left(\frac{sen3π/2}{3π/2} \right)^2 ≈ 0.045I_0$$de acuerdo con lo que encontramos anteriormente en esta sección utilizando los diámetros y circunferencias de los diagramas de fasores. Sustituyendo $φ = 5π rad$ en la ecuación 11.4 se obtiene un resultado similar para $I_2$.
Una gráfica de la Ecuación 11.4 se muestra en la y debajo de ella una fotografía de un patrón de difracción real. Observa que el pico central es mucho más brillante que los otros, y que los ceros del patrón están ubicados en aquellos puntos donde $senβ = 0$, lo que ocurre cuando $β = mπ rad$. Esto corresponde a
$$\frac{πDsenθ}{λ} = mπ$$o
$$Dsenθ = mλ$$que es la ecuación 11.1.
Ejemplo 11.2
Intensidad en la difracción de una sola rendija
La luz de $550 nm$ de longitud de onda pasa a través de una rendija de ancho de $2.00 μm$ y produce un patrón de difracción similar al que se muestra en la . (a) Encuentra las ubicaciones de los dos primeros mínimos en términos del ángulo desde el máximo central y (b) determina la intensidad relativa al máximo central en un punto a medio camino entre estos dos mínimos.
Estrategia
Los mínimos están dados por la Ecuación 11.1, $Dsenθ = mλ$. Los primeros dos mínimos son para $m = 1$ y $m = 2$. La ecuación 11.4 y la ecuación 11.2 se pueden usar para determinar la intensidad una vez que se haya encontrado el ángulo.
Solución
a. Al resolver la ecuación 11.1 para $θ$ nos da $θ_m = sen^{-1}(mλ/D)$, de modo que
$$θ_1 = sen^{-1} \left(\frac{(+1)(550 × 10^{-9} m)}{2.00 × 10^{-6} m} \right) = +16.0°$$ $$θ_2 = sen^{-1} \left(\frac{(+2)(550 × 10^{-9} m)}{2.00 × 10^{-6} m} \right) = +33.4°$$b. El punto medio entre $θ_1$ y $θ_2$ es
$$θ = (θ_1 + θ_2)/2 = (16.0° + 33.4°)/2 = 24.7°$$A partir de la ecuación 11.4, podemos calcular
$$\frac{I}{I_0} = (\frac{senβ}{β})^2 = (\frac{sen(4.77)}{4.77})^2 = (\frac{-0.9985}{4.77})^2 = 0.044$$Explicación
Esta posición, a mitad de camino entre dos mínimos, está muy cerca de la ubicación del máximo, esperada cerca de $β = 3π/2$, o $1.5π$.
 Comprueba tu aprendizaje 11.2
Comprueba tu aprendizaje 11.2
Si se varía el ancho $D$ de la rendija, la distribución de intensidad cambia, como se ilustra en la . El pico central se distribuye en la región desde $senθ = -λ/D$ a $senθ = +λ/D$. Para $θ$ pequeño, esto corresponde a un ancho angular $Δθ ≈ 2λ/D$. Por lo tanto, un aumento en el ancho de la ranura da como resultado una disminución en el ancho del pico central. Para una rendija con $D>>λ$, el pico central es muy agudo, mientras que si $D ≈ λ$, se vuelve bastante ancho.
Walter Fendt nos presenta la siguiente escena interactiva, en la cual puedes practicar para diferentes anchos de rendija, ángulos, máximos y mínimos. Puedes observar el patrón de difracción o el perfil de la intensidad de difracción.
En este otra escena interactiva, diseñada por Juan Guillermo Rivera Berrío, puedes modificar el longitud de onda ($λ$) y el ancho de la rendija ($D$), para modificar el perfil de intensidad de la difracción.
Cuando estudiamos la interferencia en el experimento de doble rendija de Young, ignoramos el efecto de difracción en cada rendija. Asumimos que las rendijas eran tan estrechas que en la pantalla solo se veía la interferencia de la luz de solo dos fuentes puntuales. Si la rendija es más pequeña que la longitud de onda, la (b) y (c) muestra que no puedes ignorar la difracción. En esta sección, estudiaremos las complicaciones del experimento de doble rendija que surgen cuando también debes tener en cuenta el efecto de difracción de cada rendija.
Para calcular el patrón de difracción para dos (o cualquier número de) rendijas, necesitamos generalizar el método que acabamos de usar para una sola rendija. Es decir, a través de cada rendija, colocamos una distribución uniforme de fuentes puntuales que irradian wavelets de Huygens, y luego sumamos las wavelets de todas las rendijas. Esto le da la intensidad en cualquier punto de la pantalla. Aunque los detalles de ese cálculo pueden ser complicados, el resultado final es bastante simple:
Patrón de difracción de dos rendijas
El patrón de difracción de dos rendijas de ancho $D$ que están separadas por una distancia $d$ es el patrón de interferencia de dos fuentes puntuales separadas por $d$ multiplicado por el patrón de difracción de una rendija de ancho $D$.
En otras palabras, las ubicaciones de las franjas de interferencia vienen dadas por la ecuación $dsenθ = mλ$, igual que cuando consideramos que las rendijas eran fuentes puntuales, pero las intensidades de las franjas ahora se reducen por efectos de difracción, de acuerdo con la Ecuación 11.4.
Tenga en cuenta que en el capítulo sobre interferencia, escribimos $dsenθ = mλ$ y usamos el entero m para referirnos a las franjas de interferencia. La ecuación 11.1 también usa m, pero esta vez para referirse a los mínimos de difracción. Si ambas ecuaciones se usan simultáneamente, es una buena práctica usar una variable diferente (como $n$) para uno de estos enteros para mantenerlos distintos.
Los efectos de interferencia y difracción operan simultáneamente y generalmente producen mínimos en diferentes ángulos. Esto da lugar a un patrón complicado en la pantalla, en el que faltan algunos de los máximos de interferencia de las dos rendijas si el máximo de la interferencia es en la misma dirección que el mínimo de la difracción.
Nos referimos a un pico faltante como un orden perdido. En la se muestra un ejemplo de un patrón de difracción en la pantalla. La línea continua con múltiples picos de varias alturas es la intensidad observada en la pantalla. Es un producto del patrón de interferencia de ondas provenientes de cortes separados y la difracción de ondas dentro de un corte.
Ejemplo 11.3
Intensidad de las franjas
La muestra que la intensidad de la franja para $m = 3$ es cero, pero ¿qué pasa con las otras franjas? Calcula la intensidad de la franja en $m = 1$ en relación con $I_0$, la intensidad del pico central.
Estrategia
Determina el ángulo para la franja de interferencia de doble rendija, usando la ecuación de Interferencia, luego determina la intensidad relativa en esa dirección debido a la difracción usando la Ecuación 1.4.
Solución
Por el capítulo sobre interferencia, sabemos que las franjas de interferencia brillantes se producen en $dsenθ = mλ$, o
$$senθ = \frac{mλ}{d}$$De la ecuación 11.4,
$$I = I_0 \left(\frac{senβ}{β} \right)^2, donde β = \frac{φ}{2} = \frac{πDsenθ}{λ}$$Sustituyendo,
$$β = \frac{πDsenθ}{λ} = \frac{πD}{λ} \cdot \frac{mλ}{d} = \frac{mπD}{d}$$Para $D = 2λ$, $d = 6λ$, y $m = 1$,
$$β = \frac{(1)π(2λ)}{6λ} = \frac{π}{3}$$Entonces, la intensidad es
$$I = I_0(senβ/β)^2 = I_0(sen(π/3)/π/3)^2 = 0.684I_0$$Explicación
Observa que este enfoque es relativamente sencillo y da un resultado que es casi exactamente el mismo que el análisis más complicado que usa fasores para calcular los valores de intensidad de la interferencia de doble rendija (línea delgada en la ). El enfoque de fasor explica la pendiente descendente en la intensidad de difracción (línea azul), de modo que el pico cerca de $m = 1$ se produce a un valor de $θ$ un poco más pequeño de lo que hemos mostrado aquí.
Ejemplo 11.4
Difracción de dos rendijas
Supongamos que en el experimento de Young, las ranuras de ancho de $0.020 mm$ están separadas por $0.20 mm$. Si las rendijas están iluminadas por una luz monocromática de $500 nm$ de longitud de onda, ¿cuántas franjas brillantes se observan en el pico central del patrón de difracción?
Solución
De la ecuación 11.1, la posición angular del primer mínimo de difracción es
$$θ ≈ senθ = \frac{λ}{d} = \frac{5.0 × 10^{-7} m}{2.0 × 10^{-5} m} = 2.5 × 10^{-2} rad$$Usando $dsenθ = mλ$ para $θ = 2.5 × 10^{-2} rad$, encontramos
$$m = \frac{dsenθ}{λ} = \frac{(0.20 mm)(2.5 × 10^{-2} rad)}{5.0 × 10^{-7} m} = 10$$que es el orden de interferencia máximo que cabe dentro del pico central. Notamos que para $m = ± 10$ faltan órdenes ya que $θ$ coincide exactamente. En consecuencia, observamos franjas brillantes para
para un total de 19 flecos brillantes.
 Comprueba tu aprendizaje 11.3
Comprueba tu aprendizaje 11.3
Finalmente, explora esta escena interactiva de Science Sims at CCNY
El análisis de la interferencia de la luz que pasa a través de dos rendijas establece el marco teórico de la interferencia y nos da una visión histórica de los experimentos de Thomas Young. Sin embargo, la mayoría de las aplicaciones modernas de la interferencia de rendijas utilizan no solo dos rendijas sino muchas, acercándose al infinito con propósitos prácticos. El elemento óptico clave se denomina rejilla de difracción, una herramienta importante en el análisis óptico.
El análisis de la interferencia de múltiples rendijas en la interferencia nos permite considerar qué sucede cuando el número de rendijas $N$ se acerca al infinito. Recuerda que los máximos secundarios $N – 2$ aparecen entre los máximos principales. Podemos ver que habrá un número infinito de máximos secundarios que aparecerán, y un número infinito de franjas oscuras entre ellos. Esto hace que el espaciado entre las franjas, y por lo tanto el ancho de los máximos, sea infinitesimalmente pequeño. Además, debido a que la intensidad de los máximos secundarios es proporcional a $1/N^2$, se aproxima a cero, por lo que ya no se ven los máximos secundarios. Lo que queda son solo los máximos principales, ahora muy brillantes y muy estrechos ().
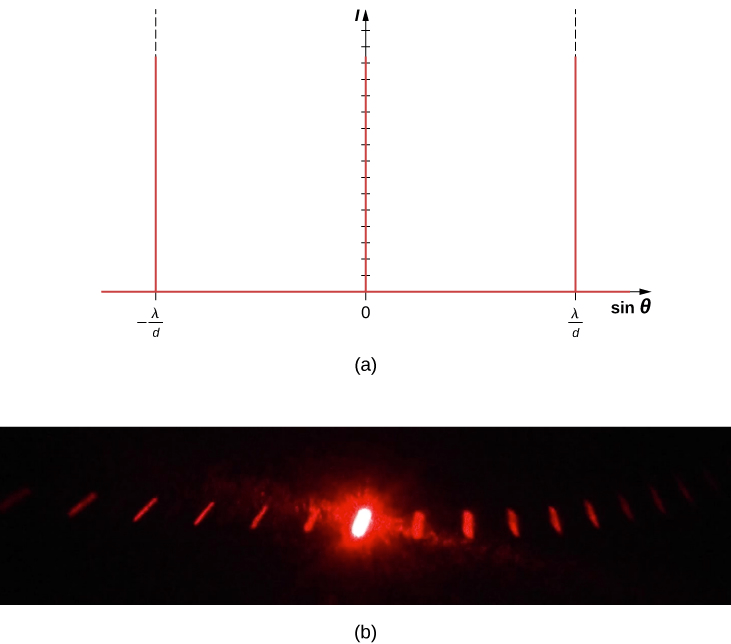
En realidad, el número de rendijas no es infinito, pero puede ser muy grande, lo suficientemente grande como para producir el efecto equivalente. Un buen ejemplo es un elemento óptico llamado rejilla de difracción. Se puede fabricar una rejilla de difracción tallando vidrio con una herramienta afilada en un gran número de líneas paralelas colocadas con precisión, con regiones intactas que actúan como rendijas (). Este tipo de rejilla se puede producir fotográficamente en masa y no de forma económica. Debido a que puede haber más de $1000$ líneas por milímetro a través de la rejilla, cuando un rayo entrante ilumina una sección tan pequeña como unos pocos milímetros, el número de rendijas iluminadas es efectivamente infinito, lo que proporciona máximos principales muy definidos.
Las rejillas de difracción funcionan tanto para la transmisión de luz, como en la . Las redes de difracción natural también ocurren en las plumas de ciertas aves como el colibrí. Las pequeñas estructuras similares a dedos en patrones regulares actúan como rejillas de reflexión, produciendo una interferencia constructiva que da a las plumas colores no solo debido a su pigmentación. Esto se llama iridiscencia.
¿Dónde se utilizan las rejillas de difracción en las aplicaciones? Las rejillas de difracción se utilizan comúnmente para la dispersión espectroscópica y el análisis de la luz. Lo que las hace particularmente útiles es el hecho de que forman un patrón más nítido que las ranuras dobles. Es decir, sus franjas brillantes son más estrechas y brillantes, mientras que sus regiones oscuras son más oscuras. Las rejillas de difracción son componentes clave de los monocromadores utilizados, por ejemplo, en imágenes ópticas de longitudes de onda particulares de muestras biológicas o médicas. Se puede elegir una rejilla de difracción para analizar específicamente una longitud de onda emitida por moléculas en células enfermas en una muestra de biopsia o para ayudar a excitar moléculas estratégicas en la muestra con una longitud de onda de luz seleccionada. Otro uso vital es en tecnologías de fibra óptica donde las fibras están diseñadas para proporcionar un rendimiento óptimo en longitudes de onda específicas. Hay disponible una gama de rejillas de difracción para seleccionar las longitudes de onda para dicho uso.

Ejemplo 11.5
Cálculo de los efectos típicos de la rejilla de difracción
Las rejillas de difracción con $10,000$ líneas por centímetro están fácilmente disponibles. Supongamos que tienes uno y envías un haz de luz blanca a una pantalla a $2 m$ de distancia. (a) Encuentra los ángulos para la difracción de primer orden de las longitudes de onda más cortas y largas de la luz visible ($380$ y $760 nm$, respectivamente). (b) ¿Cuál es la distancia entre los extremos del arco iris de luz visible producida en la pantalla para la interferencia de primer orden? (Ver .)
Estrategia
Una vez que se ha determinado un valor para el espaciado de la rendija de la rejilla de difracción, los ángulos para las líneas agudas se pueden encontrar usando la ecuación
$$dsenθ = mλ, \; \textsf{para} \; m = 0, ± 1, ± 2, ...$$Como hay $10,000$ líneas por centímetro, cada línea está separada por $1/10,000$ de un centímetro. Una vez que conocemos los ángulos, podemos encontrar las distancias a lo largo de la pantalla mediante el uso de trigonometría simple.
Solución
a. La distancia entre rendijas es $d = (1 cm)/10,000 = 1.00 × 10^{-4}cm$ o $1.00 × 10^{-6} m$. Llamemos a los dos ángulos $θ_V$ para violeta ($380 nm$) y $θ_R$ para rojo ($760 nm$). Resolviendo la ecuación $dsenθ_V = mλ$ para $senθ_V$,
$$senθ_V = \frac{mλ_V}{d}$$donde $m = 1$ para el primer orden y $λ_V = 380 nm = 3.80 × 10^{-7} m$. Sustituyendo estos valores, obtenemos:
$$senθ_V = \frac{3.80 × 10^{-7} m}{1.00 × 10^{-6} m} = 0.380$$Así, el ángulo $θ_V$ es
$$θ_V = sen^{-1}0.380 = 22.33°$$Similarmente,
$$senθ_R = \frac{7.6 × 10^{-7} m}{1.00 × 10^{-6} m} = 0.760$$Así, el ángulo $θ_R$ es
$$θ_R = sen^{-1}0.760 = 49.46°$$Observa que en ambas ecuaciones, informamos los resultados de estos cálculos intermedios a cuatro cifras significativas para usarlas en el cálculo de la parte (b).
b. Las distancias en la pantalla de seguridad están etiquetadas como $y_V$ e $y_R$ en la . Observa que $tanθ = y/x$. Podemos resolver para $y_V$ e $y_R$. Es decir,
$$y_V = xtanθ_V = (2.00 m)(tan 22.33°) = 0.815 m$$y
$$y_R = xtanθ_R = (2.00 m)(tan 49.46°) = 2.338 m$$La distancia entre ellos es por lo tanto
$$y_R - y_V = 1.523 m$$Explicación
La gran distancia entre los extremos rojo y violeta del arco iris producido a partir de la luz blanca indica el potencial que tiene esta rejilla de difracción como herramienta espectroscópica. Cuanto más puedas extender las longitudes de onda (mayor dispersión), más detalles se pueden ver en un espectro. Esto depende de la calidad de la rejilla de difracción: debe hacerse de manera muy precisa además de tener líneas muy espaciadas.
 Comprueba tu aprendizaje 11.4
Comprueba tu aprendizaje 11.4
Explora esta escena interactiva de Science Sims at CCNY en la página siguiente. Aumenta el número de rendijas $N$, los picos primarios se vuelven más nítidos, cuando alcanzas el número máximo de $N$, el sistema se está comportando de manera muy similar a una rejilla de difracción.
La luz difracta a medida que se mueve a través del espacio, doblándose alrededor de los obstáculos, interfiriendo constructivamente y destructivamente. Puede usarse como una herramienta espectroscópica, por ejemplo, una rejilla de difracción dispersa la luz según la longitud de onda y se utiliza para producir espectros, pero la difracción también limita el detalle que podemos obtener en las imágenes.
La (a) muestra el efecto de pasar la luz a través de una pequeña abertura circular. En lugar de un punto brillante con bordes afilados, obtenemos un punto con un borde difuso rodeado de círculos de luz. Este patrón es causado por la difracción, similar al producido por una sola rendija. La luz de diferentes partes de la abertura circular interfiere constructiva y destructivamente. El efecto es más notorio cuando la apertura es pequeña, pero el efecto también existe para aperturas grandes.
¿Cómo afecta la difracción al detalle que se puede observar cuando la luz pasa a través de una abertura? La (b) muestra el patrón de difracción producido por dos fuentes de luz puntual que están cerca una de la otra. El patrón es similar al de una fuente puntual única, y aún es posible decir que hay dos fuentes de luz en lugar de una. Si están más cerca, como en la (c), no podemos distinguirlos, limitando así los detalles o la resolución que podemos obtener. Este límite es una consecuencia ineludible de la naturaleza ondulatoria de la luz.
La difracción limita la resolución en muchas situaciones. La agudeza de nuestra visión es limitada porque la luz pasa a través de la pupila, que es la abertura circular del ojo. Observa que la difusión de la luz, similar a la difracción, se debe al diámetro limitado de un haz de luz, no a la interacción con una abertura.

Por lo tanto, la luz que pasa a través de una lente con un diámetro $D$ muestra este efecto y se propaga, difuminando la imagen, al igual que la luz que pasa a través de una abertura de diámetro $D$. Por lo tanto, la difracción limita la resolución de cualquier sistema que tenga una lente o espejo. Los telescopios también están limitados por difracción, debido al diámetro finito $D$ del espejo primario.
¿Cuál es el límite? Para responder a esa pregunta, considera el patrón de difracción para una abertura circular, que tiene un máximo central que es más ancho y más brillante que los máximos que lo rodean (similar a una hendidura) ( (a)). Se puede demostrar que, para una abertura circular de diámetro $D$, el primer mínimo en el patrón de difracción se produce en $1.22λ/D$ (siempre que la apertura sea grande en comparación con la longitud de onda de la luz, como es el caso de la mayoría de los instrumentos ópticos). El criterio aceptado para determinar el límite de difracción a la resolución basado en este ángulo se conoce como el criterio de Rayleigh, que fue desarrollado por Lord Rayleigh en el siglo XIX.
Criterio de rayleigh
El límite de difracción a la resolución indica que dos imágenes solo se pueden resolver cuando el centro del patrón de difracción de una está directamente sobre el primer mínimo del patrón de difracción de la otra ( (b)).
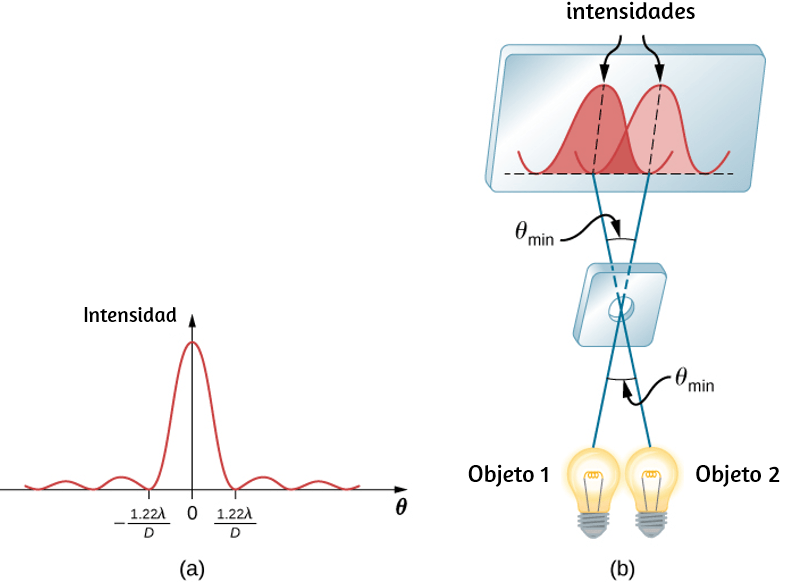
El primer mínimo está en un ángulo de $θ = 1.22λ/D$, de modo que dos objetos puntuales solo pueden resolverse si están separados por el ángulo
donde $λ$ es la longitud de onda de la luz (u otra radiación electromagnética) y $D$ es el diámetro de la abertura, lente, espejo, etc., con el que se observan los dos objetos. En esta expresión, $θ$ tiene unidades de radianes. Este ángulo también se conoce comúnmente como el límite de difracción.
Todos los intentos de observar el tamaño y la forma de los objetos están limitados por la longitud de onda. Incluso la pequeña longitud de onda de la luz prohíbe la precisión exacta. Cuando se utilizan sondas de longitud de onda extremadamente pequeñas, como con un microscopio electrónico, el sistema se ve perturbado, lo que limita nuestro conocimiento. El principio de incertidumbre de Heisenberg afirma que este límite es fundamental e ineludible.
Ejemplo 11.6
Cálculo de los límites de difracción del telescopio espacial Hubble
El espejo primario del Telescopio Espacial Hubble en órbita tiene un diámetro de $2.40 m$. Al estar en órbita, este telescopio evita los efectos degradantes de la distorsión atmosférica en su resolución. (a) ¿Cuál es el ángulo entre dos fuentes de luz puntuales de resolución justa (quizás dos estrellas)? Supongamos una longitud de onda de luz promedio de $550 nm$. (b) Si estas dos estrellas están a una distancia de 2 millones de años luz, que es la distancia de la galaxia de Andrómeda, ¿qué tan juntas pueden estar y aún estar resueltas? (Un año luz, o $ly$, es la distancia que recorre la luz en 1 año).
Estrategia
El criterio de Rayleigh establecido en la Ecuación 4.5, $θ = 1.22λ/D$, da el ángulo más pequeño posible entre las fuentes puntuales, o la mejor resolución posible. Una vez que se conoce este ángulo, podemos calcular la distancia entre las estrellas, ya que se nos da lo lejos que están.
Solución
a. El criterio de Rayleigh para el ángulo de resolución mínimo es
$$θ = 1.22\frac{λ}{D}$$Ingresando los valores conocidos, obtenemos:
$$θ = 1.22\frac{550 × 10^{-9} m}{2.40 m} = 2.80 × 10^{-7} rad$$b. La distancia $s$ entre dos objetos a una distancia $r$ y separados por un ángulo $θ$ es $s = rθ$.
Ingresando los valores conocidos, obtenemos:
$$s = (2.0 × 10^6 ly)(2.80 × 10^{-7} rad) = 0.56 ly$$Explicación
El ángulo que se encuentra en la parte (a) es extraordinariamente pequeño (menos de $1/50,000$ de grado), porque el espejo primario es muy grande en comparación con la longitud de onda de la luz. Como se notó, los efectos de difracción son más notables cuando la luz interactúa con objetos que tienen tamaños del orden de la longitud de onda de la luz. Sin embargo, el efecto todavía está allí, y hay un límite de difracción a lo observable. La resolución real del telescopio Hubble no es tan buena como la que se encuentra aquí. Al igual que con todos los instrumentos, hay otros efectos, como no uniformidades en espejos o aberraciones en lentes que limitan aún más la resolución. Sin embargo, la da una indicación de la extensión de los detalles observables con el Hubble debido a su tamaño y calidad, y especialmente porque está por encima de la atmósfera de la Tierra.


La respuesta en la parte (b) indica que se pueden resolver dos estrellas separadas por aproximadamente medio año luz. La distancia promedio entre las estrellas en una galaxia es del orden de cinco años luz en las partes externas y alrededor de un año luz cerca del centro galáctico. Por lo tanto, el Hubble puede resolver la mayoría de las estrellas individuales en la galaxia de Andrómeda, aunque se encuentra a una distancia tan enorme que su luz tarda 2 millones de años en llegar a nosotros. La muestra otro espejo utilizado para observar las ondas de radio del espacio exterior.
 Comprueba tu aprendizaje 11.5
Comprueba tu aprendizaje 11.5
La difracción no es solo un problema para los instrumentos ópticos sino también para la radiación electromagnética en sí. Cualquier haz de luz que tenga un diámetro $D$ finito y una longitud de onda $λ$ exhibe difracción de difusión. El haz se extiende con un ángulo dado por la ecuación $11.5, θ = 1.22λ/D$. Toma, por ejemplo, un rayo láser hecho de rayos lo más paralelos posible (ángulos entre los rayos tan cerca de $θ = 0°$ como sea posible) en su lugar se extiende en un ángulo $θ = 1.22λ/D$, donde $D$ es el diámetro del haz y $λ$ es su longitud de onda. Esta propagación es imposible de observar para una linterna porque su haz no es muy paralelo para empezar. Sin embargo, para la transmisión a larga distancia de rayos láser o señales de microondas, la difusión por difracción puede ser significativa (). Para evitar esto, podemos aumentar $D$. Esto se hace para la luz láser enviada a la luna para medir su distancia de la Tierra. El haz láser se expande a través de un telescopio para hacer que $D$ sea mucho más grande y más pequeño.
En la mayoría de los laboratorios de biología, la resolución es un problema cuando se introduce el uso del microscopio. Cuanto menor sea la distancia x por la cual dos objetos se pueden separar y aún se ven como distintos, mayor será la resolución. El poder de resolución de una lente se define como esa distancia $x$. Una expresión para hallar la potencia se obtiene del criterio de Rayleigh. La (a) muestra dos objetos puntuales separados por una distancia $x$. Según el criterio de Rayleigh, la resolución es posible cuando la separación angular mínima es
$$θ = 1.22\frac{550 × 10^{-9} m}{2.40 m} = \frac{x}{d}$$donde $d$ es la distancia entre el espécimen y la lente objetivo, y hemos utilizado la aproximación de ángulo pequeño (es decir, hemos asumido que $x$ es mucho más pequeño que $d$), de modo que $tanθ ≅ senθ ≅ θ$. Por lo tanto, la potencia de resolución es
$$x = 1.22\frac{λd}{D}$$Otra forma de ver esto es mediante el concepto de apertura numérica ($NA$, siglas en inglés), que es una medida del ángulo de aceptación máximo en el que una lente tomará luz y aún la contendrá dentro de la lente. La (b) muestra una lente y un objeto en el punto $P$. La $NA$ aquí es una medida de la capacidad de la lente para reunir luz y resolver detalles finos. El ángulo subtendido por la lente en su enfoque se define como $θ = 2α$. A partir de la figura y nuevamente usando la aproximación de ángulo pequeño, podemos escribir
$$senα = \frac{D/2}{d} = \frac{D}{2d}$$La $NA$ para una lente es $NA = nsenα$, donde $n$ es el índice de refracción del medio entre la lente objetivo y el objeto en el punto $P$. De esta definición para $NA$, podemos ver que
$$x = 1.22\frac{λd}{D} = 1.22\frac{λ}{2senα} = 0.61\frac{λn}{NA}$$
En un microscopio, $NA$ es importante porque se relaciona con la potencia de resolución de una lente. Una lente con una $NA$ grande es capaz de resolver detalles más finos. Las lentes con NA más grande también pueden recolectar más luz y así dar una imagen más brillante. Otra forma de describir esta situación es que cuanto mayor sea el $NA$, mayor será el cono de luz que se puede introducir en la lente, por lo que se recopilan más modos de difracción. Por lo tanto, el microscopio tiene más información para formar una imagen clara y su poder de resolución es mayor.
Una de las consecuencias de la difracción es que el punto focal de un haz tiene una distribución finita de ancho e intensidad. Imagina el enfoque cuando solo se considera la óptica geométrica, como en la figura (a). El punto focal se considera como un punto infinitamente pequeño con una intensidad enorme y la capacidad de incinerar la mayoría de las muestras, independientemente de la $NA$ de la lente objetivo, una simplificación excesiva y no física. Para la óptica de onda, debido a la difracción, tenemos en cuenta el fenómeno en el que el punto focal se propaga para convertirse en un punto focal ( (b)) con la disminución del tamaño del punto al aumentar la $NA$. En consecuencia, la intensidad en el punto focal aumenta con el aumento de $NA$. Cuanto mayor sea la $NA$, mayores serán las posibilidades de fotodegradar la muestra. Sin embargo, el enfoque nunca se convierte en un verdadero punto.
En un tipo diferente de microscopio, las moléculas dentro de un espécimen están hechas para emitir luz a través de un mecanismo llamado fluorescencia. Al controlar las moléculas que emiten luz, es posible construir imágenes con una resolución mucho más precisa que el criterio de Rayleigh, evitando así el límite de difracción. El desarrollo de la microscopía de fluorescencia súper resuelta llevó al Premio Nobel de Química en 2014.
Dado que los fotones de rayos X son muy energéticos, tienen longitudes de onda relativamente cortas, del orden de $10^{-8}$ a $10^{-12} m.$ Por lo tanto, los fotones de rayos X típicos actúan como rayos cuando se encuentran con objetos macroscópicos, como rayos, y producen sombras nítidas. Sin embargo, dado que los átomos tienen un tamaño de $0.1 nm$, los rayos X se pueden usar para detectar la ubicación, la forma y el tamaño de los átomos y las moléculas. El proceso se denomina difracción de rayos X e implica la interferencia de los rayos X para producir patrones que pueden analizarse para obtener información sobre las estructuras que dispersaron los rayos X.
Quizás el ejemplo más famoso de difracción de rayos X sea el descubrimiento de la estructura de doble hélice del ADN en 1953 por un equipo internacional de científicos que trabajan en el Laboratorio Cavendish de Inglaterra: el estadounidense James Watson, el inglés Francis Crick y el nacido en Nueva Zelanda Maurice Wilkins. Utilizando los datos de difracción de rayos X producidos por Rosalind Franklin, fueron los primeros en modelar la estructura de doble hélice del ADN que es tan crucial para la vida. Por este trabajo, Watson, Crick y Wilkins recibieron el Premio Nobel de Fisiología o Medicina de 1962 (existe cierto debate y controversia sobre el tema de que Rosalind Franklin no fue incluida en el premio, aunque murió en 1958, antes de que se otorgara el premio).

La muestra un patrón de difracción producido por la dispersión de rayos X de un cristal. Este proceso se conoce como cristalografía de rayos X debido a la información que puede proporcionar acerca de la estructura cristalina, y fue el tipo de datos que Rosalind Franklin proporcionó a Watson y Crick para el ADN. Los rayos X no solo confirman el tamaño y la forma de los átomos, sino que también proporcionan información sobre los arreglos atómicos en los materiales. Por ejemplo, una investigación más reciente en superconductores de alta temperatura involucra materiales complejos cuyas disposiciones de celosía son cruciales para obtener un material superconductor. Estos pueden ser estudiados utilizando cristalografía de rayos X.
Históricamente, la dispersión de los rayos X de los cristales se usó para probar que los rayos X son ondas electromagnéticas (EM). Esto se sospechaba desde el momento en que se descubrieron los rayos X en 1895, pero no fue hasta 1912 que el alemán Max von Laue (1879–1960) convenció a dos de sus colegas a dispersar los rayos X de los cristales. Si se obtiene un patrón de difracción, razonó, entonces los rayos X deben ser ondas, y su longitud de onda podría determinarse (el espaciado de los átomos en varios cristales era razonablemente bien conocido en ese momento, basado en los buenos valores para el número de Avogadro). Los experimentos fueron convincentes, y el Premio Nobel de Física de 1914 fue otorgado a von Laue por su sugerencia que condujo a la prueba de que los rayos X son ondas EM. En 1915, el único equipo de padre e hijo de Sir William Henry Bragg y su hijo Sir William Lawrence Bragg recibieron un Premio Nobel conjunto por inventar el espectrómetro de rayos X y la nueva ciencia del análisis de rayos X.
En formas que recuerdan a la interferencia de película delgada, consideramos dos ondas planas en longitudes de onda de rayos X, cada una reflejándose en un plano diferente de átomos dentro de la red del cristal, como se muestra en la . Desde la geometría, la diferencia en la longitud de las rutas es $2dsenθ$. La interferencia constructiva se produce cuando esta distancia es un múltiplo entero de la longitud de onda. Esta condición es capturada por la ecuación de Bragg,
donde $m$ es un entero positivo y $d$ es el espaciado entre los planos. Siguiendo la Ley de Reflexión, tanto las ondas incidentes como las reflejadas se describen con el mismo ángulo, pero a diferencia de la práctica general en la óptica geométrica, se mide con respecto a la superficie en sí, en lugar de la normal.
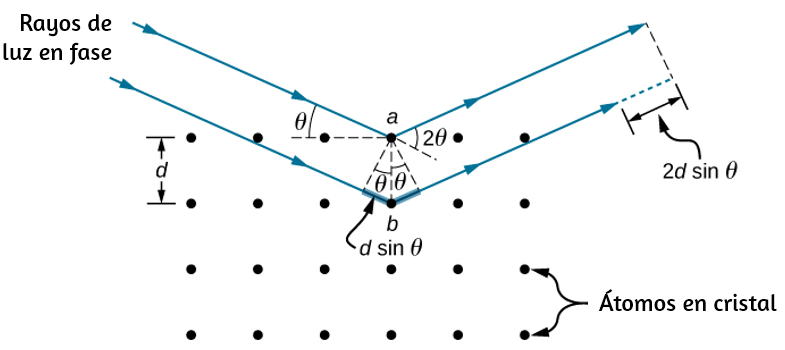
Ejemplo 11.7
Difracción de rayos X con cristales de sal
La sal de mesa común se compone principalmente de cristales de NaCl. En un cristal de NaCl, hay una familia de planos separados por $0.252 nm$. Si se observa el máximo de primer orden en un ángulo de incidencia de $18.1°$, ¿cuál es la longitud de onda de la dispersión de rayos X de este cristal?
Estrategia
Usa la ecuación de Bragg, ecuación $11.6$, $mλ = 2dsenθ$, para hallar $θ.$
Solución
Para el primer orden, $m = 1$, el espaciado plano $d$ es conocido. Resolviendo la ecuación de Bragg para la longitud de onda
Explicación
La longitud de onda determinada se ajusta dentro de la región de rayos X del espectro electromagnético. Una vez más, la naturaleza de onda de la luz se hace prominente cuando la longitud de onda ($λ = 0.157 nm$) es comparable al tamaño de las estructuras físicas ($d = 0.252 nm$) con las que interactúa.
 Comprueba tu aprendizaje 11.6
Comprueba tu aprendizaje 11.6
Aunque la muestra un cristal como una matriz bidimensional de centros de dispersión para simplificar, los cristales reales son estructuras en tres dimensiones. La dispersión puede ocurrir simultáneamente desde diferentes familias de planos en diferentes orientaciones y patrones de espaciado conocidos como planos Bragg, como se muestra en la . El patrón de interferencia resultante puede ser bastante complejo.
A continuación, presentamos una unidad didáctica del Proyecto Un_100, diseñada por Víctor Hugo García Jarillo, la cual consta de cuatro apartados. En el primero (Motivación), se presenta un video donde se muestra en que tipos de investigación se utiliza la difracción de Bragg. En el segundo (Inicio), se dará una descripción de las propiedades físicas de los rayos X y se mostrará la forma en que se producen, se muestran los tipos de estructura de los materiales en 3d de cristales utilizados para la difracción de rayos X, tales como el NaCl. El tercer apartado (Desarrollo), se dará una explicación de cómo se obtiene la ley de bragg mostrando un diagrama y analizando cómo es la interferencia de ondas, pudiendo generar con una interacción interferencias constructivas y destructivas y, finalmente, en el cuarto paratado (Cierre), se verifica la ley de Bragg mediante una interacción en la cual se podrá modificar la longitud de onda del rayo incidente, la distancia entre planos de un cristal y el ángulo de incidencia del rayo X.
Un holograma, como el de la , es una verdadera imagen tridimensional grabada en una película mediante láser. Los hologramas se utilizan para la diversión; Decoración de artículos novedosos y portadas de revistas; seguridad en tarjetas de crédito y licencias de conducir (se necesita un láser y otro equipo para reproducirlas), y para el almacenamiento de información tridimensional. Puedes ver que un holograma es una verdadera imagen tridimensional porque los objetos cambian de posición relativa en la imagen cuando se ven desde diferentes ángulos.

El nombre de holograma significa "imagen completa" (del holo griego, como en holístico) porque la imagen es tridimensional. La holografía es el proceso de producir hologramas y, aunque están grabados en una película fotográfica, el proceso es bastante diferente de la fotografía normal. La holografía utiliza interferencias de luz u óptica de ondas, mientras que la fotografía normal utiliza ópticas geométricas.
La muestra un método para producir un holograma. La luz coherente de un láser se divide por un espejo, con parte de la luz que ilumina el objeto. El resto, llamado haz de referencia, brilla directamente sobre una película. La luz dispersada desde el objeto interfiere con el haz de referencia, produciendo interferencia constructiva y destructiva.
Como resultado, la película expuesta se ve borrosa, pero un examen detallado revela un patrón de interferencia complicado almacenado en él. Donde la interferencia fue constructiva, la película (un negativo en realidad) se oscurece. La holografía a veces se denomina fotografía sin lentes, porque utiliza las características de onda de la luz, en contraste con la fotografía normal, que utiliza ópticas geométricas y requiere lentes.
La luz que cae sobre un holograma puede formar una imagen tridimensional del objeto original. El proceso es complicado en detalle, pero los conceptos básicos pueden entenderse, como se muestra en la , en la que ahora se utiliza un láser del mismo tipo que la película expuesta para iluminarla.
Las miles de pequeñas regiones expuestas de la película son oscuras y bloquean la luz, mientras que las regiones menos expuestas permiten que la luz pase. La película actúa así como una colección de rejillas de difracción con varios patrones de espaciado. La luz que pasa a través del holograma se difracta en varias direcciones, produciendo imágenes reales y virtuales del objeto utilizado para exponer la película. El patrón de interferencia es el mismo que el producido por el objeto. Mover tu ojo a varios lugares en el patrón de interferencia te brinda diferentes perspectivas, al igual que mirar directamente al objeto. La imagen se ve así como el objeto y es tridimensional como el objeto.
El holograma ilustrado en la es un holograma de transmisión. Los hologramas que se ven con luz reflejada, como los hologramas de luz blanca en las tarjetas de crédito, son hologramas de reflexión y son más comunes. Los hologramas de luz blanca a menudo aparecen un poco borrosos con los bordes del arco iris, porque los patrones de difracción de varios colores de luz se encuentran en ubicaciones ligeramente diferentes debido a sus diferentes longitudes de onda. Otros usos de la holografía incluyen todos los tipos de almacenamiento de información tridimensional, como estatuas en museos, estudios de ingeniería de estructuras e imágenes de órganos humanos.
Inventado a fines de la década de 1940 por Dennis Gabor (1900–1970), quien ganó el Premio Nobel de Física de 1971 por su trabajo, la holografía se volvió mucho más práctica con el desarrollo del láser. Dado que los láseres producen una luz de longitud de onda única coherente, sus patrones de interferencia son más pronunciados. La precisión es tan grande que incluso es posible grabar numerosos hologramas en una sola película simplemente cambiando el ángulo de la película para cada imagen sucesiva. Así es como se producen los hologramas que se mueven al caminar por ellos, una especie de película sin lentes. De manera similar, en el campo de la medicina, los hologramas han permitido exhibiciones holográficas tridimensionales completas de objetos de una pila de imágenes. Almacenar estas imágenes para uso futuro es relativamente fácil. Con el uso de un endoscopio, se pueden hacer imágenes holográficas tridimensionales de alta resolución de los órganos y tejidos internos.
Terminamos con esta unidad didáctica interactiva del proyecto @prende.mx, en la cual se describe cómo hacer la ilusión de un holograma con la técnica de la reflexión.
Aceleración angular. Tasa de cambio de la velocidad angular con respecto al tiempo
Aceleración angular instantánea. Derivada de la velocidad angular con respecto al tiempo.
Aceleración lineal total. Suma vectorial del vector de aceleración centrípeta y el vector de aceleración tangencial.
Brazo de palanca. Distancia de la perpendicular a la línea en la que se encuentra el vector de fuerza sobre un eje dado.
Cinemática del movimiento rotacional. Describe las relaciones entre el ángulo de rotación, la velocidad angular, la aceleración angular y el tiempo.
Densidad de masa lineal. La masa por unidad de longitud λ de un objeto unidimensional.
Densidad de masa superficial. Masa por unidad de área σ de un objeto bidimensional.
Dinámica de rotación. Análisis del movimiento de rotación utilizando el torque neto y el momento de inercia para encontrar la aceleración angular.
Eje paralelo. Eje de rotación que es paralelo a un eje alrededor del cual se conoce el momento de inercia de un objeto.
Energía cinética rotacional. Energía cinética debida a la rotación de un objeto; Esto es parte de su energía cinética total.
Esfuerzo de torsión. Producto cruz de una fuerza y un brazo de palanca a un eje dado.
La segunda ley de Newton para la rotación. La suma de los pares de torsión en un sistema giratorio es igual a su momento de inercia multiplicado por su aceleración angular.
Momento de inercia. Masa rotatoria de cuerpos rígidos que se relaciona con lo fácil o difícil que será cambiar la velocidad angular del cuerpo rígido giratorio.
Posición angular. Ángulo de un cuerpo que ha girado en un sistema de coordenadas fijo
Teorema de la energía de trabajo para la rotación. El trabajo de rotación total realizado en un cuerpo rígido es igual al cambio en la energía cinética de rotación del cuerpo.
Teorema de los ejes paralelos. Si el momento de inercia es conocido para un eje dado, se puede encontrar para cualquier eje paralelo a él.
Trabajo rotativo. El trabajo realizado en un cuerpo rígido debido a la suma de los pares de torsión integrados sobre el ángulo a través del cuerpo giratorio.
Velocidad angular . Tasa de cambio de la posición angular con respecto al tiempo.
Velocidad angular instantánea. Derivada de la posición angular con respecto al tiempo.
Ley de conservación del momento angular. El momento angular se conserva, es decir, el momento angular inicial es igual al momento angular final cuando no se aplica un par externo al sistema.
Momento angular. Análogo rotacional del momento lineal, encontrado al tomar el producto del momento de inercia y la velocidad angular.
Movimiento de rodadura. Combinación de movimiento de rotación y traslación con o sin deslizamiento.
Precesión. Movimiento circular del polo del eje de un objeto giratorio alrededor de otro eje debido a un torque.
Centro de gravedad. Punto donde se adjunta el vector de peso.
Comportamiento plástico. El material se deforma de manera irreversible, no vuelve a su forma y tamaño originales cuando se quita la carga y el esfuerzo desaparece.
Compresibilidad. Recíproco del módulo de volumen.
Deformación. Cantidad sin dimensiones que da la cantidad de deformación de un objeto o medio bajo esfuerzo.
Deformación a cortante. Deformación causada por el esfuerzo cortante.
Deformación por tracción. Deformación por esfuerzo de tracción, dado como un cambio fraccional en la longitud, que ocurre cuando las fuerzas estiran un objeto, causando su alargamiento.
Diagrama esfuerzo-deformación. Gráfico que muestra la relación entre el esfuerzo y la deformación, característica de un material.
Elástico. Objeto que vuelve a su tamaño y forma originales cuando la carga ya no está presente.
Esfuerzo. Cantidad que contiene información sobre la magnitud de la fuerza que causa la deformación, definida como fuerza por unidad de área.
Esfuerzo a compresión. Esfuerzo que se produce cuando las fuerzas contraen un objeto, lo que provoca su acortamiento.
Esfuerzo a granel. Esfuerzo que genera un cambio fraccional en el volumen.
Esfuerzo cortante. Esfuerzo causado por fuerzas de corte.
Esfuerzo de rotura (esfuerzo final). Valor del esfuerzo en el punto de fractura o rotura.
Esfuerzo masivo. Esfuerzo causado por fuerzas de compresión, en todas las direcciones.
Equilibrio. El cuerpo está en equilibrio cuando sus aceleraciones lineales y angulares son cero respecto a un marco de referencia inercial.
Equilibrio estático. El cuerpo está en equilibrio estático cuando está en reposo en nuestro marco de referencia inercial seleccionado.
Límite elástico. Valor de esfuerzo más allá del cual el material ya no se comporta elásticamente y se deforma permanentemente.
Límite de linealidad (límite de proporcionalidad). Mayor valor de esfuerzo más allá del cual el esfuerzo ya no es proporcional a la deformación.
Módulo de Young. Módulo elástico para esfuerzos de tracción o compresión.
Módulo elástico. Proporcionalidad constante en relación lineal entre esfuerzo y deformación, en pascales en el SI.
Módulo de corte. Módulo elástico para el esfuerzo cortante.
Módulo volumétrico. Módulo elástico para el esfuerzo a granel o por volumen.
Pascal. Unidad de esfuerzo del SI, unidad de presión del SI.
Presión. Fuerza de presión en la dirección normal en una superficie por área de superficie.
Presión normal. Presión de una atmósfera, sirve como nivel de referencia para la presión.
Primera condición de equilibrio. Expresa equilibrio traslacional; todas las fuerzas externas que actúan sobre el cuerpo se equilibran y su suma vectorial es cero.
Segunda condición de equilibrio. Expresa equilibrio rotacional; todos los torques debidos a fuerzas externas que actúan sobre el cuerpo se equilibran y su suma vectorial es cero.
Torque gravitacional. Torsión en el cuerpo causada por su peso; ocurre cuando el centro de gravedad del cuerpo no está ubicado en el eje de rotación.
Densidad. Masa por unidad de volumen de una sustancia u objeto.
Ecuación de Bernoulli. Ecuación resultante de aplicar la conservación de energía a un fluido incompresible sin fricción: $p + \frac{1}{2}ρv^2 + ρgh = constante$, en todo el fluido.
Equilibrio hidrostático. Estado en el que el agua no fluye, o es estática.
Fuerza de flotación. Fuerza neta hacia arriba sobre cualquier objeto en cualquier fluido debido a la diferencia de presión a diferentes profundidades.
Fluidos. Líquidos y gases; Un fluido es un estado de materia que cede a fuerzas de cizallamiento.
Fluido ideal. Fluido con viscosidad despreciable.
Flujo laminar. Tipo de flujo de fluido en el que las capas no se mezclan.
Flujo turbulento. Tipo de flujo en el que las capas se mezclan a través de remolinos,
Gravedad específica. Relación de la densidad de un objeto a un fluido (generalmente agua).
Numero de reynolds. Parámetro adimensional que puede revelar si un flujo particular es laminar o turbulento.
Prensa hidráulica. Máquina simple que utiliza cilindros de diferentes diámetros para distribuir la fuerza.
Presión manométrica. Presión relativa a la presión atmosférica.
Presión absoluta. Suma de presión manométrica y presión atmosférica.
Principio de Arquímedes. La fuerza de flotación sobre un objeto es igual al peso del fluido que desplaza.
Principio de Bernoulli. La ecuación de Bernoulli aplicada a profundidad constante:
$$p_1 + \frac{1}{2}ρv_1^2 = p_2 + \frac{1}{2}ρv_2^2$$Principio de Pascal. El cambio en la presión aplicada a un fluido cerrado se transmite sin disminuir a todas las porciones del fluido y a las paredes de su recipiente.
La ley de Poiseuille. Tasa de flujo laminar de un fluido incompresible en un tubo: $Q = \frac{(p_2 - p_1)πr^4}{8ηl}$.
Tasa de flujo o caudal. Abreviada $Q$, es el volumen $V$ que fluye más allá de un punto particular durante un tiempo $t$, o $Q = dV/dt$.
Viscosidad. Medida de la fricción interna en un fluido.
Amplitud ($A$). Desplazamiento máximo desde la posición de equilibrio de un objeto que oscila alrededor de la posición de equilibrio.
Cambio de fase. Ángulo, en radianes, que se utiliza en una función coseno o seno para desplazar la función hacia la izquierda o hacia la derecha, que se utiliza para hacer coincidir la función con las condiciones iniciales de los datos.
Constante del resorte ($k$). Característica de un resorte que se define como la relación entre la fuerza aplicada al resorte y el desplazamiento causado por la fuerza.
Energía potencial elástica. Energía potencial almacenada como resultado de la deformación de un objeto elástico, como el estiramiento de un resorte.
Frecuencia ($f$). Cantidad de eventos por unidad de tiempo.
Frecuencia angular natural. Frecuencia angular de un sistema oscilante en el MAS.
Fuerza restauradora. Fuerza que actúa en oposición a la fuerza causada por una deformación.
Movimiento armónico simple (MAS). Movimiento oscilatorio en un sistema donde la fuerza restauradora es proporcional al desplazamiento, que actúa en la dirección opuesta al desplazamiento.
Movimiento periódico. Movimiento que se repite a intervalos de tiempo regulares.
Oscilación crítica. Condición en la que la amortiguación de un oscilador hace que regrese lo más rápido posible a su posición de equilibrio sin oscilar hacia atrás y hacia adelante sobre esta posición.
Oscilación. Fluctuación simple de una cantidad, o fluctuaciones repetidas y regulares de una cantidad, entre dos valores extremos alrededor de un valor de equilibrio o promedio.
Oscilador armónico simple. Un dispositivo que oscila en MAS donde la fuerza restauradora es proporcional al desplazamiento y actúa en la dirección opuesta al desplazamiento.
Período ($T$). Tiempo necesario para completar una oscilación.
Péndulo físico. Cualquier objeto extendido que se balancea como un péndulo.
Péndulo simple. Punto de masa, llamado péndulo bob, unido a una cuerda casi sin masa.
Péndulo torsional. Cualquier objeto suspendido que oscile girando su suspensión.
Posición de equilibrio. Posición donde el resorte no está estirado ni comprimido.
Punto de equilibrio estable. Punto donde la fuerza neta en un sistema es cero, pero un pequeño desplazamiento de la masa causará una fuerza restauradora que apunta hacia el punto de equilibrio.
Resonancia. Oscilaciones de gran amplitud en un sistema producido por una fuerza impulsora de amplitud pequeña, que tiene una frecuencia igual a la frecuencia natural.
Sobreamortiguado. Condición en la que la amortiguación de un oscilador hace que vuelva al equilibrio sin oscilar; el oscilador se mueve más lentamente hacia el equilibrio que en el sistema críticamente amortiguado.
Antinodo. Ubicación de la máxima amplitud en ondas estacionarias.
Armónico. Frecuencia que produce ondas estacionarias y es más alta que la frecuencia fundamental.
Condición de frontera libre. Existe cuando el medio en el límite es libre de moverse.
Ecuación de onda lineal. Ecuación que describe ondas que resultan de una fuerza de restauración lineal del medio; cualquier función que sea una solución a la ecuación de onda describe una onda que se mueve en la dirección $x$ positiva o la dirección $x$ negativa con una velocidad de onda constante $v$.
Frecuencia fundamental. La frecuencia más baja que producirá una onda estacionaria.
Función de onda. Modelo matemático de la posición de las partículas del medio.
Intensidad ($I$). Potencia por unidad de área.
Interferencia. Superposición de dos o más ondas en el mismo punto y tiempo.
Interferencia constructiva. Cuando dos ondas llegan al mismo punto exactamente en fase; es decir, las crestas de las dos ondas están alineadas con precisión, al igual que los canales.
Interferencia destructiva. Cuando dos ondas idénticas llegan al mismo punto exactamente fuera de fase; es decir, se alinea de forma precisa la cresta a través de la condición de límite fijo cuando el medio en un límite se fija en su lugar para que no pueda moverse.
Longitud de onda. Distancia entre partes idénticas adyacentes de una onda.
Modo normal. Posible patrón de onda estacionaria en una cuerda.
Nodo. Punto donde la cuerda no se mueve; más generalmente, los nodos son donde la perturbación de la onda es cero en una onda estacionaria.
Número de onda. $\frac{2π}{λ}$.
Onda. Alteración que se desplaza desde su origen y transporta energía.
Onda estacionaria. Onda que puede rebotar hacia adelante y hacia atrás a través de una región en particular, convirtiéndose efectivamente en estacionaria.
Onda longitudinal. Onda en la que la perturbación es paralela a la dirección de propagación.
Onda mecánica. Onda que se rige por las leyes de Newton y requiere un medio.
Onda transversal. Onda en la que la perturbación es perpendicular a la dirección de propagación.
Pulso. Una sola perturbación que se mueve a través de un medio, transfiriendo energía pero no masa.
Rapidez de onda. Magnitud de la velocidad de la onda.
Superposición. Fenómeno que ocurre cuando dos o más ondas llegan al mismo punto.
Velocidad de onda. Velocidad a la que se mueve la perturbación; También llamada la velocidad de propagación.
Armónico. El término usado para referirse colectivamente a la frecuencia fundamental y sus connotaciones.
Armónicos. Todas las frecuencias de resonancia superiores a la fundamental.
Audición. Percepción del sonido.
Desplazamiento Doppler. Cambio real en la frecuencia debido al movimiento relativo de la fuente y el observador.
Efecto Doppler Alteración en la frecuencia observada de un sonido debido al movimiento de la fuente o del observador.
Estampido supersónico. Ruido fuerte que se produce como una onda de choque a medida que se desplaza por el suelo.
Frecuencia de latido. Frecuencia de latidos producidos por ondas de sonido que difieren en frecuencia.
Fundamental. La resonancia de frecuencia más baja.
Fonio. Unidad numérica de sonoridad.
Latidos. Interferencia constructiva y destructiva de dos o más frecuencias de sonido.
Nivel de intensidad de sonido. Cantidad sin unidades que te indica el nivel del sonido en relación con un estándar fijo.
Notas. Unidad básica de música con nombres específicos, combinada para generar melodías.
Onda de choque. Frente de onda que se produce cuando una fuente de sonido se mueve más rápido que la velocidad del sonido.
Sonar. Onda de presión viajera que puede ser periódica; La onda se puede modelar como una onda de presión o como una oscilación de moléculas.
Timbre. Número e intensidad relativa de múltiples frecuencias de sonido.
Tono. Percepción de la frecuencia de un sonido.
Transductor. Dispositivo que convierte la energía de una señal en una forma de energía medible, por ejemplo, un micrófono convierte las ondas de sonido en una señal eléctrica.
Volumen. Percepción de la intensidad del sonido.
Ángulo crítico. Angulo incidente que produce un ángulo de refracción de $90°$.
Ángulo de Brewster. Ángulo de incidencia en el que la luz reflejada está completamente polarizada.
Birrefringente. Se refiere a los cristales que dividen un haz de luz no polarizado en dos haces.
Dirección de polarización. Dirección paralela al campo eléctrico para las ondas EM.
Dispersión. Difundir la luz en su espectro de longitudes de onda.
Ley de Brewster. $tanθ_b = \frac{n_2}{n_1}$, donde $n_1$ es el medio en el que se desplaza la luz incidente y es reflejada y $n_2$ es el índice de refracción del medio que forma la interfaz que refleja la luz.
Reflector de esquina. Objeto que consta de dos (o tres) superficies reflectantes mutuamente perpendiculares, de modo que la luz que entra se refleja exactamente paralela a la dirección desde la que vino.
Fibra óptica. Campo de estudio de la transmisión de la luz a través de fibras de plástico o vidrio, aplicando el principio de reflexión total interna.
Índice de refracción. Para un material, la relación de la velocidad de la luz en el vacío a la del material.
Ley de Malus. Donde $I_0$ es la intensidad de la onda polarizada antes de pasar por el filtro.
Ley de reflexión. Ángulo de reflexión es igual al ángulo de incidencia.
Ley de refracción. Cuando un rayo de luz cruza de un medio a otro, cambia de dirección en una cantidad que depende del índice de refracción de cada medio y los senos del ángulo de incidencia y el ángulo de refracción.
Óptica de onda. Parte de la óptica que trata el aspecto de onda de la luz.
Óptica geométrica. Parte de la óptica que trata el aspecto del rayo de luz.
Polarización. Atribuye que las oscilaciones de onda tienen una dirección definida con respecto a la dirección de propagación de la onda.
Polarizado. Se refiere a las ondas que tienen las oscilaciones del campo eléctrico y magnético en una dirección definida.
Polarizado horizontalmente. Las oscilaciones están en un plano horizontal.
Polarizado verticalmente. Las oscilaciones están en un plano vertical.
Principio de Huygens. Cada punto en un frente de onda es una fuente de ondas que se extienden en la dirección hacia adelante a la misma velocidad que la onda misma. El nuevo frente de onda es un plano tangente a todas las wavelets.
Rayo. Línea recta que se origina en algún punto.
Reflexión total interna. Fenómeno en el límite entre dos medios de manera que toda la luz se refleja y no se produce refracción.
Refracción. Cambio de dirección de un rayo de luz cuando pasa a través de variaciones en la materia.
Sin polarizar. Se refiere a ondas que son polarizadas al azar.
Aberración. Distorsión en una imagen causada por desviaciones desde la aproximación de ángulo pequeño.
Aberración esférica. Distorsión en la imagen formada por un espejo esférico cuando los rayos no están todos enfocados en el mismo punto.
Acomodamiento. Uso de los músculos ciliares para ajustar la forma de la lente del ojo para enfocar objetos cercanos o lejanos.
Ampliación angular. Relación entre el ángulo subtendido por un objeto observado con una lupa y el observado a simple vista.
Aproximación de ángulo pequeño. Aproximación que es válida cuando el tamaño de un espejo esférico es significativamente más pequeño que el radio del espejo; en esta aproximación, la aberración esférica es despreciable y el espejo tiene un punto focal bien definido.
Aproximación de lente delgada. Suponiendo que la lente es muy delgada en comparación con la primera distancia de la imagen.
Aumento. Relación entre el tamaño de la imagen y el tamaño del objeto.
Aumento lineal. Relación entre la altura de la imagen y la altura del objeto.
Aumento neto. Aumento del microscopio compuesto. Es el producto del aumento lineal del objetivo y el aumento angular del ocular.
Coma. Similar a la aberración esférica, pero surge cuando los rayos entrantes no son paralelos al eje óptico.
Diseño de Cassegrain. La disposición de un objetivo y un ocular de tal manera que el espejo cóncavo que recoge la luz tiene un agujero en el medio, y la luz incide en la lente de un ocular.
Diseño newtoniano. La disposición de un objetivo y un ocular de modo que la luz enfocada del espejo cóncavo se reflejará en un lado del tubo en un ocular.
Dispositivo de carga acoplada (CCD). Chip semiconductor que convierte una imagen de luz en pequeños píxeles que se pueden convertir en señales electrónicas de color e intensidad.
Distancia de la imagen. Distancia de la imagen al eje central del elemento óptico que produce la imagen.
Distancia del objeto. Distancia del objeto al eje central del elemento óptico que produce su imagen.
Eje óptico. Eje alrededor del cual el espejo es rotacionalmente simétrico; Puedes girar el espejo sobre este eje sin cambiar nada.
Espejo cóncavo. Espejo esférico con su superficie reflectante en el lado interno de la esfera; El espejo forma una “cueva”.
Espejo convexo. Espejo esférico con su superficie reflectante en el lado exterior de la esfera.
Espejo curvo. Espejo formado por una superficie curva, como esférica, elíptica o parabólica.
Espejo plano. Superficie de reflexión plana.
Hipermetropía. Defecto visual en el que los objetos cercanos aparecen borrosos porque sus imágenes están enfocadas detrás de la retina en lugar de hacerlo en la retina; una persona con visión lejana puede ver objetos lejanos claramente, pero los objetos cercanos aparecen borrosos.
Imagen real. Imagen que puede proyectarse en una pantalla porque los rayos atraviesan físicamente la imagen.
Imagen virtual. Imagen que no se puede proyectar en una pantalla porque los rayos no atraviesan físicamente la imagen, solo parecen originarse en la imagen.
Lente convergente (o convexa). Lente en la que los rayos de luz que ingresan en paralelo convergen en un solo punto en el lado opuesto.
Lente divergente (o cóncava). Lente que hace que los rayos de luz se desvíen de su eje óptico.
Longitud focal. Distancia a lo largo del eje óptico desde el punto focal hasta el elemento óptico que enfoca los rayos de luz.
Lupa simple (o lupa). Lente convergente que produce una imagen virtual de un objeto que se encuentra dentro de la distancia focal de la lente.
Microscopio compuesto. Microscopio construido a partir de dos lentes convexas, la primera que sirve como ocular y la segunda que sirve como lente objetivo.
Miopía. Defecto visual en el que los objetos lejanos aparecen borrosos porque sus imágenes están enfocadas delante de la retina; una persona miope puede ver claramente los objetos cercanos pero los objetos lejanos aparecen borrosos.
Objetivo. Lente más cercana al objeto que está siendo examinado.
Ocular. Lente o combinación de lentes en un instrumento óptico más cercano al ojo del observador.
Plano focal. Plano que contiene el punto focal y es perpendicular al eje óptico.
Potencia óptica ($P$). Inverso de la distancia focal de una lente, con la distancia focal expresada en metros. La potencia óptica $P$ de una lente se expresa en unidades de dioptrías $D$; es decir, $1D = 1/m = 1m^{-1}$
Primer enfoque o enfoque de objeto. El objeto ubicado en este punto dará como resultado una imagen creada en el infinito en el lado opuesto de una interfaz esférica entre dos medios.
Profundidad aparente. Profundidad a la que se percibe que un objeto está ubicado con respecto a una interfaz entre dos medios.
Punto cercano. Punto más cercano que un ojo puede ver enfocado.
Punto focal. Para una lente o espejo convergente, el punto en el cual los rayos de luz convergentes se cruzan; para una lente o espejo divergente, el punto desde el cual los rayos de luz divergentes parecen originarse.
Punto lejano. Punto más lejano que un ojo puede ver enfocado.
Segundo foco o foco de la imagen. Para una interfaz convergente, el punto donde un haz de rayos paralelos se refracta en una interfaz esférica; para una interfaz divergente, el punto en el que la continuación hacia atrás de los rayos refractados convergerá entre dos medios.
Trazado de rayos. Técnica que utiliza construcciones geométricas para encontrar y caracterizar la imagen formada por un sistema óptico.
Vértice. Punto donde la superficie del espejo se interseca con el eje óptico.
Anillos de Newton. Patrón de interferencia circular creado por la interferencia entre la luz reflejada en dos superficies como resultado de un ligero espacio entre ellas.
Franjas. Brillantes y oscuros patrones de interferencia.
Incoherencia. Las ondas tienen relaciones de fase aleatorias.
Interferencia de película delgada. Interferencia entre la luz reflejada desde diferentes superficies de una película delgada.
Interferómetro. Instrumento que utiliza interferencia de ondas para realizar mediciones.
Máximo principal. Franjas de interferencia más brillantes vistas con múltiples rendijas.
Máximo secundario. Interferencias brillantes. Franjas de intensidad más bajas que los máximos principales.
Monocromo. Luz compuesta de una sola longitud de onda.
Ondas coherentes. Las ondas están en fase o tienen una relación de fase definida.
Orden. Entero m usado en las ecuaciones para interferencia constructiva y destructiva para una doble rendija.
Ancho del pico central. Ángulo entre el mínimo para $m = 1$ y $m = -1$.
Criterio de Rayleigh. Dos imágenes solo se pueden resolver cuando el centro del patrón de difracción de uno está directamente sobre el primer mínimo del patrón de difracción del otro.
Difracción. Flexión de una onda alrededor de los bordes de una abertura o un obstáculo.
Difracción de rayos X. Técnica que proporciona información detallada sobre la estructura cristalográfica de materiales naturales y manufacturados.
Holografía. Proceso de producción de hologramas con el uso de láseres.
Holograma. Imagen tridimensional grabada en película por láser. la palabra holograma significa una imagen completa (de la palabra griega holo, como en holístico).
Interferencia destructiva para una sola rendija. Ocurre cuando el ancho de la rendija es comparable a la longitud de onda de la luz que lo ilumina.
Límite de difracción. Límite fundamental de resolución debido a la difracción.
Orden perdida. Interferencia máxima que no se ve porque coincide con un mínimo de difracción.
Patrón de difracción de dos rendijas. El patrón de difracción de dos rendijas de ancho $D$ que están separadas por una distancia d es el patrón de interferencia de dos fuentes puntuales separadas por d multiplicado por el patrón de difracción de una rendija de ancho $D$.
Planos de Bragg. Familias de planos dentro de cristales que pueden dar lugar a difracción de rayos X.
Rejilla de difracción. Gran número de rendijas paralelas espaciadas uniformemente.
Resolución. Capacidad, o límite de la misma, para distinguir pequeños detalles en imágenes.