Jaime Humberto Ramírez Ríos
Institución Universitaria Pascual Bravo
Córdoba (España)
2022.
Título de la obra:
Ecuaciones Diferenciales
Autor:
Jaime Humberto Ramírez Ríos
Código JavaScript para el libro: Joel Espinosa Longi, IMATE, UNAM.
Recursos interactivos: DescartesJS
Fuentes: Lato y UbuntuMono
Red Educativa Digital Descartes
Córdoba (España)
descartes@proyectodescartes.org
https://proyectodescartes.org
Proyecto iCartesiLibri
https://proyectodescartes.org/iCartesiLibri/index.htm
https://prometeo.matem.unam.mx/recursos/VariosNiveles/iCartesiLibri/
ISBN: 978-84-18834-32-5
Esta obra está bajo una licencia Creative Commons 4.0 internacional: Reconocimiento-No Comercial-Compartir Igual.
El libro interactivo de “Ecuaciones diferenciales” se pensó para que el estudiante tenga una herramienta práctica en el estudio de las ecuaciones sin perder el rigor que ésta conlleva, el libro contiene teoría, ejemplos resueltos paso a paso y ejercicios propuestos con su respectiva respuesta, pero también, tiene escenas interactivas donde el lector puede cambiar los enunciados y visualizar las diferentes gráficas e interactuar con ellas, también cuenta con escenas para que el estudiante repase conceptos de asignaturas previas como matemáticas operativas, cálculo diferencial, cálculo integral y álgebra lineal. Recuerde que para tener un buen desempeño en esta asignatura se debe manejar muy bien los conceptos previos adquiridos en las asignaturas mencionadas anteriormente.
El texto incluye 40 escenas interactivas, diseñadas en DescartesJS y GeoGebra, para que los estudiantes y el lector puedan tener un acercamiento más práctico con las ecuaciones, también se incluyen 26 vídeos de YouTube creados por el mismo autor del libro para facilitar el desarrollo y mejor entendimiento de los diferentes contenidos.
El libro tiene cinco capítulos, introducción a las ecuaciones diferenciales, ecuaciones diferenciales de primer orden, ecuaciones diferenciales de orden superior, transformada de Laplace y series de Fourier. Con esto se puede comenzar aprendiendo a clasificar las ecuaciones para luego resolverlas de acuerdo a las características de cada una de ellas.
Para evitar, al máximo, la dependencia con la conectividad en la red, las expresiones matemáticas se han construido recurriendo al API de $\KaTeX$.
Las diferentes leyes que rigen el universo están descritas en lenguaje matemático. Cuando se deben describir fenómenos estáticos, el álgebra es suficiente para resolverlos, pero la mayoría de dichos fenómenos naturales involucran cambios que dependen del tiempo, es decir, implican una razón de cambio. Cuando un proceso describe el comportamiento de algunos fenómenos de la vida real en términos matemáticos recibe el nombre de modelo matemático y se utiliza para comprender las variables que lo conforman.
Luego de plantear un modelo, es necesario resolverlo y confrontar la solución para saber si es razonable con los datos experimentales o con los hechos conocidos. Las hipótesis que se plantean implican una razón de cambio de una o más variables independientes con respecto a una o más variables dependientes, dicho modelo matemático implica una ecuación diferencial (ED).
Las ED tienen una importancia fundamental en las matemáticas debido a que son aplicables a casi todas las ramas del saber, como: geometría, física, química y biología. Éstas permiten identificar y aplicar técnicas y conceptos matemáticos que admiten obtener e interpretar la solución de una situación problema en la que intervienen relaciones entre tasas o razones de cambio de variables definidas en diversos contextos.
Algunas aplicaciones son: movimiento rectilíneo y caída libre, deformación de resortes y vigas, mezclas de soluciones salinas, circuitos en serie, desintegración radiactiva, fechado de fósiles con carbono $14$, crecimiento y decrecimiento poblacional, propagación de virus y enfermedades, cambio en las temperaturas y reacciones químicas entre otros.
Hay dos formas de expresar ecuaciones diferenciales, las dos se van a utilizar en este libro.
a) $\dfrac {dy}{dx}+4y=1$
b) $y'''-5y''+4y=0$
NOTACIÓN:
Notación de Leibniz: Utiliza los símbolos $dy \wedge dx$ para representar incrementos infinitamente pequeños. Se representa como sigue:
$\dfrac {dy}{dx},\;\dfrac{d^{\; 2}y}{dx^2},\;\dfrac {d^{\; 3}y}{dx^3}\ldots\;\dfrac{d^{\; n}y}{dx^n}$
Notación de Primas: La notación prima se usa para denotar el número de la derivada siendo esta usada hasta tres prima ${(''')}$, de ahí en adelante se utiliza notación numérica: la cuarta derivada se denota $y^{(4)}$. La n-ésima derivada se escribe como $y^{(n)}$. Se representa como sigue:
$y',\;y''\;y'''\;y^{(4)}\ldots\;y^{(n)}$
 |
la notación de Leibniz llamada así en honor del filósofo y matemático alemán del siglo XVII Gottfried Wilhelm Leibniz, utiliza los símbolos $dx$ y $dy$ para representar incrementos infinitamente pequeños de $x\;\wedge\;y$ respectivamente, al igual que $\Delta x\;\wedge\;\Delta y$ representan incrementos finitos $x\;\wedge\;y$. |
Leibniz comenzó a usar el carácter $\int$ basándose en el carácter de la palabra latina summa, que escribió como una "s" alargada. Este uso apareció por primera vez públicamente en su artículo "De Geometría", publicado en Acta Eruditorum de junio de 1686.
La prima es un signo gráfico que se usa en matemáticas, artes, ciencias y unidades de medida. En trigonometría, la prima sencilla indica la precisión de minutos y la doble los segundos al referirse a medidas angulares, cuando se aplica la nomenclatura sexagesimal. Por ejemplo: $12^{0}18^{'}5^{''}$ denota $12$ grados, $18$ minutos y $5$ segundos.
En el caso de las funciones matemáticas la prima sencilla indica la primera derivada de la función, la doble prima indica consecuentemente la segunda derivada y así sucesivamente, de doble prima en adelante son derivadas de orden superior.
En este libro vamos a utilizar las dos notaciones, pero es importante resaltar que aunque la notación de primas es más práctica y rápida de escribir, la notación de Leibniz tiene una ventaja sobre la notación de primas y es que muestra claramente ambas variables, la dependiente y la independiente.
Se clasifican de acuerdo a tres propiedades.
Ecuación Diferencial Ordinaria (EDO): es la ecuación que contiene derivadas respecto a una sola variable independiente. (Son las que se estudiarán en este libro).
$\dfrac {dy}{dx}+y=senx$
$y'''+5y'-3y=0$
"${\color{red}x}$" Variable independiente.
"${\color{red}y}$" Variable dependiente.
Ecuación Diferencial Parcial (EDP): es la que contiene las derivadas parciales respecto a dos o más variables independientes.
$\dfrac {\partial u}{\partial y}=\dfrac {\partial v}{\partial x}$
"${\color{red}x}$" $\wedge$ "${\color{red}y}$" Variables independientes.
"${\color{red}u}$" $\wedge$ "${\color{red}v}$" Variables dependientes.
Nota:$\;\;$Como todas las ecuaciones diferenciales que vamos a trabajar en este libro son ordinarias las vamos a llamar ED.
El orden de una ED es el de la derivada de mayor orden que hay en la ecuación.
$\dfrac {d^{\;2}y}{dx^2}\;+\;5y\;=\;senx$ ED de segundo orden.
$y'''+5y''-3y'+y=0$ ED de tercer orden.
$\dfrac {d^{\;4}y}{dx^4}\;+\dfrac {d^{\;2}y}{dx^2}\;+y\;=e^x$ ED de cuarto orden.
$y'+2y=tanx$ ED de primer orden.
Se dice que una ED de n-ésimo orden es lineal si F es lineal en la variable dependiente, esto significa que una ED es lineal si tiene la forma:
$a_{n}{(x)}\dfrac {d^{\; n}y}{dx^{n}}+ a_{n-1}{(x)}\dfrac {d^{\; n-1}y}{dx^{n-1}}+\ldots+a_{1}{(x)}\dfrac {dy}{dx}+ a_{0}{(x)}y=g{(x)}$
Las características especiales son:
$xy''-4y'=x^2$ ED lineal de segundo orden.
La ecuación es lineal porque la variable que tiene exponente es la variable independiente.
$x^3y'''+xy'-y=\ln \left| {\color{red}y}\right|$ ED no lineal de tercer orden.
La ecuación no es lineal porque la función logaritmo depende de la variable dependiente.
$\dfrac {d^{\; 4}y}{dx^4}\;+17\left( \dfrac {d^{\; 2}y}{dx^2}\right) ^{\color{red}2}+16y=0$ ED no lineal de cuarto orden.
La ecuación no es lineal porque la segunda derivada está elevada a un exponente.
$y'=y-y^{\color{red}2}$ ED no lineal de primer orden.
La ecuación no es lineal porque la variable dependiente está elevada a un exponente.
En general es más fácil identificar cuándo una ED es no lineal, que cuándo es lineal.
En la siguiente escena interactiva, adaptada de Plantillas con descartes_JS, debes arrastrar la flecha desde la ED lado izquierdo hasta el texto del lado derecho para identificar el orden y la linealidad de cada ecuación diferencial. Es importante aprender a identificar las ED según el orden y la linealidad, para aplicar el método adecuado de solución que veremos más adelante.
Intervalo de definición: La solución de una ecuación diferencial debe estar definida en un intervalo. Dicho intervalo se conoce como intervalo de definición, intervalo de existencia o dominio de la solución.
Solución trivial: Es la solución de una ED que es idéntica a cero en un intervalo $I$.
Puede ocurrir que una ecuación de orden superior tenga una o varias soluciones triviales, lo que no puede ocurrir es que todas las soluciones sean triviales.
Solución explícita: Es la solución en la que la variable dependiente se expresa sólo en términos de la variable independiente $\wedge$ las constantes.
La función $y=4+\dfrac{1}{2}e^{-5x}$ es solución explícita de la ED.
$\dfrac {dy}{dx}+5y=20$
En el ejemplo $(1)$ de la página 21 se verificará que $y=4+\dfrac{1}{2}e^{-5x}$ es solución de la ED $\dfrac {dy}{dx}+5y=20$
Solución implícita: Se dice que una función $G(x,y)=0$ es una solución implícita de una ED en un intervalo $I$, suponiendo que existe al menos una función $f$ que satisface la relación así como la ED en $I$.
La función $x^2+y^2=4$ es solución implícita de la ED $\dfrac {dy}{dx}=-\dfrac {x}{y}$ en el intervalo $-2 < x < 2$
 Ejemplo 1. Verificación de una solución
Ejemplo 1. Verificación de una soluciónVerifique que la función $y=4+ce^{-5x}$ es una solución de la ED $\dfrac {dy}{dx}+5y=20$
Solución
Como la ecuación es de primer orden, se debe derivar una vez la función.
$\dfrac {dy}{dx}=-5ce^{-5x}$
Reemplazando la función $\wedge$ la derivada en la ED se tiene.
$-5ce^{-5x}+5(4 + c e^{-5x}) = 20$
Aplicando propiedad distributiva.
$-5ce^{-5x} + 20 + 5c e^{-5x} = 20$
Agrupando términos semejantes queda $20=20$
Al demostrar que el lado derecho de la ecuación es igual al lado izquierdo, se verifica que la función.
 Ejemplo 2. Verificación de una solución
Ejemplo 2. Verificación de una soluciónVerifique que la función $y=xe^{-3x}$ es una solución de la ED $y''+6y'+9y=0$
Solución
Como la ecuación es de segundo orden, se debe derivar dos veces la función, tenga en cuenta que se debe derivar como un producto.
$y=xe^{-3x}$
$y'=-3xe^{-3x}+e^{-3x}$
$y''=9xe^{-3x}-3e^{-3x}-3e^{-3x}$
Agrupando términos semejantes.
$y''=9xe^{-3x}-6e^{-3x}$
Ahora reemplazamos la función y las dos derivadas en la ED.
$9xe^{-3x}-6e^{-3x}{\color{red}+6}(-3xe^{-3x}+e^{-3x}){\color{red}+9}(xe^{-3x})=0$
Aplicando propiedad distributiva.
$9xe^{-3x}-6e^{-3x}-18xe^{-3x}+6e^{-3x}+9xe^{-3x}=0$
Agrupando términos semejantes.
$0=0$
Al demostrar que el lado derecho de la ecuación es igual al lado izquierdo, se verifica que la función.
 Ejemplo 3. Comprobación de una solución
Ejemplo 3. Comprobación de una soluciónVerificar si la función $y=xsen(\ln \left| x\right|)$ es solución explícita de la ED $x^2y''+xy'+2y=0$
Solución
Como la ecuación es de segundo orden, se debe derivar dos veces la función, tenga en cuenta que se debe derivar como un producto.
$y=xsen(\ln \left| x\right|)$
$y'=xcos(\ln \left| x\right|)\dfrac{1}{x}+sen(\ln \left| x\right|)(1)$
$y'=cos(\ln \left| x\right|)+sen(\ln \left| x\right|)$
$y''=-sen(\ln \left| x\right|)\dfrac{1}{x}+cos(\ln \left| x\right|)\dfrac{1}{x}$
Ahora se reemplaza la función y sus derivadas en la ED de segundo orden.
${\color{red}x^2}(-sen(\ln \left| x\right|)\dfrac{1}{x}+cos(\ln \left| x\right|)\dfrac{1}{x}){\color{red}+x}(cos(\ln \left| x\right|)+sen(\ln \left| x\right|)){\color{red}+2}(xsen(\ln \left| x\right|))=0$
Propiedad distributiva.
$-xsen(\ln \left| x\right|)+xcos(\ln \left| x\right|)+xcos(\ln \left| x\right|)+xsen(\ln \left| x\right|)+2xsen(\ln \left| x\right|)=0$
Agrupando términos semejantes se obtiene.
$2xcos(\ln \left| x\right|)+2xsen(\ln \left| x\right|)=0$
Como no se cumple la identidad, se puede afirmar que.
 Ejemplo 4. Comprobación de una solución implícita.
Ejemplo 4. Comprobación de una solución implícita.Demuestre que la relación $x^2+y^2=4$ es solución implícita de la ED $\dfrac {dy}{dx}=-\dfrac {x}{y}$ en el intervalo $(-2, 2)$
Solución
Se deriva dos veces la función.
$2x + 2y \dfrac {dy}{dx}=0$ despejando se obtiene $\dfrac {dy}{dx}=-\dfrac {x}{y}$
Además, resolviendo $x^2+y^2=4$ para $y$ en términos de $x$ se obtiene.
$y=\pm\sqrt{4-x^2}$
las dos funciones $y=\sqrt{4-x^2}$ $\wedge$ $y=-\sqrt{4-x^2}$ satisfacen la relación $x^2+y^2=4$ $\wedge$ son las soluciones explícitas definidas en el intervalo $(-2, 2)$
 Ejemplo 5. Comprobación de una solución implícita.
Ejemplo 5. Comprobación de una solución implícita.Demuestre que la función $x^2y-tanx+y^2=0$ es
solución implícita de la ED $(2xy-sec^2x)dx+(x^2+2y)dy=0$
Solución
Primero debemos organizar la ED, dividiéndola toda por $dx$
$(2xy-sec^2x)+(x^2+2y)\dfrac{dy}{dx}=0$
Ahora despejamos el $\dfrac{dy}{dx}$ obtenemos.
$\dfrac{dy}{dx}=\dfrac {sec^2x-2xy}{x^2+2y}$
Ahora vamos a derivar la función $x^2y-tanx+y^2=0$ aplicando derivación implícita.
$x^2\dfrac{dy}{dx}+2xy-sec^2x+2y\dfrac {dy}{dx}=0$
Agrupando los términos con $\dfrac{dy}{dx}$ al lado izquierdo y los otros términos al lado derecho, obtenemos.
$x^2\dfrac{dy}{dx}+2y\dfrac {dy}{dx}=-2xy+sec^2x$
Sacando factor común $\dfrac{dy}{dx}$
$\dfrac{dy}{dx}(x^2+2y)=-2xy+sec^2x$
Despejando $\dfrac{dy}{dx}$ obtenemos.
$\dfrac{dy}{dx}=\dfrac {sec^2x-2xy}{x^2+2y}$
Como los dos resultados son iguales, podemos decir que la función $x^2y-tanx+y^2=0$ es solución implícita de la ED
$(2xy-sec^2x)dx+(x^2+2y)dy=0$
Familias de soluciones: una ED puede tener una cantidad $\alpha$ de soluciones que corresponden a las elecciones ilimitadas de parámetros. Todas estas familias se llaman familias paramétricas de soluciones. El parámetro está directamente relacionado con el orden de la ED.
Si la ED es de primer orden, la solución es uniparamétrica. Hay un parámetro $c$ que puede tomar diferentes valores.
Si la ED es de segundo orden, la solución es biparamétrica. Hay dos parámetros $c_{1}$ $\wedge$ $c_{2}$ que pueden tomar diferentes valores.
Si la ED es de tercer orden, la solución es triparamétrica. Hay tres parámetros $c_{1}$, $c_{2}$ $\wedge$ $c_{3}$ que pueden tomar diferentes valores.
Si la ED es de orden $n$, la solución es n-paramétrica. Hay $n$ parámetros $c_{1}$, $c_{2}$, $c_{3}$ $\ldots$, $c_{n}$ que pueden tomar diferentes valores.
Solución general: Es la función que satisface a la ED $\wedge$ que contiene una o más constantes arbitrarias dependiendo del orden de la ecuación diferencial y que fueron obtenidas de las sucesivas integraciones.
La función $y=c_1xcos(\ln \left| x\right|)+c_2xsen(\ln \left| x\right|)$
Es una solución general de la ED.
$x^2y''-xy'+2y=0$
La función $y=c_1e^{2x}+c_2xe^{2x}$
Es una solución general de la ED.
$y''-4y'+4y=0$
Solución particular: Es la función que satisface a la ED $\wedge$ cuyas constantes arbitrarias toman un valor específico.
La función $y=\dfrac{2}{5}xcos(\ln \left| x\right|)-\dfrac{1}{3}xsen(\ln \left| x\right|)$
Es una solución particular de la ED.
$x^2y''-xy'+2y=0$
La función $y=\dfrac{3}{5}e^{2x}-\dfrac{1}{2}xe^{2x}$
Es una solución particular de la ED.
$y''-4y'+4y=0$
En el siguiente video, realizado por Jaime H. Ramírez Rios, podrás observar un ejemplo de comprobación de una solución explícita.
En el siguiente video, realizado por Jaime H. Ramírez Rios, podrás observar un ejemplo de comprobación de una solución explícita.
Curva solución: La gráfica de la solución de una ED se llama curva solución. Puesto que la función es derivable y continua en el intervalo de definición $I$. Es probable que la gráfica de la ED sea diferente a la gráfica de la solución, por lo cual el dominio de cada una no necesariamente debe ser igual.
Geométricamente, la solución general representa una familia de curvas. La solución general es una familia de gráficas que van cambiando dependiendo del valor del parámetro $c$, la solución particular es una de las curvas de la familia.
Geométricamente se puede hallar la solución de una ED $y'=f(x,y)$ dada. En cada punto $(x,y)$ del plano $xy$, el valor de $f(x,y)$ determina una pendiente $m=f(x,y)$, esto significa que la solución de una ED es simplemente una función derivable cuya gráfica $y = y(x)$ tiene su “pendiente correcta” en cada punto $(x, y(x))$.
Una curva solución de la ED $y'=f(x,y)$ es claramente una curva en el plano $xy$ cuya línea tangente en cada punto $(x,y)$ tiene pendiente $m=f(x,y)$.
En la siguiente escena interactiva podrás interactuar con la solución $y=\ln \left| t^{2}+1\right| +c$ de la ecuación diferencial $\dfrac {dy}{dt}=\dfrac {2t}{t^{2}+1}$.
En la siguiente escena interactiva, diseñada por Jorge L. Herrera, podrás ver cómo cambia la gráfica de una ED al cambiar el valor del parámetro $c$.
En la siguiente escena interactiva, diseñada por Adrián Rocha Ichante, podrás ver cómo cambia la gráfica de la ED al cambiar el valor del parámetro $c$. La solución es una familia de soluciones.
A menudo es interesante resolver una ecuación diferencial de primer orden de la forma $\dfrac {dy}{dx}=f(x,y)$, sujeta a la condición inicial $y(x_{0})= y_{0}$
 Ejemplo 1. PVI de primer orden
Ejemplo 1. PVI de primer orden$y = ce^x$ es una familia uniparamétrica de soluciones de la ED de primer orden $y'=y$ en el intervalo $( -\infty ,\infty)$. Determine una solución del problema de valor inicial PVI de primer orden que consiste en esta ecuación diferencial $\wedge$ la condición inicial $y(0)=5$
Solución
$y = ce^x$
Se reemplaza la condición inicial $y(0)=5$. Recuerde que la condición inicial es $y(x_{0})= y_{0}$, es decir, $y=5$ cuando $x=0$
$5 = ce^0$
El valor del parámetro es:
$c=5$
reemplazando en la solución general, obtenemos la solución particular.
 Ejemplo 2. PVI de segundo orden
Ejemplo 2. PVI de segundo orden$y = c_1e^{-x}+c_2e^{2x}$ es una familia biparamétrica de soluciones de la ED de segundo orden $y''-y'-2y=0$
Determinar $c_{1}$ $\wedge$ $c_{2}$ de modo que se cumplan las condiciones iníciales $y(0)=2$ $\wedge$ $y'(0)=-3$
Solución
$y = c_1e^{-x}+c_2e^{2x}$ es la solución general de la ED $y''-y'-2y=0$
Para hallar los valores de $c_{1}$ $\wedge$ $c_{2}$ y expresar la solución particular se debe reemplazar la condición $y(0)=2$ en la solución de la siguiente forma:
$2 = c_1e^{0}+c_2e^{0}$. Recuerde que ${\color{blue}e^0=1}$, entonces queda una ecuación con dos incógnitas $2=c_1+c_2$ y la llamamos ecuación $(1)$
Para resolver esta ecuación se necesita tener otra ecuación con dos incógnitas, entonces se deriva la solución y se reemplaza la condición $y'(0)=-3$ de la siguiente forma:
Derivando la solución obtenemos $y' =- c_1e^{-x}+2c_2e^{2x}$
Reemplazando la condición inicial $-3 =- c_1e^{0}+2c_2e^{0}$ se llega a la ecuación $-3 =- c_1+2c_2$ y la llamamos ecuación $(2)$
Con las ecuaciones $(1)$ $\wedge$ $(2)$ se puede formar un sistema de ecuaciones.
$\begin{cases}c_{1}+c_{2}=2\\ -c_{1}+2c_{2}=-3\end{cases}$
Este sistema se puede resolver por igualación, sustitución o eliminación.
Teniendo en cuenta las dos ecuaciones resultantes, lo vamos a resolver por eliminación.
$\hspace{0.6cm}{\color{Red}\bcancel {{\color{Olive}c_1}}}{+\;\; c_{2}=2}$
$\underline{\hspace{0.3cm}{\color{Red}\bcancel {{\color{Olive}-c_{1}}}}+2c_{2}=-3}$
$\hspace{1.3cm} 3c_2=-1$
Obtenemos $c_2=-\dfrac{1}{3}$
Reemplazando en la ecuación $2 = c_1+c_2$ llegamos a.
$2 = c_1-\dfrac{1}{3}$
Despejando $c_1$ se obtiene.
$c_1=\dfrac{7}{3}$
Entonces la solución particular es.
 Ejemplo 3. Intervalo de definición de una solución
Ejemplo 3. Intervalo de definición de una solución$y = \dfrac{1}{x^{2}+c}$ es una familia uniparamétrica de soluciones de la ecuación diferencial de Primer orden $y'+2xy^2=0$. Determine una solución del PVI $y(1)=4$ de primer orden que consiste en esta ecuación diferencial y las condiciones iníciales dadas. Dé el intervalo en el cual está definida la solución.
Solución
$y = \dfrac{1}{x^{2}+c}$ es la solución general de la ED $y'+2xy^2=0$
Para hallar el valor de $c$ se debe reemplazar la condición $y(1)=4$ en la solución de la siguiente forma:
$4 = \dfrac{1}{1^{2}+c}$. Despejando obtenemos. $4+4c=1$
Despejando el parámetro $c$ obtenemos $c = -\dfrac{3}{4}$
La solución particular es $y = \dfrac{1}{x^{2}-\dfrac{3}{4}}$ el dominio es $\mathbb{R} -\left\{ \pm \dfrac {\sqrt {3}}{2}\right\}$
El intervalo de definición está dado por.
$\left( -\infty\dfrac {-\sqrt {3}}{12}\right) U\left( \dfrac {-\sqrt {3}}{2},\dfrac {\sqrt {3}}{2}\right) \cup \left( \dfrac {\sqrt {3}}{2},\infty \right)$
A partir del capítulo 2 se hará un análisis de los diferentes métodos para resolver ED, para lo cual, es necesario identificar primero el tipo de ecuación para saber cuál o cuáles métodos aplicar, pero antes de proceder a dicho análisis, nos detendremos en la interpretación geométrica de las ED y sus soluciones.
Desde el punto de vista geométrico hay un método para obtener soluciones aproximadas de la ED $y'=f(x,)$ a través de cada grupo representativo de puntos $(x,y)$ en el plano se obtiene un segmento lineal con pendiente $m=f(x,y)$, todos los segmentos lineales constituyen un campo de pendientes o un campo direccional.
La terna $(x, y, y')$ determina la dirección de una recta que pasa por el punto $(x, y)$. El conjunto de los segmentos de estas rectas es la representación geométrica del campo direccional.
Una Isóclina es el conjunto de los puntos del plano en donde las rectas tangentes a las gráficas de las soluciones de la ecuación diferencial tienen la misma pendiente. Estos puntos son aquellos que satisfacen $y'=f(x,y)=c$
En las siguientes tres escenas interactivas podres ver el comportamiento de los campos direccionales y las Isóclinas de diferentes ED.
En la primera escena interactiva podrás ver el comportamiento del campo de direcciones de una ED de primer orden $\dfrac{dy}{dx}=-\dfrac{x}{y}$ y la gráfica solución para diferentes valores del parámetro (radio de circunferencia).
En la segunda escena interactiva podrás ver el comportamiento del campo de direcciones, densidad y longitud de una ED de primer orden $\dfrac{dy}{dx}=x$, pero puedes cambiar la ED ingresando otra función diferente, además, puedes visualizar soluciones particulares para diferentes valores del parámetro.
En la tercera escena interactiva podrás interactuar con las Isóclinas que están formadas por la solución de la ED.
$y'= x + y -1$.
Al mover el deslizador, podrás ver las pendientes de las rectas tangentes de acuerdo con la recta.
$k = x + y + 1$.
Las flechas indican cómo va cambiando el campo de direcciones de la ED.
En la siguiente escena interactiva, diseñada por Jorge Olivares Funes, podrás ver el campo direccional de una ED y cómo cambia el radio de la circunferencia.
En la siguiente escena interactiva, diseñada por Soed Torres, podrás ver el campo direccional de una ED.
En la siguiente escena interactiva, diseñada por Diego Sandoval, podrás ver las Isóclinas de una ED y cómo cambian a medida que se cambia el valor del parámetro.
Cuando se considera un problema de valor inicial (PVI) se deben considerar dos preguntas:
¿Existe la solución del problema? Si la respuesta es afirmativa se debe preguntar ¿La solución es única?
Dada una ED $\dfrac{dy}{dx}= f(x,y)$
Donde $f(x,y)$ está definida en una región rectangular $R$ que contiene al punto $(x_{0},y_{0})$
Si $f(x,y)$ satisface las condiciones:
1. $f(x,y)$ es continua en R,
2. $\dfrac {\partial f}{\partial y}$ es continua en $R$
Entonces existe un intervalo $I$ con centro en $x_{0}$ $\wedge$ existe una y sólo una función $y = g(x)$ definida en el intervalo $I$ que satisface la condición inicial $y(x_{0})= y_{0}$
En otras palabras, las condiciones para la existencia de la solución son:
• Continuidad de $f(x,y)$ en R,
• Acotamiento de $f(x,y)$ por R,
Y las condiciones para la unicidad son:
• Continuidad de $f(x,y)$ $\; \wedge \;$ $\dfrac {\partial f}{\partial y}$ en $R$,
• Acotamiento de $f(x,y)$ $\; \wedge \;$ $\dfrac {\partial f}{\partial y}$ por $R$,
Estas condiciones son suficientes pero no necesarias, porque puede existir una solución que satisface $y(x_{0})= y_{0}$, pero que no cumple la condición 1, o la condición 2, o ninguna de las dos.
A continuación vamos a ver un ejemplo y luego a definir la existencia y unicidad de soluciones.
 Ejemplo 1. Existencia y unicidad
Ejemplo 1. Existencia y unicidadCada una de las funciones $y=0 \; \wedge \; y=x^2$ satisface la ED $\dfrac{dy}{dx}=2\sqrt {y}$ $\wedge$ la condición inicial $y(0)=0$
Solución
El PVI $\dfrac{dy}{dx}=2\sqrt {y}$, $y(0)=0$ tiene al menos dos soluciones. como se muestra en la figura $1$.
El estudiante puede verificar que las dos funciones son solución de la ED, además, las gráficas de las dos soluciones pasan por el mismo punto $(0,0)$
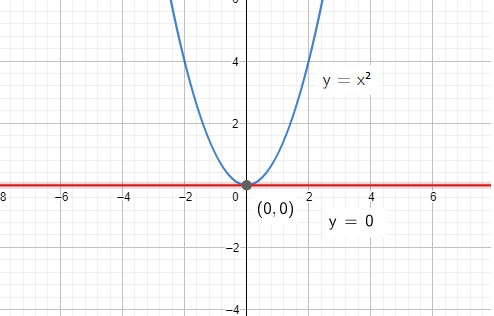
Gráfica 1 Dos soluciones del mismo PVI.
$\dfrac {dy}{dx}=f(x,y)$
Tiene una y sólo una solución que está definida en el intervalo $I$ Ejemplo 2. Existencia y unicidad
Ejemplo 2. Existencia y unicidadVerificar si la función $y=-\dfrac{x}{1+cx}$ cumple la CI. $\; \;$ $y(0)=1$
Solución
Reemplazando las condiciones iniciales $y=1$ cuando $x=0$ en la función, obtenemos.
$1=-\dfrac{0}{1+c(0)}$ nos queda la ecuación $1=0$ lo cual es un absurdo.
Esto quiere decir que es imposible que dicha solución cumpla las condiciones iniciales.
 Ejemplo 3. Existencia y unicidad
Ejemplo 3. Existencia y unicidadDemuestre que la ED $\dfrac{dy}{dx}+y=0$ tiene solución única para la CI. $\; \;$ $y(1)=3$
Solución
Vamos a demostrar que la ED tiene solución única sin resolverla, para esto debemos despejar la ED.
$\dfrac{dy}{dx}=-y$
La función $f(x,y)=-y$ es un polinomio, por lo cual es continua en todo el plano $\mathbb{R} ^{2}$
Ahora se deriva parcialmente la función respecto a $y$
$\dfrac {\partial f}{\partial y}=-1$
Es una función constante, por lo cual es continua en todo el plano $\mathbb{R} ^{2}$
Ambas funciones son continuas en cualquier rectángulo que contenga el punto $(1,3)$, como se cumplen las condiciones 1 $\wedge$ 2 en un intervalo con centro en $x_0$ entonces el PVI tiene solución única.
 Ejemplo 4. Existencia y unicidad
Ejemplo 4. Existencia y unicidadDetermine una región del plano $xy$ para el que la ED $\dfrac{dy}{dx}=\sqrt {xy}$ tiene solución única, cuyas gráficas pasen por un punto $(x_0,y_0)$ en la región.
Solución
$f(x,y)=\sqrt {xy}$
Una raíz par no puede ser negativa, pero como está en el numerador puede ser $0$
La función es continúa para $x\geq 0\wedge y\geq 0$ o para $x\leq 0 \wedge y\leq 0$
Ahora se deriva parcialmente la función respecto a $y$
$\dfrac {\partial f}{\partial y}=\dfrac {x^{\frac {1}{2}}}{y^{\frac {1}{2}}}$= $\dfrac {1}{2}\sqrt {\dfrac {x}{y}}$
Una raíz par no puede ser negativa, pero como $y$ está en el denominador no puede ser $0$
La función es continúa para $x>0 \; \wedge \; y>0$ o para $x$ < $0\wedge y$ < $0$
La función es continúa en la intercepción de los dos rectángulos es decir para $x>0 \wedge y>0$ o para $x$ < $0\wedge y$ < $0$
Como acabas de ver en los contenidos vistos hasta ahora es muy importante que manejes bien los conceptos de trigonometría básica y de derivadas, por eso vamos a repasar un poco dichos contenidos, si ya los manejas bien, pasa directamente a la página 53 para practicar lo visto hasta el momento.
A continuación encontrarás una tabla con las identidades trigonométricas básicas y pitagóricas para que uses al resolver ejercicios que contengan funciones trigonométricas.

Tabla 1. Identidades trigonométricas.
Ahora vamos a repasar derivadas. Recuerda que una derivada se puede resolver utilizando el concepto de límite, pero como ya viste la asignatura cálculo diferencial y aprendiste a derivar utilizando el concepto de límite y nuestro interés es sólo derivar de forma correcta, vamos a utilizar la siguiente tabla que contiene las derivadas básicas, la regla de la suma y de la diferencia, la regla del producto y la regla del cociente, además las derivadas de las funciones hiperbólicas las cuales vamos a utilizar cuando resolvamos ED de orden superior.
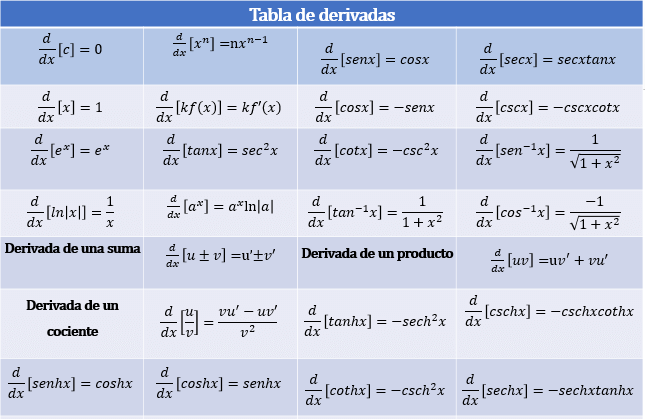
Tabla 2. Derivadas.
En la siguiente escena interactiva, resuelve los ejercicios propuestos que corresponden a la derivada de la suma y la diferencia de funciones.
Para comenzar debes recordar las siguientes propiedades.
${\color{blue}\dfrac{d}{dx}(u \pm v)=u'\pm v'}$
${\color{blue}\dfrac{d}{dx}(x)^{n}=nx^{n-1}}$
Debes resolver en tu cuaderno o libreta de apuntes cada ejercicio y después verificar que tu solución corresponda con la de cada ejemplo, luego da click en el botón otro ejemplo para resolver más ejercicios hasta que consideres que ya recuerdas bien el concepto de derivada.
En la siguiente escena interactiva, Que se encuentra en la página 112 del libro $\;$ Cálculo diferencial interactivo, podrás repasar derivadas de polinomios.
En la siguiente escena interactiva, resuelve los ejercicios propuestos que corresponden a la derivada de un producto.
Selecciona la opción apropiada y dale verificar. Si deseas ver el paso a paso, pulsa el botón Ver solución. Luego selecciona siguiente para ver otro ejercicio.
Recuerda que es muy importante derivar los productos de forma adecuada para verificar soluciones de ecuaciones diferenciales tanto de primer orden, como las de orden superior que se verán en el próximo capítulo.
En la siguiente escena interactiva, que se encuentra en la página 120 del libro $\;$ Cálculo diferencial interactivo, podrás repasar derivadas de un producto.
En la siguiente escena interactiva, resuelve los ejercicios propuestos que corresponden a la derivada de un cociente, verifica que tu solución corresponda con la de cada ejercicio, luego selecciona siguiente para ver otro ejemplo.
Cuando se deriva un cociente es muy importante tener en cuenta el orden de la derivada. La fórmula de la derivada del producto y del cociente las encuentras en la tabla de la página 45.
En la siguiente escena interactiva, que se encuentra en la página 119 del libro $\;$ Cálculo diferencial interactivo, podrás repasar derivadas de un cociente.
En la siguiente escena interactiva, resuelve cada ejercicio y selecciona la respuesta correcta, dale verificar para comprobar si es correcta, luego selecciona siguiente para ver otro ejercicio.
Podrás comprobar tu destreza para derivar un cociente en el cual hay polinomios, funciones trigonométricas, logaritmos y exponenciales.
En la siguiente escena interactiva, que se encuentra en la página 124 del libro $\;$ Cálculo diferencial interactivo, podrás repasar derivadas de un cociente.
Los siguientes ejercicios fueron diseñados por Miguel Ángel Cabezón Ochoa. En esta escena interactiva puedes realizar ejercicios aplicando regla de la cadena con diferentes funciones. Selecciona el tipo de derivada a practicar, haciendo clic en una de las opciones de la columna izquierda. La última opción muestra diferentes funciones de forma aleatoria.
Tienes a disposición una gran cantidad de ejercicios. Te sugerimos realizarlos en tu cuaderno o libreta de apuntes, cuando hayas terminado puedes verificarlos con la solución del interactivo.
Así que mucho ánimo y ponte a practicar.
En la siguiente escena interactiva, que se encuentra en la página 132 del libro $\;$ Cálculo diferencial interactivo, podrás repasar derivadas utilizando regla de la cadena.
En la siguiente escena interactiva, adaptada de Plantillas con descartes_JS, encontrarás una sopa de letras con 10 palabras relacionadas a las definiciones que acabas de estudiar en las páginas anteriores sobre clasificación de las ecuaciones diferenciales, tipos de soluciones y problemas de valor inicial entre otros. Recuerda que es muy importante comprender bien los conceptos teóricos para resolver de forma adecuada los ejercicios.
Método de solución La solución de la ED es de la forma.
Nota: No es necesario emplear dos constantes de integración al resolver la ED, porque si escribimos $\int h(y)dy+c_1=\int g(x)dx + c_2 $ la diferencia entre $c_2- c_1$ da como resultado una constante $c$
 Ejemplo 1: Solución de una ED separable
Ejemplo 1: Solución de una ED separableResolver la ED $x senx e^{-y} dx - y dy = 0$
Solución
$x \;senx\; e^{-y} dx - y \;dy = 0$
Primero debemos tener un diferencial a cada lado de la ecuación.
$x \;senx\; e^{-y} dx = y \;dy$
Ahora separamos variables.
$x \;senx\;dx =\dfrac{y}{e^{-y}}dy$
Pasamos Euler al numerador aplicando propiedades de potenciación.
$x\;senx\;dx$ = $y\;e^{y}\;dy$
Los diferenciales indican que se debe integrar.
$\int x\;senx\;dx$ = $\int y\;e^{y}\;dy$
Ahora se integra cada lado aplicando integración por partes.
$\int x\;senx\;dx$
$u=x$ $dv=senx dx$ $du=dx$ $v=-cosx$
$\int x\;senx\;dx=-x\;cosx + senx +c$
$\int y\;e^{y}\;dy$
$u=y$ $dv=e^y dy$ $du=dy$ $v=e^y$
$\int y\;e^{y}\;dy=y\; e^{-y} - e^{-y}$
Uniendo los resultados de las dos integrales obtenemos la solución de la ED.
$-x\;cosx + senx +c$ = $y\; e^{-y} - e^{-y}$
Factorizando obtenemos la solución implícita.
 Ejemplo 2: Separando variables
Ejemplo 2: Separando variablesResolver la ED $xtanxdx-ycosxdy=0$
Solución
$xtanxdx-ycosxdy=0$
Separamos variables.
$\dfrac {xtanx}{cosx}dx=ydy$
La integral no es por sustitución, entonces se debe aplicar identidades para integrar por sustitución.
Recuerde que ${\color{blue}tanx=\dfrac{senx}{cosx}}$
$x\dfrac {senx}{cos^2x}dx=ydy$
Los diferenciales indican que se debe integrar.
$\displaystyle \int x\dfrac {senx}{cos^2x}dx=\int ydy$
La integral del lado izquierdo es por partes, primero integramos el $dv$
$\displaystyle \int \dfrac {senx}{cos^2x}dx$
$u=cos x$ $du=-sen x dx$
$\displaystyle -\int \dfrac {du}{u^2}=-\int {u^{-2}}du=\dfrac {1}{u}=\dfrac {1}{cos x}=sec x$
$\displaystyle \int x\dfrac {senx}{cos^2x}dx$
$u=x$ $dv=\dfrac {senx}{cos^2x}$
$du=dx$ $v=secx$
$\displaystyle \int x\dfrac {senx}{cos^2x}=xsecx-\int secxdx$
Organizando la integral.
$xsecx-\int secx=\int ydy$
Integrando a ambos lados obtenemos la solución general.
Nota La integral de secante está en la tabla de la página $70$
$xsecx-\ln \left| secx+tanx\right|+c=\dfrac{y^2}{2}$
Despejando la $y$ obtenemos la solución explícita.
Recuerde que ${\color{blue}2c=c}$
 Ejemplo 3: Quitando logaritmos
Ejemplo 3: Quitando logaritmosResolver la ED $x\dfrac {dy}{dx}=4y$
Solución
Antes de resolver la ED es importante anotar que cuando sea posible se deben quitar los logaritmos.
$x\dfrac {dy}{dx}=4y$
Subimos el diferencial.
$x dy =4y dx$
Separamos variables.
$\dfrac {dy}{y}=4\dfrac{dx}{x}$
Los diferenciales indican que se debe integrar.
$\displaystyle \int \dfrac {dy}{y}=4 \int \dfrac {dx}{x}$
Integrando obtenemos.
$\ln \left| y\right|= 4 \ln \left| x\right| +c$
Aplicamos la propiedad de logaritmos ${\color{blue}c\ln \left| A\right|=\ln \left| A\right|^c}$
$\ln \left| y\right|= \ln \left| x\right|^4 +c$
Recuerde que ${\color{blue}e^{\ln \left| x\right|}=x}$
$e^{\ln \left| y\right|}=e^{\ln \left| x\right|^4 +c}$
Aplicando propiedades de potenciación.
$e^{\ln \left| y\right|}=e^{\ln \left| x\right|^4} \cdot {e^c}$
Teniendo en la cuenta que ${\color{blue}a^m.a^m=a^{m+n}} \; \wedge \: {\color{blue}e^c=c}$
Obtenemos la solución explícita.
 Ejemplo 4: Problema de valor inicial
Ejemplo 4: Problema de valor inicialResolver el PVI $\dfrac {dy}{dx}= -\dfrac {x}{y}$ Sujeto a la condición $y(4) = 3$
Solución
$\dfrac {dy}{dx}= -\dfrac {x}{y}$
Recuerde que para integrar no pueden haber diferenciales en el denominador.
$ y\; dy = - x\; dx$
Los diferenciales indican que se debe integrar.
$\int y\; dy = -\int x\; dx$
Integrando obtenemos.
$\dfrac {y^2}{2}= -\dfrac {x^2}{2}+c$
despejando la constante.
$\dfrac {y^2}{2}+\dfrac {x^2}{2}=c$
Simplificando.
$y^2\;+x^2=c$
Reemplazando condiciones iniciales.
$3^2\;+4^2=c$
El valor de la $c$
$c = 25$
La solución particular es.
Nota: Al multiplicar $2$ por una constante $c$ el resultado es $c$.
En el ejemplo anterior solucionamos una ecuación diferencial por variables separables y en la solución general reemplazamos las condiciones iniciales para hallar el valor de la $c$ y obtener una solución particular. noten que el valor del parámetro $"c"$ varía de acuerdo a las condiciones iniciales.
La ecuación del ejemplo 4 la vamos a graficar en la siguiente escena interactiva teniendo en la cuenta el PVI y podrás observar cómo cambia la gráfica al cambiar el valor del parámetro. La $c$ varía desde $0.1$ hasta $25$.
Las ED al igual que las ecuaciones algebraicas se pueden graficar en el plano cartesiano, algunas ED son muy sencillas de graficar, pero hay otras muy complejas.
En la siguiente escena interactiva, diseñada por Jorge Olivares Funes, podrás ver cómo cambia la gráfica del ejemplo 4 al cambiar el valor del parámetro. Al resolver la ED el parámetro se convierte en el radio de la circunferencia.
 Ejemplo 5: Problema de valor inicial
Ejemplo 5: Problema de valor inicialResolver la ED $\dfrac {dy}{dx}=-2y$
Sujeta a la condición $y(0) = -5$
Solución
$\dfrac {dy}{dx}=-2y$
Separando variables.
$\dfrac {dy}{y}=-2dx$
Los diferenciales indican que hay que integrar.
$\displaystyle \int \dfrac {dy}{y}=-2 \int dx$
Integrando obtenemos.
$\ln \left| y\right|=-2x+c$
Quitando el logaritmo.
$y = c e^{-2x}$
Reemplazando condiciones iniciales.
$-5 = c e^{0}$
El valor del parámetro es.
$c = -5$
La solución particular es.
En la siguiente escena interactiva puedes ver la gráfica del ejemplo 4. Podrás ver en la escena interactiva, cómo cambia la gráfica de la ED al cambiar el valor del parámetro en un intervalo de $[-15,15]$, el valor de la $x$ lo puedes cambiar de $[0,100]$ y el valor de la $k$ lo puedes cambiar de $[-5,5]$.
Al interactuar con los deslizadores podrás observar cómo cambia la gráfica, también podrás observar la ecuación diferencial y veras la solución particular de dicha ecuación.
En la siguiente escena interactiva, diseñada por Jorge Olivares Funes, podrás ver cómo cambia la gráfica del ejemplo 4 al cambiar el valor de la constante.
En las siguientes dos escenas interactiva podrás resolver ED por variables separables, en la primera debes tener en cuenta que el resultado se da con el parámetro despejado.
En la primera escena interactiva debes ingresar la función $f(x)$ (función con términos en la variable $x$) en la primera entrada y la función $g(y)$ (función con términos en la variable $y$) en la segunda entrada, luego vas a ver la ED igualada a cero y la solución general.
En la segunda escena interactiva encuentras una ED resuelta en dos pasos, los pasos los puedes ver interactuando con el deslizador, luego puedes practicar con diferentes ED cada una con su respectiva respuesta.
En la siguiente escena interactiva, diseñada por Ravinder Kumar, podrás resolver ED por variables separables y visualizar su gráfica.
En la siguiente escena interactiva, diseñada por Ravinder Kumar, podrás resolver ED por variables separables. Con el botón "Practice" podrás ver diferentes ejercicios y con el botón "Show" visualizarás el resultado.
En el vídeo podrás observar un ejemplo de ecuaciones diferenciales por variables separables.
En el siguiente video, realizado por Jaime H. Ramírez Rios, podrás observar un ejemplo de variables separables.
Como acabas de ver en los contenidos vistos hasta ahora es muy importante que manejes bien las integrales, por eso a continuación encontrarás una tabla con algunas de las integrales que encontrarás en los diferentes ecuaciones diferenciales que tendrás que resolver en este libro tanto en la segunda unidad como en las posteriores.
A continuación encontrarás una tabla con integrales para que uses al resolver ejercicios.
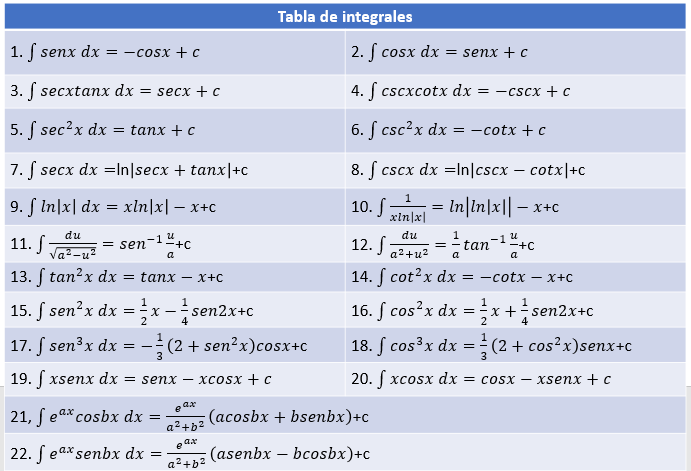
Tabla 3. Integrales.
Como acabas de ver para resolver ED es muy importante que manejes bien las diferentes técnicas de integración, por eso vamos a repasar un poco integrales, si ya los manejas bien, pasa directamente a la página 76 para resolver ED por variables separables.
En la siguiente escena interactiva, que se encuentra en la página 40 del libro $\;$ Integrando con Paco, podrás repasar integrales directas.
En la siguiente escena interactiva vamos a resolver integrales por sustitución, recuerda que si una integral no es directa, se debe examinar si una función es la derivada de la otra, para llevarla a la forma ${\color{blue}\int f(u) du}$
Puedes escoger el tipo de integral que quieres resolver, luego hazlo en tu cuaderno y verifica tu respuesta, luego da clic en el botón otro ejercicio para realizar uno diferente.
En la siguiente escena interactiva, que se encuentra en la página 77 del libro $\;$ Integrando con Paco, podrás repasar integrales por sustitución.
La única forma de volverse experto en algún contenido, es practicando, y esto se logra resolviendo muchos ejercicios, por eso aquí tienes más integrales que se resuelven por sustitución para que sigas practicando en caso de que todavía tengas dificultad con dichas integrales.
Puedes escoger el tipo de integral que quieres resolver, luego hazlo en tu cuaderno y verifica tu respuesta, luego da clic en el botón otro ejercicio para realizar uno diferente.
En la siguiente escena interactiva, que se encuentra en la página 70 del libro $\;$ Integrando con Paco, podrás repasar integrales por partes.
Cuando una integral no es directa, ni por sustitución, se verifica si es por partes. En la siguiente escena interactiva vamos a resolver integrales utilizando integración por partes.
Puedes escoger el tipo de integral que quieres resolver, luego hazlo en tu cuaderno y verifica tu respuesta, luego da clic en el botón otro ejercicio para realizar uno diferente.
Aquí encontrarás combinaciones de: algebraicas con exponencial, con logaritmo natural y con coseno; integrales logarítmicas y coseno con exponencial, las cuales son cíclicas.
Recuerda la fórmula de integración por partes ${\color{blue}\int udv=uv-\int vdu}$
En la siguiente escena interactiva, que se encuentra en la página 106 del libro $\;$ Integrando con Paco, podrás repasar integrales por partes.
La técnica de integración por partes, fuera de que es muy utilizada, a veces presenta alguna complicación al momento de iniciar a resolverla, por eso aquí encontrarás otra escena interactiva muy amigable para que sigas repasando dicha integral.
Puedes escoger el tipo de integral que quieres resolver, identificas $u$ $\wedge$ $dv$, luego buscas con los botones la respectiva derivada e integral, armas la solución y le das verificar para comprobar la respuesta.
Aquí encontrarás combinaciones diferentes a las vistas en la escena interactiva anterior.
Recuerda la fórmula de integración por partes ${\color{blue}\int udv=uv-\int vdu}$
En la siguiente escena interactiva, que se encuentra en la página 105 del libro $\;$ Integrando con Paco, podrás repasar integrales directas.
Definición: una ecuación diferencial de primer orden de la forma
$$\tag{E1} a_{1}{(x)}\dfrac {dy}{dx}+ a_{0}{(x)}y=g{(x)}$$
se dice que es una ecuación lineal en la variable dependiente $\;\;y$
Se dice que la ecuación lineal es homogénea cuando $g(x)=0$; si no es no homogénea.
Al dividir ambos lados de la ecuación $(E1)$ por el coeficiente $a_{1}{(x)}$ se obtiene la ecuación.
$\dfrac {a_{1}{(x)}}{a_{1}{(x)}}\dfrac {dy}{dx}+ \dfrac {a_{0}{(x)}}{a_{1}{(x)}}y=\dfrac {g{(x)}}{a_{1}{(x)}}$
Donde $\dfrac {a_{0}{(x)}}{a_{1}{(x)}}$ lo vamos a llamar $p(x)$ $\wedge$ $\dfrac {g{(x)}}{a_{1}{(x)}}$ lo vamos a llamar $f(x)$
Reemplazando estos valores en la ecuación $(E1)$ obtenemos la ecuación que vamos a llamar Forma estándar
Esta ecuación tiene la propiedad de que su solución es la suma de dos soluciones.
$\color{black}\fbox{$\color{blue}y = y_c + y_p$}\quad$
Donde $y_c$ es una solución de la ecuación homogénea $\wedge$ $y_p$ es una solución particular de la ecuación no homogénea.
Método de solución
Propiedad
Las ecuaciones lineales tienen la propiedad que el lado izquierdo de la ecuación resultante es la derivada del producto del factor integrante por la variable dependiente, esto es.
$\dfrac {d}{dx}\left[ e^{\int p\left( x\right) dx}y\right] =e^{\int p(x) dx}f(x)$
Reemplazando el factor integrante $e^{\int p(x) dx}$ por $F.I$ en la ecuación y despejando, llegamos a la ecuación.
Cuando se aplica la propiedad, se resuelven de forma más sencilla las ecuaciones lineales, pues sólo se debe integrar el lado derecho de la ED.
 Ejemplo 1: ED lineal homogénea
Ejemplo 1: ED lineal homogéneaResolver la ED $\dfrac {dy}{dx}=-2y$
Solución Esta ED la resolvimos por variables separables, ejemplo $5$, página $65$. Ahora la vamos a resolver como una ecuación lineal.
$\dfrac {dy}{dx}=-2y$
Pasando $-2y$ al lado izquierdo de la ecuación nos queda una ED lineal homogénea.
$\dfrac {dy}{dx}+2y=0$
Como la ecuación está en forma estándar identificamos $p(x)$ y hallamos el factor integrante.
$p(x) = 2$ $F.I = e^{2x}$
Multiplicando la forma estándar por el $F.I$
$e^{2x}\dfrac {dy}{dx}+2e^{2x}y=0$
Tenemos una ecuación de variables separables.
$\displaystyle \int_{}^{} \dfrac {dy}{y}=-2\int dx$
Ahora integramos ambos lados de la ecuación.
$\ln \left| y\right|=-2x+c$
Eliminando logaritmos llegamos a la solución.
 Ejemplo 2: ED lineal no homogénea
Ejemplo 2: ED lineal no homogéneaResolver la ED $\dfrac {dy}{dx}=-2y+10$
Solución Esta ED la resolvimos homogénea en el ejemplo 1. Ahora la vamos a resolver no homogénea, vamos a obtener la solución complementaria $y_c$ del ejemplo anterior más la solución particular $y_p$ asociada a la ED no homogénea.
$\dfrac {dy}{dx}=-2y+10$
Pasando $-2y$ al lado izquierdo de la ecuación, obtenemos una ecuación lineal no homogénea.
$\dfrac {dy}{dx}+2y=10$
ecuación en forma estándar, identificamos $p(x)$ $\wedge$ y hallamos el F.I.
$p(x) = 2$ $F.I = e^{2x}$
Multiplicando la forma estándar por el $F.I$
$e^{2x}\dfrac {dy}{dx}+2e^{2x}y=10e^{2x}$
Ahora tenemos una ecuación de variables separables.
$e^{2x}\dfrac {dy}{dx}=-2e^{2x}y+10e^{2x}$
Sacando factor común para separar variables.
$e^{2x}\dfrac {dy}{dx}=-2e^{2x}(y-5)$
ahora pasamos el $dx$ al lado derecho y separamos variables.
$\dfrac {dy}{y-5}=-2dx$
Los diferenciales indican que hay que integrar ambos lados de la ED.
$\displaystyle \int \dfrac {dy}{y-5}=-2\int dx$
Integrando.
$\ln \left| y-5\right| = -2x + c$
Quitando el logaritmo.
$e^{\ln \left| y-5\right|} =e^{ -2x + c}$
La ecuación queda de la forma.
La respuesta contiene la solución complementaria $y_c = c e^{-2x}$ la cual obtuvimos en el ejemplo 1 y también la solución particular $y_p=5$ que corresponde a la solución de la ED no homogénea, por lo cual la solución general es la suma de dos soluciones $y=y_c+y_p$
Cuando se resuelven ED lineales de primer orden, no es necesario hacer la distinción en la solución entre $y_c\; \wedge\;y_p$, pero cuando se resuelvan las ED de orden superior si es necesario, pues cada una se resuelve de forma diferente.
Otra forma de resolver una ED lineal es aplicando la propiedad.
$\color{black}\fbox{$\color{blue}F.I y = \int F.I f(x) dx$}\quad$
Observe que al usar la propiedad sólo se debe integrar el lado derecho de la ecuación y luego despejar la variable dependiente $y$ esto reduce las operaciones matemáticas para llegar a la solución de la ED.
Se debe llevar la ED a la forma estándar, identificar $p(x)$ para hallar el factor integrante. En lugar de multiplicar toda la forma estándar por el factor integrante para resolver la ecuación por variables separables, se aplica la propiedad $F.I y = \int F.I f(x) dx$
Vamos a resolver nuevamente el ejercicio anterior aplicando la propiedad.
$e^{2x} y = \int 10e^{2x}dx$
Integrando.
$e^{2x} y = 5e^{2x}+c$
Despejando $y$
$y = \dfrac {5e^{2x}}{e^{2x}}+\dfrac {c}{e^{2x}} $
La solución es.
Nota: Todas las ecuaciones diferenciales lineales se pueden resolver aplicando la propiedad $F.I y = \int F.I f(x) dx$. Observe que aplicando la propiedad se reduce el método de solución, pues sólo se debe integrar el lado derecho de la ecuación.
 Ejemplo 3: ED lineal no homogénea
Ejemplo 3: ED lineal no homogéneaResolver la ED $x\dfrac {dy}{dx}-y=x^2senx$
Solución Esta ED no está en forma estándar. Se debe dividir cada término por $x$ para llevarla a la forma estándar.
$\dfrac {dy}{dx}-\dfrac {1}{x}y=x\;senx $
Como la ecuación está en forma estándar identificamos $p(x)$ $\wedge$ hallamos el factor integrante.
$p(x)=\dfrac {-1}{x}$ $F.I = x^{-1}$
Ahora aplicamos la propiedad para resolverla.
$x^{-1} y = \int x^{-1} x\;senx dx$
Aplicando potenciación para unir términos semejantes.
$x^{-1} y = \int senx dx$
Integrando el lado derecho de la ecuación.
$x^{-1} y = -cosx +c$
Despejamos la variable dependiente $y$
$y=\dfrac {-cosx}{x^{-1}}+\dfrac {c}{x^{-1}}$
La solución es.
 Ejemplo 4: ED lineal no homogénea
Ejemplo 4: ED lineal no homogéneaResolver la ED $\dfrac {dy}{dx}+ny=e^{nx}$
Solución La ED está en forma estándar.
$\dfrac {dy}{dx}+ny=e^{nx}$
Como la ecuación está en forma estándar, identificamos $p(x)$ y hallamos el factor integrante.
$p(x)=n$ $F.I =e^{nx}$
Aplicamos la propiedad para resolver la ecuación lineal.
$e^{nx} y = \int e^{nx}\;e^{nx} dx$
Ahora aplicamos potenciación para agrupar términos semejantes.
$e^{nx} y = \int e^{2nx}dx$
Integrando el lado derecho. Recuerde que esta integral es por sustitución donde $u=nx$
$e^{nx} y = \dfrac {e^{2nx}}{2n}+c$
Despejando la $y$
$y=\dfrac{e^{2nx}}{2ne^{nx}}+\dfrac{c}{e^{nx}}$
La solución es.
En la siguiente escena interactiva, podrás ver la gráfica del ejemplo $4$, pero también podrás interactuar con los valores de $n$ para visualizar diferentes ecuaciones diferenciales y observar cómo cambia la gráfica a medida que se cambia el valor de $n$ o el valor del parámetro $c$, también podrás observar la solución particular para cada ED.
Al cambiar el valor de $n$ en la escena interactiva, la gráfica varia en la inclinación de la curva.
Al cambiar el valor de $c$ en la escena interactiva, cambia la forma de la gráfica.
En la siguiente escena interactiva, diseñada por Jorge Olivares Funes, podrás ver cómo cambia la gráfica del ejemplo 4 al cambiar los valores de $n$ y de la constante.
Es recomendable tomar tu cuaderno de apuntes y resolver varios ejercicios cuando cambies los valores de $n$ o de $c$ y luego compruebes tus resultados con los de la escena interactiva.
En la página siguiente encontrarás una escena donde puedes ingresar el $p(x)$ y el $f(x)$ para resolver diferentes ED.
En la siguiente escena interactiva, diseñada por Ravinder Kumar, podrás Resolver ecuaciones lineales.
En la siguiente escena interactiva, diseñada por Ravinder Kumar, podrás Resolver ecuaciones lineales homogéneas y no homogéneas y visualizar su gráfica.
En el siguiente video, realizado por Jaime H. Ramírez Rios, podrás observar un ejemplo de ecuación lineal.
En la siguiente escena interactiva, diseñada por Diego Sandoval, podrás resolver ED lineales y visualizar su campo de direcciones.
Una ecuación diferencial de primer orden de la forma.
$M(x,y)dx + N(x,y)dy=0$
es una ecuación exacta si la expresión del lado izquierdo es una diferencial exacta.
Teorema. Criterio para una diferencial exacta: Sean continuas $ M (x,y) dx \;\; \wedge \;\; N (x,y) dy$, con derivadas parciales continuas en una región rectangular $R$, definida por $a < x < b, c < y < d $. Entonces la condición necesaria y suficiente para que $M (x,y) dx + N (x,y) dy$ sea una diferencial exacta es que:
$\dfrac {\partial M}{\partial y}=\dfrac {\partial N}{\partial x}$
Método de solución
- Dada una función de la forma $M (x,y) dx + N (x,y) dy = 0$ se determina si es exacta. En caso afirmativo, existe una función para la cual.
- Determinamos $f$ si integramos $M (x,y)$ con respecto a $x$, manteniendo a $y$ constante.
$\color{black}\fbox{$\color{blue}f(x,y) = \int M (x,y) dx + g(y) \;\;\;\; (1)$}\quad$
Donde $g(y)$ es la constante de integración.
- Luego derivamos la ecuación $(1)$ con respecto a $y$ $\wedge$ suponemos que.
- Por último integramos con respecto a $y$ $\wedge$ sustituimos en la ecuación $(1)$
- La solución implícita de la ecuación es.
$\color{black}\fbox{$\color{blue}f(x,y) = c$}\quad$
Es importante anotar que este método de solución se puede invertir comenzando con $\dfrac {\partial f}{\partial y}=N(x,y)$ y el resultado es el mismo.
 Ejemplo 1: ED exacta
Ejemplo 1: ED exactaDeterminar si la ED $2y(y-1)dx+x(2y-1)dy=0$ es exacta, si lo es resuélvala.
Solución
$2y(y-1)dx+x(2y-1)dy=0$
Primero debemos aplicar la propiedad distributiva.
$(2y^2-2y)dx+(2xy-x)dy=0$
Determinamos si es exacta. Derivamos parcialmente $M$ con respecto a $y$ dejando $x$ constante.
$\dfrac {\partial M}{\partial y}=4y-2$
Derivamos parcialmente $N$ con respecto a $x$ dejando $y$ constante.
 Ejemplo 2: ED exacta
Ejemplo 2: ED exactaDeterminar si la ED $2xydx+(x^2-1)dy=0$ es exacta, si lo es resuélvala.
Solución
$2xydx+(x^2-1)dy=0$
Determinamos si es exacta. Derivamos parcialmente $M$ con respecto a $y$ dejando $x$ constante.
$\dfrac {\partial M}{\partial y}=2x$
Derivamos parcialmente $N$ con respecto a $x$ dejando $y$ constante.
$\dfrac {\partial N}{\partial x}=2x$
Como ${\color{blue}\;\dfrac {\partial M}{\partial y} = \dfrac {\partial N}{\partial x}}$, entonces, la ecuación es exacta.
$2xydx+(x^2-1)dy=0$
Asumimos $\dfrac {\partial f}{\partial x}=M(x,y)$.
$\partial f =(2xy){\partial x}$
Los diferenciales indican que se debe integrar.
$\int \partial f =\int 2xy {\partial x}$
Como vamos a integrar con respecto a $x$ tanto el $2$ como la $y$ son constantes.
$\int \partial f =2y \int x {\partial x}$
Integramos.
$f(x,y) = x^2 y + g(y)\;$ $(1)$
Derivamos la ecuación $(1)$ con respecto a $y$ dejando $x$ constante.
$x^2+g'(y)$
Ahora igualamos este resultado con $N$.
$x^2+g'(y)=x^2-1$
Simplificamos e integramos con respecto a $y$
$g(y)=-y$
Reemplazando este valor en la ecuación $(1)$ y como ${\color{blue}f(x,y)=c}$ obtenemos.
En la siguiente escena interactiva, diseñada por Victor Cruz, podrás resolver ED exactas y visualizar su gráfica.
En la siguiente escena interactiva, diseñada por Víctor Cruz, podrás resolver ED exactas ingresando $M(x,y) \wedge N(x,y)$
 Ejemplo 3: Resolver el PVI
Ejemplo 3: Resolver el PVIDeterminar si la ED es exacta, si lo es resuélvala.
$(y^2cosx-3x^2y-2x)dx+(2ysenx-x^3+\ln \left| y\right|)dy=0$
Sujeta a la condición inicial $y(0)=e$
Solución
Determinamos si es exacta. Derivamos parcialmente $M$ con respecto a $y$ dejando $x$ constante.
$2ycosx-3x^2$
Ahora derivamos parcialmente $N$ con respecto a $x$ dejando $y$ constante.
$2ycosx-3x^2$
Como ${\color{blue}\;\dfrac {\partial M}{\partial y} = \dfrac {\partial N}{\partial x}}$, entonces, la ecuación es exacta.
Asumimos $\dfrac {\partial f}{\partial x}=M(x,y)$
$\dfrac {\partial f}{\partial x}=y^2cosx-3x^2y-2x$
Despejamos e integramos a ambos lados.
$\int \partial f =\int (y^2cosx-3x^2y-2x) {\partial x}$
Sacamos la constante de cada integral.
$\int \partial f =y^2 \int cosx \partial x -3y \int x^2 \partial x -2 \int x \partial x $
Integramos.
$f(x,y) = y^2 senx -3y\dfrac{x^3}{3}-2\dfrac{x^2}{2}+ g(y)\;$
Simplificando obtenemos.
$f(x,y) = y^2 senx -x^3y-x^2+ g(y)\;$ $(1)$
Derivamos la ecuación $(1)$ con respecto a $y$ dejando $x$ constante.
$2ysenx-x^3+g'(y)$
Ahora igualamos este resultado con $N$.
$2ysenx-x^3+g'(y)=2ysenx-x^3+\ln \left| y\right|$
Ahora simplificamos.
$g'(y)=\ln \left| y\right|$
Integramos con respecto a $y$. Se integra por partes.
$u=\ln \left| y\right|$ $dv=dy$
$du=\dfrac{1}{y}dy$ $v=y$
$\int g'(y)\partial y=y \ln \left| y\right|-\int \partial y$
El valor $g(y)$ es.
$g(y)=y \ln \left| y\right|-y$
Reemplazando este valor en la ecuación $(1)$ y teniendo en cuenta que $f(x,y)=c$ obtenemos la solución general.
$c= y^2 senx -x^3y-x^2+y\ln \left| y\right|-y$
Ahora debemos reemplazar las condiciones iniciales.
$y(0)=e$ para obtener la solución particular.
$c= e^2 sen0 -(0)^3e-(0)^2+e\ln \left|e\right|-e$
Recuerde que ${\color{blue}\ln \left|e\right|=1}$
$c=e-e$
El valor del parámetro es $c=0$
Reemplazando este valor en la solución general.
$0= y^2 senx -x^3y-x^2+y\ln \left| y\right|-y$
Obtenemos la solución particular es.
 Ejemplo 4: ED exacta
Ejemplo 4: ED exactaDeterminar si la ED es exacta, si lo es resuélvala.
$\left(1+\ln \left| x\right|+\dfrac {y}{x}\right)dx=\left(1-\ln \left| x\right|\right)dy$
Solución
Antes de determinar si la ecuación es o no exacta se debe organizar para que cumpla la estructura $M (x,y) dx + N (x,y) dy = 0$ que vimos en la definición.
Se puede pasar cualquiera de los dos términos al otro lado, teniendo en cuenta cual es $M$ y cual es $N$ Para resolver este ejercicio pasamos el término del lado derecho al lado izquierdo.
$\left(1+\ln \left| x\right|+\dfrac {y}{x}\right)dx-(1-\ln \left| x\right|)dy=0$
Los dos términos deben ser positivos, por lo cual sacamos factor común $-1$ del segundo término.
$\left(1+\ln \left| x\right|+\dfrac {y}{x}\right)dx+(-1+\ln \left| x\right|)dy=0$
Ahora si podemos determinar si la ED es exacta. Derivamos parcialmente $M$ con respecto a $y$ dejando $x$ constante. Cuando en la ED no aparecen los dos términos al lado izquierdo o están negativos, se debe ajustar antes de comprobar si es exacta.
$\dfrac {1}{x}$
Derivamos parcialmente $N$ con respecto a $x$ dejando $y$ constante.
$\dfrac {1}{x}$
Como ${\color{blue}\;\dfrac {\partial M}{\partial y} = \dfrac {\partial N}{\partial x}}$, entonces, la ecuación es exacta.
Asumimos $\dfrac {\partial f}{\partial x}=M(x,y)$
$\displaystyle \int \partial f =\displaystyle \int \left(1+\ln \left| x\right|+\dfrac {y}{x}\right){\partial x}$
Separamos las integrales.
$\displaystyle \int \partial f =\displaystyle \int {\partial x}+\displaystyle \int \ln \left| x\right| {\partial x}+y\displaystyle \int \dfrac {1}{x}{\partial x}$
Integramos $M$ con respecto a $x$ dejando $y$ constante.
$f(x,y) = x+x\ln \left| x\right|-x+y\ln \left| x\right|+ g(y)\;$ $(1)$
Agrupando términos semejantes.
$f(x,y) = x\ln \left| x\right|+y\ln \left| x\right|+ g(y)\;$ $(1)$
Derivamos la ecuación $(1)$ con respecto a $y$ dejando $x$ constante.
$\ln \left| x\right|+g'(y)$
Ahora igualamos este resultado con $N$.
$\ln \left| x\right|+g'(y)=-1+\ln \left| x\right|$
Simplificamos.
$g'(y)=-1$
Integramos con respecto a $y$
$g(y)=-y$
Reemplazando este valor en la ecuación $(1)$
Teniendo en cuenta que $f(x,y)=c$ obtenemos la solución general.
En la siguiente escena interactiva, diseñada por Ravinder Kumar, podrás resolver ED exactas y visualizar su gráfica.
En el siguiente video, realizado por Jaime H. Ramírez Rios, podrás observar un ejemplo de ecuación exacta.
En la siguiente escena interactiva, diseñada por Ravinder Kumar, podrás resolver ED exactas.
Muchas ED que no son exactas se pueden transformar en exactas usando un factor integrante. luego de transformar la ED se utiliza el método de solución visto en las ecuaciones exactas. Si la ecuación no se puede transformar en exacta se resuelve por otro método que veremos más adelante.
Para transformar una ecuación no exacta en exacta se utiliza la siguiente sustitución.
Si $p(x)$ es función sólo de la variable $x$, entonces el factor integrante $e^{\int p(x) dx}$ la transforma en exacta.
Si $p(x)$ depende de dos variables, entonces se utiliza la siguiente sustitución.
Si $p(y)$ es función sólo de la variable $y$, entonces el factor integrante $e^{\int p(y) dy}$ la transforma en exacta.
Si una de las dos sustituciones queda en términos de una sola variable, entonces el factor integrante la transforma en exacta. es importante anotar que no todas las ED de primer orden tienen factor integrante y la sustitución tampoco permite encontrar todos los factores integrantes posibles de la ED. Sólo permite encontrar factores integrantes univariables.
 Ejemplo 1: ED reducible a exacta
Ejemplo 1: ED reducible a exactaDeterminar el factor integrante para resolver la ED.
$xydx+(2x^2+3y^2-20)dy=0$
Solución
Determinamos si es exacta. Derivamos parcialmente $M$ con respecto a $y$ dejando $x$ constante.
$x$
Ahora derivamos parcialmente $N$ con respecto a $x$ dejando $y$ constante.
$4x$
Como ${\color{blue}\;\dfrac {\partial M}{\partial y} \neq \dfrac {\partial N}{\partial x}}$, entonces, la ecuación no es exacta.
Realizamos la sustitución $p\left( x\right) =\dfrac {\dfrac {\partial M}{\partial y}-\dfrac {\partial N}{ax}}{N\left( x,y\right) }$
$\dfrac {x-4x}{2x^2+3y^2-20}=\dfrac {-3x}{2x^2+3y^2-20}$
Como el resultado depende de dos variables buscamos $p(y)$
$\dfrac {4x-x}{xy}=\dfrac {3x}{xy}=\dfrac {3}{y}$
Como el resultado depende de una variable, utilizamos $p(y)$ para hallar el factor integrante.
$F.I=e^{\int \frac {3}{y}dy}=y^3$
Ahora multiplicamos la ED no exacta por el $F.I$
$[xydx+(2x^2+3y^2-20)dy=0]y^3$
$xy^4dx+(2x^2y^3+3y^5-20y^3)dy=0$
Derivamos $M$ con respecto a $y$ dejando $x$ constante.
$4xy^3$
Derivamos $N$ con respecto a $x$ dejando $y$ constante.
$4xy^3$
Como ${\color{blue}\;\dfrac {\partial M}{\partial y} = \dfrac {\partial N}{\partial x}}$, entonces, la ecuación es exacta.
Asumimos $\dfrac {\partial f}{\partial x}=M(x,y)$
$\partial f =\left(xy^4 \right){\partial x}$
Los diferenciales indican que se debe integrar.
$\int \partial f =\int \left(xy^4 \right){\partial x}$
Integramos $M$ con respecto a $x$ dejando $y$ constante.
$f(x,y) = \dfrac {x^2y^4}{2}+ g(y)\;$ $(1)$
Derivamos la ecuación $(1)$ con respecto a $y$ dejando $x$ constante.
$2x^2y^3+g'(y)$
Igualamos este resultado con $N$.
$2x^2y^3+g'(y)=2x^2y^3+3y^5-20y^3$
Simplificando obtenemos.
$g'(y)=3y^5-20y^3$
Integramos con respecto a $y$
$\displaystyle \int g'(y) \partial y=\displaystyle \int (3y^5-20y^3)\partial y $
Integral directa.
$g(y)=\dfrac {3y^6}{6}-\dfrac {20y^4}{4}$
Simplificando.
$g(y)=\dfrac {y^6}{2}-5y^4$
Reemplazando este valor en la ecuación $(1)$ y teniendo en cuenta que $f(x,y)=c$ obtenemos la solución general.
 Ejemplo 2: ED reducible a exacta
Ejemplo 2: ED reducible a exactaDeterminar el factor integrante para resolver la ED.
$(cos2y-senx)dx+(-2tanxsen2y)dy=0$
Solución
Determinamos si es exacta. Derivamos parcialmente $M$ con respecto a $y$ dejando $x$ constante.
$-2sen2y$
Ahora derivamos parcialmente $N$ con respecto a $x$ dejando $y$ constante.
$-2sec^2xsen2y$
Como ${\color{blue}\;\dfrac {\partial M}{\partial y} \neq \dfrac {\partial N}{\partial x}}$, entonces, la ecuación no es exacta.
Realizamos la sustitución $p\left( x\right) =\dfrac {\dfrac {\partial M}{\partial y}-\dfrac {\partial N}{ax}}{N\left( x,y\right) }$
$\dfrac {-2sen2y+2sec^2xsen2y}{-2tanxsen2y}$
Sacando factor común.
$\dfrac {-2sen2y(-1+sec^2x)}{-2tanxsen2y}$
Simplificando $\wedge$ aplicando identidad pitagórica. ${\color{blue}\;-1+sec^2x=tan x}$
$\dfrac {-1+sec^2x}{-tanx}=\dfrac {tan^2x}{-tanx}$
Como el resultado depende de una variable, utilizamos $p(x)$ para hallar el factor integrante.
$F.I=e^{\int -tanxdx}=cosx$
Ahora multiplicamos la ED no exacta por el $F.I$
$[(cos2y-senx)dx+(-2tanxsen2y)dy=0]cosx$
$(cosxcos2y-senxcosx)dx+(-2senxsen2y)=0$
Tenga en cuenta que se aplicó la identidad ${\color{blue}\;cosxtanx=senx}$
Derivamos $M$ con respecto a $y$ dejando $x$ constante.
$-2cosxsen2y$
Derivamos $N$ con respecto a $x$ dejando $y$ constante.
$-2cosxsen2y$
Como ${\color{blue}\;\dfrac {\partial M}{\partial y} = \dfrac {\partial N}{\partial x}}$, entonces, la ecuación es exacta.
Asumimos $\dfrac {\partial f}{\partial x}=M(x,y)$
$\partial f =\left(cosxcos2y-senxcosx \right){\partial x}$
Los diferenciales indican que se debe integrar.
$\int \partial f =\int \left(cosxcos2y-senxcosx \right){\partial x}$
Integramos $M$ con respecto a $x$ dejando $y$ constante.
$f(x,y) = senxcos2y+ \dfrac {cos^2x}{2}+ g(y)\;$ $(1)$
Derivamos la ecuación $(1)$ con respecto a $y$ dejando $x$ constante.
$-2senxsen2y+g'(y)$
Ahora igualamos este resultado con $N$.
$-2senxsen2y+g'(y)=-2senxsen2y$
Al simplificar vemos que $g'(y)=0$. Cuando integramos el $0$ el resultado es $0+c$ como la constante sólo se tiene en cuenta en la respuesta podemos decir que:
$g(y)=0$
Reemplazando este valor en la ecuación $(1)$ $\wedge$ teniendo en cuenta que $f(x,y)=c$ obtenemos la solución general.
 Ejemplo 3: ED reducible a exacta
Ejemplo 3: ED reducible a exactaDeterminar el factor integrante para resolver la ED.
$(2xy\ln \left| y\right|)dx+(x^2+y^2\sqrt {y^{2}+1})dy=0$
Solución
Determinamos si es exacta. Derivamos parcialmente $M$ con respecto a $y$ dejando $x$ constante.
$2x+2x\ln \left| y\right|$
Derivamos parcialmente $N$ con respecto a $x$ dejando $y$ constante.
$2x$
Como ${\color{blue}\;\dfrac {\partial M}{\partial y} \neq \dfrac {\partial N}{\partial x}}$, entonces, la ecuación no es exacta.
Realizamos la sustitución $p\left( x\right) =\dfrac {\dfrac {\partial M}{\partial y}-\dfrac {\partial N}{ax}}{N\left( x,y\right) }$
$\dfrac {2x+2x\ln \left| y\right|-2x}{x^2+y^2\sqrt {y^{2}+1}}$
Simplificando.
$\dfrac {2x\ln \left| y\right|}{x^2+y^2\sqrt {y^{2}+1}}$
Como el resultado depende de dos variables, utilizamos la sustitución $p(y)$
$\dfrac {2x-2x-2x\ln \left| y\right|}{2xy\ln \left| y\right|}$
Simplificando.
$\dfrac {-2x\ln \left| y\right|}{2xy\ln \left| y\right|}=\dfrac {-1}{y}$
Hallamos el factor integrante.
$F.I=e^{\int \frac {-1}{y}dy}=y^{-1}$
Ahora multiplicamos la ED no exacta por el $F.I$
$(2x\ln \left| y\right|)dx+(x^2y^{-1}+y\sqrt {y^{2}+1})dy=0$
Derivamos $M$ con respecto a $y$ dejando $x$ constante.
$2xy^{-1}$
Derivamos $N$ con respecto a $x$ dejando $y$ constante.
$2xy^{-1}$
Como ${\color{blue}\;\dfrac {\partial M}{\partial y} = \dfrac {\partial N}{\partial x}}$, entonces, la ecuación es exacta.
Asumimos $\dfrac {\partial f}{\partial x}=M(x,y)$
$\partial f =\left (2x\ln \left| y\right|\right){\partial x}$
Los diferenciales indican que se debe integrar.
$\int \partial f = \int 2x\ln \left| y\right|{\partial x}$
Integramos $M$ con respecto a $x$ dejando $y$ constante.
$f(x,y) = x^2\ln \left| y\right|+ g(y)\;$ $(1)$
Derivamos la ecuación $(1)$ con respecto a $y$ dejando $x$ constante.
$x^2y^{-1}+g'(y)$
Ahora igualamos este resultado con $N$.
$x^2y^{-1}+g'(y)=x^2y^{-1}+y\sqrt {y^{2}+1}$
Simplificando.
$g'(y)=y\sqrt {y^{2}+1}$
Ahora integramos esta ecuación con respecto a $y$.
$\displaystyle \int g'(y) \partial y=\displaystyle \int y\sqrt {y^{2}+1}$ $\partial y $
Integral por sustitución.
$u=y^2+1$ $\wedge$ $du=2ydy$
Reemplazando en la integral.
$g'(y)=\dfrac{1}{2}\int u^{\frac{1}{2}}du$
Integrando obtenemos.
$g(y)=\dfrac{1}{3}\int u^{\frac{3}{2}}$
Reemplazamos el valor de $u$ en la respuesta.
$g(y)=\dfrac{1}{3} (y^2+1)^{\frac{3}{2}}$
Entonces $g(y)$ es:
$g(y)=\dfrac {1}{3}\sqrt {\left( y^{2}+1\right) ^{3}}$
Reemplazando este valor en la ecuación $(1)$ $\wedge$ teniendo en cuenta que $f(x,y)=c$ obtenemos la solución general.
 Ejemplo 4: Resolver el PVI
Ejemplo 4: Resolver el PVIDeterminar el factor integrante para resolver la ED.
$xtanxdx-ycosxdy=0$
Sujeta a la condición inicial $y(0)=2$
Solución
Debemos organizar la ED para que cumpla la estructura $M(x,y)dx+N(x,y)dy=0$
$xtanxdx+(-ycosx)dy=0$
Determinamos si es exacta. Derivamos parcialmente $M$ con respecto a $y$ dejando $x$ constante.
$0$
Ahora derivamos parcialmente $N$ con respecto a $x$ dejando $y$ constante.
$ysenx$
Como ${\color{blue}\;\dfrac {\partial M}{\partial y} \neq \dfrac {\partial N}{\partial x}}$, entonces, la ecuación no es exacta.
Buscamos un factor integrante para convertirla en exacta.
Realizamos la sustitución $p\left( x\right) =\dfrac {\dfrac {\partial M}{\partial y}-\dfrac {\partial N}{ax}}{N\left( x,y\right) }$
$\dfrac {0-ysenx}{-ycosx}$
Simplificando.
$\dfrac {senx}{cosx}$
hallamos el factor integrante.
$F.I=e^{\int tanx dx}=secx$
La integral de secante está en la página $70$
Ahora multiplicamos la ED no exacta por el $F.I$
$[xtanxdx+(-ycosx)dy=0]secx$
$(xsecxtanx)dx+(-y)dy=0$
Tenga en cuenta que se aplicó la identidad ${\color{blue}\;cosxsecx=1}$
Derivamos $M$ con respecto a $y$ dejando $x$ constante.
$0$
Derivamos $N$ con respecto a $x$ dejando $y$ constante.
$0$
Como ${\color{blue}\;\dfrac {\partial M}{\partial y} = \dfrac {\partial N}{\partial x}}$, entonces, la ecuación es exacta.
Asumimos $\dfrac {\partial f}{\partial x}=M(x,y)$
$\int \partial f = \int x\;secx\;tanx\;{\partial x}$
Integramos $M$ con respecto a $x$ dejando $y$ constante.
$u=x$ $dv=secxtanxdx$ $du=dx$ $v=secx$
Aplicando la fórmula de integración por partes.
$\int \partial f = xsecx-\int secxdx$
Integrando la $secx$ obtenemos.
$f(x,y) = xsecx-\ln \left| secx+tanx\right|+ g(y)\;$ $(1)$
Derivamos la ecuación $(1)$ con respecto a $y$ dejando $x$ constante y la igualamos con $N$
$g'(y)=-y$
Integramos con respecto a $y$.
$\int g'(y) \partial y=\int -y \partial y$
Integral directa.
$g(y)=-\dfrac{y^2}{2}$
Reemplazando en la ecuación $(1)$ $\wedge$ teniendo en cuenta que $f(x,y)=c$
$c = xsecx-\ln \left| secx+tanx\right| -\dfrac{y^2}{2}$
Ahora reemplazamos las condiciones iniciales $y(0)=2$
$c = 0sec0-\ln \left| sec0+tan0\right| -\dfrac{2^2}{2}$ $c = -2$
Entonces la solución particular de la ED es.
En el siguiente video, realizado por Jaime H. Ramírez Rios, podrás observar un ejemplo de una ecuación reducible a exacta.
Si una ED tiene la forma $M(x,y)dx + N(x,y)dy=0$
Tiene la siguiente propiedad.
a) $M(tx,ty)=t^nM(x,y)$
b) $N(tx,ty)=t^nN(x,y)$
Entonces se dice que tiene coeficientes homogéneos o que es una ecuación diferencial homogénea.
Nota: Una ecuación diferencial homogénea siempre se puede llevar a una ecuación diferencial de variables separables por medio de una sustitución algebraica adecuada.
$f(tx,ty)=t^nf(x,y)$
Método de solución
- Si $f(x,y)$ es una función homogénea de grado $n$, es posible hacer una sustitución con el fin de llevarla a una E.D. de variables separables.
- La sustitución que normalmente se hace es:
Recuerde que, con esta sustitución, la ecuación se vuelve variables separables, sí la integral es muy difícil o imposible de resolverse utiliza la siguiente sustitución.
 Ejemplo 1: ED homogénea
Ejemplo 1: ED homogéneaResolver la ED.
$x \dfrac{dy}{dx}=(y+xe^\frac{y}{x})$
Solución
Primero se determina si la ecuación es homogénea.
$tx \dfrac{dy}{dx}=(ty+txe^\frac{ty}{tx})$
Se simplifica $\wedge$ se saca factor común.
$tx \dfrac{dy}{dx}=t(y+xe^\frac{y}{x})$
Se determina que la ecuación es homogénea de grado 1. Ahora se hace el cambio de variable.
${\color{blue}y=ux}$ derivando ${\color{blue}dy=udx+xdu}$
$x \dfrac {udx+xdu}{dx}=(ux+xe^u)$
Al hacer la sustitución la ecuación se vuelve variables separables, subimos $dx$ y sacamos factor común $x$.
$x(udx+xdu)=x(u+e^u)dx$
Simplificamos la $x$ $\wedge$ hacemos distributiva.
$udx+xdu=udx+e^udx$
Agrupamos los $dx$ a un lado $\wedge$ el $du$ al otro lado.
$xdu=udx-udx+e^udx$
Simplificamos $\wedge$ separamos variables.
$\dfrac {du}{e^u}=\dfrac {dx}{x}$
Los diferenciales indican que se debe integrar.
$\int e^{-u}du=\displaystyle \int \dfrac {dx}{x}$
integrando obtenemos.
$-e^{-u}=\ln \left| x\right|+c$
Sustituimos nuevamente la $u$
$-e^{-\frac{y}{x}}=\ln \left| x\right|+c$
Multiplicamos por $-1$ para dar la solución.
 Ejemplo 2: ED homogénea
Ejemplo 2: ED homogéneaResolver la ED.
$(y^2+yx)dx-x^2dy=0$
Solución
Primero se determina si la ecuación es homogénea.
$(t^2y^2+tytx)dx-t^2x^2dy=0$
Se multiplica el parámetro.
$(t^2y^2+t^2yx)dx-t^2x^2dy=0$
Se saca factor común.
$t^2(y^2+yx)dx-t^2x^2dy=0$
Se determina que la ecuación es homogénea de grado 2. Ahora se hace el cambio de variable.
${\color{blue}y=ux}$ derivando ${\color{blue}dy=udx+xdu}$
$((ux)^2+uxx)dx-x^2(udx+xdu)=0$
Para resolver la ecuación se saca factor común $x^2$ $\wedge$ pasamos el segundo término a la derecha.
$x^2(u^2+u)dx=x^2(udx+xdu)$
Simplificamos $x^2$ $\wedge$ hacemos distributiva.
$u^2dx+udx=udx+xdu$
Se deben separar los diferenciales a diferente lado para poder separar variables.
$u^2dx=xdu$
Ahora se separan variables.
$\dfrac {dx}{x}=\dfrac {du}{u^2}$
Los diferenciales indican que se debe integrar.
$\displaystyle \int \dfrac {dx}{x}=\displaystyle \int u^{-2}du$
integrando obtenemos.
$\ln \left| x\right|+c=-u^{-1}$
Sustituimos nuevamente la $u$
$\ln \left| x\right|+c=-\dfrac{x}{y}$
despejando la $y$, queda la solución.
 Ejemplo 3: Resolver el PVI
Ejemplo 3: Resolver el PVIResolver la ED.
$\left( y+x\cot \dfrac{y}{x}\right) dx-xdy=0$
Solución
Primero se determina si la ecuación es homogénea.
$\left(ty+txcot\dfrac{ty}{tx}\right)dx-txdy=0$
Se simplifica $\wedge$ se saca factor común.
$t\left(y+xcot\dfrac{y}{x}\right)dx-txdy=0$
Como los dos términos tienen el mismo factor $t$, se determina que la ecuación es homogénea de grado 1. Ahora se hace el cambio de variable.
${\color{blue}y=ux}$ derivando ${\color{blue}dy=udx+xdu}$
$(ux+xcotu)dx-x(udx+xdu)=0$
Al hacer la sustitución la ecuación se vuelve variables separables, ahora sacamos factor común $x$ $\wedge$ pasamos el segundo término a la derecha.
$x(u+cotu)dx=x(udx+xdu)$
Simplificamos $x$ $\wedge$ hacemos distributiva.
$udx+cotudx=udx+xdu$
separamos diferenciales.
$udx+cotudx-udx=xdu$
Simplificamos $\wedge$ separamos variables.
$\dfrac {dx}{x}=\dfrac {du}{cotu}$
Los diferenciales indican que se debe integrar $\wedge$ se aplica la identidad ${\color{blue}\dfrac {1}{cotu}=tanu}$
$\displaystyle \int \dfrac {dx}{x}=\displaystyle \int tanudu$
integrando obtenemos.
$\ln \left| x\right|+c=\ln \left| secu\right|$
Aplicamos axioma de igualdad.
$e^{\ln \left| x\right|+c}=e^{\ln \left| secu\right|}$
Quitando logaritmos. Recuerde que ${\color{blue}e^{\ln \left| x\right|}=x}$
$cx=secu$
Sustituyendo la $u$
$cx=sec\dfrac{y}{x}$
Axioma de igualdad para despejar $y$
$sec^{-1}(cx)=sec^{-1}sec\dfrac{y}{x}$
Operando.
$sec^{-1}(cx)=\dfrac{y}{x}$
despejando la $y$ queda la solución.
 Ejemplo 4: Resolver la ED homogénea
Ejemplo 4: Resolver la ED homogéneaResolver la ED.
$2x^2ydx=(3x^3+y^3)dy$
Solución
Primero se determina si la ecuación es homogénea.
$2t^2x^2tydx=(3t^3x^3+t^3y^3)dy$
Operando y sacando factor común.
$2t^3x^2ydx=t^3(3x^3+y^3)dy$
Como los dos términos tienen el mismo factor $t^3$, se determina que la ecuación es homogénea de grado 3. Ahora hacemos el cambio de variable.
${\color{blue}y=ux}$ derivando ${\color{blue}dy=udx+xdu}$
$2x^2uxdx=(3x^3+(ux)^3)(udx+xdu)$
Al hacer la sustitución la ecuación se vuelve variables separables, ahora sacamos factor común $x^3$
$2x^3udx=x^3(3+u^3)(udx+xdu)$
Simplificamos $x^3$ $\wedge$ hacemos distributiva.
$2udx=3udx+3xdu+u^4dx+xu^3du$
separamos diferenciales.
$-udx-u^4dx=3xdu+xu^3du$
Sacamos factor común.
$-dx(u+u^4)=xdu(3+u^3)$
Separando variables.
$-\dfrac {dx}{x}=\dfrac {3+u^3}{u+u^4}du$
Los diferenciales indican que se debe integrar.
$-\displaystyle \int \dfrac {dx}{x}=\displaystyle \int \dfrac {3+u^3}{u+u^4}du$
La integral del lado derecho es muy difícil de resolver, pues no se puede hacer por sustitución $\wedge$ por fracciones parciales queda un término irreductible, cuando esto ocurre, se debe volver a comenzar el ejercicio pero utilizando la otra sustitución $x=vy$
${\color{blue}x=vy}$ derivando ${\color{blue}dx=vdy+ydv}$
$2(vy)^2y(vdy+ydv)=(3(vy)^3+y^3)dy$
Operando tenemos.
$2v^2y^3(vdy+ydv)=(3v^3y^3+y^3)dy$
Sacamos factor común $y^3$
$2v^2y^3(vdy+ydv)=y^3(3v^3+1)dy$
Simplificando $\wedge$ haciendo distributiva.
$2v^3dy+2v^2ydv=3v^3dy+dy$
separamos diferenciales y agrupamos términos semejantes.
$2v^2ydv=v^3dy+dy$
Sacamos factor común.
$2v^2ydv=dy(v^3+1)$
Separando variables.
$\dfrac {2v^2}{v^3+1}dv=\dfrac {dy}{y}$
Los diferenciales indican que se debe integrar.
$\displaystyle \int \dfrac {2v^2}{v^3+1}dv=\displaystyle \int \dfrac {dy}{y}$
La integral se resuelve por sustitución.
Es necesario hacer un cambio de variable para resolver la integral del lado izquierdo cambiamos $v^3+1$ por $u$
$u=v^3+1$ $\Rightarrow$ $du=3v^2dv$ $\Rightarrow$ $\dfrac{du}{3}=v^2dv$
$\dfrac {2}{3} \displaystyle \int \dfrac {dv}{v}=\displaystyle \int \dfrac {dy}{y}$
Integrando obtenemos.
$\dfrac {2}{3} \ln \left| u\right|+c=\ln \left| y\right|$
Se organiza el término.
$2\ln \left| v^3+1\right|+c=3\ln \left| y\right|$
Aplicamos propiedades de logaritmos.
$\ln \left| v^3+1\right|^2+c=\ln \left| y\right|^3$
Aplicamos axioma de igualdad.
$e^{\ln \left| v^3+1\right|^2+c}=e^{\ln \left| y\right|^3}$
Quitando logaritmos.
$c(v^3+1)^2=y^3$
Sustituyendo la $v$
$c\left( \dfrac {x^{3}}{y^{3}}+1\right) ^{2}=y^3$
Operando fraccionarios.
$c\left( \dfrac {x^{3}+y^{3}}{y^{3}}\right) ^{2}=y^3$
Aplicando propiedades de potenciación.
$\dfrac {C\left( x^{3}+y^{3}\right) ^{2}}{\left( y^{3}\right) ^{2}}=y^3$
Pasando $y^6$ a multiplicar obtenemos la solución.
En el siguiente video, realizado por Jaime H. Ramírez Rios, podrás observar un ejemplo de ecuación homogénea.
En la siguiente escena interactiva, diseñada por Ravinder Kumar, podrás resolver ecuaciones homogéneas.
En la siguiente escena interactiva, diseñada por Ravinder Kumar, podrás resolver ecuaciones homogéneas.
Algunas veces es necesario hacer un cambio de variable para transformar una ecuación diferencial no lineal en lineal. Lo primero que se debe hacer es llevar la ecuación a la forma estándar, lego hacer una sustitución. Si la ecuación presenta la forma:
Donde $n$ es cualquier número real, es la ecuación de Bernoulli.
Nota: Si $n=0$ $n=1$ la ecuación es lineal.
Si $n\neq 1$ la sustitución.
$\color{black}\fbox{$\color{blue}u=y^{1-n}$}\quad$
Reduce cualquier ecuación de la forma $(1)$ en una ecuación lineal.
 |
La ecuación diferencial de Bernoulli es una ecuación diferencial ordinaria de primer orden, formulada por Jacob Bernoulli. Esta ecuación fue transformada, por Gottfried Leibniz en $1693$ y por Johann Bernoulli en $1697$, es una ecuación diferencial lineal de primer orden, mediante la sustitución $u=y^{1-n}$ |
 Ejemplo 1: Resolver la ED de Bernoulli
Ejemplo 1: Resolver la ED de BernoulliResolver la ED.
$x\dfrac{dy}{dx}+y=x^2y^2$
Solución
Se determina el valor de $n$ para realizar la sustitución. En este ejercicio $n=2$
$u=y^{1-2}$ $\Rightarrow$ $u=y^{-1}$
Despejando la $y$
$y=u^{-1}$
Derivando la $y$
$dy=-u^{-2}du$
Reemplazando la $y$ $\wedge$ el $dy$ en la ecuación de Bernoulli.
$x\dfrac{-u^{-2}du}{dx}+u^{-1}=x^2(u^{-1})^2$
Después de hacer el cambio de variable, la ecuación se transforma en lineal, ahora se debe llevar a la forma estándar.
$\dfrac{-u^{-2}xdu}{-u^{-2}xdx}+\dfrac {u^{-1}}{-u^{-2}x}=\dfrac{x^2u^{-2}}{-u^{-2}x}$
Simplificando.
$\dfrac{du}{dx}-\dfrac {1}{x}u=-x$
La ecuación es lineal en la variable dependiente $u$ $\wedge$ además está en forma estándar. Ahora identificamos $p(x)$ para hallar el factor integrante.
$p(x) = -\dfrac{1}{x}$ $F.I = x^{-1}$
Ahora aplicamos la propiedad para resolver la ED lineal, multiplicando la forma estándar por el $F.I$
$x^{-1}u=-\int x^{-1}xdx$
Ahora debemos integrar el lado derecho de la ecuación.
$x^{-1}u=-x+c$
Despejamos la variable dependiente $u$
$u=-\dfrac{x}{x^{-1}}+\dfrac{c}{x^{-1}}$
Sustituyendo $u$ $\wedge$ aplicando potenciación.
$\dfrac{1}{y}=-x^2+cx$
Despejando $y$ se llega a la solución.
 Ejemplo 2: Resolver la ED de Bernoulli
Ejemplo 2: Resolver la ED de BernoulliResolver la ED.
$\dfrac{dy}{dx}=y(xy^3-1)$
Solución
Se aplica propiedad distributiva.
$\dfrac{dy}{dx}=xy^4-y$
Se organiza la ecuación para que la variable lineal quede al lado izquierdo.
$\dfrac{dy}{dx}+y=xy^4$
La ecuación ya está en la forma de la ecuación de Bernoulli.
${\color{blue}\dfrac {dy}{dx}+ p(x)y=f{(x)}y^{n}}$, ahora se determina el valor de $n$ para realizar la sustitución. En este ejercicio $n=4$
$u=y^{1-4}$ $\Rightarrow$ $u=y^{-3}$
Despejando la $y$
$y=u^{- \frac{1}{3}}$
Derivando la $y$
$dy=-\dfrac{1}{3}u^{- \frac{4}{3}}du$
Reemplazando la $y$ $\wedge$ el $dy$ en la ecuación de Bernoulli.
$\dfrac{-\frac{1}{3}u^{- \frac{4}{3}}du}{dx}+{u^{- \frac{1}{3}}}=x{u^{- \frac{4}{3}}}$
Después de hacer el cambio de variable, la ecuación se transforma en lineal, ahora se debe llevar a la forma estándar.
$\dfrac{-\frac{1}{3}u^{- \frac{4}{3}du}}{-\frac{1}{3}u^{- \frac{4}{3}dx}}+\dfrac {u^{- \frac{1}{3}}}{-\frac{1}{3}u^{- \frac{4}{3}}}=\dfrac{xu^{- \frac{4}{3}}}{-\frac{1}{3}u^{- \frac{4}{3}}}$
Simplificando.
$\dfrac{du}{dx}-3u=-3x$
La ecuación es lineal en la variable dependiente $u$ $\wedge$ además está en forma estándar.
$p(x) = -3$ $F.I = e^{-3x}$
Ahora aplicamos la propiedad para resolver la ED lineal, multiplicando la forma estándar por el $F.I$
$e^{-3x}u=\int -3xe^{-3x}dx$
La integral se resuelve por partes.
$u=-3x$ $dv=e^{-3x} dx$ $du=-3dx$ $v=-\dfrac{1}{3}e^{-3x}$
Reemplazando en la fórmula de integración por partes.
$\int -3xe^{-3x}dx=xe^{-3x}+\dfrac{1}{3}e^{-3x} + c$
Ahora reemplazamos el resultado de esta integral al lado derecho de la ED.
$e^{-3x}u=xe^{-3x}+\dfrac{1}{3}e^{-3x} + c$
Despejando $u$
$u=x+\dfrac{1}{3}+ce^{3x}$
Sustituyendo $u$
$y^{-3}=x+\dfrac{1}{3}+ce^{3x}$
Despejando $y$ se llega a la solución.
 Ejemplo 3: Resolver la ED de Bernoulli
Ejemplo 3: Resolver la ED de BernoulliResolver la ED.
$x^2\dfrac{dy}{dx}+y^2=xy$
Solución
Primero se debe organizar la ecuación, pues no está en forma estándar $\wedge$ la $y$ con exponente aparece en el lado izquierdo.
$\dfrac{dy}{dx}-\dfrac{1}{x}y=-\dfrac{1}{x^2}y^2$
El valor de $n$ es $2$
$u=y^{1-2}$ $\Rightarrow$ $u=y^{-1}$
Despejando la $y$
$y=u^{-1}$
Derivando la $y$
$dy=-u^{-2}du$
Reemplazando la $y$ $\wedge$ el $dy$ en la ecuación de Bernoulli.
$\dfrac{-u^{-2}du}{dx}-\dfrac{1}{x}u^{-1}=-\dfrac{1}{x^2}(u^{-1})^2$
la ecuación ya es lineal, se debe llevar a la forma estándar.
$\dfrac{-u^{-2}du}{-u^{-2}dx}-\dfrac {u^{-1}}{-u^{-2}x}=-\dfrac{u^{-2}}{-u^{-2}x^2}$
Simplificando.
$\dfrac{du}{dx}+\dfrac {1}{x}u=\dfrac {1}{x^2}$
La ecuación es lineal en la variable dependiente $u$ $\wedge$ además está en forma estándar.
$p(x) = \dfrac{1}{x}$ $F.I = x$
Multiplicando la forma estándar por el $F.I$
$xu=\displaystyle \int \dfrac {1}{x}dx$
Integrando.
$xu=\ln \left| x\right|+c$
Despejando $u$
$u=\dfrac {\ln \left| x\right|}{x}+ \dfrac{c}{x}$
Sustituyendo $u$ $\wedge$ aplicando potenciación.
 Ejemplo 4: Resolver el PVI
Ejemplo 4: Resolver el PVIResolver la ED.
$x^2\dfrac{dy}{dx}-2xy=3y^4$ Sujeta a $y(1)=\dfrac{1}{2}$
Solución
Primero se debe llevar la ecuación a la forma estándar.
$\dfrac{dy}{dx}-\dfrac{2}{x}y=\cfrac{3}{x^2}y^4$
El valor de $n$ es $4$
$u=y^{1-4}$ $\Rightarrow$ $u=y^{-3}$
Despejando la $y$
$y=u^{-\frac{1}{3}}$
Derivando la $y$
$dy=-\dfrac{1}{3}u^{-\frac{4}{3}}du$
Reemplazando la $y$ $\wedge$ el $dy$ en la ecuación de Bernoulli.
$\dfrac{-\frac{1}{3}u^{- \frac{4}{3}}du}{dx}-\dfrac{2u^{- \frac{1}{3}}}{x}=\dfrac{3{u^{- \frac{4}{3}}}}{x^2}$
Ya la ecuación es lineal, se debe llevar a la forma estándar.
$\dfrac{-\frac{1}{3}u^{- \frac{4}{3}}du}{-\frac{1}{3}u^{- \frac{4}{3}}dx}-\dfrac{2u^{- \frac{1}{3}}}{-x\frac{1}{3}u^{- \frac{4}{3}}}=\dfrac{3{u^{- \frac{4}{3}}}}{-x^2\frac{1}{3}u^{- \frac{4}{3}}}$
Simplificando.
$\dfrac{du}{dx}+\dfrac{6}{x}u=-\dfrac{9}{x^2}$
Ecuación lineal en forma estándar.
$p(x) = \dfrac{6}{x}$ $F.I = x^6$
Multiplicando la forma estándar por el $F.I$
$x^6u=\int -9x^4dx$
integrando el lado derecho de forma directa, obtenemos.
$x^6u=\dfrac{-9}{5}x^5+c$
Despejando la $u$ y simplificando.
$u=\dfrac{-9}{5x}+\dfrac{c}{x^6}$
Sustituyendo $u$
$y^{-3}=\dfrac{-9}{5x}+\dfrac{c}{x^6}$
Reemplazando valores iniciales.
$\left( \dfrac {1}{2}\right) ^{-3}=\dfrac{-9}{5(1)}+\dfrac{c}{(1)^6}$
Operando.
$8=\dfrac{-9}{5}+c$
Despejando obtenemos el valor de $c$
$c=\dfrac{49}{5}$
Reemplazando en la respuesta obtenemos.
$y^{-3}=\dfrac{-9}{5x}+\dfrac{49}{5x^6}$
Operando el lado derecho.
$y^{-3}=\dfrac{-9x^5+49}{5x^6}$
Bajamos la $y$ para volver el exponente positivo.
$\dfrac{1}{y^3}=\dfrac{-9x^5+49}{5x^6}$
Despejando la $y$ $\wedge$ sacando raíz cúbica obtenemos la siguiente respuesta.
En la siguiente escena interactiva, diseñada por Raul Enrique Escobar Caro, podrás resolver la ecuación de Bernoulli.
En el siguiente video, realizado por Jaime H. Ramírez Rios, podrás observar un ejemplo de ecuación de Bernoulli.
Las ED tienen una importancia fundamental en las matemáticas debido a que es aplicable a casi todas las ramas del saber, entre ellas están: la geometría, la física, la química y la biología. Éstas permiten identificar y aplicar técnicas y conceptos matemáticos que admiten obtener e interpretar la solución de una situación problema en la que intervienen relaciones entre tasas o razones de cambio de variables definidas en diversos contextos.
Algunas de las aplicaciones de las ED de primer orden son: el crecimiento y decrecimiento poblacional, la desintegración radiactiva, el fechado de fósiles con carbono 14, el cambio en las temperaturas y los circuitos en serie, entre otros.
Las ED se utilizan para describir los comportamientos de algunos fenómenos de la vida real en términos matemáticos, dicho proceso recibe el nombre de modelo matemático y se utiliza para comprender las variables que lo conforman, la relación entre ellas, además de predecir el comportamiento de dicho fenómeno.
Cuando dicho modelo lo debe resolver un científico es necesario conocer la fuerza de gravedad que ejerce la tierra sobre dicho cuerpo o la temperatura de ebullición del agua dependiendo de la altitud donde se realice el experimento, más para efectos de este libro, el objetivo se reduce a resolver modelos de baja resolución por lo cual la fuerza de gravedad que se utiliza es de $9.8 \frac{m}{seg^2}$ en el sistema MKS o $32 \frac{pies}{seg^2}$ en el sistema inglés y la temperatura de ebullición del agua que se utilizará es de $100^° C$.
Es por esto que para terminar el capítulo se introduce el modelado de problemas a partir de las leyes físicas que los rigen y que conducen a EDO.
En 1798 el economista inglés Thomas Malthus intentó modelar el crecimiento de la población humana por medio de las matemáticas, su teoría dice que la rapidez con que varía la población de un país es proporcional al número de personas presentes en ese momento. En términos matemáticos, si $p(t)$ denota la población en función del tiempo, su hipótesis se puede expresar cómo.
$\dfrac{dp}{dt}\;\; \alpha p$
Recuerde que en matemáticas, si dos cantidades $x\;\; \wedge \;\; y$ son proporcionales, se escribe $x \;\; \alpha \;\; y$ significando que $x$ es un múltiplo constante de $y$, es decir, $x=ky$, por tanto, la ecuación $\dfrac{dp}{dt}\;\; \alpha p$ se puede reescribir como.
$\dfrac{dp}{dt} =kp$
Donde $k$ es una constante de proporcionalidad.
Podemos observar que la ecuación contiene la derivada de una variable dependiente (población) con respecto a una variable independiente (tiempo), a esta ecuación se le conoce como ED y al resolverla teniendo en cuenta las condiciones iniciales del modelo matemático podemos predecir la cantidad de personas presentes en cualquier momento $t$. Aunque es un modelo simple bastante exacto, puede fallar si no se tienen en cuenta algunos factores como, por ejemplo, migración, inmigración y catástrofes naturales entre otros. Cuando se habla de seres vivos se puede usar para modelar el crecimiento de pequeñas poblaciones en intervalos cortos de tiempo.
Observemos que esta es una ED de primer orden, al organizarla nos queda.
$\dfrac{dp}{dt} -kp=0$
Esta es una ED lineal y está en forma estándar. Identificamos $p(t)$ y hallamos el factor integrante.
$p(t)=-k$ $F.I = e^{-kt}$
Aplicando la propiedad.
$e^{-kt} p = \int 0 dx$
Integrando.
$e^{-kt} p = c$
despejando la $y$
$p=\dfrac {c}{e^{-kt}}$
La solución es.
Esta es la solución de la ED para resolver ejercicios de crecimiento y decrecimiento poblacional. Esta ecuación es la misma que se utiliza para ejercicios de descomposición radiactiva, carbono 14 (C-14) e interés compuesto entre otros, por lo cual para efectos de simplificación de variables cuando no estemos trabajando ejercicios de crecimiento y decrecimiento poblacional, la ecuación la vamos a trabajar con la variable $x$.
 Ejemplo 1: Crecimiento poblacional
Ejemplo 1: Crecimiento poblacionalLa población de Colombia crece a una tasa proporcional a la población presente en el tiempo $(t)$. En el año $2005$ el censo arrojó que había $41^{'}468.384$ habitantes, en $2018$ el número de habitantes era de $48^{'}258.494$. ¿Cuál será el número de personas en $2030$? Y ¿Cuándo habrá $100^{'}000.000$ de habitantes en Colombia?
Solución
Condiciones iniciales del problema. En $2005$, el cual va a ser el tiempo inicial $t=0$ el número de habitantes era de $41^{'}468.384$ y en $2018$, o sea, $13$ años más tarde el número de habitantes era de $48^{'}258.494$, las otras dos condiciones son las preguntas.
Condiciones iniciales.
$\hspace{0.6cm}t=0\hspace{1.6cm}p=41^{'}468.384$
$\hspace{0.6cm}t=13\hspace{1.35cm}p=48^{'}258.494$
$\hspace{0.6cm}t=12\hspace{1.35cm}p=?$
$\hspace{0.6cm}t=?\hspace{1.6cm}p=100^{'}000.000$
Vamos a comenzar reemplazando el primer dato $p=41^{'}468.384$ cuando $t=0$ en la ecuación $p=ce^{kt}$ $(1)$.
Note que la ecuación $(1)$ tiene cuatro incógnitas.
$41^{'}468.384=ce^{k(0)}$ $\Rightarrow$ $c=41^{'}468.384$
Reemplazando este valor en la ecuación $(1)$ queda de la siguiente forma $p=41^{'}468.384e^{kt}$ $(2)$.
Note que la ecuación $(2)$ ya tiene sólo tres incógnitas.
Ahora reemplazamos $p=48^{'}258.494$ cuando $t=13$ en la ecuación $(2)$
$48^{'}258.494=41^{'}468.384e^{k(13)}$ despejando queda.
$\dfrac{48^{'}258.494}{41^{'}468.384}=e^{13k}$
Aplicamos logaritmo natural a ambos lados de la ecuación.
$\ln \left| \dfrac{48^{'}258.494}{41^{'}468.384} \right|=\ln \left| e^{13k}\right|$
$0.1516405482=13k$ despejando obtenemos el valor de $k$
$k=0.01166465755$
Reemplazando este valor en la ecuación $(2)$ obtenemos.
$p=41^{'}468.384e^{0.01166465755t}$ $(3)$.
Ya podemos responder la primera pregunta. Cuál será la población en $2030$, es decir, en $t=25$
$p=41^{'}468.384e^{0.01166465755(25)}$ $\Rightarrow$ $p=55^{'}509.143$
Ahora vamos a responder la segunda pregunta que dice, ¿Cuándo habrá $100^{'}000.000$ de habitantes en Colombia?
$100^{'}000.000=41^{'}468.384e^{0.01166465755(t)}$ $\Rightarrow$ $t=75.46$
 Ejemplo 2: Datado con carbono
Ejemplo 2: Datado con carbonoEn una cueva de Sudáfrica se halló un cráneo humano junto con los restos de una hoguera. Los arqueólogos creen que la edad del cráneo sea igual a la edad de la hoguera. Se determinó que sólo queda el $2 \%$ de la cantidad original de $C-14$ en los restos de la madera. Estime la edad del cráneo.
 |
En 1955, Willard Frank Libby publicó una obra titulada Radiocarbon dating en la cual habla sobre la teoría del fechado con radiocarbono (carbono $14$) que se produce en la atmósfera por acción de la radiación cósmica sobre el nitrógeno. |
El carbono $14$ es un isótopo radioactivo inestable que se encuentra en la atmósfera, al oxidarse se transforma en dióxido de carbono que absorben las plantas y que se transmiten a otros organismos cuando éstas son consumidas. Este intercambio constante de carbono entre la atmósfera y los seres vivos se ve interrumpida cuando éstos mueren y es cuando comienza a desintegrarse en fracciones constantes, en los laboratorios especializados miden la cantidad de carbono $14$ que se conservó de la muestra al paso del tiempo.
Solución
Para resolver el ejercicio es necesario plantear las condiciones iniciales del problema, teniendo en cuenta que la vida media del $C-14$ es $5.600$ años. Se sabe que inicialmente el cráneo tenía el $100 \%$ de $c-14$. Siempre que un ejercicios nos hable de porcentaje lo vamos a dividir por cien.
Condiciones iniciales.
$\hspace{0.6cm}t=0\hspace{1.6cm}p=1$
$\hspace{0.6cm}t=5600\hspace{1.0cm}p=0.5$
$\hspace{0.6cm}t=?\hspace{1.6cm}p=0.02$
Vamos a comenzar reemplazando el primer dato $p=1$ cuando $t=0$ en la ecuación $p=ce^{kt}$ $(1)$.
$1=ce^{k(0)}$ $\Rightarrow$ $c=1$
Reemplazando este valor en la ecuación $(1)$ queda de la siguiente forma $p=e^{kt}$ $(2)$.
Ahora reemplazamos $p=0.5$ cuando $t=5600$ en la ecuación $(2)$
$0.5=e^{k(5600)}$
Aplicamos logaritmo natural a ambos lados de la ecuación.
$\ln \left| 0.5 \right|=\ln \left| e^{5600k}\right|$
$-0.6931471806=5600k$ despejando obtenemos el valor de $k$
$k=-0.0001237762$
Reemplazando este valor en la ecuación $(2)$ obtenemos.
$p=e^{-0.0001237762t}$ $(3)$.
Ahora vamos a calcular la edad del cráneo, teniendo en cuenta que al momento de encontrar los restos de la madera sólo quedaba el $2 \%$ de la cantidad original de $C-14$.
$0.02=e^{-0.0001237762t}$ $\Rightarrow$ $t=31.607,1$.
 Ejemplo 3: Crecimiento poblacional
Ejemplo 3: Crecimiento poblacionalLa población de cierta ciudad aumenta proporcionalmente al número de habitantes que hay en un momento dado en ella. Si después de $5$ años, la población se ha triplicado y después de $8$ años es de $45.000$ habitantes, hallar el número de ciudadanos que había inicialmente.
Solución
Se deben plantear las condiciones iniciales del problema. Como la incógnita es la población inicial, la vamos a llamar $p_0$ para poder trabajar la ecuación. Note que cuando el enunciado dice que a los $5$ años la población se ha triplicado, se representa $3p_o$
Condiciones iniciales.
$\hspace{0.6cm}t=0\hspace{1.35cm}p=p_0$
$\hspace{0.6cm}t=5\hspace{1.35cm}p=3p_0$
$\hspace{0.6cm}t=8\hspace{1.35cm}p=45.000$
Reemplazamos el primer dato $p=p_0$ cuando $t=0$ en la ecuación $p=ce^{kt}$ $(1)$.
$p_0=ce^{k(0)}$ $\Rightarrow$ $c=p_0$
Reemplazando este valor en la ecuación $(1)$ queda de la siguiente forma $p=p_0e^{kt}$ $(2)$.
Ahora reemplazamos $p=3p_0$ cuando $t=5$ en la ecuación $(2)$
$3p_0=p_0e^{k(5)}$ despejando queda.
$\dfrac{3p_0}{p_0}=e^{5k}$
Aplicamos logaritmo natural a ambos lados de la ecuación.
$\ln \left| 3 \right|=\ln \left| e^{5k}\right|$
$1.098612289=5k$ despejando obtenemos el valor de $k$
$k=0.2197224577$
Reemplazando este valor en la ecuación $(2)$ obtenemos.
$p=p_0e^{0.2197224577t}$ $(3)$.
Ahora vamos a calcular la cantidad inicial de habitantes.
$45000=p_0e^{0.2197224577(8)}$
Despejando $p_0$
$p_0=\dfrac{45000}{e^{0.2197224577(8)}}$.
 Ejemplo 4: Descomposición radiactiva
Ejemplo 4: Descomposición radiactivaSe ha detectado que el $0.5 \%$ de una sustancia radioactiva desaparece en $12$ años. ¿Qué porcentaje desaparecerá en $1. 000$ años? ¿Cuál es la vida media de dicha sustancia?
Solución
Condiciones iniciales.
$\hspace{0.6cm}t=0$
$\hspace{0.6cm}t=12$
$\hspace{0.6cm}t=?$
$\hspace{0.6cm}t=1000$
$x=1$
$x=0.995$
$x=0.5$
$x=?$
Reemplazamos el primer dato $x=1$ cuando $t=0$ en la ecuación $p=ce^{kt}$ $(1)$.
$1=ce^{k(0)}$ $\Rightarrow$ $c=1$
Reemplazando este valor en la ecuación $(1)$ queda de la siguiente forma $x=e^{kt}$ $(2)$.
Ahora reemplazamos $x=0.995$ cuando $t=12$ en la ecuación $(2)$
$0.995=e^{k(12)}$ aplicamos logaritmo natural a ambos lados de la ecuación.
$\ln \left| 0.995 \right|=\ln \left| e^{12k}\right|$
Despejando obtenemos $k=-0.00041771181$
Reemplazando este valor en la ecuación $(2)$ obtenemos.
$x=e^{-0.00041771181t}$ $(3)$.
Ahora vamos a calcular qué porcentaje desaparecerá en $1.000$ años.
$x=e^{-0.00041771181(1000)}$
$x=65.85$ Esto quiere decir que a los mil años quedará el $65.85 \%$
Ahora vamos a calcular la vida media de la sustancia radiactiva.
$0.5=e^{-0.00041771181(t)}$.
$\ln \left| 0.5 \right|=\ln \left| e^{-0.00041771181(t)}\right|$
$t=\dfrac{-0.6931471806}{-0.00041771181}$
 Ejemplo 5: Interés compuesto
Ejemplo 5: Interés compuestoPrevio al nacimiento de su primer hijo, una pareja deposita $5.000$ dólares en una cuenta que paga el $8 \%$ de interés compuesto. Los pagos de interés son acumulables al capital. ¿Cuánto habrá en la cuenta en el dieciochoavo cumpleaños del niño?
Solución
En los ejercicios de modelado la $k$ es la constante de crecimiento o decrecimiento del ejercicio, es la que determina a qué velocidad está creciendo o decreciendo una población o se descompone el carbono 14 o se desintegra determinado material radiactivo, en los ejercicios de interés compuesto el interés determina la rapidez de crecimiento del capital, es decir, que la $k$ es el interés compuesto, para este ejercicio $k=0.08$
Condiciones iniciales.
$\hspace{0.6cm}t=0$
$\hspace{0.6cm}t=18$
$x=5000$
$x=?$
Reemplazamos el primer dato $x=5000$ cuando $t=0$ en la ecuación $p=ce^{kt}$ $(1)$.
$5000=ce^{k(0)}$ $\Rightarrow$ $c=5000$
Reemplazando este valor en la ecuación $(1)$ queda de la siguiente forma $x=5000e^{kt}$ $(2)$.
Ahora reemplazamos $k=0.08$ $\wedge$ $t=18$ en la ecuación $(2)$
$x=5000e^{(0.08)(18)}$ $x=21103,47$.En la página 199 puedes observar un vídeo de aplicación de crecimiento y decrecimiento.
En la siguiente escena interactiva, podrás resolver ejercicios de crecimiento poblacional, debes ingresar las condiciones iniciales del ejercicio.
La ley de enfriamiento de Newton dice que en un cuerpo que se está enfriando, la rapidez con que la temperatura $T$ cambia, es proporcional a la diferencia entre la temperatura del cuerpo y la temperatura constante $T_m$ del medio que lo rodea, esto es:
$\dfrac {dT}{dt}=k(T-T_m)$
Podemos ver que esta es una ED de variables separables. Separando variables tenemos.
$\dfrac {dT}{(T-T_m)}=kdt$
Integrando ambos lados de la ED. El lado izquierdo se integra por sustitución.
$\ln \left| T-T_m\right|=kt+c$
Quitando el logaritmo.
$e^{\ln \left| T-T_m\right|}=e^{kt+c}$
$T-T_m=ce^{kt}$
Despejando la temperatura obtenemos la solución.
La solución es muy similar a la de crecimiento y decrecimiento, se diferencia en que tenemos un dato más que es la temperatura del medio $T_m$, por esto los ejercicios se resuelven de forma similar.
 Ejemplo 1: Temperatura
Ejemplo 1: TemperaturaUna taza de café se sirve a una temperatura de $70^{\circ }C$ en un cuarto cuya temperatura es de $17^{\circ }C$. Dos minutos más tarde la temperatura del café es de $60^{\circ }C$. ¿Después de cuánto tiempo la taza de café alcanza la temperatura de $20^{\circ }C$?
Solución
Se plantean las condiciones iniciales del problema.
Condiciones iniciales.
$\hspace{0.6cm}t=0$
$\hspace{0.6cm}t=2$
$\hspace{0.6cm}t=?$
$T=70^{\circ }C$
$T=60^{\circ }C$
$T=20^{\circ }C$
$T_m=17^{\circ }C$
Vamos a comenzar reemplazando el primer dato $T=70^{\circ }C$ cuando $t=0$ en la ecuación $T=T_m+ce^{kt}$ $(1)$.
$70=17+ce^{k(0)}$ $\Rightarrow$ $c=53$
Reemplazando este valor en la ecuación $(1)$ queda de la siguiente forma $T=17+53e^{kt}$ $(2)$.
Ahora reemplazamos $T=60$ cuando $t=2$ en la ecuación $(2)$
$60=17+53e^{k(2)}$ despejando queda $\dfrac {43}{53}=e^{k(2)}$
Aplicamos logaritmo natural a ambos lados de la ecuación.
$\ln \left| \dfrac {43}{53} \right|=\ln \left| e^{2k}\right|$
$-0.2090917979=2k$ despejando obtenemos el valor de $k$
$k=-0.1045458989$
Reemplazando este valor en la ecuación $(2)$ obtenemos.
$T=17+53e^{-0.1045458989t}$ $(3)$.
Ahora vamos a calcular cuánto tiempo se demora la taza de café para llegar a $20°C$
$20=17+53e^{-0.1045458989t}$ $\Rightarrow$ $t=27,46$.
 Ejemplo 2: Temperatura
Ejemplo 2: TemperaturaUn termómetro que indica $70^{\circ } F$ se coloca en un horno precalentado a temperatura constante. A través de una ventana de vidrio del horno, un observador registra que la temperatura es de $110^{\circ } F$ después de medio minuto y de $145^{\circ } F$ después de un minuto. ¿A qué temperatura está el horno?
Solución
Se plantean las condiciones iniciales del problema.
Condiciones iniciales.
$\hspace{0.6cm}t=0$
$\hspace{0.6cm}t=0.5$
$\hspace{0.6cm}t=1$
$T=70^{\circ }F$
$T=110^{\circ }F$
$T=145^{\circ }F$
$T_m=?$
Vamos a comenzar reemplazando el primer dato $T=70^{\circ }C$ cuando $t=0$ en la ecuación $T=T_m+ce^{kt}$ $(1)$.
$70=T_m+ce^{k(0)}$ $\Rightarrow$ $c=70-T_m$
Reemplazando este valor en la ecuación $(1)$ queda de la siguiente forma $T=T_m+(70-T_m)e^{kt}$ $(2)$.
Ahora reemplazamos $T=110$ cuando $t=0.5$ en la ecuación $(2)$
$110=T_m+(70-T_m)e^{k(0.5)}$ $(3)$ Nos queda una ecuación con dos incógnitas, como no se puede resolver una ecuación con dos incógnitas, entonces, reemplazamos la otra condición para tener una segunda ecuación.
$145=T_m+(70-T_m)e^{k(1)}$ $(4)$
Despejando Euler de la ecuación $(3)$ $e^{0.5k}= \dfrac {110-T_m}{70-T_m}$ $(5)$
Despejando Euler de la ecuación $(4)$ $e^{k}= \dfrac {145-T_m}{70-T_m}$ $(6)$
No podemos igualar las ecuaciones $(5)$ $\wedge$ $(6)$
Aplicamos axioma de igualdad a la ecuación $(5)$ elevando al cuadrado a ambos lados.
$ \left [e^{0.5k}\right] ^{2}=\left[ \dfrac {110-T_{m}}{70-T_m}\right] ^{2}$ $\Rightarrow$ $ e^k=\left[ \dfrac {110-T_{m}}{70-T_m}\right] ^{2}$ $(7)$
Ahora igualamos las ecuaciones $(6)$ $\wedge$ $(7)$
$\dfrac {145-T_m}{70-T_m}=\left[ \dfrac {110-T_{m}}{70-T_m}\right] ^{2}$
Aplicando potenciación.
$\dfrac {145-T_m}{70-T_m}=\dfrac {[110-T_{m}]^2}{[70-T_m]^2}$
Simplificando.
$145-T_m=\dfrac {[110-T_{m}]^2}{70-T_m}$
Despejando.
$(145-T_m)(70-T_m)=[110-T_{m}]^2$
Haciendo distributiva y desarrollando el binomio.
$10.150-215T_m+[T_m]^2=12100-220T_m+[T_m]^2$
Agrupando términos semejantes.
$5T_m=1950$
Despejando $T_m$
$T_m=\dfrac{1950}{5}$
Cuando se resuelven ejercicios de crecimiento y decrecimiento o de temperaturas y piden población inicial, temperatura inicial o temperatura del medio, siempre se debe plantear un sistema de ecuaciones para poder resolver el ejercicio.
 Ejemplo 3: Temperatura
Ejemplo 3: TemperaturaUn termómetro se lleva del interior de una habitación donde la temperatura del aire es de $80^{\circ } F$ al exterior donde la temperatura del aire es de $15^{\circ } F$. después de un minuto el termómetro indica $55^{\circ } F$. ¿Cuál es la temperatura del termómetro en $t=2$ minutosS? ¿Cuánto tiempo le tomará alcanzar $19^{\circ } F$
Solución Se plantean las condiciones iniciales del problema.
Condiciones iniciales.
$\hspace{0.6cm}t=0$
$\hspace{0.6cm}t=1$
$\hspace{0.6cm}t=2$
$\hspace{0.6cm}t=?$
$T=80^{\circ }F$
$T=55^{\circ }F$
$T=?$
$T=19^{\circ }F$
$Tm=15^{\circ }F$
Vamos a comenzar reemplazando el primer dato $T=80^{\circ }C$ cuando $t=0$ en la ecuación $T=T_m+ce^{kt}$ $(1)$.
$80=15+ce^{k(0)}$ $\Rightarrow$ $c=65$
Reemplazando este valor en la ecuación $(1)$ queda de la siguiente forma $T=15+65e^{kt}$ $(2)$.
Ahora reemplazamos $T=55$ cuando $t=1$ en la ecuación $(2)$
$55=15+65e^{k(1)}$ despejando queda $\dfrac {40}{65}=e^{k}$
Aplicamos logaritmo natural a ambos lados de la ecuación.
$\ln \left| \dfrac {40}{65} \right|=\ln \left| e^{k}\right|$ obtenemos el valor de $k$
$k=-0.4855078$
Reemplazando este valor en la ecuación $(2)$ obtenemos.
$T=15+65e^{-0.4855078t}$ $(3)$.
Ahora vamos a calcular la temperatura a los $2$ minutos.
$T=15+65e^{(-0.4855078)(2)}$ $\Rightarrow$ $T=39.61$.
Ahora vamos a calcular cuánto tiempo se demora el termómetro para llegar a $19^{\circ }F$
$19=15+65e^{-0.4855078t}$ $
$\ln \left| \dfrac {4}{65} \right|=\ln \left| e^{-0.4855078t}\right|$ $\Rightarrow$ $t=5,74$
 Ejemplo 4: Temperatura
Ejemplo 4: TemperaturaSe sumerge una barra de acero en un líquido que está a una temperatura de $110^{\circ } C$, la barra está a $32^{\circ } C$, un segundo después su temperatura aumenta $4^{\circ } C$. ¿Cuál será la temperatura de la barra a los $10$ segundos? ¿Cuánto tiempo le tomará alcanzar $100^{\circ } C$
Solución
Tenga en cuenta que la temperatura de la barra aumenta $4^{\circ } C$ en un segundo, es decir en $t=1$ la temperatura es $36^{\circ } C$.
Condiciones iniciales.
$\hspace{0.6cm}t=0$
$\hspace{0.6cm}t=1$
$\hspace{0.6cm}t=10$
$\hspace{0.6cm}t=?$
$T=32^{\circ }C$
$T=36^{\circ }C$
$T=?$
$T=100^{\circ }C$
$Tm=110^{\circ }C$
Vamos a comenzar reemplazando el primer dato $T=32^{\circ }C$ cuando $t=0$ en la ecuación $T=T_m+ce^{kt}$ $(1)$.
$32=110+ce^{k(0)}$ $\Rightarrow$ $c=-78$
Reemplazando este valor en la ecuación $(1)$ queda de la siguiente forma $T=110-78e^{kt}$ $(2)$.
Ahora reemplazamos $T=36$ cuando $t=1$ en la ecuación $(2)$
$36=110-78e^{k(1)}$ despejando queda $\dfrac {-74}{-78}=e^{k}$
Aplicamos logaritmo natural a ambos lados de la ecuación.
$\ln \left| \dfrac {74}{78} \right|=\ln \left| e^{k}\right|$ obtenemos el valor de $k$
$k=-0.05264373$
Reemplazando este valor en la ecuación $(2)$ obtenemos.
$T=110-78e^{-0.05264373t}$ $(3)$.
Ahora vamos a calcular la temperatura a los $10$ segundos.
$T=110-78e^{(-0.05264373)(10)}$ $\Rightarrow$ $T=63.92$.
Ahora vamos a calcular cuánto tiempo se demora el termómetro para llegar a $100^{\circ }C$
$100=110-78e^{-0.05264373t}$ despejando queda.
$\dfrac {-10}{-78}=e^{-0.05264373t}$
Aplicamos logaritmo natural a ambos lados de la ecuación.
$\ln \left| \dfrac {10}{78} \right|=\ln \left| e^{-0.05264373t}\right|$ $\Rightarrow$ $t=39.01$
 Ejemplo 5: Temperatura
Ejemplo 5: TemperaturaSe encuentra el cuerpo de un hombre una mañana fría en una habitación cuya temperatura es $15^{\circ } C$, un detective mide la temperatura del cuerpo y el termómetro indica $36^{\circ } C$, una hora después vuelve a medir la temperatura del cuerpo y el termómetro indica $35.2^{\circ } C$. En qué momento ocurrió el asesinato.
[Sugerencia: La temperatura normal del cuerpo es de $37^{\circ } C$].
Solución
Condiciones iniciales.
$\hspace{0.6cm}t=0$
$\hspace{0.6cm}t=t$
$\hspace{0.6cm}t=t+1$
$T=37^{\circ }C$
$T=33^{\circ }C$
$T=32.1$
$Tm=15^{\circ }C$
Vamos a comenzar reemplazando el primer dato $T=37^{\circ }C$ cuando $t=0$ en la ecuación $T=T_m+ce^{kt}$ $(1)$.
$37=15+ce^{k(0)}$ $\Rightarrow$ $c=22$
La ecuación $(1)$ queda de la siguiente forma $T=15+22e^{kt}$ $(2)$.
Ahora reemplazamos $T=33$ cuando $t=t$ en la ecuación $(2)$
$33=15+22e^{k(t)}$ despejando queda $\dfrac {18}{22}=e^{kt}$
Aplicamos logaritmo natural a ambos lados de la ecuación.
$\ln \left| \dfrac {18}{22} \right|=\ln \left| e^{kt}\right|$ obtenemos una ecuación con dos incógnitas$
$kt=-0.20067079$ $(3)$ Nos queda una ecuación con dos incógnitas, como no se puede resolver, reemplazamos la otra condición para tener una segunda ecuación.
$32.1=15+22e^{k(t+1)}$ despejando queda $\dfrac {17.1}{22}=e^{k(t+1)}$
Aplicamos logaritmo natural a ambos lados de la ecuación.
$\ln \left| \dfrac {17.1}{22} \right|=\ln \left| e^{k(t+1)}\right|$ obtenemos.
$k(t+1)=-0.25196398$ $(4)$
Despejamos $k$ de las ecuaciones $(3)$
$k=\dfrac {-0.20067079}{t}$ $(5)$
Despejamos $k$ de las ecuaciones $(4)$
$k=\dfrac {-0.25196398}{t+1}$ $(6)$
Igualamos $(5)$ $\wedge$ $(6)$
$\dfrac {-0.20067069}{t}=\dfrac {-0.25196398}{t+1}$
Operando obtenemos.
$-0.20067069t-0.20067069=-0.25196398t$
Agrupando términos semejantes.
$0.05129329t=0.20067069$ despejando $ t=3.912$
$3.912$ horas equivale a 235 minutos.
En la página $199$ puedes observar un vídeo de aplicación de temperaturas.
las soluciones químicas, entendiéndose estas como un sistema homogéneo donde hay mayor proporción de soluto que de solvente, conllevan la necesidad de comprender el concepto de concentración, el cual no es más que la relación entre la cantidad de soluto y la cantidad de solvente. Las ED son una herramienta para comprender el comportamiento de las mezclas de dos o más soluciones en un recipiente bajo ciertas condiciones.
Se tomará la sal como soluto para definir la ED, pero es importante resaltar que es igualmente aplicable a todo tipo de soluciones homogéneas, pues la ecuación mide la variación de la cantidad de soluto presente en la mezcla en cualquier momento $t$
Al mezclar dos soluciones salinas de distintas concentraciones surge una ecuación diferencial de primer orden, que define la cantidad de sal contenida en la mezcla. $A(t)$ denota la cantidad de sal (medida en libras) en el tanque en el tiempo $t$, entonces la razón con la que $A(t)$ cambia es una razón neta:
$\color{black}\fbox{$\color{blue}\dfrac{dA}{dt}=R_1-R_2$}\quad$
La rapidez está dada por.
$R_1=$ Velocidad de entrada por concentración.
$R_2=$ Velocidad de salida por concentración.
La rapidez con la que la sal entra es $\frac{lbs}{min}$
 Ejemplo 1: Mezclas
Ejemplo 1: MezclasSe disuelve inicialmente $50$ libras de sal en un tanque con $300$ galones de agua. Se bombea Salmuera al tanque a razón $3 \frac{gal}{min}$ y luego la solución adecuadamente mezclada se bombea fuera del tanque a razón de $3 \frac{gal}{min}$. Si la concentración de la solución que entra es de $2 \frac{lib}{gal}$, determine la cantidad de sal que hay en el tanque en un instante cualquiera. ¿Cuánta sal hay después de $50$ min? ¿Cuánta después de un largo tiempo?
Solución
La ilustración ayuda a comprender lo que está pasando en el tanque.
En el tanque está entrando salmuera a razón de $3 \frac{gal}{min}$ con una concentración de $2 \frac{lib}{gal}$. Es decir, $R_1= 3 \frac{gal}{min}.2 \frac{lib}{gal}=6\frac{lib}{min}$
Inicialmente en el tanque hay $300$ galones de salmuera, entonces para hallar $R_2$ se plantea la ecuación ${\color{blue}R_2=r_e. \frac{A}{V+(r_e-r_s)t}}$.
Reemplazando datos en la ecuación.
$R_2=3\dfrac{gal}{min}. \dfrac{A}{300+(3-3)t}\dfrac{lib}{gal}=\dfrac{A}{100}\dfrac{lib}{min}$.
Reemplazando estos datos en la ED $\dfrac{dA}{dt}=R_1-R_2$ nos queda.
$\dfrac{dA}{dt}=6-\dfrac{A}{100}$ organizando la ED.
$\dfrac{dA}{dt}+\dfrac{1}{100}A=6$
Tenemos una ED lineal no homogénea y está en forma estándar. Identificamos $p(t)$ $\wedge$ hallamos el factor integrante.
$p(t)=\dfrac {1}{100}$ $F.I = e^{\frac {t}{100}}$
Aplicamos la propiedad para resolverla.
${\color{blue} F.I y = \int F.I f(x) dx}$
$e^{\frac {t}{100}} A = \int 6e^{\frac {t}{100}} dt$
Integrando el lado derecho.
$e^{\frac {t}{100}} A= 600e^{\frac {t}{100}}+c$
Despejamos la variable dependiente $A$
$A=600+ce^{-\frac {t}{100}}$
Ahora reemplazamos condiciones iniciales $A(0)=50$ para hallar la $c$
$50=600+ce^{0}$
El valor de la constante es.
$c=-550$
La solución es.
Teniendo la ecuación de concentración de sal, podemos responder las dos preguntas.
Para saber la cantidad de sal a los 50 minutos se reemplaza, la $t=50$
$A(50)=600-550e^{-\frac {50}{100}}$
$A(50)=266.4$
Ahora necesitamos saber la cantidad de sal después de un largo tiempo, es decir, $t=\infty$
$A(\infty)=600-550e^{-\frac {\infty}{100}}$
$A(\infty)=600$
 Ejemplo 2: Mezclas
Ejemplo 2: MezclasUn tanque contiene $450$ litros de agua en el que se disuelven $30$ gramos de sal: Una salmuera que contiene $3 \frac{gr}{l}$ se bombea al tanque con una intensidad de $6 \frac{l}{min}$, la solución adecuadamente mezclada se bombea hacia afuera con una intensidad de $8 \frac{l}{min}$. Determine la cantidad de libras de sal que hay en el tanque en cualquier instante. ¿Cuándo se vacía el tanque?
Solución
En el tanque está entrando salmuera a razón de $ 6 \frac{l}{min}$ con una.
concentración de $3 \frac{gr}{l}$. Es decir, $R_1= 6 \frac{l}{min}.3 \frac{gr}{l}=18\frac{gr}{min}$
Inicialmente en el tanque hay $450$ litros de salmuera, entonces para hallar $R_2$ se plantea la ecuación ${\color{blue}R_2=r_e. \dfrac{A}{V+(r_e-r_s)t}}$.
Reemplazando datos en la ecuación.
$R_2=8\dfrac{l}{min}. \dfrac{A}{450+(6-8)t}\dfrac{lib}{gal}=8\dfrac{A}{450-2t}\dfrac{gr}{min}$.
Reemplazando estos datos en la ED $\dfrac{dA}{dt}=R_1-R_2$ nos queda.
$\dfrac{dA}{dt}=18-4\dfrac{A}{225-t}$ organizando la ED.
$\dfrac{dA}{dt}+\dfrac{4}{225-t}A=18$
Tenemos una ED lineal no homogénea y está en forma estándar. Identificamos $p(t)$ $\wedge$ hallamos el factor integrante.
$p(t)=\dfrac{4}{225-t}$ $F.I = (225-t)^{-4}$
Ahora aplicamos la propiedad para resolverla.
$(225-t)^{-4} A = \int 18(225-t)^{-4}dt$
Integrando el lado derecho de la ecuación.
$(225-t)^{-4} A = 6(225-t)^{-3}+c$
Despejamos la variable dependiente $A$
$A = 6(225-t)+c(225-t)^{4}$
Ahora reemplazamos condiciones iniciales $A(0)=30$ para hallar la $c$
$30 = 6(225)+c(225)^{4}$
El valor de la constante es.
$c=-\dfrac{1320}{(225)^4}$
La solución es.
La ecuación que nos ayuda a determinar la cantidad de sal que hay en el tanque en cualquier momento es.
$A(t)=6\left( 225-t\right) -1320\left( \dfrac {225-t}{225}\right) ^{4}$
Ahora necesitamos saber cuándo se vacía el tanque. Como la intensidad de salida es mayor que la intensidad de entrada, es lógico que llega un momento en que el tanque estará vacío.
Utilizamos la condición $450+(6-8)t$. entonces es necesario igualar esta ecuación a cero y despejar $t$
 Ejemplo 3: Mezclas
Ejemplo 3: MezclasUn estanque contiene $100 m^3$ de agua contaminada. Con el propósito de descontaminarlo se introduce agua limpia a razón de $2 \frac{m^3}{min}$ y el agua contaminada (uniformemente mezclada) se deja salir del estanque a la misma razón. ¿Qué porcentaje de contaminantes se habrá eliminado después de $1$ h? ¿Qué tiempo debe transcurrir para que los contaminantes disminuyan en un $90 \%$?
Solución
La ilustración ayuda a comprender lo que está pasando en el tanque.
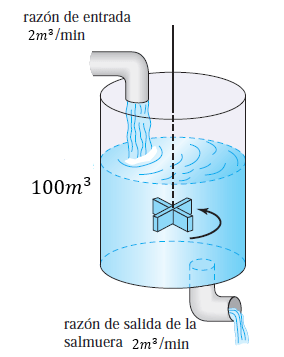
En el tanque está entrando agua limpia a razón de $2 \frac{m^3}{min}$ con una concentración de $0$ contaminación. Es decir, $R_1= 2 \frac{m^3}{min}.0=0$
Inicialmente en el tanque hay $100 m^3$ de agua contaminada, entonces para hallar $R_2$ se plantea la ecuación ${\color{blue}R_2=r_e. \frac{A}{V+(r_e-r_s)t}}$.
Reemplazando datos en la ecuación.
$R_2=2. \dfrac{A}{100+(2-2)t}=\dfrac{A}{50}\dfrac{m^3}{min}$.
Reemplazando estos datos en la ED $\dfrac{dA}{dt}=R_1-R_2$ nos queda.
$\dfrac{dA}{dt}=0-\dfrac{A}{50}$ organizando la ED.
$\dfrac{dA}{dt}+\dfrac{1}{50}A=0$
ED lineal homogénea en forma estándar. Identificamos $p(t)$
$p(t)=\dfrac {1}{50}$ $F.I = e^{\frac {t}{50}}$
Ahora aplicamos la propiedad para resolverla.
$e^{\frac {t}{50}} A = \int 0 dt$
Integrando obtenemos.
$e^{\frac {t}{50}} A=c$
Despejamos la variable dependiente $A$
$A=ce^{\frac {t}{50}}$
Ahora reemplazamos condiciones iniciales $A(0)=A_0$ para hallar la $c$
$A_0=ce^{\frac {0}{50}}$
El valor de la constante es.
$c=A_0$
La solución es.
Teniendo la ecuación de concentración de contaminante, podemos responder las dos preguntas.
Para saber el porcentaje de contaminante que se habrá eliminado después de $60$ minutos.
$A(t)=A_0e^{\frac {60}{50}}$
Ahora vamos a calcular qué porcentaje es esta cantidad de $A_0$
$\dfrac{A_0-0.3012A_0}{A_0}=\dfrac{A_0(1-0.3012)}{A_0}=0.6989$
 Ejemplo 4: Mezclas
Ejemplo 4: MezclasEl aire del interior de un pequeño cuarto con dimensiones de $12x8x8$ metros contiene $3 \%$ de monóxido de carbono. Empezando en $t=0$, se sopla aire fresco que no contiene monóxido de carbono hacía el interior del cuarto a razón de $100 \frac{m^3}{min}$. Si el aire del cuarto sale al exterior a través de una abertura a la misma velocidad.
¿Cuándo tendrá el aire del interior del cuarto $0.01 \%$ de monóxido de carbono?
Solución
La cantidad de monóxido de carbono que hay inicialmente en el cuarto es el $3 \%$ del volumen $V=768 m^3$
$A(0)=\dfrac{768x3}{100}=23.04$
En el cuarto entra aire limpio a razón de $100 \frac{m^3}{min}$. Es decir, $R_1=100 \frac{m^3}{min}.0=0$
Inicialmente en el cuarto hay $768m^3$ litros de salmuera, entonces para hallar $R_2$ se plantea la ecuación ${\color{blue}R_2=r_e. \dfrac{A}{V+(r_e-r_s)t}}$.
Reemplazando datos en la ecuación.
$R_2=100. \dfrac{A}{768+(100-100)t}=\dfrac{100A}{768}=\dfrac{25A}{192}$.
Reemplazando estos datos en la ED $\dfrac{dA}{dt}=R_1-R_2$ nos queda.
$\dfrac{dA}{dt}=0-\dfrac{25A}{192}$ organizando la ED.
$\dfrac{dA}{dt}+\dfrac{25}{192}A=0$
ED lineal homogénea en forma estándar. Identificamos $p(t)$ $\wedge$ hallamos el factor integrante.
$p(t)=\dfrac{25}{192}$ $F.I = e^{\frac{25}{192}t}$
Ahora aplicamos la propiedad para resolverla.
$e^{\frac{25}{192}t} A = \int 0 dt$
Integrando el lado derecho de la ecuación.
$e^{\frac{25}{192}t} A =c$
Despejamos $A$
$A = ce^{-\frac{25}{192}t}$
Ahora reemplazamos condiciones iniciales $A(0)=23.04$ para hallar la $c$
$23.04 = ce^{-\frac{25}{192}(0)}$
El valor de la constante es.
$c=23.04$
La solución es.
La ecuación que determina la concentración de monóxido de carbono en función del tiempo es:
Ahora podemos responder la pregunta. ¿Cuándo tendrá el aire del interior del cuarto $0.01 \%$ de monóxido de carbono?
$0.0768 = 23.04e^{-\frac{25}{192}t}$
$\ln \left| \dfrac {0.0768}{23.04} \right|=\ln \left| e^{-\frac{25}{192}t}\right|$ obtenemos.
$t = 43.805$
En la página $200$ puedes observar un vídeo de aplicación de mezclas.
Circuitos $LR$: Cuando un circuito en serie sólo contiene un inductor $(L)$ y un resistor $(R)$, la segunda ley de Kirchhoff establece que:
la suma de las caídas de voltaje a través de un inductor $L\dfrac{di}{dt}$ y de un resistor $(iR)$ es igual al voltaje aplicado $E(t)$ al circuito.
Circuito LR en serie.
Circuitos $RC$: Cuando un circuito en serie sólo contiene un resistor $(R)$ y un capacitor $(C)$, la caída de voltaje a través de un capacitor de capacitancia $(C)$ es.
$\dfrac{Q(t)}{c}$ donde $q$ es la carga en el capacitor.
Por la segunda ley de kirchhoff $\;\;\;Ri+\dfrac{i}{C}+q=E(t)\;\;\; (2)$
La corriente $(i)$ y la carga $(q)$ se relacionan mediante $i\dfrac{dq}{dt}$.
Así la ecuación $(2)$ se transforma en.
Circuito RC en serie.
 Ejemplo 1: Circuito en serie $LR$
Ejemplo 1: Circuito en serie $LR$Se conecta una batería de $20$ Voltios a un circuito en serie $LR$ con $0.2$ henry de inductancia y $30$ Ohms de resistencia. Determine la corriente $i(t)$ sí $i(0)=0$.
Solución
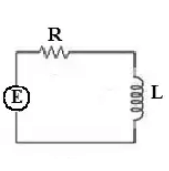
Recordemos que.
$\;\;\;L\dfrac{di}{dt}+Ri=E(t)$
Reemplazando valores tenemos $\;\;\;0.2\dfrac{di}{dt}+30i=20$
Es una ED lineal pero no está en forma estándar.
LLevándola a la forma estándar, obtenemos.
$\dfrac{di}{dt}+150i=100$
Identificamos $p(t)$ y hallamos el FI.
$p(t)=150$ $F.I = e^{150t}$
Ahora aplicamos la propiedad para resolverla.
$e^{150t} i = \int 100e^{150t}dt$
Integrando el lado derecho de la ecuación.
$e^{150t} i = \dfrac{100}{150}e^{150t}+c$
Despejamos la variable dependiente $i$
$i = \dfrac{2}{3}+ce^{-150t}$
Ahora reemplazamos condiciones iniciales $i(0)=0$ para hallar la $c$
$0 = \dfrac{2}{3}+ce^{0}$
El valor de la constante es.
$c=-\dfrac{2}{3}$
La corriente en función del tiempo es.
 Ejemplo 2: Circuito en serie $RC$
Ejemplo 2: Circuito en serie $RC$Se aplica una fuerza electromotriz de $100$ Voltios a un circuito en serie $RC$, donde la resistencia es de $200$ Ohms y la capacitancia es de $10^{-4}$ farads. Determine la carga $q(t)$ en el capacitor, Si $q(0)=0$. Encuentre la corriente $i(t)$
Solución
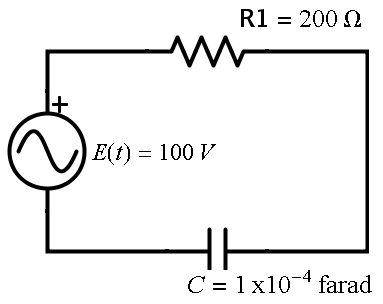
Recordemos que.
$\;\;\;R\dfrac{dq}{dt}+\dfrac{1}{C}q=E(t)$
Reemplazando valores tenemos.
$\;\;\;200\dfrac{dq}{dt}+\dfrac{1}{10^{-4}}q=100$
Es una ED lineal pero no está en forma estándar.
LLevándola a la forma estándar, obtenemos.
$\dfrac{dq}{dt}+50q=\dfrac{1}{2}$
Identificamos $p(t)$ y hallamos el FI.
$p(t)=50$ $F.I = e^{50t}$
Ahora aplicamos la propiedad para resolverla.
$e^{50t} q =\displaystyle \int \dfrac{1}{2}e^{50t}dt$
Integrando el lado derecho de la ecuación.
$e^{50t} q = \dfrac{1}{100}e^{50t}+c$
Despejamos la variable dependiente $q$
$q = \dfrac{1}{100}+ce^{-50t}$
Ahora reemplazamos condiciones iniciales $q(0)=0$ para hallar la $c$
$c=-\dfrac{1}{100}$
La carga en función del tiempo es.
$q(t) = \dfrac{1}{100}- \dfrac{1}{100}e^{-50t}$
La corriente es la derivada de la carga, por lo cual debemos derivar la respuesta anterior.
$q^{'}(t) = \dfrac{50}{100}e^{-50t}$
Entonces la corriente en función del tiempo es:
 Ejemplo 3: Circuito en serie $LR$
Ejemplo 3: Circuito en serie $LR$Se aplica una fuerza electromotriz de $450$ voltios a un circuito LR con $0.25$ henry de inductancia y $90$ ohms de resistencia. Determine la corriente $i(t)$ sí $i(0)=0$. Cuando $t$ tiende al infinito.
Solución

Recordemos que $\;L\dfrac{di}{dt}+Ri=E(t)$
Reemplazando valores tenemos $\;\;\;0.25\dfrac{di}{dt}+90i=450$
Es una ED lineal pero no está en forma estándar.
LLevándola a la forma estándar, obtenemos.
$\dfrac{di}{dt}+360i=1800$
Identificamos $p(t)$ y hallamos el FI.
$p(t)=360$ $F.I = e^{360t}$
Ahora aplicamos la propiedad para resolverla.
$e^{360t} i = \int 1800e^{360t}dt$
Integrando el lado derecho de la ecuación.
$e^{360t} i = \dfrac{1800}{360}e^{360t}+c$
Despejamos la variable dependiente $i$
$i = \dfrac{5e^{360t}}{e^{360t}}+\dfrac{c}{e^{360t}}$
Simplificando.
$i = 5+ce^{-360t}$
Ahora reemplazamos condiciones iniciales $i(0)=0$ para hallar la $c$
$0 = 5+ce^{0}$
El valor de la constante es.
$c=-5$
La corriente en función del tiempo es.
La corriente cuando $t$ tiende a infinito es.
$i(t) = 5-5e^{(-360)(\infty)}$
 Ejemplo 4: Circuito en serie $RC$
Ejemplo 4: Circuito en serie $RC$Se aplica una fuerza electromotriz de $200cos2t$ Voltios a un circuito en serie $RC$, donde la resistencia es de $50$ Ohms y la capacitancia es de $10^{-2}$ farads. Determine la carga $q(t)$ en el capacitor, Si $q(0)=0$. Encuentre la corriente $i(t)$
Solución
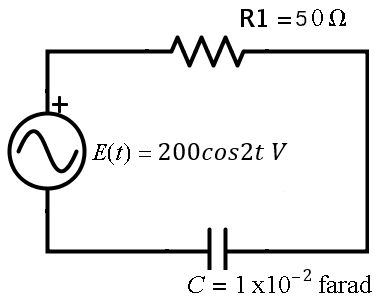
Recordemos que.
$\;\;\;R\dfrac{dq}{dt}+\dfrac{1}{C}q=E(t)$
Reemplazando valores tenemos.
$\;\;\;50\dfrac{dq}{dt}+\dfrac{1}{10^{-2}}q=200cos2t$
$\;\;\;50\dfrac{dq}{dt}+100q=200cos2t$
Es una ED lineal pero no está en forma estándar.
LLevándola a la forma estándar, obtenemos.
$\dfrac{dq}{dt}+2q=4cos2t$
Identificamos $p(t)$ y hallamos el FI.
$p(t)=2$ $F.I = e^{2t}$
Ahora aplicamos la propiedad para resolverla.
$e^{2t} q = 4\int e^{2t}cos2tdt$
Utilizamos el siguiente resultado de la tabla de integrales.
$\color{black}\fbox{$\color{blue}\int e^{ax}cosbxdx=\dfrac{e^{ax}}{a^2+b^2}(acosbx+bsenbx)+c$}\quad$
$\int e^{2t}cos2tdt=\dfrac{e^{2t}}{4+4}(2cos2t+2sen2t)+c$
$4\int e^{2t}cos2tdt=4\left( \dfrac {e^{2t}}{8}\right) 2\left( \cos ^{2}t+sen2t\right) +c$
Simplificando.
$4\int e^{2t}cos2tdt={e^{2t}}(cos2t+sen2t)+c$
Reemplazando este resultado en la ED.
$e^{2t} q = e^{2t}(cos2t+sen2t)+c$
Despejamos la variable dependiente $q$
$q = \dfrac{e^{2t}(cos2t+sen2t)}{e^{2t}}+\dfrac{c}{e^{2t}}$
Simplificando.
$q = cos2t+sen2t+ce^{-2t}$
Ahora reemplazamos condiciones iniciales $q(0)=0$ para hallar la $c$
$0 = cos2(0)+sen2(0)+ce^{-2(0)}$
El valor de la constante es.
$c=-1$
La carga en función del tiempo es.
Para calcular la corriente recuerde que $I=\dfrac{dq}{dt}$
$I =-2sen2t+2cos2t+2e^{-2t}$
La corriente en función del tiempo es.
En la página $200$ puedes observar un vídeo de aplicación de circuitos.
En el siguiente video, realizado por Jaime H. Ramírez Rios, podrás observar un ejemplo de aplicación de crecimiento.
En el siguiente video, realizado por Jaime H. Ramírez Rios, podrás observar un ejemplo de aplicación de temperatura.
En el siguiente video, realizado por Jaime H. Ramírez Rios, podrás observar un ejemplo de aplicación de mezclas.
En el siguiente video, realizado por Jaime H. Ramírez Rios, podrás observar un ejemplo de aplicación de circuitos.
En la segunda unidad se estudiaron ED de primer orden. En esta unidad se estudiarán las ecuaciones de orden superior $n\geq 2$ comenzando con las ecuaciones lineales.
Una ED lineal de orden superior es de la forma:
$a_{n}y^{(n)}+ a_{n-1}y^{(n-1)}+\ldots+a_{2}y''+a_{1}y'+ a_{0}y=g{(x)}$
Cuando $g(x)=0$ se dice que la ED es homogénea, en caso contrario es no homogénea.
Soluciones
La función $y=h(x)$ se llama solución de la ED si está definida y es derivable $n$ veces en algún intervalo de tal manera que al sustituirla en la ecuación junto con sus derivadas se obtenga una identidad.
$y=c_{1}y_{1}(x)+ c_{2}y_{2}(x)+\ldots+c_{n}y_{n}(x)$
Donde $c_{1},c_{2},\ldots,c_{n}$ son constantes arbitrarias, también es una solución en el intervalo.
 Ejemplo 1. Principio de superposición
Ejemplo 1. Principio de superposiciónUsando el principio de superposición, probar que las funciones.
$y_1=c_1e^{-x}$, $y_2=c_2xe^{-x}$ son soluciones de la ED $y''+2y'+y=0$
Solución
Escribimos la solución como una combinación lineal de las soluciones.
$y=c_1e^{-x}+c_2xe^{-x}$
$y'=-c_1e^{-x}-c_2xe^{-x}+c_2e^{-x}$
$y''=c_1e^{-x}+c_2xe^{-x}-2c_2e^{-x}$
Reemplazando en la ED.
$c_1e^{-x}+c_2xe^{-x}-2c_2e^{-x}-2c_1e^{-x}-2c_2xe^{-x}+2c_2e^{-x}+c_1e^{-x}+c_2xe^{-x}=0$
Agrupando términos semejantes queda $0=0$
Como se cumple la identidad, se prueba por el principio de superposición que las funciones.
$c_{1}f_{1}(x)+ c_{2}f_{2}(x)+\ldots+c_{n}f_{n}(x)=0$
Para toda $x$ en el intervalo. Si el conjunto de funciones no es linealmente dependiente en el intervalo, se dice que es linealmente independiente.
$w \left( f_{1}\left( x\right) ,f_{2}\left( x\right) ,\ldots ,f_{n}\left( x\right) \right) =\begin{vmatrix} f_{1} & f_{2} & . & . & . & f_{n} \\ \\ f_{1}' & f_{2}' & . & . & . & f'_{n} \\ \vdots & \vdots & & & & \vdots \\ f^{\left( n-1\right) }_{1} & f^{\left( n-1\right) }_{2} & . & . & . & f^{\left( n-1\right) }_{n} \end{vmatrix}$
Donde las primas denotan derivadas, se llama el Wronskiano de las funciones.
 Ejemplo 1. Dependencia e independencia lineal
Ejemplo 1. Dependencia e independencia linealVerificar si el conjunto de funciones $f_1(x)=e^{3x}, f_2(x)=5e^{3x}$ es linealmente dependiente (LD) o linealmente independiente (LI) en el intervalo $(-\infty, \infty)$
Solución
Para determinar si el conjunto de funciones es LI o LD se deben analizar las dos funciones.
Si multiplicamos $f_1$ por 5, obtenemos $f_2$ , es decir, $5f_1=f_2$
Entonces $f_1$ es múltiplo escalar de $f_2$
Si dos funciones son múltiplo escalar, son LD.
Otra forma de resolver el ejercicio es aplicando el Wronskiano de las funciones.
$w \left( f_{1}\left( x\right) ,f_{2}\left( x\right) \right) =\begin{vmatrix} e^{3x} & & 5e^{3x} \\ 3e^{3x} & & 15e^{3x} \end{vmatrix}=15e^{6x}{\color{red}-}15e^{6x}=0$
 Ejemplo 2. Dependencia e independencia lineal
Ejemplo 2. Dependencia e independencia linealVerificar si el conjunto de funciones $f_1(x)=e^{3x}, f_2(x)=e^{4x}$ es LD o LI en el intervalo $(-\infty, \infty)$
Solución
Para determinar si el conjunto de funciones es LI o LD se deben analizar las dos funciones.
Si multiplicamos cada función por una constante diferente, $A \wedge B$ y las igualamos, $\;\;$ $Ae^{3x} = Be^{4x}$.$\;\;$ La igualdad sólo se cumple cuando $A=0 \wedge B=0$
Por definición es LD si existen constantes no todas ceros. como las dos constantes son cero el conjunto de funciones es LI.
Otra forma de resolver el ejercicio es aplicando el Wronskiano de las funciones.
$w \left( f_{1}\left( x\right) ,f_{2}\left( x\right) \right) =\begin{vmatrix} e^{3x} & & e^{4x} \\ 3e^{3x} & & 4e^{4x} \end{vmatrix}=4e^{7x}{\color{red}-}3e^{7x}=e^{7x}$
 Ejemplo 3. Dependencia e independencia lineal
Ejemplo 3. Dependencia e independencia linealVerificar si el conjunto de funciones $f_1(x)=x, f_2(x)=x^2\;\;\wedge\;\;f_3(x)=3x^2-2x$ es LD o LI en el intervalo $(-\infty, \infty)$
Solución
Para determinar si el conjunto de funciones es LI o LD se deben analizar las tres funciones.
La función $f_3(x)$ se puede escribir como una combinación lineal de las otras dos funciones $f_3(x)=3f_2(x)-2f_1(x)$, entonces,
Nota un conjunto de funciones $f_1(x), f_2(x),\ldots, f_n(x)$ es LD en un intervalo, si por lo menos una función se puede expresar como una combinación lineal de las otras funciones.
Ahora lo vamos a resolver aplicando el Wronskiano de las funciones.
$w \left( f_{1}\left( x\right) ,f_{2}\left( x\right) , f_{3}\left( x\right) \right) =\begin{vmatrix} x & x^{2} & 3x^{2}-2x \\ 1 & 2x & 6x-2 \\ 0 & 2 & 6 \end{vmatrix}$
Nota Si tienes dificultad para recordar cómo calcular determinantes de matrices de $2\times2$ $\wedge$ $3\times3$ puedes pasar a la página 210 para repasar dicho tema.
Lo vamos a resolver expandiendo la fila 1.
$w=x\begin{bmatrix} 2x & 6x-2 \\ 2 & 6 \end{bmatrix}{\color{red}-}x^{2}\begin{bmatrix} 1 & 6x-2 \\ 0 & 6 \end{bmatrix}+\left( 3x^2-2x\right) \begin{bmatrix} 1 & 2x \\ 0 & 2 \end{bmatrix}$
$w=x(12x{\color{red}-}(12x-4)){\color{red}-}x^{2}(6{\color{red}-}0)+( 3x^2-2x)(2{\color{red}-}0)$
$w=x(12x-12x+4)-x^{2}(6)+( 3x^2-2x)(2)$
$w=4x-6x^{2}+6x^2-4x$ $\;\;\Rightarrow\;\; w=0$
 Ejemplo 4. Dependencia e independencia lineal
Ejemplo 4. Dependencia e independencia linealVerificar si el conjunto de funciones $f_1(x)=e^{x}, f_2(x)=e^{2x}\;\;\wedge\;\;f_3(x)=e^{3x}$ es LD o LI en el intervalo $(-\infty, \infty)$
Solución
Lo vamos a resolver aplicando el Wronskiano de las funciones.
$w \left( f_{1}\left( x\right) ,f_{2}\left( x\right) , f_{3}\left( x\right) \right) =\begin{vmatrix} e^{x} & e^{2x} & e^{3x} \\ e^{x} & 2e^{2x} & 3e^{3x} \\ e^{x} & 4e^{2x} & 9e^{3x} \end{vmatrix}$
$w=e^{x}\begin{bmatrix} 2e^{2x} & 3e^{3x} \\ 4e^{2x} & 9e^{3x} \end{bmatrix}{\color{red}-}e^{2x}\begin{bmatrix} e^{x} & 3e^{3x} \\ e^{x} & 9e^{3x} \end{bmatrix}+ e^{3x} \begin{bmatrix} e^{x} & 2e^{2x} \\ e^{x} & 4e^{2x} \end{bmatrix}$
$w=e^{x}(18e^{5x}{\color{red}-}12e^{5x}){\color{red}-}e^{2x}(9e^{4x}{\color{red}-}3e^{4x})+e^{3x}(4e^{3x}{\color{red}-}2e^{3x})$
$w=e^{x}(6e^{5x})-e^{2x}(6e^{4x})+e^{3x}(2e^{3x})$
$w=6e^{6x}-6e^{6x}+2e^{6x}$ $\;\;\Rightarrow\;\;\;\;\;\;\;\;w=2e^{6x}$
En la página 231 puedes observar un vídeo de dependencia e independencia lineal.
Asociado a cada matriz cuadrada $A$ hay un número llamado determinante de $A$ denotado como $“det A”$ o también por $\left| A\right|$ (no confundir con el valor absoluto). Los determinantes nos proporcionan un método para el cálculo de la matriz inversa (en caso de existir) y un criterio para estudiar si una matriz es o no invertible. Sus aplicaciones son múltiples en todas las ramas de las ciencias que tratan problemas lineales en los que necesariamente aparecen matrices y por tanto, determinantes. Sólo se puede calcular el determinante si la matriz es cuadrada o de orden $n$.
En la escena interactiva que aparece a continuación se explica, el cálculo del determinante de matrices de orden $2$ y $3$. Es importante que repase el concepto antes de resolver ejercicios.
$y=c_{1}y_{1}(x)+ c_{2}y_{2}(x)+\ldots+c_{n}y_{n}(x)$
Donde $c_{1}, c_{2}, \ldots ,c_{n}$, son constantes arbitrarias.
 Ejemplo 1. Conjunto fundamental de soluciones
Ejemplo 1. Conjunto fundamental de solucionesCompruebe que las funciones $e^{-3x}, e^{4x}$ forman un CFS de la ecuación diferencial $y''-y'-12y=0$ en el intervalo $(-\infty, \infty)$.
Forme la solución general y demuestre que son la solución de la ED.
Solución
Para demostrar que las funciones forman un CFS, se debe demostrar que las funciones son LI.
$w \left( f_{1}\left( x\right) ,f_{2}\left( x\right) \right) =\begin{vmatrix} e^{-3x} & & e^{4x} \\ -3e^{-3x} & & 4e^{4x} \end{vmatrix}=4e^{x}{\color{red}-}(-3e^{x})=7e^{x}$
Como $W \neq 0$ las funciones son LI.
Solución general
Como la ecuación es de segundo orden, se debe derivar dos veces la función.
$y=c_1e^{-3x}+c_2e^{4x}$
$y'=-3c_1e^{-3x}+4c_2e^{4x}$
$y''=9c_1e^{-3x}+16c_2e^{4x}$
Ahora reemplazamos la función y las dos derivadas en la ED.
$9c_1e^{-3x}+16c_2e^{4x}+3c_1e^{-3x}-4c_2e^{4x}-12c_1e^{-3x}-12c_2e^{4x}=0$
Aplicando propiedad distributiva $\wedge$ agrupando términos semejantes.
Obtenemos $0=0$
Al demostrar que el lado derecho de la ecuación es igual al lado izquierdo, se verifica que la función.
 Ejemplo 2. Conjunto fundamental de soluciones
Ejemplo 2. Conjunto fundamental de solucionesCompruebe que las funciones $cos(2\ln \left| x\right|), sen(2\ln \left| x\right|)$ forman un CFS de la ecuación diferencial $x^2y''+xy'+4y=0$ en el intervalo $(0, \infty)$.
Forme la solución general y demuestre que son la solución de la ED.
Solución
Para demostrar que las funciones forman un conjunto fundamental de soluciones, se debe demostrar que las funciones son linealmente independientes.
$w \left( f_{1}\left( x\right) ,f_{2}\left( x\right) \right) =\begin{vmatrix} cos(2\ln \left| x\right|) & & sen(2\ln \left| x\right|) \\ -2x^{-1}sen(2\ln \left| x\right|) & & 2x^{-1}cos(2\ln \left| x\right|) \end{vmatrix}$
$=2x^{-1}cos^{2}(2\ln \left| x\right|){\color{red}-}(-2x^{-1}sen^{2}(2\ln \left| x\right|))$
$=2x^{-1}(cos^{2}(2\ln \left| x\right|)+sen^{2}(2\ln \left| x\right|))$
Aplicando la identidad fundamental ${\color{blue}sen^2x+cos^2x=1}$
Obtenemos.
$w=2x^{-1}$
Como $W \neq 0$ las funciones son LI.
Solución general
Como la ecuación es de segundo orden, se debe derivar dos veces la función.
$y=c_1cos(2\ln \left| x\right|)+c_2sen(2\ln \left| x\right|)$
$y'=-2c_1x^{-1}sen(2\ln \left| x\right|)+2c_2x^{-1}cos(2\ln \left| x\right|)$
$y''=-4c_1x^{-2}cos(2\ln \left| x\right|)+2c_1x^{-2}sen(2\ln \left| x\right|)-4c_2x^{-2}sen(2\ln \left| x\right|)-2c_2x^{-2}cos(2\ln \left| x\right|)$
Ahora reemplazamos la función y las dos derivadas en la ED.
${\color{red}x^2}(-4c_1x^{-2}cos(2\ln \left| x\right|)+2c_1x^{-2}sen(2\ln \left| x\right|)-4c_2x^{-2}sen(2\ln \left| x\right|)-2c_2x^{-2}cos(2\ln \left| x\right|))+{\color{red}x}(-2c_1x^{-1}sen(2\ln \left| x\right|)+2c_2x^{-1}cos(2\ln \left| x\right|))+{\color{red}4}(c_1cos(2\ln \left| x\right|)+c_2sen(2\ln \left| x\right|))=0$
Aplicando propiedad distributiva.
$-4c_1cos(2\ln \left| x\right|)+2c_1sen(2\ln \left| x\right|)-4c_2sen(2\ln \left| x\right|)-2c_2cos(2\ln \left| x\right|))-2c_1sen(2\ln \left| x\right|)+2c_2cos(2\ln \left| x\right|))+4c_1cos(2\ln \left| x\right|)+4c_2sen(2\ln \left| x\right|))=0$
Agrupando términos semejantes Obtenemos.
$0=0$
Al demostrar que el lado derecho de la ecuación es igual al lado izquierdo, se verifica que la función.
Cuando un conjunto de funciones es LD, significa que esas funciones no son la solución de ninguna ED, sólo se verifica si son la solución de un ED cuando son LI, es decir, si forman un CFS.
En la sección anterior vimos que la solución general de una ecuación diferencial lineal homogénea de segundo orden.
$$\tag{E1}a_{2}y''+a_{1}y'+ a_{0}y=0$$
Es una combinación lineal $y=c_{1}y_{1}(x)+ c_{2}y_{2}(x)$ donde $y_{1} \;\; \wedge \;\; y_{2}$ son soluciones linealmente independientes en un intervalo $I$.
En esta sección vamos a ver un método para determinar dichas soluciones cuando los coeficientes de la ED en $(E1)$ son constantes.
Se busca una segunda solución $y_2$ tal que $y_{1} \;\; \wedge \;\; y_{2}$ sean un conjunto LI en $I$.
$y''+ P(x)y'+ Q(x)y=0$
Para encontrar la segunda solución se reemplaza en la ecuación:
 Ejemplo 1. Reducción de orden
Ejemplo 1. Reducción de ordenLa función $y_1=e^{-3x}$ es una solución de la ED $y''-y'-12y=0$. Use reducción de orden para encontrar una segunda solución $y_2$. Forme la solución General.
Solución
Este ejercicio lo resolvimos como un CFS en la página $180$, demostramos que las soluciones $e^{-3x}, e^{4x}$ forman un CFS, luego demostramos que son la solución de la ED $y''-y'-12y=0$. Ahora vamos a comenzar con la solución $e^{-3x}$ y utilizando reducción de orden vamos a hallar la segunda solución $e^{4x}$
Como la ED está en forma estándar identificamos $p(x)$ que es el término que acompaña a $y'$
$p(x)=-1$
El $p(x)$ y la solución $y_1=e^{-3x}$ los reemplazamos en la ecuación $(E2)$ para hallar la segunda solución $y_2$
$y_{2}=e^{-3x}\displaystyle \int \dfrac {e^{\int dx}}{\left[ e^{-3x}\right] ^{2}}dx$
Integramos el numerado y operamos el denominador.
$y_{2}=e^{-3x}\displaystyle \int \dfrac {e^{dx}}{e^{-6x}}dx$
Aplicando potenciación.
$y_{2}=e^{-3x}\int e^{7x}dx$
Integrando.
$y_{2}=e^{-3x}\left( \dfrac {1}{7}e^{7x}\right)$
Operando.
Solución general
 Ejemplo 2. Reducción de orden
Ejemplo 2. Reducción de ordenLa función $y_1=sen3x$ es una solución de la ED $y''+9y=0$. Use reducción de orden para encontrar una segunda solución $y_2$. Forme la solución General.
Solución
En la ED no hay $y'$, eso quiere decir que el número que acompaña este término es $0$
$p(x)=0$
El $p(x)$ y la solución $y_1=sen3x$ los reemplazamos en la ecuación $(E2)$ para hallar la segunda solución $y_2$
$y_{2}=sen3x \displaystyle \int \dfrac {e^{\int 0 dx}}{\left[ sen3x\right] ^{2}}dx$
La integral queda de la forma.
$y_{2}=sen3x \displaystyle \int \dfrac {1}{sen^{2}3x}dx$
Identidad.
$y_{2}=sen3x\int csc^{2}3x dx$
Integrando.
$y_{2}=sen3x\left( -\dfrac {1}{3}\cot {3x}\right)$
Identidad.
$y_{2}=-\dfrac {1}{3}sen3x\left( \dfrac{cos3x}{sen3x}\right)$
Simplificando.
Solución general
 Ejemplo 3. Reducción de orden
Ejemplo 3. Reducción de ordenLa función $y_1=e^{\frac{2x}{3}}$ es una solución de la ED $9y''-12y'+4y=0$. Use reducción de orden para encontrar una segunda solución $y_2$.
Forme la solución General.
Solución
A diferencia de los ejemplos anteriores, esta ED no está en forma estándar, entonces debemos dividir toda la ecuación por $9$ antes de identificar $p(x)$
$\dfrac{9y''}{9}-\dfrac{12y'}{9}+\dfrac{4y}{9}=\dfrac{0}{9}$
Simplificando.
$y''-\dfrac{4}{3}y'+\dfrac{4}{9}y=0$
Identificamos $p(x)$
$p(x)=\dfrac{4}{3}$
El $p(x)$ y la solución $y_1=e^{\frac{2x}{3}}$ los reemplazamos en la ecuación $(E2)$ para hallar la segunda solución $y_2$
$y_{2}=e^{\frac{2x}{3}} \displaystyle \int \dfrac {e^{\int \frac{4x}{3} dx}}{\left[ e^{\frac{2x}{3}}\right] ^{2}}dx$
La integral queda de la forma.
$y_{2}=e^{\frac{2x}{3}} \displaystyle \int \dfrac {e^{\frac{4x}{3}}}{\left[ e^{\frac{4x}{3}}\right]}dx$
Simplificando.
$y_{2}=e^{\frac{2x}{3}}\int dx$
Integrando.
$y_{2}=e^{\frac{2x}{3}}x$
La segunda solución es.
Solución general
 Ejemplo 4. Reducción de orden
Ejemplo 4. Reducción de ordenLa función $y_1=xcos(\ln \left| x\right|)$ es una solución de la ED $x^2y''-xy'+2y=0$. Use reducción de orden para encontrar una segunda solución $y_2$. Forme la solución General.
Solución
Como la ED no está en forma estándar, debemos dividir toda la ecuación por $x^2$ para identificar $p(x)$
$\dfrac{x^2y''}{x^2}-\dfrac{xy'}{x^2}+\dfrac{2y}{x^2}=\dfrac{0}{x^2}$
Simplificando.
$y''-\dfrac{1}{x}y'+\dfrac{2}{x^2}y=0$
Identificamos $p(x)$
$p(x)=-\dfrac{1}{x}$
El $p(x)$ y la solución $y_1=xcos(\ln \left| x\right|)$ los reemplazamos en la ecuación $(E2)$ para hallar la segunda solución $y_2$
$y_{2}=xcos(\ln \left| x\right|) \displaystyle \int \dfrac {e^{\int \frac{1}{x} dx}}{\left[ xcos(\ln \left| x\right|)\right] ^{2}}dx$
La integral queda de la forma.
$y_{2}=xcos(\ln \left| x\right|) \displaystyle \int \dfrac {x}{x^2cos^2(\ln \left| x\right|)}dx$
Simplificando y aplicando identidades.
$y_{2}=xcos(\ln \left| x\right|) \displaystyle \int \dfrac {sec^2(\ln \left| x\right|)}{x}dx$
Esta integral se resuelve por sustitución, siendo $u=(\ln \left| x\right|)$ $\wedge$ $du=\dfrac{1}{x}dx$
$y_{2}=xcos(\ln \left| x\right|) \int sec^2u du$
Integrando.
$y_{2}=xcos(\ln \left| x\right|) tanu$
Identidad.
$y_{2}=xcos(\ln \left| x\right|) \left( \dfrac{senu}{cosu}\right)$
Sustituyendo $u$
$y_{2}=xcos(\ln \left| x\right|) \left( \dfrac{sen(\ln \left| x\right|)}{cos(\ln \left| x\right|)}\right)$
Simplificando obtenemos la segunda solución.
Solución general
En el siguiente video, realizado por Jaime H. Ramírez Rios, podrás observar un ejemplo de dependencia e independencia lineal.
En el siguiente video, realizado por Jaime H. Ramírez Rios, podrás observar un ejemplo de reducción de orden.
Se trata de determinar si existen soluciones exponenciales en $(-\infty, \infty)$ de las ecuaciones lineales homogéneas de orden superior del tipo.
$a_{n}y^{(n)}+ a_{n-1}y^{(n-1)}+\ldots+a_{2}y''+a_{1}y'+ a_{0}y=0$
Donde los coeficientes $a_{n},a_{n-1},\ldots,a_{2},a_{1},a_{0}$ son constantes reales $\wedge$ $a_{n}\neq 0$
Método de solución: comenzamos para el caso especial de la ecuación de segundo orden.
$a_{2}y''+a_{1}y'+ a_{0}y=0$
La única función elemental no trivial cuya derivada es una constante múltiple de sí misma es la función exponencial $e^{mx}$, entonces la solución es de la forma $y=e^{mx}$
Vamos a reemplazar la solución $y=e^{mx}$ y sus derivadas en la ED de segundo orden y vamos a cambiar $a_{2},a_{1},a_{0}$, $\;\;$ por $\;\;$ $a,b,c$ puesto que sólo necesitamos tres constantes.
$y=e^{mx}$ $\;\;\;\;$ $y'=me^{mx}$ $\;\;\;\;$ $y''=m^2e^{mx}$
$am^2e^{mx}+bme^{mx}+ce^{mx}=0$
Factor común.
$e^{mx}(am^2+bm+c)=0$
Simplificando.
Esta solución se conoce como ecuación auxiliar o ecuación característica. Existen tres formas de la solución general que corresponden a los tres casos:

Tabla 4. Soluciones ED homogéneas.
 Ejemplo 1. Coeficientes constantes
Ejemplo 1. Coeficientes constantesResolver la ED $2y''-5y'-3y=0$.
Solución
Primero se lleva la ED a la ecuación auxiliar.
$2m^2-5m-3=0$
Se determinan los coeficientes.
$a=2, \;\; b=-5, \;\; c=-3$
Se reemplazan en la ecuación cuadrática.
$m=\dfrac {-\left( -5\right) \pm \sqrt {\left( -5\right) ^{2}-4\left( 2\right) \left( -3\right) }}{2\left( 2\right) }$
Operando.
$m=\dfrac {5\pm \sqrt {49}}{4}$
Como el discriminante es $49>0$ obtenemos dos respuestas diferentes.
$m=\dfrac {5+7}{4} \;\;\wedge\;\; m=\dfrac {5-7}{4}$
Simplificando.
$m_1=3 \;\;\;\; m_2=-\dfrac{1}{2}$
Las dos soluciones se reemplazan en las soluciones de la ED de la tabla 4.
$y_1=e^{3x} \;\;\;\; y_2=e^{-\frac{1}{2}x}$
Solución general.
 Ejemplo 2. Coeficientes constantes
Ejemplo 2. Coeficientes constantesResolver la ED $y''+6y'+9y=0$.
Solución
Primero se lleva la ED a la ecuación auxiliar.
$m^2+6m+9=0$
Se factoriza.
$m=\dfrac {-\left( 6\right) \pm \sqrt {\left( 6\right) ^{2}-4\left( 1\right) \left( 9\right) }}{2\left( 1\right) }$
Operando.
$m=\dfrac {-6\pm \sqrt {0}}{2}$
Como el discriminante es $0$ obtenemos dos respuestas iguales.
$m_1=-3 \;\;\;\ m_2=-3$
Las dos soluciones son.
$y_1=e^{-3x} \;\;\;\; y_2=xe^{-3}$
Solución general.
 Ejemplo 3. Coeficientes constantes
Ejemplo 3. Coeficientes constantesResolver la ED $y''+4y'+7y=0$.
Solución
Primero se lleva la ED a la ecuación auxiliar.
$m^2+4m+7=0$
Se factoriza.
$m=\dfrac {-\left( 4\right) \pm \sqrt {\left( 4\right) ^{2}-4\left( 1\right) \left( 7\right) }}{2\left( 1\right) }$
Operando.
$m=\dfrac {-4\pm \sqrt {-12}}{2}$
Como el discriminante es $-12<0$ Multiplicamos por $i^2=-1$
$m=\dfrac {-4\pm \sqrt {12i^2}}{2}$
Obtenemos dos respuestas complejas.
$m=\dfrac {-4\pm 2\sqrt {3}i}{2}$
Obtenemos la solución de la ecuación auxiliar.
$m=-2\pm \sqrt {3}i$
Los valores de $\alpha \wedge \beta$ son.
$\alpha=-2 \;\;\;\; \beta=\sqrt {3}$
Las soluciones utilizando la tabla $4$ son.
$y_1=e^{-2x}cos\sqrt {3}x$
$y_2=e^{-2x}sen\sqrt {3}x$
Solución general.
Cuando las respuestas son complejas no se tiene en cuenta los signos más y menos, pues la función $coseno$ es una función par y la función $seno$ es impar, por tanto, no se colocan los signos, quedan de forma implícita, tampoco se coloca la $i$ que indica imaginarios y que la respuesta es compleja.
Para resolver la ecuación auxiliar no es necesario utilizar la ecuación cuadrática, se pueden usar todas las técnicas de factorización.
 Ejemplo 4. Coeficientes constantes
Ejemplo 4. Coeficientes constantesResolver la ED $y''-25y=0$.
Solución
Primero se lleva la ED a la ecuación auxiliar.
$m^2-25=0$
Se factoriza como una diferencia de cuadrados.
$(m+5)(m-5)=0$
Obtenemos las soluciones de la ecuación auxiliar.
$m_1=5 \;\;\;\; m_2=-5$
Las dos soluciones son.
$y_1=e^{5x} \;\;\;\; y_2=e^{-5x}$
Solución general.
 Ejemplo 5. Coeficientes constantes
Ejemplo 5. Coeficientes constantesResolver la ED $y''+25y=0$.
Solución
Primero se lleva la ED a la ecuación auxiliar.
$m^2+25=0$
La suma de cuadrados no se puede factorizar, entonces despejamos la variable.
$m=\pm \sqrt {-25}$
Obtenemos la solución de la ecuación auxiliar.
$m=0\pm 5i$
Los valores de $\alpha \wedge \beta$ son.
$\alpha=0 \;\;\;\; \beta=5$
Las dos soluciones son.
$y_1=e^{0}cos5x \;\;\;\; y_2=e^{0}sen5x$
Solución general.
 Ejemplo 6. Resolver el PVI
Ejemplo 6. Resolver el PVIResolver la ED $y^{\prime\prime} +y=0$ Sujeta a $y\left( \dfrac {\pi }{3}\right)=0$ $\wedge$ $y'\left( \dfrac {\pi }{3}\right)=2$
Solución
Primero se lleva la ED a la ecuación auxiliar.
$m^2+1=0$
Despejamos la variable pues no es factorizable.
$m=\pm \sqrt {-1}$
Obtenemos la solución de la ecuación auxiliar.
$m=0\pm i$
Los valores de $\alpha \wedge \beta$ son.
$\alpha=0$ $\beta=1$
Las dos soluciones son.
$y_1=e^{0}cosx$ $y_2=e^{0}senx$
Solución general.
$y=c_1cosx+c_2senx$
Como la ED tiene condiciones iniciales, debemos pasar de la solución general a la solución particular, para esto, reemplazamos las condiciones iniciales en la solución general.
$0=c_1cos\left( \dfrac {\pi }{3}\right)+c_2sen\left( \dfrac {\pi }{3}\right)$
Evaluando obtenemos la ecuación $(1)$
$0=\dfrac {1}{2}c_1+\dfrac {\sqrt 3}{2}c_2$
Derivamos la solución general.
$y'=-c_1senx+c_2cosx$
Reemplazamos condiciones iniciales.
$2=-c_1sen\left( \dfrac {\pi }{3}\right)+c_2cos\left( \dfrac {\pi }{3}\right)$
Evaluando obtenemos la ecuación $(2)$
$2=-\dfrac {\sqrt 3}{2}c_1+\dfrac {1}{2}c_2$
Tenemos un sistema de ecuaciones.
$\begin{cases}0=\dfrac {1}{2}c_1+\dfrac {\sqrt 3}{2}c_2\\ 2=-\dfrac {\sqrt 3}{2}c_1+\dfrac {1}{2}c_2\end{cases}$
Multiplicamos la ecuación $(1)$ por $\sqrt 3$ y resolvemos el sistema de ecuaciones por eliminación.
$\begin{cases}0=\dfrac {\sqrt 3}{2}{\color{Red}\bcancel {{\color{black}c_{1}}}}+\dfrac {3}{2}c_2\\ 2=-\dfrac {\sqrt 3}{2}{\color{Red}\bcancel {{\color{black}c_{1}}}}+\dfrac {1}{2}c_2\end{cases}$
$\hspace{0.6cm}2=\;\; 2c_{2}$
Obtenemos $c_2=1$
Reemplazando este valor en la ecuación $(1)$ llegamos a.
$0=\dfrac {1}{2}c_1+\dfrac {\sqrt 3}{2}$
Despejando obtenemos $\;\;\;\;c_1=-{\sqrt 3}$
Entonces la solución particular es.
Ecuaciones de orden superior: para resolver una ecuación diferencial de n-ésimo orden de la forma.
$a_{n}m^{(n)}+ a_{n-1}m^{(n-1)}+\ldots+a_{2}m^{2}+a_{1}m+ a_{0}=0$
Si todas las raíces son reales y distintas, entonces se tiene la solución:
$\color{black}\fbox{$\color{blue}y=c_{1}e^{m_1x}+ c_2e^{m_2x}+\ldots+c_ce^{m_nx}$}\quad$
Si es de multiplicidad $k$, entonces se tiene la solución:
$\color{black}\fbox{$\color{blue}y=c_{1}e^{m_1x}+ c_2xe^{m_1x}+c_2x^2e^{m_1x}+\ldots+c_kx^{k-1}e^{m_1x}$}\quad$
Una ED de orden superior puede tener una combinación de soluciones diferentes, repetidas y complejas, para expresar la solución se utiliza la tabla $4$
 Ejemplo 7. Coeficientes constantes
Ejemplo 7. Coeficientes constantesResolver la ED $y'''+3y''-4y=0$
Solución
Primero se lleva la ED a la ecuación auxiliar.
$m^3+3m^2-4=0$
para factorizarla se hace división sintética.
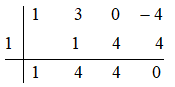
Con la división sintética obtenemos una raíz $m=1$ y con el residuo obtenemos una ecuación de segundo grado.
$(m-1)(m^2+4m+4)$
Factorizando el trinomio cuadrado perfecto.
$(m-1)(m+2)^2$
Tenemos tres soluciones, una diferente y otra de multiplicidad dos.
$y_1=e^{x}$ $y_2=e^{-2x}$ $y_3=xe^{-2x}$
Solución general.
 Ejemplo 8. Coeficientes constantes
Ejemplo 8. Coeficientes constantesResolver la ED $\dfrac{d^4y}{dx^4}+2\dfrac{d^2y}{dx^2}+y=0$
Solución
Primero se lleva la ED a la ecuación auxiliar.
$m^4+2m^2+1=0$
Es un polinomio de cuarto grado y se factoriza como un trinomio cuadrado perfecto.
$(m^2+1)^2=0$
El exponente indica que la solución es de multiplicidad dos. Se soluciona la ecuación de segundo grado.
$m^2+1=0$
Al despejar y sacar raíz cuadrada obtenemos.
$m=\pm \sqrt {-i}\;\;\;\;\Rightarrow \;\;\;\;m=\pm i$
Tenemos una raíz compleja, buscamos en la tabla $4$ y obtenemos dos soluciones.
$y_1=e^{0}cosx \;\;\;\; y_2=e^{0}senx$
Como la solución es de multiplicidad dos.
$y_1=cosx \;\;\;\; y_2=senx$ $\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;$ $y_3=xcosx \;\;\;\; y_4=xsenx$
Solución general.
En la siguiente escena interactiva, podrás resolver ED de segundo orden por medio de coeficientes constantes.
En la siguiente escena interactiva, diseñada por Marco Peñaloza, podrás resolver ED de segundo orden homogéneas.
En el siguiente video, realizado por Jaime H. Ramírez Rios, podrás observar un ejemplo de coeficientes constantes.
En el siguiente video, realizado por Jaime H. Ramírez Rios, podrás observar un ejemplo de coeficientes constantes.
Para resolver una ecuación diferencial lineal no homogénea.
$a_{n}y^{(n)}+ a_{n-1}y^{(n-1)}+\ldots+a_{2}y''+a_{1}y'+ a_{0}y=g{(x)}$
Se debe hacer dos cosas.
• Encontrar la función complementaria $y_c$ de la ecuación homogénea asociada.
• Encontrar alguna solución particular $y_p$ de la ecuación no homogénea asociada.
Es un camino directo y sencillo para determinar una solución de una ecuación lineal no homogénea con coeficientes constantes. El método consiste en hacer una conjetura acerca de la forma del $y_p$, motivada por las clases de funciones que conforman $g(x)$. El método general se limita a ED lineales donde.
• Los coeficientes $a_i, i=0,1,2...,n$ son constantes y.
• La función $g(x)$ es una constante $k$, una función polinomial, una función exponencial $e^{\alpha x}$ una función $seno$ o $coseno$ $sen\beta x, cos\beta x$ o combinaciones de estas funciones.
El método de coeficientes indeterminados no es aplicable a ecuaciones cuando la función $g(x)$ corresponde a: $\ln \left| x\right|$, $\dfrac{1}{x}$, $tanx$, $sen^{-1}x$, etc. Las ecuaciones en las que $g(x)$ es una de estas funciones se consideran en la sección $3.8$
 $$
$$
Tabla 5. Soluciones particulares de prueba.
 Ejemplo 1. Coeficientes indeterminados
Ejemplo 1. Coeficientes indeterminadosResolver la ED $y''+4y'-2y=2x^2-3x+6$
Solución
Primero se debe resolver la ED homogénea.
$y''+4y'-2y=0$
Se lleva a la ecuación auxiliar.
$m^2+4m-2=0$
Se factoriza.
$m=\dfrac {-4\pm \sqrt {24}}{2}$
Obtenemos la solución de la ecuación auxiliar.
$m=-2\pm \sqrt {6}$
La solución de la ecuación homogénea es.
$y_c=c_1e^{(-2+ \sqrt {6})x}+c_2e^{(-2- \sqrt {6})x}$
Factorizando.
Ahora vamos a calcular $y_p$, para eso buscamos en la tabla de la página $243$ el $y_p$ de prueba para un polinomio de grado $2$
$y_p=Ax^2+Bx+C$
Ahora vamos a reemplazar el $y_p$ y sus derivadas en la ED para calcular las constantes.
$y'_p=2Ax+B$
$y''_p=2A$
$2A{\color{red}+4}(2Ax+B){\color{red}-2}(Ax^2+Bx+C)=2x^2-3x+6$
Se aplica propiedad distributiva.
$2A+8Ax+4B-2Ax^2-2Bx-2C=2x^2-3x+6$
Con esta información vamos a construir un sistema de ecuaciones de tres ecuaciones con tres incógnitas.
$\begin{cases}2=-2A\\ -3=8A-2B\\ 6=2A+4B-2C\end{cases}$
Resolviendo el sistema de ecuaciones obtenemos los siguientes valores.
$A=-1 \;\;\;\;\;\;\;\; B=-\frac{5}{2} \;\;\;\;\;\;\;\; c=-9$
La solución particular es:
$y_p=-x^2-\frac{5}{2}x-9$
La solución general de la ED es:
 Ejemplo 2. Coeficientes indeterminados
Ejemplo 2. Coeficientes indeterminadosResolver la ED $y''+9y=2sen3x$
Solución
Primero se debe resolver la ED homogénea.
$y''+9y=0$
Se lleva a la ecuación auxiliar.
$m^2+9=0$
Despejamos la $m$
$m=\pm 3i$
La solución de la ecuación homogénea es.
$y_c=c_1cos3x+c_2sen3x$
Para hallar el $y_p$, buscamos en la tabla de la página $250$ para la función seno.
$y_p=Acos3x+Bsen3x$
Derivamos y reemplazamos en la ED.
$y'_p=-3Asen3x+3Bcos3x$
$y''_p=-9Acos3x-9Bsen3x$
$-9Acos3x-9Bsen3x{\color{red}+9}(Acos3x+Bsen3x)=2sen3x$
Se aplica propiedad distributiva.
$-9Acos3x-9Bsen3x+9Acos3x+9Bsen3x)=2sen3x$
Agrupando términos semejantes obtenemos.
$0=2sen3x$
El resultado es contradictorio, lo que demuestra que $y_p$ no es el adecuado. Esto ocurre porque la solución complementaria $y_c$ ya tiene $sen3x$, entonces para solucionar el problema se debe multiplicar todo el $y_p$ por $x$
$y_p=Axcos3x+Bxsen3x$
Ahora vamos a reemplazar el $y_p$ y sus derivadas en la ED para calcular las constantes.
$y'_p=-3Axsen3x+Acos3x+3Bxcos3x+Bsen3x$
$y''_p=-9Axcos3x-3Asen3x-3Asen3x-9Bxsen3x+3Bcos3x+3Bcos3x$
Agrupando términos semejantes obtenemos.
$y''_p=-9Axcos3x-6Asen3x-9Bxsen3x+6Bcos3x$
Ahora reemplazamos la segunda derivada y el $y_p$ en la ED.
$-9Axcos3x-6Asen3x-9Bxsen3x+6Bcos3x{\color{red}+9}(Axcos3x+Bxsen3x)=2sen3x$
Se aplica propiedad distributiva.
$-9Axcos3x-6Asen3x-9Bxsen3x+6Bcos3x+9Axcos3x+9Bxsen3x=2sen3x$
Agrupando términos semejantes obtenemos.
$-6Asen3x+6Bcos3x=2sen3x$
Con esta información vamos a construir un sistema de ecuaciones de dos ecuaciones con dos incógnitas.
$\begin{cases}2=-6A\\ 0=6B\end{cases}$
Los valores de las incógnitas son:
$A=-\frac{1}{6} \;\;\;\;\;\;\;\; B=0$
La solución particular es:
$y_p=-\frac{1}{6}xcos3x$
La solución general de la ED es:
 Ejemplo 3. Coeficientes indeterminados
Ejemplo 3. Coeficientes indeterminadosResolver la ED $y''-2y'-3y=4x-5+6xe^{2x}$
Solución
Primero se debe resolver la ED homogénea.
$y''-2y'-3y=0$
Se lleva a la ecuación auxiliar.
$m^2-2m-3=0$
Se factoriza.
$(m-3)(m+1)$
Las raíces del polinomio son.
$m=3 \;\;\;\;\;\;\;\; \wedge \;\;\;\;\;\;\;\;m=-1$
La solución de la ecuación homogénea es.
$y_c=c_1e^{3x}+c_2e^{-x}$
Ahora vamos a calcular $y_p$
Es importante anotar que aparecen dos $y_p$, un $y_{p_{1}}$ que corresponde a un polinomio de grado $1$ y un $y_{p_{2}}$ que corresponde a la función exponencial combinada con un polinomio de primer grado.
$y_p=y_{p_{1}}+y_{p_{2}}$
$y_p=Ax+B+(Cx+E)e^{2x}$
$y_p=Ax+B+Cxe^{2x}+Ee^{2x}$
$y'_p=A+2Cxe^{2x}+Ce^{2x}+2Ee^{2x}$
$y''_p=4Cxe^{2x}+2Ce^{2x}+2Ce^{2x}+4Ee^{2x}$
Agrupando términos semejantes.
$y''_p=4Cxe^{2x}+4Ce^{2x}+4Ee^{2x}$
Se reemplaza en la ED.
$4Cxe^{2x}+4Ce^{2x}+4Ee^{2x}{\color{red}-2}(A+2Cxe^{2x}+Ce^{2x}+2Ee^{2x}){\color{red}-3}(Ax+B+Cxe^{2x}+Ee^{2x})=4x-5+6xe^{2x}$
Se aplica propiedad distributiva.
$4Cxe^{2x}+4Ce^{2x}+4Ee^{2x}-2A-4Cxe^{2x}-2Ce^{2x}-4Ee^{2x}-3Ax-3B-3Cxe^{2x}-3Ee^{2x}=4x-5+6xe^{2x}$
Se agrupan términos semejantes.
$-3Cxe^{2x}+2Ce^{2x}-3Ee^{2x}-2A-3Ax-3B=4x-5+6xe^{2x}$
Con esta información vamos a construir un sistema de ecuaciones de cuatro ecuaciones con cuatro incógnitas.
$\begin{cases}4=-3A\\ -5=-2A-3B\\ 0=2C-3E\\ 6=-3C\end{cases}$
Los valores de las incógnitas son:
$A=-\frac{4}{3} \;\;\;\;\;\;\;\; B=\frac{23}{9} \;\;\;\;\;\;\;\; C=-2 \;\;\;\;\;\;\;\; E=-\frac{4}{3}$
La solución particular es:
$y_p=-\frac{4}{3}x+\frac{23}{9}-2xe^{2x}-\frac{4}{3}e^{2x}$
La solución general de la ED es:
 Ejemplo 4. Coeficientes indeterminados
Ejemplo 4. Coeficientes indeterminadosResolver la ED $y''+9y=xsen3x$
Solución
Primero se debe resolver la ED homogénea.
$y''+9y=0$
Se lleva a la ecuación auxiliar.
$m^2+9=0$
El término no es factorizable, entonces se despeja la $m$
$m^2=-9$
Sacamos raíz a ambos lados.
$m=\pm \sqrt {-9}$
Obtenemos la solución.
$m=0\pm 3i$
Los valores de $\alpha \wedge \beta$ son.
$\alpha=0$ $\beta=3$
Solución complementaria.
$y_c=c_1cos3x+c_2sen3x$
Ahora vamos a calcular $y_p$
$y_p=(Ax+B)cos3x+(Cx+E)sen3x$
Se puede observar que la solución complementaria ya tiene $sen3x \wedge cos3x$ entonces se debe multiplicar el $y_p$ por $x$
$y_p=(Ax^2+Bx)cos3x+(Cx^2+Ex)sen3x$
Se puede derivar así como está o hacer distributiva antes de derivar.
$y_p=Ax^2cos3x+Bxcos3x+Cx^2sen3x+Exsen3x$
$y'_p=-3Ax^2sen3x+2Axcos3x-3Bxsen3x+Bcos3x+3Cx^2cos3x+2Cxsen3x+3Excos3x+Esen3x$
$y''_p=-9Ax^2cos3x-6Axsen3x-6Axsen3x+2Acos3x-9Bxcos3x-3Bsen3x-3Bsen3x-9Cx^2sen3x+6Cxcos3x+6Cxcos3x+2Csen3x-9Exsen3x+3Ecos3x+3Ecos3x$
Se agrupan términos semejantes y se reemplaza $y_p$ y sus derivadas en la ED.
$-9Ax^2cos3x-12Axsen3x+2Acos3x-9Bxcos3x-6Bsen3x-9Cx^2sen3x+12Cxcos3x+2Csen3x-9Exsen3x+6Ecos3x{\color{red}+9}(Ax^2cos3x+Bxcos3x+Cx^2sen3x+Exsen3x)=xsen3x$
Se aplica propiedad distributiva.
$-9Ax^2cos3x-12Axsen3x+2Acos3x-9Bxcos3x-6Bsen3x-9Cx^2sen3x+12Cxcos3x+2Csen3x-9Exsen3x+6Ecos3x+9Ax^2cos3x+9Bxcos3x+9Cx^2sen3x+9Exsen3x=xsen3x$
Se agrupan términos semejantes.
$-12Axsen3x+2Acos3x-6Bsen3x+12Cxcos3x+2Csen3x+6Ecos3x=xsen3x$
Con esta información vamos a construir un sistema de ecuaciones de cuatro ecuaciones con cuatro incógnitas.
$\begin{cases}1=-12A\\ 0=2A+6E\\ 0=-6B+2C\\ 0=12C\end{cases}$
Los valores de las incógnitas son:
$A=-\frac{1}{12} \;\;\;\;\;\;\;\; B=0 \;\;\;\;\;\;\;\; C=0 \;\;\;\;\;\;\;\; E=\frac{1}{36}$
La solución particular es:
$y_p=-\frac{1}{12}x^2cos3x+\frac{1}{36}xsen3x$
La solución general de la ED es:
 Ejemplo 5. Coeficientes indeterminados
Ejemplo 5. Coeficientes indeterminadosDetermine la forma de la solución particular de $y''+2y'+y=x^{2}e^{-x}+2cos2x-3sen2x$
Solución
Al término $x^{2}e^{-x}$ le corresponde $(Ax^2+Bx+C)e^{-x}$
Al término $2cos2x-3sen2x$ le corresponde.
$(Ex+F)cos2x+(Gx+H)sen2x$
El $y_{p1}$ es equivalente a los términos de.
$y_c=c_1e^{-x}+c_2xe^{-x}$
Los términos se repiten dos veces, entonces se multiplica por $x^2$
$y_{p1}=(Ax^4+Bx^3+Cx^2)e^{-x}$
Entonces la solución particular es la suma de las dos soluciones particulares:
 Ejemplo 6. Coeficientes indeterminados
Ejemplo 6. Coeficientes indeterminadosDetermine la forma de la solución particular de.
$y''+5y'+4y=5xe^{-7x}-4x^2+3sen2x$
Solución
Al término $5xe^{7x}$ le corresponde $(Ax+B)e^{-7x}$
Al término $4x^2$ le corresponde $(Cx^2+Ex+F)$
Al término $3sen2x$ le corresponde.
$(Gx+H)cos2x+(Ix+J)sen2x \;\;\;\;\;\;\;\;$ La solución es:
 Ejemplo 5. Resolver el PVI.
Ejemplo 5. Resolver el PVI.Resolver la ED $y''+25y=4sen5x$ Sujeta a $y\left( \dfrac {\pi }{5}\right)=3$
Solución
Primero se debe resolver la ED homogénea.
$y''+25y=0$
Se lleva a la ecuación auxiliar.
$m^2+25=0$
Como no se puede factorizar, se despeja.
$m^2=-25$
Sacamos raíz a ambos lados.
$m=\pm \sqrt {-25}$
Obtenemos la solución de la ecuación auxiliar.
$m=0\pm 5i$
La solución complementaria es:
$y_c=c_1cos5x+c_2sen5x$
Ahora vamos a calcular $y_p$
$y_p=Acos5x+Bsen5x$
Se puede observar que la solución complementaria ya tiene $sen5x \wedge cos5x$ entonces se debe multiplicar el $y_p$ por $x$
$y_p=Axcos5x+Bxsen5x$
Derivamos el $y_p$ dos veces para reemplazar en la ED y calcular los valores de las constantes.
$y'_p=-5Axsen5x+Acos5x+5Bcos5x+Bcos5x$
$y''_p=-25Axsen5x-5Asen5x-5Asen5x-25Bxsen5x+5Bcos5x+5Bcos5x$
Se reemplaza $y_p$ y sus derivadas en la ED.
$-25Axsen5x-10Asen5x-25Bxsen5x+10Bcos5x{\color{red}+25}(Axcos5x+Bxsen5x)=4xsen5x$
Se aplica propiedad distributiva.
$-25Axsen5x-10Asen5x-25Bxsen5x+10Bcos5x+25Axcos5x+25Bxsen5x=4xsen5x$
Se agrupan términos semejantes.
$-10Asen5x+10Bcos5x=4sen5x$
Los valores de las incógnitas son:
$A=-\frac{2}{5} \;\;\;\;\;\;\;\; B=0$
La solución particular es:
$y_p=-\frac{2}{5}xcos5x$
La solución general de la ED es:
 Ejemplo 6. ED de tercer orden
Ejemplo 6. ED de tercer ordenDetermine la forma de la solución particular de $y'''-2y''-y'+2y=-8e^{x}+6e^{-x} $
Solución
Primero se debe resolver la ED homogénea.
$y'''-2y''-y'+2y=0$
Se lleva a la ecuación auxiliar.
$m^3-2m^2-m+2=0$
Se saca factor común por agrupación.
$m^2(m-2)-(m-2)=0$
Obtenemos dos paréntesis.
$(m^2-1)(m-2)=0$
Factorizando el primer paréntesis.
$(m+1)(m-1)(m-2)=0$
Tenemos tres raíces diferentes.
$m=-1\;\;\;\;m=1\;\;\;\;m=2$
La solución complementaria es.
$y_c=c_1e^{x}+c_2e^{-x}+c_3e^{2x}$
Ahora vamos a calcular $y_p$. Tenemos dos $y_p$ diferentes.
$y_{p1}=Ae^{x} \;\;\;\;\;\;\;\; \wedge \;\;\;\;\;\;\;\; y_{p2}=Be^{-x}$
La solución complementaria ya tiene $e^{x} \;\;\; \wedge \;\;\; e^{-x}$ entonces se multiplican cada $y_p$ por $x$ y se suman para derivar más fácil y rápido.
$y_p=Axe^{x}+Bxe^{-x}$
Se deriva tres veces la solución particular.
$y'_p=Axe^{x}+Ae^{x}-Bxe^{-x}+Be^{-x}$
$y''_p=Axe^{x}+2Ae^{x}+Bxe^{-x}-2Be^{-x}$
$y'''_p=Axe^{x}+3Ae^{x}-Bxe^{-x}+3Be^{-x}$
Se reemplaza $y_p$ y sus derivadas en la ED.
$Axe^{x}+3Ae^{x}-Bxe^{-x}+3Be^{-x}{\color{red}-2}(Axe^{x}+2Ae^{x}+Bxe^{-x}-2Be^{-x}){\color{red}-}(Axe^{x}+Ae^{x}-Bxe^{-x}+Be^{-x}){\color{red}+2}(Axe^{x}+Bxe^{-x})=-8e^{x}+6e^{-x} $
Se aplica propiedad distributiva.
$Axe^{x}+3Ae^{x}-Bxe^{-x}+3Be^{-x}-2Axe^{x}-4Ae^{x}-2Bxe^{-x}+4Be^{-x}-Axe^{x}-Ae^{x}+Bxe^{-x}-Be^{-x}+2Axe^{x}+2Bxe^{-x}=-8e^{x}+6e^{-x} $
Se agrupan términos semejantes.
$-2Ae^{x}+6Be^{-x}=-8e^{x}+6e^{-x}$
Los valores de las incógnitas son:
$A=4 \;\;\;\;\;\;\;\; B=1$
La solución particular es:
$y_p=4xe^{x}+xe^{-x}$
La solución general de la ED es:
En el siguiente video, realizado por Jaime H. Ramírez Rios, podrás observar un ejemplo de coeficientes indeterminados.
$L\left(f\left(x\right)\right)=0$
Entonces se dice que $L$ es un anulador de la función.
El operador diferencial.
$\color{black}\fbox{$\color{blue}D^{n}$}\quad$
Anula cada una de las funciones ${\color{purple} 1, x, x^2, ... , x^{n-1}}$
El operador diferencial.
$\color{black}\fbox{$\color{blue}(D-\alpha)^{n}$}\quad$
Anula cada una de las funciones ${\color{purple}e^{\alpha x}, xe^{\alpha x}, x^2e^{\alpha x}, ... , x^{n-1}e^{\alpha x}}$
El operador diferencial.
$\color{black}\fbox{$\color{blue}\left[ D^{2}-2\alpha D+\left( \alpha ^{2}+\beta ^{2}\right) \right] ^{n}$}\quad$
Anula cada una de las funciones.
${\color{purple}e^{\alpha x}cos{\beta x}, xe^{\alpha x}cos{\beta x}, x^2e^{\alpha x}cos{\beta x}, ... , x^{n-1}e^{\alpha x}cos{\beta x}}$
${\color{purple}e^{\alpha x}sen{\beta x}, xe^{\alpha x}sen{\beta x}, x^2e^{\alpha x}sen{\beta x}, ... , x^{n-1}e^{\alpha x}sen{\beta x}}$
 Ejemplo 1. Método del anulador
Ejemplo 1. Método del anuladorEncuentre un operador diferencial que anule la función.
$6-3x-7x^3$
Solución
Para anular $x^3$ se debe derivar cuatro veces, entonces el operador diferencial que anula la función es:
 Ejemplo 2. Método del anulador
Ejemplo 2. Método del anuladorEncuentre un operador diferencial que anule la función.
$e^{-5x}$
Solución
Como $\alpha=-5 \;\; \wedge \;\; n=1$ se anula la función con el operador diferencial:
 Ejemplo 3. Método del anulador
Ejemplo 3. Método del anuladorEncuentre un operador diferencial que anule la función.
$6e^{2x}+2xe^{2x}$
Solución
Como $\alpha=2 \;\; \wedge \;\; n=2$ se anula la función con el operador diferencial:
 Ejemplo 4. Método del anulador
Ejemplo 4. Método del anuladorEncuentre un operador diferencial que anule la función.
Solución
Como $\alpha=-1 \;\; \beta=2 \;\; \wedge \;\; n=1$ se anula la función con el operador diferencial:
 Ejemplo 5. Método del anulador
Ejemplo 5. Método del anuladorResolver la ED $y''+3y'+2y=4x^2$ por el método del anulador.
Solución
La ecuación auxiliar es $\;\;\;\; m^2+3m+2=0$
Factorizando $\;\;\;\; (m+2)(m+1)=0$
Las raíces son $\;\;\;\; m=-2 \;\;\;\; \wedge \;\;\;\;m=-1$
Solución complementaria ${\color{brown}y_c=c_1e^{-2x}+c_2e^{-x}}$
Como $4x^2$ se anula con el operador $D^3$
Se puede apreciar que $D^3(D^2+3D+2)y=4x^2$ es similar que $D^3(D^2+3D+2)y=0$
La ecuación auxiliar queda de la forma $\;\;\;\; m^3(m^2+3m+2)=0$
Factorizando $\;\;\;\; m^3(m+2)(m+1)=0$
Las raíces son $\;\;\;\; m_1=m_2=m_3=0,\;\; m=-2, \;\; m=-1$
La solución general es $\;\;\;\; y=c_1+c_2x+c_ex^2{\color{brown}+c_4e^{-2x}+c_5e^{-x}}$
La parte en marrón es la solución complementaria $\;\;\;\; y_c$, entonces $y_p=c_1+c_2x+c_ex^2$
Que corresponde a $\;\;\;\; y_p=A+Bx+Cx^2\;\;\;\;$ se deriva y se sustituye en la ED.
$y_p=A+Bx+Cx^2$
$y'_p=B+2Cx$
$y''_p=2C$
Se reemplaza $y_p$ y sus derivadas en la ED.
$2c{\color{red}+3}(B+2Cx){\color{red}+2}(A+Bx+Cx^2)=4x^{2}$
Se aplica propiedad distributiva.
$2c+3B+6Cx+2A+2Bx+2Cx^2=4x^{2}$
Los valores de las incógnitas son:
$A=7 \;\;\;\;\;\;\;\; B=-6 \;\;\;\;\;\;\;\; \wedge \;\;\;\;\;\;\;\; c=2$
La solución particular es:
$y_p=7-6x+2x^{2}$
La solución general de la ED es:
 Ejemplo 6. Método del anulador
Ejemplo 6. Método del anuladorResolver la ED $y''-3y'=8e^{3x}+4senx$ por el método del anulador.
Solución
La ecuación auxiliar es $\;\;\;\; m^2-3m=0$
Factorizando $\;\;\;\; m(m-3)=0$
Las raíces son $\;\;\;\; m=0 \;\;\;\; \wedge \;\;\;\;m=3$
Solución complementaria ${\color{brown}y_c=c_1+c_2e^{3x}}$
Como $\alpha=3\;\;\;\; \wedge \;\;\;\;n=1\;\;\;\;$ se anula con los operadores.
$(D-3)e^{3x}=0 \;\;\;\; \wedge \;\;\;\;(D^2+1)senx=0$
Entonces el anulador queda de la forma.
$(D-3)(D^2+1)(D^2-3D)=0$
La ecuación auxiliar queda de la forma.
$(m-3)(m^2+1)(m^2-3m)=0$
Factorizando $\;\;\;\; (m-3)(m^2+1)(m(m-3))=0$
Las raíces son $\;\;\;\; m_1=0\;\; m_2=m_3=3,\;\; m_4=i, \;\; m_5=-i$
La solución general es.
${\color{brown}y=c_1+c_2e^{3x}}+c_3xe^{3x}+c_4cosx+c_5senx$
La parte marrón es la solución complementaria $\;\;\;\; y_c$
Entonces $y_p=c_3xe^{3x}+c_4cosx+c_5senx$
Que corresponde a $\;\;\;\; y_p=Axe^{3x}+Bcosx+Csenx\;\;\;\;$ se deriva y se sustituye en la ED.
$y'_p=3Axe^{3x}+Ae^{3x}-Bsenx+Ccosx$
$y''_p=9Axe^{3x}+6Ae^{3x}-Bcosx-Csenx$
Se reemplaza $y_p$ y sus derivadas en la ED.
$9Axe^{3x}+6Ae^{3x}-Bcosx-Csenx{\color{red}-3}(3Axe^{3x}+Ae^{3x}-Bsenx+Ccosx)=8e^{3x}+4senx$
Se aplica propiedad distributiva.
$9Axe^{3x}+6Ae^{3x}-Bcosx-Csenx-9Axe^{3x}-3Ae^{3x}+3Bsenx-3Ccosx=8e^{3x}+4senx$
Se agrupan términos semejantes.
$3Ae^{3x}-Bcosx-Csenx+3Bsenx-3Ccosx=8e^{3x}+4senx$
Los valores de las incógnitas son:
$A=\dfrac{8}{3} \;\;\;\;\;\;\;\; B=\dfrac{6}{5} \;\;\;\;\;\;\;\; \wedge \;\;\;\;\;\;\;\; c=-\dfrac{2}{5}$
La solución particular es:
$y_p=\dfrac{6}{5}xe^{3x}+\dfrac{6}{5}cosx-\dfrac{2}{5}senx$
 Ejemplo 7. Método del anulador
Ejemplo 7. Método del anuladorResolver la ED $y''+y=xcosx-cosx$ por el método del anulador.
Solución
La ecuación auxiliar es $\;\;\;\; m^2+1=0$
Despejando $\;\;\;\; m^2=-1$
Las raíces son $\;\;\;\; m=i \;\;\;\; \wedge \;\;\;\;m=-i$
Solución complementaria ${\color{brown}y_c=c_1cosx+c_2senx}$
Como $\alpha=0\;\;\;\; \wedge \;\;\;\;n=2\;\;\;\;$ se anula con el operador.
$(D^2+1)^{2}=0$
Entonces el anulador queda de la forma.
$(D^2+1)^{2}(D^2+1)y=0$
La ecuación auxiliar queda de la forma.
$(m^2+1)^{2}(m^2+1)=0$
Operando.
$(m^2+1)^{3}=0$
Las raíces son $\;\;\;\; m=0\pm i\;\;\;\;$ de multiplicidad tres.
La solución general es.
${\color{brown}y=c_1cosx+c_2senx}+c_3xcosx+c_4xsenx+c_5x^2cosx+c_6x^2senx$
La parte marrón es la solución complementaria $\;\;\;\; y_c$
Entonces $y_p=c_3xcosx+c_4xsenx+c_5x^2cosx+c_6x^2senx$
Construimos la solución particular.
$y_p=Axcosx+Bxsenx+Cx^2cosx+Ex^2senx$
Se deriva y se sustituye en la ED.
$y_p=Axcosx+Bxsenx+Cx^2cosx+Ex^2senx$
$y'_p=-Axsenx+Acosx+Bxcosx+Bsenx-Cx^2senx+2Cxcosx+Ex^2cosx+2Exsenx$
$y''_p=-Axcosx-2Asenx-Bxsenx+2Bcosx-Cx^2cosx-4Cxsenx+2Ccosx-Ex^2senx+4Excosx+2Esenx$
Se reemplaza $y_p$ y sus derivadas en la ED.
$-Axcosx-2Asenx-Bxsenx+2Bcosx-Cx^2cosx-4Cxsenx+2Ccosx-Ex^2senx+4Excosx+2Esenx+Axcosx+Bxsenx+Cx^2cosx+Ex^2senx=8e^{3x}+4senx=xcosx-cosx$
Se agrupan términos semejantes.
$-2Asenx+2Bcosx-4Cxsenx+2Ccosx+4Excosx+2Esenx=8e^{3x}+4senx=xcosx-cosx$
Los valores de las incógnitas son:
$A=\dfrac{1}{4} \;\;\;\;\;\;\;\; B=-\dfrac{1}{2} \;\;\;\;\;\;\;\; C=0 \;\;\;\;\;\;\;\; \wedge \;\;\;\;\;\;\;\; E=\dfrac{1}{4}$
La solución particular es:
$y_p=\dfrac{1}{4}xcosx-\dfrac{1}{2}xsenx+\dfrac{1}{4}x^2senx$
El procedimiento utilizado para resolver una E.D. lineal de primer orden es también aplicable para resolver una E.D. de orden superior. Para adaptar el método de variación de parámetros a una ecuación diferencial de segundo orden.
$a_{2}(x)y''+a_{1}(x)y'+ a_{0}(x)y=g{(x)}$
Se debe llevar la ecuación a la forma estándar.
$\color{black}\fbox{$\color{blue}y''+P(x)y'+Q(x)y=f{(x)}$}\quad$
$P(x) \;\; Q(x) \;\; \wedge \;\; f(x) \;\;$ con continuas en $I$. Se halla $y_c$, la solución general de la ecuación homogénea. La solución particular para la ecuación lineal de segundo orden tiene la forma.
$\color{black}\fbox{$\color{blue}y_p=u_1(x)y_1(x)+u_2(x)y_2(x)$}\quad$
Donde $\;\; y_1 \;\; \wedge \;\; y_2 \;\;$ forman un conjunto fundamental de soluciones en $I$ de la forma homogénea. Como la ecuación busca determinar dos funciones desconocidas $\;\; u_1 \;\; \wedge \;\; u_2 \;\;$ y se cuenta con una sola ecuación, se deriva dos veces $y_p$ y se sustituye en la ecuación en forma estándar obteniendo las ecuaciones:
$y_1u_1+y_2u_2=0$
$y'_1u_1+y'_2u_2=f(x)$
Este sistema de dos ecuaciones con dos incógnitas se puede resolver por la regla de Cramer.
$\color{black}\fbox{$\color{blue}u'_{1}=\dfrac {W_{1}}{W}=-\dfrac {y_{2}f\left( x\right) }{W}$}\quad$ $\wedge \;\;$ $\color{black}\fbox{$\color{blue}u'_{2}=\dfrac {W_{2}}{W}=\dfrac {y_{1}f\left( x\right) }{W}$}\quad$
De donde:
$W=\begin{bmatrix} y_{1} & y_{2} \\ y'_{1} & y'_{2} \end{bmatrix} \;\; W_1=\begin{bmatrix} 0 & y_{2} \\ f(x) & y'_{2} \end{bmatrix} \;\; \wedge \;\; W_2=\begin{bmatrix} y_{1} & 0 \\ y'_{1} & f(x) \end{bmatrix}$
Las funciones $\;\; u_1 \;\; \wedge \;\; u_2 \;\;$ se obtienen integrando $\;\; u'_1 \;\; \wedge \;\; u'_2 \;\;$.
 Ejemplo 1. Variación de parámetros
Ejemplo 1. Variación de parámetrosResolver la ED $y''+2y'+y=x^2e^{-x}$ por variación de parámetros.
Solución
La ecuación auxiliar es $\;\;\;\; m^2+2m+1=0$
Factorizando $\;\;\;\; (m+1)^2=0$
Las raíces son $\;\;\;\; m=-1 \;\;\;\;$ raíz de multiplicidad dos.
Solución complementaria ${\color{brown}y_c=c_1e^{-x}+c_2xe^{-x}}$
Calculamos el Wronskiano $\;\;W=\begin{bmatrix} e^{-x} & xe^{-x} \\ -e^{-x} & -xe^{-x}+e^{-x} \end{bmatrix}$
$W=-xe^{-2x}+e^{-2x}{\color{red}-}(-xe^{-2x})=-xe^{-2x}+e^{-2x}+-xe^{-2x}$
$W=e^{-2x}$
Ahora calculamos $\;\;W_1=\begin{bmatrix} 0 & x^2e^{-x} \\ x^2e^{-x} & -xe^{-x}+e^{-x} \end{bmatrix}$
$W_1=0{\color{red}-}(x^3e^{-2x})={\color{brown}-x^3e^{-2x}}$
Ahora calculamos $\;\;W_2=\begin{bmatrix} e^{-x} & 0 \\ -e^{-x} & x^2e^{-x} \end{bmatrix}$
$W_2=x^2e^{-2x}{\color{red}-}0={\color{brown}x^2e^{-2x}}$
Entonces $\;\;u'_1=\dfrac{-x^3e^{-2x}}{e^{-2x}}\;\;$ para calcular $u_1$ se integra.
$\int {-x^3}dx$ $\;\;\;\; \Rightarrow \;\;\;\; u_1=-\dfrac{x^4}{4}$
$\;\;u'_2=\dfrac{x^2e^{-2x}}{e^{-2x}}\;\;$ para calcular $u_2$ se integra.
$\int {x^2}dx$ $\;\;\;\; \Rightarrow \;\;\;\; u_2=\dfrac{x^3}{3}\;\;\;\;$ Recuerde que.
$y_p=u_1y_1+u_2y_2$
Entonces $\;\;y_p=-\dfrac{x^4}{4}e^{-x}+\dfrac{x^3}{3}xe^{-x}$
Operando $\;\;y_p=-\dfrac{x^4e^{-x}}{4}+\dfrac{x^4e^{-x}}{3}=\dfrac{x^4e^{-x}}{12}$
No es necesario verificar si hay respuestas repetidas, el método le coloca el exponente a las respuestas repetidas. Observe que la respuesta del $y_p$ tiene exponente $x^4$, significa que estaba repetida.
 Ejemplo 2. Variación de parámetros
Ejemplo 2. Variación de parámetrosResolver la ED $y''+25y=sen5x\;\;$ por variación de parámetros.
Solución
La ecuación auxiliar es $\;\;\;\; m^2+25=0$
Como no se puede factorizar, se despeja $\;\;\;\; m^2=-25$
Las raíces son $\;\;\;\; m=\pm 5i \;\;\;\;$ raíz compleja.
Solución complementaria ${\color{brown}y_c=c_1cos5x+c_2sen5x}$
Calculamos el Wronskiano $\;\;W=\begin{bmatrix} cos5x & sen5x \\ -5sen5x & 5cos5x \end{bmatrix}$
$W=5cos^5x{\color{red}-}(-5sen^5x)=5cos^5x+5sen^5x$
$W=5$
Ahora calculamos $\;\;W_1=\begin{bmatrix} 0 & sen5x \\ sen5x & 5cos5x \end{bmatrix}$
$W_1=0{\color{red}-}(sen^25x)={\color{brown}-sen^25x}$
Ahora calculamos $\;\;W_2=\begin{bmatrix} cos5x & 0 \\ -5sen5x & sen5x \end{bmatrix}$
$W_2=cos5xsen5x{\color{red}-}0={\color{brown}sen5xcos5x}$
Entonces $\;\;u'_1=\dfrac{-sen^25x}{5}\;\;$ para calcular $u_1$ se integra.
Recuerde la identidad ${\color{blue}sen^2x=\dfrac{1-sen(2x)}{2}}$
$-\dfrac{1}{5} \displaystyle \int \dfrac{1-sen(10x)}{2}$
$\Rightarrow \;\;\;\; u_1={\color{brown}-\dfrac{x}{10}+\dfrac{1}{100}cos10x}$
$u'_2=\dfrac{sen5xcos5x}{5}\;\;$ para calcular $u_2$ se integra por sustitución.
$\dfrac{1}{5}\int sen5xcos5xdx$ $\;\;\;\; \Rightarrow \;\;\;\; u=cos5x \;\;\;\; du=-5sen5xdx$
$\dfrac{1}{5}\int sen5xcos5xdx$ $\;\;\;\; \Rightarrow \;\;\;\; u_2={\color{brown}-\dfrac{1}{50}cos^25x}$
$y_p=-\dfrac{x}{10}cos5x+\dfrac{1}{100}cos5xcos10x-\dfrac{1}{50}sen5xcos^25x$
 Ejemplo 3. Variación de parámetros
Ejemplo 3. Variación de parámetrosResolver la ED $\dfrac{1}{4}y''+y'+y=x^2-x\;\;$ por variación de parámetros.
Solución
La ecuación auxiliar es $\;\;\;\; \dfrac{1}{4}m^2+m+1=0$
Se factoriza $\;\;\;\; \left( \dfrac {1}{2}m+1\right) ^{2}=0$
Las raíces son $\;\;\;\; m=-2 \;\;\;\;$ raíz de multiplicidad dos.
Solución complementaria ${\color{brown}y_c=c_1e^{-2x}+c_2xe^{-2x}}$
Calculamos el Wronskiano $\;\;W=\begin{bmatrix} e^{-2x} & xe^{-2x} \\ -2e^{-2x} & -2xe^{-2x}+e^{-2x} \end{bmatrix}$
$W=-2xe^{-4x}+e^{-4x}{\color{red}-}(-2xe^{-4x})=-2xe^{-4x}+e^{-4x}+2xe^{-4x}$
$W=e^{-4x}$
$f(x)\;\;$ se lee cuando la ED esté en forma estándar.
Ahora calculamos $\;\;W_1=\begin{bmatrix} 0 & xe^{-2x} \\ 4x^2-4x & -2xe^{-2x}+e^{-2x} \end{bmatrix}$
$W_1=0{\color{red}-}4(x^3-x^2)e^{-2x}={\color{brown}-4(x^3-x^2)e^{-2x}}$
Ahora calculamos $\;\;W_2=\begin{bmatrix} e^{-2x} & 0 \\ -2e^{-2x} & 4x^2-4x \end{bmatrix}$
$W_2=4(x^2-x)e^{-2x}{\color{red}-}0={\color{brown}4(x^2-x)e^{-2x}}$
Entonces $\;\;u'_1=\dfrac{-4(x^3-x^2)e^{-2x}}{e^{-4x}}\;\;$ para calcular $u_1$ se integra.
$\int (-4x^3+4x^2)e^{2x}dx \;\;\;\; \Rightarrow \;\;\;\;$ se integra por partes.
$u_1=-2x^3e^{2x}+2x^2e^{2x}+3x^2e^{2x}-2xe^{2x}-3xe^{2x}+e^{2x}+\dfrac{3}{2}e^{2x}$
Agrupando términos semejantes.
$u_1=-2x^3e^{2x}+5x^2e^{2x}-5xe^{2x}+\dfrac{5}{2}e^{2x}$
$u'_2=\dfrac{4(x^2-x)e^{-2x}}{e^{-4x}}\;\;$ para calcular $u_2$ se integra.
$\int (4x^2-4x)e^{2x}dx \;\;\;\; \Rightarrow \;\;\;\;$ se integra por partes.

$u_2=2x^2e^{2x}-2xe^{2x}-2xe^{2x}+e^{2x}+e^{2x}$
Agrupando términos semejantes.
$u_2=2x^2e^{2x}-4xe^{2x}+2e^{2x}$
Entonces $\;\;y_p=-2x^3+5x^2-5x+\dfrac{5}{2}+2x^2-4x+2$
Operando $\;\;y_p=-2x^3+7x^2-9x+\dfrac{9}{2}$
 Ejemplo 2. Variación de parámetros
Ejemplo 2. Variación de parámetrosResolver la ED $y''+y=sec^2x$ por variación de parámetros.
Sujeta a la condición $y(0)=2 \;\; \wedge \;\;y'(0)=5$
Solución
Se resuelve la ED, luego se hallan los valores de las constantes.
La ecuación auxiliar es $\;\;\;\; m^2+1=0$
Como no se puede factorizar, se despeja $\;\;\;\; m^2=-1$
Las raíces son $\;\;\;\; m=\pm i \;\;\;\;$ raíz compleja.
Solución complementaria ${\color{brown}y_c=c_1cosx+c_2senx}$
Calculamos el Wronskiano $\;\;W=\begin{bmatrix} cosx & senx \\ -senx & cosx \end{bmatrix}$
$W=cos^2x{\color{red}-}(-sen^2x)=cos^2x+sen^2x={\color{brown}1}$
Ahora calculamos $\;\;W_1=\begin{bmatrix} 0 & senx \\ sec^2x & cosx \end{bmatrix}$
$W_1=0{\color{red}-}(sec^2xsenx)={\color{brown}-sec^2xsenx}$
Ahora calculamos $\;\;W_2=\begin{bmatrix} cosx & 0 \\ -senx & sec^2x \end{bmatrix}$
$W_2=cosxsec^2x{\color{red}-}0={\color{brown}cosxsec^2x}$
Entonces $\;\;u'_1=\dfrac{-sec^2xsenx}{1}\;\;$ para calcular $u_1$ se integra.
Recuerde la identidad ${\color{blue}secxsenx=tanx}$
$\int -secxtanxdx \;\;\;\; \Rightarrow \;\;\;\; u_1={\color{brown}-secx}$
$u'_2=\dfrac{cosxsec^2x}{1}\;\;$ para calcular $u_2$ se integra.
Recuerde la identidad ${\color{blue}secxcosx=1}$
$\int {secx}dx$ $\;\;\;\; \Rightarrow \;\;\;\; u_2={\color{brown}\ln \left| secx+tanx\right|}\;\;\;\;$
Recuerde que ${\color{brown}y_p=u_1y_1+u_2y_2}$
Entonces $\;\;y_p=-secxcosx+\ln \left| secx+tanx\right|senx$
Operando $\;\;y_p=-1+senx\ln \left| secx+tanx\right|$
$y=c_1cosx+c_2senx-1+senx\ln \left| secx+tanx\right|$
Reemplazamos la condición $y(0)=2$
$2=c_1cos0+c_2sen0-1+sen0\ln \left| sec0+tan0\right|$
$2=c_1-1\;\;\;\; \Rightarrow \;\;\;\;c_1=3$
$y'=-c_1senx+c_2cosx+senx.\dfrac{1}{secx+tanx}(secxtanx+sec^2x)+cosx\ln \left| secx+tanx\right|$
$y'=-c_1senx+c_2cosx+senxsecx+cosx\ln \left| secx+tanx\right|$
Reemplazamos la condición $y'(0)=5$
$5=-c_1sen0+c_2cos0+sen0sec0+cos0\ln \left| sec0+tan0\right|$
$c_2=5$
Reemplazando el valor de las constantes en la solución general, obtenemos la solución particular.
En el siguiente video, realizado por Jaime H. Ramírez Rios, podrás observar un ejemplo de variación de parámetros.
Una ecuación diferencial de la forma.
$a_{n}x^ny^{(n)}+ a_{n-1}x^{n-1}y^{(n-1)}+\ldots+a_{2}x^2y''+a_{1}xy'+ a_{0}y=g{(x)}$
Donde los coeficientes $a_{n}, a_{n-1}, ..., a_{2}, a_{1}, a_{0}$ son constantes se conoce como ecuación de Cauchy-Euler. Tiene como característica que el grado de los coeficientes nominales coincide con el orden de la ecuación. La ecuación de segundo orden tiene la forma:
$ax^2y''+bxy'+cy=0$
Método de solución: La función elemental no trivial cuya derivada es una constante múltiple de sí misma es la función exponencial $x^{m}$, entonces la solución es de la forma $y=x^{m}$

Tabla 6. Soluciones ecuación de Cauchy homogéneas.
 Ejemplo 1. ecuación homogénea
Ejemplo 1. ecuación homogéneaResolver la ecuación de Cauchy Euler $x^2y''+xy'-y=0$
Solución
Vamos a reemplazar la solución $y=x^{m}$ y sus derivadas en la ED de segundo orden.
$y=x^{m}$ $\;\;\;\;$ $y'=mx^{m-1}$ $\;\;\;\;$ $y''=m(m-1)x^{m-2}$
$x^2m(m-1)x^{m-2}+xmx^{m-1}-x^{m}=0$
Agrupamos las $x$ aplicando propiedades de potenciación.
$m(m-1)x^{m}+mx^{m}-x^{m}=0$
Factor común.
$x^{m}(m(m-1)+m-1)=0$
Propiedad distributiva.
$m^2-m+m-1=0$
Agrupando términos semejantes.
$m^2-1=0$
Factorizando obtenemos.
$m_1=1\;\;\;\; \wedge \;\;\;\;m_2=-1$
La solución general es.
 Ejemplo 2. ecuación homogénea
Ejemplo 2. ecuación homogéneaResolver la ecuación de Cauchy Euler $x^2y''+3xy'+y=0$
Solución
Vamos a reemplazar la solución $y=x^{m}$ y sus derivadas en la ED de segundo orden.
$y=x^{m}$ $\;\;\;\;$ $y'=mx^{m-1}$ $\;\;\;\;$ $y''=m(m-1)x^{m-2}$
$x^2m(m-1)x^{m-2}+3xmx^{m-1}+x^{m}=0$
Agrupamos las $x$ aplicando propiedades de potenciación.
$m(m-1)x^{m}+3mx^{m}+x^{m}=0$
Factor común.
$x^{m}(m(m-1)+3m+1)=0$
Se pasa $x^m$ a dividir al lado derecho y se aplica propiedad distributiva.
$m^2+2m+1=0$
Factorizando.
$(m+1)^2=0$
Tenemos dos raíces iguales. $m=-1$. La solución general es.
 Ejemplo 3. ecuación homogénea
Ejemplo 3. ecuación homogéneaResolver la ecuación de Cauchy Euler $x^2y''-xy'+2y=0$
Solución
Vamos a reemplazar la solución $y=x^{m}$ y sus derivadas en la ED de segundo orden.
$y=x^{m}$ $\;\;\;\;$ $y'=mx^{m-1}$ $\;\;\;\;$ $y''=m(m-1)x^{m-2}$
$x^2m(m-1)x^{m-2}-xmx^{m-1}+2x^{m}=0$
Agrupamos las $x$ aplicando propiedades de potenciación.
$m(m-1)x^{m}-mx^{m}+2x^{m}=0$
Factor común.
$x^{m}(m(m-1)-m+2)=0$
Se pasa $x^m$ a dividir al lado derecho y se aplica propiedad distributiva.
$m^2-2m+2=0$
Como el polinomio no es factorizable, usamos la ecuación cuadrática.
$m=\dfrac {2\pm \sqrt {4-8}}{2}$
Obtenemos la solución de la ecuación auxiliar.
$m=\dfrac {2\pm \sqrt {-4}}{2}$
Raíz negativa, entonces obtenemos solución compleja.
$m=1 \pm i$
Solución general.
 Ejemplo 4. ecuación homogénea
Ejemplo 4. ecuación homogéneaResolver la ecuación de Cauchy Euler $x^3y'''-6y=0$
Solución
Vamos a reemplazar la solución $y=x^{m}$ y sus derivadas en la ED de segundo orden.
$y=x^{m}$ $\;\;\;\;$ $y'=mx^{m-1}$ $\;\;\;\;$ $y''=m(m-1)x^{m-2}$
$y'''=m(m-1)(m-2)x^{m-3}$
$x^3m(m-1)(m-2)x^{m-3}-6x^{m}=0$
Agrupamos las $x$ aplicando propiedades de potenciación.
$m(m-1)(m-2)x^{m}-6x^{m}=0$
Factor común.
$x^{m}(m(m-1)(m-2)-6)=0$
Se pasa $x^m$ a dividir al lado derecho, se aplica propiedad distributiva y se agrupan términos semejantes.
$m^3-3m^2+2m-6=0$
Con la división sintética obtenemos una raíz $m=3$ y con el residuo obtenemos una ecuación de segundo grado.
$(m-3)(m^2+2)=0$
Se despeja el segundo término para hallar las tres raíces de la ecuación auxiliar.
$m=3 \;\;\;\; \wedge \;\;\;\;m= \pm \sqrt{2}$
Solución general.
 Ejemplo 5. ecuación no homogénea
Ejemplo 5. ecuación no homogéneaResolver la ecuación de Cauchy Euler $x^2y''-3xy'+3y=2x^4e^x$
Solución
Vamos a reemplazar la solución $y=x^{m}$ y sus derivadas en la ED de segundo orden.
$y=x^{m}$ $\;\;\;\;$ $y'=mx^{m-1}$ $\;\;\;\;$ $y''=m(m-1)x^{m-2}$
$x^2m(m-1)x^{m-2}-3xmx^{m-1}+3x^{m}=0$
Agrupamos las $x$ aplicando propiedades de potenciación.
$m(m-1)x^{m}-3mx^{m}+3x^{m}=0$
Factor común.
$x^{m}(m(m-1)-3m+3)=0$
Se pasa $x^m$ a dividir al lado derecho y se aplica distributiva.
$m^2-4m+3=0$
Factorizando.
$(m-3)(m-1)=0$
Las dos raíces son.
$m=3 \;\;\;\; \wedge \;\;\;\; m=1$
La solución complementaria es:
$y_c=c_1x^3+c_2x$
Calculamos el Wronskiano $\;\;W=\begin{bmatrix} x^3 & x \\ 3x^2 & 1 \end{bmatrix}$
$W=x^3-3x^3$
$W=-2x^3$
para calcular $W_1 \;\;\;\; \wedge \;\;\;\; W_2$ debemos llevar la ED a la forma estándar.
$y''-\dfrac{3}{x}y'+\dfrac{3}{x^2}y=2x^2e^x \;\;\;\; \Rightarrow \;\;\;\; f(x)=2x^2e^x$
Ahora calculamos $\;\;W_1=\begin{bmatrix} 0 & x \\ 2x^2e^x & 1 \end{bmatrix}$
$W_1=0{\color{red}-}(2x^3e^x)={\color{brown}-2x^3e^x}$
Ahora calculamos $\;\;W_2=\begin{bmatrix} x^3 & 0 \\ 3x^2 & 2x^2e^x \end{bmatrix}$
$W_2=2x^5e^x{\color{red}-}0={\color{brown}2x^5e^x}$
Entonces $\;\;u'_1=\dfrac{-2x^3e^x}{-2x^3}\;\;$ para calcular $u_1$ se integra.
$\int e^xdx \;\;\;\; \Rightarrow \;\;\;\; u_1={\color{brown}e^x}$
$u'_2=\dfrac{2x^5e^x}{-2x^3}\;\;$ para calcular $u_2$ se integra.
$\int {-x^2e^2}dx \;\;\;\; \Rightarrow \;\;\;\;$ Se integra por partes.
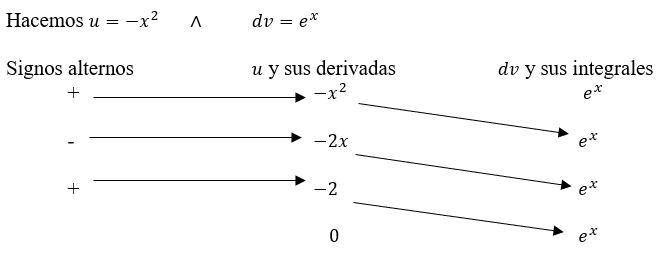
$u_2=-x^2e^x+2xe^x-2e^x$
Recuerde que $y_p=u_1y_1+u_2y_2$
Entonces $\;\;y_p=(e^x)(x^3)+(-x^2e^x+2xe^x-2e^x)(x)$
$y_p=x^3e^x-x^3e^x+2x^2e^x-2xe^x$
Agrupando términos semejantes obtenemos.
$y_p=2x^2e^x-2xe^x$
La solución general es:
 Ejemplo 6. ecuación no homogénea
Ejemplo 6. ecuación no homogéneaResolver la ecuación de Cauchy Euler $x^2y''+8xy'+10y=x^{-1}\ln \left| x\right|$
Solución
Vamos a reemplazar la solución $y=x^{m}$ y sus derivadas en la ED de segundo orden.
$y=x^{m}$ $\;\;\;\;$ $y'=mx^{m-1}$ $\;\;\;\;$ $y''=m(m-1)x^{m-2}$
$x^2m(m-1)x^{m-2}+8xmx^{m-1}+10x^{m}=0$
Agrupamos las $x$ aplicando propiedades de potenciación.
$m(m-1)x^{m}+8mx^{m}+10x^{m}=0$
Factor común.
$x^{m}(m(m-1)+8m+10)=0$
Se pasa $x^m$ a dividir al lado derecho y se aplica distributiva.
$m^2+7m+10=0$
Factorizando.
$(m+5)(m+2)=0$
Las dos raíces son.
$m=-5 \;\;\;\; \wedge \;\;\;\; m=-2$
La solución complementaria es:
$y_c=c_1x^{-5}+c_2x^{-2}$
Calculamos el Wronskiano $\;\;W=\begin{bmatrix} x^{-5} & x^{-2} \\ -5x^{-6} & -2x^{-3} \end{bmatrix}$
$W=-2x^{-8}+5x^{-8}$
$W=3x^{-8}$
para calcular $W_1 \;\;\;\; \wedge \;\;\;\; W_2$ debemos llevar la ED a la forma estándar.
$y''+\dfrac{8}{x}y'+\dfrac{10}{x^2}y=\dfrac{x^{-1}\ln \left| x\right|}{x^2} \;\;\;\; \Rightarrow \;\;\;\; f(x)=x^{-3}\ln \left| x\right|$
Ahora calculamos $\;\;W_1=\begin{bmatrix} 0 & x^{-2} \\ x^{-3}\ln \left| x\right| & -2x^{-3} \end{bmatrix}$
$W_1=0{\color{red}-}(x^{-5}\ln \left| x\right|)={\color{brown}-x^{-5}\ln \left| x\right|}$
Ahora calculamos $\;\;W_2=\begin{bmatrix} x^{-5} & 0 \\ -5x^{-6} & x^{-3}\ln \left| x\right| \end{bmatrix}$
$W_2=x^{-8}\ln \left| x\right|{\color{red}-}0={\color{brown}x^{-8}\ln \left| x\right|}$
Entonces $\;\;u'_1=\dfrac{-x^{-5}\ln \left| x\right|}{3x^{-8}}\;\;$ para calcular $u_1$ se integra.
$\displaystyle \int \dfrac{-x^{3}\ln \left| x\right|}{3}dx$
Se integra por partes.
$u=\ln \left| x\right|$ $dv=-\dfrac{x^3}{3}dx$
$du=\dfrac{1}{x}dx$ $v=-\dfrac{x^4}{12}$
Aplicando la fórmula de integración por partes.
$u_1=-\dfrac{x^4\ln \left| x\right|}{12}+\dfrac{1}{12} \int x^3dx$
$u_1$ es.
$u_1=-\dfrac{x^4\ln \left| x\right|}{12}+\dfrac{1}{48}x^4$
Ahora calculamos $u_2$
$u'_2=\dfrac{x^{-8}\ln \left| x\right|}{3x^{-8}}\;\;$ para calcular $u_2$ se integra.
$\displaystyle \int \dfrac{\ln \left| x\right|}{3}dx$
Se integra por partes.
$u=\dfrac {\ln \left| x\right|}{3}$ $dv=dx$
$du=\dfrac{1}{3x}dx$ $v=x$
Aplicando la fórmula de integración por partes.
$u_2=\dfrac{x\ln \left| x\right|}{3}-\dfrac{1}{3} \int dx$
$u_2=\dfrac{x\ln \left| x\right|}{3}-\dfrac{x}{3}$
Ahora calculamos $y_p$
$y_p=u_1y_1+u_2y_2$
$y_p=\left( -\dfrac{x^{4}\ln \left| x\right| }{12}+\dfrac{x^{4}}{48}\right) x^{-5}+\left( \dfrac{x\ln \left| x\right|}{3}-\dfrac{x}{3}\right) x^{-2}$
Aplicando distributiva.
$y_p=-\dfrac{x^{-1}\ln \left| x\right|}{12}+\dfrac{x^{-1}}{48}+\dfrac{x^{-1}\ln \left| x\right|}{3}-\dfrac{x^{-1}}{3}$
Agrupando términos semejantes obtenemos.
$y_p=-\dfrac{x^{-1}\ln \left| x\right|}{4}-\dfrac{5x^{-1}}{16}$
La solución general es:
Ahora vamos a resolver una ED de Cauchy Euler con valores iniciales.
 Ejemplo 7. Ecuación no homogénea
Ejemplo 7. Ecuación no homogéneaResolver la ecuación de Cauchy Euler $x^2y''-5xy'+8y=8x^{6}$
Sujeta a la condición $y\left( \dfrac{1}{2}\right) =0 \;\; \wedge \;\;y'\left( \dfrac{1}{2}\right) =0$
Solución
Reemplazamos la solución $y=x^{m}$ y sus derivadas en la ED.
$y=x^{m}$ $\;\;\;\;$ $y'=mx^{m-1}$ $\;\;\;\;$ $y''=m(m-1)x^{m-2}$
$x^2m(m-1)x^{m-2}-5xmx^{m-1}+8x^{m}=0$
Agrupamos las $x$ aplicando propiedades de potenciación.
$m(m-1)x^{m}-5mx^{m}+8x^{m}=0$
Factor común.
$x^{m}(m(m-1)-5m+8)=0$
Se pasa $x^m$ a dividir al lado derecho y se aplica distributiva.
$m^2-6m+8=0$
Factorizando.
$(m-2)(m-4)=0$
Las dos raíces son.
$m=2 \;\;\;\; \wedge \;\;\;\; m=4$
La solución complementaria es:
$y_c=c_1x^{2}+c_2x^{4}$
Calculamos el Wronskiano $\;\;W=\begin{bmatrix} x^{2} & x^{4} \\ 2x & 4x^{3} \end{bmatrix}$
$W=4x^{5}-2x^{5}$
$W=2x^{5}$
para calcular $W_1 \;\;\;\; \wedge \;\;\;\; W_2$ debemos llevar la ED a la forma estándar.
$y''-\dfrac{5}{x}y'+\dfrac{8}{x^2}y=8x^4 \;\;\;\; \Rightarrow \;\;\;\; f(x)=8x^{4}$
Ahora calculamos $\;\;W_1=\begin{bmatrix} 0 & x^{4} \\ 8x^{4} & 4x^{3} \end{bmatrix}$
$W_1=0{\color{red}-}(8x^{8})={\color{brown}-8x^{8}}$
Ahora calculamos $\;\;W_2=\begin{bmatrix} x^{2} & 0 \\ 2x & 8x^{4} \end{bmatrix}$
$W_2=8x^{6}{\color{red}-}0={\color{brown}8x^{6}}$
Entonces $\;\;u'_1=\dfrac{-8x^{8}}{2x^{5}}\;\;$ para calcular $u_1$ se integra.
$\int -4x^{3}dx$
$u_1=-x^4$
Ahora calculamos $u_2$
$u'_2=\dfrac{8x^{6}}{2x^{5}}\;\;$ para calcular $u_2$ se integra.
$\int 4xdx$
$u_2=2x^2$
Ahora calculamos $y_p$
$y_p=u_1y_1+u_2y_2$
$y_p=(-x^4)(x^2)+(2x^{2})(x^4)$
$y_p=-x^{6}+2x^{6}$
Agrupando términos semejantes obtenemos.
$y_p=x^{6}$
La solución general es:
$y=c_1x^{2}+c_2x^{4}+x^{6}$
Reemplazamos las condiciones iniciales en la solución general.
$0=\dfrac{1}{4}c_1+\dfrac{1}{16}c_2+\dfrac{1}{64}$
ecuación $(1)$
Derivamos la solución general para reemplazar la otra condición.
$y'=2c_1x+4c_2x^{3}+6x^{5}$
Reemplazamos C.I.
$0=c_1+\dfrac{1}{2}c_2+\dfrac{3}{16}$
ecuación $(2)$. Resolvemos el sistema de ecuaciones.
$\begin{cases}0=\dfrac{1}{4}c_1+\dfrac{1}{16}c_2+\dfrac{1}{64}\\ 0=c_1+\dfrac{1}{2}c_2+\dfrac{3}{16}\end{cases}$
Multiplicamos la ecuación $(2)$ por $-\dfrac{1}{4}$ y resolvemos el sistema de ecuaciones por eliminación.
$\begin{cases}-\dfrac{1}{64}=\dfrac{1}{4}{\color{Red}\bcancel {{\color{black}c_{1}}}}+\dfrac{1}{16}c_2\\ \;\; \dfrac{3}{64}=-\dfrac{1}{4}{\color{Red}\bcancel {{\color{black}c_{1}}}}-\dfrac{1}{8}c_2\end{cases}$
$\hspace{0.6cm}\dfrac{1}{32}=\;\; -\dfrac{1}{16}c_{2}$
Obtenemos $c_2=-\dfrac{1}{2}$
Reemplazando en la ecuación $(1)$ obtenemos $c_1=\dfrac{1}{16}$
La solución particular es:
En el siguiente video, realizado por Jaime H. Ramírez Rios, podrás observar un ejemplo de Cauchy Euler homogénea.
En el siguiente video, realizado por Jaime H. Ramírez Rios, podrás observar un ejemplo de Cauchy Euler no homogénea.
En este capítulo se examina un tipo especial de transformada integral llamada transformada de Laplace. Además de tener la propiedad de linealidad, la transformada de Laplace tiene muchas otras propiedades interesantes que la hacen muy útil para resolver problemas lineales con valores iniciales.
La Transformada de Laplace corresponde a un operador $T(f)$ definido por la integral.
$$\tag{E1}f\left( t\right) =\int _{0}^{\infty }k\left( s,t\right) f\left( t\right) dt $$
Con $f(t)$ definido para $T≥0$
Transforma una función $f$ de la variable $t$ en una función $F$ de la variable $s$.
La integral $(E1)$ se define como un límite.
$$\int _{0}^{\infty }k\left( s,t\right) f\left( t\right) dt=\displaystyle\lim_{b \to\infty}\int _{0}^{b}k\left( s,t\right) f\left( t\right) dt $$
Si el límite existe se dice que la integral converge, en caso contrario diverge. En general el límite existirá sólo para ciertos valores de la variable $s$.
La función $k\left( s,t\right)$ en la ecuación $(E 1)$ se llama Kernel o Núcleo de la transformada. La elección de $k\left( s,t\right)=e^{-st}$ como el núcleo nos proporciona una integral especialmente importante, la cual vamos a definir a continuación.
Definición: sea $f$ una función definida por $t≥0$ entonces se dice que la integral
$$\tag{E2} \mathscr{L}\left\{ f\left( t\right) \right\}=\int _{0}^{\infty }e^{-st} f\left( t\right) dt$$
Es la transformada de Laplace de $f$, siempre que la integral converja.
Cuando la integral de la ecuación $(E2)$ converge el resultado es una función de $s$. En el análisis general se usa una letra minúscula para denotar la función que se transforma y la letra mayúscula correspondiente para denotar su transformada, por ejemplo:
$\mathscr{L}\left\{ f\left( t\right) \right\}=F(s)\;\;\;\;\mathscr{L}\left\{ g\left( t\right) \right\}=G(s)\;\;\;\;\mathscr{L}\left\{ y\left( t\right) \right\}=Y(s)$
 Ejemplo 1. Transformada de Laplace
Ejemplo 1. Transformada de LaplaceEvaluar la Transformada de Laplace de $k$
Solución
$\mathscr{L}\left\{ k \right\}=\int _{0}^{\infty }ke^{-st} dt$
Como no se puede evaluar una integral con un integrando infinito, transformamos la integral en un límite.
$\displaystyle\lim_{b \to\infty}\int _{0}^{b}ke^{-st} dt $
Sacamos la constante $k$
$\displaystyle\lim_{b \to\infty}k\int _{0}^{b}e^{-st} dt $
Se integra por sustitución.
$\displaystyle\lim_{b \to\infty}-\left[\dfrac{e^{-st}}{s}\right] _{0}^{b}$
Evaluamos la integral.
$\displaystyle\lim_{b \to\infty}-\dfrac{e^{-sb}}{s}+\dfrac{e^{0}}{s}$
Evaluamos el límite.
$\displaystyle\lim_{b \to\infty}-\dfrac{e^{-sb}}{s}+\dfrac{e^{0}}{s}=\dfrac{1}{s}$
Concluimos que la Transformada de Laplace de la función constante $k$ es:
Este resultado es válido para $s>0$
Ahora vamos a evaluar la Transformada de Laplace de la función identidad $t$
 Ejemplo 2. Transformada de Laplace
Ejemplo 2. Transformada de LaplaceEvaluar la Transformada de Laplace de $t$
Solución
$\mathscr{L}\left\{ t \right\}=\int _{0}^{\infty }te^{-st} dt$
Como no se puede evaluar una integral con un integrando infinito, transformamos la integral en un límite. También se debe tener en cuenta que esta integral es diferente a la anterior porque la $t$ es una variable.
$\displaystyle\lim_{b \to\infty}\int _{0}^{t}te^{-st} dt $
Se integra por partes.
$u=t$ $dv=e^{-st}$
$du=dt$ $v=-\dfrac{e^{-st}}{s}$
Aplicando la fórmula de integración por partes.
$\displaystyle\lim_{b \to\infty}-\dfrac{te^{-st}}{s}+\dfrac{1}{s}\int _{0}^{t}e^{-st} dt$
Se integra por sustitución.
$\displaystyle\lim_{b \to\infty}\left[-\dfrac{te^{-st}}{s}-\dfrac{1}{s^2}e^{-st}\right] _{0}^{b}$
Evaluamos la integral.
$\displaystyle\lim_{b \to\infty}\left[-\dfrac{be^{-sb}}{s}-\dfrac{1}{s^2}e^{-sb}\right]-\left[-\dfrac{0e^{0}}{s}-\dfrac{1}{s^2}e^{0}\right]$
$\displaystyle\lim_{b \to\infty}\left[-\dfrac{be^{-sb}}{s}-\dfrac{1}{s^2}e^{-sb}\right]+\dfrac{1}{s^2}$
Evaluamos el límite. Se debe notar que el primer término es una indeterminación, pues multiplicamos $\infty$ por $0$. Por tanto, debemos aplicar el teorema de L´H$\widehat{o}$pital.
Recuerde que para aplicar el teorema debemos tener un cociente.
$\displaystyle\lim_{b \to\infty}-\dfrac{b}{e^{sb}}=-\dfrac{1}{s^2e^{sb}}=0$
Al evaluar el límite nos da $0$
Concluimos que la Transformada de Laplace de la función identidad $t$ es:
Este resultado es válido para $s>0$
Con los dos ejemplos anteriores se establece la generalización de la Transformada de Laplace mediante el siguiente teorema llamado transformadas básicas. Se sobreentiende la restricción de $s$ para la convergencia de cada Transformada de Laplace.

Tabla 7. Transformada de funciones básicas.
Mediante integrales básicas como sustitución y partes vistas en cálculo integral el estudiante puede verificar las transformadas básicas que están en la tabla $7$
La transformada de Laplace corresponde a un operador lineal.
$\mathscr{L}\left\{ \alpha f\left( t\right) \pm \beta g\left( t\right) \right\}$
Podemos aplicar las mismas propiedades de las integrales porque la transformada de Laplace es una integral, entonces podemos dividir la función anterior en dos transformadas.
$\mathscr{L}\left\{ \alpha f\left( t\right)\right\} \pm \mathscr{L}\left\{\beta g\left( t\right) \right\}$
Ahora sacamos las constantes de las transformadas.
$\alpha \; \mathscr{L}\left\{ f\left( t\right)\right\} \pm \beta \; \mathscr{L}\left\{ g\left( t\right) \right\}$
 Ejemplo 3. Transformada básica
Ejemplo 3. Transformada básicaEvaluar la Transformada $\mathscr{L}\left\{ 5t+2-4sen5t \right\}$
Solución
Como la transformada de Laplace es un operador lineal podemos separar la función en tres transformadas.
$\mathscr{L}\left\{ 5t \right\}+\mathscr{L}\left\{ 2 \right\}-\mathscr{L}\left\{ 4sen5t \right\}$
Sacamos las constantes de cada transformada.
$5\mathscr{L}\left\{ t \right\}+2\mathscr{L}\left\{ 1 \right\}-4\mathscr{L}\left\{ sen5t \right\}$
Ahora aplicamos las transformadas básicas del teorema $1$, aplicamos las propiedades $2$, $1$ y $5$
$5\dfrac{1}{s^2}+2\dfrac{1}{s}-4\dfrac{5}{s^2+5^2}$
Operando los términos obtenemos:
Estos resultados también se pueden obtener integrando cada término.
 Ejemplo 4. Transformada básica
Ejemplo 4. Transformada básicaEvaluar la Transformada $\mathscr{L}\left\{ 3t^4+3cos4t-8e^{-3t}+2senh5t \right\}$
Solución
Separamos la función en cuatro transformadas, esto se puede hacer cuando los términos estén separados por sumas o restas.
$\mathscr{L}\left\{ 3t^4 \right\}+\mathscr{L}\left\{ 3cos4t \right\}-\mathscr{L}\left\{ 8e^{-3t} \right\}+ \mathscr{L}\left\{ 2senh5t \right\}$
Ahora sacamos la constante de cada transformadas.
$3\mathscr{L}\left\{ t^4 \right\}+3\mathscr{L}\left\{ cos4t \right\}-8\mathscr{L}\left\{ e^{-3t} \right\}+2 \mathscr{L}\left\{ senh5t \right\}$
Ahora aplicamos las transformadas básicas del teorema $1$, aplicamos las propiedades $3$, $4$, $6$ y $8$
$3\dfrac{4!}{s^{4+1}}+3\dfrac{s}{s^2+4^2}-8\dfrac{1}{s-(-3)}+2\dfrac{5}{s^2-5^2}$
Operando los términos obtenemos:
 Ejemplo 5. Transformada básica
Ejemplo 5. Transformada básicaEvaluar la Transformada $\mathscr{L}\left\{ cos^2t \right\}$
Solución
La transformada de Laplace de $cos^2t$ no está en las transformadas básicas, entonces es necesario aplicar identidades para transformar la función.
Recuerde la identidad ${\color{blue}cos^2t=\dfrac{1+cos2t}{2}}$
$\mathscr{L}\left\{ cos^2t \right\}=\mathscr{L}\left\{ \dfrac{1+cos2t}{2} \right\}=$
$\mathscr{L}\left\{ \dfrac{1}{2} \right\}+\dfrac{1}{2}\mathscr{L}\left\{ cos2t \right\}$
Ahora aplicamos las transformadas básicas del teorema $1$, aplicamos las propiedades $1$, y $6$
Operando los términos obtenemos:
 Ejemplo 6. Transformada de una función continua por tramos
Ejemplo 6. Transformada de una función continua por tramosEvalúe $\mathscr{L}\left\{ f\left( t\right) \right\}$ donde $f\left( t\right) =\begin{cases}0 \;\;\;\;\;\;\;\;0\leq t=3\\ 2 \;\;\;\;\;\;\;\;\;\;\;\;\;\; t\geq 3\end{cases}$
Solución
La función que se muestra en la figura, es continua por tramos y de orden exponencial para $t>0$, la función $f$ se define en dos tramos, la $\mathscr{L}\left\{ f\left( t\right) \right\}$ se expresa como la suma de dos integrales.
$\mathscr{L}\left\{ f\left( t\right) \right\}=\int ^{3}_{0}0e^{-st}dt+\int ^{\infty }_{3}2e^{-st}dt$
Sólo se evalúa la segunda integral, la primera es $0$
$\displaystyle\lim_{b \to\infty}\int ^{b}_{3}2e^{-st}dt $
Se saca la constante de la integral.
$\displaystyle\lim_{b \to\infty}2\int ^{b}_{3}e^{-st}dt $
Integrando.
$\displaystyle\lim_{b \to\infty}\left[-\dfrac{2e^{-st}}{s}\right] _{3}^{b}$
Evaluamos la integral.
$\displaystyle\lim_{b \to\infty}\left[-\dfrac{2e^{-sb}}{s}\right]-\left[-\dfrac{2e^{-3s}}{s}\right]$
Evaluando el límite obtenemos.
En el siguiente video, realizado por Jaime H. Ramírez Rios, podrás observar un ejemplo de Transformada de Laplace por tramos.
El problema inverso:
Si $F(s)$ representa la transformada de Laplace de una función $f(s)$, es decir, $\mathscr{L}\left\{ f\left( t\right) \right\}=F(s)$. Se dice entonces que $f(t)$ es la transformada de Laplace inversa de $F(s)$ y se escribe:
$f(t)=\mathscr{L} ^{-1} \left\{ f\left( s\right) \right\}$
Al igual que la transformada de Laplace básica, existe un teorema para generalizar las transformadas básicas inversas.

Tabla 8. Transformada de funciones inversas.
La transformada de Laplace inversa corresponde a un operador lineal.
$\mathscr{L} ^{-1} \left\{ \alpha f\left( t\right) \pm \beta g\left( t\right) \right\}$
Podemos aplicar las mismas propiedades de las integrales porque la transformada de Laplace es una integral, entonces podemos dividir la función anterior en dos transformadas.
$\mathscr{L} ^{-1} \left\{ \alpha f\left( t\right)\right\} \pm \mathscr{L} ^{-1} \left\{\beta g\left( t\right) \right\}$
Ahora sacamos las constantes de las transformadas.
$\alpha \; \mathscr{L} ^{-1} \left\{ f\left( t\right)\right\} \pm \beta \; \mathscr{L} ^{-1} \left\{ g\left( t\right) \right\}$
 Ejemplo 1. Transformada inversa
Ejemplo 1. Transformada inversaEvalúe $\mathscr{L} ^{-1}\left\{ \dfrac{3s}{s^{2}-16}\right\}$
Solución
Como la transformada inversa es un operador lineal, primero se debe sacar la constante de la transformada y descomponer el $16$
$3 \mathscr{L} ^{-1}\left\{ \dfrac{s}{s^{2}-(4)^2}\right\}$
La función corresponde a la propiedad $8$ de la tabla $8$, donde $k=4$
En ocasiones se debe ajustar la función.
 Ejemplo 2. Transformada inversa
Ejemplo 2. Transformada inversaEvalúe $\mathscr{L} ^{-1}\left\{ \dfrac{1}{s^{5}}\right\}$
Solución
Corresponde a la propiedad $3$ de la tabla $8$, pero se debe ajustar.
$n+1=5$, entonces $n=4$, por tanto, la función se debe multiplicar y dividir por $4!$
$\dfrac{1}{{\color{blue}4!}} \mathscr{L} ^{-1}\left\{ \dfrac{{\color{blue}4!}}{s^{5}}\right\}$
 Ejemplo 3. Transformada inversa
Ejemplo 3. Transformada inversaEvalúe $\mathscr{L} ^{-1}\left\{ \dfrac{1}{s^{2}+7}\right\}$
Solución
Corresponde a la propiedad $5$ de la tabla $8$, pero se debe ajustar.
$k^2=7$, entonces $k=\sqrt{7}$, por tanto, la función se debe multiplicar y dividir por $\sqrt{7}$
$\dfrac{1}{{\color{blue}\sqrt{7}}} \mathscr{L} ^{-1}\left\{ \dfrac{{\color{blue}\sqrt{7}}}{s^{2}+7}\right\}$
 Ejemplo 4. Transformada inversa
Ejemplo 4. Transformada inversaEvalúe $\mathscr{L} ^{-1}\left\{ \dfrac{s+4}{s^{2}+5}\right\}$
Solución
Se debe separar en dos transformadas y sacar la constante.
$\mathscr{L} ^{-1}\left\{ \dfrac{s}{s^{2}+5}\right\}+4\mathscr{L} ^{-1}\left\{ \dfrac{1}{s^{2}+5}\right\}$
Corresponde a las propiedades $6$ y $5$ respectivamente pero se debe ajustar el segundo término para que coincida con la propiedad $5$. Se puede apreciar que $k^2=5$, por tanto, $k=\sqrt{5}$. Se debe ajustar multiplicando y dividiendo por $\sqrt{5}$
$\mathscr{L} ^{-1}\left\{ \dfrac{s}{s^{2}+5}\right\}+\dfrac{4}{{\color{blue}\sqrt{5}}}\mathscr{L} ^{-1}\left\{ \dfrac{{\color{blue}\sqrt{5}}}{s^{2}+5}\right\}$
 Ejemplo 4. Transformada inversa
Ejemplo 4. Transformada inversaEvalúe $\mathscr{L} ^{-1}\left\{ \dfrac{s^2+2s-1}{2s^{3}+3s^2-2s}\right\}$
Solución
La función no corresponde a ninguna de las propiedades de la tabla $8$, se debe separar el denominador.
$\mathscr{L} ^{-1}\left\{ \dfrac{s^2+2s-1}{s(2s-1)(s+2)}\right\}$
Se aplica fracciones parciales. Se factoriza el denominador.
$\dfrac{s^2+2s-1}{s(2s-1)(s+2)}$
El denominador tiene tres factores lineales distintos, por lo cual corresponde al caso 1 de fracciones parciales y se organiza de la siguiente manera:
El denominador tiene tres factores lineales distintos, por lo cual corresponde al caso 1 de fracciones parciales.
$\dfrac{s^2+2s-1}{s(2s-1)(s+2)}=\dfrac{A}{s}+\dfrac{B}{2s-1}+\dfrac{C}{s+2}$
Esta identidad es válida para todos los valores de $s$ excepto $s=0, s=1/2 \wedge s=-2$. Para hallar los valores de $A$, $B \;\; \wedge \;\; C$, multiplicamos ambos lados de esta ecuación por $s(2s-1)(s+2)$
$s^2+2s-1=A(2s-1)(s+2)+Bs(s+2)+Cs(2s-1)$
Ahora reemplazamos esos valores en la ecuación para hallar $A$, $B \;\; \wedge \;\; C$
Cuando $s=0$
$-1=A(-1)(2)$
$A=\dfrac{1}{2}$
Cuando $s=1/2$
$\dfrac{1}{4}=B\left( \dfrac{1}{2}\right) \left( \dfrac{5}{2}\right)$
$B=\dfrac{1}{5}$
Cuando $s=-2$
$-1=C(-2)(-5)\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; C=-\dfrac{1}{10}$
Con los valores de la constante procedemos a evaluar la transformada inversa.
$\mathscr{L} ^{-1}\left\{ \dfrac{s^2+2s-1}{s(2s-1)(s+2)}\right\}=$
$\dfrac{1}{2} \mathscr{L} ^{-1}\left\{ \dfrac{1}{s}\right\}+\dfrac{1}{5}\mathscr{L} ^{-1}\left\{ \dfrac{1}{(2s-1)}\right\}-\dfrac{1}{10}\mathscr{L} ^{-1}\left\{ \dfrac{1}{(s+2)}\right\}$
Las transformadas corresponden a la propiedad $1$ y $4$ de la tabla $8$, pero el segundo término hay que ajustarlo antes de aplicar las propiedades.
$\dfrac{1}{2} \mathscr{L} ^{-1}\left\{ \dfrac{1}{s}\right\}+\dfrac{1}{5}\mathscr{L} ^{-1}\left\{ \dfrac{\frac{1}{{\color{blue}{2}}}}{(\frac{2s}{{\color{blue}{2}}}-\frac{1}{{\color{blue}{2}}})}\right\}-\dfrac{1}{10}\mathscr{L} ^{-1}\left\{ \dfrac{1}{(s+2)}\right\}$
$\dfrac{1}{2} \mathscr{L} ^{-1}\left\{ \dfrac{1}{s}\right\}+\dfrac{1}{10}\mathscr{L} ^{-1}\left\{ \dfrac{1}{(s-\frac{1}{2})}\right\}-\dfrac{1}{10}\mathscr{L} ^{-1}\left\{ \dfrac{1}{(s+2)}\right\}$
 Ejemplo 5. Transformada inversa
Ejemplo 5. Transformada inversaEvalúe $\mathscr{L} ^{-1}\left\{ \dfrac{1}{s^{3}+5s}\right\}$
Solución
La función no corresponde a ninguna de las propiedades de la tabla $8$, se debe hacer fracciones parciales para separar el denominador.
$\dfrac{1}{s(s^2+5)}$
El denominador tiene dos factores, uno lineal y uno cuadrático distintos, por lo cual corresponde al caso 3 de fracciones parciales y se organiza de la siguiente manera:
$\dfrac{1}{s(s^2+5)}=\dfrac{A}{s}+\dfrac{Bs+C}{s^2+5}$
Esta identidad es válida para todos los valores de $s$ excepto $s=0$. Para hallar los valores de $A$, $B \;\; \wedge \;\; C$, multiplicamos ambos lados de esta ecuación por $s(s^2+5)$ y obtenemos.
$1=A(s^2+5)+(Bs+C)(s)$
Para hallar los valores de las constantes debemos hacer distributiva y armar un sistema de ecuaciones.
$1=As^2+5A+Bs^2+Cs$
Con esta información vamos a construir un sistema de ecuaciones de tres ecuaciones con tres incógnitas.
$\begin{cases}0=A+B\\ 0=C\\ 1=5A\end{cases}$
Resolviendo el sistema de ecuaciones obtenemos los siguientes valores.
$A=\dfrac{1}{5} \;\;\;\;\;\;\;\; B=-\frac{1}{5} \;\;\;\;\;\;\;\; c=0$
Con los valores de la constante procedemos a evaluar la transformada inversa.
$\mathscr{L} ^{-1}\left\{ \dfrac{1}{s^{3}+5s}\right\}=\dfrac{1}{5} \mathscr{L} ^{-1}\left\{ \dfrac{1}{s}\right\}-\dfrac{1}{5}\mathscr{L} ^{-1}\left\{ \dfrac{s}{s^2+5}\right\}$
Las transformadas corresponden a la propiedad $1$ y $6$ de la tabla $8$
En el siguiente video, realizado por Jaime H. Ramírez Rios, podrás observar un ejemplo de Transformada de Laplace inversa.
En la escena interactiva que aparece a continuación se explica, el caso 1 de fracciones parciales. Es importante que repase el concepto antes de resolver ejercicios.
TEOREMA 3. Transformada de una derivada: Si $f,f ',f '',\ldots, f^{(n-1)}$ son continuas en $\left[0,\infty\right)$ y son de orden exponencial y si $f^{\left(n\right)}(t)$ es continua por tramos en $\left[0,\infty\right)$, entonces
$\mathscr{L}f^n(t)=s^nF(s)-s^{(n-1)}f(0)-s^{(n-2)}f'(0)-\ldots-f^{(n-1)}(0)$
Donde $F(s)=\mathscr{L}f(t)$
Solución de problemas con valores iniciales
Para resolver una ecuación diferencial lineal con coeficientes constantes sujeta a condiciones iniciales se utiliza:
$\mathscr{L}\left\{ y'\right\}=sY(s)-y(0)$
$\mathscr{L}\left\{ y''\right\}=s^2Y(s)-sy(0)-y'(0)$
$\mathscr{L}\left\{ y'''\right\}=s^3Y(s)-s^2y(0)-sy'(0)-y''(0)$
la transformada de Laplace de una ecuación diferencial lineal con coeficientes constantes se convierte en una ecuación algebraica en Y(s).
En el ejemplo siguiente se ilustra el método para resolver una ED, así como la descomposición en fracciones parciales.
 Ejemplo 1. Resolver el PVI
Ejemplo 1. Resolver el PVIResolver la Ed $y'+2y=t$ sujeta a la condición inicial $y(0)=-1$
Solución
Para resolver la ED se reemplaza el teorema tres al lado izquierdo y el teorema uno al lado derecho.
$sY(s)-y(0)+2Y(s)=\dfrac{1}{s^2}$
Se reemplazan las condiciones iniciales.
$sY(s)-(-1)+2Y(s)=\dfrac{1}{s^2}$
Se saca factor común $Y(s)$
$Y(s)(s+2)+1=\dfrac{1}{s^2}$
Se despeja el factor común.
$Y(s)(s+2)=\dfrac{1}{s^2}-1$
Se opera el lado derecho.
$Y(s)(s+2)=\dfrac{1-s^2}{s^2}$
Se despeja $Y(s)$
$Y(s)=\dfrac{1-s^2}{s^2(s+2)}$
La solución $y(t)$ del PVI original es $y(t)=\mathscr{L} ^{-1}\left\{ Y\left( s\right) \right\}$, donde la transformada inversa se hace término a término, por tanto, es necesario descomponer la expresión del lado derecho en fracciones parciales para poder aplicar el teorema dos.
$\dfrac{1-s^2}{s^2(s+2)}=\dfrac{A}{s}+\dfrac{B}{s^2}+\dfrac{C}{s+2}$
Esta identidad es válida para todos los valores de $s$ excepto $s=0 \wedge s=-2$. Para hallar los valores de $A$, $B \;\; \wedge \;\; C$, multiplicamos ambos lados de esta ecuación por $s^2(s+2)$ y obtenemos.
$1-s^2=As(s+2)+B(s+2)+C(s^2)$
Para hallar los valores de las constantes debemos hacer distributiva y armar un sistema de ecuaciones.
$1-s^2=As^2+2As+Bs+2B+Cs^2$
Con esta información vamos a construir un sistema de ecuaciones de tres ecuaciones con tres incógnitas.
$\begin{cases}-1=A+C\\ 2A+B=0\\ 1=2B\end{cases}$
Resolviendo el sistema de ecuaciones obtenemos los siguientes valores.
$A=-\dfrac{1}{4} \;\;\;\;\;\;\;\; B=\dfrac{1}{2} \;\;\;\;\;\;\;\; c=-\dfrac{3}{4}$
Con los valores de la constante procedemos a evaluar la transformada inversa.
$Y(s)=-\dfrac{1}{4}\mathscr{L} ^{-1}\left\{ \dfrac{1}{s}\right\}+\dfrac{1}{2} \mathscr{L} ^{-1}\left\{ \dfrac{1}{s^2}\right\}-\dfrac{3}{4}\mathscr{L} ^{-1}\left\{ \dfrac{1}{s+2}\right\}$
Aplicando la transformada inversa obtenemos la solución de la ED.
 Ejemplo 2. Resolver el PVI
Ejemplo 2. Resolver el PVIResolver la ED $y''+3y'=0$ sujeta a la condición inicial $y(0)=1$ $\wedge$ $y'(0)= -1$
Solución
Para resolver la ED se reemplaza el teorema tres al lado izquierdo.
$s^2Y(s)-sy(0)-y'(0)+3sY(s)-3y(0)=0$
Se reemplazan las condiciones iniciales.
$s^2Y(s)-s+1+3sY(s)-3=0$
Se saca factor común $Y(s)$
$Y(s)(s^2+3s)-s-2=0$
Se despeja el factor común.
$Y(s)(s^2+3s)=s+2$
Se despeja $Y(s)$ y se saca factor común.
$Y(s)=\dfrac{s+2}{s(s+3)}$
La solución $y(t)$ del PVI original es $y(t)=\mathscr{L} ^{-1}\left\{ Y\left( s\right) \right\}$, donde la transformada inversa se hace término a término, por tanto, es necesario descomponer la expresión del lado derecho en fracciones parciales para poder aplicar el teorema dos.
$\dfrac{s+2}{s(s+3)}=\dfrac{A}{s}+\dfrac{B}{s+3}$
Esta identidad es válida para todos los valores de $s$ excepto $s=0 \wedge s=-3$. Para hallar los valores de $A \;\; \wedge \;\; B$, multiplicamos ambos lados de esta ecuación por $s(s+3)$ y obtenemos.
$s+2=A(s+3)+Bs$
Ahora reemplazamos esos valores en la ecuación para hallar $A \;\; \wedge \;\; B$
Cuando $s=0$
$2=A(3)$
$A=\dfrac{2}{3}$
Cuando $s=-3$
$-1=B(-3)$
$B=\dfrac{1}{3}$
Con los valores de la constante procedemos a evaluar la transformada inversa.
$Y(s)=\dfrac{2}{3}\mathscr{L} ^{-1}\left\{ \dfrac{1}{s}\right\}+\dfrac{1}{3} \mathscr{L} ^{-1}\left\{ \dfrac{1}{s+3}\right\}$
Aplicando la transformada inversa obtenemos la solución de la ED.
 Ejemplo 3. Resolver el PVI
Ejemplo 3. Resolver el PVIResolver la ED $y''-3y'+2y=e^{-4t}$ sujeta a la condición inicial $y(0)=1$ $\wedge$ $y'(0)= 5$
Solución
Para resolver la ED se reemplaza el teorema tres al lado izquierdo y el teorema uno al lado derecho.
$s^2Y(s)-sy(0)-y'(0)-3sY(s)+3y(0)+2Y(s)=\dfrac{1}{s+4}$
Se reemplazan las condiciones iniciales.
$s^2Y(s)-s-5-3sY(s)+3+2Y(s)=\dfrac{1}{s+4}$
Se saca factor común $Y(s)$
$Y(s)(s^2-3s+2)-s-2=\dfrac{1}{s+4}$
Se despeja el factor común.
$Y(s)(s^2-3s+2)=\dfrac{1}{s+4}+s+2$
Se opera el lado derecho.
$Y(s)(s^2-3s+2)=\dfrac{s^2+6s+9}{s+4}$
Se despeja $Y(s)$ y se factoriza el trinomio.
$Y(s)=\dfrac{s^2+6s+9}{(s+4)(s-2)(s-1)}$
Se descompone el lado derecho en fracciones parciales para poder aplicar el teorema dos.
$\dfrac{s^2+6s+9}{(s+4)(s-2)(s-1)}=\dfrac{A}{s+4}+\dfrac{B}{s-2}+\dfrac{C}{s-1}$
Esta identidad es válida para todos los valores de $s$ excepto $s=-4, s=2 \wedge s=1$. Para hallar los valores de $A$, $B \;\; \wedge \;\; C$, multiplicamos ambos lados de esta ecuación por $(s+4)(s-2)(s-1)$ y obtenemos.
$s^2+6s+9=A(s-2)(s-1)+B(s+4)(s-1)+C(s+4)(s-2)$
Cuando $s=-4$
$1=A(-6)(-5)$
$A=\dfrac{1}{30}$
Cuando $s=2$
$25=B(6)(1)$
$B=\dfrac{25}{6}$
Cuando $s=1$
$16=C(5)(-1)$
$C=-\dfrac{16}{5}$
Con los valores de la constante procedemos a evaluar la transformada inversa.
$Y(s)=\dfrac{1}{30}\mathscr{L} ^{-1}\left\{ \dfrac{1}{s+4}\right\}+\dfrac{25}{6} \mathscr{L} ^{-1}\left\{ \dfrac{1}{s-2}\right\}$
$-\dfrac{16}{5}\mathscr{L} ^{-1}\left\{ \dfrac{1}{s-1}\right\}$
Aplicando la transformada inversa obtenemos la solución de la ED.
 Ejemplo 4. Resolver el PVI
Ejemplo 4. Resolver el PVIResolver la Ed $2y´´+y'-y=t+1$ sujeta a la condición inicial $y(0)=1$ $\wedge$ $y'(0)= 0$
Solución
Para resolver la ED se reemplaza el teorema tres al lado izquierdo y el teorema uno al lado derecho.
$2s^2Y(s)-2sy(0)-2y'(0)+sY(s)-y(0)-Y(s)=\dfrac{1}{s^2}+\dfrac{1}{s}$
Se reemplazan las condiciones iniciales.
$2s^2Y(s)-2s(1)-2(0)+sY(s)-(1)-Y(s)=\dfrac{1}{s^2}+\dfrac{1}{s}$
$2s^2Y(s)-2s+sY(s)-1-Y(s)=\dfrac{1}{s^2}+\dfrac{1}{s}$
Se saca factor común $Y(s)$
$Y(s)\left(2s^2+s-1\right)-2s-1=\dfrac{1+s}{s^2}$
Se pasan al lado derecho el término que no dependen de $Y(s)$
$Y(s)\left(2s^2+s-1\right)=\dfrac{1+s}{s^2}+2s+1$
Se opera el lado derecho.
$Y(s)\left(2s^2+s-1\right)=\dfrac{{2s}^3+s^2+s+1}{s^2}$
Se despeja $Y(s)$ y se factoriza el trinomio.
$Y(s)=\dfrac{{2s}^3+s^2+s+1}{s^2\left(2s-1\right)\left(s+1\right)}$
Se descompone el lado derecho en fracciones parciales.
$\dfrac{{2s}^3+s^2+s+1}{s^2\left(2s-1\right)\left(s+1\right)}=\dfrac{A}{s}+\dfrac{B}{s^2}+\dfrac{C}{2s-1}+\dfrac{D}{s+1}$
Esta identidad es válida para todos los valores de $s$ excepto $s=-\ \dfrac{1}{2},0,1$. Para hallar los valores de $A,B,\ C\ \land\ D$, multiplicamos ambos lados de esta ecuación por $s^2\left(2s-1\right)\left(s+1\right)$ y obtenemos.
${2s}^3+s^2+s+1=As\left(2s-1\right)\left(s+1\right)+B\left(2s-1\right)\left(s+1\right)+Cs^2\left(s+1\right)+Ds^2\left(2s-1\right)$
Hacemos distributiva y armamos un sistema de ecuaciones.
${2s}^3+s^2+s+1=2As^3+As^2-As+2Bs^2+Bs-B+Cs^3+Cs^2+2Ds^3-Ds^2$
$\begin{matrix}\begin{matrix}2A+C+2D\\A+2B+C-D\\\end{matrix}&\begin{matrix}=\\=\\\end{matrix}&\begin{matrix}2\\1\\\end{matrix}\\\begin{matrix}-A+B\\-B\\\end{matrix}&\begin{matrix}=\\=\\\end{matrix}&\begin{matrix}1\\1\\\end{matrix}\\\end{matrix}$
Resolviendo el sistema de ecuaciones obtenemos los siguientes valores.
$A=-2\;\;\;\;\;\;\;\;B=-1\;\;\;\;\;\;\;\;C=\dfrac{16}{3}\;\;\;\;\;\;\;\;D=\dfrac{1}{3}$
Con los valores de la constante procedemos a evaluar la transformada inversa.
$Y(s)=-2\mathscr{L} ^{-1}\left\{ \dfrac{1}{s}\right\}-\mathscr{L} ^{-1}\left\{ \dfrac{1}{s^2}\right\}+\dfrac{16}{3}\mathscr{L} ^{-1}\left\{ \dfrac{1}{2s-1}\right\}+\dfrac{1}{3}\mathscr{L} ^{-1}\left\{ \dfrac{1}{s+1}\right\}$
El tercer término es necesario ajustarlo antes de aplicar el teorema inverso, por tanto, dividimos todos por $2$
$Y(s)=-2\mathscr{L} ^{-1}\left\{ \dfrac{1}{s}\right\}-\mathscr{L} ^{-1}\left\{ \dfrac{1}{s^2}\right\}+\dfrac{16}{3}\mathscr{L} ^{-1}\left\{ \dfrac{\frac{1}{2}}{s-\frac{1}{2}}\right\}+\dfrac{1}{3}\mathscr{L} ^{-1}\left\{ \dfrac{1}{s+1}\right\}$
Ahora sacamos la constante.
$Y(s)=-2\mathscr{L} ^{-1}\left\{ \dfrac{1}{s}\right\}-\mathscr{L} ^{-1}\left\{ \dfrac{1}{s^2}\right\}+\dfrac{8}{3}\mathscr{L} ^{-1}\left\{ \dfrac{1}{s-\frac{1}{2}}\right\}+\dfrac{1}{3}\mathscr{L} ^{-1}\left\{ \dfrac{1}{s+1}\right\}$
Aplicando la transformada inversa obtenemos la solución de la ED.
En la siguiente escena interactiva, diseñada por Carlos Olvera, podrás resolver ED usando la Transformada de Laplace.
En el siguiente video, realizado por Jaime H. Ramírez Rios, podrás observar un ejemplo de Transformada de derivada.
Este teorema facilita encontrar transformadas sin resolver la integral, basta con recorrer la función. Gráficamente se vería así:
Si se considera $s$ una variable real, entonces la gráfica de $F(s-a)$ es la gráfica de $F(s)$ desplazada en el eje $s$ por la cantidad $\left|a\right|$. Si $a>0$, la gráfica de $F(s)$ se desplaza $a$ unidades a la derecha, mientras que si $a<0$, la gráfica se desplaza $a$ unidades a la izquierda.
Evaluar transformadas tales como $\left\{e^{-2t}t^4\right\}$ o $\left\{e^{3t}\mathrm{cosh5t} \right\}$ se puede hacer de forma directa siempre que se conozca $\left\{t^4\right\}$ o $\left\{\mathrm{cosh5t}\right\}$. si se conoce la Transformada de Laplace de una función $f(t)$, es posible calcular la Transformada de Laplace de un múltiplo exponencial de $f$, es decir, $\left\{e^{-at}f(t)\right\}$, sólo con trasladar o desplazar, $F(s)$ a $F(s-a)$. El resultado se conoce como primer teorema de traslación.
Primer teorema de traslación: Si $\mathscr{L}f(t)=F(s)$ y $a$ es cualquier número real, entonces
$\mathscr{L}\left\{e^{at}f(t)\right\}=F(s-a)$
 Ejemplo 1. Uso del primer teorema de traslación
Ejemplo 1. Uso del primer teorema de traslaciónEvalúe $\mathscr{L}\left\{e^{-2t}t^4\right\}$
Solución
Se utiliza la transformada básica (teorema $1$)
El denominador de la transformada de Euler se coloca a la derecha.
$\mathscr{L}\left\{e^{-2t}t^4\right\}=\mathscr{L}\left\{t^4|_{s\rightarrow s+2}\right\}$
Luego se aplica el teorema $1$ a la función y donde va la $s$ se coloca la traslación.
 Ejemplo 2. Uso del primer teorema de traslación
Ejemplo 2. Uso del primer teorema de traslaciónEvalúe $\mathscr{L}\left\{e^{3t}cosh5t\right\}$
Solución
Se utiliza la transformada básica (teorema $1$)
El denominador de la transformada de Euler se coloca a la derecha.
$\mathscr{L}\left\{e^{3t}cosh5t\right\}=\mathscr{L}\left\{cosh5t|_{s\rightarrow s-3}\right\}$
Luego se aplica el teorema $1$ a la función, $cosh5t$
$\mathscr{L}\left\{e^{3t}cosh5t\right\}=\mathscr{L}\left\{\dfrac{s}{s^2-25}|_{s\rightarrow s-3}\right\}$
Para terminar se debe colocar la traslación que está al lado derecho, en la función, donde esté la $s$, tanto en el numerador como en el denominador.
 Ejemplo 3. Uso del primer teorema de traslación
Ejemplo 3. Uso del primer teorema de traslaciónEvalúe $\mathscr{L}\left\{e^{-4t}sen3t\right\}$
Solución
Se utiliza la transformada básica (teorema $1$)
El denominador de la transformada de Euler se coloca a la derecha.
$\mathscr{L}\left\{e^{-4t}sen3t\right\}=\mathscr{L}\left\{sen3t|_{s\rightarrow s+4}\right\}$
Luego se aplica el teorema $1$ a la función $sen3t$
$\mathscr{L}\left\{e^{-4t}sen3t\right\}=\mathscr{L}\left\{\dfrac{3}{s^2+9}|_{s\rightarrow s+4}\right\}$
Donde está la $s$ se coloca la traslación.
Forma inversa del teorema:
$\mathscr{L} ^{-1}\left\{F(s-a)\right\}=\mathscr{L} ^{-1}\left\{\left.F(s)\right|_{s\rightarrow s-a}\right\}$
 Ejemplo 1. Forma inversa del teorema
Ejemplo 1. Forma inversa del teoremaEvalúe $\mathscr{L} ^{-1}\left\{\dfrac{5}{(s-3)^2}\right\}$
Solución
Se utiliza la transformada inversa (teorema $2$)
Se saca la constante de la transformada y la traslación se coloca a un lado.
$\mathscr{L} ^{-1}\left\{\dfrac{5}{(s-3)^2}\right\}=5\mathscr{L}^{-1}\left\{\dfrac{1}{s^2}|s\rightarrow s-3\right\}$
Se aplica el teorema $2$ a la función y a la traslación.
 Ejemplo 2. Forma inversa del teorema
Ejemplo 2. Forma inversa del teoremaEvalúe $\mathscr{L}^{-1}\left\{\dfrac{2s+5}{(s-3)^2+16}\right\}$
Solución
Antes de aplicar el teorema dos se debe ajustar el numerador, se busca que la traslación del denominador también esté en el numerador, por ese motivo se suma y se resta $6$
$\mathscr{L}^{-1}\left\{\dfrac{2s{\color{red}-6}{\color{red}+6} +5}{(s-3)^2+16}\right\}$
Luego se saca factor común y se suma el $6$ y el $5$
$\mathscr{L}^{-1}\left\{\dfrac{2(s-3)+11}{(s-3)^2+16}\right\}$
Se separan las dos traslaciones y se sacan las constantes.
$2\mathscr{L}^{-1}\left\{\dfrac{(s-3)}{(s-3)^2+16}\right\}+11\mathscr{L}^{-1}\left\{\dfrac{1}{(s-3)^2+16}\right\}$
La traslación se coloca a un lado.
$2\mathscr{L}^{-1}\left\{\dfrac{s}{s^2+16}|s\rightarrow s-3\right\}+11\mathscr{L}^{-1}\left\{\dfrac{1}{s^2+16}|s\rightarrow s-3\right\}$
Antes de aplicar el teorema $2$ se debe ajustar el segundo termino.
$2\mathscr{L}^{-1}\left\{\dfrac{s}{s^2+16}|s\rightarrow s-3\right\}+\dfrac{11}{\color{red}4}\mathscr{L}^{-1}\left\{\dfrac{{\color{red}4}}{s^2+16}|s\rightarrow s-3\right\}$
Se aplica el teorema $2$ a la función y a la traslación.
 Ejemplo 3. Resolver el PVI
Ejemplo 3. Resolver el PVIResolver la Ed $y\prime\prime-y\prime=e^{-2t}cos{2}t$ sujeta a la condición inicial $y(0)=0$ $\wedge$ $y'(0)= 1$
Solución
Se utiliza la transformada de la primera derivada (teorema $3$) para el lado izquierdo y la transformada básica (teorema $1$) para el lado derecho como sigue.
$s^2Y(s)-sy(0)-y\prime(0)-sY(s)+y(0)=\dfrac{s+2}{\left(s+2\right)^2+4}$
Se reemplazan las condiciones iníciales.
$s^2Y(s)-s-sY(s)+1=\dfrac{s+2}{\left(s+2\right)^2+4}$
factor común $Y(s)$ y se opera el denominador del lado derecho.
$Y(s)\left(s^2-s\right)-s+1=\dfrac{s+2}{s^2+4s+8}$
Se pasan los términos que no están en el factor común al lado derecho.
$Y(s)\left(s^2-s\right)=\dfrac{s+2}{s^2+4s+8}+s-1$
Se operan los fraccionarios del lado derecho.
$Y\left(s\right)(s^2-s)=\dfrac{s^3+3s^2+5s-6}{s^2+4s+8}$
Se despeja $Y(s)$
$Y\left(s\right)=\dfrac{s^3+3s^2+5s-6}{s(s-1)(s^2+4s+8)}$
Se descompone el lado derecho en fracciones parciales.
$\dfrac{s^3+3s^2+5s-6}{s(s-1)(s^2+4s+8)}=\dfrac{A}{s}+\dfrac{B}{s-1}+\dfrac{Cs+D}{s^2+4s+8}$
Esta identidad es válida para todos los valores de $s$ excepto $s=0,1$. Para hallar los valores de $A,B,\ C\ \land\ D$, multiplicamos ambos lados de esta ecuación por $s(s-1)(s^2+4s+8)$ y obtenemos.
$s^3+3s^2+5s-6=A(s-1)(s^2+4s+8)+Bs(s^2+4s+$
$8)+\left(Cs+D\right)s(s-1)$
Propiedad distributiva y se construye un sistema de ecuaciones.
$s^3+3s^2+5s-6=As^3+3As^2+4As-8A+Bs^3+4Bs^2+$
$8Bs+Cs^3-{Cs}^2+Ds^2-Ds$
$\begin{matrix}\begin{matrix}A+B+C\\3A+4B-C+D\\\end{matrix}&\begin{matrix}=\\=\\\end{matrix}&\begin{matrix}1\\3\\\end{matrix}\\\begin{matrix}4A+8B-D\\-8A\\\end{matrix}&\begin{matrix}=\\=\\\end{matrix}&\begin{matrix}5\\-6\\\end{matrix}\\\end{matrix}$
Resolviendo el sistema de ecuaciones obtenemos:
$A=\dfrac{3}{4}\;\;\;\;\;\;\;\;B=\dfrac{3}{13}\;\;\;\;\;\;\;\;C=\dfrac{1}{52}\;\;\;\;\;\;\;\;D=\dfrac{2}{13}$
Con los valores de la constante procedemos a evaluar la transformada inversa.
$Y(s)=\dfrac{3}{4}\mathscr{L} ^{-1}\left\{ \dfrac{1}{s}\right\}+\dfrac{3}{13}\mathscr{L} ^{-1}\left\{ \dfrac{1}{s-1}\right\}+$
$\dfrac{1}{52}\mathscr{L} ^{-1}\left\{ \dfrac{s+8}{s^2+4s+8}\right\}$
El tercer término es necesario factorizar el denominador, se ajusta el trinomio cuadrado perfecto y luego se factoriza.
$Y(s)=\dfrac{3}{4}\mathscr{L} ^{-1}\left\{ \dfrac{1}{s}\right\}+\dfrac{3}{13}\mathscr{L} ^{-1}\left\{ \dfrac{1}{s-1}\right\}+$
$\dfrac{1}{52}\mathscr{L} ^{-1}\left\{ \dfrac{s+8}{\left(s+2\right)^2+4}\right\}$
Ahora se ajusta el numerador.
$Y(s)=\dfrac{3}{4}\mathscr{L} ^{-1}\left\{ \dfrac{1}{s}\right\}+\dfrac{3}{13}\mathscr{L} ^{-1}\left\{ \dfrac{1}{s-1}\right\}+$
$\dfrac{1}{52}\mathscr{L} ^{-1}\left\{ \dfrac{s+2+6}{\left(s+2\right)^2+4}\right\}$
Se divide el tercer término en dos y se sacan las constantes.
$Y(s)=\dfrac{3}{4}\mathscr{L} ^{-1}\left\{ \dfrac{1}{s}\right\}+\dfrac{3}{13}\mathscr{L} ^{-1}\left\{ \dfrac{1}{s-1}\right\}+$
$\dfrac{1}{52}\mathscr{L} ^{-1}\left\{ \dfrac{s+2}{\left(s+2\right)^2+4}\right\}+\dfrac{6}{52}\mathscr{L} ^{-1}\left\{ \dfrac{1}{\left(s+2\right)^2+4}\right\}$
Se coloca la traslación a un lado.
$Y(s)=\dfrac{3}{4}\mathscr{L} ^{-1}\left\{ \dfrac{1}{s}\right\}+\dfrac{3}{13}\mathscr{L} ^{-1}\left\{ \dfrac{1}{s-1}\right\}+$
$\dfrac{1}{52}\mathscr{L}^{-1}\left\{\dfrac{s}{s^2+4}|s\rightarrow s+2\right\}+\dfrac{3}{26}\mathscr{L}^{-1}\left\{\dfrac{1}{s^2+4}|s\rightarrow s+2\right\}$
Antes de aplicar el teorema $2$ se debe ajustar el último término.
$Y(s)=\dfrac{3}{4}\mathscr{L} ^{-1}\left\{ \dfrac{1}{s}\right\}+\dfrac{3}{13}\mathscr{L} ^{-1}\left\{ \dfrac{1}{s-1}\right\}+$
$\dfrac{1}{52}\mathscr{L}^{-1}\left\{\dfrac{s}{s^2+4}|s\rightarrow s+2\right\}+\dfrac{3}{(26)\color{red}2}\mathscr{L}^{-1}\left\{\dfrac{\color{red}2}{s^2+4}|s\rightarrow s+2\right\}$
Se aplica el teorema $2$ a la función y a la traslación.
En el siguiente video, realizado por Jaime H. Ramírez Rios, podrás observar un ejemplo de Traslación en el eje $s$.
En el siguiente video, realizado por Jaime H. Ramírez Rios, podrás observar un ejemplo de Traslación en el eje $s$.
$\mu\left(t-a\right)=\left\{\begin{matrix}0,&0\le t<{a}\\1,&t\geq{a}\\\end{matrix}\right.$
La función escalón unitario es útil para representar funciones definidas a trozos. Gráficamente se vería así:
 Ejemplo 1. Función escalón
Ejemplo 1. Función escalónsuponer $f(t)=\left\{\begin{matrix}g(t),&0\le t<{a}\\h(t),&t\geq{a}\\\end{matrix}\right.$ escribir como escalones unitarios.
Solución
La función escalón está dada por:
$f(t)=g\left(t\right)+\left[h\left(t\right)-g\left(t\right)\right]\mu\left(t-a\right)$
Aplicando propiedad distributiva queda de la forma:
 Ejemplo 2. Función escalón
Ejemplo 2. Función escalónsuponer $f(t)=\left\{\begin{matrix}g(t),&0\le t<{a}\\h(t),&{a}\le t<{b}\\0,&t\geq{b}\\\end{matrix}\right.$ escribir como escalones unitarios.
Solución
La función escalón está dada por:
$f\left(t\right)=g\left(t\right)+\left[h\left(t\right)-g\left(t\right)\right]\mu\left(t-a\right)+\left[0-h\left(t\right)\right]\mu\left(t-b\right)$
Aplicando propiedad distributiva queda de la forma:
 Ejemplo 3. Función escalón
Ejemplo 3. Función escalónExprese $f\left(t\right)=\left(\begin{matrix}20t&Si&0\le t<5\\0&Si&t\geq5\\\end{matrix}\right.$ en términos de la función escalón unitario.
Solución
La función escalón está dada por:
$f\left(t\right)=20t+\left[0-20t\right]\mu\left(t-5\right)$
Aplicando propiedad distributiva queda de la forma:
$\mathscr{L}\left\{f\left(\mathrm{t-a}\right)\mu\left(t-a\right)\right.=e^{-as}F(s)$
Ahora vamos a evaluar la transformada de Laplace con traslación en el eje $t$. es importante recordar que se utilizan los tres teoremas vistos desde el comienzo de la unidad.
 Ejemplo 4
Ejemplo 4evaluar $\mathscr{L}\left\{\left(t-1\right)\mu\left(t-1\right)\right\}$
Solución
La función cumple con el segundo teorema, entonces se aplica la transformada de Laplace básica.
 Ejemplo 5
Ejemplo 5evaluar $\mathscr{L}\left\{\left(3t+1\right)\mu\left(t-2\right)\right\}$
Solución
se debe ajustar la función para que cumpla el segundo teorema de traslación.
$\mathscr{L}\left\{\left(3t\color{red}-6\color{red}+6+1\right)\mu\left(t-2\right)\right\}$
$\mathscr{L}\left\{\left(3t-6+7\right)\mu\left(t-2\right)\right\}$
Factor común y propiedad distributiva.
$\mathscr{L}\left\{3\left(t-2\right)\mu\left(t-2\right)+7\mu\left(t-2\right)\right\}$
Ahora se aplica la transformada de Laplace básica.
 Ejemplo 6
Ejemplo 6evaluar $\mathscr{L}\left\{cos{t}\;\;\mu\left(t-\pi\right)\right\}$
Solución
se debe ajustar la función para que cumpla el segundo teorema de traslación.
$\mathscr{L}\left\{cos{\left(t-\pi\right)}\mu\left(t-\pi\right)\right\}$
Como no se puede restar y sumar dentro del ángulo porque vuelve a dar lo mismo, se aplica la identidad de suma y resta de ángulos del coseno.
$\mathscr{L}\left\{\left(cos{t}cos{\pi}+sentsen\pi\right)\mu\left(t-\pi\right)\right\}$
Evaluando obtenemos.
$\mathscr{L}\left\{-cos{t}\;\mu\left(t-\pi\right)\right\}$
Ahora se aplica la transformada de Laplace básica.
$\mathscr{L} ^{-1}\left\{e^{-as}F(s)\right\}=f\left(\mathrm{t-a}\right)\mu\left(t-a\right)$
 Ejemplo 7
Ejemplo 7evaluar $\mathscr{L}^{-1}\left\{\frac{1}{s-4}e^{-2s}\right\}$
Solución
Se resuelve con la transformada de Laplace inversa para $\;\;\;\;\;\;\;\; \left\{\dfrac{1}{s-4}\right\}=e^{4t}$
Ahora donde está la $t$ se debe colocar la traslación.
 Ejemplo 8
Ejemplo 8evaluar $\mathscr{L}^{-1}\left\{\dfrac{s}{s^2+9}e^{-\frac{\pi}{2}s}\right\}$
Solución
Transformada de Laplace inversa para $\left\{\dfrac{s}{s^2+9}\right\}=cos 3t$
Ahora donde está la $t$ se debe colocar la traslación.
$\mathscr{L}^{-1}\left\{\dfrac{s}{s^2+9}e^{-\frac{\pi}{2}s}\right\}=cos{3}\left(t-\dfrac{\pi}{2}\right)\mu\left(t-\dfrac{\pi}{2}\right)$
Aplicando la identidad para el coseno.
$cos{3}\left(t-\dfrac{\pi}{2}\right)\mu\left(t-\dfrac{\pi}{2}\right)=cos{3}tcos{3}\dfrac{\pi}{2}+sen3tsen3\dfrac{\pi}{2}$
Evaluando obtenemos.
$cos{3}\left(t-\dfrac{\pi}{2}\right)\mu\left(t-\dfrac{\pi}{2}\right)=cos{3}t(0)+sen3t(-1)$
La solución es:
 Ejemplo 9
Ejemplo 9Evalúe la función $f(t)=\left\{\begin{matrix}2&0\le t<3\\-2&t\geq3\\\end{matrix}\right.$
Solución
se escribe $f(t)$ como función escalón unitario.
$f\left(t\right)=2+\left[-2-2\right]\mu\left(t-3\right)$
$f\left(t\right)=2-4\ \mu\left(t-3\right)$
Se aplica la transformada de Laplace básica.
 Ejemplo 10
Ejemplo 10Evalúe la función $f(t)=\left\{\begin{matrix}0,&0\le t<\dfrac{3\pi}{2}\\sent,&\ t\geq\dfrac{3\pi}{2}\\\end{matrix}\right.$
Solución
Se escribe $f(t)$ como función escalón unitario.
$f\left(t\right)=0+\left[sent-0\right]\mu\left(t-\dfrac{3\pi}{2}\right)$
Propiedad distributiva.
$f\left(t\right)=sen\ t\ \mu\left(t-\dfrac{3\pi}{2}\right)$
Se ajusta el ángulo.
$f\left(t\right)=sen\ \left(t-\dfrac{3\pi}{2}\right)\ \ \mu\left(t-\dfrac{3\pi}{2}\right)$
Aplicando la identidad para el seno.
$sen\left(t-\dfrac{3\pi}{2}\right)\mu\left(t-\dfrac{3\pi}{2}\right)=sen\ tcos{\dfrac{3\pi}{2}}-sen\dfrac{3\pi}{2}cost$
Evaluando.
$sen\left(t-\dfrac{3\pi}{2}\right)\mu\left(t-\dfrac{3\pi}{2}\right)=cos\ t\mu\left(t-\dfrac{3\pi}{2}\right)$
Se aplica la transformada de Laplace básica.
 Ejemplo 11
Ejemplo 11Resolver el PVI $y\prime\prime-5y\prime+6y=f(t)$ sujeta a la condición inicial.
$y(0)=0$ $\wedge$ $y'(0)= 1$ donde $f(t)=\left\{\begin{matrix}1&0\le t<1\\0&t\geq1\\\end{matrix}\right.$
Solución
se escribe $f(t)$ como función escalón unitario.
$f(t)=1-\mu\left(t-1\right)$
Vamos a resolver el PVI.
$y\prime\prime-5y\prime+6y=1-\mu\left(t-1\right)$
Se utiliza la transformada de la primera derivada (teorema $3$) para el lado izquierdo y la transformada básica (teorema $1$) para el lado derecho como sigue.
$s^2Y(s)-sy(0)-y\prime(0)-5sY(s)+5y(0)+6Y(s)=\dfrac{1}{s}-\dfrac{1}{s}e^{-s}$
Se reemplazan las condiciones iníciales.
$s^2Y(s)-s-1-5sY(s)+5+6Y(s)=\dfrac{1}{s}-\dfrac{1}{s}e^{-s}$
factor común $Y(s)$ y se despeja.
$Y(s)\left(s^2-5s+6\right)=\dfrac{1}{s}+s-4-\dfrac{1}{s}e^{-s}$
Se operan los términos semejantes al lado derecho.
$Y(s)\left(s^2-5s+6\right)=\dfrac{s^2-4s+1}{s}-\dfrac{1}{s}e^{-s}$
Se despeja $Y(s)$ y se factoriza el termino del lado izquierdo.
$Y(s)=\dfrac{s^2-4s+1}{s\left(s-2\right)\left(s-3\right)}-\dfrac{1}{s\left(s-2\right)\left(s-3\right)}e^{-s}$
Para aplicar la transformada inversa se debe hacer fracciones parciales a los dos términos por separado.
Se descompone el primer término en fracciones parciales.
$\dfrac{s^2-4s+1}{s\left(s-2\right)\left(s-3\right)}=\dfrac{A}{s}+\dfrac{B}{\left(s-2\right)}+\dfrac{C}{\left(s-3\right)}$
Esta identidad es válida para todos los valores de $s$ excepto $s=0, 2 \wedge 3$
Para hallar los valores de $A,B \wedge C$, multiplicamos ambos lados de esta ecuación por $s\left(s-2\right)\left(s-3\right)$ y obtenemos.
$s^2-4s+1=A\left(s-2\right)\left(s-3\right)+Bs\left(s-3\right)+Cs\left(s-2\right)$
Reemplazando las restricciones del dominio en la ecuación y obtenemos los valores de las constantes.
$A=\dfrac{1}{6}\;\;\;\;\;\;\;\;B=\dfrac{3}{2}\;\;\;\;\;\;\;\;C=-\dfrac{2}{3}$
Se descompone el segundo término en fracciones parciales, no vamos a tener en cuenta el signo menos y $e^{-s}$ para hacer la fracción parcial, sólo se vuelven a utilizar en la respuesta.
$\dfrac{1}{s\left(s-2\right)\left(s-3\right)}=\dfrac{A}{s}+\dfrac{B}{\left(s-2\right)}+\dfrac{C}{\left(s-3\right)}$
Esta identidad es válida para todos los valores de $s$ excepto $s=0, 2 \wedge 3$
Para hallar los valores de $A,B \wedge C$, multiplicamos ambos lados de esta ecuación por $s\left(s-2\right)\left(s-3\right)$ y obtenemos.
$1=A\left(s-2\right)\left(s-3\right)+Bs\left(s-3\right)+Cs\left(s-2\right)$
Reemplazando las restricciones en la ecuación obtenemos:
$A=\dfrac{1}{6}\;\;\;\;\;\;\;\;B=-\dfrac{1}{2}\;\;\;\;\;\;\;\;C=\dfrac{1}{3}$
$Y(s)=\dfrac{1}{6}\mathscr{L}^{-1}\left\{\dfrac{1}{s}\right\}+\dfrac{3}{2}\mathscr{L}^{-1}\left\{\dfrac{1}{s-2}\right\}-\dfrac{2}{3}\mathscr{L}^{-1}\left\{\dfrac{1}{s-3}\right\}-$
$\left(\dfrac{1}{6}\mathscr{L}^{-1}\left\{\dfrac{1}{s}\right\}-\dfrac{1}{2}\mathscr{L}^{-1}\left\{\dfrac{1}{s-2}\right\}+\dfrac{1}{3}\mathscr{L}^{-1}\left\{\dfrac{1}{s-3}\right\}\right)e^{-s}$
Aplicando la transformada inversa obtenemos:
 Ejemplo 12
Ejemplo 12Resolver el PVI $y\prime\prime+4y=sent \mu(t-2\pi)$ sujeta a la condición inicial $y(0)=1$ $\wedge$ $y'(0)= 0$
Solución
Antes de evaluar el escalón se debe ajustar el ángulo.
$\mathscr{L}\left\{sent\;\mu(t-2\pi)\right\}=\mathscr{L}\left\{sen{\left(t-2\pi\right)}\mu\left(t-2\pi\right)\right\}$
Se aplica la identidad de suma y resta de ángulos del seno.
$\mathscr{L}\left\{\left(sen{t}cos{2\pi}-costsen\pi\right)\mu\left(t-\pi\right)\right\}=\mathscr{L}\left\{sent\;\mu(t-2\pi)\right\}$
$\mathscr{L}\left\{sent\;\mu(t-2\pi)\right\}=\dfrac{1}{s^2+1}e^{-2\pi s}$
Se utiliza la transformada básica (teorema 1) para el lado derecho y se iguala al resultado que obtuvimos del escalón.
$s^2Y(s)-sy(0)-y\prime(0)+4Y(s)=\dfrac{1}{s^2+1}e^{-2\pi s}$
Se reemplazan las condiciones iníciales.
$s^2Y(s)-s+4Y(s)=\dfrac{1}{s^2+1}e^{-2\pi s}$
Se saca factor común $Y(s)$ y se despeja.
$Y(s)\left(s^2+4\right)=s+\dfrac{1}{s^2+1}e^{-2\pi s}$
Se despeja $Y(s)$
$Y(s)=\dfrac{s}{s^2+4}+\dfrac{1}{\left(s^2+4\right)\left(s^2+1\right)}e^{-2\pi s}$
Se descompone el último término en fracciones parciales.
$\dfrac{1}{\left(s^2+4\right)\left(s^2+1\right)}=\dfrac{As+B}{s^2+4}+\dfrac{Cs+D}{s^2+1}$
Para hallar los valores de $A,B\land C$, multiplicamos ambos lados de esta ecuación por $\left(s^2+4\right)\left(s^2+1\right)$ y obtenemos.
$1=\left(As+B\right)\left(s^2+1\right)+\left(Cs+D\right)\left(s^2+4\right)$
Aplicamos propiedad distributiva.
$1=As^3+As+Bs^2+B+Cs^3+4Cs+Ds^2+4D$
Construimos un sistema de ecuaciones.
$\begin{matrix}\begin{matrix}A+C\\B+D\\\end{matrix}&\begin{matrix}=\\=\\\end{matrix}&\begin{matrix}0\\0\\\end{matrix}\\\begin{matrix}A+4C\\B+4D\\\end{matrix}&\begin{matrix}=\\=\\\end{matrix}&\begin{matrix}0\\1\\\end{matrix}\\\end{matrix}$
Para resolver el sistema de ecuaciones se puede igualar la ecuación $1$ con la $3$ y la ecuación $2$ con la $4$ y hacerlo por el método de eliminación.
Se multiplica la ecuación $1$ por $(-1)$ y la sumamos a la ecuación $3$
$\hspace{0.1cm}{\color{Red}\bcancel {{\color{black}-A}}}-\;\; C=0$
$\underline{\hspace{0.3cm}{\color{Red}\bcancel {{\color{black}A}}}+4C=0}$
$\hspace{1.0cm} 3C=0$
Obtenemos el valor de la $C$ $\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;C=0$
Reemplazando en la ecuación $4$ obtenemos $\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;A=0$
Ahora se multiplica la ecuación $2$ por $(-1)$ y la sumamos a la ecuación $4$
$\hspace{0.1cm}{\color{Red}\bcancel {{\color{black}-B}}}-\;\; D=0$
$\underline{\hspace{0.3cm}{\color{Red}\bcancel {{\color{black}B}}}+4D=1}$
$\hspace{1.0cm} 3D=1$
Obtenemos el valor de la $D$ $\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;D=\dfrac{1}{3}$
Reemplazando en la ecuación $1$ obtenemos $\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;B=-\dfrac{1}{3}$
Con los valores de la constante procedemos a evaluar la transformada inversa.
$Y(s)=\mathscr{L}^{-1}\left\{\dfrac{s}{s^2+4}\right\}+$
$\left(-\dfrac{1}{3}\mathscr{L}^{-1}\left\{\dfrac{1}{s^2+4}\right\}+\dfrac{1}{3}\mathscr{L}^{-1}\left\{\dfrac{1}{s^2+1}\right\}\right)e^{-2\pi s}$
Antes de aplicar el teorema 2$$ se debe ajustar el término de la mitad.
$Y(s)=\mathscr{L}^{-1}\left\{\dfrac{s}{s^2+4}\right\}+$
$\left(-\dfrac{1}{(3){\color{red}2}}\mathscr{L}^{-1}\left\{\dfrac{{\color{red}2}}{s^2+4}\right\}+\dfrac{1}{3}\mathscr{L}^{-1}\left\{\dfrac{1}{s^2+1}\right\}\right)e^{-2\pi s}$
Aplicando la transformada inversa obtenemos:
En el siguiente video, realizado por Jaime H. Ramírez Rios, podrás observar un ejemplo de Traslación en el eje $t$.
Si $F(s)=\mathscr{L}f(t)$ $\wedge n= \mathrm{1,2,3,}\ldots$ entonces.
$\mathscr{L}\left\{t^nf(t)\right\}=(-1)^n\dfrac{d^n}{ds^n}F(s)$
 Ejemplo 1
Ejemplo 1Evaluar $\mathscr{L}\left\{t \mathrm{cosh2t})\right\}$
Solución
Para aplicar derivada de una transformada debe estar la variable "t" multiplicando cualquier función. Se determina el valor de la $n$ para saber cuántas veces se debe derivar. En este caso $n=1$
$\mathscr{L}\left\{t \mathrm{cosh2t})\right\}=\left(-1\right)\dfrac{d}{ds}\dfrac{s}{s^2-4}$
$\mathscr{L}\left\{t \mathrm{cosh2t})\right\}=\left(-1\right)\cdot\dfrac{\left(s^2-4\right)\left(1\right)-\left(s\right)\left(2s\right)}{\left(s^2-4\right)^2}$
Propiedad distributiva.
$\mathscr{L}\left\{t \mathrm{cosh2t})\right\}=\left(-1\right)\cdot\dfrac{s^2-4-2s^2}{\left(s^2-4\right)^2}$
Agrupando términos semejantes.
 Ejemplo 2
Ejemplo 2Evaluar $\mathscr{L}\left\{t^2 sen 3t)\right\}$
Solución
$n=2$ se debe derivar dos veces.
$\mathscr{L}\left\{t^2 sen 3t)\right\}=\left(-1\right)^2\dfrac{d^2}{ds^2}\dfrac{3}{s^2+9}$
Se realiza la primer derivada y se escribe de la siguiente forma.
$\mathscr{L}\left\{t^2 sen 3t)\right\}=\dfrac{d}{ds}\dfrac{\left(s^2+9\right)\left(0\right)-\left(3\right)\left(2s\right)}{\left(s^2+9\right)^2}$
$\mathscr{L}\left\{t^2 sen 3t)\right\}=\dfrac{d}{ds}\dfrac{-6s}{\left(s^2+9\right)^2}$
Se realiza la última derivada.
$\mathscr{L}\left\{t^2 sen 3t)\right\}=\dfrac{\left(s^2+9\right)^2\left(-6\right)-\left(-6s\right)\left[2\left(s^2+9\right)\left(2s\right)\right]}{\left(s^2+9\right)^4}$
Factor común.
$\mathscr{L}\left\{t^2 sen 3t)\right\}=\dfrac{\left(s^2+9\right)\left[\left(s^2+9\right)\left(-6\right)-\left(-24s^2\right)\right]}{\left(s^2+9\right)^4}$
$\mathscr{L}\left\{t^2 sen 3t)\right\}=\dfrac{-6s^2-54+24s^2}{\left(s^2+9\right)^3}$
Agrupando términos semejantes.
 Ejemplo 3
Ejemplo 3Evaluar $\mathscr{L}\left\{t^3\mathrm{e}^{-5t}\right\}$
Solución
$n=3$ se debe derivar tres veces.
$\mathscr{L}\left\{t^3{e}^{-5t}\right\}=(-1)^3\dfrac{d^3}{ds^3}\ \dfrac{1}{s+5}$
Primera derivada.
$\mathscr{L}\left\{t^3{e}^{-5t}\right\}=-\dfrac{d^2}{ds^2}\dfrac{-1}{\left(s+5\right)^2}$
Ahora se realiza la segunda derivada.
$\mathscr{L}\left\{t^3{e}^{-5t}\right\}=-\dfrac{d}{ds}\dfrac{2\left(s+5\right)}{\left(s+5\right)^4}$
Simplificando.
$\mathscr{L}\left\{t^3{e}^{-5t}\right\}=-\dfrac{d}{ds}\dfrac{2}{\left(s+5\right)^3}$
Tercera derivada.
$\mathscr{L}\left\{t^3{e}^{-5t}\right\}=-\dfrac{-2\left[3\left(s+5\right)^2\right]}{\left(s+5\right)^6}$
Simplificando obtenemos la solución.
Como hay un producto y aparece Euler también lo podemos resolver como traslación en el eje $s$
$\mathscr{L}\left\{e^{-5t}t^3\right\}=\mathscr{L}\left\{t^3|_{s\rightarrow s+5}\right\}$
$\mathscr{L}\left\{e^{-5t}t^3\right\}=\dfrac{6}{\left(s+5\right)^4}$
 Ejemplo 4
Ejemplo 4Evaluar $\mathscr{L}\left\{t{e}^{2t}{sen6t} \right\}$
Solución
$n=1$ se debe derivar una vez y se hace traslación en el eje $s$
$\mathscr{L}\left\{t{e}^{2t}{sen6t} \right\}=(-1)\dfrac{d}{ds}\ \dfrac{6}{\left(s-2\right)^2+36}$
$\mathscr{L}\left\{t{e}^{2t}{sen6t} \right\}=-\ \dfrac{-6\left[2\left(s-2\right)\right]}{\left[\left(s-2\right)^2+36\right]^2}$
La solución es:
 Ejemplo 5
Ejemplo 5Evaluar $\mathscr{L}\left\{tsenkt\right\}$
Solución
$n=1$ se debe derivar una vez y se hace traslación en el eje $s$
$\mathscr{L}\left\{tsenkt\right\}=(-1)^1\dfrac{d}{ds}\ \dfrac{k}{s^2+k^2}$
$\mathscr{L}\left\{tsenkt\right\}=-\dfrac{-k(2s)}{\left(s^2+k^2\right)^2}$
La solución es:
 Ejemplo 6
Ejemplo 6Resolver el PVI $ y''+16y={cos4t}$ sujeta a la condición inicial $y(0)=0$ $\wedge$ $y'(0)= 1$
Solución
Se utiliza la transformada de la segunda derivada (teorema $3$) al lado izquierdo y la transformada básica (teorema $1$) al lado derecho.
$s^2Y(s)-sy(0)-y\prime(0)+16Y(s)=\dfrac{s}{s^2+16}$
Se reemplazan las condiciones iniciales.
$s^2Y(s)-1+16Y(s)=\dfrac{s}{s^2+16}$
Factor común $Y(s)$ y se despeja.
$Y(s)\left(s^2+16\right)=\dfrac{s}{s^2+16}+1$
Se opera el lado derecho.
$Y(s)\left(s^2+16\right)=\dfrac{s^2+s+16}{s^2+16}$
Se despeja $Y(s)$
$Y(s)=\dfrac{s^2+s+16}{\left(s^2+16\right)^2}$
Se descompone el lado derecho en fracciones parciales.
$\dfrac{s^2+s+16}{\left(s^2+16\right)^2}=\dfrac{As+B}{s^2+16}+\dfrac{Cs+D}{\left(s^2+16\right)^2}$
Se multiplica ambos lados de la ecuación por $\left(s^2+16\right)^2$ para quitar denominadores.
$s^2+s+16=\ (As+B)\left(s^2+16\right)+Cs+D$
Propiedad distributiva.
$s^2+s+16=As^3+16As+Bs^2+16B+Cs+D$
Se arma un sistema de cuatro ecuaciones con cuatro incógnitas para hallar el valor de las constantes.
$\begin{matrix}\begin{matrix}A\\B\\\end{matrix}&\begin{matrix}=\\=\\\end{matrix}&\begin{matrix}0\\1\\\end{matrix}\\\begin{matrix}16A+C\\16B+D\\\end{matrix}&\begin{matrix}=\\=\\\end{matrix}&\begin{matrix}1\\16\\\end{matrix}\\\end{matrix}$
Los valores de las constantes son:
$A=0\;\;\;\;\;\;\;\;B=1\;\;\;\;\;\;\;\;C=1\;\;\;\;\;\;\;\;D=0$
$Y(s)=\mathscr{L}^{-1}\left\{\dfrac{1}{s^2+16}\right\}+\mathscr{L}^{-1}\left\{\dfrac{s}{\left(s^2+16\right)^2}\right\}$
Se debe ajustar el primer término y el segundo término antes de aplicar la transformada inversa, para eso se utiliza el resultado del ejemplo $5$ para ajustar el segundo término.
$Y(s)=\dfrac{1}{\color{red}4}\mathscr{L}^{-1}\left\{\dfrac{\color{red}4}{s^2+16}\right\}+\dfrac{1}{\color{red}8}\mathscr{L}^{-1}\left\{\dfrac{{\color{red}8}s}{\left(s^2+16\right)^2}\right\}$
Aplicando la transformada inversa obtenemos la solución.
 Ejemplo 7
Ejemplo 7Resolver el PVI $y'+y=tsent$ sujeta a la condición inicial $y(0)=0$
Solución
Al lado derecho hay una traslación en el eje $s$
$tsent=(-1)^1\dfrac{d}{ds}\ \dfrac{1}{s^2+1}$
$tsent=-\dfrac{-2s}{\left(s^2+1\right)^2}$
$tsent=\dfrac{2s}{\left(s^2+1\right)^2}$
Se utiliza la transformada de la segunda derivada (teorema $3$) al lado izquierdo y se iguala con el resultado de la traslación.
$sY(s)-y(0)+Y(s)=\dfrac{2s}{\left(s^2+1\right)^2}$
Se reemplazan las condiciones iniciales y se saca factor común.
$Y(s)\left(s+1\right)=\dfrac{2s}{\left(s^2+1\right)^2}$
Se despeja $Y(s)$
$Y(s)=\dfrac{2s}{{\left(s+1\right)\left(s^2+1\right)}^2}$
Se descompone el lado derecho en fracciones parciales.
$\dfrac{2s}{{\left(s+1\right)\left(s^2+1\right)}^2}=\dfrac{A}{s+1}+\dfrac{Bs+C}{s^2+1}+\dfrac{Ds+E}{\left(s^2+1\right)^2}$
Se multiplica ambos lados de la ecuación por ${\left(s+1\right)\left(s^2+1\right)}^2$ para quitar denominadores.
$2s=A\left(s^2+1\right)^2+(Bs+C)\left(s+1\right)\left(s^2+1\right)+(Ds+E)\left(s+1\right)$
Propiedad distributiva.
$2s=As^4+2As^2+A+Bs^4+Bs^2+Bs^3+Bs+Cs^3+Cs+Cs^2+C+Ds^2+Ds+Es+E$
Se arma un sistema de cinco ecuaciones con cinco incógnitas para hallar el valor de las constantes.
$\begin{matrix}\begin{matrix}A+B\\B+C\\2A+B+C+D\\\end{matrix}&\begin{matrix}=\\=\\=\\\end{matrix}&\begin{matrix}0\\0\\0\\\end{matrix}\\B+C+D+E&=&2\\A+C+E&=&0\\\end{matrix}$
Los valores de las constantes son:
$A=-\dfrac{1}{2}\;\;\;\;\;\;\;\;B=\dfrac{1}{2}\;\;\;\;\;\;\;\;C=-\dfrac{1}{2}\;\;\;\;\;\;\;\;D=1\;\;\;\;\;\;\;\;E=1$
$Y(s)=-\dfrac{1}{2}\mathscr{L}^{-1}\left\{\dfrac{1}{s+1}\right\}+\dfrac{1}{2}\mathscr{L}^{-1}\left\{\dfrac{s}{s^2+1}\right\}-\dfrac{1}{2}\mathscr{L}^{-1}\left\{\dfrac{1}{s^2+1}\right\}+\mathscr{L}^{-1}\left\{\dfrac{s}{\left(s^2+1\right)^2}\right\}+\mathscr{L}^{-1}\left\{\dfrac{1}{\left(s^2+1\right)^2}\right\}$
Para el último término no hay ninguna transformada en las tablas, entonces lo unimos con el tercer término.
$\dfrac{-\frac{1}{2}}{s^2+1}+\dfrac{1}{\left(s^2+1\right)^2}=\dfrac{-\frac{1}{2}s^2-\frac{1}{2}+1}{\left(s^2+1\right)^2}$
Agrupando términos semejantes.
$\dfrac{-\frac{1}{2}s^2+\frac{1}{2}}{\left(s^2+1\right)^2}$
Factor común.
$\dfrac{-\frac{1}{2}\left(s^2-1\right)}{\left(s^2+1\right)^2}$
$Y(s)=-\dfrac{1}{2}\mathscr{L}^{-1}\left\{\dfrac{1}{s+1}\right\}+\dfrac{1}{2}\mathscr{L}^{-1}\left\{\dfrac{s}{s^2+1}\right\}+\mathscr{L}^{-1}\left\{\dfrac{s}{\left(s^2+1\right)^2}\right\}-\dfrac{1}{2}\mathscr{L}^{-1}\left\{\dfrac{s^2-1}{\left(s^2+1\right)^2}\right\}$
Se ajusta el tercer término.
$Y(s)=-\dfrac{1}{2}\mathscr{L}^{-1}\left\{\dfrac{1}{s+1}\right\}+\dfrac{1}{2}\mathscr{L}^{-1}\left\{\dfrac{s}{s^2+1}\right\}+\dfrac{1}{\color{red}2}\mathscr{L}^{-1}\left\{\dfrac{{\color{red}2}s}{\left(s^2+1\right)^2}\right\}-\dfrac{1}{2}\mathscr{L}^{-1}\left\{\dfrac{s^2-1}{\left(s^2+1\right)^2}\right\}$
Aplicando la transformada inversa obtenemos la solución.
La transformada de Laplace de una solución desconocida de una ED, puede reconocerse algunas veces como el producto de las transformadas de dos funciones conocidas.
 Ejemplo 1
Ejemplo 1resolver el PVI $y\prime\prime+y=cost$ sujeta a la condición inicial $y(0)=0$ $\wedge$ $y'(0)= 0$
Solución
Reemplazando el teorema $1$ y el teorema $2$
$s^2Y(s)-sy(0)-y\prime(0)+Y(s)=\dfrac{s}{s^2+1}$
Se reemplazan las condiciones iniciales.
$s^2Y(s)+Y(s)=\dfrac{s}{s^2+1}$
Factor común $Y(s)$
$Y(s)\left(s^2+1\right)=\dfrac{s}{s^2+1}$
Se despeja $Y(s)$
$Y(s)=\dfrac{s}{\left(s^2+1\right)^2}$
Se descompone el lado derecho en fracciones parciales.
$\dfrac{s}{\left(s^2+1\right)^2}=\dfrac{As+B}{s^2+1}+\dfrac{Cs+D}{\left(s^2+1\right)^2}$
Se multiplica ambos lados de la ecuación por $\left(s^2+1\right)^2$ para quitar denominadores.
$s=\ (As+B)\left(s^2+1\right)+Cs+D$
Propiedad distributiva.
$s=As^3+As+Bs^2+B+Cs+D$
Se arma un sistema de cuatro ecuaciones con cuatro incógnitas para hallar el valor de las constantes.
$\begin{matrix}\begin{matrix}A\\B\\\end{matrix}&\begin{matrix}=\\=\\\end{matrix}&\begin{matrix}0\\0\\\end{matrix}\\\begin{matrix}A+C\\B+D\\\end{matrix}&\begin{matrix}=\\=\\\end{matrix}&\begin{matrix}1\\0\\\end{matrix}\\\end{matrix}$
Los valores de las constantes son:
$A=0\;\;\;\;\;\;\;\;B=0\;\;\;\;\;\;\;\;C=1\;\;\;\;\;\;\;\;D=0\;\;\;\;\;\;\;\;E=1$
$Y(s)=\mathscr{L}^{-1}\left\{\dfrac{s}{\left(s^2+1\right)^2}\right\}$
No hay una transformada que nos ayude a resolver el ejercicio. Debe haber una forma de combinar las $2$ funciones $sen{t}\ \land\ cos\ t$ para obtener $y(t)$ cuya transformada sea el producto de sus transformadas.
Pero $y(t)$ no es el producto de $cos\ t$ por $sen{t}$ debido a que:
$\mathscr{L}\left\{cos\ t\ sen{t}\right\}\mathscr{L}\left\{\ \dfrac{1}{2}\ sen{2t}\right\}$
Evaluando la transformada.
$\dfrac{1}{s^2+4\ }\neq\dfrac{s}{\left(s^2+1\right)^2}$
Se puede concluir que:
$\mathscr{L}\left\{cos\ t\ sen{t}\right\}\neq\mathscr{L}\left\{\ cos\ t\right\}\mathscr{L}\left\{\ sen{t}\right\}$
El teorema que nos ayuda a resolver el problema indica que la función:
$h(t)=\int_{0}^{t}{f(\tau)g(t-\tau)d\tau}$
Tiene la propiedad.
$\mathscr{L}\left\{\mathrm{h}\left(t\right)\right\}=H(s)=F(s)\cdot G(s)$
La función de $t$ definida como la integral.
$\int_{0}^{t}{f(\tau)g(t-\tau)d\tau}$
Depende sólo de $f\ \ \land\ g$, y se conoce como la convolución de $f\ \ \land\ g$
Se representa como $f\ast g$, de tal forma que su transformada es el producto de las transformadas de $f\ \ \land\ g$.
si las funciones $f \land g$ son continuas por tramos en el intervalo $\left[\mathrm{0,}\infty\right)$ entonces un producto especial, denotado por $f\ast g$ se define mediante la integral.
$f\ast g=\int_{0}^{t}{f(\tau)g(t-\tau)d\tau}$
Y se llama convolución de $f \land g$. La convención de $f\ast g$ es una función de $t$
si $f(t) \land g(t)$ son funciones continuas por tramos en el intervalo $\left[\mathrm{0,}\infty\right)$ y de orden exponencial, entonces.
$\mathscr{L}\left\{\mathrm{f\ \ *\ g}\right\}=\mathscr{L}\left\{f(t)\right\}\mathscr{L}\left\{g(t)\right\}=F(s)G(s)$
Para terminar el ejemplo $1$ debemos tener en cuenta que:
La convolución de $\ sen{t}\ \land\ \ cos\ t$ es.
$\ sen{t}\ast cos\ t\ =\int_{0}^{t}{sen\ \tau\ cos\left(\ t-\tau\right)d\tau}$
Aplicando la identidad de producto a suma.
$senmx.cos{n}x=\dfrac{1}{2}\left(sen\left[\left(m-n\right)x\right]+sen\left[\left(m+n\right)x\right]\right)$
$\int_{0}^{t}{sen\ \tau\ cos\left(\ t-\tau\right)d\tau}\ =\dfrac{1}{2}\int_{0}^{t}{sen\left(\ \tau-t+\tau\right)+sen\left(\tau+\ t-\tau\right)d\tau}$
Agrupando términos semejantes.
$\dfrac{1}{2}\int_{0}^{t}{sen\left(\ 2\tau-t\right)+sen\left(\ t\right)d\tau}$
Integrando obtenemos.
$\dfrac{1}{2}\left[-\frac{1}{2}cos\left(\ 2\tau-t\right)+sen\left(\ t\right)\tau\right]_0^t$
Reemplazando los límites de integración.
$\dfrac{1}{2}\left[\left(\ -\dfrac{1}{2}cos\left(\ t\right)+sen\left(\ t\right)t\right)-\left(\ -\dfrac{1}{2}cos\left(\ -t\right)+sen\left(\ t\right)0\right)\right]$
Ahora evaluamos.
$\dfrac{1}{2}\left[-\dfrac{1}{2}cos\left(\ t\right)+t\ sen\ t+\dfrac{1}{2}cos\left(\ t\right)\right]$
Agrupando términos semejantes obtenemos la solución.
$\dfrac{1}{2}t\ sen\ t$
La solución del ejemplo $1$ es:
 Ejemplo 2
Ejemplo 2Evaluar $\mathscr{L}\left\{2\ast t^2\right\}$
Solución
$\mathscr{L}\left\{2\ast t^2\right\}=\dfrac{2}{s}\cdot\dfrac{2!}{s^3}$
 Ejemplo 3
Ejemplo 3Evaluar $\mathscr{L}\left\{e^{-2t}\ast sen h3t\right\}$
Solución
$\mathscr{L}\left\{e^{-2t}\ast sen h3t\right\}=\dfrac{1}{s+2}\cdot\dfrac{3}{s^2-9}$
 Ejemplo 4
Ejemplo 4Evaluar $\mathscr{L}\left\{\int_{0}^{t}{cos{\tau} d\tau}\right\}$
Solución
La función $f(\tau)=1$ y la función $g(t-\tau)=cos{\tau}$ por tanto, se aplica el teorema de convolución.
$\mathscr{L}\left\{\int_{0}^{t}{cos{\tau} d\tau}\right\}=\dfrac{1}{s}\cdot\dfrac{s}{s^2+1}$
Al multiplicar los dos resultados obtenemos la solución:
 Ejemplo 5
Ejemplo 5Evaluar $\mathscr{L}\left\{t\int_{0}^{t}sen\tau d\tau\right\}$
Solución
La función $f(\tau)=1$ y la función $g(t-\tau)=sen{\tau}$, se aplica el teorema de convolución, pero afuera de la integral hay una $t$, por.
tanto, también se debe aplicar la derivada de una transformada.
$\mathscr{L}\left\{t\int_{0}^{t}sen\tau d\tau\right\}=\dfrac{1}{s}\cdot\left(-1\right)\dfrac{d}{ds}\dfrac{1}{s^2+1}$
$\mathscr{L}\left\{t\int_{0}^{t}sen\tau d\tau\right\}=\dfrac{1}{s}\cdot\left(-1\right)\cdot\dfrac{-2s}{\left(s^2+1\right)^2}$
Al multiplicar signos y simplificar obtenemos:
 Ejemplo 6
Ejemplo 6Hallar la convolución de $f(t)=sen\ 2t\ \ \ \ \ \ \land\ \ \ \ \ \ \ g(t)=e^t$
Solución
Para resolver el ejercicio debemos aplicar el teorema de convolución integrando las dos funciones.
$sen\ 2t\ast e^t=\int_{0}^{t}{e^{t-\tau}\ sen\ 2\tau\ d\tau}$
Aplicando propiedades de potenciación.
$\int_{0}^{t}{e^t\cdot\ e^{-\tau}sen\ 2\tau\ d\tau}=e^t\int_{0}^{t}{\ e^{-\tau}sen\ 2\tau\ d\tau}$
Recuerde la integral.
${\color{blue}cos^2t=\int{e^{ax}senbxdx=\dfrac{e^{ax}}{a^2+b^2}\left(asenbx-bcos{b}x\right)+c}}$
Reemplazamos los valores teniendo en cuenta que: $a=-1 \land b=2$, obtenemos:
$e^t\int_{0}^{t}{\ e^{-\tau}sen\ 2\tau\ d\tau}=e^t\left(\dfrac{e^{-\tau}}{5}\left(-sen\ 2\tau-2cos{2\tau}\right)\right]_{0}^{t}$
Ahora debemos evaluar la integral reemplazando los límites de integración.
$e^t\left[\left(\dfrac{e^{-t}}{5}\left(-sen\ 2t-2cos{2t}\right)\right)-\left(\dfrac{e^0}{5}\left(-sen\ 0-2cos{0}\right)\right)\right]$
Evaluando obtenemos.
$e^t\left[\left(\frac{e^{-t}}{5}\left(-sen\ 2t-2cos{2t}\right)\right)-\left(\dfrac{1}{5}\left(-2\right)\right)\right]$
Operando el último término.
$e^t\left[\left(\dfrac{e^{-t}}{5}\left(-sen\ 2t-2cos{2t}\right)\right)+\dfrac{2}{5}\right]$
Aplicando la propiedad distributiva obtenemos la solución.
Las series e integrales de Fourier establecen un tema clásico del análisis matemático. Aparecen en el siglo XVIII como resultado del estudio de las vibraciones de una cuerda, las series de Fourier han contribuido al desarrollo de los conceptos básicos del análisis –función, integral, serie, convergencia y se han obtenido por los trabajos de varios matemáticos sobre series trigonométricas.
Las series de Fourier son series de términos coseno y seno y surgen en la tarea práctica de representar funciones periódicas generales. Como aplicación constituyen una herramienta muy importante en la solución de problemas en los que intervienen ecuaciones diferenciales ordinarias y parciales.
Otra propiedad esencial de las funciones es generalizar el concepto de ortogonalidad, el concepto de producto interno de vectores pierde su interpretación geométrica en las funciones. Pero dicho concepto se ha generalizado y es común considerar una función como un vector. Entonces se puede decir que dos funciones distintas son ortogonales cuando su producto interno es cero, este producto interno es en realidad una integral definida. Este concepto se aplica en movimientos amortiguados de una masa “m” en un resorte y en oscilaciones amortiguadas forzadas.
El producto interno de dos funciones $f_1 \ \ \land\ \ \ f_2$ en un intervalo $\left[a,b\right]$ es el número.
$\left(f_1,f_2\right)=\int_{a}^{b}{f_1(x)f_2(x)dx}$
Dos funciones $f_1 \ \ \land\ \ \ f_2$ son ortogonales en un intervalo $\left[a,b\right]$ sí.
$\left(f_1,f_2\right)=\int_{a}^{b}{f_1(x)f_2(x)dx=0}$
Un conjunto de funciones de valor real $\left\{φ_0(x),φ_1(x),φ_2(x)\ldots\right\}$ se dice que es ortogonal en un intervalo $\left[a,b\right]$ si.
$\left(φ_m,φ_n\right)=\int_{a}^{b}{φ_m(x)φ_n(x)dx=0}\; \; \; m \neq n $
 Ejemplo 1
Ejemplo 1demostrar que las funciones $f_1(x)=x^2 \ \ \land\ \ \ f_2(x)=x^3$ son ortogonales en el intervalo $[-1,1]$
Solución
Se debe demostrar que el producto interno entre las dos funciones es cero.
$\left(f_1,f_2\right)=\int_{-1}^{1}{x^2x^3dx}$
Obtenemos la integral.
$\int_{-1}^{1}{x^5dx}=\left.\dfrac{x^6}{6}\right|_{-1}^1$
Evaluando los límites.
$\dfrac{1}{6}-\dfrac{1}{6}=0$
 Ejemplo 2
Ejemplo 2demostrar que las funciones $f_1(x)=cos{x} \ \ \land\ \ \ f_2(x)=sen^2x$ son ortogonales en el intervalo $[0,\pi]$
Solución
$\left(f_1,f_2\right)=\int_{0}^{\pi}{cos{x}sen^2xdx}$
Se integra por sustitución.
$u=senx\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ du=cos{x}dx$
$\int_{0}^{\pi}{cos{x}sen^2xdx=}\int_{0}^{\pi}{u^2du=}\dfrac{u^3}{3}=\left.\dfrac{sen^3x}{3}\right|_0^\pi$
Evaluando obtenemos.
$\dfrac{sen^3\pi}{3}-\dfrac{sen^30}{3}=0-0=0$
Conjuntos ortonormales: la norma o longitud $\left\| u\right\|$ de un vector $u$, se puede expresar en términos del producto interno. La expresión $\left(u,u\right)=\left\| u^2\right\|$ se llama norma cuadrada, por lo que la norma es $\left\| u\right\|=\sqrt{\left( u,u\right) }$. De igual modo la norma cuadrada de una función $φ_0$ es $\left\| φ \left( x\right) \right\| ^{2}=\left( φ_n ,φ_n\right)$ y así la norma o su longitud generalizada es $\left\| φ \left( x\right) \right\|=\sqrt{\left( φ_n ,φ_n\right)}$. En otras palabras, la norma cuadrada y la norma de una función $φ_n$ en un conjunto ortogonal $\left\{φ_n(x)\right\}$ son, respectivamente.
$\left\| φ \left( x\right) \right\| ^{2}=\int _{a}^{b}φ _{n}^{2}\left( x\right) dx$
$\left\| φ \left( x\right) \right\|=\sqrt{\int _{a}^{b}φ _{n}^{2}\left( x\right) dx}$
 Ejemplo 3
Ejemplo 3Demuestre que el conjunto $\left\{1,cos{x},cos{2}x,...\right\}$ es ortogonal en el intervalo $[-\pi,\pi]$ y encuentre las normas de cada función.
Solución
Se debe demostrar que el producto interno de las funciones $\left\{φ_0(x),φ_1(x),φ_2(x)...\right\}$ es cero, donde:
$φ_0(x)=1,\; φ_1(x)=cos{x},\; φ_2(x)=cos{2}x, \; φ_n(x)=cos{n}x...$
Primero se demuestra que $φ_0(x),φ_n(x)=0$, es decir, el $1$ con todos los cosenos.
$\left(φ_0(x),φ_n(x)\right)={\int_{-\pi}^{\pi}{1.cos(nx)dx=\left.-\dfrac{1}{n}sen(nx)\right|}}_{-\pi}^\pi=$
$-\dfrac{1}{n}sen\pi x+\frac{1}{n}sen\left(-\pi x\right)$
Recuerde que: ${\color{blue}sen\left(-x\right)=-senx}$
$\int_{-\pi}^{\pi}{1.cos(nx)dx=}-\dfrac{1}{n}sen(\pi x)-\dfrac{1}{n}sen(\pi x)=0$
Ahora se debe demostrar que cada coseno es ortogonal con los otros cosenos, es decir, $m\neq n$
$\left(φ_m(x),φ_n(x)\right)=\int_{-\pi}^{\pi}{cos(mx)cos(nx)dx}$
Recuerde que: ${\color{blue}cos{A}cos{B}=\dfrac{1}{2}\left[cos{\left(A+B\right)}+cos{\left(A-B\right)}\right]}$
$\dfrac{1}{2}\int_{-\pi}^{\pi}\left[cos{\left(m+n\right)}x+cos{\left(m-n\right)}x\right]dx$
$\left.\dfrac{1}{2\left(m+n\right)}sen\left(m+n\right)x+\dfrac{1}{2\left(m-n\right)}sen\left(m-n\right)x\right|_{-\pi}^\pi$
$\dfrac{1}{2\left(m+n\right)}sen\left(m+n\right)\pi+\dfrac{1}{2\left(m-n\right)}sen\left(m-n\right)\pi-\dfrac{1}{2\left(m+n\right)}sen\left(m+n\right)\pi+\dfrac{1}{2\left(m-n\right)}sen\left(m-n\right)\pi=0$
Queda demostrado que el conjunto de funciones es ortogonal. Ahora se deben hallar las normas de $\left\{φ_0(x),φ_1(x),φ_2(x)...\right\}$
Primero se halla la norma de $φ_0(x)$ donde.
$\left\| φ \left( x\right) \right\|=\sqrt{\int _{-\pi}^{\pi}φ _{0}^{2}\left( x\right) dx}$
$\left\| φ \left( x\right) \right\|=\sqrt{\int _{-\pi}^{\pi}1^{2} dx}=\sqrt{\left.x\right|_{-\pi}^\pi}=\sqrt{\pi-\left(-\pi\right)}=\sqrt{2\pi}$
Sólo falta hallar las normas de los cosenos. Para hacer todas las combinaciones asumimos $m=n$
$\left\| φ \left( x\right) \right\|=\sqrt{\int _{-\pi}^{\pi}φ _{n}^{2}\left( x\right) dx}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;$Reemplazando obtenemos.
$\left\| φ \left( x\right) \right\|=\sqrt{\int _{-\pi}^{\pi}cos^{2}\left( nx\right) dx}$
$\left\| φ \left( x\right) \right\|=\sqrt{\int _{-\pi}^{\pi}\dfrac{1-cos(2nx)}{2} dx}$
$\left\| φ \left( x\right) \right\|=\sqrt{\left.\dfrac{x}{2}-\dfrac{sen(2nx)}{4}\right|_{-\pi}^\pi}$
$\left\| φ \left( x\right) \right\|=\sqrt{\left(\dfrac{\pi}{2}-\dfrac{sen2n\pi}{4}\right)-\left(-\dfrac{\pi}{2}+\dfrac{sen2n\pi}{4}\right)}$
$\left\| φ \left( x\right) \right\|=\sqrt{\frac{\pi}{2}+\frac{\pi}{2}}=\sqrt\pi$
 Ejemplo 4
Ejemplo 4Demuestre que el conjunto $\left\{sen\dfrac{n\pi}{p}x\right\}$ con $n=1,2,3,4...$ es ortogonal en el intervalo $[0,p]$ y encuentre las normas de cada función.
Solución
Se debe demostrar que el producto interno de las funciones $\left\{φ_1(x),φ_2(x),φ_3(x)...\right\}$ es cero, donde:
$φ_1(x)=\left\{sen\dfrac{\pi}{p}x\right\},\; φ_2(x)=\left\{sen\dfrac{2\pi}{p}x\right\},$
$φ_3(x)=\left\{sen\dfrac{3\pi}{p}x\right\}, \; φ_n(x)=\left\{sen\dfrac{n\pi}{p}x\right\}...$
Se debe demostrar que cada $seno$ es ortogonal con los otros $senos$, es decir, $m \neq n$
$\left(φ_0(x),φ_n(x)\right)$
$\left(φ_m(x),φ_n(x)\right)=\displaystyle\int_{0}^{p} sen \dfrac{mπ}{p}x \;\;sen\dfrac{mπ}{p}x\;\;dx$
para integrar se aplica la identidad de producto a suma.
${\color{blue}sen(mx)cos(nx)=\dfrac{1}{2}\left[cos{\left(m-n\right)x}+cos{\left(m+n\right)x}\right]}$
$\dfrac{1}{2}\displaystyle\int_{0}^{p}\left[cos\dfrac{{\left(m-n\right)\pi}}{p}x+cos\dfrac{{\left(m+n\right)\pi}}{p}x\right]dx=$
$\left.\dfrac{p}{2\left(m-n\right)\pi}sen\dfrac{\left(m-n\right)\pi}{p}x-\dfrac{p}{2\left(m+n\right)\pi}sen\dfrac{\left(m+n\right)\pi}{p}x\right|_{0}^p=$
$\dfrac{p}{2\left(m-n\right)\pi}sen(m-n)\pi-\dfrac{p}{2\left(m+n\right)\pi}sen(m+n)\pi$
$\dfrac{p}{2\left(m-n\right)\pi}sen\;{0}+\dfrac{p}{2\left(m+n\right)\pi}sen\;{0}=0$
Normas de los senos. Para hacer todas las combinaciones asumimos $m=n$
$\left\| φ_n \left( x\right) \right\|=\sqrt{\displaystyle\int _{0}^{p}sen^{2}\dfrac{n\pi}{p}\; x dx}=\sqrt{\dfrac{1}{2}\displaystyle\int _{0}^{p}\left(1-cos2\dfrac{n\pi}{p}x \right)dx}$
$\sqrt{\left.\dfrac{x}{2}-\dfrac{psen2\dfrac{n\pi}{p}x}{4n\pi}\right|_{0}^p}=\sqrt{\left(\dfrac{p}{2}-\dfrac{psen(2n\pi)}{4n\pi}\right)-\left(0-\dfrac{psen0}{4n\pi}\right)}$
La serie de Fourier de una función $f$ definida en el intervalo $[-p,p]$ está dada por.
$f(x)=\dfrac{a_0}{2}+\sum_{n=1}^{\infty}\left(a_ncos{\dfrac{n\pi}{p}}x+b_nsen\dfrac{n\pi}{p}x\right)$
Donde.
${\color{blue}a_o=\dfrac{1}{p}\int_{-p}^{p}{f(x)dx}}$
${\color{blue}a_n=\dfrac{1}{p}\int_{-p}^{p}{f(x)cos{\dfrac{n\pi}{p}}xdx}}$
${\color{blue}b_n=\dfrac{1}{p}\int_{-p}^{p}{f(x)sen\dfrac{n\pi}{p}xdx}}$
 Ejemplo 1
Ejemplo 1Desarrolle la serie de Fourier $f(x)=\left\{\begin{matrix}0,&-\pi< x<0\\\pi-x,&0\le x <\pi\\\end{matrix}\right.$
Solución
Para desarrollar la serie de Fourier debemos encontrar los coeficientes $a_o,a_n \wedge b_n$, teniendo en cuenta que la serie está definida por tramos.
$a_o=\dfrac{1}{\pi}\left(\int_{-\pi}^{o}0dx+\int_{0}^{\pi}\left(\pi-x\right)dx\right)$
$a_o=\dfrac{1}{\pi}\int_{0}^{\pi}\left(\pi-x\right)dx=\left.\dfrac{1}{\pi}\left(\pi x-\frac{x^2}{2}\right)\right|_0^\pi$
$a_o=\dfrac{1}{\pi}\left[\left(\pi^2-\dfrac{\pi^2}{2}\right)-0\right]=\dfrac{1}{\pi}\left(\dfrac{\pi^2}{2}\right)$
${\color{blue}a_o=\dfrac{\pi}{2}}$
$a_n=\dfrac{1}{\pi}\left[\int_{-\pi}^{0}{0cos{\dfrac{n\pi}{\pi}}xdx}+\int_{0}^{\pi}{\left(\pi-x\right)cos{\dfrac{n\pi}{\pi}}xdx}\right]$
$a_n=\dfrac{1}{\pi}\int_{0}^{\pi}{\left(\pi-x\right)cos(nx)dx}$
Se integra por partes.
$u=\left(\pi-x\right)$ $dv=cos{(nx)}dx$
$du=-dx$ $v=\dfrac{sen(nx)}{n}$
$a_n=\dfrac{\left(\pi-x\right)sen(nx)}{n}+\dfrac{1}{n}\int_{0}^{\pi}{sen(nx)dx}$
$a_n=\dfrac{1}{\pi}\left[\left.\dfrac{\left(\pi-x\right)sen(nx)}{n}-\dfrac{cos(nx)}{n^2}\right|_0^\pi\right]$
Reemplazando los límites de integración.
$\left(\dfrac{\left(\pi-\pi\right)sen(n\pi)}{n\pi}-\dfrac{cos(n\pi)}{n^2\pi}\right)-\left(\dfrac{\left(\pi-0\right)sen0}{n\pi}-\dfrac{cos{0}}{n^2\pi}\right)$
Recuerde que $cos(n\pi)$ es $-1$ cuando $n$ es impar, es decir $n=1,3,5,7,...$ y es igual a $1$ cuando $n$ es par, es decir, $n=2,4,6,8,...$ y $sen(n\pi)=0$
Evaluando obtenemos.
$a_n=-\dfrac{(-1)^n}{n^2\pi}+\dfrac{1}{n^2\pi}$
${\color{blue}a_n=\dfrac{1-(-1)^n}{n^2\pi}}$
$b_n=\dfrac{1}{\pi}\left[\int_{-\pi}^{0}{0sen\dfrac{n\pi}{\pi}xdx}+\int_{0}^{\pi}{\left(\pi-x\right)sen\dfrac{n\pi}{\pi}xdx}\right]$
$b_n=\dfrac{1}{\pi}\int_{0}^{\pi}{\left(\pi-x\right)sen(nx)dx}$
Se integra por partes.
$u=\left(\pi-x\right)$ $dv=sen{(nx)}dx$
$du=-dx$ $v=-\dfrac{cos(nx)}{n}$
$b_n=\dfrac{-\left(\pi-x\right)cos(nx)}{n}-\dfrac{1}{n}\int_{0}^{\pi}{co s(nx)dx}$
$b_n=\dfrac{1}{\pi}\left[\left.\dfrac{-\left(\pi-x\right)cos{n}x}{n}-\dfrac{sen(nx)}{n^2}\right|_0^\pi\right]$
Reemplazando los límites de integración.
$b_n=\left(\dfrac{-\left(\pi-\pi\right)cos{(n}\pi)}{n\pi}-\dfrac{sen(n\pi)}{n^2\pi}\right)-\left(\dfrac{-\pi cos(0)}{n\pi}-\dfrac{sen(0)}{n^2\pi}\right)$
Evaluando obtenemos.
$b_n=\dfrac{\pi}{n\pi}$
${\color{blue}b_n=\dfrac{1}{n}}$
La serie de Fourier es:
 Ejemplo 2
Ejemplo 2Desarrolle la serie de Fourier $f(x)=\left\{\begin{matrix}0,&-\frac{\pi}{2}< x<0\\\cos x,&0\le x <\frac{\pi}{2}\\\end{matrix}\right.$
Solución
Para desarrollar la serie de Fourier debemos encontrar $a_o,a_n \wedge b_n$, teniendo en cuenta que la serie está definida por tramos.
$a_o=\dfrac{1}{\frac{\pi}{2}}\left(\displaystyle \int_{\frac{-\pi}{2}}^{o}0dx+ \displaystyle \int_{0}^{\frac{\pi}{2}}{cos\ x\ dx}\right)$
$a_o=\dfrac{2}{\pi}\displaystyle \int_{0}^{\frac{\pi}{2}}{cos\ x\ dx}=\left.\frac{2}{\pi}\left(sen\ x\right)\right|_0^{\frac{\pi}{2}}$
$a_o=\dfrac{2}{\pi}\left[\left(sen\frac{\pi}{2}-sen\ 0\right)-0\right]={\color{blue}\dfrac{2}{\pi}}$
$a_n=\dfrac{1}{\frac{\pi}{2}}\displaystyle\int_{0}^{\frac{\pi}{2}}{cos\ x\ cos\ \dfrac{n\pi x}{\frac{\pi}{2}}\ dx}$
$a_n=\dfrac{2}{\pi}\displaystyle\int_{0}^{\frac{\pi}{2}}{cos(x)cos\left(2nx\right)dx}$
Recuerde que: ${\color{blue}cos{A}cos{B}=\dfrac{1}{2}\left[cos{\left(A-B\right)}+cos{\left(A+B\right)}\right]}$
$a_n=\dfrac{2}{\pi}\dfrac{1}{2}\displaystyle\int_{0}^{\frac{\pi}{2}}\left(cos{\left[\left(1-2n\right)x\right]}+cos{\left[\left(1+2n\right)x\right]}\right)dx$
$a_n=\dfrac{1}{\pi}\left[\left.\dfrac{sen\left(1-2n\right)x}{1-2n}+\dfrac{sen\left(1+2n\right)x}{1+2n}\right|_0^{\frac{\pi}{2}}\right]$
$a_n=\dfrac{1}{\pi}\left[\left(\dfrac{sen\left(1-2n\right)\frac{\pi}{2}}{1-2n}+\dfrac{sen\left(1+2n\right)\frac{\pi}{2}}{1+2n}\right)-\left(\dfrac{sen\left(0\right)}{1-2n}+\dfrac{sen\left(0\right)}{1+2n}\right)\right]$
$a_n=\dfrac{1}{\pi}\left[\left(\dfrac{(-1)^n}{1-2n}+\dfrac{(-1)}{1+2n}\right)-0\right]={\color{blue}\dfrac{2(-1)^{n+1}}{\pi\left(1-4n^2\right)}}$
$b_n=\dfrac{1}{\frac{\pi}{2}}\displaystyle\int_{0}^{\frac{\pi}{2}}{cos\ x\ sen\ \dfrac{n\pi x}{\frac{\pi}{2}}\ dx}$
$b_n=\dfrac{2}{\pi}\int_{0}^{\frac{\pi}{2}}{cos(x)sen\left(2nx\right)dx}$
Recuerde que: ${\color{blue}senA.cosB=\dfrac{1}{2}\left(sen\left[\left(A-B\right)\right]+sen\left[\left(A+B\right)\right]\right)}$
$b_n=\dfrac{2}{\pi}\dfrac{1}{2}\displaystyle\int_{0}^{\frac{\pi}{2}}\left(sen{\left[\left(2n-1\right)x\right]}+sen{\left[\left(2n+1\right)x\right]}\right)dx$
$b_n=\dfrac{1}{\pi}\left[-\left.\dfrac{cos\left(2n-1\right)x}{2n-1}-\dfrac{cos\left(2n+1\right)x}{2n+1}\right|_0^{\frac{\pi}{2}}\right]$
$b_n=\dfrac{1}{\pi}\left[\left(-\dfrac{cos\left(2n-1\right)\frac{\pi}{2}}{2n-1}-\dfrac{cos\left(2n+1\right)\frac{\pi}{2}}{2n+1}\right)-\left(\dfrac{cos\left(0\right)}{2n-1}-\dfrac{cos\left(0\right)}{2n+1}\right)\right]$
$b_n=\dfrac{1}{\pi}\left[0-\left(-\dfrac{1}{2n-1}-\dfrac{(-1)}{2n+1}\right)-0\right]$
${\color{blue}b_n=\dfrac{4n}{\pi\left(4n^2-1\right)}}$
La serie de Fourier es:
Series de Fourier de senos y de cosenos
1. La serie de Fourier de una función par en el intervalo $\left[-p,p\right]$ es la serie de cosenos.
$f(x)=\dfrac{a_0}{2}+\sum_{n=1}^{\infty}{a_ncos{\dfrac{n\pi}{p}}x}$
Donde.
${\color{blue}a_o=\dfrac{2}{p}\int_{0}^{p}{f(x)dx}}$
${\color{blue}a_n=\dfrac{2}{p}\int_{0}^{p}{f(x)cos{\dfrac{n\pi}{p}}xdx}}$
2. La serie de Fourier de una función impar en el intervalo $\left[-p,p\right]$ es la serie de senos.
$f(x)=\sum_{n=1}^{\infty}{b_nsen\dfrac{n\pi}{p}x}$
Donde.
${\color{blue}b_n=\dfrac{2}{p}\int_{0}^{p}{f(x)sen\dfrac{n\pi}{p}xdx}}$
Funciones pares e impares.
$f(x)=x^2$ es par, ya que $f(-x)=\left(-x^2\right)=x^2=f(x)$
$f(x)=x^3$ es impar, ya que $f(-x)=\left(-x^3\right)=-x^3=-f(x)$
Propiedades de funciones pares e impares
a) El producto de dos funciones pares es par.
b) El producto de dos funciones impares es par.
c) El producto de una función par y una impar es impar.
d) La suma (diferencia) de dos funciones pares es par.
e) La suma (diferencia) de dos funciones impares es impar.
f) Si $f$ es par, entonces $\int_{-a}^{a}{f(x)dx=2\int_{0}^{a}{f(x)dx}}$
g) Si $f$ es impar, entonces $\int_{-a}^{a}{f(x)dx=0}$
 Ejemplo 1
Ejemplo 1Desarrolle la función $f(x)=x \;\;\;\;\;\;\;\; -2 < x < 2 $
Solución
Para desarrollar la serie de Fourier es importante graficar para saber si la función es par o impar.
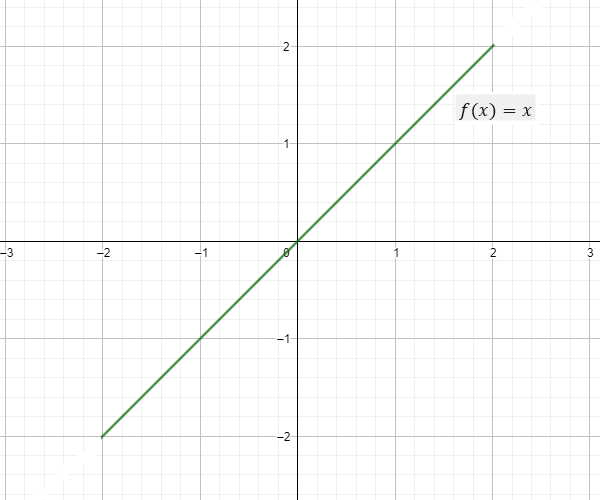
La gráfica nos muestra que es una función impar, entonces es una serie de senos, sólo se debe hallar b_n.
$b_n=\dfrac{2}{2}\int_{0}^{2}{xsen\dfrac{n\pi}{2}xdx}=\int_{0}^{2}{xsen\dfrac{n\pi}{2}xdx}$
Es una integral por partes.
$u=x$ $dv=sen\dfrac{n\pi}{2}xdx$
$du=dx$ $v=-\dfrac{2}{n\pi}cos\dfrac{n\pi}{2}x$
$\int_{0}^{2}{xsen\dfrac{n\pi}{2}xdx}=-\dfrac{2x}{n\pi}cos\dfrac{n\pi}{2}x+\dfrac{2}{n\pi}\int_{0}^{2}{co s\dfrac{n\pi}{2}xdx}$
$b_n=\int_{0}^{2}{xsen\dfrac{n\pi}{2}xdx}=\left.\dfrac{-2x}{n\pi}cos{\dfrac{n\pi}{2}}x+\dfrac{4}{n^2\pi^2}sen\dfrac{n\pi}{2}x\right|_0^2$
$b_n=\left(\dfrac{-4}{n\pi}cos{n}\pi+\dfrac{4}{n^2\pi^2}senn\pi\right)-\left(\dfrac{0}{n\pi}cos{0}+\dfrac{4}{n^2\pi^2}sen0\right)$
$b_n=\dfrac{-4\left(-1\right)^n}{n\pi}=$${\color{blue}\dfrac{4\left(-1\right)^{n+1}}{n\pi}}$
 Ejemplo 2
Ejemplo 2Desarrolle la función $f(x)=\left|sen\ x\right| \;\;\;\;\;\;\;\; -\pi < x < \pi $
Solución
Para desarrollar la serie de Fourier es importante graficar para saber si la función es par o impar.
La gráfica nos muestra que es una función par, entonces es una serie de cosenos, se debe hallar $a_0,\ \ a_n$
$a_0=\dfrac{2}{\pi}\int_{0}^{\pi}{sen\ x\ dx}=\left.-\dfrac{2}{\pi}cos{x}\right|_0^\pi$
$a_0=-\dfrac{2}{\pi}\left[\left(cos{\pi}\right)-\left(cos{0}\right)\right]=$${\color{blue}\dfrac{4}{\pi}}$
$a_n=\dfrac{2}{\pi}\int_{0}^{\pi}{sen\ x\ cos\dfrac{n\pi}{\pi}xdx=}\dfrac{2}{\pi}\int_{0}^{\pi}{sen\ x\ cos(nx)dx}$
$a_n=\dfrac{2}{\pi}\dfrac{1}{2}\int_{0}^{\pi}\left(sen{\left[\left(1+n\right)x\right]}+sen{\left[\left(1-n\right)x\right]}\right)dx$
$a_n=\dfrac{1}{\pi}\left[-\left.\dfrac{cos\left(1+n\right)x}{1+n}-\dfrac{cos\left(1-n\right)x}{1-n}\right|_0^\pi\right]$
$a_n=\dfrac{1}{\pi}\left[\left(-\dfrac{cos\left(1+n\right)\pi}{1+n}-\dfrac{cos\left(1-n\right)\pi}{1-n}\right)-\left(-\dfrac{cos\left(0\right)}{1+n}-\dfrac{cos\left(0\right)}{1-n}\right)\right]$
$a_n=\dfrac{1}{\pi}\left[\left(\dfrac{(-1)^n}{1+n}+\dfrac{(-1)^n}{1-n}\right)+\left(\dfrac{1}{1+n}+\dfrac{1}{1-n}\right)\right]$
$a_n=$${\color{blue}\dfrac{2\left((-1)^n+1\right)}{\pi\left(1-n^2\right)}}$
En la siguiente escena interactiva, diseñada por phet.colorado.edu, podrás crear las ondas de una serie de Fourier.