Cálculo Interactivo II
Héctor de Jesús Argueta Villamar
María Juana Linares Altamirano
DGTIC - Facultad de Ciencias. UNAM.
Título de la obra:
Cálculo Interactivo II
Autores:
Héctor de Jesús Argueta Villamar argueta@unam.mx
María Juana Linares Altamirano linares@unam.mx
Código JavaScript para el libro: Joel Espinosa Longi, IMATE, UNAM.
Conversión a formato de libro interactivo: Joel Espinosa Longi
Recursos interactivos: GeoGebra y DescartesJS
Fuentes tipográficas: CrimsonPro y UbuntuMono
Fórmulas matemáticas: $\KaTeX$
El programa Cálculo Interactivo II que aquí se presenta tuvo sus primeros avances en un proyecto de colaboración DGTIC - Facultad de Ciencias, para el Desarrollo de Materiales Interactivos de Apoyo a la Enseñanza del Cálculo, coordinado por la Secretaría de Apoyo Educativo de la Facultad de Ciencias de la UNAM bajo la dirección de la Maestra Guadalupe Lucio Gómez Maqueo.
Dentro de tal proyecto se definieron el contenido, la estructura y la navegación de Cálculo Interactivo II y se desarrolló la primera versión de los primeros tres capítulos de seis que contendría toda la obra, tratando de apegarse a los planes y programas de estudio del curso de Cálculo Diferencial e Integral II de la Facultad de Ciencias.
Posterior a ello y habiéndose vencido el plazo de colaboración con la Facultad de Ciencias, se continuó su desarrollo dentro de la DGTIC, dentro del Proyecto Institucional Toda la UNAM en línea, derivado de las líneas rectoras y encabezado por el Dr. Felipe Bracho Carpizo, Director General de la Dependencia.
Dentro de la Unidad de Investigación, Desarrollo e Inovación, bajo el apoyo decidido de su Director el Dr. Guillermo Rodríguez Abitia y bajo la Coordinación General de la Maestra Teresa Vázquez Mantecón y la supervisión de nuestra Jefa del Departamento de Gestión de Contenidos y Diseño Instruccional, Maestra Rebeca Valenzuela Argüelles, Cálculo Interactivo II nace en su primera versión en Java en el mes de Enero de 2013.
A los seis capítulos previstos, se agregó uno más sobre Aplicaciones de la Integral, que pensamos indispensable para redondear el trabajo. Aunque esta obra fue pensada acorde a los planes y programas de la Facultad de Ciencias, consideramos que es de utilidad para otras Escuelas de Ciencias e Ingenierías y parcialmente para las Escuelas de nivel Medio Superior, en particular para nuestros dos subsistemas del Bachillerato en la UNAM.
Dadas las dificultades por la que atraviesan actualmente diversos desarrollos realizados en Java y ante la necesidad de la Facultad de Ciencias de contar con materiales que apoyaran la construcción de sus cursos en línea, la DGTIC representada por el Dr. Guillermo Rodríguez Abitia titular de la Dirección de Innovación y Desarrollo Tecnológico y la Facultad de Ciencias representada por el Dr. Alfredo Arnaud Bobadilla, acordaron la contratación de un grupo de becarios que colaborarían en la transformación de estos materiales a HTML5, bajo la Coordinación de María Juana Linares Altamirano y Héctor de Jesús Argueta Villamar autores de Cálculo Interactivo II.
Los jóvenes participantes en esta segunda etapa de Cálculo Interactivo II son: Alanís Manríquez Jesús Felipe, Ávalos Valentín Gustavo Alejandro, Durán Méndez Abraham, Jiménez Santiago Berenice, Ku Kinil Ginni Noelia, Lerista Barrera Miguel Ángel, Rivas Robles René Alejandro, Rivaz Hernández José Amet, Vargas Mendoza Marco Antonio y parcialmente Flores Romero María Erandi, todos ellos de la Facultad de Ciencias y a quienes les expresamos nuestros más caros agradecimientos ya que con su empeño y compromiso es que entregamos la primera versión de Cálculo Interactivo II en HTML5.
En una segunda etapa, contamos con la revisión del material, de parte la becaria Salazar Navarro Itzel Adayam, a quien le expresamos nuestro más sincero agradecimiento.
27 de enero de 2018
M. en C. María Juana Linares Altamirano
M. en C. Héctor de Jesús Argueta Villamar
Aquí podrás encontrar el concepto de Integral, su construcción y desarrollo, así como su intrínseca relación con los conceptos de Derivada, Área y Área algebraica.
Calcular áreas es un problema ancestral. Los egipcios y los babilonios ya sabían de manera empírica, algunas fórmulas para el cálculo de áreas de figuras planas sencillas y para aproximar el área de un círculo.
Estos conocimientos pasaron a los griegos, quienes le dieron sustento lógico y sistemático. Entre ellos, Arquímedes fue quien más se acercó al concepto moderno de área y fue así, que con base en estas ideas Riemann en el siglo XIX, formuló su definición de Integral.
En geometría elemental se establecen fórmulas para calcular las áreas de muchas figuras planas, en particular se tienen fórmulas para calcular áreas de figuras con lados rectos, entre ellas, el área de triángulos, cuadrados, rectángulos y en general de polígonos regulares. Si un polígono es irregular se puede calcular su área recurriendo al método de triangulación.
El concepto de integral que construiremos en esta sección nos permitirá calcular áreas de figuras planas, cuyos lados no sean rectos, pero para su construcción nos basaremos en el conocimiento de la fórmula para calcular áreas de rectángulos, como podremos ver en el siguiente apartado. Por ahora establecemos las regiones con las que iniciaremos nuestro estudio.
Iniciaremos la construcción intentando calcular el área de algunas regiones muy especiales: aquellas limitadas por el eje de las $x$, las rectas verticales que pasan por $(a,0)$ y $(b,0)$ y la gráfica de una función $f$ acotada en $[a,b]$ tal que las $f(x)$ son no negativas, como se presenta en la figura.
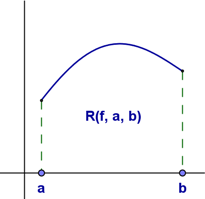
En este tipo de regiones se incluyen, desde luego, rectángulos, triángulos y muchas de las figuras de geometría plana. El número que asignaremos eventualmente como área de la región $R(f,a,b)$ le daremos el nombre de integral de $f$ sobre $[a,b]$.
Para definir la integral sobre $[a,b]$ para funciones acotadas que puedan tener valores negativos como en la figura, basta introducir el concepto de “área algebraica” considerando con valor positivo las áreas de regiones sobre el eje de las $x$ y negativo en caso que estén por abajo del eje de las $x$.
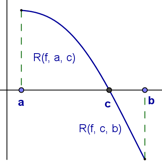
Con esta consideración del “área algebraica” el procedimiento de construcción de la integral será el mismo, y su valor será la suma algebraica de las áreas de cada una de las regiones, como veremos en la sección de Función integrable, más adelante.
Para comprender mejor la construcción del concepto de Integral, es muy importante que tengas claros los conceptos de ínfimo y supremo, relacionados por supuesto con conjuntos acotados y con el axioma del supremo, vistos en el curso de Cálculo Diferencial e Integral I. También debes tener claro el significado de función acotada y el concepto de partición de un intervalo cerrado, que incluiremos en esta sección.
Si deseas recordar estos conceptos, da clic aquí.
Si deseas recordar, da clic aquí.
Para tener presentes algunos resultados que se utilizan casi de inmediato en este apartado, incluimos las siguientes proposiciones.
Sean $\empty \neq A \subset B \subset \mathbb{R}$. Si $B$ es acotado, entonces $A$ es acotado y además, $infA \geq infB$ y $supA \leq supB$.
El ínfimo del subconjunto $A$, es mayor que el ínfimo del conjunto $B$ que lo contiene y el supremo del subconjunto $A$ es menor que el supremo del conjunto $B$ que lo contiene.
Sean $A$ y $B$ subconjutos de $\mathbb{R}$, no vacíos y acotados. Sea $A+B = \{a+b | a \in A \text{ y } b \in B\}$, entonces $(A+B)$ es acotado y además $inf(A+B) \geq inf A + inf B$ y $sup(A+B) \leq sup A + supB$.
Estas proposiciones serán de mucha utilidad, la primera para la construcción del concepto de integral y la segunda, en los teoremas de álgebra de las funciones integrables. Te conviene tenerlos en cuenta.
Sea $\empty \neq A \subset \mathbb{R}$ y acotado. Si $c \gt 0$ y $cA = \{ca | a \in A\}$, entonces $cA$ es acotado y además $inf(cA) \geq c(infA)$ y $sup(cA) \leq c(supA)$.
Los siguientes tres resultados te permitirán calcular tus primeras integrales, por medio de la definición.
$1+2+...+n = \dfrac{n(n+1)}{2} \; \forall n \in \mathbb{N}$.
$1^2+2^2+...+n^2 = \dfrac{n(n+1)(2n+1)}{6} \; \forall n \in \mathbb{N}$.
$1^3+2^3+...+n^3 = \left( \dfrac{n(n+1)}{2} \right)^2 \; \forall n \in \mathbb{N}$.
El concepto de límite lo debes tener muy bien asimilado.
$L$ es límite de $f$ en $a$, si para cada $\varepsilon \gt 0, \exist \delta \gt 0$, tal que $\forall x \in Dom f$, si $0 \lt |x-a| \lt \delta$, entonces $|f(x)-L| \lt \epsilon$.
Es decir, para cada vecindad $V_{\varepsilon}(L)$ debe existir una vecindad $V_{\delta}^0(a)$, tal que: $\forall x \in Dom f \cap V_{\delta}^0(a)$, se cumple que $f(x) \in V_{\varepsilon}(L)$.
Ya por último te recomendamos tener claro el Teorema del Valor Medio para Derivadas.
Si $f$ es continua en $[a,b]$ y derivable en $(a,b)$, entonces $\exist x \in (a,b)$ tal que $f'(x) = \dfrac{f(b)-f(a)}{b-a}$.
Sea $a \lt b$. Una partición del intervalo $[a,b]$ es una colección finita de puntos de $[a,b]$, de los cuales uno es $a$ y otro es $b$.
Como se trata de un conjunto finito de puntos, estos pueden ser numerados y ordenados como:
$t_0, t_1, ..., t_{n-1}, t_n,$ de manera que: $a=t_0 \lt t_1 \lt ... \lt t_{n-1} \lt t_n = b$
Así es que pensaremos en una partición, como un conjunto finito y ordenado de puntos, donde el primero es $a$ y el último es $b$. Es decir que siempre pensaremos en que $a \lt b$.
Sea $f$ una función acotada sobre $[a,b]$ y $P=\{t_0, ..., t_n\}$ una partición de $[a,b]$. Sean, además para $i=1, ..., n$:
$m_i = inf\{f(x) | t_{i-1} \leq x \leq t_i \}$
$M_i = sup\{f(x) | t_{i-1} \leq x \leq t_i \}$
Definimos, la suma inferior de $f$ para $P$, designada por $L(f,P)$, como:
$\displaystyle L(f,P) = \sum_{i=1}^{n} m_i (t_i-t_{i-1})$
Definimos, la suma superior de $f$ para $P$, designada por $U(f,P)$, como:
$\displaystyle U(f,P) = \sum_{i=1}^{n} M_i (t_i-t_{i-1})$
En la definición anterior:
Si $f$ es una función acotada sobre $[a,b]$ y $P=\{t_0, ..., t_n \}$ una partición de $[a,b]$, entonces $L(f,P) \leq U(f,P)$.
Esto nos indica que, la suma inferior de $f$ para la partición $P$ es menor o igual que la suma superior de $f$ para la misma partición $P$.
Para la construcción del concepto de integral sería deseable que tal desigualdad se cumpliese para particiones distintas, es decir que: $L(f,P_1) \leq U(f,P_2)$. Nos encaminamos a demostrarlo, pero antes de ello, una definición y un lema.
Sean $P$ y $Q$ particiones de $[a,b]$. Decimos que $Q$ es un refinamiento de $P,$ si $P \subset Q$.
También se acostumbra decir que $Q$ refina a $P$. Por ejemplo: $Q = \{-2,-1,0,0.5,1,1.3,2,2.5,3 \}$ es una partición de $[-2,3]$ y es un refinamiento de la partición $P = \{-2,-1,0,0.5,1.3,2,2.5,3 \}$ del mismo intervalo $[-2,3]$. En este caso $Q$ tiene un elemento de más (el $1$) con respecto a $P$, sin embargo podría tener cuantos se quisieran, pero en número finito.
Si $Q$ refina a $P$, entonces $L(f,P) \leq L(f,Q)$ y $U(f,P) \geq U(f,Q)$.
Es decir, las sumas inferiores crecen al refinar una partición y al contrario, las sumas superiores decrecen.
Sean $P_1$ y $P_2$ particiones de $[a,b]$, y sea $f$ una función acotada sobre $[a,b].$ Entonces $L(f,P_1) \leq U(f,P_2)$.
En la siguiente sección profundizaremos en estas consecuencias del teorema 1, ya que son de gran importancia para definir si una función es integrable o no.
Aquí encontrarás la definición de función integrable y ejemplos sencillos que permitan ilustrar la aplicación de la definición para corroborar si una función es o no integrable.
En la sección anterior, derivado del Teorema 1, obtuvimos una conclusión que reescribiremos utilizando $P([a,b])$ para denotar el conjunto de particiones de $[a,b]$:
$sup\{ L(f,P) | P \in P([a,b]) \} \leq inf\{ U(f,P) | P \in P([a,b]) \}$ ... (1)
Y es claro además que:
$L(f,P') \leq sup\{ L(f,P) | P \in P([a,b]) \} \leq inf\{ U(f,P) | P \in P([a,b]) \} \leq U(f,P') \forall$ partición $P'$ de $[a,b]$.
De acuerdo con la desigualdad (1), puede ocurrir que:
$sup\{ L(f,P) | P \in P([a,b]) \} = inf\{ U(f,P) | P \in P([a,b]) \}$ ... (2)
$sup\{ L(f,P) | P \in P([a,b]) \} \lt inf\{ U(f,P) | P \in P([a,b]) \}$ ... (3)
En el caso (2), existe un único número entre todas las sumas inferiores y superiores de $f$ y éste sería el candidato para representar el área de la región $R(f,a,b)$.
Por el contrario en el caso (3) habría infinidad de valores entre todas las sumas inferiores y superiores de $f$ y, por consecuencia no parece haber un candidato para el área de la región $R(f,a,b)$.
En efecto, con estas ideas, establecemos la definición de función integrable.
Una función $f$ acotada sobre $[a,b]$ es integrable sobre $[a,b]$ si $sup\{ L(f,P) | P \in P([a,b]) \} = inf\{ U(f,P) | P \in P([a,b]) \}$.
En este caso, el número común recibe el nombre de integral de $f$ sobre $[a,b]$ y se denota por $\displaystyle \int_a^b f$.
La integral $\displaystyle \int_a^b f$ recibe el nombre de área de la región $R(f,a,b)$ cuando $f(x) \geq 0 \; \forall x \in [a,b]$.
Así, si $f$ es integrable sobre $[a,b]$, entonces $\displaystyle \int_a^b f$ es el único número entre todas las sumas superiores e inferiores de $f$ en $[a,b]$.
A continuación mostramos un par de ejemplos sencillos para aplicar la definición de función integrable. En uno de ellos demostraremos que la función dada es integrable y en el otro haremos ver que no lo es.
Aquí encontrarás un criterio de integrabilidad que permite corroborar si una función es o no integrable, de una manera más sencilla que aplicando la definición de función integrable. También encontrarás la demostración del teorema 2, que establece la equivalencia entre el criterio de integrabilidad y la definición de función integrable.
Si $f$ es una función acotada sobre $[a,b]$, entonces $f$ es integrable sobre $[a,b]$, si y sólo si $\forall \varepsilon \gt 0$, existe una partición de $P$ de $[a,b]$ tal que $U(f,P)-L(f,P) \lt \varepsilon$.
Estas observaciones son con la idea de apreciar mejor la importancia del Criterio de integrabilidad (Teorema 2).
Para hacer ver que una función acotada en $[a,b]$, es integrable sobre $[a,b]$:
$sup\{ L(f,P) | P \in P([a,b]) \} = inf\{ U(f,P) | P \in P([a,b]) \}$
y para ello, hay que calcular todas las sumas superiores e inferiores, para toda partición del intervalo $[a,b]$ y recuerda que éstas son infinitas.
$U(f,P)-L(f,P) \lt \varepsilon$
Recuerda que dado $\varepsilon \gt 0$ hay que encontrar una partición $P$ de $[a,b]$, tal que la suma superior, menos la inferior sea menos que épsilon. Dicho en otras palabras, las sumas superior e inferior tienen valores tan cercanos como se quiera.
En los ejemplos siguientes se demuestra la integrabilidad de funciones acotadas en un intervalo $[0,b]$, utilizando el Criterio de integrabilidad y en particular en los ejemplos 2 y 3, se utiliza un tipo de partición que llamaremos regular.
Se dice que una partición $P_n = \{ t_0, ..., t_n \}$ de $[a,b]$ es regular, si divide al intervalo en $n$ partes iguales.
En una partición regular de $[a,b]$, ocurre que: $t_i = a + \dfrac{i(b-a)}{n}$ y $t_i-t_{i-1} = \dfrac{b-a}{n} \; \forall i$.
Es decir: $t_0 = a + \dfrac{0(b-a)}{n} = a$, $t_1 = a + \dfrac{1(b-a)}{n}$, $t_2 = a + \dfrac{2(b-a)}{n}$, $...$, $t_n = a + \dfrac{n(b-a)}{n} = b$.
En particular: si $a=0$, entonces $t_0=0$, $t_1=\dfrac{b}{n}$, $t_2=\dfrac{2b}{n}$, $...$, $t_k=\dfrac{kb}{n}$, $...$, $t_n = b$
En este apartado encontrarás fundamentalmente el teorema que asegura que toda función continua en un intervalo cerrado $[a,b]$ es integrable sobre $[a,b]$. Para la demostración de este teorema, necesitamos algunos conceptos y resultados previos sobre continuidad y continuidad uniforme, que también serán incluidos. En realidad, es un teorema fácil de aceptar, pero si gustas formalizarlo, aquí tienes esta sección.
Si $f$ es continua en $[a,b]$, entonces $f$ es acotada sobre $[a,b]$.
Este teorema es la conjunción de uno de los teoremas fuertes de continuidad, el 2 y el teorema 6 del mismo tema, en el curso de Cálculo diferencial e integral I.
Una función $f$ es uniformemente continua en un intervalo $I$, si $\forall \varepsilon \gt 0, \exist \delta \gt 0$ tal que $\forall x, y \in I$ se cumple que: si $|x-y| \lt \delta$, entonces $|f(x)-f(y)| \lt \varepsilon$.
Sean $a \lt b \lt c$ y $f$ continua en el intervalo $[a,c]$. Dado que $\varepsilon 0$, supongamos que existen $\delta_1 \gt 0$ y $\delta_2 \gt 0$, tales que:
$x, y \in [a,b]$ y $|x-y| \lt \delta_1 \implies |f(x)-f(y)| \lt \varepsilon$
$x, y \in [b,c]$ y $|x-y| \lt \delta_2 \implies |f(x)-f(y)| \lt \varepsilon$
Entonces existe $\delta \gt 0$ tal que:
$x, y \in [a,c]$ y $|x-y| \lt \delta \implies |f(x)-f(y)| \lt \varepsilon$
Si $f$ es continua en $[a,b]$, entonces $f$ es uniformemente continua en $[a,b].$
Si $f$ es continua en $[a,b]$, entonces $f$ es integrable en $[a,b].$
Con este teorema, tenemos un conjunto mucho muy grande de funciones integrables, particularmente todas las polinomiales.
En este apartado encontrarás algunos teoremas que tienen que ver con el manejo algebraico de las funciones integrables y de sus integrales.
Sea $a \lt c \lt b$. $f$ es integrable sobre $[a,b]$, si y sólo si $f$ es integrable sobre $[a,c]$ y $[c,b]$. Además $\displaystyle \int_a^b f = \int_a^c f + \int_c^b f$.
Con la idea de extender este teorema a casos más diversos, como por ejemplo para $a \lt b \lt c$ y otros posibles, se formulan las siguientes definiciones.
$\displaystyle \int_a^a f=0$ y $\displaystyle \int_a^b f = -\int_b^a f$ si $a \gt b$.
Así tenemos la siguiente:
$\displaystyle \int_a^c f + \int_c^b f = \int_a^b f \;\; \forall a, b \text{ y } c$.
Para el siguiente teorema será importante que recuerdes la Proposición 2 de la sección Conceptos previos, que establece la relación entre supremos e ínfimos de los conjuntos $A$, $B$ y $A+B$.
Si $f$ y $g$ son integrables sobre $[a,b]$, entonces $f+g$ es integrable sobre $[a,b]$ y $\displaystyle \int_a^b (f+g) = \int_a^b f + \int_a^b g$.
Para el siguiente teorema será importante que recuerdes la Proposición 3 de la sección Conceptos previos, que establece la relación entre supremos e ínfimos de los conjuntos $A$ y $cA$, para $c \gt 0$.
Si $f$ es integrable sobre $[a,b]$, entonces la función $cf$ es integrable sobre $[a,b]$ $\forall c$ y $\displaystyle \int_a^b cf = c\int_a^b f$.
Si $f$ es integrable sobre $[a,b]$ y $m \leq f(x) \leq M \;\;\; \forall x \in [a,b]$, entonces $\displaystyle m(b-a) \leq \int_a^b f \leq M(b-a)$.
Este teorema puede ser muy útil, en ocasiones, para obtener una aproximación de la integral.
En este apartado encontrarás algunos ejemplos que son posibles a partir de la aplicación de los teoremas hasta ahora vistos.
Si $f(x)=x$, $\forall x$, entonces $\displaystyle \int_0^b f = \frac{b^2}{2}$
Si $f(x)=x^2$, $\forall x$, entonces $\displaystyle \int_0^b f = \frac{b^3}{3}$
Si $f(x)=x^3$, $\forall x$, entonces $\displaystyle \int_0^b f = \frac{b^4}{4}$
Si $f(x)=x$, $\forall x$, entonces $\displaystyle \int_a^b f = \int_0^b f - \int_0^a f = \frac{b^2}{2} - \frac{a^2}{2}$
Si $f(x)=x^2$, $\forall x$, entonces $\displaystyle \int_a^b f = \int_0^b f - \int_0^a f = \frac{b^3}{3} - \frac{a^3}{3}$
Si $f(x)=x^3$, $\forall x$, entonces $\displaystyle \int_a^b f = \int_0^b f - \int_0^a f = \frac{b^4}{4} - \frac{a^4}{4}$
Una función discontinua de primera clase (o con discontinuidad removible) es integrable, como por ejemplo:
Si $f:[0,2] \to \mathbb{R}$, tal que $f(x) = \begin{cases} 1 \text{ si } x \neq 1 \\ 2 \text{ si } x = 1 \end{cases}$ entonces $\displaystyle \int_0^2 f = 2$.
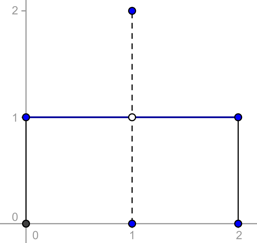
¿La recuerdas? Si no puedes ir a los ejemplos del Criterio de Integrabilidad.
Podemos hacer ver que una función continua en un intervalo cerrado, excepto en uno de sus puntos, en donde tiene una discontinuidad de segunda clase (o no removible), es integrable sobre $[a,b]$.
Por ejemplo, la función:
Si $f:[0,2] \to \mathbb{R}$, tal que $f(x) = \begin{cases} 1 \text{ si } x \in [0,1) \\ 2 \text{ si } x \in [1,2] \end{cases}$ entonces $f$ es integrable en $[0,2]$ y $\displaystyle \int_0^2 f = 3$.
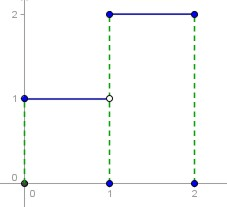
La razón es que es integrable sobre $[0,1]$ y sobre $[1,2]$, entonces, por el teorema 5 es integrable en $[0,2]$ y la integral es fácil de calcular. ¿Puedes ingeniar otras funciones discontinuas de primera y segunda clase que sean integrables?
Algunas veces resulta muy difícil calcular una integral, entonces poder aproximarla aunque sea de manera burda, será un avance.
Hasta ahora hemos utilizado una notación muy cómoda y económica para la integral: $\displaystyle \int_a^b f$. Esto es porque en nuestras expresiones hasta sólo hemos manejado una sola variable. Cuando en una expresión hay más de una variable, entonces es necesario hacer explícita la variable de integración y en ese caso, las otras se comportan como constantes respecto a ésta. Por ejemplo:
$\displaystyle \int_a^b (x+y)dx \overset{\text{Teo 5}}{=} \int_a^b xdx + \int_a^b ydx \overset{\text{Teo 6}}{=} \int_a^b xdx + y \int_a^b dx = \left( \frac{b^2}{2} - \frac{a^2}{2} \right) + y(b-a)$
$\displaystyle \int_a^b (y+t)dt \overset{\text{Teo 5}}{=} \int_a^b ydt + \int_a^b tdt \overset{\text{Teo 6}}{=} y \int_a^b dt + \int_a^b tdt = y(b-a) + \left( \frac{b^2}{2} - \frac{a^2}{2} \right)$
$\displaystyle \int_a^x (y+t)dy \overset{\text{Teo 5}}{=} \int_a^x ydy + \int_a^x tdy \overset{\text{Teo 6}}{=} \int_a^x ydy + t \int_a^x dy = \left( \frac{x^2}{2} - \frac{a^2}{2} \right) + t(x-a)$
$\displaystyle \int_a^b \left( \int_a^x tdz \right) dx \overset{\text{Teo 6}}{=} \int_a^b \left( t \int_a^x dz \right) dx = \int_a^b t(x-a)dx \underset{\text{Teo 5}}{\overset{\text{Teo 6}}{=}} t \left( \int_a^b xdx + a \int_a^b dx \right) = t \left( \frac{b^2}{2} - \frac{a^2}{2} \right) - a(b-a)$
Las integrales a continuación, significan lo mismo:
$\displaystyle \int_a^b xdx, \int_a^b ydy, \int_a^b tdt \text{ ó }\int_a^b udu$
En este apartado iniciarás el estudio de la integral como una función, lo cual te permitirá conectarla con los conceptos ya estudiados de límite, continuidad y derivada. Es decir, podrás estudiar la continuidad de una función integral, aplicarle límite y obtener su derivada.
Sea $f$ integrable sobre $[a,b]$. Definimos la función $f:[a,b] \to \mathbb{R}$, tal que $\displaystyle F(x) = \int_a^x f(t) dt$.
Por el Teorema 4, sabemos que esta función está bien definida, puesto que si $f$ es integrable sobre todo $[a,b]$, entonces $f$ es integrable sobre cualquiera subintervalo $[a,x]$, para todo $x$ en $[a,b]$.
Para la demostración del siguiente teorema, será necesario que recuerdes que:
Si $f$ es integrable sobre $[a,b]$, entonces $f$ está acotada en $[a,b]$.
Si $f$ es integrable sobre $[a,b]$ y $F:[a,b] \to \mathbb{R}$ es una función tal que $\displaystyle F(x) = \int_a^x f$ entonces $F$ es continua sobre $[a,b]$.
Esta propiedad de la integral como una función es interesante y se cumple, aun que la función $f$ sea discontinua, como podrás apreciar en los siguientes ejemplos.
En este apartado podrás encontrar una aplicación de la integral, referente al cálculo de la longitud de una curva, comúnmente llamada Longitud de arco. Empezaremos con una explicación de lo que deseamos hacer:
Para calcular la longitud de la curva la idea es hacer una partición del intervalo $[a,b]$ y, trazar una poligonal que une los puntos $(t0,f(t0)), (t1,f(t1)), ... ,(tn,f(tn)),$ como se puede ver en la construcción interactiva. Así, la longitud de la poligonal, es una aproximación a la longitud de la curva. Entre más fina resulte la partición, más próxima será la longitud de la poligonal, a la longitud de la curva.
Esta idea debemos formalizarla y para ello, empezaremos con una
Sea $f$ continua en $[a,b]$ y $P=\{t_0, t_1, ..., t_n\}$ una partición de $[a,b]$. Definimos $\displaystyle \lambda (f,P) = \sum_{i=1}^n \sqrt{(t_i-t_{i-1})^2 + (f(t_i) - f(t_{i-1}))^2}$ como la longitud de la poligonal que une consecutivamente los puntos $(t_{i-1}, f(t_{i-1}))$ y $(t_i, f(t_i)) \;\; \forall i$.
Observa que cada sumando, representa la longitud de cada segmento cuyos extremos son $(t_{i-1}, f(t_{i-1}))$ y $(t_i,f(t_i))$.
Sea $f$ continua en $[a,b]$ y $P=\{t_0, t_1, ..., t_n\}$ una partición de $[a,b]$. Definimos $ \Delta (f,P) = sup \{\lambda(f,P) | P \in \mathscr{P}([a,b])\}$ como la longitud de $f$ en $[a,b]$, suponiendo que $\{ \lambda(f,P) | P \in \mathscr{P}([a,b]) \}$ es un conjunto acotado superiormente.
Ahora estamos en posibilidad de nuestro primer teorema.
Supongamos que $f'$ es continua en $[a,b]$. Si $P$ es una partición cualquiera de $[a,b]$, entonces $L \left( \sqrt{1+(f')^2}, P \right) \leq \lambda(f,P) \leq U \left( \sqrt{1+(f')^2}, P \right)$.
De aquí nos encaminamos a obtener la expresión que nos proporciones la longitud de $f$ en $[a,b]$ y para ello, estableceremos unos cuantos razonamientos más, a partir de este teorema.
$sup \left\{ L \left( \sqrt{1+(f')^2} \right), P \right\} \leq \{\lambda(f,P)\}$.
$sup \{ \lambda(f,P) \} \leq inf \left\{ U \left( \sqrt{1+(f')^2}, P \right) \right\}$.
Y ahora el resultado importante respecto a la longitud de $f$ en $[a,b]$.
Supongamos que $f'$ es continua en $[a,b]$, entonces $\sqrt{1+(f')^2}$ es integrable y $\displaystyle \Delta(f) = \int_a^b \sqrt{1+(f')^2}$.
A continuación podrás ver algunos ejemplos, en general sencillos, porque las integrales que resultan requieren métodos de integración que aun no hemos visto.
En este apartado encontrarás algunos ejercicios selectos resueltos. Te presentamos una solución de éstos, por la importancia que tienen más adelante en el tema de Integrales impropias. Es importante que los estudies con cuidado y mejor aún que trates de desarrollar cualquier detalle que haga falta o que no entiendas.
En todos estos ejercicios requerirás un buen manejo del concepto de Partición de un intervalo $[a,b]$. Igualmente de los conceptos de supremo e ínfimo. A estas alturas suponemos que los tienes dominados.
Demostrar que $\displaystyle \int_a^b f(x)dx = \int_{a+c}^{b+c} f(x-c)dx$.
Supondremos que la función $f(x)$ es integrable en el intervalo $[a,b]$, y demostraremos que la función $g(x)=f(x-c)$ es integrable en el intervalo $[a+c,b+c]$, y que las integrales respectivas son iguales.
Sea $g(x)=f(x-c)$ para todo $x \in [a+c,b+c]$.
Puesto que $f(x)$ es integrable en el intervalo $[a,b]$, por el Criterio de integrabilidad, tenemos que:
Para todo $\varepsilon \gt 0$ existe $P=\{t_0 = a, ..., t_n = b\}$ partición de $[a,b]$ tal que $U(f,P) - L(f,P) \lt \varepsilon$.
Donde, $\displaystyle U(f,P) = \sum_{i=1}^n M_i(t_i-t_{i-1}), L(f,P) = \sum_{i=1}^n m_i(t_i-t_{i-1})$, $M_i = sup \{ f(x) : t_{i-1} \leq x \leq t_i \}, \forall i=1, ..., n$ y $m_i = inf \{ f(x) : t_{i-1} \leq x \leq t_i \}, \forall i=1, ..., n$
Sea $P' = \{ t'_0=a+c, ..., t'_i=t_i+c, ..., t'_n=b+c \}$ partición de $[a+c,b+c]$ construida a partir de la partición $P = \{ t_0=a, ..., t_n=b \}$ del intervalo $[a, b]$.
Sean $M'_i = sup \{ g(x): t'_{i-1} \leq x \leq t'_i \}$ y $m'_i = \{ g(x): t_{i-1} \leq x \leq t_i \}$ donde $t_i=t_i+c, \forall i=1,...,n$
Pero,
$M'_i = sup \{ g(x): t'_{i-1} \leq x \leq t'_i \} = sup \{ g(x): t_{i-1}+c \leq x \leq t_i+c \} = sup \{ f(x-c): t_{i-1} \leq x-c \leq t_i \} = sup \{ f(w): t_{i-1} \leq w \leq t_i \} = M_i, \forall i=1,...,n$
y
$m'_i = inf \{ g(x): t'_{i-1} \leq x \leq t'_i \} = inf \{ g(x): t_{i-1}+c \leq x \leq t_i+c \} = inf \{ f(x-c): t_{i-1} \leq x-c \leq t_i \} = inf \{ f(w): t_{i-1} \leq w \leq t_i \} = m_i, \forall i=1,...,n$
Por tanto,
$\displaystyle L(g,P') = \sum_{i=1}^n m'_i (t'_i - t'_{i-1}) = \sum_{i=1}^n m_i (t_i - t_{i-1}) = L(f,P)$.
$\displaystyle U(g,P') = \sum_{i=1}^n M'_i (t'_i - t'_{i-1}) = \sum_{i=1}^n M_i (t_i - t_{i-1}) = U(f,P)$.
Entonces, $U(g,P') = U(f(x-c),P') = U(f,P)$ y $L(g,P') = L(f(x-c),P') = L(f,P)$.
Así, dado $\varepsilon \gt 0$ existe $P' = \{ t'_0=a+c, ..., t'_i=t_i+c, ..., t_n=b+c \}$ partición de $[a+c,b+c]$ tal que $U(g,P') - L(g,P') = U(f,P)-L(f,P) \lt \varepsilon$.
Se sigue que $g(x)=f(x-c)$ es integrable en el intervalo $[a+c,b+c]$.
Además, $\displaystyle \int_a^b f(x)dx = sup \{ L(f,P) \} = sup \{ L(g,P') \} = \int_{a+c}^{b+c} f(x-c)dx$
Por tanto, $\displaystyle \int_a^b f(x)dx = \int_{a+c}^{b+c} f(x-c)dx$.
Q.E.D
Demostrar que $\displaystyle \int_1^a \frac{1}{t} dt + \int_1^b \frac{1}{t} dt = \int_1^{ab} \frac{1}{t} dt$.
La idea es demostrar que $\displaystyle \int_1^a \frac{1}{t} dt$ existe y que es igual a $\displaystyle \int_1^{ab} \frac{1}{t} dt$.
Luego aplicaremos el Teorema 4, página 368 del Spivak, para concluir la igualdad solicitada.
$f(x)=\dfrac{1}{x}, \forall x \in [1,a]$ es una función continua y decreciente en el intervalo $[1,a]$, para todo $a \gt 1$.

Por ser $f(x)=\dfrac{1}{x}$ continua en $[1,a]$, según el Teorema 3, página 366 del Spivak, se sigue que es integrable en $[1,a]$.
Por tanto, $\forall \varepsilon \gt 0 \exist P$ partición de $[1,a]$ tal que $U(f,P)-L(f,P) \lt \varepsilon$.
Esto significa, que dado $\varepsilon \gt 0$ siempre existe una $P = \{ t_0=1, ..., t_n=a \}$ partición de $[1,a]$, tal que $U(f,P)-L(f,P) \lt \varepsilon$.
Donde,
$M_i = sup \{ f(x): t_{i-1} \leq x \leq t_i \} = f(t_{i-1}) = \dfrac{1}{t_{i-1}}, \forall i=1,...,n$
$m_i = inf \{ f(x): t_{i-1} \leq x \leq t_i \} = f(t_{i-1}) = \dfrac{1}{t_i}, \forall i=1,...,n$
Y
$\displaystyle U(f,P) = \sum_{i=1}^n M_i(t_i-t_{i-1}) = \sum_{i=1}^n f(t_{i-1})(t_i-t_{i-1}) = \sum_{i=1}^n \dfrac{1}{t_{i-1}} (t_i-t_{i-1})$
$\displaystyle L(f,P) = \sum_{i=1}^n m_i(t_i-t_{i-1}) = \sum_{i=1}^n f(t_i)(t_i-t_{i-1}) = \sum_{i=1}^n \dfrac{1}{t_i} (t_i-t_{i-1})$
Esto es, dado $\varepsilon \gt 0$ y $P = \{ t_0=1, ..., t_n=a \}$ la partición de $[1,a]$ tal que:
$$U(f,P)-L(f,P) = \sum_{i=1}^n \frac{1}{t_{i-1}} (t_i,t_{i-1}) - \sum_{i=1}^n \frac{1}{t_i} (t_i,t_{i-1}) \lt \varepsilon$$Ahora, demostraremos que $f(x) = \dfrac{1}{x} \forall x \in [b,ab]$ es integrable en $[b,ab]$ y que $\displaystyle \int_1^a \frac{1}{t} dt = \int_b^{ab} \frac{1}{t} dt$.
Sabemos que $f(x)=\dfrac{1}{x}, \forall x \in [b,ab]$ es una función continua y decreciente en $[b,ab]$.
Sea $P'$ la partición de $[b,ab]$ definida con base en la partición $P$ de $[1,a]$, esto es:
$P' = \{ t'_0=b·1, t'_1=b·t_1, ..., t'_1=b·t_i, ..., t'_n=bt_n = ba\}$
Así,
$M'_i = sup \{ f(x): t'_{i-1} \leq x \leq t'_i \} = f(t'_{i-1}) = \dfrac{1}{t'_{i-1}} = \dfrac{1}{bt_{i-1}} = \dfrac{1}{b}\dfrac{1}{t_{i-1}} = \dfrac{1}{b} M_i, \forall i=1,...,n$
$m'_i = inf \{ f(x): t'_{i-1} \leq x \leq t'_i \} = f(t'_i) = \dfrac{1}{t'_i} = \dfrac{1}{bt_i} = \dfrac{1}{b}\dfrac{1}{t_i} = \dfrac{1}{b} m_i, \forall i=1,...,n$
Por lo tanto,
$\displaystyle U(f,P') = \sum_{i=1}^n M'_i(t'_i - t'_{i-1}) = \sum_{i=1}^n f(t'_{i-1})(t'_i - t'_{i-1}) = \sum_{i=1}^n \frac{1}{bt_{i-1}} (bt_i - bt_{i-1}) = \sum_{i=1}^n \frac{1}{bt_{i-1}} b(t_i - t_{i-1}) = \sum_{i=1}^n \frac{1}{t_{i-1}} (t_i - t_{i-1}) = \sum_{i=1}^n M_i (t_i - t_{i-1}) = U(f,P)$
Y
$\displaystyle L(f,P') = \sum_{i=1}^n m'_i(t'_i - t'_{i-1}) = \sum_{i=1}^n f(t'_i)(t'_i - t'_{i-1}) = \sum_{i=1}^n \frac{1}{bt_i} (bt_i - bt_{i-1}) = \sum_{i=1}^n \frac{1}{bt_i} b(t_i - t_{i-1}) = \sum_{i=1}^n \frac{1}{t_i} (t_i - t_{i-1}) = \sum_{i=1}^n m_i (t_i - t_{i-1}) = L(f,P)$
Por tanto,
$\forall \varepsilon \gt 0 \;\;\; \exist P'$ partición $[b,ab]$ tal que: $U(f,P') - L(f,P') = U(f,P) - L(f,P) \lt \varepsilon$.
Por tanto,
$\forall \varepsilon \gt 0 \;\;\; \exist P'$ partición $[b,ab]$ tal que: $U(f,P') - L(f,P') \lt \varepsilon$.
Esto significa que $f(x) = \dfrac{1}{x}$ es integrable en $[b,ab]$.
Además, $\displaystyle \int_b^{ab} \frac{1}{t} dt$ es el único número que está entre todas las sumas superiores y todas las sumas inferiores de $f(x)=\dfrac{1}{x}$ para $P'$ partición de $[b,ab]$.
Es decir, $\displaystyle U(f,P') \leq \int_b^{ab} \frac{1}{t} dt \leq L(f,P'), \; \forall P'$ partición de $[b,ab]$.
Pero, como $U(f,P') = U(f,P)$ y $L(f,P') = L(f,P)$ se sigue que:
$\displaystyle U(f,P) \leq \int_b^{ab} \frac{1}{t} dt \leq L(f,P), \; \forall P$ partición de $[1,a]$ ... (1)
Luego, por ser $f(x)=\dfrac{1}{x}$ integrable en $[1,a]$, entonces el número $\displaystyle \int_1^a \frac{1}{t} dt$ es el único número que está entre todas las sumas superiores y todas las sumas inferiores de $f(x)=\dfrac{1}{x}$ para $P$ partición de $[1,a]$.
Es decir, $\displaystyle U(f,P) \leq \int_1^a \frac{1}{t} dt \leq L(f,P), \; \forall P$ partición de $[1,a]$ ... (2)
Así, de (1) y (2) se sigue que $\displaystyle \int_1^a \frac{1}{t} dt = \int_b^{ab} \frac{1}{t} dt$ ... (3)
Por tanto, $f(x) = \dfrac{1}{x}$ es integrable en $[1,b]$ y en $[b,ab]$, por el Teorema 4, página 368 del Spivak, tenemos:
$\displaystyle \int_1^b \frac{1}{t} dt + \int_b^{ab} \frac{1}{t} dt = \int_1^{ab} \frac{1}{t} dt$ ... (4)
Pero, por (3), la expresión (4) puede escribirse de la siguiente manera:
$\displaystyle \int_1^{ab} \frac{1}{t} dt = \int_1^b \frac{1}{t} dt + \int_b^{ab} \frac{1}{t} dt = \int_1^b \frac{1}{t} dt + \int_1^a \frac{1}{t} dt$ ... (5)
Por tanto, $\displaystyle \int_1^{ab} \frac{1}{t} dt = \int_1^a \frac{1}{t} dt + \int_1^b \frac{1}{t} dt$
Q.E.D
Demostrar que $\displaystyle \int_{ca}^{cb} f(x)dx = c \int_a^b f(cx)dx$.
Supondremos que la función $f(cx)$ es integrable en el intervalo $[a,b]$, y demostraremos que $f(x)$ es integrable en el intervalo $[ca,cb]$, y que las integrales respectivas son iguales.
Supongamos que $f(cx)$ es integrable en el intervalo $[a,b]$, por el Criterio de integrabilidad sabemos que: Para todo $\varepsilon \gt 0$ existe una $P = \{ a=t_0, ..., t_n=b \}$ partición de $[a,b]$ tal que $U(f(cx),P) - L(f(cx),P) \lt \frac{\varepsilon}{c}$.
Donde $\displaystyle U(f(cx),P) = \sum_{i=1}^n M_i (t_i - t_{i-1})$, y $\displaystyle L(f(cx),P) = \sum_{i=1}^n m_i (t_i - t_{i-1})$
$M_i = sup \{ f(cx): t_{i-1} \leq x \leq t_i \} \; \forall i=1,...,n$
Y
$m_i = inf \{ f(cx): t_{i-1} \leq x \leq t_i \} \; \forall i=1,...,n$
Sea $P' = \{ t'_0=ca, ..., t'_i=ct_i, ..., t'_n=ct_n \}$ una partición del intervalo $[ca,cb]$ construida a partir de la partición $P = \{ t_0=a, ..., t_n=b \}$ del intervalo $[a,b]$.
Sean $\displaystyle U(f,P') = \sum_{i=1}^n M'_i(t'_i - t'_{i-1})$ y $\displaystyle L(f,P') = \sum_{i=1}^n m'_i (t'_i - t'_{i-1})$.
Donde $M'_i = sup \{ f(x):t_{i-1} \leq x \leq t_i \}, \; \forall i=1,...,n$ y $m'_i = inf \{ f(x):t_{i-1} \leq x \leq t_i \}, \; \forall i=1,...,n$.
Pero,
$M_i = sup \{ f(cx):t_{i-1} \leq x \leq t_i \} = sup \{ f(x):ct_{i-1} \leq x \leq ct_i \} = sup \{ f(x):t_{i-1} \leq x \leq t_i \} = M'_i, \; \forall i=1,...,n$
Y
$m_i = inf \{ f(cx):t_{i-1} \leq x \leq t_i \} = inf \{ f(x):ct_{i-1} \leq x \leq ct_i \} = inf \{ f(x):t_{i-1} \leq x \leq t_i \} = m'_i, \; \forall i=1,...,n$
Entonces
$\displaystyle U(f,P') = \sum_{i=1}^n M'_i(t'_i - t'_{i-1}) = \sum_{i=1}^n M_i(ct_i - ct_{i-1}) = c \sum_{i=1}^n M_i(t_i - t_{i-1}) = c U(f(cx),P)$.
Y
$\displaystyle L(f,P') = \sum_{i=1}^n m'_i(t'_i - t'_{i-1}) = \sum_{i=1}^n m_i(ct_i - ct_{i-1}) = c \sum_{i=1}^n m_i(t_i - t_{i-1}) = c L(f(cx),P)$.
Por tanto, dado $\varepsilon \gt 0$ existe una partición $P' = \{ t'_0=ca, ..., t'_i=ct_i, ..., t'_n=ct_n \}$ de $[ca,cb]$ tal que:
$U(f,P') - L(f,P') = cU(f(cx),P) - cL(f(cx),P) = c[U(f(cx),P) - L(f(cx),P)] \lt c (\frac{\varepsilon}{c}) = \varepsilon$
Por tanto, la función $f(x)$ es integrable en el intervalo $[ca,cb]$, siempre que la función $f(cx)$ es integrable en el intervalo $[a,b]$.
Por otro lado, $\displaystyle \int_{ca}^{cb} f(x)dx = sup \{ L(f,P') \} = sup \{ cL(f(cx),P) \} = c sup \{ L(f(cx),P) \} = \int_a^b f(cx)dx$
Por tanto, $\displaystyle \int_{ca}^{cb} f(x)dx = \int_a^b f(cx)dx$.
Demostrar que:
Puesto que $f$ es integrable en $[a,b]$ y $m \leq f(x) \leq M$ entonces por el Teorema 7, página 374 del Spivak, tenemos:
$$m(b-a) \leq \int_a^b f(x)dx \leq M(b-a)$$Se sigue que $\displaystyle \frac{1}{b-a} \int_a^b f(x)dx = \mu$ para algún número $\mu$ con $m \leq \mu \leq M.$
Q.E.D
Por ser $f$ continua en $[a,b]$, sabemos que $f$ alcanza su valor máximo y mínimo en el cerrado $[a,b]$. En consecuencia $f$ es acotada sobre $[a,b]$.
Esto es, existen $x_0, x_1$ en $[a,b]$ tales que $f(x_0) \leq f(x) \leq f(x_1), \; \forall x \in [a,b].$
Entonces aplicando el resultado del inciso (a), tenemos:
$$f(x_0)(b-a) \leq \int_a^b f(x)dx \leq f(x_1)(b-a)$$Lo cual implica,
$$f(x_0) \leq \frac{1}{b-a} \int_a^b f(x)dx \leq f(x_1)$$Esto es, el número $\displaystyle \frac{1}{b-a} \int_a^b f(x)dx$ está entre el valor mínimo y el valor máximo de $f$.
Entonces, por el Teorema del Valor intermedio, sabemos que existe un número $\xi \in [a,b]$ tal que $\displaystyle f(\xi) = \frac{1}{b-a} \int_a^b f(x)dx$.
Por tanto, $\displaystyle \frac{1}{b-a} \int_a^b f(x)dx = f(\xi)$ para algún número $\xi \in [a,b]$.
Q.E.D
Sea $f$ definida en el cerrado $[0,1]$, por $f(x) = \begin{cases} x, \text{ si } x \neq 0.5 \\ 0, \text{ si } x = 0.5 \end{cases}$
La función $f$ es integrable en $[0,1]$, pero no es continua en $[0,1]$. Además, $\displaystyle \int_0^1 f(x)dx = \frac{1}{2}$.
Entonces, al resolver la ecuación $\displaystyle \int_0^1 f(x)dx = f(\xi)$ tenemos:
$\displaystyle \int_0^1 f(x)dx = f(\xi) \implies \frac{1}{2} = f(\xi)$ pero, la última ecuación no tiene solución en $[0,1]$, por tanto, no existe ningún número $\xi$, de $[a,b]$ tal que $\displaystyle \int_0^1 f(x)dx = f(\xi)$.
Este resultado recibe el nombre de Teorema del Valor Medio para integrales.
Para la demostración, supondremos que la función $f(x)g(x)$ es integrable en $[a,b]$.
Si $g(x) = 0, \; \forall x$ de $[a,b]$, la ecuación $\displaystyle \int_a^b f(x)g(x) dx = f(\xi) \int_a^b g(x)dx$, se cumple independientemente del valor de $f(\xi)$.
De aquí en adelante, supondremos que $g(x) \gt 0, \; \forall x$ de $[a,b]$.
Por ser $f$ continua en $[a,b]$, sabemos que $f$ alcanza su valor máximo y mínimo en el cerrado $[a,b]$. En consecuencia, $f$ es acotada sobre $[a,b]$.
Esto es, existen $x_0, x_1$ en $[a,b]$ tales que $f(x_0) \leq f(x) \leq f(x_1), \; \forall x \in [a,b].$
Por tanto, al ser $g$ positiva en $[a,b]$, de la desigualdad anterior se sigue:
$$f(x_0)g(x) \leq f(x)g(x) \leq f(x_1)g(x), \; \forall x \in [a,b]$$Por tanto, de la desigualdad anterior, se sigue
$$f(x_0) \int_a^b g(x)dx \leq \int_a^b f(x)g(x)dx \leq f(x_1) \int_a^b g(x)dx$$De aquí, $\displaystyle f(x_0) \leq \frac{1}{\int_a^b g(x)dx} \int_a^b f(x)g(x)dx \leq f(x_1)$.
Esto es, el número $\displaystyle \frac{1}{\int_a^b g(x)dx} \int_a^b f(x)g(x)dx$ está entre el valor mínimo y el valor máximo de $f$ sobre $[a,b]$.
Por tanto, por el Teorema del Valor intermedio, se sigue que existe un número $\xi$ de $[a,b]$ tal que $\displaystyle f(\xi) = \frac{1}{\int_a^b g(x)dx} \int_a^b f(x)g(x)dx$
De aquí, $\displaystyle \int_a^b f(x)g(x)dx = f(\xi) \int_a^b g(x)dx$ para algún $\xi$ de $[a,b]$.
Q.E.D
Sugerencia: usar $\displaystyle \sum_{i=1}^n i = \frac{n(n+1)}{2}, \; \forall n \in \mathbb{N}$ o $\displaystyle \sum_{i=1}^n i^2 = \frac{n(n+1)(2n+1)}{6}, \; \forall n \in \mathbb{N}$ según sea el caso.
Sugerencia: Toda partición $P = \{ t'_0, ..., t'_n \}$ de $[a,b]$ da origen a una partición $P = \{ t'_0, ..., t'_n \} = \{ t'_0+c, ..., t'_n+c \}$ de $[a+c,b+c]$ y viceversa.
Sugerencia: Puede escribirse $\displaystyle \int_1^a \frac{1}{t}dt = \int_b^{ab} \frac{1}{t}dt$. Pues Toda partición $P = \{ t_0, ..., t_n \}$ de $[1,a]$ da origen a una partición $P' = \{ t'_0, ..., t'_n \} = \{ bt_0, ..., bt_n \}$ de $[b,ab]$ y viceversa.
Obsérvese que se trata de un caso particular del ejercicio anterior.
¿Es $f$ integrable en $[0,1]$? Si la respuesta es sí, calcular la integral.
Aquí podrás encontrar el primero y segundo Teorema Fundamental del Cálculo y sus consecuencias más importantes como el cálculo de áreas entre curvas y la derivada de la función integral.
También podrás encontrar un estudio sobre las integrales impropias y diversos ejemplos al respecto. Esta sección será breve, pero con mucha importancia en lo que sigue. Conviene prestarle mucha atención.
En este apartado podrás encontrar las recomendaciones de los conceptos previos que debes revisar, antes de abordar el tema del Teorema Fundamental del Cálculo.
Debes tener clara la definición de la integral como una función. ¿Recuerdas?
Sea $f$ integrable sobre $[a,b]$. Definimos la función $F: [a,b] \to \mathbb{R}$, tal que $\displaystyle F(x) = \int_a^x f(t) dt$.
Debes recordar el
También debes recordar el
Además, debes tener bien presente el
Otro resultado que te será muy necesario es el
Algo más que sería importante que recordaras, es la Regla de la cadena para derivar una composición de funciones. Basta con que recuerdes que: $(g \circ h)'(x) = g'(h(x))h'(x)$ y que puedas reconocer las componentes de una función compuesta. Por ejemplo, ¿cómo escribirías las componentes de la siguiente función?
Si no recuerdas, a continuación se presenta un pequeño repaso.
Sean $f$ y $g$ funciones reales de variable real. Definimos $(f \circ g): D \to \mathbb{R}$ tal que $(f \circ g)(x) = f(g(x))$ y $D = \{ x:x \in Dom g$ y $g(x) \in Domf \}$.
La variable $x$ debe estar en el dominio de $g$ para garantizar que exista $g(x)$ y éste a su vez debe estar en el dominio de $f$ para garantizar que exista $f(g(x))$. La composición no es conmutativa.
Sean $f: \mathbb{R} \to \mathbb{R}$ tal que $f(x)=x^2$ y $g: \mathbb{R} \to \mathbb{R}$ tal que $g(x)=sen(x)$.
$$\begin{rcases} (f \circ g)(x) = f(g(x)) = (g(x))^2 = (sen(x))^2 \\ (g \circ f)(x) = g(f(x)) = sen(f(x)) = sen(x^2) \end{rcases} \text{Pero } (sen(x))^2 \neq sen(x^2)$$¿Puede ilustrar un caso donde $Dom(f \circ g) \neq Dom(g \circ f)$?
En una función compuesta ¿cómo puedes encontrar sus componentes?. Por ejemplo en:
$$f(x) = \sqrt{sen(cos(x^3))}$$Una buena regla es leer de adentro hacia afuera. Es decir:
$$f(x) = \underbrace{\sqrt{\underbrace{sen( \underbrace{\cos (\underbrace{x^3}_{u} )}_{v} )}_{w}}}_{z} \implies \begin{array}{c} f(x)=z(w(v(u(x)))) \text{ , donde:} \\ u(x)=x^3, v(u) = cos(u), \\ w(v) = sen(v) \text{ y } z(w)=\sqrt{w} \end{array}$$Evidentemente hay más resultados que serán necesarios, pero éstos son cruciales.
En este apartado, dedicado al primer teorema fundamental del cálculo infinitesimal, podrás encontrar una relación interesante entre la función integral $F$ y la función $f$, en caso de que ésta sea continua. También podrás encontrar un corolario, consecuencia del primer teorema fundamental que facilita el cálculo de una integral definida, para ciertos casos.
En la demostración del siguiente Teorema se utilizará el Teorema 7 (teorema de acotación de integrales) de la sección anterior en el apartado de Álgebra de Funciones Integrables. También puedes verlo en Conceptos previos.
Sean $f$ integrable sobre $[a,b]$ y $F$ definida sobre $[a,b]$, tal que $\displaystyle F(x) = \int_a^x f$. Si $f$ es continua en $c \in [a,b]$, entonces $F$ es derivable en $c$ y $F'(c) = f(c)$.
Si $c=a$ o $c=b$, la derivada de $F$ se entiende por la derecha o por la izquierda, respectivamente.
En el teorema que acabamos de ver, la función $F$ se obtiene al variar la $x$, en el límite superior de la integral. Enseguida veremos el caso en que la $x$ se encuentre en el límite inferior de la integral.
Sean $f$ integrable sobre $[a,b]$ y $G$ definida sobre $[a,b]$, tal que $\displaystyle G(x) = \int_x^b f$. Si $f$ es continua en $c \in [a,b]$, entonces $G$ es derivable en $c$ y $G'(c) = -f(c)$.
El Teorema 1a, permite además extender el Teorema 1, para el caso en que $x \lt a$. En este caso, podemos escribir:
Si $x \lt a$, tenemos que $\displaystyle F(x) = \int_a^x f = -\int_x^a f$, y, si $c \lt a$, entonces $F'(c) = -(-f(c)) = f(c)$.
Por último, la generalización del teorema 1, es para el caso en que f sea continua en todo el intervalo $[a,b]$. En este caso el Teorema diría:
Sean $f$ integrable sobre $[a,b]$ y $F$ definida sobre $[a,b]$, tal que $\displaystyle F(x) = \int_a^x f$. Si $f$ es continua en $[a,b]$, entonces $F$ es derivable en todo $[a,b]$ y $F'=f$.
Y su demostración es igual a la del Teorema 1. Sólo es una extensión a cada punto de $[a,b]$. Este teorema, tiene una consecuencia muy interesante como podrás ver en el siguiente Corolario
Si $f$ es continua en todo $[a,b]$ y $f=g'$ para alguna función $g$, entonces $\displaystyle \int_a^b f=g(b)-g(a)$.
Así que para muchas funciones $f$ continuas será fácil encontrar el valor de su integral, con sólo encontrar una función $g$, cuya derivada sea $f$. En algunos textos a éste teorema se le suele llamar el segundo teorema fundamental del cálculo. En este curso el segundo teorema fundamental no exige que $f$ sea continua, así que será un resultado un poco más fuerte, como veremos en la siguiente sección.
Con sólo derivar una función $g$, ya podremos tener la certeza de la integral de $g'$. Por ejemplo, ya tenemos la certeza de que:
$$\int_a^b x^n dx = \frac{x^{n+1}}{n+1} \text{ para } n \in \mathbb{N} \;\;\; \text{ y } \;\;\; \int_a^b x^{-n} dx = \frac{x^{-n+1}}{-n+1} \text{ para } 1 \neq n \in \mathbb{N}$$En este apartado podrás encontrar el segundo teorema fundamental del cálculo y algunas de sus consecuencias.
Es aquí que requerirás de manera importante el
Si $f$ es integrable sobre $[a,b]$ y $f=g'$ para alguna función $g$, entonces $\displaystyle \int_a^b f=g(b)-g(a)$.
A continuación te presentamos un par de ejemplos sencillos, pero ilustrativos, de funciones integrables, que no son continua, pero a las cuales se les puede aplicar el segundo teorema fundamental.
Es evidente que este segundo teorema fundamental también se aplica a funciones continuas (ya que son integrables), pero para ellas, basta el Corolario del primer teorema fundamental.
En este apartado encontrarás ejemplos de cálculo de áreas entre curvas y su invariancia respecto a traslaciones. Es un apartado de mucha práctica. Trabajaremos fundamentalmente con funciones continuas. Debes tener presente el
Calcular el área entre las gráficas de las funciones $f: \mathbb{R} \to \mathbb{R}$ tal que $f(x)=x$ y $f:\mathbb{R} \to \mathbb{R}$ tal que $f(x)=x^2$.
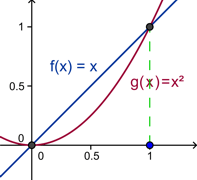
Calcular el área entre las gráficas de las funciones $f: \mathbb{R} \to \mathbb{R}$ tal que $f(x)=x^3$ y $f:\mathbb{R} \to \mathbb{R}$ tal que $f(x)=x^2$.

Calcular el área entre las gráficas de las funciones $f: \mathbb{R} \to \mathbb{R}$ tal que $f(x)=x^3-x$ y $f:\mathbb{R} \to \mathbb{R}$ tal que $f(x)=x^2$.

Antes de ver la solución, reflexionemos lo siguiente:
Los puntos de intersección se obtienen resolviendo la ecuación $x^3-x=x^2$, es decir:
$x^3-x^2-x=0 \iff x(x^2-x-1)=0 \iff x=0$ o $x=\dfrac{1-\sqrt{5}}{2}$ o $x=\dfrac{1+\sqrt{5}}{2}$.
Por tanto, los intervalos a considerar son $\left[ \dfrac{1-\sqrt{5}}{2},0 \right]$ y $\left[ \dfrac{1+\sqrt{5}}{2},0 \right]$ y para saber en cuál de ellos $f$ es mayor o igual que $g$, o $g$ mayor o igual que $f$, basta calcular un valor de $f-g$, en el interior de cada uno de ellos, puesto que $f-g$, no cambia de signo en cada uno de dichos intervalos.
Así, puedes comprobar que: $(f-g)\left( -\dfrac{1}{2} \right) = \dfrac{1}{8} \gt 0$ y $(f-g)(1) = -1 \lt 0$. Por tanto en el primer intervalo $f$ es mayor o igual que $g$ y en el segundo, $g$ es mayor o igual que $f$.
En este apartado descubrirás una relación operativa muy importante entre la derivada y la integral. Los conceptos que importa tengas muy claros, son: la integral como una función, el primer teorema fundamental del cálculo y la regla de la cadena. En Conceptos previos de esta misma sección encontrarás varios de ellos.
Hallar la derivada de la siguiente función $\displaystyle \int_a^{x^3} sen^3 t dt$.
Sea $\displaystyle H(x) = \int_a^{x^3} sen^3 t dt$
$H(x)$ es la composición de dos funciones, a saber, de la función $\displaystyle F(x) = \int_a^x sen^3 t dt$ con la función $c(x)=x^3$. Pues,
$$(F \circ g)(x) = F(g(x)) = \int_a^{g(x)} sen^3 t dt = \int_a^{x^3} sen^3 t dt = H(x)$$Puesto que $f(t)=sen^3 t$ es una función continua en todo $\mathbb{R}$, por el Primer Teorema Fundamental del Cálculo, la función $\displaystyle F(x) = \int_a^x sen^3 tdt$ es derivable y $F'(x)=f(x)$.
Por otro lado, la función $c(x)=x^3$ es también derivable para todo número $x$.
Entonces, por la Regla de la Cadena, tenemos
$H'(x) = F'(g(x))g'(x) = f(g(x))g'(x) = f(x^3)3x^2 = sen^3(x^3)3x^2 = 3x^2sen^3(x^3)$
Por tanto, $\displaystyle \left( \int_a^{x^3} sen^3 t dt \right)' = 3x^2sen^3(x^3)$.
Hallar la derivada de la siguiente función $\displaystyle \int_3^{\int_1^x sen^3 t dt} sen^3 t dt$
Sea $\displaystyle H(x) = \int_3^{\int_1^x sen^3 t dt} sen^3 t dt$.
La función $H(x)$ es la composición de dos funciones, a saber, la función $\displaystyle F(x) \int_3^x sen^3 t dt$ con la función $\displaystyle c(x) = \int_1^x sen^3 t dt$, como se muestra a continuación:
$$(F \circ c)(x) = F(c(x)) = F \left( \int_1^x sen^3 t dt \right) = \int_3^{\int_1^x sen^3 t dt} sen^3 t dt = H(x)$$Por otro lado, la función $f(t)=sen^3 t$ es continua en todo $\mathbb{R}$, entonces por el Teorema Fundamental del Cálculo, tanto la función $F(x)$ como la función $c(x)$ son derivables, y $F'(x) = sen^3(x) = c'(x)$.
Entonces por la Regla de la Cadena, tenemos:
$\displaystyle (F \circ c)'(x) = F'(c(x))c'(x) = F' \left( \int_1^x sen^3 t dt \right) sen^3 x = sen^3 \left( \int_1^x sen^3 t dt \right) sen^3 x = H'(x)$
Por tanto, $\displaystyle H'(x) = sen^3 \left( \int_1^x sen^3 t dt \right) sen^3 x$.
Hallar la derivada de la siguiente función $\displaystyle \int_{15}^x \left( \int_8^y \frac{1}{1+t^2+sen^2 t} dt \right) dy$.
Sea $\displaystyle H(x) = \int_{15}^x \left( \int_8^y \frac{1}{1+t^2+sen^2 t} dt \right) dy$.
Si denotamos por $\displaystyle \alpha(y) = \int_8^y \frac{1}{1+t^2+sen^2 t} dt$, entonces podemos escribir: $\displaystyle H(x) = \int_{15}^x \alpha(y) dy$.
Analizando la función $\alpha(y)$, vemos que la función del integrando $\displaystyle f(t) = \frac{1}{1+t^2+sen^2 t}$ es una función continua para todo número real. Así, por el Primer Teorema Fundamental del Cálculo, la función $\displaystyle \alpha(y) = \int_8^y \frac{1}{1+t^2+sen^2 t} dt$ es derivable en todo $\mathbb{R}$, y por tanto, $\alpha(y)$ es continua en $\mathbb{R}$.
Entonces, nuevamente por el Primer Teorema Fundamental del Cálculo, la función:
$\displaystyle H(x) = \int_{15}^x \alpha(y) dy$ es derivable y $H'(x)=\alpha(x)$.
Por tanto, $\displaystyle H'(x) = \int_8^x \frac{1}{1+t^2+sen^2 t} dt$.
Hallar la derivada de la siguiente función $\displaystyle \int_x^b \frac{1}{1+t^2+sen^2 t} dt$.
Sea $\displaystyle G(x) = \int_x^b \frac{1}{1+t^2+sen^2 t} dt$.
Puesto que $f(t) = \dfrac{1}{1+t^2+sen^2 t}$ es una función continua para todo número real, entonces por el Primer Teorema Fundamental del Cálculo, se sigue que la función $G(x)$ es derivable y que $G'(x)=-f(x)$.
Por tanto, $G'(x) = \dfrac{1}{1+x^2+sen^2 x}$.
Hallar la derivada de la siguiente función $\displaystyle \int_a^b \frac{x}{1+t^2+sen^2 t} dt$.
Sea $\displaystyle \beta(x) = \int_a^b \frac{x}{1+t^2+sen^2 t} dt$.
Entonces $\displaystyle \beta(x) = \int_a^b \frac{x}{1+t^2+sen^2 t} dt = x \left( \int_a^b \frac{1}{1+t^2+sen^2 t} dt \right) = \left( \int_a^b \frac{1}{1+t^2+sen^2 t} dt \right)x$ y puesto que la función $f(t) = \dfrac{1}{1+t^2+sen^2 t}$ es una función continua en todo $\mathbb{R}$, entonces la integral $\displaystyle \int_a^b \frac{1}{1+t^2+sen^2 t} dt$ es un número real.
Por tanto, la función $\beta(x)$ es una recta con pendiente $\displaystyle \int_a^b \frac{1}{1+t^2+sen^2 t} dt$.
Por tanto, $\displaystyle \beta'(x) = \int_a^b \frac{1}{1+t^2+sen^2 t} dt$.
Hallar la derivada de la siguiente función $\displaystyle sen \left( \int_0^x sen \left( \int_0^y sen^3 t dt \right) dy \right)$.
Sea $\displaystyle \rho(x) = sen \left( \int_0^x sen \left( \int_0^y sen^3 t dt \right) dy \right)$.
Denotemos por $\displaystyle \alpha(y) = \int_0^y sen^3 t dt$, entonces $\displaystyle \rho(x) = sen \left( \int_0^x sen \left( \int_0^y sen^3 t dt \right) dy \right) = sen \left( \int_0^x sen (\alpha (y)) dy \right)$.
Ahora, si denotamos por $\displaystyle F(x) = \int_0^x sen (\alpha (y)) dy$, entonces la igualdad anterior se puede escribir como:
$$\rho(x) = sen \left( \int_0^x sen (\alpha(y))dy \right) = sen(F(x))$$Por tanto, $\rho(x)=sen(F(x))$.
Así que para derivar $\rho(x)$ debemos aplicar la Regla de la Cadena. Antes, haremos algunas precisiones:
Primero, por el Primer Teorema Fundamental del Cálculo, la función $\displaystyle \alpha(y) = \int_0^y sen^3 t dt$ es una derivable, pues $sen^3 t$ es una función continua en todo $\mathbb{R}$, y en consecuencia, al ser derivable $\alpha(y)$ es continua en todo $\mathbb{R}$.
Segundo, nuevamente, por el Primer Teorema Fundamental del Cálculo, la función $\displaystyle F(x) = \int_0^x sen (\alpha (y)) dy$ es derivable, pues la función $sen(\alpha(y))$ es continua en todo $\mathbb{R}$ y $F'(x) = sen (\alpha (x))$.
Por tanto, efectivamente podemos aplicar la Regla de la Cadena y derivar $\rho(x)$.
Por tanto, $\displaystyle \rho'(x) = (sen \circ F)'(x) = sen'(F(x))F'(x) = cos(F(x))F'(x) = cos \left( \int_0^x sen(\alpha(y))dy \right) sen(\alpha(x))$ pero, $\displaystyle \alpha(y) = \int_0^y sen^3 t dt$.
Por tanto, $\displaystyle \rho'(x) = cos \left( \int_0^x sen(\alpha(y))dy \right) sen \left( \int_0^x sen^3 t dt \right)$.
Hallar la derivada de $F^{-1}$, en términos de $F^{-1}$, si $\displaystyle F(x) = \int_1^x \frac{1}{t} dt, \forall x \gt 0$.
Sabemos que si $f$ es una función uno a uno y continua en un intervalo y tal que $f'(f^{-1}(x)) \neq 0$, entonces su función inversa, $f^{-1}$, es derivable en $x$, y
$$(f^{-1})'(x) \frac{1}{f'(f^{-1}(x))} \tag{*}$$Analizando la función $\displaystyle F(x) = \int_1^x \frac{1}{t} dt, \forall x \gt 0$, obtenemos que por el Primer Teorema Fundamental del Cálculo $F(x)$ es derivable puesto que la función $f(t)=\dfrac{1}{t}$ es continua para todo real positivo. Además, $F'(x)=\dfrac{1}{x} \gt 0, \forall x \gt 0$. Y puesto que $F'(x) \gt 0, \forall x \gt 0$ entonces $F(x)$ es creciente en $(0,∞)$. Por tanto, la función $\displaystyle F(x) = \int_1^x \frac{1}{t} dt$ es uno a uno y continua en $(0,∞)$, y su derivada nunca se anula. Aplicando el resultado (*), tenemos:
$$(F^{-1})'(x) = \frac{1}{F'(F^{-1}(x))} = \frac{1}{\frac{1}{F^{-1}(x)}} = F^{-1}(x)$$Por tanto, $(F^{-1})'(x) = F^{-1}(x)$, donde $\displaystyle F(x) = \int_1^x \frac{1}{t} dt$.
Hallar la derivada de $F^{-1}$, en términos de $F^{-1}$, si $\displaystyle F(x) = \int_1^x \frac{1}{\sqrt{1-t^2}} dt, \forall x \in (-1,1)$.
Sabemos que si $f$ es una función uno a uno y continua en un intervalo y tal que $f'(f^{-1}(x)) \neq 0$, entonces su función inversa, $f^{-1}$, es derivable en $x$, y
$$(f^{-1})'(x) = \dfrac{1}{f'(f^{-1}(x))} \tag{*}$$Analizando $\displaystyle F(x) = \int_1^x \frac{1}{\sqrt{1-t^2}} dt, \forall x \in (-1,1)$, vemos que por el Primer Teorema Fundamental del Cálculo, $F(x)$ es derivable en $(-1,1)$, ya que la función $f(t) = \dfrac{1}{\sqrt{1-t^2}}$ es continua en el intervalo $(-1,1)$. Al ser $F(x)$, derivable en $(-1,1)$, entonces es continua en $(-1,1)$. Además, $F'(x) = \dfrac{1}{\sqrt{1-x^2}}$ es positiva en $(-1,1)$. Por tanto, la función $\displaystyle F(x) = \int_1^x \frac{1}{\sqrt{1-t^2}} dt$ es creciente en $(-1,1)$, y en consecuencia es uno a uno en $(-1,1)$.
Por tanto, $\displaystyle F(x) = \int_1^x \frac{1}{\sqrt{1-t^2}} dt$ es uno a uno y continua en $(-1,1)$,y su derivada nunca se anula.
Aplicando el resultado (*) tenemos:
$$(F^{-1})'(x) = \frac{1}{F'(F^{-1}(x))} = \frac{1}{\frac{1}{\sqrt{1-(F^{-1}(x))^2}}} = \sqrt{1-(F^{-1}(x))^2}$$Por tanto, $(F^{-1})'(x) = \sqrt{1-(F^{-1}(x))^2}$, donde $\displaystyle F(x) = \int_1^x \frac{1}{\sqrt{1-t^2}} dt, \forall x \in (-1,1)$.
Sea $\alpha : \mathbb{R} \to \mathbb{R}$ la función definida por $\displaystyle \alpha(x)=\int_0^x \frac{1}{1+t^2}dt$.
Realizar lo siguiente:
Puesto que $f(t)=\dfrac{1}{1+t^2}$ es continua $\forall x \in \mathbb{R}$, por el Primer Teorema Fundamental del Cálculo, se sigue que $\alpha(x)$ es derivable y $\alpha '(x)=\dfrac{1}{1+x^2}, \forall x \in \mathbb{R}$
Por otro lado, $\alpha ''(x)=\dfrac{2x}{(1+x^2)^2}, \forall x \in \mathbb{R}$.
Por el inciso anterior, $\alpha '(x)=\dfrac{1}{1+x^2}, \forall x \in \mathbb{R}$.
Por tanto $\alpha '(x) \gt 0, \forall x \in (-\infty, \infty)$. Por tanto, $\alpha(x)$ es creciente en $(-\infty, \infty)$.
Q.E.D.
$\displaystyle \alpha(-x) = \int_0^{-x} \frac{1}{1+t^2}dt = \int_0^{-x} f(t)dt$, donde $f(t)=\dfrac{1}{1+t^2}$
Sabemos que $\displaystyle \int_{ca}^{cb} f(x)dx = c \int_a^b f(cx)dx$, entonces $\displaystyle \alpha(-x) = \int_0^{-x} \frac{1}{1+t^2}dt = \int_{(-1)0}^{(-1)x} f(t)dt = (-1)\int_0^x f(-t)dt = -\int_0^x \frac{1}{1+(-t)^2}dt = -\int_0^x \frac{1}{1+t^2}dt = -\alpha(x)$
Por tanto, $\alpha(-x)=-\alpha(x)$.
Q.E.D.
Puesto que $\dfrac{1}{(1+t)^2} \leq \dfrac{1}{1+t^2}, \forall t$, entonces $\displaystyle \int_0^x \frac{1}{(1+t)^2} dt \leq \int_0^x \frac{1}{1+t^2}dt, \forall x \gt 0$ ... (1)
Por otro lado, $\dfrac{1}{1+t^2} \leq 1, \forall t \in [0,1]$ y $\dfrac{1}{1+t^2} \leq \dfrac{1}{t^2}, \forall t \gt 1$ entonces $\displaystyle \int_0^1 \frac{1}{1+t^2} dt + \int_1^x \frac{1}{1+t^2}dt \leq 1+\int_1^x \frac{1}{t^2}dt$ ... (2)

De (1) y (2), tenemos $\displaystyle \int_0^x \frac{1}{(1+t)^2} dt \leq \int_0^x \frac{1}{1+t^2}dt \leq 1 + \int_1^x \frac{1}{t^2}, \forall x \gt 1$.
Q.E.D.
Por la desigualdad (2) del inciso (d), tenemos $\displaystyle \int_0^x \frac{1}{1+t^2}dt \leq 1+\int_1^x \frac{1}{t^2}dt = 1 + [(-x^{-1})-(-1^{-1})] = 1-x^{-1}+1 = 2 - \frac{1}{x} \leq 2, \forall x \gt 1$.
Por transitividad, se sigue $\displaystyle \int_0^x \frac{1}{1+t^2}dt \leq 2, \forall x \gt 1$.
Q.E.D.
En este apartado encontrarás de funciones que no están definidas en un intervalo cerrado o bien que no están acotadas, a las que llamaremos integrales impropias en contraste con los requisitos establecidos cuando construimos el concepto de integrabilidad. ¿Recuerdas? Pedimos que $f$ fuese acotada sobre un intervalo cerrado $[a,b]$.
Este apartado, lo desarrollaremos fundamentalmente con base en ejemplos, pero es necesario antes saber cómo vamos a entender este tipo de integrales y por ello, primero una definición.
En caso de que el límite en cada caso exista, se dice que la integral converge y en caso contrario se dice que diverge.
Para los siguientes ejemplos se requieren previamente otros resultados. En el ejemplo 4, asumiremos que $arctan'(x)=\dfrac{1}{1+x^2}$ que se formaliza en una sección más adelante, pero que suponiendo algunas identidades trigonométricas es fácil demostrar.
En los ejemplos 5 y 6 se require la igualdad $\displaystyle \int_1^a \frac{1}{t}dt + \int_1^b \frac{1}{t}dt = \int_1^{ab} \frac{1}{t}dt$ demostrada en el apartado Ejercicios selectos, de la sección de Integrales y además la siguiente definición.
Si $\exist \delta \gt 0$, tal que $f$ no está acotada en $(0,\delta)$, entonces definimos $\displaystyle \int_0^{a \gt 0} f = \lim \limits_{\delta \to 0} \int_{\delta}^a f$.
Y para los siguientes ejemplos 7 y 8, aplicaremos la definición anterior.
Enseguida te presentamos algunos criterios que son muy útiles para determinar si una integral impropia es o no convergente. Estos criterios, dependen de un teorema relacionado con sucesiones y su demostración la veremos en la Sección correspondiente de Sucesiones y Series, sin embargo, consideramos de gran interés presentar su utilidad en este momento.
Supongamos que $f$ es no negativa y sean $\displaystyle y_n = \int_a^n f(x)dx$ para $a \leq n \in \mathbb{N}$ entonces: $\displaystyle \int_a^{\infty} f$ es convergente $\iff \{ y_n \}$ está acotada superiormente.
Este teorema, desencadena otros resultados, a saber:
Supongamos que $f$ es no negativa, entonces $\displaystyle \int_a^{\infty} f$ es convergente $\iff \exist M \gt 0$ tal que $\displaystyle \int_a^b f \leq M \; \forall b \gt a$.
Supongamos que $f$ y $g$ son no negativas y que $f(x) \leq g(x) \; \forall x \in [a, \infty)$, entonces:
Si $\displaystyle \int_a^{\infty} |f|$ es convergente, entonces $\displaystyle \int_a^{\infty} f$ es convergente.
En el ejemplo 9, utilizaremos los corolarios 2 y 3 y en el ejemplo 10, el Corolario 2.
En esta sección podrás encontrar la construcción de las funciones trigonométricas seno y coseno, en términos del área del sector circular que subtienden, el eje positivo de las $x$, el rayo terminal que define el ángulo y la circunferencia unitaria.
También podrás encontrar la construcción de las demás funciones trigonométricas y de los teoremas que dan como resultado, las identidades trigonométricas más importantes. Igualmente encontrarás la interpretación geométrica de estas funciones en el círculo unitario y un pequeño compendio de identidades consecuencia de los teoremas anteriores.
Aquí podrás encontrar una vista rápida, en el plano, de conceptos preliminares a la definición de las funciones trigonométricas, como los siguientes: ángulo, ángulo dirigido, ángulo incluyendo el círculo unitario, área del sector circular, entre otros.
La idea en este capítulo es construir las funciones trigonométricas a partir del concepto de área estudiado anteriormente a través de la integral. Interviene otro concepto derivado de la integral, como el de longitud de arco.
$\{l_1,l_2\}$ donde $l_1$ y $l_2$ son semirrectas con el mismo punto inicial. Es un conjunto formado por dos semirrectas con vértice común, sin importar el orden de las semirrectas. Comúnmente se hace referencia a una semirrecta con el nombre de rayo y a su punto inicial como vértice.
Así, un ángulo es un conjunto de dos rayos con vértice común.
Cuándo el orden de las semirrectas o rayos es importante, entonces se trata de un ángulo dirigido.
$(l_1,l_2)$ donde $l_1$ y $l_2$ son semirrectas con el mismo punto inicial. En este caso tendrá sentido hablar del rayo inicial (o primera semirrecta) y el rayo final (segunda semirrecta).
Si incluimos el plano cartesiano unitario y convenimos en que el rayo inicial sea el eje positivo de las $x$, entonces para definir un ángulo dirigido, basta definir el rayo final, puesto que el vértice está definido por el origen de coordenadas.
En este caso, para definir un ángulo dirigido, bastaría dar un punto sobre la circunferencia, puesto que éste, junto con el origen de coordenadas, definirían el rayo o semirrecta final.
Al sector del círculo limitado por el eje positivo de las $x$, el rayo final y la circunferencia, se le llama sector circular, lo denotaremos por $S$ y es de interés calcular su área $A(S)$, en términos de la longitud del arco $x$ entre los dos rayos.
Para ello, tendremos en cuenta que la longitud total de la circunferencia de radio $1$, es $2\pi$ y su área es $\pi$. Por ahora, nos restringiremos a la semicircunferencia superior. Así, tenemos la relación: Área del sector circular, es al área del círculo, como la longitud de arco, es a la longitud total de la circunferencia.
Es decir:
$$\frac{A(S)}{\pi} = \frac{x}{2\pi} \implies A(S) = \frac{x}{2}$$Donde $x$ es la medida del ángulo en radianes (longitud del arco) y $\theta$ su medida en grados.
Ahora podremos calcular el área del sector circular, pero con respecto a la abscisa del punto que define el rayo terminal del ángulo.
Para calcular el área del sector circular, trataremos dos casos: a) $0 \leq t \leq 1$ y b) $-1 \leq t \leq 0$.
Caso a) $0 \leq t \leq 1$. El área del sector circular se obtiene de sumar el área del triángulo, más el área de la región en verde, representada por la integral de $f(t) = \sqrt{1-t^2}$ de $t$ a $1$, es:
$\displaystyle A(S) = \frac{t\sqrt{1-t^2}}{2} + \int_t^1 \sqrt{1-u^2} du$ ... (2)
Caso b) $-1 \leq t \leq 0$. El área del sector circular se obtiene restando el área del triángulo del área de la región en verde, representada por la integral de $f(t)=\sqrt{1-t^2}$ de $t$ a $1$, es:
$\displaystyle A(S) = \frac{t\sqrt{1-t^2}}{2} + \int_t^1 \sqrt{1-u^2} du$ ... (3)
Es importante hacer notar que como en este caso $t$ es negativo o cero, la expresión $\dfrac{t\sqrt{1-t^2}}{2}$ es negativa o cero respectivamente.
Las expresiones (2) y (3) son la misma, en lo que difieren en cada caso, es en el signo de $t$, pero la fórmula para obtener el área del sector circular es la misma y además queda en función de $t$. Por lo tanto.
Si $-1 \leq t \leq 1$, entonces $\displaystyle A(t) = \frac{t\sqrt{1-t^2}}{2} + \int_t^1 \sqrt{1-u^2} du$ es el área del sector circular definido por $t$.
En este apartado encontrarás la definición de la función coseno en términos del área del sector circular y la definición de la función seno. Además encontrarás algunos teoremas, relacionados con sus derivadas.
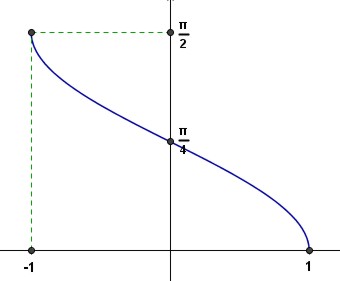
Para iniciar, estableceremos la definición para $0 \leq x \leq \pi$ y luego la extenderemos a todos los reales. En la definición siguiente es importante recordar que la función área es uno a uno y además que el área del sector circular en términos del arco $x$ es $A(S)=\dfrac{x}{2}$.
Si $0 \leq x \leq \pi$, entonces definimos $cos(x)$ como el único número en $[-1,1]$, tal que $A(cos(x))=\dfrac{x}{2}$ y $sen(x)=\sqrt{1-cos^2(x)}$.
Antes, enunciaremos un lema (sin demostración) sobre la derivada de la inversa de una función, que de aquí en adelante será sumamente utilizado.
Si $h$ es una función continua, uno a uno, definida sobre un intervalo y suponiendo que $h$ es derivable en $h^{-1}(x)$, con $h'(h^{-1}(x)) \neq 0$, entonces $h^{-1}$ es derivable en $x$ y ademas:
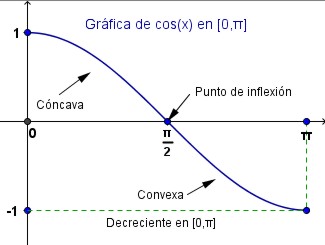
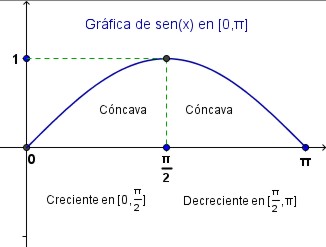
$$(h^{-1})'(x) = \frac{1}{h'(h^{-1}(x))}$$Si $0 \lt x \lt \pi$, entonces $cos'(x)=-sen(x)$ y $sen'(x)=cos(x)$
Utilizando lo ya visto, haremos un análisis de la función coseno, para hacer ver que su gráfica en $0 \leq x \leq \pi$ es la siguiente:
Similarmente, haremos un análisis de la función seno, para ver que su gráfica en $0 \leq x \leq \pi$ es la siguiente:
Falta extender la definición a todos los reales. Para ello establecemos la siguiente definición.
Si $\pi \lt x \lt 2\pi$, entonces $cos'(x)=-sen(x)$ y $sen'(x)=cos(x)$.
Para el caso de la definición anterior, las funciones seno y coseno toman los mismos valores, así que el teorema 1 queda obvio.
En este apartado encontrarás las funciones circulares que nos hacen falta y que se obtienen de las principales seno y coseno. Se definen mediante cocientes, como podrás ver y por ello, sus dominios deben evitar ceros en el denominador.
En este caso, hay que evitar los valores donde el coseno valga cero.
En este caso, hay que evitar los valores donde el seno valga cero.
Son identidades trigonométricas que se deducen con cierta facilidad, sumamente útiles para la deducción de otras identidades trigonométricas y muy especialmente para calcular la derivada de las trigonométricas inversas. trigonométricas y para el cálculo de algunas integrales.
a)$sen^2(x)+cos^2(x)=1$ b) $1+tan^2(x)=sec^2(x)$ c) $1+cot^2(x)=csc^2(x)$
Más adelante inclusive las utilizaremos para interpretar geométricamente los valores de cada una de las funciones trigonométricas.
Si $x \neq \dfrac{(2k+1)\pi}{2}$, entonces $tan'(x)=sec^2(x)$ y $sec'(x)=sec(x)tan(x)$. Si $x \neq k\pi$, entonces $cot'(x)=-csc^2(x)$ y $csc'(x)=-csc(x)cot(x)$.
En los métodos de integración, estas derivadas resultan de mucha utilidad, sobre todo en el llamado método por sustitución.
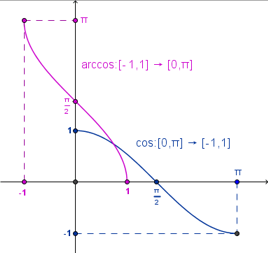
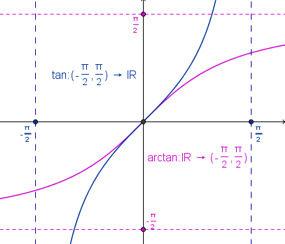
En este apartado veremos las funciones trigonométricas inversas, pero para ello como no son inyectivas, tendremos que restringir sus dominios. En particular, trabajaremos con:
$$sen: \left[ -\frac{\pi}{2}, \frac{\pi}{2} \right] \to [-1,1] \implies arcsen: [-1,1] \to \left[ -\frac{\pi}{2}, \frac{\pi}{2} \right]$$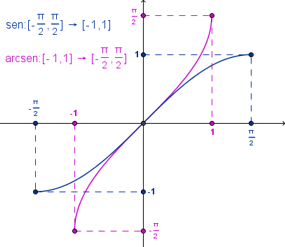
El siguiente teorema tiene que ver con la derivada de las inversas de las funciones trigonométricas y para su demostración, es importante que recuerdes:
Si $-1 \lt x \lt 1$, entonces:
En este apartado veremos otras identidades trigonométricas, además de la ya vistas anteriormente, bajo el rubro de tres identidades trigonométricas. Aquí en particular, nos interesa descubrir las identidades para $sen(x+y)$ y para $cos(x+y)$, ya que de ellas se deducen otras que tienen que ver con ángulos dobles o ángulos mitad.
Para lograr las identidades señaladas, necesitamos algunos resultados previos, entre ellos el siguiente Lema 2 y el Teorema 4.
Sea $f$ una función que tiene segunda derivada en todo $\mathbb{R}$ y que satisface:
Esto significa que sólo la función constante cero, satisface las tres condiciones dadas simultáneamente.
En cambio, si $f(0)$ o $f'(0)$ son distintos de cero, la función $f$ ya no sería idénticamente cero. Veamos el siguiente teorema.
Sea $f$ una función que tiene segunda derivada en todo $\mathbb{R}$ y que satisface:
De acuerdo con este teorema 4, en particular si $f(0)=0$ y $f'(0)=1$, entonces $f(x)=sen(x)$ y, si $f(0)=1$ y $f'(0)=0$, entonces $f(x)=cos(x)$.
Si $x, y \in \mathbb{R}$ entonces:
Utilizando el teorema 5, es posible construir otras identidades trigonométricas, como se podrá ver en el siguiente apartado.
Hasta ahora y a manera de resumen, tenemos las identidades:
De ellas se pueden obtener las siguientes:
Mediante simples despejes, en 6. y 7., se obtienen las siguientes identidades que son de mucha utilidad, en particular para el cálculo de integrales, porque permite bajar el grado de las funciones involucradas.
¿Puedes descubrir el desarrollo, para obtener la siguiente identidad?
Es seguro que encuentres o que puedas descubrir muchas identidades trigonométricas, pero las que hemos visto, son básicas.
En este apartado podrás encontrar la interpretación geométrica de las funciones trigonométricas en la circunferencia de radio $1$ y un interactivo del círculo trigonométrico, desplegando la gráfica de las funciones trigonométricas.
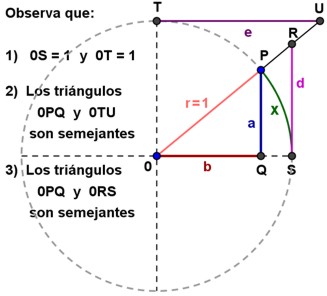
Por la definición de seno y coseno, sabemos que: $a=sen(x)$ y $b=cos(x).$ Haremos ver que $d=tan(x)$ y $e=cot(x)$.
Como los triángulos $OPQ$ y $OTU$ son semejantes, entonces:
$$\frac{PQ}{OQ} = \frac{RS}{OS} \implies \frac{a}{b} = \frac{d}{1} \implies \frac{sen(x)}{cos(x)} = d$$Como los triángulos $OPQ$ y $ORS$ son semejantes, entonces:
$$\frac{OQ}{PQ} = \frac{TU}{OT} \implies \frac{b}{a} = \frac{e}{1} \implies \frac{cos(x)}{sen(x)} = e$$Pero además, por las identidades trigonométricas 2) y 3), que establecen: 2) $1+tan^2(x)=sec^2(x)$, 3) $1+cot^2(x)=csc^2(x)$, podemos ver que $OR$ es la $sec(x)$ y $OU$ es la $csc(x)$.
Observa que las identidades 2) y 3) establecen una relación pitagórica en un triángulo rectángulo, de la forma: $a^2+b^2=c^2$.
Así, queda que:
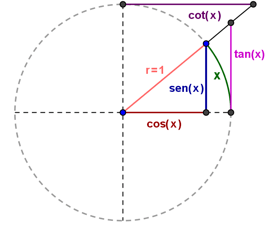
donde la hipotenusa del triángulo con catetos $1$ y tangente, es la secante y la hipotenusa del triángulo con catetos 1 y cotangente es la cosecante.
Desde luego que en cada cuadrante debe haber una adecuación del signo de cada función. Por ejemplo en el segundo cuadrante la tangente es negativa, puesto que seno es positivo y coseno es negativo. También la secante sería negativa.
Con base en las interpretaciones geométricas anteriores y con la adecuación necesaria en cada cuadrante, presentamos el siguiente graficador interactivo de las funciones trigonométricas. Por espacio, sólo presentamos seno, coseno y tangente.
Cada vez que muevas el punto $P$ en el interactivo y desees borrar las trazas, debes dar clic en el ícono de reiniciar que estará en el extremo superior derecho.
Hallar:
Indicación: en cada caso sacar $a$ del signo integral, obteniendo una expresión cuadrática en $a$.
Indicación: $y = arctan x$ significa que $x=tan y=\dfrac{sen y}{cos y} = \dfrac{sen y}{\sqrt{1-sen^2 y}}$
En esta sección encontrarás la construcción de las funciones logaritmo y exponencial, utilizando el concepto de integral, combinado con el uso de la derivada.
Igualmente encontrarás la estrecha relación entre ellas y sus propiedades más importantes. Así también verás la construcción de los logaritmos y exponenciales en diferentes bases.
En este apartado haremos ver la necesidad de trabajar con mayor formalidad los conceptos de logaritmo y exponencial, con la finalidad de poder demostrar propiedades conocidas y poderlas aplicar con la conciencia tranquila.
En los cursos elementales de matemáticas se da por hecho la siguiente ley de los exponentes,
Si $a \gt 0$, entonces $a^n a^m = a^{n + m}$
cuando mucho se ilustra de la siguiente manera para el caso de exponentes naturales:
$a^n a^m = \underbrace{a · a · ... · a}_{n \text{ veces}} = \underbrace{a · a · ... · a}_{m \text{ veces}} = \underbrace{a · a · ... · a}_{n+m \text{ veces}} = a^{n + m}$
De donde, si se quiere mantener la ley de los exponentes para el caso $n=0$, se obtiene que: $a^0 a^m = a^{0+m} = a^m$. Lo cual obliga a definir: $a^0=1.$
Igualmente, si se desea mantener la ley de los exponentes, para el caso de los enteros negativos, se tendría que: $a^{-n}a^n = a^{-n+n} = a^0 = 1$, lo cual obliga a definir: $a^{-n} = \dfrac{1}{a^n}$.
Con esta misma idea, mantener la ley de exponentes para potencias racionales, implicaría que: $\underbrace{a^{\frac{1}{n}} · a^{\frac{1}{n}} · ... · a^{\frac{1}{n}} }_{n \text{ veces}} = a^{n\frac{1}{n}} = a^1 = a$, lo cual obliga a definir: $a^{\frac{1}{n}} = \sqrt[n]{a}$. Y entonces, basta definir $a^{\frac{m}{n}} = \sqrt[n]{a^m}$.
Hasta ahí se llega generalmente, pero ¿Qué pasaría si tuviésemos un exponente irracional? Por ejemplo, cómo interpretar $3^{\sqrt{2}}$?. En todos los casos anteriores se podía contar "tantas veces". Aun más, ¿Cómo hacer ver la ley de exponentes para estos casos?
De manera similar en los cursos de matemáticas elementales, frecuentemente encontramos una presentación del concepto de logaritmo, de la siguiente manera:
El logaritmo de un número $b$, en una base $a$ positiva dada, es el exponente $x$, al cual se debe elevar $a$, para obtener $b$.
Es decir:
Si $a^x = b$, entonces $x$ es el logaritmo en base $a$, de $b$ y se denota como $x=\log_a b$.
Es decir, $x = \log_a b$, si $a^x = b$. Sin embargo, bastaría preguntar por $\log_{10} \pi = ?$ O bien, ¿Cuánto vale $x$, tal que $10^x = \pi$?
En este apartado buscaremos construir la función exponencial, definida en todos los reales. Lo hacemos pensando fundamentalmente en que ésta cumpla la ley de los exponentes:
$$a^{x+y} = a^x a^y$$desde luego para $a \gt 0$. Además, con la experiencia de la definición hasta los racionales vimos que:
$a^{\log_a x} = x$ y $\log_a a^x = x$
es decir, logaritmo y exponencial son inversa una de la otra.
Buscamos una función $f$ derivable, que no sea idénticamente cero, que satisfaga la ley de los exponentes y que tenga inversa, es decir:
Buscamos una función $f$ derivable tal que:
La propiedad (i) garantiza que $f$ cumpla la ley de los exponentes y la (ii) garantiza que no sea idénticamente cero. La buscamos derivable para poder recurrir a su derivada y obtener información de ella. Recordemos que la derivada de una función nos aporta conocimiento sobre la propia función.
Con las propiedades anteriores, tenemos que:
$f'(x) = \lim \limits_{h \to 0} \dfrac{f(x+h) - f(x)}{h} \overset{i)}{=} \lim \limits_{h \to 0} \dfrac{f(x)f(h) - f(x)}{h} = f(x) \lim \limits_{h \to 0} \dfrac{f(h)-1}{h}$ ... (1)
Pero por otra parte:
$f(x+0) = f(x)f(0) \implies f(x) = f(x)f(0) \implies f(0) = 1$ ... (2)
Luego entonces sustituyendo (2) en (1), queda que:
$f'(0) = \lim \limits_{h \to 0} \dfrac{f(h)-1}{h}$ ... (3)
Suponiendo que el límite en (3) existe, le llamaremos $k$ y sustituyendo en (1), nos quedaría finalmente que:
$f'(x) = k f(x)$ ... (4)
Aunque pudiésemos calcular el valor de $k$ en (4), de cualquier manera llegamos a una expresión donde la derivada de $f$, depende de $f$ y ésta última es la que queremos encontrar. Necesitamos explorar otro camino y para ello, aplicaremos (iii), es decir recurriendo al hecho de que f tiene inversa.
Antes de empezar la nueva exploración, sera importante que recuerdes la expresión para la derivada de la inversa, si no la recuerdas puedes dar clic en
Para ser consistente con lo desarrollado hasta los racionales, llamaremos $f^{-1}(x) = \log_a(x)$, así tendríamos que:
$$(f^{-1})'(x) = \log'_a(x) = \frac{1}{f'(f^{-1}(x))} = \frac{1}{k f(f^{-1}(x))} = \frac{1}{k x}$$De aquí, por el corolario del primer teorema fundamental, tenemos que:
$\displaystyle \frac{1}{k} \int_1^x \frac{1}{t} dt = \log_a(x) - \log_a(1)$
pero como: $\log_a(1)=0$, puesto que $a^0=1$,
entonces nos queda que: $\displaystyle \log_a(x) = \frac{1}{k} \int_1^x \frac{1}{t} dt$ ... (5)
En la expresión (5) seguimos con el problema del valor de $k$. Una manera de salvar el problema, es declarar $k=1$ y definir:
$\displaystyle \log(x) = \int_1^x \frac{1}{t} dt$
confiando en que se trata del logaritmo de $x$ en alguna base que no conocemos por ahora.
En este apartado encontrarás la definición de la función logaritmo y la demostración de sus propiedades más importantes. Con lo anterior allanaremos el camino para definir la función exponencial y para la demostración igualmente de sus propiedades más importantes.
Si $x \gt 0$, entonces definimos $\displaystyle \log(x) = \int_1^x \frac{1}{t} dt$
Puedes mover $x$ y observar que:
Estas propiedades corresponden a las propiedades de la integral que hemos visto con anticipación. Por ejemplo (a), corresponde a la propiedad $\displaystyle \int_1^x f(t)dt = - \int_x^1 f(t)dt$.
Por otra parte $\log(x)$ no es posible definirlo para $x \leq 0$, puesto que $f(t)=\dfrac{1}{t}$ no está acotada en el intervalo $[x,1]$.
Ahora estamos en posibilidad de demostrar una de las propiedades más importantes de la función logaritmo, a saber:
Si $x, y \gt 0$, entonces $\log(xy) = \log(x)+\log(y)$.
A partir de este teorema tenemos dos resultados particulares de interés.
Si $n \in \mathbb{N}$ y $x \gt 0$, entonces $\log(x^n) = n\log(x)$.
Si $x, y \gt 0$, entonces $\log \left( \dfrac{x}{y} \right) = \log(x) - \log(y)$
En este apartado encontrarás la definición de la función exponencial y la demostración de sus propiedades más importantes. Aprovecharemos la idea de que, al menos hasta los racionales, logaritmo y exponencial son inversas una de la otra. Tomamos esta idea y definimos la función exponencial, que denotaremos por $\exp$, de la siguiente manera:
$\exp : \mathbb{R} \to (0,\infty)$ tal que $\exp(x)=\log^{-1}(x)$
Para analizar su gráfica, veamos el siguiente teorema sobre su derivada. Para su demostración sera importante que recuerdes la la derivada del logaritmo y la expresión para la derivada de la inversa, si no la recuerdas puedes dar clic
$\exp'(x) = \exp(x) \; \forall x \in \mathbb{R}$.
Es decir, la derivada de la exponencial en cada punto, es igual a su propio valor en tal punto. Se sabe que a excepción de la función constante cero, la exponencial es la única con la propiedad establecida en el Teorema 2.
Para $x \lt 0$, es inmediato ya que $\exp(x) \gt 0 \; \forall x \in \mathbb{R}$.
Para $x \gt 0$, sabemos que $\log(x) \lt x-1 \implies \log(x) \lt x \implies \exp(\log(x)) \lt \exp(x) \implies x \lt \exp(x)$.
Basados en la propiedad del logaritmo, establecida en el Teorema 1 y del hecho que las funciones $\log$ y $\exp$ son inversas entre sí, demostraremos una de las propiedades más importantes de la función exponencial, a saber:
$\exp(x+y) = \exp(x) \exp(y) \; \forall x, y \in \mathbb{R}$
Esta función $\exp$, ya cumple los requisitos de la función cuya búsqueda emprendimos en el apartado 2 de este tema ¿Recuerdas?:
Buscamos una función $f$ derivable tal que:
El teorema 3, demuestra que satisface el inciso (i). Respecto a (ii), sabemos que $\exp(1) \neq 0$ puesto que $\exp(x) \gt 0 \; \forall x \in \mathbb{R}$ y por último cumple (iii), es decir, tiene inversa.
El número $\exp(1)$ será motivo de análisis en el siguiente apartado. Por ahora buscaremos graficar la función exponencial, relacionada con la gráfica de su inversa, $\log$.
En este apartado encontrarás la relación entre el número $\exp(1)$ y la función exponencial. Igualmente encontrarás las primeras aproximaciones para dicho número y la gráfica de la función exponencial, relacionada con la de su inversa, $\log(x)$.
El número $\exp(1)$, adquiere ahora mayor interés y habrá que precisar su valor. Sabemos que es un real, pero ¿será racional o irracional? Por lo pronto, le asignaremos un nombre más corto.
$e = \exp(1)$
Es decir el número $e$, es aquel para el cual $\log(e)=1$. En otras palabras:
Si mueves el punto rojo $x$, cuando la integral vale $1$, entonces $x=e$ (desde luego que en el interactivo nos dará un valor aproximado), i.e. $\displaystyle 1=\log(e) = \int_1^e \frac{1}{t} dt$.
Queda la duda sobre el valor del número $e$. Para empezar haremos ver que: $2 \lt e \lt 4$, lo cual no es muy halagüeño, pero con las herramientas teóricas que tenemos hasta ahora, es lo que podemos lograr. Veamos:
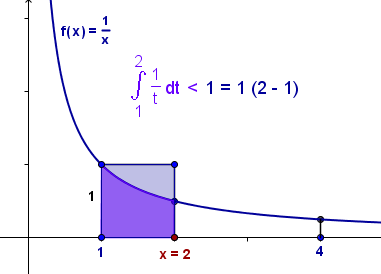
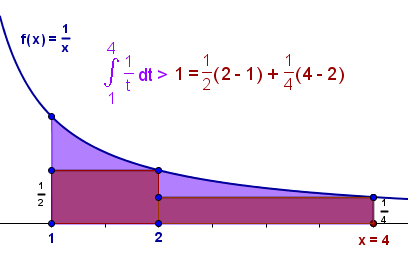
Es decir:
$$\int_1^2 \frac{1}{t} dt \lt \int_1^e \frac{1}{t} dt \lt \int_1^4 \frac{1}{t} dt \implies 2 \lt e \lt 4$$Consecuentes con el trabajo de las propiedades de los exponentes para números racionales, definiremos, la exponencial en términos del número $e=|exp(1)$, de la siguiente manera:
$\exp(x) = e^x \; \forall x \in \mathbb{R}$
En este apartado encontrarás la definición de funciones exponenciales pero con base $a \gt 0$, distinta al número $e$ y sus propiedades más importantes, referidas como propiedades de los exponentes. Tomamos $a \gt 0$ para asegurar la existencia de $\log(a)$ y para evitar problemas con algunos exponentes racionales (raíces pares de números negativos).
Sea $a \gt 0$. Entonces definimos $a^x = e^{x \log(a)} \; \forall x \in \mathbb{R}$.
Cuando $a=e$, queda la definición de la exponencial, tal como la vimos en la sección anterior, puesto que $\log(e)=1$.
Ahora veamos las leyes de los exponentes, que de paso puedes observar que coinciden con las ya conocidas en los racionales.
Si $a \gt 0$, entonces:
Ahora resulta interesante analizar esta función para distintos valores de $a \gt 0$.
Para $a=1$, $f(x)=a$ (constante). Resulta evidente.
Para $a \gt 1, f(x) = a^x$ es creciente.
Para $a \lt 1, f(x) = a^x$ es decreciente.
Así tenemos que $f(x)=a^x$ para $0 \lt a \neq 1$ es inyectiva y por lo tanto tiene inversa.
A dicha inversa le llamaremos: $f^{-1}(x) = log_a(x)$ para $0 \lt a \neq 1$ y $x \gt 0$, es decir se trata del logaritmo en base $a$, de $x$.
Es muy importante ahora, establecer la relación entre el logaritmo en base $a$, con respecto al logaritmo en base $e$. Demostraremos que: $\log_a(x) = \dfrac{\log(x)}{\log(a)}$.
Observa los cambios para $0 \lt a \lt 1$ y para $a \gt 1$.
Observa los cambios para $0 \lt a \lt 1$ y para $a \gt 1$.
$f(x)=a^x \implies f(x)=e^{x \log(a)} \implies f'(x) = \log(a) e^{x \log(a)} = \log(a) a^x$
$g(x) = \log_a(x) \implies g(x) = \dfrac{\log(x)}{\log(a)} \implies g'(x) = \dfrac{1}{x \log(a)}$
$f(x) = g(x)^{h(x)} \implies f'(x) = g(x)^{h(x)} \left[ h'(x) \log(g(x)) + h(x) \dfrac{g'(x)}{g(x)} \right]$
$f(x) = x^a \implies f'(x) = x^a \left( \dfrac{a}{x} \right) = a x^{a-1}$
En este caso basta aplicar el caso general, considerando:
$h(x) = a \implies h'(x) = 0$
$g(x) = x \implies g'(x) = 1$
En este apartado encontrarás otros resultados sobre la función exponencial, entre ellos su relación con cualquier función polinomial.
De antemano, como lo vimos en el teorema 2, sabemos que: Si $f(x)=e^x,$ entonces $f'(x)=f(x)$. Queremos saber si el recíproco del teorema 2 es cierto. Veamos entonces el siguiente teorema.
Si $f$ es derivable y $f'(x)=f(x) \; \forall x$, entonces $\exist c \in \mathbb{R}$, tal que $f(x)=ce^x \; \forall x$.
Además de las propiedades demostradas en los teoremas 2 y 3, la función exponencial tiene otra sumamente importante: "La función exponencial exponencial crece más rápidamente que cualquier polinomio". Este resultado lo demostraremos en el Teorema 6, pero antes veamos otro resultado que necesitaremos:
$\lim \limits_{x \to \infty} e^x = \infty$
Para cualquier número natural $n$, se tiene que : $\lim \limits_{x \to \infty} \dfrac{e^x}{x^n} = \infty$.
A partir de este resultado se facilita analizar un cierto tipo de funciones, tales que sus derivadas de cualquier orden, en un punto, permanecen igual a cero, como por ejemplo:
y
$$f'(0^-) = \lim \limits_{h \to 0^-} \frac{f(0+h)-f(0)}{h} = \lim \limits_{h \to 0^-} \dfrac{e^{\left( -\frac{1}{h^2} \right)}}{h} = \lim \limits_{h \to 0^-} \frac{\frac{1}{h}}{e^{\left( \frac{1}{h} \right)^2}} = \lim \limits_{x \to \infty} \frac{x}{e^{(x^2)}}$$$\lim \limits_{x \to 0^+} f'(x) = \lim \limits_{x \to 0^+} \dfrac{2 e^{\left( -\frac{1}{x^2} \right)}}{x^3} = 2 \lim \limits_{x \to 0^+} \dfrac{\left( \frac{1}{x} \right)^3}{e^{\left( \frac{1}{x} \right)^2}} = 2 \lim \limits_{h \to \infty} \dfrac{h^3}{e^{h^2}} = 0 = f'(0)$ donde $h=\dfrac{1}{x}$
$\lim \limits_{x \to 0^-} f'(x) = \lim \limits_{x \to 0^-} \dfrac{2 e^{\left( -\frac{1}{x^2} \right)}}{x^3} = 2 \lim \limits_{x \to 0^-} \dfrac{\left( \frac{1}{x} \right)^3}{e^{\left( \frac{1}{x} \right)^2}} = -2 \lim \limits_{k \to \infty} \dfrac{k^3}{e^{k^2}} = 0 = f'(0)$ donde $k=\dfrac{1}{x}$
Una situación similar ocurre con la función:
$f(x) = \begin{cases} e^{\left( -\frac{1}{x^2} \right)} sen \left( \dfrac{1}{x} \right) \; &\forall x \neq 0 \\ 0 &\text{si } x=0 \end{cases}$
Es decir, se trata de una función extremadamente plana alrededor del origen y tal que $f^{(k)}(0)=0 \; \forall k$. Observa su gráfica y las de la primera y segunda derivadas.
Existen muchas analogías entre estas funciones y las correspondientes funciones trigonométricas ordinarias.
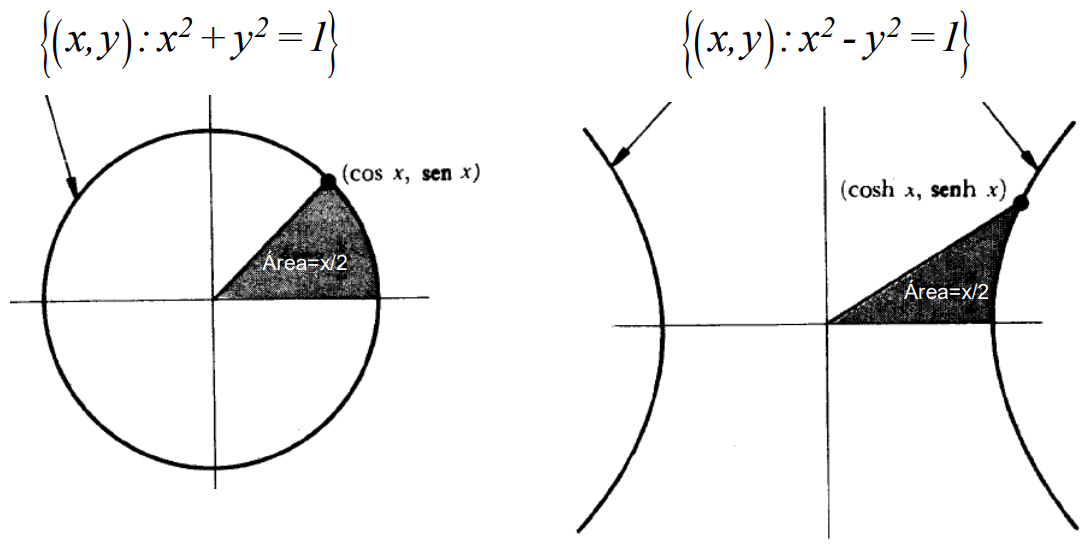
Demostrar que:
Demostrar, utilizando la información del ejercicio anterior, que:
Comparar la solución de la tercera integral con la que se obtiene escribiendo:
$$\frac{1}{1-x^2}=\frac{1}{2} \left[ \frac{1}{1-x}+\frac{1}{1+x} \right]$$$f(x) \gt \dfrac{e^n}{n^n}$ para $x \gt n$.
En esta sección encontrarás los teoremas que te permitirán construir los métodos para calcular integrales de funciones, en términos de funciones elementales.
Encontrarás los métodos de integración más conocidos, por partes, por sustitución y por fracciones parciales, enriquecidos con muchos ejemplos. Así también podrás ver la construcción de fórmulas de reducción para integrales complicadas.
Para poder abordar esta sección es muy importante que recuerdes algunos resultados tanto de derivación, como de Integrales. Los enunciaremos a continuación sin demostración, en el entendido que si las requieres las podrás consultar en Cálculo Interactivo I o en los primeros apartados de estos materiales de Cálculo Interactivo II. El interés para este apartado, son en sí los resultados y no tanto sus demostraciones.
Derivada de una suma: Si $f$ y $g$ son derivables en $a$, entonces $f+g$ es derivable en $a$ y $(f+g)'(a) = f'(a)+g'(a)$.
Derivada de un producto: Si $f$ y $g$ son derivables en $a$, entonces $fg$ es derivable en $a$ y $(fg)'(a) = f'(a)g(a) + f(a)g'(a)$.
Caso particular del producto: Si $g(x)=cf(x)$ y $f$ es derivable en $a$, entonces $g$ es derivable en $a$ y $(g)'(a) = cf'(a)$.
Derivada de un cociente: Si $f$ y $g$ son derivables en $a$ y $g(a) \neq 0$, entonces $f/g$ es derivable en $a$ y $(f/g)'(a) = \dfrac{f'(a)g(a) - f(a)g'(a)}{[g(a)]^2}$.
Derivada de una composición: Si $g$ es derivables en $a$, y $f$ es derivable en $g(a)$, entonces $f \circ g$ es derivable en $a$ y $(f \circ g)'(a) = f'(g(a))g'(a)$.
Función constante: $f(x)=c$ (constante) $\implies f'(x)=0 \; \forall x \in \mathbb{R}$.
Función idéntica: $f(x)=x \implies f'(x)=1 \; \forall x \in \mathbb{R}$.
Potencia natural: $f(x)=x^n \; (n \in \mathbb{N}) \implies f'(x) = nx^{n-1} \; \forall x \in \mathbb{R}$.
Funciones trigonométricas: $sen'(x)=cos(x)$ y $cos'(x)=-sen(x) \; \forall x \in \mathbb{R}$.
Funciones logarítmica y exponencial: $\log'(x)=\dfrac{1}{x} \; \forall x \gt 0$ y $(e^x)'=e^x \; \forall x \in \mathbb{R}$.
De acuerdo con el segundo Teorema Fundamental del Cálculo, toda derivada nos proporciona una fórmula para calcular una integral. Por ejemplo:
$\displaystyle F(x)=sen(x) \implies F'(x)=cos(x) \implies \int_a^b cos(x)dx = sen(b)-sen(a)$
$\displaystyle F(x)=\frac{x^n}{n} \implies F'(x)=\frac{nx^{n-1}}{n} = x^{n-1} \implies \int_a^b x^{n-1}dx = \frac{b^n}{n} - \frac{a^n}{n}$
$\displaystyle F(x)=e^x \implies F'(x)=e^x \implies \int_a^b e^x dx=e^b - e^a$
Así que, si deseamos calcular la integral $\displaystyle \int_a^b f$, nuestra primera reacción será localizar una función $F$ tal que $F'=f$ y entonces el valor de dicha integral sería simplemente $F(b)-F(a)$. No siempre será fácil encontrar tal función $F$, pero no estará de más intentar este primer camino.
A una función $F$ que cumpla que $F'=f$ le llamaremos función primitiva de $f$.
Apoyados en el primer Teorema Fundamental del Cálculo, sabemos que si $f$ es continua, siempre tiene una primitiva, a saber: $\displaystyle F(x)=\int_a^x f$.
Sin embargo lo que sería deseable es poder expresar tal función primitiva, en términos de funciones conocidas, sean polinomios, trigonométricas, logarítmicas, sus inversas, etc. o mediante operaciones con ellas, incluida la composición. Es decir nos gustaría poder encontrar primitivas en términos de lo que llamaremos funciones elementales.
Dada la observación anterior, el propósito del tema de Integración que nos ocupa, será desarrollar en lo posible, la teoría necesaria que nos permita establecer métodos para calcular primitivas en términos de funciones elementales.
Habrá funciones que se resistan o que definitivamente sean imposibles. En las primeras la práctica, el conocimiento de los métodos y los artificios algebraicos ayudarán a salir adelante y en las segundas habrá que dar otro tratamiento que será motivo de un trabajo posterior.
Se sabe que por ejemplo, que no existe una función elemental $F$ tal que $F'(x)=e^{-x^2}$, no obstante que $f(x)=e^{-x^2}$ es continua en todos los reales. Hay un teorema que lo demuestra, pero por su complejidad, se encuentra fuera de los propósitos de este apartado.
Para iniciar partiremos de la siguiente tabla de las siguientes integrales básicas, que se pueden comprobar mediante una simple derivación. Por economía en la escritura sólo consideraremos la primitiva básica y no sumada con constantes.
$\displaystyle \int adx=ax$,
$\displaystyle \int x^n dx = \frac{x^{n+1}}{n+1}, n \neq -1$,
$\displaystyle \int \frac{1}{x}dx = log(x)$,
$\displaystyle \int e^x dx = e^x$,
$\displaystyle \int sen(x)dx=-cos(x)$,
$\displaystyle \int cos(x)dx=sen(x)$,
$\displaystyle \int sec^2(x)dx=tan(x)$,
$\displaystyle \int sec(x)tan(x)dx=sec(x)$,
$\displaystyle \int \frac{1}{1+x^2}dx=arctan(x)$, y
$\displaystyle \int \frac{1}{\sqrt{1-x^2}}dx=arcsen(x)$
A partir de tales integrales, de los siguientes teoremas básicos ya vistos y de los métodos que vayamos encontrando, calcularemos otras integrales.
$\displaystyle \int (f(x)+g(x))dx = \int f(x)dx + \int g(x)dx$, y $\displaystyle \int cf(x)dx = c\int f(x)dx$, o $\displaystyle \int_a^b (f(x)+g(x))dx = \int_a^b f(x)dx + \int_a^b g(x)dx$, y $\displaystyle \int_a^b cf(x)dx = c\int_a^b f(x)dx$
Estos teoremas indican que es lo mismo:
En los teoremas básicos, no tenemos, como en la derivada, teoremas para el producto o el cociente de dos funciones. Esto es porque no siempre es posible tener un procedimiento general para integrar productos o cocientes, sin embargo, la teoría siguiente tratará de resolverlo para ciertos casos.
La fórmula para derivar un producto de funciones, proporciona la posibilidad de formular un teorema para integrar cierto tipo de productos de funciones como veremos enseguida.
Si $f'$ y $g'$ son funciones continuas, entonces $\displaystyle \int fg'=fg-\int gf'$
Este teorema también puede formularse incluyendo la variable $x$:
Si $f'(x)$ y $g'(x)$ son funciones continuas $\forall x$, entonces: $\displaystyle \int f(x)g'(x) = f(x)g(x) - \int g(x)f'(x)dx$.
O como una integral definida:
Si $f'(x)$ y $g'(x)$ son funciones continuas $\forall x \in [a,b]$, entonces: $\displaystyle \int_a^b f(x)g'(x) = f(x)g(x) - \int_a^b g(x)f'(x)dx$.
Este teorema 1, nos permite tener un método de integración que llamaremos "método de integración por partes" y que en general lo aplicaremos en productos de funciones polinomiales por trigonométricas, exponenciales por trigonométricas o polinomiales por exponenciales que son los casos típicos a resolver con este método. También veremos algunos casos atípicos en los que se puede aplicar tal método.
En los siguientes ejemplos, elegir $f(x)=x$ tiene la ventaja de que $f'(x)=1$ y esto permitiría simplificar la integral, al aplicar el método de integración por partes.
$\displaystyle \int x sen(x)dx$
$\displaystyle \int x e^x dx$
$\displaystyle \int x cos(x)dx$
En los siguientes ejemplos, la elección de $f$ y $g'$ es indistinta. Lo importante será que la integral en cuestión aparecerá en los dos miembros de la igualdad.
$\displaystyle \int e^x sen(x)dx$
$\displaystyle \int sen(x)cos(x)dx$
$\displaystyle \int e^x cos(x)dx$
En el siguiente ejemplo, aparentemente no hay un producto de funciones. Sin embargo, podemos considerar $f(x)=\log(x)$ y $g'(x)=1$. Veamos:
$\displaystyle \int \log(x)dx$
En los siguientes ejemplos, la elección de $f$ y $g'$ es indistinta, sin embargo en los dos primeros casos, la que utilizaremos facilita el cálculo de la integral.
$\displaystyle \int x \log(x)dx$
$\displaystyle \int \frac{1}{x} \log(x)dx$
$\displaystyle \int (\log(x))^2 dx$
En los siguientes ejemplos, la elección de $f(x)=x^2$, tiene la ventaja de que en la primera aplicación del Teorema 1: $f'(x)=2x$ y entonces la integral del segundo término queda como en los ejemplos del primer bloque arriba.
$\displaystyle \int x^2 e^x dx$
$\displaystyle \int x^2 cos(x) dx$
$\displaystyle \int x^2 sen(x) dx$
Como consecuencia de la regla de la cadena, tenemos la posibilidad de instrumentar un método de integración para ciertos productos de funciones. Presentamos enseguida el teorema que lo justifica.
Si $f$ y $g'$ son funciones continuas, entonces $\displaystyle \int_{g(a)}^{g(b)} f = \int_a^b (f \circ g) · g'$.
Este teorema también puede formularse incluyendo variables:
Si $f$ y $g'$ son funciones continuas, entonces $\displaystyle \int_{g(a)}^{g(b)} f(u)du = \int_a^b f(g(x)) · g'(x) dx$.
Al método de integración que se deriva de la aplicación de este teorema 2, le llamaremos "método de integración por sustitución" y lo aplicaremos con diversos tipos de sustituciones como podremos apreciar en los ejemplos.
En un primer momento realizaremos ejemplos considerando los límites de integración y posteriormente sólo nos preocuparemos del cálculo de las primitivas en términos elementales. Igualmente, por lo extenso, dividiremos este tema en dos apartados.
En los siguientes ejemplos, es más o menos visible la función $g$, que permitiría simplificar la integral.
$\displaystyle \int_a^b sen^7(x) cos(x) dx $
$\displaystyle \int_a^b cot(x)dx$
$\displaystyle \int_a^b tan(x)dx$
$\displaystyle \int_a^b \frac{1}{x \log(x)}dx$
$\displaystyle \int_a^b tanh(x)dx$
$\displaystyle \int_a^b cos(x)e^{sen(x)}dx$
En los siguientes ejemplos, identificaremos la función $g$ que nos ayude a simplificar la integral. Así, sustituyendo $u=g(x)$ tendremos $du=g'(x) dx$. Integramos respecto de $u$ y luego la primitiva la transformamos en términos de $x$, con la misma sustitución $u=g(x)$.
$\displaystyle \int sen^3(x) cos(x) dx$
$\displaystyle \int sen(x) cos^5(x) dx$
$\displaystyle \int sec^2(x) tan^5(x) dx$
$\displaystyle \int cos(x) e^{sen(x)} dx$
$\displaystyle \int sen(x) e^{cos(x)} dx$
$\displaystyle \int \frac{1}{x+2} dx$
$\displaystyle \int e^{3x} dx$
$\displaystyle \int cos(6x) dx$
$\displaystyle \int \frac{e^x}{\sqrt{1-e^{2x}}} dx$
En los siguientes ejemplos, no es fácil identificar la función $g$ que ayude a simplificar la integral. Es decir, no es fácil identificar el cambio de variable.
$\displaystyle \int \frac{1+e^x}{e^x-1} dx$
$\displaystyle \int \frac{e^{2x}}{\sqrt{1+e^x}} dx$
$\displaystyle \int \frac{e^{2x}}{\sqrt{e^{2x}-1}} dx$
En el siguiente apartado, seguiremos con el método de sustitución para el cálculo de integrales, pero utilizando fundamentalmente identidades trigonométricas.
En este apartado seguiremos ejemplificando el método de sustitución, derivado del teorema 2, pero ahora mediante sustituciones con expresiones trigonométricas y para las cuales será necesario tener presentes las identidades trigonométricas siguientes:
Así como algunas que se obtienen a partir de las anteriores:
Además también es importante tener presente el teorema 2:
Si $f$ y $g'$ son funciones continuas, entonces: $\displaystyle \int_{g(a)}^{g(b)} f = \int_a^b (f \circ g)·g'$.
o en esta otra formulación:
Si $f$ y $g'$ son funciones continuas, entonces: $\displaystyle \int_{g(a)}^{g(b)} f(u)du = \int_a^b f(g(x))·g'(x)dx$.
En los ejemplos que presentaremos, seguiremos insistiendo en encontrar las correspondientes sustituciones, sin preocuparnos por los límites de integración.
En los siguientes ejemplos, haremos uso de las identidades trigonométricas mencionadas arriba y nos referiremos en su aplicación al número que las identifica.
$\displaystyle \int \sqrt{1-x^2}dx$
$\displaystyle \int x \sqrt{1+x^2}dx$
$\displaystyle \int \frac{\sqrt{1-x^2}}{x^2}dx$
$\displaystyle \int \frac{1}{(1+x^2)^2}dx$
$\displaystyle \int \frac{1}{x^2 \sqrt{1+x^2}}dx$
En los siguientes ejemplos, ilustraremos la forma de trabajar integrales de potencias de funciones trigonométricas. Las identidades trigonométricas son fundamentales, sobre todo aquellas que reducen las potencias, como las 8) y 9).
$\displaystyle \int sen^4(x)dx$
$\displaystyle \int cos^4(x)dx$
$\displaystyle \int cos^3(x)dx$
$\displaystyle \int sen^3(x)dx$
$\displaystyle \int sen^3(x) cos^2(x)dx$
$\displaystyle \int sen^2(x) cos^3(x)dx$
En los siguientes ejemplos, ilustraremos cómo abordar casos generales de integración de potencias de funciones trigonométricas.
$\displaystyle \int sen^{2m+1}(x)dx$
$\displaystyle \int cos^{2m+1}(x)dx$
$\displaystyle \int cos^{2m}(x)dx$
$\displaystyle \int sen^{2m}(x)dx$
En el caso de integrales del tipo: $\displaystyle \int sen^n(x) cos^m(x)dx$ se siguen procedimientos similares ya sea utilizando la identidad 1) para los casos en que $n$ o $m$ sean impares y las identidades 8) o 9) en caso de que $n$ y $m$ sean pares.
En el siguiente apartado, seguiremos con otro método de integración, propio para integrar cocientes de funciones polinomiales.
En este apartado encontrarás un método para integrar cocientes de funciones polinomiales, también llamadas funciones racionales. La justificación teórica de dicho método se basa en el Teorema Fundamental del Álgebra y en otros resultados que se desarrollan en el estudio de las funciones complejas.
Por lo anterior, sólo exhibiremos los teoremas correspondientes, sin su demostración y lo que sí, desarrollaremos diversos ejemplos que permitan entender este método de integración por fracciones parciales.
Toda función polinómica $q(x)=x^m + b_{m-1}x^{m-1} + ... + b_1x + b_0$, se puede escribir como un producto: $q(x)=(x-\alpha_1)^{r_1} \cdot ... \cdot (x-\alpha_1)^{r_k} \cdot (x^2+\beta_1 x+\gamma_1)^{s_1} \cdot ... \cdot (x^2+\beta_1 x+\gamma_1)^{s_t}$, donde:
Es decir que toda función polinómica se puede escribir como un producto de factores reales y complejos. Los factores reales pueden ser con repetición y los factores complejos son por pares y distintos.
Sean $n \lt m$ y $p(x)=x^m+a_{n-1}x^{n-1}+...+a_1x+a_0$, $q(x)=x^m+b_{m-1}x^{m-1}+...+b_1x+b_0 = (x-\alpha_1)^{r_1} \cdot ... \cdot (x-\alpha_1)^{r_k} \cdot (x^2+\beta_1x+\gamma_1)^{s_1} \cdot ... \cdot (x^2+\beta_1x+\gamma_1)^{s_t}$, entonces $\dfrac{p(x)}{q(x)}$ se puede escribir como:
$\displaystyle \frac{p(x)}{q(x)} = \left[ \frac{a_{11}}{(x-\alpha_1)} + ... + \frac{a_{1r_1}}{(x-\alpha_1)^{r_1}} \right] + ... + \left[ \frac{a_{k1}}{(x-\alpha_k)} + ... + \frac{a_{kr_1}}{(x-\alpha_k)^{r_1}} \right] + \left[ \frac{b_{11}+c_{11}}{(x^2+\beta_1x+\gamma_1)} + ... + \frac{b_{1s_1}+c_{1s_1}}{(x^2+\beta_1x+\gamma_1)^{s_1}} \right] + ... + \left[ \frac{b_{t1}+c_{t1}}{(x^2+\beta_tx+\gamma_t)} + ... + \frac{b_{1s_t}+c_{1s_t}}{(x^2+\beta_tx+\gamma_t)^{s_t}} \right]$
Es decir:
Si $\dfrac{p(x)}{q(x)} = \dfrac{x^3+x+2}{(x-1)^2 (x^2+1)}$, entonces $\dfrac{p(x)}{q(x)} = \dfrac{A}{(x-1)} + \dfrac{B}{(x-1)^2} + \dfrac{Cx+D}{x^2+1}$.
Si $\dfrac{p(x)}{q(x)} = \dfrac{x^2-x+1}{(x-1)^2 (x^2+1)^2}$, entonces $\dfrac{p(x)}{q(x)} = \dfrac{A}{(x-1)} + \dfrac{B}{(x-1)^2} + \dfrac{Cx+D}{x^2+1} + \dfrac{Ex+F}{(x^2+1)^2}$.
Y claro, el problema es calcular las incógnitas $A$, $B$, $C$, $D$ y en su caso $E$ y $F$. Desde luego el teorema 2, asegura que existe solución.
La posibilidad que proporciona el Teorema 2, de descomponer el cociente de polinomios en fracciones, permite calcular la integral de dicho cociente como una suma de integrales de dichas fracciones, las cuales son realmente sencillas de obtener.
En los ejemplos que presentamos, consideraremos por separado los cuatro casos posibles:
En caso que existan combinaciones, que es lo más probable, se aplica lo correspondiente a cada caso.
Igualmente en los ejemplos que presentamos haremos énfasis en el cálculo de las fracciones parciales y dejaremos indicadas las integrales correspondientes.
En los siguientes ejemplos, ilustramos el caso a) en el cual, el denominador tiene raíces reales simples.
$\displaystyle \int \frac{6x^2-x+1}{x^3-x} dx$
$\displaystyle \int \frac{x}{x^2+5x+6} dx$
$\displaystyle \int \frac{x^2+2}{x(x+2)(x-1)} dx$
En los siguientes ejemplos, ilustramos el caso b) en el cual, el denominador tiene raíces reales repetidas.
$\displaystyle \int \frac{x+1}{x^2(x-1)^3} dx$
$\displaystyle \int \frac{x^3-1}{x^2(x-1)^3} dx$
$\displaystyle \int \frac{x^3-4x+3}{x^2(x+1)^2} dx$
En los siguientes ejemplos, ilustramos el caso c) en el cual, el denominador tiene raíces complejas simples.
$\displaystyle \int \frac{3x^2-1}{(x^2+1)(x^2+x+1)} dx$
$\displaystyle \int \frac{x-1}{(x^2+1)(x^2+x+1)} dx$
En el siguiente ejemplo, ilustramos el caso d) en el cual, el denominador tiene raíces complejas repetidas.
$\displaystyle \int \frac{x^3+x+2}{x^4+2x^2+1} dx$
En general las integrales que resultan después de aplicar este método de fracciones parciales, son mucho más sencillas, así justificamos el haberlas dejado indicadas.
En el siguiente apartado, veremos algunos casos de reducción de integrales a casos más sencillos, mediante fórmulas llamadas de reducción.
En este apartado encontrarás algunas fórmulas que permitirán reducir algunas integrales de potencias de funciones, a otra integral más sencilla que la original, a las cuales se les llamaremos fórmulas de reducción. Un método muy útil para encontrar dichas fórmulas será el de integración por partes.
Por lo anterior será importante que recuerdes el Teorema correspondiente.
Si $f'$ y $g'$ son funciones continuas, entonces $\displaystyle \int fg' = fg - \int gf'$.
Igualmente haremos uso de algunas identidades trigonométricas, por lo cual será bueno que recuerdes, al menos las básicas, a saber:
En estos ejemplos, presentaremos sólo algunas de las más comunes.
En los siguientes ejemplos, podrás observar cómo la integral original, depende de otra con menor potencia.
$\displaystyle \int sen^n(x)dx = -\frac{1}{n} sen^{n-1}(x)cos(x) + \frac{n-1}{n} \int sen^{n-2}(x) dx$.
$\displaystyle \int cos^n(x)dx = \frac{1}{n} sen(x)cos^{n-1}(x) + \frac{n-1}{n} \int cos^{n-2}(x) dx$.
$\displaystyle \int [\log(x)]^n dx = x[\log(x)]^n - n \int [\log(x)]^{n-1} dx$.
$\displaystyle \int x^n e^x dx = x^n e^x - n \int x^{n-1}e^x dx$.
Demostrar que para $n \gt 1$, se cumple la siguiente fórmula de reducción:
$\displaystyle \int \frac{1}{(x^2+1)^n}dx = \frac{1}{2n-2} \frac{x}{(x^2+1)^{n-1}} + \frac{2n-3}{2n-2} \int \frac{1}{(x^2+1)^{n-1}} dx$.
En primer lugar escribimos:
$\displaystyle \textcolor{blue}{\int \frac{1}{(x^2+1)^n}dx} = \int \frac{1+x^2-x^2}{(x^2+1)^n}dx = \int \frac{1}{(x^2+1)^{n-1}}dx - \textcolor{red}{\int \frac{x^2}{(x^2+1)^n} dx}$ ... (1)
Enseguida trabajamos con la integral en rojo de la expresión (1):
$\displaystyle \textcolor{red}{\int \frac{x^2}{(x^2+1)^n}dx} = \int \frac{2x^2}{2(x^2+1)^n} dx = \textcolor{red}{\int x \frac{2x}{2(x^2+1)^n}dx}$ ... (2)
Resolvemos esta última integral en (2), por el método de integración por partes. Recuerda que: $\displaystyle \int fg' = fg - \int f'g$.
Si $\displaystyle \begin{cases} f(x)=x \\ \text{y} \\ g'(x)=\dfrac{1}{2} \dfrac{2x}{(x^2+1)^n} \end{cases} \implies \begin{cases} f'(x)=1 \\ \text{y} \\ g(x)=\dfrac{1}{2} \int \dfrac{2x}{(x^2+1)^n}dx = \dfrac{1}{2} \dfrac{1}{(1-n)} \dfrac{1}{(x^2+1)^{n-1}}\end{cases}$
Para obtener $g(x)$, basta utilizar el método de sustitución, haciendo $u=x^2+1$, de donde $du=2xdx$ y por lo tanto:
$\displaystyle \int \frac{2x}{(x^2+1)^n}dx = \int \frac{1}{u^n}du = \int u^{-n}du = \frac{u^{-n+1}}{-n+1} = \frac{1}{1-n} \frac{1}{u^{n-1}} = \frac{1}{-n+1} \frac{1}{(x^2+1)^{n-1}}$
Aplicando el método de integración por partes, nos queda:
$\displaystyle \textcolor{red}{\int x \frac{2x}{2(x^2+1)^n}dx} = \frac{1}{2} \frac{1}{(1-n)} \frac{x}{(x^2+1)^{n-1}} - \frac{1}{2} \frac{1}{(1-n)} \int \frac{1}{(x^2+1)^{n-1}} dx$ ... (3)
Es decir, de (2) y (3), nos queda que:
$\displaystyle \textcolor{red}{\int \frac{x^2}{(x^2+1)^n}dx} = \frac{1}{2} \frac{1}{(1-n)} \frac{x}{(x^2+1)^{n-1}} - \frac{1}{2} \frac{1}{(1-n)} \int \frac{1}{(x^2+1)^{n-1}} dx$ ... (4)
Sustituyendo (4) en (1), nos queda:
$\displaystyle \textcolor{blue}{\int \frac{1}{(x^2+1)^n}dx} = \int \frac{1}{(x^2+1)^{n-1}}dx - \frac{1}{2} \frac{1}{(1-n)} \frac{x}{(x^2+1)^{n-1}} + \frac{1}{2} \frac{1}{(1-n)} \int \frac{1}{(x^2+1)^{n-1}} dx$ ... (5)
Agrupando los términos semejantes en la expresión de la derecha en (5), nos queda:
$\displaystyle \textcolor{blue}{\int \frac{1}{(x^2+1)^n}dx} = - \frac{1}{2} \frac{1}{(1-n)} \frac{x}{(x^2+1)^{n-1}} + \left( \frac{1}{2} \frac{1}{(1-n)} + 1 \right) \int \frac{1}{(x^2+1)^{n-1}} dx$
Cambiando el signo en el denominador de la primera expresión del lado derecho y haciendo cuentas en la segunda, nos queda:
$\displaystyle \textcolor{red}{\int \frac{1}{(x^2+1)^n}dx} = \frac{1}{(2n-2)} \frac{x}{(x^2+1)^{n-1}} + \frac{3-2n}{2-2n} \int \frac{1}{(x^2+1)^{n-1}} dx$
Por último, cambiando el signo en el numerador y denominador de la segunda expresión del lado derecho, nos queda que:
$\displaystyle \int \frac{1}{(x^2+1)^n}dx = \frac{1}{(2n-2)} \frac{x}{(x^2+1)^{n-1}} + \frac{2n-3}{2n-2} \int \frac{1}{(x^2+1)^{n-1}} dx$
Q.E.D.
Con estas fórmulas, terminamos lo referente a los métodos de integración en términos de funciones elementales y pasaremos a un nuevo tema, referente a la aproximación de funciones, mediante funciones polinomiales.
Las fórmulas de las derivadas de todas las funciones trigonométricas deben tenerse a la mano.
Justificar cada paso.
En esta sección encontrarás la teoría necesaria que justifica la aproximación de funciones mediante polinomios, en una vecindad alrededor de un punto. También encontrarás varios resultados consecuencia de los anteriores. Entre otros, el teorema general de máximos y mínimos y una demostración de que el número $e$ es irracional.
Encontrarás construcciones interactivas que te permitirán visualizar las aproximaciones, permitiéndote cambiar el punto alrededor del cual deseas establecerla.
Entre todas las funciones que se estudian en Cálculo Diferencial e Integral, las polinomiales son las más sencillas de todas. Los procedimientos para el cálculo de límites, para derivarlas o para integrarlas son bastante fáciles. Pero aún para evaluarlas en cualquier punto, se reducen a un número finito de multiplicaciones y adiciones.
En cambio el cálculo en otras funciones, como las logarítmicas, exponenciales, racionales o trigonométricas o combinaciones de ellas, pueden adquirir tintes de gran dificultad. Por ejemplo, si queremos calcular $\log(3)$, $sen(2)$ o $cos(1)$ al menos no resulta inmediato.
Ya en capítulos anteriores vimos las dificultades que se tienen para funciones que nos son polinómicas el cálculo de límites o de derivadas, por ejemplo $\lim \limits_{x \to 0} \dfrac{sen(x)}{x}$, $\lim \limits_{x \to 0} x^x$ o $(arctan(x))'$. Estas dificultades no están ausentes en el cálculo de integrales y es por todo esto que se destaca la importancia de poder aproximar funciones mediante funciones polinomiales.
Antes de incursionar en la teoría para aproximar funciones por medio de funciones polinomiales, estudiemos una propiedad particular estas.
Sea $P(x)=a_0+a_1x+a_2x^2+...+a_nx^n$ una función polinomial de grado n y con dominio en los reales.
Lo primero que podemos observar es que $P(0)=a_0$.
Derivando, tenemos: $P'(x)=a_1+2a_2x+3a_3x^2+...+na_nx^{n-1}$, de donde: $P'(0)=a_1$.
Derivando nuevamente, tenemos: $P''(x)=2a_2+(3·2)a_3x+(4·3)a_4x^2+...+n(n-1)a_nx^{n-2}$, de donde: $P''(0)=2a_2$.
Volviendo a derivar, nos queda: $P^{(3)}(x)=(3·2)a_3+(4·3·2)a_4x+...+n(n-1)(n-2)a_nx^{n-3}$, de donde: $P^{(3)}(0)=(3·2)a_3$.
Derivando una vez más, tenemos $P^{(4)}(x)=(4·3·2)a_4+...+n(n-1)(n-2)(n-3)a_nx^{n-4}$, de donde: $P^{(4)}(0)=(4·3·2)a_4$.
Podemos observar en general que: $P^{(k)}(0)=k(k-1)(k-2) \cdot ... \cdot 1a_k = k!a_k$ para $k=0, ..., n$, asumiendo que: $0!=1$ y $P^{(0)}(x)=P(x)$.
Es decir, los coeficientes del polinomio se pueden escribir de la siguiente forma:
$a_k = \dfrac{P^{(k)}(0)}{k!}$ para $0 \leq k \leq n$ asumiendo que: $0! = 1$ y $P^{(0)}(x)=P(x)$ ... (1)
En resumen un polinomio de grado $n$, lo podemos escribir de la siguiente forma:
$\displaystyle P(x)=\frac{P^{(0)}(0)}{0!} + \frac{P'(0)}{1!}x + \frac{P''(0)}{2!}x^2 + ... + \frac{P^{(n)}(0)}{n!}x^n = \sum_{k=0}^n \frac{P^{(k)}(0)}{k!} x^k$ ... (2)
Es fácil observar que si:
$P(x)=a_0+a_1(x-a)+a_2(x-a)^2+...+a_n(x-a)^n$, entonces: $a_k=\dfrac{P^{(k)}(a)}{k!}$ para $0 \leq k \leq n$ ... (3)
con las mismas suposiciones anteriores: $0!=1$ y $P^{(0)}(x)=P(x)$.
En el siguiente apartado será muy importante tener en cuenta las expresiones (1), (2) y (3).
En este apartado encontrarás la definición del Polinomio de Taylor para una función $f$ que cumpla ciertas características y algunos de los ejemplos más sencillos.
Para la siguiente definición, será importante recordar del apartado anterior, que si:
$$P(x)=a_0+a_1(x-a)+a_2(x-a)^2+...+a_n(x-a)^n$$es un polinomio de grado $n$ en $(x-a)$, entonces los coeficientes tienen la siguiente expresión:
$a_k=\dfrac{P^{(k)}(a)}{k!}$ para $0 \leq k \leq n$ ... (3)
Sea $f$ una función tal que $f'(a), f''(a), ..., f^{(n)}(a)$ existen y sean $a_k=\dfrac{f^{(k)}(a)}{k!}$ para $0 \leq k \leq n$. Definimos el polinomio de grado $n$ en $(x-a)$ como $P_{n,a,f}(x)=a_0+a_1(x-a)+...+a_n(x-a)^n$, al que llamaremos polinomio de Taylor de grado $n$ para $f$ en $a$.
Una primera pregunta que podría surgir, es la siguiente:
¿Qué relación existe entre $f$ y su polinomio de Taylor $P_{n,a,f}(x)$?
El resultado siguiente nos dará una primera respuesta:
Sea $f$ una función tal que $f'(a), f''(a), ..., f^{(n)}(a)$ existen y $P_{n,a,f}(x)=a_0+a_1(x-a)+...+a_n(x-a)^n$, donde $a_k=\dfrac{f^{(k)}(a)}{k!}$ para $0 \leq k \leq n$, entonces $P^{(k)}_{n,a,f}(a)=f^{(k)}(a)$ para $0 \leq k \leq n$.
Es decir, $f$ y su polinomio de Taylor $P_{n,a,f}(x)$ coinciden en todas sus derivadas desde $0$ hasta $n$, al ser evaluadas en $a$.
Calcularemos el Polinomio de Taylor para funciones más o menos sencillas, pero también veremos algún caso con complicaciones, lo cual nos llevará a buscar métodos alternativos.
Una primera función para la cual es relativamente fácil calcular su polinomio de Taylor de grado $n$ en $a=0$, es $f(x)=e^x$. Sabemos que existen todas sus derivadas hasta el orden $n$ y son ella misma.
$P_{n,0,e^x}(x)=1+x+\dfrac{x^2}{2!}+...+\dfrac{x^n}{n!}$
Otro ejemplo mas o menos sencillo es la función seno, de la cual sabemos que es derivable siempre y se puede evaluar fácilmente en $0$.
$P_{2n+1,0,sen(x)}(x)=x-\dfrac{x^3}{3!}+\dfrac{x^5}{5!}-\dfrac{x^7}{7!}+...+(-1)^n \dfrac{x^{2n+1}}{(2n+1)!}$
Otro ejemplo mas o menos sencillo es la función coseno, de la cual sabemos que es derivable siempre y se puede evaluar fácilmente en $0$.
$P_{2n,0,cos(x)}(x)=1-\dfrac{x^2}{2!}+\dfrac{x^4}{4!}-\dfrac{x^6}{6!}+...+(-1)^n \dfrac{x^{2n}}{(2n)!}$
Otros ejemplo mas o menos sencillo es $\log(x)$ que igualmente es $n$ veces derivable, pero al no estar definida en $0$, haremos el cálculo de su polinomio de Taylor en $1$.
$P_{n,1,\log(x)}(x)=(x-1)-\dfrac{(x-1)^2}{2}+\dfrac{(x-1)^3}{3}-\dfrac{(x-1)^4}{4}+...+(-1)^{n-1} \dfrac{(x-1)^n}{n}$
Con el mismo método del ejemplo anterior te será posible descubrir que:
$P_{n,0,\log(x+1)}(x)=x-\dfrac{x^2}{2}+\dfrac{x^3}{3}-\dfrac{x^4}{4}+...+(-1)^{n-1} \dfrac{x^n}{n}$
Un ejemplo complicado, que nos obliga a buscar métodos alternativos.
$P_{n,0,arctan(x)}(x)=?$
En lo subsecuente necesitaremos construir la teoría necesaria para resolver casos como el anterior u otros.
En la sección anterior, en la Proposición 0, vimos que $f$ y su polinomio de Taylor coinciden en $a$, hasta la n-ésima derivada. En esta sección veremos que la relación entre $f$ y su polinomio de Taylor es aun más profunda que la establecida en la proposición anterior, para ello empezaremos con una definición.
Dos funciones $f$ y $g$ son iguales hasta el orden $n$ en $a$, si $\lim \limits_{x \to a} \dfrac{f(x)-g(x)}{(x-a)^n}=0$
$f(x)=e^x$ y $g(x)=1+x$ son iguales hasta el orden $1$ en $a=0$.
$f(x)=e^x$ y $g(x)=1+x+\dfrac{x^2}{2}$ son iguales hasta el orden $2$ en $a=0$.
$f(x)=e^x$ y $g(x)=1+x+\dfrac{x^2}{2}+\dfrac{x^3}{3!}$ son iguales hasta el orden $3$ en $a=0$.
$f(x)=sen(x)$ y $g(x)=x$ son iguales hasta el orden $1$ en $a=0$.
$f(x)=sen(x)$ y $g(x)=x-\dfrac{x^3}{3!}$ son iguales hasta el orden $3$ en $a=0$.
$f(x)=cos(x)$ y $g(x)=1-\dfrac{x^2}{2!}+\dfrac{x^4}{4!}$ son iguales hasta el orden $4$ en $a=0$.
$f(x)=\log(x)$ y $g(x)=(x-1)-\dfrac{(x-1)^2}{2!}$ son iguales hasta el orden $2$ en $a=1$.
En todos y cada uno de los ejemplos anteriores, puedes observar que: $g(x)$ es polinomio de Taylor de $f(x)$ del orden dado y en el punto indicado.
De manera sencilla y tratando de generalizar, podemos ver que: $f(x)$ y $P_{1,a,f}(x)$ son iguales hasta el orden $1$ en $a$.
Así mismo: $f(x)$ y $P_{2,a,f}(x)$ son iguales hasta el orden $2$ en $a$.
En general esperamos poder demostrar que:
$f(x)$ y $P_{n,a,f}(x)$ son iguales hasta el orden $n$ en $a$.
Esto lo haremos en nuestro siguiente apartado, después de un pequeño conjunto de resultados que facilitarán la demostración del mismo.
En esta sección podrás encontrar la relación profunda entre $f$ y su polinomio de Taylor en el sentido de ser iguales hasta el orden $n$ en el punto $a$. Para facilitar el entendimiento de su demostración la separaremos en varios resultados.
Sea $f$ una función tal que $f'(a), ..., f^{(n)}(a)$ existen. Sean $a_k=\dfrac{f^{(k)}(a)}{k!}$ para $k=0, ...,n$ y $P_{n,a,f}(x)$ polinomio de Taylor de grado $n$, en $a$, para $f$, entonces: $\dfrac{f(x)-P_{n,a,f}(x)}{(x-a)^n} = \dfrac{f(x)-Q(x)}{(x-a)^n} - \dfrac{f^{(n)}(a)}{n!}$, donde $\displaystyle Q(x) = \sum_{k=0}^{n-1} \frac{f^{(k)}(a)}{k!} (x-a)^k$.
Sea $f$ una función tal que $f'(a), ..., f^{(n)}(a)$ existen. Sean $a_k=\dfrac{f^{(k)}(a)}{k!}$ para $k=0, ...,n$ y $\displaystyle Q(x)=\sum_{k=0}^{n-1} \dfrac{f^{(k)}(a)}{k!} (x-a)^k$ entonces $Q^{(k)}(a)=f^{(k)}(a)$ para $k=0,...,n-2$ y $Q^{(n-1)}(x)=f^{(n-1)}(a)$.
Si $g(x)=(x-a)^n$, entonces $g^{(k)}(x)=\dfrac{n!(x-a)^{n-k}}{(n-k)!}$ para $k=1,...,n$.
$\displaystyle \lim_{x \to a} \frac{f(x)-Q(x)}{(x-a)^n} = \lim_{x \to a} \frac{f^{(n-1)}(x)-Q^{(n-1)}(x)}{n!(x-a)} = \frac{f^{(n)}(a)}{n!}$.
Sea $f$ una función tal que $f'(a),...,f^{(n)}(a)$ existen. Sean además $a_k=\dfrac{f^{(k)}(a)}{k!}$ para $k=0,...,n$ y $P_{n,a,f}(x)=a_0+a_1(x-a)+...+a_n(x-a)^n$ entonces $\lim \limits_{x \to a} \dfrac{f(x)-P_{n,a,f}(x)}{(x-a)^n}=0$.
Sean $P$ y $Q$ dos polinomios en $(x-a)$ de grados $\leq n$ y tales que son iguales hasta el orden $n$ en $a$, entonces $P=Q$.
Si $f$ es $n$ veces derivable en $a$ y $P$ es un polinomio en $(x-a)$ de grado $\leq n$, igual a $f$ hasta el orden $n$ en $a$, entonces $P=P_{n,a,f}$.
Una consecuencia importante del teorema 1, es el siguiente teorema sobre máximos y mínimos locales de una función.
Supongamos que $f'(a)=f''(a)=...=f^{(n-1)}(a)=0$ y que $f^{(n)}(a) \neq 0$.
Con la teoría anterior en nuestro haber, retomaremos en el apartado siguiente el cálculo del polinomio de Taylor para la función $arctan(x)$.
Cuando una función $f$ es $n$ veces derivable en un punto $a$, el Corolario del apartado anterior, nos ofrece un método útil para calcular su polinomio de Taylor en $a$. Ilustraremos este hecho con la función $f(x)=arctan(x)$.
$\dfrac{1}{1+t^2}=1-t^2+t^4-t^6+...+(-1)^nt^{2n}+(-1)^{n+1} \dfrac{t^{2n+2}}{1+t^2}$.
$\displaystyle arctan(x)=x-\dfrac{x^3}{3} + \dfrac{x^5}{5} - \dfrac{x^7}{7} + ... + (-1)^n \dfrac{x^{2n+1}}{2n+1} + (-1)^{n+1} \int_0^x \dfrac{t^{2n+2}}{1+t^2}dt$.
$P(x)=x-\dfrac{x^3}{3} + \dfrac{x^5}{5} - \dfrac{x^7}{7} + ... + (-1)^n \dfrac{x^{2n+1}}{2n+1}$.
sería el polinomio de Taylor de grado $2n+1$ en $0$, para $f(x)=arctan(x)$ siempre que:
$\lim \limits_{x \to 0} \dfrac{f(x)-P(x)}{x^{2n+1}}=0$, es decir si $\displaystyle \lim_{x \to 0} \dfrac{\int_0^x \frac{t^{2n+2}}{1+t^2}dt}{x^{2n+1}}=0$.
$\displaystyle \left| \frac{\int_0^x \frac{t^{2n+2}}{1+t^2}dt}{x^{2n+1}} \right| \leq \frac{\frac{|x|^{2n+3}}{2n+3}}{|x|^{2n+1}} = \frac{|x|^2}{2n+3} = \frac{x^2}{2n+3}$
$\displaystyle |x| \leq 1 \implies \left| \int_0^x \frac{t^{2n+2}}{1+t^2}dt \right| \leq \frac{1}{2n+3}$
Es decir, entre mayor sea el grado del polinomio de Taylor, más parecido será a la función $f(x)=arctan(x)$.
En el siguiente apartado, trataremos de extender estas ideas a otras funciones y haremos el análisis de los polinomios de Taylor, con relación a su grado.
En este apartado, extenderemos las ideas que experimentamos en el apartado anterior con la función $arctan(x)$, hasta la formulación del Teorema de Taylor, el cual establece una relación bastante buena entre una función y su polinomio de Taylor.
El resto $R_{n,a,f}(x)$ de $f$ respecto a su polinomio de Taylor $P_{n,a,f}(x)$ se define como $R_{n,a,f}(x)=f(x)-P_{n,a,f}(x)$. Es decir, $f(x)=P_{n,a,f}(x)+R_{n,a,f}(x)$.
Sería muy importante poder calcular una expresión general para el resto $R_{n,a,f}(x)$, sobre todo para poder cuantificarlo y así poder saber la proximidad de $P_{n,a,f}(x)$ con $f(x)$ alrededor de $a$. Por ejemplo, en el apartado anterior vimos que:
$\displaystyle f(x)=arctan(x) \implies R_{2n+1,0,f}(x) = (-1)^{n+1} \int_0^x \frac{t^{2n+2}}{1+t^2}dt$ y $\lim \limits_{n \to \infty} R_{2n+1,0,f}(x)=0$.
Empezaremos con el caso más sencillo para $n=0$.
$\displaystyle f(x)=f(a)+R_{0,a,f}(x) \implies \R_{0,a,f} \int_a^x f'(t)dt$.
Ahora para $n=1$.
$\displaystyle f(x)=f(a)+f'(a)(x-a)+R_{1,a,f}(x) \implies \R_{1,a,f} \int_a^x f''(t)(x-t)dt$.
Ahora para $n=2$.
$\displaystyle f(x)= \sum_{k=0}^{k=2} \frac{f^{(k)}(t)}{2!} + R_{2,a,f}(x) \implies R_{2,a,f}(x) = \int_a^x \frac{f^{(3)}(t)}{2!}(x-t)^2 dt$.
Siguiendo con el procedimiento anterior de manera recursiva, podemos intuir la forma general del resto, como lo demostraremos enseguida por el método de inducción matemática, incluyendo la hipótesis de que $f^{(n+1)}(t)$ sea continua en $[a,x]$, debido a los requerimientos del teorema de integración por partes:
$\displaystyle f(x)= \sum_{k=0}^{k=n} \frac{f^{(k)}(t)}{n!} + R_{n,a,f}(x) \implies R_{n,a,f}(x) = \int_a^x \frac{f^{(n+1)}(t)}{n!}(x-t)^n dt$.
Sabemos que: $f(x)=f(a)+R_{0,a,f}(x)$ ... (1)
Y por el teorema fundamental del Cálculo, tenemos que: $\displaystyle \int_a^x f'(t)dt = f(x)-f(a)$.
De donde nos queda que: $\displaystyle f(x)=f(a)+ \int_a^x f'(t)dt$ ... (2)
Y así, de (1) y (2) nos queda que: $\displaystyle R_{0,a,f}(x)= \int_a^x f'(t)dt$.
$\displaystyle R_{k,a,f}(x) = \int_a^x \frac{f^{(k+1)}(t)}{k!} (x-t)^k dt$ ... (hi)
$u(t)=f^{(k+1)}(t)$ y $v'(t)=\dfrac{(x-t)^k}{k!}$ ... (3)
de donde: $u'(t)=f^{(k+2)}(t)$ y $v(t)=-\dfrac{(x-t)^{k+1}}{(k+1)!}$ ... (4)
Recordando el teorema de integración por partes:
Si $u'$ y $v'$ son continuas, entonces $\displaystyle \int uv'=uv-\int u'v$.
Al sustituir las expresiones (3) y (4) en (hi) nos queda:
$\displaystyle R_{k,a,f}(x) = \int_a^x \frac{f^{(k+1)}(t)}{k!} (x-t)^k dt = u(t)v(t) {\LARGE |}_a^x + \int_a^x f^{(k+2)}(t) \frac{(x-t)^{k+1}}{(k+1)!}dt$
Como: $v(x)=0, u(a)=f^{(k+1)}(a)$ y $v(a)=-\dfrac{(x-a)^{k+1}}{(k+1)!}$, entonces nos queda:
$\displaystyle R_{k,a,f}(x) = \frac{f^{(k+1)}(a)}{(k+1)!} (x-a)^{k+1} + \int_a^x \frac{f^{(k+2)}(t)}{(k+1)!} (x-t)^{k+1}dt$ ... (5)
Ahora bien, sabemos que para $n=k$ tenemos que: $\displaystyle f(x) = \sum_{i=0}^k \frac{f^{(i)}(a)}{i!} (x-a)^i + R_{k,a,f}(x)$ ... (6)
Sustituyendo (5) en la expresión (6), nos queda:
$\displaystyle f(x)=\sum_{i=0}^{k+1} \frac{f^{(i)}(a)}{i!} (x-a)^i + \int_a^x \frac{f^{(k+1)}(t)}{k!} (x-t)^k dt$ ... (7)
$\displaystyle R_{k+1,a,f}(x) = \int_a^x \frac{f^{(k+1)}(t)}{k!} (x-t)^k$
Es decir que se cumple para $n=k+1$ y por tanto, queda demostrado que:
$\displaystyle R_{n,a,f}(x)=\int_a^x \frac{f^{(n+1)}(t)}{n!} (x-t)^n dt$ es verdadera $\forall n \geq 0$.
Estamos ahora en posibilidad de abordar nuestro teorema más general y más importante, en cuya demostración utilizaremos teoremas importantes del tema de derivadas como el Teorema del Valor Medio y el Teorema del Valor Medio de Cauchy.
Supongamos que $f', ..., f^{(n+1)}$ están definidas sobre $[a,x]$ y que $R_{n,a,f}(x)$ está definido por $f(x)=f(a)+f'(a)(x-a)+...+\dfrac{f^{(n)}(a)}{n!}(x-a)^n + R_{n,a,f}(x)$, entonces:
Además si $f^{(n+1)}$ es integrable sobre $[a,x]$, entonces:
$\forall t \in [a,x]$, tenemos que: $f(x)=f(t)+f'(t)(x-t)+\dfrac{f''(t)}{2!}(x-t)^2+...+\dfrac{f^{(n)}(t)}{n!}(x-t)^n+R_{n,t,f}(x)$.
Para cada $t \in [a,x]$, definimos $S(t)=R_{n,t,f}(x)$. Entonces, nos queda $f(x)=f(t)+f'(t)(x-t)+\dfrac{f''(t)}{2!}(x-t)^2+...+\dfrac{f^{(n)}(t)}{n!}(x-t)^n +s(t)$ ... (1)
Derivaremos ambos miembros con respecto a $t$, pero antes es conveniente observar qué ocurre con la derivada de dos términos consecutivos:
$U_k(t)=\dfrac{f^{(k)}(t)}{k!}(x-t)^k \implies U'_k(t)=-\dfrac{f^{(k)}}{(k-1)!}(x-t)^{k-1} + \dfrac{f^{(k+1)}(t)}{k!}(x-t)^k$
$U_{k+1}(t)=\dfrac{f^{(k+1)}(t)}{(k+1)!}(x-t)^{k+1} \implies U'_{k+1}(t)=-\dfrac{f^{(k+1)}}{k!}(x-t)^k + \dfrac{f^{(k+2)}(t)}{(k+1)!}(x-t)^{k+1}$
Se puede observar que en ambas expresiones aparece un término común, pero con signo contrario, de tal manera que en la suma se anulan. Esto significa que al derivar se irán anulando en cadena términos consecutivos y sólo prevalecerá el n-ésimo con signo positivo, más la derivada de $S(t)$.
Es decir, derivando (1) nos queda:
$0=f'(t)+[-f'(t)+f''(t)(x-t)]+...+\left[ -\dfrac{f^{(n)}}{(n-1)!}(x-t)^{n-1} + \dfrac{f^{(n+1)}(t)}{n!}(x-t)^n \right] +S'(t)$
Por lo tanto $S'(t)=-\dfrac{f^{(n+1)}(t)}{n!}(x-t)^n$ ... (2)
Por otra parte, como $S$ es continua en $[a,x]$ y derivable en $(a,x)$, entonces, por el teorema del valor medio,
$\exist t \in (a,x)$ tal que $\dfrac{S(x)-S(a)}{x-a}=S'(t)$ ... (3)
Combinando (2) y (3) y, la definición de $S(t)$, nos queda:
$\dfrac{S(x)-S(a)}{x-a} = -\dfrac{f^{(n+1)}(t)}{n!}(x-t)^n$ ... (4)
Además, recordando que:
$S(t)=R_{n,t,f}(x)=f(x)-\left[ f(t)+f'(t)(x-t)+\dfrac{f''(t)}{2!}(x-t)^2 +...+ \dfrac{f^{(n)}(t)}{n!}(x-t)^n \right]$
Se puede observar que: $S(x)=R_{n,x,f}(x)=0$ y $S(a)=R_{n,a,f}(x)$ ... (5)
Sustituyendo (5) en (4), nos queda:
$-\dfrac{R_{n,a,f}(x)}{x-a}=-\dfrac{f^{(n+1)}(t)}{n!}(x-t)^n \implies R_{n,a,f}(x) \dfrac{f^{(n+1)}(t)}{n!}(x-t)^n(x-a)$ para alguna $t \in (a,x)$ ... (Forma de Cauchy)
Ahora bien, para deducir la Forma de Lagrange, aplicamos el Teorema del Valor Medio de Cauchy a las funciones: $S(t)=R_{n,t,f}(x)$ y $g(t)=(x-t)^{n+1}$, es decir:
Como $S(t)$ y $g(t)$ son continuas en $[a,x]$ y derivables en $(a,x)$, entonces $\exist t \in (a,x)$ tal que:
$\dfrac{S(x)-S(a)}{g(x)-g(a)} = \dfrac{S'(t)}{g'(t)}$ ... (6)
Como $S(x)=0=g(x)$ y sustituyendo en (6), $g'(t)$ y la expresión (2) correspondiente a $S'(t)$, nos queda:
$\dfrac{S(a)}{g(a)} = \dfrac{-\frac{f^{(n+1)}(t)}{n!}(x-t)^n}{-(n+1)(x-t)^n} \implies S(a)=\dfrac{f^{(n+1)}(t)}{(n+1)!} g(a)$
Es decir: $R_{n,a,f}(x)=\dfrac{f^{(n+1)}(t)}{(n+1)!}(x-a)^{n+1}$ para alguna $t \in (a,x)$ ... (Forma de Lagrange)
Para la forma integral del resto, aplicamos que: $f^{(n+1)}(t)$ es integrable en $[a,x]$. Entonces:
$\displaystyle S(x)-S(a) = \int_a^x S'(t)dt = -\int_a^x \frac{f^{(n+1)}(t)}{n!}(x-t)^n dt$
Como $S(x)=0$, entonces finalmente queda:
$\displaystyle R_{n,a,f}(x) = \int_a^x \frac{f^{(n+1)}(t)}{n!}(x-t)^n dt$ ... (Forma de Integral)
En el siguiente apartado veremos como estimar restos para algunas de las funciones más conocidas. Igualmente veremos algunas aplicaciones de este teorema.
En este apartado, intentaremos estimar los restos de algunas funciones respecto a sus polinomios de Taylor, utilizando para ello, su forma integral.
El resto $R_{n,a,f}(x)$ está definido por $f(x)=P_{n,a,f}(x)+R_{n,a,f}(x)$ y de acuerdo con el Teorema 4 (teorema de Taylor) su forma Integral es la siguiente: $\displaystyle R_{n,a,f}(x) = \int_a^x \frac{f^{(n+1)}(t)}{n!}(x-t)^n dt$.
Para la función exponencial. Si $0 \lt x \leq 1$, entonces $0 \lt R_{n,0,e^x}(x) \lt \dfrac{4}{(n+1)!}$
Para la función seno: $|R_{2n,0,sen(x)}(x)| \leq \dfrac{|x|^{2n+2}}{(2n+2)!}$
Para la función coseno: $|R_{2n,0,cos(x)}(x)| \leq \dfrac{|x|^{2n+1}}{(2n+1)!}$
Para la función arcotangente: $|R_{2n+1,0,arctan(x)}(x)| \leq \dfrac{|x|^{2n+3}}{2n+3}$
En todas las estimaciones anteriores, se puede observar que los restos se pueden hacer tan pequeños como se desee dando a $n$ valores suficientemente grandes, especialmente si se trabaja con valores de $x$ en el el intervalo $[-1,1]$.
Los polinomios de Taylor y la estimación de los restos, vistos en el apartado anterior, nos permite calcular valores aproximados de cantidades diversas con un error deseado. Por ejemplo:
Podemos utilizar la estimación del resto para la función exponencial, para obtener una mejor aproximación del número $e$, de la que teníamos en un capítulo anterior, a saber: $2 \lt e \lt 4$.
$$2 \lt e \lt 2.75$$Sabemos que, si $f(x)=e^x$ y $0 \lt x \leq 1$, entonces $0 \lt R_{n,0,f}(x) \lt \dfrac{4}{(n+1)!}$.
Por tanto, si $n=4$, entonces $0 \lt R_{4,0,f}(x) \lt \dfrac{4}{5!}=\dfrac{1}{30} \lt \dfrac{1}{24}$ ... (1)
También sabemos que $e^x=1+x+\dfrac{x^2}{2!}+...+\dfrac{x^n}{n!}+R_{n,0,f}(x)$ ... (2)
Así, de (1) y (2), tenemos que, si $x=1$ y $n=4$, entonces $e \lt 1+1+\dfrac{1}{2}+\dfrac{1}{6}+\dfrac{1}{24}+\dfrac{1}{24}$.
Es decir, si $x=1$ y $n=4$, entonces $e \lt 2 + \dfrac{18}{24}=2.75$.
Asi tenemos una mejor aproximación de la que teníamos en un capítulo anterior: $2 \lt e \lt 2.75$.
Para valores de $n$ cada vez mayores, obtenemos mejores aproximaciones, por ejemplo para $n=5$, nos queda: $2 \lt e \lt 2.7222$.
Similarmente podemos utilizar el polinomio de Taylor de la función exponencial, para aproximar el número $e$ con la cantidad de cifras decimales que pudiéramos desear. Puedes dar clic en la siguiente imagen para que puedas acceder a una tabla con algunas aproximaciones.
$e \approx 2.7182815$
Podemos utilizar la estimación del resto para la función seno.
Para resolver el siguiente problema, calcular $sen(2)$ con un error menor que $10^{-5}$.
Podemos utilizar la estimación del resto para la función coseno.
Para resolver el siguiente problema, calcular $cos(1)$ con un error menor que $10^{-5}$.
Como en los casos anteriores es posible aproximar muchos otros valores. Muchas de las tablas de logaritmos, de funciones trigonométricas, de raíces entre otras, fueron construidas con base en aproximaciones de este estilo. Igualmente ocurre con los algoritmos de aproximación en las calculadoras.
En este apartado te presentamos una aplicación muy particular del polinomio de Taylor de la función exponencial, con la idea de demostrar que el número $e$ es irracional.
Recuerda que en el apartado anterior vimos que $2 \lt e \lt 2.75$.
Para los efectos de la aplicación que te queremos presentar, nos será suficiente y de mayor utilidad tomar la desigualdad $2 \lt e \lt 3$.
Además utilizaremos la estimación del resto que hicimos para la función exponencial, a saber:
Si $0 \lt x \leq 1$, entonces $0 \lt R_{n,0,e^x}(x) \lt \dfrac{e^x x^{n+1}}{(n+1)!}$
Y por otra parte que con base en el conocimiento de que la función exponencial es creciente, utilizaremos la siguiente desigualdad:
$\dfrac{e^x x^{n+1}}{(n+1)!} \leq \dfrac{e}{(n+1)!} \; \forall x \in (0,1]$
Para no hacer tan larga la demostración que nos ocupa primero demostraremos el siguiente lema, que establece una nueva aproximación del resto para la función exponencial y luego nuestro teorema final.
Si $0 \lt x \leq 1$ y $2 \lt e \lt 3$ entonces $0 \lt R_{n,0,e^x}(x) \lt \dfrac{3}{(n+1)!}$
Este será nuestro teorema de cierre, con lo cual esperamos te proporcione mucha idea de las posibilidades del Teorema de Taylor.
El número $e$ es irracional.
Por facilidad denotaremos el resto por $R_n$. Así, tomando $x=1$, podemos escribir: $e=e^1=1+1+\dfrac{1}{2!}+\dfrac{1}{3!}+...+\dfrac{1}{n!}+R_n$ donde $0 \lt R_n \lt \dfrac{3}{(n+1)!}$.
Ahora bien, si $e \in \mathbb{Q}$, entonces existen $p, q \in \mathbb{Z}^+$, con $q \neq 0$, tales que $e=\dfrac{p}{q}$.
Entonces $\dfrac{p}{q}=1+1+\dfrac{1}{2!}+\dfrac{1}{3!}+...+\dfrac{1}{n!}+R_n$.
Multiplicando por $n!$, nos queda: $\dfrac{n!p}{q} = n!+n!+\dfrac{n!}{2!}+\dfrac{n!}{3!}+...+\dfrac{n!}{n!}+n!R_n$.
Si $n>q$ y $n>3$ (lo cual es posible), tenemos que: $\dfrac{n!p}{q}$ y $n!+n!+\dfrac{n!}{2!}+\dfrac{n!}{3!}+...+\dfrac{n!}{n!}$ son enteros.
Por lo tanto $n!R_n$ debe ser entero ... (1)
Pero como sabemos $0 \lt R_n \lt \dfrac{3}{(n+1)!} \implies 0 \lt n!R_n \lt \dfrac{3n!}{(n+1)!}=\dfrac{3}{n+1}$.
Y para $n>3$, tenemos que $0 \lt n!R_n \lt 1$. ¡Contradicción con (1)!
Q.E.D.
Con esto cerramos el tema, no obstante que hay mucha tela de dónde cortar. Nuestra siguiente sección la dedicaremos a las aplicaciones del Cálculo Integral.
$P_{n,a,f}(x)=a_0+a_1(x-a)+...+a_n(x-a)^n$
Escribir la expresión de los coeficientes $a_k$ para $0 \leq k \leq n$.
Sugerencia: Graficar con Maple o cualquier otro software, las funciones y tres polinomios de Taylor de diferente grado.
Sugerencia: Ver las páginas 582 y 583 del Spivak.
Sugerencia: Recordar que el Teorema 4 afirma que $f(x)=f(a)+f'(a)+\dfrac{f''(a)}{2!}(x-a)^2+\dfrac{f^{(3)}(a)}{3!}(x-a)^3+...+\dfrac{f^{(n)}(a)}{n!}(x-a)^n+R_{n,f,a}(x)$.
Revisar también las páginas 587 y 588 del Spivak.
En esta sección encontrarás algunas aplicaciones de la integral, tanto en matemáticas como en otras disciplinas, como la física. Tendrás a la mano teoría, conceptos previos y recursos gráficos e interactivos, para entender mejor tales aplicaciones.
En esta sección trabajaremos con regiones planas limitadas por funciones continuas (por tanto integrables) definidas en un intervalo cerrado $[a,b]$. Es decir, regiones $R(f,a,b)$ como las que se muestran en las figuras siguientes:
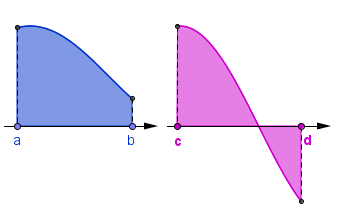
Calcular las áreas de regiones $R(f,a,b)$ como las que se muestran en la figura anterior.
Para tener éxito, es importante recordar que:
Si $f$ es continua en todo $[a,b]$ y $f=g'$ para alguna función $g$, entonces $\displaystyle \int_a^b f=g(b)-g(a)$.
Si $f$ y $g$ son integrables sobre $[a,b]$, entonces $f+g$ es integrable sobre $[a,b]$ y $\displaystyle \int_a^b (f+g)=\int_a^b f + \int_a^b g$.
Si $f$ es integrable sobre $[a,b]$, entonces la función $cf$ es integrable sobre $[a,b] \; \forall c$ y $\displaystyle \int_a^b cf = c \int_a^b f$.
En los ejemplos, se realiza el cálculo de áreas para diversas funciones continuas, definidas en un intervalo cerrado.
Los valores de las integrales son aproximados.
Se plantea un problema sencillo para el cálculo del área bajo la gráfica de una función. No olvides tomar tu cuaderno y tu lápiz para realizar tus cálculos.
En esta sección trabajaremos con regiones planas limitadas por dos funciones continuas (por tanto integrables) definidas en un intervalo cerrado $[a,b]$. Es decir, regiones $R(f,a,b)$ como la que se muestra en las figuras siguiente:
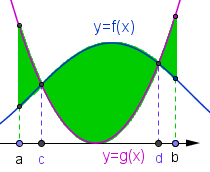
Calcular las áreas de regiones $R(f,a,b)$ como las que se muestran en la figura anterior.
Para tener éxito, es importante tener en cuenta:
$f(x) \geq g(x) \; \forall x \in [c,d]$, mientras que $g(x) \geq f(x) \; \forall x \in [a,c] \cup [d,b]$.
$\displaystyle \text{Área } = \int_a^c (g(x)-f(x))dx + \int_c^d (f(x)-g(x))dx + \int_d^b (g(x)-f(x))dx$
Si $f$ es continua en todo $[a,b]$ y $f=g'$ para alguna función $g$, entonce $\displaystyle \int_a^b f=g(b)-g(a)$.
Si $f$ y $g$ son integrables sobre $[a,b]$, entonces $f+g$ es integrable sobre $[a,b]$ y $\displaystyle \int_a^b (f+g) = \int_a^b f + \int_a^b g$.
Si $f$ es integrable sobre $[a,b]$, entonces la función $cf$ es integrable sobre $[a,b] \; \forall c$ y $\displaystyle \int_a^b cf = c \int_a^b f$.
En los ejemplos, se realiza el cálculo de áreas entre curvas, para diversas funciones continuas.
Los valores de las integrales son aproximados.
Se plantea un problema sencillo para el cálculo del área entre las gráficas de dos funciones. No olvides tomar tu cuaderno y tu lápiz para realizar tus cálculos.
Esta aplicación se refiere al cálculo de la longitud de una curva. En particular, en este apartado, trabajaremos con funciones continuas definidas en intervalos cerrados.
Calcular longitudes de arco para funciones continuas definidas en intervalos cerrados.
Sea $f:[a,b] \to \mathbb{R}$ tal que $f'$ es continua en $[a,b]$, entonces la longitud de arco de $f$, se define como $\displaystyle \Delta(f)= \int_a^b \sqrt{1+(f')^2}$.
A continuación podrás ver algunos ejemplos de cálculo de longitudes de arco. Para el cálculo de las integrales, consultaremos las tablas de integrales y en caso de que lo amerite, exhibiremos el procedimiento en una ventana flotante.
A continuación podrás practicar tus conocimientos sobre longitud de arco. Recuerda que es muy importante que tomes tu papel y lápiz, para realizar los cálculos correspondientes.
Cuando un objeto se mueve en línea recta debido a la aplicación de una fuerza, decimos que tal fuerza ha desarrollado un Trabajo. Cuando la fuerza que se aplica es constante y se aplica en la dirección del movimiento, el trabajo realizado se calcula multiplicando el valor de la fuerza por la distancia recorrida, es decir $T=F \cdot d$. Sin embargo, el interés en este apartado es calcular el trabajo realizado por fuerzas que no necesariamente sean constantes.
Calcular el Trabajo realizado por una fuerza $F$ variable al mover un objeto en forma rectilínea de punto a otro.
A continuación podrás ver algunos ejemplos de cálculo del Trabajo realizado por una fuerza al mover un objeto. Para el cálculo de las integrales, consultaremos las tablas de integrales y en caso de que lo amerite, exhibiremos el procedimiento en una ventana flotante.
A continuación podrás practicar tus conocimientos adquiridos sobre el trabajo realizado por una fuerza. Recuerda que es muy importante que tomes tu papel y lápiz, para realizar los cálculos correspondientes.
En este apartado podrás encontrar algunas aplicaciones de la integral, relacionadas con el movimiento de un objeto. Por ejemplo conociendo la velocidad de un móvil, se trata de conocer la distancia recorrida o conociendo su aceleración sería deseable conocer su velocidad.
Calcular distancias o velocidades de un móvil, a partir de la velocidad o la aceleración respectivamente.
Si $f$ es continua en todo $[a,b]$ y $f=g'$ para alguna función $g$, entonces $\displaystyle \int_a^b f=g(b)-g(a)$.
A continuación podrás ver algunos ejemplos de aplicaciones de la integral en problemas de movimiento. Para el cálculo de las integrales, consultaremos las tablas de integrales y en caso de que lo amerite, exhibiremos el procedimiento en una ventana flotante.
A continuación podrás practicar tus conocimientos adquiridos sobre los problemas de movimiento. Recuerda que es muy importante que tomes tu papel y lápiz, para realizar los cálculos correspondientes.
En este apartado podrás encontrar algunas aplicaciones de la integral, relacionadas con los volúmenes contenidos al rotar la gráfica de una función definida en un intervalo cerrado $[a,b]$, alrededor de uno de los ejes y que son los llamados sólidos de revolución. En este trabajo los ejemplos serán de rotaciones alrededor del eje de las $x$. Por ejemplo, imagina una función constante en $[0,2]$, al rotarla alrededor del eje $x$, se formaría un cilindro, pero si la función fuese la idéntica tendríamos un cono.
Calcular los volúmenes contenidos al rotar la gráfica de una función definida en un intervalo cerrado $[a,b]$.
Si $f$ es continua en todo $[a,b]$ y $f=g'$ para alguna función $g$, entonces $\displaystyle \int_a^b f=g(b)-g(a)$.
A continuación podrás ver algunos ejemplos de aplicaciones de la integral en el cálculo de volúmenes de sólidos de revolución. Para el cálculo de las integrales, consultaremos las tablas de integrales y en caso de que lo amerite, exhibiremos el procedimiento en una ventana flotante.
En todos los ejemplos, excepto en el último, el cálculo de las integrales es sencillo, a continuación se muestran dichos cálculos.
$\displaystyle \int sen^2(x)dx = \int \left( \frac{1}{2} - \frac{1}{2} cos(2x) \right)dx = \frac{1}{2} \int dx - \frac{1}{2} \int cos(2x)dx \overset{u=2x}{=} \frac{1}{2}x - \frac{1}{2} \int \frac{1}{2} cos(u)du = \frac{1}{2}x - \frac{1}{4} \int cos(u)du = \frac{1}{2}x - \frac{1}{4} sen(u) = \frac{1}{2}x - \frac{1}{4}sen(2x)$
A continuación podrás practicar tus conocimientos adquiridos sobre los problemas de sólidos de revolución. Recuerda que es muy importante que tomes tu papel y lápiz, para realizar los cálculos correspondientes.
En este apartado podrás encontrar algunas aplicaciones de la integral, relacionadas con las áreas de las superficies que se generan al rotar la gráfica de una función definida en un intervalo cerrado $[a,b]$, alrededor de uno de los ejes y que son las llamadas áreas de superficies de revolución. En este trabajo los ejemplos serán de rotaciones alrededor del eje de las $x$.
Por ejemplo, imagina una función constante en $[0,2]$, al rotarla alrededor del eje $x$, se formaría un cilindro, pero si la función fuese la idéntica tendríamos un cono. En el apartado anterior calculamos el volumen generado, ahora calcularemos las áreas de las superficies generadas.
Calcular las áreas de las superficies generadas al rotar la gráfica de una función definida en un intervalo cerrado $[a,b]$.
Si $f$ es continua en todo $[a,b]$ y $f=g'$ para alguna función $g$, entonces $\displaystyle \int_a^b f=g(b)-g(a)$.
$\displaystyle A = 2\pi \int_a^b f(x) \sqrt{1+[f'(x)]^2}dx$
A continuación podrás ver algunos ejemplos de aplicaciones de la integral en el cálculo de áreas de superficies de revolución. Para el cálculo de las integrales, consultaremos las tablas de integrales y en caso de que lo amerite, exhibiremos el procedimiento en una ventana flotante.
$\displaystyle \int \sqrt{4x+1}dx \overset{u=\sqrt{4x+1}}{=} \int \frac{1}{2}u^2 du = \frac{1}{2} \int u^2 du = \frac{1}{6} u^3 \overset{u=\sqrt{4x+1}}{=} \frac{1}{6} (4x+1)^{\frac{3}{2}}$
$\displaystyle \int sen(x) \sqrt{1+cos^2x} dx = \int -\sqrt{u^2+1} du = -\int \sqrt{u^2+1} du = - \int sec^3 u_1 du_1 = -sec(u_1)tan(u_1) + \int sec(u_1)tan^2 u_1 d_1 = -sec(u_1)tan(u_1) + \int sec(u_1)(sec^2 u_1 -1) du_1 = -sec(u_1)tan(u_1) + \int (sec^3 u_1 - sec(u_1)) du_1 = -sec(u_1)tan(u_1) + \int sec^3 u_1 du_1 + \int -sec(u_1) du_1 = -\frac{1}{2} sec(u_1) tan(u_1) + \frac{1}{2} \int -sec(u_1) du_1 = -\frac{1}{2} sec(u_1) tan(u_1) -\frac{1}{2} \int sec(u_1)du_1 = -\frac{1}{2} sec(u_1) tan(u_1) -\frac{1}{2} \int \frac{sec^2 (u_1) + sec(u_1) tan(u_1)}{sec(u_1)+tan(u_1)} du_1 = -\frac{1}{2} sec(u_1) tan(u_1) - \frac{1}{2} \int \frac{1}{u_2} du_2 = -\frac{1}{2} sec(u_1) tan(u_1) - \frac{1}{2} \ln(u_2) = -\frac{1}{2} sec(u_1) tan(u_1) - \frac{1}{2} \ln(sec(u_1) + tan(u_1)) = -\frac{1}{2} \sqrt{u^2+1} u - \frac{1}{2} \ln(\sqrt{u^2+1} + u) = -\frac{1}{2} \sqrt{1+cos^2 x} cos(x) - \frac{1}{2} \ln (\sqrt{1+cos^2 x} + cos(x))$
Otra manera, tal vez más sencilla, de comprobar que la integral es correcta, es derivándola y observar que su resultado es el integrando.
A continuación podrás practicar tus conocimientos adquiridos sobre los problemas de superficies de revolución. Recuerda que es muy importante que tomes tu papel y lápiz, para realizar los cálculos correspondientes.