Cálculo Interactivo I
Héctor de Jesús Argueta Villamar
María Juana Linares Altamirano
DGTIC - Facultad de Ciencias. UNAM.
Título de la obra:
Cálculo Interactivo I
Autores:
Héctor de Jesús Argueta Villamar argueta@unam.mx
María Juana Linares Altamirano linares@unam.mx
Código JavaScript para el libro: Joel Espinosa Longi, IMATE, UNAM.
Conversión a formato de libro interactivo: Joel Espinosa Longi
Recursos interactivos: GeoGebra y DescartesJS
Fuentes tipográficas: CrimsonPro y UbuntuMono
Fórmulas matemáticas: $\KaTeX$
El programa Cálculo Interactivo I que presentamos tuvo sus inicios en el proyecto Precálculo Interactivo, desarrollado como tesis de Maestría en Ciencias (Matemáticas) de Héctor de Jesús Argueta Villamar y dirigida por el Dr. Carlos Hernández Garciadiego investigador del Instituto de Matemáticas de la UNAM. Los temas desarrollados fueron Lógica, Números reales y Funciones y el software matemático utilizado esencialmente fue The Geometer's Sketchpad y su componente JavaSketchpad.
A partir de ello y del desarrollo de Geometría Interactiva, proyecto de tesis de Maestría en Ciencias (Matemáticas) de María Juana Linares Altamirano dirigida igualmente por el Dr. Carlos Hernández Garciadiego, es que la Maestra Guadalupe Lucio Gómez-Maqueo titular de la Secretaría de Apoyo Educativo de la Facultad de Ciencias y por recomendación del Maestro Wilfrido Martínez Torres, nos invita a colaborar en la construcción de un Centro Virtual para la Enseñanza de las Ciencias, con el encargo de construir en primera instancia el material de apoyo interactivo para el curso de Cálculo diferencial e integral I.
Así es que emprendemos el proyecto Cálculo Interactivo I, tratando de mejorar lo ya hecho en Precálculo Interactivo y completando los temas del curso. En este nuevo proyecto se incorporaron otras herramientas de software matemático como GeoGebra, Descartes y Arquímedes. Este trabajo fue finalmente revisado y avalado por una comisión nombrada por el Consejo Técnico, de Profesores de tiempo completo de la Facultad de Ciencias de la UNAM.
Con la experiencia adquirida, nos dimos a la tarea de desarrollar Cálculo interactivo II basados en los temas que señalan los planes de estudio de la Facultad de Ciencias de la UNAM. Para el desarrollo de Cálculo Interactivo II se utilizó software como The Geometer's Sketchpad, GeoGebra y Arquímedes.
Con el tiempo, desarrollamos dos módulos de Aplicaciones, uno para la Derivada y otro para la Integral, mismos que incorporamos en los respectivos materiales. Posterior a ello, como invitados a participar en el Proyecto Comunidades de Aprendizaje en la Facultad de Ciencias, coordinado a nivel universitario por la Dra. María Ascención Morales Ramírez, Secretaria Ejecutiva del Colegio de Directores de Facultades y Escuelas, nos dimos a la tarea de desarrollar en html5, un pequeño módulo de introducción a Conjuntos y mejoramos sustancialmente el de Lógica, mismos que se incorporaron al material de Cálculo Interactivo I.
A excepción de estos últimos, todos los demás materiales fueron desarrollados con software basado en Java y con las actualizaciones de la máquina virtual de Java, se empezaron a tener problemas para acceder a ellos, por lo cual se hacía necesario emigrarlos a HTML5, lo cual implicaba un trabajo verdaderamente titánico por la cantidad de interactivos que contienen.
Con estos antecedentes y ante la necesidad de la Facultad de Ciencias de la UNAM de empezar a construir sus primeros cursos en línea, fuimos llamados por el Dr. Alfredo Arnaud Bobadilla titular de la Secretaría de Educación Abierta y Continua, con la idea de que pudiéramos compartir dichos materiales.
Con nuestra mayor disposición a compartir, planteamos el problema de la transformación aHTML5, lo cual propició un acuerdo entre la DGTIC representada por el Dr. Guillermo Rodríguez Abitia titular de la Dirección de Innovación y Desarrollo Tecnológico y la Facultad de Ciencias representada por el Dr. Alfredo Arnaud Bobadilla, que significó la contratación de un grupo de becarios que colaborarían en esta tarea, bajo la Coordinación de María Juana Linares Altamirano y Héctor de Jesús Argueta Villamar autores de Cálculo Interactivo I y Cálculo Interactivo II.
Los jóvenes participantes en esta primera etapa de Cálculo Interactivo I son: Alanís Manríquez Jesús Felipe, Ávalos Valentín Gustavo Alejandro, Chimal Hernández Manuel de Jesús, Durán Méndez Abraham, Flores Romero María Erandi, Jiménez Santiago Berenice, Ku Kinil Ginni Noelia, Lerista Barrera Miguel Ángel, Rivas Robles René Alejandro, Rivaz Hernández José Amet, Ramos Tort Andrea Berenice y Vargas Mendoza Marco Antonio, todos ellos de la Facultad de Ciencias y a quienes les expresamos nuestros más caros agradecimientos ya que con su empeño y compromiso es que entregamos Cálculo Interactivo I en HTML5.
En una segunda etapa, contamos con la revisión del material, de parte del becario González Casanova Azuela Daniel, a quien le expresamos nuestro más sincero agradecimiento.
27 de enero de 2018
M. en C. María Juana Linares Altamirano
M. en C. Héctor de Jesús Argueta Villamar
Aquí podrás encontrar un breve resumen sobre los conjuntos, sus operaciones básicas y sus propiedades más importante.
No es un tratado exhaustivo sobre la teoría de conjuntos. Se trata de presentarte lo mínimo indispensable para que puedas utilizarlos en las secciones de Lógica, Ejercicios y Problemas.
La teoría de los Conjuntos fue desarrollada de manera rigurosa en la segunda mitad del siglo XIX y principios del XX. Su desarrollo se atribuye fundamentalmente al matemático alemán Georg Cantor (1845-1918) por sus investigaciones sobre conjuntos infinitos. Sin embargo, han intervenido muchos otros matemáticos de gran talla, como Gottlob Frege, Bertrand Russel, Ernst Zermelo y Abraham Fraenkel, entre otros. La importancia de esta teoría es que vino a dar a la matemática una mejor fundamentación y precisión en su lenguaje.
Lejos de la fundamentación axiomática de la teoría de conjuntos y de las discusiones filosóficas en la matemática moderna, en este apartado nos interesa estudiar las nociones más elementales de los conjuntos, sus operaciones y propiedades más importantes. Por lo mismo, partiremos de ideas muy intuitivas y de definiciones básicas.
Así, diremos de manera muy sencilla que un CONJUNTO está determinado por sus ELEMENTOS.
Es decir, dado un elemento y un conjunto, se debe cumplir una y sólo una de ambas proposiciones:
No debe haber ambigüedad alguna. O la proposición 1 es verdadera y la 2 falsa, o viceversa.
En general seguiremos la siguiente notación:
Conjuntos: $A$, $B$, $C$, $...$
Elementos: $a$, $b$, $c$, $...$
$x$ pertenece al conjunto $A$: $x \in A$
$x$ no pertenece al conjunto $A$: $x \notin A$
De esta manera si representamos al conjunto $A$ por un círculo y al elemento $x$ por un punto, podemos experimentar la relación de pertenencia mediante la siguiente construcción interactiva:
Y como mucho del trabajo que realizaremos estará centrado en ciertos conjuntos numéricos, a éstos en particular los denotaremos de la siguiente manera:
Hay dos formas para describir a un conjunto:
La segunda es muy propia para describir conjuntos finitos con muchos elementos que posean alguna o algunas propiedades que los describan y es la única forma para poder describir conjuntos infinitos.
En ambos casos utilizaremos como es costumbre, la notación con corchetes, como veremos enseguida.
| $A = \{1, a, 2, b, ✓, ✕\}$ | Finito | Por extensión |
| $B = \{Δ, ∇, α, β, \downarrow, \uparrow \}$ | Finito |
Por extensión |
| $C = \{x \in \mathbb{N} | x$ es un número primo$\}$ | Infinito |
Por compresión |
| $D = \{x \in \mathbb{Z} | x$ es múltiplo de $3\}$ | Infinito | Por compresión |
| $E = \{s \in \mathbb{N} | s^2 \lt 55 \}$ | Finito | Por compresión |
Estos conjuntos son importantes en la medida que establecen el contexto en el que se trabaja en determinada teoría o problema.
Por ejemplo, si planteamos la ecuación: $3x + 2 = 0$ y nos preguntamos por su solución en el conjunto de los números enteros, encontraremos que no existe entero alguno tal que cumpla la igualdad. Es decir, el conjunto de enteros que satisface la ecuación es vacío.
En cambio si planteamos la misma ecuación: $3x + 2 = 0$ y nos preguntamos por su solución en el conjunto de los números racionales, será fácil ver que sí existe un racional que cumple con la igualdad. Es decir, el conjunto de racionales que satisfacen la ecuación no es vacío.
En los casos anteriores, $\mathbb{Z}$ y $\mathbb{Q}$ respectivamente fueron establecidos como conjuntos universo para tales problemas.
Así, diremos que: el CONJUNTO UNIVERSAL establece el contexto de trabajo. Es decir, es el conjunto en el que se enmarca una determinada teoría o problema.
Por otra parte el CONJUNTO VACÍO está íntimamente ligado al conjunto universal y es aquel que no tiene ningún elemento de tal universo.
Denotaremos:
Con la notación anterior, podemos expresar los casos anteriores de la siguiente manera:
$$\{x \in \mathbb{Z} | 3x + 2 = 0\} = ∅ \;\;\;\; \{ x \in \mathbb{Q} | 3x + 2 = 0 \} = ∅$$$A = \{x \in \mathbb{N}| 5x^2 - 1 = 0 \} = ∅$
$Ω = \mathbb{N}$
$B = \{x \in \mathbb{Z}| 0 \lt x \lt 1 \} = ∅$
$Ω = \mathbb{Z}$
$C = \{x \in \mathbb{R}| x^2 + 2 \lt 0 \} = ∅$
$Ω = \mathbb{R}$
$D = \{x \in \mathbb{Q}| 5x + 3 = 0 \} = \left\{ -\dfrac{3}{5} \right\}$
$Ω = \mathbb{Q}$
$E = \{x \in \mathbb{Z}| 2x^3 - 1 \gt 0 \} = \{x \in \mathbb{Z}| x \ge 1 \}$
$Ω = \mathbb{Z}$
$F = \{x \in \mathbb{R}| x^2 + x + 1 = 0 \} = ∅$
$Ω = \mathbb{R}$
$G = \{x \in \mathbb{R}| x^2 + 3x + 2 = 0 \} = \{ -2, -1 \}$
$Ω = \mathbb{R}$
$H = \{x \in \mathbb{Q}| 3x \in \mathbb{Z} \} = \{ x \in \mathbb{Q}| x = \dfrac{p}{3} \text{ con } p \in \mathbb{Z} \}$
$Ω = \mathbb{Q}$
$K = \{x \in \mathbb{R}| x^2 + 1 = 0 \} = ∅$
$Ω = \mathbb{R}$
En cada uno de los ejemplos anteriores, se establece cuál es el conjunto que se toma como universal, desde el momento en que se especifica de qué conjunto se toman los elementos. A la derecha en cada caso, se hacen explícitos.
En general es fácil descubrir las igualdades o desigualdades en cada conjunto. Sin embargo, te dejamos el reto de contestar la siguiente pregunta: ¿Puedes explicar porqué: $C = ∅$, $F = ∅$ y $K = ∅$?
Lo importante es darse cuenta que los conceptos de Conjunto Universal y Conjunto vacío, son relativos. El conjunto Universal establece el contexto y el vacío depende de ello.
Las operaciones básicas que trataremos en este apartado, serán: UNIÓN, INTERSECCIÓN y COMPLEMENTO de conjuntos. Sin embargo, antes de ello, deberemos distinguir cuándo dos conjuntos son iguales y cuándo un conjunto es subconjunto de otro.
Sean $A$, $B$ conjuntos.
$A$ es igual a $B$ si tiene los mismos elementos.
Notación: $A = B$.
$A$ es subconjunto de $B$ si todo elemento de $A$, es elemento de $B$.
Notación: $A \subset B$.
Es relativamente fácil comprender que, si $A = B$ entonces $A \subset B$ y $B \subset A$.
Igualmente no es difícil entender que, si $A \subset B$ y $B \subset A$ entonces $A = B$.
Es decir, podemos establecer sin dificultad el siguiente resultado:
$A = B$ sí y sólo si $A \subset B$ y $B \subset A$
$\{1, 2, 3\} = \{1, 1, 2, 3\}$
$\{1, 2, 3\} = \{2, 3, 1\}$
$\{x \in \mathbb{N}|3x - 6 = 0\} = \{2\}$
$\{x \in \mathbb{Z}|x^2 + 3x + 2 = 0\} = \{-2, -1\}$
$\{x \in \mathbb{Z}|2x^3 - 1 \gt 0\} = \{x \in \mathbb{Z}|x \ge 1\}$
$\{x \in \mathbb{Z}|2x + 1 \lt 3\} = \{x \in \mathbb{Z}|x \lt 1\}$
$\{x \in \mathbb{N}|x^2 - 3x + 2 = 0\} \subset \{1, 2, 3\}$
$\{x \in \mathbb{Z}|x \ge 1\} \subset \{x \in \mathbb{R}|2x - 1 \gt 0\}$
Sean $A$, $B$ conjuntos.
$A \cup B = \{x \in Ω | x \in A$ o $x \in B\}$ llamada $A$ unión $B$.
$A \cap B = \{x \in Ω | x \in A$ y $x \in B\}$ llamada $A$ intersección $B$.
$A - B = \{x \in Ω | x \in A$ y $x \notin B\}$ llamada complemento de $B$ respecto de $A$ o de manera sencilla: $A$ menos $B$.
En particular: $A^c = \{x \in Ω | x \notin A\}$ llamada complemento de $A$.
$\{1, 2, 3, 4\} \cup \{a, b\} = \{1, a, 2, b, 3, 4\}$
$\{1, 2, 3, 4\} \cap \{2, 3, a, b\} = \{2, 3\}$
$\{x \in \mathbb{N} | 2x - 6 = 0\} \cup \{x \in \mathbb{N} | x^2 - 3x + 2 = 0\} = \{2, 1, 3\}$
$\{x \in \mathbb{Z} | 2x^3 - 1 \gt 0\} \cap \{x \in \mathbb{Z} | 2x \lt 3\} = \{1\}$
$\{x \in \mathbb{N} | x^2 - 3x + 2 = 0\} - \{x \in \mathbb{N} | x - 1 = 0\} = \{2\}$
Si $Ω = \mathbb{N}$ y $A = \{x \in \mathbb{N} | x \text{ es impar}\}$ entonces $A^c = \{x \in \mathbb{N} | x \text{ es par}\}$
En la teoría de conjuntos, hay muchas propiedades interesantes, sin embargo en este apartado sólo veremos algunas muy básicas.
Reservaremos muchas otras, para cuando veamos los métodos de demostración que será en el siguiente apartado de Lógica.
Sean $A, B \in Ω$. Podemos ver que:
Por la definición de unión $A \cup B = \{x \in Ω | x \in A$ o $x \in B\},$ sabemos que si $x \in A$, entonces $x \in A \cup B$. Por lo tanto, $A \subset A \cup B$.
Por la definición de intersección: $A \cap B = \{x \in Ω | x \in A$ y $x \in B\},$ sabemos que si $x \in A \cap B$, entonces $x \in A$. Por lo tanto, $A \cap B \subset A$.
Por la definición de complemento: $A - B = \{x \in Ω | x \in A$ y $x \notin B\},$ sabemos que si $x \in A - B$, entonces $x \in A$. Por lo tanto, $A - B \subset A$.
Por la definición de unión: $A \cup B = \{x \in Ω | x \in A$ o $x \in B\},$ sabemos que si $x \in B$, entonces $x \in A \cup B$. Por lo tanto, $B \subset A \cup B$.
Por la definición de intersección: $A \cap B = \{x \in Ω | x \in A$ y $x \in B\},$ sabemos que si $x \in A \cap B$, entonces $x \in B$. Por lo tanto, $A \cap B \subset B$.
Por la definición de complemento $B - A = \{x \in Ω | x \in B$ y $x \notin A\},$ sabemos que si $x \in B - A$, entonces $x \in B$. Por lo tanto, $B - A \subset B$.
Por la definición de unión: $A \cup B = \{x \in Ω | x \in A$ o $x \in B\}$, sabemos que si $x \in A$, entonces $x \in A \cup ∅$. Por lo tanto, $A \subset A \cup ∅$ ... ( 1 ).
Además, si $x \in A \cup ∅$, entonces $x \in A$. Por lo tanto, $A \cup ∅ \subset A$ ... ( 2 ).
Así, de ( 1 ) y ( 2 ), tenemos que: $A \cup ∅ = A$.
Por la definición de intersección $A \cap B = \{x \in Ω | x \in A$ y $x \in B\}$, sabemos que si $x \in A \cap Ω$, entonces $x \in A$. Por lo tanto, $A \cap Ω \subset A$ ... ( 1 ).
Además, si $x \in A$, entonces $x \in A \cap Ω$. Por lo tanto, $A \subset A \cap Ω$ ... ( 2 ).
Así, de ( 1 ) y ( 2 ), tenemos que: $A \cap Ω = A$.
Por la definición de complemento $A - B = \{x \in Ω | x \in A$ y $x \notin B\},$ sabemos que si $x \in A - ∅$, entonces $x \in A$. Por lo tanto, $A - ∅ \subset A$ ... ( 1 ).
Además, si $x \in A$, entonces $x \in A - ∅$. Por lo tanto, $A \subset A - ∅$ ... ( 2 ).
Así, de ( 1 ) y ( 2 ), tenemos que: $A - ∅ = A$.
Haremos ver que:
Si $x \in (A \cup B)^c$, entonces $x \notin A \cup B$. Por lo tanto, $x \notin A$ y $x \notin B$ (si estuviera en alguno, estaría en la unión). De donde, $x \in A^c$ y $x \in B^c$, entonces $x \in A^c \cap B^c$. Por lo tanto, $(A \cup B)^c \subset A^c \cap B^c$ ... ( 1 ).
Si $x \in A^c \cap B^c$, entonces $x \in A^c$ y $x \in B^c$. Por lo tanto, $x \notin A$ y $x \notin B$. De donde, $x \notin A \cup B$, entonces $x \in (A \cup B)^c$ (si estuviera en la unión, estaría en alguno). Por lo tanto, $A^c \cap B^c \subset (A \cup B)^c$ ... ( 2 ).
Así, de ( 1 ) y ( 2 ), tenemos que: $(A \cup B)^c = A^c \cap B^c$.
Haremos ver que:
Si $x \in (A \cap B)^c$, entonces $x \notin A \cap B$. Por lo tanto, $x \notin A$ o $x \notin B$ (basta que no esté en alguno para que no esté en la intersección). De donde, $x \in A^c$ o $x \in B^c$, entonces $x \in A^c \cup B^c.$ Por lo tanto, $(A \cap B)^c \subset A^c \cup B^c$ ... ( 1 ).
Si $x \in A^c \cup B^c$, entonces $x \in A^c$ o $x \in B^c$. Por lo tanto, $x \notin A$ o $x \notin B$. De donde, $x \notin A \cap B$, entonces $x \in (A \cap B)^c$ (si no está en alguno, no está en la intersección). Por lo tanto, $A^c \cup B^c \subset (A \cap B)^c$ ... ( 2 ).
Así, de ( 1 ) y ( 2 ), tenemos que: $(A \cap B)^c = A^c \cup B^c$.
En la siguiente construcción interactiva puedes practicar los conocimientos adquiridos, de manera gráfica mediante diagramas de Venn.
El interactivo anterior también te podrá servir para observar de manera gráfica, las siguientes propiedades.
Sean $A, B \subset Ω$. Podemos ver que:
$A \cap B = B \cap A$
$A \cup B = B \cup A$
$A - B \neq B - A$
$A \subset A \cup B$
$A \cap B \subset A$
$A - B \subset A$
$B \subset A \cup B$
$A \cap B \subset B$
$B - A \subset B$
$(A \cup B)^c = A^c \cap B^c$
$(A \cap B)^c = A^c \cup B^c$
La Facultad de Ciencias está organizando sus equipos para participar en las Olimpiadas nacionales de Matemáticas, Física y Biología. Cientos de jóvenes han acudido a la Convocatoria con la intención de participar en una o más de las disciplinas. Después de varias encuestas y rondas de exámenes diagnósticos, la computadora arrojó los siguientes resultados:
Urge tomar una decisión y como siempre, por cuestiones presupuestales, el Consejo Técnico urge a la Comisión de Organización, saber lo siguiente:
¿Cuántos jóvenes están en condiciones de participar en las olimpiadas de las tres disciplinas?
Denotaremos los conjuntos de jóvenes en condiciones de participar en las olimpiadas por cada disciplina, por sus letras iniciales: $M$ para Matemáticas, $F$ para Física y $B$ para Biología.
Así, tenemos, los siguientes números:
Para responder a este problema, será necesario calcular $\#(M \cap F \cap B)$.
Sabemos que: $\#(M \cup F) = \#(M) + \#(F) - \#(M \cap F)$.
De donde: $\#(M \cap F) = \#(M) + \#(F) - \#(M \cup F) = 400 + 390 - 680 = 110$ ... ( 1 ).
Además: $M \cap F = (M \cap F) \cap Ω = (M \cap F) \cap (B^c \cup B) = (M \cap F \cap B^c) \cup (M \cap F \cap B)$.
Y como $(M \cap F \cap B^c) \cap (M \cap F \cap B) = ∅$, entonces:
$\#(M \cap F) = \#(M \cap F \cap B^c) + \#(M \cap F \cap B)$ ... ( 2 ).
Despejando de ( 2 ), nos queda:
$\#(M \cap F \cap B) = \#(M \cap F) - \#(M \cap F \cap B^c)$ ... ( 3 ).
Sustituyendo ( 1 ) en ( 3 ) y el valor de $\#(M \cap F \cap B^c) = 90$, nos queda:
$\#(M \cap F \cap B) = 110 - 90 = 20$
En conclusión, solamente $20$ de los cientos de jóvenes, estarían en posibilidad de participar en las olimpiadas de las tres disciplinas
Aquí podrás encontrar un resumen sobre las proposiciones lógicas, sus operaciones, propiedades importantes y sobre todo, los métodos de demostración con algunos ejemplos interactivos.
Encontrarás también la ayuda necesaria para comprender lo que significa demostrar y para comprender los diferentes métodos de demostración que puedes utilizar.
Esta breve lección de lógica está pensada para ofrecerte lo mínimo necesario para que puedas entrarle a hacer demostraciones y con ello, facilitarte el tránsito en tus primeros cursos, particularmente en el de Cálculo Diferencial e Integral I.
Utilizaremos alguna otra simbología como la siguiente:
Si buscas en el diccionario encontrarás lo siguiente acerca del término Proposición:
Para abreviar diremos que gramaticalmente una proposición, es una oración, que afirma o niega algo de alguien, donde ese alguien puede ser singular o plural, masculino, femenino o neutro.
Por ejemplo, “Los triángulos son las figuras geométricas más bonitas” es una oración que afirma algo sobre los triángulos y por lo mismo es una proposición gramatical.
Sin embargo “El dulce de la miel” es tan solo una frase que no afirma, ni niega algo sobre el dulce de la miel, como pudiera ser “me empalaga”. Distinto sería decir: “La miel es dulce”, en este caso, sí sería una proposición gramatical.
Una proposición lógica, es una proposición gramatical, pero con la característica fundamental de que pueda ser VERDADERA o FALSA, pero no ambas.
En el diccionario la acepción matemática de proposición es: “Enunciación de una verdad demostrada o que se trata de demostrar”. Obviamente esto no sería posible si la expresión misma tuviese ambigüedades en sus valores de verdad.
Es decir, una proposición lógica debe tener perfectamente definido su valor de verdad: o FALSA o VERDADERA.
Nos referiremos a una proposición lógica simplemente con el nombre de PROPOSICIÓN, entendiendo que sus valores de verdad están bien definidos.
Recordemos que en adelante nos referiremos a las proposiciones lógicas, simplemente como PROPOSICIONES.
Las proposiciones se clasifican en dos tipos: Simples y Compuestas, dependiendo de como están conformadas.
Son aquellas que no tienen oraciones componentes afectadas por negaciones (“no”) o términos de enlace como conjunciones (“y”), disyunciones (“o”) o implicaciones (“si ... entonces”). Pueden aparecer términos de enlace en el sujeto o en el predicado, pero no entre oraciones componentes.
Una proposición será compuesta si no es simple. Es decir, si está afectada por negaciones o términos de enlace entre oraciones componentes.
En los siguientes ejemplos usaremos S para las simples y C para las compuestas:
| Las medianas de un triángulo se intersecan. | S | No existen negaciones, ni términos de enlace. |
| El 14 y el 7 son factores del 42. | S | Aunque hay un término de enlace, éste afecta al sujeto. |
| El 14 es factor del 42 y el 7 también es factor del 42. | C | Existen dos proposiciones enlazadas por una conjunción. |
| El 2 o el 5 son divisores de 48. | S | Aunque hay un término de enlace, éste afecta al sujeto. |
| El 2 es divisor de 48 o el 5 es divisor de 48. | C | Existen dos proposiciones enlazadas por una disyunción. |
| No todos los números primos son impares. | C | Existe una negación que afecta a una proposición. |
| Un entero no primo mayor de 1, es divisible por un primo | S | Aunque existe un no, éste afecta al sujeto. |
| Si sumamos dos primos, entonces la suma es un primo. | C | Existe una implicación como término de enlace. |
| La suma de dos primos es un primo. | S | No existen negaciones, ni términos de enlace. |
Existen proposiciones, Simples o Compuestas, que están formuladas en términos de una o más variables como por ejemplo:
A este tipo de proposiciones se les conoce como Abiertas dado que son falsas o verdaderas, dependiendo del valor de la variable (o las variables).
Sin embargo algo muy importante al respecto, es que la o las variables deben tener definido un Dominio que hagan que tales proposiciones sea lógicas.
Por ejemplo en la 1., no valdría sustituir $x$ por un número complejo o por una persona. De inmediato se antoja que el Dominio sean números reales.
Este tipo de proposiciones son frecuentes, si no es que las más, en nuestros cursos de matemáticas.
Denotaremos la proposiciones simples como $p$, $q$, $r$, etc. y definiremos cuatro operaciones básicas entre proposiciones: la negación (no), la conjunción (y), la disyunción (o) y la implicación ($⟹$).
Dada una proposición $p$, su negación $no \; p$ es aquella proposición que es falsa cuando $P$ es verdadera y, es verdadera cuando $p$ es falsa.
Dadas las proposiciones $p$, $q$. La conjunción $p$ y $q$ es aquella proposición que sólo es verdadera, cuando ambas son verdaderas. En cualquier otro caso es falsa.
Dadas las proposiciones $p$, $q$. La disyunción $p$ o $q$ es aquella proposición que sólo es falsa, cuando ambas son falsas. En cualquier otro caso es verdadera.
Dadas las proposiciones $p$, $q$. La implicación $p ⟹ q$ es aquella proposición que sólo es falsa, cuando $p$ es verdadera y $q$ es falsa. En cualquier otro caso es verdadera.
Una manera de representar visualmente los valores de verdad de una proposición compuesta de acuerdo con las combinaciones posibles de los valores de verdad de sus componentes, es mediante las llamadas tablas de verdad, las cuales son un arreglo con renglones y columnas.
En el primer renglón se colocan ordenadamente las proposiciones componentes y la proposición resultante y en los siguientes, las combinaciones posibles de los valores de verdad de las componentes y los correspondientes de la resultante. Veamos:
| $p$ | $no \; p$ |
| V | F |
| F | V |
$p$ verdadera, $no \; p$ falsa y viceversa.
| $p$ | $q$ | $p$ y $q$ |
| V | V | V |
| V | F | F |
| F | V | F |
| F | F | F |
Sólo es verdadera cuando ambas son verdaderas.
| $p$ | $q$ | $p$ o $q$ |
| V | V | V |
| V | F | V |
| F | V | V |
| F | F | F |
Sólo es falsa cuando ambas son falsas.
| $p$ | $q$ | $p ⟹ q$ |
| V | V | V |
| V | F | F |
| F | V | V |
| F | F | V |
Sólo es falsa cuando $p$ es verdadera y $q$ falsa.
Las propiedades que veremos en esta sección, serán fundamentales para entender los métodos de demostración.
Definición 1. Dos proposiciones $p$, $q$ son equivalentes si siempre que $p$ es verdadera, también lo es $q$ y viceversa. Notación: $p ≈ q$.
Definición 2. En la proposición $p ⟹ q$, a $p$ se le llama antecedente y a $q$ consecuente, o también hipótesis y conclusión, respectivamente.
Definición 3. A la proposición $q ⟹ p$, se le llama la recíproca de $p ⟹ q$. Algunos autores también le llaman la inversa de $p ⟹ q$.
Definición 4. $p ⟺ q$ se lee: “$p$ si y sólo si $q$” y significa la conjunción de $p ⟹ q$ y $q ⟹ p$.
En la construcción de verdades matemáticas, es muy importante saber construir negaciones de proposiciones compuestas. Aquí presentamos algunas de las más usuales:
$no (no \; p) ≈ p$
$no (p$ y $q) ≈ no \; p$ o $no \; q$
$no (p$ o $q) ≈ no \; p$ y $no \; q$
$no (p ⟹ q) ≈ p$ y $no \; q$
Definición 5. A la proposición $no \; q ⟹ no \; p$ se le llama la contrarrecíproca de $p ⟹ q$. A esta proposición algunos autores también le llaman contrapuesta.
Con esta proposición se puede formular la siguiente equivalencia:
$p ⟹ q ≈ no \; q ⟹ no \; p$.
Definición 6. Un absurdo (o contradicción) es la conjunción de una proposición $w$ cualquiera con su negación.
Es decir, un absurdo es una proposición de la forma: $w$ y $no \; w$ para alguna proposición $w$.
Importa que reflexiones en que un absurdo es una proposición que siempre es falsa.
Con un absurdo, se puede formular una equivalencia muy importante.
$p ⟹ q ≈ (p$ y $no \; q ⟹ w$ y $no \; w$ para alguna $w)$.
Definición 7. Si $p = p_1$ o $p_2$ o $...$ o $p_n$, entonces se dice que $p ⟹ q$, es una implicación por casos y además:
$p ⟹ q ≈ (p_1 ⟹ q$ y $p_2 ⟹ q$ y $...$ y $p_n ⟹ q)$.
Sabemos que las proposiciones afirman o niegan algo de un sujeto.
Dependiendo del sujeto, incluyen un cuantificador.
Ejemplifiquemos y analicemos caso por caso:
En las proposiciones 1., 2., 3. y 4. se afirma algo sobre un todo.
Es decir, se afirma algo sobre todos los elementos de un cierto conjunto.
Por ello se dice que tales proposiciones incluyen un “cuantificador universal”.
En cambio en las proposiciones 5. y 6. la afirmación es sobre alguien singular.
Por ello se dice que tales proposiciones incluyen un “cuantificador existencial”.
Reflexionando sobre la proposición 1., se puede descubrir que no todos los múltiplos de 2 son múltiplos de 4, es decir:
La proposición 1. es falsa porque “Existe un múltiplo de 2 (por ejemplo el 6), que no es múltiplo de 4”.
Similarmente, reflexionando sobre la proposición 3., se pueden encontrar números pares divisibles por 3, es decir:
La proposición 3. es falsa porque “Existe un entero par (por ejemplo el 12), que si es divisible por 3”.
Así mismo, resolviendo la ecuación dada en la proposición 5., se da uno cuenta que las soluciones no son naturales ($x_1 = -1$, $x_2 = -2$), es decir:
La proposición 5. es falsa porque “Ninguna de las soluciones de la ecuación $x^2 + 3x + 2 = 0$, son naturales”.
¡Observa que un universal se niega con un existencial y viceversa!
Las proposiciones 2., 4. y 6. son verdaderas y por lo tanto requieren de demostración.
En este caso, son muy sencillas, pero las dejaremos para los ejemplos de demostraciones, más adelante.
Con cierta frecuencia, los cuantificadores en la proposiciones, no aparecen de manera explícita, por ejemplo:
La proposición 1. podría redactarse del siguiente modo:
Si $x$ es múltiplo de 2, entonces $x$ es múltiplo de 4.
Igualmente la proposición 5. podría redactarse del siguiente modo:
El conjunto solución de la ecuación $x^2 + 3x + 2 = 0$, es subconjunto del conjunto de los números Naturales.
Se aplican cuando se desea deducir una proposición $q$, a partir de una proposición $p$ que se considera verdadera.
Es decir, se aplican para demostrar la veracidad de $q$, suponiendo la veracidad de $p$.
Considerando la hipótesis $p$ verdadera, si la implicación se construye utilizando los métodos de demostración y una sucesión de razonamientos verdaderos, por consecuencia se arribará a una conclusión $q$ verdadera.
Veamos en este sentido lo que significa demostrar para algunos autores:
“Demostrar un teorema significa que el matemático lo deduzca, mediante un razonamiento lógico, a partir de propiedades fundamentales de los conceptos que aparecen en el teorema. De este modo, no sólo los conceptos, sino también los métodos de la matemática, son abstractos y teóricos”
La matemática: su contenido, métodos y significado, Aleksandrov, Kolmogorov, Laurentiev y otros, Alianza universidad.
“...una demostración es un sistema de razonamientos por medio de los cuales la veracidad de la proposición que se demuestra se deduce de axiomas y de verdades antes demostradas”
Acerca de la demostración en Geometría, A. I. Fetísov, Lecciones Populares de Matemáticas, Editorial MIR.
“Dada una proposición de la forma Si $A$ entonces $B$, llamamos a $A$ hipótesis y a $B$ conclusión. Así, la idea de demostrar una proposición del tipo anterior, consiste en suponer que $A$ es verdadero, y al construir una cadena de argumentos, obtener que $B$ es verdadero.”
Esto es, con los métodos de demostración se trata de validar el primer caso de la tabla de verdad de la implicación:
| $p$ | $q$ | $p ⟹ q$ |
| V | V | V |
| V | F | F |
| F | V | V |
| F | F | V |
Es importante recordar que si se parte de $p$ verdadera y la implicación o algunos de los argumentos en la cadena de razonamientos es falsa, no se puede arribar a $q$ verdadera (segundo caso de su tabla de verdad).
De manera similar, si la proposición $p$ de la cual se parte es falsa, no obstante que la cadena de razonamientos sea correcta, no se puede garantizar el arribo a $q$ verdadera.
En los siguientes apartados veremos los distintos métodos de demostración, para lo cual se recomienda tener en cuenta las distintas equivalencias vistas en el apartado de Propiedades importantes.
Este método consiste en construir una sucesión de proposiciones $p_1$, $p_2$, $...$, $p_n$, todas ellas verdaderas, partiendo de $p = p_1$ y terminando en $p_n = q$. En cada paso, se pueden usar la hipótesis $p$ y resultados previamente establecidos, como definiciones, axiomas u otras proposiciones, incluyendo las que se van construyendo en la sucesión.
La expresión lógica de este método es la siguiente:
$$\underbrace{(p_1 \text{ o } p_2 \text{ o } ... \text{ o } p_{i-1}) ⟹ p_i}_{\text{verdadera}} \;\;\;\; \forall i = 2, ..., n$$$k$ impar $⟹ k^2$ impar
$k$ par $⟹ k^2$ par
$\sqrt{x^2 + 1} = x - 1 ⟹ x = 0$
$\Large x + 2y = 5 \atop 3x - y = 1$ $⟹ x = 1$ y $y = 2$
$9x^2 + 4y^2 - 8y - 32 = 0 ⟹ \dfrac{x^2}{4} + \dfrac{(y - 1)^2}{9} = 1$
Suma de par con impar es impar
Suma de dos impares es par
Suma de par con par es par
$A \subset B ⟹ B^c \subset A^c$
Te habrás dado cuenta que ya has usado este método, por ejemplo cuando resuelves un sistema de ecuaciones, cuando deduces una fórmula o cuando deduces propiedades geométricas, etc.
Dependiendo de la proposición a demostrar puedes usar uno u otro método, pero frecuentemente cuando una proposición $p ⟹ q$, se te resista al método directo, podrás usar otros métodos como los que verás en este y los siguientes apartados, en particular éste de la contrarrecíproca.
Este método está basado en la equivalencia:
$p ⟹ q ≈ no \; q ⟹ no \; p$
Por ello, para demostrar que $p ⟹ q$, se parte de la negación de la conclusión $no \; q$ y de ello se deduce la negación de la hipótesis $no \; p$.
Este método también se enuncia del siguiente modo:
Para demostrar que $p ⟹ q$, se parte de suponer que la conclusión $q$ es falsa y de ahí se deduce que la hipótesis $p$ es falsa.
En adelante denotaremos por $∅$ al conjunto vacío.
$A \subset B ⟹ B^c \subset A^c$
Sea $k \in \mathbb{Z}. k^2$ par $⟹ k$ par
Sea $k \in \mathbb{Z}. k^2$ impar $⟹ k$ impar
Si $A$ es cualquier conjunto, entonces $A \cap A^c = ∅$
Existen proposiciones que es posible demostrarlas mediante el método directo y también por Contrarrecíproca, pero también las hay que no permiten ser demostrados por el método directo.
En los ejemplos anteriores, el primero es posible hacerlo por el método directo o por contrarrecíproca. Sin embargo, el segundo, el tercero y el cuarto no son posibles por método directo. En esos casos nos queda recurrir al de la Contrarrecíproca o inclusive al de Reducción al absurdo.
Este método es frecuentemente utilizado y aveces, hasta el favorito de muchos matemáticos, por la gran versatilidad que ofrece. Dependiendo de la proposición a demostrar puedes usar uno u otro método, pero frecuentemente cuando una proposición $p ⟹ q$, se te resista al método directo, podrás usar otros métodos como éste de reducción al absurdo.
Este método está basado en la equivalencia:
$p ⟹ q ≈ (p$ y $no \; q ⟹ w$ y $no \; w$ para alguna $w)$
Así, en este método, para demostrar que $p ⟹ q$, se construye un absurdo usando la hipótesis $p$ y la negación de la conclusión $no \; q$.
Este método también se enuncia del siguiente modo:
Para demostrar que $p ⟹ q$, se construye un absurdo, suponiendo falsa la conclusión $q$ y usando la hipótesis $p$.
En adelante denotaremos por $∅$ al conjunto vacío.
Si $A \subset B$, entonces $A - B = ∅$
Sean $n, m \in \mathbb{N}$. Si $nm$ es impar, entonces $n$ y $m$ son impares
Si $A - B = ∅$, entonces $A \subset B$
Si A es cualquier conjunto, entonces $A \cap A^c = ∅$
Si $A \cup B \subset B$, entonces $A - B = ∅$
Los métodos por contrarrecíproca y de reducción al absurdo se parecen en que en ambos se construye una contradicción usando la negación de la conclusión.
Sin embargo, la diferencia es que, en el primero la contradicción es con la hipótesis y en el segundo la hipótesis también se utiliza y la contradicción es con cualquier otra proposición, axioma, definición, postulado, etc.
En muchas proposiciones es posible aplicar cualquiera de ambos métodos para su demostración, como se puede observar en los ejemplos de arriba. Están demostrados por reducción al absurdo, pero bien pudieron demostrarse por Contrarrecíproca.
Este método solamente es posible utilizarlo cuando la hipótesis $p$ es una disyunción de casos, es decir cuando $p = p_1$ o $p_2$ o $...$ o $p_n$.
Este método está basado en la equivalencia:
$p ⟹ q ≈ (p_1 ⟹ q$ y $p_2 ⟹ q$ y $...$ $p_n ⟹ q)$
Este método se explica señalando que para demostrar que $p ⟹ q$, es necesario demostrar que todos los casos de la hipótesis implican la conclusión.
Si $n \in \mathbb{Z}$, entonces $n^2 + n + 1$ es impar
Si $a \in \mathbb{R}$, entonces $|a| \ge 0$
Si $a \in \mathbb{R}$, entonces $|a| = |-a|$
En el método por casos, como ya señalamos, es necesario demostrar que todos los casos de la hipótesis implican la conclusión.
Sin embargo, para la demostración en cada uno de los casos, se tendrán que aplicar alguno de lo métodos ya vistos.
Puede suceder inclusive que en una demostración se apliquen varios métodos en diversas partes de la misma.
El método por contraejemplo se aplica de manera muy particular para demostrar la falsedad de proposiciones cuya hipótesis está construida mediante un “cuantificador universal”. Esto es, se aplica para demostrar la falsedad de una proposición que tenga una conclusión referida para “todos los elementos de un cierto conjunto”.
Para demostrar la falsedad de proposiciones de este tipo, basta exhibir un elemento que satisfaga la hipótesis de la proposición, pero que no satisfaga su conclusión. A dicho elemento se le conoce con el nombre de contraejemplo.
El uso del contraejemplo, es muy útil cuando uno se encuentra ante una proposición con cuantificador universal, de la cuál no se sabe si es verdadera o falsa.
La primera idea es buscar un contraejemplo. Si no se encuentra en una primera instancia, se intentará demostrar su veracidad aplicando los otros métodos o una combinación de ellos.
Demostrar que son FALSAS las siguientes proposiciones:
$a, b \in \mathbb{R} ⟹ |a + b| = |a| + |b|$
$a, b \in \mathbb{R}$ y $a^2 = b^2 ⟹ a = b$
$A - B = B - A \;\;\; \forall A$ y $B$ conjuntos
No obstante que pueda haber muchos casos en los que sí se satisfaga la implicación, basta con uno sólo en el que no ocurra, para asegurar que tales proposiciones son falsas.
Aquí podrás encontrar unas cuantas notas sobre el concepto de número y su desarrollo.
El concepto de número no fue elaborado por la humanidad de una vez y para siempre, tuvo que pasar por un proceso sumamente lento, acorde a su desigual desarrollo y a sus necesidades sociales. Algunos pueblos no sobrepasaban a unos cuantos números, los mínimos necesarios para resolver sus problemas cotidianos.
Aún actualmente se da este fenómeno, como lo reporta un estudio realizado en Agosto del 2004 en una tribu amazónica, en donde se contesta negativamente a la pregunta ¿Es innato el concepto de número?.
Estos pueblos aunque podían juzgar, a su modo, sobre el tamaño de una u otra colección de objetos con los que se encontraban a diario, aun no tenían la noción de número. De hecho los números eran directamente percibidos por ellos como una propiedad inseparable de una colección de objetos, propiedad que sin embargo no podían distinguir claramente.
A un nivel inmediatamente superior, el número aparece ya como una propiedad de una colección de objetos, aunque no se distingue todavía de la colección, en cuanto número no relacionado con objetos concretos. Esto salta a la vista si se observan los nombres que reciben algunos números entre ciertos pueblos: “mano” para cinco, “hombre” completo para veinte, por ejemplo.
El número de objetos de una colección dada es una propiedad de la colección, pero el número en sí, es una propiedad que no era aún abstraída de la colección concreta y considerada simplemente en sí misma. Por consecuencia aun no era abstraída la idea de que un número podía representar la propiedad común de un universo de colecciones. Por ejemplo, aun no se concebía al número “cinco” como la propiedad común a todas las colecciones que contienen tantos objetos como dedos hay en una mano.
Es seguro que el carácter abstracto de la idea de número requiere de un estado algo avanzado del desarrollo intelectual, mismo que ocurre después de diversas y múltiples experiencias en la labor de contar y, de comparar y comparar colecciones. En el pensamiento infantil la idea de número permanece siempre relacionado con objetos tangibles a su alcance, como por ejemplo los dedos de la mano.
Entre otras cosas, la dificultad en la construcción de la idea abstracta de número es porque en ella, se encuentra implícito el concepto de relación biunívoca. Si entre dos colecciones cualesquiera existe una relación biunívoca, entonces tienen una misma propiedad representada por un mismo número.
Es decir, se podría establecer la siguiente definición:
Un número es aquella propiedad de las colecciones de objetos cuyos objetos pueden ponerse en correspondencia biunívoca unos con otros, y que es diferente en aquellas otras colecciones para las cuales tal correspondencia es imposible.
En el proceso de contar, la humanidad no sólo descubrió y asimiló las relaciones entre los números, sino que por consecuencia fueron construyendo operaciones, nuevos números como los enteros y gradualmente fueron estableciendo leyes generales.
Fueron comprendiendo los números no como entidades separadas, sino como un sistema con sus relaciones mutuas y sus reglas generales, igualmente fueron comprendiendo el concepto de infinitud en los números y así de esta manera nace el objeto de estudio de la aritmética.
La introducción de símbolos numéricos fue producto del desarrollo social, pero a su vez, ésto jugó un papel muy importante en el desarrollo de la aritmética. Los símbolos numéricos no sólo significaron una materialización del concepto de número abstracto, sino que además proporcionaron un medio sencillo para realizar operaciones.
Además la introducción de símbolos numéricos marcó la primera etapa hacia la simbología matemática, la segunda etapa, que se produjo mucho más tarde, fue la introducción de signos para las operaciones y la designación de literales para las incógnitas.
Los números fraccionarios fueron producto de la interrelación entre la aritmética y la geometría.
La simple medición de una línea representa una fusión de estas ramas de la matemática. Para medir la longitud de un objeto se le aplica a éste una cierta unidad de longitud y se calcula cuántas veces es posible repetir esta operación.
Sin embargo en este proceso de medición ocurre con frecuencia que la unidad elegida no está contenida un número entero de veces en el objeto a medir. Así surge la necesidad de fraccionar la unidad de medida para poder expresar el resultado con mayor exactitud, en fracciones de la misma unidad.
En todo este desarrollo, el elemento común era el de contar, contar y contar. Desde contar objetos enteros, hasta contar fracciones.
Pero la aparición de las fracciones fue solo la primera etapa. La siguiente etapa y muy importante, fue el descubrimiento de los intervalos inconmensurables y que dieron origen a los llamados números irracionales, mismos que no pueden expresarse por una fracción ordinaria de enteros.
Con el descubrimiento de estos números, la construcción de los reales se dio a partir de la conjunción de los racionales (fracciones) y los irracionales (inconmensurables), con reglas y operaciones comunes.
Se pudieron axiomatizar y a partir de esto, se han demostrado diversas propiedades como las leyes de cancelación, las leyes de los signos, etc.
Todo conjunto $A$ (no vacío) de reales, acotado superiormente posee un supremo, es decir, existe un real $s$ que es la mínima de las cotas superiores de $A$ ($s = sup A$).
fue clave en la construcción de los irracionales y por consecuencia en la posibilidad de axiomatizar los números reales.
Con este axioma ha sido posible atribuir a los números reales la propiedad de continuidad, es decir, de poder establecer una correspondencia biunívoca de los reales con los puntos de una recta.
En la construcción del concepto de número, se pueden distinguir tres etapas, íntimamente relacionadas y de ninguna manera, separadas tajantemente unas de otras.
A pesar de que el concepto de número, fue elaborado con tanta dificultad y a través de tanto tiempo, hoy para los niños es relativamente fácil de dominar. La primera razón es que el niño vive en un medio donde los números son de uso común y le enseñan a manejarlos, pero la segunda razón es que el niño actual ya dispone de palabras y signos para los números.
La axiomatización de los números reales, permite un estudio más sistemático de ellos y permite generalizar sus leyes a otras estructuras algebraicas que satisfagan estos mismo axiomas. Aún más, el modelo de axiomatización ha sido la base para el estudio de muchas más estructuras algebraicas.
La Matemática: Su contenido, métodos y significado. Aleksandrov, Kolmogorov, Laurentiev y otros Alianza Editorial.
| Nombre | Adición | Multiplicación |
| Cerradura | A1) $\forall a, b \in \mathbb{R}, a + b \in \mathbb{R}$ | M1) $\forall a, b \in \mathbb{R}, ab \in \mathbb{R}$ |
| Conmutativa | A2) $\forall a, b \in \mathbb{R}, a + b = b + a$ | M2) $\forall a, b \in \mathbb{R}, ab = ba$ |
| Asociativa | A3) $\forall a, b, c \in \mathbb{R}, a + (b + c) = (a + b) + c$ | M3) $\forall a, b, c \in \mathbb{R}, a(bc) = (ab)c$ |
| Neutro | A4) $\exist 0 \in \mathbb{R}$ tal que $\forall a \in \mathbb{R}, a + 0 = 0 + a = a$ | M4) $\exist 1 \in \mathbb{R}$ con $1 \neq 0$ tal que $\forall a \in \mathbb{R}, a1 = 1a = a$ |
| Inverso | A5) Para cada $a \in \mathbb{R}, \exist -a \in \mathbb{R}$ tal que $a + (-a) = (-a) + a = 0$ | M5) Para cada $a \in \mathbb{R}$ con $a \neq 0, \exist a^{-1} \in \mathbb{R}$ tal que $aa^{-1} = a^{-1}a = 1$ |
| Nombre | Orden |
| Tricotomía | O1) $\forall a, b \in \mathbb{R}$, se cumple una y sólo una de las siguientes relaciones: $a = b$ o $a \lt b$ o $b \lt a$ |
| Transitiva | O2) Si $a \lt b$ y $b \lt c$, entonces $a \lt c$ |
| Preserva Orden bajo Adición | O3) Si $a \lt b$ entonces $a + c \lt b + c \;\;\;\; \forall c \in \mathbb{R}$ |
| Preserva Orden bajo Multiplicación ($0 \lt c$) | O4) Si $0 \lt c$ y $a \lt b$ entonces $ac \lt bc$ |
| Axioma del Supremo | S) En la sección “Otros modelos de números” encontrarás su enunciado y algunas aplicaciones |
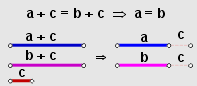
Así se conoce este teorema, cuya demostración puedes ir descubriendo paso a paso, en el siguiente interactivo.
La idea es partir de $a$, y mediante una cadena de igualdades llegar a $b$, utilizando el llamado
Para construir tal cadena de igualdades se deben utilizar exclusivamente los
“Si en una expresión se sustituye un objeto por otro igual, la expresión resultante es igual a la anterior”.
En adelante nos referiremos a éste como Principio de sustitución.
Si $a = b$, entonces $a + c = b + c$.
Basta que en la expresión $a + c$, se sustituya $a$ por $b$ y entonces queda que $a + c = b + c$.
Así, juntando la ley de cancelación para la adición y el recíproco, mostrado en el ejemplo anterior, se tiene un resultado más general, es decir:
$a + c = b + c ⟺ a = b$
Este resultado permite tanto sumar como cancelar una misma cantidad en ambos lados de una igualdad, lo cual es de suma importancia en la resolución de ecuaciones.
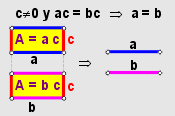
Así se conoce este teorema, cuya demostración puedes ir descubriendo paso a paso, en el siguiente interactivo.
La idea es partir de a, y mediante una cadena de igualdades llegar a b, utilizando el llamado
Para construir tal cadena de igualdades se deben utilizar exclusivamente los
Si $a = b$, entonces $ac = bc$
Basta que en la expresión $ac$, se sustituya $a$ por $b$ y entonces queda que $ac = bc$.
Así, juntando la ley de cancelación para la multiplicación y su recíproco mostrado en el ejemplo anterior, se tiene un resultado más general, es decir:
Si $c \neq$, entonces $ac = bc ⟺ a = b$
Este resultado permite tanto multiplicar como cancelar una misma cantidad (distinta de cero), en ambos lados de una igualdad, lo cual es de suma importancia en la resolución de ecuaciones.
Así se conoce este teorema, cuya demostración puedes ir descubriendo paso a paso, en el siguiente interactivo.
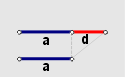
La idea es partir de la hipótesis de que $d$, es un neutro aditivo y demostrar que $d = 0$, utilizando el llamado
Con esto se demuestra que no hay otro elemento, más que el $0$, que satisfaga el axioma (A4).
Para construir esta demostración se deben utilizar exclusivamente los
Este teorema permitirá referirnos de aquí en adelante al $0$, como el neutro aditivo de los números reales.
Además la unicidad del neutro aditivo, junto con la relación de orden, permite definir los reales positivos y negativos:
$a$ es positivo, si $0 \lt a$
y
$a$ es negativo, si $a \lt 0$
Así se conoce este teorema, cuya demostración puedes ir descubriendo paso a paso, en el siguiente interactivo.
La idea es partir de suponer que $d$ es un inverso aditivo de $a$ y demostrar que $d = -a$, utilizando el llamado
Con esto se demuestra que no hay otro elemento, más que $-a$, que satisfaga el axioma (A5) y de ahí también se justifica el nombre que se le ha asignado en los axiomas.
Para construir la demostración se deben utilizar exclusivamente los
La unicidad del inverso aditivo permitirá de aquí en adelante, referirnos a $-a$, como el inverso aditivo de $a$.
Es decir, que cada número real sólo posee un inverso aditivo.
Igualmente $a$ es el inverso aditivo de $-a$.
Así se conoce este teorema, cuya demostración puedes ir descubriendo paso a paso, en el siguiente interactivo.
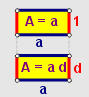
La idea es partir de suponer que $d$, es un neutro multiplicativo y demostrar que debe ser igual a $1$, utilizando el llamado
Con esto se demuestra que no hay otro elemento, más que $1$, que satisfaga el axioma (M4).
Para construir tal demostración se deben utilizar exclusivamente los
La unicidad del Neutro Multiplicativo permitirá de aquí en adelante, referirnos al $1$ como el neutro multiplicativo de los números reales. Es decir, que en los reales sólo hay un elemento unidad.
Así se conoce este teorema, cuya demostración puedes ir descubriendo paso a paso, en el siguiente interactivo.
La idea es partir de suponer que $d$, es un inverso multiplicativo de $a$ y demostrar que $d = a^{-1}$, utilizando el llamado
Con esto se demuestra que no hay otro elemento, más que $a^{-1}$, que satisfaga el axioma (M5) y de ahí también se justifica el nombre que se le ha dado en los axiomas.
Para construir tal cadena de igualdades se deben utilizar exclusivamente los
La unicidad del inverso multiplicativo, permitirá referirnos a $a^{-1}$ como el inverso multiplicativo de $a$ (distinto de cero). Es decir que cada real diferente de cero, sólo posee un inverso multiplicativo. Igualmente diremos que $a$ es el inverso multiplicativo de $a^{-1}$.
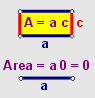
Así se puede nombrar este teorema, cuya demostración puedes ir descubriendo paso a paso, en el siguiente interactivo.
La idea es partir de $a0$, y mediante una cadena de igualdades llegar a $0$, utilizando el llamado
Para construir tal cadena de igualdades se deben utilizar exclusivamente los
Este teorema será de importancia para el siguiente teorema que permite manejar los inversos aditivos en relación a la operación multiplicación, lo que algunos autores llaman las leyes de los signos.
Así se puede nombrar este teorema, cuya demostración puedes ir descubriendo paso a paso, en el siguiente interactivo.
La idea es hacer ver que $(-1)a$ es inverso aditivo de $a$ y, dado que por el Teorema 4, sólo existe un inverso aditivo de $a$, entonces: $(-1)a = -a$.
Para hacer ver que $(-1)a$ es inverso aditivo de $a$, basta demostrar que $a + (-1)a = 0$. Por ello, se trata de iniciar en $a + (-1)a$ y mediante una cadena de igualdades llegar a $0$, utilizando el llamado
Para construir tal cadena de igualdades se deben utilizar exclusivamente los
En particular se hace uso del Teorema 4 que establece:
Dado $a \in \mathbb{R}$, si $a + d = 0$, entonces $d = -a$
y del Teorema 7 que establece:
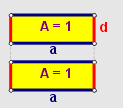
$a0 = 0 \;\;\;\; \forall a \in \mathbb{R}$.
Este teorema es de gran importancia para demostrar las leyes de los signos.
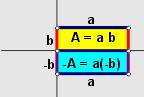
Así se conoce este teorema, que es una de las leyes de los signos, cuya demostración puedes ir descubriendo paso a paso, en el siguiente interactivo.
La idea es partir de $a(-b)$, y mediante una cadena de igualdades llegar a $-(ab)$, utilizando el llamado
Para construir tal cadena de igualdades se deben utilizar exclusivamente los
En particular se hace uso del Teorema 8 que establece:
$-a = (-1)a \;\;\;\; \forall a \in \mathbb{R}$
Este resultado es fundamental en la manipulación de expresiones algebraicas.
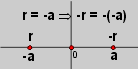
Así se conoce este teorema, cuya demostración puedes ir descubriendo paso a paso, en el siguiente interactivo. A este teorema también se le puede nombrar de la siguiente forma: el inverso aditivo del inverso aditivo de $a$, es $a$.
La idea es hacer ver que $-(-a)$ es inverso aditivo de $(-a)$, y dado que por el Teorema 4, sólo existe un inverso aditivo, entonces $a = -(-a)$.
Así, la idea es iniciar en $-(-a) + (-a)$ y, mediante una cadena de igualdades llegar a 0, utilizando el llamado
Para construir tal cadena de igualdades se deben utilizar exclusivamente los
En particular se hace uso del Teorema 4 que establece:
Dado $a \in \mathbb{R}$, si $a + d = 0$, entonces $d = -a$.
Este teorema prepara la demostración de la ley de los signos que dice: el inverso aditivo de $a$, por el inverso aditivo de $b$, es $ab$.
Así se conoce este teorema, que es una de las leyes de los signos, cuya demostración puedes ir descubriendo paso a paso, en el siguiente interactivo.
La idea es partir de $(-a)(-b)$, y mediante una cadena de igualdades llegar a $(ab)$, utilizando el llamado
Para construir tal cadena de igualdades se deben utilizar exclusivamente los
En particular se hace uso del Teorema 8 que establece:
$-a = (-1)a \;\;\;\; \forall a, b \in \mathbb{R}$.
del Teorema 9 que establece:
$a(-b) = -(ab) \;\;\;\; \forall a, b \in \mathbb{R}$.
y del Teorema 10 que establece:
$-(-a) = a \;\;\;\; \forall a \in \mathbb{R}$.
Este es un buen momento para establecer las siguientes definiciones:
Resta: $a - b = a + (-b)$.
División: $\dfrac{a}{b} = ab^{-1} \;\;\;\; (b \neq 0)$.
Estas definiciones son fundamentales para facilitar la manipulación de expresiones.
Es decir, cuando el producto de dos números es cero, al menos uno de ellos, es cero. La demostración de este teorema la puedes ir descubriendo paso a paso, en el siguiente interactivo.
La idea es suponer que uno de ellos no es cero y demostrar que por fuerza el otro debe ser cero. Así se usa el
La demostración es similar en cualquier caso: o bien, suponiendo que $a$ no es cero y demostrando que $b$ debe ser cero, o bien, suponiendo que $b$ no es cero y demostrando que $a$ debe ser cero.
En la demostración que se presenta se realiza uno de los casos. ¿Puedes realizar el otro caso?
Para construir tal cadena de igualdades se deben utilizar exclusivamente los
En particular se hace uso del Teorema 7 que establece:
$a0 = 0 \;\;\;\; \forall a \in \mathbb{R}$.
El recíproco de este Teorema: Si $a = 0$ o $b = 0$, entonces $ab = 0$, cuya demostración es consecuencia inmediata del Teorema 7 (cualquier real por cero, es cero), se deja como ejercicio.
Así, juntando ambos resultados, se tiene un resultado más general, es decir: $ab = 0 ⟺ a = 0$ o $b = 0$.
Este resultado es fundamental en la manipulación de expresiones y para obtener diversos resultados algebraicos.
Así se puede nombrar este teorema, cuya demostración puedes ir descubriendo paso a paso, en el siguiente interactivo.
La idea es partir de la hipótesis $a^2 = b^2$, y mediante una cadena de $⟺$ (si y sólo si), llegar a la conclusión $a = b$ o $a = -b$, utilizando el llamado
Para construir tal cadena de igualdades se deben utilizar exclusivamente los
En particular se hace uso del Teorema 1 y su recíproco que establecen:
$a + c = b + c ⟺ a = b$.
y del Teorema 12 que establece:
Si $ab = 0$, entonces $a = 0$ o $b = 0$.
Además de la definición de la Resta: $a - b = a + (-b)$.
Este resultado es fundamental para resolver ecuaciones que involucran expresiones cuadráticas.
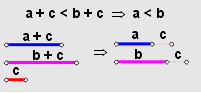
Así se conoce este teorema, cuya demostración puedes ir descubriendo paso a paso, en el siguiente interactivo.
La idea es partir de la hipótesis $a + c \lt b + c$, y mediante una cadena de implicaciones llegar a la conclusión $a \lt b$ utilizando el llamado
Para construir tal cadena de implicaciones se deben utilizar exclusivamente los
El recíproco de este Teorema, es el axioma (O3) que dice: Si $a \lt b$ entonces $a + c \lt b + c \;\;\;\; \forall c \in \mathbb{R}$.
Así, juntando la ley de cancelación para la adición en desigualdades y su recíproco, el axioma (O3), se tiene un resultado más general, es decir:
$a + c \lt b + c ⟺ a \lt b$
Este resultado permite tanto sumar como cancelar una misma cantidad, en ambos lados de una desigualdad, lo cual es de suma importancia en la resolución de desigualdades.
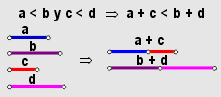
Así se puede nombrar este teorema, cuya demostración puedes ir descubriendo paso a paso, en el siguiente interactivo.
En tal demostración, la idea es, a partir de la hipótesis construir una cantidad $z$, que sea mayor que la suma de menores y menor que la suma de mayores, utilizando el llamado
Para construir tal cantidad $z$ se deben utilizar exclusivamente los
El recíproco de este Teorema: Si $a + c \lt b + d$, entonces $a \lt b$ y $c \lt d$ es FALSO, sería importante que pudieras intentar dar un CONTRAEJEMPLO, es decir, dar cuatro números $a$, $b$, $c$ y $d$, tales que satisfagan la hipótesis $a + c \lt b + d$, pero que no satisfagan la conclusión $a \lt b$ y $c \lt d$.
No todo Teorema tiene un recíproco verdadero. Por ejemplo: “Todo entero múltiplo de 4, es múltiplo de 2”. Sin embargo el recíproco es falso.
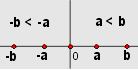
Así se puede nombrar este teorema, cuya demostración puedes ir descubriendo paso a paso, en el siguiente interactivo.
En tal demostración, la idea es partir de la hipótesis $a \lt b$, y mediante una cadena de implicaciones, llegar a la conclusión $-b \lt -a$, utilizando el llamado
Para construir tal cadena de implicaciones se deben utilizar exclusivamente los
El recíproco de este Teorema: Si $-b \lt -a$, entonces $a \lt b$, es en realidad el mismo Teorema 16, ya que $a$ y $-a$ son recíprocos uno de otro. De manera similar $b$ y $-b$. Sin embargo, con los mismos argumentos del teorema, puedes intentar demostrarlo.
Así, juntando ambos resultados, se tiene un resultado más general, es decir:
$a \lt b \iff -b \lt -a$
Este resultado permite decir que los inversos aditivos invierten la desigualdad.
Así se puede recordar este teorema, cuya demostración puedes ir descubriendo paso a paso, en el siguiente interactivo.
La idea es aprovechar el hecho de que si $c \lt 0$, entonces $-c \gt 0$ y entonces utilizar el axioma (O4) de orden, que establece que al multiplicar una desigualdad por un positivo, ésta se conserva. Se utilizará el
Para construir tal cadena de implicaciones se deben utilizar exclusivamente los
En particular se hace uso del Teorema 16 que establece:
Si $a \lt b$, entonces $-b \lt -a$.
y del Teorema 9 que establece:
$a(-b) = -(ab) \;\;\;\; \forall a, b \in \mathbb{R}$.
El recíproco de este Teorema: sea $c \lt 0$, si $ac \gt bc$, entonces $a \lt b$, es verdadero y su demostración, se deja como un ejercicio interesante. Seguro que tendrás que utilizar varios resultados ya vistos.
Así, juntando la ley de cancelación para la adición y su recíproco, se tiene un resultado más general, es decir:
Sea $c \lt 0$, entonces, $ac \gt bc \iff a \lt b$.
Este resultado permite decir que, al multiplicar o cancelar un factor negativo, en ambos lados de una desigualdad, ésta se invierte. Frecuentemente esta propiedad se pasa por alto en la resolución de desigualdades y por supuesto no considerarla, conduce a errores graves.
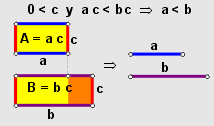
Así se conoce este teorema, cuya demostración puedes ir descubriendo paso a paso, en el siguiente interactivo.
En tal demostración, la idea es utilizar el ejercicio 6 que establece que $c$ y $c^{-1}$ tienen el mismo signo y de ahí, utilizar el cuarto axioma de orden (O4). Así, si $c \gt 0$, entonces $c^{-1} \gt 0$ y viceversa. Se utilizará el
Para construir la cadena de implicaciones de la demostración, se deben utilizar exclusivamente los
El recíproco de este Teorema es el Axioma O4:
Si $0 \lt c$ y $a \lt b$ entonces $ac \lt bc$.
Así, juntando ambos resultados, el axioma O4 y su recíproco, se tiene un resultado más general, es decir: sea $0 \lt c$, entonces, $a \lt b \iff ac \lt bc$.
Este resultado permite decir que al multiplicar o cancelar un mismo factor positivo, en ambos lados de una desigualdad, ésta se conserva. Este resultado es de suma importancia en la resolución de desigualdades.

Así se puede nombrar este teorema, cuya demostración puedes ir descubriendo paso a paso, en el siguiente interactivo.
La idea es usar el ejercicio 7 y el cuarto axioma de orden (O4). Así, partir de la hipótesis $a \lt b$ y mediante una cadena de implicaciones, llegar a la conclusión $b^{-1} \lt a^{-1}$ utilizando el llamado
Para construir tal cadena de implicaciones se deben utilizar exclusivamente los
El recíproco de este Teorema es: sea $ab \gt 0$, si $b^{-1} \lt a^{-1}$, entonces $a \lt b$, es en realidad el mismo Teorema 19, ya que $a$ y $a^{-1}$ son recíprocos uno de otro. De manera similar $b$ y $b^{-1}$. Sin embargo, con los mismos argumentos del teorema, puedes intentar demostrarlo.
Así, juntando ambos resultados, se tiene un resultado más general, es decir:
Sea $ab \gt 0$, entonces $a \lt \iff b^{-1} \lt a^{-1}$.
Este resultado permite refrendar que inversos multiplicativos del mismo signo, invierten la desigualdad. Esto es muy importante considerarlo en la resolución de desigualdades.
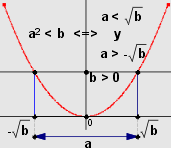
Así se puede nombrar este teorema, cuya demostración puedes ir descubriendo paso a paso, en el siguiente interactivo.
La idea es partir de la hipótesis, y mediante una cadena de dobles implicaciones $\iff$ llegar a la conclusión, utilizando el
Para construir tal cadena de dobles implicaciones se deben utilizar exclusivamente los
En particular se hace uso del Teorema 14 y su recíproco que establecen:
$a + c \lt b + c \iff a \lt b$
Este resultado es muy importante para resolver desigualdades cuadráticas.
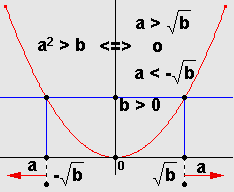
Así se puede nombrar este teorema, cuya demostración puedes ir descubriendo paso a paso, en el siguiente interactivo.
En tal demostración, la idea es partir de la hipótesis, y mediante una cadena de dobles implicaciones $\iff$ llegar a la conclusión, utilizando el llamado
Para construir tal cadena de dobles implicaciones se deben utilizar exclusivamente los
En particular se hace uso del Teorema 14 y su recíproco que establecen:
$a + c \lt b + c \iff a \lt b$.
Este resultado es muy importante para resolver desigualdades cuadráticas.
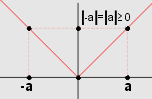
Así se puede nombrar este teorema, cuya demostración puedes ir descubriendo paso a paso, en el siguiente interactivo.
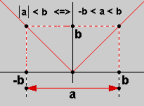
El valor absoluto de un número real $a$, se define de la siguiente manera:
$$|a| = \begin{cases} a &\text{si } a \ge 0 \\ -a &\text{si } a \lt 0 \end{cases}$$Es decir, si $a$ es positivo o cero, su valor absoluto es el mismo $a$, pero si $a$ es negativo, su valor absoluto es el inverso aditivo de $a$.
La idea es hacer ver que los dos únicos casos posibles:
conducen a la conclusión mediante cadenas de implicaciones. Es claro que se usará el
Para construir tales cadenas se deben utilizar exclusivamente los
En particular se hace uso del Teorema 16 que establece:
Si $a \lt b$, entonces $-b \lt -a$.
Este resultado es muy importante, entre otras cosas, para definir el concepto de distancia y de vecindades.
Así se puede nombrar este teorema, cuya demostración puedes ir descubriendo paso a paso, en el siguiente interactivo.
En tal demostración, la idea es hacer ver que los únicos tres casos posibles, que en realidad por la conmutatividad, se pueden reducir a dos:
Caso 1) $a \ge 0$ y $b \ge 0$
Caso 2) $a \ge 0$ y $b \lt 0$
Caso 3) $a \lt 0$ y $b \ge 0$
conducen a la conclusión mediante cadenas de implicaciones, usando el
En la demostración sólo se realizarán los casos 1) y 2). El caso 3) es en realidad el caso 2).
Para construir tales cadenas se deben utilizar exclusivamente los
En particular se hace uso del Teorema 17 que establece:
Sea $c \lt 0$, si $a \lt b$, entonces $ac \gt bc$.
En particular se hace uso del Teorema 9 que establece:
$a (-b) = -(ab) \;\;\;\; \forall a, b \in \mathbb{R}$.
Este resultado es muy importante para el manejo de expresiones con valores absolutos.
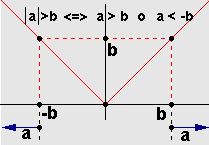
Así se puede recordar este teorema, cuya demostración puedes ir descubriendo paso a paso, en el siguiente interactivo.
La idea es empezar con la hipótesis y mediante una cadena de dobles implicaciones llegar a la conclusión, utilizando el llamado
Es importante recordar que por la ley de tricotomía un real es mayor que cero o igual a cero o menor que cero. Por ello, la definición incluye la disyunción, aunque en general en los libros no aparece explícitamente.
Para construir tales cadenas se deben utilizar exclusivamente los
En particular se hace uso del Teorema 16 y su recíproco que establecen:
$a \lt b \iff -b \lt -a$
Este resultado es muy importante para resolver desigualdades con valores absolutos.
Así se puede recordar este teorema, cuya demostración puedes ir descubriendo paso a paso, en el siguiente interactivo.
La idea es empezar con la hipótesis y mediante una cadena de dobles implicaciones llegar a la conclusión, utilizando el llamado
Es importante recordar que por la ley de tricotomía un real es mayor que cero o igual a cero o menor que cero. Por ello, la definición incluye la disyunción, aunque en los libros no aparece explícitamente.
Para construir tales cadenas se deben utilizar exclusivamente los axiomas de los reales, las hipótesis del teorema, la definición de valor absoluto, teoremas o resultados anteriores.
En particular se hace uso del Teorema 16 y su recíproco que establecen:
$a \lt b \iff -b \lt -a$
Este resultado es muy importante para resolver desigualdades con valores absolutos.
Los números naturales son un conjunto que satisface los siguientes axiomas:
P1)
$1 \in \mathbb{N}$.
P2)
Si $n \in \mathbb{N}$, entonces $\exist n'$ único, sucesor de $n$.
P3)
El $1$ no es sucesor de ningún natural.
P4)
Si $n' = m'$, entonces $n = m$.
P5)
Si $M \subset \mathbb{N}$ y cumple las propiedades: i) $1 \in M$, ii) $n' \in M$ siempre que $n \in M$, entonces $M = \mathbb{N}$.
Conocidos como Axiomas de Peano, en honor al matemático italiano Giuseppe Peano (1858 - 1932), quien los estableciera de manera precisa.
Los axiomas de Peano definen de manera univoca a los números Naturales, es decir, cualquier conjunto que satisfaga los Axiomas de Peano, no será otro que los Naturales.
Entre otras cosas, éstos axiomas permiten definir su adición, considerando que el sucesor $n' = n+1$ y su multiplicación como adición repetida. Así tenemos $2 = 1' = 1+1$, $3 = 2' = 2+1$, etc.
Los naturales no satisfacen todos los
Los Naturales, son el punto de partida acostumbrado para la construcción de la aritmética y como consecuencia, para los subsecuentes sistemas numéricos. Su formulación axiomática es fundamental en la construcción de propiedades de los naturales y de otras estructuras algebraicas.
Teorema. $a + c = b + c \implies a = b \;\;\;\; \forall a, b, c \in \mathbb{N}$.
Como ya sabes, los naturales no satisfacen todos los
A pesar de lo anterior, en los Naturales se cumple la Ley de Cancelación para la Adición, aunque su demostración ya no puede hacerse como en el
Puedes ver la demostración paso a paso en el siguiente interactivo, en donde se utiliza el
El recíproco de este teorema es: si $a = b$, entonces $a + c = b + c$, y es cierto en los naturales y su demostración se realiza mediante una inducción finita, es decir: $a = b \implies a + 1 = b + 1, \implies a+2 = b+2$, etc. Puedes escribir detalladamente la demostración.
Así, juntando la ley de cancelación para la adición y su recíproco, se tiene un resultado más general en los naturales, es decir:
$a + c = b + c \iff a = b$
Así en los naturales, en una igualdad, se puede sumar o cancelar una misma cantidad.
De los
En la mayoría de los libros aparece la siguiente formulación de este Principio de Inducción Matemática:
Una proposición $P$ es válida $\forall n \in \mathbb{N}$, si:
Un ejemplo del uso de este principio se da en la demostración de la fórmula para la llamada progresión aritmética:
En el siguiente interactivo se presenta la demostración de la fórmula: $1 + 2 + ... + n = \dfrac{n(n + 1)}{2} \;\;\;\; \forall n \in \mathbb{N}$.
Otro ejemplo de las propiedades de naturales es la suma de los primeros $n$ impares que consiste en descubrir una fórmula para la suma de los primeros $n$ naturales impares.
En el siguiente interactivo se presenta la demostración de la fórmula: $1 + 3 + ... + (2n-1) = n^2 \;\;\;\; \forall n \in \mathbb{N}$.
Estos ejemplos se presentan aquí sólo para ilustrar el uso de este principio, pero hay una gran variedad de propiedades, demostrables mediante este principio. Una buena referencia es: Método de Inducción Matemática, I. S. Sominski, Lecciones Populares de Matemáticas, Editorial Mir.
Los números enteros son una consecuencia de los Naturales, en los cuales, cualquier ecuación de la forma $m + x = n$ con $m$ y $n$ enteros, tiene solución.
Lo anterior se debe a que los enteros, respecto a la adición, satisfacen todos los
Sin embargo, respecto a la multiplicación, no satisface el axioma M5, es decir, no existen inversos multiplicativos. Por esta razón, una ecuación de la forma $mx = n$ con $m$ y $n$ enteros, no siempre tiene solución en los enteros.
Estructuras algebraicas como la de los enteros que satisfacen los axiomas: A1, ..., A5, M1, ..., M4 y D, no son únicas. Como veremos en otra sección, existe por ejemplo Z4.
Los Enteros se diferencian de los Naturales, fundamentalmente en que los Naturales satisfacen el Principio del Buen Orden y los Enteros no. Es decir: “Todo subconjunto (no vacío) de los Naturales tiene elemento mínimo”. Esto no es cierto en los enteros.
Principio del buen orden: si $A \neq ∅$ y $A \subset \mathbb{N}$, entonces $A$ tiene un elemento mínimo.
Para demostrar el Principio del Buen Orden se utilizó el
Los Enteros, son un sistema numérico, consecuencia inmediata de los Naturales y el enlace para construir los números Racionales, que veremos adelante.
Teorema. $c \neq 0$, $ac = bc \implies a = b \;\;\;\; \forall a, b, c \in \mathbb{Z}$.
Como ya sabes, los enteros no satisfacen todos los
A pesar de lo anterior, en los Enteros se cumple la Ley de Cancelación para la Multiplicación, aunque su demostración ya no puede hacerse como en el
Puedes ver la demostración paso a paso en el siguiente interactivo, en donde se utiliza el método de inducción matemática.
El recíproco de este teorema: si $a = b$, entonces $ac = bc$, es cierto en los enteros y su demostración se realiza igualmente por inducción. Puedes intentar escribir la demostración.
Así, juntando la ley de cancelación para la adición y su recíproco, se tiene un resultado más general en los enteros, es decir:
Si $c \neq 0$, entonces $ac = bc \iff a = b$.
Así en los enteros, en una igualdad, se puede multiplicar o cancelar una misma cantidad.
Los múltiplos de $2$, $k = 2m$, con $m \in \mathbb{Z}$, se llaman Enteros Pares.
El resto de ellos, $k = 2m+1$, con $m \in \mathbb{Z}$, se llaman Enteros Impares.
Te presentamos varias proposiciones que relacionan $k^2$ con $k$, todas demostradas con el
Proposición e1, $k \in \mathbb{Z}$ y $k^2$ par $\implies k$ es par.
Proposición e2, $k \in \mathbb{Z}$ y $k^2$ impar $\implies k$ es impar.
La conjunción de ambas proposiciones es el siguiente Teorema: $k \in \mathbb{Z}$, $k^2$ par $\iff k$ es par.
O equivalentemente el Teorema: $k \in \mathbb{Z}$, $k^2$ impart $\iff k$ es impar.
También podemos clasificar los enteros en los que son múltiplos de $3$ y los que no lo son.
Los múltiplos de $3$ son de la forma: $k = 3m$, con $m \in \mathbb{Z}$ y los que no, pueden ser de la forma $k = 3m+1$, con $m \in \mathbb{Z}$ o de la forma $k = 3m+2,$ con $m \in \mathbb{Z}$.
Proposición e3, $k \in \mathbb{Z}$ y $k^2$ múltiplo de $3 \implies k$ es múltiplo de $3$.
Como el recíproco de esta proposición es inmediato, se tiene el teorema:
$k \in \mathbb{Z}$, $k^2$ múltiplo de $3 \iff k$ es múltiplo de $3$.
Esta proposición no se puede extender a todos los enteros, por ejemplo, la proposición $k \in \mathbb{Z}$ y $k^2$ múltiplo de $4 \implies k$ es múltiplo de 4, ES FALSA, púes $k=6$ no es múltiplo de $4$ y sin embargo $k^2=36$ si es múltiplo de $4$.
La generalización de estos resultados, es posible para los números primos, pero para ello, se requiere el siguiente Lema:
Si $p$ primo no divide a $r$, entonces $p$ no divide a $r^2$.
Cuya demostración se basa en el Teorema fundamental de la Aritmética que establece: “Todo número entero $k \gt 1$, se puede factorizar de manera única (salvo orden) como producto de números primos”. Es decir:
Dado $1 \lt k \in \mathbb{Z}$, existen $p_1 \gt p_2 \gt ... \gt p_i$ primos y $s_i$ con $i = 1, ..., t$ naturales, tales que $k = p_1^{s_1} p_2^{s_2} ... p_i^{s_i}$.
Proposición e4, sean $k \in \mathbb{Z}$ y $p$ primo, entonces, $k^2$ es múltiplo de $p$ si y solo sí, $k$ es múltiplo de $p$.
Del Teorema Fundamental de la Aritmética sólo dejaremos la referencia, ya que su demostración se escapa de los propósitos de este trabajo: I.N. Herstein. Topics in Algebra. Blaisdell Publishing Company.
En los Enteros hay muchos resultados interesantes, varios de ellos relacionados con los números primos. Existen también diversas Conjeturas interesantes (Proposiciones que permanecen sin demostración y que hoy día, aún con la utilización de las computadoras, no se ha encontrado contraejemplo alguno).
Tal es el caso de la Conjetura de Golbach cuyo planteamiento se remonta a 1742, en una carta que escribe Christian Golbach a Leonard Euler y que dice: “Todo número par (mayor de 2) se puede escribir como la suma de dos números primos”.
Con paciencia se pueden comprobar muchos casos: $4=3+1$, $6=3+3,$ $8=3+5$, $10=5+5$, etc. El hecho es que hasta la fecha con las computadoras se han podido comprobar cientos de billones de pares y no aparece contraejemplo alguno, pero tampoco hay alguna demostración.
Para ver más puedes visitar el sitio: https://mathworld.wolfram.com.
Los números racionales son cocientes de enteros y con las operaciones de adición y multiplicación, satisfacen todos los
Así que todos los resultados que hemos demostrado para los Reales, se aplican a los Racionales. En particular las leyes de cancelación y el hecho de que toda ecuación del tipo $mx + b = c$ con $m$, $b$ y $c$ racionales, tiene solución en $\mathbb{Q}$.
Como los Racionales satisfacen los Axiomas Campo y de Orden, se dice que son un Campo ordenado, al igual que los Reales.
Los Racionales difieren de los Reales en el Axioma del Supremo, cuya importancia consiste en la posibilidad de poder establecer una correspondencia biunívoca entre los Reales y los puntos de una recta. Los Racionales por sí mismos no llenan la recta, no obstante que “entre dos racionales cualesquiera hay una infinidad de ellos”, como veremos en el siguiente apartado.
Los griegos, con el Teorema de Pitágoras aplicado a un triángulo rectángulo con catetos igual a $1$, descubrieron el número $\sqrt{2}$ que no es posible escribirlo como cociente de enteros, es decir, no es racional. A este tipo de números les llamaron inconmensurables y actualmente se les llaman Irracionales. En la siguiente sección podremos ver algunas de estas demostraciones.
Los Racionales difieren de los Naturales o los Enteros en la propiedad de los sucesores. Recuerda que en todo Natural o Entero tiene un sucesor. Esto no es así en $\mathbb{Q}$, como podremos ver en el siguiente apartado.
Proposición 1, $r, s \in \mathbb{Q}, r \lt s \implies \exist t \in \mathbb{Q}$ tal que $r \lt t \lt s$.
En la Proposición 1 encontrarás la demostración de que “entre cualesquiera dos racionales, hay otro racional”. En realidad de la proposición anterior se deduce fácilmente que “entre cualesquiera dos racionales, hay una infinidad de racionales”.
Los Racionales, al ser un campo satisfacen todas las propiedades algebraicas de los reales, pero la diferencia sustancial entre ambos es el Axioma del Supremo. Los Racionales no satisfacen este axioma.
Los griegos, con el Teorema de Pitágoras aplicado a un triángulo rectángulo con catetos igual a $1$, descubrieron el número $\sqrt{2}$, siendo seguramente este el primier irracional que registraron.
Proposición i1, $\sqrt{2} \notin \mathbb{Q}$, es decir, $\sqrt{2}$ es racional. A continuación se presenta la demostración, por
Llamando $\mathbb{I}$ a los números irracionales (que los Griegos llamaron inconmensurables), tenemos que $\sqrt{2} \in \mathbb{I}$.
Proposición i2, $\sqrt{3} \notin \mathbb{Q}$, es decir, $\sqrt{3}$ es irracional, (i.e. $\sqrt{3} \in \mathbb{I}$).
Proposición i3, si $p$ es primo, entonces $\sqrt{p} \notin \mathbb{Q}$, (i.e. $\sqrt{p} \in \mathbb{I}$).
Se tiene el siguiente resultado: Proposición i4, si $k \in \mathbb{N}$ y $\sqrt{k} \notin \mathbb{N}$, entonces $\sqrt{k} \notin \mathbb{Q}$. Es decir: si $k \in \mathbb{N}$ y $\sqrt{k} \notin \mathbb{N}$, entonces $\sqrt{k} \in \mathbb{I}$.
Proposición i5, si $\alpha \in \mathbb{I}$ y $r \in \mathbb{Q}$, entonces $\alpha + r \in \mathbb{I}$.
Proposición i6, si $\alpha \in \mathbb{I}$ y $r \in \mathbb{Q}, r \neq 0$, entonces $\alpha r \in \mathbb{I}$.
No obstante las anteriores construcciones, aun así, no habríamos agotado todos los los números irracionales, como veremos adelante.
Se pueden encontrar fácilmente dos irracionales cuya suma sea racional o también cuyo producto sea racional, ¿Lo puedes intentar? Con lo anterior se concluye que no satisfacen los axiomas A1 y M1 de los
Un número real, o es racional o es irracional. Es decir:
$\mathbb{R} = \mathbb{Q} \cup \mathbb{I}$ y $\mathbb{Q} \cap \mathbb{I} = ∅$.
Los Racionales y los Reales son un campo, mientras que los irracionales no. Los Reales satisfacen el Axioma del Supremo, pero los Racionales no y los Irracionales tampoco. El Axioma del Supremo está estrechamente ligado con la existencia de los números irracionales.
De los axiomas de los reales, éste es el que nos faltaba. A diferencia de los demás axiomas que tiene que ver más con propiedades algebraicas, aplicables a diversos campos, éste es realmente característico de los reales.
Todo conjunto $A$ (no vacío) de reales, acotado superiormente posee un supremo, es decir, existe un real $s$ que es la mínima de las cotas superiores de $A$ ($s = supA$).
En donde: $A$ está acotado superiormente si $\exist$ un real $M$ tal que $x \leq M \;\;\;\; \forall x \in A$. Además: a todo número $M$ con esta propiedad se le llama cota superior de $A$, entonces, $s = supA$ si, $s$ es cota superior de $A$, y si $t$ es cota superior de $A \implies s \leq t$, es decir, $s$ es la mínima de todas las cotas superiores de $A$.
Sea $A = \{ x \in \mathbb{Q} | x^2 \lt 2 \}$, $A \neq ∅$, pues al menos $1 \in A$. Además, por ejemplo, $2$ es una cota superior de $A$. Sin embargo, no existe $sup A$. Es decir, no existe un racional que sea la mínima de todas las cotas superiores.
Observe que: todos los racionales que son cotas superiores de $A$ son mayores que $\sqrt{2}$, pero a la vez existen racionales tan cerca de $\sqrt{2}$ como se quiera.
Demostración:
Sean $S_1$ y $S_2$ supremos de $A \neq ∅$ (acotado superiormente). De la definición tenemos que si $t$ es cota superior de $A \implies s \leq t$, por lo que $S_1 \leq S_2$ y $S_2 \leq S_1$, entonces $S_1 = S_2$.
En pocas palabras, el axioma del supremo es fundamental para el desarrollo del cálculo diferencial e integral. En la siguiente página podremos ver proposiciones interesantes que no serían posibles sin el axioma del supremo.
Para comprender un poco más la importancia del axioma del supremo presentamos una secuencia de proposiciones muy interesantes cuyas demostraciones están estrechamente relacionadas con tal axioma. Las primeras tres son formas equivalentes de la llamada propiedad arquimediana de los números reales.
Proposición S1, el conjunto $\mathbb{N}$ no está acotado superiormente.
Es claro que los naturales son un conjunto acotado inferiormente, sin embargo aunque de manera intuitiva se observa que no lo están superiormente, la demostración formal es indispensable.
Proposición S2, $\forall \alpha \in \mathbb{R}$, existe $n \in \mathbb{N}$ tal que $\alpha \lt n$.
Es decir, dado cualquier real, siempre es posible encontrar un natural mayor que él.
Proposición S3, $\forall \varepsilon \gt 0$, existe $n \in \mathbb{N}$ tal que $\dfrac{1}{n} \lt \varepsilon$.
Es decir, dado un número arbitrariamente pequeño, siempre existe un natural, tal que su inverso multiplicativo es aun menor.
Con un poco de esfuerzo, es posible demostrar la equivalencia de las proposiciones S1, S2 y S3. ¿Podrías intentarlo?
También es posible encontrar otras formas, desde luego equivalentes, de la propiedad arquimediana de los números reales.
Por ejemplo: sean $a, b \in \mathbb{R}$, si $0 \lt a \lt b$, entonces $\exist n \in \mathbb{N}$ tal que $na \gt b$.
Para la siguiente proposición necesitamos un nuevo concepto, que lo establecemos en la siguiente definición:
Sea $x \in \mathbb{R}$. Definimos $[x]$ como el mayor entero $k$, tal que $k \leq x$.
Por ejemplo: $$\begin{align*} x = 2.5 &\implies [x]=2 \\ x = -3.1 &\implies [x]=-4 \\ x = 5 &\implies [x]=5 \\ x = k \in \mathbb{Z} &\implies [x]=k \end{align*}$$
Proposición S4, si $x, y \in \mathbb{R}$ y $y - x \gt 1$, entonces $\exist k \in \mathbb{Z}$ tal que $x \lt k \lt y$.
Es decir, entre dos reales que distan en más de $1$, existe un entero.
Proposición S5, si $x, y \in \mathbb{R}$ y $x \lt y$, entonces $\exist r \in \mathbb{Q}$ tal que $x \lt r \lt y$.
Es decir, entre dos reales cualesquiera, existe un racional. Es sencillo deducir que si existe uno, existe una infinidad (¿puedes argumentarlo?).
Proposición S6, si $r, s \in \mathbb{Q}$ y $r \lt s$, entonces $\exist j \in \mathbb{I}$ tal que $x \lt j \lt y$.
Es decir, entre dos racionales cualesquiera, existe un irracional.
Proposición S7, si $x, y \in \mathbb{R}$ y $x \lt y$, entonces $\exist j \in \mathbb{I}$ tal que $x \lt j \lt y$.
Es decir, entre dos reales cualesquiera, existe un irracional.
Juntando todas estas proposiciones se puede concluir que entre dos reales cualesquiera, existen infinidad de racionales y también infinidad de irracionales. ¿Podrías argumentarlo?
Para comprender un poco más las relaciones entre los conjuntos de números, será importante referirnos al concepto de cardinalidad, que tiene que ver con la “cantidad” de elementos de un conjunto infinito. Podríamos decir que el concepto de cardinalidad es una extensión del concepto de cantidad para conjuntos finitos.
Para saber si dos conjuntos finitos $A$ y $B$, tienen la misma cantidad de elementos, bastaría hacer corresponder cada uno de los elementos de A con cada uno de los de B y si no sobra ningún elemento, se concluye que si tienen la misma cantidad de elementos.
Este método, consiste matemáticamente en establecer una relación biyectiva (uno a uno y sobre) entre $A$ y $B$, el cual se puede extender a conjuntos infinitos, de la siguiente manera:
Dos conjuntos infinitos $A$ y $B$, tienen la misma cardinalidad si entre ellos se puede establecer una relación biyectiva.
Denotaremos por $\#(A)$ la cardinalidad del conjunto $A$.
Proposición r1, $f:\mathbb{N} \rightarrow I$ tal que $f(n) = 2n-1$ es biyectiva, es decir, los impares positivos tienen la misma cardinalidad que los Naturales.
Proposición r2, $f:\mathbb{N} \rightarrow P$ tal que $f(n) = 2n$ es biyectiva, es decir, los pares positivos tienen la misma cardinalidad que los Naturales.
Así, no obstante que los naturales impares y los naturales pares son subconjuntos propios de los naturales, tenemos que: $\#(I) = \#(P) = \#(\mathbb{N})$.
Un subconjunto puede tener la misma cardinalidad del conjunto que lo contiene, pero nunca mayor, ¿Puedes explicarlo? Así, podemos entender que: $\#(\mathbb{N}) \leq \#(\mathbb{R})$. Más adelante haremos ver que la igualdad no puede ser.
Proposición r3, $\mathbb{N} \rightarrow \mathbb{Z}$ tal que $f(n) = \begin{cases} \dfrac{n+1}{2} \text{ si } n \text{ es impar} \\ -\dfrac{n}{2} + 1 \text{ si } n \text{es par} \end{cases}$ es biyectiva.
Proposición r4, $\#(\mathbb{Z}) = \#(\mathbb{Q})$. A continuación verás la ilustración de la relación biyectiva entre los Naturales y los racionales positivos (por las proposiciones anteriores con eso basta). El método consiste en ir relacionando los naturales con los racionales en forma diagonal.
Basta demostrar que no es posible establecer una relación sobre entre los naturales y los reales del intervalo $[0,1]$.
Proposición r5, no existe una relación sobre los naturales en $[0, 1]$. Daremos dos demostraciones, la primera demostración se presenta en el siguiente interactivo.
Para la segunda demostración partiremos del siguiente resultado que llamaremos:
R1. La intersección de intervalos cerrados anidados y no vacíos, es no vacía.
Demostración: la intersección de intervalos cerrados anidados y no vacíos, es no vacía. Si definimos dos conjuntos: $A$ el conjunto de extremos izquierdos de los intervalos y $B$ el conjunto de extremos derechos de los intervalos. Podemos deducir que: $∅ \neq A \subset \mathbb{R}$ y está acotado superiormente por cualquier $b \in B$. Entonces por el Axioma del supremo: $\exist \alpha \in \mathbb{R}$, tal que $\alpha = sup A$. Por lo tanto: $a \leq \alpha \leq b \;\;\;\; \forall a \in A$ y $\forall b \in B$. Así: $\alpha$ pertenece a todos los intervalos anidados.
En el siguiente interactivo se muestra la segunda demostración.
Los naturales, los enteros y los racionales por tener la misma cardinalidad, se dice que son conjuntos numerables.
Cualquier subconjunto infinito de los naturales tiene la cardinalidad de los naturales.
Todo conjunto numerable tiene la misma cardinalidad que los naturales.
Los irracionales y por tanto los reales, son conjuntos no numerables.
En resumen, tenemos que:
$\#(\mathbb{N}) = \#(\mathbb{Z}) = \#(\mathbb{Q}) \lt \#(\mathbb{R})$
Existen otras estructuras algebraicas finitas, que dependiendo del valor de $n$ natural, son o no, un campo. En el caso de aquellas que no son un campo, se dan situaciones muy interesantes, como ecuaciones sin solución o leyes algebraicas que no se cumplen.
Presentamos a continuación la más sencilla de estas estructuras: $(\mathbb{Z}_2, +, *)$, donde $\mathbb{Z}_2 = \{0, 1\}$ y
| $+$ | $0$ | $1$ |
| $0$ | $0$ | $1$ |
| $1$ | $1$ | $0$ |
| $*$ | $0$ | $1$ |
| $0$ | $0$ | $0$ |
| $1$ | $0$ | $1$ |
Es relativamente sencillo hacer ver que cumple todos los axiomas de campo.
Similarmente, tenemos: $(\mathbb{Z}_3, +, *)$, donde $\mathbb{Z}_3 = \{0, 1, 2\}$ y
| $+$ | $0$ | $1$ | $2$ |
| $0$ | $0$ | $1$ | $2$ |
| $1$ | $1$ | $2$ | $0$ |
| $2$ | $2$ | $0$ | $1$ |
| $*$ | $0$ | $1$ | $2$ |
| $0$ | $0$ | $0$ | $0$ |
| $1$ | $0$ | $1$ | $2$ |
| $2$ | $0$ | $2$ | $1$ |
De seguro, las más laboriosas de comprobar sean la asociatividad y la distributiva, pero al igual que la anterior, es posible ver que cumple todos los axiomas de campo.
En general estas estructuras se describen de la siguiente forma:
Sea $\mathbb{Z}_n = \{0, 1, ..., n-1\}$, en donde se tienen dos operaciones, adición $(+)$ y multiplicación $(*)$, definidas de la siguiente forma:
Se suma de manera usual en los enteros: $k+l = s$ y entonces en los enteros módulo $n$:
donde $r$ es el residuo entero que queda al dividir $s$ entre $n$.
Similarmente, se multiplica de manera usual en los enteros: $k*l = m$ y entonces en los enteros módulos $n$:
donde $r$ es el residuo entero que queda al dividir $m$ entre $n$.
Si $n=6$, entonces $\mathbb{Z}_6 = \{0, 1, 2, 3, 4, 5\}$.
Así:
A continuación, verás la ilustración interactiva de las tablas se adición y multiplicación de los enteros módulo 4, y podrás observar algunas de sus propiedades, en particular que no conforman un campo, puesto que falla la existencia del inverso multiplicativo y por lo mismo no se cumple la respectiva ley de cancelación.
Ahora verás la ilustración interactiva de sus tablas se adición y multiplicación y podrás observar algunas de sus propiedades, en particular que sí conforman un campo.
Se observa fácilmente que las operaciones son cerradas, conmutativas y que existen neutros e inversos. Es un poco laborioso ver que en efecto se cumplen las asociativas y la distributiva.
De lo anterior se desprende que al ser un campo, cumplen todos los teoremas que demostramos para los reales, en particular las leyes de cancelación para ambas operaciones.
Así, en los enteros módulo 5, toda ecuación de la forma:
$a * x + b = 0 \implies x = a^{-1} * (-b)$ si $a \neq 0$.
Por ejemplo: $3*x + 2 = 0 \implies x = 3^{-1}*(-2) = 2*3 = 1$.
Comprobación: $3*1 + 2 = 3 + 2 = 5$, pero $5$ dividido entre $5$ es $1$ con residuo $0$, entonces en efecto $x = 1$.
Aunque aquí no haremos la demostración, se sabe que: $(\mathbb{Z}_n, +, *)$ es campo $\iff n = p$ primo.
En todos los campos se cumplen las leyes de cancelación, tanto para la adición como para la multiplicación. En todos los campos tiene solución cualquier ecuación de la forma: $a*x + b = 0$
A pesar de que los irracionales no son un campo, existen subconjuntos de irracionales que en unión con los racionales y con las operaciones usuales en los reales, conforman un campo, por ejemplo:
$F = \{ a+b\sqrt{2} | a, b \in \mathbb{Q}\}$
con cierta dificultad, pero se pueden comprobar todas las propiedades de campo. En particular se puede ver que:
$0 + 0\sqrt{2}$ es el neutro aditivo.
$1 + 0\sqrt{2}$ es el neutro multiplicativo.
y aun más, se puede comprobar que: $\left(\dfrac{a}{a^2 - 2b^2} \right) - \left(\dfrac{b}{a^2 - 2b^2} \right) \sqrt{2}$ es el inverso multiplicativo de $a+b \sqrt{2}$.
Por ejemplo: $3-2 \sqrt{2}$ es el inverso multiplicativo de $3+2 \sqrt{2}$.
Similarmente se puede construir el campo: $G = \{a+b\sqrt{3} | a, b \in \mathbb{Q} \}$.
En este caso: ¿Quienes serían los neutros aditivo y multiplicativo? y ¿Cuál sería la expresión para los inversos multiplicativos?
Extendiendo el concepto tendríamos que los siguientes también serían campos:
$L = \{a+b \sqrt{p} | a, b \in \mathbb{Q}$ y $p$ primo $\}$
$M = \{a+b \sqrt{k} | a, b \in \mathbb{Q}$ y $\sqrt{k} \in \mathbb{I} \}$
En ambos casos: ¿Quienes serían los inversos multiplicativos?
No obstante lo poderoso que es el campo de los reales, se presentan situaciones algebraicas donde no basta. Por ejemplo, la ecuación:
$x^2 + 1 = 0$ no tiene solución en $\mathbb{R}$
Esta situación motiva la aparición de nuevas estructuras algebraicas, en este caso la de los números complejos, cuya definición, se basa en el número complejo, llamado: $i = \sqrt{-1}$.
Así que: $i^2 = -1$, $i^3 = -i$, $i^4 = 1$, etc.
Los números complejos se definen como:
$\mathbb{C} = \{\alpha + i\beta | \alpha, \beta \in \mathbb{R} \}$
Sean $z = \alpha_1 + i \beta_1$ y $w = \alpha_2 + i \beta_2$, entonces:
Sean $z = 2 + i 3$ y $w = 1 + i 4$, entonces:
Con cierta dificultad, pero se puede comprobar que $(\mathbb{C}, +, *)$ es un campo. Generalmente la parte mas complicada es descubrir el inverso multiplicativo.
En todos los campos se cumplen las leyes de cancelación, tanto para la adición como para la multiplicación. En todos los campos tiene solución cualquier ecuación de la forma: $a*x + b = 0$
En los complejos tiene solución cualquier ecuación de la forma:
$a_n x^n + a_{n-1} x^{n-1} + ... + a_1 x + a_0 = 0$
Resultado que se conoce como el Teorema Fundamental del Algebra, cuya primera prueba se le atribuye a F. Gauss en su tesis doctoral en 1799.
Precisamente la idea de ir construyendo los conjuntos numéricos desde los Naturales a los Complejos, pasando por los Enteros, Racionales y Reales es suplir las deficiencias que presentan en la resolución de ecuaciones algebraicas. Llegar al Teorema Fundamental de la Aritmética fue toda una travesía histórica en el desarrollo de las matemáticas.
Aquí podrás encontrar el concepto de función, sus operaciones básicas y los tipos de funciones más importantes en el cálculo diferencial e integral de una variable real.
También encontrarás graficadores de funciones, que los podrás usar para representar operaciones o para visualizar mejor aquellas que requieren un zoom o para construir funciones con parámetros.
También encontrarás ejercicios interactivos para el reconocimiento de funciones.
Sean $A$ y $B$ conjuntos no vacíos. Una función $f$ de $A$ en $B$ es una regla de correspondencia tal que, a cada elemento de $A$ le asocia un único elemento en $B$.
La anterior definición aunque es útil, no es rigurosa. Se cuestiona qué entender por “regla de correspondencia”. Así que a continuación se proporciona una definición formal de función.
Sean $A$ y $B$ conjuntos. El producto cartesiano $A \times B$ de $A$ y $B$, se define como:
$A \times B = \{(a,b) | a \in A$ y $b \in B\}$
es decir, es el conjunto de todas las parejas ordenadas, donde el primer elemento pertenece a $A$ y el segundo pertenece a $B$.
Una relación $R$ entre $A$ y $B$ es un subconjunto del producto cartesiano $A \times B$.
Una función $f$ de $A$ en $B$ es una relación entre $A$ y $B$ que satisface las siguientes condiciones:
La condición i. establece que todo elemento de $A$, tenga relación con algún elemento de $B$.
La condición ii. establece que ningún elemento de $A$, puede tener relación con más de un elemento en $B$.
Aunque las definiciones formales, no establecen que $A$ y $B$ deban ser no vacíos, para los propósitos de nuestro curso nosotros si lo haremos.
Cada elemento del Dominio tiene asociado un único elemento en el Codominio. Así, son reglas de asociación que establecen una función.
Varios elementos del dominio pueden tener asociado el mismo elemento del codominio. Es seguro que muchos seres humanos hayan nacido en la misma fecha.
Es seguro que haya alumnos que no tengan computadora o inclusive puede ser que haya alumnos que tengan más de una. Es una regla de asociación que no establece una función.
$f : A \rightarrow B$ es una función con valor real de variable real, si $A \subset \mathbb{R}$ y $B \subset \mathbb{R}$. Es decir, cada real de $A$, tiene asociado un único real en $B$. En adelante, a menos que se diga lo contrario, se tomará $B = \mathbb{R}$.
Como $B \subset \mathbb{R}$, se le llama función con valor real y como $A \subset \mathbb{R}$, se le llama de variable real.
Observa que $f(1)$ no existe.
Observa que $f(-1) \notin \mathbb{R}$.
Observa que el $1$ se aplica con las dos expresiones y por consecuencia tiene dos asociados: $f(1) = \begin{cases} 1+2 = 3 \\ 1+1 = 2 \end{cases}$
Observa que el $3$ se aplica con las dos expresiones y por consecuencia tiene dos asociados: $f(3) = \begin{cases} 1-3 = -2 \\ 3+1 = 4 \end{cases}$
Los cuatro casos anteriores podrían ser funciones con sólo corregir el dominio. Por ejemplo en a. bastaría quitar del dominio el valor $1$ y en b. bastaría tomar como dominio los reales no negativos. ¿Qué correcciones habría que hacer en los otros dos casos?
Función constante $f : \mathbb{R} \rightarrow \mathbb{R}$ tal que $f(x) = b$.
Función idéntica $f : \mathbb{R} \rightarrow \mathbb{R}$ tal que $f(x) = x$.
Función valor absoluto $f : \mathbb{R} \rightarrow \mathbb{R}$ tal que $f(x) = |x|$.
Función raíz cuadrada $f : \mathbb{R}^+ \cup \{0\} \rightarrow \mathbb{R}$ tal que $f(x) = \sqrt{x}$.
Función mayor entero, menor o igual a $x$ $f : \mathbb{R} \rightarrow \mathbb{R}$ tal que $f(x) = [x]$.
Función raíz cúbica $f : \mathbb{R} \rightarrow \mathbb{R}$ tal que $f(x) = \sqrt[3]{x}$.
Función hipérbola equilátera $f : \mathbb{R} - \{0\} \rightarrow \mathbb{R}$ tal que $f(x) = \dfrac{1}{x}$.
Función por pedazos $f : [-6, 5] \rightarrow \mathbb{R}$ tal que $f(x) = \begin{cases} -2 \text{ si } x \in [-6, 1] \\ x \text{ si } x \in (1, 5] \end{cases}$
Función seno $f : \mathbb{R} \rightarrow \mathbb{R}$ tal que $f(x) = sen(x)$.
Función coseno $f : \mathbb{R} \rightarrow \mathbb{R}$ tal que $f(x) = cos(x)$.
Función exponencial $f : \mathbb{R} \rightarrow \mathbb{R}$ tal que $f(x) = e^x$.
Función logarítmica $f : \mathbb{R}^+ \rightarrow \mathbb{R}$ tal que $f(x) = \ln(x)$.
Sean las funciones $f : A \rightarrow \mathbb{R}$ y $g : B \rightarrow \mathbb{R}$, entonces definimos:
$(f + g) : A \cap B \rightarrow \mathbb{R}$ tal que $(f + g)(x) = f(x) + g(x)$.
$(f - g) : A \cap B \rightarrow \mathbb{R}$ tal que $(f - g)(x) = f(x) - g(x)$.
$(fg) : A \cap B \rightarrow \mathbb{R}$ tal que $(fg)(x) = f(x)g(x)$.
$\left(\dfrac{f}{g}\right) : C \rightarrow \mathbb{R}$ tal que $\left(\dfrac{f}{g}\right)(x) = \dfrac{f(x)}{g(x)}$, donde $C = A \cap B - \{x: g(x) = 0\}$.
En todos los casos el dominio debe ser la intersección de $A$ y $B$ para garantizar la existencia de $f(x)$ y $g(x)$ y por consecuencia poderlas sumar. Pero además en la división se deben quitar los valores donde el denominador $g(x)$ sea cero.
Sean $f$ y $g$ funciones reales de variable real. Definimos $(f \circ g) : D \rightarrow \mathbb{R}$ tal que $(f \circ g)(x) = f(g(x))$ y $D = \{x : x \in Dom g$ y $g(x) \in Dom f\}$
La variable $x$ debe estar en el dominio de $g$ para garantizar que exista y éste a su vez debe estar en el dominio de $f$ para garantizar que exista $f(g(x))$.
Reglas de asociación distintas: sean $f : \mathbb{R} \rightarrow \mathbb{R}$ tal que $f(x) = x^2$ y $g : \mathbb{R} \rightarrow \mathbb{R}$ tal que $g(x) = sen(x)$
$\begin{rcases} (f \circ g)(x) = f(g(x)) = (g(x))^2 = (sen(x))^2 \\ (g \circ f)(x) = g(f(x)) = sen(f(x)) = sen(x^2) \end{rcases}$ pero $(sen(x))^2 \neq sen(x^2)$
¿Puede ilustrar un caso donde $Dom(f \circ g) \neq Dom(g \circ f)$?
En una función compuesta ¿cómo puedes encontrar sus componentes? Por ejemplo en:
$f(x) = \sqrt{sen(cos(x^3))}$
Una buena regla es leer de adentro hacia afuera. Es decir:
$f(x) = \underbrace{\sqrt{\underbrace{sen (\underbrace{(cos \underbrace{(x^3)}_{u})}_{v})}_{w}}}_{z} \implies f(x) = z(w(v(u(x))))$, donde, $u(x) = x^3$, $v(u) = cos(u)$, $w(v) = sen(v)$ y $z(w) = \sqrt{w}$.
La operación composición es muy útil para generar una gran diversidad de funciones.
Ilustraremos algunos ejemplos de familias de funciones variando coeficientes.
Función lineal, $f(x) = ax + b$ con $x \in \mathbb{R}$.
Función cuadrática, $f(x) = ax^2 + bx + c$ con $x \in \mathbb{R}$.
Una familia con valor absoluto, $f(x) = a|x + b| + c$ con $x \in \mathbb{R}$.
Una familia con raíz cuadrada, $f(x) = a \sqrt{x} + b$ con $x \geq 0$.
Una familia con mayor entero, $f(x) = a[x] + b$ con $x \in \mathbb{R}$.
Una familia de hipérbolas equiláteras, $f(x) = \dfrac{a}{x} + b$ con $x \neq 0$.
Una familia de senoidales, $f(x) = asen(bx + c) + d$ con $x \in \mathbb{R}$.
Una familia de cosenoidales, $f(x) = acos(bx + c) + d$ con $x \in \mathbb{R}$.
Una familia de exponenciales, $f(x) = ae^x + b$ con $x \in \mathbb{R}$.
Una familia de logarítmicas, $f(x) = a\ln(x) + b$ con $x \gt 0$.
Un cociente de polinomios, $f(x) = \dfrac{ax^2 + b + c}{x + d}$ con $x \neq -d$.
Una composición de funciones, $f(x) = a cos(bx^2)$ con $x \in \mathbb{R}$.
Para definir las funciones biyectivas, requerimos definir las funciones inyectivas (también llamadas uno a uno) y las suprayectivas (también llamadas sobre).
Una función $f : A \rightarrow B$ es inyectiva, si para todo $a_1, a_2 \in A$ tales que $a_1 \neq a_2 \implies f(a_1) \neq f(a_2)$.
Elementos distintos del dominio, tienen imágenes distintas en el codominio, es decir, elementos distintos del dominio, no pueden tener la misma imagen en el codominio.
Una función $f : A \rightarrow B$ es sobre, si para cada $b \in B$, existe $a \in A$ tal que $f(a) = b$.
Significa que todo elemento del codominio es imagen de algún elemento del dominio. Aquí es bueno hacer notar que toda función es suprayectiva sobre su Rango.
Una función $f : A \rightarrow B$ es biyectiva, si es a la vez inyectiva y suprayectiva (llamada brevemente: uno a uno y sobre).
No es inyectiva, no es sobre, $f : \mathbb{R} \rightarrow \mathbb{R}$ tal que $f(x) = x^2 + x -2$.
Es inyectiva y es sobre (es biyectiva), $f : \mathbb{R} \rightarrow \mathbb{R}$ tal que $f(x) = 2x + 1$.
No es inyectiva, pero si es sobre, $f : [-3, 3] \rightarrow [-0.5, 4]$ tal que $f(x) = \dfrac{4-x^2}{x^2+1}$
Es inyectiva, pero no sobre, $f : [0, \infty) \rightarrow \mathbb{R}$ tal que $f(x) = \dfrac{x^2}{x^2+1}$
Para una función $f : I \rightarrow \mathbb{R}$ definida en un intervalo $I$, existen 4 casos posibles de monotonía.
A continuación se presentan ejemplos de los diversos tipos de funciones monótonas.
Es monótona creciente, $f : \mathbb{R} \rightarrow \mathbb{R}$ tal que $f(x) = x^3$.
Es monótona decreciente, $f : [0, \infty) \rightarrow \mathbb{R}$ tal que $f(x) = \dfrac{1}{x^2+1}$
Es monótona no decreciente, $f : \mathbb{R} \rightarrow \mathbb{R}$ tal que $f(x) = [x]$.
Es monótona no creciente, $f : \mathbb{R} \rightarrow \mathbb{R}$ tal que $f(x) = 1-[x]$.
Parecería ser monótona decreciente, $f : \mathbb{R} - \{0\} \rightarrow \mathbb{R}$ tal que $f(x) = \dfrac{1}{x}$
Se llaman así porque tienen simetría, respecto al eje vertical o respecto al origen. Así, sus dominios son simétricos al origen, es decir: $x \in Dom f \iff -x \in Dom f$.
$f$ es par, si: $f(-x) = f(x) \;\;\;\; \forall x \in Dom f$. Tiene simetría respecto al eje vertical.
$f$ es impar, si: $f(-x) = -f(x) \;\;\;\; \forall x \in Dom f$. Tiene simetría respecto al origen.
$(gh)(-x) = g(-x)h(-x) = g(x)h(x) = (gh)(x)$.
$(gh)(-x) = g(-x)h(-x) = g(x)(-h(x)) = -(gh)(x)$.
$(gh)(-x) = g(-x)h(-x) = (-g(x))(-h(x)) = (gh)(x)$.
Es par, $f : \mathbb{R} \rightarrow \mathbb{R}$ tal que $f(x) = \dfrac{1}{x^2+1}$
Es par, $f : \mathbb{R} \rightarrow \mathbb{R}$ tal que $f(x) = \dfrac{x^2}{x^2+1}$
Es impar, $f : \mathbb{R} \rightarrow \mathbb{R}$ tal que $f(x) = x^3$
Es impar, $f : \mathbb{R} \rightarrow \mathbb{R}$ tal que $f(x) = \dfrac{x}{x^2+1}$
Cualquiera $f$ se puede expresar de la siguiente forma:
$f(x) = \left( \dfrac{f(x)+f(-x)}{2} \right) + \left( \dfrac{f(x)-f(-x)}{2} \right) = (g(x)) + (h(x))$.
Puedes checar la igualdad y que, $g$ es par y $h$ impar.
Se dice que $f$ es acotada si: existe $M$ tal que $|f(x)| \leq M \;\;\;\; \forall x \in Dom f$.
De manera equivalente se dice es acotada si: existen $m$ y $M$ tales que $m \leq f(x) \leq M \;\;\;\; \forall x \in Dom f$.
Esta segunda definición permite tipificar si $f$ está acotada superior o inferiormente según existan $M$ o $m$, respectivamente.
Sus demostraciones en realidad son sencillas y puedes realizarlas sin mucha dificultad.
Es acotada, $f : \mathbb{R} \rightarrow \mathbb{R}$ tal que $f(x) = \dfrac{1}{x^2+1}$
Es acotada, $f : \mathbb{R} \rightarrow \mathbb{R}$ tal que $f(x) = \dfrac{x^2}{x^2+1}$
Es acotada, $f : \mathbb{R} \rightarrow \mathbb{R}$ tal que $f(x) = \dfrac{x}{x^2+1}$
No es acotada, $f : \mathbb{R} \rightarrow \mathbb{R}$ tal que $f(x) = [x]$
No es acotada, $f : \mathbb{R} - \{0\} \rightarrow \mathbb{R}$ tal que $f(x) = \dfrac{1}{x}$
No es acotada, $f : \mathbb{R} \rightarrow \mathbb{R}$ tal que $f(x) = x^3$
Las funciones acotadas no pueden crecer o decrecer al infinito. Más bien sus gráficas se encuentran entre dos rectas paralelas al eje de las $x$, las que pasan por $m$ y $M$.
Una función $f$ es periódica con un período $t \neq 0$, si:
Si una función es periódica puede haber varios valores de $t$ que cumplan con dicha propiedad. Por ello, al mínimo valor positivo de $t$ para el cual se cumple esta propiedad, se le llama el período de $t$.
Si es $t$ periódica significa que sus valores se repiten con regularidad. De manera práctica significa que la gráfica de la función en un cierto dominio, se repite a la derecha y la izquierda.
Es periódica, $f : \mathbb{R} \rightarrow \mathbb{R}$ tal que $f(x) = x-[x]$
Es periódica, $f : \mathbb{R} \rightarrow \mathbb{R}$ tal que $f(x) = sen(x)$
Es periódica, $f : \mathbb{R} \rightarrow \mathbb{R}$ tal que $f(x) = cos(x)$
No es periódica (¡es monótona!), $f : \mathbb{R} \rightarrow \mathbb{R}$ tal que $f(x) = [x]$
No es periódica, $f : \mathbb{R} \rightarrow \mathbb{R}$ tal que $f(x) = sen(x^2)$
No es periódica (¡es monótona!), $f : \mathbb{R} \rightarrow \mathbb{R}$ tal que $f(x) = x^3$
i) $f(x) = [x]+x$
ii) $f(x) = x^3$
iii) $f(x) = -x+3$
iv) $f(x) = sen(x)$
v) $f(x) = x^2-2x$
vi) $f(x) = cos(x)$
i) $f(x)=x^3$
ii) $f(x)=\dfrac{1}{x^2+1}$
iii) $\dfrac{x}{x^2+1}$
iv) $\dfrac{x^2}{x^2+1}$
i) $f(x)=x^3$
ii) $f(x)=\dfrac{1}{x^2+1}$
iii) $\dfrac{x}{x^2+1}$
iv) $\dfrac{x^2}{x^2+1}$
i) $f(x)=x^2$
ii) $f(x)=\dfrac{1}{x^2+1}$
iii) $\dfrac{x^2}{x^2+1}$
iv) $|x|$
i) $f(x) = x + \dfrac{1}{x}$. ¿Qué ocurre cuando $x$ está próximo a $0$ y cuando $x$ es grande? ¿Qué posición ocupa la gráfica en relación con la gráfica de la función identidad? ¿Porqué es suficiente considerar primero sólo $x$ positivos?
ii) $f(x) = x - \dfrac{1}{x}$
iii) $f(x) = x^2 + \dfrac{1}{x^2}$
iv) $x^2 - \dfrac{1}{x^2}$
i) $g(x) = f(x) + c$
ii) $g(x) = f(x+c)$ ¡Cuidado, es fácil equivocarse!
iii) $g(x) = cf(x)$ Distinguir los casos: $c = 0$, $c \gt 0$ y $c \lt 0$
iv) $g(x) = f(cx)$ Distinguir los casos: $c = 0$, $c \gt 0$ y $c \lt 0$
v) $g(x) = f \dfrac{1}{x}$
vi) $g(x) = f(|x|)$
vii) $g(x) = |f(x)|$
viii) $g(x) = max(f, 0)$
ix) $g(x) = min(f, 0)$
x) $g(x) = max(f, 1)$
i) $f(f(x))$ ¿Para que $x$ tiene sentido?
ii) $f \dfrac{1}{x}$
iii) $f(cx)$
iv) $f(x+y)$
v) $f(x) + f(y)$
vi) $f(|x|)$
i) ¿Para cuáles $y$ es $h(y) \leq y $?
ii) ¿Para cuáles $y$ es $h(y) \leq g(y)$?
iii) ¿Qué es $g(h(z)) - h(z)$?
iv) ¿Para cuáles $w$ es $g(w) \leq w$?
v) ¿Para cuáles $\varepsilon$ es $g(g(\varepsilon)) = \varepsilon$?
i) $f(x) = \sqrt{1-x^2}$
ii) $f(x) = \sqrt{1-\sqrt{1-x^2}}$
iii) $f(x) = \dfrac{1}{x-1} + \dfrac{1}{x-2}$
iv) $f(x) = \sqrt{1-x^2} + \sqrt{x^2-1}$
v) $f(x) = \sqrt{1-x} + \sqrt{x-2}$
i) $(S \circ P)(y)$
ii) $(S \circ s)(y)$
iii) $(f \circ g)(u)$
iv) $(S \circ P \circ s)(t) + (s \circ P)(t)$
v) $s(t^3)$
vi) $(g \circ f)(u)$
vii) $(f \circ g)(v) + (g \circ f)(v)$
vii) $f^{-1}(x)$
ix) $g^{-1}(x)$
i) $|x-3| \lt 1$
ii) $|x-3| \leq 1$
iii) $|x-a| \lt \varepsilon$
iv) $|x^2-1| \lt \dfrac{1}{2}$
v) $\dfrac{1}{1+x^2} \geq \dfrac{1}{5}$
vi) $x^2+1 \geq 2$
vii) $(x+1)(x-1)(x-2) \gt 0$
Aquí encontrarás el concepto de límite de una función en un punto, tratado con un enfoque intuitivo y formalizado por medio de vecindades.
Este concepto es de los más importantes en el Cálculo,porque de él dependen otros,como los de Continuidad,Derivada e Integral. En sí mismo el concepto de límite es interesante porque proporciona información sobre el comportamiento de una función alrededor de un punto.
Encontrarás las demostraciones de los teoremas, paso a paso, así como ejemplos y ejercicios interactivos. También encontrarás construcciones interactivas con el propósito de ayudar a una mejor comprensión.
Aquí encontrarás algunos conceptos necesarios para abordar el concepto de límite.
Recuerda que:
$|x-a| \lt r \iff -r \lt x-a \lt r \iff a-r \lt x \lt a+r \iff x \in (a-r, a+r)$
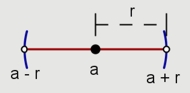
Se trata de las $x$ que distan de $a$ en menos que $r$, o bien, de las $x$ que pertenecen al intervalo abierto con centro en $a$ y radio $r$. A estos intervalos les llamaremos Vecindad de $a$ de radio $r$ y la denotaremos por: $\nu_r(a)$.
En el tema de límites, son importantes las vecindades de $a$ de radio $r$, pero excluyendo al punto $a$. Es decir:
$\nu_r(a) - \{a\}$, o también $0 \lt |x-a| \lt r$
A este tipo de vecindad le llamaremos Vecindad agujerada de $a$ de radio $r$ y la denotaremos por: $\nu_r^o(a)$
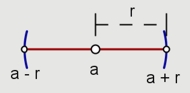
También en el tema de límites es importante el concepto de punto de acumulación de un conjunto $A$.
Se dice que $a$ es punto de acumulación de un conjunto $A$, si: $\nu_r^o(a) \cap A \neq ∅ \;\;\;\; \forall r \gt 0$
Es decir cualquier vecindad agujerada de $a$, tiene al menos un elemento de $A$.
Cuando hablemos de límite de una función en un punto $a$, será necesario que cualquier vecindad agujerada de $a$, tenga al menos un elemento del dominio de la función, es decir que $a$ sea punto de acumulación del dominio de la función.
En este apartado encontrarás una introducción un tanto intuitiva al concepto de límite de una función en un punto.
Es importante que consideres, que cuando se habla del concepto de límite, se tienen en juego los siguientes elementos:
Y con tales elementos se formula la pregunta: ¿Todos los valores $x$, “cerca” de $a$, tienen sus imágenes $f(x)$ “cerca” de $L$?
Si es así, intuimos que $L$ es límite de $f$ en $a$, pero en caso contrario decimos que $L$ no es límite de $f$ en $a$.
¿Cuál sería el caso contrario? Que existiera una $x$ “cerca” de $a$, cuya imagen $f(x)$ quedara “lejos” de $L$.
En esta visión intuitiva, se tiene un problema: las nociones “cerca de” o “lejos de”, no son tan precisas como lo requiere una definición matemáticamente correcta.
Por lo anterior, para definir adecuadamente el concepto de límite de una función en un punto, tendremos que recurrir a conceptos ya definidos anteriormente como son los intervalos abiertos con centro en un punto, llamadas comúnmente vecindades alrededor de dicho punto.
La cercanía de valores a un punto, se puede referir a que tales valores se encuentren en una vecindad del punto, del radio arbitrario. Es decir no se trata de una distancia particular para definir si se está cerca o no de un punto, más bien se trata de un proceso de acercamiento que no se detiene.
Por último, en el caso del concepto de límite, tendríamos que relacionar dos tipos de vecindades, las que se toman arbitrarias alrededor del punto $L$ y las que se encuentran alrededor de punto $a$.
Tratando de redondear las ideas anteriores, para hacer ver que $L$ es límite de $f$ en $a$, tendríamos que hacer lo siguiente:
Es importante desde luego usar una notación adecuada. Es decir,
La definición formal, que verás en la siguiente sección, se acostumbra formularla con vecindades expresadas en términos del valor absoluto. Por ello, te sugerimos estudiar detenidamente la sección de Conceptos previos.
Mientras tanto puedes analizar las siguientes construcciones interactivas.
$L$ es límite de $f$ en $a$, si para cada $\varepsilon \gt 0, \exist \delta \gt 0$, tal que $\forall x \in Dom f$, si $0 \lt |x-a| \lt \delta$, entonces $|f(x) - L| \lt \varepsilon$.
Es decir, para cada vecindad $\nu_{\varepsilon}(L)$ debe existir una vecindad $\nu_{\delta}^o(a)$, tal que: $\forall x \in Dom f \cap \nu_{\delta}^o(a)$ se cumpla que: $f(x) \in \nu_{\varepsilon}(L)$.
La notación que se utiliza en tal caso es: $L = \lim\limits_{x \to a} f(x)$.
En esta definición:
$L$ no es límite de $f$ en $a$, si $\exist \varepsilon \gt 0$, tal que $\forall \delta \gt 0$.
$\exist x \in Dom f$, que cumple $0 \lt |x-a| \lt \delta$, pero $|f(x)-L| \geq \varepsilon$.
Es decir, que existe una vecindad particular $\nu_{\varepsilon}(L)$ tal que cualquiera que sea $\nu_{\delta}^o(a)$, $\exist x \in Dom f \cap \nu_{\delta}^o(a)$ y que sin embargo: $f(x) \notin \nu_{\varepsilon}(L)$.
En algunos libros para referirse a una vecindad particular de $L$, utilizan $\varepsilon_0$. Es decir, establecen que:
$L$ no es límite de $f$ en $a$, si $\exist \varepsilon_0 \gt 0$, tal que $\forall \delta \gt 0$.
$\exist x \in Dom f$, que cumple $0 \lt |x-a| \lt \delta$, pero $|f(x)-L| \geq \varepsilon_0$.
Recuerda: la negación de un cuantificador universal se logra mediante un existencial y viceversa. (Ver Cuantificadores en Tema de Lógica).
Teorema: Si una función $f$ tiene límite en $a$, éste es único.
Si $\lim\limits_{x \to a} f(x) = L_1$ y $\lim\limits_{x \to a} f(x) = L_2$ entonces $L_1 = L_2$.
En muchas ocasiones es útil analizar el comportamiento de una función alrededor de un punto $a$, pero de manera lateral. Es decir, por la derecha o por la izquierda del punto $a$. Así tendríamos:
$L_d$ es límite lateral derecho de $f$ en $a$, si para cada $\varepsilon \gt 0, \exist \delta \gt 0$, tal que $\forall x \in Dom f$, si $a \lt x \lt a + \delta$, entonces $|f(x) - L_d| \lt \varepsilon$.
De manera similar, $L_i$ es límite lateral izquierdo de $f$ en $a$, si para cada $\varepsilon \gt 0, \exist \delta \gt 0$, tal que $\forall x \in Dom f$, si $a - \delta \lt x \lt a$, entonces $|f(x) - L_i| \lt \varepsilon$.
Y se denotan respectivamente por: $L_d = \lim\limits_{x \to a^+} f(x)$ y $L_i = \lim\limits_{x \to a^-} f(x)$.
$L = \lim\limits_{x \to a} f(x) \iff \lim\limits_{x \to a^-} f(x) = \lim\limits_{x \to a^+} f(x) = L$
Esto significa que el límite existe y es igual a $L$, sí y sólo sí los límites laterales existen y son iguales a $L$. Puedes deducirlo observando la equivalencia siguiente:
$0 \lt |x-a| \lt \delta$ sí y sólo sí $(a \lt x \lt a + \delta)$ y $(a - \delta \lt x \lt a)$.
Si alguno de los límites laterales no existe o si existen, pero no son iguales, entonces la función no tiene límite.
En muchas ocasiones el cálculo de la delta en términos de la épsilon, no es tan sencillo como en los ejemplos del apartado 2 de este tema. A continuación te explicaremos un procedimiento para aligerar esta tarea.
De acuerdo con la definición de límite: Dada $\varepsilon \gt 0$ se trata de encontrar $\delta \gt 0$ tal que si $0 \lt |x-a| \lt \delta$, entonces $|f(x) - L| \lt \varepsilon$.
El procedimiento:
Observación: Si en 2) no requieres $\delta_0 \gt 0$ para acotar a $g(x)$, entonces basta tomar $\delta = \dfrac{\varepsilon}{M}$ o una menor.
Ejemplo 1. Demostrar que: $\lim\limits_{x \to 0} x \, sen \left(\dfrac{1}{x} \right) = 0$.
Demostración: Sea $\varepsilon \gt 0$ arbitrario. Queremos $\delta \gt 0$ tal que si $0 \lt |x-0| \lt \delta$, entonces $\left|x\,sen \left(\dfrac{1}{x} \right) - 0 \right| \lt \varepsilon$.
Apliquemos el procedimiento:
Ejemplo 2. Demostrar que: $\lim\limits_{x \to 2} x^2 = 4$.
Demostración: Sea $\varepsilon \gt 0$ arbitrario. Queremos $\delta \gt 0$ tal que si $0 \lt |x-2| \lt \delta$, entonces $|x^2-4| \lt \varepsilon$
Apliquemos el procedimiento:
En este apartado encontrarás los teoremas relacionados con el límite de una suma, resta, producto y división de funciones. Para ello iniciaremos con el siguiente:
1) Si $|x-x_0| \lt \dfrac{\varepsilon}{2}$ y $|y-y_0| \lt \dfrac{\varepsilon}{2}$, entonces $|(x+y) - (x_0+y_0)| \lt \varepsilon$.
2) Si $|x-x_0| \lt min \left\{1, \dfrac{\varepsilon}{2(|y_0|+1)} \right\}$ y $|y-y_0| \lt min \left\{1, \dfrac{\varepsilon}{2(|x_0|+1)} \right\}$.
Si tienes la curiosidad de saber porqué se eligieron $\delta_1 \gt 0$ y $\delta_2 \gt 0$ tal como aparecen en 2), lee la siguiente información.
Dado $\varepsilon \gt 0$, se trata de encontrar $\delta_1 \gt 0$ y $\delta_2 \gt 0$ tales que:
$|x - x_0| \lt \delta_1$ y $|y - y_0| \lt \delta_2 \implies |xy - x_0 y_0| \lt \varepsilon$ ... ( 1 ).
Podemos escribir ( 1 ) de las siguientes dos formas:
$|xy - x_0 y_0| = |xy - x_0 y + x_0 y - x_0 y_0| \leq |y| |x - x_0| + |x_0| |y - y_0| \lt |y| \delta_1 + |x_0| \delta_2$ y
$|xy - x_0 y_0| = |xy - x y_0 + x y_0 - x_0 y_0| \leq |x| |y - y_0| + |y_0| |x - x_0| \lt |x| \delta_2 + |y_0| \delta_1$
Así, para que se cumpla ( 1 ), podemos buscar $\delta_1 \gt 0$ y $\delta_2 \gt 0$ tales que:
$|y| \delta_1 \lt \dfrac{\varepsilon}{2}$ y $|x_0| \delta_2 \lt \dfrac{\varepsilon}{2}$ y $|x| \delta_2 \lt \dfrac{\varepsilon}{2}$ y $|y_0| \delta_1 \lt \dfrac{\varepsilon}{2}$.
Recordando además que:
$|x| - |x_0| \leq |x - x_0| \lt \delta_1 \implies |x| \lt \delta_1 + |x_0|$ y $|y| - |y_0| \leq |y - y_0| \lt \delta_2 \implies |y| \lt \delta_2 + |y_0|$.
Podemos buscar $\delta_1 \gt 0$ y $\delta_2 \gt 0$ tales que:
$|y| \delta_1 \lt (\delta_2 + |y_0|) \delta_1 \lt \dfrac{\varepsilon}{2}$ ... ( 2 ),
$|x_0| \delta_2 \lt \dfrac{\varepsilon}{2}$ ... ( 3 ),
$|x| \delta_2 \lt (\delta_1 + |x_0|) \delta_2 \lt \dfrac{\varepsilon}{2}$ ... ( 4 ) y
$|y_0| \delta_1 \lt \dfrac{\varepsilon}{2}$ ... ( 5 ).
Se cumplen ( 3 ) y ( 5 ) si $\delta_1 = \dfrac{\varepsilon}{2(|y_0| + 1)}$ y $\delta_2 = \dfrac{\varepsilon}{2(|x_0| + 1)}$ y, sustituyendo en ( 2 ) y ( 4 ), queda:
$|y| \delta_1 \lt (\delta_2 + |y_0|) \dfrac{\varepsilon}{2(|y_0| + 1)} \stackrel{\delta_2 = 1}{=} \dfrac{\varepsilon}{2}$ y $|x| \delta_2 \lt (\delta_1 + |x_0|) \dfrac{\varepsilon}{2(|x_0| + 1)} \stackrel{\delta_1 = 1}{=} \dfrac{\varepsilon}{2}$.
Así, debemos tomar $\delta_1 = min \left\{1, \dfrac{\varepsilon}{2(|y_0| +1)} \right\}$ y $\delta_2 = min \left\{1, \dfrac{\varepsilon}{2(|x_0| +1)} \right\}$.
3) Si $y_0 \neq 0$ y $|y - y_0| \lt min \left\{ \dfrac{|y_0|}{2}, \dfrac{\varepsilon|y_0|^2}{2} \right\}$, entonces $y \neq 0$ y $\left| \dfrac{1}{y} - \dfrac{1}{y_0} \right| \lt \varepsilon$.
Si tienes la curiosidad de saber porqué se eligió $\delta \gt 0$ tal como aparece en 3), lee el siguiente texto.
Dado $\varepsilon \gt 0$, se trata de encontrar $\delta \gt 0$ tal que:
$y_0 \neq 0$ y $|y-y_0| \lt \delta \implies y \neq 0$ y $\left| \dfrac{1}{y} - \dfrac{1}{y_0} \right| \lt \varepsilon$ ... ( 1 ).
Por un lado, recordando que:
$|y_0| - |y| \leq |y_0 - y| \lt \delta \implies |y| \gt |y_0| - \delta$ ... ( 2 ).
Por otro lado, podemos escribir ( 1 ) de la siguiente forma:
$\left| \dfrac{1}{y} - \dfrac{1}{y_0} \right| = \dfrac{|y_0 - y|}{y y_0} = \dfrac{|y - y_0|}{|y y_0|} \lt \dfrac{\delta}{|y| |y_0|} \stackrel{(2)}{\lt} \dfrac{\delta}{(|y_0| - \delta) |y_0|} = \dfrac{\delta}{|y_0|^2} - \dfrac{1}{|y_0|} \lt \dfrac{\delta}{|y_0|^2}$ ... ( 3 ).
Así, a fin de que: $|y| \gt 0$ y $\left|\dfrac{1}{y} - \dfrac{1}{y_0} \right| \lt \varepsilon$, necesitamos que: $|y| \gt |y_0| - \delta \gt 0$ ... ( 4 ) y $\dfrac{\delta}{|y_0|^2} \lt \varepsilon$.
Es decir, podemos tomar $\delta = \dfrac{|y_0|}{2}$ para ( 4 ) y $\delta = \dfrac{\varepsilon |y_0|^2}{2}$ para ( 5 ).
En resumen podemos tomar $\delta = min \left\{ \dfrac{|y_0|}{2}, \dfrac{\varepsilon|y_0|^2}{2} \right\}$.
Si $\lim\limits_{x \to a} f(x) = L$ y $\lim\limits_{x \to a} g(x) = M$, entonces:
1) $\lim\limits_{x \to a} (f+g) = L+M$
2) $\lim\limits_{x \to a} (fg) = LM$
3) Si además $M \neq 0$, $\lim\limits_{x \to a} \left(\dfrac{1}{g}\right)(x) = \dfrac{1}{M}$
Con las mismas hipótesis del teorema y combinando 2) y 3) del teorema, se obtiene:
4) Si además $M \neq 0$, entonces $\lim\limits_{x \to a} \left(\dfrac{f}{g} \right)(x) = \dfrac{L}{M}$.
Es decir:
En este apartado encontrarás otros teoremas que facilitan el cálculo o manejo de algunos límites de interés.
Si $f(x) = g(x) \;\; \forall x \in \nu_{\delta_0}^o(a)$ y $\lim\limits_{x \to a} g(x) = L$, entonces $\lim\limits_{x \to a} f(x) = L$
Si $f(x) \geq 0 \;\; \forall x \in \nu_{\delta_0}^o(a)$ y $\lim\limits_{x \to a} f(x) = L$, entonces $L \geq 0$
Sea $f(x) \geq g(x) \;\; \forall x \in \nu_{\delta_0}^o(a)$. Si $\lim\limits_{x \to a} f(x) = L$ y $\lim\limits_{x \to a} g(x) = M$, entonces $L \geq M$.
Si $h(x) \leq f(x) \leq g(x) \;\; \forall x \in \nu_{\delta_0}^o(a)$ y $\lim\limits_{x \to a} h(x) = \lim\limits_{x \to a} g(x) = L$, entonces $\lim\limits_{x \to a} f(x) = L$.
En este apartado encontrarás algunos límites interesantes, como por ejemplo:
Demostrar que $\lim\limits_{x \to 0} \dfrac{sen(x)}{x} = 1$.
$P = (cos(x), sen(x))$.
$Q = (1, 0)$.
$S = (1, tan(x))$.
$QS$ segmento tangente a $C$ en $Q$.
$PR$ segmento tangente a $C$ en $P$.
$SQ = tan(x)$.
Para $x \gt 0$ (cercano a $0$)
$sen(x) \leq x \leq tan(x) \iff \begin{cases} sen(x) \leq x \;\;\; \textbf{( 1 )} \\ x \leq tan(x) \;\;\; \textbf{( 2 )} \end{cases}$
De $\textbf{( 1 )}$, tenemos que: $\dfrac{sen(x)}{x} \leq 1 \;\;\; $ ( 3 )
De $\textbf{( 2 )}$, tenemos que: $x \leq \dfrac{sen(x)}{cos(x)} \implies cos(x) \leq \dfrac{sen(x)}{x} \;\;\;$ ( 4 )
Juntando ( 3 ) y ( 4 ), tenemos que: $cos(x) \leq \dfrac{sen(x)}{x} \leq 1$
Y aplicando: $\lim\limits_{x \to 0} [cos(x)] = cos(0) = 1$ y $\lim\limits_{x \to 0} [1] = 1$
Así, por el teorema del sandwich, se tiene que: $\lim\limits_{x \to 0^+} \dfrac{sen(x)}{x} = 1$ (Recordar que $x \lt 0$).
Pero como: $\dfrac{sen(-x)}{-x} = \dfrac{-sen(x)}{-x} = \dfrac{sen(x)}{x}$, entonces: $\lim\limits_{x \to 0^-} \dfrac{sen(x)}{x} = 1$
Entonces: $\lim\limits_{x \to 0} \dfrac{sen(x)}{x} = 1$ (los límites laterales existen y son iguales).
Q.E.D.
Demostrar que $\lim\limits_{x \to 0} \dfrac{1-cos(x)}{x} = 0$.
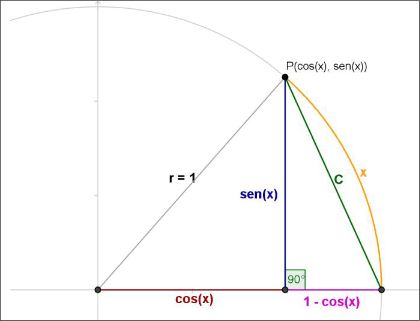
Observa que estamos tomando $x \gt 0$ y cercana a cero.
Así, por el Teorema de Pitágoras: $\sqrt{(1-cos(x))^2 + sen^2(x)} = C$
Pero además: $C \lt x$
Entonces: $\sqrt{(1-cos(x))^2 + sen^2(x)} \lt x$ ( 1 )
Así, de la desigualdad ( 1 ), al elevar al cuadrado, tenemos que: $0 \leq (1-cos(x))^2 + sen^2(x) \lt x^2$
De donde: $0 \leq 1 - 2cos(x)+ cos^2(x) + sen^2(x) \lt x^2$
Como $cos^2(x) + sen^2(x) = 1$ nos queda: $0 \leq 2 - 2cos(x) \lt x^2$
Como además $x \gt 0$, dividiendo por $2x$, tenemos: $0 \leq \dfrac{1-cos(x)}{x} \lt \dfrac{x}{2} \lt x$
Y aplicando el teorema del Sandwich, tenemos que: $\lim\limits_{x \to 0^+} \dfrac{1-cos(x)}{x} = 0$
Ahora, para el caso negativo, tenemos que: $\dfrac{1-cos(-x)}{-x} = \dfrac{1-cos(x)}{-x} = \dfrac{1-cos(x)}{x}$
Así $\lim\limits_{x \to 0^-} \dfrac{1-cos(x)}{x} = -\lim\limits_{x \to 0^-} \dfrac{1-cos(x)}{x} = 0$
$\therefore \lim\limits_{x \to 0} \dfrac{1-cos(x)}{x} = 0$
Q.E.D.
Calcular $\lim\limits_{x \to 0} \dfrac{sen(ax)}{x}$ para $a \neq 0$.
Dado que $a \neq 0$, podemos escribir: $\dfrac{sen(ax)}{x} = \dfrac{a \, sen(ax)}{ax}$
De este modo, queda: $\lim\limits_{x \to 0} \dfrac{sen(ax)}{x} = \lim\limits_{x \to 0} \dfrac{a \, sen(ax)}{ax} = a \lim\limits_{x \to 0} \dfrac{sen(ax)}{ax}$
Pero además: $x \rightarrow 0 \iff ax \rightarrow 0$
Entonces, aplicando el hecho de que $\lim\limits_{u \to 0} \dfrac{sen(u)}{u} = 1$, nos queda:
$a \lim\limits_{x \to 0} \dfrac{sen(ax)}{ax} = a \lim\limits_{ax \to 0} \dfrac{sen(ax)}{ax} = a(1) = a$
Y por lo tanto: $\lim\limits_{x \to 0} \dfrac{sen(ax)}{x} = a$
Calcular $\lim\limits_{x \to 0} \dfrac{sen^2(x)}{x \, tan(x)}$.
Podemos escribir: $\dfrac{sen^2(x)}{x \, tan(x)} = \dfrac{sen(x)}{x} \dfrac{sen(x)}{tan(x)} = \dfrac{sen(x)}{x} \dfrac{sen(x)}{\frac{sen(x)}{cos(x)}} = \dfrac{sen(x)}{x} cos(x)$
De este modo, queda: $\lim\limits_{x \to 0} \dfrac{sen^2 (x)}{x \, tan(x)} = \lim\limits_{x \to 0} \dfrac{sen(x)}{x} cos(x) = \lim\limits_{x \to 0} \dfrac{sen(x)}{x} \lim\limits_{x \to 0} cos(x)$
Entonces, aplicando el hecho de que $\lim\limits_{u \to 0} \dfrac{sen(x)}{u}$, nos queda: $\lim\limits_{x \to 0} \dfrac{sen^2(x)}{x \, tan(x)} = \lim\limits_{x \to 0} cos(x) = 1$
Calcular $\lim\limits_{x \to 0} \dfrac{sen(ax)}{sen(bx)}$ para $a, b \neq 0$.
Dados que $a, b \; (\neq 0)$, podemos escribir:
$\dfrac{sen(ax)}{sen(bx)} = \left( \dfrac{a}{b} \right) \left( \dfrac{b}{a} \right) \left( \dfrac{x}{x} \right) \left( \dfrac{sen(ax)}{sen(bx)} \right) = \left( \dfrac{a}{b} \right) \left( \dfrac{\dfrac{sen(ax)}{ax}}{\dfrac{sen(bx)}{bx}} \right)$
De este modo, queda: $\lim\limits_{x \to 0} \dfrac{sen(ax)}{sen(bx)} = \left( \dfrac{a}{b} \right) \lim\limits_{x \to 0} \left( \dfrac{\dfrac{sen(ax)}{ax}}{\dfrac{sen(bx)}{bx}} \right)$
Pero como además: $ax \rightarrow 0$ y $bx \rightarrow 0 \iff x \rightarrow 0$
Entonces, aplicando el cociente de límites y el hecho de que $\lim\limits_{u \to 0} \dfrac{sen(u)}{u} = 1$, nos queda:
$\lim\limits_{x \to 0} \dfrac{sen(ax)}{sen(bx)} = \left( \dfrac{a}{b} \right) \dfrac{\lim\limits_{ax \to 0} \dfrac{sen(ax)}{ax}}{\lim\limits_{bx \to 0} \dfrac{sen(bx)}{bx}} = \dfrac{a}{b}$
Es decir: $\lim\limits_{x \to 0} \dfrac{sen(ax)}{sen(bx)} = \dfrac{a}{b}$
Calcular $\lim\limits_{x \to 1} \dfrac{x^3-1}{x^2-1}$.
Sabemos que: $\dfrac{x^3 - 1}{x^2 - 1} = \dfrac{(x-1)(x^2 + x + 1)}{(x-1)(x+1)} \stackrel{x \neq 1}{=} \dfrac{x^2 + x + 1}{x+1}$
Entonces: $\lim\limits_{x \to 1} \dfrac{x^3 - 1}{x^2 - 1} = \lim\limits_{x \to 1} \dfrac{x^2 + x + 1}{x+1}$
Y aplicando los teoremas sobre álgebra de límites:
$\lim\limits_{x \to 1} \dfrac{x^3 - 1}{x^2 - 1} = \dfrac{\lim\limits_{x \to 1} (x^2 + x + 1)}{\lim\limits_{x \to 1} (x+1)} = \dfrac{3}{2}$
Es decir: $\lim\limits_{x \to 1} \dfrac{x^3 - 1}{x^2 - 1} = \dfrac{3}{2}$
Calcular $\lim\limits_{x \to 1} \dfrac{\sqrt{x}-1}{x-1}$.
Haciendo el cambio de variable $y = \sqrt{x}$, podemos escribir: $\dfrac{\sqrt{x}-1}{x-1} \stackrel{y=\sqrt{x}}{=} \dfrac{y-1}{y^2 - 1} = \dfrac{y-1}{(y-1)(y+1)} \stackrel{y \neq 1}{=} \dfrac{1}{y+1}$
Como además $x \to 1 \iff y \to 1$, tenemos que:
$\lim\limits_{x \to 1} \dfrac{\sqrt{x}-1}{x-1} = \lim\limits_{y \to 1} \dfrac{1}{y+1}$
Y aplicando los teoremas sobre álgebra de límites: $\lim\limits_{y \to 1} \dfrac{1}{y+1} = \dfrac{1}{2}$
Es decir: $\lim\limits_{x \to 1} \dfrac{\sqrt{x}-1}{x-1} = \dfrac{1}{2}$
Calcular $\lim\limits_{x \to 0} \dfrac{\sqrt{1+x}-1}{\sqrt[3]{1+x}-1}$.
Haciendo el cambio de variable $1+x = y^6$, podemos escribir:
$\dfrac{\sqrt{1+x}-1}{\sqrt[3]{1+x}-1} \stackrel{1+x=y^6}{=} \dfrac{y^3 - 1}{y^2 - 1} = \dfrac{(y-1)(y^2 + y + 1)}{(y-1)(y+1)} \stackrel{y \neq 1}{=} \dfrac{y^2 + y + 1}{y+1}$
Como además $x \to \iff y \to 1$, tenemos que:
$\lim\limits_{x \to 0} \dfrac{\sqrt{1+x}-1}{\sqrt[3]{1+x}-1} = \lim\limits_{y \to 1} = \dfrac{y^2 + y + 1}{y+1}$
Y aplicando los teoremas sobre álgebra de límites: $\lim\limits_{y \to 1} \dfrac{y^2 + y + 1}{y+1} = \dfrac{3}{2}$
Es decir: $\lim\limits_{x \to 0} \dfrac{\sqrt{1+x}-1}{\sqrt[3]{1+x}-1} = \dfrac{3}{2}$
Calcular $\lim\limits_{x \to a} \dfrac{sen(x) - sen(a)}{x-a}$.
Sabemos que: $sen(x) - sen(a) = 2 sen \left( \dfrac{x-1}{2} \right) cos \left( \dfrac{x+a}{2} \right)$
Por lo tanto: $\dfrac{sen(x) - sen(a)}{x-a} = \dfrac{ 2sen \left( \dfrac{x-a}{2} \right) cos \left( \dfrac{x+a}{2} \right) }{x-a} = \dfrac{sen \left( \dfrac{x-a}{2} \right) }{\left( \dfrac{x-a}{2} \right) } cos \left( \dfrac{x+a}{2} \right)$
De este modo, queda:
$\lim\limits_{x \to a} \dfrac{sen(x) - sen(a)}{x-a} = \lim\limits_{x \to a} \left( \dfrac{ sen \left( \dfrac{x-a}{2} \right) }{ \left( \dfrac{x-a}{2} \right) } cos \dfrac{x-a}{2} \right)$
Y como: $\lim\limits_{x \to a} \left( \dfrac{ sen \left( \dfrac{x-a}{2} \right) }{ \left( \dfrac{x-a}{2} \right) } \right) = 1$ y $\lim\limits_{x \to a} cos \left( \dfrac{x+a}{2} \right) = cos(a)$
Entonces, aplicando el producto de límites,nos queda:
$\lim\limits_{x \to a} \dfrac{sen(x) - sen(a)}{x-a} = \lim\limits_{x \to a} \left( \dfrac{ sen \left( \dfrac{x-a}{2} \right) }{ \left( \dfrac{x-a}{2} \right) } \right) \lim\limits_{x \to a} cos \left( \dfrac{x+a}{2} \right) = cos(a)$
Es decir: $\lim\limits_{x \to a} \dfrac{sen(x) - sen(a)}{x-a} = cos(a)$
Calcular $\lim\limits_{h \to 0} \dfrac{sen(x+h) - sen(x)}{h}$.
Sabemos que: $sen(x+h) = sen(x) cos(h) + sen(h) cos(x)$
Por lo tanto:
$\dfrac{sen(x+h) - sen(x)}{h} = \dfrac{sen(x)cos(h) + sen(h)cos(x) - sen(x)}{h}$
Factorizando y separando los sumandos, queda:
$\dfrac{sen(x+h) - sen(x)}{h} = -sen(x) \left( \dfrac{1 - cos(h)}{h} \right) + cos(x) \left( \dfrac{sen(h)}{h} \right)$
Y como: $\lim\limits_{h \to 0} \left( \dfrac{1 - cos(h)}{h} \right) = 0$ y $\lim\limits_{h \to 0} \dfrac{sen(h)}{h} = 1$
Entonces, aplicando la suma y el producto de límites,nos queda:
$\lim\limits_{h \to 0} \dfrac{sen(x+h) - sen(x)}{h} = sen(x) \lim\limits_{h \to 0} \left( \dfrac{1 - cos(h)}{h} \right) + cos(x) \lim\limits_{h \to 0} \left( \dfrac{sen(h)}{h} \right) = cos(x)$
Es decir: $\lim\limits_{h \to 0} \dfrac{sen(x+h) - sen(x)}{h} = cos(x)$
Si utilizas el graficador a continuación, para aquellas funciones donde tengas constantes, como $a$ o $b$, debes darles un valor numérico particular, pues de otra manera el graficador la tomará como otra variable y no le será posible darte una respuesta.
Existen algunas variantes en el concepto de límite que resultan muy útiles para analizar el comportamiento de ciertas funciones. Algunas de estas variantes se pueden representar simbólicamente del siguiente modo:
$\lim\limits_{x \to \infty} f(x) = L$,
$\lim\limits_{x \to a} f(x) = \infty$,
$\lim\limits_{x \to \infty} f(x) = \infty$
También se incluyen las variantes de tendencia a menos infinito y la combinación con los límites laterales.
$\lim\limits_{x \to \infty} f(x) = L$, significa que para cada $\varepsilon \gt 0, \exist N \gt 0$ tal que, si $x \in Dom f$ y $x \gt N$, entonces $|f(x) - L| \lt \varepsilon$.
$\lim\limits_{x \to a} f(x) = \infty$, significa que para cada $M \gt 0, \exist \delta \gt 0$ tal que, si $x \in Dom f$ y $0 \lt |x-a| \lt \delta$, entones $f(x) \gt M$.
$\lim\limits_{x \to \infty} f(x) = \infty$, significa que para cada $M \gt 0, \exist N \gt 0$ tal que, si $x \in Dom f$ y $x \gt N$, entonces $f(x) \gt M$.
$\lim\limits_{x \to \infty} \dfrac{1}{x} = 0$
$\lim\limits_{x \to 0^+} \dfrac{1}{x} = \infty$
$\lim\limits_{x \to \infty} \dfrac{1}{x^2}$
$\lim\limits_{x \to \infty} \dfrac{x^2}{x^2+1}$
$\lim\limits_{x \to 0} \dfrac{1}{x^2}$
$\lim\limits_{x \to \infty} \dfrac{sen(x)}{x}$
$\lim\limits_{x \to \infty} sen \left( \dfrac{1}{x} \right)$
Si utilizas el graficador a continuación, para aquellas funciones donde tengas constantes, como $a$ o $b$, debes darles un valor numérico particular, pues de otra manera el graficador la tomará como otra variable y no le será posible darte una respuesta.
En este apartado podrás probar tus conocimientos en el cálculo de algunos límites, por ejemplo:
$\lim\limits_{x \to a} \dfrac{x^2 - a^2}{x-a}$
$\lim\limits_{x \to a} \dfrac{\sqrt{x} - \sqrt{a}}{x-a}$
$\lim\limits_{x \to 0} \dfrac{b \, sen(ax)}{x}$ para $a, b \neq 0$
$\lim\limits_{x \to a} \dfrac{b \, sen(ax)}{sen(bx)}$ para $a, b \neq 0$
$\lim\limits_{x \to \infty} \dfrac{ax^2}{x^2 + b^2}$
$\lim\limits_{x \to \infty} \dfrac{x^2 - bx + x}{ax^2 + b^2}$
Si utilizas el graficador a continuación, para aquellas funciones donde tengas constantes, como $a$ o $b$, debes darles un valor numérico particular, pues de otra manera el graficador la tomará como otra variable y no le será posible darte una respuesta.
Los ejercicios siguientes los puedes consultar en el Libro de Cálculo de M. Spivak.
i) $\lim\limits_{x \to 1} \dfrac{x^2-1}{x+1}$
ii) $\lim\limits_{x \to 2} \dfrac{x^3 - 8}{x-2}$
iii) $\lim\limits_{x \to 3} \dfrac{x^3 - 8}{x-2}$
iv) $\lim\limits_{x \to y} \dfrac{x^n - y^n}{x-y}$
v) $\lim\limits_{y \to x} \dfrac{x^n - y^n}{x-y}$
vi) $\lim\limits_{h \to 0} \dfrac{\sqrt{a+h} - \sqrt{a}}{h}$
i) $f(x) = x^2; l=a^2$
ii) $f(x) = \dfrac{x}{1+sen^2 x}; a=0, l=0$
iii) $f(x) = \dfrac{1}{x}; a=1, l=1$
iv) $f(x) = \sqrt{|x|}; a=0, l=0$
v) $f(x) = x^2 + \dfrac{1}{x}; a=1, l=2$
vi) $f(x) = \sqrt{x}; a=1, l=1$
(¿Cómo puede verse esto gráficamente? Indicación: ¿Porqué basta con demostrar que $l-1 \lt f(x) \lt l+1$ pra $0 \lt |x-a| \lt \delta$?).
[Naturalmente la parte a) es innecesaria si se consigue hacer la parte b)]
Los siguientes ejercicios los puedes consultar en el libro: Cálculo de Arizmendi, Carrillo y Lara. Procedimientos para el Cálculo de Algunos Límites.
i) $f(x) = 1-2x$, $x_0 = -1$, $L=3$ y $\varepsilon=0.01$, $\varepsilon=0.0001$, $\varepsilon=0.02$
ii) $f(x) = x^2 - 4$, $x_0 = 2$, $L=0$ y $\varepsilon=0.01$, $\varepsilon=0.0001$, $\varepsilon=0.02$
iii) $f(x) = \dfrac{x^2-9}{x+3}$, $x_0 = -3$, $L=-6$ y $\varepsilon=0.05$, $\varepsilon=0.001$, $\varepsilon=0.0004$
iv) $f(x) = \sqrt[3]{x}$, $x_0 = 1$, $L=1$ y $\varepsilon=0.002$, $\varepsilon=0.0001$, $\varepsilon=0.01$
v) $f(x) = \dfrac{x+1}{x}$, $x_0 = 1$, $L=2$ y $\varepsilon=0.001$, $\varepsilon=0.002$, $\varepsilon=0.003$
vi) $f(x) = \dfrac{1}{x}$, $x_0 = 2$, $L=\dfrac{1}{2}$ y $\varepsilon=0.002$, $\varepsilon=0.02$, $\varepsilon=0.2$
i) $\lim\limits_{x \to 2} \dfrac{x^2 - 4}{x-2} = 4$
ii) $\lim\limits_{x \to 2} x = 2$
iii) $\lim\limits_{x \to 3} \sqrt[3]{x} = \sqrt[3]{3}$
iv) $\lim\limits_{x \to 2} \dfrac{1}{x+1} = \dfrac{1}{3}$
v) $\lim\limits_{x \to -3} \dfrac{1}{x+2} = -1$
vi) $\lim\limits_{h \to 0} \dfrac{x + h^3 - x^3}{h} = 3x^2$
vii) $\lim\limits_{x \to 1} 1-x^2 = 0$
viii) $\lim\limits_{x \to 0} \dfrac{2x}{1+x} = 0$
ix) $\lim\limits_{x \to a} |x| = a$
i) $\lim\limits_{x \to 0} \dfrac{sen(5x)}{x}$
ii) $\lim\limits_{h \to 0} \dfrac{sen(h^2)}{h}$
iii) $\lim\limits_{x \to 0} \dfrac{sen(ax)}{x}$
iv) $\lim\limits_{x \to 0} \dfrac{sen(5x)}{sen(2x)}$
v) $\lim\limits_{x \to 0} \dfrac{sen^2(x)}{x \, tan(x)}$
vi) $\lim\limits_{h \to 0} \left( h \dfrac{sen(h)}{sen(2h^2)} \right)$
vii) $\lim\limits_{x \to \frac{\pi}{4}} \dfrac{sen(x) - cos(x)}{1 - tan(x)}$
viii) $\lim\limits_{x \to 0} \dfrac{sen(x) tan(x)}{x^2}$
ix) $\lim\limits_{x \to a} \dfrac{cos(x) - cos(a)}{x-a}$
x) $\lim\limits_{h \to 0} \dfrac{cos(x+h) - cos(x)}{h}$
i) $\lim\limits_{x \to 1} \dfrac{x-1}{x^2-1}$
ii) $\lim\limits_{x \to 3} \dfrac{x^6 - 729}{x-3}$
iii) $\lim\limits_{x \to 2} \dfrac{x^2 + 6x + 8}{x^2 - 2x - 8}$
iv) $\lim\limits_{x \to 2} \dfrac{x^2 - 4}{x^3 + 8}$
v) $\lim\limits_{x \to 1} \dfrac{x^4 + x^2 - 2}{x^4 - 10x^2 + 9}$
vi) $\lim\limits_{x \to 2} \dfrac{3x^2 - 5x -2}{x^3 - 2x^2 + 3x - 6}$
vii) $\lim\limits_{x \to -1} \dfrac{x^9 + 1}{x^3 + 1}$
viii) $\lim\limits_{x \to 4} \dfrac{x^2 + x - 20}{x^2 - 2x - 8}$
ix) $\lim\limits_{x \to 2} \dfrac{x^2 + 6x - 16}{x^2 + 10x - 16}$
Aquí podrás encontrar el concepto de función continua en un punto y los teoremas de continuidad más importantes.
En particular encontrarás los teoremas sobre álgebra de funciones continuas y otros teoremas cuyas demostraciones son un resultado interesante del axioma del supremo.
Encontrarás las demostraciones de los teoremas, paso a paso, así como ejemplos y ejercicios interactivos. También encontrarás construcciones interactivas con el propósito de ayudar a una mejor comprensión.
Antes de establecer la definición, diremos que una condición indispensable para decir si una función es continua en un punto $a$, es que tal punto pertenezca a su dominio. De otra manera no tendría sentido. Así, una función $f$ es continua en $a \in Dom f$, si para cada $\varepsilon \gt 0, \exist \delta \gt 0$, tal que $\forall x \in Dom f$ y $|x-a| \lt \delta \implies |f(x) - f(a)| \lt \varepsilon$.
En esta definición se puede observar que a diferencia de la definición de límite:
Una función $f$ es continua en $a \in Dom f$, si $\lim\limits_{x \to a} f(x) = f(a)$.
Una función $f$ no es continua en $a \in Dom f$, sí:
Igual que en la continuidad, tiene sentido hablar de la discontinuidad de una función, en puntos que pertenecen a su dominio.
Una función $f$ es discontinua en $a \in Dom f$, si no es continua en $a$.
Una función $f$ es discontinua en $a \in Dom f$, sí:
Cuando una función $f$ tiene una discontinuidad removible en $a$, se puede definir una función $F$ igual a $f$ (excepto en $a$), pero que sea continua en $a$.
En este apartado veremos los teoremas relacionados con el álgebra de funciones continuas.
Si $f$ y $g$ son continuas en $a$, entonces:
Además si $g(a) \neq 0$, entonces:
Si $f$ y $g$ son continuas en $a$ y $g(a) \neq 0$, entonces $\dfrac{f}{g}$ es continua en $a.$
Si $g$ es continua en $a$ y $f$ es continua en $g(a)$, entonces $f \circ g$ es continua en $a$.
$f$ es continua en $(a, b)$, si es continua $\forall x \in (a, b)$.
$f$ es continua en $[a, b]$, si es continua $\forall x \in (a, b)$ y además:
$\lim\limits_{x \to a^+} f(x) = f(a)$ y $\lim\limits_{x \to b^-} f(x) = f(b)$.
Sea $f$ continua en $a$ y $f(a) \gt 0$, entonces $\exist \delta \gt 0$ tal que $f(x) \gt 0 \; \forall x \in \nu_{\delta} (a)$. Similarmente si $f(a) \lt 0$, entonces $\exist \delta \gt 0$ tal que $f(x) \lt 0 \; \forall x \in \nu_{\delta}(a)$.
En este apartado veremos teoremas de gran importancia en la teoría de funciones continuas en intervalos cerrados.
Para la demostración de tales teoremas será indispensable recordar el Axioma del supremo de los números reales:
Todo conjunto $A$ (no vacío) de reales, acotado superiormente posee un supremo, es decir, existe un real $s$ que es la mínima de las cotas superiores de $A$ ($s = sup A$).
En el siguiente teorema se utilizará el Teorema 3 de la sección anterior, en donde se estable que una función continua en un punto, mantiene su signo, en una vecindad de dicho punto.
Si $f$ es continua en $[a, b]$ y $f(a) \lt 0 \lt f(b)$, entonces existe $x \in (a, b)$, tal que $f(x)=0$.
Este teorema es muy útil, en particular para aproximar raíces de polinomios.
Si $f$ es continua en $a$, entonces $\exist \delta \gt 0$ tal que $f$ está acotada en $(a-\delta, a+\delta)$.
En la demostración del siguiente teorema, jugará un papel muy importante este Lema 1. Revísalo con cuidado antes de entrar a la demostración del Teorema 2.
Si $f$ es continua en $[a,b]$, entonces $f$ está acotada superiormente en $[a,b].$
Si $f$ es continua en $[a,b]$, entonces existe $x_0 \in [a,b]$, tal que $f(x_0) \geq f(x) \; \forall x \in [a,b]$. En este caso se dice que $f$ “alcanza el máximo” en $x_0$.
Tales demostraciones las haremos en el siguiente apartado.
En este apartado veremos teoremas que se deducen con cierta facilidad, de los tres teoremas fuertes y que completan los resultados importantes para funciones continuas en intervalos cerrados. Les asignaremos números consecutivos.
Si $f$ es continua en $[a,b]$ y $f(a) \lt c \lt f(b)$, entonces existe $x \in (a,b)$ tal que $f(x)=c$.
Si $f$ es continua en $[a,b]$ y $f(a) \gt c \gt f(b)$, entonces existe $x \in [a,b]$ tal que $f(x)=c$.
Los teoremas 4 y 5 juntos demuestran que $f$ toma todos los valores entre $f(a)$ y $f(b)$. Se puede decir más: Si $c$ y $d$ están en $[a,b]$, entonces $f$ toma todos los valores comprendidos entre $f(c)$ y $f(d)$. En resumen, si una función continua en un intervalo cerrado $[a,b]$ toma dos valores, entonces toma todos los valores comprendidos entre ellos; esta generalización del teorema fuerte 1, recibe a menudo el nombre de Teorema del valor intermedio.
Si $f$ es continua en $[a,b]$, entonces $f$ está acotada inferiormente en $[a,b]$.
El teorema fuerte 2 y el 6 juntos demuestran que una función continua $f$ en $[a,b]$ está acotada en $[a,b]$.
Si $f$ es continua en $[a,b]$, entonces existe $x_0 \in [a,b]$ tal que $f(x_0) \leq f(x) \; \forall x \in [a,b]$.
En este caso se dice que $f$ “alcanza el mínimo” en $x_0$.
El teorema fuerte 3 y el 7 juntos demuestran que una función continua $f$ en $[a,b]$ alcanza su máximo y mínimo en $[a,b]$.
Juntando los teoremas 3, 4, 5 y 7, se establece la siguiente generalización:
Si $f$ es continua en $[a,b]$, entonces $f$ toma todos los valores entre su mínimo y su máximo.
En este apartado veremos algunas aplicaciones de los teoremas fuertes y sus consecuencias.
Si $\alpha \gt 0$, entonces $\exist b$ tal que $b^2 = \alpha$.
Esto significa que todo número positivo posee una raíz cuadrada. Un razonamiento similar, al presentado en la demostración, se puede utilizar para demostrar que todo real positivo tiene una raíz enésima.
La ecuación $sen(x^2-1) = 2x + 1$ tiene al menos una solución real.
$|x| \gt 1, 2n |a_{n-1}|, ..., 2n|a_0| \implies \dfrac{1}{2} \leq 1 + \dfrac{a_{n-1}}{x} + ... + \dfrac{a_0}{x^n}$
La hipótesis en esta implicación significa que $|x|$ es mayor que cada uno de los elementos enlistados.
Si $n$ es impar, entonces cualquier ecuación $x^n + a_{n-1}x^{n-1} + ... + a_0 = 0$ posee una raíz real.
Si $n$ es par y $f(x) = x^n + a_{n-1}x^{n-1} + ... + a_0$, entonces $\exist x_0$ tal que $f(x_0) \leq f(x) \; \forall x$.
En este apartado podrás probar tus conocimientos sobre las funciones continuas.
i) $f(x)=x^2; l=a^2$
ii) $f(x)=\dfrac{1}{x}; a=1, l=1$
iii) $f(x)=x^2+\dfrac{1}{x}; a=1, l=2$
iv) $f(x)=\dfrac{x}{1+sen^2 x}; a=0, l=0$
v) $f(x)=\sqrt{|x|}; a=0, l=0$
vi) $f(x)=\sqrt{x}; a=1, l=1$
Los siguientes ejercicios los puedes consultar en el libro: Cálculo de Arizmendi, Carrillo y Lara.
i) $f(x)=\begin{cases} \sqrt{x^2}-1 & x \geq 1 \\ x^2-2x+1 & x \in [0,1] \end{cases}$ en $x_0=1$
ii) $h(x)=\begin{cases} \dfrac{|x|}{x} & x \neq 0 \\ 1 & x=0 \end{cases}$ en $x_0=0$
iii) $g(x)=\begin{cases} \sqrt{1-x^2} & x \in [0,1] \\ -\sqrt{1-(x-2)^2} & x \in [1,2] \end{cases}$ en $x_0=1$
iv) $k(x)=\begin{cases} s(x) & x \in (a,b] \\ t(x) & x \in [b,c) \end{cases}$ en $x_0=b$
(si $s(x)$ y $t(x)$ son continuas en $b$)
i) $f(x)=3x-5$ en $x_0=1$
ii) $g(x)=-\dfrac{1}{2}x + \sqrt{3}$ en $x_0=-1$
iii) $f(x)=3x^2-5x+1$ en $x_0=0$
iv) $g(x)=\dfrac{1}{2}x^2 + \sqrt{3x}$ en $x_0=2$
v) $h(x)=\dfrac{2x^2-1}{3x+2}$ en $x_0=-1$
vi) $k(x)=2^3+x^2-x+3$ en $x_0=1$
vii) $f(x)=\dfrac{1}{kx}$ en $x_0=1, k \neq 0$
viii) $g(x)=|x|$ en $x_0=0.75$
ix) $h(x)=|x-3|$ en $x_0=\dfrac{1}{2}$
x) $f(x)=\sqrt{2x-5}$ en $x_0=3$
Los ejercicios siguientes los puedes consultar en el Libro de Cálculo de M. Spivak.
i) $f(x)=x^3-x+3$
ii) $f(x)=x^5+5x^4+2x+1$
iii) $x^5+x+1$
iv) $4x^2-4x+1$
i) $sen x = x-1$
ii) $x^{179} + \dfrac{163}{1+x^2+sen^2 x} = 119$
iii) $cos(x)-\dfrac{1}{2} = x-1$
iv) $(2x^2-2)^4 = -x+1$
Los siguientes ejercicios los puedes consultar en el libro: Cálculo de Arizmendi, Carrillo y Lara.
i) $f(x)=x^3$ en $[-1,1]$
ii) $g(x)=x^3-1$ en $[0,3]$
iii) $h(x)=x^2+4x+4$ en $[0,1]$
iv) $k(x)=3x^2-x-1$ en $[-1,1]$
i) $x^3+7x^2-3x-5=0$ en $[-3.2,0.1]$
ii) $x^5-4x^3+x^2-1=0$ en $[-2.1,1.5]$
iii) $x^4-3^3+x^2-4x+3=0$ en $[-1.3,1.5]$
iv) $x sen(x)-\dfrac{1}{2}=0$ en $[-1,2]$
v) $x cos(x)+\dfrac{1}{2}=0$ en $[1,3.5]$
Ejercicios opcionales
i) $\left\{ \dfrac{1}{n} : n \text{ en } \mathbb{N} \right\}$
ii) $\left\{ \dfrac{1}{n} : n \text{ en } \mathbb{Z} \text{ y } n \neq 0 \right\}$
iii) $\left\{ x : x=0 \text{ ó } x=\dfrac{1}{n} \text{ para algún } n \text{ en } \mathbb{N} \right\}$
iv) $\left\{ x : 0 \leq x \leq \sqrt{2} \text{ y } x \text{ es racional } \right\}$
v) $\left\{ x : x^2+x+1 \geq 0 \right\}$
vi) $\left\{ x : x^2+x-1 \lt 0 \right\}$
vii) $\left\{ x : x \lt 0 \text{ y } x^2+x-1 \lt 0 \right\}$
viii) $\left\{ \dfrac{1}{n}+(-1)^n : n \text{ en } \mathbb{N} \right\}$
Aquí encontrarás el concepto de derivada de una función en un punto, sus diferentes interpretaciones y una gran diversidad de teoremas que construyen la teoría necesaria para graficar funciones y para comprender muchas de sus aplicaciones.
En particular encontrarás los teoremas sobre álgebra de derivadas, los teoremas de Rolle, del Valor medio, el del Valor medio de Cauchy y la Regla de L'Hôpital, entre otros.
Encontrarás las demostraciones de los teoremas, paso a paso, así como ejemplos, ejercicios y construcciones interactivas con el propósito de ayudar a una mejor comprensión.
En este apartado podrás encontrar la definición de función derivable, su relación con la continuidad, ejemplos, no ejemplos y su significado.
$f$ es derivable en $a$, si $\lim \limits_{h \to 0} \dfrac{f(a+h)-f(a)}{h}$ existe.
En tal caso, se establece la siguiente notación: $f'(a) = \lim \limits_{h \to 0} \dfrac{f(a+h)-f(a)}{h}$ y, a dicho número se le conoce como la derivada de $f$ en $a$.
Por su importancia en el concepto de Derivada, destacamos que a la expresión $\dfrac{f(a+h)-f(a)}{h}$ se le conoce como el cociente de Newton de $f$ en $a$.
De la definición es claro que si el límite del cociente de Newton existe, cuando $h$ tiende a cero, entonces $f$ es derivable en $a$.
Si $f$ es derivable en $a$, entonces $f$ es continua en $a$.
Este teorema expresado en su forma contrarrecíproca, establece que:
Si $f$ no es continua en $a$, entonces $f$ no es derivable en $a$.
Así, una condición necesaria para que una función sea derivable en un punto, es que sea continua en tal punto. Sin embargo, esta condición no es suficiente.
Existen funciones continuas en un punto, que no son derivables en tal punto.
Al ver los ejemplos intenta sacar una conclusión del porqué no son derivables en el punto dado. Además observa que en estos casos, el dominio de la función derivada se reduce respecto al dominio de $f$.
En este apartado podrás encontrar las interpretaciones de la derivada, tanto desde el punto de vista de la geometría como de la física y aun de manera general.
La interpretación de este cociente, es básico para la interpretación de la derivada de una función en un punto.
$\dfrac{f(a+h)-f(a)}{h} =$ pendiente de la recta secante que pasa por los puntos $P(a,f(a))$ y $Q(a+h,f(a+h))$.
$f'(a) =$ pendiente de la recta tangente a la gráfica de $f$ en $(a, f(a))$.
$y-f(a) = f'(a)(x-a) \implies y = f'(a)x+b$, donde $b=f(a)-af'(a)$.
Cuando las variables que se relacionan en la función $s(t)$ sean distancia-tiempo, tendríamos que $\dfrac{s(a+h)-s(a)}{h}$ representa la velocidad media de una partícula en el intervalo de tiempo transcurrido entre $a$ y $a+h$.
Así, la derivada desde el punto de vista de la física $s'(a) = \lim \limits_{h \to 0} \dfrac{s(a+h)-s(a)}{h}$ se podrá interpretar como la velocidad instantánea de dicha partícula en el tiempo $a$.
En general cuando la función relaciona la variación de cualquier cantidad respecto al tiempo, se dice que la derivada representa la razón de cambio o tasa de variación de dicha cantidad a un tiempo dado.
Igualmente si la función relaciona cualesquiera variables (presión-temperatura, volumen-radio, etc), significará la razón de cambio de una variable respecto a un valor específico de la otra.
En este apartado podrás encontrar una conclusión sobre la derivabilidad, algunos ejemplos de funciones derivables y los teoremas sobre álgebra de funciones derivables.
Los ejemplos vistos en el apartado 1, de este tema así lo confirman. Son funciones que tienen un “quiebre” en $a$, o la pendiente de la recta tangente no es finita o la gráfica parece muy intrincada en las cercanías de $a$.
Una función es derivable, si es derivable en todos los puntos de su dominio.
Así, una función derivable, en primer lugar debe ser continua en todos los puntos de su dominio y tener una gráfica “suave”, de tal manera que en todos sus puntos sea posible trazar una recta tangente.
Sea $f: \mathbb{R} \to \mathbb{R}$ tal que $f(x)=c$ (constante), entonces $f'(a)=0 \; \forall a$.
$f'(a) = \lim \limits_{h \to 0} \dfrac{f(a+h)-f(a)}{h} = \lim \limits_{h \to 0} \dfrac{c - c}{h} = 0$. Q.E.D.
Sea $f: \mathbb{R} \to \mathbb{R}$ tal que $f(x)=x$, entonces $f'(a)=1 \; \forall a$.
$f'(a) = \lim \limits_{h \to 0} \dfrac{f(a+h)-f(a)}{h} = \dfrac{a+h-a}{h} = \dfrac{h}{h} =1$. Q.E.D.
Si $f$ y $g$ son derivables en $a$, entonces $f+g$ es derivable en $a$ y $(f+g)'(a) = f'(a)+g'(a)$.
Si $f$ y $g$ son derivables en $a$, entonces $fg$ es derivable en $a$ y $(fg)'(a) = f'(a)g(a) + f(a)g'(a)$.
Si $g(x)=cf(x)$ y $f$ es derivable en $a$, entonces $g$ es derivable en $a$ y $(g)'(a) = cf'(a)$.
Si $f(x)=x^n$ para $n \in \mathbb{N}$, entonces $f'(a) = na^{n-1} \; \forall a$.
Si $f$ es una función derivable, entonces su derivada $f'$ es a su vez una función, que puede o no ser derivable. Si lo es, entonces, se produce otra función, la derivada de la derivada de $f$ y así sucesivamente. Por ello, es posible definir de manera recursiva las derivadas de orden superior:
$f'' = (f')', \; f''' = (f''')', \; f^{(n)} = \left(f^{(n-1)} \right)'$
Con los teoremas vistos en este apartado y con la definición recursiva de las derivadas se tiene una primera conclusión sobre las derivadas de un polinomio:
$$\begin{align*} f(x) &= a_nx^n + a_{n-1}x^{n-1} + ... + a_1x + a_0 \implies \\ f'(x) &= na_nx^{n-1} + (n-1)a_{n-1}x^{n-2} + ... + 2a_2x + a_1 \implies \\ f''(x) &= n(n-1)a_nx^{n-2} + (n-1)(n-2)a_{n-1}x^{n-3} + ... + 2a_2 \implies \\ \vdots & \\ f^{(n)}(x) &= (n!)a_n \end{align*}$$Es decir, las funciones polinomiales son derivables y sus derivadas también y así sucesivamente. Como la derivada enésima es constante, de ahí las demás son cero. Como veremos más adelante, hay funciones cuya derivada no siempre es derivable.
$f''(a) =$ pendiente de la recta tangente a la gráfica de $f'$ en $(a,f'(a))$ y así, se puede extender.
$s''(a) = \lim \limits_{h \to 0} \dfrac{s'(a+h)-s'(a)}{h} $ se interpreta como el cambio instantáneo de la velocidad de una partícula en el tiempo $a$, es decir, la aceleración de la misma. Y así puede extenderse.
La segunda derivada $f''(a)$ significa la razón de cambio de $f'$ respecto a su variable, en $a$. Y así puede extenderse.
En este apartado continuaremos con los teoremas sobre la derivabilidad que nos hacen falta, tanto para la división, como para la composición de funciones y diversos ejemplos.
En la demostración del siguiente teorema necesitaremos el teorema 3 (en Álgebra de funciones continuas), que asegura que una función continua en $a$, conserva el signo en una cierta vecindad de $a$. Esto garantizará que $g(a+h)$ sea distinto de cero en dicha vecindad.
Si $g$ es derivable en $a$ y $g(a) \neq 0$, entonces $\dfrac{1}{g}$ es derivable en $a$ y $\left( \dfrac{1}{g} \right)'(a) = \dfrac{-g'(a)}{(g(a))^2}$.
Si $f(x) = x^{-n} = \dfrac{1}{x^n}$, para $n \in \mathbb{N}$, entonces $f'(x) = -nx^{-n-1} = \dfrac{-n}{x^{n+1}}$.
Puedes intentar demostrarlo, para lo cual puedes aplicar el teorema 7. Esto generaliza el Teorema 6 a los negativos y además interpretando:
$f(x)=x^0$, como $f(x)=1$ y $f'(x)=0x^{-1}$ como $f'(x)=0$, entonces el Teorema 6 se cumple para $n=0$.
Si $f$ y $g$ son derivables en $a$ y $g(a) \neq 0$, entonces $\dfrac{f}{g}$ es derivable en $a$ y $\left(\dfrac{f}{g} \right)'(a) = \dfrac{f'(a)g(a)-f(a)g'(a)}{(g(a))^2}$.
Si $g$ es derivable en $a$, y $f$ es derivable en $g(a)$, entonces $f \circ g$ es derivable en $a$ y $(f \circ g)'(a) = f'(g(a))g'(a)$.
Con los teoremas anteriores se tienen reglas para derivar una gran variedad de funciones. A continuación algunos ejemplos.
En este apartado estudiaremos los conceptos de máximos y mínimos de una función. Lo relacionaremos con la derivada en caso de ser posible y trabajaremos con funciones definidas en intervalos cerrados $[a,b]$.
Sea $f$ una función y $x_0 \in A \subset Dom f$. Se dice que $f$ alcanza su valor máximo sobre $A$ en $x_0$, si $f(x_0) \geq f(x) \; \forall x \in A$.
Similarmente se establece la definición para el valor mínimo de $f$ sobre $A$.
Se aprecia en la gráfica, que puede haber muchos puntos en $A$, donde $f$ alcanza su valor máximo (o mínimo), pero sólo puede haber un valor máximo (o mínimo) de $f$ sobre $A$. Será de interés en este estudio el caso en que $A = [a,b]$.
Sea $f$ una función definida sobre $(a,b)$ y $x_0 \in (a,b)$. Si $f$ alcanza en $x_0$ su valor máximo (o mínimo) sobre $(a,b)$ y $f$ es derivable en $x_0$, entonces $f'(x_0)=0$.
Sea $f$ una función y $x_0 \in A \subset Dom f$. Se dice que $f$ alcanza en $x_0$, un máximo local sobre $A$, si $\exist \delta \gt 0$ tal que $f(x_0) \geq f(x) \; \forall x \in A \cap (x_0-\delta,x_0+\delta)$. Es decir, si $f$ alcanza en $x_0$ un máximo sobre $A \cap (x_0-\delta,x_0+\delta)$.
Puedes construir una definición similar para un mínimo local.
Sea $f$ una función definida sobre $(a,b)$ que alcanza en $x_0 \in (a,b)$ un máximo (o mínimo) local sobre $A = (a,b)$. Si $f$ es derivable en $x_0$, entonces $f'(x_0)=0$.
Este teorema es una consecuencia casi inmediata del teorema 1, sin embargo, el recíproco de este teorema es falso. Existen funciones con derivada $0$ en un punto, donde no hay máximo, ni mínimo local. Por ejemplo: $f(x)=x^3$ en $0$.
Se dice que $x_0$ es un punto crítico de una función $f$, si $f'(x_0)=0$. Al número $f(x_0)$ se le llama valor crítico de la función $f$.
Consideremos el problema de calcular el máximo y el mínimo de una función continua en un intervalo cerrado $[a,b]$. Para ello, debemos considerar tres clases de puntos:
De todos ellos, se eligen los puntos donde la función “alcanza su máximo” y donde “alcanza su mínimo”.
En este apartado veremos un conjunto de teoremas de mucha importancia para el significado de la derivada.
Sea $f$ continua en $[a,b]$ y derivable en $(a,b)$. Si $f(a)=f(b)$, entonces $\exist x \in (a,b)$ tal que $f'(x)=0$.
Lo que asegura este teorema es que $f$ alcanza un máximo o mínimo local en $(a,b)$. Al partir de $(a,f(a))$, si “sube” o “baja”, tiene que regresar a $(b,f(b))$ sin rupturas ni saltos y al ser derivable en $(a,b)$, así debe alcanzar un máximo o un mínimo y como es derivable en $(a,b)$ se tiene que debe ser una función “suave”, sin quiebres y entonces la derivada existe y deberá ser cero.
Si $f$ es continua en $[a,b]$ y derivable en $(a,b)$, entonces $\exist x \in (a,b)$ tal que $f'(x) = \dfrac{f(b)-f(a)}{b-a}$.
Este teorema es una generalización del Teorema de Rolle. Si $f(a) = f(b),$ tendríamos como caso particular a dicho teorema. El teorema del valor medio asegura que existe $x$ en $(a,b)$, donde la pendiente de la recta tangente es igual a la pendiente de la recta secante que pasa por $(a,f(a))$ y $(b,f(b))$.
Del teorema 4 (Teorema del valor medio) se desprenden varios corolarios interesantes que ayudan a ir configurando cada vez más, el significado de la derivada.
Sea $f$ definida en un intervalo $I$. Si $f'(x)=0 \; \forall x \in I$, entonces $f$ es constante en $I$.
Sean $f$ y $g$ definidas en el mismo intervalo $I$. Si $f'(x) = g'(x) \; \forall x \in I$, entonces $\exist c$ (constante), tal que $f(x) = g(x)+c \; \forall x \in I$.
Si $f'(x) \gt 0 \; \forall x \in I$, entonces $f$ es creciente en $I$.
Si $f'(x) \lt 0 \; \forall x \in I$, entonces $f$ es decreciente en $I$.
Este corolario 3, permite calcular los intervalos de crecimiento y decrecimiento de una función y combinado con los máximos y mínimos locales facilitan ir configurando la gráfica de una función.
Un problema importante es el trazo de la gráfica de una función y en ese caso es recomendable, determinar:
Lo anterior, aunado a una inspección rápida para ver si la función es par o impar, monótona, etc., ayudará mucho a configurar su gráfica. Existe un criterio para los máximos y mínimos locales que sólo depende del comportamiento de $f$ en el punto crítico, como veremos en el siguiente teorema.
Si $f'(a)=0$ y $f''(a) \gt 0$, entonces $f$ alcanza un mínimo local en $a$.
Si $f'(a)=0$ y $f''(a) \lt 0$, entonces $f$ alcanza un máximo local en $a$.
Este teorema 5 es muy útil sobre todo para funciones polinómicas, sin embargo, para muchas funciones la expresión de la segunda derivada es tan complicada, que es preferible recurrir al recomendable punto 3, es decir, a analizar el signo de la primera derivada antes y después de un punto crítico.
Aun más, es posible que $f''(a)=0$ y en ese caso, el teorema 5 no proporciona información, puede ser máximo o mínimo local o ninguno de los dos. Esto lo confirma el siguiente teorema.
Supongamos que $f''(a)$ existe. Si $f$ alcanza un mínimo local en $a$, entonces $f''(a) \geq 0$, pero si $f$ alcanza un máximo local en $a$, entonces $f''(a) \leq 0$.
Para confirmar el teorema 5, en estos ejemplos, podrías calcular el valor de la segunda derivada en cada punto crítico.
Enseguida presentaremos tres resultados importantes, consecuencia del Teorema del valor medio. Tres notas para entender el significado del siguiente teorema 7:
Supongamos que $f$ es continua en $a$ y que $\exist f'(x) \; \forall x \in I$, excepto posiblemente para $x=a$. Supongamos además que $\lim \limits_{x \to a} f'(x)$ existe, entonces $f'(a)$ existe y $\lim \limits_{x \to a} f'(x) = f'(a)$.
Dicho de otro modo. Una función con una discontinuidad removible, no puede ser derivada de ninguna función.
Un ejemplo interesante, que permite reforzar que aunque una función pueda ser derivable en todas partes, es posible que su derivada sea discontinua y su discontinuidad no puede ser removible, es la siguiente:
$f(x)=\begin{cases} x^2 sen\left( \dfrac{1}{x} \right) &\text{ si } x \neq 0 \\ 0 &\text{ si } x=0\end{cases}$ es derivable $\forall x \in \mathbb{R}$, $f'$ no es continua en $x=0$ y $\lim \limits_{x \to 0} f'(x)$ no existe.
Las lineas de la demostración son las siguientes:
Como $\lim \limits_{x \to 0} x^2 sen\left( \dfrac{1}{x} \right) = 0$, es claro que $f$ es continua en $0$.
Además $f$ es derivable para toda $x$ diferente de cero y como:
$f'(0) = \lim \limits_{h \to 0} \dfrac{f(0+h)-f(0)}{h} = \lim \limits_{h \to 0} \dfrac{h^2 sen \left( \dfrac{1}{h} \right)}{h} = \lim \limits_{h \to 0} h sen \left( \dfrac{1}{h} \right) = 0$.
Entonces $f$ es derivable en los reales y la derivada queda así:
$f'(x) = \begin{cases} 2x sen \left( \dfrac{1}{x} \right) - cos \left( \dfrac{1}{x} \right) &\text{ si } x \neq 0 \\ 0 &\text{ si } x=0 \end{cases}$
Sin embargo $\lim \limits_{x \to 0} f'(x) = \lim \limits_{x \to 0} \left[ 2x sen \left( \dfrac{1}{x} \right) - cos \left( \dfrac{1}{x} \right) \right]$ no existe.
Y por tanto $f'$ no es continua en $0$.
El siguiente teorema es una generalización del Teorema del valor medio, que a su vez es una generalización del Teorema de Rolle. Dicho de otro modo, el teorema de Rolle es un caso particular del Teorema del Valor Medio y éste del siguiente teorema llamado: Teorema del Valor Medio de Cauchy.
Si $f$ y $g$ son continuas en $[a,b]$ y derivables en $(a,b)$, entonces $\exist x_0 \in (a,b)$ tal que $[f(b)-f(a)] g'(x_0) = [g(b)-g(a)] f'(x_0)$.
$\dfrac{f(b)-f(a)}{g(b)-g(a)} = \dfrac{f'(x_0)}{g'(x_0)}$
$\lim \limits_{x \to a} \dfrac{f(x)}{g(x)}$, cuando $\lim \limits_{x \to a} f(x)=0$ y $\lim \limits_{x \to a} g(x)=0$.
En este sentido es que tenemos el siguiente resultado, que generaliza el resultado del Teorema 7.
Si $\lim \limits_{x \to a} f(x)=0$, $\lim \limits_{x \to a} g(x)=0$ y $\lim \limits_{x \to a} \dfrac{f'(x)}{g'(x)}$ existe, entonces $\lim \limits_{x \to a} \dfrac{f(x)}{g(x)}$ existe y $\lim \limits_{x \to a}\dfrac{f(x)}{g(x)} = \lim \limits_{x \to a} \dfrac{f'(x)}{g'(x)}$
Existen diversas formas de la Regla de L'Hôpital. Ninguna de ellas requieren un razonamiento esencialmente nuevo al que se utilizó en la demostración del teorema 9 y otras se obtienen por procedimientos meramente algebraicos. También hay otro tipo de indeterminaciones, que se pueden reducir al caso del teorema 9.
Aquí encontrarás los conceptos de convexidad y concavidad y los teoremas relacionados.
Una función $f$ es convexa en un intervalo $I$, si $\forall a, b \in I$, el segmento rectilíneo que une $(a, f(a))$ y $(b, f(b))$ queda por encima de su gráfica. $f$ es cóncava en $I$, si tal segmento queda por debajo de su gráfica.
Esta condición geométrica de la definición, queda expresada de manera analítica, en el siguiente teorema.
Una función $f$ es convexa en un intervalo $I$, si $\forall a, b \in I$ y $\forall x \in (a,b)$, se tiene que: $\dfrac{f(x)-f(a)}{x-a} \lt \dfrac{f(b)-f(a)}{b-a}$.
Si se invierte la desigualdad, queda definida analíticamente la concavidad.
Será de gran interés analizar la convexidad y la concavidad para funciones derivables.
Sea $f$ convexa en $I$. Si $f$ es derivable en $a \in I$, entonces la gráfica de $f$ queda por encima de la tangente por $(a, f(a))$, excepto en $(a, f(a))$. Además, si $a \lt b$ y $f$ es derivable en $a$ y $b$, entonces $f'(a) \lt f'(b)$.
Sea $f$ derivable y $f'$ creciente. Si $a \lt b$ y $f(a) = f(b)$, entonces $f(x) \lt f(a) \; \forall x \in (a,b)$.
El siguiente teorema facilita saber si una función es convexa.
Si $f$ es derivable y $f'$ creciente, entonces $f$ es convexa.
$f''(x) \gt 0 \; \forall x \in (a-\delta,a) \implies f'(x)$ es creciente $\implies f$ es convexa, $f''(x) \lt 0 \; \forall x \in (a,a+\delta) \implies f'(x)$ es decreciente $\implies f$ es cóncava, y viceversa.
Aquí encontrarás algunos problemas de aplicación de las derivadas.
El vértice de la parábola $y^2 = 2px$ es el centro de una elipse. El foco de la parábola, es un extremo de uno de los ejes principales de la elipse y además la parábola y la elipse se cortan en un ángulo recto. Hallar la ecuación de la elipse.
Sabemos que la ecuación de la elipse es:
$b^2 x^2 + a^2 y^2 = a^2 b^2$ ... (1)
Por tanto para conocer su ecuación, necesitamos conocer $a$ y $b$.
Por las hipótesis sobre el vértice $V$ y el foco $F$ de la parábola, tenemos que: $a = \dfrac{p}{2}$.
Así, sólo falta conocer el valor de $b$.
Para ello requerimos aplicar la hipótesis sobre la perpendicularidad del corte entre la elipse y la parábola.
Para ello nos sirve la derivada, que representa la pendiente de la recta tangente a una curva en un cierto punto.
Derivamos (1) con respecto a $x$ y nos queda:
$2b^2x + 2a^2y \frac{dy}{dx} = 0$ ... (2)
Despejando de (2) la derivada, tenemos:
$\frac{dy}{dx} = - \frac{b^2x}{a^2y} = m_1$ ... (3)
$m_1$, pendiente de la recta tangente a la elipse en $x$.
Ahora derivamos la ecuación de la parábola respecto de $x$:
$2y\frac{dy}{dx} = 2p \implies \frac{dy}{dx} = \frac{p}{y} = m_2$ ... (4)
$m_2$, pendiente de la recta tangente a la parábola en $x$.
Por la hipótesis de perpendicularidad en un cierto punto, tenemos que:
$m_2 m_1 = -1$ ... (5)
Sustituyendo en (5) los valores de (3) y (4):
$\dfrac{p}{y} \left( -\dfrac{b^2x}{a^2y} \right) = -1 \implies \dfrac{pb^2x}{a^2 y^2} = 1$ ... (6)
Sustituyendo ahora en el denominador de (6), el valor de $y^2$, según la ecuación de la parábola, tenemos que:
$\dfrac{pb^2x}{2pxa^2} = \dfrac{b^2}{2a^2} = 1 \implies b^2 = 2a^2$ ... (7)
Así, sustituyendo (7) en la ecuación (1), tenemos:
$2a^2x^2 + a^2y^2 = a^2(2a^2) \stackrel{a=\frac{p}{2}}{\implies} \dfrac{p^2}{2}x^2 + \dfrac{p^2}{4}y^2 = \dfrac{p^4}{8}$
De donde queda: $4x^2 + 2y^2 = p^2$. Que es la ecuación de la elipse buscada.
Calcular el área del triángulo formado por el eje de las $x$, la tangente y la normal a la gráfica de $f(x)=6x-x^2$ en el punto $(5,5)$.
Como $\measuredangle ABC = 90º$, entonces: Área del triángulo $= \dfrac{(AB)(BC)}{2}$.
Así que el problema se reduce a conocer la longitud de los segmentos $AB$ y $BC$. Para ello, falta conocer las ecuaciones de las rectas tangente $L_1$ y normal $L_2$ y, su respectiva intersección con el eje de las $x$.
$f'(x)=6-2x \implies f'(5)=-4=m_1$ pendiente de $L_1$.
Así, la ecuación punto pendiente de $L_1$, queda: $y=-4(x-5)+5$, por tanto, su intersección con el eje de las $x$, se da cuando $y=0$.
$-4(x-5)+5=0 \implies -4x+20+5=0 \implies x=\dfrac{-25}{-4}=\dfrac{25}{4}$.
Así: $C \left( \dfrac{25}{4}, 0 \right)$ es uno de los vértices del triángulo.
Pendiente de $L_2$: $m_2= -\dfrac{1}{m_1} = \dfrac{1}{4}$.
Así, la ecuación punto pendiente de $L_2$, queda: $y=\dfrac{1}{4}(x-5)+5$, por tanto, su intersección con el eje de las $x$, se da cuando $y=0$.
$\dfrac{1}{4}(x-5)+5=0 \implies \dfrac{1}{4}x-\dfrac{5}{4}+5=0 \implies x=-15$
Así: $A(15,0)$ es otro de los vértices del triángulo.
$d(A,B)=\sqrt{(5-(-15))^2 + (5-0)^2} = \sqrt{20^2 + 5^2} = \sqrt{425}$
$d(B,C)=\sqrt{\left( \dfrac{25}{4}-5 \right)^2 + (0-5)^2} = \sqrt{\left( \dfrac{5}{4} \right)^2 + 5^2} = \dfrac{\sqrt{425}}{4}$
$Area(\triangle ABC) = \dfrac{\left( \sqrt{425} \right) \left( \dfrac{\sqrt{425}}{4} \right)}{2} = \dfrac{425}{8}$
Calcular la altura del cono de volumen máximo que puede inscribirse en una esfera de radio $r$.
Podemos observar que $h=c+r$. $r$ es fijo, pero $c$ cambia conforme cambia el radio $x$ de la base del cono.
Sabemos que el volumen del cono es igual a:
$V=\dfrac{1}{3} \pi x^2 h$ ... (1)
Esta cantidad debemos maximizarla y por lo tanto debemos dejarla en términos de una variable. En particular debe quedar en términos de $h$, que es la incógnita y del radio $r$ de la esfera que contiene al cono. Entonces el objetivo es $x$, hay que escribirla en términos de $h$.
Por el Teorema de Pitágoras, tenemos:
$r^2=x^2+c^2 \implies x^2=r^2-c^2$ ... (2)
Sustituyendo (2) en (1), tenemos:
$V=\dfrac{1}{3} \pi (r^2-c^2) h$ ... (3)
Pero como:
$h=c+r \implies c=h-r \implies c^2=h^2-2hr+r^2$ ... (4)
Sustituyendo (4) en (3), tenemos:
$V=\dfrac{1}{3} \pi (r^2-(h^2-2hr+r^2))h \implies V=\dfrac{1}{3} \pi (2hr-h^2)h$
Es decir:
$V=\dfrac{1}{3} \pi (2h^2r-h^3)$ ... (5)
Que es la fórmula del volumen del cono, pero en términos de la variable $h$ y ahora sí, vamos a maximizar dicho volumen.
$\dfrac{dV}{dh} = \dfrac{1}{3} \pi (4rh-3h^2)=0 \implies (4rh-3h^2)=0 \implies h(4r-3h)=0$
Es decir:
$h=0$ ó $4rh-3h^2=0$
Pero para que el volumen sea máximo, sólo queda que:
$h=\dfrac{4}{3}r$
Una esfera sólida homogénea pesa $P$kg. ¿Cuál es el peso $Q$ del mayor cilindro circular recto que puede cortarse de la esfera?
Por ser una esfera homogénea, el cilindro de mayor peso que se puede cortar de la esfera, es aquel cuyo volumen sea máximo.
Así, la proporción entre volúmenes, es la misma que entre los pesos.
Sabemos que el volumen del cilindro está dado por:
$V=\pi r^2 h$ ... (1)
Esta cantidad hay que maximizarla, pero para ello hay que ponerla en términos de la altura $h$ del cilindro y del radio $R$ de la esfera que lo contiene.
Se observa que: $R^2 = \left( \dfrac{h}{2} \right)^2 + r^2 \implies r^2=R^2 - \left( \dfrac{h}{2} \right)^2$ ... (2)
Sustituyendo (2) en (1), nos queda: $V(h)=\pi \left(R^2 - \left( \dfrac{h}{2} \right)^2 \right) h$
De donde: $V'(h) = \pi \left( R^2 - \dfrac{3h^2}{4} \right)$ ... (3)
Para obtener el máximo, debemos tener que: $V'(h)=0 \implies h=\dfrac{2R}{\sqrt{3}}$ ... (4)
Sustituyendo (2) y (4) en (1), tenemos que: $V=\pi \left( R^2 - \left( \dfrac{R}{\sqrt{3}} \right)^2 \right) \dfrac{2R}{\sqrt{3}} =\dfrac{4}{3 \sqrt{3}} \pi R^3$. Volumen máximo del cilindro.
Realizando el cociente: $\dfrac{\text{Volumen cilindro}}{\text{Volumen esfera}} = \dfrac{\dfrac{4}{3\sqrt{3}} \pi R^3}{\dfrac{4}{3} \pi R^3} = \dfrac{1}{\sqrt{3}}$, que es la proporción entre los volúmenes y como es la misma proporción entre los pesos, tenemos que: $\dfrac{Q}{P} = \dfrac{1}{\sqrt{3}}$, de donde:
$Q = \dfrac{P}{\sqrt{3}} kg$
Peso del cilindro circular recto que puede cortarse de la esfera
Encontrar el punto para el cual la recta tangente a la parábola $f(x)=x^2-2x+1$, es paralela a la recta $3x+2y=6$.

Sabemos que la pendiente de la recta tangente a la gráfica de $f$ en $x$, es: $f'(x)=2x-2$ y debe ser igual a la pendiente de la recta dada: $3x+2y-6=0$.
Entonces, como la recta dada: $y=-\dfrac{3}{2}x+3$ tiene pendiente $-\dfrac{3}{2}$, entonces:
$f'(x)=2x-2 = -\dfrac{3}{2} \implies x=\dfrac{1}{4}$
Que es el punto donde la recta tangente a la gráfica de $f$, es paralela a la recta dada.
Sabiendo que si $f(x)=e^x$, entonces $f'(x)=e^x$, demostrar que la ecuación $e^x=x+1$ sólo tiene una raíz real, a saber $x=0$.
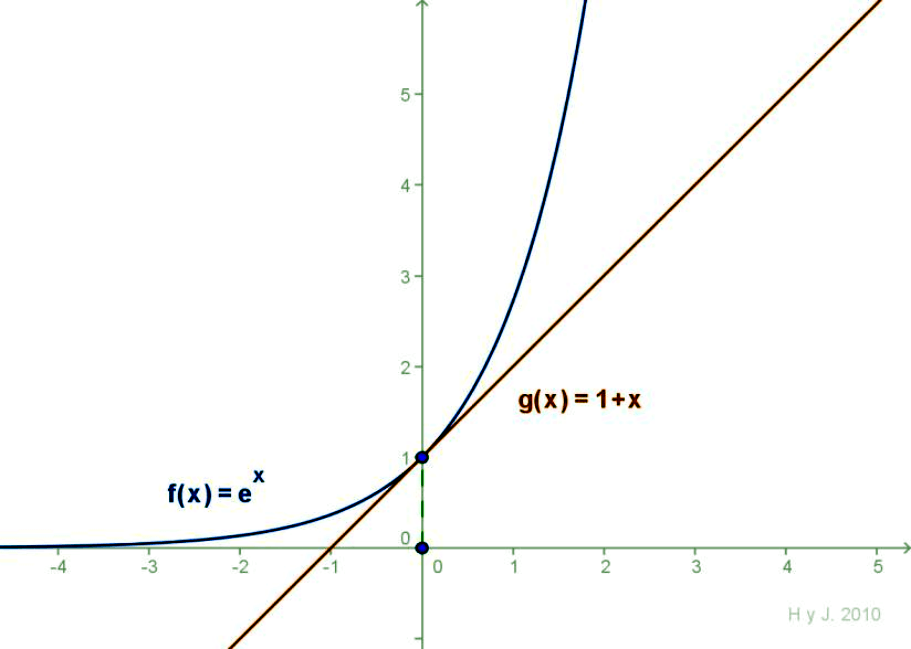
Es fácil ver que $x=0$ es solución de la ecuación dada. La demostración estará completa, cuando hagamos ver que es la única.
Para ello, definimos: $f(x)=e^x-x-1$. Demostraremos que ésta función sólo tiene un mínimo, a saber $x=0$ y su valor mínimo es $f(0)=0$. Veamos:
$f'(x)=e^x-1=0 \implies x=0$, único punto singular. Ahora obtenemos la segunda derivada:
$f''(x)=e^x \gt 0 \; \forall x$, en particular, para $x=0$. Por lo tanto, en $x=0$, hay un mínimo local y además, $f(0)=e^0-0-1=0$.
Así, la ecuación dada: $e^x=x+1$, sólo tiene una raíz real, $x=0$.
Sea $f:[-1,2] \to \mathbb{R}$ tal que $f(x)=x^2$. ¿En qué punto del intervalo $[-1,2]$ la recta tangente a $f$, coincide con la pendiente de la recta que pasa por los puntos $(-1,f(-1))$ y $(2,f(2))$?

Por el teorema del valor medio, sabemos que: $\exist x_0 \in (a,b)$ tal que $f'(x_0)=\dfrac{f(b)-f(a)}{b-a}$, entonces: $f'(x_0) = \dfrac{f(2) - f(-1)}{2-(-1)} = \dfrac{4-1}{3} = 1$ y como $f'(x_0) = 2x_0$, entonces, nos queda:
$2x_0=1 \implies x_0=\dfrac{1}{2}$ valor intermedio.
Demostrar que entre todos los rectángulos de área $A \gt 0$, dada, el cuadrado es el de perímetro mínimo.

Sabemos que:
$A=xy$ ... (1) área
$P=2x+2y$ ... (2) perímetro
Como queremos minimizar el perímetro, entonces requerimos expresar su fórmula en términos de una sola variable y luego aplicarle el procedimiento para calcular los puntos singulares, etc.
Despejando $y$ de (1), tenemos que:
$y=\dfrac{A}{x} \implies P(x)=2x + 2 \left( \dfrac{A}{x} \right)$
Entonces: $P'(x)=\dfrac{2x^2-2A}{x^2}=0 \implies x=\sqrt{A}$, único punto singular.
Ahora bien, $P''(x)=\dfrac{4A}{x^3} \implies P''(\sqrt{A}) = \dfrac{4A}{(\sqrt{A})^3} = \dfrac{4}{\sqrt{A}} \gt 0$.
De donde tenemos que el perímetro mínimo es cuando: $x=\sqrt{A} \stackrel{\text{sust. en (1)}}{\implies} y=\sqrt{A}$ y por lo tanto se trata de un cuadrado.
En una avenida principal de la ciudad de México, un automóvil pasa frente a una cámara de vigilancia y 10 segundos después, pasa por la siguiente cámara de vigilancia que se encuentra a 225 metros de la primera. Investigue si en algún momento dicho automóvil ha rebasado el límite de velocidad que es de 80 Km/hora.
Ubicamos la primera cámara de vigilancia en el origen $(0,0)$ y la segunda en las coordenadas $(10,225)$.
Por otra parte, sabemos que la función $s(t)$ que representa el desplazamiento del automóvil con respecto al tiempo, es una función continua en el intervalo $[0,10]$ y derivable en el intervalo $(0,10)$.
Así que por el Teorema del valor medio:
$\exist t_0 \in (0,10)$ tal que $s'(t_0) = \dfrac{225-0}{10-0} = 22.5 m/seg.$
Es decir, en $t_0 \in (0,10)$, la velocidad del automóvil es $s'(t_0)=22.5m/seg.$
Realizando la conversión a $metros/minuto$, luego a $metros/hora$ y, finalmente a $kilómetros/hora$, tenemos:
$s'(t_0) = 22.5m/seg = 1350m/min = 81000m/hr = 81km/hr$
Es resumen, en algún momento, dentro de los 10 segundos, el automóvil rebasó el límite de velocidad.
$f:[-1,1] \to \mathbb{R}$ donde $f(x)=2x^2-x-1$?
$f:(-0.5,1) \to \mathbb{R}$ donde $f(x)=2x^2-x-1$?
$f:[-3,3] \to \mathbb{R}$ donde $f(x) = \dfrac{x^2-4}{x-2}$ si $x \neq 2$ y $f(x)=5$ si $x=2$.
$\lim \limits_{x \to -1} \dfrac{x^3-3x+2}{x^2+2x+2} = \lim \limits_{x \to -1} \dfrac{3x^2-3}{2x+2} = \lim \limits_{x \to -1} \dfrac{6x}{2} = -3$
$\lim \limits_{x \to 2} \dfrac{x^3-3x^2+2x}{x^2-x-2} = \lim \limits_{x \to 2} \dfrac{3x^2-6x+2}{2x-1} = \lim \limits_{x \to 2} \dfrac{6x-6}{2} = 3$
Aquí encontrarás varias aplicaciones de la Derivada, algunas de ellas en ramas propias de las Matemáticas y en disciplinas como la Física, la Termodinámica y la Economía.
Tendrás a la mano la teoría necesaria y gráficos interactivos que te permitirán entender mejor las aplicaciones. Contarás con referencias bibliográficas y de Internet, para temas en los que requieras profundizar.
Calcular las ecuaciones de rectas tangentes y rectas normales a una curva en un punto dado $(a,f(a))$.
Para tener éxito, es importante recordar que:
$y-f(a)=f'(a)(x-a)$, es decir: $y=f'(a)x+(f(a)-af'(a))$ ... (1)
$y-f(a)=\dfrac{1}{f'(a)}(x-a)$, es decir: $y=-\dfrac{1}{f'(a)}x + \left( f(a)+a \dfrac{1}{f'(a)} \right)$ ... (2)
En los ejemplos, dada una función y un punto sobre su gráfica, se calculan las ecuaciones de la recta tangente y la recta normal correspondientes. Recuerda utilizar (1) y (2). Da clic en un ejemplo, ejecútalo y luego da clic en el botón de reiniciar
En la siguiente construcción, dada una función y un punto a cualquiera sobre el eje $x$, podrás ver las ecuaciones de la recta tangente y la recta normal correspondientes en el punto $(a,f(a))$.
Sea $f(a)=g(a)$. Se llama ángulo de intersección de $f$ y $g$ en $(a,f(a))$, al ángulo $\theta \leq 90º$ que forman sus rectas tangentes en el punto de intersección $(a,f(a))$.
Calcular el ángulo $\theta \leq 90º$, que forman la gráfica de dos funciones $f$ y $g$, en un punto de intersección.
Suponiendo que $f(a)=g(a)$, es importante recordar que:
$tan(\theta)=\left| \dfrac{tan(\alpha)-tan(\beta)}{1+tan(\alpha)tan(\beta)} \right|$
$tan(\theta)=\left| \dfrac{g'(a)-f'(a)}{1+g'(a)f'(a)} \right|$ ... (1)
En los ejemplos, dadas dos funciones y un punto de intersección, se calcula la tangente del ángulo de intersección correspondiente. Recuerda utilizar (1).
En esta lección será de gran utilidad recordar los conceptos de recta tangente y recta normal. La relación de estos conceptos con la derivada es fundamental para entender y resolver los problemas geométricos que aquí se tratarán.
Resolver algunos problemas de geometría analítica, relacionados con el cálculo de rectas tangentes y normales.
Dada una función $f$ derivable en $a$, es importante recordar que:
En los ejemplos, se calculan las ecuaciones de rectas tangentes a la gráfica de una función, bajo condiciones de paralelismo o perpendicularidad a otras rectas.
En la siguiente construcción mueve el punto $A$ y observa las ecuaciones de las rectas tangentes a la gráfica de $f$ y que pasan por el punto $A$.
Cuando tenemos dos cantidades relacionadas que varían con respecto a una misma variable y deseamos obtener la razón de cambio de una de ellas, respecto a la otra, decimos que tenemos razones de cambio relacionadas. Por ejemplo:
En fín, si $y=y(u)$ y $x=x(u)$ y, existe una relación entre $x$ e $y$, es deseable obtener la razón de cambio de $y$ respecto de $x$ o viceversa.
Resolver problemas donde se tengan razones de cambio relacionadas.
Es importante recordar que:
En los ejemplos siguientes, se resuelven problemas de razones de cambio relacionadas.
En los ejercicios siguientes, se plantea un fenómeno sísmico con datos que pueden no estar apegados a la realidad, pero que permiten, ilustrar un problema de tal naturaleza. Recuerda que debes tomar lápiz y papel para intentar resolverlo.
En la Economía también es importante considerar la variación de una cantidad respecto a otra. Por ejemplo la demanda de un producto respecto a su precio, o el precio de un producto respecto a su costo de producción o la utilidad obtenida en la venta de un producto, con relación al costo de producción, etc.
Por lo anterior, es muy importante la representación de las cantidades relacionadas en forma de funciones que puedan ser derivables, no obstante que los datos que se manejan sean discretos, por ejemplo cuando se establece la función de costo $C(x)$, la variable $x$ representa unidades de cierta mercancía.
Resolver algunos problemas sencillos en Economía.
En Economía se suele describir la variación de una cantidad respecto a otra mediante un concepto llamado promedio que expresa la variación de una cantidad sobre un rango específico de valores de otra y un concepto llamado marginal que expresa el cambio instantáneo en una cantidad respecto a la otra.
Un símil de los conceptos anteriores en Física serían los conceptos de velocidad promedio y velocidad instantánea o lo que geométricamente serían la pendiente de la recta secante y la pendiente de la recta tangente, respectivamente.
Si $C(x)$ es la función que representa el Costo Total en unidades monetarias para producir $x$ unidades de cierta mercancía:
Si $p$ es el precio de unitario de cierta mercancía y $x$ el número de unidades de dicha mercancía. Es natural pensar que la cantidad solicitada por los consumidores en el mercado, dependa de su precio. Es natural pensar que “a menor precio, mayor demanda y a mayor precio, menor demanda”.
A veces también es posible considerar que el precio de un producto se puede establecer en función de su demanda: “a mayor demanda menor precio”. En este caso, tendríamos $p=g(x)$ que se llamaría función de demanda o inclusive podría establecerse mediante una ecuación de demanda. A la gráfica correspondiente que relaciona cantidad $x$ solicitada y el precio $p$, los economistas acostumbran llamarle curva de la demanda.
Un caso típico: La demanda de un cierto producto es nula cuando el precio es muy alto ($p=18$), mientras que el consumo máximo de dicho producto en una familia no puede pasar de cierto valor ($6$ unidades) aunque el precio fuese cero.
Derivado de estos conceptos, se tiene la función de Ingreso Total, $R(x)=x P(x)$, es decir: la cantidad de unidades vendidas, por el precio de las mismas.
Y además la función de Ingreso Marginal, $R'(x)=P(x)+x P'(x)$, que representaría la razón de cambio del ingreso total para cada $x$.
En los ejemplos se realizan diversos cálculos referentes a los conceptos anteriores de Economía.
En los ejercicios siguientes, se plantea un problema sobre la producción de ciertas mercancías, conociendo la función del Costo Total y donde se desea conocer la razón de cambio en los costos de producción, para valorar la conveniencia de la inversión. Recuerda que debes tomar lápiz y papel para intentar resolverlo.
La Física y sus problemas en relación con el movimiento fueron relevantes en el desarrollo del concepto de la derivada.
Si un móvil recorre una cierta distancia $s$ en una cantidad de tiempo $t$, se puede conocer la velocidad promedio en que hizo tal recorrido, pero también se podría saber su velocidad en cada instante de dicho recorrido gracias a la derivada. Así mismo en problemas de caída libre o de objetos con movimientos acelerados, la derivada tiene un papel fundamental.
Resolver algunos problemas sencillos en Física.
Es importante recordar que:
En los ejemplos se resuelven problemas sencillos de Física y en todos ellos se desprecia la fricción del aire.
En los ejercicios siguientes, se plantea un problema sobre caída libre y se pide que encuentres la mejor aproximación a la solución. Recuerda que debes tomar lápiz y papel para intentar resolverlo.
En muchos casos, el estado de un sistema termodinámico se puede determinar mediante los valores de tres variables: la presión $P$ que se ejerce sobre el sistema, su temperatura $T$ y el volumen que ocupa $V$. Cuando el sistema está en equilibrio, estas tres variables no cambian de manera espontánea.
El comportamiento de un sistema termodinámico queda descrito por una ecuación $T=T(P,V)$, llamada ecuación de estado del sistema, que hace depender una variable de las otras dos, por ejemplo para un gas ideal (un gas hipotético, formado por partículas puntuales, sin atracción ni repulsión y cuyos choques entre ellas, son perfectamente elásticos), la ecuación de estado para un mol de gas está dada por: $PV=RT$ donde $R$ es la constante universal de los gases, $P$ la presión medida en atmósferas, $T$ la temperatura absoluta medida en grados Kelvin y $V$ el volumen en unidades cúbicas.
Si el número de moles fuese $n$, la fórmula anterior para gases ideales queda: $PV=nRT$.
Para fines de estudio de un sistema termodinámico, usualmente se mantiene constante una de las tres variables y así se estudia el cambio de la segunda, respecto a la tercera. Por ejemplo, si pensamos en un gas dentro de un recipiente rígido, el Volumen es constante, mientras que podemos relacionar los cambios de la temperatura respecto a la presión o de la presión respecto a la temperatura.
Resolver algunos problemas sencillos de Termodinámica, particularmente para gases ideales. Es importante aclarar que en este trabajo omitiremos el detalle de las unidades y concentraremos la atención en las aplicaciones de la derivada.
Dependiendo de la variable $T$, $P$ o $V$, que se mantenga constante, se definen tres cantidades de importancia para la Termodinámica, a saber:
$\alpha=\dfrac{1}{V} V'(T)$
$\kappa=-\dfrac{1}{V}V'(P)$
$\beta=\dfrac{1}{P}P'(T)$
En los ejemplos se resuelven problemas muy sencillos de Termodinámica, para gases ideales.
En los ejercicios siguientes, se plantea un problema muy parecido al de los ejemplos, en el sentido de poder calcular los coeficientes de expansión térmica isobárica, de compresibilidad isobárica y de tensión isocórica, para $n$ moles de un gas ideal. No olvides tomar tu lápiz y cuaderno para realizar tus cálculos.
Se trata de un procedimiento basado en la derivada, para encontrar aproximaciones a las raíces de una función real de variable real que sea derivable.
Es muy útil en análisis numérico, sobre todo para aproximar raíces de polinomios en los cuales los métodos conocidos no funcionan (por ejemplo: $x^3+2x-5=0$, $x^5-x+1=0$) o para otro tipo de funciones, como por ejemplo: $2cos(x)-x^2$ o $x-cos(x)=0$.
Este método sirve inclusive para aproximar valores como por ejemplo: $\sqrt{3}, \sqrt[4]{3}, \sqrt[5]{247}, \pi$, encontrando de manera aproximada las raíces de las siguientes ecuaciones $x^2-3=0, x^4-3=0, x^5-247=0, cos(x)+1=0$, respectivamente.
No es un método infalible, pero más adelante explicaremos las condiciones para su eficiente funcionamiento.
Resolver algunos problemas sencillos de aproximación de raíces con el Método de Newton.
En economía, como en cualquiera otra disciplina, se suele describir la variación de una cantidad respecto a otra mediante:
$y-f(a)=f'(a)(x-a)$, es decir: $y=f'(a)x + (f(a)-af'(a))$
Sea $f:[a,b] \to \mathbb{R}$ una función derivable, de la cual sabemos que tiene una raíz en dicho intervalo y queremos encontrar una aproximación que nos satisfaga. ¿Qué hacemos? Veamos:
$y-f(x_0)=f'(x_0)(x-x_0)$ ... (1)
$0-f(x_0)=f'(x_0)(x_1-x_0)$ ... (2)
$x_{n+1} = x_n-\dfrac{f(x_n)}{f'(x_n)}$
Debe ser claro que si alguna de las condiciones en los pasos anteriores falla, entonces el Método de Newton no puede funcionar.
En los ejemplos se resuelven problemas sencillos de aproximaciones aplicando el Método de Newton.
Al ver estos ejemplos, podrás pensar que es más fácil tomar una calculadora o cualquier programa de computadora que haga los cálculos. En este caso, es importante pensar que las calculadoras realizan sus cálculos, con base en métodos como el de Newton.
En los ejercicios siguientes, se plantea la resolución de problemas de aproximación utilizando el Método de Newton. No olvides que debes tomar lápiz y papel para intentar resolverlos.
Se llama así a un problema que busca minimizar o maximizar el valor de una variable. Dicho en otras palabras, es un problema que trata de calcular el valor máximo o mínimo de una función, en nuestro caso, de una variable. Por ejemplo: minimizar el error en una medición, minimizar la cantidad de material para construir un contenedor, maximizar el volumen de un contenedor, minimizar el tiempo de espera o de recorrido, etc.
Los problemas que aquí trataremos tendrán la restricción que genera el hecho de que las funciones a optimizar, sólo dependerán de una variable. Sin embargo lo que importa entender es el método y las herramientas de matemáticas de máximos y mínimos a utilizar.
En la mayoría de los libros de Cálculo de una variable, podremos encontrar una variedad importante de estos problemas de optimización, en algunos de ellos, tipificados como problemas de máximos y mínimos.
Resolver algunos problemas sencillos de optimización.
En los problemas de optimización es muy importante recordar varios conceptos y resultados sobre la derivada:
Si $f'(a)=0$ y $f''(a) \gt 0$, entonces $f$ alcanza un mínimo local en $a$. Si $f'(a)=0$ y $f''(a) \lt 0$, entonces $f$ alcanza un máximo local en $a$.
En los ejemplos se resuelven problemas sencillos de Optimización.
En los ejercicios siguientes, se plantea un problema relacionado con la optimización de un área rectangular con perímetro constante. Recuerda que debes tomar lápiz y papel para intentar resolverlo.