Productos en hex (un ejemplo)
Anteriormente se te hicieron algunas preguntas sobre el número de unidades máximo que se pueden acarrear en el caso de la multiplicación. Aprovechemos esta página para tratar de obtener la respuesta. Y además veamos el ejemplo de la multiplicación en una base mayor a la decimal, como lo es la hexadecimal.
Sólo se presenta un ejemplo. No hay ejercicios. Sin embargo, trata de entender cómo funciona. Y presta atención a que, finalmente, lo más importante que debes saber es cómo contar (que lo aprendiste en la unidad sobre Cambio de base). Cómo resuelvas las operaciones puede depender de preferencias personales (por ejemplo, el usar una recta numérica, o usar los dedos, etc.). Pero lo más importante es saber contar.
Para este ejemplo, recuerda cómo haces las multiplicaciones de números decimales de forma manual. Por ejemplo, \(387\times12\). Recuerda que primero multiplicas \(387\) por el \(2\) del \(12\). Eso te da un primer sumando. Después multiplicas el \(387\) por el \(1\) del \(12\), con lo que obtienes el segundo sumando, que va recorrido un lugar a la izquierda respecto del primero. Al final, sumas los sumandos tomando en cuenta sus posiciones y con eso obtienes el resultado del producto.
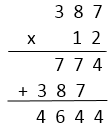
En el ejemplo a continuación se construirá el primer sumando. Una vez construido, se construirá el segundo sumando. La parte de la suma de estos sumandos (que da el resultado final del producto) ya no se aborda, debido a que eso ya lo sabes hacer de los interactivos pasados de la unidad.
En el siguiente interactivo podrás ver ejemplos del producto de dos números hexadecimales dados al azar. Revisa cada ejemplo hasta el final y al final podrás generar otro ejemplo. Se consideran números hexadecimales de sólo tres dígitos, debido a que, al ser un producto, el resultado involucra más dígitos.
En este interactivo pudiste ver que para el caso de la multiplicación ya no es una regla que siempre se acarrea una unidad. Ello es válido para la suma de dos números, pero para el caso de la multiplicación se pueden acarrear valores mayores a una unidad. Ello tiene una razón sencilla: cuando multiplicas un número lo estás sumando varias veces. Puedes tener, así pues, más de dos sumandos (si, por ejemplo, lo multiplicas por \(9\), tendrás nueve veces el valor sumado consigo mismo).
Este comportamiento es también válido para el caso binario. Trata de hacer tus propios ejemplos de productos de números binarios siguiendo lo que aprendiste para el caso hexadecimal, que es considerablemente más complicado que el binario.
Algo que conviene mencionar también es una forma de valerte de la notación decimal cuando calculas un producto en hexadecimal. En este interactivo se hizo todo con puntitos. No obstante, nota que se puede resumir, usando la notación decimal, con los siguientes pasos:
- El número de puntitos corresponde, en decimal, al producto de los valores puestos en decimal. Por ejemplo, \(A\times9\) corresponde a multiplicar \(10\times9=90\) en decimal.
- Una vez que tienes dicho número, buscas cuál es el residuo del número en base dieciséis. Ello se logra dividiendo el número entre \(16\) y viendo cuántos puntitos sobraron. En el ejemplo, tendrías que \(16\) cabe en \(90\) un total de cinco veces y sobran diez puntitos (en decimal). Estos deiz puntitos en hexadecimal corresponden a \(A\), por lo que el residuo sería \(A\), y es lo que va como resultado del dígito del producto.
- El dígito que acarreas a la siguiente columna es el número de veces enteras que cupo dieciséis en el producto que obtuviste. En este ejemplo, cupo completamente un total de cinco veces, por lo que acarreas \(5\) a la siguiente columna. Claro, puedes representar en el dígito el residuo, pero todo lo demás (el \(5\times16\) que falta debe ir como parte del acarreo de una columna de orden mayor.
- El proceso continúa de esta forma con una salvedad: el resultado del producto del nuevo dígito debe añadirse al valor acarreado del producto de los dígitos de la columna anterior. Esto es muy similar al caso de la suma.
Créditos
Escena original
| Diseño del contenido | Alejandro Radillo Díaz, LITE |
| Diseño funcional | Alejandro Radillo Díaz, LITE |
| Programación | Alejandro Radillo Díaz, LITE |
| Asesoría de programación | Oscar Escamilla González, LITE |
| Diseño gráfico | Francisco Varela Fuentes |
| Coordinación | Leticia Montserrat Vargas Rocha, LITE |
Los contenidos de esta unidad didáctica interactiva están bajo una licencia Creative Commons Reconocimiento-NoComercial-CompartirIgual.
La unidad didáctica fue creada con Arquímedes, una herramienta de código abierto.
La unidad didáctica contiene escenas elaboradas con Descartes, una herramienta de código abierto.
LITE - UnADM 2014


