Relaciones
Ejemplos de relaciones
Si consideramos un conjunto de tareas que deben ser realizadas para llevar a cabo un proyecto, nos podemos preguntar si, dadas dos tareas \(S\) y \(T\), una debe llevarse a cabo antes de empezar con la otra. También podemos preguntar cómo asignarle personas de un equipo a las tareas. La afirmación "\(S\) debe realizarse antes de tarea \(T\)" puede ser cierta o falsa, así como la afirmación "persona \(P\) está asignada a realizar la tarea \(T\)".
Como se mencionó en la escena de Motivación, el concepto de relación es ubicuo en todos los aspectos del mundo. El lenguaje de relaciones nos permite no solo estudiar situaciones como la del ejemplo anterior, sino cualquier situación donde existe alguna o múltiples relaciones entre los elementos de varios conjuntos. Vamos a ilustrarlo viendo con cierto detalle el ejemplo considerado.
Supongamos que un proyecto consiste de 5 tareas \(T_i\) (\(i=1,…,5\)), y cuatro personas \(P_j\) (\(j=1,…,4\)), que deben ser asignadas a varias tareas para llevar a cabo el proyecto. Supongamos que las tareas están representadas por segmentos cuya longitud representa el número de unidades de tiempo para completar las tareas. Además, los segmentos se dibujan con relación a una línea de tiempo, como lo ilustra el diagrama. Junto a cada segmento aparece el nombre de la tarea y la persona o personas asignadas a ella.
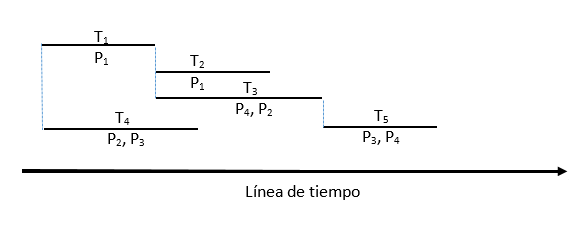
Usando el diagrama podemos ver las asignaciones de las diversas tareas, por ejemplo, la tarea \(T_1\) está asignada a la persona \(P_1\) y la tarea \(T_5\) está asignada a las personas \(P_3\) y \(P_4\). También podemos decir que la persona \(P_1\) tiene asignadas las tareas \(T_1\) y \(T_2\) y que la persona \(P_3\) tiene asignadas las tareas \(T_4\) y \(T_5\).
Podemos describir estas relaciones por medio parejas como esta: \((Tarea, Persona)\), o con parejas como esta: \((Persona, Tarea)\). Consideremos los conjuntos \(T = \lbrace T_1, T_2, T_3, T_4, T_5\rbrace\) y \(P = \lbrace P_1, P_2, P_3, P_4\rbrace\) respectivamante. Los conjuntos que resultan de todas las asociaciones \((Tarea,Persona)\) o \((Persona, Tarea) \) definidas por el diagrama son:
\(R = \lbrace (T_1, P_1), (T_2, P_1), (T_3, P_2), (T_3, P_4), (T_4, P_2), (T_4, P_3), (T_5, P_3), (T_5, P_4)\rbrace\)
\(S = \lbrace(P_1, T_1), (P_1, T_2), (P_2, T_3), (P_2, T_4), (P_3, T_4), (P_3, T_5), (P_4, T_3), (P_4, T_5)\rbrace\)
Podemos también inferir del diagrama algunas de las relaciones de precedencia, por ejemplo, las tareas \(T_2\) y \(T_3\) deben ocurrir después de la tarea \(T_1\) y \(T_5\) debe ocurrir después de la tarea \(T_3\), pero \(T_1\) y \(T_4\) son independientes y pueden ocurrir simultáneamente. Sin embargo, no podemos decir si la tarea \(T_2\) debe ocurrir antes de la tarea \(T_5\). La relación de precedencia se puede representar completamente con el siguiente diagrama:
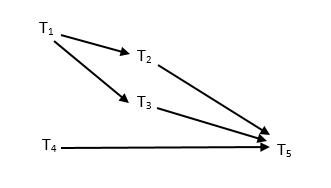
De este diagrama podemos construir el siguiente conjunto de relación de precedencia de tareas:
\(U = \lbrace(T_1, T_2), (T_1, T_3), (T_1, T_5), (T_2, T_5), (T_3, T_5), (T_4, T_5) \rbrace\)
La relación de precedencia \((T_1, T_5)\) está implicada implícitamente porque si \(T_5\) no puede ocurrir antes de \(T_2\) o de \(T_3\), y \(T_2\) o \(T_3\) no pueden ocurrir antes de \(T_1\), entonces
\(T_5\) no puede ocurrir antes de \(T_1\).
Como se puede observar, \(R\) es un subconjunto del producto cartesiano
\(T \times P\), \(S\) es un subconjunto del producto
cartesiano \(P \times T\) y \(U\) es un subconjunto de \(T \times
T\).
También se puede
observar que \(S\) puede obtenerse directamente de \(R\)
simplemente cambiando el orden de los elementos de cada par ordenado en \(R\). En este caso decimos que \(S\) es la relación inversa
de \(R\) y escribimos \(S = R^{-1}.\)
Definición y algunas propiedades de relación
Este ejemplo nos permite visualizar la definición de relación entre los elementos de dos conjuntos dados, digamos \(A\) y \(B\). Una relación \(R\) es simplemente un subconjunto del producto cartesiano \(A \times B\). Es posible que los dos conjuntos coincidan, como en el caso del conjunto \(U\) del ejemplo anterior, sin embargo los conjuntos \(A\) y \(B\) son dos conjuntos arbitrarios.
En
el caso de que los conjuntos \(A\) y \(B\) coincidan, podemos
definir ciertas propiedades de las relaciones en el conjunto
\(A\). Para
ilustrarlo, consideremos el conjunto de todas las líneas del
plano. Una relación
básica entre ellas resulta de los axiomas de la geometría
euclidiana:
la relación de paralelismo entre líneas. Decimos que dos líneas \(L_1\) y \(L_2\) son paralelas si
su intersección, como subconjuntos del plano, es vacía o si las
líneas coinciden en todos sus puntos.
Si
\(\Lambda\) denota al conjunto de todas las líneas del
plano, podemos definir la relación de paralelismo como el
subconjunto de \(\Lambda \times \Lambda\) que consiste de todas las parejas \((L_1,L_2)\)
tales que \(L_1\) y \(l_2\) son paralelas.
Para simplificar la notación escribimos \(L_1 \parallel
L_2\) para decir que las líneas son paralelas.
Por
definición de paralelismo, claramente tenemos que
1. \(L_1 \parallel L_1\)
2. Si \(L_1 \parallel L_2\), entonces \(L_2 \parallel L_1\)
3. Si \(L_1 \parallel L_2\) y \(L_2 \parallel L_3\) entonces \(L_1 \parallel L_3\)
A
la propiedad 1 se le llama reflexividad, a la 2
se le llama
simetría y a la 3 se le llama transitividad.
En general, una relación arbitraria en \(A\), i.e. la relación es un subconjunto de \(A \times A\), no tiene ninguna de estas propiedades. Vamos a decir que la relación es reflexiva, simétrica o transitiva si la relación tiene la propiedad 1, 2 o 3 respectivamente. Cuando una relación tiene estas 3 propiedades, decimos que tenemos una relación de equivalencia.
Una
relación
muy simple pero importante es la relación
de identidad \( \Delta_A\) que consiste de la diagonal de
\(A \times
A\), es decir todas las parejas \( (a, a)\), con \(a\) un elemento de
\(A\).
Composición
de relaciones
Una operación importante entre relaciones es la composición. Consideremos una relación \(R\) tal que \(R \subseteq A \times B\) y una relación \(S\) tal que \(S \subseteq B \times C\). Podemos formar una nueva relación, denotada por \(S \circ R\), subconjunto de \(A \times C\) de la siguiente manera: Los elementos de \(S \circ R\) son todas las parejas \((a, c)\) para las cuales existe un elemento \(b\) en \(B\) tal que \((a, b)\) está en \(R\) y \((b, c)\) está en \(S\). A la relación \(S \circ R\) es la composición de \(R\) y \(S\).
Es
fácil de ver que si componemos \( \Delta_A\) con
\(R\), obtenemos que \(R \circ \Delta_A = R\) y
\( \Delta_A \circ Q = Q\), donde \(Q\) es una relación en \(B
\times A\). Tampoco
es difícil verificar que la composición es asociativa,
es decir que si \(T\) es una relación contenida en \(C \times D\), entonces \((T
\circ S) \circ R = T \circ (S \circ R)\). Podemos expresar las
propiedades de reflexividad, simetría y transitividad en términos de la composición como sigue:
- Una relación \(R\) en \(A \times A\) es reflexiva, si y solo si \(\Delta_A \subseteq R\)
- Una relación \(R\) en \(A \times A\) es simétrica, si y solo si \(R^{-1} = R\)
- Una relación \(R\) en \(A \times A\) es transitiva, si y solo si \(R \circ R \subseteq R\)
Créditos
Escena original
| Diseño del contenido | Julio Arnoldo Prado Saavedra Víctor Manuel Amezcua Y Raz |
| Diseño funcional | Julio Arnoldo Prado Saavedra Víctor Manuel Amezcua Y Raz |
| Programación | Julio Arnoldo Prado Saavedra |
| Asesoría de programación | Víctor Manuel Amezcua Y Raz |
| Diseño gráfico | Ricardo López Gómez |
| Coordinación | Leticia Montserrat Vargas Rocha |
Adaptación
| Diseño funcional | Julio Arnoldo Prado Saavedra Oscar Escamilla González |
| Programación | Julio Arnoldo Prado Saavedra |
| Asesoría de programación | Oscar Escamilla González Leticia Montserrat Vargas Rocha |
| Diseño gráfico | Francisco Varela Fuentes |
| Coordinación | Leticia Montserrat Vargas Rocha |
Los contenidos de esta unidad didáctica interactiva están bajo una licencia Creative Commons Reconocimiento-NoComercial-CompartirIgual.
La unidad didáctica fue creada con Arquímedes, una herramienta de código abierto.
La unidad didáctica contiene escenas elaboradas con Descartes, una herramienta de código abierto.
LITE - UnADM 2014